- 1Department of Neurorehabilitation, Scientific Institute of Pavia via Boezio, IRCCS, ‘Salvatore Maugeri’ Foundation, Pavia, Italy
- 2Department of Informatics, Bioengineering, Robotics, System Engineering (DIBRIS), University of Genova, Genova, Italy
Antidromic action potentials following distal stimulation of motor axons occasionally fail to invade the soma of alpha motoneurons in spinal cord, due to their passing through regions of high non-uniformity. Morphologically detailed conductance-based models of cat spinal alpha motoneurons have been developed, with the aim to reproduce and clarify some aspects of the electrophysiological behavior of the antidromic axon-somatic spike propagation. Fourteen 3D morphologically detailed somata and dendrites of cat spinal alpha motoneurons have been imported from an open-access web-based database of neuronal morphologies, NeuroMorpho.org, and instantiated in neurocomputational models. An axon hillock, an axonal initial segment and a myelinated axon are added to each model. By sweeping the diameter of the axonal initial segment (AIS) and the axon hillock, as well as the maximal conductances of sodium channels at the AIS and at the soma, the developed models are able to show the relationships between different geometric and electrophysiological configurations and the voltage attenuation of the antidromically traveling wave. In particular, a greater than usually admitted sodium conductance at AIS is necessary and sufficient to overcome the dramatic voltage attenuation occurring during antidromic spike propagation both at the myelinated axon-AIS and at the AIS-soma transitions.
Introduction
Since the early Fifties of the last century, microelectrode intracellular recordings from spinal motoneurons allowed the detailed analysis of the electrophysiological events generated at the soma by an antidromic spike evoked at the distal part of a motor fiber (Brock et al., 1953; Eccles, 1955). This technique, compared to the extracellular recordings which usually collected potentials from a population of neurons, provides much of the most direct information on antidromic invasion of single motoneurons. Thus, it was possible to study the central effect of stimuli applied to motor nerves and antidromically conducted to the soma of spinal alpha motoneurons.
It was evident that, due to the geometric inhomogeneity of the cable conductor which reduces the safety factor of the conduction along the nerve fiber, the antidromic traveling wave was not always able to invade the soma (Eccles, 1955; Goldstein and Rall, 1974; Joyner et al., 1980; Moore et al., 1983).
Classically, three transition regions have been hypothesized to dampen the antidromic spike conduction: (i) the myelinated axon to the unmyelinated axon initial segment (AIS), (ii) the AIS to the soma, and (iii) the profusely branching dendritic tree (Eccles, 1955). In particular, at the AIS to soma transition, a junctional delay or a block of the conduction may happen, due to the increased capacitive load carried by the somato-dendritic region downstream of the antidromically traveling wave (Joyner et al., 1980; Moore et al., 1983). The magnitude of the delay at the AIS to soma transition, or the presence of a complete block at this point depends on morphologic and electrophysiological (mainly the Na+ conductance) properties at the transition region (Goldstein and Rall, 1974).
Nowadays, the occurrence of soma invasion has been used in reduced computational models of spinal motoneurons with the aim to indirectly set the values of Na+ channel densities onto somatic and AIS membranes (Powers et al., 2012), with the implicit assumption that the somatic invasion always follows an antidromic spike propagation.
In a previous study (Balbi et al., 2014), we developed a reduced model of spinal alpha-motoneuron to investigate the reciprocal interplay between AIS and soma during the antidromic conduction of a spike, and to explore the associated phenomenon of the recurrent discharge.
In the present study, detailed models of spinal motoneurons have been developed and described, taking advantage of both the web-based database NeuroMorpho of somato-dendritic morphologically detailed reconstructions (Ascoli et al., 2007) and a previous model of mammalian nerve fiber (McIntyre et al., 2002). We aimed at exploring the axon-somatic back-propagation in detailed models of spinal motoneurons, with different morphologies of the somato-dendritic part.
In particular, by using detailed models, we derive more plausible and realistic conductances values of the ionic channels responsible of antidromic propagation from axonal to somatic regions.
Finally, the present study also provides a novel yet tentative modeling investigation of the spike propagation at the myelinated-unmyelinated region of the AIS.
Materials and Methods
The proposed models were developed and run in the NEURON v7.3 simulation environment (Carnevale and Hines, 2006). Full details and the source code will be provided as a ModelDB entry (https://senselab.med.yale.edu/ModelDB; accession number: to be defined).
Geometric Properties of the Models
The morphologically detailed models are made up of three parts: (a) the soma and a highly detailed three-dimensional dendritic tree, (b) a frustum-shaped axon hillock with the proximal enlarged end attached to the soma, and the opposite end attached to the unmyelinated axonal initial segment (AIS), (c) a myelinated axon (23 mm long) attached to the distal end of the AIS.
Soma and dendrites
In the simulations, we used reconstructed 3D morphologies of dendritic tree and soma from 14 cat spinal motoneurons (Figure 1), available from the NeuroMorpho database (Ascoli et al., 2007).
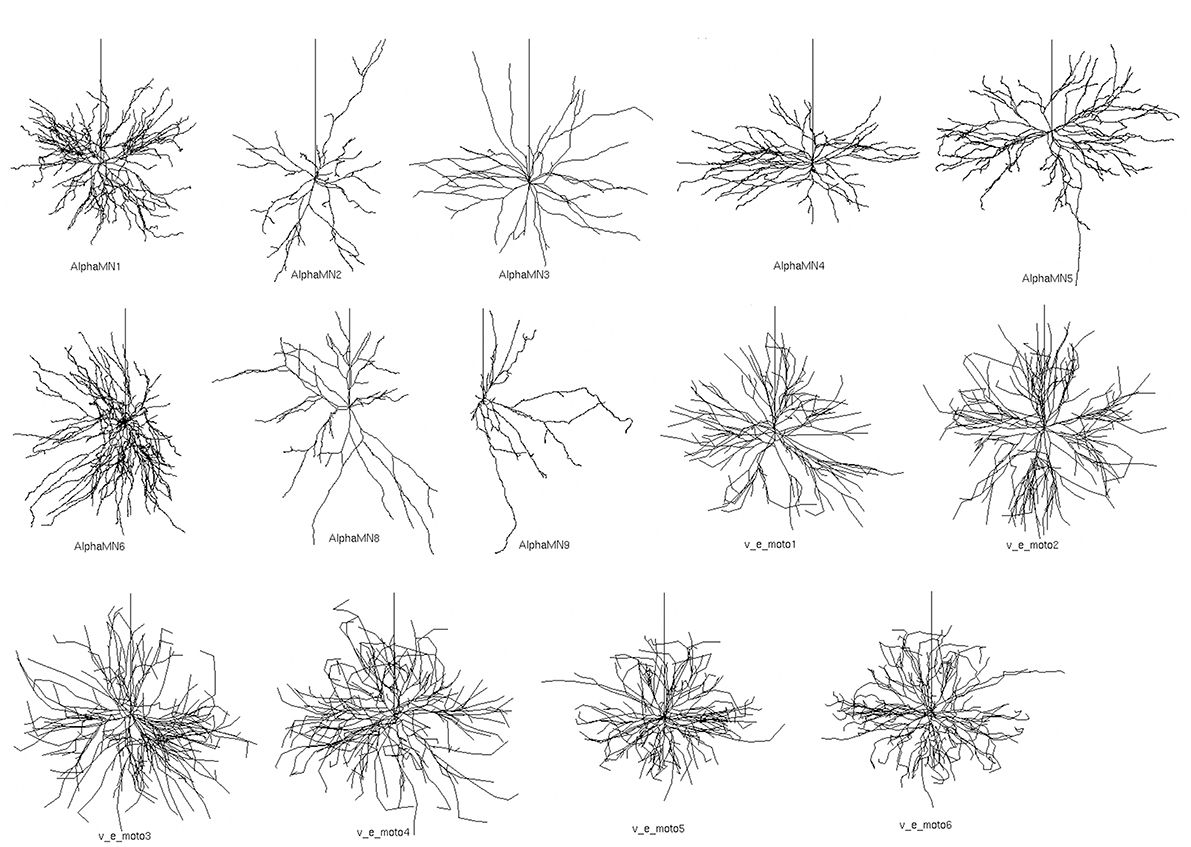
Figure 1. Fourteen detailed 3D somato-dendritic morphologies of cat spinal alpha-motoneuron imported from NeuroMorpho.org (Ascoli et al., 2007). The vertical upward neurite in each neuron represents the proximal part of the axon and was added after importing the somato-dendrite morphologies.
The morphologies belong to distinct sets of data from two different works (Cullheim et al., 1987; Alvarez et al., 1998), and morphometric details are provided in Table 1. All 3D morphologies derive from alpha motoneurons of the cat lumbar spinal cord. In NeuroMorpho database reconstruction, the original spherical somata are converted in two cylindrical compartments with identical diameters and lengths; the length of each compartment is half the diameter.
On the other way round, the dendritic tree is converted in multiple compartments, adopting the convention that a compartment is made by a neurite without ramifications, i.e., the compartment ends when it divides in branches or when it is a terminal ramification. This implies that a single compartment usually has different diameters along its course and that it can run considerably far from its beginning.
Since a poor spatial discretization could lower the performance of the models, we increased the number of dendritic compartments of the reconstructed dendritic tree after importing them in NEURON. In particular, we split in multiple compartments every branch longer than 20 μm, obtaining a nearly 15-fold increase of the average number of dendritic compartments, as displayed in the third and fourth columns of Table 1. The number of compartments in which a section should be divided (spatial discretization) to preserve consistent computational results usually relies on the value of the DC length constant (λDC) of an infinite cylinder with identical anatomical and biophysical properties. A more thorough approach, considering the transient characteristics of the neural signals, takes into account the AC length constant λf computed at a frequency f that is high enough for transmembrane current to be primarily capacitative, yet still in the range of frequencies relevant to neural function (Carnevale and Hines, 2006). By using the NEURON built-in function d_lambda, we checked that the final spatial grid of the dendritic tree was consistent with the AC length constant rule.
AIS and axon hillock
As the reconstructed 3D morphologies are limited to the somato-dendritic part of the spinal motoneurons, we modeled the efferent pathway (i.e., the axon hillock, the AIS and the myelinated axon) based on average measures of cat spinal motoneurons (Conradi, 1969; Burke et al., 1977; Cullheim and Kellerth, 1978; Ulfhake and Kellerth, 1982, 1984; Cullheim et al., 1987). As a result, the cylindrical AIS was divided in 9 compartments, 3 μm wide and 50 μm long. The frustum-shaped axon hillock, formed by 7 compartments, has been modeled 25 μm long and connects the soma with the AIS; its diameter ranges from a value similar to the AIS at one end, to a value similar to the soma at the opposite side, so that a linear transition occurs between the soma and AIS diameters along the axon hillock.
Myelinated axon
The myelinated part of the axon has been modeled according to the study of McIntyre et al. (2002), who developed a geometrically and electrically accurate model of mammalian motor nerve fiber. In particular, adopting a double cable structure with a finite impedance myelin sheath, the model details the node of Ranvier, the adjacent paranodal myelin attachment segment, the juxtaparanodal segment and the internodal segment. The geometric details are summarized in Table 2.
Biophysical Properties
Passive and active properties of the model, derived from previous in silico (McIntyre and Grill, 2002; McIntyre et al., 2002; Powers et al., 2012) and in vivo (Araki and Terzuolo, 1962; Kernell, 1966; Barrett and Crill, 1974, 1980; Barrett et al., 1980; Zengel et al., 1985; Morales et al., 1987; Fleshman et al., 1988; Clements and Redman, 1989; Yamuy et al., 1992; Liu et al., 1995) studies are provided in Tables 3, 4; the rate functions of the ionic channels, according to the Hodgkin-Huxley formalism (Hodgkin and Huxley, 1952), are described in Supplemental Material.
Passive properties
All the neuronal segments have been modeled with axial and external resistivity set at 70 Ω · cm. Specific capacitance has been set at 1 μF/cm2 (Barrett and Crill, 1974; Gentet et al., 2000), except in myelin, where a value of 0.1 μF/cm2 has been adopted, and in nodal and internodal axonal membrane, where it has been set at 2 μF/cm2 (McIntyre et al., 2002).
The Na+ equilibrium potential has been set to +50 mV, the K+ to −77 mV, while the Ca2+ equilibrium potential dynamically changed depending on the variations of internal and external ion concentrations. The Ca2+ dynamics were represented by a simple, first-order process representing influx through Ca2+ channels and decay with a single time constant (see Supplemental Material for details).
Active properties
Soma and proximal dendrites. We considered proximal dendrites those parts of the primary dendrites extending from the soma along a distance equal to the 10% of the average dendritic length for each neuron model. The soma and the proximal dendrites include conductances representing non-linear fast Na+, persistent Na+, delayed rectifier K+, hyperpolarization-activated mixed cation, high-threshold Ca2+, and Ca2+-activated K+ channels as well as a linear leakage conductance (Table 3). The somatic Ca2+-activated K+ channel is responsible for the after-hyperpolarization (AHP). Along the proximal dendrites, each conductance linearly decreases to the respective value set in the distal part of the dendritic tree, except for the hyperpolarization-activated conductance, which has the same value in soma and dendrites.
As regard as the sodium currents, we decided to adopt separate models for the transient and the persistent component of the Na+ channels. In real neurons the persistent sodium current is not provided by a separate channel, but it is a feature of the Nav1.6 channel electrophysiological behavior. However, accurate representation of both of these components requires a multi-state kinetics model (Kuo and Bean, 1994). In addition, a series of unknowns undermine the possibility to exactly reproduce the electrophysiological features of cat motoneuron sodium channels: (a) detailed voltage clamp studies of isolated Nav1.6 (and Nav1.2) channels heterologously expressed in (preferibly mammalian) cell systems exist for mouse or human sodium channels (which are in turn different), not for cats (Catterall et al., 2014); (b) it is neither exactly known the compartmental distribution in cat motoneurons of the different isoforms of sodium channels; (c) nor their fractional contribution to the global sodium currents is known. Given these limitations, we chose to implement in our models a previously described model of sodium channel (Powers et al., 2012), which proved useful to reproduce many of the experimental electrophysiological behavior of cat motoneurons.
However, due to the poor alignment of the fast and persistent sodium current as originally set, we modified the hemi-activation voltage of the gating variables of the two current in order to obtain a more plausible electrophysiological behavior of the current-voltage relationships. In particular, we shifted the hemi-activation voltage of the gating variables for the persistent current toward more depolarized values (+15 mV) and that for the fast current toward more hyperpolarized values (−5 mV) (see Supplemental Material).
Moreover, we set the persistent sodium conductance at a value able to produce a proportion of persistent current of about 20% compared to the peak of the transient one (Burbidge et al., 2002).
Medium and distal dendrites. The distal parts of the dendritic tree have been modeled with the lowest densities of the same conductances present at the soma, according to previous in silico studies (Powers et al., 2012). Moreover, in the dendritic branches far from the soma between 30 and 60% of the average dendritic length, a low-threshold Ca2+ conductance has been set to take into account the dendritic persistent inward current. Ca2+-activated K+ channels have also been uniformly distributed along these same regions of the dendrites.
Axon hillock and AIS. The axon hillock and the AIS include conductances modeling non-linear fast Na+, persistent Na+, and delayed rectifier K+ channel as well as a linear leakage conductance (Table 3). At the axon hillock, by varying the respective densities, the active channels of soma progressively replace those of the initial segment section, so that a gradual transition between active conductances has been set.
Myelinated axon. The nodes of Ranvier bring the parallel combination of non-linear fast Na+, persistent Na+, and slow K+ conductances, a linear leakage conductance, and the membrane capacitance (Table 4).
The paranodal and internodal compartments consisted of two layers, each including a linear conductance in parallel with the membrane capacitance, representing the myelin sheath and underlying axolemma.
Simulation Protocol
Due to the presence of active yet small conductances of the ionic channels at the depolarization starting value (−70 mV), few milliseconds were necessary to settle down a stable equilibrium potential, which slightly varied through the different sections. Thus, each simulation starts from a previously saved steady-state (300 ms without perturbations).
An integration time-step of 0.025 ms was adopted for all the simulations.
Results
Basal Electrophysiological Behavior of the Models
The electrophysiological features of the simulated models are summarized in Table 5. The rheobase (minimal intensity of an infinitely long stimulus able to evoke a spike) was evaluated with a stimulus duration up to 1 s. Figure 2A shows four examples of stimulus intensity-duration curve relative to four alpha motoneuron models of different size.
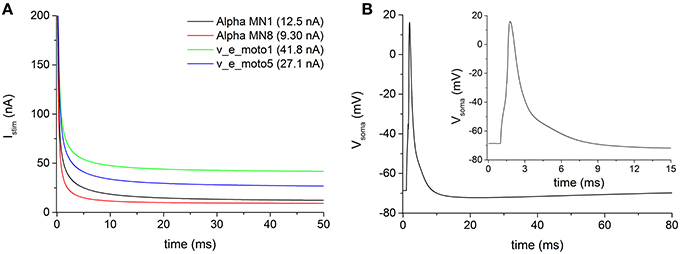
Figure 2. (A) Examples of stimulus intensity-duration curve, for measuring the rheobase, in four representative motoneurons of the pool. (B) Action potentials following a brief (0.5 ms) somatic depolarizing current recorded from soma of the motoneuron v_e_moto5. The inset shows the first 15 ms of the induced action potential.
The modeled motoneurons predominantly belong to cells of big dimension (considering an average soma diameter of about 50 μm in alpha motoneurons). The increased motoneuronal size, especially in motoneurons from the second pool (i.e., v_e_moto1 to v_e_moto6, Table 1), results in relatively low values of input impedance (ZIN) and high values of rheobase (Figure 2A, green and blue traces).
The duration of the stimulus adopted to evoke an action potential at the soma was set to 0.5 ms. Figure 2B shows an example of somatic spike relative to the motoneuron v_e_moto5, elicited by a stimulus at the soma. It can be noticed the entire after-hyperpolarization that lasts about 80 ms.
Voltage Attenuation from First Node to AIS
We examined the antidromic propagation of the action potential from the myelinated axon through the AIS to the soma, following a distal stimulation of the axon. The distal node[15], located 17.25 mm far from the soma, was stimulated by means of a virtual electric pulse with a duration of 0.1 ms and an intensity of 5 nA. Given the extensive voltage attenuation that the antidromic traveling wave encounters along the axon-somatic junction, no antidromic spike is able to invade the soma in all neuron models bringing the basal biophysical and geometric parameters (Figure 3A). Figure 3A also shows a significant spike attenuation (mainly sustained by the dramatic geometric inhomogeneity of the axon-somatic junction), which already appears at the first node of Ranvier (green trace of Figure 3A), as well as the regularly conducted spike at the node[10] (blue trace of Figure 3A).
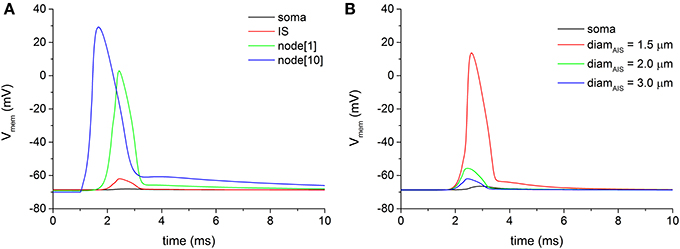
Figure 3. (A) Voltage attenuation encountered by the antidromically traveling wave at the transition regions between the first node of Ranvier (node[1], green trace) and the soma (black trace). Distal electric stimulation was applied at node[15]. (B) By decreasing the diameter of the axonal initial segment (IS), the voltage attenuation at the IS progressively lessens until the threshold for an action potential can be reached (red line).
To overcome the wide voltage attenuation between the myelinated axon and the AIS, the geometric parameters of the AIS were swept. As Figure 3B shows, a reduction of the AIS diameter was able to decrease the attenuation at the point when the threshold for a spike is reached at the AIS. The reduced diameter, indeed, decreased the voltage attenuation for depolarization's approaching the AIS from the myelinated axon, due to a sealed end effect.
However, even with a fully delivered action potential at AIS, the voltage at the soma still remains well below the threshold (Figure 3B, black line), and, in each neuron model of the pool, no somatic antidromic propagation is possible. Therefore, it appears evident that two different sites of voltage attenuation are serially involved in preventing the antidromic somatic spike invasion: from myelinated axon to AIS and from AIS to soma.
Voltage Attenuation from AIS to Soma
As we arbitrarily chose the geometric AIS parameters, we have been able to sweep them in a realistic range to search for possible values which allow the spike antidromic propagation from myelinated axon to AIS. Regarding the voltage attenuation from AIS to soma, given the constraint of the imported and fixed morphological values of soma and dendrites, we needed a different way to facilitate the antidromic somatic spike invasion. Then, we increased the density of the somatic inactivating fast Na+ channels, because they are directly responsible for the spike initiation. However, even with extremely large increments of channels density at soma with respect to the initial conductance value, no soma invasion occurred (Figure 4A, red and blue solid lines). Values of Na+ channel density at soma higher than 10 S/cm2 induced a spontaneous and sustained depolarization of the motoneurons, not consistent with the experimental data.
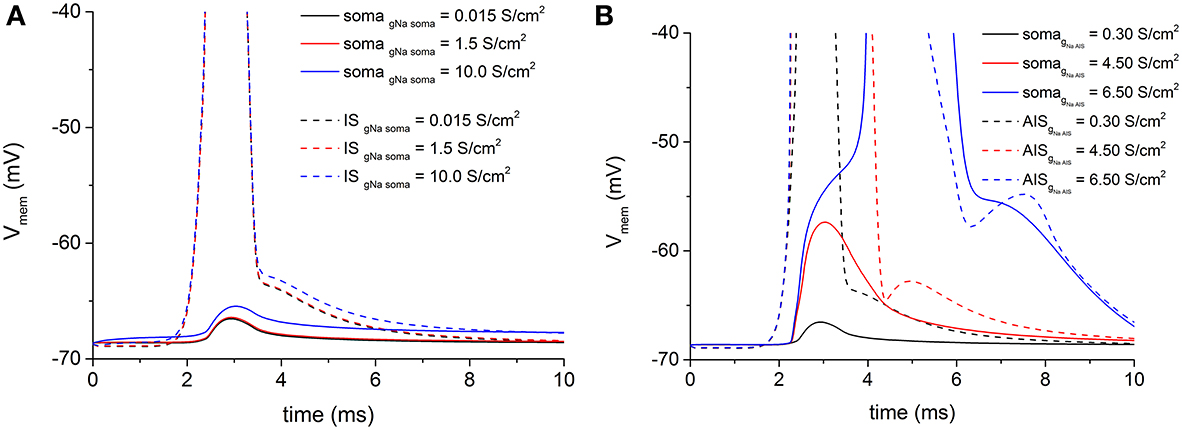
Figure 4. (A) Persistent voltage attenuation at soma (solid lines) blocks antidromic somatic spike propagation, notwithstanding increasing values of somatic fast Na+ conductance. As in Figure 3, an antidromic spike at IS (dashed lines) regularly develops for all Na+ conductance values. Basal Na+ maximal conductance at soma = 0.015 S/cm2. (B) The increase of fast Na+ channels conductance at the IS (dashed lines) is able to overcome the AIS-to-soma voltage attenuation and permits the antidromic spike propagation to the soma (solid lines). Basal Na+ maximal conductance at IS = 0.3 S/cm2.
On the contrary, when the density of the same channels at the AIS was increased to overcome the capacitive load of the soma and dendrites, it was sufficient to reach about 20-fold increments of the basal density to obtain a somatic spike (Figure 4B blue solid line).
Therefore, our simulations showed that changes in geometric and biophysical parameters of the AIS were necessary and sufficient to overcome the antidromic propagation failure both at the myelinated-unmyelinated axon and at AIS-soma transitions.
Table 6 shows a set of minimal values for AIS diameter and Na+ conductance in each neuron model able to permit the antidromic soma spike propagation.
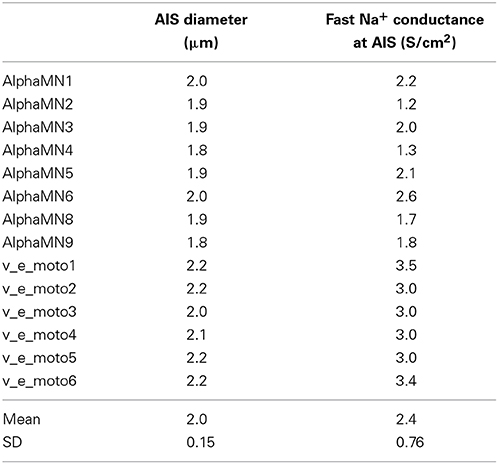
Table 6. Values of AIS parameters able to make the soma invasion of antidromic action potential possible.
Voltage Attenuations and the Electrotonic Distance
The myelinated axon-to-AIS and the AIS-to-soma voltage attenuations are principally sustained by the dramatically increased capacitive load downstream the antidromically traveling wave.
Based on the passive electrical properties of an ideal conductor, along infinite cables of uniform geometry the stationary voltage attenuation follows the well-known exponential cable equation:
with λ, the length constant, depending on the diameter of the cable conductor:
where Rm is the resistance across a unit area of passive membrane, Ri the volume resistivity of the intracellular medium, and d the diameter of the cable.
However, due to the wide difference between real neurites and an ideal cable conductor, and to the changing Rm in different regions of the neurons, according to previous studies on the measure of the electrotonic space (Carnevale et al., 1995) in real neurons, it can be useful to consider the electrotonic distance (X = x/λ) between two points in terms of voltage attenuation:
By adopting the previous definition of electrotonic distance and by using the NEURON's tool for the study of electrotonus (Carnevale et al., 1995), it has been convenient to compute the different length constants in both the directions (ortho- and antidromic) of impulse propagation (Table 7).
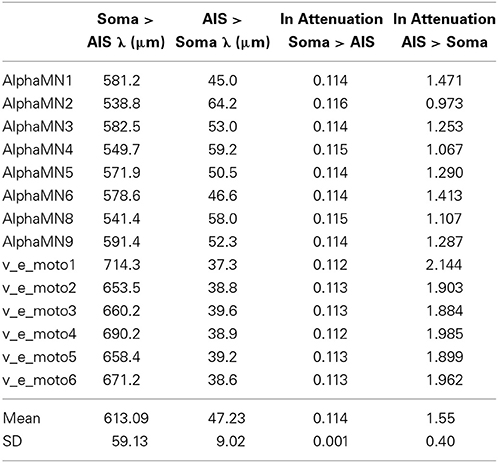
Table 7. Spatial constants and electrotonic distances in every neuron model, between AIS and soma and in both directions of impulse propagation.
Table 7 shows how much the length constants between two points with high geometric non-uniformity do change depending on the direction of current flow, a longer length constant implying a more favorable progression of the spike.
As already described (Goldstein and Rall, 1974; Joyner et al., 1980; López-Aguado et al., 2002), indeed, at the site of an abrupt increase of diameter, significant changes happen both in voltage and ionic and axial currents. When the antidromic wave approaches the non-uniform region of the axon-soma junction, it must charge a larger capacity through a reduced axial resistance. As the action potential comes closer to the abrupt increase in diameter, its ability to provide the depolarizing current begins to be strained by the heavier load, resulting in a slower rise of the action potential and an attenuated amplitude. Even little changes of action potential amplitude cause an abnormally elevated sodium influx, because the driving force (V − ENa) remains large, which in turn can provide additional charge for depolarizing the adjacent region of increased diameter. However, as the axial current progressively increases, even the extra charge from the elevated inward sodium flux can become insufficient to depolarize the soma or the AIS membrane to threshold level.
Discussion
In this study, we modeled the antidromic propagation of the action potential along a single motor fiber from the myelinated axon through the unmyelinated AIS to the soma of a spinal alpha motoneuron. To this purpose, we used a pool of morphologically detailed models of alpha motoneuron, exploiting the open-access web-based database of three-dimensional somato-dendritic reconstructions (www.neuromorpho.org) (Ascoli et al., 2007).
In addition, we adopted a highly detailed model of myelinated axon (McIntyre et al., 2002), which provided a realistic saltatory conduction in the myelinated part of the model. By using initial Na+ conductances similar to those adopted in previous in silico studies (Dodge and Cooley, 1973; Traub, 1977; Fleshman et al., 1988; Booth et al., 1997; Safronov et al., 2000; McIntyre et al., 2002; ElBasiouny et al., 2005; Shapiro and Lee, 2007; Cisi and Kohn, 2008; Powers et al., 2012) (Table 8), we unexpectedly found that in all neuron models no antidromic spike propagation occurred neither at the soma nor at the AIS.
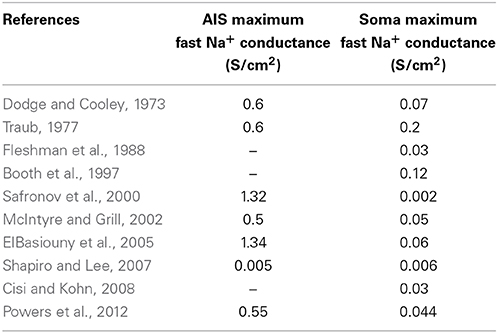
Table 8. Values of maximum conductance of fast inactivating Na+ channels in AIS and soma of previously developed models of alpha motoneurons in vertebrates.
Does the Somatic Invasion of An Antidromic Traveling Wave Always Occur in Real Neurons?
In real intracellular recordings, a failure of the antidromic somatic invasion represents an exception, and is often the result of experimental artifacts, like an induced somatic hyperpolarization or a repetitive antidromic stimulation (Eccles, 1955). In these cases, a subthreshold depolarization at soma is usually recorded and called NM (i.e., non-medullated) spike, according to the assumption that it is related to an action potential at the AIS. The antidromic spike propagation, in other words, reaches the AIS but fails to depolarize to the threshold the soma.
Too Big Cells for Somatic Invasion to Happen?
It can be hypothesized that spontaneous not induced blockages of antidromic spike mainly happen in motoneurons of larger size, due to the greater capacitive load provided by their soma and dendrites. Thus, the prevalence of large motoneurons in our pool of neuron models could bias our results toward a failure of the somatic invasion. As established in previous studies (Zengel et al., 1985), the relatively high values of rheobase of our pool, as well as the low ones of the input impedance, are in agreement with this dimensional bias. However, the failure of propagation was also detected in neuron models of the pool of smaller size. In addition, in every neuron model in basal configurations we were barely able to see even a slight depolarization at the soma following the antidromic spike propagation, which is in contrast with a main role of the excessively high neurons size in explaining our results.
How Many Sites of Dramatic Voltage Attenuation?
Our models provide for the first time a neurocomputational validation of a classical hypothesis carried out by the early electrophysiological studies, i.e., the probable failure of the antidromic propagation at the transition zone between the myelinated axon and the AIS (Eccles, 1955), in addition to the one occurring at the junction between AIS and soma. A substantial voltage attenuation, indeed, can be observed at these sites, mainly as a result of their marked geometric inhomogeneity.
Biophysical Significance of the Study
Our study clearly shows that, when dealing with detailed morphological reconstructions of motoneurons, a much higher density of Na+ channels at the AIS has to be hypothesized to make the antidromic soma invasion to happen. Given that a precise and direct measure of Na+ channels density at the AIS of spinal motoneurons is still lacking, our hypothesis represents a neurocomputational prediction, which can be confirmed or contradicted by future experimental data.
Our findings show that the Na+ channels density at AIS should be set much higher than at the soma (Table 6). These data are in agreement with those of a previous study (Kole et al., 2008), which explored the densities of the Na+ channels at AIS and at the somato-dendritic compartment in cortical layer 5 pyramidal neurons by means of whole-cell patch clamping recordings, immunocytochemical imaging and neurocomputational models. That study found a value for Na+ channels density at AIS ~50 times higher than at the soma.
The AIS
The AIS is a highly organized cellular domain specialized to function as the site of spike initiation in neurons (Clark et al., 2009). Its geometric and biophysical properties greatly influence the spiking features of the neurons. In addition, the segregation of ionic channels and their isoforms in different AIS subregions may explain a key role of the AIS in regulating the neuronal spike timing and frequency (Clark et al., 2009). In particular, a differential clustering of Nav1.2 and Nav1.6 sodium channel subtypes in the proximal or the distal region, respectively, of the AIS has been considered as the basis of two distinct tasks of the AIS: spike initiation and action potential back-propagation (Hu et al., 2009). The lowest threshold for spike initiation at the distal AIS should be determined by the high density of low-threshold Nav1.6 channels, while the high-threshold Nav1.2 channels control spike back-propagation because of their high density at the proximal AIS.
Although the present study did not adopt distinct subtypes of fast sodium channel, our findings are in agreement with this unique role of the AIS in spike back-propagation.
In our models, we directly attached the distal end of the AIS to the proximal edge of the first myelin attachment segment, so that the transition between these two segments was similar to that between a node and the myelin attachment segments. This agrees with the discovery that the axonal region where the myelin sheath begins seems organized with para-AIS and juxtapara-AIS, similar to the nodal regions (Duflocq et al., 2011).
Detailed Models
In this study, the development of detailed models of spinal motoneurons has provided novel insights about the voltage attenuation in proximal segments of the axon. Some experimentally testable predictions about the values of the densities of the Na+ channels at AIS and soma are also suggested.
Morphologically detailed models, indeed, have already demonstrated to provide more suitable results, compared to the reduced ones, especially when the examined events involve the integration of multiple synaptic inputs, or dendritic active conductances, or somato-dendritic back-propagation (Hendrickson et al., 2011). In particular, somato-dendritic back-propagation is considered a key mechanism for coincidence detection and synaptic long-term plasticity in neurons, and has been modeled in different types of neurons (Lüscher and Larkum, 1998; Diwakar et al., 2009; Hay et al., 2011). In these studies, morphologically detailed models have been successfully developed to simulate the spike back-propagation from soma to dendrites.
The implementation and the use of high-detailed neuron models to characterize the back-propagation from the myelinated axon through the initial segment to the soma, has been studied only in few cases. López-Aguado et al. (2002) modeled a single CA1 pyramidal cell obtained from detailed morphometric studies to describe the subcellular and macroscopic currents during axon-somatic or synaptic impulse propagation. This experimental and modeling work was able to show how the somatic transmembrane currents are entirely different during backward and forward spike propagation, and how the main cell axis behaves as a totally different cable when the action potential propagate in one direction or another. As above showed, a similar dichotomy is also clear from our results.
More recently, Kole et al. (2008) solved the discrepancies between cell-attached or outside-out patch-clamp studies, and whole-cell voltage-clamp data, by demonstrating a much higher density of Na+ channels at AIS than at the soma. Also in this work the computational part of the study was carried out by implementing highly detailed morphological reconstructions of the examined neuronal type (Kole et al., 2008).
Herein an axon-somatic back-propagation modeling study was performed for the first time in detailed models of spinal motoneurons, and further evidence was provided about the role of higher than usually admitted values of Na+ channel density at AIS.
Finally, our study also supports the view that the electrophysiological behavior of detailed models may help to guide the process of complexity reduction: the detailed model can prevent modelers from adopting minimizing strategies carrying to reduced models incompatible with the experimental neuronal features.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: http://www.frontiersin.org/journal/10.3389/fncom.2015.00015/abstract
References
Alvarez, F. J., Pearson, J. C., Harrington, D., Dewey, D., Torbeck, L., and Fyffe, R. E. (1998). Distribution of 5-hydroxytryptamine-immunoreactive boutons on alpha-motoneurons in the lumbar spinal cord of adult cats. J. Comp. Neurol. 393, 69–83.
Araki, T., and Terzuolo, A. C. (1962). Membrane currents in spinal motoneurons associated with the action potential and synaptic activity. J. Neurophysiol. 25, 772–789.
Ascoli, G. A., Donohue, D. E., and Halavi, M. (2007). NeuroMorpho.org: a central resource for neuronal morphologies. J. Neurosci. 27, 9247–9251. doi: 10.1523/JNEUROSCI.2055-07.2007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Balbi, P., Martinoia, S., Colombo, R., and Massobrio, P. (2014). Modelling recurrent discharge in the spinal α-motoneuron: reappraisal of the F wave. Clin. Neurophysiol. 125, 427–429. doi: 10.1016/j.clinph.2013.09.025
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Barrett, E. F., Barrett, J. N., and Crill, W. E. (1980). Voltage-sensitive outward currents in cat motoneurones. J. Physiol. 304, 251–276. doi: 10.1113/jphysiol.1980.sp013323
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Barrett, J. N., and Crill, W. E. (1974). Specific membrane properties of cat motoneurones. J. Physiol. 239, 301–324. doi: 10.1113/jphysiol.1974.sp010570
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Barrett, J. N., and Crill, W. E. (1980). Voltage clamp of cat motoneurone somata: properties of the fast inward current. J. Physiol. 30, 231–249. doi: 10.1113/jphysiol.1980.sp013322
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Berthold, C. H., Nilsson, I., and Rydmark, M. (1983). Axon diameter and myelin sheath thickness in nerve fibres of the ventral spinal root of the seventh lumbar nerve of the adult and developing cat. J. Anat. 136, 483–508.
Berthold, C. H., and Rydmark, M. (1983). Electrophysiology and morphology of myelinated nerve fibers. VI. Anatomy of the paranode-node-paranode region in the cat. Experientia 39, 964–976. doi: 10.1007/BF01989761
Booth, V., Rinzel, J., and Kiehn, O. (1997). Compartmental model of vertebrate motoneurons for Ca2+-dependent spiking and plateau potentials under pharmacological treatment. J. Neurophysiol. 78, 3371–3385.
Brock, L. G., Coombs, J. S., and Eccles, J. C. (1953). Intracellular Recording From Antidromically Activated Motoneurones. J. Physiol. 122, 429–461. doi: 10.1113/jphysiol.1953.sp005013
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Burbidge, S. A., Daleb, T. J., Powell, A. J., Whitaker, W. R. J., Xie, X. M., Romanos, M. A., et al. (2002). Molecular cloning, distribution and functional analysis of the Nav 1.6 voltage-gated sodium channel from human brain. Mol. Brain Res. 103, 80–90. doi: 10.1016/S0169-328X(02)00188-2
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Burke, R. E., Strick, P. L., Kanda, K., Kim, C. C., and Walmsley, B. (1977). Anatomy of medial gastrocnemius and soleus motor nuclei in cat spinal cord. J. Neurophysiol. 40, 667–680.
Carnevale, T. N., Tsai, K. Y., Claiborne, B. J., and Brown, T. H. (1995). “The electrotonic transformation: a tool for relating neuronal form to function,” in Advances in Neural Information Processing Systems. Vol. 7, eds G. Tesauro, D. S. Touretzky, and T. K. Leen (Cambridge, MA: MIT Press), 69–76.
Catterall, W. A., Goldin, A. L., and Waxman, S. G. (2014). Voltage-Gated Sodium Channels, Introduction. IUPHAR/BPS Guide to PHARMACOLOGY. Available online at: http://www.guidetopharmacology.org/GRAC/FamilyIntroductionForward?familyId=82(Last modified on March 06, 2014; Accessed February 02, 2015).
Cisi, R. R., and Kohn, A. F. (2008). Simulation system of spinal cord motor nuclei and associated nerves and muscles, in a Web-based architecture. J. Comput. Neurosci. 25, 520–542. doi: 10.1007/s10827-008-0092-8
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Clark, B. D., Goldberg, E. M., and Rudy, B. (2009). Electrogenic tuning of the axon initial segment. Neuroscientist 16, 651–668. doi: 10.1177/1073858409341973
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Clements, J. D., and Redman, S. J. (1989). Cable properties of cat spinal motoneurones measured by combining voltage clamp, current clamp and intracellular staining. J. Physiol. 409, 63–87. doi: 10.1113/jphysiol.1989.sp017485
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Conradi, S. (1969). Observation on the ultrastructure of the axon hillock and initial axon segment of lumbosacral motoneurons in the cat. Acta Physiol. Scan Suppl. 332, 65–84.
Cullheim, S., Fleshman, J. W., Glenn, L. L., and Burke, R. E. (1987). Membrane area and dendritic structure in type-identified triceps surae alpha motoneurons. J. Comp. Neurol. 255, 68–81. doi: 10.1002/cne.902550106
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Cullheim, S., and Kellerth, J.-O. (1978). A morphological study of the axon and recurrent axon collaterals of cat sciatic α-motoneurons after intracellular staining with horseradish peroxidase. J. Comp. Neurol. 178, 537–558. doi: 10.1002/cne.901780309
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Diwakar, S., Magistretti, J., Goldfarb, M., Naldi, G., and D'Angelo, E. (2009). Axonal Na+ channels ensure fast spike activation and back-propagation in cerebellar granule cells. J. Neurophysiol. 101, 519–532. doi: 10.1152/jn.90382.2008
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dodge, F. A., and Cooley, J. (1973). W. Action potential of the motorneuron. IBM J. Res. Dev. 17, 219–229. doi: 10.1147/rd.173.0219
Duflocq, A., Chareyre, F., Giovannini, M., Couraud, F., and Davenne, M. (2011). Characterization of the axon initial segment (AIS) of motor neurons and identification of a para-AIS and a juxtapara-AIS, organized by protein 4.1B. BMC Biol. 9:66. doi: 10.1186/1741-7007-9-66
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Eccles, J. C. (1955). The central action of antidromic impulses in motor nerves fibers. Pflügers Arch. 260, 385–415. doi: 10.1007/BF00363548
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
ElBasiouny, S. M., Bennett, D. J., and Mushahwar, V. K. (2005). Simulation of dendritic CaV1.3 channels in cat lumbar motoneurons: spatial distribution. J. Neurophysiol. 94, 3961–3974. doi: 10.1152/jn.00391.2005
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Fleshman, J. W., Segev, I., and Burke, R. E. (1988). Electrotonic architecture of type-identified α-motoneurons in the cat spinal cord. J. Neurophysiol. 60, 60–85.
Gentet, L. J., Stuart, G. J., and Clements, J. D. (2000). Direct measurement of specific membrane capacitance in neurons. Biophys. J. 79, 314–320. doi: 10.1016/S0006-3495(00)76293-X
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Goldstein, S. S., and Rall, W. (1974). Changes of action potential shape and velocity for changing core conductor geometry. Biophys. J. 14, 731–757. doi: 10.1016/S0006-3495(74)85947-3
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hay, E., Hill, S., Schürmann, F., Markram, H., and Segev, I. (2011). Models of neocortical layer 5b pyramidal cells capturing a wide range of dendritic and perisomatic active properties. PLoS Comput. Biol. 7:e1002107. doi: 10.1371/journal.pcbi.1002107
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hendrickson, E. B., Edgerton, J. R., and Jaeger, D. (2011). The capabilities and limitations of conductance-based compartmental neuron models with reduced branched or unbranched morphologies and active dendrites. J. Comput. Neurosci. 30, 301–321. doi: 10.1007/s10827-010-0258-z
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544. doi: 10.1113/jphysiol.1952.sp004764
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hu, W., Tian, C., Yang, M., Hou, H., and Shu, Y. (2009). Distinct contributions of Nav1.6 and Nav1.2 in action potential initiation and backpropagation. Nat. Neurosci. 12, 996–1002. doi: 10.1038/nn.2359
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Joyner, R. W., Westerfield, M., and Moore, J. W. (1980). Effects of cellular geometry on current flow during a propagated action potential. Biophys. J. 31, 183–194. doi: 10.1016/S0006-3495(80)85049-1
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kernell, D. (1966). Input resistance, electrical excitability, and size of ventral horn cells in cat spinal cord. Science 152, 1638–1640. doi: 10.1126/science.152.3729.1637
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kole, M. H., Ilshner, S. U., Kampa, B. M., Williams, S. R., Ruben, P. C., and Stuart, G. J. (2008). Action potential generation requires a high sodium channel density in the axon initial segment. Nat. Neurosci. 11, 178–186. doi: 10.1038/nn2040
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kuo, C., and Bean, B. P. (1994). Na+ channels must deactivate to recover from inactivation. Neuron 12, 819–829. doi: 10.1016/0896-6273(94)90335-2
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Liu, R.-H., Yamuy, J., Xi, M.-C., Morales, F. R., and Chase, M. H. (1995). Changes in electrophysiological properties of cat spinal motoneurons following the intramuscular injection of adriamycin compared with changes in the properties of motoneurons in aged cats. J. Neurophysiol. 74, 1972–1981.
López-Aguado, L., Ibarz, J. M., Varona, P., and Herreras, O. (2002). Structural inhomogeneities differentially modulate action currents and population spikes initiated in the axon or dendrites. J. Neurophysiol. 88, 2809–2820. doi: 10.1152/jn.00183.2002
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Lüscher, H. R., and Larkum, M. E. (1998). Modeling action potential initiation and back-propagation in dendrites of cultured rat motoneurons. J. Neurophysiol. 80, 715–729.
McIntyre, C. C., and Grill, W. M. (2002). Extracellular stimulation of central neurons: influence of stimulus waveform and frequency on neuronal output. J. Neurophysiol. 88, 1592–1604. doi: 10.1152/jn.00147.2002
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
McIntyre, C. C., Richardson, A. G., and Grill, W. M. (2002). Modeling the excitability of mammalian nerve fibers: influence of afterpotentials on the recovery cycle. J. Neurophysiol. 87, 995–1006. doi: 10.1152/jn.00353.2001
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Moore, J. W., Stockbridge, N., and Westerfield, M. (1983). On the site of impulse initiation in a neurone. J. Physiol. 336, 301–311. doi: 10.1113/jphysiol.1983.sp014582
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Morales, F. R., Boxer, P. A., Fung, S. J., and Chase, M. H. (1987). Basic electrophysiological properties of spinal cord motoneurons during old age in the cat. J. Neurophysiol. 58, 180–194.
Nilsson, I., and Berthold, C. H. (1988). Axon classes and internodal growth in the ventral spinal root L7 of adult and developing cats. J. Anat. 156, 71–96.
Powers, R. K., ElBasiouny, S. M., Rymer, W. Z., and Heckman, C. J. (2012). Contribution of intrinsic properties and synaptic inputs to motoneuron discharge patterns: a simulation study. J. Neurophysiol. 107, 808–823. doi: 10.1152/jn.00510.2011
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rydmark, M. (1981). Nodal axon diameter correlates linearly with internodal axon diameter in spinal roots of the cat. Neurosci. Lett. 24, 247–250. doi: 10.1016/0304-3940(81)90165-8
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rydmark, M., and Berthold, C. H. (1983). Electron microscopic serial section analysis of nodes of Ranvier in lumbar spinal roots of the cat: a morphometric study of nodal compartments in fibres of different sizes. J. Neurocytol. 12, 537–565. doi: 10.1007/BF01181523
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Safronov, B. V., Wolff, M., and Vogel, W. (2000). Excitability of the soma in central nervous system neurons. Biophys. J. 78, 2998–3010. doi: 10.1016/s0006-3495(00)76838-x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Shapiro, N. P., and Lee, R. H. (2007). Synaptic amplification versus bistability in motoneuron dendritic processing: a top-down modeling approach. J. Neurophysiol. 97, 3948–3960. doi: 10.1152/jn.00084.2007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Traub, R. D. (1977). Motorneurons of different geometry and the size principle. Biol. Cybern. 25, 163–176. doi: 10.1007/bf00365213
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Ulfhake, B., and Kellerth, J.-O. (1982). Does alpha-motoneuron size correlate with motor unit type in cat triceps surae? Brain Res. 251, 201–209. doi: 10.1016/0006-8993(82)90738-7
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Ulfhake, B., and Kellerth, J.-O. (1984). Electrophysiological and morphological measurements in cat gastrocnemius and soleus alpha-motoneurons. Brain Res. 307, 167–179. doi: 10.1016/0006-8993(84)90471-2
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Yamuy, J., Englehardt, J. K., Morales, F. R., and Chase, M. H. (1992). Active electrophysiological properties of spinal motoneurons in aged cats following axotomy. Neurobiol. Aging 13, 231–238. doi: 10.1016/0197-4580(92)90035-V
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keywords: spinal motoneuron, detailed model, back-propagation, axonal initial segment, sodium channel density
Citation: Balbi P, Martinoia S and Massobrio P (2015) Axon-somatic back-propagation in detailed models of spinal alpha motoneurons. Front. Comput. Neurosci. 9:15. doi: 10.3389/fncom.2015.00015
Received: 31 July 2014; Accepted: 27 January 2015;
Published online: 12 February 2015.
Edited by:
Martin Giese, University Clinic Tübingen, GermanyCopyright © 2015 Balbi, Martinoia and Massobrio. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pietro Balbi, Department of Neurorehabilitation, Scientific Institute of Pavia via Boezio, IRCCS, ‘Salvatore Maugeri’ Foundation, via Boezio n. 28, 27100 Pavia, Italy e-mail:cGJhbGJpQGZzbS5pdA==
 Pietro Balbi
Pietro Balbi Sergio Martinoia
Sergio Martinoia Paolo Massobrio
Paolo Massobrio