- 1Department of Mathematical Sciences, Xi'an Jiaotong-Liverpool University, Suzhou, China
- 2Department of Public Health, Faculty of Health Sciences, Ben-Gurion University of the Negev, Beer-Sheva, Israel
- 3Allen Institute for Brain Science, Seattle, WA, USA
Two cliques of genes identified computationally for their high co-expression in the mouse brain according to the Allen Brain Atlas, and for their enrichment in genes related to autism spectrum disorder (ASD), have recently been shown to be highly co-expressed in the cerebellar cortex, compared to what could be expected by chance. Moreover, the expression of these cliques of genes is not homogeneous across the cerebellar cortex, and it has been noted that their expression pattern seems to highlight the granular layer. However, this observation was only made by eye, and recent advances in computational neuroanatomy allow to rank cell types in the mouse brain (characterized by their transcriptome profiles) according to the similarity between their spatial density profiles and the spatial expression profiles of the cliques. We establish by Monte Carlo simulation that with probability at least 99%, the expression profiles of the two cliques are more similar to the density profile of granule cells than 99% of the expression of cliques containing the same number of genes (Purkinje cells also score above 99% in one of the cliques). Thresholding the expression profiles shows that the signal is more intense in the granular layer. Finally, we work out pairs of cell types whose combined expression profiles are more similar to the expression profiles of the cliques than any single cell type. These pairs predominantly consist of one cortical pyramidal cell and one cerebellar cell (which can be either a granule cell or a Purkinje cell).
1. Introduction
The neuroanatomical structures underlying autism spectrum disorder (ASD) traits are the subject of intense research efforts, as ASD is one of the most prevalent and highly heritable neurodevelopmental disorders in humans (Newschaffer et al., 2007; Amaral et al., 2008; Levy, 2009; Lord, 2011). Recent genomic advances have led to the association of more than 300 candidate genes with ASD susceptibility (Jacquemont et al., 2006; Szatmari et al., 2007; Cook and Scherer, 2008; Basu et al., 2009; Gilman et al., 2011; Kumar et al., 2011; Levy et al., 2011; Myers et al., 2011; Anney et al., 2012; Iossifov et al., 2012; Neale et al., 2012; O'Roak et al., 2012; Sanders et al., 2012). However, the list is far from closed and the molecular mechanisms and brain regions underlying ASD traits remain largely unclear. While no major anatomical pathology has been observed in brains of ASD cases, various molecular and neuroimaging studies have linked several brain regions to ASD. The cortex is often associated to capacities, such as planning and interpreting language, that are impaired in autism. Indeed, differences in gene expression patterns in the cortex of ASD brain have been found in Voineagu et al. (2011). On the other hand, the cerebellum, which appeared much earlier in evolution than the cortex, is a less likely candidate for implication in autism, because it is more often associated to motor skills. However, a strong body of evidence, in particular from the from the study of post-mortem autistic brains (Skefos et al., 2014), suggests an implication of the cerebellum in ASD. Moreover, the cerebellum may be connected to remote parts of the brain, including the neocortex involved in cognitive development and social interaction (see Wang et al., 2014).
The mouse model has recently benefited from an unprecedented flow of data, which begs for computational analysis. Important sources of data include:
1. genetic databases of ASD, such as AutDB (Basu et al., 2009; Kumar et al., 2011);
2. gene-based maps: the Allen Brain Atlas (ABA) of the adult mouse (Ng et al., 2005, 2007a,b, 2009; Lein et al., 2006; Sunkin and Hohmann, 2007; Lee et al., 2008; Hawrylycz et al., 2011a,b), which consists of thousands of brain-wide in situ hybridization (ISH) gene-expression profiles, digitized, and co-registered to the Allen Reference Atlas (ARA) (Dong, 2008);
3. cell-based maps: the ongoing development of a classification of cell types in the mouse brain based on their transcriptome profiles (Arlotta et al., 2005; Chung et al., 2005; Sugino et al., 2005; Rossner et al., 2006; Cahoy et al., 2008; Doyle et al., 2008; Heiman et al., 2008; Okaty et al., 2009, 2011).
These sources of data are complementary to each other. Recently, we used the ABA to examine the spatial co-expression characteristics of genes associated with ASD susceptibility in the AutDB database (Menashe et al., 2013). We identified two networks of highly co-expressed genes that are enriched with autism genes and significantly overexpressed in the cerebellar cortex. These results added to the mounting evidence of the involvement of the cerebellum in autism (Vargas et al., 2005; Lotta et al., 2014). However, the complex internal structure of the cerebellum requires a further investigation of the specific cerebellar regions or cell types associated with ASD.
On the other hand, cell-type-specific transcriptomes were recently combined with the ABA in order to estimate the brain-wide density of cell types (Grange et al., 2014), using a linear mathematical model, which amounts to decomposing the gene expression data of the ABA over a set of measured cell-type-specific transcriptomes (see also Ko et al., 2013; Tan et al., 2013 for cell-type-specific analyses of the ABA, and Abbas et al., 2009 for a similar mathematical approach in the context of blood cells). These estimates have potential application to the neuroanatomy of ASD: whenever a brain region exhibits over-expression of ASD-related genes, this region can also be compared to the neuroanatomical patterns of cell types, revealing which cell types are involved. Computational neuroanatomy has so far combined the AutDB and the ABA one one hand (Menashe et al., 2013), and cell-type-specific transcriptomes and the ABA on the other hand (Grange et al., 2014). In this paper we will close this loop by looking for computational links between ASD-related genes from AutDB and cell-type-specific transcriptomes.
It was observed in Menashe et al. (2013) that two cliques of co-expressed autism genes appear to be overexpressed in the granular layer of the cerebellum. However, this observation was based on visual comparison of the expression patterns of the genes in these two cliques to sections of the estimated density patterns of cell types1. This approach by mere visual inspection is far from satisfactory since it does not make use of the computational potential of the ABA (Bohland et al., 2010; Grange and Mitra, 2012; Grange et al., 2013). Moreover, post-mortem studies of brains of autistic patients (Skefos et al., 2014) have shown alterations in the Purkinje layer of the cerebellum, rather than in the granule cells.
In the present study we re-examine the two cliques discovered in Menashe et al. (2013) using recent developments of computational neuroanatomy relating cell-type-specificity of gene expression to neuroanatomy. We extend the Monte Carlo methods developed in Menashe et al. (2013) (to estimate the probability of co-expression among a set of genes) to the comparison between the expression of a set of genes and the spatial density profile of a cell type. This allows to estimate the probability of similarity between gene-expression profiles of cliques and spatial distributions of all cell types considered in Grange et al. (2014). Finally, we look for linear combinations of pairs of density profiles of cell types that are more similar to the expression profiles of cliques of genes than any single cell type.
2. Methods
2.1. Cosine Similarity between the Expression Profile of a Clique of Genes and the Density of a Cell Type
2.1.1. Cliques of genes
We re-examine the brain-wide expression profiles of the two cliques  1 and
1 and  2 of genes identified in Menashe et al. (2013) based on their exceptional co-expression properties, which consist of 33 and 6 genes, respectively:
2 of genes identified in Menashe et al. (2013) based on their exceptional co-expression properties, which consist of 33 and 6 genes, respectively:

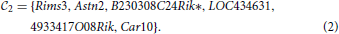
They both contain genes from the AutDB database (Basu et al., 2009; Kumar et al., 2011) of ASD-related genes(Ptchd1, Galnt13, Dpp6 and Astn2 for the first clique, Astn2 and Rims3 for the second).
2.1.2. Gene expression energies from the Allen Brain Atlas
The adult mouse brain is partitioned into V = 49,742 cubic voxels of side 200 microns, to which ISH data are registered (Lein et al., 2006; Dong, 2008) for thousands of genes. For computational purposes, these gene-expression data can be arranged into a voxel-by-gene matrix2. For a cubic voxel labeled v, the expression energy of the gene g is a weighted sum of the grayscale-value intensities evaluated at the pixels intersecting the voxel:
Like the analysis of Grange et al. (2013) and Menashe et al. (2013), the present analysis is restricted to the coronal ABA, for which the entire mouse brain was processed in the ABA pipeline (whereas only the left hemisphere was processed for the sagittal atlas).
2.1.3. Cell-type-specific microarray data and estimated cell-type-specific density profiles
The cell-type-specific microarray reads collated in Okaty et al. (2011) from the studies (Arlotta et al., 2005; Chung et al., 2005; Sugino et al., 2005; Rossner et al., 2006; Cahoy et al., 2008; Doyle et al., 2008; Heiman et al., 2008; Okaty et al., 2009) (for T = 64 different cell-type-specific samples) are arranged in a type-by-gene matrix denoted by C, such that
and the columns are arranged in the same order as in the matrix E of expression energies defined in Equation (3). In Grange et al. (2014), we proposed a simple linear model for a voxel-based gene-expression atlas in terms of the transcriptome profiles of cell types and their spatial densities:
where the index t denotes the t-th cell type, and ρt(v) denotes its density at voxel labeled v. The profile ρt is a spatial density, to be distinguished from the expression profile of a fixed cell type across all genes. More precisely, the values of the cell-type-specific density profiles were computed in Grange et al. (2014) by minimizing the value of the residual term in Equation (5) over all the (positive) density profiles, which amounts to solving a quadratic optimization problem (with positivity constraint) at each voxel:
The solution of this problem at every voxel happens to be quite sparse (with fewer than 6 distinct cell types detected at most voxels). Adding a term proportional to the L1-norm of ν in the above objective function can increase sparsity (adapting the search for marker genes implemented in Grange et al. 2013), but the diversity of cell types present in a given voxel is expected to be larger in reality than in our model, and should be increased if the model is refitted to a richer panel of cell-type-specific transcriptomes. However, if data sets increase to dramatically higher values than T = 64, L1-penalization could become necessary to increase sparsity (or to match it with known results in well-studied voxels).
2.1.4. Cosine similarity between spatial gene-expression patterns and cell-type-specific spatial density patterns
The quantitative study of spatial co-expression of genes in Menashe et al. (2013) combines the columns of the matrix of gene-expression energies (Equation 3) by computing the cosine similarities of all pairs of genes in the cliques  1 and
1 and  2. These cosine similarities are then compared to those obtained from random sets of genes containing the same numbers of elements as
2. These cosine similarities are then compared to those obtained from random sets of genes containing the same numbers of elements as  1 and
1 and  2, respectively. This technique can be adapted to compare brain-wide gene-expression profiles to the spatial density of cell types, simply by considering cosine similarities between gene-expression profiles and cell-type-specific density profiles.
2, respectively. This technique can be adapted to compare brain-wide gene-expression profiles to the spatial density of cell types, simply by considering cosine similarities between gene-expression profiles and cell-type-specific density profiles.
Given a set  of genes from the coronal ABA (selected either computationally based on their co-expression properties, or based on curation of the biomedical literature, for instance
of genes from the coronal ABA (selected either computationally based on their co-expression properties, or based on curation of the biomedical literature, for instance  =
=  1 or
1 or  =
=  2), we can compute the sum of their expression profiles:
2), we can compute the sum of their expression profiles:
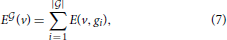
where gi is the column index in the matrix of expression energies (Equation 3) corresponding to the i-th gene in the set  , and |
, and | | denotes the number of genes in this set. The quantity E
| denotes the number of genes in this set. The quantity E is an element of RV+, just as the brain-wide density profile of a cell type estimated from Equation (6). We can therefore estimate the similarity between E
is an element of RV+, just as the brain-wide density profile of a cell type estimated from Equation (6). We can therefore estimate the similarity between E and the density of cell type labeled t by computing the cosine similarity
and the density of cell type labeled t by computing the cosine similarity
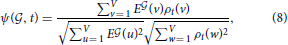
which is a number between 0 and 1 by construction.
Our model assumes that various sources of noise result in an additive term. However, the efficacy and stability of the biological agent binding to mRNA can vary from gene to gene, resulting in multiplicative noise. The model of Equation (5) assumes that the expression energies depend linearly on the quantity of mRNA present at each voxel (ignoring saturation effects for strong expression), and with a gene-independent coefficient (ignoring multiplicative noise). Multiplicative noise could have a strong influence when studying the sum of expression profiles of several genes in a clique. However, it was checked in Menashe et al. (2013) that the two cliques of genes in the present study are over-expressed in the cerebellar cortex, even if gene-expression profiles are separately normalized before the sum (Equation 7) is performed, which reduces the influence of multiplicative noise.
2.1.5. Statistical significance of the similarity between expression profiles of genes and density profiles of cell types
Furthermore, for a fixed cell type, we can estimate how exceptional the similarity ψ( , t) is, compared to what would be expected from random sets of |
, t) is, compared to what would be expected from random sets of | | genes drawn from the coronal ABA. This is a finite problem, but it becomes hugely complex in a regime where |
| genes drawn from the coronal ABA. This is a finite problem, but it becomes hugely complex in a regime where | | is relatively large but still small compared to the size of the entire atlas (which is the case for both cliques in the present study). We can take a Monte Carlo approach, draw R random sets of |
| is relatively large but still small compared to the size of the entire atlas (which is the case for both cliques in the present study). We can take a Monte Carlo approach, draw R random sets of | | genes and simulate the cumulative distribution function (CDF) of the cosine similarity3 between the expression profile of a random set of |
| genes and simulate the cumulative distribution function (CDF) of the cosine similarity3 between the expression profile of a random set of | | genes and the density profile of cell-type labeled t (this CDF depends only on the cell type and on the number of genes |
| genes and the density profile of cell-type labeled t (this CDF depends only on the cell type and on the number of genes | |, so we can denote it by CDFt, |
|, so we can denote it by CDFt, | |). By the law of large numbers, we obtain an estimate of this CDF by taking an average of R random sets, and the probability
|). By the law of large numbers, we obtain an estimate of this CDF by taking an average of R random sets, and the probability 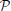 R(
R( , t) of getting a lower value of cosine similarity than ψ(
, t) of getting a lower value of cosine similarity than ψ( , t) after R random draws converges to the true probability when R is large enough (in the present case the problem is finite, see Menashe et al., 2013 for details of the method).
, t) after R random draws converges to the true probability when R is large enough (in the present case the problem is finite, see Menashe et al., 2013 for details of the method).
The precision of our estimates depends on the value of R. We can use Hoeffding's inequality to control the probability of being within a known error from the true CDF, as a function of the number R of random draws. As we are estimating the probability of having larger cosine similarity than expected by chance by summing R Bernoulli variables, Hoeffding's inequality (see Hastie et al., 2009 for instance) states that for any τ, the probability of missing the true value of the probability  (
( , t) by τ is bounded in terms of τ and the number of random draws R as follows:
, t) by τ is bounded in terms of τ and the number of random draws R as follows:
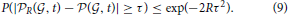
For instance, taking τ = 0.01 and R = 26,500 leads to a value of 0.01 for the bound on the r.h.s. of the inequality (Equation 9), so it is enough to draw this number of random sets of genes to obtain an estimator within 1 percent of the true probabilities, with probability at least 99 percent.
Having conducted the simulation of the distribution of cosine similarities for a choice of R based on Hoeffding's inequality, we can rank cell types for a fixed clique  by decreasing values of statistical significance:
by decreasing values of statistical significance:
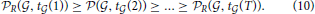
2.1.6. Similarity between thresholded gene-expression energies and cell-type-specific densities
Given that the expression profiles of the cliques of interest in this study is much less sparse than any of the densities of cell types estimated in Grange et al. (2014), the genes in the cliques must be expressed in several different cell types, but there are large differences in expression between cortical voxels and cerebellar voxels for instance, and also within the cerebellar cortex (see Figures 2A,B). We propose to threshold brain-wide expression profile of each clique, and to recompute the cosine similarities with density profiles, in order to discover which neuroanatomical cell-type-specific patterns are highlighted with more intensity. If the profile of a given cell type is highlighted by a given clique, when the threshold grows from zero to low values of the threshold, the cosine similarity is expected to grow, since many voxels with low values of expression energy, that penalize the cosine similarity to the cell type, are put to zero by the threshold. Let us denote by τ the value of the threshold. We compute the thresholded expression energies of the cliques and cosine similarities as follows:
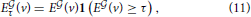
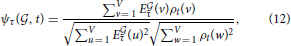
At very large values of the threshold, expression energies are going to be put to zero everywhere, and the cosine similarities decrease to zero (for all cell types). So the cosine similarity between the expression of the two gene cliques and the cell types they highlight are expected to exhibit peaks when plotted as a function of the threshold. The higher the peak, and the higher the corresponding value of the threshold, the more intensely the cell type is highlighted.
2.2. Cosine Similarity Between Expression of a Clique of Genes and the Density of a Pair of Cell Types
Instead of ranking single cell types by the significance of the similarity between their density profile and the (possibly thresholded) expression of a given clique, we can extend our analysis to combinations of cell types. The simplest modification of our similarity analysis consists of a search for pairs of cell types whose combined density profile is more similar to the expression profile of a given clique than any single cell type in the data set.
As the density profiles of two cell types labeled t1 and t2 are two vectors in the voxel space RV, they define a plane in voxel space, and they provide a base of this plane (provided the two vectors ρt1 and ρt2 are linearly independent, which is the case for all pairs (t1, t2) in the present study). To characterize how well the expression profile of a clique of genes coincides with the reunion of two given cell types labeled t1 and t2, we have to solve the following minimization problem:
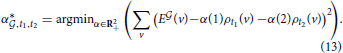
This problem is analogous to the one stated in Equation (6), but it corresponds to fitting one vector in voxel space by linear combination of two vectors with positive coefficients, not V vectors in gene space using T vectors with positive coefficients. Having solved this problem for a given pair of cell types labeled by (t1, t2), we know the closest vector to the clique  that can be obtained by combining these two cell types. We can compute the cosine similarity between this optimal vector and the expression profile of the clique (and denote it by ψ(
that can be obtained by combining these two cell types. We can compute the cosine similarity between this optimal vector and the expression profile of the clique (and denote it by ψ( , t1, t2), which symbol will be used in Table 3 and in the caption of Figure 5). We can repeat this computation in order to obtain a Monte Carlo simulation of this cosine similarity, just as we did in the case of single cell types. More precisely, we compute the closest vector to E
, t1, t2), which symbol will be used in Table 3 and in the caption of Figure 5). We can repeat this computation in order to obtain a Monte Carlo simulation of this cosine similarity, just as we did in the case of single cell types. More precisely, we compute the closest vector to E in the plane of voxel space spanned by ρt1 and ρt2, which we denote by
in the plane of voxel space spanned by ρt1 and ρt2, which we denote by 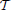
 , t1, t2:
, t1, t2:
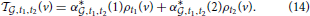
The cosine similarity between this optimal vector and the expression vector E is readily computed as:
is readily computed as:
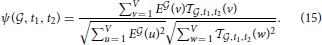
Having computed this quantity for a given clique  and all pairs of cell types in our data set, we can detect the pairs of cell types for which the optimization of Equation (13) leads to the largest improvement in cosine similarity, for instance by providing a better fitting than any single cell type. This motivates us to consider the following pairs of cell types:
and all pairs of cell types in our data set, we can detect the pairs of cell types for which the optimization of Equation (13) leads to the largest improvement in cosine similarity, for instance by providing a better fitting than any single cell type. This motivates us to consider the following pairs of cell types:
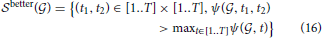
Again, for a given pair of cell types, the value of the cosine similarity can be biased by the size of the support of the two underlying cell types, but we can estimate the probability of getting a lower cosine similarity from random cliques of genes ( 1,
1,  2, …,
2, …,  R, with |
R, with | | genes each), simply by repeating the computation of cosine similarities (Equation 8), with the optimal vector
| genes each), simply by repeating the computation of cosine similarities (Equation 8), with the optimal vector 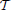
 , t1, t2 (defined in Equation 14) substituted to the single density profile:
, t1, t2 (defined in Equation 14) substituted to the single density profile:
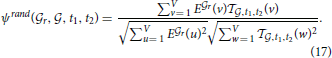
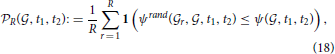
where R can again be worked out for given thresholds using Hoeffding's inequality.
2.3. Cosine Similarity between a Brain-Wide Density Profile and a Brain Region
Given a brain region ω defined in the ARA, we define the normalized vector χω in voxel space whose non-zero entries correspond to the voxels belonging to the region ω:
Given a density profile ρt, we can compute its cosine similarity to χω, in the same way that was used in Menashe et al. (2013) with gene-expression profiles:
The quantities ϕω(E 1) and ϕω(E
1) and ϕω(E 2) were shown in Menashe et al. (2013) to be exceptionally large compared to quantities obtained from cliques of the same size, when ω is taken to be the cerebellar cortex. In this study the quantity ϕω will be used to study the neuroanatomy of density profiles of cell types shown to be highly similar to expression profiles (see Figure 7 for sorted values of ϕω(ρt) with ω taken to be the cerebral cortex).
2) were shown in Menashe et al. (2013) to be exceptionally large compared to quantities obtained from cliques of the same size, when ω is taken to be the cerebellar cortex. In this study the quantity ϕω will be used to study the neuroanatomy of density profiles of cell types shown to be highly similar to expression profiles (see Figure 7 for sorted values of ϕω(ρt) with ω taken to be the cerebral cortex).
3. Results
3.1. Granule Cells and Purkinje Cells are the Most Significantly Similar Cell Types to Both Cliques
We computed the cosine similarities between the expression profiles of the two cliques  1 and
1 and  2 and the density profiles of the T = 64 cell types estimated in Grange et al. (2014), using Equation (8). The sorted values are plotted on Figure 1. It appears that the ranking of the cell types by cosine similarity is roughly conserved between the two cliques, and that no more than a third of the cell types have a cosine similarity of more than 10% to either clique.
2 and the density profiles of the T = 64 cell types estimated in Grange et al. (2014), using Equation (8). The sorted values are plotted on Figure 1. It appears that the ranking of the cell types by cosine similarity is roughly conserved between the two cliques, and that no more than a third of the cell types have a cosine similarity of more than 10% to either clique.
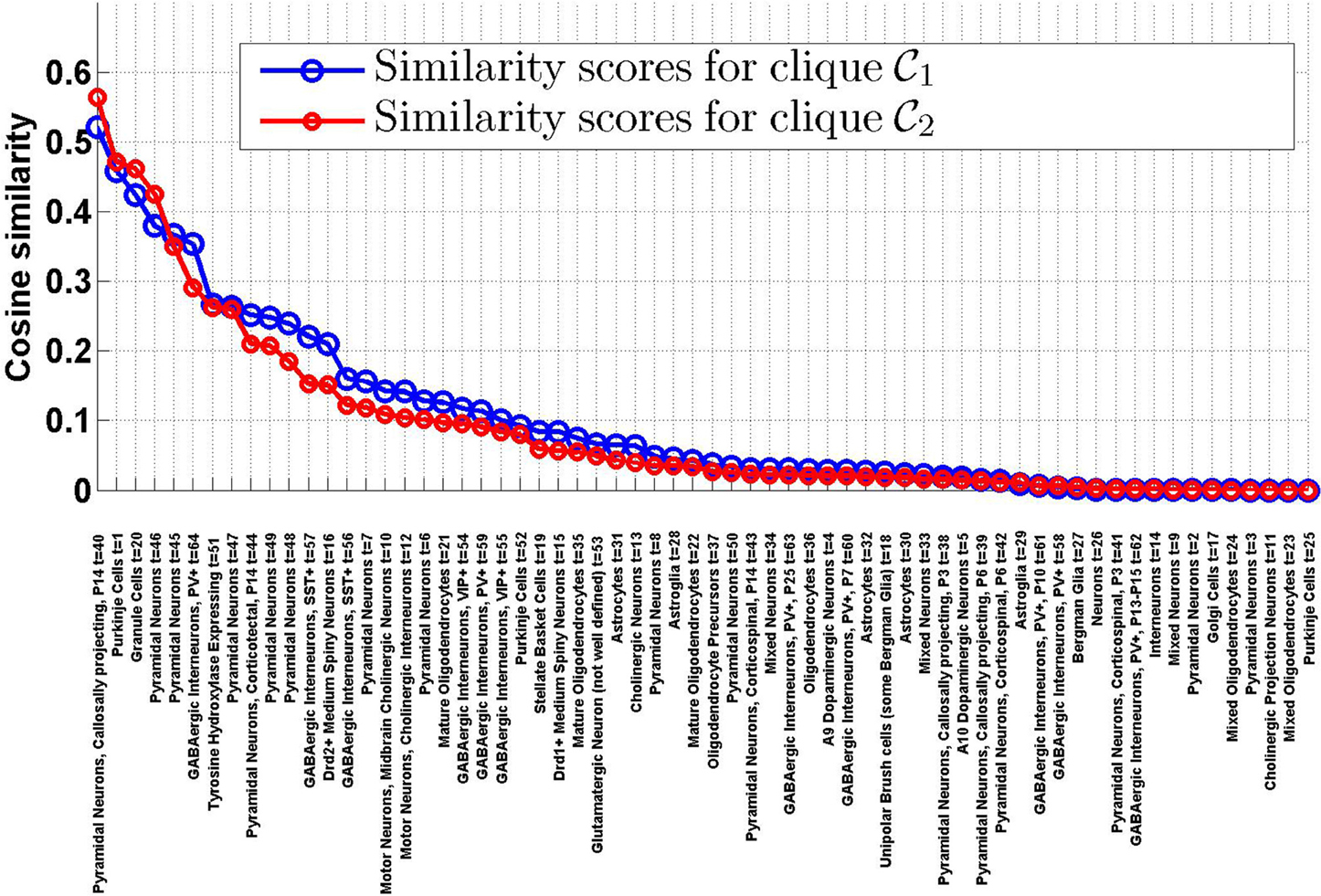
Figure 1. Similarity scores between the T = 64 densities of cell types in our data set and the cliques  1 and
1 and  2, sorted by decreasing order of ψ(
2, sorted by decreasing order of ψ( 1, t). There is a good agreement between the rankings of cell types induced by the two cliques. The first four cell types in both cliques are labeled t = 40 (pyramidal neurons), t = 1 (Purkinje cells), t = 20 (granule cells), t = 46 (pyramidal neurons).
1, t). There is a good agreement between the rankings of cell types induced by the two cliques. The first four cell types in both cliques are labeled t = 40 (pyramidal neurons), t = 1 (Purkinje cells), t = 20 (granule cells), t = 46 (pyramidal neurons).
For each cell type, we computed the probabilities 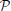 R(
R( 1, t) and
1, t) and 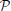 R(
R( 2, t) for R = 27,000 random sets (of 33 genes each for clique
2, t) for R = 27,000 random sets (of 33 genes each for clique  1, of 6 genes each for clique
1, of 6 genes each for clique  2). Tables 1, 2 show the cell types for which the cosine similarity is larger than 10%, ordered by decreasing values of statistical significance. For both cliques, granule cells (labeled t = 20) and Purkinje cells (labeled t = 1), have the highest value of PR (more than 99% for both cliques in the case of granule cells). For each of the two cliques, one more cell type has a value of PR larger than 80% (mature oligodendrocytes, labeled t = 21, in the case of
2). Tables 1, 2 show the cell types for which the cosine similarity is larger than 10%, ordered by decreasing values of statistical significance. For both cliques, granule cells (labeled t = 20) and Purkinje cells (labeled t = 1), have the highest value of PR (more than 99% for both cliques in the case of granule cells). For each of the two cliques, one more cell type has a value of PR larger than 80% (mature oligodendrocytes, labeled t = 21, in the case of  1, pyramidal neurons, labeled t = 46, in the case of
1, pyramidal neurons, labeled t = 46, in the case of  2). The statistical significance (i.e., the value of
2). The statistical significance (i.e., the value of 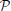 R) drops sharply after the third rank for both cliques. Our computational analysis therefore returns a list of four cell types to which at least one of the two cliques in this study is significantly similar (more similar than at least 80% of the sets of genes in our Monte CArlo simulations).
R) drops sharply after the third rank for both cliques. Our computational analysis therefore returns a list of four cell types to which at least one of the two cliques in this study is significantly similar (more similar than at least 80% of the sets of genes in our Monte CArlo simulations).
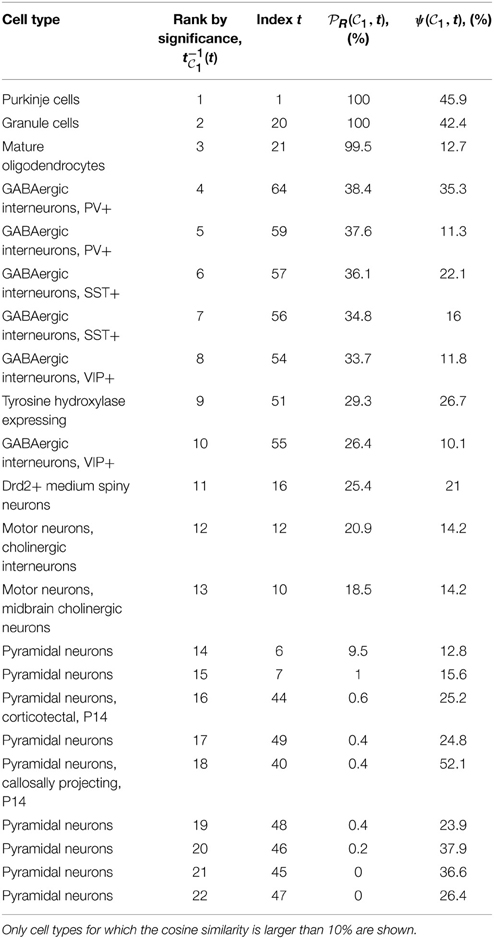
Table 1. Table of cell types sorted by decreasing values of statistical significance for clique  1 (see Equation 10), measured by the probability
1 (see Equation 10), measured by the probability 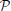 R(
R( 1, t), for R = 27,000.
1, t), for R = 27,000.
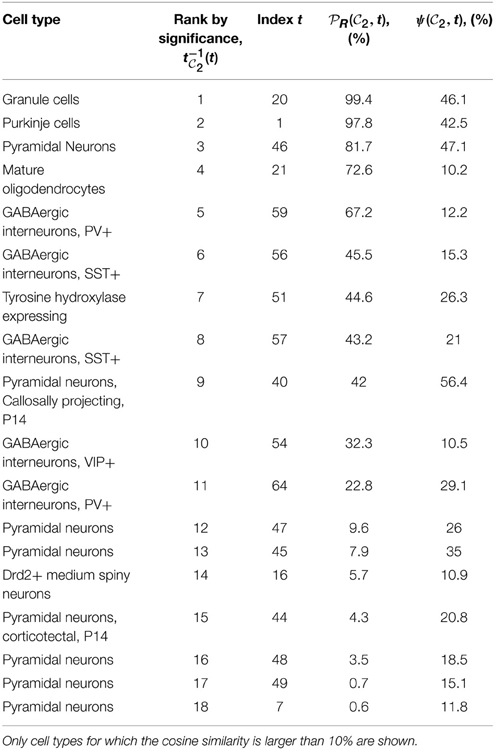
Table 2. Table of cell types sorted by decreasing values of statistical significance for clique  2 (see Equation 10), measured by the probability
2 (see Equation 10), measured by the probability  R(
R( 2, t), for R = 27,000.
2, t), for R = 27,000.
Figure 2 shows heat maps of the expression profiles of the two cliques and of the density profiles of these four cell types. The expression profiles of both cliques highlight the cerebellum, but they are non-zero in many more voxels than any of the densities of cell types illustrated in Figures 2C1–C4. These densities are highly concentrated in the cerebellum (indeed the corresponding cell-type-specific samples were extracted from the cerebellum, see Rossner et al., 2006 for Purkinje cells, see Doyle et al., 2008 for granule cells and mature oligodendrocytes), with the exception of the pyramidal neurons (labeled t = 46) which are highly localized in the cerebral cortex (the corresponding cell-type-specific samples were extracted from the layer 5 of the cerebral cortex, see Sugino et al., 2005).
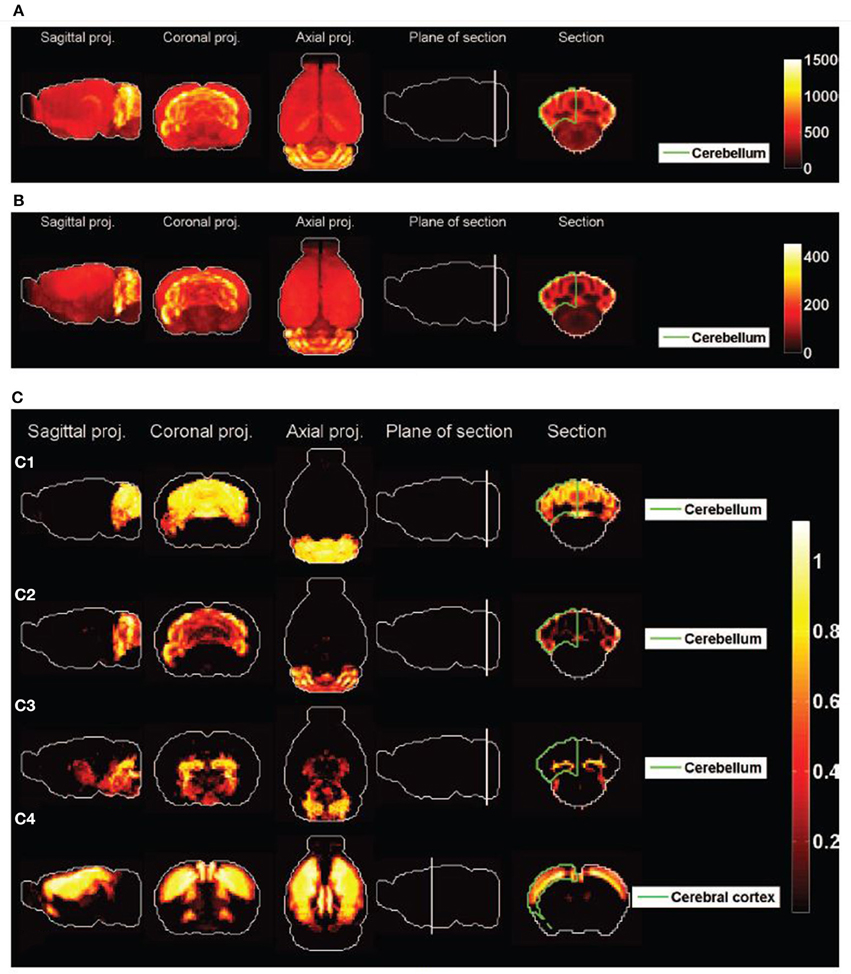
Figure 2. Heat maps of gene-expression of gene cliques, and of density profiles of cell types. (A) Heat map of the sum of expression energies of the 33 genes in the clique C1. (B) Heat map of the sum of expression energies of the 6 genes in the clique C2. (C) Heat maps of brain-wide densities (denoted by ρt for cell type labeled t) of cell types estimated based on the model of Equation (5), for Purkinje cells (C1, labeled t = 1), granule cells (C2, labeled t = 20), cerebellar mature oligodendrocytes (C3, labeled t = 21), and cortical pyramidal neurons extracted from layer 5 (C4, labeled t = 46). These four cell types are the ones that are ranked the most highly by statistical significance of similarity to either of the cliques  1 and
1 and  2 (
2 ( R > 80% in Tables 1, 2).
R > 80% in Tables 1, 2).
The cell-type-specific sample of granule cells (labeled t = 20) is the only cell type that has a score higher than 99% in both cliques. Figure 2 shows plots of the simulated CDFs of the cosine similarities between the top three cell types by significance and sets of genes of the same size as  1 (Figure 3A) and
1 (Figure 3A) and  2 (Figure 3B). One can observe that both granule cells and Purkinje cells sit more comfortably at the top of the distribution than the cell type ranked third by statistical significance, especially for clique
2 (Figure 3B). One can observe that both granule cells and Purkinje cells sit more comfortably at the top of the distribution than the cell type ranked third by statistical significance, especially for clique  2.
2.
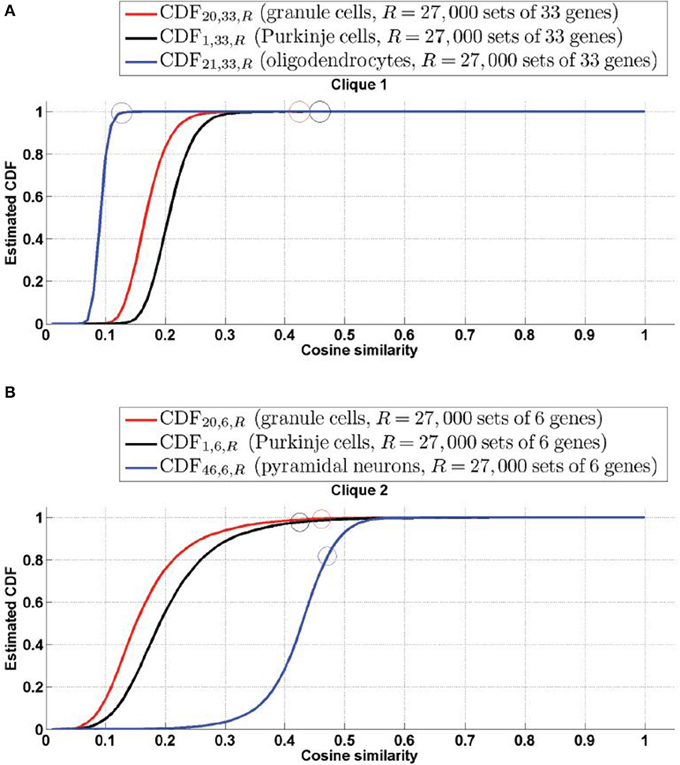
Figure 3. Simulated cumulative distribution functions (CDFs) of cosine similarities between gene-expression of cliques and the estimated density profile of the three cell types with most significant cosine similarity (granule cells and Purkinje cells for both cliques, along with mature oligodendrocytes for Clique  1 and pyramidal neurons for Cliques
1 and pyramidal neurons for Cliques  2, as per Tables 1, 2). The values of the CDFs at the cosine similarities ψ(
2, as per Tables 1, 2). The values of the CDFs at the cosine similarities ψ( , t), for clique labeled
, t), for clique labeled  and cell type labeled t, are plotted as colored circles. The plots show that granule cells and Purkinje cells both sit extremely comfortably at the top of the distribution of cosine similarities to the expression of both cliques. (A)
and cell type labeled t, are plotted as colored circles. The plots show that granule cells and Purkinje cells both sit extremely comfortably at the top of the distribution of cosine similarities to the expression of both cliques. (A)  =
=  1, (B)
1, (B)  =
=  2.
2.
We therefore need to vary the contrast in the presentation of the expression patterns, in order to decide in which sense, if any, the density profiles of granule cells and Purkinje cells are highlighted differently by the cliques  1 and
1 and  2. We computed the cosine similarities between the thresholded expression profiles of each of the two cliques of interest, and the top-three cell types by significance (found in Tables 1, 2), as defined by Equation (12). The values are plotted as a function of the threshold in Figures 4A,C (the expression profiles of the cliques are L2-normalized so that thresholding parameter τ interpolates between the minimum and maximum value of each of them, and stays in the same range). Granule cells present a peak for both cliques (Purkinje cells do only for the clique
2. We computed the cosine similarities between the thresholded expression profiles of each of the two cliques of interest, and the top-three cell types by significance (found in Tables 1, 2), as defined by Equation (12). The values are plotted as a function of the threshold in Figures 4A,C (the expression profiles of the cliques are L2-normalized so that thresholding parameter τ interpolates between the minimum and maximum value of each of them, and stays in the same range). Granule cells present a peak for both cliques (Purkinje cells do only for the clique  1, but at a lower value of the threshold, and the peak is lower, even though Purkinje cells start from a larger similarity to the clique
1, but at a lower value of the threshold, and the peak is lower, even though Purkinje cells start from a larger similarity to the clique  1 than granule cells before any threshold is applied). On the other hand, the thresholding procedure lowers the similarity between both cliques and the third cell type returned by the statistical analysis (oligodendrocytes for clique
1 than granule cells before any threshold is applied). On the other hand, the thresholding procedure lowers the similarity between both cliques and the third cell type returned by the statistical analysis (oligodendrocytes for clique  1 and pyramidal neurons for clique
1 and pyramidal neurons for clique  2. Moreover, Figures 4B,D) shows heat maps of the expression profiles of both cliques, at the values corresponding to the peak of cosine similarity to granule cells. Indeed the coronal sections through the cerebellum exhibit the characteristic layered, hollow profile of the density of granule cells observed in Figure 2C2, which confirms that the granular layer is highlighted with more intensity by the cliques than the Purkinje layer. Maximal-intensity projections of the thresholded expression profiles exhibit residual expression in the cortex for clique
2. Moreover, Figures 4B,D) shows heat maps of the expression profiles of both cliques, at the values corresponding to the peak of cosine similarity to granule cells. Indeed the coronal sections through the cerebellum exhibit the characteristic layered, hollow profile of the density of granule cells observed in Figure 2C2, which confirms that the granular layer is highlighted with more intensity by the cliques than the Purkinje layer. Maximal-intensity projections of the thresholded expression profiles exhibit residual expression in the cortex for clique  2, and to a lesser extent in the hippocampus for clique
2, and to a lesser extent in the hippocampus for clique  1 (but it should be noted that genes are more highly expressed in the hippocampus than in any other region of the brain on average in the coronal ABA).
1 (but it should be noted that genes are more highly expressed in the hippocampus than in any other region of the brain on average in the coronal ABA).
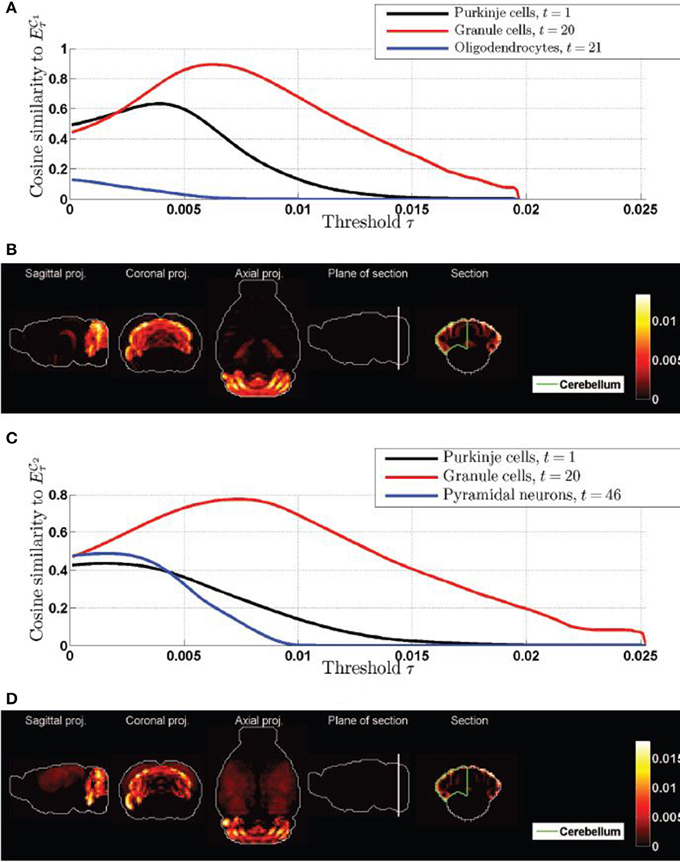
Figure 4. Cosine similarities of thresolded gene expression energies of cliques, as a function of the threshold. (A) Plot of ψτ( 1, t) as a function of τ for the top three cell types in Table 1. (B) Heat map of the expression energy of clique
1, t) as a function of τ for the top three cell types in Table 1. (B) Heat map of the expression energy of clique  1 at the value of the threshold τ for which ψτ(
1 at the value of the threshold τ for which ψτ( 1, 20) is maximum. (C) Plot of ψτ(
1, 20) is maximum. (C) Plot of ψτ( 2, t) as a function of τ for the top three cell types in Table 2. (D) Heat map of the expression energy of clique
2, t) as a function of τ for the top three cell types in Table 2. (D) Heat map of the expression energy of clique  2 at the value of the threshold τ for which ψτ(
2 at the value of the threshold τ for which ψτ( 2, 20) is maximum. Compare the two coronal sections to the one of the density of granule cells in Figure 2C2.
2, 20) is maximum. Compare the two coronal sections to the one of the density of granule cells in Figure 2C2.
We therefore conclude that the gene expression profiles of the two cliques of genes in this study highlight the cerebellum with more intensity in the granular layer than in the Purkinje layer, but these two neuroanatomical structures are by far the most exceptionally similar to the expression profiles of the cliques.
3.2. Pairs of Cell Types with Exceptional Cosine Similarities to Expression of Cliques Predominantly Involve One Cortical and One Cerebellar Cell Type
If we do not threshold the expression profiles of the cliques, they have a non-zero value in the cerebral cortex, albeit lower than in the cerebellum (Figures 2A,B). This combination of cortical and cerebellar expression is not achieved by any of the cell types in our data set, even those that are singled out by our statistical analysis of cosine similarity (as can be checked by visual inspection of Figures 2C1–C4). This compels us to explore better fittings of the expression of the two cliques  1 and
1 and  2 using more cell types.
2 using more cell types.
We computed the optimal cosine similarity scores defined in Equation (17) for the T(T − 1)/2 = 2016 possible pairs of cell types from our data set (the results are plotted in matrix form as a heat map on Figure 5). Many of the maxima visibly involve the cell type labeled t = 40 which consists of pyramidal neurons, calosally projecting. This cell type also gave rise to high values of cosine similarity between single cell types and both cliques (Figure 1). However, the values  R(
R( 1, 40) = 0.4% (rank 59 out of 64) and
1, 40) = 0.4% (rank 59 out of 64) and  R(
R( 2, 40) = 42% (rank 25 out of 64) reflect the fact the values of the cosine similarities to ρ40 are biased upwards by the large support of ρ40. Other strinking horizontal and vertical lines in the heat maps of Figure 5 correspond to cell types that were already singled out by the above statistical analysis of cosine similarities to single cell types.
2, 40) = 42% (rank 25 out of 64) reflect the fact the values of the cosine similarities to ρ40 are biased upwards by the large support of ρ40. Other strinking horizontal and vertical lines in the heat maps of Figure 5 correspond to cell types that were already singled out by the above statistical analysis of cosine similarities to single cell types.
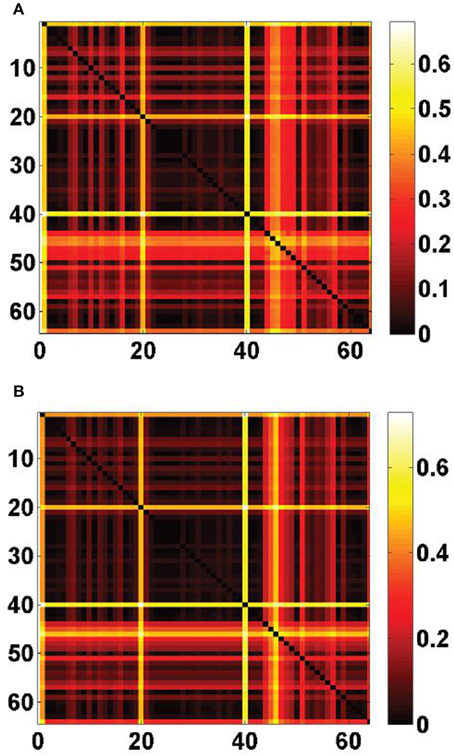
Figure 5. Optimal cosine similarities between cliques of ASD-related genes and pairs of cell types drawn from the fitting panel of T = 64 cell-type-specific transcriptomes, defined in Equation (17). (A) Heat map of the matrix ψ( 1, t1, t2), for 1 ≤ t1, t2 ≤ 64. (B) Heat map of the matrix ψ(
1, t1, t2), for 1 ≤ t1, t2 ≤ 64. (B) Heat map of the matrix ψ( 2, t1, t2), for 1 ≤ t1, t2 ≤ 64. Striking horizontal and vertical lines correspond to the labels t = 1 (Purkinje cells), t = 20 (granule cells), that are returned by the analysis of similarity between cliques and single cell types, but also to the label t = 40 (pyramidal neurons, calosally projecting).
2, t1, t2), for 1 ≤ t1, t2 ≤ 64. Striking horizontal and vertical lines correspond to the labels t = 1 (Purkinje cells), t = 20 (granule cells), that are returned by the analysis of similarity between cliques and single cell types, but also to the label t = 40 (pyramidal neurons, calosally projecting).
For some pairs of cell types, the optimized cosine similarity between a clique of genes and a linear combination of the densities of cell types labeled t1 and t2 is not only larger than the similarities with individual density profiles ψ( , t1) and ψ(
, t1) and ψ( , t2), but it is also larger than the maximum of all the cosine similarities to a single cell type, whose values for the two cliques in this study are:
, t2), but it is also larger than the maximum of all the cosine similarities to a single cell type, whose values for the two cliques in this study are:
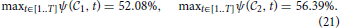
The sets of such pairs of cell types (denoted by  better(
better( 1) and
1) and  better(
better( 2) in Equation 16) consist of 62 and 66 elements, respectively for cliques
2) in Equation 16) consist of 62 and 66 elements, respectively for cliques  1 and
1 and  2 (which represents 3.08% and 3.27% of the 2016 distinct possible pairs of cell types from our data set). We counted the occurrences of each of the cell types in these special pairs and presented the result in histograms (Figure 6). It appears from both histograms that cell type labeled t = 40, plays a special role. This cell type was extracted from the cerebral cortex, and indeed its estimated density profile ρ40 is highly localized in the cortex. Moreover, this cell type is the one that has the highest cosine similarity to an ideal density χcortex that would be uniform in the cerebral cortex and zero elsewhere (see Equation 20 with ω chosen to be the cerebral cortex). A sorted plot of the cosine similarities between estimated density profiles of cell types and χcortex is presented on Figure 7, showing that four classes of cortical pyramidal neurons stand out, the first of which is labeled t = 40.
2 (which represents 3.08% and 3.27% of the 2016 distinct possible pairs of cell types from our data set). We counted the occurrences of each of the cell types in these special pairs and presented the result in histograms (Figure 6). It appears from both histograms that cell type labeled t = 40, plays a special role. This cell type was extracted from the cerebral cortex, and indeed its estimated density profile ρ40 is highly localized in the cortex. Moreover, this cell type is the one that has the highest cosine similarity to an ideal density χcortex that would be uniform in the cerebral cortex and zero elsewhere (see Equation 20 with ω chosen to be the cerebral cortex). A sorted plot of the cosine similarities between estimated density profiles of cell types and χcortex is presented on Figure 7, showing that four classes of cortical pyramidal neurons stand out, the first of which is labeled t = 40.
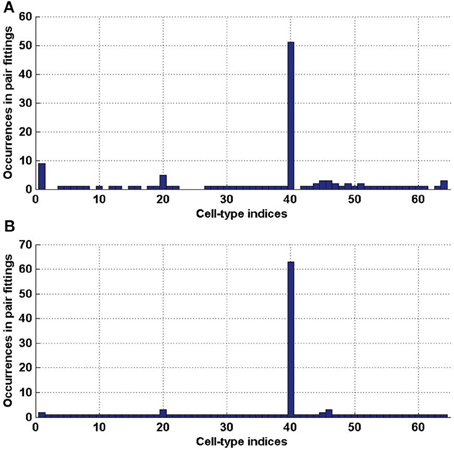
Figure 6. Histograms of the indices of cell types (in [1..64]), that are involved in a pair of cell types with a better cosine similarity to the expression profile of a clique than any single cell type. (A) For clique  1 (total number of elements 124). (B) For clique
1 (total number of elements 124). (B) For clique  2 (total number of elements 132).
2 (total number of elements 132).
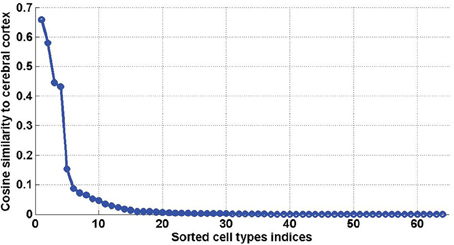
Figure 7. Sorted values of the cosine similarities between density profiles of cell types and the cerebral cortex (defined in Equation 20, for ω = cerebral cortex). The first four values, which stand out, correspond to t = 40, t = 46, t = 47, t = 45, which are all pyramidal neurons extracted from the cerebral cortex.
Again, for the best fits to pairs of densities of cell types, we have to estimate the probability of obtaining the same results by chance. For each of the cliques, we ran a Monte Carlo simulation of the similarity scores to the 62 and 66 optimal combinations of cell types returned by the above analysis (this simulation is the extension of the quantity PR of Equation (10) to two cell types, see Equation 18). The combinations of pairs of cell types which have higher cosine similarity to one of the two cliques  1 and
1 and  2 with probability larger than 99 % are presented in Table 3. They consist of 13 and 5 pairs of cell types, respectively, and the highest-ranking pairs for both cliques (by value of cosine similarity) contain the pyramidal neurons labeled t = 40, along with granule cells or Purkinje cells (see Figures 8A,B). For a heat map of the two combinations of cell types presented at the top of Tables 3A,B, see Figures 8A,B, where a distinct cortico-cerebellar pattern appears.
2 with probability larger than 99 % are presented in Table 3. They consist of 13 and 5 pairs of cell types, respectively, and the highest-ranking pairs for both cliques (by value of cosine similarity) contain the pyramidal neurons labeled t = 40, along with granule cells or Purkinje cells (see Figures 8A,B). For a heat map of the two combinations of cell types presented at the top of Tables 3A,B, see Figures 8A,B, where a distinct cortico-cerebellar pattern appears.
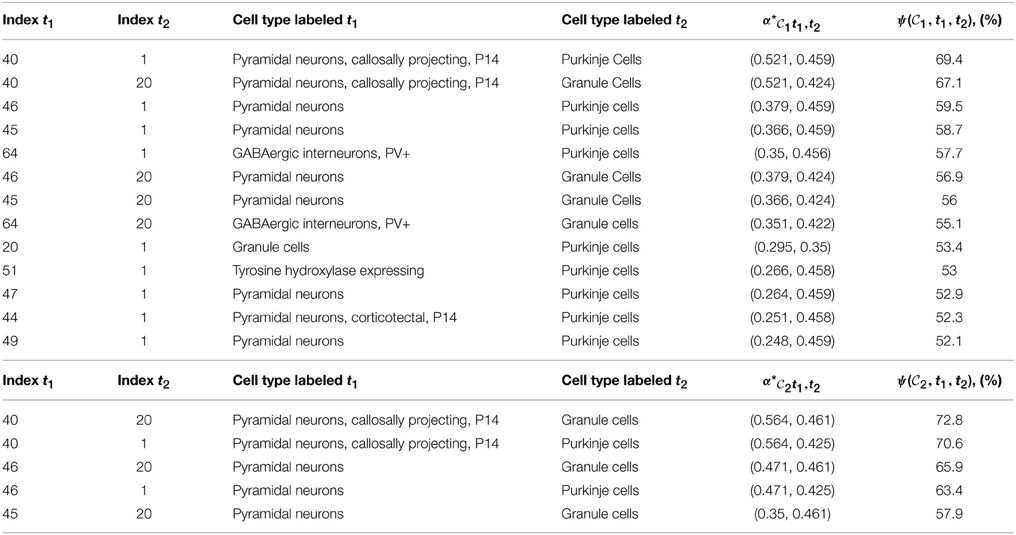
Table 3. Tables of pairs of cell types with higher cosine similarity to a clique of ASD-related genes than any single cell type, for which the value of  R(
R( , t1,t2) is larger than 99 percent. (A) For clique
, t1,t2) is larger than 99 percent. (A) For clique  1,
1,  =
=  1. (B) For clique
1. (B) For clique  2,
2,  =
=  2.
2.
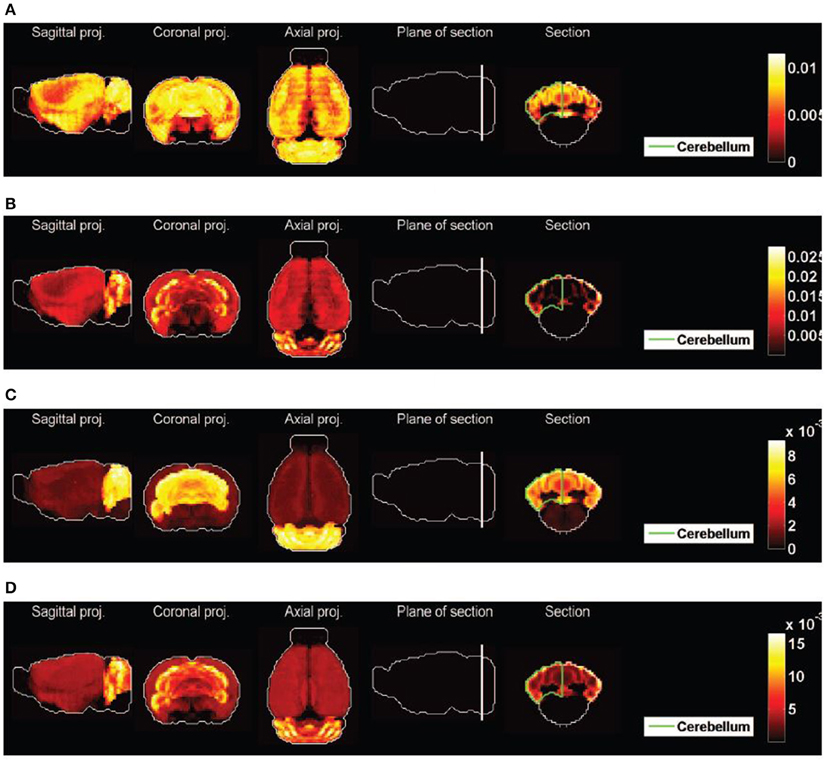
Figure 8. Heat maps of best-fitted sums of densities of cell types. (A) Purkinje cells (t = 1) and pyramidal neurons (t = 40), best fit to clique  1, second best fit to clique
1, second best fit to clique  2. (B) Granule cells (t = 20) and pyramidal neurons (t = 40), best fit to clique
2. (B) Granule cells (t = 20) and pyramidal neurons (t = 40), best fit to clique  2, second best fit to clique
2, second best fit to clique  1. (C) The average of the 13 pairs of cell types illustrated in Table 2A for clique
1. (C) The average of the 13 pairs of cell types illustrated in Table 2A for clique  1. (D) The average of the 5 pairs of cell types illustrated in Table 2B for clique
1. (D) The average of the 5 pairs of cell types illustrated in Table 2B for clique  2.
2.
This reflects the fact that the combination of the cerebral cortex and cerebellar cortex (with relative weights specified by the optimal coefficients given in the fifth columns of Table 3) is highly similar to the expression profiles of the two cliques. Moreover, 9 out of the 13 pairs in Table 3A and all the pairs in Table 3B contain a pyramidal neuron (and all pairs contain either Purkinje cells or granule cells). We therefore conclude that allowing one more cell-type-specific degree of freedom to fit the expression profiles of both cliques gives rise to a predominant contribution from pyramidal neurons, all of which are cortical except the hippocampal cell type labeled t = 49, and all of which had a much lower statistical significance as single cell types. It can be noted that the four pyramidal neurons with largest similarity to the cerebral cortex (which stand out on Figure 7) are all represented in Table 3.
The averages of all the pairs of cell types returned by our analysis are plotted as heat maps on Figures 8C,D, which can be visually compared to the heat maps of Figures 2A,B. The effect is much better than for any of the heat maps Figures 2C1–C4, even though the heterogeneity of the expression of clique  2 across the cerebral cortex is not reproduced.
2 across the cerebral cortex is not reproduced.
4. Discussion
Our computational analysis shows that among the cell types collated in Okaty et al. (2011) and analyzed together with the ABA in Grange et al. (2014), the similarity of the expression of both cliques  1 and
1 and  2 to granule cells and Purkinje cells is larger than the similarity of more than 97% of the cliques of the same size. These two cell types are the only cell types in our data set to have this property. The statistical significance of the similarity to the spatial density of granule cells is larger than the one of Purkinje cells for the clique
2 to granule cells and Purkinje cells is larger than the similarity of more than 97% of the cliques of the same size. These two cell types are the only cell types in our data set to have this property. The statistical significance of the similarity to the spatial density of granule cells is larger than the one of Purkinje cells for the clique  2, but Purkinje cells still stand out together with granule cells (which makes sense with the involvement of Purkinje cells in autism discovered in post-mortem studies Skefos et al., 2014). This completes the observation made in Menashe et al. (2013) based on visual inspection of the Purkinje and granular layers of the cerebellar cortex. Granule cells (and not Purkinje cells) may be present in some superficial voxels in which both cliques are highly expressed (see the coronal sections in Figure 2), but as brain-wide neuroanatomical patterns, granule cells and Purkinje cells are both exceptionally similar to the expression profiles of the two cliques in this study. The spatial resolution of the voxelized ISH data of the mouse ABA (200 microns) complicates the separation between granule cells and Purkinje cells, which we attempted here by our thresholding procedure, due to the extreme difference in size between the two cell types. Granule cells and Purkinje cells may be present in the same voxel, and registration errors are therefore much larger in scale of a granule cell than in scale of a Purkinje cell. An interesting direction for a deeper analysis can be found in Ko et al. (2013) and Li et al. (2014), where image series rather than voxelized data are used.
2, but Purkinje cells still stand out together with granule cells (which makes sense with the involvement of Purkinje cells in autism discovered in post-mortem studies Skefos et al., 2014). This completes the observation made in Menashe et al. (2013) based on visual inspection of the Purkinje and granular layers of the cerebellar cortex. Granule cells (and not Purkinje cells) may be present in some superficial voxels in which both cliques are highly expressed (see the coronal sections in Figure 2), but as brain-wide neuroanatomical patterns, granule cells and Purkinje cells are both exceptionally similar to the expression profiles of the two cliques in this study. The spatial resolution of the voxelized ISH data of the mouse ABA (200 microns) complicates the separation between granule cells and Purkinje cells, which we attempted here by our thresholding procedure, due to the extreme difference in size between the two cell types. Granule cells and Purkinje cells may be present in the same voxel, and registration errors are therefore much larger in scale of a granule cell than in scale of a Purkinje cell. An interesting direction for a deeper analysis can be found in Ko et al. (2013) and Li et al. (2014), where image series rather than voxelized data are used.
The values of the cosine similarities are not necessarily ranked in the same order as the statistical significances (indeed their values are not decreasing in the fourth columns of Tables 1, 2, which are organized by decreasing order of significance). This is related to the fact that the cosine similarity is biased in favor of cell types present in a larger number of voxels (for example pyramidal neurons, labeled t = 46, have a larger support, at 8980 voxels, than granule cells, at 3351 voxels). So, if a clique of genes has a large support (which is the case of both cliques in this study, which have non-zero expression in more than 98% of voxels), it can have a larger cosine similarity to pyramidal neurons than to granule cells, but its similarity to granule cells may be more statistically significant. This is the case for clique  2, and the fact is illustrated in more detail on Figure 3B, where it is clear that the similarity between pyramidal neurons (labeled t = 46) and clique
2, and the fact is illustrated in more detail on Figure 3B, where it is clear that the similarity between pyramidal neurons (labeled t = 46) and clique  2, albeit larger than the value for granule cells and Purkinje cells, sits lower in the distribution of cosine similarities. Our probabilistic approach is therefore a necessary complement to the computation of similarities.
2, albeit larger than the value for granule cells and Purkinje cells, sits lower in the distribution of cosine similarities. Our probabilistic approach is therefore a necessary complement to the computation of similarities.
However, two more transcriptomes of Purkinje cells are present in our data set (labeled t = 25 and t = 52), and they do not stand out in our analysis (their cosine similarity to cliques  1 and
1 and  2 are 0 for t = 25 and 9.2 and 9.5% for t = 52, respectively), even though these three transcriptome profiles are close to each other. The difference in cosine similarities is due to the fact that the density profiles ρ25 and ρ52 are much sparser than ρ1, especially in the cerebellum. When fitting the cell-type-based model (Equation 5), similar profiles compete against each other, and the sample t = 1 wins in most cerebellar voxels. In Grange et al. (2014), we checked that keeping only one sample of Purkinje cells (t = 52, chosen for further numerical exploration as it was independently estimated in Okaty et al. (2009) to be less contaminated by other cell types) and refitting the model yields to similar results as the complete data set, except for the density ρ52, which inherits most of the density from ρ1. We reran the analysis that returned Tables 1, 2 using these refitted densities, and found that the remaining Purkinje cells occupies the rank of t = 1 (with scores
2 are 0 for t = 25 and 9.2 and 9.5% for t = 52, respectively), even though these three transcriptome profiles are close to each other. The difference in cosine similarities is due to the fact that the density profiles ρ25 and ρ52 are much sparser than ρ1, especially in the cerebellum. When fitting the cell-type-based model (Equation 5), similar profiles compete against each other, and the sample t = 1 wins in most cerebellar voxels. In Grange et al. (2014), we checked that keeping only one sample of Purkinje cells (t = 52, chosen for further numerical exploration as it was independently estimated in Okaty et al. (2009) to be less contaminated by other cell types) and refitting the model yields to similar results as the complete data set, except for the density ρ52, which inherits most of the density from ρ1. We reran the analysis that returned Tables 1, 2 using these refitted densities, and found that the remaining Purkinje cells occupies the rank of t = 1 (with scores 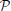 R(
R( 1, 52) = 98.8% and
1, 52) = 98.8% and 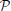 R(
R( 2, 52) = 96.5%, respectively), while the other ranks are conserved. Restricting the number of cell types in the panel therefore yields results compatible with the hierarchical nature of cell types. On the other hand, it is crucial to keep a number of genes that is large enough to sample a large subspace of the span of the columns of the matrix E in voxel space In Grange et al. (2014), we simulated a thalamic cell type by choosing the 200 genes that are are the most expressed in the thalamus, and constructing a fictitious transcriptome in which the expression of these genes is higher than average. This was shown to be enough to transfer the thalamic density from t = 52 to this cell simulated cell type. Hence the signal in a small fraction of a data set can control the competition between two cell types. However, the presence of all the other genes in the data set is necessary to ensure that the densities of other cell types are stable under the inclusion of the simulated cell type, and the (possibly small) sets of genes that control the competition between cells vary from cell to cell.
2, 52) = 96.5%, respectively), while the other ranks are conserved. Restricting the number of cell types in the panel therefore yields results compatible with the hierarchical nature of cell types. On the other hand, it is crucial to keep a number of genes that is large enough to sample a large subspace of the span of the columns of the matrix E in voxel space In Grange et al. (2014), we simulated a thalamic cell type by choosing the 200 genes that are are the most expressed in the thalamus, and constructing a fictitious transcriptome in which the expression of these genes is higher than average. This was shown to be enough to transfer the thalamic density from t = 52 to this cell simulated cell type. Hence the signal in a small fraction of a data set can control the competition between two cell types. However, the presence of all the other genes in the data set is necessary to ensure that the densities of other cell types are stable under the inclusion of the simulated cell type, and the (possibly small) sets of genes that control the competition between cells vary from cell to cell.
The robustness of the neuroanatomical density patterns of cell types was shown in Grange et al. (2014) to vary between cell types, but the most unstable spatial density profiles tend to be the sparsest (the T cell types were ranked by deceasing stability against subsampling of genes). The cell types that stand out in our results are not among the sparsest ones, as they exhibit striking neuroanatomical patterns. To investigate the stability of our results against the exclusion of cell types, we refitted the model of Equation (5) to a panel of cell types including only the 23 cell types ranked highest for stability (this rank was chosen as it is the lowest rank among those of the 4 distinct cell types presented in Figure 3. The estimated CDFs are stable after refitting (and the values corresponding to statistical significance are within one percent of the values estimated from the full panel).
Moreover, some of the densities of cell types estimated computationally in Grange et al. (2014) can be combined pairwise in order to match the expression of ASD-related cliques of genes better than any single cell types. The optimal combinations we worked out reconcile the involvement of the cerebellum in ASD and the role of the cerebral cortex which had been thought to be predominant. In fact, the use of pairs of cell types to fit the expression of cliques singles out pairs of cell types consisting of one pyramidal neuron and either granule or Purkinje cells. It would be interesting if this association between cortical and cerebellar neurons could be related to connections between the cerebellum and the cerebral cortex (Oh et al., 2014). The improvement of the similarity scores brought by considering pairs of cell types, within this still relatively modest cell-type-specific data set consisting of less than 100 cell types, while a complete taxonomy of neuronal cell types could well be more detailed by orders of magnitude, indicates that the cell-type-specificity of ASD needs multiple genes and multiple cell types (beyond pairs) to be worked out.
One may wonder if our method is not circuitous, compared to the one of Menashe et al. (2013) (in which cosine similarities are computed to estimate the similarity between the spatial expression profile of a clique and a region of the brain defined by classical neuroanatomy and not by gene-expression data). In the present study, given that the expression of a clique of genes is included in the data set that has been used to fit the model of Equation (5). Taking the entire set of genes in the coronal ABA into account allows one to stabilize the results in the sense that we do not need to select genes that are over-expressed in one cell type relative to the others (which choice would have to be refined whenever the set of cell-type-specific transcriptome is modified), and the optimization procedure is equivalent to a competition between cell-type-specific transcriptome profiles. As a numerical experiment, we refitted the model of Equation (5) twice for each clique, using only the genes in the clique the first time, and using its complement the second time. Given that the two cliques of genes of genes contain only 1.1 and 0.2% of the coronal atlas, with expression profiles exceptionally between each other and to the cerebellar cortex, the results of the first refitting cannot detect densities of non-cerebellar cell types, while the results of the second refitting is very close to the original results. As the cliques are small enough not to contain all the genes that are over-expressed in cerebellar cell types, the study of cosine similarities is not too circuitous.
Our analysis shows that the gene-based approach of the ABA and the cell-based approach of the transcriptional classification of cell types in the brain can be combined in order to quantify the similarity between expression patterns of condition-related genes and the spatial density of cell types, even though the region-specificity of transcriptomes of cell types is only accessible computationally. Our results are limited by the paucity of the cell-type-specific data, since the number of transcriptionally distinct neuronal cell types is presumably much larger than 64. However, the classification of cell types is a hierarchical problem, and it is plausible that granule cells and Purkinje cells branch early from each other (and from cortical pyramidal neurons and oligodendrocytes) in the classification, which makes the available data set reasonably effective as a first draft in the context of this study. The computational methods we devised can be easily reapplied when more cell-type-specific microarray data become available. Moreover, alternative measures of similarity can easily be substituted to the cosine similarity, without modifying the analysis of statistical significance and contrast, or the number of random draws dictated by Hoeffding's inequality.
Within data sets of the mouse model organism, the Allen Atlas of the developing mouse brain (http://developingmouse.brain-map.org/) could be used to detect stage-specific changes in expression profiles, as the development of ASD is known to take place in early developmental stages of the brain. However, the current data sets do not allow to repeat the fitting of the model, as the developmental atlas is not co-registered and voxelized, moreover most of the cell type-specific transcriptomes come from adult mouse brains. One can note from Grange et al. (2014) that corticospinal neurons from non-adult mice fit poorly, which could be traced to late maturation of these neurons.
The translation of results from the mouse model to humans is extremely challenging, even though the ABA of the human brain has been released (Hawrylycz et al., 2012), because the human atlas cannot be voxelized, due to the size and paucity of the specimens.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research is supported by Xi'an Jiaotong-Liverpool University (Research Development Fund) and by the Allen Institute for Brain Science.
Footnotes
1. ^which at the time were available as preprint: Grange et al. (2013). Cell-type-specific microarray data and the Allen atlas: quantitative analysis of brain-wide patterns of correlation and density. arXiv preprint arXiv:1303.0013. The correspondence between cell types and their integer labels is the same as in Tables 64, 65 of this preprint. See also the extended discussion of Grange et al. (2014). Cell-type-specific transcriptomes and the Allen Atlas (II): discussion of the linear model of brain-wide densities of cell types. arXiv preprint arXiv:1402.2820.
2. ^These data were downloaded from the ABA website http://mouse.brain-map.org, and are included in the MATLAB toolbox with which the results of the present study were obtained. See the current version of the manual and download link in Grange et al. (2012).
3. ^or any other measure of similarity.
References
Abbas, A. R., Wolslegel, K., Seshasayee, D., Modrusan, Z., and Clark, H. F. (2009). Deconvolution of blood microarray data identifies cellular activation patterns in systemic lupus erythematosus. PLoS ONE 4:e6098. doi: 10.1371/journal.pone.0006098
Amaral, D. G., Schumann, C. M., and Nordahl, C. W. (2008). Neuroanatomy of autism. Trends Neurosci. 31, 137–145. doi: 10.1016/j.tins.2007.12.005
Anney, R., Klei, L., Pinto, D., Almeida, J., Bacchelli, E., Baird, G., et al. (2012). Individual common variants exert weak effects on the risk for autism spectrum disorders. Hum. Mol. Genet. 21, 4781–4792. doi: 10.1093/hmg/dds301
Arlotta, P., Molyneaux, B. J., Chen, J., Inoue, J., Kominami, R., and Macklis, J. D. (2005). Neuronal subtype-specific genes that control corticospinal motor neuron development in vivo. Neuron 45, 207–221. doi: 10.1016/j.neuron.2004.12.036
Basu, S. N., Kollu, R., and Banerjee-Basu, S. (2009). Autdb: a gene reference resource for autism research. Nucl. Acids Res. 37(Suppl. 1), D832–D836. doi: 10.1093/nar/gkn835
Bohland, J. W., Bokil, H., Pathak, S. D., Lee, C.-K., Ng, L., Lau, C., et al. (2010). Clustering of spatial gene expression patterns in the mouse brain and comparison with classical neuroanatomy. Methods 50, 105–112. doi: 10.1016/j.ymeth.2009.09.001
Cahoy, J. D., Emery, B., Kaushal, A., Foo, L. C., Zamanian, J. L., Christopherson, K. S., et al. (2008). A transcriptome database for astrocytes, neurons, and oligodendrocytes: a new resource for understanding brain development and function. J. Neurosci. 28, 264–278. doi: 10.1523/JNEUROSCI.4178-07.2008
Chung, C. Y., Seo, H., Sonntag, K. C., Brooks, A., Lin, L., and Isacson, O. (2005). Cell type-specific gene expression of midbrain dopaminergic neurons reveals molecules involved in their vulnerability and protection. Hum. Mol. Genet. 14, 1709–1725. doi: 10.1093/hmg/ddi178
Cook, E. H. Jr., and Scherer, S. W. (2008). Copy-number variations associated with neuropsychiatric conditions. Nature 455, 919–923. doi: 10.1038/nature07458
Dong, H. W. (2008). The Allen Reference Atlas: A Digital Color Brain Atlas of the C57Bl/6J Male Mouse. Hoboken, NJ: John Wiley & Sons Inc.
Doyle, J. P., Dougherty, J. D., Heiman, M., Schmidt, E. F., Stevens, T. R., Ma, G., et al. (2008). Application of a translational profiling approach for the comparative analysis of cns cell types. Cell 135, 749–762. doi: 10.1016/j.cell.2008.10.029
Gilman, S. R., Iossifov, I., Levy, D., Ronemus, M., Wigler, M., and Vitkup, D. (2011). Rare de novo variants associated with autism implicate a large functional network of genes involved in formation and function of synapses. Neuron 70, 898–907. doi: 10.1016/j.neuron.2011.05.021
Grange, P., Bohland, J. W., Hawrylycz, M., and Mitra, P. P. (2012). Brain Gene Expression Analysis: a MATLAB Toolbox for the Analysis of Brain-Wide Gene-expression Data. Available online at: arXiv preprint arXiv:1211.6177.
Grange, P., Bohland, J. W., Okaty, B. W., Sugino, K., Bokil, H., Nelson, S. B., et al. (2014). Cell-type–based model explaining coexpression patterns of genes in the brain. Proc. Natl. Acad. Sci. U.S.A. 111, 5397–5402. doi: 10.1073/pnas.1312098111
Grange, P., Hawrylycz, M., and Mitra, P. P. (2013). Computational neuroanatomy and co-expression of genes in the adult mouse brain, analysis tools for the allen brain atlas. Quant. Biol. 1, 91–100. doi: 10.1007/s40484-013-0011-5
Grange, P., and Mitra, P. P. (2012). “Computational neuroanatomy and gene expression: optimal sets of marker genes for brain regions,” in 2012 46th Annual Conference on Information Sciences and Systems (CISS) (Princeton, NJ: IEEE), 1–6.
Hastie, T., Tibshirani, R., and Friedman, J. (2009). The Elements of Statistical Learning, Vol. 2. New York, NY: Springer. doi: 10.1007/978-0-387-84858-7
Hawrylycz, M., Baldock, R. A., Burger, A., Hashikawa, T., Johnson, G. A., Martone, M., et al. (2011a). Digital atlasing and standardization in the mouse brain. PLoS Comput. Biol. 7:e1001065. doi: 10.1371/journal.pcbi.1001065
Hawrylycz, M., Ng, L., Page, D., Morris, J., Lau, C., Faber, S., et al. (2011b). Multi-scale correlation structure of gene expression in the brain. Neural Netw. 24, 933–942. doi: 10.1016/j.neunet.2011.06.012
Hawrylycz, M. J., Lein, E. S., Guillozet-Bongaarts, A. L., Shen, E. H., Ng, L., Miller, J. A., et al. (2012). An anatomically comprehensive atlas of the adult human brain transcriptome. Nature 489, 391–399. doi: 10.1038/nature11405
Heiman, M., Schaefer, A., Gong, S., Peterson, J. D., Day, M., Ramsey, K. E., et al. (2008). A translational profiling approach for the molecular characterization of cns cell types. Cell 135, 738–748. doi: 10.1016/j.cell.2008.10.028
Iossifov, I., Ronemus, M., Levy, D., Wang, Z., Hakker, I., Rosenbaum, J., et al. (2012). De novo gene disruptions in children on the autistic spectrum. Neuron 74, 285–299. doi: 10.1016/j.neuron.2012.04.009
Jacquemont, M.-L., Sanlaville, D., Redon, R., Raoul, O., Cormier-Daire, V., Lyonnet, S., et al. (2006). Array-based comparative genomic hybridisation identifies high frequency of cryptic chromosomal rearrangements in patients with syndromic autism spectrum disorders. J. Med. Genet. 43, 843–849. doi: 10.1136/jmg.2006.043166
Ko, Y., Ament, S. A., Eddy, J. A., Caballero, J., Earls, J. C., Hood, L., et al. (2013). Cell type-specific genes show striking and distinct patterns of spatial expression in the mouse brain. Proc. Natl. Acad. Sci. U.S.A. 110, 3095–3100. doi: 10.1073/pnas.1222897110
Kumar, A., Wadhawan, R., Swanwick, C. C., Kollu, R., Basu, S. N., and Banerjee-Basu, S. (2011). Animal model integration to autdb, a genetic database for autism. BMC Med. Genomics 4:15. doi: 10.1186/1755-8794-4-15
Lee, C.-K., Sunkin, S. M., Kuan, C., Thompson, C. L., Pathak, S., Ng, L., et al. (2008). Quantitative methods for genome-scale analysis of in situ hybridization and correlation with microarray data. Genome Biol. 9:R23. doi: 10.1186/gb-2008-9-1-r23
Lein, E. S., Hawrylycz, M. J., Ao, N., Ayres, M., Bensinger, A., Bernard, A., et al. (2006). Genome-wide atlas of gene expression in the adult mouse brain. Nature 445, 168–176. doi: 10.1038/nature05453
Levy, D., Ronemus, M., Yamrom, B., Lee, Y.-H., Leotta, A., Kendall, et al. (2011). Rare de novo and transmitted copy-number variation in autistic spectrum disorders. Neuron 70, 886–897. doi: 10.1016/j.neuron.2011.05.015
Li, R., Zhang, W., and Ji, S. (2014). Automated identification of cell-type-specific genes in the mouse brain by image computing of expression patterns. BMC Bioinformatics 15:209. doi: 10.1186/1471-2105-15-209
Lotta, L., Conrad, K., Cory-Slechta, D., and Schor, N. (2014). Cerebellar purkinje cell p75 neurotrophin receptor and autistic behavior. Transl. Psychiatry 4, e416. doi: 10.1038/tp.2014.55
Menashe, I., Grange, P., Larsen, E. C., Banerjee-Basu, S., and Mitra, P. P. (2013). Co-expression profiling of autism genes in the mouse brain. PLoS Comput. Biol. 9:e1003128. doi: 10.1371/journal.pcbi.1003128
Myers, R. A., Casals, F., Gauthier, J., Hamdan, F. F., Keebler, J., Boyko, A. R., et al. (2011). A population genetic approach to mapping neurological disorder genes using deep resequencing. PLoS Genet. 7:e1001318. doi: 10.1371/journal.pgen.1001318
Neale, B. M., Kou, Y., Liu, L., MaAyan, A., Samocha, K. E., Sabo, A., et al. (2012). Patterns and rates of exonic de novo mutations in autism spectrum disorders. Nature 485, 242–245. doi: 10.1038/nature11011
Newschaffer, C. J., Croen, L. A., Daniels, J., Giarelli, E., Grether, J. K., Levy, S. E., et al. (2007). The epidemiology of autism spectrum disorders*. Annu. Rev. Public Health 28, 235–258. doi: 10.1146/annurev.publhealth.28.021406.144007
Ng, L., Bernard, A., Lau, C., Overly, C. C., Dong, H.-W., Kuan, C., et al. (2009). An anatomic gene expression atlas of the adult mouse brain. Nat. Neurosci. 12, 356–362. doi: 10.1038/nn.2281
Ng, L., Hawrylycz, M., and Haynor, D. (2005). “Automated high-throughput registration for localizing 3d mouse brain gene expression using itk,” in IJ–2005 MICCAI Open-Source Workshop (Chapel Hill, NC).
Ng, L., Lau, C., Young, R., Pathak, S., Kuan, L., Sodt, A., et al. (2007a). Neuroblast: a 3d spatial homology search tool for gene expression. BMC Neurosci. 8(Suppl. 2):P11. doi: 10.1186/1471-2202-8-S2-P11
Ng, L., Pathak, S. D., Kuan, C., Lau, C., Dong, H., Sodt, A., et al. (2007b). Neuroinformatics for genome-wide 3-d gene expression mapping in the mouse brain. IEEE/ACM Trans. Comput. Biol. Bioinformat. 4, 382–393. doi: 10.1109/tcbb.2007.1035
Oh, S. W., Harris, J. A., Ng, L., Winslow, B., Cain, N., Mihalas, S., et al. (2014). A mesoscale connectome of the mouse brain. Nature 508, 207–214. doi: 10.1038/nature13186
Okaty, B. W., Miller, M. N., Sugino, K., Hempel, C. M., and Nelson, S. B. (2009). Transcriptional and electrophysiological maturation of neocortical fast-spiking gabaergic interneurons. J. Neurosci. 29, 7040–7052. doi: 10.1523/JNEUROSCI.0105-09.2009
Okaty, B. W., Sugino, K., and Nelson, S. B. (2011). A quantitative comparison of cell-type-specific microarray gene expression profiling methods in the mouse brain. PLoS ONE 6:e16493. doi: 10.1371/journal.pone.0016493
O'Roak, B. J., Vives, L., Girirajan, S., Karakoc, E., Krumm, N., Coe, B. P., et al. (2012). Sporadic autism exomes reveal a highly interconnected protein network of de novo mutations. Nature 485, 246–250. doi: 10.1038/nature10989
Rossner, M. J., Hirrlinger, J., Wichert, S. P., Boehm, C., Newrzella, D., Hiemisch, H., et al. (2006). Global transcriptome analysis of genetically identified neurons in the adult cortex. J. Neurosci. 26, 9956–9966. doi: 10.1523/JNEUROSCI.0468-06.2006
Sanders, S. J., Murtha, M. T., Gupta, A. R., Murdoch, J. D., Raubeson, M. J., Willsey, A. J., et al. (2012). De novo mutations revealed by whole-exome sequencing are strongly associated with autism. Nature 485, 237–241. doi: 10.1038/nature10945
Skefos, J., Cummings, C., Enzer, K., Holiday, J., Weed, K., Levy, E., et al. (2014). Regional alterations in purkinje cell density in patients with autism. PLoS ONE 9:e81255. doi: 10.1371/journal.pone.0081255
Sugino, K., Hempel, C. M., Miller, M. N., Hattox, A. M., Shapiro, P., Wu, C., et al. (2005). Molecular taxonomy of major neuronal classes in the adult mouse forebrain. Nat. Neurosci. 9, 99–107. doi: 10.1038/nn1618
Sunkin, S. M., and Hohmann, J. G. (2007). Insights from spatially mapped gene expression in the mouse brain. Hum. Mol. Genet. 16, R209–R219. doi: 10.1093/hmg/ddm183
Szatmari, P., Paterson, A. D., Zwaigenbaum, L., Roberts, W., Brian, J., Liu, X.-Q., et al. (2007). Mapping autism risk loci using genetic linkage and chromosomal rearrangements. Nat. Genet. 39, 319–328. doi: 10.1038/ng1985
Tan, P. P. C., French, L., and Pavlidis, P. (2013). Neuron-enriched gene expression patterns are regionally anti-correlated with oligodendrocyte-enriched patterns in the adult mouse and human brain. Front. Neurosci. 7:5. doi: 10.3389/fnins.2013.00005
Vargas, D. L., Nascimbene, C., Krishnan, C., Zimmerman, A. W., and Pardo, C. A. (2005). Neuroglial activation and neuroinflammation in the brain of patients with autism. Ann. Neurol. 57, 67–81. doi: 10.1002/ana.20315
Voineagu, I., Wang, X., Johnston, P., Lowe, J. K., Tian, Y., Horvath, S., et al. (2011). Transcriptomic analysis of autistic brain reveals convergent molecular pathology. Nature 474, 380–384. doi: 10.1038/nature10110
Keywords: computational neuroanatomy, gene expression, cerebellum, cell types, autism spectrum disorder
Citation: Grange P, Menashe I and Hawrylycz M (2015) Cell-type-specific neuroanatomy of cliques of autism-related genes in the mouse brain. Front. Comput. Neurosci. 9:55. doi: 10.3389/fncom.2015.00055
Received: 14 November 2014; Accepted: 25 April 2015;
Published: 29 May 2015.
Edited by:
David Hansel, University of Paris, FranceReviewed by:
Gal Chechik, Bar-Ilan University, IsraelAaditya Viswanath Rangan, New York University, USA
Copyright © 2015 Grange, Menashe and Hawrylycz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pascal Grange, Department of Mathematical Sciences, Xi'an Jiaotong-Liverpool University, 111 Ren'Ai Road, Science Building D, Dushu Lake Higher Education Town, Suzhou 215123, China,cGFzY2FsLmdyYW5nZUBwb2x5dGVjaG5pcXVlLm9yZw==
 Pascal Grange
Pascal Grange Idan Menashe2
Idan Menashe2 Michael Hawrylycz
Michael Hawrylycz