- 1Department of Industrial Design, Eindhoven University of Technology, Eindhoven, Netherlands
- 2Department of Naval, Electric, Electronic, and Telecommunications Engineering, University of Genova, Genoa, Italy
Estimation of emotions is an essential aspect in developing intelligent systems intended for crowded environments. However, emotion estimation in crowds remains a challenging problem due to the complexity in which human emotions are manifested and the capability of a system to perceive them in such conditions. This paper proposes a hierarchical Bayesian model to learn in unsupervised manner the behavior of individuals and of the crowd as a single entity, and explore the relation between behavior and emotions to infer emotional states. Information about the motion patterns of individuals are described using a self-organizing map, and a hierarchical Bayesian network builds probabilistic models to identify behaviors and infer the emotional state of individuals and the crowd. This model is trained and tested using data produced from simulated scenarios that resemble real-life environments. The conducted experiments tested the efficiency of our method to learn, detect and associate behaviors with emotional states yielding accuracy levels of 74% for individuals and 81% for the crowd, similar in performance with existing methods for pedestrian behavior detection but with novel concepts regarding the analysis of crowds.
1. Introduction
The tendency of the urban development toward Smart cities (Chourabi et al., 2012) poses a number of research and engineering challenges among which crowd emotion management and prevention of escalations is of vital importance. Furthermore, with the fast growth of population in urban areas around the world, the phenomenon of crowds is set to become commonplace in the near future. The purpose of this work is to present an approach for estimating emotions of single individuals and of a crowd as a whole. In this work, we use the working definition of the crowd as a group of people in proximity, where a common motivation or set of emotions may exist as in the case of sports events and concerts, or merely individuals with different motivations and emotions walking around a busy area. In both instances, the term crowd behavior refers to the behavior adopted by individuals when becoming part of a crowd.
Research on crowd emotions differs significantly from the research on individual emotions in several ways. de Gelder (2006) and Huis in 't Veld and De Gelder (2015) propose that crowd emotions are a delicate balance between the emotions of the individuals and the emotions of the crowd. They found that the interactive or panicked crowds, as opposed to the individually fearful crowds, triggered more anticipatory and preparation action activity, whereas the brain was less sensitive to the dynamics of individuals in a happy or neutral crowd.
Despite the dissimilarities among the most prominent theories addressing crowds from psychologists and sociologist such as Le Bon (2001), Freud (1921), and Allett (1996) among others, there is a consensus on the important role of emotions in the phenomenon of crowd behavior (Challenger et al., 2009). Emotions can be thought as manifestations of our internal state of well-being utilizing psychophysiological and behavioral reactions. In more practical terms, emotions serve as a response to internal or external events experienced by a subject and are manifested over brief periods of time (Plutchik, 2011). Also, supported by the work done by Matsumoto (2004), Ekman et al. (1987) and Keltner and Ekman (2000) we have learn that emotions are discrete and measurable, also that certain emotions appear to be universally recognized despite cultural context or learned associations.
The use of facial and vocal expressions to infer emotions becomes unfeasible in crowded environments. Hence, in this work we propose the use of behaviors described as motion patterns to identify emotional states. This approach is supported by de Gelder et al. (2010), Van den Stock (2007) and Frijda (2010) where they suggest that the whole body expressions of emotion are primary carriers of emotion and action information and may thus play a more important role in a crowd situation than facial expressions. Emotions expressed by dancers and music instrument players have been simulated on robot agents by Barakova and Lourens (2010). The relationship between emotional states and behaviors is further supported by Damasio's Somatic Marker hypothesis (Bechara and Damasio, 2005) in which he explains that decision making involves both cognitive and emotional processes. However, it is important to point out that the relationship between emotions and behaviors is not straightforward as shown in appraisal theory (Moors et al., 2013) proposed by Arnold and developed Lazarus to explain how the same event can provoke different emotions in different individuals and occasions. Moreover, the contemporary appraisal theories define emotions as processes rather than states (Moors et al., 2013), which is in line with the modeling of the movement behavior of the individuals in the crowd.
The work presented in this paper proposes a hierarchical Bayesian model suited for crowded environments. Our model is capable to learn behaviors and associate them with emotions during the training phase, and to estimate emotional states based on partial observations of behaviors during the testing phase; we apply this for both the individuals in the crowd and the crowd as a whole. We consider two types of entities, namely the individual and the crowd. The entity individual describes the behavior and associated emotion of individual people walking across the observed environment. Hence, an instance of entity individual is implemented for each pedestrian detected. The entity crowd describes the whole congregation of people as a single being subjected to the laws of mental unity as explained in Le Bon (2001), hence having its own behavior and associated emotional state. In this work, we limit to describe emotional states in one dimension, ranging from positive to negative according to the principle of valence (Rosenhan and Messick, 1966).
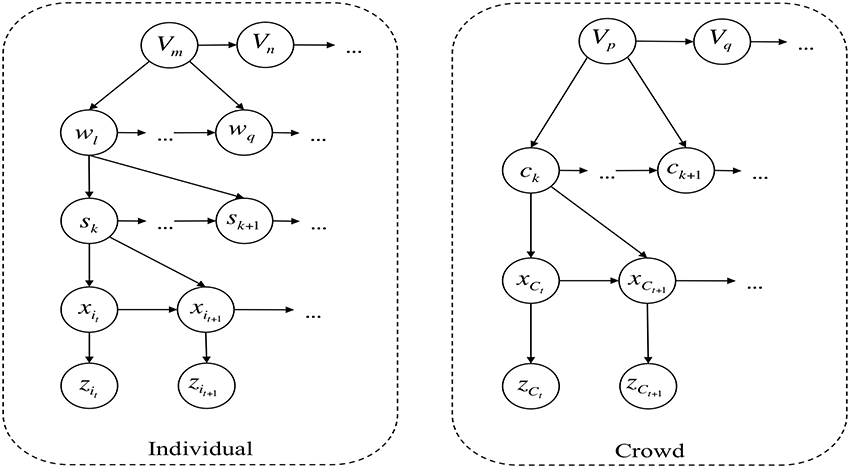
In the proposed approach, the topology of an environment is learned from observed trajectories of individuals employing a self-organizing map SOMI, where each node of SOMI represents a mutually exclusive zone. The path of individuals is expressed as a sequence of transitions among these zones, and a hierarchical Bayesian network builds probabilistic models to describe and group similar behaviors. The learned behaviors are associated with certain emotional states in an empirical fashion. We describe the configuration of the crowd in a given instant with a state vector containing the estimated density level in each zone of the environment. Employing a second self-organizing map SOMC we cluster similar configurations of the crowd into a node of SOMC, enabling us to describe the behavior of a crowd as a transition of nodes of SOMC using a similar hierarchical Bayesian network. The proposed hierarchical Bayesian model is presented in Figure 1. Finally, the emotional states are associated to crowd behaviors in an empirical way. The association between behaviors and emotions is done empirically because the interpretation of a behavior greatly depends on the context of the environment, for example, a fast-paced walk with sudden turns during rush-hour in a train station could have a different emotion associated if the same behavior was displayed in a museum.
The remaining of this work is organized as follow: Section 2 presents a brief survey of previous approaches to estimate emotions. A comprehensive description of our proposed model is presented in Section 3. Experiments and results to validate our model are given in Section 4. Finally, in Section 5 we state our conclusions and intended future work.
2. Related Work
Most of the existing literature in the subject of human emotion recognition has been focused on individuals rather than crowds (Horlings et al., 2008; Izar, 2013). Facial and vocal expressions are useful indicators to infer emotional states, Ekman proposed in Ekman and Friesen (2002) a system based on sets of action units (AU) to recognize emotions based on facial movements. Juslin and Scherer explore the use of pitch and context to infer emotions, as presented in Juslin and Scherer (2008). However, the use of facial and vocal expressions to identify emotions is not feasible in crowded environments. Observation of behaviors seems more appropriate for estimating emotions in crowded scenarios but the relationship between behaviors and emotions is not straightforward as shown in Moors et al. (2013) as it varies depending on the context of the situation and environment. However, promising research has emerged in recent years proposing solutions to this problem. An interesting experiment in Novelli et al. (2013) tested a self-categorization theory to estimate positive and negative emotional responses to crowded environments under different circumstances. Inspired from the highly crowded cities in China, Liu et al. (2013) analyze the contagion of emotions among individuals, particularly under abnormal (panic) scenarios. A more relevant research and the starting point for the work presented here was done by Baig et al. (2014) with a probabilistic model to estimate emotional state of individuals as positive or negative based on the time and trajectory taken to traverse a simple scenario. Our contribution differs from Novelli et al. (2013) and Liu et al. (2013) in that we provide a method for online estimation of emotions of both individuals and the crowd as a whole. Also, unlike the work in Baig et al. (2014) that models only individuals that have the same motivation, we provide a more robust and adaptable framework that treats individuals and the crowd as separate entities to estimate emotions under environments where multiple types of behaviors are observed.
3. Methods
This section describes the proposed hierarchical Bayesian model to describe behaviors and associated emotional states of both entities individual and crowd. In this work, we define a behavior as the way in which an entity transits among different states to achieve its goal (destination). For individual, a state corresponds to a physical region of the environment whereas for the crowd a state corresponds to a given configuration of people's density distribution in the observed environment. Behaviors for both individual and crowd are labeled empirically by a human operator knowledgeable of the environment using the labels of positive, normal or negative to denote the emotional state.
In overall, our approach starts by learning the topology of the observed environment from the trajectory of individuals using a self-organizing map (SOM) (Kohonen, 1990) which divides the physical space into regions. Trajectories of individuals are represented as transition of regions, and all trajectories with similar destination are classified to a same behavior, to finally build a probabilistic model that describe this behavior. Likewise for the crowd, similar sequences of state transitions are grouped into a same behavior which is described by means of a probabilistic model. The bayesian network for both individual and crowd entities is presented in Figure 1.
Once the topology of the environment and behaviors of both the individual and the crowd are learned, we can test the ability of the model to produce estimation of emotions.
3.1. Environment Representation
We first address the problem of obtaining a topological representation of the environment of interest as this is necessary to describe behaviors of individuals. Let us consider an environment monitored by a surveillance camera that captures the motion of individuals as illustrated in Figure 2A. By applying state of the art techniques for multi-target tracking in camera networks (Antonini et al., 2006; Ali and Shah, 2008) it is possible to obtain the trajectory of each individual and collect this data into a training set X
where ∈ ℝ2 is a coordinate estimation of individual ϑi at time t, in a period of observation from 1 to τk for a total of N individuals. Using X we train a self-organizing map SOMI containing a set of nodes S = {s1, …, sm×n} where m is the number of rows and n is the number of columns in an hexagonal topology. As a result of the training phase, SOMI provides a complete topological representation of the environment, where node sj ∈ S represents a mutually exclusive zone in the environment as shown in Figures 3A,B. Representing the environment utilizing a self-organizing map encompasses several advantages including (a) unsupervised learning of the environment's topological configuration, (b) clustering and reduction of data and (c) a simpler way to describe individual's trajectories.
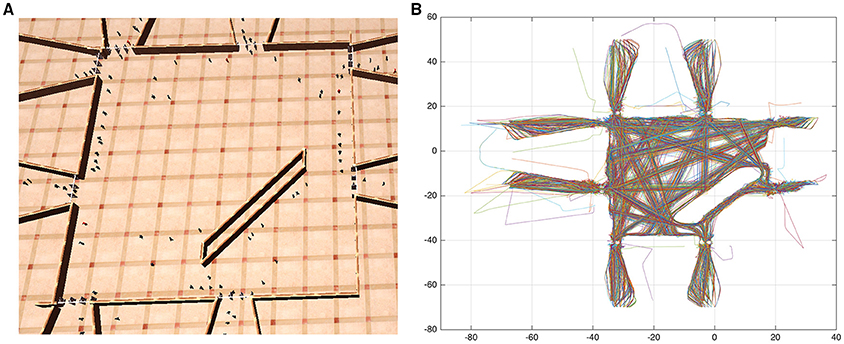
Figure 2. (A) Simulation of a crowded environment. (B) Plot of individual's trajectories, colors are assigned randomly.
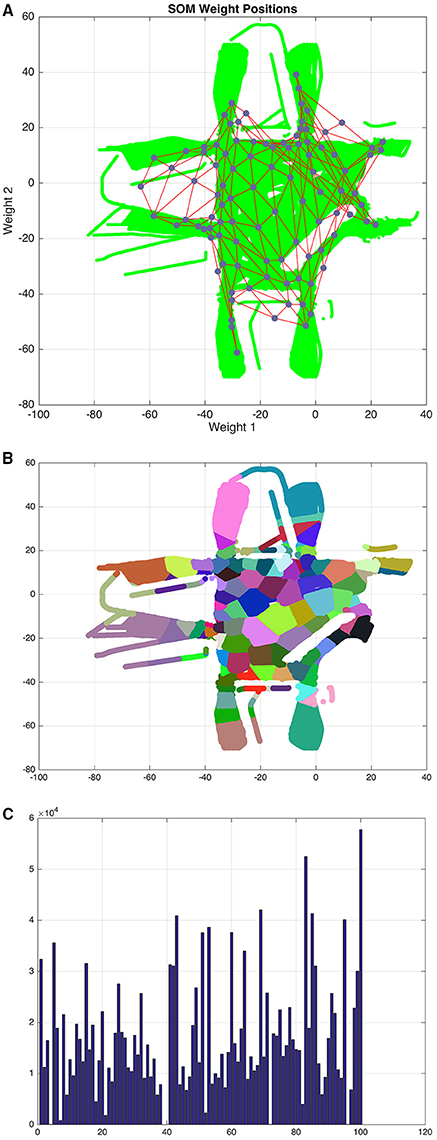
Figure 3. (A) Training data (green) and the self-organizing map SOMI (red edges and blue nodes). (B) Environment partitioned into zones, colors are assigned to zones in a random fashion. (C) Clustering distribution of training data among zones.
3.2. Entity Individual
We describe each observed individual ϑi in the environment with an instance of the entity Individual hence in a crowd with N people detected, a total of N instances will be implemented. The hierarchical model of entity Individual is presented in Figure 1. We describe the trajectory of ϑi as a discrete-controlled process with a state vector xit ∈ ℝ2
and observation vector zit ∈ ℝ2
Where gik and hik represent the process and observation noise, both assumed to be independent, white, with Gaussian distribution. Applying an Extended Kalman Filter (EKF) over the observation and state vectors we obtain an estimation . The trajectory Xi of ϑi is described as a sequence of estimations
and represents the trajectories of individuals . Using the zones of S and SOMI produced in Section 3.1, we can cluster every estimation into a zone sk ∈ S as . Furthermore, we can express the trajectory Xi as a sequence of zones
where wi is called a word. Words are grouped into a vocabulary Vl = {w1, …, wq} given the condition that ∀wa, wb ∈ Vl, s1 ∈ wa = s1 ∈ wb and sn ∈ wa = sm ∈ wb where |wa| = n and |wb| = m, that is, words with similar origin and destination. The notion of words provides a simplified way to describe trajectories whereas the notion of vocabularies allows to group trajectories that correspond to the same behavior, aiming to reach the same destination. Hence, each vocabulary Vl indicates a different behavior. Each learned behavior is modeled with two conditional probability distributions (CPDs)
and
where sα is the initial state, sβ is the final state and sb+1 is the predicted next state given the partial observed trajectory wa:b from time instant a to b in Equation (6). Δt is the transition time given the current state sb and the predicted next state sb+1 in Equation (7). The purpose of Equation (6) is to estimate the origin, destination and next state of ϑi by matching wa:b to the most similar existing word wk with the highest likelihood. On the other hand, Equation (7) estimates the time required for the next transition time. Notice that in both Equations (6) and (7), the superscript l is used to indicate the behavior (vocabulary) to which the CPDs correspond to. Given the estimation of trajectory (Equation 6) and transition time (Equation 7) we can proceed to estimate the emotional state using Bayes rule (Equation 8)
where E is the emotional state labeled as positive, normal or negative, and p(E) is the prior probability learned from the training data and assumed to be uniform. We evaluate Equation (8) for each possible value of E in order to find the emotional state with the highest likelihood. Given that the association between behavior and emotion depends on the context of the situation, the rules for labeling are to be determined for each particular scenario. However, in Section 4 we explain the labeling criteria applied to the experiments presented here.
3.3. Entity Crowd
Supported by the work presented in Le Bon (2007) and Reicher (2012) we argue that a crowd behaves as a collective minded entity and therefore we can model behaviors and infer emotional states for the entity crowd in a similar way to that of the entity individual. One single instance of the entity crowd is employed in a given environment. We start our description of the entity crowd by defining a state vector XCt
and observation vector ZCt
where xit and zit are the state and observation vectors of ϑi as defined in Equations (2) and (3), respectively, for a total of N individuals. In a similar way we could define = as an estimation of the state vector of entity Crowd, however the difficulty of using that definition is that is prompt to irregular dimensionality between samples as individuals join or leave the crowd. Instead we define as
where ŷkt is an estimated amount of individuals in zone sk ∈ S at time t, for a total of m × n zones in S as produced by SOMI in Section 3.1. In this sense, the crowd's state vector estimation is implicitly dependent on the estimation of the individuals' trajectories. This definition of is more advantageous as it provides a vector with uniform dimensionality while maintaining meaningful information. Also, since the focus of is density estimation rather than trajectory tracking, we could employ crowd density algorithms (Cho et al., 1999; Rahmalan et al., 2006) to achieve this task. We collect the estimations into a training set
and use this set to train a self-organizing map SOMC that further reduces dimensionality and provides a representation of states transitions. It is important to mention that SOMC does not provide topological information as SOMI does. SOMC is composed by p rows, q columns and a set of nodes C = {c1, …, cp×q} where the node ck represents a state of the crowd. This enables us to classify each estimation to a state.
For the entity crowd we do not define words to describe state transition sequences because unlike the entity individual where there is a finite trajectory, the sequence of state transitions in a crowd emerges as a cyclic process with people continuously joining and leaving the crowd. As explained in Section 5 we aim to explore the cyclic behaviors of a crowd in a more comprehensive way in future work, but for the work presented here we describe a crowd behavior as a first order Markov process with two CPDs to estimate the change of states and transition time
and
where ck and ck+1 are the current and next state, respectively, and Δt is the transition time. The emotional state of the crowd is assigned to be the same as the experienced for the majority of individuals, hence no labeling is applied to specific state or transition time of the entity crowd.
4. Experiments and Results
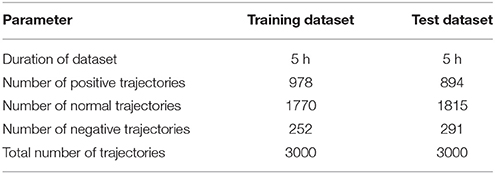
To validate our proposed model we employ data produced by a realistic crowd simulator first introduced in Chiappino et al. (2012, 2015), based on social forces (Helbing and Molnar, 1995) where each individual in the environment is treated as a particle subject to 2D forces, deriving its motion equations from Newtons law F = ma and accounting for its motivation as an attraction force pulling the individual toward its destination and repulsive forces from physical objects and other individuals in the environment. We have recreated a scenario similar to that of a train station as shown in Figure 2A, the produced trajectories are plotted in Figure 2B. The information of individual's trajectories is provided directly from the crowd simulator, hence the steps for detection and tracking of people are omitted. Simulations were carried out under different levels of crowdedness, details for the training and testing datasets produced from simulations are presented in Table 1.
The self-organizing maps SOMI and SOMC are initialized with similar parameters. The set of neurons on each SOM is initialized with random weights and in a hexagonal arrangement spread across the corresponding input space. Distance between neurons is calculated by the number of links among them. The initial neighborhood size is 3 with 100 steps for the ordering phase. The training phase is done over 500 epochs by competitive layer but without bias, updating the winning neuron and all other neurons within the given neighborhood using Kohonen rule.
The first task addressed is to use the trajectory of individuals to obtain a topological representation of the environment with the help of a self-organizing map SOMI as shown in Figures 3A,B. We can observe from Figure 3C the distribution of training data among zones after the clustering process, which is important when describing trajectories, larger zones indicate that more trajectories traverse this area whereas the opposite is also true for smaller zones. The decision of how many zones to employ to describe trajectories has a direct impact on the reliability of our model to estimate the emotion of individuals; this happens because we describe the behavior of individuals by transition of zones, and with fewer zones there is a higher uncertainty of the motion of individuals. In these experiments, SOMI is composed of 100 zones (10 rows and 10 columns) in a hexagonal topology. After testing our model with different dimensions, we found this size to be a suitable balance between predictability and topological representativeness.
Employing SOMI, the trajectories of the training set were evaluated, and a total of 41 different behaviors were identified, a few examples of the learned behaviors are shown in Figure 4.
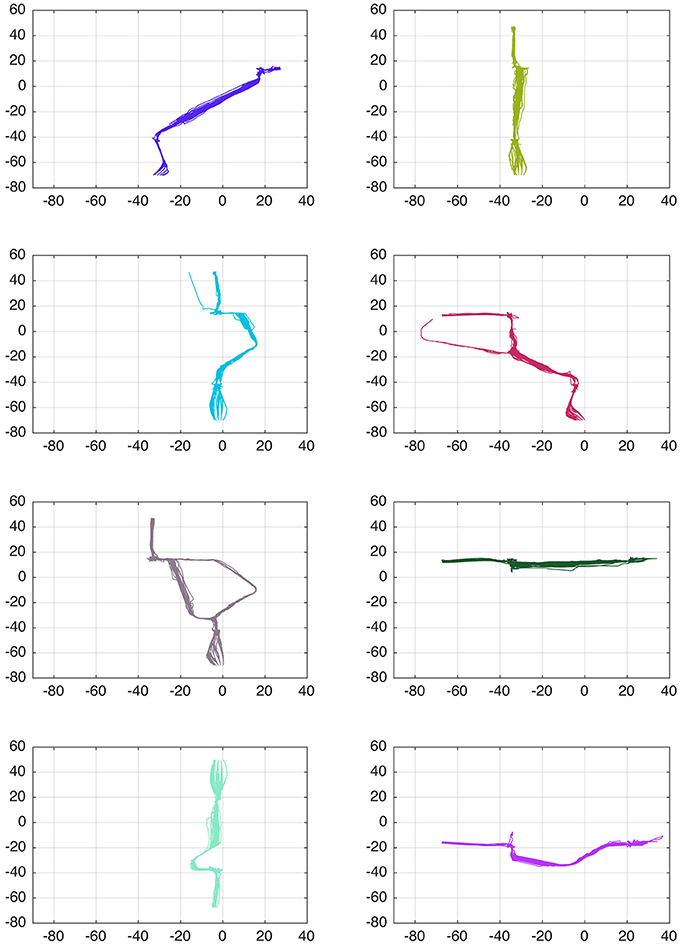
Figure 4. Examples of learned behaviors from the trajectories in the training phase, a total of 41 different behaviors where identified. Colors are assigned randomly.
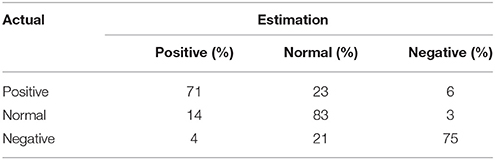
The scenario replicated in the experiments corresponds to that of a train station. Hence, the criteria for labeling behaviors follows from the assumption that people aim to reach their destination in the briefest possible time. The behaviors with the minimum number of state transitions and the shortest transition time are labeled with a positive emotion. The behaviors with the higher frequency of occurrence are associated with a normal emotion. Finally, the behaviors with the highest number of transitions and longer transition time are assigned a negative emotion. During the testing phase, for the purpose of estimating emotional state on individuals, our hierarchical model predicts the zones transitions and transition time for each individual in real time based on the learned behaviors. In our model, the accuracy level to estimate the emotion of individuals depends on the model's capability to predict the individual's behavior. In Figure 5A we show the behavior prediction success rate during a period of 100 s where the average rate was of 76%. Throughout the entire length of the simulations, the prediction success rate oscillated between 74 and 82%. A summary of the model's performance to estimate emotional states is presented in Table 2. In Figure 5B we present a snapshot of the online emotion estimation of individuals.
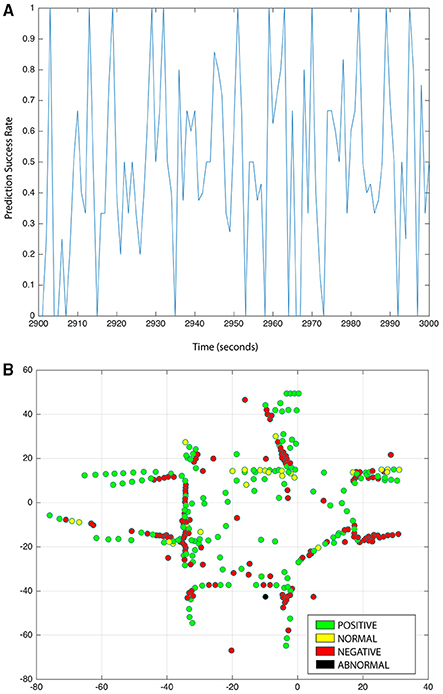
Figure 5. (A) Overall success rate in behavior prediction of individuals. (B) Online emotion estimation of individuals.
The behavior of the crowd is described with a second self-organizing map SOMC, also composed of 100 zones (10 rows and 10 columns), which allow us to build a probabilistic model for its behavior. However, unlike SOMI, a plot of SOMC does not provide a visual semantic due to the high dimensionality of its state vector. Using the same simulations applied to test our model for individuals, we test the ability of the crowd model to predict its behavior, that is, the next state and transition time among states of SOMC. In Figure 6A we can observe the behavior prediction success rate of the crowd oscillating more consistently between 50 and 94%, with an average rate of 81%. In the work proposed here, the emotional state of the crowd is not correlated to its behavior, instead is assigned to be the same as the experienced for the majority of individuals. In Figure 6B we display the summary of detected emotions in an observation period of 600 s, during which a positive emotion becomes predominant as the number of individuals joining the crowd increases.
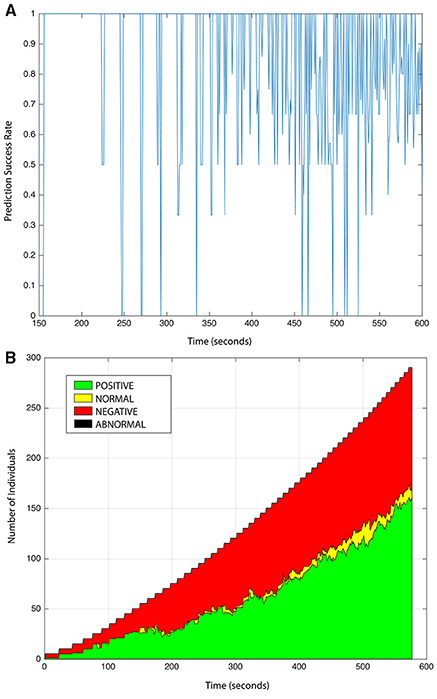
Figure 6. (A) Success rate in behavior prediction of crowd entity. (B) Online emotion estimation of the crowd.
5. Conclusions and Future Work
In this work, we presented a robust model for the estimation of emotions on single individuals and the crowd as a whole, under complex crowded environments. In comparison with (Baig et al., 2014), our approach provides significant improvements: (1) accounts for scenarios with multiple origin and destination points, (2) introduces the idea of vocabularies to describe behaviors which help to reduce data sparsity, and (3) explores the idea of the crowd as a single entity with its own behavior and emotional state.
Our overall hypothesis is that crowd emotion is a combination of individual's emotion estimation, as suggested by neuroscience studies (de Gelder et al., 2010). In this particular study, we have a rather simple model that treats the crowd emotion as a sum of the emotions of the individuals in the crowd. The emotion of the crowd is estimated by a deviation of normal patterns and speed of movement identified in normal situations.
The approach presented here is applicable to real-life crowded environments for monitoring automation intended to identify and prevent dangerous situations as well as to improve crowd control. Furthermore, contributions of this nature are essential for the development of robust cognitive dynamic systems intended for smart cities.
Future development of this work will focus on extending the model to consider the interaction of individual and crowd emotions enabling us to explore causality and contagion of emotional states among individuals and its impact in the crowd as a whole. The result of the simulations performed show the behavior of the crowd to emerge in a cyclic manner; we are interested in further explore this phenomenon and to provide a more comprehensive model for describing such behavior of the crowd. Finally, we aim to extend this model to enable its use in first person perspective models and applications.
Author Contributions
The central idea of this work was developed jointly with CR throughout extensive discussions. MB implemented modifications to the employed software to suit the experiments needs. LM helped in several technical aspects to facilitate the execution of the simulations. EB provided essential insights in the fundamentals of emotion theory and contributed to writing the manuscript. MR assisted with valuable insights and revision of the manuscript. All authors contributed significantly to the work presented in this paper.
Funding
This work was produced under the program of Erasmus Mundus Joint Doctorate in Interactive and Cognitive Environments (EMJD ICE), funded by the Education, Audiovisual and Culture Executive Agency (EACEA).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Sincere thanks to the members of the Information and Signal Processing for Telecommunications Laboratory from the University of Genoa for their valuable insights. This work was produced under the program of Erasmus Mundus Joint Doctorate in Interactive and Cognitive Environments (EMJD ICE), funded by the Education, Audiovisual and Culture Executive Agency (EACEA).
References
Ali, S., and Shah, M. (2008). “Floor fields for tracking in high density crowd scenes,” in Proceedings of European Conference on Computer Vision. Marseille.
Allett, J. (1996). Crowd psychology and the theory of democratic elitism: the contribution of William McDougall. Pol. Psychol. 17, 213–227.
Antonini, G., Martinez, S., Bierlaire, M., and Thiran, J. (2006). Behavioral priors for detection and tracking of pedestrians in video sequences. Intl J. Comput. Vis. 69, 159–180. doi: 10.1007/s11263-005-4797-0
Baig, M. W., Barakova, E. I., Marcenaro, L., Regazzoni, C. S., and Rauterberg, M. (2014). “Bio-inspired probabilistic model for crowd emotion detection,” in 2014 International Joint Conference on Neural Networks (IJCNN) (Beijing), 3966–3973.
Barakova, E. I., and Lourens, T. (2010). Expressing and interpreting emotional movements in social games with robots. Pers. Ubiquitous Comput. 14, 457–467. doi: 10.1007/s00779-009-0263-2
Bechara, A., and Damasio, A. (2005). The somatic marker hypothesis: a neural theory of economic decision. Games Econ. Behav. 52, 336–372. doi: 10.1016/j.geb.2004.06.010
Challenger, R., Clegg, C., and Robinson, M. (2009). Understanding Crowd Behaviours. Multi-Volume Report for the UK Government's Cabinet Office.
Chiappino, S., Morerio, P., Marcenaro, L., Fuiano, E., Repetto, G., and Regazzoni, C. S. (2012). “A multi-sensor cognitive approach for active security monitoring of abnormal overcrowding situations in critical infrastructure,” in 15th International Conference on Information Fusion, Singapore.
Chiappino, S., Morerio, P., Marcenaro, L., and Regazzoni, C. S. (2015). Bio-inspired relevant interaction modelling in cognitive crowd management. J. Ambient Intell. Humaniz. Comput. 6, 171–192. doi: 10.1007/s12652-014-0224-0
Cho, S., Chow, T., and Leung, C. (1999). A neural-based crowd estimation by hybrid global learning algorithm. IEEE Trans. Syst. Man Cybern. 10, 535–541.
Chourabi, H., Nam, T., Walker, S., Gil-Garcia, J. R., Mellouli, S., Nahon, K., et al. (2012). “Understanding smart cities: an integrative framework,” in 45th Hawaii International Conference on System Science (HICSS) (Maui, HI), 2289–2297.
de Gelder, B. (2006). Towards the neurobiology of emotional body language. Nat. Rev. Neurosci. 7, 242–249. doi: 10.1038/nrn1872
de Gelder, B., Van den Stock, J., Meeren, H. K., Sinke, C. B., Kret, M. E., and Tamietto, M. (2010). Standing up for the body. Recent progress in uncovering the networks involved in the perception of bodies and bodily expressions. Neurosci. Biobehav. Rev. 34, 513–527. doi: 10.1016/j.neubiorev.2009.10.008
Ekman, P., and Friesen, W. (2002). The Facial Action Coding System. Salt Lake City, UT: Research Nexus eBook.
Ekman, P., Friesen, W. V., O'Sullivan, M., Chan, A., Diacoyanni-Tarlatzis, I., Heider, K., et al. (1987). Universals and cultural differences in the judgments of facial expressions of emotion. J. Pers. Soc. Psychol. 53, 712–717.
Frijda, N. (2010). Impulsive action and motivation. Biol. Psychol. 84, 570–579. doi: 10.1016/j.biopsycho.2010.01.005
Helbing, D., and Molnar, P. (1995). Social force model for pedestrian dynamics. Phys. Rev. E 51, 4282–4286.
Horlings, R., Datcu, D., and Rothkrantz, L. J. M. (2008). “Emotion recognition using brain activity,” in 9th International Conference on Computer Systems and Technologies. (New York, NY).
Huis in 't Veld, E. M. J., and De Gelder, B. (2015). From personal fear to mass panic: the neurological basis of crowd perception. Hum. Brain Mapp. 36, 2338–2351. doi: 10.1002/hbm.22774
Izar, C. E. (2013). “The emotions in life and science,” in Human Emotions, 2nd Edn (New York, NY: Springer Science & Business Media), 1–18.
Juslin, P., and Scherer, K. (2008). “Vocal expression of affect,” in The New Handbook of Methods in Nonverbal Behavior Research, eds J. A. Harrigan, R. Rosenthal, and K. R. Scherer (New York, NY: Oxford University Press), 65–116.
Keltner, D., and Ekman, P. (2000). “Facial expression of emotion,” in Handbook of Emotions, 2nd Edn., eds M. Lewis and J. Haviland-Jones (New York, NY: Guilford Publications, Inc.).
Le Bon, G. (2007). “General characteristics of crowds-psychological law of their mental unity,” in The Crowd, English Edn (London: Transactions Publishers).
Liu, Z., Jin, W., Huang, P., and Chai, Y. (2013). An emotion contagion simulation model for crowd events. Jisuanji Yanjiu yu Fazhan/Comput. Res. Dev. 50, 2578–2589.
Matsumoto, D. (2004). Paul Ekman and the legacy of universals. J. Res. Pers. 38, 45–51. doi: 10.1016/j.jrp.2003.09.005
Moors, A., Ellsworth, P. C., Scherer, K. R., and Frijda, N. H. (2013). Appraisal theories of emotion: state of the art and future development. Emot. Rev. 5, 119–124. doi: 10.1177/1754073912468165
Novelli, D., Drury, J., Reicher, S., and Stott, C. (2013). Crowdedness mediates the effect of social identification on positive emotion in a crowd: a survey of two crowd events. PLoS ONE 8:e78983. doi: 10.1371/journal.pone.0078983
Rahmalan, H., Nixon, M., and Carter, J. (2006). “On Crowd Density Estimation for Sourveillance,” The Institution of Engineering and Technology Conference on Crime and Security, 540–545.
Reicher, S. (2012). “Crowd psychology,” in Encyclopedia of Human Behavior, 2nd Edn., ed V. S. Ramachandran (San Diego, CA: Academic Press), 631–637.
Keywords: crowd behavior, emotion estimation in crowds, estimation of individual and collective emotions
Citation: Urizar OJ, Baig MS, Barakova EI, Regazzoni CS, Marcenaro L and Rauterberg M (2016) A Hierarchical Bayesian Model for Crowd Emotions. Front. Comput. Neurosci. 10:63. doi: 10.3389/fncom.2016.00063
Received: 04 April 2016; Accepted: 09 June 2016;
Published: 08 July 2016.
Edited by:
Jose Manuel Ferrandez, Universidad Politecnica de Cartagena, SpainReviewed by:
Antonio Fernández-Caballero, Universidad de Castilla-La Mancha, SpainAndres Ortiz, Universidad de Málaga, Spain
Copyright © 2016 Urizar, Baig, Barakova, Regazzoni, Marcenaro and Rauterberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Oscar J. Urizar, b3Nzc2trYXJAZ21haWwuY29t
 Oscar J. Urizar
Oscar J. Urizar Mirza S. Baig
Mirza S. Baig Emilia I. Barakova
Emilia I. Barakova Carlo S. Regazzoni
Carlo S. Regazzoni Lucio Marcenaro2
Lucio Marcenaro2 Matthias Rauterberg
Matthias Rauterberg