Combined Effects of Feedforward Inhibition and Excitation in Thalamocortical Circuit on the Transitions of Epileptic Seizures

1. Introduction

Epilepsy is a debilitating condition of chronic neurological unprovoked seizures (Kramer et al., 2005; Vaurio et al., 2017), which can induce the cognitive, linguistic and behavioral disorders (Barnes and Paolicchi, 2008; Caplan et al., 2008), extending well beyond the immediate effect from seizures (Vaurio et al., 2017). The seizure classifications of epilepsy can be divided into simple partial seizures (Devinsky et al., 1989; Kim et al., 2016), complex partial seizures (Jeniffer et al., 2015; Mohamed and Burnham, 2016) and generalized seizures (Youngblood et al., 2015). Experimental and computational evidences have suggested that these seizures are closely related to each other (Devinsky et al., 1988; Rogers et al., 2012; Varon Perez et al., 2012; Fan et al., 2015; Li et al., 2016a,b; Liu et al., 2016). This could be attributable to concomitance of multiple intricate mechanisms.

Absence and tonic-clonic seizures are both the form of generalized epileptic seizures, i.e., the involvements of whole cortical region in humans during the pathological brain rhythms of epileptic seizures. In the electroencephalogram (EEG), generalized absence seizures of epilepsy, mainly occurring in children and juvenile (Marten et al., 2009), are typically characterized by bilaterally highly synchronized 2–4 Hz spike and wave discharges (SWD) (Meeren et al., 2002; Sitnikova, 2010) with a brief impairment of consciousness (i.e., absence) (Panayiotopoulos, 2001; Sitnikova, 2010). In addition, absence epilepsy is the petit-mal onset and never accompanied by aura and convulsions. In contrast to the absence epilepsy, the generalized tonic-clonic seizures are the grand-mal type of epilepsy (Wang et al., 2011). In clinic, the onset of this typical tonic-clonic seizures is characterized by the tense of muscles (Quiroga et al., 1997). In EEG, it can be identified as the paroxysmal fast activity of tonic phase with high frequency (>13 Hz) and low amplitude, which particularly accompanied by the evolutions into clonic phase with low frequency (<10 Hz) and high amplitude slow-wave oscillations (Ji et al., 2014). It has been demonstrated that both the absence and tonic-clonic seizures can generally appear in one complete recording from the same patient (Fong et al., 1998; Wakamoto et al., 2011; Shinnar et al., 2015). In particular, as seen from Figure 1, clinical and eletrographical evidences showed that absence seizures can evolve into the tonic-clonic oscillations of epilepsy (i.e., absence-tonic-clonic seizures, Figure 1B) (Mayville et al., 2000) and a tonic seizure can also be followed by the absence seizure (tonic-absence seizures, Figure 1A) (Shih and Hirsch, 2003). Although extensive observations and research have elucidated the mechanisms underlying the absence and tonic-clonic seizures, how these two seizures transit from each other remains an unanswered question in epileptology.

FIGURE 1

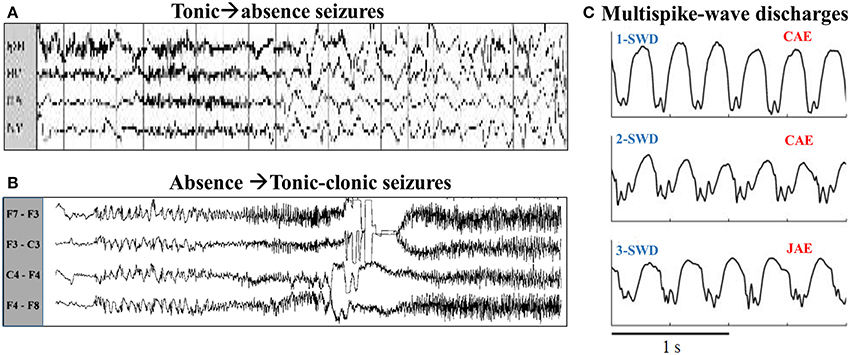
Figure 1. (A) The typical tonic-absence EEG pattern, modified from Shih and Hirsch (2003). (B) Electrographic evolution of an absence seizure to generalized tonic-clonic activity in patient, modified from Mayville et al. (2000). (C) EEG recordings from three different patients with an absence seizure, modified from Marten et al. (2009). The first two patients are diagnosed with CAE (childhood absence epilepsy) (Upper and Middle panels), while the patient in the lower panel is diagnosed with JAE (juvenile absence epilepsy).

Neural field model can be used to characterize the macroscopic dynamics of neuronal populations. By introducing the disinhibition mechanism into the cerebral cortex, Fan et al. (2015) proposed a modified spatially-extended neural field model of cortex to computationally represent the physiologically plausible two-way transitions of epilepsy between absence and tonic-clonic seizures. However, the simultaneous recordings from cortex and thalamus of either the rodent animal models (Crunelli and Leresche, 2009) or clinical patients with epilepsies (Freestone et al., 2009) have shown that the pathological rhythms in cortex during epileptic seizures arise from the abnormal interactions within corticothalamic circuit (Coenen and Van Luijtelaar, 2003; Timofeev and Steriade, 2004; Millard et al., 2011; Sherman, 2012; Fan et al., 2016). This can also be supported by the interactions of ionic conductances in cells of both thalamus and cortex based on the specific anatomy of thalamocortical circuitry, which gives rise to the multiple modes of activities characterizing behavioral states of generalized epilepsy (Kush et al., 2016). These results provide the causal support for the involvement of subcortical thalamus in the initiations and developments of generalized epilepsies such as absence seizures and tonic-clonic seizures. Nevertheless, the thalamocortical mechanisms underlying the transitions between absence seizures and tonic-clonic seizures still need to be explored.

In this paper, we employ the recently developed thalamocortical neural field model (Taylor et al., 2014) to characterize the macroscopic dynamics of neuronal populations within the thalamocortical circuit. Neural field models (Taylor et al., 2014; Wang and Wang, 2017) have been successfully applied to investigate the effect of stimulation on the SWD of absence seizures in epilepsy. As seen in Figure 2, the thalamocortical loop consists of cortical subsystem and thalamic subsystem. The cortical subsystem is composed of the excitatory (EX) neuronal population and inhibitory (IN) neuronal population, and the thalamic subsystem is composed of the thalamocortical (TC) relay neuronal populations and the thalamic reticular (RE) neuronal populations. The linking rules of intra-cortical EX-IN circuit and intra-thalamic TC-EX circuit, as well as the inter-thalamocortical loop, follow the work of Pinault and O'Brien (2005). However, in the previous model network, they didn't consider the feedforward inhibition from TC to IN. In fact, TC projects excitatory synaptic functions into both the cortical IN (inhibitory) and EX (excitatory) neuronal populations to comprehensively regulate the cortical firing activities by activating IN and EX, respectively. Therein, we refer to the projection from TC to IN as the feedforward inhibition of TC, which can first activate IN and the activated IN then further inhibits the abnormal discharges of EX. Hence, the feedforward inhibition, in effect, represents the TC-IN-EX pathway, in which the IN-EX pathway is inhibitory. Similarly, we refer to the direct projection from TC to EX as the feedforward excitation of TC. It is thought that in some cortical areas feedforward inhibition has even more stronger functions on cortex than the feedforward excitation from TC to EX (Porter et al., 2001; Sasaki et al., 2006; Cruikshank et al., 2007; Delevich et al., 2015; Herrera et al., 2015; Paz and Huguenard, 2015). Inspired by this, we propose a modified model by adding feedforward inhibition into the thalamocortical loop. Based on this modified model, we will systematically investigate the combined effects of feedforward inhibition and excitation from thalamus to cortex on the transition behaviors of epileptic seizures including tonic-clonic and absence seizures.

FIGURE 2

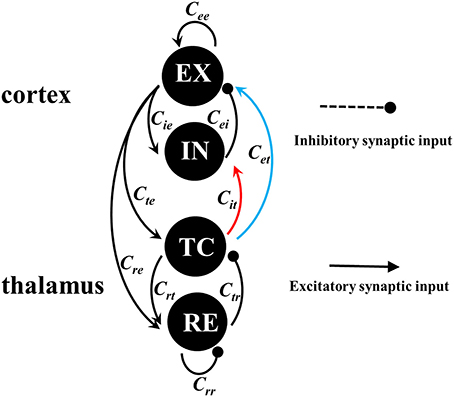
Figure 2. (Color online) Framework of the cortico-thalamic network. The cortical subsystem consists of excitatory (EX) pyramidal neuronal population and inhibitory (IN) interneuronal population. The thalamic subsystem consists of thalamus reticular (RE) nucleus and specific relay nuclei (TC). Excitatory projections are mediated by glutamate, which are denoted by the lines with arrow heads, while the inhibitory projections are mediated by GABA receptors, which are represented by the lines with round heads, respectively. The red and blue lines represent the feedforward inhibitory and excitatory connectivities, which are the only parameters we allow to vary.

The organization of this paper is as follows. In Section 2, we review the model equations and the parametric variables of principal interest. The dynamical analysis for the model used here is also conducted in this section. In Section 3, we consider the feedforward effects from thalamus to cortex on the generalized epileptic seizures. In Sections 3.1 and 3.2, we compute the 1-D bifurcation diagrams to explore the effects of feedforward excitation and inhibition on the transition dynamics of generalized absence and tonic-clonic seizures, respectively. In Section 3.3, the combined effects of feedforward excitation and inhibition on the transition dynamics are explored by plotting 2-D bifurcation diagrams. In Section 4 we discuss these results.

2. Models and Methods

2.1. Description of the Model

In this paper, we propose a modified thalamocortical neural field model originally from Taylor et al. (2014), where we introduce the feedforward inhibition from TC to IN into the thalamocortical network. As seen in Figure 2, connection schematic of this modified neural field model is composed of the thalamocortical loop, which consists of the cortical EX-IN circuit and thalamic TC-RE circuit. The current improved model equations can be written as follows:

$\begin{array}{ll}\frac{dEX}{dt}=(h_e-EX+C_{ee}f\left[EX\right]-C_{ei}f\left[IN\right]+C_{et}f\left[TC\right]){\tau }_e,& (1)\end{array}$

$\begin{array}{ll}\frac{dIN}{dt}=(h_i-IN+C_{ie}f\left[EX\right]+C_{it}f\left[TC\right]){\tau }_i,& (2)\end{array}$

$\begin{array}{ll}\frac{dTC}{dt}=(h_t-TC+C_{te}f\left[EX\right]-C_{tr}g\left[RE\right]){\tau }_t,& (3)\end{array}$

$\begin{array}{ll}\frac{dRE}{dt}=(h_r-RE+C_{re}f\left[EX\right]+C_{rt}g\left[TC\right]-C_{rr}g\left[RE\right]){\tau }_r& (4)\end{array}$

Each equation is a rate equation with the units of voltage (activity) per time, where EX, IN, TC, RE are firing rates, i.e., the fractional firing activity in each neuronal populations, the parameters h_e,i,t,r are additive input constants to EX, IN, TC and RE, respectively. τ_e,i,t,r are the timescale parameters having the unit of s⁻¹. C_{ee,ei,et,ie,it,te,tr,re,rt,rr} are the connectivity strengths within different neuronal populations whose linking rules essentially follow the experimentally known connection values. In particular, C_it and C_et represent the feedforward inhibition and excitation from TC to cortex. f[·] and g[·] are the activation functions of the cortical subsystem and thalamic subsystem, respectively:

$\begin{array}{ll}f(x)=1/(1+{\theta }^{-x})& (5)\end{array}$

$\begin{array}{ll}g(y)=\alpha y+\beta & (6)\end{array}$

with x = EX, IN, TC and RE, y = TC, RE, and θ determines the steepness.

2.2. Dynamical Analysis

The thalamocortical model can be represented as follows (Rodrigues et al., 2007, 2009):

$\begin{array}{ll}\dot{X}=F(X(t),\nu ),& (7)\end{array}$

where F = (F₁, F₂, F₃, F₄)∈C^k(ℝ⁴ × ℝ²¹, ℝ⁴) is the vector field for large enough k, X = (EX, IN, TC, RE), ν∈ℝ²¹ is the total parameter space, but in this present study, the parameters of interest are the feedforward excitation and inhibition of cortico-thalamic synaptic circuit, w = (C_et, C_it) ⊂ ν, due to its physiological relevance in studies of absence seizures. Because C_et, C_it are the only parameters we allow to vary, in fact, F ∈C^k(ℝ⁴ × ℝ², ℝ⁴) and the system can be rewritten as

$\begin{array}{ll}\dot{X}=F\left(X\left(t\right)w\right)=\{\begin{array}{r}\hfill F_1\left(X\left(t\right),C_{et}\right)\\ \hfill F_2\left(X\left(t\right),C_{it}\right)\\ \hfill F_3\left(X\left(t\right)\right)\\ \hfill F_4\left(X\left(t\right)\right)\end{array}& (8)\end{array}$

Let X*(t) = (EX*, IN*, TC*, RE*) be fixed point of the system (8), i.e., equilibrium state being determined by setting the RHS (Borisyuk and Kirillov, 1992) of vector field of system (8) equal to 0,

$\begin{array}{ll}F\left(X\left(t\right)w\right)=0& (9)\end{array}$

The stability of equilibrium points can be analyzed by ensuring that the linearized version of (8) satisfies the Hartman-Groβman theorem (Kuznetsov et al., 1998). Consequently, we consider the Jacobian matrix (linearization matrix) of (8):

$\begin{array}{ll}\text{J}=\left[\begin{array}{cccc}-{\tau }_e+{\tau }_e{C}_{ee}{f}^{\prime }(EX)& -{\tau }_e{C}_{ei}{f}^{\prime }(IN)& {\tau }_e{C}_{et}{f}^{\prime }(TC)& 0\\ {\tau }_i{C}_{ie}{f}^{\prime }(EX)& -{\tau }_i& {\tau }_i{C}_{it}{f}^{\prime }(TC)& 0\\ {\tau }_t{C}_{te}{f}^{\prime }(EX)& 0& -{\tau }_t& {\tau }_t{C}_{tr}\alpha \\ {\tau }_r{C}_{re}{f}^{\prime }(EX)& 0& {\tau }_r{C}_{rt}\alpha & -{\tau }_r-{\tau }_r{C}_{rr}\alpha \end{array}\right]& (10)\end{array}$

Assume that for $C_{et}=C_{et}^{*}$ and $C_{it}=C_{it}^{*}$ at least one of the eigenvalues of the Jacobian matrix calculated at X*(t) is zero. This is valid if and only if the matrix determinant $\Delta (X^{*}(t),w^{*})=|J{|}_{X^{*}(t),C_{et}^{*},C_{it}^{*}}=0$. We then consider the following equations

$\begin{array}{ll}\{\begin{array}{r}\hfill F(X(t),w)=0\\ \hfill {\Delta }_{\text{J}}(\text{X}(\text{t}),{\text{C}}_{\text{et}},{\text{C}}_{\text{it}})=0\end{array}& (11)\end{array}$

which defines a curve in the six-dimensional space (EX, IN, TC, RE, C_et, C_it). The projection of this curve onto the plane w = (C_et, C_it) is called the fold point bifurcation curve.

In the 4-dimensional system of differential equations, the necessary and sufficient condition for a sum of two eigenvalues to be zero is that 3th Gurvitz determinant Δ_G(X(t), C_et, C_it) = 0 (Gantmakher, 1967). If there exists a pair of eigenvalues of $J_{X^{*}(t)}$, λ₁ and λ₂, the sum of which is zero (i.e., either λ_{1, 2} = ±iω, or λ₁= −λ₂ are real), we consider the following equations,

$\begin{array}{ll}\{\begin{array}{r}\hfill F(X(t),w)=0\\ \hfill {\Delta }_{\text{G}}(\text{X}(\text{t}),{\text{C}}_{\text{et}},{\text{C}}_{\text{it}})=0\end{array}& (12)\end{array}$

which define a curve in the six-dimension space (EX, IN, TC, RE, C_et, C_it). We call the projection of the curve onto the plane w = (C_et, C_it) the Andronov-Hopf bifurcation curve.

The double limit cycle curve can be defined by considering a fixed point of the Poincare map. Here the condition that the point (EX, IN, TC, RE, C_et, C_it) belongs to the double limit cycle curve can be written as a system of five equations, where four equations define that the point is the fixed point of Poincare map, and the fifth one defines that the point is a multiple fixed point of this map. The projection of this curve onto the plane w = (C_et, C_it) is called the double limit cycle curve. When parameters pass through this curve two limit cycles appear or disappear.

In addition, setting the linear change of variables to $\widehat{X}=X-X^{*}$ and substituting appropriately into equations we obtain the following $\dot{\widehat{X}}=F(\widehat{X},w)$ where now F(0,w) = 0. Therefore, without loss of generalization, the state X = 0 is chosen to be the state of low level background activity. That is X = 0 is the steady state solutions of (1–4). h_e,i,t,r are external inputs into EX, IN, TC and RE neuronal populations, which can qualitatively induce the transitions between pathological state and non-seizure state of system. In the presence of external input (i.e., h_e,i,t,r ≠ 0), substituting X = 0 into the RHS of (1–4), we can quantitatively identify h_e,i,t,r as follows (Equation 13) through the interactive intensities among different neuronal populations, C_{ee,ei,et,ie,it,te,tr,re,rt,rr}, within the thalamocortical circuit,

$\begin{array}{ll}\{\begin{array}{rr}\hfill 2h_e=& \hfill C_{ei}-C_{ee}-C_{et}\\ \hfill 2h_i=& \hfill -C_{ie}-C_{it}\\ \hfill 2h_t=& \hfill C_{tr}-C_{te}\\ \hfill 2h_r=& \hfill C_{rr}-C_{rt}-C_{re}\end{array}& (13)\end{array}$

Finally, epileptic absence seizures are characterized by SWD which is essentially the bursting oscillations. Bursting is one of the most important firing activities of neuronal systems. Rinzel (1985) firstly made some theoretical analysis on bursting and recognized that bursting exhibits a transition between a slow wave (or resting state) and a spiking state, owning to slow variation process modulating fast firing activities. In this system, TC can be considered as the slow variables in the model subsystem (3), which controls the dynamics of the fast subsystem (1), (2), and (4). Therefore, the fast-slow dynamics analysis plays an important role for the dynamical behavior of firing patterns (Rinzel, 1985; Izhikevich, 2000; Duan et al., 2008), especially bursting-like SWD discharges of absence seizure in epilepsy.

2.3. Simulation Method and Data Analysis

All model parameters used to make simulations in this manuscript are listed in Table 1. The standard fourth-order Runge-Kutta integration scheme under the MATLAB (MathWorks, USA) simulating environment was used with Equations (1–4). The model EEG is taken as the mean of two cortical populations, EX and IN. Both the bifurcation and frequency analysis (Chen et al., 2014, 2015, 2017) are utilized to characterize the critical state transitions and neural oscillations generated by our model. Firstly, the bifurcation analysis is performed by calculating the stable local minimum and maximum values of the mean for EX and IN. Furthermore, to evaluate the dominant frequency of neural oscillations, the power spectral density (PSD) is estimated using the fast Fourier transform (FFT) for the time series of the mean for EX and IN. Then the maximum peak frequency is defined as the dominant frequency of neural oscillations. We further investigated the interesting dynamical features of the modified model numerically using the software package XPPAut (Ermentrout, 2002). The bifurcation diagrams were computed by using AUTO as incorporated in XPPAut.

TABLE 1

Table 1. Parameter values of system (1)–(4) used in the manuscript.

3. Results

3.1. Feedforward Excitation TC → EX Inducing Tonic-Absence Seizures with Weak Feedforward Inhibition

Tonic-absence seizures, originally termed by Shih and Hirsch (2003), consist of a tonic seizure with generalized paroxysmal fast activity (>13 Hz) which is followed by an absence seizure with generalized slow spike-wave activity (~2–4 Hz). Clinically and electrographically, this is a poorly characterized seizure type in patients with symptomatic generalized epilepsy. The typical tonic-absence EEG pattern can be found in the Figure 1A, modified from Figure 2A in the work of Shih and Hirsch (2003). In this section, we computationally investigate the effect of feedforward excitation from TC to EX, i.e., C_et, on the generation of tonic-absence seizures, based on the modified thalamocortical network model.

3.1.1. Firing Transitions of Modified Model System

Figure 3 gives an overall view of cortical various state transitions with the increasing of C_et and fixing C_it = 0.05, i.e., under the condition of weak feedforward inhibition from TC to IN. It is seen from the upper panel of Figure 3 that the small values of C_et, e.g., C_et <≈1.2, can induce the simple oscillations. The exemplary time series for this is given in Figure 4A. Compared to the lower panel of Figure 3, it is seen that the corresponding dominant frequencies of simple oscillations are larger than 13 Hz, which hence represents the generalized tonic seizures of epilepsy. Electrophysiologically, this is because that the weak feedforward inhibition is unable to effectively activate the cortical inhibitory neuronal populations (IN), which cannot further confront the abnormal discharges of excitatory neuronal populations (EX). Especially, it can also be observed that with the increasing of C_et, the amplitudes of tonic oscillations gradually decrease, while the vibration frequencies are amplified step by step. As 1.22 <≈ C_et <≈1.25, tonic oscillations decay to steady values. Accordingly, the system enters into the transient low saturated (LS) firing states.

FIGURE 3

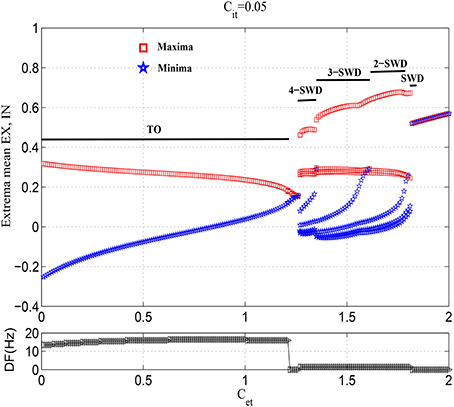
Figure 3. Bifurcation diagrams (upper panel) and corresponding dominant frequencies (lower panel) showing model dynamics of a single compartment over changes in C_et with C_it fixed at 0.05. The system transits from the tonic oscillations (TO) to 4-spike and wave discharges (4-SWD), 3-spike and wave discharges (3-SWD), 2-spike and wave discharges (2-SWD), spike and wave discharges (SWD) and to high saturated state (HS), respectively.

FIGURE 4

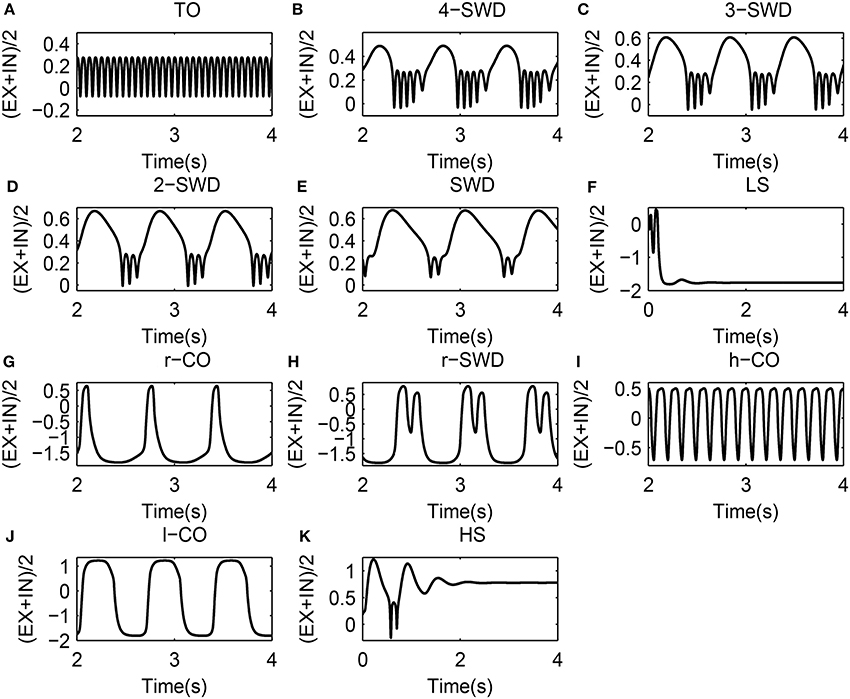
Figure 4. 11 solutions along with the marker style used to represent them. (A) TO (tonic oscillations): C_it = 0.05, C_et = 0.5; (B) 4-SWD (4-spike and wave diacharges): C_it = 0.05, C_et = 1.3; (C) 3-SWD (3-spike and wave discharges): C_it = 0.05, C_et = 1.5; (D) 2-SWD (2-spike and wave discharges): C_it = 0.05, C_et = 1.7; (E) SWD (spike and wave discharges): C_it = 0.05, C_et = 1.81; (F) LS (low saturated state): C_it = 1.0, C_et=0.05; (G)r-CO (reversed clonic oscillations): C_it = 1.0, C_et = 0.2; (H) r-SWD (reversed SWD): C_it = 1.0, C_et = 0.4; (I) h-CO (high-frequency CO): C_it = 1.0, C_et = 0.8; (J) l-CO (low-frequency CO): C_it = 1.0, C_et = 1.2; (K) HS (High saturated state): C_it = 1.0, C_et = 2. For clarity, these solutions are also indicated by text labels in each figure.

However, as the further increasing of C_et, the system transits into the multi-spike and wave discharges (m-SWD) from the low saturated firing states. Firstly, the system shows the periodic 4-spike and wave discharges (4-SWD) within the parameter region 1.25 <≈ C_et <≈1.35. Then, the system successively transits from 4-SWD to the periodic 3-/2-spike and wave discharges (3-/2-SWD), corresponding to the parameter regions, 1.35 <≈ C_et <≈1.6 and 1.6 <≈ C_et <≈1.78, respectively. Immediately after the m-SWD, the system transits into the SWD (i.e., periodic 1-spike and wave discharges, SWD), corresponding to 1.78 <≈ C_et <≈1.8, which is the characteristic of epileptic absence seizures. Finally, for the much large values of C_et, the system shows the high saturated (HS) firing states. Overall, the feedforward inhibition, i.e., C_et, can induce the transitions from tonic oscillations to SWD discharges, which mathematically describes the clinically and electrographically observed tonic-absence seizures process of epilepsy.

The exemplary time series for the solutions of 4-/3-/2-/1-SWD are displayed in the Figures 4B–E, which also serve as the legends for the subsequent bifurcation diagrams. In order to make a link between the above-mentioned time series and the real patient EEG data, Figure 1C gives the EEG traces from seizure database, taken from two different patients with childhood absence epilepsy (CAE, upper and middle panels) and one patient with juvenile absence epilepsy (JAE, lower panel). Specifically, EEG traces show the 1-SWD and 2-SWD discharges for patients with CAE and 3-SWD discharges for patient with JAE, respectivley. In particular, through the qualitative comparison between the human EEG data (Figure 1C) and the time traces of cortico-thalamic model (Figures 4C–E) we can find an interesting qualitative agreement between the data and the model.

3.1.2. The Dynamical Mechanisms Underlying the Tonic-Absence Seizures

Figure 5 shows the dynamical explanations for the bifurcation diagram of these state behaviors corresponding to Figure 3 and Figure 4. It is seen that for small values of C_et, the solutions of the system are either fixed points or tonic oscillation (TO). Among these solutions, there is a region of bistability (BS₁) consisting of a stable fixed point and a stable limit cycle, corresponding to C_et <≈0.24. At C_et ≈0.24, the stable fixed point disappears due to a fold of fixed point bifurcation (LPF). After that, the system enters into the monostable regions composed of stable limit cycle and stable focus, corresponding to 0.24 <≈ C_et <≈1.22 (i.e., MS₁) and 1.22 <≈ C_et <≈1.25 (i.e., MS₂), respectively. In particular, at C_et = 1.22, the stabilities of focuses switch following a supercritical Hopf bifurcation (HB₁). The m-SWD solutions emerge for larger C_et (e.g., 1.25 <≈ C_et <≈1.8) successively following a fold of cycles bifurcation (LPC₁), LPC₂, LPC₃, HB₂ and HB₃ bifurcations, which give rise to the monostable regions (MS₃), bistable regions (BS₂, BS₃, BS₄) and tristable region (TS₁), respectively. In particular, compared to the Figure 3, SWD solution occurs in the bistable region of 1.78 <≈ C_et <≈1.8. Finally, the system undergoes another LPC₄ and enters into the monostable fixed points (MS₄).

FIGURE 5

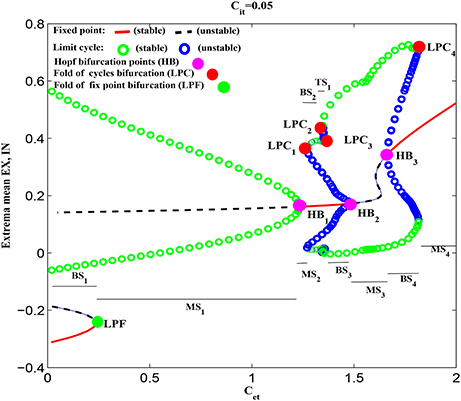
Figure 5. (Color online) Dynamical bifurcation diagram corresponding to the state transitions in Figure 3. As C_et increasing, the system successively undergoes the fold of fixed point bifurcation (LPF), Hopf bifurcation (HB₁), the fold of cycles bifurcation (LPC₁), LPC₂, LPC₃, HB₂, HB₃, and LPC₄, respectively. The parameter regions consist of monostable region (“MS”) including stable fixed point (MS₂, MS₄), and stable limit cycles (MS₁, MS₃), bistable regions (“BS,” BS₁ − BS₄) composed of stable limit cycle and stable fixed point, and tristable region (“TS”) composed of stable fixed point and two stable limit cycles, respectively.

It is noted that the system status in the multistable regions is dependent on the initial values of the four state variables. From the mathematical standpoint, there exist separating manifolds, i.e., separatrix, between the attraction basins of various stable states. Specifically, when the initial values of the four state variables are close to the side of separatrix near the stable fixed points, the system will converge to the steady states, otherwise the system will show the tonic oscillations or m-SWD discharges when the initial values fall into the attraction basin of stable limit cycle. In particular, during the simulations, all the initial values of the four state variables are set to [0.1724 0.1787 – 0.0818 0.2775] which is within the attraction basins of stable limit cycle. Hence the system displays the periodic simple tonic oscillations or m-SWD discharges. Note that, the dynamical explanations also serve as a legend for the subsequent state bifurcation diagrams.

3.1.3. Fast-slow Decomposition Analysis

The fast-slow dynamics underlies the basis of dynamical behavior of bursting firing patterns (Rinzel, 1985; Izhikevich, 2000; Duan et al., 2008), especially bursting-like SWD discharges of absence seizure in epilepsy. Figure 6 shows the fast-slow dynamical analysis for the multi-spike and wave discharges (m-SWD). The equilibrium points form a lay down “L”-shaped curve, in which the stable and unstable focus curves are described with the solid and dashed line respectively, which are separated by the supercritical Hopf bifurcation point (HB). The stable limit cycles occur at the supercritical Hopf bifurcation (HB). The maximal and minimal values of the limit cycles of EX are described with green solid dot. The oscillations (spikes) emerge because of the stable limit cycles which bifurcate from the HB point. For 4-spike and wave discharges at C_et = 1.3, the supercritical Hopf bifurcation occurs at TC = −0.03338 (Figure 6A), 3-spike at TC = −0.0532311 (Figure 6B), 2-spike at TC = −0.06917 (Figure 6C) and 1-spike at TC = −0.07676 (Figure 6D). With the increase of parameter C_et, the HB moves left which results in the decrease of number and amplitude of spikes. So the bursting transits from 4-spike to 1-spike.

FIGURE 6

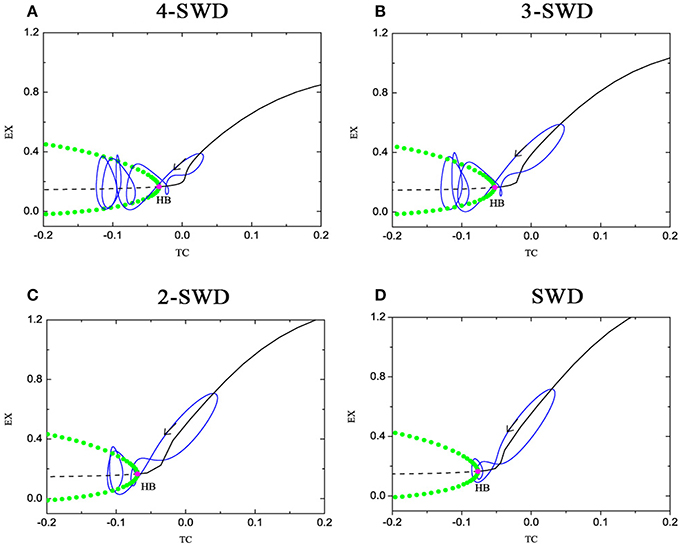
Figure 6. (Color online) Fast-slow dynamical analysis of fast subsystem (1), (2), and (4) with respect to the slow variable TC at (A) C_it = 0.05, C_et = 1.3; (B) C_it = 0, 05, C_et = 1.5; (C) C_it = 0.05, C_et = 1.7; (D) C_it = 0.05, C_et = 1.81, corresponding to Figures 4B–E, respectively. The solid and dashed curve represent the stable and unstable focus. HB refer to the supercritical Hopf bifurcation and the trajectory of the system (1)–(4) is also superimposed on it. The other parameter values are same as that in Figure 5.

3.2. Feedforward Inhibition TC → IN Inducing Absence-Clonic Seizures with Strong Feedforward Excitation

In order to investigate the modulation functions of feedforward inhibition on the feedforward excitation inducing tonic-absence seizures, we gradually increase the feedforward inhibition, i.e., C_it, to observe the state transitions from the various phases of tonic-absence seizures. Figure 7 captures the typical state transitions under the different functions of feedforward inhibitions with fixing C_it at 0.1 (Figure 7A), 0.2 (Figure 7B), 0.4 (Figure 7C), 0.7 (Figure 7D), 1.0 (Figure 7E), and 1.8 (Figure 7F), respectively. In what follows, for the sake of clearness, the investigations for the state transitions are mainly focused on the three parameters intervals of C_et, i.e., C_et ∈ [0, 0.2], C_et ∈ [0.2, 0.6] and C_et ∈ [0.6, 2], respectively.

FIGURE 7

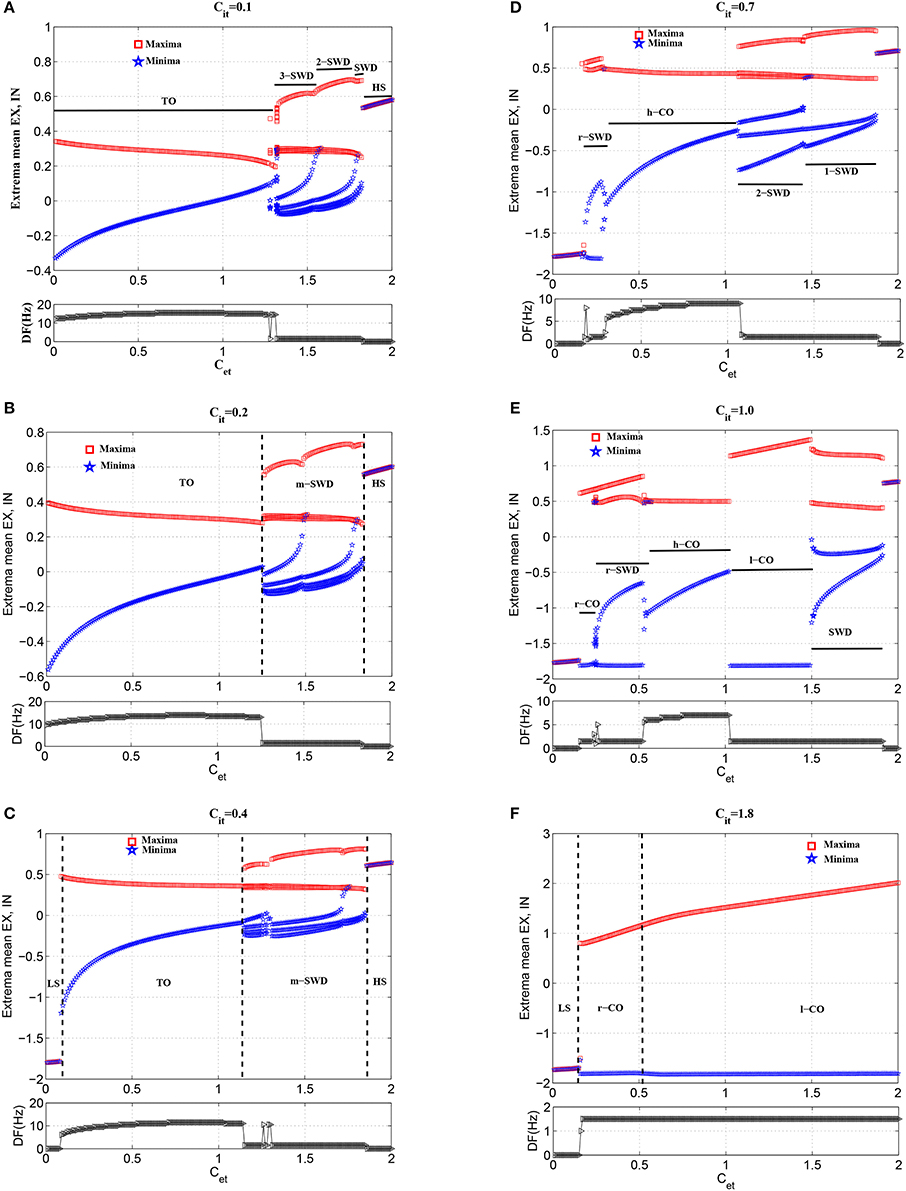
Figure 7. Bifurcation diagrams (upper panels) and corresponding dominant frequencies (lower panels) showing model dynamics of a single compartment over changes in Cet with Cit fixed at (A) 0.1, (B) 0.2, (C) 0.4, (D) 0.7, (E) 1.0, and (F) 1.8, respectively. For clarity, TO, m-SWD (m = 1,2,3), r-SWD (reversed SWD discharges), LS (low saturated state), HS, and r/h/l-CO (reversed/high-frequency/low-frequency clonic oscillations) solutions are indicated by text labels in each figure.

3.2.1. Delayed Onset of Epileptiform Discharges

As shown in Figures 7A,B, the weak feedforward inhibition, C_it, can not effectively inhibit the cortical activity motivated by the feedforward excitations, C_et, which can immediately induce the high-frequency tonic oscillations. However, as shown in Figure 7C, with the feedforward inhibition getting large, e.g., C_it = 0.4, the feedforward excitation induced tonic oscillations can be suppressed and the system transits into the low saturated state (LS). This means feedforward inhibition can delay the onset of epileptic tonic seizures by inhibiting the abnormal epileptic activities activated by feedforward excitations. Interestingly, compared Figure 7C with Figure 7D, we can find that with C_et further increasing the postponed onset of tonic oscillations in the modified model can be prolonged. Dynamically, this state transition from tonic oscillations to low saturated firing is attributed to the bistability mechanism composed of stable limit cycle and stable fixed point. Specifically, when C_it is set at small values, e.g., C_it = 0.1 or 0.2, weak feedforward inhibition fails to drive the system to escape from the attractor basin of limit cycle representing the tonic oscillations. However, as C_it increased, e.g., C_it = 0.4, for the small feedforward excitation, e.g., C_et < 0.1, which leads to the tonic oscillations with lower dominant frequency, the feedforward inhibition can successfully drive the system beyond the separatrix and into the attractor basin of fixed point, and the system will eventually converge to the steady saturated states. In particular, with C_it further increasing, the tonic oscillations with higher-frequency induced by the larger 0.1 < C_et < 0.2 can also be terminated through driving the system to escape away from the attractor basin of limit cycle with smaller period. Exemplary time series for the solutions of low saturated firing and tonic oscillations are shown in Figures 4A,F.

3.2.2. Seizure Transitions between m-SWD (r-SWD) Discharges and Clonic (r-Clonic) Oscillations

Compared Figures 7D–F to Figure 7C, it can be seen that for 0.2 < C_et < 0.6, the larger feedforward inhibitions can not abate the tonic oscillations again, but induce the more richer slow-wave dynamics. In particular, for C_it = 0.7 (Figure 7D), the whole system shows the low-frequency (<10 Hz) oscillations, along with the shift of tonic oscillations (TO) to high-frequency clonic oscillations (h-CO). Also, for 0.2 < C_et < 0.3 the reversed SWD discharges (r-SWD) emerge from the tonic-clonic oscillations. With the further increasing of C_it, e.g., C_it = 1.0, r-SWD discharges are gradually transformed into the reversed clonic oscillations (r-CO). Along with this transformations is the emergence of new r-SWD discharges from the h-CO oscillations in the larger parameter region, 0.3 < C_et < 0.6. For the much large C_it = 1.8, r-SWD discharges can eventually transit into the r-CO oscillations. In some sense, under the condition of weak feedforward excitation (e.g., C_et < 0.6), with the increasing of feedforward inhibition, the state evolutions from tonic-clonic oscillations to reversed SWD (r-SWD) discharges and clonic oscillations (r-CO) describe the physiological transitions between tonic-clonic and absence epileptic seizures. Exemplary time series for the solutions of r-CO, r-SWD and h-CO are shown in Figures 4G,H,I.

In addition, Figures 7A–E also show that with C_it increasing from 0.1, 0.2, 0.4 to 0.7, the parameter region of C_et corresponding to SWD is getting larger. And within the parameter region of larger C_et corresponding to m-SWD, the system transits from 4-SWD, 3-SWD to 2-SWD, respectively. As C_it further increased, e.g., C_it = 1.0, the 2-SWD and SWD discharges of the system within 1.0 < C_et < 1.5 can be further suppressed and turned into low-frequency (<5 Hz) clonic oscillations (l-CO, see Figure 4J). For the much large C_it = 1.8, within 0.6 < C_et < 2.0, the whole system is inhibited by the large enough feedforward inhibitions and only shows the ~1.5 Hz slow-wave clonic oscillations. These transitions from m-SWD (m = 1,2,3,4) to clonic oscillations induced by the feedforward inhibition represent the physiologically observed absence-clonic seizures shown in Figure 1B.

3.3. Combined Effects of Feedforward Inhibition and Excitation on Epileptic Seizures

In order to observe the overall dynamics transition of the modified Taylor model as shown in Figure 2, we depict the state transitions (Figure 8A) and corresponding dominant frequency (Figure 8B) as the feedforward excitation and inhibition from subcortical thalamus to cortex, C_et and C_it, are changed in 2-D plane [0, 2] × [0, 2]. It can be seen in Figure 8A that there are ten types of firing states, which are denoted as: LS/HS: low/high saturated firings, TO: tonic oscillations with high frequency (>10 Hz) and low amplitude, h/l-CO: clonic oscillations with high (>5 Hz & <10 Hz) and low (~2 Hz) frequencies, r-CO: reversed clonic oscillations, m-SWD: multi-spike and wave discharges (m = 2,3), SWD: spike and wave discharges (m = 1), r-SWD: reversed SWD discharges.

FIGURE 8

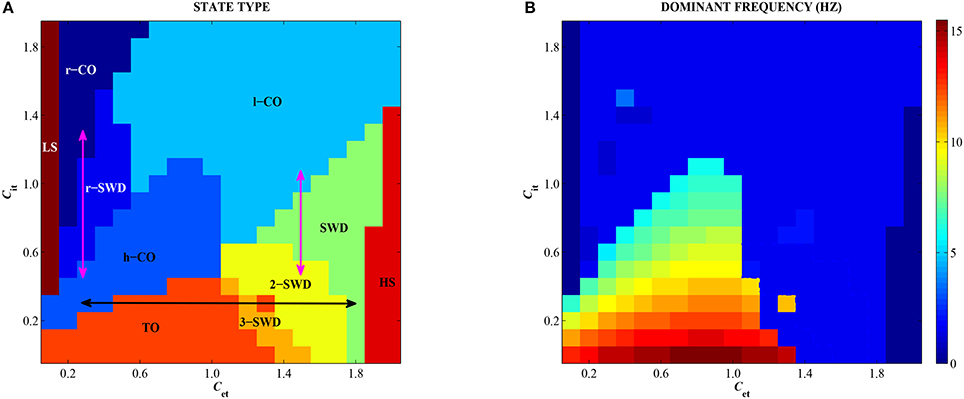
Figure 8. (Color online) Different firing states (A) and variations of corresponding dominant frequency (B) of the single modified Taylor model are shown on the parameter plane (C_et, C_it). TO, m/r-SWD (m = 1,2,3), LS, HS, and r/h/l-CO solutions are indicated by text labels. Double arrows indicate the possible transition pathways between different firing states.

Specifically, for the both small values of C_et and C_it, the system exhibits the epileptic tonic-clonic oscillations. By contrast, the much large C_et and C_it can suppress the system to show low-frequency clonic oscillations. However, the unbalanced functions between feedforward excitation and inhibition can induce the epileptic spike-wave discharges. For example, for the small C_it (e.g., <1, i.e., the weak feedforward inhibition), the strong feedforward excitation (e.g., C_et > 1) can activate the system to display typical m-SWD (m = 2, 3) and SWD (m = 1) discharges of absence seizures in epilepsy. Conversely, for the small C_et (e.g., <0.6, i.e., the weak feedforward excitation), the stronger feedforward inhibition can induce the reversed SWD (r-SWD) discharges and clonic (r-CO) oscillations. In particular, the horizontal double black arrow and the left vertical double pink arrow represent the physiologically observed epileptic transitions from tonic-clonic oscillations to absence seizures (see Figure 1A), which corresponds to the results of Sections 3.1.1 and 3.2.2, respectively. The right vertical pink arrow represents the physiologically observed seizure transitions from absence seizures to clonic oscillations of epilepsy (see Figure 1B), which also corresponds to the result of Section 3.2.2. In addition, non-oscillation activities, i.e., saturated states, occur for the small C_et and large C_it, or the large C_et and small C_it, corresponding to regions LS and HS, respectively. What's more, as shown in Figure 8B, only both weak feedforward excitation and inhibition, corresponding the parameter region of small C_et and C_it, can result in the high-frequency oscillations, while the other parameter regions correspond to the low-frequency oscillations.

4. Conclusion

In this paper, using a modified thalamocortical neural field model network, we systematically investigated the combined effects of feedforward inhibition and excitation from thalamus to cortex on the epileptic seizure transitions. Electrophysiological experiments have long revealed the existence of two-way transitions between absence and tonic-clonic epileptic seizures in the cerebral cortex (Mayville et al., 2000; Shih and Hirsch, 2003). By computational modeling, we first demonstrated that under the condition of weak feedforward inhibition, the enhancement of feedforward excitation can induce the transitions from tonic-clonic oscillations of epilepsy to SWD of absence seizures. More importantly, we showed that the phase of absence seizures corresponding to strong feedforward excitation can be further transformed into the clonic oscillations with the enhancement of feedforward inhibition, representing the epileptic absence-clonic seizure transitions. Our findings highlight the functional importance of thalamic feedforward inhibition and excitation, which might contribute to the emergences and transitions of epileptic seizures including tonic-clonic oscillations and absence epilepsy.

Inhibitory interneuronal population plays a crucial role in the seizure suppressions. It can confront the abnormal discharges of excitatory neuronal population to control epileptic seizures. Hence, our model can be extended to investigate the opposite issues such as the modulations or suppressions of absence seizures by balancing thalamic feedforward inhibition and excitation. However, it remains difficult to discern whether the feedforward inhibition are leading the feedforward excitation or vice versa. In addition, previous experimental study has shown that RE can facilitate sharing information and consolidate new memories by coordinating the slow-wave oscillations of different brain regions (Lewis et al., 2015). Hence, we will explore the modulating role of RE for the feedforward effect of TC on the transitional dynamics of epileptic seizures.

Author Contributions

DF, LD, QW, and GL designed and performed the research as well as wrote the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research is supported by the National Natural Science Foundation of China (Grant Nos. 11325208, 11472009, 11572015, 11172017, and 81671285), the Construction Plan for Innovative Research Team of North China University of Technology (XN018010), the Capital Health Research and Development of Special (2016-1-8012), Beijing Municipal Science & Technology Commission (Z161100000516230, Z161100002616016), the Project funded by China Postdoctoral Science Foundation (Grant No. 2016M600037) and the Fundamental Research Funds for the Central Universities (FRF-TP-16-068A1).

References

Barnes, G. N., and Paolicchi, J. M. (2008). Neuropsychiatric comorbidities in childhood absence epilepsy. Nat. Clin. Pract. Neurol. 4, 650–651. doi: 10.1038/ncpneuro0947

PubMed Abstract | CrossRef Full Text | Google Scholar

Borisyuk, R. M., and Kirillov, A. B. (1992). Bifurcation analysis of a neural network model. Biol. Cybernet. 66, 319–325. doi: 10.1007/BF00203668

PubMed Abstract | CrossRef Full Text | Google Scholar

Caplan, R., Siddarth, P., Stahl, L., Lanphier, E., Vona, P., and Gurbani, S., et al. (2008). Childhood absence epilepsy: behavioral, cognitive, and linguistic comorbidities. Epilepsia 49, 1838–1846. doi: 10.1111/j.1528-1167.2008.01680.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, M., Guo, D., Wang, T., Jing, W., Xia, Y., and Xu, P., et al. (2014). Bidirectional control of absence seizures by the basal ganglia: a computational evidence. PLoS Comput. Biol. 10:e1003495. doi: 10.1371/journal.pcbi.1003495

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, M., Guo, D., Li, M., Ma, T., Wu, S., and Ma, J., et al. (2015). Critical roles of the direct gabaergic pallido-cortical pathway in controlling absence seizures. PLoS Comput. Biol. 11:e1004539. doi: 10.1371/journal.pcbi.1004539

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, M., Guo, D., Xia, Y., and Yao, D. (2017). Control of Absence Seizures by the Thalamic Feed-Forward Inhibition. Front. Comput. Neurosci. 11:31. doi: 10.3389/fncom.2017.00031

PubMed Abstract | CrossRef Full Text | Google Scholar

Coenen, A. M., and Van Luijtelaar, E. L. (2003). Genetic animal models for absence epilepsy: a review of the WAG/Rij strain of rats. Behav. Genet. 33, 635–655. doi: 10.1023/A:1026179013847

PubMed Abstract | CrossRef Full Text | Google Scholar

Cruikshank, S. J., Lewis, T. J., and Connors, B. W. (2007). Synaptic basis for intense thalamocortical activation of feedforward inhibitory cells in neocortex. Nat. Neurosci. 10, 462–468. doi: 10.1038/nn1861

PubMed Abstract | CrossRef Full Text | Google Scholar

Crunelli, V., and Leresche, N. (2009). “Absence seizures: oscillations in thalamocortical networks and the putative 'initiation site' of typical absence seizures,” in Encyclopedia of Basic Epilepsy Research, ed P. A. Schwartzkroin (Elsevier), 15–21. doi: 10.1016/B978-012373961-2.00053-9

CrossRef Full Text

Delevich, K., Tucciarone, J., Huang, Z. J., and Li, B. (2015). The mediodorsal thalamus drives feedforward inhibition in the anterior cingulate cortex via parvalbumin interneurons. J. Neurosci. Off. J. Soc. Neurosci. 35, 5743–5753. doi: 10.1523/JNEUROSCI.4565-14.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Devinsky, O., Nadi, S., Theodore, W. H., and Porter, R. J. (1988). Cerebrospinal fluid pleocytosis following simple, complex partial, and generalized tonic-clonic seizures. Ann. Neurol. 23, 402–403. doi: 10.1002/ana.410230418

PubMed Abstract | CrossRef Full Text | Google Scholar

Devinsky, O., Sato, S., Kufta, C. V., Ito, B., Rose, D. F., and Theodore, W. H., et al. (1989). Electroencephalographic studies of simple partial seizures with subdural electrode recordings. Neurology 39, 527–533. doi: 10.1212/WNL.39.4.527

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, L., Lu, Q., and Wang, Q. (2008). Two-parameter bifurcation analysis of firing activities in the chay neuronal model. Neurocomputing 72, 341–351. doi: 10.1016/j.neucom.2008.01.019

CrossRef Full Text | Google Scholar

Ermentrout, G. B. (2002). Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students. Philadelphia: Society for Industrial and Applied Mathematics. doi: 10.1137/1.9780898718195

CrossRef Full Text | Google Scholar

Fan, D., Liu, S., and Wang, Q. (2016). Stimulus-induced epileptic spike-wave discharges in thalamocortical model with disinhibition. Sci. Rep. 6, 37703. doi: 10.1038/srep37703

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, D., Wang, Q., and Perc, M. (2015). Disinhibition-induced transitions between absence and tonic-clonic epileptic seizures. Sci. Rep. 5, 12618. doi: 10.1038/srep12618

PubMed Abstract | CrossRef Full Text | Google Scholar

Fong, G. C., Shah, P. U., Gee, M. N., Serratosa, J. M., Castroviejo, I. P., Khan, S., et al. (1998). Childhood absence epilepsy with tonic-clonic seizures and electroencephalogram 3-4-hz spike and multispike-slow wave complexes: linkage to chromosome 8q24. Am. J. Hum. Genet. 63, 1117–1129. doi: 10.1086/302066

PubMed Abstract | CrossRef Full Text | Google Scholar

Freestone, D. R., Grayden, D. B., Lai, A., and Nelson, T. S. (2009). “The thalamocortical circuit and the generation of epileptic spikes in rat models of focal epilepsy,” in International Conference of the IEEE Engineering in Medicine & Biology Society (Minneapolis, MN). doi: 10.1109/iembs.2009.5333073

CrossRef Full Text | Google Scholar

Gantmakher, F. R. (1967). The theory of matrices. Monatshefte Fur Mathematik Und Physik 2, 63–72.

Google Scholar

Herrera, C. G., Cadavieco, M. C., Jego, S., Ponomarenko, A., Korotkova, T., and Adamantidis, A. (2015). Hypothalamic feedforward inhibition of thalamocortical network controls arousal and consciousness. Nat. Neurosci. 19:290. doi: 10.1038/nn.4209

PubMed Abstract | CrossRef Full Text | Google Scholar

Izhikevich, E. M. (2000). Neural excitabilility, spiking and bursting. Int. J. Bifurcation Chaos 10, 1171–1266. doi: 10.1142/S0218127400000840

CrossRef Full Text | Google Scholar

Jeniffer, V. N., Udayakumar, S., and Pushpalatha, K. (2015). A clinical study to identify the possible etiology of complex partial seizures using magnetic resonance imaging brain findings and its implications on treatment. J. Pediatr. Neurosci. 10:350. doi: 10.4103/1817-1745.174435

PubMed Abstract | CrossRef Full Text | Google Scholar

Ji, G. J., Zhang, Z., Xu, Q., Zang, Y. F., Liao, W., and Lu, G. (2014). Generalized tonic-clonic seizures: aberrant interhemispheric functional and anatomical connectivity. Radiology 271, 839–847. doi: 10.1148/radiol.13131638

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, H. I., Baek, M. R., Cho, K. H., Cho, Y. J., and Heo, K. (2016). Simple partial seizures aggravated or induced by benzodiazepine injection. Seizure 41, 6–8. doi: 10.1016/j.seizure.2016.06.020

CrossRef Full Text | Google Scholar

Kramer, M. A., Kirsch, H. E., and Szeri, A. J. (2005). Pathological pattern formation and cortical propagation of epileptic seizures. J. Roy. Soc. Inter. 2, 113–127. doi: 10.1098/rsif.2004.0028

PubMed Abstract | CrossRef Full Text | Google Scholar

Kush, P., Cauller, L. J., and Llano, D. A. (2016). Presence of a chaotic region at the sleep-wake transition in a simplified thalamocortical circuit model. Front. Comput. Neurosci. 10:91. doi: 10.3389/fncom.2016.00091

CrossRef Full Text | Google Scholar

Kuznetsov, Y., Kuznetsov, L., and Marsden, J. (1998). Elements of Applied Bifurcation Theory. New York, NY: Springer-Verlag.

Google Scholar

Lewis, L. D., Voigts, J., Flores, F. J., Schmitt, L. I., Wilson, M. A., and Halassa, M. M., et al. (2015). Thalamic reticular nucleus induces fast and local modulation of arousal state. Elife Sci. 4:e08760. doi: 10.7554/eLife.08760

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Tang, J., Ma, J., Du, M., Wang, R., and Wu, Y. (2016a). Dynamic transition of neuronal firing induced by abnormal astrocytic glutamate oscillation. Sci. Rep. 6:32343. doi: 10.1038/srep32343

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Wang, R., Du, M., Tang, J., and Wu, Y. (2016b). Dynamic transition on the seizure-like neuronal activity by astrocytic calcium channel block. Chaos Solit. Fract. 91, 702–708. doi: 10.1016/j.chaos.2016.08.009

CrossRef Full Text | Google Scholar

Liu, S., Wang, Q., and Fan, D. (2016). Disinhibition-induced delayed onset of epileptic spike-wave discharges in a five variable model of cortex and thalamus. Front. Comput. Neurosci. 10:81. doi: 10.3389/fncom.2016.00028

PubMed Abstract | CrossRef Full Text | Google Scholar

Marten, F., Rodrigues, S., Benjamin, O., Richardson, M. P., and Terry, J. R. (2009). Onset of polyspike complexes in a mean-field model of human electroencephalography and its application to absence epilepsy. Philos. Trans. Roy. Soc. Lond. A Math. Phys. Eng. Sci. 367, 1145–1161. doi: 10.1098/rsta.2008.0255

PubMed Abstract | CrossRef Full Text | Google Scholar

Mayville, C., Fakhoury, T., and Abou-Khalil, B. (2000). Absence seizures with evolution into generalized tonic-clonic activity: clinical and eeg features. Epilepsia 41, 391–394. doi: 10.1111/j.1528-1157.2000.tb00178.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Meeren, H. K., Pijn, J. P. M., Van Luijtelaar, E. L., Coenen, A. M., and da Silva, F. H. L. (2002). Cortical focus drives widespread corticothalamic networks during spontaneous absence seizures in rats. J. Neurosci. 22, 1480–1495. Available online at: http://www.jneurosci.org/content/22/4/1480.short

PubMed Abstract | Google Scholar

Millard, D. C., Wang, Q., and Stanley, G. B. (2011). Nonlinear system identification of the thalamocortical circuit in response to thalamic microstimulation. Int. Ieee/embs Conf. Neural Eng. 1359, 1–4. doi: 10.1109/ner.2011.5910475

CrossRef Full Text | Google Scholar

Mohamed, J., and Burnham, M. I. (2016). Identifying the pathological substrate(s) of complex partial seizures: blumenfelds network inhibition hypothesis. Clin. Neurophysiol. 127:e163. doi: 10.1016/j.clinph.2015.10.058

CrossRef Full Text | Google Scholar

Panayiotopoulos, C. P. (2001). Treatment of typical absence seizures and related epileptic syndromes. Pediatr. Drugs 3, 379–403. doi: 10.2165/00128072-200103050-00006

PubMed Abstract | CrossRef Full Text | Google Scholar

Paz, J. T., and Huguenard, J. R. (2015). Microcircuits and their interactions in epilepsy: is the focus out of focus? Nat. Neurosci. 18, 351–359. doi: 10.1038/nn.3950

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinault, D., and O'Brien, T. J. (2005). Cellular and network mechanisms of genetically-determined absence seizures. Thalamus Rel. Syst. 3:181. doi: 10.1017/S1472928807000209

PubMed Abstract | CrossRef Full Text | Google Scholar

Porter, J. T., Johnson, C. K., and Agmon, A. (2001). Diverse types of interneurons generate thalamus-evoked feedforward inhibition in the mouse barrel cortex. J. Neurosci. Offic. J. Soc. Neurosci. 21, 2699–2710. Available online at: http://www.jneurosci.org/content/21/8/2699.short

PubMed Abstract | Google Scholar

Quiroga, R. Q., Blanco, S., Rosso, O. A., Garcia, H., and Rabinowicz, A. (1997). Searching for hidden information with Gabor Transform in generalized tonic-clonic seizures. Electroencephalogr. Clin. Neurophysiol. 103, 434–439. doi: 10.1016/S0013-4694(97)00031-X

CrossRef Full Text | Google Scholar

Rinzel, J. (1985). “Bursting oscillations in an excitable membrane model,” in Ordinary and Partial Differential Equations, Lecture Notes in Mathematics, eds B. D. Sleeman and R. J. Jarvis (New York, NY: Springer), 304–316.

Google Scholar

Rodrigues, S., Barton, D., Szalai, R., Benjamin, O., Richardson, M. P., and Terry, J. R. (2009). Transitions to spike-wave oscillations and epileptic dynamics in a human cortico-thalamic mean-field model. J. Comput. Neurosci. 27, 507–526. doi: 10.1007/s10827-009-0166-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodrigues, S., Goncalves, J., and Terry, J. R. (2007). Existence and stability of limit cycles in a macroscopic neuronal population model. Phys. D Nonlin. Phenom. 233, 39–65. doi: 10.1016/j.physd.2007.06.010

CrossRef Full Text | Google Scholar

Rogers, J. K., Hutton, J., Marson, A. G., and Chadwick, D. W. (2012). Assessing the risk of subsequent tonic-clonic seizures in patients with a history of simple or complex partial seizures. J. Neurol. Neurosur. Psychiat. 83, 803–809. doi: 10.1136/jnnp-2011-300917

CrossRef Full Text | Google Scholar

Sasaki, S., Huda, K., Inoue, T., Miyata, M., and Imoto, K. (2006). Impaired feedforward inhibition of the thalamocortical projection in epileptic ca²⁺ channel mutant mice, tottering. J. Neurosci. Offic. J. Soc. Neurosci. 26, 3056–3065. doi: 10.1523/JNEUROSCI.5422-05.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Sherman, S. M. (2012). Thalamocortical interactions. Curr. Opin. Neurobiol. 22, 575–579. doi: 10.1016/j.conb.2012.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Shih, T. T., and Hirsch, L. J. (2003). Tonic-absence seizures: an underrecognized seizuretype. Epilepsia 44, 461–465. doi: 10.1046/j.1528-1157.2003.39602.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Shinnar, S., Cnaan, A., Hu, F., Clark, P., Dlugos, D., Hirtz, D. G., et al. (2015). Long-term outcomes of generalized tonic-clonic seizures in a childhood absence epilepsy trial. Neurology 85, 1108–1114. doi: 10.1212/WNL.0000000000001971

PubMed Abstract | CrossRef Full Text | Google Scholar

Sitnikova, E. (2010). Thalamo-cortical mechanisms of sleep spindles and spike-wave discharges in rat model of absence epilepsy (a review). Epilep. Res. 89, 17–26. doi: 10.1016/j.eplepsyres.2009.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Taylor, P. N., Wang, Y., Goodfellow, M., Dauwels, J., Moeller, F., Stephani, U., et al. (2014). A computational study of stimulus driven epileptic seizure abatement. PLoS ONE 9:e114316. doi: 10.1371/journal.pone.0114316

PubMed Abstract | CrossRef Full Text | Google Scholar

Timofeev, I., and Steriade, M. (2004). Neocortical seizures: initiation, development and cessation. Neuroscience 123, 299–336. doi: 10.1016/j.neuroscience.2003.08.051

PubMed Abstract | CrossRef Full Text | Google Scholar

Wakamoto, H., Fukuda, M., Shigemi, R., Murakami, Y., Motoki, T., Ohmori, H., et al. (2011). Atypical childhood absence epilepsy with preceding or simultaneous generalized tonic clonic seizures. Brain Dev. 33, 589–592. doi: 10.1016/j.braindev.2010.09.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Lu, G., Zhang, Z., Zhong, Y., Jiao, Q., Zhang, Z., et al. (2011). Altered resting state networks in epileptic patients with generalized tonic-clonic seizures. Brain Res. 1374, 134–141. doi: 10.1016/j.brainres.2010.12.034

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., and Wang, Q. (2017). Eliminating Absence Seizures through the Deep Brain Stimulation to Thalamus Reticular Nucleus. Front. Comput. Neurosci. 11:22. doi: 10.3389/fncom.2017.00022

PubMed Abstract | CrossRef Full Text | Google Scholar

Varon Perez, J. C., Jansen, K., Lagae, L., and Van Huffel, S. (2012). Cardiorespiratory analysis on children suffering from absence and complex partial seizures. Arch. Gen. Psychiatry 39, 113–116. Available online at: http://ieeexplore.ieee.org/abstract/document/6420343/

Vaurio, L., Karantzoulis, S., and Barr, W. B. (2017). “The Impact of Epilepsy on Quality of Life,” in Changes in the Brain (New York, NY: Springer), 167–187. doi: 10.1007/978-0-387-98188-8_8

CrossRef Full Text | Google Scholar

Youngblood, M. W., Chen, W. C., Mishra, A. M., Enamandram, S., Sanganahalli, B. G., Motelow, J. E., et al. (2015). Rhythmic 3-4 Hz discharge is insufficient to produce cortical bold fmri decreases in generalized seizures. Neuroimage 109, 368–377. doi: 10.1016/j.neuroimage.2014.12.066

CrossRef Full Text | Google Scholar