- 1Computational Intelligence Lab, Department of Scientific Computing, Florida State University, Tallahassee, FL, United States
- 2Institute of Biomedical and Clinical Science, University of Exeter Medical School, Exeter, United Kingdom
Intracellular Ca2+ dynamics in astrocytes can be triggered by neuronal activity and in turn regulate a variety of downstream processes that modulate neuronal function. In this fashion, astrocytic Ca2+ signaling is regarded as a processor of neural network activity by means of complex spatial and temporal Ca2+ dynamics. Accordingly, a key step is to understand how different patterns of neural activity translate into spatiotemporal dynamics of intracellular Ca2+ in astrocytes. Here, we introduce a minimal compartmental model for astrocytes that can qualitatively reproduce essential hierarchical features of spatiotemporal Ca2+ dynamics in astrocytes. We find that the rate of neuronal firing determines the rate of Ca2+ spikes in single individual processes as well as in the soma of the cell, while correlations of incoming neuronal activity are important in determining the rate of “global” Ca2+ spikes that can engulf soma and the majority of processes. Significantly, our model predicts that whether the endoplasmic reticulum is shared between soma and processes or not determines the relationship between the firing rate of somatic Ca2+ events and the rate of neural network activity. Together these results provide intuition about how neural activity in combination with inherent cellular properties shapes spatiotemporal astrocytic Ca2+ dynamics, and provide experimentally testable predictions.
1. Introduction
In the last 25 years, the prevailing notion that astrocytes serve purely as structural and metabolic support has evolved to viewing them as units that interact with neuronal inputs and alter neuronal activity. This new paradigm of astrocyte function emerged after it was discovered that astrocytes possess Ca2+ excitability in the form of Ca2+ spikes and oscillations. These can be triggered by neuronal activity and the subsequent release of neurotransmitters and increase in extracellular K+. Following Ca2+ activity, astrocytes can release gliotransmitters that act at the synaptic or perisynaptic level to strengthen or weaken synapses, or to change neuronal activity. This fueled a number of modeling studies that investigated the mechanisms through which synaptic activity triggers Ca2+ spikes in astrocytes and how, in turn, the astrocyte response affects the synapses (Nadkarni and Jung, 2007; Postnov et al., 2007; De Pitta et al., 2009; Wade et al., 2011; Tewari and Majumdar, 2012; Khalid et al., 2017). These studies naturally focused on temporal Ca2+ dynamics.
Astrocyte-to-neuron signaling directly and indirectly impacts the dynamics of synapses and neurons (Halassa et al., 2009b; Henneberger et al., 2010; Kimelberg and Nedergaard, 2010; Perea and Araque, 2010). These effects can have a short or long duration, and they can affect single or multiple neurons (Halassa et al., 2009a). Paralleling this multiplicity of actions on different temporal and spatial scales, recent in vivo imaging of astrocyte Ca2+ activity in response to neuronal activity has revealed a spatiotemporal hierarchy of Ca2+ events. They range from fast Ca2+ fluctuations in the astrocyte periphery to Ca2+ spiking across the astrocyte branches and in the cell body (Di Castro et al., 2011; Araque et al., 2014; Kanemaru et al., 2014; Rusakov et al., 2014; Bindocci et al., 2017).
These spatiotemporal events interact in complex ways with governing rules that are important to clarify (Volterra et al., 2014; Bazargani and Attwell, 2016; Bindocci et al., 2017) since they may underlie different classes of astrocyte-to-neuron signaling. Recent work suggests that the most distal processes, which receive synaptic inputs, possess channels that allow fast, localized extracellular Ca2+ influx (Di Castro et al., 2011; Bindocci et al., 2017). However these peripheral perisynaptic processes lack the Ca2+ stores to trigger Ca2+-induced Ca2+ release (CICR) (Patrushev et al., 2013; Rusakov, 2015). Thus, wider Ca2+ events resulting from CICR are only observed in larger, more proximal processes, away from neuronal synapses (Rusakov, 2015). Bindocci et al. (2017) have used three-dimensional imaging and reconstructions of astrocytes to describe fast and local Ca2+ events scattered in the astrocyte gliapil (optically unresolved perisynaptic processes) and the larger events occuring in the astrocyte core (soma and major processes). Of those larger events, a much greater fraction occured in major processes than in the soma. Occasionally, global events that invaded most of the core were observed. These events were not sweeping waves, but were triggered by the simultaneous occurence of Ca2+ events in multiple loci, generally in the gliopil, and presumably due to synchronous neuronal activity.
This diversity and complexity of Ca2+ events calls for spatial models to understand astrocyte Ca2+ dynamics and how they affect neurons and synapses. To date, there are only a handful of spatial models designed to study the spatio-temporal Ca2+ dynamics in astrocytes. Kang and Othmer (2009) developed a 2D spatial model with realistic cellular morphology. Their goal, however, was not to study the dynamics of Ca2+ events within an astrocyte, but to study how network connectivity, IP3 diffusion, and ATP transport affected the propagation of Ca2+ waves across astrocyte networks. Wu et al. (2014) modeled Ca2+ and IP3 dynamics based on a temporal single point model (Ullah et al., 2006) extended to a homogeneous square domain. This model could reproduce the power-law distribution of Ca2+ event duration and intensity observed in hippocampal astrocytes, demonstrating that scale-free Ca2+ dynamics can arise from intracellular IP3 diffusion. Gordleeva et al. (2018) developed a multi-compartmental model of an astrocyte with realistic morphology. They stimulated the most distal compartments on each of their astrocytic processes and considered how the resulting Ca2+ signal propagated toward the soma. Synchronous stimulation of multiple processes was necessary for activation of the astrocyte soma, suggesting that astrocytes can serve as detectors of spatial synchronization in a neural network. Finally, Savtchenko et al. (2018) developed a compartmental astrocyte-model builder to reproduce astrocyte morphology and function with high detail. They were able to fit parameters of such a model to physiological data, and demonstrated the use of the model to examine the role of fine details of astrocyte functional morphology, such as the distance between IP3 receptor clusters, on Ca2+ dynamics.
Here, we develop an astrocyte compartmental model to study how stochastic Ca2+ influx due to neuronal activity triggers Ca2+ spikes in the main astrocyte processes and how this in turn triggers Ca2+ spikes in the soma and global events involving the soma and most major processes. This is similar to the work of Gordleeva et al. (2018), but here we distinguish between fast Ca2+ events due to synaptic activity and slower events involving CICR, inspired by the hierarchy of Ca2+ events described by Araque et al. (2014). We use a model of complexity intermediate between the single point model of Postnov et al. (2007) and the model of Gordleeva et al. (2018). Keeping the number of compartments and biophysical complexity to a minimum limits the number of variables and free parameters, providing better intuition and understanding of the model dynamics. We use this simple model architecture to ask the following questions:
1. How are neuronal inputs integrated to produce Ca2+ spikes in the astrocyte soma?
2. How do neuronal input properties, such as their correlations and distribution over the astrocyte, facilitate Ca2+ spikes in the soma and global events involving most processes?
3. How do diffusive properties of the cytosol and Ca2+ stores impact the production of soma Ca2+ spikes?
2. Methods and Model Description
2.1. Compartmental Model
We model the astrocyte as a soma with five major processes (see Figure 1). Each compartment defines its own single point model assuming homogeneization of Ca2+ concentration and interacts with the other compartments through diffusion. Compartmental Ca2+ in the cytosol and endoplasmic reticulum (ER) is expressed in terms of its concentrations and for process i, and and in the soma. Diffusion of Ca2+ between the soma and the process is proportional to the difference in Ca2+ concentration between the two compartments.
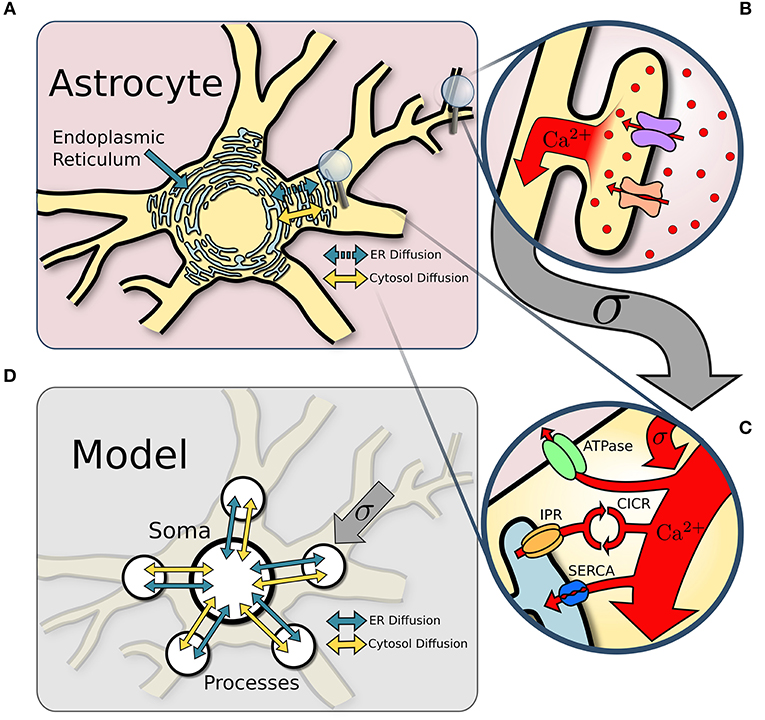
Figure 1. Model structure. (A) Overview of an astrocyte structure. The endoplasmic reticulum (ER) covers the astrocyte core (soma and major processes). (B) In response to neuronal activity, Ca2+ enters the perisynaptic astrocyte processes via the Na+/Ca2+ exchanger and other Ca2+ channels. (C) Ca2+ influx from perisynaptic processes sums at the larger ER-holding processes, which can activate Ca2+-induced-Ca2+-release (CICR). Removal of Ca2+ occurs via ATPase and SERCA pumps. (D) The astrocyte soma and five of its major processes are approximated with single point models connected via diffusion across both the ER and the cytosol.
The Ca2+ dynamics is governed by a system of ODEs based on the non-dimensional functional model of Postnov et al. (2007). The explicit influence of the neurons is described by a source term that models the input of extracellular Ca2+ into the process cytosol via a variety of channels. Model dynamics are governed by the fluxes between cytosol and ER due to IPR activation and reuptake of Ca2+ by the ER through SERCA pumps. Finally, Ca2+ ions diffuse through the cytosol between soma and processes; we also include in the model the possibility for Ca2+ ions to diffuse through the ER. The Ca2+ thus satisfies the following set of equations:
where Equations 1 and 3 represent process Ca2+ dynamics and Equations 4 and 5 represent Ca2+ dynamics in the soma. Diffusion of Ca2+ ions between process i and the soma in the cytosol and the ER are respectively denoted by and . The small parameter ϵc in Equation 5 controls the separation of timescales of the calcium in the cytosol and the ER.
Table 1 lists the model parameters and their default values.
The parameter r controls the intrinsic Ca2+ excitability of each compartment, which may include a contribution from TRPA1 channels to basal Ca2+(Shigetomi et al., 2012). We set r = 0.31, which is just below the threshold for spontaneous Ca2+ spikes, as in Postnov et al. (2007). The effect of distal neuronal sources on the dynamics of Ca2+ in process i is captured by the source term σξi, where ξi is sampled from N(0, 1). This fluctuating Ca2+ term is due in part to the Na+/Ca2+ exchanger (NCX), which is co-localized with Na+-dependent glutamate transporters, as well as neurotransmitter-gated Ca2+-permeable ion channels such as AMPA, NMDA, or P2X receptors (Kirischuk et al., 1997, 2007; Bazargani and Attwell, 2016). These Ca2+ signals combine with many others upon reaching the primary branch (Araque et al., 2014; Bindocci et al., 2017).
The diffusion coefficient DI is set to 0.05 unless otherwise noted. The role played by the distribution and the geometry of the ER in glial cells has been under debate with evidence supporting varying degrees of ER interaction between domains of the astrocyte (Blaustein and Golovina, 2001; Petersen et al., 2001; Levine and Rabouille, 2005). To be consistent with these recent findings, we start by setting DE = 0, but later consider the influence of non-zero values.
In Equations 1 and 5, the Ca2+ flux from ER to cytosol through IPR is represented by Jr, while the flux from cytosol to ER due to SERCA pumps is represented by Jp. To simplify the notation, we express these fluxes below in terms of Hill functions, defined by:
Excitability of Ca2+ dynamics is the result of Ca2+ flow between the cytosol and IP3-sensitive internal Ca2+ stores, which is initiated by the influx of either IP3 or extracellular Ca2+. There is a large spectrum of IPR models that vary in their consideration of IP3 and Ca2+. The primary characteristics that all IPR models share is that the steady-state open probability of the IPR channels are represented by a bell shaped function of Ca2+ (Dupont et al., 2016), which results in Ca2+-induced Ca2+ release (CICR) from internal stores. This work utilizes a representation of IPR flux taken from (Goldbeter et al., 1990) that assumes a sufficient level of IP3 and models the release of Ca2+ from the ER by an interaction between the two Ca2+ pools,
where CI and CE are the non-dimensional Ca2+ concentrations for the cytosol and ER respectively, and b2 sets the half-activation value of CI for the IP3 channel. This model approximates IPR dynamics with a fast activation and slow inactivation of the channel by Ca2+ Dupont et al. (2016). We omit IP3 dynamics and diffusion in order to present the simplest possible framework through which a hierarchy of Ca2+ activity can be represented and explored.
Cells continuously pump Ca2+ from the cytosol into the ER through SERCA pumps on the ER membrane, modeled as
where b1 is the maximum velocity of the reaction Dupont et al. (2016). SERCA pumps are influential in sustaining non-linear dynamics because they replenish the ER which is the source of excitable behavior.
2.2. Numerical Method
The governing Equations (1-4) are solved numerically using a first order Euler-Maruyama method (Kloeden and Platen, 1992) to properly treat the stochastic neuronal input term σξi. To establish the appropriate time discretization, several simulations were run with σ = 0, with default model parameters found in Table 1, except for r, which was set to r = 0.32, just beyond the threshold for spontaneous spike generation. To establish the appropriate step size we ran a simulation of 10,000 time units with successively smaller Δt. We found that below Δt = 0.5, the change in all spike times in the processes and in the soma satisfied
where tspikeΔt is a spike time for a step size Δt. Spike times are identified by CI crossing a threshold of 1.2 while increasing Meyer and Stryer (1991). The numerical code is freely available and can be downloaded from https://github.com/FSUcilab/Compartmental_model_astrocytes.git
2.3. Correlated Neural Inputs
Astrocyte processes likely receive correlated input since the neuronal populations that contribute input to each process may overlap or have correlated activities (Averbeck et al., 2006; López-Hidalgo and Schummers, 2014). To allow flexible experimentation with correlated input, we construct a function that generates k input signals that have a fixed pairwise correlation coefficient ρ, where k is the number of active astrocyte processes. Starting with k uncorrelated signals ξ sampled from a normal distribution N(0, 1), we first compute the correlation matrix Σ such that Σij = (1−δij)ρ+δij (where δij is the Kronecker Delta) and perform a Cholesky factorization Σ = LLT (Johnson, 1994). Multiplication of L by the vector of uncorrelated signals ξ produces k signals with the desired correlation ρ:
2.4. Spike-Triggered Average
To analyze the relationship between the activity in the different compartments, we use spike-triggered averaging (STA) (Schwartz et al., 2006). For each soma spike, the Ca2+ trace of a process is selected within a time window preceding the soma spike. This ensemble of Ca2+ traces are then averaged. For comparison, we compute a baseline for which Ca2+ traces of the same length are selected at random times and averaged.
3. Results
3.1. Response of a Compartmental Astrocyte Model to Neuronal Activity
Several studies have demonstrated that Ca2+ undergoes small, localized, oscillatory Ca2+ responses within the processes (Perea and Araque, 2002; Di Castro et al., 2011; Panatier et al., 2011; Araque et al., 2014; Bindocci et al., 2017). Integration of this activity may lead to local spiking in individual processes, which can recruit the soma and produce global spikes encompassing the soma and additional processes (Araque et al., 2014; Bindocci et al., 2017). In our model, each process i receives a neuronal input modeled as a Ca2+ source term ξi(t). We explore how this leads to CICR-driven spikes in processes and soma. In general, nearby neurons can be correlated (Averbeck et al., 2006), and thus, the Ca2+ dynamics in the different processes might be correlated as well. As mentioned in section 2.3, we assume a pairwise correlation between input sources of ρ and explore the effect of ρ on the spiking frequency in the processes and the soma. We begin our simulations with zero signal correlation.
A time course of cytosolic Ca2+ in each process and in the soma is shown in Figure 2A, which includes an insert that zooms in on the subthreshold Ca2+ activity in two processes in response to the noisy neural input. The neuronal input signal amplitude (defined as the standard deviation of the signal) is initially set to σ = 0.2 . One of the soma spikes is identified as a global event, defined when at least four of five processes spike within a period of 12.5 time units from the soma spike. Thus our model covers the three scales of Ca2+ activity observed experimentally (Araque et al., 2014): a small scale for subthreshold Ca2+ activity due to neuronal inputs (hundreds of ms, spatially restricted to < 5μm), an intermediate timescale set by the process spikes (seconds, spatially extending over the length of a process), and the large scale of global events (up to 10 s, extending to most of the astrocyte core). The interval between successive spikes in a given process follows a sharp, approximately log-normal distribution (Figure 2B). The soma spikes at a lower frequency than the processes, as observed experimentally (Nimmerjahn et al., 2009; Kanemaru et al., 2014; Bindocci et al., 2017) and the distribution of interspike intervals is much wider for the soma than for the processes (Figure 2B), that is, there is more randomness in spike timing in the soma than in the processes.
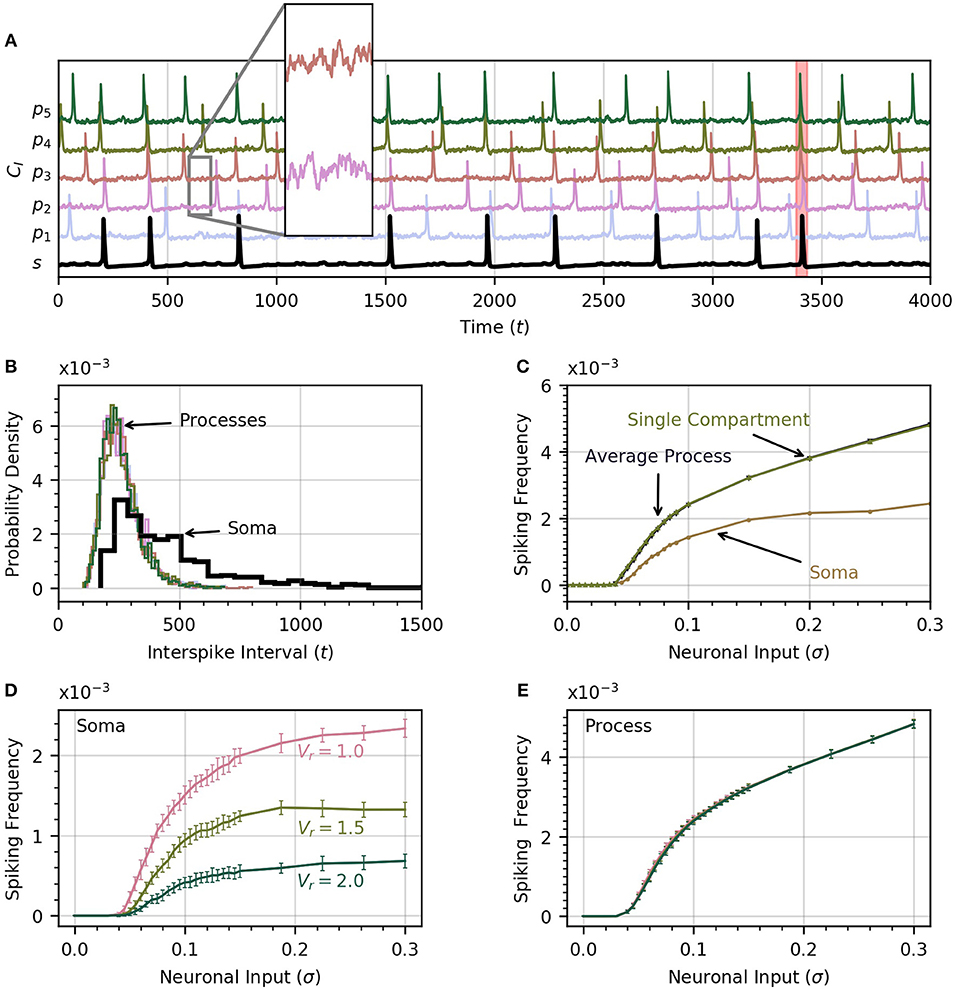
Figure 2. Astrocyte activity under random neuronal input. (A) Time course of cytosolic Ca2+ concentration in five processes (color) and the soma (black, bottom trace) over a 4000 time unit interval. All time traces have been normalized to their maximum value. Subthreshold oscillations are depicted in the inset. The shaded rectangle in the proximity of t = 3500 indicates a global event when at least four of five processes spike within 12.5 time units of the soma spike. (B) Histograms of interspike intervals for all processes and the soma are unimodal and follow an approximate log-normal distribution. (C) Both soma and average process spike frequency increase monotonically with neuronal input intensity. The variation of average process frequency with σ is identical to that for a single compartment model. (D) Spike frequency in the soma depends on the ratio Vr of soma to process volume. As Vr increases, the soma spikes less frequently. (E) On the other hand, spiking rates in the processes depend only very weakly on Vr. When process and soma have equal volume, the process spikes at about half the rate as the soma. In (D,E), error bars were obtained by breaking up a simulation over 106 time units into 20 equal intervals and computing the standard deviation across each interval. The same approach is adoped in subsequent experiments. Note that in our functional model, all units in this and subsequent figures are arbitrary. Simulation parameters: ρ = 0.0, DI = 0.05 and DE = 0 (A–D), Vr = 1 (A–C).
As the intensity of the neuronal input σ is increased from 0 to 0.3, both the processes and the soma start to spike and the spiking rate increases monotonically with σ (Figure 2C). The soma spikes at a lower rate, and appears to saturate for σ>0.2. Below a threshold value of σ = 0.04, there are no process or soma spikes. The threshold is slightly higher for soma spikes that depend on one or more processes spiking before a sufficient amount of Ca2+ can diffuse into the soma. We examine the conditions that induce soma spikes in a later section. To determine how Ca2+ dynamics in the processes are affected by their connection to the soma, and via the soma by the other processes, we plot the spiking rate as a function of σ in a single compartment model. This curve is almost identical to the average spiking rate across processes for a low value of DI. This suggests that in this diffusion regime, the processes of our astrocyte model behave similarly to single compartment models, with little effect from interactions between compartments.
3.1.1. Effect of Larger Soma Volume
For simplicity, we have assumed that all compartments have equal surface and equal volume. However, a recent investigation into the three-dimensional morphology of astrocytes implied that the volume of the soma is about 1.5 times the volume of a major process (Bindocci et al., 2017). To consider the effect of a larger soma volume on the spiking activity, we define the soma to process volume ratio
under the assumption that all the processes have identical geometry.
Taking this volume ratio into account, the equations for Ca2+ dynamics in the soma become
where accounts for the increase in membrane surface area through which Ca2+ flux occurs. Thus, the increased volume in the soma slows down its Ca2+ dynamics.
Through Figures 2D,E, we examine the effect of volume ratio on spiking rate in the soma and the processes for the three volume ratios 1, 1.5, and 2. Larger volume ratios decrease the average soma spiking frequency for all values of neuronal input. On the other hand, the spiking rate in the processes are independent of the volume ratio. A larger soma volume requires a larger amount of Ca2+ to diffuse to the soma before rises enough to trigger CICR. In the remainder of the paper we set Vr = 1 to reduce the computation time, and allow the collection of a large enough number of soma spikes to perform statistical analysis.
3.2. Effects of Input Distribution Onto the Astrocyte Model
3.2.1. Correlated Inputs Trigger Soma Spikes More Effectively and Produce Global Events
The amplitude of inputs is not the only factor that affects astrocyte Ca2+ dynamics. Since neurons in a given cortical area can have correlated activities, it is likely the case that the inputs to the different astrocyte processes also exhibit a (potentially variable) degree of correlation (Averbeck et al., 2006). To simulate this correlation, we generate input signals ξi(t) with pairwise correlation ρ. We then compute the activity in the processes and soma as a function of σ for different values of ρ. Frequency curves are shown in Figure 3A. As the correlation coefficient increases, soma spiking frequency increases, and plateaus at higher values.
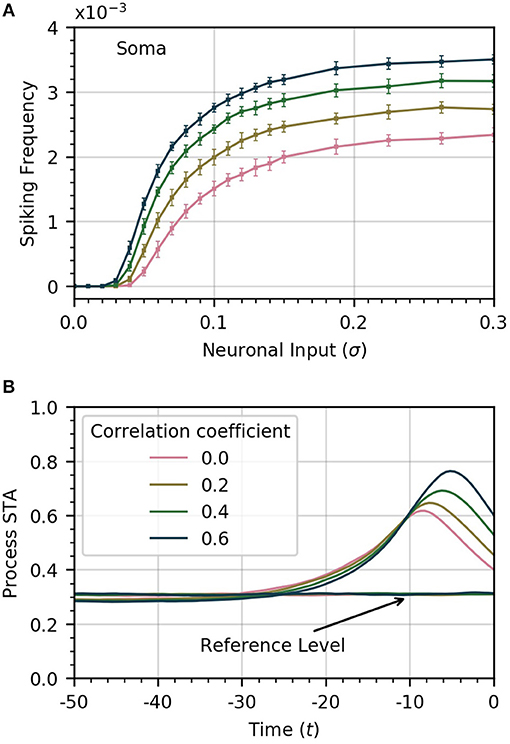
Figure 3. Increased correlation between neuronal inputs facilitates soma spike activity. (A) Variations of soma spike frequency with σ for different values of ρ. Higher input signal correlation raises the soma spiking frequency and decreases the threshold σ for soma spikes. (B) Spike-triggered average of CI conditioned on the soma spikes within a window of 50 time units ahead of the soma spikes. At higher values of correlation, the process spikes are more concentrated and trigger closer to the soma spike. For reference, we show the average of CI over random time windows. Simulation parameters: σ = 0.2, DI = 0.05, DE = 0.0, Vr = 1.0.
We also find that higher correlation between Ca2+ influx signals decreases the threshold σ necessary for the soma to spike. In Figure 3B, we plot the STA of process activity conditioned on soma spikes for various values of ρ. At higher levels of correlation, the STA is sharper and closer to the soma spike. This suggests that synchrony between process spikes facilitates soma spiking.
Finally, we show in Figure 4 that the occurrence of global events strongly increases with ρ. Thus, while finite correlation between input sources have a moderate effect on soma spiking, they greatly increase the number of global events. For the remainder of the paper, we set the pairwise correlation coefficient between neuronal signals to ρ = 0.2, unless explicitly stated otherwise.
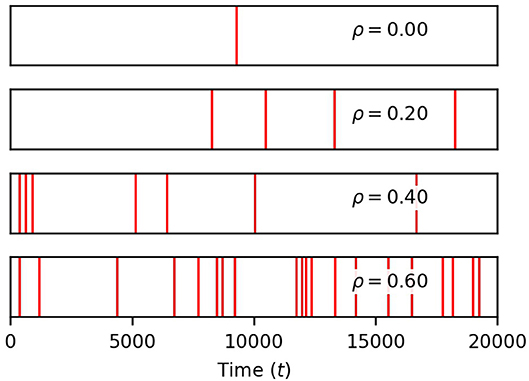
Figure 4. Correlation between neuronal inputs induce global events. Each red vertical bar marks the occurrence of a global event (four or more process spikes within a window of 12.5 time units of a soma spike). Their density rises with ρ. Simulation parameters: σ = 0.2, DI = 0.05, DE = 0.0, Vr = 1.0 .
3.2.2. Concentrating Neuronal Inputs Helps Trigger Soma Spikes
Up until this point, we have assumed a uniform distribution of Ca2+ due to neuronal activity. However, our model provides the ability to stagger the level of Ca2+ input between processes. We wish to better understand whether neuronal inputs should be distributed over many processes to effectively evoke somatic Ca2+ spikes.
To gain some insight into this question, we perform three experiments in which we vary the number of processes subject to neuronal input (Figure 5). In the base case, all five processes receive the same level of neuronal activity, denoted by σ. In the second case, each of three processes receives a level σ3, and in the third case, a single process is active, with neuronal activity σ1. We choose the levels σ1 and σ3 to ensure that in each case the sum of all active signals has identical variance.
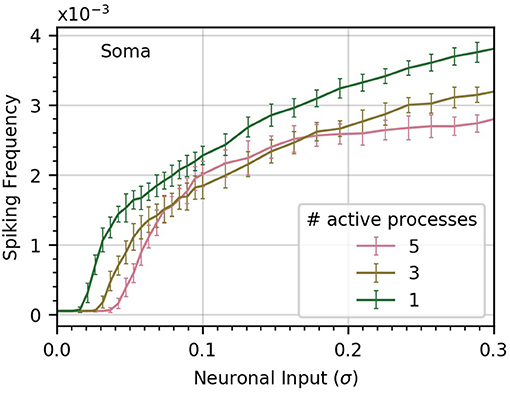
Figure 5. Concentrating inputs into fewer processes facilitates soma spiking. Curves (a-c) correspond respectively to 5, 3, and 1 processes receiving neuronal input; these are the active processes. By definition, σ is the standard deviation of the neuronal input signal into five processes, as in previous figures. As the number of active processes is decreased, σ is scaled up to maintain a constant standard deviation of the sum of the inputs. Concentrating the neuronal inputs into fewer processes increases soma spike rate across most of the σ range and decreases the threshold σ for soma spiking. Simulation parameters: ρ = 0.2, DI = 0.05, DE = 0.0 .
More generally, consider the sum Sm of m signals si with pairwise correlation ρ and variance σ2. It can easily be shown that the standard deviation of Sm is given by
With the help of Equation 14, we obtain relationships that ensure comparative total input between the standard deviations of the process neuronal input when one and three processes are active:
We find that concentrating inputs onto fewer processes slightly increases spiking frequency in the soma, and decreases the threshold σ required to evoke soma spiking (Figure 5). At higher values of σ, concentrating inputs in fewer processes only has a small effect on somatic frequency. This suggests that neuronal inputs concentrated in only a few processes are more likely to trigger soma spikes than if they are distributed throughout the astrocyte processes.
3.3. Compartmental Diffusion Effects
Calcium gradients across neighboring cell regions are accounted for in our model by diffusion fluxes between adjacent processes, either through the cytosol (JI, d) or through the ER (JE, d). Accordingly, we set out to investigate how variations of diffusion coefficients DI and DE affect somatic spiking.
3.3.1. Diffusion Between Soma and Process Cytosol
The soma receives no input from neuronal activity, so it only becomes active because of the diffusion of cytosolic Ca2+ from spiking processes. Thus, the soma spiking rate should increase with DI, as seen in Figure 6A. Curves (a) through (c) correspond to increasing levels of DI (0.025, 0.050, 0.1). Increasing DI also slightly decreases the threshold value of σ for soma spikes. To determine how the rate of diffusive Ca2+ transfer impacts the relationship between process and soma spiking, we plot the average spike-triggered average of processes Ca2+ conditioned on soma spikes for different values of DI in Figure 6B. At higher values of DI, the STA of process activity narrows and moves closer to the soma spike, suggesting that for higher values of DI fewer process spikes occurring within a short time frame are needed to elicit a soma spike. To confirm this, we plot the likelihood of different process spike counts preceding a soma spike for several values of cytosolic diffusion. This information is summarized in Figure 6C. It shows that for DI = 0.05 or less, most soma spikes are triggered only once two or three process spikes occur close to each other. Thus, soma spikes occur less frequently and less regularly than process spikes, explaining the wider distribution of ISI for soma spikes (Figure 2B).
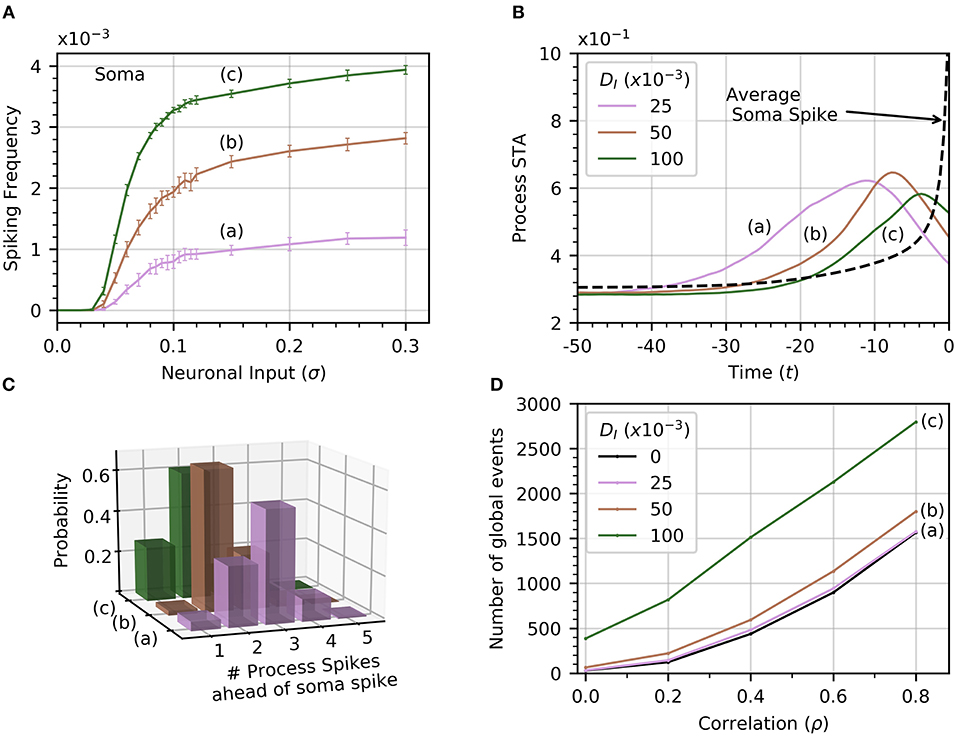
Figure 6. Effect of cytosolic diffusion on soma and global activity. (A) Soma spiking rate increases with cytosolic diffusion DI for all levels of neuronal input. Higher DI also decreases the threshold input for soma spikes. In (A,B,D), curves (a) through (c) correspond to DI = 0.025, 0.05, 0.1, respectively. (B) Spike-triggered averages of in a single process (all processes produce a very similar curve) were computed in a window of 50 times units ahead of the soma spikes. Higher DI shortens the average interval between soma spike and preceding process spikes. (C) The distribution of number of process spikes preceding a soma spike shifts toward lower values at higher DI. The number of process spikes were only counted within a window of 30 time units ahead of the soma spikes. (D) Variations of the number of global events (defined by at least four processes spiking within a time window of 25, with or without a soma spike) with ρ. Cytosolic diffusion determines whether the soma directly influences the number of global events, or whether they are due to random process spike co-occurrences. As input correlation increases in the absence of soma activity (DI = 0), so do the number of randomly occurring global events (dashed curve). Note that in the absence of cytosolic diffusion, the soma does not spike. When DI increases to 0.025, the soma begins to spike [panel A, curve (a)], but the number of global events does not increase significantly. Further increases of DI to 0.05 and 0.1 shows a substantial increase in the number of global events, which are almost certainly associated with soma spikes. That this is so is substantiated by noticing that process spiking frequency is unaffected by DI, as seen in Figure 2C, which shows that the process spiking frequency at DI = 0.05 is the same as in the single compartment (equivalent DI = 0). Given a sufficiently strong cytosolic diffusion (DI = 0.1), soma spikes help generate significantly more global events than those generated by input signal correlation alone. Simulation parameters: DE = 0, σ = 0.2, Vr = 1 .
3.3.2. Are Global Events Random?
From Figure 4, we recall that increasing ρ increases the number of global events. Are these events the result of spike propagation from the soma to other processes, or are they simply random synchronizations between process spikes due to the correlation between neuronal inputs? To answer this question, we set DI = 0 to ensure that events that involve four or more process spikes within 25 time units can only occur as random coincidence of process spikes. We plot the number of such global events for increasing signal correlation in Figure 6D. When DI lies between 0.025 and 0.05, there is little difference with the number of global events found for DI = 0. Thus, these global events are simply due to random occurrences. However, when DI = 0.1, the number of global events rises markedly. This demonstrates that the soma is involved with the global event generation. Therefore, the strength of diffusion between compartments can change the nature of global events.
3.3.3. Diffusion Within the Endoplasmic Reticulum
Up until now, we have assumed that there was no connection between process and soma ER. We now relax this assumption and consider the impact of diffusion between the two. Since the extent of diffusion within the astrocyte ER is unknown, we consider a range of ER diffusivities. We set DI = 0.05, which allows high frequency spiking in the soma when no diffusion occurs between ERs (see Figure 6A). Next, we compute the average soma frequency as a function of σ for three values of DE in the range 0 to 0.002 . As soon as DE > 0, the relationship between soma frequency and σ becomes non-monotonic (Figure 7A). As σ increases, the spike frequency in the soma initially increases toward a maximum value, and then decreases as σ continues to increase. This effect becomes stronger, limiting the maximum soma spike frequency, for larger values of DE. Thus, diffusion between the soma and process ER impedes soma activity at high levels of neuronal inputs. Spiking activity in each process remains unchanged as shown in Figure 7B.
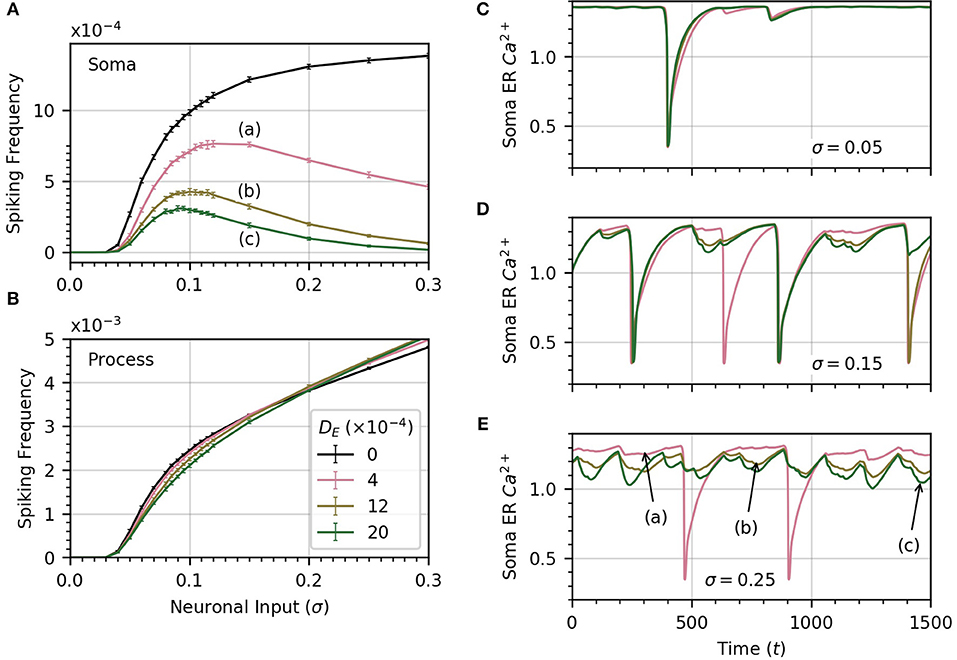
Figure 7. ER diffusion leads to non-monotonic variation of soma spike frequency with σ. (A) Non-monotonic variations of soma spike frequency with σ for non-zero DE. The maximum soma spike frequency decreases and shifts toward lower σ for higher values of DE (from a to c). The DE = 0 curve is drawn in black. (B) The process spike frequency is mostly independent of DE, except in the region near σ = 0.1 where the frequency is slightly elevated at lower DE. Note that the error bars have similar magnitude to those in (A). Simulation parameters: ρ = 0.2, DI = 0.05, Vr = 1 . (C–E) The bell-shaped curves in (A) are explained by examining the time course of soma ER Ca2+ for different levels of DE at three levels of σ. At low σ (C), the level of the soma ER Ca2+ does not vary significantly with DE. (D,E) At high σ, depletion increases with DE, leading to missed soma spikes. Large downward deflections result from soma spikes while small downward deflections result from process spikes. All simulations were conducted with the same initial random seed to generate a consistent sequence of process spikes as DE is varied. Simulation parameters: DI = 0.05, ρ = 0.2 .
To explain why the soma spikes at a lower rate at high σ, we note that two opposite factors shape the relationship between the rate of spikes in the soma and the neuronal input intensity. As σ increases initially, the spike rate in the processes rises, which leads to more spikes in the soma. Accordingly, the first part of the curves in Figure 7A shows an increase in spiking frequency with σ. However, this picture changes at higher σ when DE > 0. In that case, each process spike causes a flow of Ca2+ from the soma ER to the process ER, because process ER Ca2+ has rushed into the process cytosol. Thus, following a process spike, the soma ER becomes transiently depleted. The opposite is also true: a soma spike causes flow of Ca2+ from the process ER to the soma ER, but the soma spikes less frequently than the processes. Therefore, the net effect is that soma ER Ca2+ level will decrease, this effect becoming stronger with larger σ. This lowers soma excitability, lowering the soma spike frequency. (Below, we illustrate the ER Ca2+ depletion by process spikes.)
To summarize, at low σ, the spike rate increases as the slope of frequency vs σ is quite large. On the other hand, as σ increases, the higher spike rate due to higher excitation slows down, while the soma ER gets further depleted with increased process spike frequency. Around σ = 0.1, this depletion of soma ER Ca2+ lowers soma excitability so much that soma spike rate decreases with σ.
We confirm the above by displaying the time course of soma ER Ca2+ for , at three values of σ in panels C (σ = 0.05), D (σ = 0.15), E (σ = 0.25), of Figure 7. At low σ, the time course of the soma ER Ca2+ does not vary significantly over the range of DE considered. At higher values of σ (Figures 7D,E), the differences between ER soma Ca2+ at different DE levels grow, which leads to some missed soma spikes. Large downward deflections result from soma spikes while small downward deflections result from process spikes. At higher values of σ, the soma ER can be depleted for DE > 0, causing the soma to miss some spikes.
4. Discussion
Astrocytes play a range of roles on neural circuits at different spatial and temporal scales. This range of astrocytic effects on neural circuits is mediated by a hierarchy of Ca2+ events in astrocytes. In turn, these events are a response to neuronal activity (Shigetomi et al., 2016; Bindocci et al., 2017). These events range from fast, localized transients, to slower global events that recruit the soma and major processes. To better understand the spatiotemporal propagation of Ca2+ signals in the cell and how these signals might be altered in neurodegenerative diseases, we need to investigate how neuronal inputs give rise to this hierarchy of Ca2+ events.
In this paper, we applied a compartmental model to investigate how the properties of neuronal inputs give rise to a variety of Ca2+ events in astrocytes. The model is adapted from the single compartment, functional model of Postnov et al. (2007) that describes astrocyte response to perisynaptic Ca2+ influx. We added compartments representing major astrocyte processes that couple to the soma through diffusion.
In this simple model, we demonstrated that the Ca2+ influx into each process in response to neuronal activity controls the occurrence of process Ca2+ spikes, and in turn soma Ca2+ spikes. The degree of correlation between the process neuronal inputs determines the frequency of global events involving the soma and at least four processes. These global events, in the model, are simply due to the random co-occurrence of process spikes in response to correlated neuronal inputs, unless cytosolic diffusion is large enough for soma spikes to trigger spikes in processes. Our simulations also indicate that the exchange of Ca2+ between the soma and process ER compartments severely curtails the number of somatic spikes in response to high levels of neural activity.
4.1. A First Model to Build Intuition
Our goal was to build an initial model that incorporates the spatial structure of astrocytes to explore their hierarchy of Ca2+ dynamics. This model investigates questions related to astrocyte geometry, Ca2+ diffusion across its compartments, the distribution of neuronal inputs received by its perisynaptic processes and the effect of these inputs on Ca2+ activity in both the soma and major processes. The adoption of a simple model as a starting point in our investigation helps build intuition about the origin of astrocytic Ca2+ events. Indeed, only a small number of variables interact to produce these events. A more complex model that incorporates details of astrocyte geometry and signaling pathways would be required to match experimental data. Such models, however, come at the expense of a large number of parameters and variables, which would make the analysis less intuitive and prone to fine tuning of parameters. Our model is built on reasonable assumptions, can be extended to ask more detailed questions, and may guide further model development and experiments since it provides a series of testable predictions.
One important assumption in our work is that all major processes possess Ca2+ excitability, and that neuronal activity only affects processes, not the soma. Experiments have shown that neuronal activity causes fast, local Ca2+ transients in distal, fine process branches that do not contain IP3 receptors and therefore show no Ca2+ excitability. These Ca2+ events may be triggered by the opening of Ca2+-permeable channels in response to neuronal activity (Hamilton et al., 2008; Shigetomi et al., 2012; Lind et al., 2013; Srinivasan et al., 2015). Herein, we model the effects of the distant Ca2+ transients onto the major processes as a Gaussian distribution of Ca2+ input. We have implicitly assumed a constant level of IP3, such that integration of the random Ca2+ influx events could trigger CICR. This is because Ca2+ entry through channels can happen without activation of G-protein coupled receptors that lead to the production of IP3, and because IP3 concentration within the astrocyte should equilibrate faster than the Ca2+ concentration. Since Ca2+ excitability in the processes may not require IP3 receptors (Srinivasan et al., 2015), we did not use a model of Ca2+ excitability that explicitly depends on intracellular IP3 levels. There is evidence, however, that the Ca2+ levels resulting from Ca2+ spikes may affect IP3 levels, which may be important for the production of multiple modes of Ca2+ dynamics (De Pitta et al., 2009).
In addition, all processes have a basal rate of Ca2+ influx that brings them close to threshold for a Ca2+ spike in the absence of neuronal activity. We identify the level of astrocyte excitability with the spike frequency in the soma and in the processes. The implicit assumption is that spiking rate in response to sustained activity serves as a good measure of the effectiveness of the neuronal input patterns in evoking Ca2+ responses.
4.2. Control of Astrocyte Ca2+ Dynamics by Neuronal Activity
The framework underlying this work, and discussed further below, was built up from a series of experimental results summarized by Carmignoto (2000), Volterra and Meldolesi (2005), and Zorec et al. (2012), which in turn led to the presentation in Araque et al. (2014). According to this framework, neuronal activity causes fast, localized Ca2+ events that occur in distal branches, which can result in regenerative Ca2+ events in the main process through a process of integration not unlike integration of synaptic inputs by neurons. As neuronal activity increases, spikes in processes can in turn be integrated and trigger soma spikes and global events. To our knowledge, however, this has not been demonstrated experimentally and recent work, while not contradicting this simple framework, suggest that Ca2+ dynamics in astrocytes may exhibit a wide range of events (Wu et al., 2014; Bindocci et al., 2017), possibly with more complex rules than assumed here.
The model generates four types of Ca2+ events: (1) fast transients due to neuronal activity onto each process; (2) process spikes; (3) soma spikes; and (4) global events that involve spikes in soma and several processes within a short time window. Fast transients (1) are always produced as long as there is neuronal activity (σ > 0). Astrocyte processes integrate fast Ca2+ transients caused by neuronal inputs, leading to process spikes. The soma Ca2+ rises due to process spikes. We have not observed soma spikes (3) without process spikes (2) and rarely observed global events (4) without soma spikes (3). Thus the chain (1)-(4) of observable Ca2+ events defines a hierarchy, whereby an event high in the hierarchy only occurs when preceding events in the hierarchy have already been reached.
The particular Ca2+ events (1)-(4) observed in the hierarchy depend on the parameters σ and ρ, which respectively describe neuronal activity and input correlation. At very low σ, we do not observe spikes in either processes or soma: only fast Ca2+ transients (1) occur in the processes. At higher σ, processes begin to spike (2) and their spike rate increases with σ. The spiking frequency in the process reproduces the behavior of the spiking rate in a single compartment model with identical σ (Figure 2B). As σ is increased further, soma spikes appear and their spiking rate dependence on σ is similar to that of the processes. The soma spikes less frequently than the processes, as observed experimentally (Araque et al., 2014; Bindocci et al., 2017). Taking into account the fact that the soma volume is about 1.5 times the volume of a major process leads to an even lower soma spike rate than in the processes, since larger volume ratio slows down Ca2+ variations.
The role played by correlation between neuronal inputs on astrocyte Ca2+ dynamics differs from that played by σ. Increasing ρ has practically no effect on the average process spiking rate and only a modest effect on that of the soma (Figure 3A), except at low σ. In that case, increasing ρ facilitates soma spikes, and lowers the σ threshold for soma spikes. Beyond this effect of correlation on the soma spike rate, increasing ρ mainly increases the frequency of global events. That is, the proportion of soma spikes that are global events increases with ρ, but not with σ. Thus, the amount of neuronal input onto the processes controls the rate of spiking in the processes and in the soma, while the degree of correlation between neuronal inputs controls the frequency of global events.
4.3. Implications for the Role of Astrocytes in Neural Computations
In addition to many roles played by astrocytes as neuron support cells and regulators of blood flow, there is growing evidence that astrocytes also modulate the activity of neural circuits by acting on neuronal excitability and on synaptic activity and plasticity. It has been suggested that the spatiotemporal distribution of neuronal activity determines the profile of Ca2+ transients evoked in astrocytes. This in turn determines the extent of synaptic modifications by astrocytes (Araque et al., 2014). According to that hypothesis, localized and short-lived synaptic activity only evokes fast, local astrocyte transients–event (1) above–which in turn only affect synapses directly involved in triggering the fast Ca2+ events. Stronger, longer lasting, or slightly more widespread synaptic activity in the same area could trigger a spike in one major process (2). In turn, this affects synapses under its control, active or not. Finally, synaptic activity occurring in more than one process may evoke somatic spikes and global events, (3) and (4), depending on the degree of synchrony of synaptic activation. These events in turn may lead to synaptic plasticity in all synapses covered by the astrocyte. Araque's hypothesis only holds if a hierarchy of Ca2+ events results from a hierarchy of network synaptic activity. Our results support this hypothesis by demonstrating that the different types of astrocyte Ca2+ events follow such a hierarchy. The higher in the hierarchy, the more synapses over a larger area may be affected synchronously by astrocyte signaling.
Our results may also explain why astrocytes in the visual cortex maps have sharper tuning curves than do neurons. Schummers et al. (2008) measured global events in astrocytes in response to visual inputs with different orientation or spatial frequency. Astrocytes responded according to which orientation domain they belonged to, but their tuning curves were sharper than that of neurons within the same domain. These sharper tuning curves may result from the fact that the distributed activation of synapses over the whole astrocyte must exhibit a significant degree of temporal correlation to induce global events. However, by the same reasoning, astrocytes located around pinwheel centers, which do not receive tuned inputs, should therefore have an untuned response. This does not seem to be the case, as astrocytes located close to a pinwheel center still exhibit sharp tuning curves (López-Hidalgo and Schummers, 2014).
4.4. ER Geometry Affects the Soma Response to Inputs
CICR generates spikes while somatic and global events rely on diffusion between processes and the soma. Therefore the ER, which is the main store of astrocytic Ca2+, plays an important role in these Ca2+ events. Spiking in the soma occurs as a response to increased levels of neuronal activity when the ERs in the soma and processes connect through diffusion. Setting DE to a non-zero value resulted in a qualitative change in the relationship between the amount of neural activity and the soma spike frequency. More specifically, the graph of average frequency vs. σ becomes non-monotonic, initially increasing at low values of σ, then decreasing back toward 0. During a process spike ER, Ca2+ in the process becomes depleted, which leads to diffusion of Ca2+ from the soma ER to the ER in the processes. Since the processes spike more frequently than the soma, the net result is a decrease of Ca2+ in the soma ER and lower soma excitability.
We note that in this model of Ca2+ excitability, Ca2+ in ER plays the role of the recovery variable. Thus, the loss of Ca2+ by the soma ER engenders a decrease in soma excitability as σ increases from the lower levels. With a different model with de-inactivation of IP3R channels by Ca2+ as the recovery variable, we may not see the drop in soma spike frequency as some ER Ca2+ becomes depleted, but rather a drop in soma spike amplitude.
Our model does take into account the effect of store-operated Ca2+ channels. Store-operated Ca2+ entry would activate once the ER Ca2+ reaches a low level, potentially resulting in an influx of Ca2+ through the cytoplasm. This could prevent the decrease in soma excitability at high σ. Thus, a modification in the parametrization of Ca2+ excitability in the model might impact cause and effect between processes and soma ER.
4.5. Relevance to Neurodegenerative Diseases
Pathological changes in astrocytes alter Ca2+ activity in several forms of neurodegenerative disease (Nedergaard et al., 2010; Hamby et al., 2012; Sofroniew, 2014; Ben Haim et al., 2015; Rodŕıguez-Arellano et al., 2016; Verkhratsky et al., 2016). Neurological diseases can be viewed as a homeostatic failure and astrocytes are affected through alterations in multiple disease-specific homeostatic mechanisms generally known as reactive gliosis (Sofroniew, 2005; Nedergaard et al., 2010; Rodŕıguez-Arellano et al., 2016; Verkhratsky et al., 2016). Reactive gliosis is an evolutionarily conserved defense mechanism associated with neurodegenerative disease; the resultant remodeling undergone by astrocytes can contribute to pathological progression and alter Ca2+ dynamics (Verkhratsky et al., 2016).
In Alzheimer's disease (AD), β-amyloid buildup has been shown to initiate reactivity in astrocytes (Alberdi et al., 2013). For instance, exposure of astrocytes to β-amyloid in hippocampal slices resulted in Ca2+ release from the ER, which instigated astroglial reactivity (Alberdi et al., 2013). β-amyloid plaques also lead to aberrant physiology in the form of spontaneous Ca2+ oscillations as well as intercellular Ca2+ waves (Kuchibhotla et al., 2009; Lim et al., 2014).
Prior to the development of β-amyloid plaques, astrocytes undergo atrophy as a result of reactive gliosis (Verkhratsky et al., 2016). Atrophy in turn leads to decreased volume of the soma as well as a reduction in the number of primary processes (Olabarria et al., 2010; Yeh et al., 2011; Kulijewicz-Nawrot et al., 2012). A model like the one developed here may be used to predict the consequences of these morphological changes, together with functional changes in Ca2+ influx, on Ca2+ spiking and global events.
5. Conclusion
We have demonstrated that a functional compartmental model can answer questions about the rules that govern the generation of Ca2+ events observed in astrocytes. A parametric study conducted with respect to Ca2+ influx intensity and pairwise correlation, DI, and DE, suggests that the variability of neuronal activity seen by the astrocyte sets the spiking frequency in both the processes and in the soma. The correlation between the neuronal activity in the different processes controls the number of global events. Our calculations also suggest that diffusion between the ER of the soma and of the major processes has an important effect on the dynamics of Ca2+ events in astrocytes. A detailed look at the mechanics behind the global events and the conditions under which synchronization occurs remains a subject of future investigation.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Alberdi, E., Wyssenbach, A., Alberdi, M., Sánchez-Gómez, M. V., Cavaliere, F., Rodríguez, J. J., et al. (2013). Ca2+-dependent endoplasmic reticulum stress correlates with astrogliosis in oligomeric amyloid β-treated astrocytes and in a model of a lzheimer's disease. Aging Cell 12, 292–302. doi: 10.1111/acel.12054
Araque, A., Carmignoto, G., Haydon, P. G., Oliet, S. H., Robitaille, R., and Volterra, A. (2014). Gliotransmitters travel in time and space. Neuron 81, 728–739. doi: 10.1016/j.neuron.2014.02.007
Averbeck, B. B., Latham, P. E., and Pouget, A. (2006). Neural correlations, population coding and computation. Nat. Rev. Neurosci. 7, 358–366. doi: 10.1038/nrn1888
Bazargani, N., and Attwell, D. (2016). Astrocyte calcium signaling: the third wave. Nat. Neurosci. 19, 182–189. doi: 10.1038/nn.4201
Ben Haim, L., Carrillo-de Sauvage, M.-A., Ceyzériat, K., and Escartin, C. (2015). Elusive roles for reactive astrocytes in neurodegenerative diseases. Front. Cell. Neurosci. 9:278. doi: 10.3389/fncel.2015.00278
Bindocci, E., Savtchouk, I., Liaudet, N., Becker, D., Carriero, G., and Volterra, A. (2017). Three-dimensional Ca2+ imaging advances understanding of astrocyte biology. Science 356, 715–724. doi: 10.1126/science.aai8185
Blaustein, M. P., and Golovina, V. A. (2001). Structural complexity and functional diversity of endoplasmic reticulum Ca2+ stores. Trends Neurosci. 24, 602–608. doi: 10.1016/S0166-2236(00)01891-9
Carmignoto, G. (2000). Reciprocal communication systems between astrocytes and neurones. Progr. Neurobiol. 62, 561–581. doi: 10.1016/S0301-0082(00)00029-0
De Pitta, M., Volman, V., Levine, H., and Ben-Jacob, E. (2009). Multimodal encoding in a simplified model of intracellular calcium signaling. Cogn. Process. 10, S55–S70. doi: 10.1007/s10339-008-0242-y
Di Castro, M. A., Chuquet, J., Liaudet, N., Bhaukaurally, K., Santello, M., Bouvier, D., et al. (2011). Local Ca2+ detection and modulation of synaptic release by astrocytes. Natl. Neurosci. 14, 1276–1284. doi: 10.1038/nn.2929
Dupont, G., Falcke, M., Kirk, V., and Sneyd, J. (2016). “Nonlinear dynamics of calcium,” in Models of Calcium Signalling, eds S. S. Antman, L. Greengard, and P. J. Holmes (Springer), 207–242. Available online at: https://www.springer.com/series/1390
Goldbeter, D. G., and Berridge, M. J. (1990). Minimal model for signal-induced Ca2+ oscillations and for their frequency encoding through protein phosphorylation. Proc. Natl. Acad. Sci. U.S.A. 87, 1461–1465. doi: 10.1073/pnas.87.4.1461
Gordleeva, S. Y., Lebedev, S., Rumyantseva, M., and Kazantsev, V. (2018). Astrocyte as a detector of synchronous events of a neural network. JETP Lett. 107, 440–445. doi: 10.1134/S0021364018070032
Halassa, M. M., Fellin, T., and Haydon, P. G. (2009a). Tripartite synapses: roles for astrocytic purines in the control of synaptic physiology and behavior. Neuropharmacology 57, 343–346. doi: 10.1016/j.neuropharm.2009.06.031
Halassa, M. M., Florian, C., Fellin, T., Munoz, J. R., Lee, S.-Y., Abel, T., et al. (2009b). Astrocytic modulation of sleep homeostasis and cognitive consequences of sleep loss. Neuron 61, 213–219. doi: 10.1016/j.neuron.2008.11.024
Hamby, M. E., Coppola, G., Ao, Y., Geschwind, D. H., Khakh, B. S., and Sofroniew, M. V. (2012). Inflammatory mediators alter the astrocyte transcriptome and calcium signaling elicited by multiple g-protein-coupled receptors. J. Neurosci. 32, 14489–14510. doi: 10.1523/JNEUROSCI.1256-12.2012
Hamilton, N., Vayro, S., Kirchhoff, F., Verkhratsky, A., Robbins, J., Gorecki, D. C., et al. (2008). Mechanisms of ATP-and glutamate-mediated calcium signaling in white matter astrocytes. Glia 56, 734–749. doi: 10.1002/glia.20649
Henneberger, C., Papouin, T., Oliet, S. H., and Rusakov, D. A. (2010). Long-term potentiation depends on release of d-serine from astrocytes. Nature 463:232. doi: 10.1038/nature08673
Johnson, G. E. (1994). Constructions of particular random processes. Proc. IEEE 82, 270–285. doi: 10.1109/5.265353
Kanemaru, K., Sekiya, H., Xu, M., Satoh, K., Kitajima, N., Yoshida, K., et al. (2014). In vivo visualization of subtle, transient, and local activity of astrocytes using an ultrasensitive Ca2+ indicator. Cell Reports 8, 311–318. doi: 10.1016/j.celrep.2014.05.056
Kang, M., and Othmer, H. G. (2009). Spatiotemporal characteristics of calcium dynamics in astrocytes. Chaos 19:037116. doi: 10.1063/1.3206698
Khalid, M. U., Tervonen, A., Korkka, I., Hyttinen, J., and Lenk, K. (2017). “Geometry-based computational modeling of calcium signaling in an astrocyte,” in EMBEC & NBC 2017 (Singapore: Springer), 157–160. doi: 10.1007/978-981-10-5122-7_40
Kimelberg, H. K., and Nedergaard, M. (2010). Functions of astrocytes and their potential as therapeutic targets. Neurotherapeutics 7, 338–353. doi: 10.1016/j.nurt.2010.07.006
Kirischuk, S., Kettenmann, H., and Verkhratsky, A. (1997). Na+/Ca2+ exchanger modulates kainate-triggered Ca2+ signaling in Bergmann glial cells in situ. FASEB J. 11, 566–572. doi: 10.1096/fasebj.11.7.9212080
Kirischuk, S., Kettenmann, H., and Verkhratsky, A. (2007). Membrane currents and cytoplasmic sodium transients generated by glutamate transport in Bergmann glial cells. Pflügers Archiv. Eur. J. Physiol. 454, 245–252. doi: 10.1007/s00424-007-0207-5
Kloeden, P. E., and Platen, E. (1992). Numerical Solution of Stochastic Differential Equations. Berlin; Heidelberg: Springer-Verlag Berlin Heidelberg, 636.
Kuchibhotla, K. V., Lattarulo, C. R., Hyman, B. T., and Bacskai, B. J. (2009). Synchronous hyperactivity and intercellular calcium waves in astrocytes in alzheimer mice. Science 323, 1211–1215. doi: 10.1126/science.1169096
Kulijewicz-Nawrot, M., Verkhratsky, A., Chvátal, A., Syková, E., and Rodríguez, J. J. (2012). Astrocytic cytoskeletal atrophy in the medial prefrontal cortex of a triple transgenic mouse model of alzheimer's disease. J. Anat. 221, 252–262. doi: 10.1111/j.1469-7580.2012.01536.x
Levine, T., and Rabouille, C. (2005). Endoplasmic reticulum: one continuous network compartmentalized by extrinsic cues. Curr. Opin. Cell Biol. 17, 362–368. doi: 10.1016/j.ceb.2005.06.005
Lim, D., Ronco, V., Grolla, A. A., Verkhratsky, A., and Genazzani, A. A. (2014). Glial calcium signalling in alzheimer's disease. Rev. Physiol. Biochem. Pharmacol. 167, 45–65. doi: 10.1007/112_2014_19
Lind, B. L., Brazhe, A. R., Jessen, S. B., Tan, F. C., and Lauritzen, M. J. (2013). Rapid stimulus-evoked astrocyte Ca2+ elevations and hemodynamic responses in mouse somatosensory cortex in vivo. Proc. Natl. Acad. Sci. U.S.A. 110, E4678–E4687. doi: 10.1073/pnas.1310065110
López-Hidalgo, M., and Schummers, J. (2014). Cortical maps: a role for astrocytes? Curr. Opin. Neurobiol. 24, 176–189. doi: 10.1016/j.conb.2013.11.001
Nadkarni, S., and Jung, P. (2007). Modeling synaptic transmission of the tripartite synapse. Phys. Biol. 4, 1–9. doi: 10.1088/1478-3975/4/1/001
Nedergaard, M., Rodríguez, J. J., and Verkhratsky, A. (2010). Glial calcium and diseases of the nervous system. Cell Calc. 47, 140–149. doi: 10.1016/j.ceca.2009.11.010
Nimmerjahn, A., Mukamel, E. A., and Schnitzer, M. J. (2009). Motor behavior activates Bergmann glial networks. Neuron 62, 400–412. doi: 10.1016/j.neuron.2009.03.019
Olabarria, M., Noristani, H. N., Verkhratsky, A., and Rodríguez, J. J. (2010). Concomitant astroglial atrophy and astrogliosis in a triple transgenic animal model of alzheimer's disease. Glia 58, 831–838. doi: 10.1002/glia.20967
Panatier, A., Vallée, J., Haber, M., Murai, K. K., Lacaille, J. C., and Robitaille, R. (2011). Astrocytes are endogenous regulators of basal transmission at central synapses. Cell 146, 785–798. doi: 10.1016/j.cell.2011.07.022
Patrushev, I., Gavrilov, N., Turlapov, V., and Semyanov, A. (2013). Subcellular location of astrocytic calcium stores favors extrasynaptic neuron-astrocyte communication. Cell Calc. 54, 343–349. doi: 10.1016/j.ceca.2013.08.003
Perea, G., and Araque, A. (2002). Communication between astrocytes and neurons: a complex language. J. Physiol. 96, 199–207. doi: 10.1016/S0928-4257(02)00007-4
Perea, G., and Araque, A. (2010). Glia modulates synaptic transmission. Brain Res. Rev. 63, 93–102. doi: 10.1016/j.brainresrev.2009.10.005
Petersen, O. H., Tepikin, A., and Park, M. K. (2001). The endoplasmic reticulum: one continuous or several separate Ca2+ stores? Trends Neurosci. 24, 271–276. doi: 10.1016/S0166-2236(00)01787-2
Postnov, D. E., Ryazanova, L. S., and Sosnovtseva, O. V. (2007). Functional modeling of neural-glial interaction. Biosystems 89, 84–91. doi: 10.1016/j.biosystems.2006.04.012
Rodríguez-Arellano, J., Parpura, V., Zorec, R., and Verkhratsky, A. (2016). Astrocytes in physiological aging and alzheimer's disease. Neuroscience 323, 170–182. doi: 10.1016/j.neuroscience.2015.01.007
Rusakov, D. A. (2015). Disentangling calcium-driven astrocyte physiology. Nat. Rev. Neurosci. 16, 226–233. doi: 10.1038/nrn3878
Rusakov, D. A., Bard, L., Stewart, M. G., and Henneberger, C. (2014). Diversity of astroglial functions alludes to subcellular specialisation. Trends Neurosci. 37, 228–242. doi: 10.1016/j.tins.2014.02.008
Savtchenko, L. P., Bard, L., Jansen, T. P., Reynolds, J. P., Kraev, I., Medvidov, M., et al. (2018). Biophysical underpinning of astroglial physiology probed with realistic cell models. bioRxiv, 1–25. doi: 10.1101/336974
Schummers, J., Yu, H., and Sur, M. (2008). Tuned responses of astrocytes and their influence on hemodynamic signals in the visual cortex. Science 320, 1638–1643. doi: 10.1126/science.1156120
Schwartz, O., Pillow, J., Rust, N., and Simoncelli, E. (2006). Spike-triggered neural characterization. J. Vis. 6, 484–507. doi: 10.1167/6.4.13
Shigetomi, E., Patel, S., and Khakh, B. S. (2016). Probing the complexities of astrocyte calcium signaling. Trends Cell Biol. 26, 300–312. doi: 10.1016/j.tcb.2016.01.003
Shigetomi, E., Tong, X., Kwan, K. Y., Corey, D. P., and Khakh, B. S. (2012). TRPA1 channels regulate astrocyte resting calcium and inhibitory synapse efficacy through GAT-3. Nat. Neurosci. 15, 70–80. doi: 10.1038/nn.3000
Sofroniew, M. V. (2005). Reactive astrocytes in neural repair and protection. Neuroscientist 11, 400–407. doi: 10.1177/1073858405278321
Sofroniew, M. V. (2014). Astrogliosis. Cold Spring Harbor Perspect. Biol. 7:a020420. doi: 10.1101/cshperspect.a020420
Srinivasan, R., Huang, B. S., Venugopal, S., Johnston, A. D., Chai, H., Zeng, H., et al. (2015). Ca2+ signaling in astrocytes from IP3R2-/- mice in brain slices and during startle responses in vivo. Nature Neurosci. 18, 708–717. doi: 10.1038/nn.4001
Tewari, S., and Majumdar, K. K. (2012). A mathematical model of the tripartite synapse: astrocyte-induced synaptic plasticity. J. Biol. Phys. 38, 465–496. doi: 10.1007/s10867-012-9267-7
Ullah, G., Jung, P., and Cornell-Bell, A. H. (2006). Anti-phase calcium oscillations in astrocytes via inositol (1, 4, 5)-trisphosphate regeneration. Cell Calc. 39, 197–208. doi: 10.1016/j.ceca.2005.10.009
Verkhratsky, A., Zorec, R., Rodriguez, J. J., and Parpura, V. (2016). Pathobiology of neurodegeneration: the role for astroglia. Opera Med. Physiol. 1, 13–22.
Volterra, A., Liaudet, N., and Savtchouk, I. (2014). Astrocyte Ca2+ signalling: an unexpected complexity. Nat. Rev. Neurosci. 15, 327–335. doi: 10.1038/nrn3725
Volterra, A., and Meldolesi, J. (2005). Astrocytes, from brain glue to communication elements: the revolution continues. Nat. Rev. Neurosci. 6:626. doi: 10.1038/nrn1722
Wade, J. J., McDaid, L. J., Harkin, J., Crunelli, V., and Kelso, J. A. S. (2011). Bidirectional coupling between astrocytes and neurons mediates learning and dynamic coordination in the brain: a multiple modeling approach. PLoS ONE 6:e29445. doi: 10.1371/journal.pone.0029445
Wu, Y.-W., Tang, X., Arizono, M., Bannai, H., Shih, P.-Y., Dembitskaya, Y., et al. (2014). Spatiotemporal calcium dynamics in single astrocytes and its modulation by neuronal activity. Cell Calc. 55, 119–129. doi: 10.1016/j.ceca.2013.12.006
Yeh, C.-Y., Vadhwana, B., Verkhratsky, A., and Rodríguez, J. J. (2011). Early astrocytic atrophy in the entorhinal cortex of a triple transgenic animal model of alzheimer's disease. ASN Neuro 3, 271–279. doi: 10.1042/AN20110025
Keywords: calcium spike, spatiotemporal dynamics, diffusion, IP3 receptor, endoplasmic reticulum, glia
Citation: Cresswell-Clay E, Crock N, Tabak J and Erlebacher G (2018) A Compartmental Model to Investigate Local and Global Ca2+ Dynamics in Astrocytes. Front. Comput. Neurosci. 12:94. doi: 10.3389/fncom.2018.00094
Received: 31 May 2018; Accepted: 08 November 2018;
Published: 30 November 2018.
Edited by:
Yang Tang, Humboldt-Universität zu Berlin, GermanyReviewed by:
Maurizio De Pittà, Basque Center for Applied Mathematics, SpainShuai Mao, East China University of Science and Technology, China
Copyright © 2018 Cresswell-Clay, Crock, Tabak and Erlebacher. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joël Tabak, ai50YWJha0BleGV0ZXIuYWMudWs=
Gordon Erlebacher, Z2VybGViYWNoZXJAZnN1LmVkdQ==
 Evan Cresswell-Clay
Evan Cresswell-Clay Nathan Crock
Nathan Crock Joël Tabak
Joël Tabak Gordon Erlebacher
Gordon Erlebacher