- 1Mathematical Center, University of Lund, Lund, Sweden
- 2IMPB - The Keldysh Institute of Applied Mathematics of the Russian Academy of Sciences, Moscow, Russia
- 3Oxford Centre for Computational Neuroscience, Oxford, United Kingdom
- 4Department of Computer Science, University of Warwick, Coventry, United Kingdom
- 5Institute of Science and Technology for Brain-Inspired Intelligence, Fudan University, Shanghai, China
A new approach to understanding the interaction between cortical areas is provided by a mathematical analysis of biased competition, which describes many interactions between cortical areas, including those involved in top-down attention. The analysis helps to elucidate the principles of operation of such cortical systems, and in particular the parameter values within which biased competition operates. The analytic results are supported by simulations that illustrate the operation of the system with parameters selected from the analysis. The findings provide a detailed mathematical analysis of the operation of these neural systems with nodes connected by feedforward (bottom-up) and feedback (top-down) connections. The analysis provides the critical value of the top-down attentional bias that enables biased competition to operate for a range of input values to the network, and derives this as a function of all the parameters in the model. The critical value of the top-down bias depends linearly on the value of the other inputs, but the coefficients in the function reveal non-linear relations between the remaining parameters. The results provide reasons why the backprojections should not be very much weaker than the forward connections between two cortical areas. The major advantage of the analytical approach is that it discloses relations between all the parameters of the model.
1. Introduction
Biological systems employ a selection processing strategy for managing the enormous amount of information resulting from their interaction with the environment. This selection of relevant information is referred to as attention. One type of visual attention is the result of top-down influences on the processing of sensory information in the visual cortex, and therefore is intrinsically associated with neural interactions within and between cortical areas. Thus, elucidating the neural basis of visual attention is an excellent paradigm for understanding some of the basic mechanisms for interactions between cortical areas.
Observations from a number of cognitive neuroscience experiments have led to an account of attention termed the “biased competition hypothesis,” which aims to explain the computational processes governing visual attention and their implementation in the brain's neural circuits and neural systems. According to this hypothesis, attentional selection operates in parallel by biasing an underlying competitive interaction between multiple stimuli in the visual field toward one stimulus or another, so that behaviorally relevant stimuli are processed in the cortex while irrelevant stimuli are filtered out (Chelazzi et al., 1993; Duncan, 1996; Chelazzi, 1998; Reynolds and Desimone, 1999). Thus, attending to a stimulus at a particular location or with a particular feature biases the underlying neural competition in a certain brain area in favor of neurons that respond to the location, or the features, of the attended stimulus. This attentional effect is produced by generating signals in areas outside the visual cortex which are then fed back to extrastriate visual cortical areas, where they bias the competition such that when multiple stimuli appear in the visual field, the cells representing the attended stimulus win, thereby suppressing the firing of cells representing distracting stimuli (Duncan and Humphreys, 1989; Desimone and Duncan, 1995; Duncan, 1996; Reynolds et al., 1999). According to this line of work, attention appears as a property of competitive/cooperative interactions that work in parallel across the cortical modules. Neurophysiological experiments are consistent with this hypothesis in showing that attention serves to modulate the suppressive interaction between the neuronal firing elicited by two or more stimuli within the receptive field (Miller et al., 1993; Motter, 1993; Chelazzi, 1998; Reynolds and Desimone, 1999; Reynolds et al., 1999). Further evidence comes from functional magnetic resonance imaging (fMRI) in humans (Kastner et al., 1998, 1999) which indicates that when multiple stimuli are present simultaneously in the visual field, their cortical representations within the object recognition pathway interact in a competitive, suppressive fashion, which is not the case when the stimuli are presented sequentially. It was also observed that directing attention to one of the stimuli counteracts the suppressive influence of nearby stimuli.
Neurodynamical models providing a theoretical framework for biased competition have been proposed and successfully applied in the context of attention and working memory (Rolls and Deco, 2002; Rolls, 2016). In the context of attention, Usher and Niebur (1996) introduced an early model of biased competition to explain the attentional effects in neural responses observed in the inferior temporal cortex, and this was followed by a model for V2 and V4 by Reynolds et al. (1999) based on the shunting equations of Grossberg (1988). Deco and Zihl (2001) extended Usher and Niebur's model to simulate the psychophysics of visual attention by visual search experiments in humans. Their neurodynamical formulation is a large-scale hierarchical model of the visual cortex whose global dynamics is based on biased competition mechanisms at the neural level. Attention then appears as an effect related to the dynamical evolution of the whole network. This large-scale formulation has been able to simulate and explain in a unifying framework visual attention in a variety of tasks and at different cognitive neuroscience experimental measurement levels, namely: single-cells (Deco and Lee, 2002; Rolls and Deco, 2002), fMRI (Corchs and Deco, 2002, 2004), psychophysics (Deco et al., 2002; Deco and Rolls, 2004), and neuropsychology (Deco and Rolls, 2002; Heinke et al., 2002). In the context of working memory, further developments (Deco and Rolls, 2003; Deco et al., 2004; Szabo et al., 2004) managed to model in a unifying form attentional and memory effects in the prefrontal cortex integrating single-cell and fMRI data, and different paradigms in the framework of biased competition.
A detailed dynamical analysis of the synaptic and spiking mechanisms underlying biased competition was produced by Deco and Rolls (2005). However, the parameter regions within which biased competition operates were identified by a mean field analysis, which consisted of testing a set of parameters until effective regions in the state spaces were identified.
Here we treat the biased competition system analytically for the first time. This mathematical analysis complements previous numerical results and improves our understanding of the principles of operation of the system. Although the results are presented in the context of attention, they apply more generally to interactions between cortical areas. The dynamics of cortical attractor networks, and the dynamical interactions between cortical areas and the strength of the connections between them that enable them to interact usefully for short-term memory and attention yet maintain separate attractors have been analyzed with the rather different approaches of theoretical physics elsewhere (Treves, 1993; Battaglia and Treves, 1998; Renart et al., 1999a,b, 2000, 2001; Panzeri et al., 2001; Rolls, 2016).
2. Methods
2.1. The Biased Competition Network
The network to be analyzed is shown in Figure 1, and has the same general architecture used by Deco and Rolls (2005) to investigate the mechanisms of biased competition in a range of neurophysiological experiments. The system has forward connections Jf and Kf, and top-down backprojection connections Jb and Kb, as shown in Figure 1. The top-down connections are weaker, so that they can bias the bottom up inputs, but not dominate them, so that the system remains driven by the world. The top-down connections in the model correspond to the backprojections found between adjacent cortical areas in a cortical hierarchy, and in the area of memory recall, to the backprojections from the hippocampus to the neocortex (Kesner and Rolls, 2015; Rolls, 2016, 2018). The anatomical arrangement that facilitates this is that the backprojections end on the apical dendrites of cortical pyramidal cells far from the cell body, where their effects can be shunted by forward inputs that terminate on the parts of the dendrite that are electrically closer to the cell body (Rolls, 2016). In both top-down attention, and in memory recall, it is important that any bottom-up inputs from the world take priority, so that the organism is sensitive to events in the world, rather than being dominated by internal processing (Rolls, 2016). Interestingly, there is evidence that this situation is less the case in schizophrenia, in which some key forward connections are reduced in magnitude relative to the backprojections (Rolls et al., 2019). The type of neurophysiological experiment for which this model was designed is described by Deco and Rolls (2005), with one of the original neurophysiological investigations performed on object-based attention in the inferior temporal visual cortex (IT) by Chelazzi et al. (1993). The overall operation of this architecture is conceptualized as follows [see Deco and Rolls (2005)]. Activity in neuron or population of neurons L1 have a strong driving effect on H1 (via Jf), as stimulus 1 acting via λ1 is the preferred (i.e., most effective) stimulus, and a weaker effect on H2 (via the crossed connection Kf) for which stimulus 1 is the less preferred stimulus. There are weaker corresponding backprojections Jb and Kb. Correspondingly, L2 has a strong driving effect on H2 (via Jf) as stimulus 2 acting via λ2 is the preferred stimulus, and a weaker effect on H1 (via the crossed connection Kf) for which stimulus 2 is the less preferred stimulus. L1 is in competition with L2 (with strength cL), and H1 is in competition with H2 (with strength cH). The present model does not imply that L1 and L2 are in different areas in a topographical map, but that can be easily implemented by decreasing the strength of cL if L1 and L2 are not close together in the map, and the same general results hold (see Deco and Rolls, 2005). It is noted that convergence in topographically mapped systems from stage to stage is important in providing one of the bases for translation invariant visual object recognition as modeled in VisNet (Rolls, 2012, 2016), and that the dendritic morphology at different stages of processing in the visual cortical hierarchy may facilitate this (Elston, 2002; Elston and Fujita, 2014).
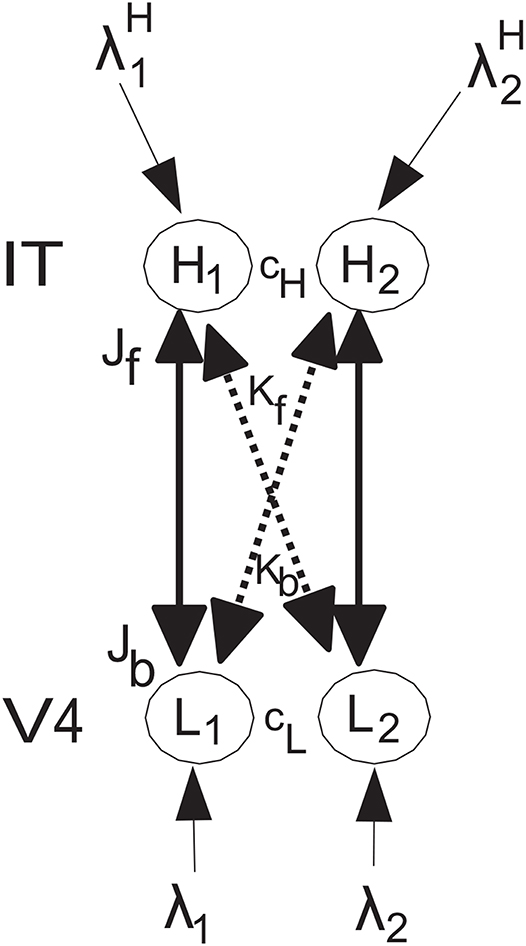
Figure 1. Model architecture. The lower nodes are L1 and L2, and receive inputs λ1 and λ2. L1 has forward connections of strength Jf to higher node H1 for which stimulus 1 acting via λ1 is the preferred input, and L2 has forward connections of strength Jf to higher node H2 for which stimulus 2 acting via λ2 is the preferred input. The corresponding backprojections have weaker strength Jb. In addition, there are crossed connections shown with dashed lines. In particular, L1 has forward connections of weak strength Kf to higher node H2 as stimulus 1 is not the preferred stimulus for H2, and L2 has forward connections of strength Kf to higher node H1 as stimulus 2 is not the preferred stimulus for H1. The corresponding backprojections have weaker strength Kb. A top-down attentional bias signal can be applied to node H2, and can bias the network to emphasize the effects of λ2 even if λ2 is less than or equal to λ1. There is competition within a level, with H1 and H2 competing with strength cH, and L1 and L2 competing with strength cL. The conditions for these effects to occur and for the network to be stable are analyzed. In addition, all four of the nodes can in the simulations have recurrent collateral connections that produce self-excitatory effects, consistent with cortical architecture, and these produce the expected effects, but are not considered further here because the mathematical analysis focusses on the tractable case in which they are not present. The nodes L correspond to V4, and the nodes H to inferior temporal visual cortex, in the neurophysiological experiment of Chelazzi et al. (1993) on object-based top-down attention.
The nodes L correspond to V4, and the nodes H to inferior temporal visual cortex, in the neurophysiological experiment of Chelazzi et al. (1993) on object-based top-down attention. The lower nodes are L1 and L2, and receive inputs λ1 and λ2. L1 has forward connections of strength Jf to higher node H1, and L2 has forward connections of strength Jf to higher node H2. The corresponding backprojections have strength Jb. In addition, there are crossed connections Kf and Kb shown with dashed lines. The rationale for this connectivity is that the preferred stimulus for L1 has strong effects on H1, but weaker effects on H2 for which it is not the preferred stimulus. In a corresponding way, the preferred stimulus for L2 has strong effects on H2, but weaker effects on H1 for which it is not the preferred stimulus. This is implemented as follows. L1 has forward connections of strength Kf to higher node H2, and L2 has forward connections of strength Kf to higher node H1. The corresponding backprojections have strength Kb. The K connections are weaker that the J connections. A top-down attentional bias signal can be applied to node H2, and can bias the network to emphasize the effects of λ2 even if λ2 is less than or equal to λ1. There is competition within a level, with H1 and H2 competing with strength cH, and L1 and L2 competing with strength cL. The conditions for these effects to occur and for the network to be stable are analyzed. In addition, all four of the nodes can have recurrent collateral connections that produce self-excitatory effects, but the effects of these in the simulations do not affect the generic results obtained, and are not included for simplicity in the mathematical analyses.
The network can operate as follows. If a weaker than λ1 input λ2 is applied to L2, then neural populations L1 and H1 win the competition. However, if a top-down biased competition input is applied to H2, then this can bias the network so that H2 wins the competition over H1, but also L2 has higher activity than L1. Here we analyse the relation between the parameters shown in Figure 1 that enable these effects to emerge and to be stable.
A feature of the model described here and also by Deco and Rolls (2005) is that local attractor dynamics are implemented within each of the neuronal populations, as recurrent collateral connections are a feature of the cerebral neocortex, and are one way to incorporate non-linear effects into the operation of the system. The new results are derived here analytically, and are illustrated with simulations with the parameters originating from the formulas obtained.
2.2. The Attentional Effects to be Modeled: Investigation 1
One top-down biased competition effect to be considered is as follows. If λ1 is greater than λ2, then the activity of L1 will be greater than the activity of L2. But if we apply a top-down biased competition input to H2, then at some value of the top-down bias will result in L2 having as much activity as L1. We seek to analyse the exact conditions under which this biased competition effect occurs, in terms of all the parameters of the system.
This system has been studied previously as follows, but with a mean-field analysis to search the parameter space, rather than the analytic approach described here. Figure 1 shows a design associated with a prediction that can be made by setting the contrast-attention interaction study in the framework of the experimental biased competition design of Chelazzi et al. (1993) involving object attention. Deco and Rolls (2005) modeled this experiment by measuring neuronal responses from neurons in neuronal population (or pool) H1 in the inferior temporal cortex (IT) to a preferred and a non-preferred stimulus simultaneously presented within the receptive field. They manipulated the contrast or efficacy of the stimulus that was non-preferred for the neurons H1. They analyzed the effects of this manipulation for two conditions, namely without object attention, or with top-down object attention on the non-preferred stimulus 2 that produced input λ2, implemented by adding an extra bias to H2. In the previous integrate-and-fire simulations (Deco and Rolls, 2005), top-down biased competition was demonstrated, and it was found that the attentional suppressive effect implemented through on the responses of neurons H1 to the competing non-preferred stimulus (2) was higher when the contrast of the non-preferred stimulus (2) was at intermediate values. However, the operation of this type of network was not examined analytically, which is the aim of the present investigation.
2.3. The Attentional Effects to be Modeled: Investigation 2
A second top-down competition effect might be considered as follows. If λ1 is greater than λ2 and both are applied simultaneously, then the activity of H1 will be greater than the activity of H2. However, if we apply top-down bias to H2, then we can influence the activity of H2 and H1 (through all the connections in the system) until H2 and H1 have the same activity (and at the same time there will be an effect on L1 and L2). We wish to quantify these effects analytically in terms of all the parameters of the system.
3. Dynamics
We shall use the notation that [x]+ = max{x, 0} for any rational value of x. We assume that L1(t), L2(t), H1(t), H2(t) are defined by the following system of recurrent equations in discrete time t = 0, 1, …:
One can also use here any time step t = 0, τ, 2τ,…, treating τ as another parameter. Here I denotes the indicator function, i.e.,
and similarly for I{Li(t) > TL}. This means that the terms in (3.1) and (3.2) which involve these indicator functions for the recurrent dynamics are present only if the activity in Li(t) or Hi(t) is greater than the corresponding threshold TL or TH. In the analysis described here, we assumed that TL and TH were infinity, so that the recurrent dynamics were not in operation, but the recurrent dynamics were tested in the simulations.
The constants represent the synaptic weight of the connection from node Lj to node Hi, while is the synaptic weight of the connection from node Hj to node Li. We shall assume that
for all i = 1, 2, i ≠ j, where indexes b and f correspond to “back” and “forward”. Furthermore, we assume that for some non-negative coefficient q (typically 0 ≤ q < 1, see more comments below)
Functions represent the external inputs.
All the remaining constants in the system (3.1), (3.2) are free parameters; they are assumed to be non-negative, as they represent the following characteristics:
βL is the decay term for the L nodes,
cL is the competition between the L nodes,
TL is the threshold at which an L node enters its attractor dynamics as was explained above,
αL is the gain factor for self-excitation in an L node for attractor dynamics,
βH is the decay term for the H nodes,
cH is the competition between the H nodes,
TH is the threshold at which an H node enters its attractor dynamics,
αH is the gain factor for self-excitation in an H node for attractor dynamics.
Note that when all the constant parameters of the system are set to be zero, including the input functions , then the system
remains at the initial state (L1(0), L2(0), H1(0), H2(0)).
We shall assume that
and that all the input functions are non-negative constants, i.e.,
We shall address the following problems. Assume, that λ1 > λ2 > 0.
Problem I. Are there such that L1(t) ≤ L2(t) for all large values of t? This is investigated in Investigation 1.
Problem II. Are there such that H1(t) ≤ H2(t) for all large values of t? This is investigated in Investigation 2.
In other words we are looking for the conditions for the parameters of the system which allow the biased competition. Deco and Rolls (2005) found numerically an area of parameters which yields such effect. Here we derive this analytically. This allows us to treat a wide range of parameters and moreover to find out the exact relations between all the parameters of the network when the biased competition takes place.
4. Simulations of the Operation of the Network With Parameters Selected Based on the Analysis That Follows
4.1. Investigation 1
The top-down biased competition effect to be considered here is as follows. If λ1 is greater than λ2, then the activity of L1 will be greater than the activity of L2. But if we apply a top-down biased competition input λH to H2, then at some value of λH the top-down bias will result in L2 having as much activity as L1. The aim was to discover the critical value of λH by simulation, for comparison with the analytic value.
The system specified by (3.1) and (3.2) was implemented in Matlab. The parameters shown in (3.1) and (3.2) were set as follows:
Jf = 0.15 / 3 (the values for these synaptic weights are in the same ratio as in Deco and Rolls, 2005)
Jb = 0.05 / 3
Kf = 0.015 /3
Kb = 0.005 / 3
βL = 0.35 (the decay term for the L nodes)
cL = 0.3 (the competition between the L nodes)
TL = 5.0 (the threshold at which an L node enters its attractor dynamics; in practice this was set to infinity in most of the work described, in order to prevent attractor dynamics operation in the nodes)
αL = 0.0 (the gain factor for self-excitation in an L node for attractor dynamics, αL can be set as well to 0.1 if recurrent dynamics are required)
βH = 0.35 (the decay term for the H nodes)
cH = 0.3 (the competition between the H nodes)
TH = 5.0 (the threshold at which an H node enters its attractor dynamics; in practice this was set to infinity in most of the work described, in order to prevent attractor dynamics operation in the nodes)
αH = 0.0 (the gain factor for self-excitation in an H node for attractor dynamics, αH can be set to 0.1)
λ1 = 6.0
λ2 = 5.0
= 0.0 or the critical value of derived below in the analysis for the top-down bias to overcome the bottom-up inputs shown as λ1 and λ2.
For all of the simulations illustrated in this paper and for the analytic investigations, the recurrent collateral self-excitatory effects were turned off (i.e., the α values were set to zero, and the parameters TL and TH were set to infinity). However, as stated in the Legend to Figure 1, the effects obtained when these were enabled were generically the same with respect to the biased competition effects described in this research.
Simulation results for a system with λ1 = 6.0, λ2 = 5.0, and the top-down bias λH = are shown in Figure 2. is the value derived in the analysis for the top-down bias to just overcome the bottom-up inputs shown as λ1 and λ2, as shown below in (5.54). was 22.816. Now the H2 node has high activity as expected due to the application of , but this has the effect that the network settles into a state where the L2 node has just higher activity than the L1 node, despite λ1 > λ2. This demonstrates that the analysis described below that derives the critical value for the biased attention signal to just reverse the difference between the bottom up inputs to make the network respond preferentially to the weaker incoming signal, is accurate.
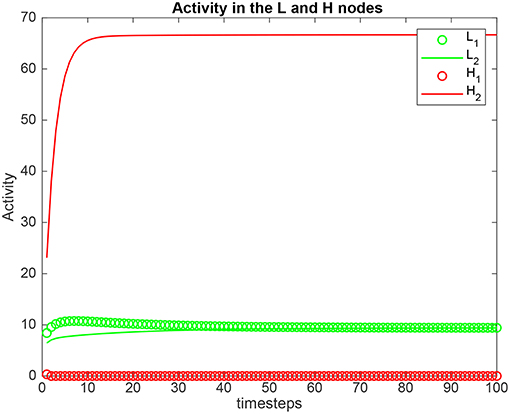
Figure 2. Simulation results for Investigation 1 for a system with λ1 = 6.0, λ2 = 5.0, and the top-down bias = 22.816. = 22.816 is the value derived in the analysis for the top-down bias to just overcome the difference between the bottom-up inputs shown as λ1 and λ2.
In further investigations, it was found that the analysis made correct predictions over a wide range of values of the parameters that were confirmed by numerical simulations. For example, the value was correctly calculated by the analysis over a 10-fold variation of Kf and Kb as shown by the performance of the numerical simulations. It was also found in the simulations that ratios for Jb/Jf and kb/kf in the range of 0.1–0.5 produced top-down biased competition effects with values for that were in the range of the other activities in the system.
The interpretation of the analytical results shown in for example (5.54) is now facilitated by graphical analysis. Figure 3 for Investigation 1 shows the top-down bias needed to make the activity of L2 as large as L1 as a function of λ1 − λ2 which is termed δλ. λ1 was fixed at 6, and = 0. Figure 3 shows that is a linear function of δλ. The slope of this function is high (140/6). The implication is that for reasonable values of the top-down bias limited to perhaps 50 in this model, the working range for δλ is relatively small, approximately 2.
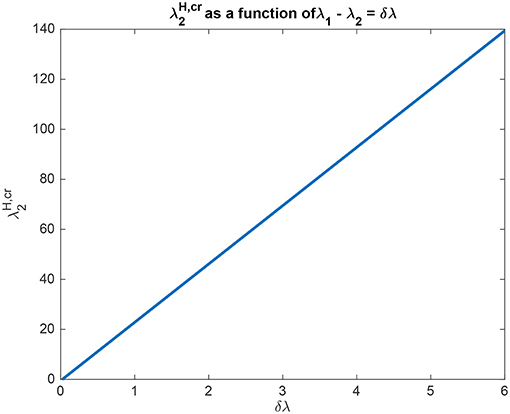
Figure 3. Analytical results for Investigation 1 showing the top-down bias needed to make the activity of L2 as large as L1 as a function of λ1 − λ2 denoted δλ. λ1 was fixed at 6.
In another example to illustrate the utility of the analysis that produced (5.54), it was found that the top-down bias needed to make the activity of L2 as large as L1 was relatively independent of the absolute values of λ1 and λ2, and so depended on the difference between them, i.e., λ1 − λ2 termed δλ. This is illustrated in Figure 4 in which δλ was set to 1.0, and the value of λ1 was increased from 1 to 10. It is clear that the top-down bias required depends very little on the absolute values of λ1 and λ2, but instead on their difference as shown in Figure 3.
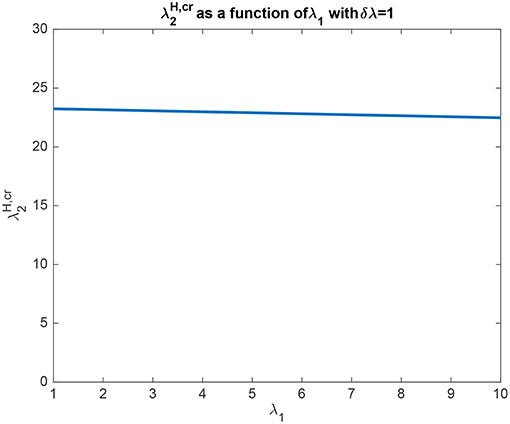
Figure 4. Analytical results for Investigation 1 for a system with λ1 − λ2 which is termed δλ fixed at 1. It is shown that the top-down bias needed to make the activity of L2 as large as L1 was relatively independent of the absolute values of λ1 and λ2.
We can also understand quantitatively the effect of the other parameters using (5.54). For example, if Jb is increased from its default value of 0.05/3 to 0.1/3, then the slope of the function illustrated in Figure 3 falls to a lower value (66/6). This makes the important point that top-down biased competition can only operate with rates for the top-down bias (in this case ) in a reasonable range (not too high) if the backward connection strength (here Jb with a default value of 0.05/3) is not too low compared to the forward connection strength (here Jf with a default value of 0.13/3). This places important constraints on the ratio of the strengths of backprojections relative to forward projections between cortical areas (Rolls, 2016).
In another example to illustrate the utility of the analysis that produced (5.54), it was found that if the crossed connections Kb (default 0.005/3) were increased (for example to 0.01/3), then more top-down bias was needed, with the slope of the function shown in Figure 3 now 158/6. The reason for this is clear, that some of the top-down bias acts on λ1 via Kb, but the analytic result in (5.54) quantifies this, as it does the effects of the other parameters involved in this approach to biased competition.
4.2. Investigation 2
The second top-down competition effect considered was as follows. If λ1 is greater than λ2 and both are applied simultaneously, then the activity of H1 will be greater than the activity of H2. However, if we apply top down biased competition λH to H2, then we can influence the rates H2 and H1 (through all the connections in the system) until H2 and H1 have the same activity (and at the same time there will be an effect on L1 and L2). We wished to quantify these effects analytically in terms of all the parameters of the system.
Simulation results for a system with λ1 = 6.0, λ2 = 5.0, and the top-down bias = 0 or = are shown in Figure 5. is the value derived in the analysis for the top-down bias to make the rates in H1 equal those in H2, to just overcome the difference between the bottom-up inputs λ1 and λ2, as shown in (5.60). The upper graph in Figure 5 shows the results when the top-down bias λH = 0. It can be seen that the rates in H1 are higher than in H2, which is as expected, because λ1 = 6.0, and λ2 = 5.0. In the lower part of Figure 5 the top-down bias = 0.775, the value derived in the analysis for the top-down bias to just produce equal rates in H1 and H2, overcoming the difference between the bottom-up inputs shown as λ1 and λ2. The simulation illustrated in the lower part of the figure thus shows that when the analytically calculated value for is used, the numerical simulation confirms that this is the correct value. When a different value is used, as shown in the top part of Figure 5, then the correct results are not obtained.
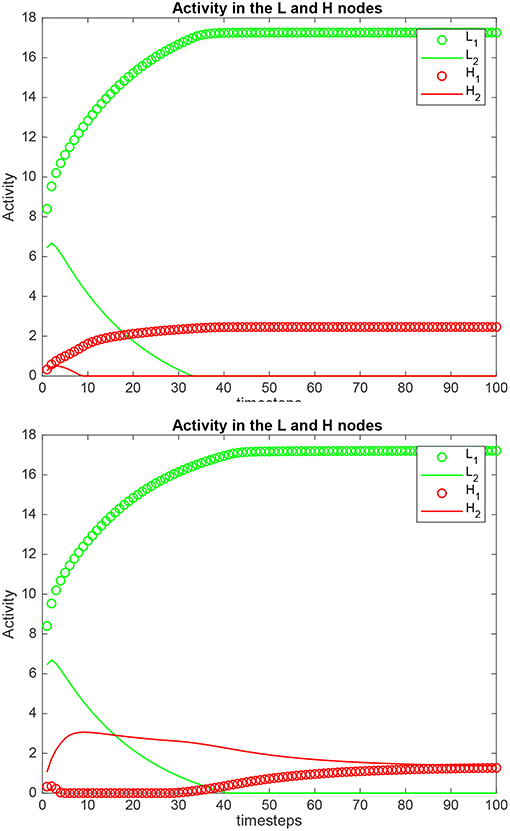
Figure 5. Simulation results for Investigation 2 for a system with λ1 = 6.0, λ2 = 5.0. (Upper) The top-down bias = 0. (Lower) The top-down bias = = 0.775. = is the value derived in the analysis for the top-down bias to just produce equal rates in H1 and H2, overcoming the difference between the bottom-up inputs shown as λ1 and λ2.
The interpretation of the analytical results shown in for example (5.60) for Investigation 2 is now facilitated by graphical analysis. Analytical results for Investigation 2 to show how is a function of λ1 are shown in Figure 6, for a system with λ2 = 5.0. is the value derived in the analysis for the top-down bias to just produce equal rates in H1 and H2, overcoming the difference between the bottom-up inputs shown as λ1 and λ2. Figure 6 shows that is a linear function of λ1, when λ2 = 5.0. Moreover, Figure 6 shows that only a small variation of is sufficient to counteract large changes in λ1. Moreover, the implication of 5.60 is that provided that the conditions shown in (5.59) are met, the operation is relatively independent of λ2. The understanding to which this leads is that the relative outputs measured at the H nodes are relatively little affected by the values of λ1 and λ2, compared to the effects of the input biases to and . An implication for the operation of the brain is that top-down biased competition can have useful effects on the lower (L) nodes in the system, which could then influence other systems. Another implication is that the output from the higher (H) nodes is relatively strongly affected by any direct inputs to the H nodes, compared to effects mediated by top-down biases acting through the backward connections to the L nodes, and on systems connected to these L nodes.
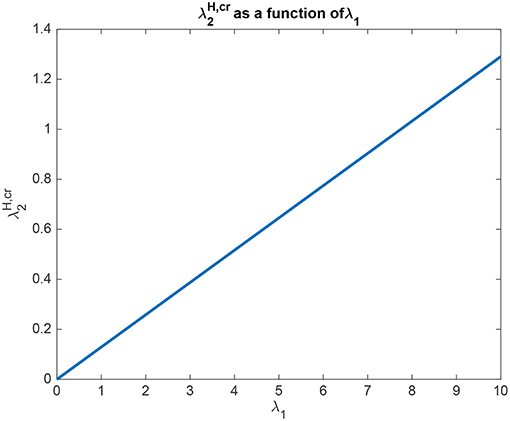
Figure 6. Analytical results for Investigation 2 for a system with λ2 = 5.0. is shown as a function of λ1. is the value derived in the analysis for the top-down bias to just produce equal rates in H1 and H2, overcoming the difference between the bottom-up inputs shown as λ1 and λ2.
Analytical results for Investigation 2 to show how depends on are shown in Figure 7, for a system with λ2 = 5.0. is the value derived in the analysis for the top-down bias to just produce equal rates in H1 and H2, overcoming the difference between the bottom-up inputs shown as λ1 and λ2. This figure shows that is a linear function of with a slope of approximately 1. The implication here is that inputs to the H nodes influence each other almost equally, and this will occur primarily through the inhibition between these nodes implemented by cH, rather than through the top-down connections to the L nodes, and then the return effects from the L to the H nodes.
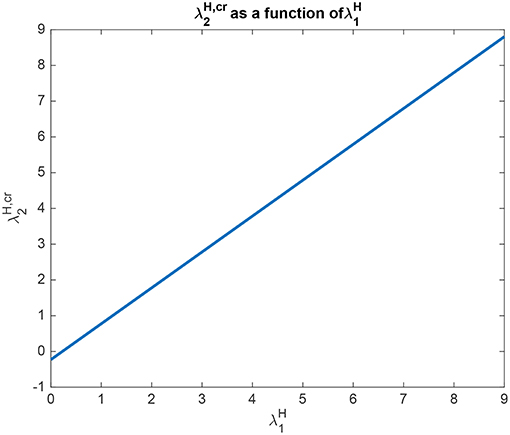
Figure 7. Analytical results for Investigation 2 for a system with λ1 = 6.0, λ2 = 5.0. is shown as a function of . is the value derived in the analysis for the top-down bias to just produce equal rates in H1 and H2, overcoming the difference between the bottom-up inputs shown as λ1 and λ2.
5. Mathematical Analysis
To solve the named problems we shall study the system (3.1) and (3.2) which describes the dynamics of (L1(t), L2(t), H1(t), H2(t)) in . Note that the entire state space is decomposed into 24 = 16 areas depending on whether xi ∈ [0, TL], yi ∈ [0, TH]:
where
In each area Xe1 × Xe2 × Ye3 × Ye4 the behavior of a system (3.1), (3.2) is linear; the non-linear nature of this system is seen, roughly speaking, only at the borders of these areas. In particular, there is a “cut” or “threshold” at zero for all involved functions, as their meaning as rates assumes only non-negative values.
We are mostly interested in modeling dynamics of a vector (L1(t), L2(t), H1(t), H2(t)) which does not escape to infinity in any coordinate. Therefore, we shall first study the system in the area
Let us assume first the following simplifying assumption. Set
which means that there is no facilitation of rates in the network.
Consider the linear system associated with the system (3.1), (3.2):
Let us fix
Then assuming also as in (3.5) the zero initial conditions
we observe that as long as
i.e., and [recall assumption (5.9)], the system (5.10) describes exactly the same system as in (3.1) and (3.2), i.e.,
Therefore we first derive the conditions for the matrix in (5.10) under which relations (5.12) hold for all t ≥ 0, i.e., the system remains to be in the bounded area S.
The boundedness of the solution to (5.10) is defined entirely by the eigenvalues of the corresponding matrix. However, deriving the eigenvalues even for a (4 × 4)-matrix requires already heavy computations. Instead we shall take advantage of some particular properties and symmetries of our model which allow us to reduce the original 4 dimensions of the system.
5.1. Boundedness of the Trajectories
Let us consider the dynamics of two systems related to (5.10):
and
Observe that H(t) → ∞ or ΔH(t) → ∞ if and only if at least one , in which case the original system (L1(t), L2(t), H1(t), H2(t)) cannot remain in the bounded area S. A similar statement holds about L(t) and ΔL(t). Therefore, we begin the analysis by providing the necessary conditions for the stability of systems (5.14) and (5.15), and thus for the stability of (5.10).
Then assuming that the connection parameters provide stability for the sums (5.14) we investigate the behavior of the system of differences (5.15) for different inputs
Our goal here is to find parameters such that given asymmetric inputs λ1 > λ2 we want to find such that ΔL(t) converges to a negative value for large t or that ΔH(t) converges to a negative value for large t.
If the equality (5.13) still holds for all t this means that correspondingly, L1(t) < L2(t) or H1(t) < H2(t) for large t as well. Hence, correspondingly, we have a solution to Problem I or Problem II.
First we derive from (5.10):
where
and
Similarly,
where
and
Effectively, using the symmetries we reduced the 4 dimensions of our model to 2 dimensions, as the solution to our original system (5.10) is given by
and
Recall that for a 2x2 matrix
where all the entries are positive (as in our model) the eigenvalues are given by
and
Note that due to the assumption of positivity of entries we have here
Hence, we have two (not linearly dependent) eigenvectors
Note here for further reference that the inequalities
and
hold for all positive parameters A, B, C, D.
Let us consider a linear transformation in R2:
where and ȳ = (y1, y2) is any vector.
Since vectors E1 and E2 make a basis in R2, for any vector ȳ there are numbers q1 and q2, such that
Then the solution to (5.29) is given by
Observe that
The last system together with the assumption that both C and D are positive yields
Under the last condition equation (5.31) yields the following convergence to the fixed point:
as t → ∞.
Consider WS defined in (5.17) as an example of the generic matrix M in (5.22). Let us denote its eigenvalues κi(WS), i = 1, 2, κ1(WS) ≥ κ2(WS). Under assumption
we have according to (5.33):
Next we study the eigenvalues κ1(WΔ) ≥ κ2(WΔ) of WΔ. Under assumption
which holds whenever (5.35) holds, we have according to (5.33):
Observe that when cL = cH = 0, condition (5.38) follows by the above condition (5.36).
Notice that together with the assumption (3.3) when all the parameters except Jb, Kb are fixed, the ratio q = Jb/Jf has to be small to ensure the boundedness of the functions Li(t), Hi(t).
In words, conditions (5.36) and (5.38) tell us that under the assumption (5.35) the stability of the system (or boundedness of the trajectories) requires that at least some of the connections, forward or backward ones, have to be sufficiently small.
5.2. Dynamics of (ΔL(t), ΔH(t)) for a Biased Input When All Rates Remain to be Strictly Positive
Here we study the system (3.1)–(3.2) assuming conditions when the functions Li(t), Hi(t) remain to be strictly positive and bounded. This means that the dynamics is described by linear system.
Assume that initially the input to is greater than the one to , i.e., Δλ > 0. We shall find here the sufficient conditions on the parameters of the connections which yield existence of the values
such that eventually, contrary to the initial bias, the state of the system satisfies
for all large t.
We shall assume first of all that the above conditions (5.35), (5.36), (5.37), and (5.38) are satisfied.
Consider system (5.19) with input
Let us decompose this vector along the eigenvectors of WΔ as in (5.30):
where Ei(WΔ) and κi(WΔ), i = 1, 2, denote, correspondingly the eigenvectors and the eigenvalues of WΔ, and here [compare matrices (5.19) and (5.22)]
Then by (5.34) the following convergence takes place when t → ∞:
Hence, given a positive
we want to find value x = x(Δλ) which satisfies condition
and moreover minimizes function [see (5.40)]
From (5.42) we get
which is negative. Then for all the x which satisfy (5.44) we have
Finally, we can define a negative ΔλH such that (5.40) holds, and moreover the limiting state as defined in the first row on the right in (5.41) satisfies (5.42). Observe that condition (5.42) by (5.41) guarantees condition (5.39). Substituting previously derived formulas into (5.45) we derive that for any given positive Δλ and any such that
we have (5.39).
We conclude that in the case when (5.13) still holds for all large t, i.e., if the system remains to be in the positive area, we have L2(t) ≥ L1(t) for all large t if conditions (5.35), (5.36), and (5.38) are fulfilled and is greater than the following critical value:
5.3. Operation With a Threshold at a Rate of Zero
Here we explore the non-linear effects of the system (3.1)–(3.2) considering the case when some of the rates Li(t) or Hi(t) become zero and may stay at zero due to the non-linear threshold function that does not allow negative rates (·)+.
5.3.1. Equality in the L-Nodes
We shall find here the conditions when a state
with strictly positive L and H can be a fixed point for the dynamical system (3.1)-(3.2) under assumption that
and also (5.9) holds, i.e., when a facilitation of rate above a certain threshold is not applied.
Assuming that the trajectories of L1(t), L2(t), and H2(t) remain to be strictly positive and do not hit zero, while H1(t) does decay to zero, the constants in (5.48) should satisfy the following system derived from (5.10) [see also 3.1)–(3.2)]:
Observe that the inequality in the third line in (5.49) after the threshold at a rate of zero as in the original system (3.1)-(3.2) yields limiting state H1(t) = 0.
The system (5.49) is equivalent to
This requires the following conditions for the parameters in order for the last system to have a solution:
which in turn requires
Observe that when the last condition is equivalent to
Assuming that (5.52) holds we derive from (5.51) the following critical value
The above analysis yields the following statement.
Proposition 5.1. Let conditions (5.36) and (5.38) hold, and let
Assume also (5.52) (or (5.53) if ) and
Then the system (3.1)-(3.2) converges to a state where
Notice that the limiting state described in the last Proposition satisfies (5.48).
Observe that the formula (5.54) for the critical value is in a good agreement with the previous case (5.47); in fact the same condition as in (5.47) reads directly from the inequality in (5.50). However, this is precisely the non-linearity of the system that we use here to derive the exact formula (5.54) for the critical value.
5.3.2. Equality in the H-Nodes
We shall find here the conditions when a state
with strictly positive L and H can be a fixed point for the dynamical system (3.1)-(3.2) under the assumption that
and also (5.9) holds, i.e., when a facilitation of rate above a certain threshold is not applied.
Assuming that the trajectories of L1(t), H1(t), and H2(t) remain to be strictly positive and do not hit zero, while L2(t) does decay to zero, the constants in (5.56) should satisfy the following system derived from (5.10) [see also 3.1)–(3.2)]:
Observe that the inequality in the second line in (5.57) after the threshold at zero as in the original system (3.1)–(3.2) yields limiting state L2(t) = 0. The system (5.57) is equivalent to
First we derive the conditions for the parameters in order for the last system to have a solution:
Assuming that the latter holds we derive from (5.57) the following critical value
If then the system ends up in a state where L1(t) = L > L2(t) = 0 and H2(t) = H1(t) = H.
6. Discussion
6.1. The Analysis
We consider here a 4-dimensional system of linear equations with thresholds for the rates at zero. Although it is “almost” a linear system, which admits rather straightforward analysis, the focus is on the relations between the numerous parameters. Notably, the latter relations are mostly non-linear.
Our approach takes advantage of the authentic symmetries in the system which allowed us to reduce the original 4 dimensions to 2 dimensions. This method may have some interest on its own as it can be used in other similar situations.
The derived conditions for the parameters which yield certain desired properties (specified as Problems I and II) disclose non-trivial relations between the parameters.
We considered several cases: (i) when the system keeps a positive rate at each node (section 5.2), and (ii) when the rate at one node, namely L2(t) (section 5.3.2), or H2(t) (section 5.3.1) is suppressed to zero after a long enough time.
Consider first our solution to Problem I. Remarkably the formulas for the critical value of the bias to yield the success of competition are different for the above two cases, namely when all the rates are strictly positive or when one rate is zero. These formulas are given by (5.47) and (5.54). This level of accuracy would not be possible without analytic formulas. Observe that (5.47) is the first condition in system (5.50), which also has to be fulfilled for the formula (5.54) to work.
As we mentioned above, formula (5.47) holds only under assumption that all the rates remain to be strictly positive, that can be achieved, for example, by choosing sufficiently large.
Further, we notice that the solution to Problem II provided by formula (5.60) reveals an interesting relation: as long as λ2 satisfies condition (5.59) it does not enter directly formula (5.60).
Deco and Rolls (2005) inferred from their particular simulations that the ratio of 2.5 between Jf and Jb provides a good working point for the biased competition. As we do not find any universal ratio between Jf and Jb in our analysis we conclude that the ratio 2.5 reflects particular scaling when the remaining parameters are fixed at certain values. On the other hand, our analysis tells us that the product JfJb has to be sufficiently small for the boundedness of the trajectories. More precisely, (5.36) and (5.38) under assumption (3.3) require the following sufficient conditions for our analysis
Furthermore, each of formulas (5.54) or (5.47) works under additional conditions as specified in the text. In particular, formula (5.54) requires (5.53), which is
A reasonably large set of parameters satisfies the above conditions, as shown by the computational results.
6.2. Implications for Understanding Biased Competition and the Interaction Between Neural Systems
The analysis elucidates some interesting properties of the biased competition system described. For example, the system is sensitive to the difference between λ1 and λ2, with the amount of biased competition required to produce the biased competition effects described related to this difference, as shown by the analytical results leading to (5.54), and the results shown in Figures 3, 4. These analyses and results show that while the system tolerates a wide range for the absolute values of λ1 and λ2, the difference between then δλ must be relatively small for the values of the top-down bias to be within a reasonable range of activity values, which in the context of the simulations described here might be up to 50.
The mean value of the λ inputs on the other hand influences how high the rates are of the output neurons. Another feature revealed by the analysis is how the parameters can be set to achieve asymptotically stable performance.
The analysis has interesting implications for understanding the operation of the backprojections that are important in top-down biased competition mechanisms of attention. Equation (5.54) and Figure 3, the associated results show that in order for the top down critical value not to have to be too large, the backprojections Jb must not be too weak. At the same time, Jb must be less than Jf, so that perceptual bottom-up inputs can dominate neural processing, which must not be dominated by internally generated top-down signals. This leaves a relatively small region for Jb/Jf between perhaps < 1.0 and 0.3. However, this ratio must be kept fairly low so that the two systems being coupled in this way can operate with separate attractors at the bottom (L) and top (H) ends (Renart et al., 1999a,b).
Another interesting property of this top-down biased competition system elucidated by the analysis is that the operation of the system, including the effects of the top-down bias , was influenced especially by the difference δλ between λ1 and λ2, rather than by their absolute value, as shown in (5.54) and illustrated in Figures 3, 4. This is similar to the operation of integrate-and-fire decision-making networks (Rolls and Deco, 2010; Deco et al., 2013; Rolls, 2016), with the similarity reflecting the way in which the competition between the nodes or attractors operates.
The key correspondence between the mathematical analysis and the numerical simulations is that the simulations show that the mathematical analysis very accurately specifies the exact value of the top-down bias that is needed. That is useful confirmation that the analysis accurately specifies the interactions between the parameters in the biased competition system. The simulations are additionally useful in illustrating the operation of the biased competition system investigated analytically.
In conclusion, the major advantage of the analytical approach brought to bear here for the first time on biased competition between cortical areas is that it discloses relations between all the parameters of the model, and helps to identify those values that yield the desired effect of biased competition. This task cannot be fulfilled purely by numerical simulations.
Data Availability
All datasets analyzed for this study are included in the manuscript and the supplementary files.
Author Contributions
TT performed the mathematical analyses. ER performed the numerical simulations and assessments. ER and TT wrote the paper jointly.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
TT acknowledges support of a COSTNET EU grant for supporting the collaboration with Oxford. ER acknowledges support for the collaboration with Lund from a grant of the Swedish Academy of Science (VR). The authors thank Y. Kazanovich (Institute of Applied Mathematics, Russian Academy of Sciences) for helpful discussion and comments.
References
Battaglia, F., and Treves, A. (1998). Stable and rapid recurrent processing in realistic autoassociative memories. Neural Comput. 10, 431–450. doi: 10.1162/089976698300017827
Chelazzi, L. (1998). Serial attention mechanisms in visual search: a critical look at the evidence. Psychol. Res. 62, 195–219. doi: 10.1007/s004260050051
Chelazzi, L., Miller, E., Duncan, J., and Desimone, R. (1993). A neural basis for visual search in inferior temporal cortex. Nature 363, 345–347. doi: 10.1038/363345a0
Corchs, S., and Deco, G. (2002). Large-scale neural model for visual attention: integration of experimental single cell and fMRI data. Cereb. Cortex 12, 339–348. doi: 10.1093/cercor/12.4.339
Corchs, S., and Deco, G. (2004). Feature-based attention in human visual cortex: simulation of fMRI data. Neuroimage 21, 36–45. doi: 10.1016/j.neuroimage.2003.08.045
Deco, G., and Lee, T. S. (2002). A unified model of spatial and object attention based on inter-cortical biased competition. Neurocomputing 44–46, 775–781. doi: 10.1016/S0925-2312(02)00471-X
Deco, G., Pollatos, O., and Zihl, J. (2002). The time course of selective visual attention: theory and experiments. Vision Res. 42, 2925–2945. doi: 10.1016/S0042-6989(02)00358-9
Deco, G., and Rolls, E. T. (2002). Object-based visual neglect: a computational hypothesis. Eur. J. Neurosci. 16, 1994–2000. doi: 10.1046/j.1460-9568.2002.02279.x
Deco, G., and Rolls, E. T. (2003). Attention and working memory: a dynamical model of neuronal activity in the prefrontal cortex. Eur. J. Neurosci. 18, 2374–2390. doi: 10.1046/j.1460-9568.2003.02956.x
Deco, G., and Rolls, E. T. (2004). A neurodynamical cortical model of visual attention and invariant object recognition. Vision Res. 44, 621–644. doi: 10.1016/j.visres.2003.09.037
Deco, G., and Rolls, E. T. (2005). Neurodynamics of biased competition and cooperation for attention: a model with spiking neurons. J. Neurophysiol. 94, 295–313. doi: 10.1152/jn.01095.2004
Deco, G., Rolls, E. T., Albantakis, L., and Romo, R. (2013). Brain mechanisms for perceptual and reward-related decision-making. Prog. Neurobiol. 103, 194–213. doi: 10.1016/j.pneurobio.2012.01.010
Deco, G., Rolls, E. T., and Horwitz, B. (2004). ‘What’ and ‘where’ in visual working memory: a computational neurodynamical perspective for integrating fMRI and single-neuron data. J. Cogn. Neurosci. 16, 683–701. doi: 10.1162/089892904323057380
Deco, G., and Zihl, J. (2001). Top-down selective visual attention: a neurodynamical approach. Vis. Cogn. 8, 119–140. doi: 10.1080/13506280042000054
Desimone, R., and Duncan, J. (1995). Neural mechanisms of selective visual attention. Annu. Rev. Neurosci. 18, 193–222. doi: 10.1146/annurev.ne.18.030195.001205
Duncan, J. (1996). “Cooperating brain systems in selective perception and action,” in Attention and Performance XVI, eds T. Inui and J. L. McClelland (Cambridge, MA: MIT Press), 549–578.
Duncan, J., and Humphreys, G. (1989). Visual search and stimulus similarity. Psychol. Rev. 96, 433–458. doi: 10.1037//0033-295X.96.3.433
Elston, G. N. (2002). Cortical heterogeneity: implications for visual processing and polysensory integration. J. Neurocytol. 31, 317–335. doi: 10.1023/A:1024182228103
Elston, G. N., and Fujita, I. (2014). Pyramidal cell development: postnatal spinogenesis, dendritic growth, axon growth, and electrophysiology. Front. Neuroanat. 8:78. doi: 10.3389/fnana.2014.00078
Grossberg, S. (1988). Non-linear neural networks: principles, mechanisms, and architectures. Neural Netw. 1, 17–61. doi: 10.1016/0893-6080(88)90021-4
Heinke, D., Deco, G., Zihl, J., and Humphreys, G. (2002). A computational neuroscience account of visual neglect. Neurocomputing 44–46, 811–816. doi: 10.1016/S0925-2312(02)00477-0
Kastner, S., De Weerd, P., Desimone, R., and Ungerleider, L. (1998). Mechanisms of directed attention in the human extrastriate cortex as revealed by functional MRI. Science 282, 108–111. doi: 10.1126/science.282.5386.108
Kastner, S., Pinsk, M., De Weerd, P., Desimone, R., and Ungerleider, L. (1999). Increased activity in human visual cortex during directed attention in the absence of visual stimulation. Neuron 22, 751–761. doi: 10.1016/S0896-6273(00)80734-5
Kesner, R. P., and Rolls, E. T. (2015). A computational theory of hippocampal function, and tests of the theory: new developments. Neurosci. Biobehav. Rev. 48, 92–147. doi: 10.1016/j.neubiorev.2014.11.009
Miller, E. K., Gochin, P. M., and Gross, C. G. (1993). Suppression of visual responses of neurons in inferior temporal cortex of the awake macaque by addition of a second stimulus. Brain Res. 616, 25–29. doi: 10.1016/0006-8993(93)90187-R
Motter, B. C. (1993). Focal attention produces spatially selective processing in visual cortical areas V1, V2, and V4 in the presence of competing stimuli. J. Neurophysiol. 70, 909–919. doi: 10.1152/jn.1993.70.3.909
Panzeri, S., Rolls, E. T., Battaglia, F., and Lavis, R. (2001). Speed of feedforward and recurrent processing in multilayer networks of integrate-and-fire neurons. Netw. Comput. Neural Syst. 12, 423–440. doi: 10.1088/0954-898X/12/4/302
Renart, A., Moreno, R., Rocha, J., Parga, N., and Rolls, E. T. (2001). A model of the IT–PF network in object working memory which includes balanced persistent activity and tuned inhibition. Neurocomputing 38–40, 1525–1531. doi: 10.1016/S0925-2312(01)00548-3
Renart, A., Parga, N., and Rolls, E. T. (1999a). Associative memory properties of multiple cortical modules. Network 10, 237–255. doi: 10.1088/0954-898X_10_3_303
Renart, A., Parga, N., and Rolls, E. T. (1999b). Backprojections in the cerebral cortex: implications for memory storage. Neural Comput. 11, 1349–1388. doi: 10.1162/089976699300016278
Renart, A., Parga, N., and Rolls, E. T. (2000). “A recurrent model of the interaction between the prefrontal cortex and inferior temporal cortex in delay memory tasks,” in Advances in Neural Information Processing Systems, Vol. 12, eds S. Solla, T. Leen, and K.-R. Mueller (Cambridge, MA: MIT Press), 171–177.
Reynolds, J., and Desimone, R. (1999). The role of neural mechanisms of attention in solving the binding problem. Neuron 24, 19–29. doi: 10.1016/S0896-6273(00)80819-3
Reynolds, J. H., Chelazzi, L., and Desimone, R. (1999). Competitive mechanisms subserve attention in macaque areas V2 and V4. J. Neurosci. 19, 1736–1753. doi: 10.1523/JNEUROSCI.19-05-01736.1999
Rolls, E. T. (2012). Invariant visual object and face recognition: neural and computational bases, and a model, VisNet. Front. Comput. Neurosci. 6:35. doi: 10.3389/fncom.2012.00035
Rolls, E. T. (2018). The storage and recall of memories in the hippocampo-cortical system. Cell Tissue Res. 373, 577–604. doi: 10.1007/s00441-017-2744-3
Rolls, E. T., Cheng, W., Gilson, M., Gong, W., Deco, G., Zac Lo, C.-Y., et al. (2019). Beyond the disconnectivity hypothesis of schizophrenia. Cereb. Cortex.
Rolls, E. T., and Deco, G. (2002). Computational Neuroscience of Vision. Oxford: Oxford University Press.
Rolls, E. T., and Deco, G. (2010). The Noisy Brain: Stochastic Dynamics as a Principle of Brain Function. Oxford: Oxford University Press.
Szabo, M., Almeida, R., Deco, G., and Stetter, M. (2004). Cooperation and biased competition model can explain attentional filtering in the prefrontal cortex. Eur. J. Neurosci. 19, 1969–1977. doi: 10.1111/j.1460-9568.2004.03211.x
Treves, A. (1993). Mean-field analysis of neuronal spike dynamics. Network 4, 259–284. doi: 10.1088/0954-898X/4/3/002
Keywords: biased competition, attention, cerebral cortex, mathematical analysis, neural networks, top-down connections, bottom-up connections
Citation: Turova T and Rolls ET (2019) Analysis of Biased Competition and Cooperation for Attention in the Cerebral Cortex. Front. Comput. Neurosci. 13:51. doi: 10.3389/fncom.2019.00051
Received: 08 May 2019; Accepted: 04 July 2019;
Published: 31 July 2019.
Edited by:
Paul Miller, Brandeis University, United StatesReviewed by:
Guy Elston, University of South Australia, AustraliaAdam Ponzi, Okinawa Institute of Science and Technology Graduate University, Japan
Copyright © 2019 Turova and Rolls. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Edmund T. Rolls, ZWRtdW5kLlJvbGxzQG94Y25zLm9yZw==
 Tatyana Turova1,2
Tatyana Turova1,2 Edmund T. Rolls
Edmund T. Rolls