- 1Department of Physics and Astronomy, Ohio University, Athens, OH, United States
- 2Neuroscience Program, Ohio University, Athens, OH, United States
- 3Bernstein Center for Computational Neuroscience Berlin, Berlin, Germany
- 4Department of Physics, Humboldt University Berlin, Berlin, Germany
It has been shown before that two species of diffusing particles can separate from each other by the mechanism of reciprocally concentration-dependent diffusivity: the presence of one species amplifies the diffusion coefficient of the respective other one, causing the two densities of particles to separate spontaneously. In a minimal model, this could be observed with a quadratic dependence of the diffusion coefficient on the density of the other species. Here, we consider a more realistic sigmoidal dependence as a logistic function on the other particle’s density averaged over a finite sensing radius. The sigmoidal dependence accounts for the saturation effects of the diffusion coefficients, which cannot grow without bounds. We show that sigmoidal (logistic) cross-diffusion leads to a new regime in which a homogeneous disordered (well-mixed) state and a spontaneously separated ordered (demixed) state coexist, forming two long-lived metastable configurations. In systems with a finite number of particles, random fluctuations induce repeated transitions between these two states. By tracking an order parameter that distinguishes mixed from demixed phases, we measure the corresponding mean residence in each state and demonstrate that one lifetime increases and the other decreases as the logistic coupling parameter is varied. The system thus displays typical features of a first-order phase transition, including hysteresis for large particle numbers. In addition, we compute the correlation time of the order parameter and show that it exhibits a pronounced maximum within the bistable parameter range, growing exponentially with the total particle number.
1 Introduction
The emergence of spatiotemporal structures in suspensions of active particles is an important topic in the current research in nonequilibrium statistical physics (Romanczuk et al., 2012; Marchetti et al., 2013; Costanzo et al., 2014; Grossmann et al., 2014; O’Keeffe et al., 2017; Granek et al., 2024). Interestingly, in such settings, order in terms of separation of different sorts of particles may emerge other than by repelling or attracting forces but via the mutual control of motility.
A particularly striking example is the demixing of two different strains of Escherichia coli bacteria with reciprocal motility interaction, studied experimentally and in a reaction-diffusion model by Curatolo et al. (2020). A central part of the mechanism of particle separation was a mutual amplification of the diffusion strength caused by the presence of the respective other bacteria. This could be mimicked in the paper by Schimansky-Geier et al. (2021), which presented, simulated, and studied analytically a minimal model in which two populations of overdamped Brownian particles mutually control their strength of diffusivity (the noise intensity of driving fluctuations increases with the concentration of the respective other sort of particles). The dependence of the diffusion coefficient has to be strong enough (qualitatively and quantitatively) to observe a demixing of the two population densities.
Here, we study a variant of the model suggested by Schimansky-Geier et al. (2021) and demonstrate a novel bistability between a well-mixed and a demixed state that results in a system with finite particles in stochastic transitions between an ordered and a disordered state. This result might be interesting and also observable experimentally when the reciprocal motility interaction is particularly tailored.
Our paper is organized as follows. In the next section, we introduce the studied model, focusing on the novel aspect, the sigmoidal diffusion coefficient. In Section 3, we derive the conditions under which a single demixed state, a single homogeneous (well-mixed) state, and bistability between both states can be observed in the model and present the system bifurcation diagram. In Section 4, we show and discuss the results of simulations in the bistable parameter regime, in which we measure the mean times that the system spends in the two bistable states and inspect how these times depend on the bifurcation parameter. We conclude in Section 5 with a discussion of our results.
2 Model and measures
We consider two populations of Brownian particles, A and B, each of size
Here
Averaging close to the boundaries is implemented in a reduced window over an inside range of the respective densities; see below for an explanation. The case of local interaction where
Our model belongs to the broad class of active matter systems, ensembles of particles that continuously consume energy and therefore operate out of equilibrium (Romanczuk et al., 2012; Marchetti et al., 2013). In Equation 1, noise represents fluctuations in the internal drive of the particles. The time-dependent local density of the opposite species modulates each particle’s effective diffusivity (noise intensity). This reciprocal motility control represents energy influx at the microscopic scale, breaking detailed balance. Consequently, the observed steady states are maintained by a sustained flux of energy.
For the nonlinear function,
a function that monotonically grows with its argument (hence, the fluctuations driving the A particles at
Implementing the average of the densities as estimated from simulations of a finite number of particles deserves some comments, see Schimansky-Geier et al. (2021) for details. In our numerical simulations, the sensing radius accounts for a moving average of binned probability density functions (PDF). For each bin and a given time instant, the PDF is estimated by the number of particles that have fallen into this bin. To estimate
In the limit of infinite particle numbers,
We emphasize that these nonlinear diffusion equations may permit more than one steady-state solution. We implement a numerical solution of these equations by a finite-difference scheme described in detail in Appendix B of Schimansky-Geier et al. (2021), testing different initial conditions to determine the number and stability of asymptotic solutions. The integration of the Smoluchowski equations was terminated once the probability distributions at two consecutive time steps differed by less than
As in Schimansky-Geier et al. (2021), the system admits a homogeneous steady-state solution
which becomes significantly larger than zero whenever the system is demixed. This quantity can be computed from both finite-population simulations and from numerical solutions of the coupled Smoluchowski equations.
As an additional measure of order in the system, we consider the instantaneous mean position of the A particles:
which should remain close to zero when the A-particle distribution is homogeneous, but will deviate if A particles preferentially occupy one side of the interval (negative for the left side, positive for the right). Compared to
For finite
The simulation time window was chosen to ensure a sufficient number of transitions between metastable states in the bistable parameter regime for reliable estimation of the mean residence times, the probability density, and the correlation function of the order parameter. For exponentially distributed residence times, the standard error of the sample mean
3 State diagram for
We start with the numerical analysis of Equation 4 and find the asymptotic state(s) of the system by solving the nonlinear equations for various initial conditions on a grid.
When we vary the parameters
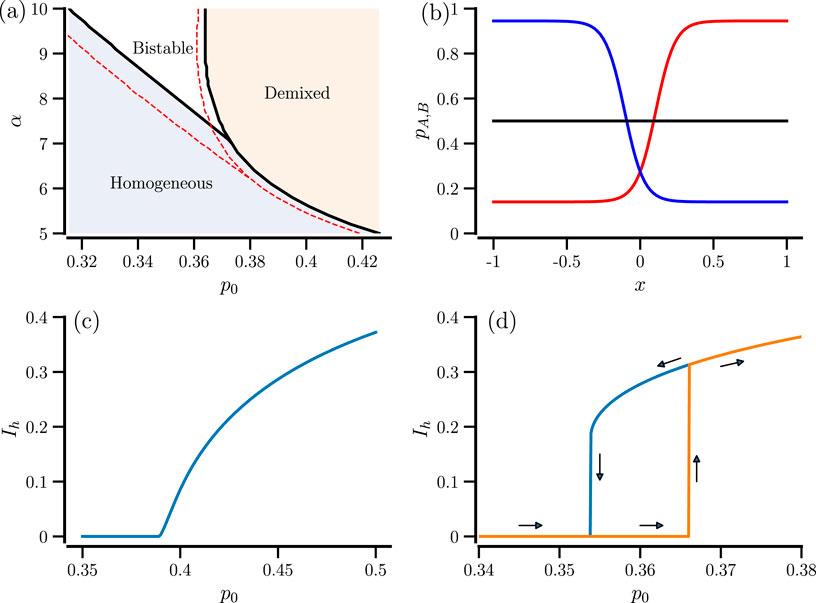
Figure 1. State transitions in the case
As a consequence of the different parameter regimes, we see different types of transitions when the inflection point
The observed bistability in the system with an infinite number of A and B particles (corresponding to the Smoluchowski equations) raises the interesting question of what will happen in a system with a finite number of particles that is prone to fluctuations. We explore the bifurcation in a system with many but finite particles next and then turn to smaller systems in which finite-size fluctuations may trigger transitions between bistable states.
4 First-order-like transition in finite but large systems
We now turn to a large system with
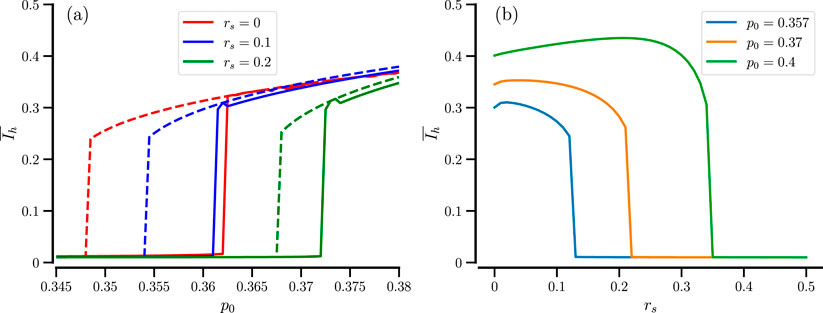
Figure 2. Effect of the sensing radius. (a) Time-averaged order parameter vs.
How does the bifurcation plot depend on the number of used particles? This is exhibited in Figure 3 for our standard value of sensing radius,
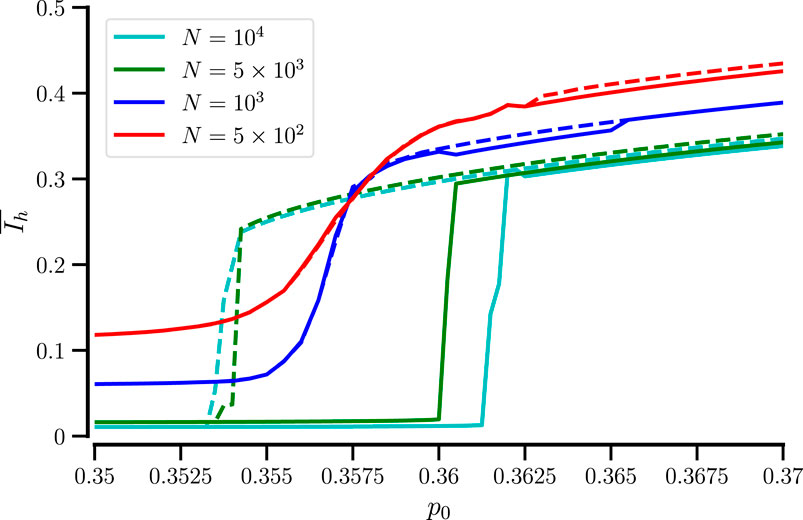
Figure 3. Hysteresis in the time-averaged order parameter is only seen for sufficiently large systems. Time-averaged order parameter vs.
5 Switching between mixed and demixed state in the bistable regime for small
For small
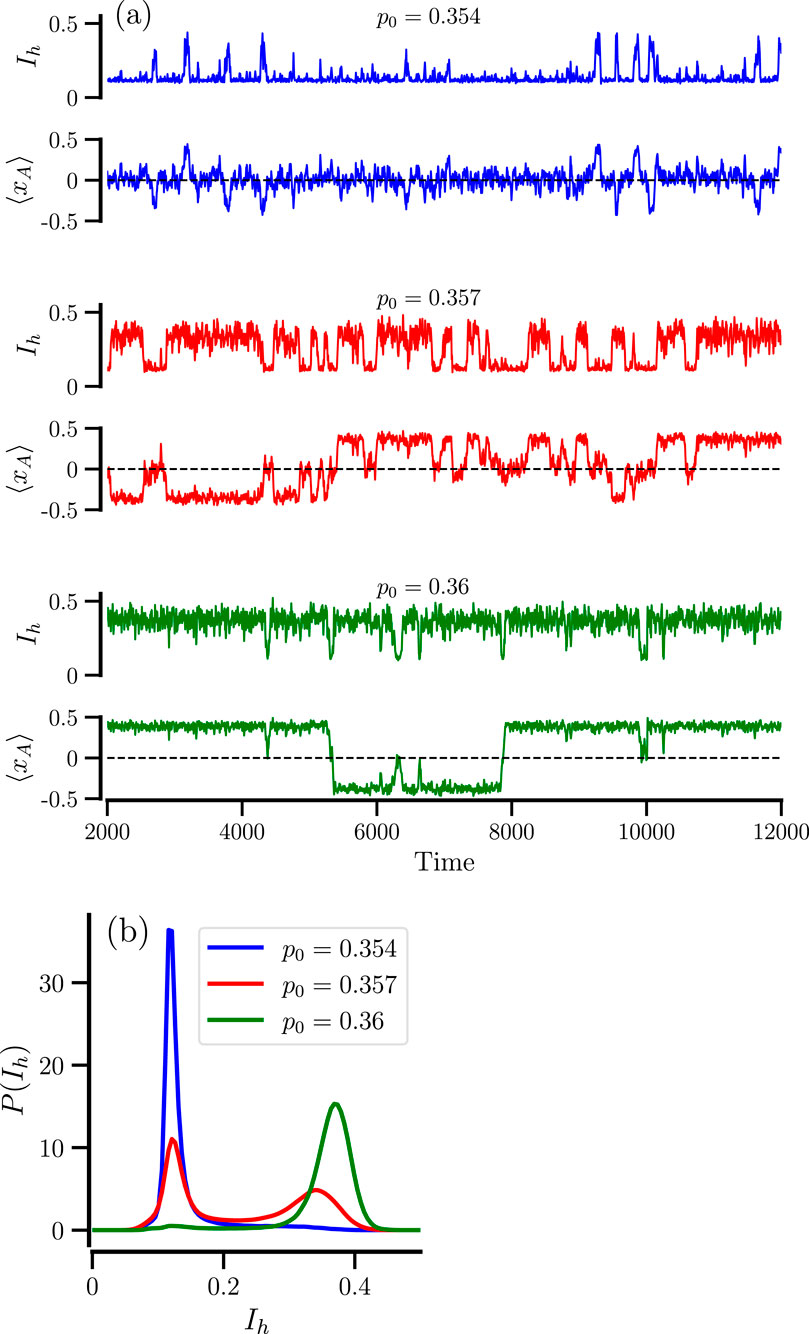
Figure 4. Stochastic transitions between mixed and remixed states for small particle numbers. Fragments of time traces of
From Figure 4a we can also conclude that both
Figure 5 shows a complete picture of
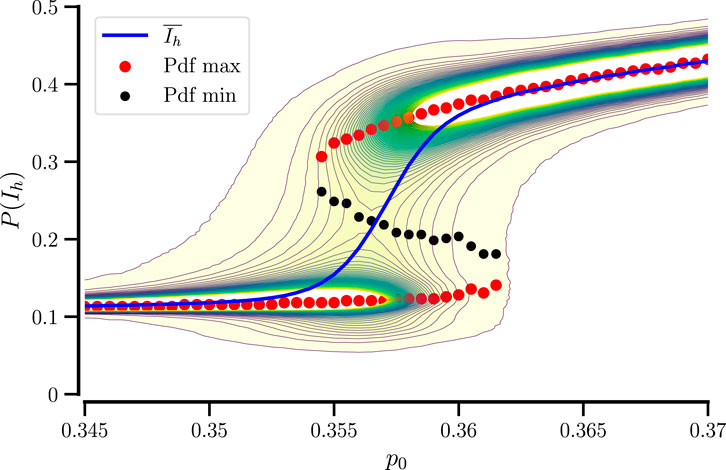
Figure 5. Probability distribution of
The stochastic transitions can be most appropriately characterized by the mean residence times in the mixed and demixed states. To this end, we extract many
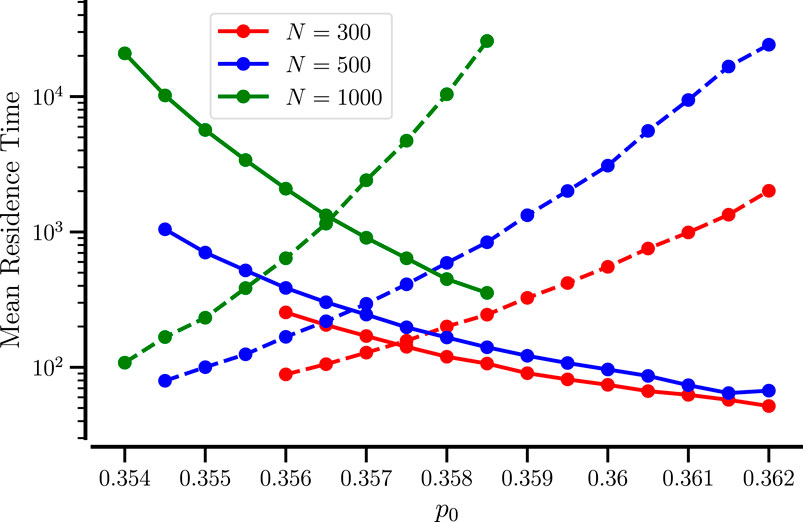
Figure 6. Mean residence times of mixed and demixed states for small systems. The mean duration of mixed (solid line) and demixed epochs (dashed line) vs.
Clearly, a larger number of particles implies ‘more waiting’: for
There is a particular value of
The slow back and forth between the different states of the system (especially at larger particle numbers and amid the bistable regime) may lead to long temporal correlations. We inspect their dependence on the system parameter by calculating the normalized correlation function of the order parameter
and extracting its typical decay time, the correlation time by the following estimate
We note that the correlation time is easier to calculate than the residence times, as one does not need to define and use a threshold to determine the residence epochs. In Figure 7a, the correlation time Equation 7 displays a pronounced maximum at the sweet spot
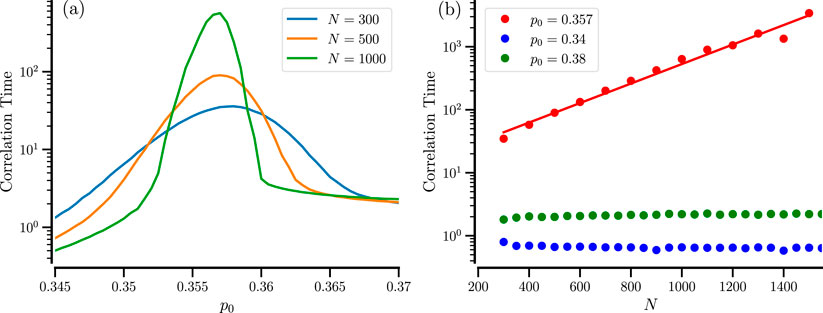
Figure 7. Correlation time of the order parameter. (a) Correlation time vs.
Furthermore, when the number of particles
6 Summary and discussion
We have inspected a minimalistic model of two populations of Brownian particles that mutually enhance by their presence the diffusion coefficient of the respective other population. Building on the results from Schimansky-Geier et al. (2021), as a new model ingredients we used here a sigmoidal nonlinearity characterized by an inflection point
Exploring the case of finite particle numbers using Langevin equations revealed the emergence of repeated stochastic transitions between the homogeneous (disordered) mixed state and a demixed state in which one kind of particle is in excess in one region while the other one is in excess in another region. Hence, in a strong formulation, the system switches back and forth between order and chaos, which we quantified by an order parameter that measures the deviation from a uniform distribution. We note that another measure would be the entropy of the two distributions: we have verified that the entropy indeed displays stochastic transitions between two values corresponding to the more ordered, demixed state and the more disordered, homogeneously distributed state (not shown). Repeated back-and-forth transitions between order and disorder have been observed experimentally in several systems (Pufall et al., 2004; Paul et al., 2022); interestingly, in the context of our work, the simplicity of the model leads to such transitions between high- and low-entropy states.
We have furthermore explored the transitions using the residence times and the correlation time of the order parameter and, specifically, their dependence on the bifurcation parameters and the system size. Typical for a symmetric bistable setup, the correlation time is maximized and displays an exponential growth in the system size.
It would be fascinating to observe this type of transition between mixed and demixed states in experimental systems of active matter. The new feature of our nonlinear dependence of the diffusion coefficient on the probability density seems to be rather realistic: diffusion coefficients can certainly not grow unbounded with the number of opposite particles (at some point, the presence of other particles may even hinder and limit diffusion), hence a saturation of
Our logistic mutual diffusion model captures self-organized demixing and noise-induced transitions between mixed and demixed states, behavior that resembles a thermodynamic first-order phase separation transition as in liquid-liquid phase separation (LLPS) (Banani et al., 2017; Zeigler et al., 2021). Further, cross-diffusion systems can be recast formally as Cahn–Hilliard–type equations (Berendsen et al., 2017) and therefore may share phenomenological features with LLPS models (Laghmach and Potoyan, 2020; Li and Hou, 2022). Conceptually, however, our model is an active media system and is not an LLPS model. In our model, the demixing is driven by reciprocal modulation of diffusion rather than by intermolecular interaction energies, as in LLPS.
The observed behavior in our model is a form of self-organization—more precisely, a transient self-organization that repeatedly emerges and decays. It may be useful to regard the spontaneous formation of high-concentration domains as a dynamical network whose nodes exchange particles and either adjust their size (approaching a single-interface metastable state) or disaggregate (transitioning to the disordered state). Methods from the theory of adaptive networks (Gross and Sayama, 2009; Berner et al., 2023) could be used to extend and analyze our framework in settings where state-dependent (context-dependent) interactions are expected. In our model, “state-dependent coupling” refers to the cross-diffusion gains depending on the locally averaged density of the partner species. Beyond microbial consortia, analogous activity-dependent couplings occur in several physiological contexts, for example, cancer–immune crosstalk in tissues (Hsieh et al., 2022; Marzban et al., 2024) and organ–organ interactions discussed in Network Physiology (Bashan et al., 2012; Qi et al., 2024; Lehnertz et al., 2020; Ivanov, 2021). We emphasize that these connections are qualitative, as quantitative mapping would require system-specific variables and timescales.
Our results may be viewed in the broader framework of synergetics, originally proposed by Hermann Haken, wherein emergent macroscopic patterns and states in nonlinear systems are cast via a small set of order parameters that “enslave” microscopic degrees of freedom (Haken, 1977; Haken 1983; Haken, 2012). In particular, our model’s demixing phenomenon, driven by reciprocal diffusivity feedback, exemplifies the hallmark of self-organization: above a threshold in the control parameter (here, the sigmoidal strength), a new collective state emerges and coexists with the homogeneous state, leading to noise-induced transitions between these metastable configurations.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
AN: Writing – review and editing, Methodology, Data curation, Formal Analysis, Investigation, Software, Conceptualization, Resources. XD: Data curation, Investigation, Formal Analysis, Writing – original draft. BL: Investigation, Methodology, Writing – review and editing, Supervision, Writing – original draft, Formal Analysis, Data curation, Conceptualization.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Acknowledgments
AcknowledgementsThe authors thank Michael Zaks (Humboldt University Berlin, Germany) for insightful discussions. AN thanks the Quantitative Biology Institute at Ohio University for providing computational resources.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that one of them (ABN) was an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Generative AI statement
The author(s) declare that Generative AI was used in the creation of this manuscript. Generative AI was used only for grammar and spelling checking.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnetp.2025.1612495/full#supplementary-material
References
Banani, S. F., Lee, H. O., Hyman, A. A., and Rosen, M. K. (2017). Biomolecular condensates: organizers of cellular biochemistry. Nat. Rev. Mol. cell Biol. 18, 285–298. doi:10.1038/nrm.2017.7
Bashan, A., Bartsch, R. P., Kantelhardt, J. W., Havlin, S., and Ivanov, P. C. (2012). Network physiology reveals relations between network topology and physiological function. Nat. Commun. 3, 702. doi:10.1038/ncomms1705
Bendat, J. S., and Piersol, A. G. (2011). Random data: analysis and measurement procedures. John Wiley and Sons.
Berendsen, J., Burger, M., and Pietschmann, J.-F. (2017). On a cross-diffusion model for multiple species with nonlocal interaction and size exclusion. Nonlinear Anal. 159, 10–39. doi:10.1016/j.na.2017.03.010
Berner, R., Gross, T., Kuehn, C., Kurths, J., and Yanchuk, S. (2023). Adaptive dynamical networks. Phys. Rep. 1031, 1–59. doi:10.1016/j.physrep.2023.08.001
Cates, M. E., and Tailleur, J. (2015). Motility-induced phase separation. Annu. Rev. Condens. Matter Phys. 6, 219–244. doi:10.1146/annurev-conmatphys-031214-014710
Costanzo, A., Elgeti, J., Auth, T., Gompper, G., and Ripoll, M. (2014). Motility-sorting of self-propelled particles in microchannels. Europhys. Lett. 107, 36003. doi:10.1209/0295-5075/107/36003
Curatolo, A. I., Zhou, N., Zhao, Y., Liu, C., Daerr, A., Tailleur, J., et al. (2020). Cooperative pattern formation in multi-component bacterial systems through reciprocal motility regulation. Nat. Phys. 16, 1152–1157. doi:10.1038/s41567-020-0964-z
Granek, O., Kafri, Y., Kardar, M., Ro, S., Tailleur, J., and Solon, A. (2024). Colloquium: inclusions, boundaries, and disorder in scalar active matter. Rev. Mod. Phys. 96, 031003. doi:10.1103/revmodphys.96.031003
Grossmann, R., Romanczuk, P., Baer, M., and Schimansky-Geier, L. (2014). Vortex arrays and mesoscale turbulence of self-propelled particles. Phys. Rev. Lett. 113, 258104. doi:10.1103/PhysRevLett.113.258104
Haken, H. (1983). Synergetics: an introduction: nonequilibrium phase transitions and self-organization in physics, chemistry, and biology. Springer.
Haken, H. (2012). Advanced synergetics: instability hierarchies of self-organizing systems and dDvices. Springer Science and Business Media.
Heinen, L., Groh, S., and Dzubiella, J. (2024). Tuning nonequilibrium colloidal structure in external fields by density-dependent state switching. Phys. Rev. E 110, 024604. doi:10.1103/PhysRevE.110.024604
Hsieh, W.-C., Budiarto, B. R., Wang, Y.-F., Lin, C.-Y., Gwo, M.-C., So, D. K., et al. (2022). Spatial multi-omics analyses of the tumor immune microenvironment. J. Biomed. Sci. 29, 96. doi:10.1186/s12929-022-00879-y
Ivanov, P. C. (2021). The new field of network physiology: building the human physiolome. Front. Netw. physiology 1, 711778. doi:10.3389/fnetp.2021.711778
Kullmann, R., Knoll, G., Bernardi, D., and Lindner, B. (2022). Critical current for giant fano factor in neural models with bistable firing dynamics and implications for signal transmission. Phys. Rev. E 105, 014416. doi:10.1103/PhysRevE.105.014416
Laghmach, R., and Potoyan, D. A. (2020). Liquid–liquid phase separation driven compartmentalization of reactive nucleoplasm. Phys. Biol. 18, 015001. doi:10.1088/1478-3975/abc5ad
Lehnertz, K., Bröhl, T., and Rings, T. (2020). The human organism as an integrated interaction network: recent conceptual and methodological challenges. Front. Physiology 11, 598694. doi:10.3389/fphys.2020.598694
Li, L.-g., and Hou, Z. (2022). Theoretical modelling of liquid–liquid phase separation: from particle-based to field-based simulation. Biophys. Rep. 8, 55–67. doi:10.52601/bpr.2022.210029
Lindner, B., and Nicola, E. M. (2008). Critical asymmetry for giant diffusion of active Brownian particles. Phys. Rev. Lett. 101, 190603. doi:10.1103/PhysRevLett.101.190603
Lindner, B., and Sokolov, I. (2016). Giant diffusion of underdamped particles in a biased periodic potential. Phys. Rev. E 93, 042106. doi:10.1103/PhysRevE.93.042106
Marchetti, M. C., Joanny, J.-F., Ramaswamy, S., Liverpool, T. B., Prost, J., Rao, M., et al. (2013). Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189. doi:10.1103/revmodphys.85.1143
Marzban, S., Srivastava, S., Kartika, S., Bravo, R., Safriel, R., Zarski, A., et al. (2024). Spatial interactions modulate tumor growth and immune infiltration. NPJ Syst. Biol. Appl. 10, 106. doi:10.1038/s41540-024-00438-1
O’Keeffe, K. P., Hong, H., and Strogatz, S. H. (2017). Oscillators that sync and swarm. Nat. Commun. 8 (1), 1504. doi:10.1038/s41467-017-01190-3
Paul, S., Hsu, W.-L., Ito, Y., and Daiguji, H. (2022). Boiling in nanopores through localized joule heating: transition between nucleate and film boiling. Phys. Rev. Res. 4, 043110. doi:10.1103/physrevresearch.4.043110
Pufall, M. R., Rippard, W. H., Kaka, S., Russek, S. E., Silva, T. J., Katine, J., et al. (2004). Large-angle, gigahertz-rate random telegraph switching induced by spin-momentum transfer. Phys. Rev. B—Condensed Matter Mater. Phys. 69, 214409. doi:10.1103/physrevb.69.214409
Qi, C., Wang, W., Liu, Y., Hua, T., Yang, M., and Liu, Y. (2024). Heart-brain interactions: clinical evidence and mechanisms based on critical care medicine. Front. Cardiovasc. Med. 11, 1483482. doi:10.3389/fcvm.2024.1483482
Romanczuk, P., Bär, M., Ebeling, W., Lindner, B., and Schimansky-Geier, L. (2012). Active brownian particles. Eur. Phys. J. Spec. Top. 202, 1–162. doi:10.1140/epjst/e2012-01529-y
Schimansky-Geier, L., Lindner, B., Milster, S., and Neiman, A. B. (2021). Demixing of two species via reciprocally concentration-dependent diffusivity. Phys. Rev. E 103, 022113. doi:10.1103/PhysRevE.103.022113
Keywords: Brownian particles, pattern formation, bistability, active matter, noise-induced switching, network physiology, self-organization
Citation: Neiman AB, Dong X and Lindner B (2025) Metastability in the mixing/demixing of two species with reciprocally concentration-dependent diffusivity. Front. Netw. Physiol. 5:1612495. doi: 10.3389/fnetp.2025.1612495
Received: 15 April 2025; Accepted: 20 October 2025;
Published: 17 November 2025.
Edited by:
Plamen Ch. Ivanov, Boston University, United StatesReviewed by:
Aneta Stefanovska, Lancaster University, United KingdomSonya Bahar, University of Missouri–St. Louis, United States
Copyright © 2025 Neiman, Dong and Lindner. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alexander B. Neiman, bmVpbWFuYUBvaGlvLmVkdQ==; Benjamin Lindner, YmVuamFtaW4ubGluZG5lckBwaHlzaWsuaHUtYmVybGluLmRl
 Alexander B. Neiman
Alexander B. Neiman Xiaochen Dong
Xiaochen Dong Benjamin Lindner
Benjamin Lindner