Large deformation diffeomorphic metric mapping registration of reconstructed 3D histological section images and in vivo MR images

Our current understanding of neuroanatomical abnormalities in neuropsychiatric diseases is based largely on magnetic resonance imaging (MRI) and post mortem histological analyses of the brain. Further advances in elucidating altered brain structure in these human conditions might emerge from combining MRI and histological methods. We propose a multistage method for registering 3D volumes reconstructed from histological sections to corresponding in vivo MRI volumes from the same subjects: (1) manual segmentation of white matter (WM), gray matter (GM) and cerebrospinal fluid (CSF) compartments in histological sections, (2) alignment of consecutive histological sections using 2D rigid transformation to construct a 3D histological image volume from the aligned sections, (3) registration of reconstructed 3D histological volumes to the corresponding 3D MRI volumes using 3D affine transformation, (4) intensity normalization of images via histogram matching, and (5) registration of the volumes via intensity based large deformation diffeomorphic metric (LDDMM) image matching algorithm. Here we demonstrate the utility of our method in the transfer of cytoarchitectonic information from histological sections to identify regions of interest in MRI scans of nine adult macaque brains for morphometric analyses. LDDMM improved the accuracy of the registration via decreased distances between GM/CSF surfaces after LDDMM (0.39 ± 0.13 mm) compared to distances after affine registration (0.76 ± 0.41 mm). Similarly, WM/GM distances decreased to 0.28 ± 0.16 mm after LDDMM compared to 0.54 ± 0.39 mm after affine registration. The multistage registration method may find broad application for mapping histologically based information, for example, receptor distributions, gene expression, onto MRI volumes.

Introduction

High resolution magnetic resonance imaging (MRI) technology has rendered in vivo brain structure accessible to morphometric analysis, an approach that has found widespread application in studies of anatomic changes associated with neuropsychiatric disorders, see papers in Thompson et al. (2004 , 2008b) . However, the cytoarchitectonic boundaries that define individual functional units in the brain, as for example the borders between neighboring cortical areas, cannot be captured at the resolution of MRI images. Such cellular detail is available only from post mortem microscopic analysis of histologically processed brains. Therefore, using histological sections to define anatomic boundaries in the MRI images would elevate the morphometric analyses of in vivo brain structure to a more refined, functionally meaningful level.

Combining the two techniques requires precise registration of histological section images and MRI images, a process that is difficult due to the deformations introduced by histological processing (Dauguet et al., 2007 ). Brain extraction commonly leads to nonlinear deformation such as shrinkage because of the fluid loss in the tissue. Fixation results in further shrinkage and distortion of brain volume. Histological processing such as sectioning, staining, and mounting on glass slides can cause further shrinkage, spatial deformations, or tissue damage such as shears or tears. In general, any histology to in vivo modality registration method requires: (1) alignment of photographic images of histological sections and their stacking to reconstruct a 3D histological volume, and (2) matching of the 3D histological volume to the 3D MRI volume. Sometimes the photographic images of the brain taken prior to sectioning, that is, blockface images, have been used as an intermediate modality to aid in the 3D histological volume reconstruction and to facilitate alignment to 3D MRI volumes (Table 1 ).

TABLE 1

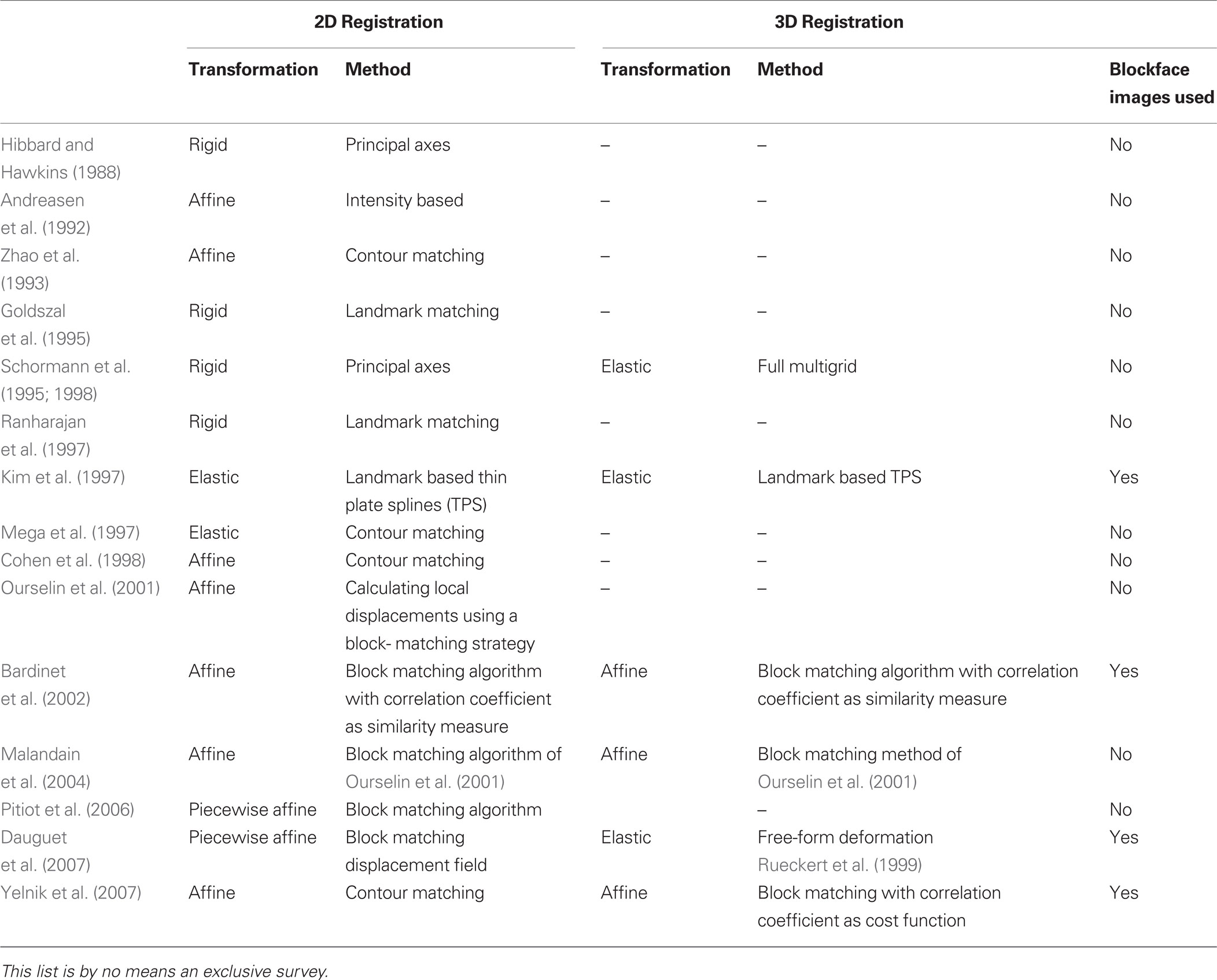
Table 1. Summary of previous work for reconstruction of 3D histological volume and histology to in vivo modality registration.

Here we describe a multistage method that allows direct registration of the histological volume to the MRI volume when blockface images are not available. The major innovative feature of our method is the incorporation of large deformation diffeomorphic metric mapping (LDDMM) (Beg et al., 2005 ) for final registration of the 3D volumes. LDDMM is a nonlinear registration algorithm that calculates diffeomorphic transformations between images in which anatomical structures and sub-structures are faithfully preserved. As demonstrated here, the addition of LDDMM greatly enhances the precision of the registration.

In this paper, we describe the data used to test our method and describe our registration algorithm in detail (see Materials and methods). We then provide visual examples of the registration and give validation results for registration accuracy (see Results). Finally, we conclude our work with a discussion of our method and possible improvements.

Materials and Methods

The registration method we have developed consists of five steps that constitute a new method for generating anatomical correspondences between the histology and the MRI volumes (Figure 1 ). Step 1 is the manual white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) segmentation of histological sections. Step 2 is the 2D rigid alignment and stacking of histological sections. Step 3 is the affine registration of the 3D histological image to the MRI volume. Step 4 is matching the histogram of 3D histological image to the MRI histogram. Step 5 is the 3D LDDMM image matching between the 3D histological image and the MRI volume. These individual steps are described in detail below.

FIGURE 1

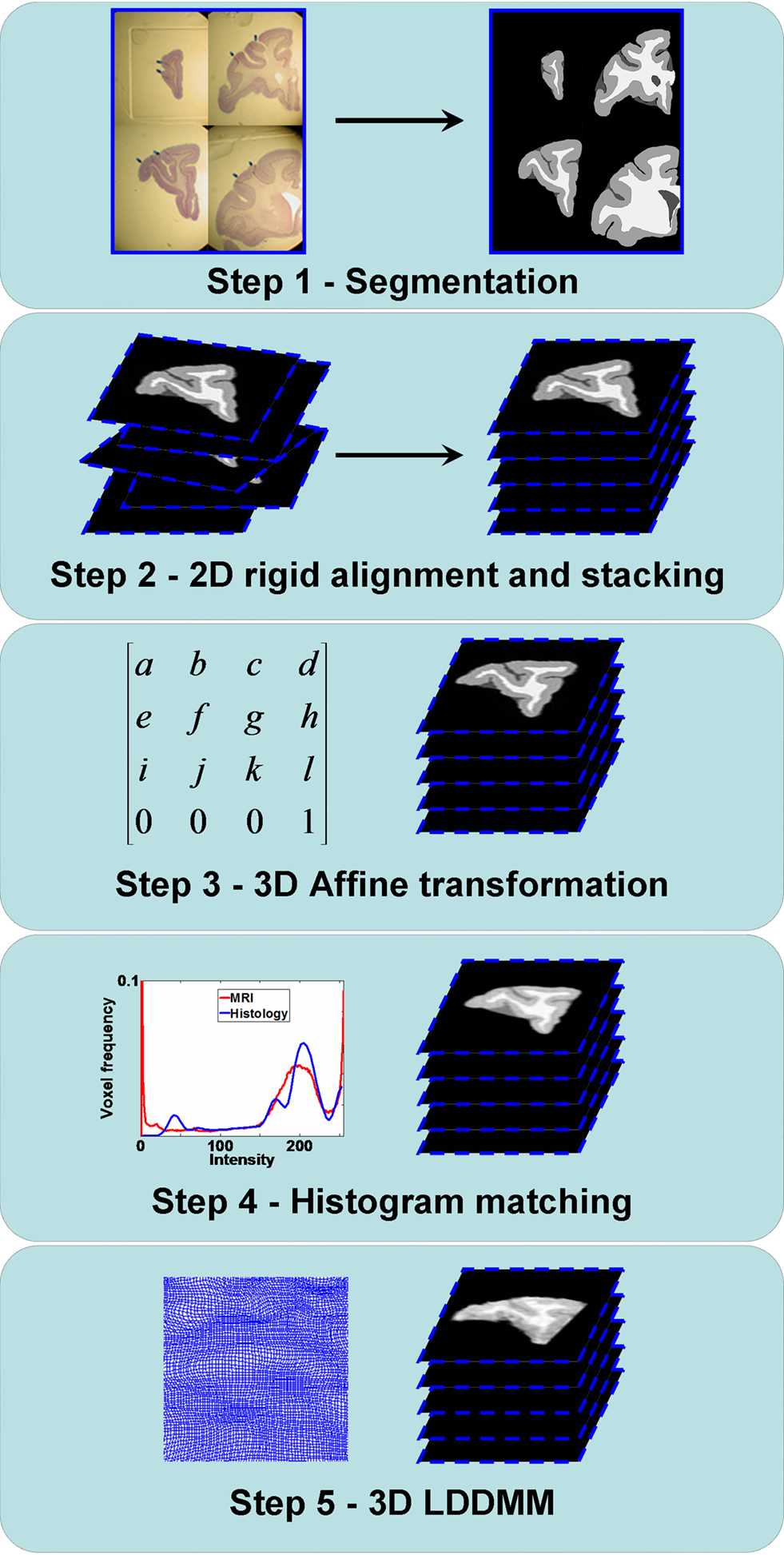
Figure 1. Flowchart illustrating the registration steps from the histology to the MRI volumes. Step 1: GM/WM/CSF segmentation of the histological sections. Step 2: 2D rigid alignment and stacking of histological sections. Step 3: 3D affine registration of the 3D histological image to the MRI volume. Step 4: Histogram matching between the 3D histological image and the MRI volume. Step 5: 3D LDDMM image matching between the 3D histological image and the MRI volume.

Subjects

Brains from nine adult Rhesus macaque monkeys (age at scanning 5.5–9.25 years; age at sacrifice 6.42–12.42 years) were used in this study. Three (1M, 2F) were normal untreated adult animals, three (2M, 1F) were exposed to x-irradiation (175–200 cGy) in early gestation, and three (2M, 1F) were exposed to x-irradiation (300–600 cGy) in midgestation. All procedures involving non-human primate subjects, including in utero exposure to irradiation, surgical C-section, housing, feeding, veterinary care, MRI, and sacrifice were performed in accordance with guidelines established by the Yale Institutional Animal Care and Use Committee. Irradiation exposure for these animals has been described elsewhere (Selemon et al., 2009 ).

The MRI scans of the monkeys were acquired in vivo on a 1.5 Tesla LX GE Advantage scanner S using the following protocol: A T1-weighted spoiled gradient recalled acquisition at steady state (SPGR) sequence (repetition time = 25 ms, echo time = 4 ms, flip angle = 30°, acquisitions = 124, matrix = 256 × 256 was used to collect the scans. Voxel resolution was 0.625 × 0.625 mm, and slice thickness was 0.7 mm. Note that one normal female subject was scanned on a 3.0 Tesla Siemens Trio scanner with a similar MPRAGE sequence.

A series of celloidin-embedded, 40-μm thick Nissl-stained sections through the frontal lobe for the same subject post mortem at approximately every 0.8 mm (every 20th section) was also generated. The procedures for sacrifice via intracardial perfusion, celloidin embedding of brain tissue, and histological processing have been described elsewhere (Selemon et al., 2009 ). High resolution digital photographic images (0.005534 × 0.005534 mm²/pixel) were acquired of each histological section.

Multistage Registration

GM/WM/CSF segmentation of histological sections

In photomicrographs of histological sections, GM and WM of the prefrontal cortex were manually segmented based on microscopic observation (Leica MZ75 low power scope, variable magnification of 0.63–5.0×) of corresponding histology sections that had been Nissl stained with cresyl violet for cytoarchitectonic analysis (Figure 2 , top row). During the segmentation process, we identified the MRI slice that was visually the most similar to a given histological section. Although CSF is not present in sections after histological processing of the brain, its labeling is necessary for the intensity normalization and LDDMM image matching (see Histogram matching and Nonlinear registration with LDDMM) steps of our registration method, because four classes or four intensity levels of MR image (i.e., WM, GM, CSF, and background) need to be accounted for. We therefore also identified sulcal and ventricular spaces of the histology sections that corresponded to similar spaces in the MRI slices and labeled those as CSF. Then, each compartment was assigned an arbitrary constant intensity value, that is, WM = 240, GM = 160 and CSF = 80 (Figure 2 , bottom row).

FIGURE 2

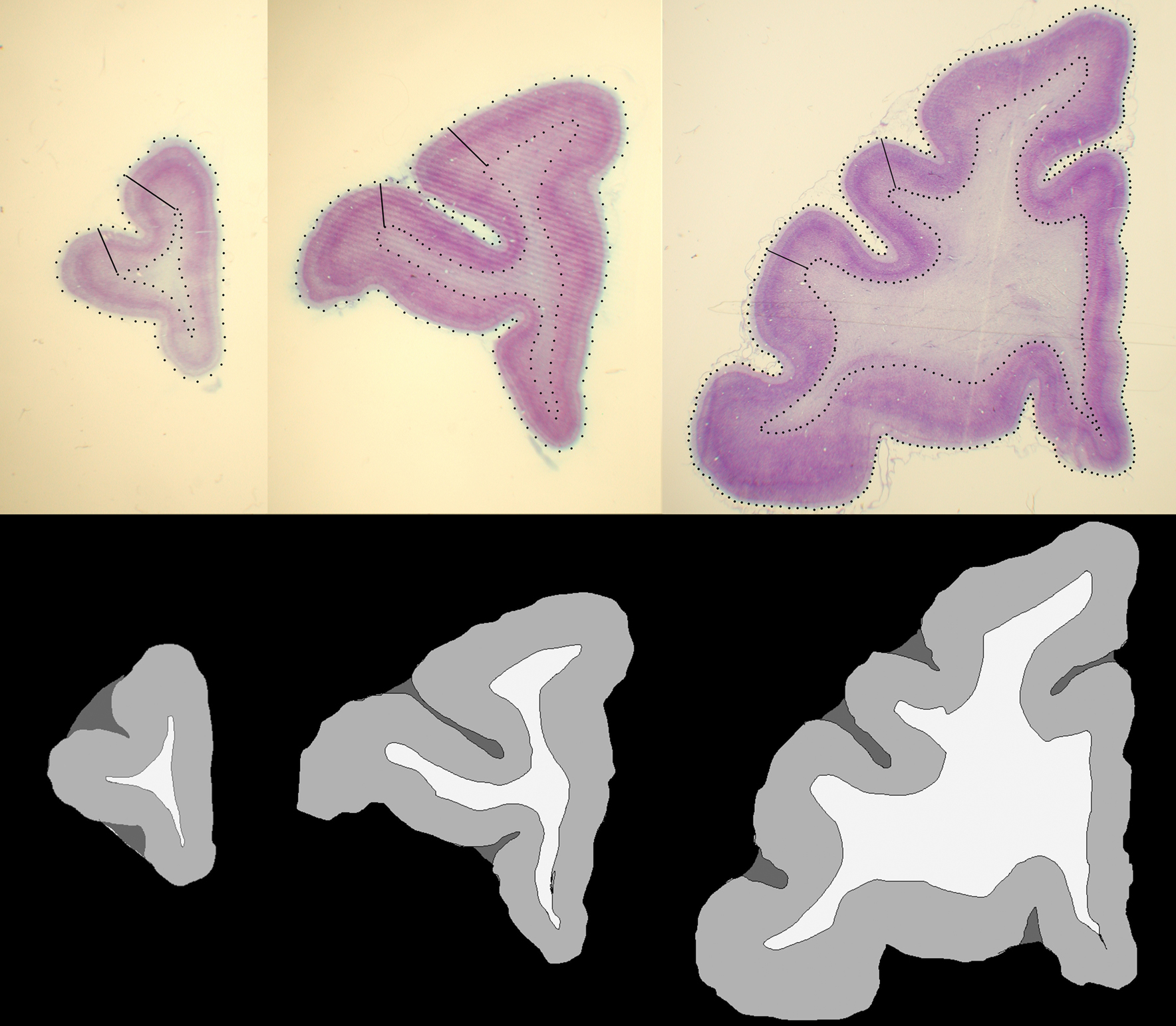
Figure 2. Examples of histological sections (top row) and corresponding GM, WM, CSF segmentations (bottom row).

2D rigid registration of histological sections

Rigid registration (rotation and translation) was used to align each consecutive segmented histological section similar to Malandain et al. (2004) . Each section was registered to the previous section starting from the second. Then starting from the section before the last one, each section was registered to the next section. So, if there are N section images,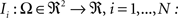

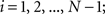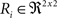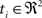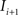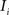(1) For (a) Calculate (rotation matrix) and (translation vector) registering to and (b) resample image 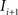with 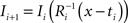using nearest neighbor interpolation.

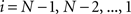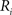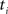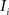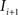(2) For ; (a) Calculate and registering to and (b) resample image 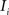with 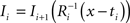using nearest neighbor interpolation.

The transformation parameters were calculated with the automatic image registration (AIR) package (Woods et al., 1998 ). AIR minimizes a least-squared difference image cost function (Friston et al., 1995 ; Hajnal et al., 1995 ) using full Newton-type minimization with a multi-resolution approach. At each resolution level, the derivatives of the cost function with respect to the three parameters of the 2D rigid transformation model are computed and they are used to update the estimated parameters and to iteratively minimize the cost function. Assuming that the histological sections were cut parallel to each other and since the thickness of the sections was small (0.8 mm), this procedure aligns the tissue boundaries in consecutive slices successfully achieving a global alignment of all sections. After the alignment of histological sections, they were stacked to form a 3D histological image.

3D Affine registration

In preparation for registration with the histological volumes, the prefrontal cortex was manually segmented using previously published protocols (Selemon et al., 2005 ) in each 3D MRI volume and the coronal slices of the segmented 3D prefrontal cortex region-of-interest (ROI) image were resampled using bilinear interpolation to a resolution of 0.15625 × 0.15625 mm²/pixel.

After the reconstruction of the 3D histological image, AIR was used to align it to the 3D MRI volume with an affine transformation. Since the intensities of tissues between images were different, normalized least-squared difference cost function was used in AIR. The 3D affine transformation corrects any orientation and other global shape differences between the 3D histology image and the MRI volume.

Histogram matching

In order to apply LDDMM, structures that will be registered must have similar intensity profiles because it is an intensity-based algorithm which minimizes the image differences. Therefore, we used a histogram-matching algorithm to make the GM, WM, and CSF intensity values of the 3D histology images similar to the values of the same regions in the MRI volume. During the manual segmentation of GM, WM and CSF regions in histological sections, these ROIs were labeled by three different intensity values. The 3D histological images were first smoothed with a Gaussian filter (SD = 0.5) to make their histograms a continuous function.

Then we used the histogram matching or histogram specification algorithm (Gonzalez and Woods, 2002 ) to match the histogram of the histological image to the MRI volume. This algorithm calculates histograms of two images and uses them as probability density functions to find a transformation between the intensity values of these images.

This algorithm can be summarized as follows. For two images 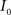and :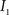

(1) Calculate the histograms for the images 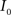and 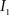with 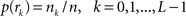, where 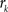is an intensity level, 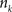is the number of voxels that have intensity level 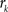, n is the total number of voxels and 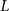is the total number of possible intensity levels in an image. Histogram is a discrete approximation for the probability density function of the occurrence of intensity levels.

(2) Calculate the cumulative distribution functions (CDF) for the images 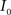and 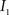using

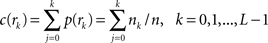
(3) If 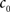and 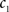are the calculated CDFs for the images 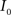and 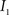, calculate the mapping 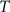between the intensity level indices of these images using

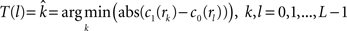
(4) Update the intensities in image using the transformation .

Non-linear registration with LDDMM

Registration between the 3D histological image and the 3D MRI volume is completed via LDDMM. For two images 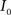and 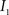in a collection of anatomies, there exists a diffeomorphism (one-to-one, differentiable, invertible and smooth mapping) 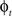such that 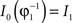. The map is constructed as a flow of ordinary differential equations 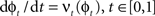where 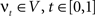is smooth time-dependent vector field. The optimal transformation between the two images is obtained from the vector field satisfying the variational problem (Beg et al., 2005 ; Ceritoglu et al., 2009 ).

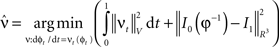
Large deformation diffeomorphic metric calculations were performed using the Diffeomap software (Li et al., 2001) .

Measurement of Registration Quality

To measure the registration accuracy we compared the distances between GM/CSF and WM/GM boundaries in the MRI volume with the same boundaries in the 3D histological images at each registration step. These boundaries were defined as 3D surfaces represented by triangulated meshes via isosurface generation (Gueziec and Hummel 1995). The distance 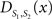between two surfaces 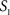and 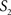was calculated for each vertex 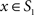as the Euclidian distance to the nearest vertex 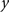of the surface 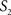from 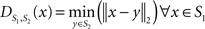(Ceritoglu et al., 2009) .

The CDF of the distances between the histology image surfaces and the corresponding MRI surfaces was used to compute the 90th percentile distance. The mean and the SD of these distances were also computed.

Application to Delineation of Area 46 and Cortical Layers

Prefrontal cortical area 46 borders with neighboring cortical areas and the boundaries between layers I/II and IV/V were segmented manually in the histological sections based on cytoarchitectonic criteria (Walker, 1940 ). Previously calculated 2D rigid transformations were used to align the 2D area 46 layer images. They were stacked to reconstruct a 3D ROI. Finally, the 3D affine and the LDDMM transformations were applied to the area 46 ROIs to transform it onto the MRI space for morphometric analysis of area 46 and its layers.

Histology to MRI Registration Using Grayscale Histological Section Images

In order to assess the impact of manual segmentation of GM/WM and GM/CSF boundaries on the serial alignment of sections, the entire registration process was repeated using the original photographic histological section images after they were converted to grayscale.

Similarly to the process described in Section “2D rigid registration of histological sections”, each grayscale section was registered to the previous section starting from the second. Then, each section was registered to the next section starting from the one before last section. The intensity profiles of tissues and layers were very different across sections after the grayscale conversion. Thus, the minimization of the least-squared difference cost function was not suitable to calculate the rigid transformation parameters and to register the grayscale histological sections. Instead FMRIB’s linear image registration tool (FLIRT) (Jenkinson and Smith, 2001 ) which minimizes the negative of the normalized mutual information cost function (Maes, 1998 ; Studholme et al., 1999 ) was used to calculate the transformation parameters. FLIRT uses a global optimization method that includes a multi-resolution approach and Powell’s method (Press et al., 1995 ) for local optimization to minimize the cost function iteratively.

After the consecutive alignment of the grayscale histological images, the intensity differences between sections were also corrected. First, the intensity range of every section image was scaled to [0,255]. Then, one of the middle sections was selected as the target section and the histogram of all the sections were matched to the histogram of the target section using the histogram-matching algorithm described in Section “Histogram matching”.

The intensity corrected section images were stacked to form a second set of 3D images for each subject. The other steps of our multistage registration method were repeated. Manually segmented tissue boundaries were transformed using the computed transformations. Finally, the tissue boundary surface distances between the MRI volume and the 3D histological images at each registration step were calculated.

Results

The intermediate results at different registration steps are illustrated for one subject. The irregular, non-smooth, GM/CSF and WM/GM boundaries observed in the stacked histological image without any serial alignment (Figure 3 , top row) were transformed into smooth, spatially consistent 3D GM/CSF and GM/WM boundaries, with 2D rigid registration (Figure 3 , bottom row).

FIGURE 3

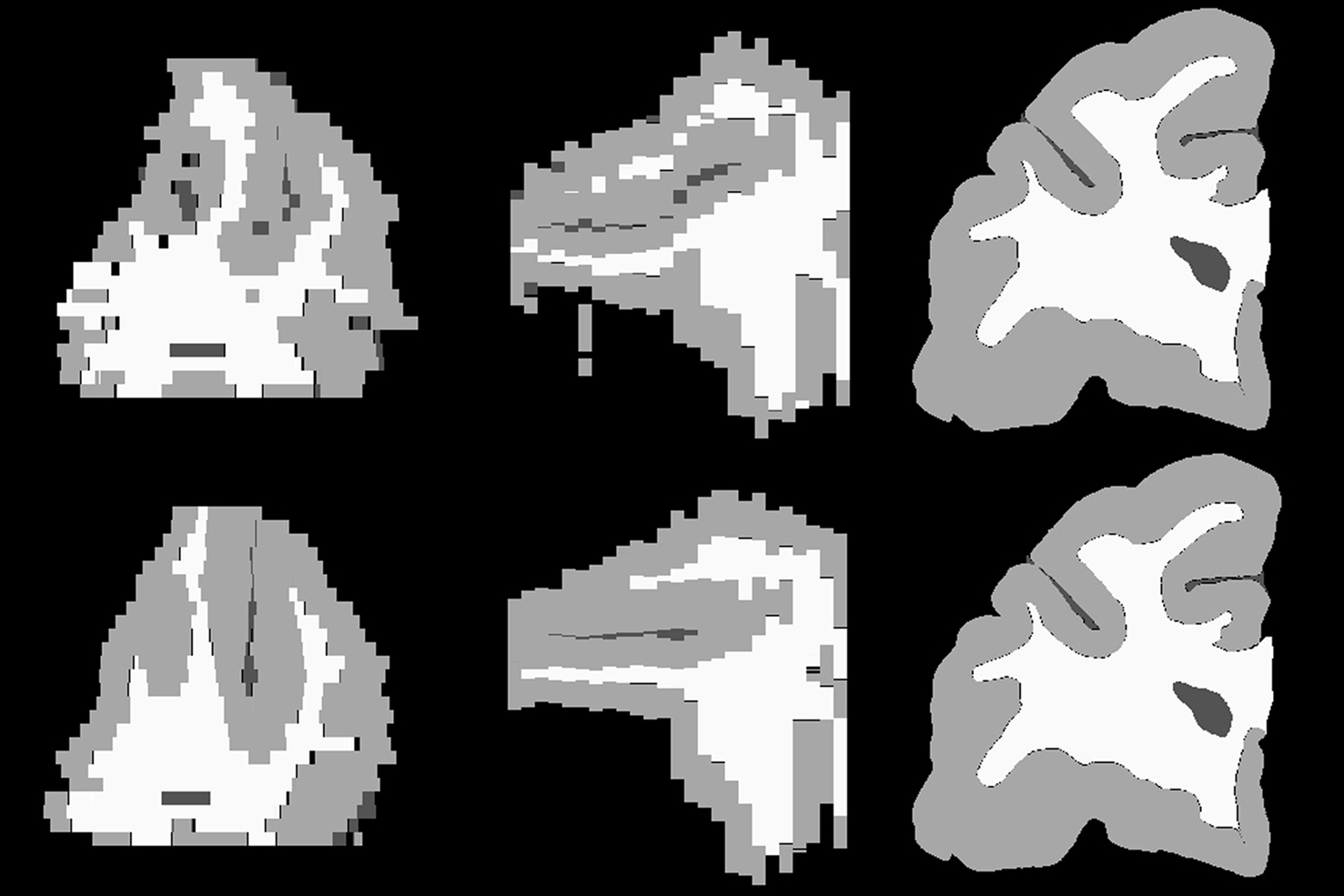
Figure 3. Axial (left), sagittal (middle), and coronal (right) slices of reconstructed 3D histology image without (top) and with (bottom) 2D rigid registration.

After stacking, the 3D histological image was aligned to the MRI volume with the 3D affine transformation. In theory, affine registration following the 2D rigid alignment and stacking improves the correspondence between GM/CSF and WM/GM surfaces in the histology images and the MRI images by calculating the optimal global axes stretch that would compensate for differences in slice thicknesses across different histology slices. However, because the resolution of the stacked histology image are estimates from slice thicknesses, the distance between corresponding surfaces in the MRI volume and stacked histology image (i.e., quantification of such correspondence) cannot be exactly computed.

After affine registration, the histogram of the histological image was matched to the histogram of MRI volume (Figure 4 ) before LDDMM registration. The smoothed and histogram matched histology image and the MR volume was used in LDDMM computations to calculate a transformation. Then the transformation was used to transform the unsmoothed histology image.

FIGURE 4

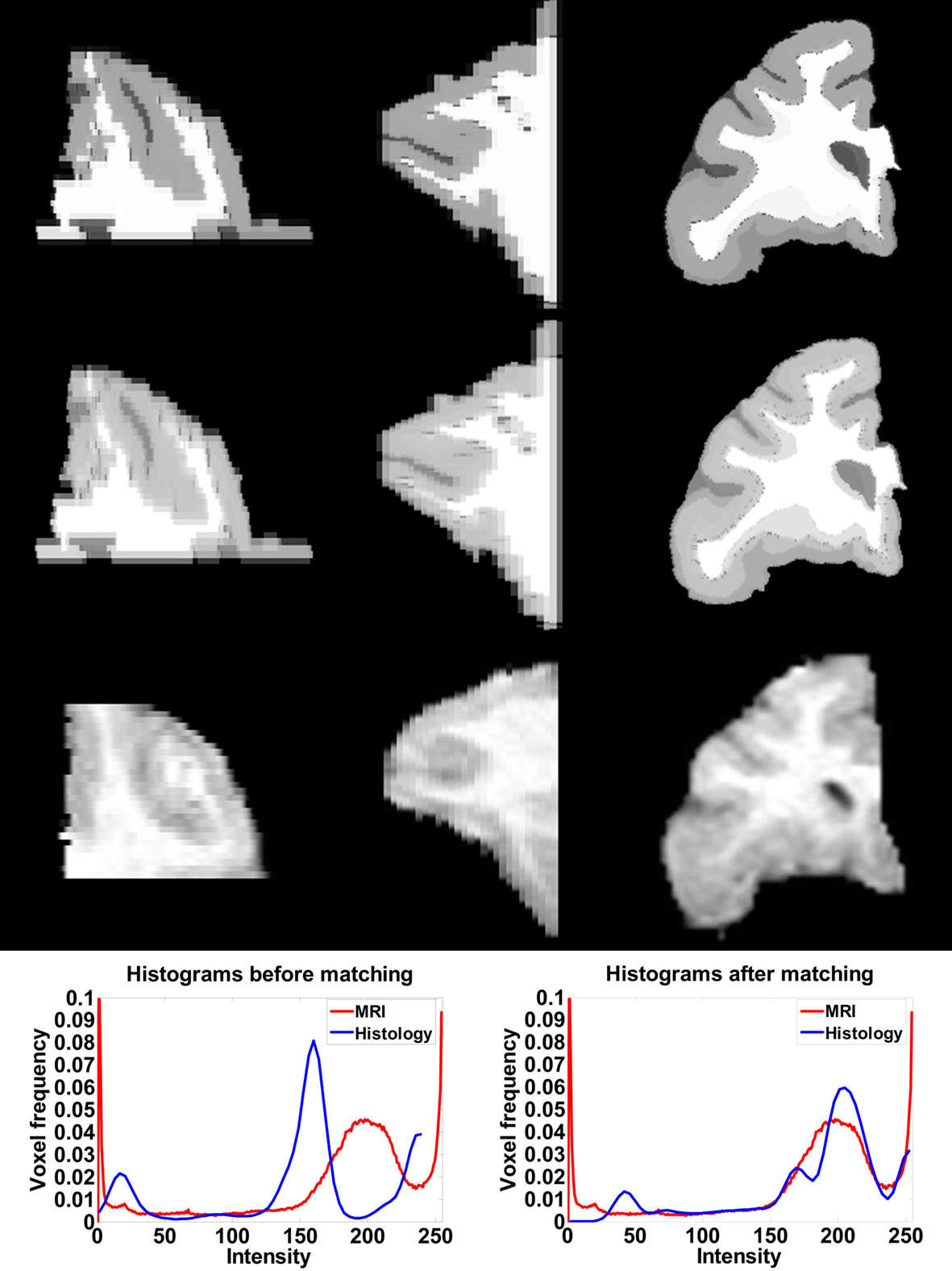
Figure 4. Axial (left), sagittal (middle), and coronal (right) slices of histology image before (first row) and after histogram matching (second row), the corresponding MRI slices (third row). Histograms of the histology image before (fourth row left) and after (fourth row right) histogram matching together with the histogram of MRI volume.

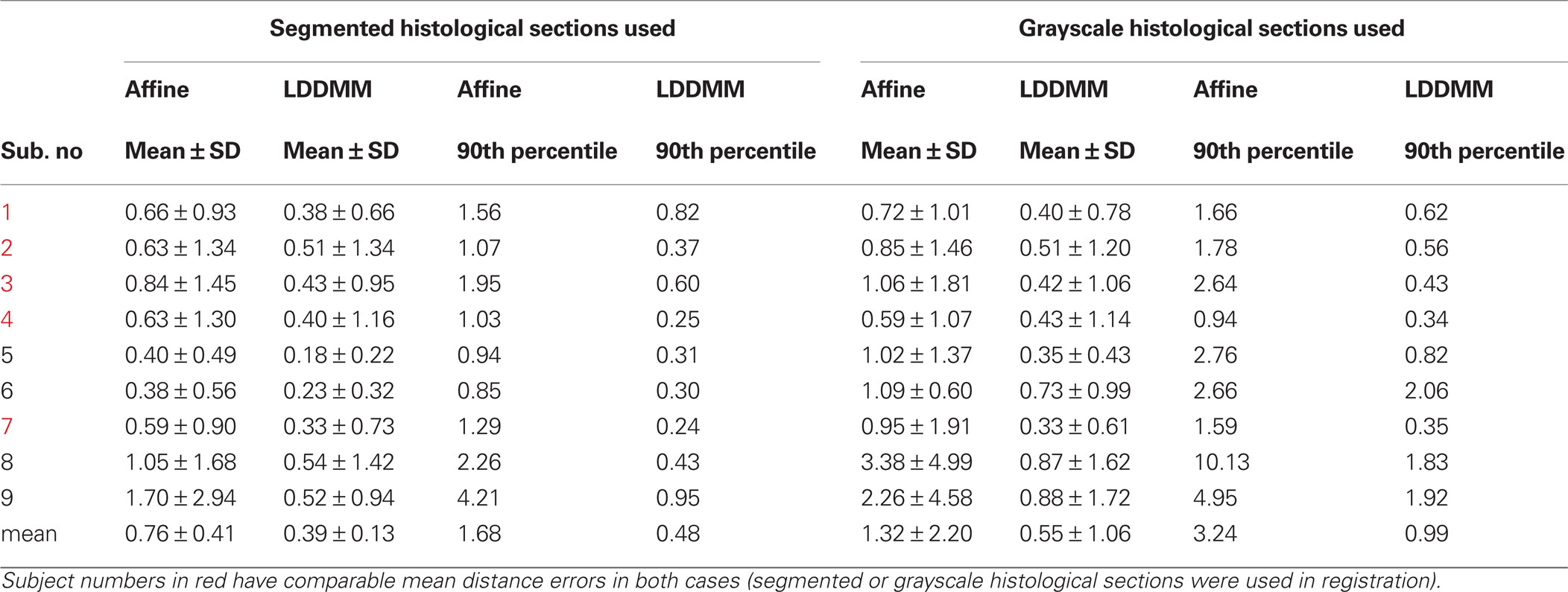
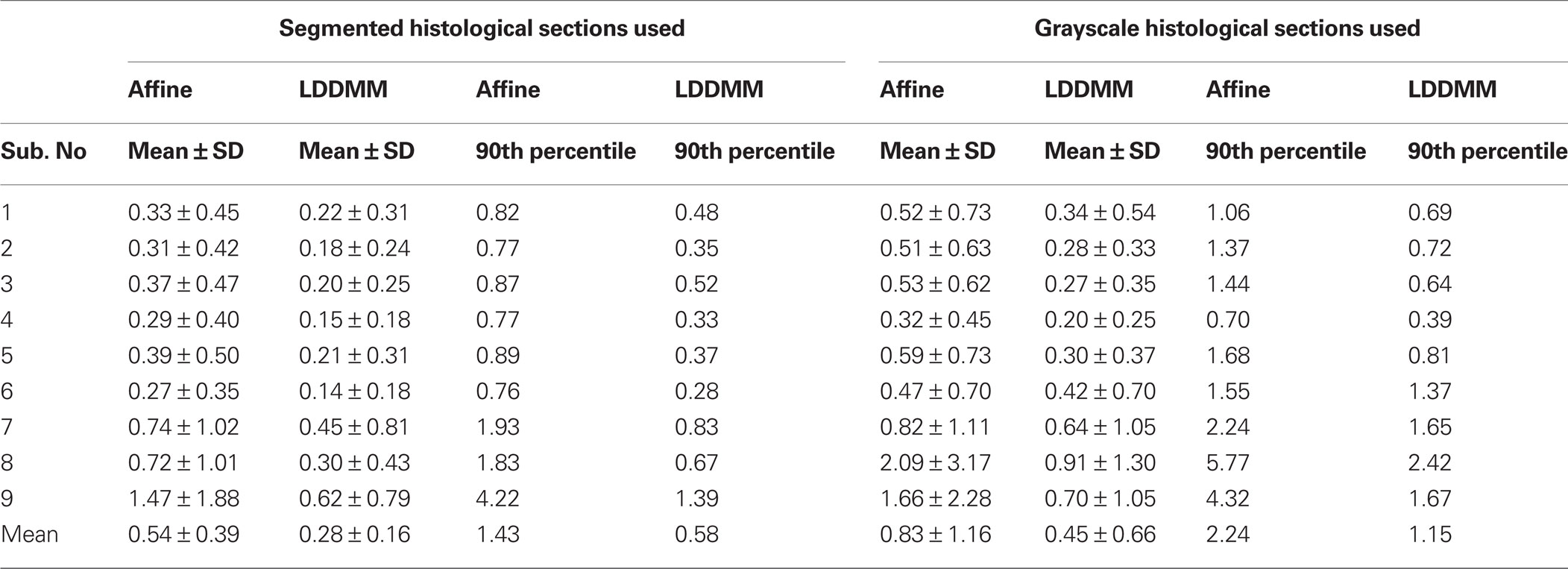
Correspondence between GM/CSF and WM/GM surfaces in the affine-registered histology images (Figure 5 , top row) and the MRI images was further improved by LDDMM registration (Figure 5 , middle row), resulting in better registration with the corresponding MRI surfaces (Figure 5 , bottom row). The improvement was quantified via distances between corresponding surfaces in the MRI volume and histological sections. After affine registration, mean GM/CSF distance was 0.76 ± 0.41 mm; the mean distance decreased to 0.39 ± 0.13 mm following LDDMM. For LDDMM, 90% of the histology surface vertices were within 0.5 mm of the MRI surfaces (Table 2 ). Likewise, mean WM/GM distance following affine registration (0.54 ± 0.39 mm) decreased to 0.28 ± 0.16 mm following LDDMM (Table 2 ). For WM/GM surfaces, 90% of the histology WM/GM surface vertices were within 0.6 mm of the MRI surfaces after LDDMM (Table 3 ).

FIGURE 5

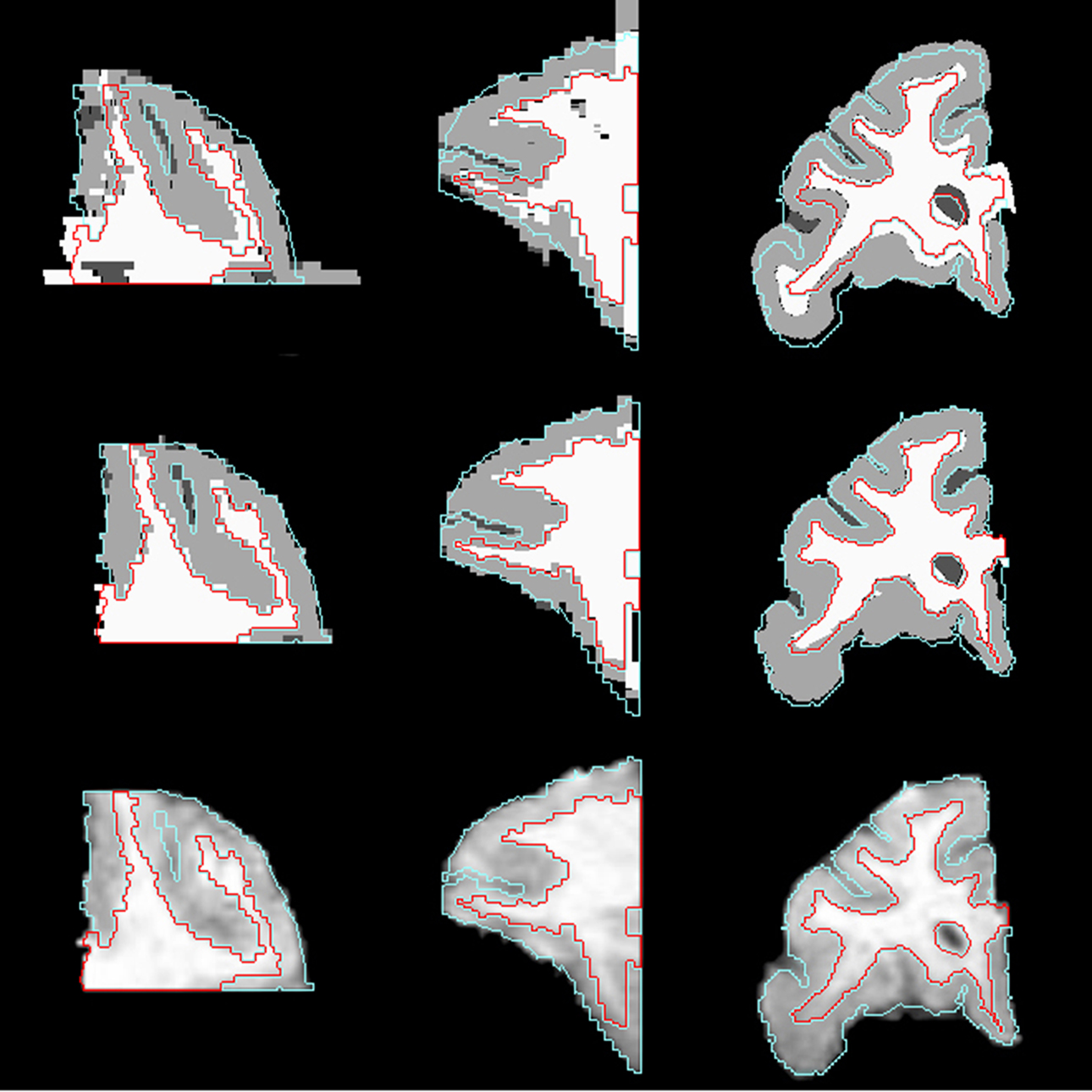
Figure 5. Axial (left), sagittal (middle), and coronal (right) slices of histology image after affine transformation (top row) and after LDDMM (middle row). Last row shows corresponding MR image slices. In each image, the GM/CSF boundaries (cyan) and the WM/GM boundaries (red) defined in the MRI volume are overlaid to illustrate the improvement of registration accuracy with LDDMM.

TABLE 2

Table 2. GM/CSF surface distance errors (mm).

TABLE 3

Table 3. WM/GM surface distance errors (mm).

If the sagittal and coronal slices of the histological image after affine transformation (Figure 5 , top row) and the same slices of MR image (Figure 5 , bottom row) are compared, it can be seen that some of the curvature of white matter structures was lost after 2D rigid registration and stacking of sections. This is the banana problem explained in Malandain et al. (2004) in detail. After the slicing process, a curved object cannot be absolutely recovered without external information. In our method, we aim to correct the banana problem with LDDMM transformation using the MR images as the external reference assuming that the object is smooth enough. The method that we developed seems to visually correct the curvature problem (Figure 5 , middle row).

After the multistage registration was complete, the borders of area 46 and laminar boundaries were transferred from the histology to the MRI volumes (Figure 6 , top and middle rows respectively). Area 46 layers for two subjects were also represented on a 3D surface in the MRI space (Figure 6 , bottom row).

FIGURE 6

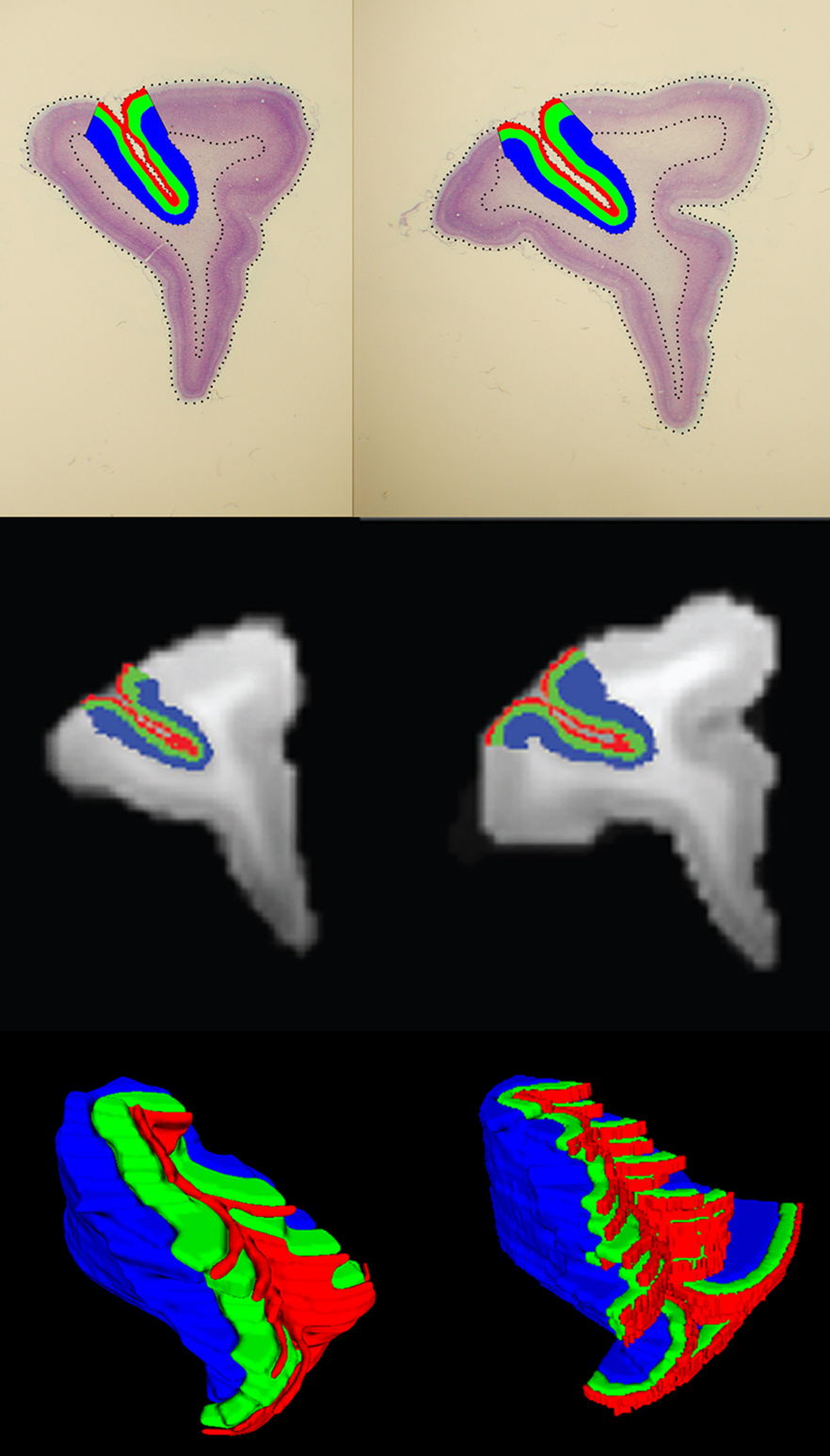
Figure 6. Area 46 layers (red: layer I, green: layers II–III–IV, blue: layers V–VI) on histological sections (top row) and the same layers on the MRI slices (middle row) after registration. Example 3D surfaces for area 46 layers in the MRI space (bottom row).

In order to evaluate whether labor-intensive manual segmentation of histology sections had an appreciable effect on the serial alignment of the histology sections to generate a 3D volume, we repeated the alignment using the intensity information in photographic images. As described in Section “Histology to MRI Registration using grayscale histological section images”, we converted the photographic images to grayscale and we did serial alignment of consecutive slices rigidly using an algorithm based on maximization of normalized mutual information. After intensity correction between sections and after repeating other steps of our method, distances between tissue surface boundaries were calculated.

When the grayscale histological images were used, mean GM/CSF distance was 1.32 ± 2.20 mm after affine registration; the mean distance decreased to 0.55 ± 1.06 mm following LDDMM (Table 2 ). Mean WM/GM distance following affine registration (0.83 ± 1.16 mm) decreased to 0.45 ± 0.66 mm following LDDMM (Table 3 ). For some of the subjects, GM/CSF mean distances were comparable with the results obtained when the segmented histological images were used in registration (Table 2 , subject numbers in red). However, because of the torn and missing tissues in some of the histological sections, using intensity information directly in registration resulted in large errors for other subjects.

Discussion

We have described a novel, multistage, method for registration of post mortem histology sections, to in vivo MRI sub-volumes of the same brains. We demonstrated that our method yielded a progressively more accurate alignment of the WM/GM and GM/CSF boundaries in the histological and the MRI volumes with each step in the registration algorithm. Smooth 3D WM/GM and GM/CSF surfaces were generated after the 3D histology image reconstruction, and these surfaces were registered to the same surfaces in the MRI volume with an average error less than 0.4 mm. As illustrated in this report, our method can be used to transfer cortical and laminar boundaries from the histology sections to the MRI volumes and therefore may facilitate analysis of cytoarchitectonically parcellated and therefore more functionally homogeneous regions of interest in the MRI scans.

The method we have developed is unique in several important ways. Perhaps the most important innovation in our method is the incorporation of LDDMM (Beg et al., 2005 ; Ceritoglu et al., 2009 ). LDDMM ensures that disjoint shapes remain disjoint and there is no fusion of points because of the one-to-one property of diffeomorphisms. Connected shapes remain connected because of the continuity property and the smoothness of the object boundaries are preserved because of the smoothness property of the diffeomorphisms. This ensures that sub-structures within transformed structures are preserved during the mapping (Boothby, 2002) such as the cortical layers delineated in the histological volumes. Recently, Klein et al. (2009) reviewed 14 different registration methods and showed increased fidelity is associated with increased dimensions. In particular, diffeomorphic mappings were among those that yielded increased fidelity. Although LDDMM was not included in that study, its infinite dimensional formulation ensures high registration fidelity and therefore should compare favorably with other methods.

If the two images that are registered with LDDMM have same modality or if they have similar structures and similar intensity profiles on these structures, the highly elastic LDDMM transformation improves registration accuracy (Miller et al., 2005 ; Ceritoglu et al., 2009 ). In histology to MRI registration, although the photographic images of the histological sections and the MRI have similar tissues (GM and WM regions), some subjects have substantial number of sections featuring large tears or missing areas and they have sections with different intensity profiles. Therefore, it is difficult to apply LDDMM directly on the original histological images. In our method, we used manually segmented histological sections to reconstruct a 3D histological volume that has tissue regions with smooth boundaries and intensity profiles similar to the MRI data which allows LDDMM to perform better.

We used a simple rigid registration procedure for between-section registration of manually segmented histology images. In comparison, existing methods align serial 2D biological images (histological sections or autoradiographs) to reconstruct a 3D volume using principal axes (Hibbard and Hawkins, 1988 ; Schormann et al., 1995 ; Schormann and Zilles, 1998 ), affine transformations (Andreasen et al., 1992 ; Ourselin et al., 2001 ; Malandain et al., 2004 ) contour matching (Zhao et al., 1993 ; Cohen et al., 1998 ; Yelnik et al., 2007 ), elastic transformations (Mega et al., 1997 ), piecewise affine (Pitiot et al., 2006) and adaptive piecewise affine registration algorithms (Dauguet et al., 2007 ). Some of these methods use intensity information for the serial alignment of sections. Similarly, we repeated our experiments using the grayscale intensity information in histological sections for serial alignment using a linear registration algorithm which is based on the maximization of mutual information. This algorithm is robust for the estimation of the rigid body transformation parameters even if the intensity profiles are very different in images. When the distances of tissue boundaries between the reconstructed 3D histological image and the MRI image were compared (Tables 2 and 3 ), it was observed that registration accuracy was lower when compared to using the segmented histological images in serial alignment and in LDDMM because of the missing or torn tissues and different intensity profiles in some of the histological sections. In the future, we aim to replace manual segmentation of histological sections with automated or semi-automated segmentation.

The robustness of serial alignment with rigid registration depends mainly on the assumption that the histological sections were cut parallel to each other and the tissue boundaries in consecutive sections are close to each other. If there are imperfections in the histological sectioning process and if some sections are cut oblique compared to others, a more complex procedure should be used with an improved algorithm used for serial alignment.

We developed this histology-MRI registration method to optimize morphometric measurement of area 46 in the macaque brain. Combining the two techniques allows us to capitalize on the strengths of each method, that is, the precise delineation of functionally distinct units of brain structure as discernable on post mortem histology sections and the visualization of in vivo brain structure, undistorted by post mortem fixation and processing, on the MRI scans. Once the boundaries of area 46 have been transferred to the MRI volumes, we can apply state-of-the-art computational anatomy methods, such as LCDM (Miller et al., 2003 ), to quantify the volume, surface area and thickness of area 46, as well as volume and thickness of delineated layers. These structural parameters cannot be obtained with either method alone since measurement in post mortem histological sections would be skewed by shrinkage and distortion due to fixation and processing while discrimination of the boundaries of area 46 and its layers is not possible in the MRI scans. It should be noted that we applied our method to a single ROI, that is, prefrontal cortex, in only one of the hemispheres. However, the same method could be used for alignment of the whole brain although piecewise affine transformations as described in (Dauguet et al., 2007 ) might be necessary for serial alignment if the hemispheres exhibited different deformations due to histological processing.

Our method has a potential application in human databases where both MRI scans and post mortem histological sections are available from the same subjects to analyze structural alteration in cytoarchitectonically parcellated, and therefore more functionally homogenous, ROIs. With respect to analysis of the cerebral cortex, it is all the more important to use cytoarchitectonic criteria to distinguish individual cortical areas in the human brain where the borders of areas show marked individual variability and exhibit little correspondence to sulcal landmarks (Rajkowska and Goldman-Rakic, 1995 ). Moreover, in diseases thought to have a developmental origin, as for example schizophrenia, application of this method would make it possible to determine whether the expanse of a specific cortical region, for example, area 46, is altered relative to the size of the frontal lobe as a whole. Thus, the application of this registration method may allow for more detailed and functionally relevant analyses of neuropsychiatric illness that could significantly advance our understanding of these human diseases.

This registration method also has more general utility in superimposition of any histologically based information onto the MRI volumes. Currently, atlases of the mouse brain (Lein et al., 2007) and human brain (Chakravarty et al., 2009 ) are being developed to integrate multiple data modalities derived from histological analysis, including cytoarchitectonic delineation, immunohistochemical staining, and gene expression, onto the MRI volumes of the same brains. Registration of multi-modal and multi-scale anatomical atlases is used increasingly to generate maps of genomic expression (Thompson et al., 2008a ), receptor localization (Zilles and Amunts, 2009 ) and other histologically based information (Toga et al., 2005 ). Our method which incorporates LDDMM as a final step in the registration process and significantly improves the correspondence between maps may be useful in these diverse applications.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work reported here was made possible by grants from NIH (P50-MH071616; P41-RR15241 and R01-MH59329) and NSF (DMS-0456253). We thank Neha Malhotra and Matt Trachtenberg for technical assistance.

References

Andreasen, A., Drewes, A. M., Assentoft, J. E., and Larsen, N. E. (1992). Computer-assisted alignment of standard serial sections without use of artificial landmarks. A practical approach to the utilization of incomplete information in 3-D reconstruction of the hippocampal region. J. Neurosci. Methods 45, 199–207.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bardinet, E., Ourselin, S., Dormont, D., Malandain, G., Tandé, D., Parain, K., Ayache, N., and Yelnik, J. (2002). Co-registration of histological, optical and MR data of the human brain. LNCS 2488, 548–555.

Beg, M. F., Miller, M. I., Trouvé, A., and Younes, L. (2005). Computing large deformation metric mappings via geodesic flows of diffeomorphisms. Int. J. Comput. Vision 61, 139–157.

CrossRef Full Text

Boothby, W. M. (2002). An Introduction to Differentiable Manifolds and Riemannian Geometry, 2nd edn. New York: Academic Press.

Ceritoglu, C., Oishi, K., Li, X., Chou, M. C., Younes, L., Albert, M., Lyketsos, C., van Zijl, P. C. M., Miller, M. I., and Mori, S. (2009). Multi-contrast large deformation diffeomorphic metric mapping for diffusion tensor imaging. Neuroimage 47, 618–627.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chakravarty, M. M., Hawrylycz, M., Bertagnollo, D., Cartagena, P., Daly, B., Dee, N., Guillozet-Bongaarts, A., Jeromin, A., Lazarz, E., Overly, C. C., Riley, Z., Shen, E., Slaughterbeck, C., Smith, K., Vawter, M., and Jones, A. (2009). Informatics and imaging pipeline for development of a new multi-modal atlas of the human brain: imaging, anatomy, and gene expression. Human Brain Mapping 15th Annual Meeting, San Francisco, CA.

Cohen, F. S., Zhengwei, Y., Zhaohui, H., and Nianov, J. (1998). Automatic matching of homologous histological sections. IEEE Trans. Biomed. Eng. 45, 642–649.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dauguet, J., Delzescaux, T., Condé, F., Mangin, J. F., Ayache, N., Hantraye, P., and Frouin, V. (2007). Three-dimensional reconstruction of stained histological slices and 3D non-linear registration with in-vivo MRI for whole baboon brain. J. Neurosci. Methods 164, 191–204.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Friston, K., Ashburner, J., Frith, C. D., Poline, J. B., Heather, J. D., and Frackowiak, R. S. J. (1995). Spatial registration and normalization of images. Hum. Brain Mapp. 3, 165–189.

CrossRef Full Text

Goldszal, A. F., Tretiak, O. J., Hand, P. J., Bhasin, S., and McEachron, D. L. (1995). Three-dimensional reconstruction of activated columns from 2-[14C]deoxy-D-glucose data. Neuroimage 2, 9–20.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gonzalez, R. C., and Woods, R. E. (2002). Digital Image Processing, 2nd edn. Upper Saddle River, NJ: Prentice Hall.

Hajnal, J. V., Saeed, N., Soar, E. J., Oatridge, A., Young, I. R., and Bydder, G. M. (1995). A registration and interpolation procedure for subvoxel matching of serially acquired MR images. J. Comput. Assist. Tomogr. 19, 289–296.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hibbard, L. S., and Hawkins, R. A. (1988). Objective image alignment for three-dimensional reconstruction of digital autoradiograms. J. Neurosci. Methods 26, 55–74.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jenkinson, M., and Smith, S. (2001). A global optimisation method for robust affine registration of brain images. Med. Image Anal. 5, 143–156.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kim, B., Boes, J. L., Frey, K. A., and Meyer, C. R. (1997). Mutual information for automated unwarping of rat brain autoradiographs. Neuroimage 5, 31–40.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Klein, A., Andersson, J., Ardekani, B. A., Ashburner, J., Avants, B., Chiang, M. C., Christensen, G. E., Collins, D. L., Gee, J., Hellier, P., Song, J. H., Jenkinson, M., Lepage, C., Rueckert, D., Thompson, P., Vercauteren, T., Woods, R. P., Mann, J. J., and Parsey, R. V. (2009). Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage 46, 786–802.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lein, E. S., Hawrylycz, M. J., Ao, N., Ayres, M., Bensinger, A., Bernard, A., Boe, A. F., Boguski, M. S., Brockway, K. S., Byrnes, E. J., Chen, L., Chen, L., Chen, T. M., Chin, M. C., Chong, J., Crook, B. E., Czaplinska, A., Dang, C. N., Datta, S., Dee, N. R., Desaki, A. L., Desta, T., Diep, E., Dolbeare, T. A., Donelan, M. J., Dong, H. W., Dougherty, J. G., Duncan, B. J., Ebbert, A. J., Eichele, G., Estin, L. K., Faber, C., Facer, B. A., Fields, R., Fischer, S. R., Fliss, T. P., Frensley, C., Gates, S. N., Glattfelder, K. J., Halverson, K. R., Hart, M. R., Hohmann, J. G., Howell, M. P., Jeung, D. P., Johnson, R. A., Karr, P. T., Kawal, R., Kidney, J. M., Knapik, R. H., Kuan, C. L., Lake, J. H., Laramee, A. R., Larsen, K. D., Lau, C., Lemon, T. A., Liang, A. J., Liu, Y., Luong, L. T., Michaels, J., Morgan, J. J., Morgan, R. J., Mortrud, M. T., Mosqueda, N. F., Ng, L. L., Ng, R., Orta, G. J., Overly, C. C., Pak, T. H., Parry, S. E., Pathak, S. D., Pearson, O. C., Puchalski, R. B., Riley, Z. L., Rockett, H. R., Rowland, S. A., Royall, J. J., Ruiz, M. J., Sarno, N. R., Schaffnit, K., Shapovalova, N. V., Sivisay, T., Slaughterbeck, C. R., Smith, S. C., Smith, K. A., Smith, B. I., Sodt, A. J., Stewart, N. N., Stumpf, K. R., Sunkin, S. M., Sutram, M., Tam, A., Teemer, C. D., Thaller, C., Thompson, C. L., Varnam, L. R., Visel, A., Whitlock, R. M., Wohnoutka, P. E., Wolkey, C. K., Wong, V. Y., Wood, M., Yaylaoglu, M. B., Young, R. C., Youngstrom, B. L., Yuan, X. F., Zhang, B., Zwingman, T. A., and Jones, A. R. (2007). Genome-wide atlas of gene expression in the adult mouse brain. Nature 445, 168–176.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Li, X., Jiang, H., and Mori, S. (2001). Diffeomap, Kennedy Krieger Insitute & Johns Hopkins University, www.MriStudio.org .

Maes, F. (1998). Segmentation and Registration of Multimodal Medical Images: From Theory, Implementation and Validation to a Useful Tool in Clinical Practice. Ph.D. Thesis, Catholic University of Leuven, Belgium.

Malandain, G., Bardinet, E., Nelissen, K., and Vanduffel, W. (2004). Fusion of autoradiographs with an MR volume using 2-D and 3-D linear transformations. Neuroimage 23, 111–127.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mega, M. S., Chen, S. S., Thompson, P. M., Woods, R. P., Karaca, T. J., Tiwari, A., Vinters, H. V., Small, G. W., and Toga, A. W. (1997). Mapping histology to metabolism: coregistration of stained whole-brain sections to premortem PET in Alzheimer’s disease. Neuroimage 5, 147–153.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Miller, M. I., Beg, M. F., Ceritoglu, C., and Stark, C. (2005). Increasing the power of functional maps of the medial temporal lobe by using large deformation diffeomorphic metric mapping. Proc. Natl. Acad. Sci. USA 102, 9685–9690.

CrossRef Full Text

Miller, M. I., Hosakere, M., Barker, A. R., Priebe, C. E., Lee, N., Ratnanather, J. T., Wang, L., Gado, M., Morris, J. C., and Csernansky, J. G. (2003). Labeled cortical mantle distance maps of the cingulate quantify differences between dementia of the Alzheimer type and healthy aging. Proc. Natl. Acad. Sci. USA 100, 15172–15177.

CrossRef Full Text

Ourselin, S., Roche, A., Subsol, G., Pennec, X., and Ayache, N. (2001). Reconstructing a 3D structure from serial histological sections. Image Vis. Comput. 19, 25–31.

CrossRef Full Text

Pitiot, A., Bardinet, E., Thompson, P. M., and Malandain, G. (2006). Piecewise affine registration of biological images for volume reconstruction. Med. Image Anal. 10, 465–483.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Press, W, H, Teukolsky, S, A., Vetterling, W, T., Flannery, B, P. (1995). Numerical recipes in C: The Art of Scientific Computing, 2nd edn. Cambridge: Cambridge University Press.

Rajkowska, G., and Goldman-Rakic, P. S. (1995). Cytoarchitectonic definition of prefrontal areas in the normal human cortex: II. Variability in locations of areas 9 and 46 and relationship to the Talairach coordinate system. Cereb. Cortex 5, 323–337.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rangarajan, A., Chui, H., Mjolsness, E., Pappu, S., Davachi, L., Goldman-Rakic, P., and Duncan, J. (1997). A robust point-matching algorithm for autoradiograph alignment. Med. Image Anal. 1, 379–398.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rueckert, D., Sonoda, L. I., Hayes, C., Hill, D. L., Leach, M. O., and Hawkes, D. J. (1999). Nonrigid registration using free-form deformations: application to breast MR images. IEEE Trans. Med. Imaging 18, 712–721.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schormann, T., and Zilles, K. (1998). Three-dimensional linear and nonlinear transformations: an integration of light microscopical and MRI data. Hum. Brain Mapp. 6, 339–347.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schormann, T., Dabringhaus, A., and Zilles, K. (1995). Statistics of deformations in histology and application to improved alignment with MRI. IEEE Trans. Med. Imaging 14, 25–35.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Selemon, L. D., Begovic, A., and Rakic, P. (2009). Selective reduction of neuron number and volume of the mediodorsal nucleus of the thalamus in macaques following irradiation at early gestational ages. J. Comp. Neurol. 515, 454–464.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Selemon, L. D., Wang, L., Nebel, M. B., Csernansky, J. G., Goldman-Rakic, P. S., and Rakic, P. (2005). Direct and indirect effects of fetal irradiation on cortical gray and white matter volume in the macaque. Biol. Psychiatry 57, 83–90.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Studholme, C., Hill, D. L. G., and Hawkes, D. J. (1999). An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognit. 32, 71–86.

CrossRef Full Text

Thompson, C. L., Pathak, S. D., Jeromin, A., Ng, L. L., MacPherson, C. R., Mortrud, M. T., Cusick, A., Riley, Z. L., Sunkin, S. M., Bernard, A., Puchalski, R. B., Gage, F. H., Jones, A. R., Bajic, V. B., Hawrylycz, M. J., and Lein, E. S. (2008a). Genomic anatomy of the hippocampus. Neuron 60, 1010–1021.

CrossRef Full Text

Thompson, P. M., Miller, M. I., Poldrack, R. A., Nichols, T. E., Taylor, J. E., Worsley, K. J., and Ratnanather, J. T. (2008b). Special issue on mathematics in brain imaging. Neuroimage 45, S1–S2.

CrossRef Full Text

Thompson, P. M., Miller, M. I., Ratnanather, J. T., Poldrack, R. A., and Nichols, T. E. (2004). Special issue on mathematics in brain imaging. Neuroimage 23, S1–S2.

Toga A. W., Thompson, P. M., and Michael, F. G. (2005). Brain atlases of normal and diseased populations. Int. Rev. Neurobiol. 66, 1–54.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Walker, A. E. (1940). A cytoarchitectural study of the prefrontal area of the macaque monkey. J. Comp. Neurol. 73, 59–86.

CrossRef Full Text

Woods, R. P., Grafton, S. T., Holmes, C. J., Cherry, S. R., and Mazziotta, J. C. (1998). Automated image registration: I. General methods and intrasubject, intramodality validation. J. Comput. Assist Tomogr. 22, 139–152.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yelnik, J., Bardinet, E., Dormont, D., Malandain, G., Ourselin, S., Tande, D., Karachi, C., Ayache, N., Cornu, P., and Agid, Y. (2007). A three-dimensional, histological and deformable atlas of the human basal ganglia. I. Atlas construction based on immunohistochemical and MRI data. Neuroimage 34, 618–638.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zhao, W., Young, T. Y., and Ginsberg, M. D. (1993). Registration and three-dimensional reconstruction of autoradiographic images by the disparity analysis method. IEEE Trans. Med. Imaging 12, 782–791.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zilles, K., and Amunts, K. (2009). Receptor mapping: architecture of the human cerebral cortex. Curr. Opin. Neurol. 22, 331–339.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text