- 1 Computational Neuroscience Laboratory, The Salk Institute, La Jolla, CA, USA
- 2 Cognitive Brain Mapping Laboratory, RIKEN Brain Science Institute, Wako-shi, Saitama, Japan
Incompatible images presented to the two eyes lead to perceptual oscillations in which one image at a time is visible. Early models portrayed this binocular rivalry as involving reciprocal inhibition between monocular representations of images, occurring at an early visual stage prior to binocular mixing. However, psychophysical experiments found conditions where rivalry could also occur at a higher, more abstract level of representation. In those cases, the rivalry was between image representations dissociated from eye-of-origin information, rather than between monocular representations from the two eyes. Moreover, neurophysiological recordings found the strongest rivalry correlate in inferotemporal cortex, a high-level, predominantly binocular visual area involved in object recognition, rather than early visual structures. An unresolved issue is how can the separate identities of the two images be maintained after binocular mixing in order for rivalry to be possible at higher levels? Here we demonstrate that after the two images are mixed, they can be unmixed at any subsequent stage using a physiologically plausible non-linear signal-processing algorithm, non-negative matrix factorization, previously proposed for parsing object parts during object recognition. The possibility that unmixed left and right images can be regenerated at late stages within the visual system provides a mechanism for creating various binocular representations and interactions de novo in different cortical areas for different purposes, rather than inheriting then from early areas. This is a clear example how non-linear algorithms can lead to highly non-intuitive behavior in neural information processing.
When incompatible images are presented to the two eyes, the visual system is thrown into oscillations. First one image is visible and then the other, typically alternating with a period of a couple of seconds. This is known as binocular rivalry. A commonly used rivalrous stimulus is a pair of orthogonal gratings, one grating presented to each eye. However, non-matching stimuli in general will work, such as a face and a house. Seminal psychophysical work on rivalry was done by Levelt (1965), who studied how the time course of the oscillations depended on the nature of the stimuli. In recent years the study of rivalry has expanded from psychophysics to neurophysiology and functional MRI (fMRI) brain imaging, as described in various reviews (Leopold and Logothetis, 1999; Blake and Logothetis, 2002; Lee, 2004; Tong et al., 2006; Sterzer et al., 2009).
Early models portrayed binocular rivalry as involving reciprocal inhibition between monocular representations of the two images, occurring at an early visual stage prior to binocular mixing (Lehky, 1988; Blake, 1989). (See Wilson, 2007, for a more recent and elaborate version of this idea.) Low-level monocular representations postulated by such models would make the striate cortex or the lateral geniculate nucleus likely locations for rivalry.
However, psychophysical experiments found conditions where rivalry appeared to occur at a higher, more abstract level of representation. In those cases, the rivalry was between image representations dissociated from eye-of-origin information, rather than directly between monocular signals from the two eyes. Evidence for this higher-level “image rivalry” came from two types of experiments. One involved studies in which two rivalrous images were physically switched back and forth rapidly between the two eyes, typically at a rate of around three times per second (Logothetis et al., 1996; Lee and Blake, 1999). For particular stimulus configurations under those conditions, the rivalrous percept oscillated much more slowly than the physical switching of the stimuli, at a rate of around 1 cycle every 2 s. That suggested the rivalry was between representations of the images divorced or abstracted from the direct monocular representations coming from each eye. The second type of experiment involved rivalrous stimuli that were patchworks synthesized from two incompatible images. For example, the left eye stimulus might be composed of randomly intermixed patches of image A and image B. The right eye image would then be a complementary patchwork, having a patch of the image B where the other eye had a patch of image A. Using those stimuli, the rivalrous percept was not of oscillations between the two patchworks. Rather, what occurred was rivalry between a coherent image A and a coherent image B, showing that the patches had been grouped before rivalry (Dörrenhaus, 1975; Kovács et al., 1996; Ngo et al., 2000). Again this indicated that rivalry was occurring at a more abstract level of image representation than direct monocular signals from the two eyes.
Neurophysiological recordings in monkeys corroborated the psychophysical finding that in some situations rivalry could involve higher-level image representations. The strongest neurophysiological correlate of rivalry was found in inferotemporal cortex (Sheinberg and Logothetis, 1997), a high-level, binocularly driven visual area involved in object recognition. In contrast early visual areas, where large populations of monocular neurons exist, showed modest rivalry effects. Weak correlates of rivalry were reported for single-cell recordings in striate cortex (Leopold and Logothetis, 1996), and no rivalry related activity was reported for single-cell recordings in lateral geniculate nucleus (Lehky and Maunsell, 1996; Wilke et al., 2009). FMRI studies, on the other hand produced somewhat different results from single-cell physiology, showing vigorous rivalry correlates in striate cortex (Polonsky et al., 2000; Tong and Engel, 2001; Lee et al., 2007) and to some extent in lateral geniculate nucleus as well (Haynes et al., 2005; Wunderlich et al., 2005).
Overall, examining the psychophysical, neurophysiological, and fMRI data, there is evidence for rivalry occurring at a wide range of levels within the visual system. Faced with this body of results, a new class of “hierarchical” binocular rivalry models was created (Wilson, 2003; Freeman, 2005). Earlier models had postulated reciprocal inhibition between monocular representations of images tied to signals from left and right eyes. Hierarchical models augmented that with an additional stage (or stages) involving inhibition between higher-level, binocular representations of images, where eye-of-origin was lost. That allowed “eye rivalry” to occur at lower levels of the visual system and “image rivalry” to occur at higher levels.
An unresolved issue in hierarchical models is how can the separate identities of the two images be maintained after binocular mixing in order for rivalry to be possible at higher levels? We suggest that a way for left and right images to retain their separate identities after binocular mixing is to simply unmix them. Recently a new class of non-linear signal-processing algorithms has been developed that has the potential to do that, called blind source separation (BSS) algorithms (Choi et al., 2005; Cichocki et al., 2009; Comon and Jutten, 2010). BSS algorithms separate signal mixtures into component “sources.” The algorithms are called “blind” because they are given little or no information about the nature of the underlying source signals they are trying to recover. Because they are blind, they fall into the category of unsupervised learning algorithms.
From amongst the various BSS algorithms we focus on one, non-negative matrix factorization (NMF; Lee and Seung, 1999). The non-negativity constraint in NMF is appealing for applications in neural processing as firing rates must be non-negative. However the ability to do binocular unmixing is not unique to NMF, and we shall also demonstrate it using a second, unrelated BSS algorithm called independent component analysis (ICA). Matlab code for NMF was obtained from Hoyer (2011) and for ICA from Hyvarinen (2011). We believe that this is the first suggestion that BSS algorithms may be dynamically operating within the brain for real-time visual processing.
Results
Two pairs of images were used to test the algorithms (Figure 1), a pair of orthogonal sinusoidal gratings and a face/house pair. Both stimulus classes are widely used in binocular rivalry studies. Each pair was linearly mixed in various proportions to form five mixed images. This variable mixing in the algorithm corresponds to physiological observations that binocular neurons in striate cortex of macaque monkey occur in various ocular dominance mixtures (Hubel and Wiesel, 1968). In the words of Hubel and Wiesel (1977), “Just why the two eyes should be brought together in this elaborate but incomplete way is not yet clear. What the ocular dominance columns appear to achieve is a partial mixing of influences from the two eyes, with all shades of ocular dominance throughout the entire binocular field of vision.” Whatever the reason for this variable binocular mixing, it is precisely what is needed for BSS algorithms to work. The algorithms would not work if only a single binocular mixture were available. fMRI studies also show ocular dominance columns in humans (Cheng et al., 2001; Yacoub et al., 2007), suggesting variable binocular mixing may be similar in humans and macaque monkeys.
Variable ocular dominance also occurs in extrastriate visual cortex. Ocular dominances in extrastriate cortex are more narrowly spread than in striate cortex, as indicated by data from inferotemporal cortex (Uka et al., 2000) and area MT (Kiorpes et al., 1996). The unmixing results reported here were produced using left/right ocular dominance mixtures spread over the range 67%/33%–33%/67%, as shown in Figure 1. However, similar results were obtained using an even narrower spectrum of ocular dominances, going from 55/45 to 45%/55%, so it does not take a large range to allow the BSS algorithms to work. The variability of ocular dominances in extrastriate cortex appears sufficient to support the sort of binocular unmixing being proposed here.
The NMF algorithm was implemented in terms of matrix algebra (Figure 2A). The procedure was to factorize the binocular mixture matrix B into two matrices, B = M × A, subject to the constraint M and A were non-negative. Each column in the binocular mixture matrix B corresponded to one mixed image (there are five mixed images in this example). Each row corresponded to a different image pixel. Starting from random values of M and A, the algorithm iteratively updated their values so as to reduce error between M × A and B, following standard update rules for the algorithm using an error measure based on entropy divergence (Lee and Seung, 1999, 2001). (The error measure used is not critical for the algorithm.) Gradually the two images unmixed as M × A converged to B. The binocular mixture matrix B was now expressed in terms of the multiplication of M, a matrix containing the two unmixed monocular images, by A, a matrix containing mixing coefficients.
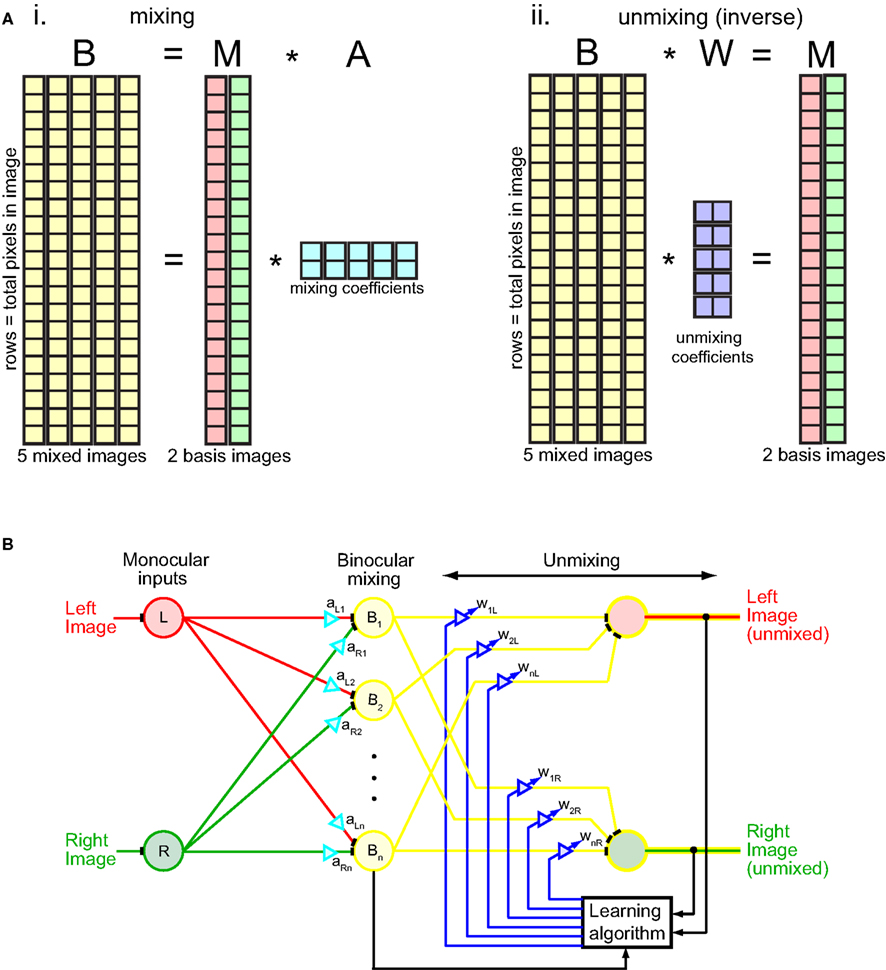
Figure 2. Mechanics of the unmixing algorithm. (Ai) Matrix representation of binocular mixing. The binocular mixture matrix B had five columns, representing the five mixed images depicted in Figure 1. Each column had 40,000 rows, corresponding to 40,000 pixels in each image (200 × 200 pixels). Thus each image is “unfolded” from a 2D array to a 1D column of pixels. The binocular matrix B was factored into two non-negative matrices M and A such that B = M × A. The factorization was done by iteratively updating M and A in accord with the NMF algorithm so as to gradually reduce error between B and M × A, with error based on entropy divergence (Lee and Seung, 1999, 2001). The matrix M had two columns, containing left and right source images, and 40,000 rows. The matrix A contained mixing coefficients, which combined the two source images in M to form different binocular mixtures. Matrix A had five columns and two rows, corresponding to five pairs of mixing coefficients to produce five different binocular mixtures. (Aii) Matrix representation of binocular unmixing. The matrix W of unmixing coefficients is the Moore–Penrose generalized inverse of the mixing matrix A. (B) Neural network interpretation of the unmixing algorithm. Diagram adapted from Cichocki et al. (2009).
What we really want to solve, however, is the inverse problem to that described above. Rather than find the matrix A of mixing coefficients used to combine monocular images into binocular mixtures (Figure 2Ai), we want an unmixing matrix W that can decompose the binocular mixtures into component monocular images: B × W = M (Figure 2Aii). Fortunately there is a simple relationship between the mixing and unmixing matrices: they are inverses of each other: W = A+. (In this case, because the mixing and unmixing matrices are not square, the Moore–Penrose generalized inverse A+ must be used rather than the regular matrix inverse A−1). Although we applied the algorithm directly to image pixel values, the principle remains the same whether the numbers in matrices M and B represent pixel values or neural firing rates derived by convolving receptive fields with the image.
The unmixing algorithm can be given a more physiological interpretation by formulating it in terms of a neural network rather than matrix algebra (Figure 2B). The iterative nature of the algorithm is indicated by the feedback loop originating from the outputs. The gradual unmixing of the binocular signal as it cycles through the feedback loop may have a perceptual correlate in binocular rivalry. When orthogonal gratings are briefly flashed to the two eyes for less than 150 ms they appear mixed, in a checkerboard pattern (Wolfe, 1983). It is only after longer exposure that the mixture disappears and the image from one eye or the other starts to predominate.
Feedback was mathematically implemented here as discrete time updates on a set of matrices. It could equivalently be expressed within a network as a non-linear dynamical system operating in continuous time, expressed as a set of coupled differential equations. As the dynamical system evolves to a stable point (unmixed images at the output), it is not only neural activities that must change dynamically, but also the strengths of synaptic interactions. There is indeed evidence for rapid dynamic modulation of neural connectivity in a network (Vaadia et al., 1995), and rapid synaptic plasticity as a mechanism for implementing neural computations has been reviewed by Abbott and Regehr (2004).
Unmixing produced by the NMF algorithm was not perfect. There was residual crosstalk within the two unmixed images. This was apparent when an unmixed image was subtracted from the original source image (Figure 3). The crosstalk was small enough, however, that in most trials it was not apparent upon inspection of the unmixed images. However, in some trials (around 25% for the face/house pair), the NMF algorithm converged to a situation with visible crosstalk, possibly because lack of noise in the algorithm allowed it get stuck in a local error minimum. Details of the crosstalk pattern varied from trial to trial as the algorithm started from different random states.
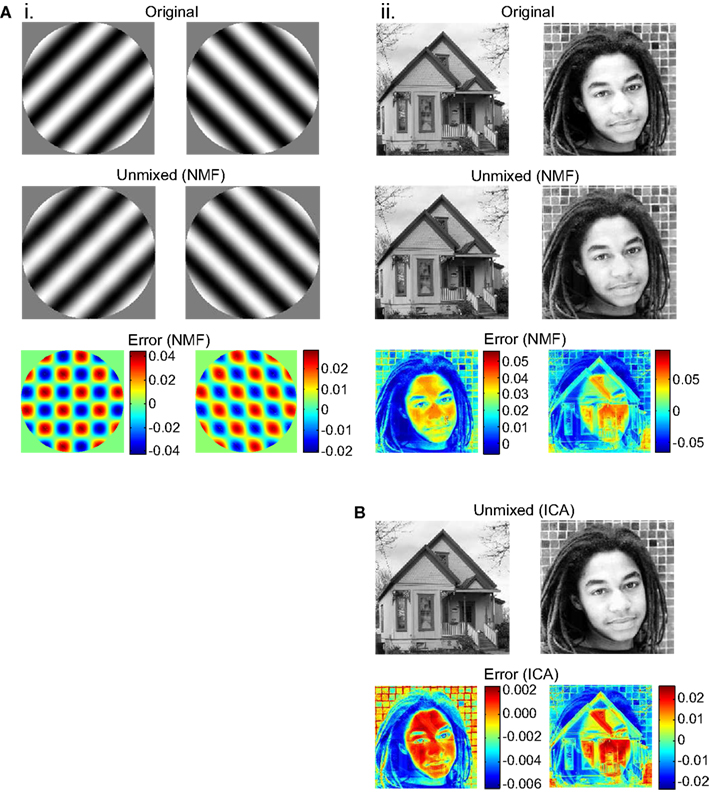
Figure 3. Unmixing results and errors, for example runs of the NMF and ICA algorithms. Source images are shown, together with images recovered after the source images were binocularly mixed and then unmixed. Error indicates pixel subtraction (original image)–(unmixed image). Gray levels in source and unmixed images fell in the range 0.0–1.0. (A) Results for NMF unmixing algorithm. (B) Results for ICA unmixing algorithm.
In addition to NMF, we tried another BSS algorithm, ICA (Bell and Sejnowski, 1995; Hyvärinen and Oja, 2000; Stone, 2002). Instead of being constrained to finding non-negative factors of a matrix, this algorithm was constrained to find a set of unmixed images that were as statistically independent as possible from each other. FastICA (Hyvärinen and Oja, 2000) was the specific variant of the ICA algorithm used. ICA was able to unmix binocular images in a manner similar to NMF (compare Figures 3Aii,B). Unlike NMF, ICA never converged to produce visible crosstalk between unmixed images, although subliminal crosstalk remained. The ICA algorithm, on the other hand, did have the disadvantage that in 50% of unmixing trials the recovered images were contrast reversed, as ICA did not have a non-negativity constraint.
The NMF algorithm was able to unmix gratings with small orientation differences, down to the smallest difference tested of 1°. In contrast, the ICA algorithm had an increasing probability of finding an incorrect solution to the unmixing problem as the orientation difference dropped below 15°.
Although both BSS algorithms were capable of unmixing images, they differed in the details of their behavior. Presumably other BSS algorithms would each have their own mix of characteristics.
Discussion
Binocular unmixing neatly solves the problem of how two images can retain their separate identities after binocular mixing, so that rivalry can occur between high-level binocular representations of incompatible images. Although unmixed images appear virtually identical to the original monocular images (Figure 3), they are binocularly driven (Figure 2B).
The ability of two unrelated algorithms, NMF and ICA, to unmix binocular signals suggests that there is a whole class of BSS algorithms having similar capabilities. This opens the opportunity for combined theoretical and experimental investigations to uncover the particular implementation that may be occurring biologically.
The binocular unmixing model does not consider how the oscillations of rivalry themselves are produced. The actual oscillations during rivalry would require further interactions between the two images after unmixing. Mechanisms to produce oscillations have already been extensively modeled (among them Lehky, 1988; Lumer, 1998; Laing and Chow, 2002; Wilson, 2003, 2007; Freeman, 2005; Grossberg et al., 2008; Gigante et al., 2009). Binocular unmixing augments those models of oscillations by creating conditions at higher visual levels that allow them to operate.
The binocular mixing model also does not consider mechanisms of perceptual grouping that occur under some rivalry conditions (Dörrenhaus, 1975; Kovács et al., 1996; Ngo et al., 2000). Grouping mechanisms in rivalry have received less theoretical attention than oscillatory mechanisms (although see Grossberg et al., 2008). Binocular unmixing again serves to create conditions at higher visual levels that would allow grouping algorithms to operate.
As signals pass through the unmixing circuitry, eye-of-origin labeling is lost in the recovered left and right images. There is no way to tell which image originated from the left eye and which originated from the right eye. This lose of eye-of-origin information is consistent with the psychophysical data outlined earlier, and is in fact a defining characteristic of high-level “image rivalry.” The situation is different for stereopsis, where the preservation of disparity sign (near/far) indicates that eye-of-origin information is implicitly retained within the population of binocular cells. That was emphasized by Assee and Qian (2007) in a model of da Vinci stereopsis that extracted eye-of-origin information for occluded monocular regions using binocular cells. While the BSS algorithms used here lose eye-of-origin information, in the future it might be possible to devise binocular unmixing models that do retain such information, for applications other than rivalry.
We found a low level of crosstalk in the unmixed left and right images (Figure 3). Binocular crosstalk has not been a prediction of previous binocular models. In experimental observations under conditions of high-level “image rivalry,” we would expect a strong level of crosstalk immediately following the initial presentation of rivalrous stimuli, with the crosstalk smoothly decaying over time to some non-zero value before the oscillations started. Subliminal crosstalk would remain during the oscillatory period.
Non-negative matrix factorization was introduced as a possible mechanism for parsing objects into parts for object recognition (Lee and Seung, 1999). We see that it may also be involved in binocular rivalry. At the single neuron level, neurophysiological correlates of binocular rivalry are strongest in inferotemporal cortex (Sheinberg and Logothetis, 1997), a ventral visual area associated with object recognition, and weaker in striate cortex (Leopold and Logothetis, 1996) or in the dorsal visual pathway (Logothetis and Schall, 1989). Although as a binocular phenomenon rivalry tends to be most associated with stereopsis, we suggest at higher levels it may also have connections with mechanisms of shape representation during object recognition.
Besides binocular rivalry in inferotemporal cortex, another example that might use binocular unmixing involves area MT, a cortical area believed to represent visual motion. There is evidence that area MT can support comparisons between velocities in left and right images for computation of 3D motion (Rokers et al., 2009, 2011), despite being binocularly driven. In this case, MT appears to be performing visual processing as if it had access to the original unmixed images.
Binocular unmixing thus raises the possibility that new binocular interactions between left and right images can be created in different cortical areas for different purposes, rather than being inherited from striate cortex.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I thank Saumil Patel, Anne Sereno, and Christian Wehrhahn for comments on the manuscript.
References
Assee, A., and Qian, N. (2007). Solving da Vinci stereopsis with depth-edge-selective V2 cells. Vision Res. 47, 2585–2602.
Bell, A. J., and Sejnowski, T. J. (1995). An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 7, 1129–1159.
Cheng, K., Waggoner, R. A., and Tanaka, K. (2001). Human ocular dominance columns as revealed by high-field functional magnetic resonance imaging. Neuron 32, 359–374.
Choi, S., Cichocki, A., Park, H.-M., and Lee, S.-Y. (2005). Blind source separation and independent component analysis: a review. Neural Inform. Process. Lett. Rev. 6, 1–57.
Cichocki, A., Zdunek, R., Phan, A. H., and Amari, S.-I. (2009). Nonnegative Matrix and Tensor Factorizations: Applications to Exploratory Multi-Way Data Analysis and Blind Source Separation. Chichester: Wiley.
Comon, P., and Jutten, C. (eds). (2010). Handbook of Blind Source Separation: Independent Component Analysis and Applications. New York: Academic Press.
Gigante, G., Mattia, M., Braun, J., and Del Giudice, P. (2009). Bistable perception modeled as competing stochastic integrations at two levels. PLoS Comput. Biol. 5, e1000430. doi: 10.1371/journal.pcbi.1000430
Grossberg, S., Yazdanbakhsh, A., Cao, Y., and Swaminathan, G. (2008). How does binocular rivalry emerge from cortical mechanisms of 3-D vision? Vision Res. 48, 2232–2250.
Haynes, J.-D., Deichmann, R., and Rees, G. (2005). Eye-specific effects of binocular rivalry in the human lateral geniculate nucleus. Nature 438, 496–499.
Hoyer, P.O. (2011). NMF Matlab Code (nmfpack). Available at: http://www.cs.helsinki.fi/u/phoyer/software.html
Hubel, D. H., and Wiesel, T. N. (1968). Receptive fields and functional architecture of monkey striate cortex. J. Physiol. (Lond.) 195, 215–243.
Hubel, D. H., and Wiesel, T. N. (1977). Ferrier lecture. Functional architecture of macaque monkey visual cortex. Proc. R. Soc. Lond. B Biol. Sci. 198, 1–59.
Hyvarinen, A. (2011). FastICA Matlab Code. Available at: http://research.ics.tkk.fi/ica/fastica/
Hyvärinen, A., and Oja, E. (2000). Independent component analysis: algorithms and applications. Neural Netw. 13, 411–430.
Kiorpes, L., Walton, P. J., O’Keefe, L. P., Movshon, J. A., and Lisberger, S. G. (1996). Effects of early-onset artificial strabismus on pursuit eye movements and on neuronal responses in area MT of macaque monkeys. J. Neurosci. 16, 6537–6553.
Kovács, I., Papathomas, T. V., Yang, M., and Fehér, Á. (1996). When the brain changes its mind: interocular grouping during binocular rivalry. Proc. Natl. Acad. Sci. U.S.A. 93, 15508–15511.
Laing, C. R., and Chow, C. C. (2002). A spiking neuron model for binocular rivalry. J. Comput. Neurosci. 12, 39–53.
Lee, D. D., and Seung, H. S. (1999). Learning the parts of objects by non-negative matrix factorization. Nature 401, 788–791.
Lee, D. D., and Seung, H. S. (2001). “Algorithms for non-negative matrix factorization,” in Advances in Neural Information Processing Systems, Vol. 13, eds T. Leen, T. Dietterich, and V. Tresp (Cambridge: MIT Press), 556–562.
Lee, S.-H., Blake, R., and Heeger, D. J. (2007). Hierarchy of cortical responses underlying binocular rivalry. Nat. Neurosci. 10, 1048–1054.
Lehky, S. R., and Maunsell, J. H. (1996). No binocular rivalry in LGN of alert macaque monkeys. Vision Res. 36, 1225–1234.
Leopold, D. A., and Logothetis, N. K. (1996). Activity changes in early visual cortex reflect monkeys’ percepts during binocular rivalry. Nature 379, 549–553.
Leopold, D. A., and Logothetis, N. K. (1999). Multistable phenomena: changing views in perception. Trends Cogn. Sci. (Regul. Ed.) 3, 254–264.
Logothetis, N. K., Leopold, D. A., and Sheinberg, D. L. (1996). What is rivalling during binocular rivalry? Nature 380, 621–624.
Logothetis, N. K., and Schall, J. D. (1989). Neuronal correlates of subjective visual perception. Science 245, 761–763.
Lumer, E. D. (1998). A neural model of binocular integration and rivalry based on the coordination of action-potential timing in primary visual cortex. Cereb. Cortex 8, 553–561.
Ngo, T. T., Miller, S. M., Liu, G. B., and Pettigrew, J. D. (2000). Binocular rivalry and perceptual coherence. Curr. Biol. 10, R134–R136.
Polonsky, A., Blake, R., Braun, J., and Heeger, D. J. (2000). Neuronal activity in human primary visual cortex correlates with perception during binocular rivalry. Nat. Neurosci. 3, 1153–1159.
Rokers, B., Cormack, L. K., and Huk, A. C. (2009). Disparity- and velocity-based signals for three-dimensional motion perception in human MT+. Nat. Neurosci. 12, 1050–1055.
Rokers, B., Czuba, T. B., Cormack, L. K., and Huk, A. C. (2011). Motion processing with two eyes in three dimensions. J. Vis. 11, doi: 10.1167/11.2.10. [Epub ahead of print].
Sheinberg, D. L., and Logothetis, N. K. (1997). The role of temporal cortical areas in perceptual organization. Proc. Natl. Acad. Sci. U.S.A. 94, 3408–3413.
Sterzer, P., Kleinschmidt, A., and Rees, G. (2009). The neural bases of multistable perception. Trends Cogn. Sci. (Regul. Ed.) 13, 310–318.
Stone, J. V. (2002). Independent component analysis: an introduction. Trends Cogn. Sci. (Regul. Ed.) 6, 59–64.
Tong, F., and Engel, S. A. (2001). Interocular rivalry revealed in the human cortical blind-spot representation. Nature 411, 195–199.
Tong, F., Meng, M., and Blake, R. (2006). Neural bases of binocular rivalry. Trends Cogn. Sci. (Regul. Ed.) 10, 502–511.
Uka, T., Tanaka, H., Yoshiyama, K., Kato, M., and Fujita, I. (2000). Disparity selectivity of neurons in monkey inferior temporal cortex. J. Neurophysiol. 84, 120–132.
Vaadia, E., Haalman, I., Abeles, M., Bergman, H., Prut, J., Slovin, H., and Aertsen, A. (1995). Dynamics of neuronal interactions in monkey cortex in relation to behavioural events. Nature 373, 515–518.
Wilke, M., Mueller, K.-M., and Leopold, D. A. (2009). Neural activity in the visual thalamus reflects perceptual suppression. Proc. Natl. Acad. Sci. U.S.A. 106, 9465–9470.
Wilson, H. R. (2003). Computational evidence for a rivalry hierarchy in vision. Proc. Natl. Acad. Sci. U.S.A. 100, 14499–14503.
Wilson, H. R. (2007). Minimal physiological conditions for binocular rivalry and rivalry memory. Vision Res. 47, 2741–2750.
Wolfe, J. M. (1983). Influence of spatial frequency, luminance, and duration on binocular rivalry and abnormal fusion of briefly presented dichoptic stimuli. Perception 12, 447–456.
Wunderlich, K., Schneider, K. A., and Kastner, S. (2005). Neural correlates of binocular rivalry in the human lateral geniculate nucleus. Nat. Neurosci. 8, 1595–1602.
Keywords: binocular rivalry, blind source separation, non-linear dynamical systems, non-negative matrix factorization, independent component analysis
Citation: Lehky SR (2011) Unmixing binocular signals. Front. Hum. Neurosci. 5:78. doi: 10.3389/fnhum.2011.00078
Received: 21 April 2011; Paper pending published: 14 June 2011;
Accepted: 22 July 2011; Published online: 09 August 2011.
Edited by:
Naotsugu Tsuchiya, RIKEN, JapanReviewed by:
Ning Qian, Columbia University (New York City), USAIzumi Ohzawa, Osaka University, Japan
Copyright: © 2011 Lehky. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Sidney R. Lehky, Computational Neuroscience Laboratory, The Salk Institute, 10010 North Torrey Pines Road, La Jolla, CA 92037, USA. e-mail:c2lkbmV5QHNhbGsuZWR1

