- Instituto de Ingeniería Biomédica, Facultad de Ingeniería, Universidad de Buenos Aires, Buenos Aires, Argentina
Equivalence relations (ERs) are logical entities that emerge concurrently with the development of language capabilities. In this work we propose a computational model that learns to build ERs by learning simple conditional rules. The model includes visual areas, dopaminergic, and noradrenergic structures as well as prefrontal and motor areas, each of them modeled as a group of continuous valued units that simulate clusters of real neurons. In the model, lateral interaction between neurons of visual structures and top-down modulation of prefrontal/premotor structures over the activity of neurons in visual structures are necessary conditions for learning the paradigm. In terms of the number of neurons and their interaction, we show that a minimal structural complexity is required for learning ERs among conditioned stimuli. Paradoxically, the emergence of the ER drives a reduction in the number of neurons needed to maintain those previously specific stimulus–response learned rules, allowing an efficient use of neuronal resources.
Introduction
Logic categories are classes composed of elements that verify an equivalence relation (ER) among them, that is to say, they are reflexive, symmetric, and transitive.
Mainly in human subjects, training conditional rules among stimuli produce the emergence of ER between those stimuli that were directly or indirectly associated (Hayes, 1989; Sidman et al., 1989; Kastak et al., 2001). A strong coexistence between the emergence of ER and the capabilities of developing a language was shown in children. In fact, only those children that developed a language, at least using signs, have performed correctly in equivalence tests (Devany et al., 1986). Indeed, emergence of symmetry has been studied in groups of monkeys, baboons, and children giving positive results only for the last group (Sidman et al., 1982).
Understanding the neural mechanisms that underlie the emergence of ER should give us a deeper knowledge about language development.
In many computational papers, rule learning has been explained from the point of view of how the model reacts and adapts to changing environments (Cohen et al., 2007; Rey et al., 2007), paying special attention to the tradeoff between dopamine and norepinephrine release in the cerebral cortex and how these neuromodulators switch between exploratory and exploitatory behavior. In O’Reilly et al. (2002), a computational model of the intradimensional/extradimensional task is presented and, as in the models aforementioned, the focus is on the ability of switching between different learned rules for normal or pathological cases. However, few computational models simulate ER learning (Martin et al., 2008; García et al., 2010).
Human beings are unique among other species in that ER emerge as a natural consequence of training conditional rules. For that reason, the study of the mechanisms and structures involved in the learning of this paradigm is limited to cases of patients with brain injuries or learning deficiencies. In this sense, computational models can help to understand what structures and mechanisms could be interacting in order to produce the emergence of ER.
Herein, we introduce a computational model to explain the emergence of the ERs from the learning of simple conditional rules. The model accounts for psychological and neurophysiological data in primates and by means of lesions; we will explain how certain mechanisms affect the emergence of ER as a natural consequence of training simple conditional rules. Among these mechanisms, top-down modulation of neurons in the visual pathway together with Hebbian learning and lateral interactions seem to be necessary.
Materials and Methods
The experimental paradigms used to train and test the models are the same as those used in Devany et al. (1986) and Sidman et al. (1982) to teach ER to humans and monkeys.
Briefly, a stimulus (sample) is presented at the center of the display during 500 ms, followed by a delay interval of 1 s without stimuli. After that, two stimuli (comparisons) are presented at the sides, left and right of the central position.
At this moment, the subject has to choose one of the comparison stimuli in order to be rewarded.
Figure 1 shows some examples of delayed matching to sample (DMTS) training, ER testing, and the timing diagram of stimuli presentation, response and reward during one trial.
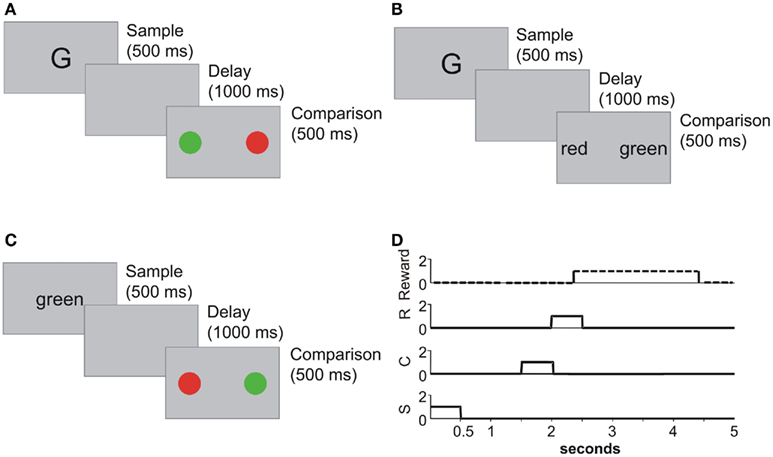
Figure 1. (A) A trial in DMTS training. A sample stimulus is presented during 500 ms, a 1-s delay is interposed, and after that delay two comparison stimuli are presented. The subject must choose between these stimuli in order to receive a reward. In this trial, letters were paired to colors. (B) A DMTS trial where letters are paired to words. (C) A test trial where unpaired stimuli are presented, it is a test for equivalence relation between words and colors. (D) Stimuli timing, responses, and reward along trials. Sample stimuli (S) are presented for 500 ms at the beginning of the trial. After a 1-s delay the comparison stimuli (S) are presented. Comparison stimuli are held until a response (R) is executed, or the end of the trial is reached. Every time a correct response is executed a reward is delivered. Rewards last 2 s for simulation purposes.
Sample and comparison stimuli belong to different classes that could be perceptually different. In the paradigm used here (Figure 2A), stimuli of class A = {ai} are presented as samples and stimuli of classes B = {bi} and C = {ci} are used as comparisons. As an example, stimulus G (from class A) is paired to the green color and the word “GREEN,” from classes B and C respectively. The same occurs for the other stimuli (R, “RED” and color red). Trained conditionals and tested relations are shown in continuous and dashed lines respectively in Figure 2. After reaching criteria in A → B and A → C rules, the subject is tested in reflexivity (A → A, B → B, C → C), symmetry (B → A and C → A) and the combined test for symmetry and transitivity (B → C and C → B).
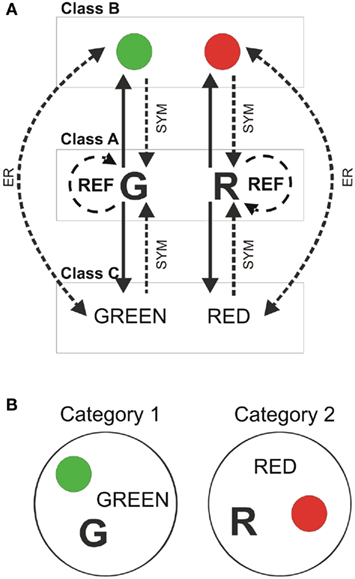
Figure 2. Training and testing equivalence relations. (A) Three classes of perceptually different stimuli were used to train and test the paradigm. Simple conditional rules (continuous line) were reinforced in a delayed matching to sample experiment. Once individuals reached criteria in DMTS, they were tested in equivalence relations (dashed lines). REF: reflexivity test, SYM: symmetry test, and ER: equivalence relation test. (B) If the performance in the equivalence relations test is higher than 80%, the set of stimuli can be split in two new subsets, two logic categories of equivalent stimuli (Category 1 and Category 2).
If the subject succeeds in more than 80% of the tested relations, it is considered as having the capability of learning ERs. When this happens, equivalent stimuli can be rearranged in two logical categories (see Figure 2B).
Model
In previous computational models we explained the neural mechanisms and neural structures that allow them to perform efficiently in visual discrimination (VD) and DMTS paradigm (A → B, A → C), and also how these structures interact to allow flexible behavior in changing environments (Rey et al., 2007; Lew et al., 2008; Rapanelli et al., 2010). Nonetheless, when we tested those models in ERs learning, they performed at random.
In order to produce the emergence of ERs from the training of simple conditional rules, we included three neurophysiological hypotheses in the original model.
First, neurons in the input layer of the model are selective to objects and places. A certain stimulus placed at position i (center of the screen) produces the activation of neurons selective for the same stimulus when that stimulus appears in other positions (left and right parts of the screen; Suzuki et al., 1997).
Second, associative memories of paired stimuli emerge as a consequence of reinforced learning in a delayed paired association task (Naya et al., 2001).
Third, prefrontal and premotor areas modulate selectively the excitability of neurons at early stages of the visual pathway (Tomita et al., 1999; Ekstrom et al., 2008).
Neurons in the model represent functional clusters of biological neurons, see Figure 3. The output of these neurons is the average firing rate of those clusters. This is a real time model and variables are updated every 100 ms.
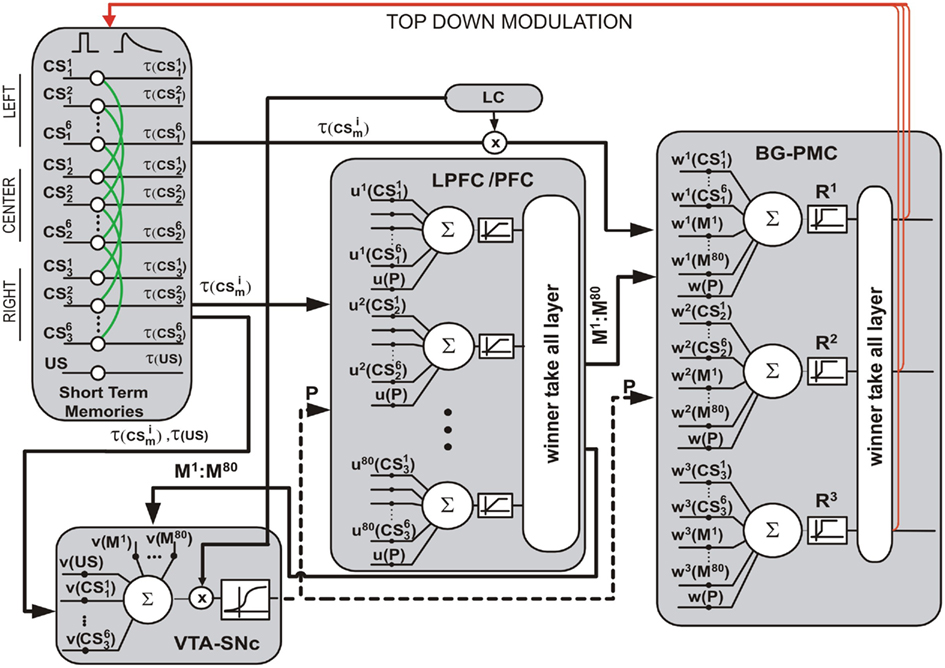
Figure 3. Computational model. The input layer contains units that compute short term memories of input conditional stimuli (CS) and the reward (US). These memories are inputs to other blocks of the models. The VTA–SNc block computes P, the prediction of the US. The LC block computes a long term memory of the US, and this quantity modulates both: the excitability VTA–SNc neurons and the strength of visual inputs that project onto the output layer. The LPFC structure contains neurons that compute their outputs based on short term memories of the visual inputs and the value of P. Outputs of these neurons compete in a winner-take-all mechanism and project onto the output layer and onto the VTA–SNc. The quantity of neurons in the LPFC structure is one of the subjects of this research and by default its value is 80. Here, the BG–PMC block is the output layer of the model. This layer executes the behavioral responses R1, R2, or R3. Neurons in this structure integrate information from visual inputs, the LPFC, and the VTA–SNc. As in the LPFC structure, a winner-take-all mechanism is applied to the output of the neurons in order to avoid the execution of multiple responses. Top-down modulation is shown in red whereas Hebbian-like synapses at visual stages are shown in green. A glossary containing parameters values and their definitions is appended at the end of this work.
When certain conditioned stimulus i
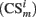 is present in position m (center, left, or right), its value is set to
is present in position m (center, left, or right), its value is set to 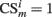 , otherwise
, otherwise 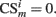
Every time a correct response is executed, the unconditioned stimulus (US) is set to a positive value for the next 20 time steps (2 s), otherwise its value is set to zero. This positive value represents the strength of the reward.
The input layer of the model computes the short term memory (STM) of input stimuli:
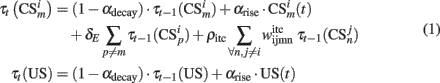
where 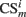 is the conditioned stimulus i presented at the position m (center, left, or right), US is the unconditioned stimulus (reward), t is the time step and τ means the stimulus trace.
is the conditioned stimulus i presented at the position m (center, left, or right), US is the unconditioned stimulus (reward), t is the time step and τ means the stimulus trace.
In the case of 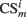 traces, the third term in Eq. 1is the information that responsive neurons for stimulus i at position m receive from the neuron that responds to stimulus i at position p. The last term involves weighted contributions of any other stimuli than
traces, the third term in Eq. 1is the information that responsive neurons for stimulus i at position m receive from the neuron that responds to stimulus i at position p. The last term involves weighted contributions of any other stimuli than 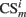 present at time step t. Synaptic weights
present at time step t. Synaptic weights 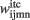 are computed by Hebbian learning (see Eq. 13). They represent the associative memory found in inferotemporal cortex (ITC) after training in a delayed paired associated experiment (Naya et al., 2001).
are computed by Hebbian learning (see Eq. 13). They represent the associative memory found in inferotemporal cortex (ITC) after training in a delayed paired associated experiment (Naya et al., 2001).
The output layer of the model includes those areas related to the execution of a response, that is, the premotor cortex, the basal ganglia, and/or the frontal eye field.
If throughout a trial the activity of the output neurons do not exceed the activation threshold, a random response is executed with probability of 1/3. This random response is executed 900 ms after the end of the delay period. When a response is executed, the activity of its associated neuron is set to 1 during five time steps, while the others are clamped to 0 for the same time.
Responses represent both, saccadic movements or touching to the right (R1), left (R2), and to any other non-rewarded direction (R3). All are codified at the motor-related structure layer.
Experimental data suggest that stimulation of the ventro tegmental area (VTA) decreases spontaneous firing rates of PFC pyramidal neurons, mainly by exciting interneurons (Tseng et al., 2006; Tseng and O’Donnell, 2007). In our model, such inhibition is represented by constant negative synaptic weights ut(P) from the VTA to the PFC. However, due to the synergism between NMDA and D1 dopamine receptors (Lewis and O’Donnell, 2000), we postulate that initially inhibited PFC pyramidal neurons will fire strongly when afferent inputs release large amounts of glutamate. This activated cluster will then inhibit other clusters (Durstewitz et al., 2000). To model this effect, we apply a winner-take-all mechanism at the PFC output. The following equations show how the output of PFC neurons is computed along a trial:
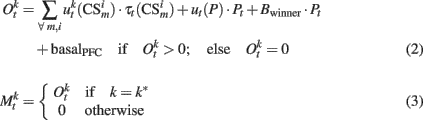
where 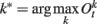 represents the index of the winner neuron, Bwinner stands for the synergism between D1 dopamine receptors and NMDA receptors, and basalPFC is the baseline firing rate of PFC neurons.
represents the index of the winner neuron, Bwinner stands for the synergism between D1 dopamine receptors and NMDA receptors, and basalPFC is the baseline firing rate of PFC neurons.
It has been hypothesized that dopamine (DA) modulates the excitability of striatal neurons allowing the BG to inhibit competent programs and to release the correct one (Mink, 1996). As in the PFC, in our model DA inhibits the motor area through constant negative synaptic weight wt(P), and, in contrast to this general inhibition, the winner neuron is excited proportionally to the released DA. This mechanism applies a “brake” over all possible motor programs releasing that program whose activity surpasses a fixed threshold. The output of the response neurons is computed as:
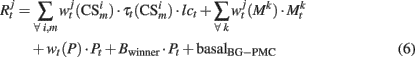
basalBG–PMC is the baseline firing rate of BG–PMC neurons and lct represents a modulation exerted by noradrenergic neurons of the Locus Coeruleus (LC) over visual and somatosensory cortical neurons. Effects of norepinephrine (NE) on the modulation of glutamate-evoked responses have been proved to have an inverted U shape (Berridge and Waterhouse, 2003), that is, low and high doses of NE produce a decrease on neuron excitability, while medium doses increase their excitability. In behaving monkeys, tonic firing of LC neurons shows a defined correlation with performance (Usher et al., 1999). Tonic frequencies of 2–3 Hz are associated with good performance periods while frequencies >3 Hz are related to periods where erratic performance and distractibility are observed. This gives a hint of the function of the noradrenergic system in the regulation of exploratory behavior (Aston-Jones and Cohen, 2005). We model tonic firing of LC neurons as a function of the reward received in the last trials:
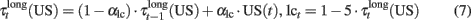
Short term memories for the response neurons are computed by
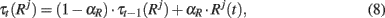
and as in Eq. 2, for the PFC area, a winner-take-all rule is applied.
In addition to excitability, dopamine effects on PFC pyramidal neurons are also related to modifications of synaptic efficacy via LTP and LTD (Reynolds and Wickens, 2002; Pan et al., 2005). For this reason, previous models have used the DA signal in the modulation of synaptic weights modifications (Lew et al., 2001, 2008; O’Reilly et al., 2002). Although the temporal differences (TD) model simulates accurately the firing rates of VTA neurons (Schultz et al., 1997), dopamine effects in PFC and BG–PMC are observed for hundreds of milliseconds after DA release. In this work, for computationally reasons, we used a simple algorithm to model the presence of extracellular DA in the PFC and the BG–PMC; however, the same results were obtained when a TD model was used as the VTA–SNc block (Lew et al., 2008). Prediction of incoming reward Pt was computed based on the stimuli present at time t
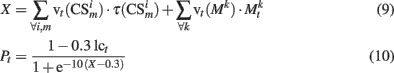
where the negative term in the numerator of Eq. 8stands for noradrenergic inhibition of dopaminergic neurons (Paladini and Williams, 2004) and vt are synaptic weights that represent learned associations between conditioned stimuli, PFC neuron responses, and the US
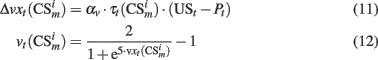
Equation 9 is the Rescorla–Wagner like model of associative learning in conditioning paradigms (Rescorla and Wagner, 1972; Schmajuk and Zanutto, 1997; Lew et al., 2001), 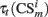 represent traces of both, conditioned stimuli and PFC neurons responses and vt is used to clump those associations between −1 and 1.
represent traces of both, conditioned stimuli and PFC neurons responses and vt is used to clump those associations between −1 and 1.
As in our previous models DA modulates learning in both, PFC and BG–PMC neurons (Lew et al., 2001, 2008; Rey et al., 2007; Rapanelli et al., 2010). If Pt > h, Hebbian learning computes the synaptic weights of both, PFC and BG–PMC neurons. The opposite occurs if Pt < h. Thus, synaptic weights of the PFC winner neuron k* and BG–PMC neurons and also those synaptic weights that connect input units at the input layer are updated according to:
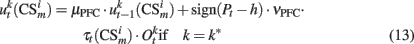
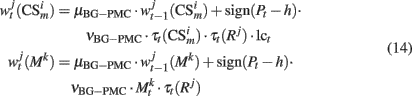
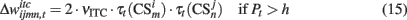
In the previous equations, μPFC and μBG–PMC are first order momentum constants while νPFC, νGB–PMC, and νITC are learning rates for the PFC, BG–PMC, and units at the input layer respectively.
Top-down modulation mechanisms were found in monkeys during learning of association tasks and memory retrieval (Tomita et al., 1999). Lateral Intraparietal (LIP) neurons modulate the activity of V1 neurons in humans (Saalmann et al., 2007) whereas FEF transmagnetic stimulation influences the modulation of visual activity (Taylor et al., 2007; Ekstrom et al., 2008). In our model, we propose selective top-down modulation of frontal and premotor areas over visual inputs. The main purpose of this selective modulation is to control the extinction of short term memories according to the executed response. The STM extinction rate αdecay of Eq. 1is modulated selectively when a comparison stimulus is chosen, increasing the original value of αdecay in 2% for non-selected stimuli while keeping its original value for the selected one. In the model, this effect produces a faster extinction of short term memories for non-selected stimuli.
Simulations and Results
Learning of Reinforced Conditionals
In the learning phase the model was trained in DMTS. Sample stimuli belonging to class A were presented during 500 ms followed by a delay of 1000 ms without stimuli presented. After that, two stimuli, both of them belonging to classes B and C respectively were presented as comparison stimuli. Responses of the model, indicated as direct conditional relations in Figure 2A, were reinforced. A total of 500 simulations were performed using a DMTS paradigm in order to analyze the statistical properties of the ensemble. From these simulations, 394 (78%) reached a performance of 100% and were used to test the emergence of equivalent relation.
In Figure 4, the dynamic of learning is shown as training progresses. Average values of performance in DMTS as well as dopaminergic and noradrenergic activation and reaction times are plotted against training trials.
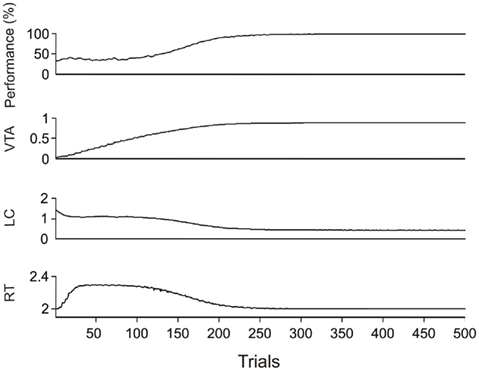
Figure 4. Average values of performance in DMTS acquisition, activation levels of VTA–SNc and LC and reaction times from 394 from 500 (78%) DMTS experiments where the performance reached 100%.
Before proceeding with the formal test to evaluate the model in ERs, we tested it in symmetry. Experimental results obtained with monkeys, baboons, and children have shown that only children can pass a symmetry test (Sidman et al., 1982).
After training the model in DMTS, symmetry was tested in the 394 models of the ensemble that reached a performance of 100%. Sample stimuli were chosen from classes B or C while comparison stimuli were chosen from class A. From the 394 models of the ensemble, symmetry was proved positively in 354 cases. Also, reflexivity was proved positively in 368 models.
To test reflexivity, models had to choose correctly those comparison stimuli that were presented previously as samples. In the symmetry and reflexivity tests, all possible combinations of sample and comparison stimuli were tested. Here, a relation is learned when at least 80% of correct responses were executed. Reflexivity, symmetry, and ERs were tested positively in 94, 93.6, and 87% of the models able to learn DMTS. In spite of the proportion of models that learn DMTS and ER (394/500 and 344/500), the averaged performances after the training phase were 95.7 and 88.9% respectively, as can be seen Figure 5A. In that sense, the distribution of performances in the ensemble showed a broad spectrum with a peak for values higher than 90%, see Figure 5B.
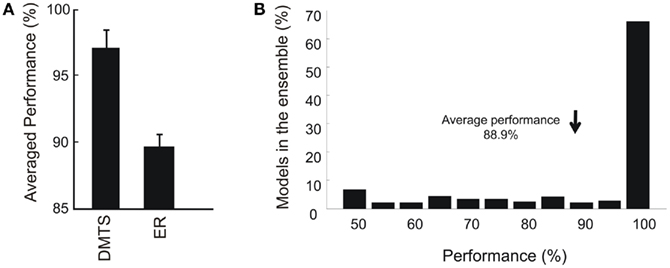
Figure 5. (A) Performance in DMTS and ER. Mean values and SEM were calculated using the first 20 trials after the plateau in correct responses was reached, that is, the same number of trials used for testing equivalence relations (all combinations indicated by dashed lines in Figure 2). (B) Normalized distribution of performances in the ensemble. It can be noted that while less than 70% of the models performs better than 90% in ER, the average performance of the ensemble is 88.9%.
Figure 6 shows the dynamics of learning ERs for the ensemble of 500 models as a function of the number of trials. To study the behavior of the ensemble, simulations were performed for different numbers of training trials, from 1 to 720 in steps of 40 trials. This figure shows the percentage of models in the ensemble whose performances were 100 and 80% in DMTS and ER tests respectively.
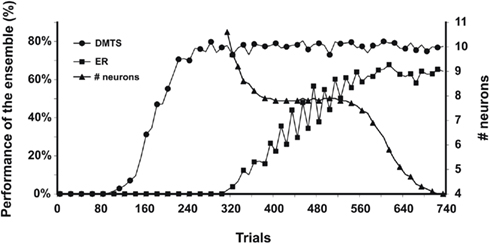
Figure 6. Performance in DMTS and equivalence relations (ER) are shown as a function of training trials. Both performances were calculated as the percentage of models of the ensemble that perform at 100% in DMTS and over criteria (80%) in equivalence relations. The right axis shows the number of neurons necessary to codify the rules tested in the equivalence relation.
As can be seen, after trial 280, DMTS could be tested positively in approximately 80% of the models. However, ERs emerge 40 trials after DMTS reached performance plateau. The percentage of models in the ensemble that pass ER tests increases until trial 600, where a plateau of 63% is reached. Additionally, we show the average of PFC neurons used by the ensemble of models to map rules. This quantity is calculated as the average of PFC neurons that won the winner-take-all competence during the last 100 training trials. As can be seen, that average reaches a first plateau after 400 training trials. During this plateau, eight PFC neurons were necessary to map the complete set of trained rules. It is interesting to note that after some time of overtraining in DMTS and, concurrently with the plateau in the emergence of ERs, the number of neurons decrease to four, the smallest amount required to map all learned rules.
Figure 7 shows the dependence of DMTS and ER learning as a function of the number of PFC neurons. It can be seen that a minimal complexity is required to learn those paradigms. The DMTS and ER paradigms cannot be learned if the number of neurons in the PFC structure is less than 16. On the other end, increasing the PFC size over 128 neurons does not increase significantly the number of models that learn DMTS as well as ER paradigms. To understand how the amount of neuronal resources affect the behavior of the models during training and testing of DMTS and ER paradigms, we calculated the average of winner neurons in the last 100 trials of these stages of the experiment. As displayed in Figure 6, if the number of neurons assigned to the PFC is over a certain minimum (64 neurons), both, DMTS and ER are learned. However, the number of neurons that finally mapped learned rules remains constant and independent of this minimum. On the other hand, although the amount of neuronal resources assigned to PFC increases exponentially, the maximum number of neurons used at the beginning of the training increases linearly.
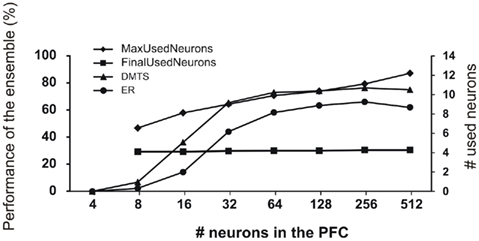
Figure 7. Use of neuronal resources. Left axis: the percentage of models in the ensemble that reaches criteria in DMTS and ER test is shown as a function of the number of neurons in the PFC. Right axis: number of neurons in the PFC that won at least once during the training phase (MaxUsedNeurons) and the number of neurons in the PFC that won at least once in the last 100 trials of the training phase (FinalUsedNeurons).
Producing Lesions in the Model
We produced lesions to components of the model that we postulated as necessary for ER learning, that is, the dopamine systems, the Hebbian learning mechanism at the input layer and top-down inhibition.
For each simulated lesion, an ensemble of 500 models was run and the mean performance across the ensemble for tasks of different complexities was calculated. In all cases, mean performances were calculated after the plateau in correct responses was reached. The average performance for each type of lesion is shown in Figure 8.
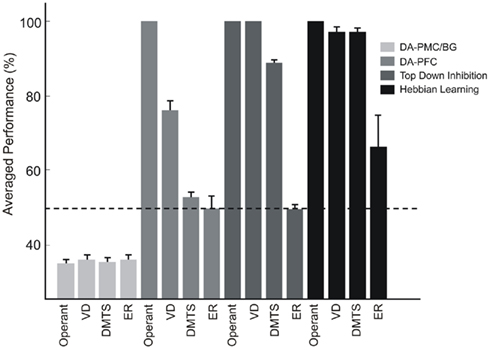
Figure 8. Effects of lesions. Four types of lesions were conducted over the necessary mechanisms for ER learning. Lesions to the dopaminergic afferents to the output layer (DA–PMC/BG) impair the ability to build stimuli responses mappings, and models perform at chance, that is, all responses have the same probability of being executed. On the other hand, lesions to the PFC dopamine afferents only impair the acquisition of DMTS and ER, both tasks containing non-linear separable input patterns. Disruption of Hebbian learning at the input structures and top-down inhibition mechanisms does not affect the learning of simple operant tasks neither DMTS. In contrast, ER cannot be learned if any of the mechanisms here lesioned are not working properly. Dashed line indicates chance level.
Lesions to the dopamine system were simulated by inhibiting the VTA/SN block output. Dopamine signal (P) affects both, learning and excitability in the PFC and the BG–PMC structures. We produced independent lesions to the dopamine–PFC system and to the dopamine–PMC/BG system.
Lesions to the dopamine–PMC/BG systems impair the ability to reinforce stimulus–response paths and, as a consequence of that, the models perform at chance no matter what the tasks are. On the other hand, lesions to the dopamine–PFC system impair the acquisition of complex tasks, like DMTS and ER, keeping intact the ability of acquiring the simple ones. For simple operant tasks, like pressing a level to receive reward (OPER) or to discriminate two different visual stimuli (VD), models of the ensemble perform significantly better than chance. This result is consistent with the linear separability of the patterns involved in each task (Roychowdhury et al., 1995; Lew et al., 2008).
Disruptions to Hebbian learning mechanisms at the input structure of the model decrease the probability of learning ER. Simulations were performed by setting the value of vITC, which is the parameter that controls Hebbian learning rates at the input layer, to zero. Despite the fact that the lesioned models did not learn ER, the performances in operant learning, VD, and DMTS were significantly higher than chance, as can be seen in Figure 8. The models performed as if they were stimulus specific mappings. In this sense, it is known that lesions of the parahippocampal gyrus, which contains the perirhinal and entorhinal cortices and where associative visual memory formation is found (Naya et al., 2001), impair the formation and retrieval of associative memories in human subjects (Weniger et al., 2004; Gold et al., 2006).
In monkeys, transection of the posterior corpus callosum and the anterior commissure, severely impairs the performance in a delayed pair associated paradigm by means of a lack in top-down inhibition (Tomita et al., 1999). This kind of lesions gives us an insight about the function of feedback projection from the frontal lobe over visual structures, while learning and recalling associative memories. We simulated this lesion by disrupting top-down inhibition in the models and computing their performances during the last part of the training phase. Operant learning, VD, and DMTS tasks could be learned with performances higher than chance as it is shown in Figure 8. However, as in the rest of the simulated lesions, ERs did not emerge as a consequence of learning simple conditional rules.
In terms of the subject performances, it is reasonable to think that VD, DMTS, and ER tasks posses increasing levels of complexity. In a previous work (Lew et al., 2008) we have shown how the PFC and the PMC–BG can interact in order to allow simple (VD) and complex (DMTS) tasks learning. Here, we include in that model three mechanisms, Hebbian learning and lateral interactions at the input stage and top-down inhibition, which allow ERs learning.
Discussion
Among the large variety of primates, human is the unique species that can develop a formal language. Whether building logic categories of equivalent stimuli is a necessary condition or a consequence of the ability to acquire formal languages still remains to be elucidated. However, it has been shown that these capabilities emerge concurrently in human subjects who have the ability to communicate at least using signs.
We introduced a computational model that explains how ERs of unrelated visual stimuli can be learned as a consequence of the reinforced training of simple conditional rules.
Unlike other computational models that learn ER between stimuli (Martin et al., 2008; García et al., 2010), our model proposes the biological mechanisms that give to the system a new emergent property: the ability to learn ERs from the training of simple conditionals.
It is important to note that the model is also able to learn many other relevant behavioral paradigms like simple operant learning, VD and, of course, DMTS. Not all of these behaviors need all the structures and mechanisms involved in the model presented here. Operant learning can be learned by means of an input structure, a dopaminergic system that rules Hebbian or anti-Hebbian learning and an output structure that executes behavioral responses (Lew et al., 2001). However, that model is not able to learn paradigms where the stimuli are not linearly separable, as in DMTS. The addition of a PFC-like structure to the model, with neurons that adapt their synaptic weights by means of Hebbian rule, provides the system with the capability of learning this kind of paradigms (Lew et al., 2008). Adding Hebbian learning at the input structures and top-down inhibition brings ability of learning ERs. This sequence of improvements can explain from an evolutionary point of view, how new nervous structures allow learning more complex paradigms.
In our model, functional blocks representing neuroanatomic structures as the main components of the visual pathway, the lateral prefrontal cortex, dopaminergic, and noradrenergic areas, interact in order to learn correct behavioral responses. Also, Hebbian-like association learning at the visual stages and top-down modulation of PFC and motor-related neurons over visual inputs are included as a key component in the learning of logic categories.
We showed how disrupting these mechanisms impacts over the performance of the system in operant tasks, DMTS, and ER paradigms. In the case of dopaminergic afferents to the output structures, lesioning the dopamine system undermines the ability to learn stimulus specific relations. On the other hand, simple operant tasks including VD can be learned if the lesion only affects dopaminergic afferent to the PFC-like structure. Both types of lesions impair the acquisition of paradigms where there exists non-separability of the input patterns, as can be found in DMTS and ER.
On the contrary, lesions to the Hebbian learning mechanisms impair the ability of learning ER while the performance in DMTS remains almost unaffected. In this way, this mechanism appears to be necessary for the learning of paradigms where rule extraction and concept learning are involved. Rule extraction and concept learning result in a reduction in the number of active PFC neurons in the last phase of DMTS training and ER testing.
Finally, top-down inhibition degradation showed the deterioration of both, the DMTS and ER performances.
Summarizing, none of the mechanisms here proposed as necessary for ER emergence affect the abilities to learn paradigms where rule extraction can be replaced by specific stimuli–response mappings. However, in the light of our results, all of them are required if the emergence of ER is expected as a consequence of the learning of simple conditional rules.
The model suggests that a minimal structural complexity is necessary to allow the emergence of ERs after learning simple conditional rules. In fact, as it is shown in Figure 7, the number of ensemble models that learn ERs depends on the number of PFC neurons. However, it is also shown that the maximum number of neurons used to codify all the rules contained in an ER remains fixed.
It is reasonable to ask why, in spite of the fact that the mechanisms we proposed as necessary for ER learning exist in the primate brain; the only subjects able to learn ER are human beings with language abilities. Our results suggest two possible answers to this question. First, the emergence of ERs occurs after some overtraining in a DMTS task. It would be interesting to test if overtraining improves the emergence of ER in human subjects with language disabilities. Second, there exists a region in the parametrical space which rules top-down inhibition as well as Hebbian learning and lateral interaction. In such region, VD, DMTS, and ER can be learned. Although the model showed a robust behavior against perturbations of those parameters, the lack of top-down inhibition and Hebbian learning severely impacts on the learning of complex tasks as well. It is, then, reasonable to think that a balance between them is required in order to learn VD and DMTS tasks before ER can emerge as a consequence of that learning.
Regarding the number of necessary neurons to learn the ERs, it is important to note the dynamics of this value. As can be seen in Figure 6, more than 10 neurons (average) are necessary to learn the ER, but after overtraining, this number of neurons decreases to eight for approximately 150 trials. Even though during overtraining there are no changes in the performance in DMTS, the performance in ERs tests improves progressively. It is important to note that when this performance reaches a plateau, the number of neurons decreases to four; half of the neurons that are needed to learn stimulus specific simple conditionals. Learning ERs that arise from the reinforcing of simple conditionals rules requires a large number of neurons at the beginning of the training phase. After the ER is learned, the number of recruited neurons necessary to map the relations is reduced to the minimum value.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Glossary and Parameters

Acknowledgments
Supported by PICT 2485 and UBACYT I027. We wish to thank Dr. Max Valentinuzzi, Michelle Bridger, and Fabiana Vega for their helpful comments.
References
Aston-Jones, G., and Cohen, J. D. (2005). An integrative theory of locus coeruleus-norepinephrine function: adaptive gain and optimal performance. Annu. Rev. Neurosci. 28, 403–450.
Berridge, C. W., and Waterhouse, B. D. (2003). The locus coeruleus-noradrenergic system: modulation of behavioral state and state-dependent cognitive processes. Brain Res. Rev. 42, 33–84.
Cohen, J. D., McClure, S. M., and Yu, A. J. (2007). Should I stay or should I go? How the human brain manages the trade-off between exploitation and exploration. Philos. Trans. R. Soc. Lond. B Biol. Sci. 362, 933–942.
Devany, J. M., Hayes, S. C., and Nelson, R. O. (1986). Equivalence class formation in language-able and language-disabled children. J. Exp. Anal. Behav. 46, 243–257.
Durstewitz, D., Seamans, J. K., and Sejnowski, T. J. (2000). Dopamine-mediated stabilization of delay-period activity in a network model of prefrontal cortex. J. Neurophysiol. 83, 1733–1750.
Ekstrom, L. B., Roelfsema, P. R., Arsenault, J. T., Bonmassar, G., and Vanduffel, W. (2008). Bottom-up dependent gating of frontal signals in early visual cortex. Science 321, 414–417.
García, A., Hernández, J. A. M., and Gutiérrez Domíng, M. T. (2010). A computational model for the formation of equivalence classes. Int. J. Psychol. Psychol. Ther. 10, 163–176.
Gold, J., Hopkins, R. O., and Squire1, L. R. (2006). Single-item memory, associative memory, and the human hippocampus. Learn. Mem. 13, 644–649.
Hayes, S. C. (1989). Non-humans have not yet shown stimulus equivalence. J. Exp. Anal. Behav. 51, 385–392.
Kastak, C. R., Schusterman, R. J., and Kastak, D. (2001). Equivalence classification by California sea lions using class-specific reinforcers. J. Exp. Anal. Behav. 76, 131–158.
Lew, S. E., Rey, H. G., Gutnisky, D. A., and Zanutto, B. S. (2008). Differences in prefrontal and motor structures learning dynamics depend on task complexity: a neural network model. Neurocomputing 71, 2782–2793.
Lew, S. E., Wedemeyer, C., and Zanutto, B. S. (2001). “Role of unconditioned stimulus prediction in the operant learning: a neural network model,” in Proceedings of IJCNN ’01, Washington DC, 331–336.
Lewis, B. L., and O’Donnell, P. (2000). Ventral tegmental area afferents to the prefrontal cortex maintain membrane potential ‘up’ states in pyramidal neurons via D(1) dopamine receptors. Cereb. Cortex 10, 1168–1175.
Martin, H. J. A., Santos, M., García, A., and de Lope Asiaín, J. (2008). “A computational model of the equivalence class formation psychological phenomenon,” in Innovations in Hybrid Intelligent Systems, eds C. Emilio, C. M. Juan, and E. A. Ajith Salamanca, 44, 104–111.
Mink, J. W. (1996). The basal ganglia: focused selection and inhibition of competing motor programs. Prog. Neurobiol. 50, 381–425.
Naya, Y., Yoshida, M., and Miyashita, Y. (2001). Backward spreading of memory-retrieval signal in the primate temporal cortex. Science 291, 661–664.
O’Reilly, R. C., Noelle, D. C., Braver, T. C., and Cohen, J. D. (2002). Prefrontal cortex and dynamic categorization tasks: representational organization and neuromodulatory control. Cereb. Cortex 12, 246–257.
Paladini, C. A., and Williams, J. T. (2004). Noradrenergic inhibition of midbrain dopamine neurons. J. Neurosci. 24, 4568–4575.
Pan, W. X., Schmidt, R., Wickens, J. R., and Hyland, B. I. (2005). Dopamine cells respond to predicted events during classical conditioning: evidence for eligibility traces in the reward-learning network. J. Neurosci. 25, 6235–6242.
Rapanelli, M., Lew, S. E., Frick, L., and Zanutto, B. S. (2010). Plasticity in the rat prefrontal cortex: linking gene expression and an operant learning with a computational theory. PLoS ONE 5, e8656.
Rescorla, R. A., and Wagner, A. R. (1972). “A theory of Pavlovian conditioning: variations in the effectiveness of reinforcement and non-reinforcement,” in Classical Conditioning II: Current Research and Theory, eds A. H. Black, and W. F. Prokasy (New York: Appleton Century Crofts), 64–99.
Rey, H. G., Lew, S. E., and Zanutto, B. S. (2007). “Dopamine and norepinephrine modulation of cortical and sub-cortical dynamics during visuomotor learning,” in Monoaminergic Modulation of Cortical Excitability, eds K. Y. Tseng, and M. Atzori (Springer), 247–260.
Reynolds, J. N. J., and Wickens, J. R. (2002). Dopamine-dependent plasticity of corticostriatal synapses. Neural Netw. 15, 507–521.
Roychowdhury, V. P., Siu, K.-Y., and Kailath, T. (1995). Classification of linearly non-separable patterns by linear threshold elements. IEEE Trans. Neural Netw. 6, 318–331.
Saalmann, Y. B., Pigarev, I. N., and Vidyasagar, T. R. (2007). Neural mechanisms of visual attention: how top-down feedback highlights relevant locations. Science 16, 1612–1615.
Schmajuk, N., and Zanutto, B. S. (1997). Escape, avoidance, and imitation: a neural network approach. Adapt. Behav. 6, 63–129.
Schultz, W., Dayan, P., and Montague, P. R. (1997). A neural substrate of prediction and reward. Science, 275, 1593–1599.
Sidman, M., Rauzin, R., Lazar, R., Cunningham, S., Tailby, W., and Carrigan, P. (1982). A search for symmetry in the conditional discriminations of rhesus monkeys, baboons, and children. J. Exp. Anal. Behav. 37, 23–44.
Sidman, M., Wynne, C. K., Maguire, R. W., and Barnes, T. (1989). Functional classes and equivalence relations. J. Exp. Anal. Behav. 52, 261–274.
Suzuki, W. A., Miller, E. K., and Desimone, R. (1997). Object and place memory in the macaque entorhinal cortex. J. Neurophysiol. 78, 1062–1081.
Taylor, P. C., Nobre, A. C., and Rushworth, M. F. (2007). FEF TMS affects visual cortical activity. Cereb. Cortex 17, 391–399.
Tomita, H., Ohbayashi, M., Nakahara, K., Hasegawa, I., and Miyashita, Y. (1999). Top-down signal from prefrontal cortex in executive control of memory retrieval. Nature 401, 699–703.
Tseng, K. Y., Mallet, N., Toreson, K. L., Le Moine, C., Gonon, F., and O’Donnell, P. (2006). Excitatory response of prefrontal cortical fast-spiking interneurons to ventral tegmental area stimulation in vivo. Synapse 59, 412–417.
Tseng, K. Y., and O’Donnell, P. (2007). D2 dopamine receptors recruit a GABA component for their attenuation of excitatory synaptic transmission in the adult rat prefrontal cortex. Synapse 61, 843–850.
Usher, M., Cohen, J. D., Servan-Schreiber, D., Rajkowski, J., and Aston-Jones, G. (1999). The role of locus coeruleus in the regulation of cognitive performance. Science 283, 549–554.
Keywords: language, neural network, equivalence relations
Citation: Lew SE and Zanutto BS (2011) A computational theory for the learning of equivalence relations. Front. Hum. Neurosci. 5:113. doi: 10.3389/fnhum.2011.00113
Received: 01 May 2010; Accepted: 19 September 2011;
Published online: 18 October 2011.
Edited by:
Ivan Toni, Radboud University, NetherlandsReviewed by:
Ivan Toni, Radboud University, NetherlandsFrank Leone, Radboud University, Netherlands
Copyright: © 2011 Lew and Zanutto. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Sergio E. Lew, Instituto de Ingeniería Biomédica, Universidad de Buenos Aires, Paseo Colon 850, Buenos Aires, Argentina. e-mail:c2VyZ2lvbGV3QGdtYWlsLmNvbQ==

