- Center of Cognitive Neuroscience, Institute of Psychology, Catholic University of Louvain, Louvain-la-Neuve, Belgium
Studies on developmental dyscalculia (DD) have tried to identify a basic numerical deficit that could account for this specific learning disability. The first proposition was that the number magnitude representation of these children was impaired. However, Rousselle and Noël (2007) brought data showing that this was not the case but rather that these children were impaired when processing the magnitude of symbolic numbers only. Since then, incongruent results have been published. In this paper, we will propose a developmental perspective on this issue. We will argue that the first deficit shown in DD regards the building of an exact representation of numerical value, thanks to the learning of symbolic numbers, and that the reduced acuity of the approximate number magnitude system appears only later and is secondary to the first deficit.
Developmental dyscalculia (DD) is a persistent and specific disorder of the numerical development and mathematical learning. In the recent years, several authors have proposed that DD arises from a fundamental impairment in the representation of number magnitudes (e.g., Butterworth, 1999, 2005; Wilson and Dehaene, 2007). In this paper, we will argue that the first deficit shown in DD does not support the hypothesis of an impairment at that level. Rather, we will argue that the first deficits of DD regards the construction of an exact representation of numerical value, that builds on the acquisition of symbolic number meaning1. The reduced acuity of the approximate number magnitude system would only appear later and would be secondary to the first deficit.
According to what we will call the simple story, babies are born with an innate analog magnitude system specifically tuned to numerical information (Xu and Spelke, 2000; Lipton and Spelke, 2003, 2004; Xu, 2003; Feigenson et al., 2004; Xu et al., 2005). This system yields approximate, noisy representations and is thus called the approximate number system or ANS. Throughout the development, the acuity of that system increases (Halberda and Feigenson, 2008). When the child learns the number words in the counting routine, these symbols take their meaning from the connections they establish with this ANS (Dehaene, 1992; Gallistel and Gelman, 1992; Dehaene and Cohen, 1995, 1997). Finally, this ANS would also be crucial for more advanced numerical learning as individual differences in the acuity of that representation correlate with mathematics achievement (Halberda et al., 2008). Accordingly, some researchers have argued that DD could result from a core dysfunction of that representation (Butterworth, 1999, 2005; Landerl et al., 2004; Wilson and Dehaene, 2007). Indeed, several authors found that, when comparing sets of dots, DD children showed less sensitivity to numerical differences than control children, thus showing a reduced number acuity (Piazza et al., 2010; Mazzocco et al., 2011). Similarly, Mussolin et al. (2010) observed that DD children were slower and less accurate than control children when comparing small and close numerosities. Finally, using a free estimation production task with completely non-symbolic input and output, Mejias et al. (in press) observed that the estimates produced by DD children were less precise and more variable that those of typically achieving children (see also Mazzocco et al., 2011 for similar observations). All these data thus support the hypothesis of a deficient ANS in DDs.
However, a number of researches brought data that are inconsistent with this view. First, in unselected populations, performance in the comparison of two sets of dots failed to account for individual difference in mathematics (Holloway and Ansari, 2009; Mundy and Gilmore, 2009). Second, when comparing the magnitude of two sets of dots, a series of studies (Rousselle and Noël, 2007; Iuculano et al., 2008; Landerl and Kölle, 2009; De Smedt and Gilmore, 2011) failed to find any difference between the performance of DD and control children. However, in all these studies, DD children displayed significant impairment in Arabic number comparison and calculation. Accordingly, Rousselle and Noël (2007) proposed that the central deficit in DD children would not be a defect of the ANS itself but rather in accessing the numerical magnitude information conveyed by symbols such as Arabic numbers or number words.
How can we account for this contradictory pattern of results? We could first consider the type of measure used. For instance, Piazza et al. (2010) and Mazzocco et al. (2011) measured the acuity of the ANS by calculating the index w. Such a method was not used by the other authors. However, among those who measured a distance effect, another indicator of the precision of the ANS, some found significant difference between DD and control children (e.g., Price et al., 2007; Mussolin et al., 2010) and some did not (e.g., Landerl and Kölle, 2009; De Smedt and Gilmore, 2011). If we list all the studies that have compared DD and control children’s ability to process the magnitude of non-symbolic (i.e., dot collections) or symbolic numbers (Arabic digits or number words) and order them according to the age of the children tested (see Table 1), a clear picture emerges. First, at all ages, DD children perform significantly lower than controls in the magnitude comparison tasks using symbolic numbers. Second, for tasks using non-symbolic numbers, a dissociation appears between the studies which tested younger (6–9 years old) versus older children (10 years old and above): only the latter showed some significant difference2. Thus, the first deficit seen in DD children is specific to the magnitude processing of symbolic numbers. Dyscalculia children’s deficit in processing non-symbolic number magnitude only appears later, on a second time.
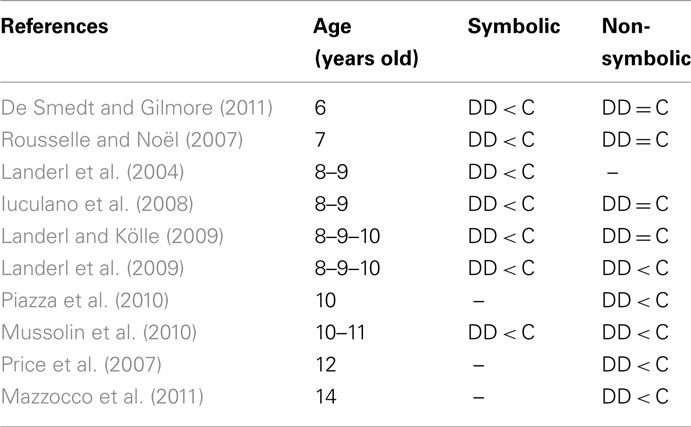
Table 1. Comparison of the performance of DD and Control children in the symbolic or non-symbolic number comparison.
Given the changing profile of DD according to their age, a developmental perspective must be adopted. However, considering this picture, it should be acknowledged that the simple story can not easily explain why DD children would have a first difficulty with number symbols and only later with the ANS, especially if we consider than the meaning of number symbols is learned through the mapping with the ANS. At this point, it is thus necessary to consider other theoretical perspectives.
More and more recent developmental data support the idea that the meaning of number words is not gained through the simple mapping between these number words and the ANS. First, if the child simply has to map number symbols to the ANS, why would it take so long before he/she understands the meaning of the number words? At least a year elapses between the time a child is able to recite the counting sequence and the moment he/she comes to understand the cardinal value of the verbal numerals in the sequence (as demonstrated by succeeding at tasks such as “What is on this card?” or “Give me n items”; Wynn, 1992). Second, young children who do not yet understand the precise meaning of the number words in their counting sequence do not show the typical characteristics of ANS when required to estimate the number of items in a set (Lipton and Spelke, 2005; Le Corre and Carey, 2007).
For these reasons, another set of theories has been put forward which argue that the learning of symbolic numbers would lead to the emergence of a new numerical representation system in human ontogeny (see Carey, 2001, 2004; Wiese, 2003b, 2007; Noël et al., 2008). Endowed with a semantic content based on the ordinal information enclosed in the symbol sequence, this new representation would allow representing exact numerical value, contrary to the ANS which is only an approximate representation of number magnitude.
Carey’s (2001, 2004, 2009) developmental model perfectly illustrates this standpoint. She proposes that representations of natural numbers are first built on a “parallel individuation” system allowing babies to keep track of the items in a small set through mental models which encode their spatio-temporal properties (Kahneman et al., 1992; Trick and Pylyshyn, 1994; Simon, 1997). Indeed, contrarily to the ANS, the parallel individuation system provides an exact, although implicit, representation of small numerosities and, by creating a mental model for each new element, provides a natural representation of the operation of “adding one” to an array. The capacity to represent ordered relations, and the sensitivity to syntactico-semantic markers of quantification present in language, could also play a significant role in this developmental step (see also Wiese, 2003a,b; Sarnecka et al., 2007). All these tools would help children gradually learn the meaning of the number words one, then a few months later two, then again a few months later three, and then four. As this parallel individuation system is very limited and only allows the child to track 3 or 4 items in parallel, another processing is required for the next developmental step.
At this point, the child has to discover that the cardinal value of a number word is determined by its order on the list, and that successive numbers are related by the function “+1”: For any known number n in the list, the value of the next number is n + 1. This successor function is probably worked out by induction on the basis of the child’s knowledge of the cardinal meaning of one, two, three, and four. Sarnecka and Carey (2008) have shown that this conceptual jump is, at least, a two-stage process. First, children understand that adding one item to a set leads to a cardinal which is labeled by a word further away in the counting list than the word denoting the initial cardinal. Second, children understand that adding one item to a set leads to a cardinal labeled by the word just after the one used to tag the initial cardinal. At this point, children master the successor function and have discovered how verbal numerals represent the natural numbers.
In Carey’s view, it is only after children have created this new representation of exact numbers that they start to map it with the ANS (see Le Corre and Carey, 2007) and thus establish connections between the old, approximate representation of number magnitude and the new, exact representation of natural numbers (see Figure 1).
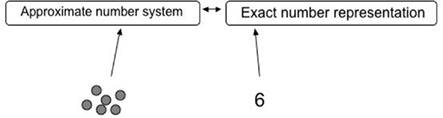
Figure 1. A two semantic number representation model with an approximate representation for non-symbolic numbers and an exact representation for symbolic numbers.
This distinction between an approximate and an exact representation is also consistent with cross-cultural evidence showing that adults leaving in cultures with very limited number lexicon and no counting system are unable to develop an exact representation of numbers beyond 3 or 4, although their ANS is quite normal (Gordon, 2004; Pica et al., 2004). Similarly, deaf adults leaving in numerate communities who have developed their own signs for numbers but not embedded in a counting system do not develop representations of large exact numerosities (Spaepen et al., 2011). In summary, although we share an ANS with animals, it is only if we have the chance to learn a number system based on the successor function and embedded in a counting process that we can develop an exact representation of large numbers which is the basis of exact mathematics.
How can this developmental perspective shed light on the data of DD? As we saw, the first difficulties seen in DD children concern the processing of symbolic number magnitude. Accordingly, we propose that the first difficulty of DD children is to develop an exact representation of natural numbers. As for the first numbers, this representation is assumed to build on the parallel individuation system, DD children’s difficulty to elaborate an exact numerical representation could originate from the limitation of this parallel tracking system, as manifested by the reduction of the subitizing range in children with DD (see Koontz and Berch, 1996; Schleifer and Landerl, 2011). But this initial limitation is probably not the only difficulty they would encounter in constructing an exact numerical representation. Later, the induction process needed to discover the successor function might also be impaired in DD children.
In Carey’s (2004, 2009) model, once the child has developed an exact representation of natural numbers, he/she starts to connect it with the ANS. Because the representation of natural numbers is precise, some authors have assumed that its mapping onto the ANS would increase the precision of that intrinsically approximate system (see Halberda et al., 2008; Piazza et al., 2010). Indeed, change in number acuity are seen throughout the child’s development (going from a w = 0.525 at age 3 to a w = 0.179 at age 6) up to adulthood (w = 0.108, Halberda and Feigenson, 2008). Of course, these changes might be due to natural brain maturation but concurrently, they might be stimulated by the manipulation, processing, and calculation of exact numbers. In the same way as color names in language defines category boundaries which influence color perception (Regier and Kay, 2009), the existence of number words referring to exact numerosities could in turn shape the perceived boundaries between numerosities at the non-symbolic level. In fact, the same kind of reciprocal influence has long been recognized in reading development: phonological abilities facilitate the development of reading but reading in turn improves phonological sensitivity as well (Perfetti et al., 1987; Bentin and Leshem, 1993; Burgess and Lonigan, 1998).
Such a hypothesis could explain why an initial difficulty with symbolic numbers and the manipulation of exact number processing would prevent DD children from refining their ANS in the same way as typically developing children do. This inefficient refinement would predict a slower growth of number acuity in DD children. This delayed maturation of number acuity would lead to increasing difference in number acuity between DD and control children over development. Thus, while only small and non-significant differences between DD and control children are measured in tasks tapping the precision of the ANS in young populations, larger and significant differences are reported in populations of older children.
To sum up, the simple story fails to give a plausible account for the developmental trajectory of the basic deficits actually reported in DD children. Here we argue that developmental theories assuming the construction of an exact representation of symbolic numbers (based on the ordinal properties of numbers in the counting sequence) offer a more powerful explanation for the pattern of results actually depicted in the literature. Considering the developmental course of DD children’s impairments, we hypothesize that their first deficit, manifested in symbolic number processing tasks, would result from a basic dysfunction in the building process of this exact representation of symbolic numbers. Appearing later, the reduced acuity of the ANS would be the consequence, rather than the cause, of this first deficit.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The two authors of this paper are supported by the National Research Fund of Belgium.
Footnotes
- ^In this paper, the terms “symbolic numbers” must be understood as every symbols that bear a precise cardinal meaning and that are part of an ordered sequence. In typical development, the first symbols referring to a precise numerosity are certainly verbal number words but in other culture, it could be body part counting for example.
- ^Let us however note a difference in the profiles obtained by Landerl et al. (2009) and by Landerl and Kölle (2009). Although they used the same tasks and the same age range for participants, only the first one showed slower RTs in the non-symbolic magnitude comparison task. The only difference between the studies is that the cutoff criteria to define MLD is 1 SD below the mean in the first one and 1.5 SD below the mean in the second one.
References
Bentin, S., and Leshem, H. (1993). On the interaction between phonological awareness and reading acquisition: it’s a two-way street. Ann. Dyslexia 43, 125–148.
Burgess, S. R., and Lonigan, C. J. (1998). Bidirectional relations of phonological sensitivity and prereading abilities: evidence from a preschool sample. J. Exp. Child. Psychol. 70, 117–141.
Butterworth, B. (2005). “Developmental dyscalculia,” in Handbook of Mathematical Cognition, ed. J. I. D. Campbell (New York: Psychology Press), 298–318.
Carey, S. (2001). Cognitive foundations of arithmetic: evolution and ontogenesis. Mind Lang. 16, 37–55.
Carey, S. (2009). The Origin of Concepts (Oxford series in cognitive development). New York: Oxford University Press.
De Smedt, B., and Gilmore, C. K. (2011). Defective number module or impaired access? Numerical magnitude processing in first graders with mathematical difficulties. J. Exp. Child. Psychol. 108, 278–292.
Dehaene, S., and Cohen, L. (1995). Towards an anatomical and functional model of number processing. Math. Cogn. 1, 83–120.
Dehaene, S., and Cohen, L. (1997). Cerebral pathways for calculation: double dissociation between rote verbal and quantities knowledge of arithmetic. Cortex 33, 219–250.
Feigenson, L., Dehaene, S., and Spelke, E. (2004). Core systems of number. Trends Cogn. Sci. (Regul. Ed.) 8, 307–314.
Gallistel, C. R., and Gelman, R. (1992). Preverbal and verbal counting and computation. Cognition 44, 43–74.
Halberda, J., and Feigenson, L. (2008). Developmental change in the acuity of the “number sense”: the approximate number system in 3-, 4-, 5-, and 6-year-olds and adults. Dev. Psychol. 44, 1457–1465.
Halberda, J., Mazzocco, M. M. M., and Feigenson, L. (2008). Individual differences in non-verbal number acuity correlate with maths achievement. Nature 455, 665–668.
Holloway, I. D., and Ansari, D. (2009). Mapping numerical magnitudes onto symbols: the numerical distance effect and individual differences in children’s mathematics achievement. J. Exp. Child. Psychol. 103, 17–29.
Iuculano, T., Tang, J., Hall, C. W. B., and Butterworth, B. (2008). Core information processing deficits in developmental dyscalculia and low numeracy. Dev. Sci. 11, 669–680.
Kahneman, D., Treisman, A., and Gibbs, B. J. (1992). The reviewing of parallel individuations: object specific integration of information. Cogn. Psychol. 24, 174–219.
Koontz, K. L., and Berch, D. B. (1996). Identifying simple numerical stimuli: processing inefficiencies exhibited by arithmetic learning disabled children. Math. Cogn. 2, 1–23.
Landerl, K., Bevan, A., and Butterworth, B. (2004). Developmental dyscalculia and basic numerical capacities: a study of 8-9-year-old students. Cognition 93, 99–125.
Landerl, K., Fussenegger, B., Moll, K., and Willburger, E. (2009). Dyslexia and dyscalculia: two learning disorders with different cognitive profiles. J. Exp. Child. Psychol. 103, 309–324.
Landerl, K., and Kölle, C. (2009). Typical and atypical development of basic numerical skills in elementary school. J. Exp. Child. Psychol. 103, 546–565.
Le Corre, M., and Carey, S. (2007). One, two, three, four, nothing more: an investigation of the conceptual sources of the verbal counting principles. Cognition 105, 395–438.
Lipton, J. S., and Spelke, E. S. (2003). Origins of the number sense: large-number discrimination in human infants. Psychol. Sci. 14, 396–401.
Lipton, J. S., and Spelke, E. S. (2004). Discrimination of large and small numerosities by human infants. Infancy 5, 271–290.
Lipton, J. S., and Spelke, E. S. (2005). Preschool children’s mapping of number words to non-symbolic numerosities. Child Dev. 76, 978–988.
Mazzocco, M. M., Feigenson, L., and Halberda, J. (2011). Impaired acuity of the approximate number system underlies mathematical learning disability (dyscalculia). Child Dev. 82, 1224–1237.
Mejias, S., Mussolin, C., Rousselle, L., Grégoire, J., and Noël, M.-P. (in press). Numerical and non-numerical estimation in children with and without mathematical learning disabilities. Child Neuropsychol. http://dx.doi.org/10.1080/09297049.2011.625355
Mundy, E., and Gilmore, C. K. (2009). Children’s mapping between symbolic and non-symbolic representation of number. J. Exp. Child. Psychol. 103, 490–502.
Mussolin, C., Mejias, S., and Noël, M.-P. (2010). Symbolic and non-symbolic number comparison in children with and without dyscalculia. Cognition 115, 10–25.
Noël, M.-P., Grégoire, J., Meert, G., and Seron, X. (2008). The innate schema of natural numbers does not explain historical, cultural, and developmental differences. Behav. Brain Sci. 31, 6, 664–665.
Perfetti, C. A., Beck, I., Bell, L., and Hughes, C. (1987). Phonemic knowledge and learning to read are reciprocal: a longitudinal study of first grade children. Merrill Palmer Q. 33, 283–319.
Piazza, M., Facoetti, A., Trussardi, A. N., Berteletti, I., Conte, S., Lucangeli, D., Dehaene, S., and Zorzi, M. (2010). Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition 116, 33–41.
Pica, P., Lemer, C., Izard, V., and Dehaene, S. (2004). Exact and approximate arithmetic in an Amazonian indigene group. Science 306, 499–503.
Price, G. R., Holloway, I., Rasanen, P., Vesterinen, M., and Ansari, D. (2007). Impaired parietal magnitude processing in developmental dyscalculia. Curr. Biol. 17, R1042–R1043.
Regier, T., and Kay, P. (2009). Language, thought, and color: Whorf was half right. Trends Cogn. Sci. (Regul. Ed.) 13, 439–446.
Rousselle, L., and Noël, M.-P. (2007). Basic numerical skills in children with mathematics learning disabilities: a comparison of symbolic versus non-symbolic number magnitude processing. Cognition 102, 361–395.
Sarnecka, B. W., and Carey, S. (2008). How counting represents number: what children must learn and when they learn it. Cognition 108, 662–674.
Sarnecka, B. W., Kamenskaya, V. G., Yamana, Y., Ogura, T., and Yudovina, Y. B. (2007). From grammatical number to exact numbers: early meanings of ‘one’, ‘two’, and ‘three’ in English, Russian and Japanese. Cogn. Psychol. 55, 136–168.
Schleifer, P., and Landerl, K. (2011). Subitizing and counting in typical and atypical development. Dev. Sci. 14, 280–291.
Simon, T. J. (1997). Reconceptualizing the origins of number knowledge: a “non-numerical” account. Cogn. Dev. 12, 349–372.
Spaepen, E., Coppola, M., Spelke, E. S., Carey, S. E., and Goldin-Meadow, S. (2011). Number without a language model. Proc. Natl. Acad. Sci. U.S.A. 108, 3163–3168.
Trick, L. M., and Pylyshyn, Z. W. (1994). Why are small and large numbers enumerated differently? A limited-capacity preattentive stage in vision. Psychol. Rev. 101, 80–102.
Wiese, H. (2003a). Iconic and non-iconic stages in number development: the role of language. Trends Cogn. Sci. (Regul. Ed.) 7, 385–390.
Wilson, A. J., and Dehaene, S. (2007). “Number sense and developmental dyscalculia,” in Human Behavior, Learning, and the Developing Brain: Atypical Development, 2nd Edn, eds D. Coch, G. Dawson, and K. Fischer (New York: Guilford Press), 212–237.
Wynn, K. (1992). Children’s acquisition of the number words and the counting system. Cogn. Psychol. 24, 220–251.
Xu, F. (2003). Numerosity discrimination in infants: evidence for two systems of representations. Cognition 89, B15–B25.
Xu, F., and Spelke, E. S. (2000). Large number discrimination in 6-month-old infants. Cognition 74, B1–B11.
Keywords: developmental dyscalculia, number processing, approximate number representation, exact number representation
Citation: Noël M-P and Rousselle L (2011) Developmental changes in the profiles of dyscalculia: an explanation based on a double exact-and-approximate number representation model. Front. Hum. Neurosci. 5:165. doi: 10.3389/fnhum.2011.00165
Received: 23 August 2011;
Accepted: 27 November 2011;
Published online: 21 December 2011.
Edited by:
Daniel Ansari, The University of Western Ontario, CanadaReviewed by:
Avishai Henik, Ben-Gurion University of the Negev, IsraelGavin Price, The University of Western Ontario, Canada
Copyright: © 2011 Noël and Rousselle. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Marie-Pascale Noël, Faculté de psychologie, 10 place C. Mercier, 1348 Louvain-la-Neuve, Belgium. e-mail:bWFyaWUtcGFzY2FsZS5ub2VsQHVjbG91dmFpbi5iZQ==

