Digitoids: a novel computational platform for mimicking oxygen-dependent firing of neurons in vitro

Introduction: Computational models are valuable tools for understanding and studying a wide range of characteristics and mechanisms of the brain. Furthermore, they can also be exploited to explore biological neural networks from neuronal cultures. However, few of the current in silico approaches consider the energetic demand of neurons to sustain their electrophysiological functions, specifically their well-known oxygen-dependent firing.

Methods: In this work, we introduce Digitoids, a computational platform which integrates a Hodgkin-Huxley-like model to describe the time-dependent oscillations of the neuronal membrane potential with oxygen dynamics in the culture environment. In Digitoids, neurons are connected to each other according to Small-World topologies observed in cell cultures, and oxygen consumption by cells is modeled as limited by diffusion through the culture medium. The oxygen consumed is used to fuel their basal metabolism and the activity of Na⁺-K⁺-ATP membrane pumps, thus it modulates neuronal firing.

Results: Our simulations show that the characteristics of neuronal firing predicted throughout the network are related to oxygen availability. In addition, the average firing rate predicted by Digitoids is statistically similar to that measured in neuronal networks in vitro, further proving the relevance of this platform.

Dicussion: Digitoids paves the way for a new generation of in silico models of neuronal networks, establishing the oxygen dependence of electrophysiological dynamics as a fundamental requirement to improve their physiological relevance.

1 Introduction

Exploring how neurons process and transmit information is crucial for advancing our knowledge of the brain. Along with the study of biological neural networks in cultures or in in vitro slices (Chiappalone et al., 2019; Compte et al., 2003; Humpel, 2015; Van Pelt et al., 2005), computational, or in silico, models have been successfully exploited, e.g., to support the study of neuronal network modulation and delineate potential mechanisms underlying activity patterns (Doorn et al., 2023; Masquelier and Deco, 2013; Sukenik et al., 2021; Wen et al., 2022). Several model-based solutions for generating virtual representations of neural cells able to replicate the salient properties of experimentally observed behaviors have been proposed (Lonardoni et al., 2015). For instance, intuitive and easy to use simulators (e.g., BRIAN 2, NEST, NEURON) have been employed to simulate spiking neural network models (Gewaltig and Diesmann, 2007; Hines and Carnevale, 2001; Stimberg et al., 2019). Traditionally, they include mathematical descriptions of the single-neuron activity, ranging from simple phenomenological characterization of neuronal spiking (Izhikevich, 2003) to more complex, biophysical conductance-based simulations of ion fluxes between the intra and the extracellular space (Hodgkin and Huxley, 1952b), as well as models of cell-cell connections to replicate the neuronal network architecture (Markram et al., 2015; Masoli et al., 2022; Potjans and Diesmann, 2014). Some studies also incorporate more sophisticated models, e.g., including astrocytes via tripartite synapses (Lenk et al., 2020).

However, few of these approaches include energetic considerations, i.e., the dynamics of ATP hydrolysis (Kuznetsov, 2024; Wei et al., 2014). It is well-known that metabolism is involved in brain functionality: nutrients—and, in particular, oxygen (O₂)—fuel brain specialized functions, determining the electrophysiological dynamics and brain plasticity, up to cognitive functions (Watts et al., 2018). More specifically, beyond the basic activities common to other cells (e.g., DNA and RNA synthesis), resource uptake in neurons is also dedicated to support spiking, because of the role of the Na⁺-K⁺-ATP pump in signal propagation (Attwell and Laughlin, 2001; Lennie, 2003). Since ATP dephosphorylation depends on the rate of O₂ consumption, its dynamics can be monitored (Brosel et al., 2018; Özugur et al., 2020). O₂ dependence is also crucial for in vitro slice preparations, requiring humid and well-oxygenated environment for their culturing (Sanchez-Vives et al., 2000). An analytical formulation describing O₂-dependent firing was proposed by Wei and collaborators (Wei et al., 2014) to elucidate the mechanisms of seizure development and termination, as well as their interaction with energy metabolism. This model assumes that O₂ variations depend on the diffusion from the bath solution and on the neuronal consumption rate for firing, but it does not consider that O₂ can also be consumed for sustaining other metabolic functions of the cell (Attwell and Laughlin, 2001; Lennie, 2003).

The formulation proposed by Wei’s team was applied to brain tissue slices. However, O₂ is also crucial in in vitro cultures: for example, in traditional monolayers, cells are inevitably exposed to different O₂ levels when varying the amount of medium or the O₂ boundary concentration (Al-Ani et al., 2018; Gordon and Amini, 2021; Pacitti et al., 2019; Walsh et al., 2005). Starting from Wei et al.’s model, we have developed a computational platform able to mimic the in vitro electrophysiological behavior of neuronal cultures at the single-cell and network level. We refer to Digitoids as the digitalized versions of in vitro neuronal monolayers obtained from dissociated neurons, in which the dependence on O₂ concentration of network dynamics is considered. As in vitro networks can have different culture conditions and layouts (Antonello et al., 2022; Downes et al., 2012; Emre Kapucu et al., 2022; Hyvärinen et al., 2019), the platform is purposely designed to be modular, thus the user can generate Digitoids matching any type of in vitro neuronal network. Here we describe the theory and computational setup of Digitoids. For testing the performance and highlighting the crucial role of O₂ in describing firing dynamics in neuronal cultures, we digitalized the layouts of neuron monolayers seeded on commercial micro-electrode arrays (MEAs). The O₂-dependent model of firing and metabolism was implemented on digitalized networks to assess if a degree of similarity can be found between the Digitoids’ output and the corresponding experimental data from MEA recordings, comparing the predictivity of our platform to that of traditional models which neglect the dependence of firing activity on O₂ supply. Albeit preliminary, these results highlight the significant role of O₂ dynamics in network behaviors and thus the necessity of including energetic considerations while mathematically describing electrophysiological activity in cell cultures.

2 Materials and methods

2.1 Theory and outline of the computational platform

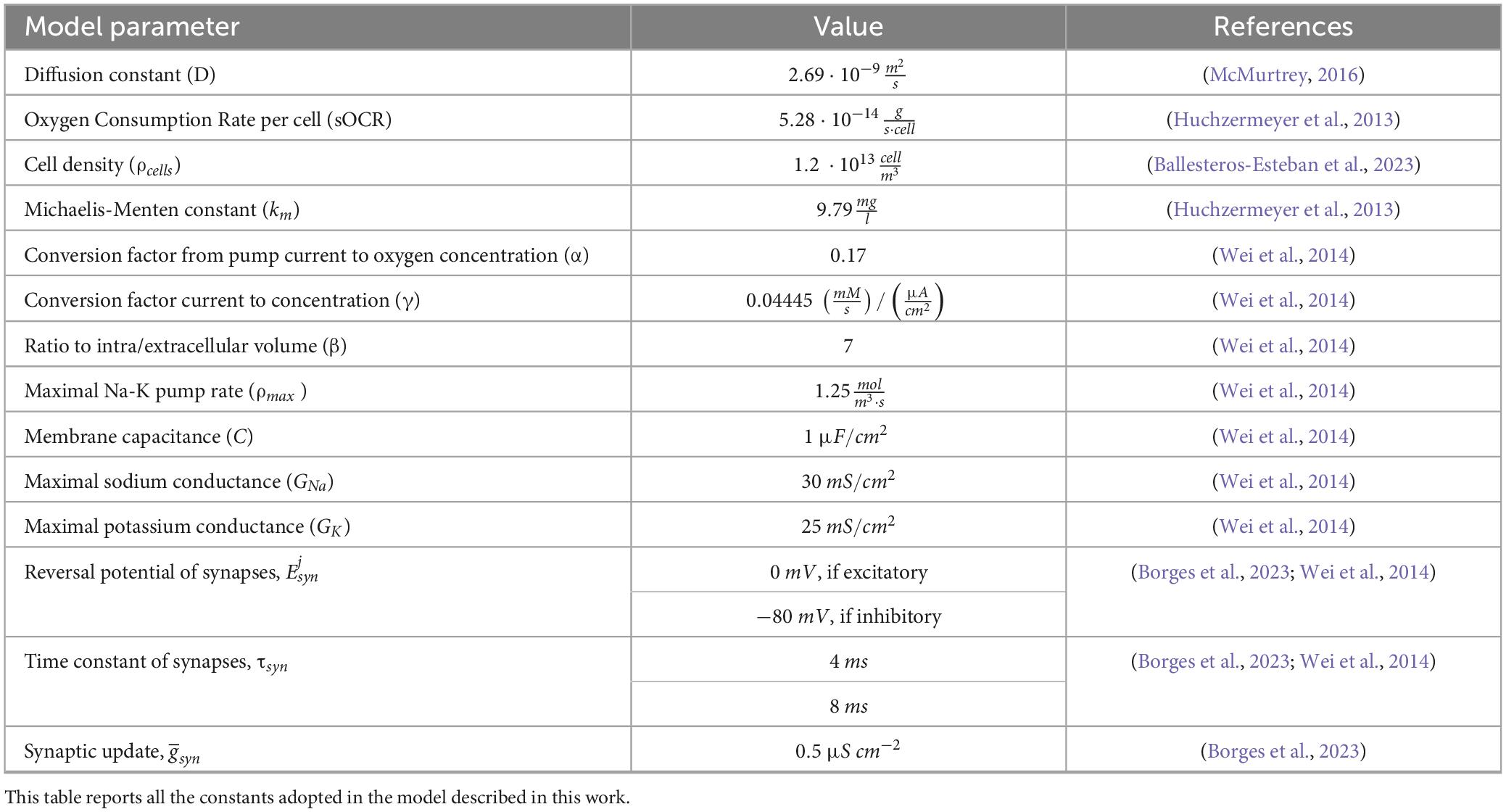
Figure 1. A shows the in vitro scenario simulated by the Digitoids. It is composed of a well seeded with neurons, supplied with a layer of culture medium of height h. The cells are assumed to be homogeneously distributed on the bottom of the well (at z = 0). Four phenomena occur in the system: i) O₂ diffusion through the medium, ii) O₂ consumption by neurons to fuel both basic cellular processes and electrophysiological activity, iii) neuron firing and iv) neural network dynamics, i.e., the transfer of electrical information via synaptic-mediated connections among cells. Considering the symmetry of the system, O₂ diffusion can be assumed to occur only along the z axis and independently of the x and y directions (McMurtrey, 2016; Patterson and Mazurek, 2010; Place et al., 2017). Each neuron at z = 0 consumes O₂ as described in the subsection 2.1.2 Single-neuron model, generating an axial concentration gradient and a consequent downward flux. Moreover, O₂ diffusion and reaction can be simulated as “background dynamics”, given that their characteristic times are significantly longer than those of the electrophysiological phenomena occurring on the x,y plane, where the neuron monolayer lies (Table 1). Transfer information is mainly influenced by the strength and number of synaptic connections between neurons. Thus, the O₂-dependent single-neuron dynamics can be decoupled from those of the network as a whole. As such, the network (Figure 1A) can be considered as the integration of modules describing the O₂ consumption—depending on its downward diffusion—as well as the firing for a single neuron (Figure 1B), modulated through the extent of its in-plane connectivity. Under these assumptions, the single-neuron metabolic and electrophysiological activity can be determined at each time step according to the O₂ concentration perceived by the cells at z = 0, which is in turn updated depending on the single-neuron consumption and allows computing the diffusive flux magnitude along the medium column. On this basis, the O₂ concentration profile at the subsequent time step can be estimated and the process iterated over time.

TABLE 1

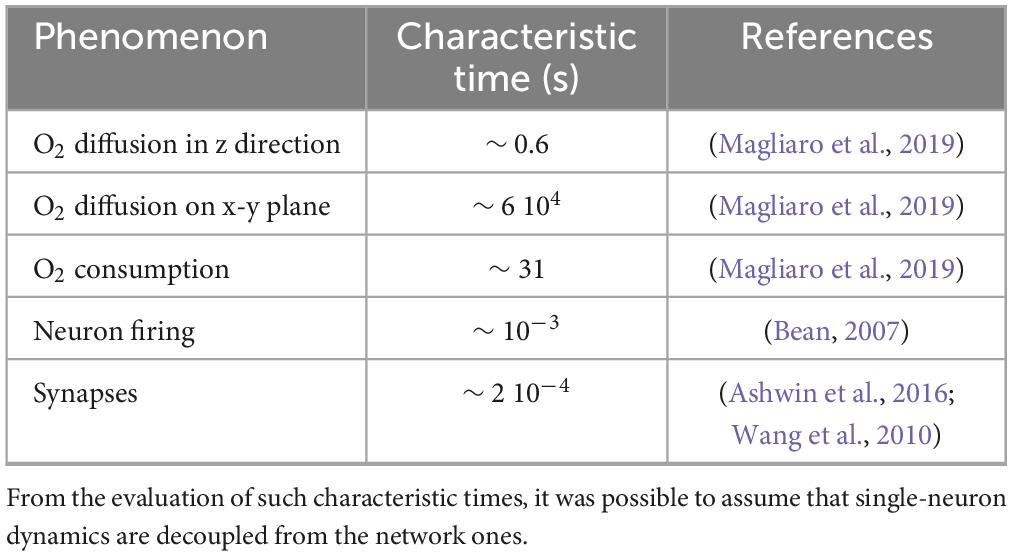
Table 1. Characteristic times of the phenomena involved in the single-neuron model: O₂ diffusion—in the x direction and in the x-y plane, O₂ consumption, neuron firing and synapses.

FIGURE 1

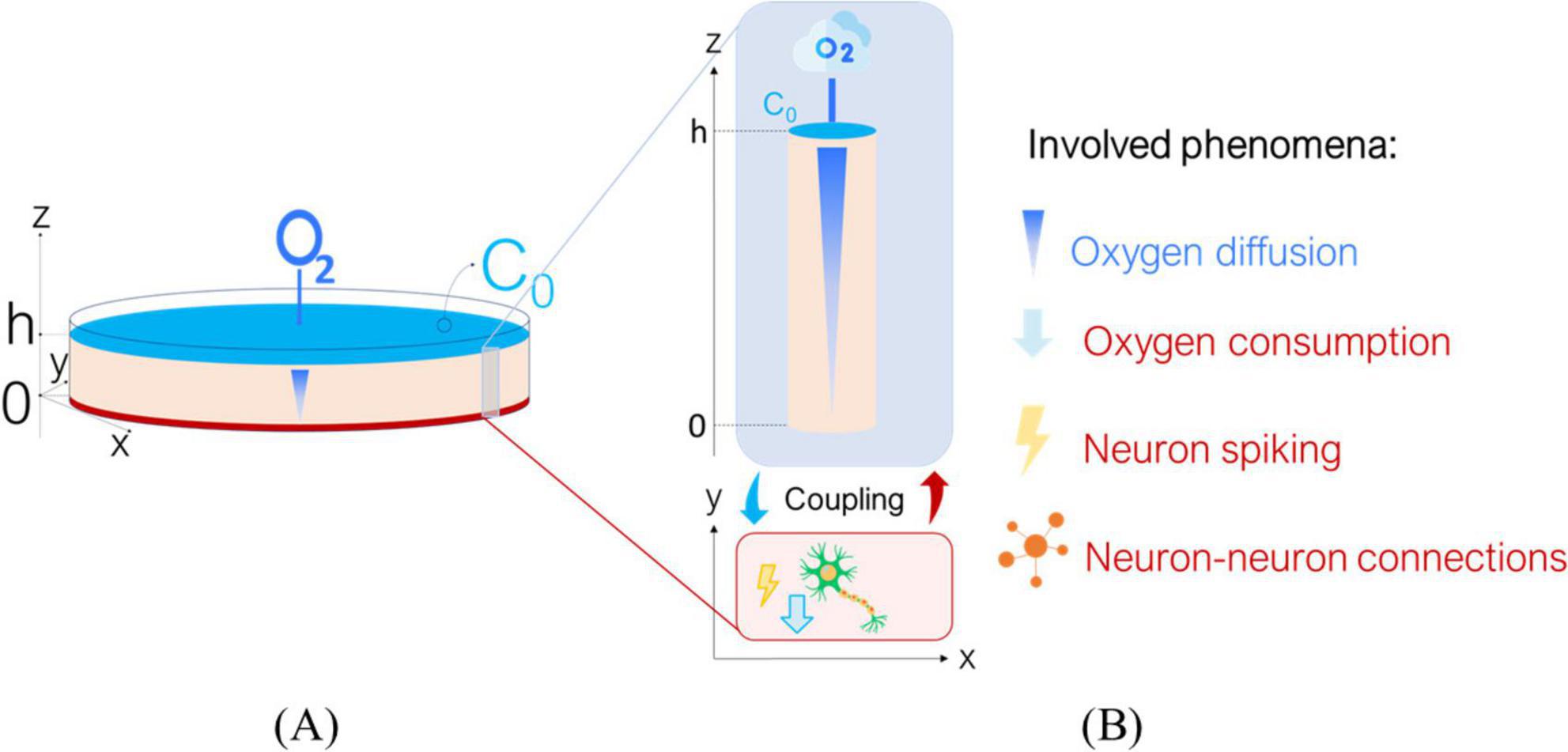
Figure 1. Overview of the Digitoids platform. (A) The in vitro scenario to be modeled: we describe a neuronal monolayer where cells are seeded at the bottom of a well, filled with culture medium reaching height h. The top layer of culture medium interfaces with air, allowing O₂ to diffuse and reach the cells, which consume it to sustain their metabolism and for firing. (B) Sketch of the coupling between O₂ diffusion through the culture medium and single-neuron activity. We assume that single-cell dynamics can be decoupled from the network ones: a neuron lies in plane x-y and is covered by a medium column of height h, where O₂ diffuses from top to the bottom along z axis. The biophysical phenomena involved are listed on the right: O₂ diffusion, O₂ consumption, neuron spiking and neuron-to-neuron connections.

The computational platform was developed in Matlab (version R2023b the Mathworks Inc., Boston Massachusetts), exploiting the Simulink toolbox.

2.1.1 Diffusion model

O₂ diffusion through the culture medium is modeled as a one-dimensional phenomenon governed by the Fick’s second law:

$\frac{\partial c}{\partial t}=D\frac{{\partial }^{2}c}{\partial z^2}(1)$

where c (mol m^–3) is the O₂ concentration and D (m² s^–1) is the diffusion constant of O₂ in the culture medium. Eq. (1) is solved using the finite difference method according to the initial and boundary conditions. Specifically, assuming that the well is initially filled with O₂-saturated culture medium, the initial condition is c(z, 0) = c₀, and the air-medium interface maintains a uniform and time-invariant O₂ concentration, i.e., c(h,t) = c₀. Note that, as neurons consume O₂ by means of a surface reaction (i.e., they sink O₂ as an outward flux through the well bottom), there is no volumetric reaction term to include in Eq. (1).

2.1.2 Single-neuron model

The single-neuron model describes the O₂ consumption for maintaining both vital and electrophysiological functions and the O₂-dependent dynamics in each cell of the network as a function of the current O₂ availability [i.e., c(0,t)] as input.

Regarding the O₂ consumption, we assume that 75% of the available O₂ is devoted to fuel neuronal spiking activity (namely, c_f = 0.75⋅c), and the remaining 25% (namely, c_nf = 0.25⋅c) to sustain basic cell processes (Attwell and Laughlin, 2001; Lennie, 2003). The O₂ consumption rate of the whole neuron network (R(c), in mol m^–3 s^–1) can be thus expressed as:

$R\left(c\right)=R_{nf}\left(c_{nf}\right)+R_f\left(c_f\right)(2)$

where R_nf(c_nf) is the rate at which O₂ is consumed for cellular and sub-cellular processes not directly linked to electrophysiological activity, and R_f(c_f) is the O₂ consumption contributing to neuron firing. Specifically, R_nf(c_nf) can be formulated according to the Michaelis-Menten kinetics (Berger et al., 2018; Magliaro et al., 2019):

$R_{nf}\left(c_{nf}\right)=\frac{sOCR\cdot {\mathrm{\rho }}_{cells}\cdot c_{nf}}{k_m+c_{nf}}(3)$

where sOCR (mol s^–1) is the maximal consumption rate of a single cell in the network, ρ_cells (m^–3) is the volumetric cell density of the monolayer and k_m (mol m^–3) is the Michaelis-Menten constant, i.e., the O₂ concentration corresponding to half saturation of the consumption rate. On the other hand, R_f(c_f) was described by Wei and co-workers (Wei et al., 2014) as:

$R_f\left(c_f\right)=\mathrm{\alpha }\cdot I_{pump}\left(c_f\right)(4)$

where I_pump (mol m^–3 s^–1) is the transport rate of ions across the membrane and α (a.u.) is a conversion factor from pump transport rate to time variation of O₂ concentration. I_pump is related to intracellular (subscript i) sodium and the extracellular (subscript o) potassium concentrations as in the following equation:

$I_{pump}=\frac{\mathrm{\rho }}{1.0+\exp \left(\frac{25-{\left[Na\right]}_i}{3}\right)}\times \frac{1}{1.0+\exp \left(5.5-{\left[K^{+}\right]}_o\right)}(5)$

in which we assume that the rate ρ (mol m^–3 s^–1) at which the pumps transport ions across the membrane depends on the O₂ concentration according to a sigmoidal function.

$\mathrm{\rho }\left(c_f\right)=\frac{{\mathrm{\rho }}_{max}}{1+{\text{exp}}^{\left(20-\frac{c_f}{3}\right)}}(6)$

In Eq. (6), ρ_max (mol m^–3 s^–1) is the maximal rate at which the pump operates, i.e., when the medium is fully oxygenated. Therefore, I_pump regulates the trans-membrane electrochemical gradient depending on the O₂ availability, which thus influences the membrane potential V (mV) and the firing activity of the neuron. The Hodgkin-Huxley (HH) model is used to describe the dynamics of V (Hodgkin et al., 1952; Hodgkin and Huxley, 1952a):

$\frac{dV}{dt}=\frac{1}{C}\left(I_{ext}-I_{Na}-I_K-I_{Cl}\right)(7)$

where C (μF cm^–2) is the membrane capacitance, I_ext (μA cm^–2) is the external applied or synaptic current from other neurons, I_Na,I_K,I_Cl (μA cm^–2) are the sodium, potassium and chloride currents. The latter corresponds to a leakage current, as it is mainly represented by flux of Cl^– ions (Hodgkin and Huxley, 1952a).

It is worth highlighting that—as in the traditional formulation of the HH model—the membrane potential V (Eq. 7) depends on the potassium and sodium currents I_Na and I_K:

${\mathrm{I}}_{Na}\approx G_{Na}{m}^{3}p\left(V-E_{Na}\right)(8)$

$\mathrm{I}\approx {}_{K}G_K{n}^4\left(V-E_K\right)(9)$

where m,p, and n are activation and inactivation variables (their description is given by Supplementary Eqs. 1–7) of voltage-gated ionic channels, whose values range from 0 to 1 and define the fraction of open and closed channels throughout the membrane. For the sake of simplicity, the non-voltage-sensitive leaks were not reported. As detailed in Eqs. (8) and (9), I_Na and I_K are in turn functions of the reversal potential E_Na and E_K, respectively, given by the Nernst equation:

$E_{Na}=26.64\ln \left(\frac{{[N{a}^{+}]}_o}{{[N{a}^{+}]}_i}\right)(10)$

$E_K=26.64\ln \left(\frac{{[K^{+}]}_o}{{[K^{+}]}_i}\right)(11)$

However, while in the HH model the intracellular concentration of sodium and the extracellular concentration of potassium are considered as constants, in this formulation they are modulated by I_pump, which is a function of the local O₂ concentration, as described through Eqs. (5) and (6). Thus, Nernst potentials of sodium and potassium (Eqs. 10 and 11) vary with O₂. All the dynamics describing neuronal functioning are here assumed to occur at 37°C, corresponding to the physiological temperature for eukaryotic cells. Intracellular sodium and extracellular potassium concentrations are in turn modulated by I_Na, I_K and I_pump, as described by the following equations (Eqs. 12 and 13):

$\frac{d{\left[K^{+}\right]}_o}{dt}=\mathrm{\gamma }\mathrm{\beta }{I}_K-2.0\mathrm{\beta }{I}_{pump}(12)$

$\frac{d{\left[N{a}^{+}\right]}_i}{dt}=-\mathrm{\gamma }{I}_{Na}-3.0I_{pump}(13)$

More details on the model are provided in the Supplementary Text 1 (Eqs. 8–10).

2.1.3 Connectivity model

The neuronal network is generated connecting the single neurons. In this study, we implemented the neuron-to-neuron coupling via chemical synapses (Roth and van Rossum, 2009). Thus, the membrane potential of the i-th neuron is described by the following equation.

$\frac{d{V}_i}{dt}=\frac{1}{C^i}\left(I_{ext}^i-I_{Na}^i-I_K^i-I_{Cl}^i+I_{syn}^i\right)(14)$

$I_{syn}^i$ in Eq. (14) is the synaptic current input to the post-synaptic neuron i and it is modeled as:

$I_{syn}^i=\sum _{\begin{array}{c}\hfill j=1\hfill \\ \hfill j\ne i\hfill \end{array}}^N{g}_{syn}^{ji}\cdot a_{ij}\cdot \left(E_{syn}^j-V_i\right)(15)$

in which we assume that the i-th neuron receives inputs from N pre-synaptic neurons. a_ij is the coefficient describing the connection between vertices i and j of the adjacency matrix A, obtained through the Watts-Strogaz method (more details in the next Section and in Supplementary Table 2). $E_{syn}^i$ (mV) is the reversal potential of the synapse for the j-th pre-synaptic neuron and can assume the following values according to the nature of the synaptic connection (Borges et al., 2023; Wei et al., 2014).

$E_{syn}^j=\{\begin{array}{c}\hfill 0mV,excitatoryconnection\hfill \\ \hfill -80mV,inhibitoryconnection\hfill \end{array}(16)$

The value of the synaptic conductance $g_{syn}^i$ (μS cm^–2) is modified every time the pre-synaptic neuron fires, i.e., every time V_i exceeds the threshold value of 0mV with a positive derivative. At each spike, there is a release of neurotransmitter into the synaptic cleft, thus the synaptic conductance over time is modeled as an exponential decay:

$g_{syn}^{ji}\left(t\right)={\overline{g}}_{syn,}^{ji}\cdot e^{-\frac{(t-t_0)}{{\mathrm{\tau }}_{syn}}}(17)$

where t₀ is the time at which the spike is fired by the pre-synaptic neuron, ${\overline{g}}_{syn}^{ji}$ is the maximal conductance value and τ_syn is the decay time constant, which assumes the following values (Wei et al., 2014).

${\mathrm{\tau }}_{syn}=\{\begin{array}{c}\hfill 4ms,\mathrm{excitatory}\mathrm{connection}\hfill \\ \hfill 8ms,\mathrm{inhibitory}\mathrm{connection}\hfill \end{array}(18)$

The synaptic dynamics are implemented in the model by updating the value of the synaptic conductance $g_{syn}^i$ as follows (Borges et al., 2023; Roth and van Rossum, 2009):

$g_{syn}^{ji}\to g_{syn}^{ji}+{\overline{g}}_{syn}(19)$

$\frac{d{g}_{syn}^{ji}}{dt}=-\frac{g_{syn}^{ji}}{{\mathrm{\tau }}_{syn}}(20)$

where ${\overline{g}}_{syn}=0.5$μS cm^–2 is the intensity of the synaptic update, the same for both excitatory and inhibitory synapses. In Digitoids, 80% of neurons are excitatory and 20% inhibitory.

2.1.4 Network model

It has been observed that the structure of neuronal networks in both brain tissues and cellular monolayers can be described by Small-World (SW) graphs (Antonello et al., 2022; Bettencourt et al., 2007; de Santos-Sierra et al., 2014). Specifically, a SW graph shows intermediate characteristics between a random and a regular graph, with dense clustering of neighboring vertices and short distances between pair of vertices. Indeed, in vivo chemical synapses typically facilitate the formation of dense local connections between neurons, thus giving rise to clusters, as well as of long-range connections allowing clusters of neurons to communicate (Bassett and Bullmore, 2006). Given a network composed of n vertices and m edges, it can be described by the metrics reported in Supplementary Table 2 (Humphries and Gurney, 2008; Watts and Strogatz, 1998).

We generated SW neural networks in a purposely developed Simulink library, which describes the wiring information through an adjacency matrix A, usually used to represent inter-neuron connections (de Santos-Sierra et al., 2014; Poli et al., 2015; Shefi et al., 2002). Starting from the number of vertices and edges and the metrics characterizing the networks, A can be obtained using the Watts-Strogatz method (Chen et al., 2007). Each coefficient of the matrix describes the connectivity between vertex i and j. Specifically, a_ij = 1 if an edge exists from vertex i to vertex j, otherwise it is 0. We thus exploited such adjacency matrices to create connections between neurons, defined by chemical synapses (Eqs. 14–20). Both the O₂ diffusion and the single-neuron models were integrated in the library, which allows defining: (i) the initial and boundary O₂ concentration c₀ at the air-medium interface, (ii) the height of the medium h, and (iii) the metabolic and firing parameters of the neuron.

2.2 Impact of oxygen on single-neuron activity

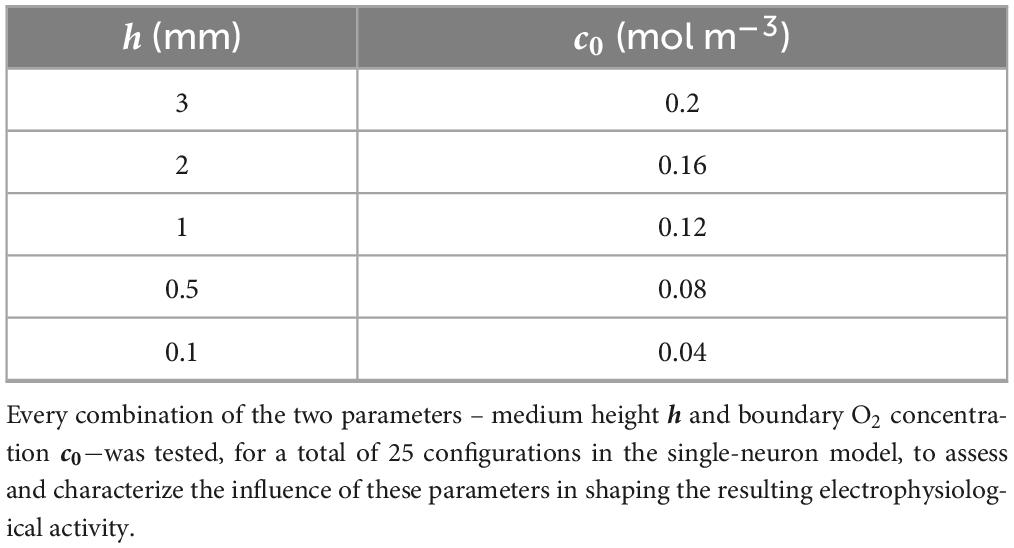
For assessing the influence of O₂ availability on firing, the single-neuron model coupled with O₂ diffusion was first computed using stepwise variations of both (i) the boundary concentration of O₂ from 0.2 mol m^–3 (i.e., the maximum available oxygen concentration in water) to 0.04 mol m^–3 [i.e., the critical oxygen concentration for cell survival (Berger et al., 2018)] and (ii) the culture medium height h from 0.1 to 3 mm, based on the conditions usually used for neuron electrophysiological recordings (Ballesteros-Esteban et al., 2023; Negri et al., 2020; Scelfo et al., 2012). All the parameter combinations were simulated for 20 s (variable step solver “ode15s” by Simulink) and are summarized in Table 2.

TABLE 2

Table 2. Values of the parameters simulated in the single-neuron configuration.

2.3 Analysis of single-neuron membrane potential

To characterize how the shape of the spike trains and the single-spike waveforms are influenced by the different combinations of c₀ and h–and, thus, by the overall O₂ availability within the system—we defined two new metrics: the Aspect Ratio (AR, expressed in logarithmically-scaled mV s^–1) and the Dissipation Rate (DR, expressed in s^–1), defined as follows:

$AR={\log }_{10}\frac{\mathrm{\Delta }{V}_{max}}{t_{train}}(21)$

$DR=\frac{\mathrm{\alpha }}{\mathrm{\Delta }{V}_{max}}(22)$

where ΔV_max is the peak-to-peak amplitude of the highest spike in the train, t_train is the time duration of the train and α (in mV s^–1) is the average value of the first derivative of the envelope of the peaks in the train. t_train was expressed as the difference between the end and start times t_end and t_start, identified as the time at which the first derivative of the signal is equal to 0 and the time at which the signal amplitude > −60 mV (Di Florio et al., 2022; Wilson and Emerson, 2002), respectively. Figure 2A reports a typical spike train, and a graphical representation of the quantities used to calculate AR and DR.

FIGURE 2

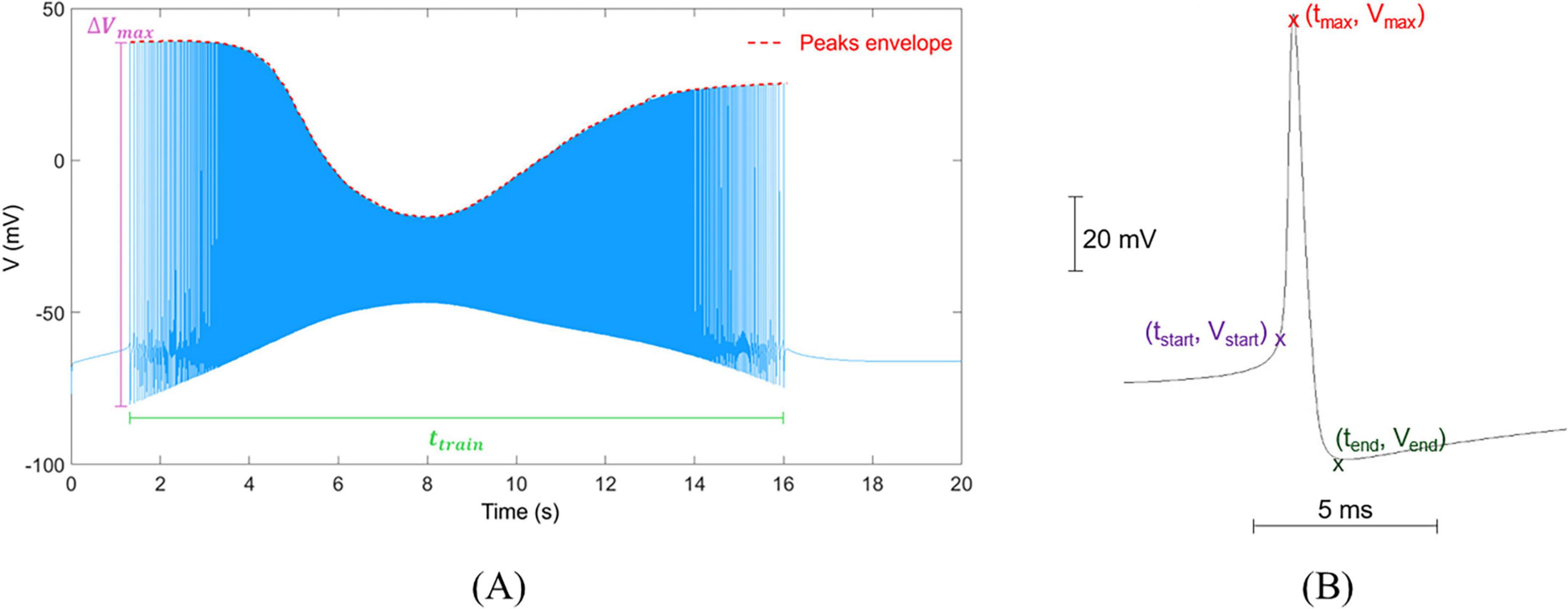
Figure 2. Visual representation of trains and single spikes, and their metrics. (A) Example of a spike train simulated for a single neuron, in which membrane voltage V (mV) varies in time (s). The plot reports the parameters used to calculate AR and DR: Δ V_max is the maximal peak-to-peak amplitude, t_train is the time duration of the train, and the peak envelope is used to calculate the average value of its first derivative, α. (B) Waveform of a single spike isolated from the train with indication of reference points for calculating its electrophysiological characteristics (v_pp, rr and fr).

We separately assessed the correlation of each of the three metrics–t_train, AR and DR—with the boundary O₂ concentration c₀ and the medium height h by computing the non-parametric Spearman coefficient (significance level of 0.05).

The shape of single spikes was also evaluated, calculating the peak-to-peak amplitude (v_pp = v_max−v_min, expressed in mV), rise rate (rr = (v_max−v_start)/(t_max−t_start), in mV s^–1) and fall rate (fr = (v_max−v_end)/(t_max−t_end) in mV s^–1), where t_max is calculated as the time corresponding to the maximum of the spike (Figure 2B; Ghaderi et al., 2018; Zaitsev et al., 2012).

Finally, to describe the features of the spikes fired by single neurons as a function of the balance between diffusive O₂ supply and its consumption by the neurons irrespective of the specific setup of the simulation, we exploited the Thiele Modulus, Φ². Specifically, Φ² is defined as the ratio between the characteristic diffusion (τ_d) and reaction (τ_r) times. Since metabolism and firing occur simultaneously in the neuron domain, the reaction dynamics is driven by the faster of the two phenomena. Given that the reaction is described by the sum of two rates (Eq. 2), Φ² can be formulated as follows:

${\mathrm{\Phi }}^2=\frac{{\mathrm{\tau }}_d}{{\mathrm{\tau }}_r}={\mathrm{\tau }}_d\left(\frac{1}{{\mathrm{\tau }}_{nf}}+\frac{1}{{\mathrm{\tau }}_f}\right)=\frac{{\mathrm{\tau }}_d\left({\mathrm{\tau }}_{nf}+{\mathrm{\tau }}_f\right)}{{\mathrm{\tau }}_{nf}\cdot {\mathrm{\tau }}_f}(23)$

where τ_nf and τ_f indicate the characteristic times of basal and firing-related O₂ consumption, respectively. Refer to Supplementary Text 2 for further details on the derivation of Eq. (23). The shape metrics of the spike trains–AR and DR−were then also evaluated as a function of Φ².

2.4 Assessment of digitoids performance

2.4.1 Digitoids versus experimental data

Digitoids performance was evaluated using the experimental data presented in Ballesteros-Esteban et al. (2023), following the pipeline shown in Figure 3. In ref. (Ballesteros-Esteban et al., 2023), the authors describe the morphology and the electrophysiological activity of neuron networks in vitro. The network activity was recorded via a MEA, and the mean Firing Rate (mFR) as well as the event synchronization were extracted. The topological evolution of the networks was mapped to a network graph, where neurons are represented as vertices and their physical connections as edges, and the SW metrics were defined. Their experimental setup and SW metrics are detailed in Supplementary Tables 1, 2, and a more in-depth description of the experimental set-up and procedures is provided in Supplementary Text 4. In our work, measurements from Day In Vitro (DIV) 11 to DIV 16—i.e., when the network exhibits a SW layout (Ballesteros-Esteban et al., 2023) —were exploited, without the intention of mapping the temporal evolution of the in vitro neuronal cultures. Given the number of vertices and edges for those DIVs reported in Ballesteros-Esteban and co-workers and the metrics characterizing the networks, the adjacency matrix was obtained through the Watts-Strogatz method, setting the rewiring probability to 0.5 (Watts and Strogatz, 1998). Three SW graphs were obtained for each DIV considered. The outcoming connectivity models are sparse (i.e., the number of edges is less than the possible number of edges in the order of O(q), where q is the total number of vertices), with a mean edge density (defined in Supplementary Table 2) of 2.5%, in consistence with previously reported experimental values (Antonello et al., 2022; Downes et al., 2012).

FIGURE 3

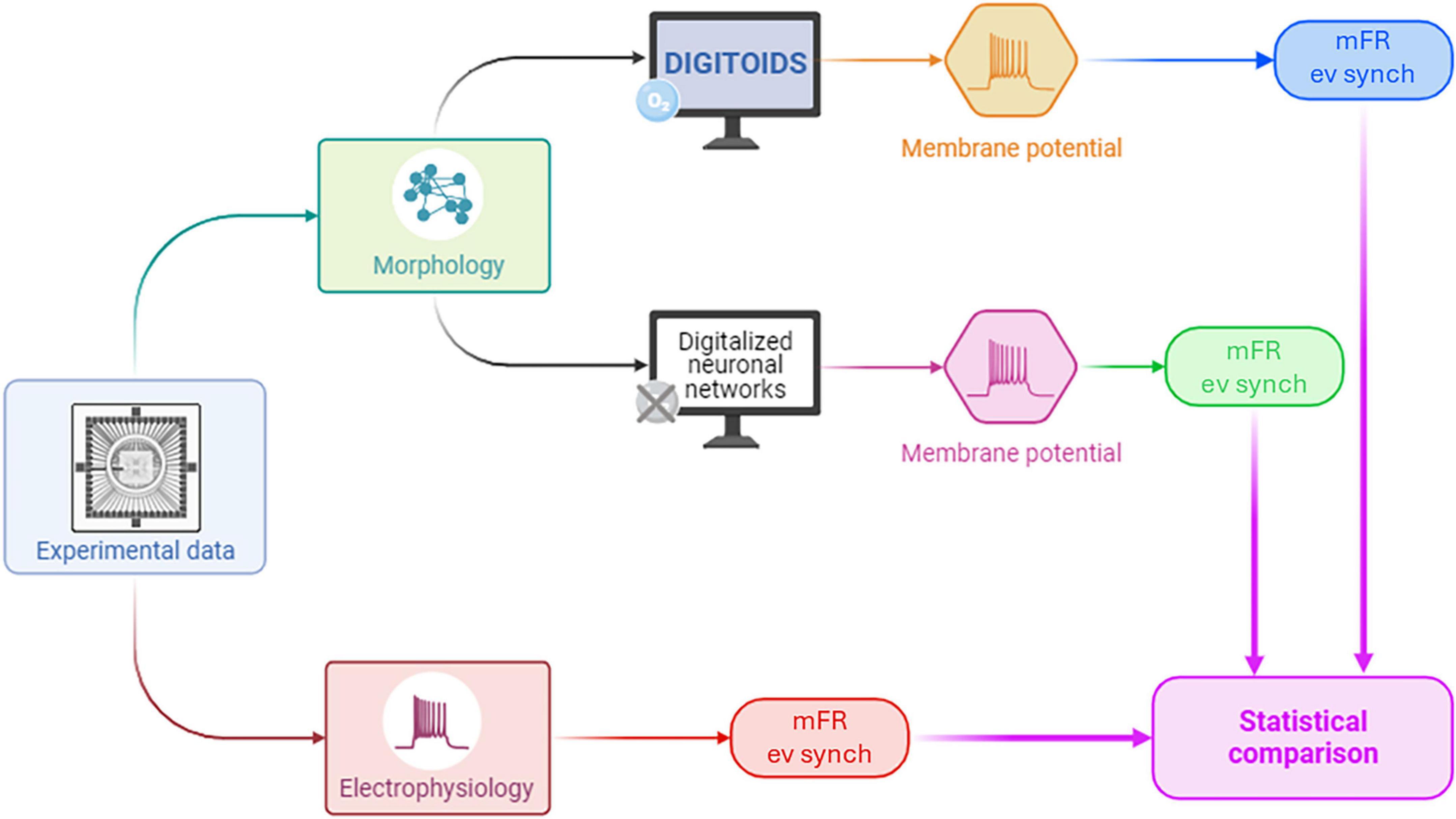
Figure 3. The pipeline adopted for assessing the performance of Digitoids using experimental data. Experimental topological parameters from neurons cultured on MEAs were used to build the Digitoids and the HH (i.e., O₂-independent models) neuronal networks. The Digitoids and HH models were simulated, and their membrane potentials were processed in the same way as the experimental electrophysiological data to extract mFR. Finally, mFRs from the two computational models – Digitoids and HH – and experimental neuronal cultures were statistically compared to assess whether a similarity exists.

The SW layouts and the adjacency matrices were used to generate the corresponding Digitoids. The layouts, along with their number of vertices and edges, are reported in Supplementary Table 3, while the model parameters are listed in Table 3. The same SW layouts were used to build in silico neuronal networks where the traditional HH model was implemented instead of the O₂-dependent one, described in Section 2.1.2. The single-neuron description was obtained by imposing the membrane pump to work optimally, i.e., with fixed pump rate ρ_max (Table 3). The current components of the model are the same of the single-neuron model (Section 2.1.2)—i.e, I_Na, I_K and I_Cl−−consistently with the model developed by Wei and co-workers (Wei et al., 2014). The neurons in the computational network models are spontaneously active due to potassium concentration in the bath. All the network models were simulated for 20 s with the variable-step solver “ode15s” of Simulink, with maximal step size of 0.4.

TABLE 3

Table 3. Values of the parameters used in the model.

2.4.2 Impact of oxygen on network-level activity

Six Digitoids (with SW layout size described in Supplementary Table 3) were developed and simulated to explore the effects of O₂ deprivation on the network activity. For this purpose, the six Digitoids were first simulated in normal oxygenation conditions for cell culture, i.e., considering a boundary concentration c₀ = 0.2mM. Then, the same networks were simulated lowering c₀ to 0.04mM, i.e., the threshold O₂ concentration ensuring physiological cell functioning and survival (Berger et al., 2018).

2.5 Statistical analysis

Statistical analyses were performed using GraphPad Prism 8 (GraphPad Software, Boston, Massachusetts United States) to identify any significant differences between the mFR of the computational models and the experimental data. Thus, firstly, the distributions of mFR of the O₂-dependent firing in Digitoids, the mFR experimentally measured in cultured neurons and the mFR values from the traditional HH model were tested for normality, by adopting the Shapiro-Wilk test (α = 0.05). Since the distributions were not Gaussian, the non-parametric Kruskal-Wallis test was used (α = 0.05). To compare mFR and event synchronization between the Digitoids simulated in normal (i.e., c₀ = 0.2mM) and O₂ deprivation (i.e., c₀ = 0.04mM) conditions, the Mann-Whitney test was instead adopted (α = 0.05).

3 Results

3.1 Dependence of firing on oxygen availability

Figure 4 shows examples of the outcome of the Digitoids, i.e., the neuron membrane potential and the O₂ concentration at the cell level (z = 0) taken over a time window of 20 s for different values of the boundary O₂ concentration. As expected, the plots indicate that single neurons exhibit an O₂-dependent firing, with reduced activity when the local concentration decreases. Indeed, when the neuron fires, the Na⁺-K⁺-ATP pump is activated, thus O₂ is consumed (Eqs. 2–4), and its concentration at z = 0 decreases. Longer spike trains are generated if O₂ availability is high.

FIGURE 4

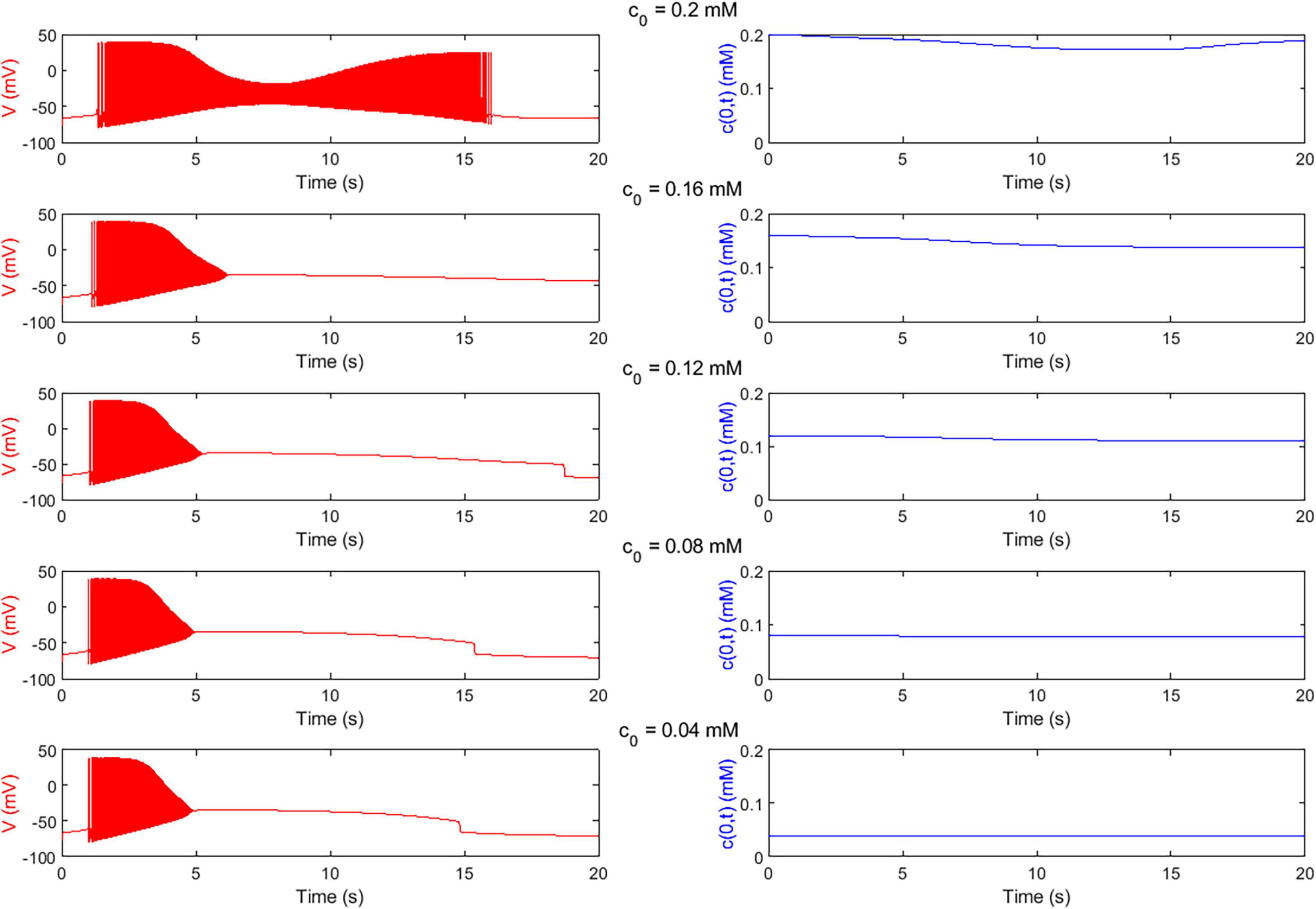
Figure 4. O₂-dependent electrophysiological activity of single neurons predicted by Digitoids. Membrane potential (V, left column) and O₂ concentration at the neuron level (c(0,t), right column) over the first 20 s of the simulation of the single-neuron model with h = 0.1 mm for different values of boundary O₂ concentration c₀ (reported in Table 2). In the upper panel, the output of the configuration with highest O₂ availability is depicted. The neuron is able to fire a long train of action potentials. In correspondence of the firing, c(0,t) decreases because O₂ is consumed by the cell to sustain metabolism and electrical activity.

For what concerns the sensitivity of the shape metrics to the parameters c₀ and h, plots are reported in Supplementary Figures 5, 6. Specifically, Supplementary Figure 5 graphically depicts the dependence of t_train, AR and DR (Eqs. 21 and 22) on c₀ for each of the tested medium heights, while Supplementary Figure 6 reports their dependence on h parametrized with respect to c₀. From the visual analysis of the plots, a monotonic relation can be identified between the parameters c₀ and h–which set the availability of O₂ over time to the neuron—and the train metrics. This suggests that the neuron is able to fire longer trains of action potentials when the O₂ availability in the system is not a limiting factor, i.e., with highest c₀ and lowest h. Furthermore, the Spearman correlation coefficient r was computed to provide a quantitative means of such dependencies. Numerical values of r are reported in Supplementary Tables 4–9 together with corresponding p-values. All the metrics display significant correlation with c₀, while they significantly correlate with the medium height only when boundary O₂ is maximal. Indeed, the single-neuron output is more sensitive to growing medium heights when O₂ availability is not limited yet by reduced air saturation, that is c₀ < 0.2 mM. Otherwise, supply constraints due to the increased diffusive path do not significantly affect the duration of spike trains.

Moreover, single spikes were identified for each combination of h and c₀; for each spike, v_pp, rr and fr were calculated, and their trend over time are shown in Supplementary Figures 1–3. At the beginning of the simulation (i.e., when O₂ availability is high), v_pp values appear independent of h and c₀ (see Supplementary Figure 1). Then, v_pp decreases over time with a rate depending on c₀. In particular, we observed that the rate at which v_pp decreases at the end of the spike train is higher for the lower values of c₀. This is reported in Figure 5A, where the slope of v_pp (dV_pp) over the last four time points considered in the simulation is shown to better highlight the dependence on the different values of h and c₀.

FIGURE 5

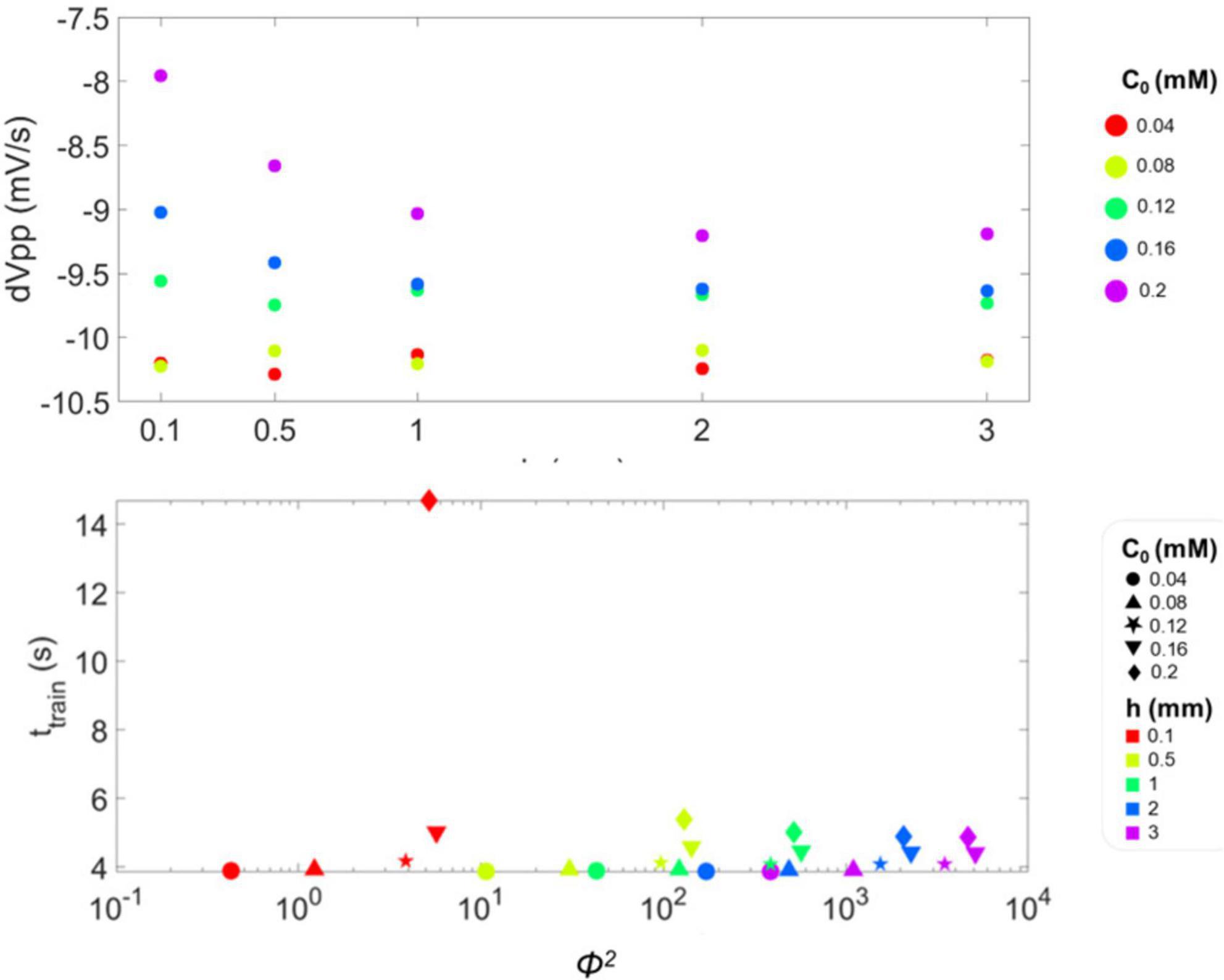
Figure 5. (A) Slope of the peak-to-peak amplitude of single spikes (dV_pp) calculated for the last four points of v_pp in the spike train and plotted as a function of medium height h. For the three lowest values of h − 0.5, 1 and 2 mm −, the value of dV_pp is more negative when c₀ is lower. This means that the train of action potentials fired by the single-neuron model is terminated with a steeper slope, i.e., faster with respect to conditions of higher c₀. (B) Duration of the spike train, t_train, as a function of Φ², whose values are reported in log-scale. Datapoints correspond to the considered combinations of c₀ and h, reported in Table 2: different symbols correspond to different values of c₀, while colors to h.

Figure 5B depicts t_train as a function of Φ². Notably, t_train is sensitive to the level of O₂ available to the neuron, as reported in Bean (2007), since it decreases with higher Φ² (that is with lower c₀ and higher h). This implies that firing is a diffusion-limited phenomenon, which is suppressed when it cannot be energetically sustained due to O₂ depletion (Nieber, 1999; Pires Monteiro et al., 2021; Santiago et al., 2023). Moreover, the dispersion of t_train values becomes narrower with increasing Φ², indicating that the firing threshold is governed by O₂ availability, which is in turn increasingly limited by diffusion as h increases.

The same trends with respect to Φ² are observable for DR and AR−see Supplementary Text 3 and Supplementary Figure 4 for details.

3.2 Performance of the digitoids

Figure 6 shows the mFR obtained from: (i) the experimental in vitro recordings reported in Ballesteros-Esteban et al. (2023); (ii) the output from the corresponding Digitoids; (iii) the firing activity of the network with the same topological layout but the traditional formulation of electrophysiology according to the HH model. For all the DIV considered, no statistically significant differences were found between the mFR of Digitoids and the corresponding experimental data. On the other hand, the values of mFR of the traditional O₂-independent HH model were significantly different if compared to both the in vitro observations and Digitoids predictions. The associated p-values are reported in Supplementary Table 10.

FIGURE 6

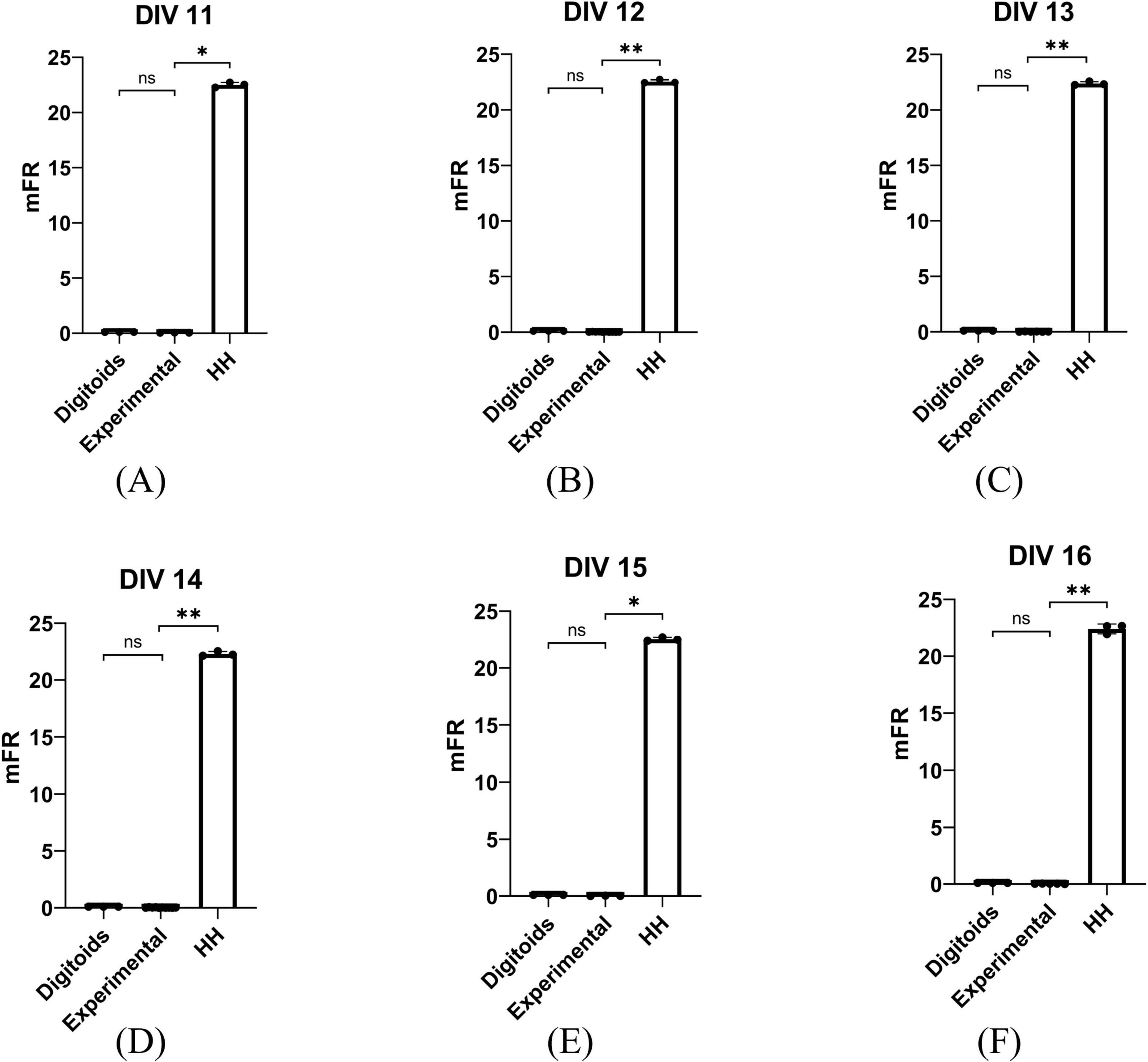
Figure 6. Statistical comparison between mFR (spikes s^–1) values obtained from experimental measurements, the Digitoids and the HH model for the six different Day In Vitro (DIV) considered for analyses: (A) DIV 11, (B) DIV 12, (C) DIV 13, (D) DIV 14, (E) DIV 15, (F) DIV 16. At each DIV, mFR calculated from Digitoids and Experimental data exhibits no tatistically significant differences, while Experimental and Digitoids are always different. *p < 0.05, **p < 0.005.

Further, the whole-network effect of O₂ deprivation on mFR predicted by Digitoids is shown in Figure 7A. When accounting for reduced O₂ availability (c₀ = 0.04mM), Digitoids coherently predicted significantly lower mFR than that obtained for c₀ = 0.2mM. The event synchronization was also evaluated in such conditions. Also in this case, O₂ deprivation lowers the predicted synchronization values, with significant differences with respect to values predicted by the Digitoids with normoxic conditions (Figure 7B).

FIGURE 7

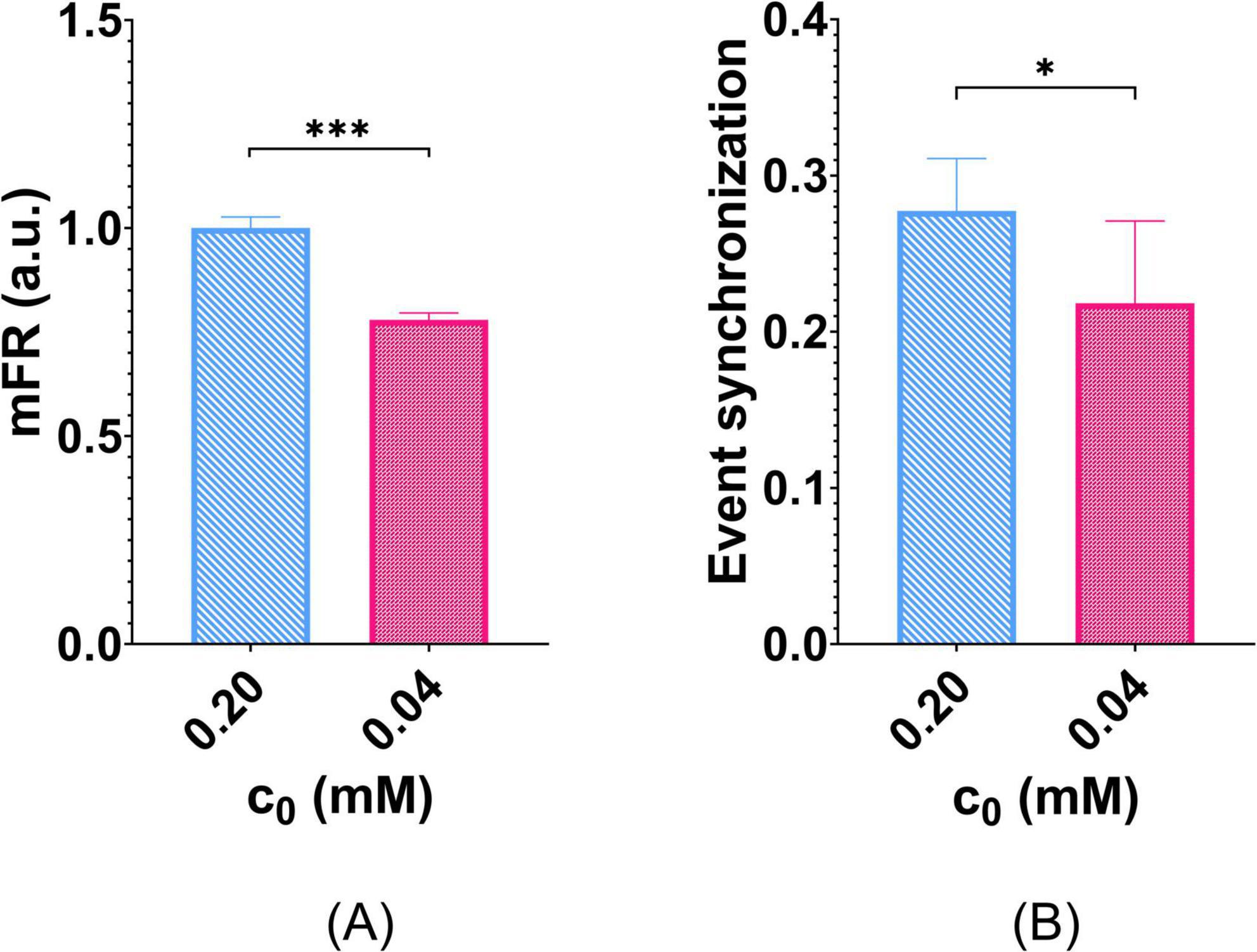
Figure 7. Effects of O₂ deprivation on network activity. Six Digitoids were simulated with normal O₂ and with deprived O₂ in culture medium to compare their mFR. (A) mFR is significantly reduced when the networks are simulated in O₂ deprivation conditions. mFR values are reported in a.u. since they were normalized for the average value calculated in normoxic conditions (i.e., c₀ = 0.20mM). ***p < 0.001. (B) O₂ deprivation also reduces the event synchronization of the networks, with statistically significant differences with respect to the normoxic condition. *p < 0.05.

Supplementary Figure 7 depicts an example of the event synchronization calculated from one of the simulated Digitoids.

4 Discussion

O₂ levels are crucial to neuronal function in vitro: they significantly affect viability, oxidative stress and mitochondrial function (Zhu et al., 2012). However, the influence of O₂ on in vitro electrophysiological behavior is often neglected. In this work, we developed a computational platform—Digitoids—able to replicate a neuronal network in vitro. Digitoids embeds a model of neuron firing in which the O₂ dynamics of diffusion and consumption are introduced and coupled with ionic transport across the cell membrane. The novelty of the proposed model resides in the coupling of O₂ diffusion and consumption dynamics with neuronal electrical activity. Thanks to this approach, different culture conditions and layouts can be replicated obtaining descriptions of O₂-dependent activity tailored on the specific system under study.

To demonstrate the importance of O₂ in neuron firing, we computed different metrics of the spike train as well as of single spikes and assessed their dependency on O₂ availability. Overall, the observed trends confirm that the electrophysiological behavior of single neurons is modulated by O₂ supply. These results are supported by the significant correlation between the train metrics and the boundary O₂ concentration, c₀. Interestingly, neuron firing was found to be less sensitive to O₂ fluctuations in conditions of limited resource availability (i.e., for high Φ ² values). Indeed, reduced—or even non-significant—correlation coefficients of spike train characteristics with medium height are found when boundary O₂ does not correspond to air saturation (i.e., c = 0.2 mM).

This behavior can be explained considering that reduced O₂ hinders the homeostatic maintenance of ion concentrations between the intra and extracellular environments, which is responsible for sustaining the electrical activity of the neuron, as reported for both brain slices and in vitro cultures exposed to hypoxia (Brisson et al., 2013; Fiskum et al., 2021; Pires Monteiro et al., 2021; Spong et al., 2016; Zanelli et al., 2015). Under these conditions, the Na⁺-K⁺-ATP pump lacks sufficient resources to fuel ion transport, and thus firing decreases or even ceases (Nieber, 1999). The preliminary results obtained simulating O₂ deprivation at the network level corroborate this evidence, suggesting that cells reduce their electrical activity and synchronization than in standard oxygenation at both the single-neuron and whole-network scale. These results are consistent with studies which reported reduced firing rate of cultured neurons when exposed to hypoxia (Fiskum et al., 2021; Hofmeijer et al., 2014).

As a first preliminary assessment of the goodness of Digitoids predictions, we compared the simulated firing rate to that measured in neuronal networks seeded on commercial MEAs. No statistically significant differences were found between the experimentally measured mFRs and those predicted by Digitoids. Additionally, we compared the mFRs observed in vitro to predictions by the classic HH model applied to the same network layouts. The results are significantly different, highlighting that the mutual influence between local O₂ concentration and the ion pump activity affects electrophysiological dynamics, as also captured by the analyses performed on the single-neuron output. It is worth highlighting that for Digitoids and experimental data the mFR is much lower than in the traditional HH model. In the latter, the initial values of simulation parameters (described in Section 2.4) indeed induce neurons to fire longer trains of APs, which are not limited by reduced O₂ availability. Including O₂ dynamics instead allows Digitoids to mimic its potential deprivation due to neuronal uptake, hindering the cross-membrane transport of ions as the energetic demand of membrane pumps cannot be satisfied.

The platform is designed to be modular and adaptable to different culture conditions by tuning the cell metabolic and electrophysiological parameters. More complex models of neuronal cultures, (e.g., co-cultures) can be developed by adding different single-cell blocks to the Simulink library to mimic other neural phenotypes. Following the approach described in Callegari et al. (2023), three-dimensional (3D) neuronal constructs can also be built by overlaying monolayers on each other. Thus, Digitoids can be extended to the simulation of neurospheres and cerebral organoids (Poli et al., 2019), supporting the investigation of their biophysical mechanisms. These constructs are particularly susceptible to O₂ availability, as its depletion can lead to the formation of non-viable cores, hindering the development of mature traits and of a 3D neural network (Poli et al., 2019).

It is important to note that the experimental data used for comparison were derived from insect neurons, while the model parameters are typical of mammalian neurons. Nevertheless, the fundamental mechanisms underlying spike generation are similar across different species (Spong et al., 2016), and invertebrates are widely used to advance our understanding of more complex organisms (Newcomb et al., 2023; Sattelle and Buckingham, 2006). A more in-depth validation of our platform would require parallel recordings of electrophysiological and O₂ dynamics in in vitro neurons. Specifically, perturbations will be added in the model and the predicted output will be compared to an experimental setting where the same perturbation is introduced (e.g., incubator O₂ level drop). Furthermore, future effort will be carried out to integrate in the model also the O₂ demand of synaptic activity (Faria-Pereira and Morais, 2022). For what concerns the parameters specific of the electrophysiological model, they will be tuned to better fit the recorded electrophysiology of in vitro neurons.

To proof the feasibility of using Digitoids, we exploited topological and electrophysiological data acquired on low density cultured networks. Thus, the simulated networks involve a relatively limited number of neurons and connections. To further expand the relevance of this work, larger networks can be developed and simulated. Larger-sized Digitoids can be developed with the same approach described in this work (Section 2.4.1) by defining a bioinspired (i.e., based on biologically observed features) adjacency matrix to layout the spatial distribution of single neurons and their connections within the Simulink framework.

In conclusion, this work represents a promising first step towards creating “digital twins” of in vitro neuronal networks. The approach implemented in Digitoids can be exploited for gaining important insights into brain pathophysiology. As an example, stroke and ischemia are characterized by low O₂ levels, which lead to cognitive decline, neuronal damage and cell death (Klein Gunnewiek et al., 2020; Radenkovic et al., 2024; Voogd et al., 2023). In addition, neurodegeneration is known to be intimately linked to mitochondrial—and thus bioenergetic—dysfunctions (Bustamante-Barrientos et al., 2023). Hence, Digitoids hold the potential to support, or even replace, primary neuronal cultures, as they are cost-effective, have a longer lifespan and allow high-throughput experiments that would be unfeasible in vitro (Velasco et al., 2020). Ongoing efforts include further model validation through detailed O₂ and electrophysiological measurements, as well as expanding the model to include additional modules for different neuron types and 3D networks.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding authors.

Ethics statement

The manuscript presents research on animals that do not require ethical approval for their study.

Author contributions

RF: Data curation, Formal Analysis, Software, Visualization, Writing – original draft. EB: Data curation, Formal Analysis, Visualization, Writing – review & editing. AA: Supervision, Writing – review & editing. CM: Conceptualization, Funding acquisition, Methodology, Project administration, Supervision, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work has received funding from the NAP project (HORIZON-EIC-2022-PathfinderOpen) under grant agreement No. 101099310.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fninf.2025.1549916/full#supplementary-material

References

Al-Ani, A., Toms, D., Kondro, D., Thundathil, J., Yu, Y., and Ungrin, M. (2018). Oxygenation in cell culture: Critical parameters for reproducibility are routinely not reported. PLoS One 13:e0204269. doi: 10.1371/journal.pone.0204269

PubMed Abstract | Crossref Full Text | Google Scholar

Antonello, P. C., Varley, T. F., Beggs, J., Porcionatto, M., Sporns, O., and Faber, J. (2022). Self-organization of in vitro neuronal assemblies drives to complex network topology. eLife 11:e74921. doi: 10.7554/ELIFE.74921

PubMed Abstract | Crossref Full Text | Google Scholar

Ashwin, P., Coombes, S., and Nicks, R. (2016). Mathematical frameworks for oscillatory network dynamics in neuroscience. J. Math. Neurosci. 6:92. doi: 10.1186/S13408-015-0033-6

PubMed Abstract | Crossref Full Text | Google Scholar

Attwell, D., and Laughlin, S. B. (2001). An energy budget for signaling in the grey matter of the brain. J. Cereb. Blood Flow Metab. 21, 1133–1145. doi: 10.1097/00004647-200110000-00001

PubMed Abstract | Crossref Full Text | Google Scholar

Ballesteros-Esteban, L. M., Leyva, I., Almendral, J. A., and Sendiña-Nadal, I. (2023). Self-organization and evolution of structure and function in cultured neuronal networks. Chaos Solitons Fractals 173:113764. doi: 10.1016/j.chaos.2023.113764

Crossref Full Text | Google Scholar

Bassett, D. S., and Bullmore, E. (2006). Small-world brain networks. Neuroscientist 12, 512–523. doi: 10.1177/1073858406293182

PubMed Abstract | Crossref Full Text | Google Scholar

Bean, B. P. (2007). The action potential in mammalian central neurons. Nat. Rev. Neurosci. 8, 451–465. doi: 10.1038/nrn2148

PubMed Abstract | Crossref Full Text | Google Scholar

Berger, E., Magliaro, C., Paczia, N., Monzel, A. S., Antony, P., Linster, C. L., et al. (2018). Millifluidic culture improves human midbrain organoid vitality and differentiation. Lab Chip 18, 3172–3183. doi: 10.1039/C8LC00206A

PubMed Abstract | Crossref Full Text | Google Scholar

Bettencourt, L. M. A., Stephens, G. J., Ham, M. I., and Gross, G. W. (2007). Functional structure of cortical neuronal networks grown in vitro. Phys. Rev. E - Statist. Nonlinear Soft Matter Phys. 75:021915. doi: 10.1103/PhysRevE.75.021915

PubMed Abstract | Crossref Full Text | Google Scholar

Borges, F. S., Protachevicz, P. R., Souza, D. L. M., Bittencourt, C. F., Gabrick, E. C., Bentivoglio, L. E., et al. (2023). The roles of potassium and calcium currents in the bistable firing transition. Brain Sci. 13:1347. doi: 10.3390/brainsci13091347

PubMed Abstract | Crossref Full Text | Google Scholar

Brisson, C. D., Lukewich, M. K., and Andrew, R. D. (2013). A distinct boundary between the higher brain’s susceptibility to ischemia and the lower brain’s resistance. PLoS One 8:e79589. doi: 10.1371/journal.pone.0079589

PubMed Abstract | Crossref Full Text | Google Scholar

Brosel, S., Grothe, B., and Kunz, L. (2018). An auditory brainstem nucleus as a model system for neuronal metabolic demands. Eur. J. Neurosci. 47, 222–235. doi: 10.1111/ejn.13789

PubMed Abstract | Crossref Full Text | Google Scholar

Bustamante-Barrientos, F. A., Luque-Campos, N., Araya, M. J., Lara-Barba, E., de Solminihac, J., Pradenas, C., et al. (2023). Mitochondrial dysfunction in neurodegenerative disorders: Potential therapeutic application of mitochondrial transfer to central nervous system-residing cells. J. Trans. Med. 21:613. doi: 10.1186/s12967-023-04493-w

PubMed Abstract | Crossref Full Text | Google Scholar

Callegari, F., Brofiga, M., and Massobrio, P. (2023). Modeling the three-dimensional connectivity of in vitro cortical ensembles coupled to micro-electrode arrays. PLoS Comp. Biol. 19:e1010825. doi: 10.1371/journal.pcbi.1010825

PubMed Abstract | Crossref Full Text | Google Scholar

Chen, Y. W., Zhang, L. F., and Huang, J. P. (2007). The Watts–Strogatz network model developed by including degree distribution: Theory and computer simulation. J. Phys. Math. Theoret. 40, 8237–8246. doi: 10.1088/1751-8113/40/29/003

Crossref Full Text | Google Scholar

Chiappalone, M., Pasquale, V., and Frega, M. (2019). “Preface: In vitro neuronal networks,” in In vitro neuronal networks: From culturing methods to neuro-technological applications. advances in neurobiology, eds M. Chiappalone, V. Pasquale, and M. Frega (Berlin: Springer). doi: 10.1111/jnc.16121

PubMed Abstract | Crossref Full Text | Google Scholar

Compte, A., Sanchez-Vives, M. V., McCormick, D. A., and Wang, X.-J. (2003). Cellular and network mechanisms of slow oscillatory activity (<1 Hz) and wave propagations in a cortical network model. J. Neurophysiol. 89, 2707–2725. doi: 10.1152/jn.00845.2002

PubMed Abstract | Crossref Full Text | Google Scholar

de Santos-Sierra, D., Sendiña-Nadal, I., Leyva, I., Almendral, J. A., Anava, S., Ayali, A., et al. (2014). Emergence of small-world anatomical networks in self-organizing clustered neuronal cultures. PLoS One 9:e85828. doi: 10.1371/journal.pone.0085828

PubMed Abstract | Crossref Full Text | Google Scholar

Di Florio, M., Iyer, V., Rajhans, A., Buccelli, S., and Chiappalone, M. (2022). “Model-based online implementation of spike detection algorithms for neuroengineering applications,” in Proceedings of the 2022 44th annual international conference of the IEEE Engineering in Medicine & Biology Society (EMBC), (Piscataway, NJ: IEEE). doi: 10.1109/EMBC48229.2022.9871444

PubMed Abstract | Crossref Full Text | Google Scholar

Doorn, N., van Hugte, E. J. H., Ciptasari, U., Mordelt, A., Meijer, H. G. E., Schubert, D., et al. (2023). An in silico and in vitro human neuronal network model reveals cellular mechanisms beyond NaV1. 1 underlying Dravet syndrome. Stem Cell Rep. 18, 1686–1700. doi: 10.1016/j.stemcr.2023.06.003

PubMed Abstract | Crossref Full Text | Google Scholar

Downes, J. H., Hammond, M. W., Xydas, D., Spencer, M. C., Becerra, V. M., Warwick, K., et al. (2012). Emergence of a small-world functional network in cultured neurons. PLoS Comp. Biol. 8:e1002522. doi: 10.1371/JOURNAL.PCBI.1002522

PubMed Abstract | Crossref Full Text | Google Scholar

Emre Kapucu, F., Vinogradov, A., Hyvärinen, T., Ylä-Outinen, L., and Narkilahti, S. (2022). Comparative microelectrode array data of the functional development of hPSC-derived and rat neuronal networks. Sci. Data 9:120. doi: 10.1038/s41597-022-01242-4

PubMed Abstract | Crossref Full Text | Google Scholar

Faria-Pereira, A., and Morais, V. A. (2022). Synapses: The Brain’s energy-demanding sites. Int. J. Mol. Sci. 23:3627. doi: 10.3390/ijms23073627

PubMed Abstract | Crossref Full Text | Google Scholar

Fiskum, V., Sandvig, A., and Sandvig, I. (2021). Silencing of activity during hypoxia improves functional outcomes in motor neuron networks in vitro. Front. Integrat. Neurosci. 15:792863. doi: 10.3389/fnint.2021.792863

PubMed Abstract | Crossref Full Text | Google Scholar

Gewaltig, M.-O., and Diesmann, M. (2007). NEST (NEural Simulation Tool). Scholarpedia 2:1430. doi: 10.4249/SCHOLARPEDIA.1430

Crossref Full Text | Google Scholar

Ghaderi, P., Marateb, H. R., and Safari, M.-S. (2018). Electrophysiological profiling of neocortical neural subtypes: A semi-supervised method applied to in vivo whole-cell patch-clamp data. Front. Neurosci. 12:823. doi: 10.3389/fnins.2018.00823

PubMed Abstract | Crossref Full Text | Google Scholar

Gordon, J., and Amini, S. (2021). General overview of neuronal cell culture. Methods Mol. Biol. 2311, 1–8. doi: 10.1007/978-1-0716-1437-2_1

PubMed Abstract | Crossref Full Text | Google Scholar

Hines, M. L., and Carnevale, N. T. (2001). Neuron: A tool for neuroscientists. Neuroscientist 7, 123–135. doi: 10.1177/107385840100700207

PubMed Abstract | Crossref Full Text | Google Scholar

Hodgkin, A. L., and Huxley, A. F. (1952a). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544. doi: 10.1113/JPHYSIOL.1952.SP004764

PubMed Abstract | Crossref Full Text | Google Scholar

Hodgkin, A. L., and Huxley, A. F. (1952b). Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. J. Physiol. 116, 449–472. doi: 10.1113/JPHYSIOL.1952.SP004717

PubMed Abstract | Crossref Full Text | Google Scholar

Hodgkin, A. L., Huxley, A. F., and Katz, B. (1952). Measurement of current- voltage relations in the membrane of the giant axon of Loligo. J. Physiol. 116, 424–448. doi: 10.1113/JPHYSIOL.1952.SP004716

PubMed Abstract | Crossref Full Text | Google Scholar

Hofmeijer, J., Mulder, A. T. B., Farinha, A. C., van Putten, M. J. A. M., and le Feber, J. (2014). Mild hypoxia affects synaptic connectivity in cultured neuronal networks. Brain Res. 1557, 180–189. doi: 10.1016/j.brainres.2014.02.027

PubMed Abstract | Crossref Full Text | Google Scholar

Huchzermeyer, C., Berndt, N., Holzhü Tter, H.-G., and Kann, O. (2013). Oxygen consumption rates during three different neuronal activity states in the hippocampal CA3 network. J. Cereb. Blood Flow Metab. 33, 263–271. doi: 10.1038/jcbfm.2012.165

PubMed Abstract | Crossref Full Text | Google Scholar

Humpel, C. (2015). Organotypic brain slice cultures: A review. Neuroscience 305, 86–98. doi: 10.1016/J.NEUROSCIENCE.2015.07.086

PubMed Abstract | Crossref Full Text | Google Scholar

Humphries, M. D., and Gurney, K. (2008). Network “small-world-ness”: A quantitative method for determining canonical network equivalence. PLoS One 3:e0002051. doi: 10.1371/journal.pone.0002051

PubMed Abstract | Crossref Full Text | Google Scholar

Hyvärinen, T., Hyysalo, A., Kapucu, E., Aarnos, L., Vinogradov, A., Eglen, S. J., et al. (2019). Functional characterization of human pluripotent stem cell-derived cortical networks differentiated on laminin-521 substrate: Comparison to rat cortical cultures. Sci. Rep. 9:17125. doi: 10.1038/s41598-019-53647-8

PubMed Abstract | Crossref Full Text | Google Scholar

Izhikevich, E. M. (2003). Simple model of spiking neurons. IEEE Trans. Neural Netw. 14, 1569–1572. doi: 10.1109/TNN.2003.820440

PubMed Abstract | Crossref Full Text | Google Scholar

Klein Gunnewiek, T. M., Van Hugte, E. J. H., Frega, M., Guardia, G. S., Foreman, K., Panneman, D., et al. (2020). m.3243A &gt G-Induced mitochondrial dysfunction impairs human neuronal development and reduces neuronal network activity and synchronicity. Cell Rep. 31:107538. doi: 10.1016/j.celrep.2020.107538

PubMed Abstract | Crossref Full Text | Google Scholar

Kuznetsov, A. V. (2024). Effects of time-dependent adenosine triphosphate consumption caused by neuron firing on adenosine triphosphate concentrations in synaptic boutons containing and lacking a stationary mitochondrion. J. Biomechan. Eng. 146:111002. doi: 10.1115/1.4065743

PubMed Abstract | Crossref Full Text | Google Scholar

Lenk, K., Satuvuori, E., Lallouette, J., Ladrón-de-Guevara, A., Berry, H., and Hyttinen, J. A. K. (2020). A computational model of interactions between neuronal and astrocytic networks: The role of astrocytes in the stability of the neuronal firing rate. Front. Comp. Neurosci. 13:92. doi: 10.3389/fncom.2019.00092

PubMed Abstract | Crossref Full Text | Google Scholar

Lennie, P. (2003). The cost of cortical computation. Curr. Biol. 13, 493–497. doi: 10.1016/S0960-9822(03)00135-0

PubMed Abstract | Crossref Full Text | Google Scholar

Lonardoni, D., Di Marco, S., Amin, H., Berdondini, L., and Nieus, T. (2015). A computational model of cell culture dynamics: The role of connectivity and synaptic receptors in the appearance of synchronized bursting events. BMC Neurosci. 16:177. doi: 10.1186/1471-2202-16-S1-P177

Crossref Full Text | Google Scholar

Magliaro, C., Rinaldo, A., and Ahluwalia, A. (2019). Allometric scaling of physiologically-relevant organoids. Sci. Rep. 9:11890. doi: 10.1038/s41598-019-48347-2

PubMed Abstract | Crossref Full Text | Google Scholar

Markram, H., Muller, E., Ramaswamy, S., Reimann, M. W., Abdellah, M., Sanchez, C. A., et al. (2015). Reconstruction and simulation of neocortical microcircuitry. Cell 163, 456–492. doi: 10.1016/j.cell.2015.09.029

PubMed Abstract | Crossref Full Text | Google Scholar

Masoli, S., Rizza, M. F., Tognolina, M., Prestori, F., and D’Angelo, E. (2022). Computational models of neurotransmission at cerebellar synapses unveil the impact on network computation. Front. Comp. Neurosci. 16:1006989. doi: 10.3389/fncom.2022.1006989

PubMed Abstract | Crossref Full Text | Google Scholar

Masquelier, T., and Deco, G. (2013). Network bursting dynamics in excitatory cortical neuron cultures results from the combination of different adaptive mechanism. PLoS One 8:e75824. doi: 10.1371/journal.pone.0075824

PubMed Abstract | Crossref Full Text | Google Scholar

McMurtrey, R. J. (2016). Analytic models of oxygen and nutrient diffusion, metabolism dynamics, and architecture optimization in three-dimensional tissue constructs with applications and insights in cerebral organoids. Tissue Eng. Part C Methods 22, 221–249. doi: 10.1089/ten.TEC.2015.0375

PubMed Abstract | Crossref Full Text | Google Scholar

Negri, J., Menon, V., and Young-Pearse, T. L. (2020). Assessment of spontaneous neuronal activity in vitro using multi-well multi-electrode arrays: Implications for assay development. Eneuro 7:ENEURO.0080-19.2019. doi: 10.1523/ENEURO.0080-19.2019.

PubMed Abstract | Crossref Full Text | Google Scholar

Newcomb, J. M., Todd, K., and Buhl, E. (2023). Editorial: Invertebrate neurophysiology—of currents, cells, and circuits. Front. Neurosci. 17:1303574. doi: 10.3389/fnins.2023.1303574

PubMed Abstract | Crossref Full Text | Google Scholar

Nieber, K. (1999). Hypoxia and neuronal function under in vitro conditions. Pharmacol. Therapeut. 82, 71–86. doi: 10.1016/S0163-7258(98)00061-8

PubMed Abstract | Crossref Full Text | Google Scholar

Özugur, S., Kunz, L., and Straka, H. (2020). Relationship between oxygen consumption and neuronal activity in a defined neural circuit. BMC Biol. 18:76. doi: 10.1186/s12915-020-00811-6

PubMed Abstract | Crossref Full Text | Google Scholar

Pacitti, D., Privolizzi, R., and Bax, B. E. (2019). Organs to cells and cells to organoids: The evolution of in vitro central nervous system modelling. Front. Cell. Neurosci. 13:129. doi: 10.3389/fncel.2019.00129

PubMed Abstract | Crossref Full Text | Google Scholar

Patterson, M. S., and Mazurek, E. (2010). Calculation of cellular oxygen concentration for photodynamic therapy in vitro. Methods Mol. Biol. 635, 195–205. doi: 10.1007/978-1-60761-697-9_14

PubMed Abstract | Crossref Full Text | Google Scholar

Pires Monteiro, S., Voogd, E., Muzzi, L., De Vecchis, G., Mossink, B., Levers, M., et al. (2021). Neuroprotective effect of hypoxic preconditioning and neuronal activation in a in vitro human model of the ischemic penumbra. J. Neural Eng. 18:036016. doi: 10.1088/1741-2552/abe68a

PubMed Abstract | Crossref Full Text | Google Scholar

Place, T. L., Domann, F. E., and Case, A. J. (2017). Limitations of oxygen delivery to cells in culture: An underappreciated problem in basic and translational research. Free Radical Biol. Med. 113, 311–322. doi: 10.1016/J.FREERADBIOMED.2017.10.003

PubMed Abstract | Crossref Full Text | Google Scholar

Poli, D., Magliaro, C., and Ahluwalia, A. (2019). Experimental and computational methods for the study of cerebral organoids: A review. Front. Neurosci. 13:162. doi: 10.3389/fnins.2019.00162

PubMed Abstract | Crossref Full Text | Google Scholar

Poli, D., Pastore, V. P., and Massobrio, P. (2015). Functional connectivity in in vitro neuronal assemblies. Front. Neural Circuits 9:57. doi: 10.3389/fncir.2015.00057

PubMed Abstract | Crossref Full Text | Google Scholar

Potjans, T. C., and Diesmann, M. (2014). The cell-type specific cortical microcircuit: Relating structure and activity in a full-scale spiking network model. Cereb. Cortex 24, 785–806. doi: 10.1093/cercor/bhs358

PubMed Abstract | Crossref Full Text | Google Scholar

Radenkovic, S., Budhraja, R., Klein-Gunnewiek, T., King, A. T., Bhatia, T. N., Ligezka, A. N., et al. (2024). Neural and metabolic dysregulation in PMM2-deficient human in vitro neural models. Cell Rep. 43:113883. doi: 10.1016/j.celrep.2024.113883

PubMed Abstract | Crossref Full Text | Google Scholar

Roth, A., and van Rossum, M. C. W. (2009). Modeling synapses. Comp. Model. Methods Neuroscient. 6, 139–160. doi: 10.7551/mitpress/7543.003.0008

Crossref Full Text | Google Scholar

Sanchez-Vives, M. V., Nowak, L. G., and McCormick, D. A. (2000). Cellular mechanisms of long-lasting adaptation in visual cortical neurons in vitro. J. Neurosci. 20, 4286–4299. doi: 10.1523/JNEUROSCI.20-11-04286.2000

PubMed Abstract | Crossref Full Text | Google Scholar

Santiago, J., Kreutzer, J., Bossink, E., Kallio, P., and le Feber, J. (2023). Oxygen gradient generator to improve in vitro modeling of ischemic stroke. Front. Neurosci. 17:1110083. doi: 10.3389/fnins.2023.1110083

PubMed Abstract | Crossref Full Text | Google Scholar

Sattelle, D. B., and Buckingham, S. D. (2006). Invertebrate studies and their ongoing contributions to neuroscience. Invertebrate Neurosci. 6, 1–3. doi: 10.1007/s10158-005-0014-7

PubMed Abstract | Crossref Full Text | Google Scholar

Scelfo, B., Politi, M., Reniero, F., Palosaari, T., Whelan, M., and Zaldívar, J.-M. (2012). Application of multielectrode array (MEA) chips for the evaluation of mixtures neurotoxicity. Toxicology 299, 172–183. doi: 10.1016/j.tox.2012.05.020

PubMed Abstract | Crossref Full Text | Google Scholar

Shefi, O., Golding, I., Segev, R., Ben-Jacob, E., and Ayali, A. (2002). Morphological characterization of in vitro neuronal networks. Phys. Rev. E 66:021905. doi: 10.1103/PhysRevE.66.021905

PubMed Abstract | Crossref Full Text | Google Scholar

Spong, K. E., Andrew, R. D., and Robertson, R. M. (2016). Mechanisms of spreading depolarization in vertebrate and insect central nervous systems. J. Neurophysiol. 116, 1117–1127. doi: 10.1152/jn.00352.2016

PubMed Abstract | Crossref Full Text | Google Scholar

Stimberg, M., Brette, R., and Goodman, D. F. M. (2019). Brian 2, an intuitive and efficient neural simulator. eLife 8:e47314. doi: 10.7554/ELIFE.47314

PubMed Abstract | Crossref Full Text | Google Scholar

Sukenik, N., Vinogradov, O., Weinreb, E., Segal, M., Levina, A., and Moses, E. (2021). Neuronal circuits overcome imbalance in excitation and inhibition by adjusting connection numbers. Proc. Natl. Acad. Sci. U. S. A. 118:e2018459118. doi: 10.1073/pnas.2018459118

PubMed Abstract | Crossref Full Text | Google Scholar

Van Pelt, J., Vajda, I., Wolters, P. S., Corner, M. A., and Ramakers, G. J. A. (2005). Dynamics and plasticity in developing neuronal networks in vitro. Prog. Brain Res. 147, 171–188. doi: 10.1016/S0079-6123(04)47013-7

PubMed Abstract | Crossref Full Text | Google Scholar

Velasco, V., Shariati, S. A., and Esfandyarpour, R. (2020). Microtechnology-based methods for organoid models. Microsyst. Nanoeng. 6:76. doi: 10.1038/s41378-020-00185-3

PubMed Abstract | Crossref Full Text | Google Scholar

Voogd, E. J. H. F., Frega, M., and Hofmeijer, J. (2023). Neuronal responses to ischemia: Scoping review of insights from human-derived in vitro models. Cell. Mol. Neurobiol. 43, 3137–3160. doi: 10.1007/s10571-023-01368-y

PubMed Abstract | Crossref Full Text | Google Scholar

Walsh, K., Megyesi, J., and Hammond, R. (2005). Human central nervous system tissue culture: A historical review and examination of recent advances. Neurobiol. Dis. 18, 2–18. doi: 10.1016/j.nbd.2004.09.002

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, Q., Perc, M., Duan, Z., and Chen, G. (2010). Impact of delays and rewiring on the dynamics of small-world neuronal networks with two types of coupling. Phys. Statist. Mechan. Appl. 389, 3299–3306. doi: 10.1016/J.PHYSA.2010.03.031

Crossref Full Text | Google Scholar

Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442. doi: 10.1038/30918

PubMed Abstract | Crossref Full Text | Google Scholar

Watts, M. E., Pocock, R., and Claudianos, C. (2018). Brain energy and oxygen metabolism: Emerging role in normal function and disease. Front. Mol. Neurosci. 11:216. doi: 10.3389/fnmol.2018.00216

PubMed Abstract | Crossref Full Text | Google Scholar

Wei, Y., Ullah, G., Ingram, J., and Schiff, S. J. (2014). Oxygen and seizure dynamics: II. Computational modeling. J. Neurophysiol. 112, 213–223. doi: 10.1152/jn.00541.2013

PubMed Abstract | Crossref Full Text | Google Scholar

Wen, J., Peitz, M., and Brüstle, O. (2022). A defined human-specific platform for modeling neuronal network stimulation in vitro and in silico. J. Neurosci. Methods 373:109562. doi: 10.1016/j.jneumeth.2022.109562

PubMed Abstract | Crossref Full Text | Google Scholar

Wilson, S. B., and Emerson, R. (2002). Spike detection: A review and comparison of algorithms. Clin. Neurophysiol. 113, 1873–1881. doi: 10.1016/S1388-2457(02)00297-3

PubMed Abstract | Crossref Full Text | Google Scholar

Zaitsev, A. V., Povysheva, N. V., Gonzalez-Burgos, G., and Lewis, D. A. (2012). Electrophysiological classes of layer 2/3 pyramidal cells in monkey prefrontal cortex. J. Neurophysiol. 108, 595–609. doi: 10.1152/jn.00859.2011

PubMed Abstract | Crossref Full Text | Google Scholar

Zanelli, S. A., Rajasekaran, K., Grosenbaugh, D. K., and Kapur, J. (2015). Increased excitability and excitatory synaptic transmission during in vitro ischemia in the neonatal mouse hippocampus. Neuroscience 310, 279–289. doi: 10.1016/J.NEUROSCIENCE.2015.09.046

PubMed Abstract | Crossref Full Text | Google Scholar

Zhu, J., Aja, S., Kim, E.-K., Park, M. J., Ramamurthy, S., Jia, J., et al. (2012). Physiological oxygen level is critical for modeling neuronal metabolism in vitro. J. Neurosci. Res. 90, 422–434. doi: 10.1002/jnr.22765

PubMed Abstract | Crossref Full Text | Google Scholar