From Hebb rules to spike-timing-dependent plasticity: a personal account
- Laboratory of Computational Neuroscience, Brain Mind Institute, École Polytechnique FÉdÉrale de Lausanne, Lausanne, Switzerland
For my master thesis in physics, I spent my days in an experimental lab working with electronics, liquid nitrogen, vacuum pumps, and tiny semiconductor lasers. It seemed every day another component of the set-up would fail–I felt utterly misplaced. But then a friend told me about an a fascinating new field in physics that linked statistical physics to brain science. It was an exciting period: the papers by Hopfield (Hopfield, 1982) and their mathematical analysis (Amit et al., 1985) were all new, and the Kohonen self-organizing map (Kohonen, 1984) was analyzed by physicists next door (Ritter and Schulten, 1988). In 1988, I decided to change field and apply my theoretical modeling skills to neuroscience.
I learned the tricks of mathematical analysis of Hopfield networks during an internship with Leo van Hemmen at the university of Munich early in 1989, which filled the time before I started a one-year stay as a visiting scholar at Berkeley in the lab of Bill Bialek. The hot topic in Munich (Herz et al., 1989) as well as in some other labs (Kleinfeld, 1986; Sompolinsky and Kanter, 1986) was an extension of the Hopfield model so as to store memories not in the form of stationary attractors, but as sequences of activity patterns (Herz et al., 1989). The networks were constructed with binary neurons that are either “on” or “off” and evolved in discrete time. Andreas Herz, who was then a student of Leo van Hemmen’s, discovered that, when signal transmission delays are correctly taken into account, both static and dynamic memories can be stored by the same Hebb rule (Herz et al., 1989). But what puzzled me at that time was the assumption of discrete time: Is it 1 ms per memory pattern or 2 ms, why not 20 or 0.5 ms? What sets this time scale?
When I moved to Berkeley in the summer of 1989, I was strongly impressed by the ideas of spike-based coding (Bialek et al., 1991), a topic of intense discussions in the Bialek lab at that time. My personal goal became to translate Hopfield models into spiking networks where the intrinsic neuronal time scale would be clearly defined (Gerstner, 1991; Gerstner and van Hemmen, 1992). After my return to Munich, I wondered whether my spiking networks would be able to learn spatio-temporal spike patterns. In analogy to earlier work on sequence learning (Herz et al., 1991), I realized that this would only be possible if I used a Hebbian learning rule which reflects the causality principle implicit in Hebb’s formulation: the timing must be such that synapses that contribute to firing the postsynaptic neuron are maximally strengthened. Hence long-term potentiation (LTP) must be maximal if the spike arrives at the synapse 1 or 2 ms before the postsynaptic spike so as to compensate for the rise time of the excitatory postsynaptic potential (Gerstner et al., 1993). The timing conditions were summarized in a figure, reprinted here as Figure 1. I also realized that I needed to postulate a back propagating action potential, so as to inform the synapse about the timing of postsynaptic spikes. For the sake of a little anecdote: one referee did not like such a naive postulate and asked me to mention explicitly that such a back propagating spike had never been found – so that’s what I wrote in the 1993 paper (Gerstner et al., 1993). Interestingly, 20 years earlier Leon Cooper had also seen the need to transmit information to the site of the synapse, but formulated his idea in a rate-coding picture (Cooper, 1973).
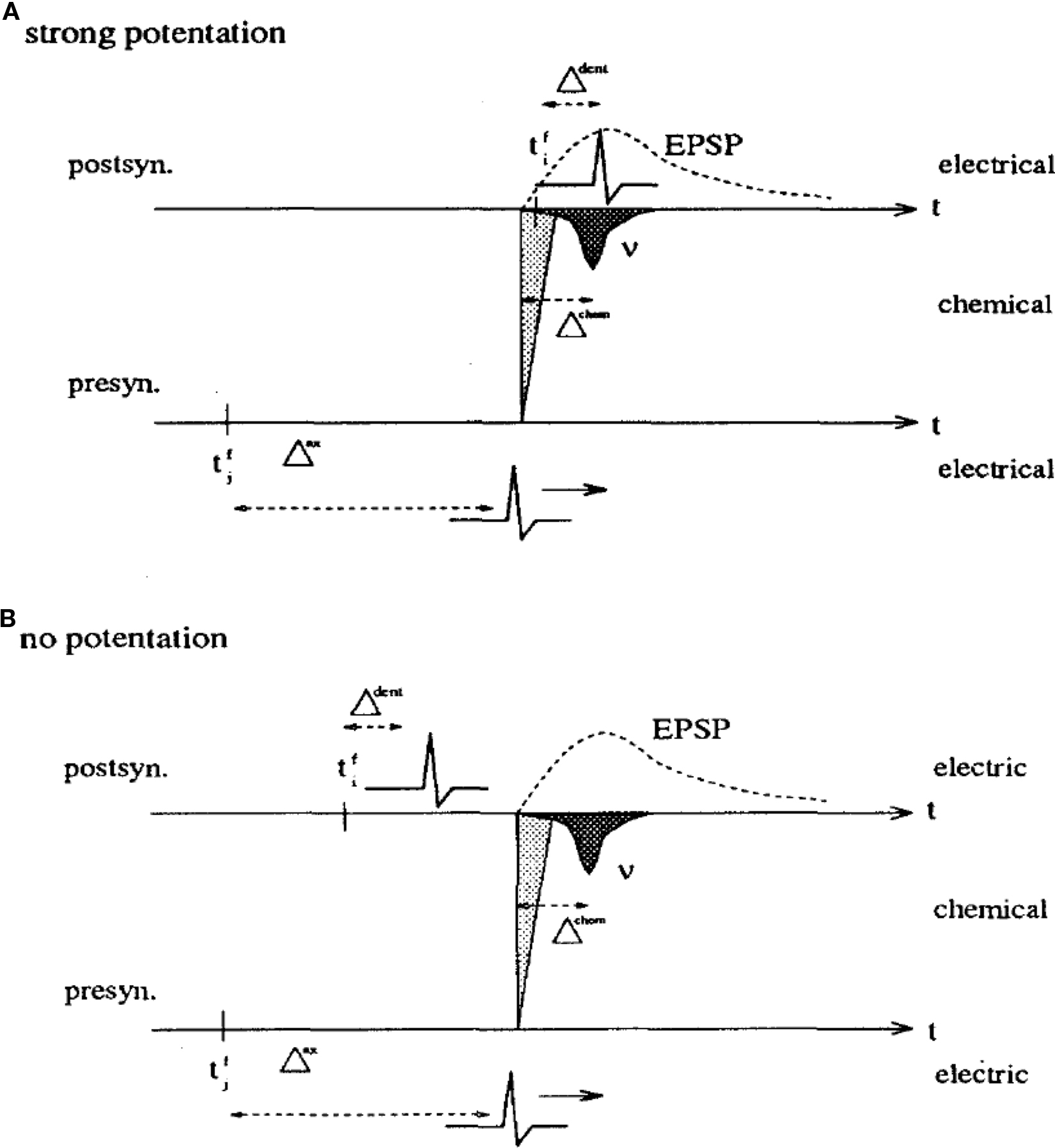
Figure 1. A copy of Figure 3 in Gerstner et al. (1993) with caption: Hebbian learning at the synapse. The presynaptic neuron j fires at time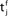 
and the postsynaptic neuron i at 
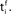It takes a time Δax and Δdent, respectively, before the signal arrives at the synapse. At the presynaptic terminal neurotransmitter is released (shaded) and evokes an EPSP (dashed) at the postsynaptic neuron. In (A) the dendritic spike arrives slightly after the neurotransmitter release and matches the time window defined by some chemical processes, so the synaptic efficacy is enhanced. In (B) the postsynaptic neuron fired too early and no strengthening of the synapse occurs.
In the 1993 paper, I assumed some unspecified chemical process that would set the “window of coincidences” for the causal pre-before-post situation. I postulated a coincidence window for asymmetric Hebbian learning with millisecond resolution, in order for the network to learn on this time scale. In the summer of 1994, Hermann Wagner, a barn owl expert, joined the Technical University of Munich for a sabbatical. He told us about the astonishing capacity of the owl’s auditory system to resolve time on the sub-millisecond scale, which is necessary to locate prey in complete darkness. Different neurons in the auditory nucleus in charge of detecting coincidences between spikes arriving from the left and right ears have different receptive fields in the temporal domain – for the theoreticians in the group of Leo van Hemmen a wonderful challenge.
Von der Malsburg, Kohonen, Bienenstock and colleagues as well as many others (von der Malsburg, 1973; Willshaw and von der Malsburg, 1976; Bienenstock et al., 1982; Kohonen, 1984) had shown in the 1970s and 1980s that the development of spatial receptive fields can be described by models based on Hebbian learning, but how could learning be possible for spiking neurons that have to learn features in the temporal domain? That was the topic of many discussions in the lab, in particular with Richard Kempter, a bright PhD student. From my previous experience with referees, it was clear that I could not simply postulate a Hebbian coincidence window of learning with a resolution of 10 μs to solve the task of learning temporal structures at that time scale – time constants in the auditory nuclei are faster than in visual cortex, but probably do not go below 1 ms.
After several nights of intense thinking, I suggested one morning to Richard that we should somehow exploit competition between good and bad timings, similar to spatial competition in networks with center excitation and surround inhibition, but translated to the problem of learning in the temporal domain. We therefore postulated what we called a Hebbian learning window with two regimes: good timings (i.e., presynaptic spikes arriving just before a postsynaptic firing event) should lead to a potentiation of the synapses, while bad timings (presynaptic spikes arriving after a postsynaptic spike) should lead to depression. Richard implemented the idea in a simulation and it worked beautifully. The graph of our hypothetical Spike-Timing-Dependent Plasticity (STDP) function as published in 1996 is included here as Figure 2.
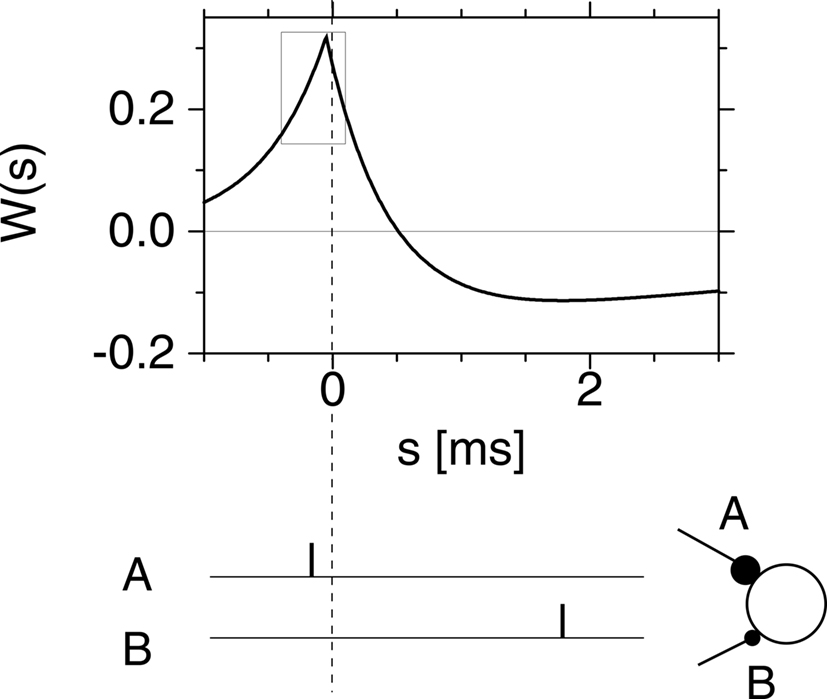
Figure 2. A copy of Figure 2d in Gerstner et al. (1996), with caption: “The postsynaptic firing occurs at time s = 0 (vertical dashed line). Learning is most efficient if presynaptic spikes arrive shortly before the postsynaptic neuron starts firing as in synapse A. Another synapse B which fires after the postsynaptic spike is weakened.”
We submitted our results in May 1995 to the 8th Neural Information Processing Conference (NIPS8) where we presented them in December that year (Kempter et al., 1996). The writing of the full paper started in the summer of 1995, before I left for a short postdoctoral period at Brandeis, where I stayed from September to December 1995. By the time we finally submitted the paper in February 1996, an abstract of Henry Markram and Bert Sakmann had been published in the Society of Neuroscience meeting from November 1995, which we cited in the final version of our manuscript, together with the paper of Debanne et al. (1994) for synaptic depression, so as to convince the referees that our assumptions were not entirely outrageous. For some reason, we missed to cite the paper of Levy and Stewart (Levy and Stewart, 1983).
While at Brandeis, I also learned that Larry Abbott and Kenny Blum had been working on ideas of asymmetric Hebbian learning in the context of hippocampal circuits involved in a navigation problem (Abbott and Blum, 1996). The Abbott-Blum paper from 1996 is formulated in a rate-coding picture and implements asymmetric Hebbian learning with a time window for LTP for pre-before-post (and the possibility of LTD for reverse timing) in the range of a few hundred milliseconds or a few seconds, but the formalism can easily be reinterpreted as STDP. When I joined Brandeis in 1995, the paper was already submitted and Kenny Blum had left, but Larry Abbott and myself continued this line of work together (Gerstner and Abbott, 1997).
References
Abbott, L. F., and Blum, K. I. (1996). Functional significance of long-term potentiation for sequence learning and prediction. Cereb. Cortex 6, 406–416.
Amit, D. J., Gutfreund, H., and Sompolinsky, H. (1985). Spin–glass models of neural networks. Phys. Rev. A 32, 1007–1032.
Bialek, W., Rieke, F., de Ruyter van Stevenick, R. R., and Warland, D. (1991). Reading a neural code. Science 252, 1854–1857.
Bienenstock, E. L., Cooper, L. N., and Munroe, P. W. (1982). Theory of the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. J. Neurosci. 2, 32–48.
Cooper, L. N. (1973) “A possible organization of animal memory and learning,” in Nobel Symposium on Collective Properties of Physical Systems, eds B. Lundquist and S. Lundquist (New York: Academic Press), 252–264.
Debanne, D., Gähwiler, B. H., and Thompson, S. M. (1994). Asynchronous pre- and postsynaptic activity induces associative long-term depression in area CA1 of the rat Hippocampus in vitro. Proc. Natl. Acad. Sci. U.S.A. 91, 1148–1152.
Gerstner, W. (1991) “Associative memory in a network of “biological” neurons,” in Advances in Neural Information Processing Systems 3, Conference in Denver 1990, eds R. P. Lippmann, J. E. Moody, and D. S. Touretzky (San Mateo, CA: Morgan Kaufmann Publishers), 84–90.
Gerstner, W., and Abbott, L. F. (1997). Learning navigational maps through potentiation and modulation of hippocampal place cells. J. Comput. Neurosci. 4, 79–94.
Gerstner, W., Kempter, R., van Hemmen, J. L., and Wagner, H. (1996). A neuronal learning rule for sub-millisecond temporal coding. Nature 383, 76–78.
Gerstner, W., Ritz, R., and van Hemmen, J. L. (1993). Why spikes? Hebbian learning and retrieval of time–resolved excitation patterns. Biol. Cybern. 69, 503–515.
Gerstner, W., and van Hemmen, J. L. (1992). Associative memory in a network of “spiking” neurons. Network 3, 139–164.
Herz, A. V. M., Li, Z., and van Hemmen, J. L. (1991). Statistical mechanics of temporal association in neural networks with transmission delays. Phys. Rev. Lett. 66, 1370–1373.
Herz, A. V. M., Sulzer, B., Kühn, R., and van Hemmen, J. L. (1989). Hebbian learning reconsidered: representation of static and dynamic objects in associative neural nets. Biol. Cybern. 60, 457–467.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U.S.A. 79, 2554–2558.
Kempter, R., Gerstner, W., van Hemmen, J. L., and Wagner, H. (1996). “Temporal coding in the sub-millisecond range: model of barn owl auditory pathway,” in Advances in Neural Information Processing Systems 8, conference in Denver 1995, (Cambridge: MIT Press), 124–130.
Kleinfeld, D. (1986). Sequential state generation by model neural networks. Proc. Natl. Acad. Sci. U.S.A. 83, 9469–9473.
Kohonen, T. (1984). Self-Organization and Associative Memory. Berlin, Heidelberg, New York: Springer-Verlag.
Levy, W. B., and Stewart, D. (1983). Temporal contiguity requirements for long-term associative potentiation/depression in hippocampus. Neuroscience 8, 791–797.
Ritter, H., and Schulten, K. (1988). Convergency properties of kohonen’s topology conserving maps: fluctuations, stability and dimension selection. Biol. Cybern. 60, 59–71.
Sompolinsky, H., and Kanter, I. (1986). Temporal association in asymmetric neural networks. Phys. Rev. Lett. 57, 2861–2864.
von der Malsburg, C. (1973). Self-organization of orientation selective cells in the striate cortex. Kybernetik 14, 85–100.
Citation: Gerstner W (2010) From Hebb rules to spike-timing-dependent plasticity: a personal account. Front. Syn. Neurosci. 2:151. doi: 10.3389/fnsyn.2010.00151
Received: 19 May 2010;
Accepted: 11 November 2010;
Published online: 09 December 2010.
Copyright: © 2010 Gerstner. This is an open-access publication subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: wulfram.gerstner@epfl.ch