- 1Department Biologie II, Ludwig-Maximilians-Universität München, Munich, Germany
- 2Bernstein Center for Computational Neuroscience Munich, Munich, Germany
Recurrent networks have been proposed as a model of associative memory. In such models, memory items are stored in the strength of connections between neurons. These modifiable connections or synapses constitute a shared resource among all stored memories, limiting the capacity of the network. Synaptic plasticity at different time scales can play an important role in optimizing the representation of associative memories, by keeping them sparse, uncorrelated and non-redundant. Here, we use a model of sequence memory to illustrate how plasticity allows a recurrent network to self-optimize by gradually re-encoding the representation of its memory items. A learning rule is used to sparsify large patterns, i.e., patterns with many active units. As a result, pattern sizes become more homogeneous, which increases the network's dynamical stability during sequence recall and allows more patterns to be stored. Last, we show that the learning rule allows for online learning in that it keeps the network in a robust dynamical steady state while storing new memories and overwriting old ones.
Introduction
Memories are based on synaptically induced changes of intrinsically generated brain activity. Examples for such intrinsic activities are the recurring sequences of neuronal activity patterns in the hippocampus (Wilson and McNaughton, 1994; Nadasdy et al., 1999; Lee and Wilson, 2002; Davidson et al., 2009); see Buhry et al. (2011); Wikenheiser and Redish (2012) for review. Classically, these sequences were interpreted as replaying previous activity patterns. Meanwhile they have been found to also preplay future behavior (Diba and Buzsaki, 2007) or reverse replay past behavior (Foster and Wilson, 2006; Diba and Buzsaki, 2007). More recently, it has been shown that they even predict future behaviors (Gupta et al., 2010; Dragoi and Tonegawa, 2011, 2013; Pfeiffer and Foster, 2013). The diversity of these sequences has generated an equally diverse set of possible functional explanations, ranging from memory consolidation (Nakashiba et al., 2009; Jadhav et al., 2012) to memory deletion (Hoffman et al., 2007) and path planning (Azizi et al., 2013; Ponulak and Hopfield, 2013).
In this paper, we will specifically address one variant of the memory consolidation and deletion hypothesis, viz. whether these sequences can be used to drive a learning rule that allows for efficiently re-encoding memories and thereby solve the problem of catastrophic forgetting. The basic idea of this hypothesis is that new memories might be encoded by assemblies that are not optimally sparse and thus allow secure retrieval. A retrograde learning rule that propagates long-term depression (LTD) will be shown to be able to reduce these assemblies toward a level of sparseness, which is optimal from the retrieval point of view and, at the same time, allows the network to operate in a stable regime of online learning, in which old memories are overwritten by new ones. This learning rule operates on a time scale that is slower than the fast time scale of initial imprinting. As a result, new memories will be represented by a larger number of neurons (and synapses) than old memories, which are encoded more efficiently and will eventually be forgotten.
Materials and Methods
Here, we investigate memory consolidation and retrieval in a network which stores sequential associations of binary patterns (Nadal, 1991; Gibson and Robinson, 1992; Hirase and Recce, 1996; Leibold and Kempter, 2006; Kammerer et al., 2013). As in these previous papers, the dynamics is formulated in discrete time. The individual time steps can be biologically interpreted as the cycles of a collective network oscillation (e.g., hippocampal ripple oscillations; Maier et al., 2011). The employed network model is identical to that described in Medina and Leibold (2013) and lays particular emphasis on handling heterogeneous pattern sizes, i.e., the number of active neurons at any time may be different. Formally, this is expressed by the vector of coding ratios
where Mk = fk N is the number of active neurons in the k-th binary pattern ξk ∈ {0, 1}N, N is the number of neurons in the network, and the indices k = 0, …, P represent each of the P + 1 patterns that are connected by the P pairwise directed associations. Unless mentioned otherwise, the coding ratios fk are randomly drawn from a gamma distribution (to avoid negative patterns sizes) with mean coding ratio ϕ0 and standard deviation σϕ.
The associations between the individual patterns of the sequence ξ0, ξ1, ξ2, … are stored in the synaptic weight matrix, which is chosen according to a clipped Hebbian rule (Willshaw et al., 1969): a synapse from neuron j to i has weight sij = 0 only if a spike of neuron i never follows one of neuron j in any of the P associations, otherwise sij = 1. In addition to this Willshaw rule, we also allow for a morphological connectivity, i.e., a synapse from neuron j to neuron i only exists with probability cm (Gibson and Robinson, 1992; Leibold and Kempter, 2006). This implies a second set of binary synaptic variables wij, with wij = 1 if the respective synapse exists and wij = 0 otherwise. For such a learning rule and heterogeneous pattern sizes, it was shown in Medina and Leibold (2013) that the probability c of a potentiated synaptic connection (sij = 1) equals
In this and related models, the choice of binary synapses facilitates the mathematical tractability of the theory, although, in biology, synaptic weights generally follow long-tailed distributions (Song et al., 2005). The long tail, however, allows one to subdivide synapses into weak and strong ones, which could be considered as being approximated by a noisy binary approach.
Synaptic Metaplasticity
According to Willshaw's learning rule, a synapse is in the potentiated state (sij = 1) if it connects two neurons that fire in sequence at least once. However, some neuron pairs may fire in sequence multiple times if they are part of the representation of consecutive patterns more than once. Although disregarded so far, the number of times a neuron pair fires in sequence is important since it tells us how many associations rely on this connection being potentiated. In order to conserve this information while using binary synapses, we consider synaptic meta levels with serial state transitions, a model similar to that proposed in Amit and Fusi (1994); Leibold and Kempter (2008).
A state diagram of our plasticity model is shown in Figure 1A. After a synapse has been potentiated once, every further occurrence of sequential firing in the sequence activation schedule increments the meta level by one, leaving the synaptic weight sij unchanged. Figure 1B shows the distribution of synaptic states in the network for three different pattern loads P. At higher loads, synapses are more likely to reach higher meta levels.
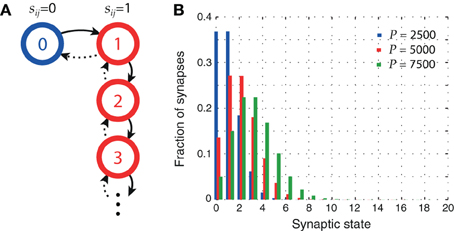
Figure 1. Synaptic metaplasticity. (A) Synaptic meta levels with serial state transitions. Learning initially potentiates the state (solid lines), whereas LTD signals decrement it (dotted lines) with probability q. (B) Distribution of synaptic states after storage of P patterns. The higher the network load, the more likely synapses are to be in higher meta levels. Parameters: N = 105, cm = 0.1, ϕ0 = 0.02, and σϕ = 0.1 ϕ0.
Network Dynamics
Following Medina and Leibold (2013), neurons are modeled using a simple threshold dynamics that translates the synaptic matrix Jij = sij wij into an activity sequence: a neuron i fires a spike at cycle t + 1 if its postsynaptic potential at time t exceeds the threshold θ. Here, xj(t) ∈ {0, 1} represents the binary state of neuron j at time t and b denotes the strength of a linear instantaneous feedback inhibition (Hirase and Recce, 1996; Kammerer et al., 2013). The negative feedback constant is chosen b = c for all subsequent simulations (Medina and Leibold, 2013).
To save computational time, most of the upcoming results are derived in a mean field approximation. To this end, in each time step, neurons are subdivided into two populations: an On population which is supposed to fire according to the sequence schedule and an Off population which is supposed to be silent (Leibold and Kempter, 2006). The number of active neurons at time step t can thus be divided into a number mt of correctly activated neurons (hits) and a number nt of incorrectly activated neurons (false alarms). Using these conventions yields the mean field dynamics (Medina and Leibold, 2013)
with
and denoting the cumulative distribution function of the normal distribution. Here, the mean number of synaptic inputs μ ≡ 〈h(t)〉 and the variance σ2 ≡ 〈h(t)2〉 − 〈h(t)〉2, for the On population, are
with ς = c/cm; see Equation (2). The analog expressions for the Off population are
Finally, the variability coefficient V2ς used in Equations (7) and (9) is given by
Retrosynaptic LTD
The replay model in Medina and Leibold (2013) assumed the synaptic matrix Jij to remain constant. Synaptic plasticity may, however, take place on a slower time scale and change network dynamics between consecutive replay events. In this paper, we investigate the idea that replay evokes a retrosynaptic LTD to achieve a more efficient utilization of synaptic resources, thereby increasing storage capacity. We therefore assume that the stored patterns are initially too large and, over time, are reduced by learning such that the coding ratios fk converge to an optimal value.
This idea is implemented as shown in Figure 2. During replay of association ξt → ξt + 1 (Figure 2A), active cells that receive excessive synaptic input send a retrosynaptic LTD signal to all presynaptic cells which were active in the previous time step. The emission of such a signal is modeled as a stochastic process in which the emission probability ψ increases with the number h of synaptic inputs received by the cell like
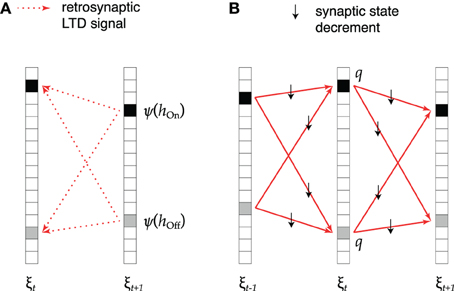
Figure 2. Retrosynaptic LTD. (A) During sequence replay, excessive depolarization h at time t + 1 triggers a retrosynaptic LTD signal that is propagated with probability ψ(h) to all presynaptic cells that were active at time t (black squares denote hits, gray squares denote false alarms). (B) Each cell receiving an LTD signal responds with probability q by decrementing the state of all its input synapses from cells that fired at time t − 1 and all its output synapses to cells that fired at time t + 1.
Here the parameter h0 defines a minimal pattern size M = h0/cm beyond which plasticity signals can occur. Its choice determines the optimal memory capacity of the network, as this minimal pattern size can become a stable fixed point of the dynamics of pattern sizes.
To combine this learning rule with the mean field network dynamics, we have to find an expression for the probability Ps that a presynaptic cell receives at least one retrosynaptic signal. The number of inputs received at time t + 1 is on average μOn for an On cell, and μOff for an Off cell. Thus, for an On cell, we have a probability (1 − ψ(μOn))cmmt + 1 of receiving no retrograde LTD signal from any active cell in the On population, and a probability (1 − ψ(μOff))cmnt + 1 of receiving no retrograde LTD signal from the Off population. Similarly, for an Off cell, these probabilities are (1 − ψ(μOn))cmmt + 1 and (1 − ψ(μOff))cmnt + 1, and thus
As illustrated in Figure 2B, upon receiving one or more LTD signals, with probability q, the presynaptic cell decrements by one the meta state of all its input synapses from the mt − 1 + nt − 1 cells that were active in the previous time step, as well as the meta state of all its output synapses to the mt + 1 + nt + 1 cells that are active in the following time step. Each synapse in the subset of decremented synapses therefore takes part in one association less. As a result, the cell no longer takes part in the neural representation of pattern ξt, although it might still be spuriously activated during replay. On average, the size of pattern ξt is therefore updated according to
where .
Online Learning
If associations are stored in the network one after another (online learning), new memories will overwrite old memories (Nadal et al., 1986; Amit and Fusi, 1994), which is also known as palimpsest learning, and thereby the connectivity between On neurons of old associations is increasingly diluted. The remaining signal strength of an association k depends on the probability yk = 1 − p(0|k) that a synapse is not in state zero, given that it participates in association ξk → ξk + 1 (i.e., it connects neurons that fired in sequence during the storage of that association). To account for overwriting, the dynamical Equations (6) and (7) are modified as follows
In our model framework, the synaptic connectivity is changed in two ways. First, during imprinting of a new association, synapses increment their meta state level. Second, synaptic states are decremented via retrosynaptic LTD. To capture these changes, we define the average state distribution ρ(s), which describes the probability that an arbitrarily chosen synapse is in state s, and thus c/cm = 1 − ρ(0).
Effect of synaptic potentiation on state distribution
If a new association is added that links pattern ξk to pattern ξk + 1, a random synapse increases its state with probability fkfk + 1 and thus the change in the state distribution is
where
and 1I is the unit matrix.
Effect of synaptic depression on state distribution.
Conversely, retrograde LTD is described by the matrix multiplication
where
and ps, p′s are the probabilities that a replay event decreases the state s of a random synapse by 1 and 2, respectively.
To obtain ps and p′s, we define the probability p(s, ↓) = ρ(s) ps that a synapse is in state s and receives the signal to go down one meta level. Similarly, p(s, ↓↓) = ρ(s) p′s is the probability that a synapse is in state s and receives the signal to go down two meta levels.
A depression event ↓ during replay of the association ξk → ξk + 1 can have two origins: (1) the depression signal ↓(k+) that is sent by a neuron of pattern ξk to its output synapses, and (2) the depression signal ↓(k−) the neuron sends to its input synapses. Since a subpopulation of synapses may be part of both the inputs and the outputs of pattern ξk, a synapse may be depressed twice and thus go down two levels. Since the patterns are statistically independent, both depression events are independent and thus the probability that a synapse is in state s and goes down by two levels upon replay of association ξk → ξk + 1 is given by
Similarly, the probability p(s, −) that a synapse stays in state s is
A synapse either stays in state s, it goes down by one state or goes down by two states, and thus
This normalization condition then yields the probability p(s, ↓) that a synapse is in state s and is decreased by one, viz.
The probabilities p(s, ↓(k±)) can be further split up into two non-overlapping subsets of synapses, one (called k) that connects the On populations of association k and another one (called k) denoting all other synapses. Therefore we have
Since the LTD signal ↓ is independent of the synapse state s, we have
and in analogy for k − 1. The last terms on the right-hand side are obtained from equations (12) and (13) as follows
and
What remains to be obtained in Equations (27) and (28) are the conditional probabilities p(s|k) and p(s|k). From heuristic considerations, we approximate
Equation (33) assumes that the presence of association ξk → ξk + 1 can affect the conditional state distribution p(s|k) in two ways: either it increases the state by one (p(s − 1|k) rk), or it has no effect on the state (p(s|k) (1 − rk)). The constants rk can be interpreted as the fraction of synapses for which association ξk → ξk + 1 contributes to the next meta level. We will refer to them as the remaining memory strength of association k.
Combining equation (33) with
we can recursively compute
and in particular provide a connection between rk and yk via
Effect of synaptic depression on signal connectivity
In addition to changes in the state distribution ρ that describes the noise connectivity during associations, retrosynaptic LTD also specifically influences the synapses between the On populations according to yl = 1 − p(0|l). For more recent associations yl will be large, whereas for older associations yl will be small. The change in yl that results from retrosynaptic LTD while replaying association ξk → ξk + 1 is computed from the change in p(0|l),
For associations l ∉ {k − 1, k} the conditional probabilities of depression are independent of the association l, i.e., p(↓|s, l) = p(↓|s) = ps and p(↓↓|s, l) = p′s. The conditional state occupancies are obtained via the r-factors from Equation (36) as p(s|l) = p(s − 1|l) rl + p(s|l) (1 − rl).
For associations k − 1 and k, synapses can only experience by-chance LTD from one of the two signals (association k − 1 from ↓(k+) and association k from ↓(k−)), since LTD from the other signal would result in a decrease of the pattern size (with undiluted connectivity). Likewise there is no double decrement for these associations. As a result, the update rules for these associations are
and, replacing k − 1 by k,
The probabilities p(1|k, k − 1), p(1|k, k − 1) and p(1|k, k − 1) in Equations (38) and (39) can be obtained in analogy to
due to statistical independence of the patterns.
Effect of synaptic depression on subthreshold variance
The dynamics of sequence replay not only depends on the mean connectivities c and cm yk but also on the second moment of the connectivity matrix as captured by V2ς from Equation (10). Retrosynaptic LTD will also affect this second moment. As an approximation, we again use the r-factors from Equation (36), which are an estimate of the fraction of presynaptic On neurons that contribute to the meta level of association k. Thus, we can replace the coding ratio fk − 1 in Equations (2) and (10) by the diluted coding ratio rk − 1 fk − 1 and obtain
Since the definition of the r-factors in Equation (33) implements only an approximation, the two ways of computing the mean connectivities via c/cm = 1 − ρ(0) and c/cm = 1 − ∏Pk = 1 (1 − fk fk − 1rk − 1) are slightly different. To achieve numerical robustness we obtain ρ(0) by applying Newton's method to solve the implicit Equation
for ρ(0) in which the r-factors have been expressed via Equation (36).
Results
Retrosynaptic LTD During Sequence Replay Sparsifies Large Patterns
The mean field description for the pattern size changes from Equation (14) can be interpreted as a dynamical system itself, since it constitutes a discrete-time iterated map on the pattern sizes. The time scale of this dynamics is slower than the time scale of sequence replay since, during the replay of a sequence, the pattern sizes change only by a small amount. Figures 3A,B show the temporal evolution of the sizes of some example patterns and of the full distribution of pattern sizes for q = 0.1 that results from the mean field Equation (14). The simulations show that the pattern sizes converge to a common fixed point and, as a result, the pattern size distribution becomes delta-like. For such homogeneous pattern sizes the memory capacity is maximized (Medina and Leibold, 2013).
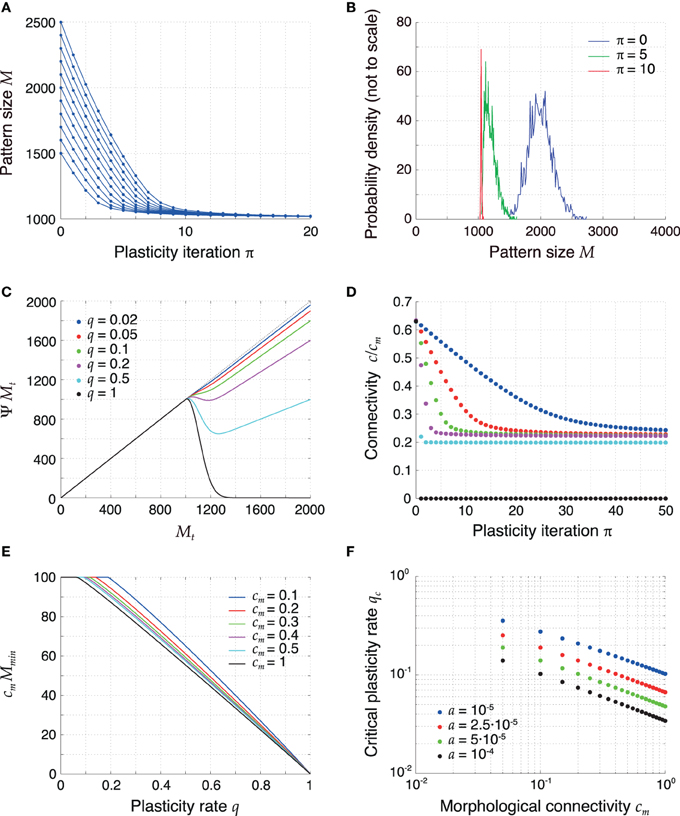
Figure 3. Retrosynaptic LTD signals sparsify and homogenize the pattern size distribution. (A) Evolution of the sizes of a few sample patterns for q = 0.1. (B) Evolution of the full pattern size distribution. Initially (blue), sizes are very inhomogeneous (σϕ/ϕ0 = 10%). After 5 iterations (green) of plasticity, patterns are encoded more sparsely and the sequence becomes more homogeneous. After 10 iterations (red), the sequence is essentially homogeneous. (C) The plasticity map given by (14), showing how a pattern size Mt is sparsified as a function of q. The curves shown were obtained with parameters a = 2.5·10−5 and h0 = 100 in (11) and setting mt + 1 = ϕ0 N and nt + 1 = 0 in (12). For too high q values (q ⪆ 0.2), the fixed point of the dynamics of pattern sizes at M = h0/cm = 1000 is surpassed. (D) Connectivity decreases as a result of plasticity sparsifying stored patterns (P = 2500). The rate of decrease increases with q. (E) Minimal value of cm Ψ M as a function of q for different values of cm and constant h0. At the critical value of q the curves bend down in a non-differentiable way. (F) Critical LTD probability qc as a function of cm for constant h0. Other parameters: N = 105, ϕ0 = 0.02, and cm = 0.1 unless mentioned otherwise.
To more systematically analyze plasticity on the slow time scale, we revisit dynamical Equation (14) and interpret it as a one-dimensional iterated map Mt → Ψ Mt. Figure 3C visualizes the iteration function Ψ M for different values of q. For small q, the fixed-point Equation M = Ψ M has a solution for a maximal pattern size M = h0/cm, which serves as an attractor of the discrete dynamics for all starting values M > h0/cm. If q is too high, the iteration function bends down for M > h0/cm and there is no longer a single fixed point for all initial pattern sizes M > h0/cm. The critical value of q is thus determined by the condition
which means that the minimum of the iteration function Ψ M for M > h0/cm is smaller or equal h0/cm. The critical value qc is the smallest value of q for which condition (43) is fulfilled and is indicated by the kink of the graphs in Figure 3E. For larger q the iterated map can produce pattern sizes below h0/cm, which are then marginally stable fix points but the resulting pattern sizes may be too small for successful replay. The critical qc is not universal and depends on parameters. Most importantly, it decreases with cm and a (Figure 3F). The critical value remained above a few percent for a wide range of parameters. Specifically, in sparsely connected networks (cm ≪ 1), the choice q ≈ 0.05 is generally subcritical and thus allows for an optimal storage capacity.
The dynamics of pattern sizes is paralleled by a dynamics of the mean network connectivity from Equation (2); Figure 3D. A reduction of the pattern sizes leads to a corresponding decrease in connectivity. The rate of this decrease is higher for higher values of q. For subcritical values of q (0 < q ≤ qc) the average connectivity converges to a fixed point that is independent of q. For supercritical q (1 > q > qc) the connectivity converges to a lower fixed-point connectivity, indicating a substantial fraction of too small pattern sizes. In the extreme case q = 1 all synapses are depotentiated and the connectivity converges to 0.
Plasticity During Sequence Replay Increases Dynamic Stability
The changes in connectivity due to retrosynaptic LTD are paralleled by changes of fast dynamics of sequence replay according to Equations (3) as exemplarily illustrated for three different plasticity stages (initial, after 5 and 10 iterations) and firing thresholds in Figure 4. As plasticity proceeds and the pattern size distribution in the sequence becomes more homogeneous, the activity fluctuations during replay are reduced and, eventually, allow for the whole sequence to be retrieved successfully.
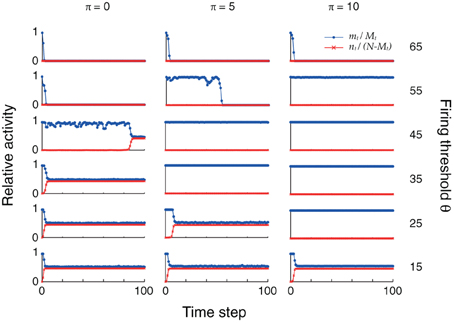
Figure 4. Plasticity of pattern sizes increases the dynamic stability during sequence replay. In all graphs, we show the fraction mt/Mt of hits (blue) at time step t and the fraction nt/(N − Mt) of false alarms (red) during the replay of a sequence (only the first 100 time steps are shown), using the mean field model of Equations (3) and following. Left to right: increasing plasticity iterations. Bottom to top: increasing firing thresholds θ. The initial pattern size distribution had parameters ϕ0 = 0.02 and σϕ/ϕ0 = 10%. Other parameters were N = 105, cm = 0.1 and P = 2500.
In the example of Figure 4, learning extends the range of thresholds under which the network successfully replays the full sequence if the network was perfectly initialized (m0 = M0, n0 = 0). For a large threshold (e.g., θ = 55), learning allows for the emergence of ongoing sequence replay in a regime where initially no self-sustained network activity was possible. Before any plasticity takes place, the pattern sizes are highly inhomogeneous and the network falls silent almost immediately. After 5 plasticity iterations, fluctuations are reduced and the network is able to successfully retrieve more items in the sequence. Near perfect pattern retrieval (mt/Mt = 1 and nt/(N − Mt) = 0) is made possible after 10 iterations. Similarly, for low thresholds (e.g., θ = 25), replay initially drives the network into an epileptic state (mt/Mt ≈ nt/(N − Mt) ≈ 0.5). The reduction of pattern sizes due to learning, again, allows for ongoing sequence replay.
Defining the retrieval quality (Leibold and Kempter, 2006)
as the relative difference between hit ratio and false alarm ratio, allows a better comparison of the replay performance for a large set of parameter choices. Formally this is done via the replay success rate, which is the fraction of runs for which at time t the replay quality Γt is above 0.5 (Medina and Leibold, 2013).
Figure 5A shows the evolution of replay success rates for three plasticity stages and three different memory loads P. Initially, the pattern sizes are large and inhomogeneous, and ongoing sequence replay is not possible. Only for small loads (P = 2500) and for a small firing threshold range (θ ≈ 45), can the first items be retrieved with high probability. As plasticity reduces inhomogeneity and sparsifies the patterns, the range of firing thresholds θ for which the full sequence can be retrieved expands. This is made possible by a decrease in the noise connectivity c, shown in Figure 5B and verified through cellular simulations. In a modified model without synaptic meta states there was no improvement by applying repeated learning steps, since synapses were switched to an inactive state too quickly (Figure 5C).
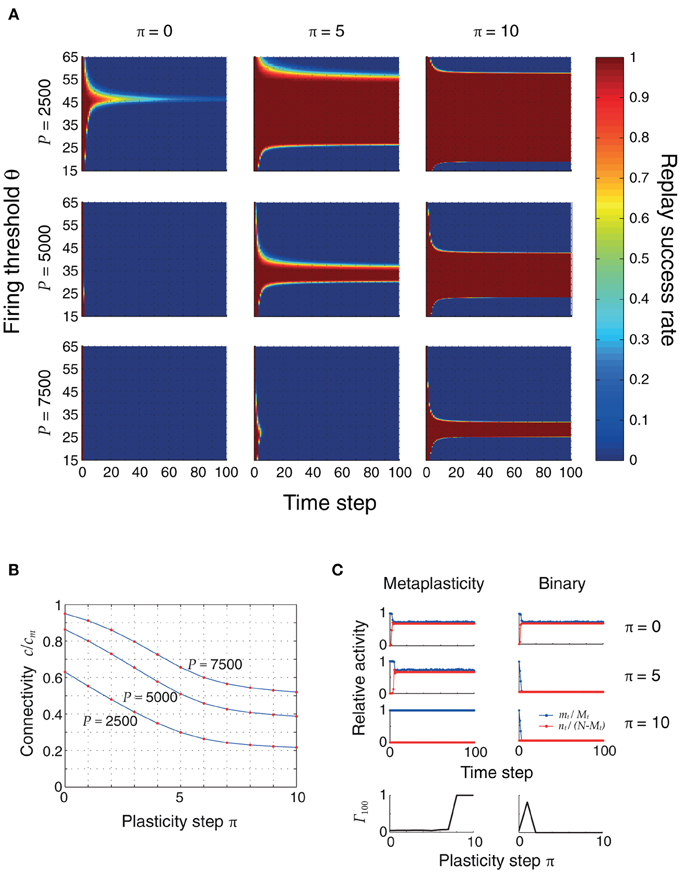
Figure 5. (A) Replay success rate over time for different firing thresholds θ and a sequence of length Q = 100. These plots were obtained using the mean field model, and were verified using cellular simulations. Left to right: increasing plasticity iterations. Top to bottom: increasing pattern load P. The initial pattern size distribution had parameters ϕ0 = 0.02 and σϕ/ϕ0 = 10%. Other parameters were: N = 105, cm = 0.1. (B) Connectivity decreases as the network sparsifies its stored associations. This plot was obtained by simulating the actual neural network with three different pattern loads P and a randomly generated coding ratio vector ϕ. The connectivity was calculated both using the mean field equation (2) (blue) and counting the actual number of potentiated synapses (red dots), showing a perfect match. (C) Advantage of metaplasticity (left) over simple binary synapses (right) during retrosynaptic LTD. Blue and red traces indicate hits and false alarms (as in Figure 4) for 0, 5 and 10 learning steps. The bottom row depicts the replay quality of the 100th pattern in the sequence as a function of the number of learning steps. Only with metaplasticity the replay remains stable for many learning steps.
Online Learning
So far, the initial distribution of pattern sizes was centered at mean values far above the fixed point M = h0/cm. However, once the pattern size distribution has reached this optimal value, retrosynaptic LTD will only take place if a new association with an oversized pattern is added into the synaptic matrix. In our model, this can be simulated as a homogeneous sequence with one pattern of size larger than M = h0/cm, as illustrated in Figure 6: for low firing thresholds (θ = 26), the excess synaptic drive generated by an oversized pattern initially leads to sequence termination by setting the network into an epileptic state. Plasticity via retrosynaptic signals gradually reduces the size of the problematic pattern, eventually allowing for successful replay of the full sequence. This shows that retrosynaptic LTD in principle makes it possible to integrate new associations into the network, and therefore provides a possible basis for online learning, i.e., the ongoing storage of new memories.
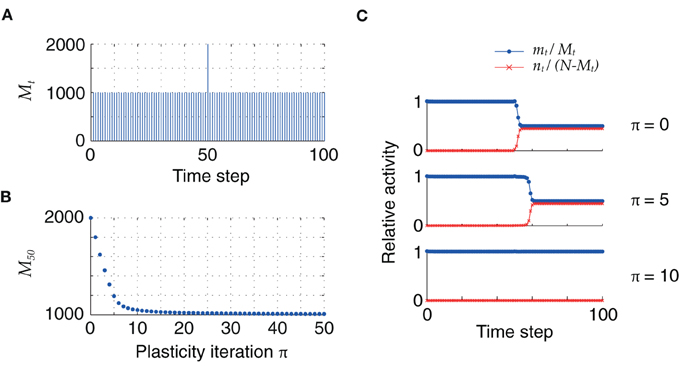
Figure 6. (A) Homogeneous sequence with a double-sized pattern at t = 50. (B) Evolution of oversized pattern with plasticity (q = 0.1). (C) Initially, sequence replay fails at t = 50 because of the excessive synaptic drive generated by the oversized pattern, which leads the network to an epileptic state (top). After 5 iterations, the network explosion is slower but still present (middle). Successful replay of the full sequence is possible after 10 iterations (bottom). Parameters: N = 105, cm = 0.1, c = 5%, ϕ0 = 0.01, θ = 26.
Of course, adding new associations (increasing P) will consequently also increase the mean connectivity c, up to a point at which classically memories can no longer be retrieved (Willshaw et al., 1969; Nadal, 1991; Kammerer et al., 2013). For these large connectivities c the false alarms add considerable synaptic inputs such that a neuron is no longer always able to correctly decide whether it should fire or not. Using our present model of retrograde LTD, however, neurons could detect such over-excitation and may subsequently depress synapses.
To investigate whether this mechanism allows for self-organized sequence replay in a steady state, we set up a simulation in which we add sequences of 7 new patterns before each plasticity episode and monitor the retrieval quality as well as the mean connectivity. The dynamics of the connectivity c and cm yk is thereby simulated according to Section 2.4.
The result of one such simulation is summarized in Figure 7. The simulation starts with an empty network, i.e., all synapses are in state 0. Each time after storing a new sequence, the newest 60 sequences (if already available) are replayed starting with perfect initialization of the first pattern, m = M and n = 0. These replays induce retrosynaptic LTD. Before the network has reached a steady state, replay is generally successful for all sequences (Figure 7A) and is worse for the last recalled patterns in younger sequences, because there the pattern sizes have not yet converged to their optimum h0/cm = 1000. This is because oversized patterns tend to evoke dynamical instabilities that lead to many false alarms and bad replay quality. After the network has reached a steady state, the first of the 60 replays generally fail, whereas the younger sequences can be replayed at high quality (Figure 7B). Interestingly, the mean connectivity c converges to its steady state more quickly than the replay dynamics (Figure 7C). The pattern sizes are slightly above their optimum h0/cm (Figure 7D; note that each 7th pattern is the final pattern of each sequence and does not shrink according to the learning rule. These final patterns stay at their initial size). Only for the newest patterns the sizes reflect the initial distribution (here a uniform distribution between 1000 and 2000).
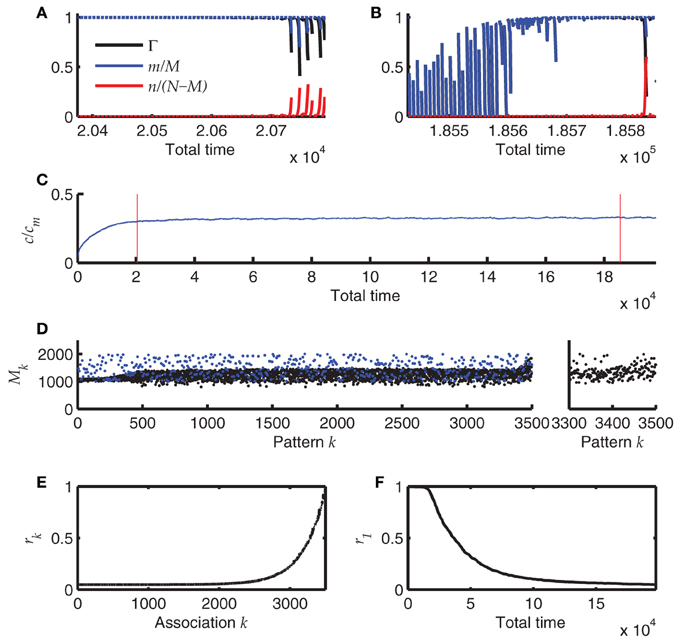
Figure 7. Online learning. (A) Replay of the 60 most recent sequences before the network has reached a steady state. Blue and red lines depict hits and false alarms, respectively, black line indicates the retrieval quality Γ. (B) Same as A after the network has reached its steady state. (C) Mean connectivity c as a function of time. (D) Pattern sizes. Blue dots indicate the sizes of the last (7th) pattern of each sequence. (E) The remaining memory strength r of all associations at the end of the simulation (500 sequences; 3500 patterns). (F) The memory strength of the oldest association as a function of simulation time. Parameters of the simulation were N = 4 · 104, cm = 0.1, b = 0.03, θ = 30, h0 = 100, a = 10−5. The simulation was terminated after having stored 500 sequences of length 7.
The r values that measure the remaining memory strength of an association (see Methods), provide an additional view on the memory capacity of the network; Figure 7E. Their convergence to zero for old memories reflects the memory time scale of the network. Additionally, the approach to the steady state is made visible if one monitors the r value of the oldest memory (r1) over time (Figure 7F). The convergence of r is much slower than the convergence of the mean connectivity c (Figure 7C), explaining why the replay dynamics further changes long after the mean connectivity has reached its steady state.
Discussion
Fast hippocampal activity sequences have been hypothesized to underlie memory consolidation (Ego-Stengel and Wilson, 2010; Mölle and Born, 2011; Jadhav et al., 2012). On the cellular level, the associated re-encoding of episodic memories can either occur at the synapses between hippocampus and neocortex (Buzsaki, 1996; Frankland and Bontempi, 2005) or within the hippocampus itself. So far, hypotheses for hippocampus-intrinsic consolidation were mainly focusing on synaptic mechanisms (Frey and Morris, 1997; Milekic and Alberini, 2002; Päpper et al., 2011). The present paper provides a mechanistic model of memory re-encoding on the circuit level whereby associations between assemblies of neurons are not strengthened over time, but assemblies are reduced in size to utilize the hippocampal resources more efficiently.
Retroaxonal learning affecting both input and output synapses of a neuron has been suggested to aid stabilization of recent memories previously (Harris, 2008), although only in the context of synaptic potentiation. There, neurotrophins have been hypothesized to constitute a plausible underlying biochemical pathway. Here, we suggest a specific functional role for a retroaxonal spread of depression and have shown that it may allow a network to operate in an online mode where old memories are overwritten by new memories. Moreover, the suggested retrograde LTD predicts that depression in output synapses should be correlated with depression in input synapses.
A different mechanism suggested to reduce the overall excitatory drive in a network is synaptic scaling, whereby all synapses of an overexcited neuron undergo LTD (Turrigiano et al., 1998; Watt et al., 2000; Turrigiano, 2008; Savin et al., 2009). Retroaxonal learning is a more content-specific mechanism than synaptic scaling since it only affects synapses that have been active in the recent past and thus generally accounts for longer retention times.
Previous models of online learning (Amit and Fusi, 1994; Fusi et al., 2005; Ben Dayan Rubin and Fusi, 2007; Leibold and Kempter, 2008; Amit and Huang, 2010; Huang and Amit, 2011) usually do not explicitly take into account the network dynamics underlying the induction of plasticity. This paper presents a hypothesis of how LTD can be derived from network dynamics. The initial imprinting of the memories by LTP is still ad-hoc since we assume it to be occurring via extra-hippocampal signals.
Several other theoretical explanations for sequence replay and the sharp-wave ripple state have been suggested. (1) Sequences can be seen as avalanche-like activity patterns that are amplified by dendritic non-linearities (Memmesheimer, 2010; Jahnke et al., 2012, 2013). (2) CA1 pyramidal cell spike patterns may be triggered by strong feedforward excitation from CA3 inputs that are temporally coordinated by fast recurrent inhibition (Ylinen et al., 1995; Geisler et al., 2005; Taxidis et al., 2012). (3) The ripple oscillation may result from a network of gap-junction coupled axons (Traub et al., 1999; Traub and Bibbig, 2000; Vladimirov et al., 2013). (4) Sequences may result from a few overlapping attractor states in a recurrent network of neurons (Azizi et al., 2013). So far, these models are hardly evaluated with respect to their memory capacity (although coding capacity was probed in Azizi et al., 2013).
High memory capacities have been found in classical models of memory networks, developed independently of the hippocampal physiology, that suppose neuronal sequences to result from attractor networks with asymmetrically biased synaptic matrices (Dehaene et al., 1987; Buhmann and Schulten, 1988) in discrete time. One major drawback of these classical theories as well as the model presented here is their formulation in discrete time, which makes them hard to connect to cell-physiological properties of pyramidal cells. On the cellular level, sequence replay is most likely associated with the presence of huge precisely timed excitatory and inhibitory synaptic conductances (Maier et al., 2011). Whether and how under such conditions a neuron can fire and, more specifically, can select to fire at one specific oscillation cycle during a ripple, remains to be shown.
Sparsification of the hippocampal code may be an important intermediate step to prepare consolidation of memories in the hippocampal-neocortical loop, since generally storage capacity increases with sparseness (Nadal, 1991; Leibold and Kempter, 2006) and associating large hippocampal assemblies with neocortical states might be too costly. On the other hand, initially large assemblies might have the advantage that new associations can be retrieved more robustly. Optimal sparseness cannot be obtained by translating from one brain area to another via a random connectivity matrix, since then associations get lost as they may fall in the lower tail of the statistical distribution of the number of synaptic connections and thus do not give rise to sufficient excitation in the downstream brain area. Optimally sparse codes, hence, always require additional plasticity rules that carve out the subset of neurons that can fire reliably. The activity-driven increase in sparseness could also explain the prevalence of a few dominant preplay sequences (Dragoi and Tonegawa, 2013) that may provide an easily addressable substrate for future associations. Our model predicts that, once these sequences are connected with a memory item, the internal representation becomes more sparse and the sequences are no longer spontaneously visible. However, they are nevertheless stored within the hippocampal synaptic matrix and can be retrieved upon presentation of appropriate cue patterns.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was funded by the German Federal Ministry for Education and Research (BMBF) under grant numbers 01GQ0981 (Bernstein Fokus on Neuronal Basis of Learning: Plasticity of Neuronal Dynamics) and 01GQ1004A (Bernstein Center for Computational Neuroscience Munich).
References
Amit, D. J., and Fusi, S. (1994). Learning in neural networks with material synapses. Neural Comput. 6, 957–982. doi: 10.1162/neco.1994.6.5.957
Amit, Y., and Huang, Y. (2010). Precise capacity analysis in binary networks with multiple coding level inputs. Neural Comput. 22, 660–688. doi: 10.1162/neco.2009.02-09-967
Azizi, A. H., Wiskott, L., and Cheng, S. (2013). A computational model for preplay in the hippocampus. Front. Comput. Neurosci. 7:161. doi: 10.3389/fncom.2013.00161
Ben Dayan Rubin, D. D., and Fusi, S. (2007). Long memory lifetimes require complex synapses and limited sparseness. Front. Comput. Neurosci. 1:7. doi: 10.3389/neuro.10.007.2007
Buhmann, J., and Schulten, K. (1988). “Storing sequences of biased patterns in neural networks with stochastic dynamics,” in Neural Computers, Vol. 41, eds R. Eckmiller and V. D. C. Malsburg (Berlin, Heidelberg: Springer-Verlag), 231–242.
Buhry, L., Azizi, A. H., and Cheng, S. (2011). Reactivation, replay, and preplay: how it might all fit together. Neural Plast. 2011, 203462. doi: 10.1155/2011/203462
Buzsaki, G. (1996). The hippocampo-neocortical dialogue. Cereb. Cortex 6, 81–92. doi: 10.1093/cercor/6.2.81
Davidson, T. J., Kloosterman, F., and Wilson, M. A. (2009). Hippocampal replay of extended experience. Neuron 63, 497–507. doi: 10.1016/j.neuron.2009.07.027
Dehaene, S., Changeux, J. P., and Nadal, J. P. (1987). Neural networks that learn temporal sequences by selection. Proc. Natl. Acad. Sci. U.S.A. 84, 2727–2731. doi: 10.1073/pnas.84.9.2727
Diba, K., and Buzsaki, G. (2007). Forward and reverse hippocampal place-cell sequences during ripples. Nat. Neurosci. 10, 1241–1242. doi: 10.1038/nn1961
Dragoi, G., and Tonegawa, S. (2011). Preplay of future place cell sequences by hippocampal cellular assemblies. Nature 469, 397–401. doi: 10.1038/nature09633
Dragoi, G., and Tonegawa, S. (2013). Distinct preplay of multiple novel spatial experiences in the rat. Proc. Natl. Acad. Sci. U.S.A. 110, 9100–9105. doi: 10.1073/pnas.1306031110
Ego-Stengel, V., and Wilson, M. A. (2010). Disruption of ripple-associated hippocampal activity during rest impairs spatial learning in the rat. Hippocampus 20, 1–10. doi: 10.1002/hipo.20707
Foster, D. J., and Wilson, M. A. (2006). Reverse replay of behavioural sequences in hippocampal place cells during the awake state. Nature 440, 680–683. doi: 10.1038/nature04587
Frankland, P. W., and Bontempi, B. (2005). The organization of recent and remote memories. Nat. Rev. Neurosci. 6, 119–130. doi: 10.1038/nrn1607
Frey, U., and Morris, R. G. (1997). Synaptic tagging and long-term potentiation. Nature 385, 533–536. doi: 10.1038/385533a0
Fusi, S., Drew, P. J., and Abbott, L. F. (2005). Cascade models of synaptically stored memories. Neuron 45, 599–611. doi: 10.1016/j.neuron.2005.02.001
Geisler, C., Brunel, N., and Wang, X. J. (2005). Contributions of intrinsic membrane dynamics to fast network oscillations with irregular neuronal discharges. J. Neurophysiol. 94, 4344–4361. doi: 10.1152/jn.00510.2004
Gibson, W. G., and Robinson, J. (1992). Statistical analysis of the dynamics of a sparse associative memory. Neural Netw. 5, 645–661. doi: 10.1016/S0893-6080(05)80042-5
Gupta, A. S., van der Meer, M. A., Touretzky, D. S., and Redish, A. D. (2010). Hippocampal replay is not a simple function of experience. Neuron 65, 695–705. doi: 10.1016/j.neuron.2010.01.034
Harris, K. D. (2008). Stability of the fittest: organizing learning through retroaxonal signals. Trends Neurosci. 31, 130–136. doi: 10.1016/j.tins.2007.12.002
Hirase, H., and Recce, M. (1996). A search for the optimal thresholding sequence in an associative memory. Network 4, 741–756. doi: 10.1088/0954-898X/7/4/008
Hoffman, K. L., Battaglia, F. P., Harris, K., MacLean, J. N., Marshall, L., and Mehta, M. R. (2007). The upshot of up states in the neocortex: from slow oscillations to memory formation. J. Neurosci. 27, 11838–11841. doi: 10.1523/JNEUROSCI.3501-07.2007
Huang, Y., and Amit, Y. (2011). Capacity analysis in multi-state synaptic models: a retrieval probability perspective. J. Comput. Neurosci. 30, 699–720. doi: 10.1007/s10827-010-0287-7
Jadhav, S. P., Kemere, C., German, P. W., and Frank, L. M. (2012). Awake hippocampal sharp-wave ripples support spatial memory. Science 336, 1454–1458. doi: 10.1126/science.1217230
Jahnke, S., Memmesheimer, R. M., and Timme, M. (2013). Propagating synchrony in feed-forward networks. Front. Comput. Neurosci. 7:153. doi: 10.3389/fncom.2013.00153
Jahnke, S., Timme, M., and Memmesheimer, R.-M. (2012). Guiding synchrony through random networks. Phys. Rev. X 2, 041016. doi: 10.1103/PhysRevX.2.041016
Kammerer, A., Tejero-Cantero, Á., and Leibold, C. (2013). Inhibition enhances memory capacity: optimal feedback, transient replay and oscillations. J. Comput. Neurosci. 34, 125–136. doi: 10.1007/s10827-012-0410-z
Lee, A. K., and Wilson, M. A. (2002). Memory of sequential experience in the hippocampus during slow wave sleep. Neuron 36, 1183–1194. doi: 10.1016/S0896-6273(02)01096-6
Leibold, C., and Kempter, R. (2006). Memory capacity for sequences in a recurrent network with biological constraints. Neural Comput. 18, 904–941. doi: 10.1162/089976606775774714
Leibold, C., and Kempter, R. (2008). Sparseness constrains the prolongation of memory lifetime via synaptic metaplasticity. Cereb. Cortex 18, 67–77. doi: 10.1093/cercor/bhm037
Maier, N., Tejero-Cantero, Á., Dorrn, A. L., Winterer, J., Beed, P. S., Morris, G., et al. (2011). Coherent phasic excitation during hippocampal ripples. Neuron 72, 137–152. doi: 10.1016/j.neuron.2011.08.016
Medina, D., and Leibold, C. (2013). Inhomogeneous sparseness leads to dynamic instability during sequence memory recall in a recurrent neural network model. J. Math. Neurosci. 3, 8. doi: 10.1186/2190-8567-3-8
Memmesheimer, R. M. (2010). Quantitative prediction of intermittent high-frequency oscillations in neural networks with supralinear dendritic interactions. Proc. Natl. Acad. Sci. U.S.A. 107, 11092–11097. doi: 10.1073/pnas.0909615107
Milekic, M. H., and Alberini, C. M. (2002). Temporally graded requirement for protein synthesis following memory reactivation. Neuron 36, 521–525. doi: 10.1016/S0896-6273(02)00976-5
Mölle, M., and Born, J. (2011). Slow oscillations orchestrating fast oscillations and memory consolidation. Prog. Brain Res. 193, 93–110. doi: 10.1016/B978-0-444-53839-0.00007-7
Nadal, J.-P. (1991). Associative memory: on the (puzzling) sparse coding limit. J. Phys. A 24, 1093–1101. doi: 10.1088/0305-4470/24/5/023
Nadal, J. P., Toulouse, G., Changeux, J. P., and Dehaene, S. (1986). Networks of formal neurons and memory palimpsests. Europhys. Lett. 1, 535–542. doi: 10.1209/0295-5075/1/10/008
Nadasdy, Z., Hirase, H., Czurko, A., Csicsvari, J., and Buzsaki, G. (1999). Replay and time compression of recurring spike sequences in the hippocampus. J. Neurosci. 19, 9497–9507.
Nakashiba, T., Buhl, D. L., McHugh, T. J., and Tonegawa, S. (2009). Hippocampal CA3 output is crucial for ripple-associated reactivation and consolidation of memory. Neuron 62, 781–787. doi: 10.1016/j.neuron.2009.05.013
Päpper, M., Kempter, R., and Leibold, C. (2011). Synaptic tagging, evaluation of memories, and the distal reward problem. Learn. Mem. 18, 58–70. doi: 10.1101/lm.2024811
Pfeiffer, B. E., and Foster, D. J. (2013). Hippocampal place-cell sequences depict future paths to remembered goals. Nature 497, 74–79. doi: 10.1038/nature12112
Ponulak, F., and Hopfield, J. J. (2013). Rapid, parallel path planning by propagating wavefronts of spiking neural activity. Front. Comput. Neurosci. 7:98. doi: 10.3389/fncom.2013.00098
Savin, C., Triesch, J., and Meyer-Hermann, M. (2009). Epileptogenesis due to glia-mediated synaptic scaling. J. R. Soc. Interface 6, 655–668. doi: 10.1098/rsif.2008.0387
Song, S., Sjostrom, P. J., Reigl, M., Nelson, S., and Chklovskii, D. B. (2005). Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 3:e68. doi: 10.1371/journal.pbio.0030068
Taxidis, J., Coombes, S., Mason, R., and Owen, M. R. (2012). Modeling sharp wave-ripple complexes through a CA3-CA1 network model with chemical synapses. Hippocampus 22, 995–1017. doi: 10.1002/hipo.20930
Traub, R. D., and Bibbig, A. (2000). A model of high-frequency ripples in the hippocampus based on synaptic coupling plus axon-axon gap junctions between pyramidal neurons. J. Neurosci. 20, 2086–2093.
Traub, R. D., Schmitz, D., Jefferys, J. G., and Draguhn, A. (1999). High-frequency population oscillations are predicted to occur in hippocampal pyramidal neuronal networks interconnected by axoaxonal gap junctions. Neuroscience 92, 407–426. doi: 10.1016/S0306-4522(98)00755-6
Turrigiano, G. G. (2008). The self-tuning neuron: synaptic scaling of excitatory synapses. Cell 135, 422–435. doi: 10.1016/j.cell.2008.10.008
Turrigiano, G. G., Leslie, K. R., Desai, N. S., Rutherford, L. C., and Nelson, S. B. (1998). Activity-dependent scaling of quantal amplitude in neocortical neurons. Nature 391, 892–896. doi: 10.1038/36103
Vladimirov, N., Tu, Y., and Traub, R. D. (2013). Synaptic gating at axonal branches, and sharp-wave ripples with replay: a simulation study. Eur. J. Neurosci. 38, 3435–3447. doi: 10.1111/ejn.12342
Watt, A. J., van Rossum, M. C., MacLeod, K. M., Nelson, S. B., and Turrigiano, G. G. (2000). Activity coregulates quantal AMPA and NMDA currents at neocortical synapses. Neuron 26, 659–670. doi: 10.1016/S0896-6273(00)81202-7
Wikenheiser, A. M., and Redish, A. D. (2012). Hippocampal sequences link past, present, and future. Trends Cogn. Sci. (Regul. Ed.) 16, 361–362. doi: 10.1016/j.tics.2012.05.005
Willshaw, D. J., Buneman, O. P., and Longuet-Higgins, H. C. (1969). Non-holographic associative memory. Nature 222, 960–962. doi: 10.1038/222960a0
Wilson, M. A., and McNaughton, B. L. (1994). Reactivation of hippocampal ensemble memories during sleep. Science 265, 676–679. doi: 10.1126/science.8036517
Keywords: associative memory, memory capacity, sparse coding, recurrent plasticity, memory consolidation
Citation: Medina D and Leibold C (2014) Re-encoding of associations by recurrent plasticity increases memory capacity. Front. Synaptic Neurosci. 6:13. doi: 10.3389/fnsyn.2014.00013
Received: 30 December 2013; Accepted: 19 May 2014;
Published online: 10 June 2014.
Edited by:
Florentin Wörgötter, University Goettingen, GermanyReviewed by:
Jochen Triesch, Johann Wolfgang Goethe University, GermanyRaoul-Martin Memmesheimer, Radboud University Nijmegen, Netherlands
Copyright © 2014 Medina and Leibold. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daniel Medina, Department Biologie II, Ludwig-Maximilians-Universität München, Großhaderner Strasse 2, 82152 Planegg, Munich, Germany e-mail:bWVkaW5hQGJpb2xvZ2llLnVuaS1tdWVuY2hlbi5kZQ==
 Daniel Medina
Daniel Medina Christian Leibold
Christian Leibold