- 1School of Instrumentation and Optoelectronic Engineering, Beihang University, Beijing, China
- 2School of Electrical and Computer Engineering, Seoul National University, Seoul, South Korea
Holography has emerged as one of the most attractive three-dimensional display technologies. With the technological development of computer science and coherent light source, the computer-generated holography has been applied in many fields. However, the speckle noise of the holographic reconstructed image seriously affects the viewing experience. In this paper, the cause of speckle noise generation in holographic display is introduced. Then, discussions about the speckle noise suppression methods are provided. The discussions are categorized into iterative and non-iterative approaches. Besides, we also introduce other speckle noise suppression techniques which are proposed from the perspective of light coherence, human visual system and optical system. Finally, the prospects of different types of approaches are summarized.
Introduction
Holography was first proposed by D. Gabor in 1948 (Gabor, 1948). It can record and reconstruct the entire wave-front information of the object. In 1965, A.W. Roman successfully made the first computer-generated hologram (CGH) and the theoretical foundation of CGH was established (Brown and Lohmann, 1966). In this period, the researchers mainly focused on the hologram encoding methods, and the main device for producing holograms was a plotter. Then, Lohmann proposed three different forms of circuitous phase-encoded holograms (Brown and Lohmann, 1969). Subsequently, Paris applied the fast Fourier transform (FFT) algorithm to speed up the calculation of the Fourier hologram, which greatly shortened the calculation time (Lohmann and Paris, 1967). After the 1980s, various types of spatial light modulators (SLMs) and new recording materials were developed (Zhan et al., 2020), which created new opportunities for holographic display. Many researchers gradually paid attention to the display effects of the different types of SLMs, and the researchers focused on the various hologram generation algorithms. So, different methods were developed, such as the look-up table method (Lucente, 1993), stereo holography method (Yamaguchi et al., 1992) and integrated holography method (St. Hilaire et al., 1992). Since 2000, liquid crystal on silicon (LCoS) has become a new research hotspot. The LCoS uses electrical signals to control the deflection of liquid crystal molecules for achieving modulation of the incident light phase (Chen et al., 2018). Then, the focus of researches was to improve the calculation speed of holograms by using GPU acceleration and optimizing physical models based on the LCoS (Nishitsuji et al., 2018; Lin et al., 2021). In addition, an increasing number of researchers paid attention to the field of view (FOV) and image quality of the holographic display (Maimone et al., 2017; Shi et al., 2017; Jang et al., 2018; Wang et al., 2020a; Zhao et al., 2020; Wu and Zhang, 2021; Yoo et al., 2021).
Although CGH has many advantages, there still exists many problems needed to be solved in the display field. One of the key issues is the speckle noise because it seriously affects the viewing experience. It is generally considered that the speckle noise in holographic displays is generated from the quantization error and the spatial coherence. In the past 20 years, more and more researchers have focused on the method for speckle noise suppression. Recently, the requirements to improve the quality of reconstructed images become more urgent. There are a large variety of methods for speckle noise reduction.
This paper gives the overview on the speckle noise suppression of holographic display based on spatial light modulator, and the main body is divided into the following sections. Firstly, the reason for speckle noise in CGH is described. Meanwhile, three criteria for quantizing the effect of speckle noise in the holographic reconstruction are provided. Besides, we introduce the speckle noise suppression process by considering various strategies. The described speckle noise reduction methods are mainly categorized into iterative method and non-iterative methods. In addition, other speckle noise suppression techniques are also introduced, which are proposed from the perspective of light coherence, human visual system and optical system. Finally, the prospects of these methods are summarized.
Speckle Noise Problem in Holographic Display
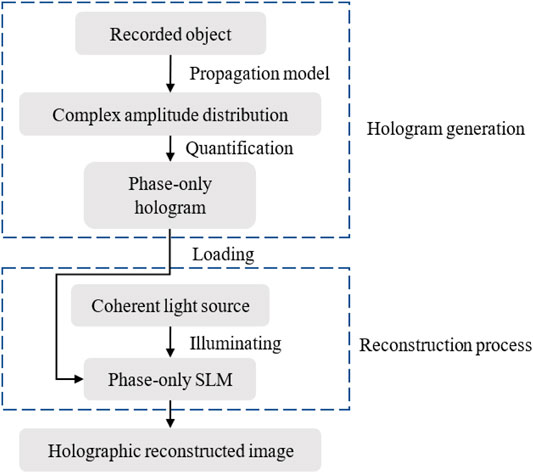
Since the commercial SLMs are either phase-only type or amplitude-only type, the holograms need to be encoded into phase-only or amplitude-only type to fit the type of SLM. Among them, the phase-only SLM has higher diffraction efficiency, so it is currently widely used in the holographic display. The principle of CGH display based on the phase-only SLM is shown in Figure 1. In the hologram generation process, the complex amplitude distribution of the recorded object can be obtained by using the point-based propagation model. Then, the phase-only hologram can be generated by encoding the complex amplitude distribution of the recorded object. The encoding process can also be regarded as a quantization process, which is the sampling and approximation of the complex amplitude distribution. In the reconstruction process, the phase-only SLM is needed to realize the optical reconstruction of the CGH. By loading the phase-only hologram on the phase-only SLM and illuminating it with the coherent light source, the image can be reconstructed.
In general, the speckle noise in holographic display is considered generated from the perspective of software and hardware. The software and hardware refer to the computer generation process of the hologram and the optical reconstruction process, respectively. Speckle noise results from the interference. In encoding process, the approximate sampling is regarded as the quantization error of the holographic reconstruction and it is inevitable. Due to the quantization error, the speckle noise is generated by the uncontrolled coherence effects of the reconstructed image. When the phase in the reconstructed image is a random distribution, the reconstructed image points will disturb each other and produce a randomly changed intensity because of the phase difference. In order to simulate the scattered light on the surface of the recorded object, the random phase is added to the recorded object in hologram algorithms. As shown in Figure 2, the recorded object consists of parts with low frequencies and high spatial frequencies. For a recorded object without random phase, only high-frequency and part of low-frequency of the information can be recorded on the CGH, while the edge of the low-frequency cannot be recorded. Although the random phase is a generator to ensure that the recorded object information spread completely over the CGH, it is also the main cause of the speckle noise generation (Shimobaba and Ito, 2015).
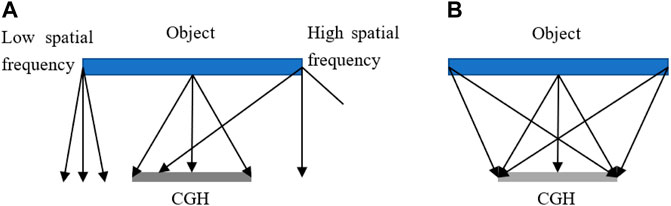
FIGURE 2. Propagation model for the hologram generation (A) without random phase (B) with random phase.
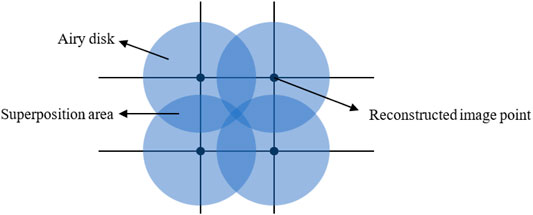
Moreover, during the optical holographic reconstruction, coherent light sources and optical devices are also the causes of the speckle noise generation. The reconstructed points exist in the form of Airy disks because of the limited aperture of the optical elements and the diffraction effects, as shown in Figure 3. The speckle noise becomes more serious with increasing of the superposition area. The optical reconstruction process is imperfect since the dust, scratches in the lens and aberrations can produce additional speckle noises. Different from the quantization error, this kind of error caused by the hardware is called systematic error.
Finally, to assess the speckle noise suppression effect, three criteria can be used to investigate: the peak signal-to-noise ratio (PSNR), structural similarity (SSIM) index and speckle contrast (SC). Besides, the foveal perception, wirtinger flow method and subjective quality evaluation can also be used for evaluation (Bolek and Makowski, 2019; Chakravarthula et al., 2021). PSNR is the most commonly used objective measurement method for evaluating image quality, which can be defined as follows:
where X and Y represent the object image and the reconstructed image, respectively, m and n represent the resolutions. The unit of PSNR is 1dB. A higher value of the PSNR usually means the effect of speckle noise suppression is better.
SSIM is also a very important parameter for evaluating the reconstructed image quality. For the holographic reconstructed image x and recorded object y, the SSIM of the two images can be expressed as follows:
where µx and µy are the average of image x and image y, respectively. σx2 and σy2 are the variance of image x and image y, respectively. σxy is the covariance between images x and y. c1=(k1L)2 and c2=(k2L)2 are two constants used to maintain stability and L is the dynamic range of pixel values, where K1 equals to 0.01 and K2 equals to 0.02 (Duan et al., 2019).
SC is the simplest parameter to evaluate the speckle noise of the reconstructed image, and it satisfies the following equation:
where σ and Ī represent the standard deviation of intensity and the average of intensity, respectively. The lower SC indicates the less speckle noise in the reconstructed image.
Methods of Speckle Noise Suppression
There are many kinds of methods for suppressing the speckle noise, and they can be discussed based on the hologram generation process and the reconstruction process. Based on the hologram generation process, the CGH algorithm can be divided into two categories: iterative and non-iterative methods. Based on the reconstruction process, we also introduce other speckle noise suppression techniques which are proposed from the perspective of light coherence, human visual system and optical system.
Iterative Methods
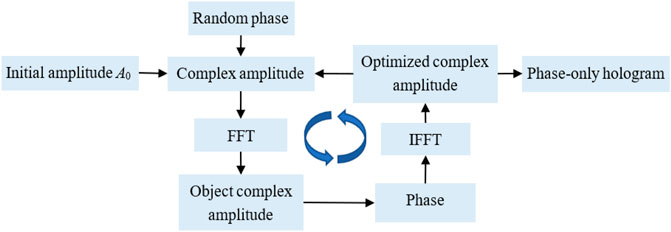
Among the iterative methods that can generate phase-only holograms, the iterative Fourier transform algorithm is a representative method. The characteristic of this type of algorithm is the iterative propagation in two planes by using the Fourier transform (Bu et al., 2021). The most famous and mostly used method is the Gerchberg-Saxton (GS) algorithm (Gerchberg and Saxton, 1972). As shown in Figure 4, the amplitude constraint is imposed on the object plane and hologram plane, then the phase is continuously iterated between the hologram plane and object plane. After several iterations, the phase distribution on the hologram plane converges to an optimal value. Therefore, the amplitude information of the object can be encoded into the phase-only hologram. Moreover, it is also possible to use the Fresnel transform instead of the Fourier transform to simulate light field propagation.
Many improved CGH algorithms have been developed based on the GS algorithm. The GS algorithm with weight coefficients (GSWC) has been proposed to improve the convergence rate and suppress the speckle noise (Kuzmenko et al., 2011; Wu et al., 2021a). The GSWC algorithm replaces the original constraint with the weight coefficients multiplied by the amplitude of the recorded object. The quality of the reconstructed image using the GSWC algorithm is improved by 75% compared with the GS algorithm. Moreover, the uniform random phase generator used by the GS algorithm is also an important cause of the speckle noise. To optimize the random phase generator, an iterative method with bandwidth constraint strategy has been proposed (Chen et al., 2021a). As shown in Figure 5, in order to suppress the speckle noise and provide effectively controls of the reconstructed intensity fluctuations, the iterative method can optimize the phase of the CGH by using the bandwidth constraint strategy of the reconstructed image and quadratic initial phase. The SC of the method with bandwidth constraint strategy is 46% lower than that of the GS method.
Different from the iteration between the object plane and the hologram plane, the error diffusion (ED) method is another type of iterative algorithm, which iterates between the pixels of the hologram (Barnard et al., 1989). As shown in Figure 6, H represents a pixel of the CGH, (x, y) represents the pixel coordinate point, E and k represent the quantization error of the pixel point and the weight coefficient, respectively. Since the ED method diffuses the quantization error to adjacent pixels of the phase-only hologram and homogenizes them, the speckle noise generated by the quantization error can be suppressed. However, the calculation time of the ED method increases proportionally with the resolution of the hologram.
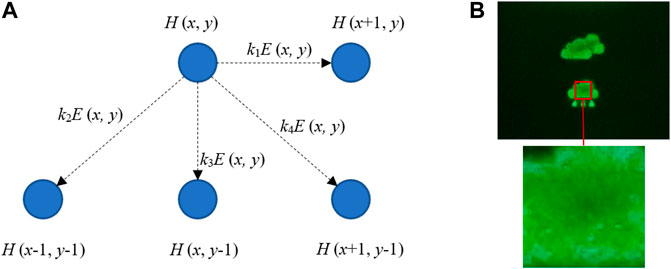
FIGURE 6. Illustration of the ED method. (A) Schematic diagram of the ED method and (B) the reconstructed image by using the ED method.
Based on the ED method, some researchers have introduced two enhanced methods which are known as the localized error diffusion and redistribution (LERDR) and bidirectional error diffusion (BERD). In these methods, the conversion of a complex Fresnel hologram to a phase-only hologram can be conducted in a parallel manner (Ysang et al., 2014). Compared with the localized error diffusion (LERD) algorithm, the PSNR of the reconstructed image by using LERDR and BERD algorithm is nearly 10 dB higher on average. Besides, the combination of the ED and the digital lens has been proposed (Chang et al., 2015; Wang et al., 2020b; Jiao et al., 2020; Li et al., 2020). The suppression effect of speckle noise can be improved by more than 60% on average compared with the ED method.
Recently, with the rapid development of the camera and computation, the camera with an algorithm can be used to optimize the phase distribution of the CGH. Camera-in-the-loop (CITL) holographic algorithm has been proposed to reduce the gap between the numerical simulation and optical reconstruction, since the optical system is imperfect. However, the direct current (DC) noise from the SLM cannot be eliminated in CITL on-axis setup. To solve this problem, a holographic display system has been proposed by using a new CITL optimization and two phase-only SLM (Choi et al., 2021a). This display system is inspired by the design of Michelson interferometers, so that called Michelson holography (MH). Compared with the double phase-amplitude coding (DPAC) method, the PSNR of the reconstructed image by using MH method is about 6 dB higher in the optical experiment. Nonetheless, the calculation time of the MH method is too much for the multi-depth recorded object. To solve this problem, a multi-depth holographic display method has been proposed by using stochastic gradient descent (SGD) with complex loss function (Chen et al., 2021b). For the recorded object with 20 depth layers, the calculation time of the proposed method is faster 94.36% than that of the SGD based on amplitude loss method.
Non-Iterative Methods
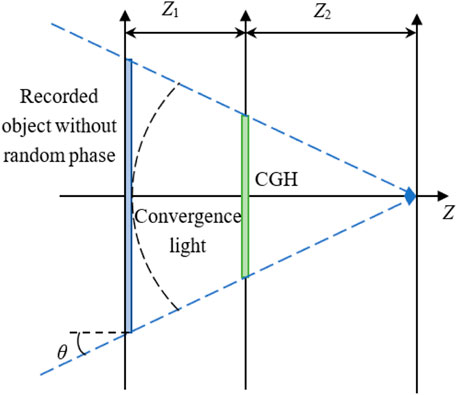
As non-iterative methods, the multi-random phase method and multiple fractional Fourier transform method have been used for reducing the speckle noise (Jun et al., 1995; Zheng et al., 2009; Wang et al., 2020c). These methods are effective in speckle noise suppression, but they are time-consuming. To reduce the calculation time and suppress the speckle noise at the same time, the random phase-free method has been proposed by multiplying the recorded object with the virtual convergence light (Shimobaba and Ito, 2015; Nagahama et al., 2019). As shown in Figure 7, the recorded object multiplies with the virtual convergence light instead of the random phase. The recorded object information is completely diffused in the CGH by using the virtual convergence light. The virtual convergence light also avoids the speckle noise generated by the random phase. It should be noted that the incident angle θ of the convergence light must be smaller than the maximum diffraction angle of the SLM to avoid the aliasing error. Compared with the random phase method, the PSNR of the numerically reconstructed image using the random-phase-free method is nearly 30 dB higher.
Since the random phase could lead to the excessive diffusion of information and degrades the image quality, the gradient-limited random phase (GL-RP) addition method and the limited-random-phase (L-RP) time average method have been developed to avoid excessive diffusion of the object information (Ma et al., 2017; Zhao et al., 2019). In the numeral simulation of the GL-RP method, the PSNR and SSIM of the reconstructed image increase by 10 and 13%, respectively. The L-RP method finds that the random phase of the recorded object has an appropriate range, which is limited to 1.2π–1.5π. When the limited random phase is applied in the hologram generation process, the speckle noise can be reduced significantly.
The pixel separation method is also one of the most famous methods. The recorded object is separated into different point groups by pixel separation. For each point group, the sub-CGHs with independent initial random phases are generated. Then, the speckle noise is reduced by the time average (Mori et al., 2014; Liu et al., 2019; Masaya and Yuji, 2019). Compared with the non-separation method, the speckle contrast of the reconstructed image by using these methods is reduced by more than 80%. Therefore, a combination of the pixel separation method and the time average can suppress the speckle noise effectively. However, the high-refresh SLM is necessary for these methods since the time average reduces frame rates of the holographic display. The speckle noise can be further suppressed with the increase of the separated interval and the number of the sub-CGHs.
In the generation process, the Fresnel CGH can be binarized in a non-iterative manner through down-sampling the recorded object with a grid lattice prior. Meanwhile, the down-sampling method can suppress the speckle noise as well. However, the results of the down-sampling method have a prominent texture of regularly that is spaced voids in the shaded regions. To solve this problem, an enhanced method based on grid-cross down-sampling (GCD) has been proposed (Cheung et al., 2011; Tsang et al., 2013). The reconstructed images of these methods have proved that the speckle noise can be suppressed effectively. However, a sparse appearance with many empty voids is generated in reconstructed image when using the GCD method. To suppress the speckle noise and the sparse appearance at the same time, a combination of the GCD and a time-division comb filtering (TDCF) approach has been proposed (Liu et al., 2020; Tsang et al., 2020). The PSNR of the reconstructed image by using the LRDS method can reach almost 30 dB. Moreover, the intermediate angular-spectrum method (IASM) has been proposed by avoiding the numerical circular convolution (Chen et al., 2019). Compared with the zero-padding method, the PSNR of the reconstructed image based on the IASM method can be improved by 36%.
On the other hand, the size of the diffraction region affects the quality of the reconstructed image. In order to reduce the speckle noise caused by the useless diffraction region, a wave-front recording plane (WRP) method with a limiting diffraction region has been proposed (Yanagihara et al., 2020). As shown the green area in Figure 8, the useless diffraction region can be avoided in CGH generation process. The experimental results demonstrate that the speckle noise can be reduced efficiently by using the WRP method with the limited circular diffraction region. Besides, a method to suppress the speckle noise in the holographic display based on effective utilization of two phase-only SLMs has also been verified availably (Wang et al., 2019). This method combines the pixel separation, the time multiplexing and the limit diffraction region to reduce the speckle noise. Compared with the conventional point-based method, the speckle contrast of the reconstructed image by using this method is reduced by 21.57%, and the calculation time is reduced by 48.53%.
The speckle noise can also be efficiently suppressed by using the complex amplitude encoding method. For the speckle reduction, an efficient coding method by using lossy compression has been verified (Bernardo et al., 2021). Both the effect of the speckle noise caused by the encoding process and the speckle noise caused by the compression in the recorded object have been discussed in this method. In addition, a combination of the time-multiplexing and the hologram optimization approach has been proposed (Hamann et al., 2018). This approach suppresses the speckle noise by an alternating direction method of multipliers optimization. The simulation demonstrates a significant improvement in the PSNR of the reconstructed image under higher rank factorization. Besides, the double-phase hologram (DPH) provides a better approximation to encode complex amplitude fields. Recently, the speckle-less holographic display based on DPH method has been proposed (Mendoza-Yero et al., 2014; Qi et al., 2016). In DPH method, the complex amplitude information is encoded as two-phase values, then the two phase values are combined into the pixel of the phase-only CGH by using two binary complementary chessboard masks. Since the two-phase values can be synthesized into the corresponding complex amplitude values, the quantization error is reduced and the speckle noise is suppressed. Furthermore, these methods can suppress the speckle noise and reduce the calculation time at the same time because of the free of iteration. Compared with the iterative Fourier transform algorithm, the speckle contrast of the reconstructed image by using the DPH method is reduced by more than 60%.
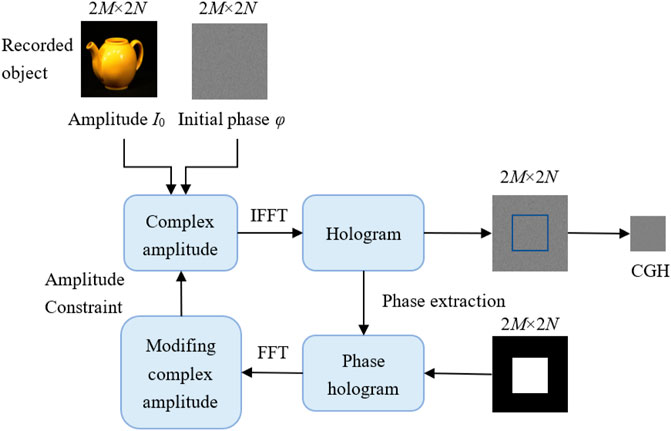
The hologram generation method based on deep learning is also a non-iterative method, which has great potential to realize real-time and speckle-free holographic display (LeCun et al., 2015; Horisaki et al., 2018; Eybposh et al., 2020; Lee et al., 2020a; Curtis et al., 2021; Park and Park, 2020). The convolutional neural network (CNN) has been demonstrated usefully in revealing the deep relationships between the input object and output hologram (Lee et al., 2020a). The learned CNN has the advantages of speckle reduction and fast calculation speed. Recently, a combination of the CNN and a modified double phase approach has been proposed to achieve a high-quality real-time holographic display (Shi et al., 2021). As shown in Figure 9, they introduce an anti-aliasing double phase method (AA-DPM) to generate the hologram dataset, which can reduce both high-frequency noise and speckle noise. The CNN is utilized to learn the relationship between the input 3D object and the Fresnel hologram dataset. The loss function in the training period consists of two types of loss functions: one is to measure the error of the predicted hologram, and the other one is to measure the quality of the reconstructed 3D object. Through the training strategy, the CNN can learn the characteristic of the hologram with high precision, so as to eliminate speckle noise effectively (Chakravarthula et al., 2020; Peng et al., 2020; Choi et al., 2021b; Wu et al., 2021b).
Methods Based on the Light Coherence and Optical System
During the optical holographic reconstruction, the coherent light source is one of the main causes of speckle noise generation. Therefore, reducing the coherence of the light source is helpful to suppress the speckle noise. To reduce the coherence, a random laser has been demonstrated usefully (Redding et al., 2012). In conventional coherent light sources, the low spatial coherence and the laser-level intensity are mutually exclusive. As a new kind of light source, the random laser is ideal for display because it has both properties.
Furthermore, in conventional holographic display, the reconstructed images suffer from the trade-off between the speckle noise and the resolution. To alleviate the trade-off problem, the theoretical models for quantifying the effect of the low-coherence have been introduced (Lee et al., 2020b). In this theoretical model, an optimal coherence light source with the maximum effect of the speckle suppression can be found. However, although the light source is optimized for considerable speckle noise suppression, the sacrifice of the resolution and the depth of field is inevitable. Then, this method has been demonstrated to alleviate the trade-off. Moreover, by combining the tunable-focus lens and the local illumination module, a speckle reduced holographic display prototype has been built (Lee et al., 2020c). In order to reduce the speckle noise while maintaining resolution, depth of field and frame rate, the tomographic synthesis method has been applied. The experimental results demonstrate that this method can suppress the speckle contrast averagely by 37.8% while keeping the resolution and depth of field unchanged.
Besides, a novel CGH encoding method based on a low-coherence light source has also been proved feasible for speckle noise reduction (Duan et al., 2019). Compared with the angular spectrum method, the PSNR of the reconstructed image by using this novel encoding method is improving by more than 60%. It is meaningful that this novel encoding method can be combined with other algorithms based on the low-coherence light source. The previous methods of suppressing speckle noise do not take the perceptual characteristics of the human visual system (HVS) into account (Chakravarthula et al., 2021). Considering the HVS, a method by incorporating anatomically-informed model of human perception has been proposed to reduce the speckle noise. Some users have been invited to evaluate the reconstructed image by using the proposed method.
Finally, we summarize the prospects of three types of methods. Iterative algorithms based on GS method have good flexibility to suppress the speckle noise. However, the computational speed of these algorithms is limited by the number of iterations, which makes it difficult to implement real-time holographic display. As another iterative method, the ED method requires fewer computational resources and reduces the speckle noise well. However, it is not suitable for the CGH with random phase involved because of the limited complex amplitude information correction ability.
As the non-iterative algorithms, the random-phase-free method, the pixel separation method, the down-sampling method, the double phase method and the deep learning method can suppress the speckle noise and improve the quality of the reconstructed image. Generally, the non-iterative algorithms are suitable for the real-time holographic display because they occupy less computational resources. Among them, deep-learning-based hologram generation methods are the most promising one because of the effectiveness in the speckle noise suppression. However, although the speckle noise suppression method based on the current deep-learning-based algorithms is impressive, the whole display system is still a bit huge and complex to commercialization.
On the other hand, reducing the coherence of the light source and systematic errors are also helpful to suppress the speckle noise. However, the low-coherence light source has drawbacks, which are the serious impact on the sharpness and contrast of the reconstructed image (Memmolo et al., 2014; Montrésor et al., 2019). It is important to find an intermediate point balance value between the coherence and incoherence of the light source. In practice, the strategy can include one or more of these methods.
Conclusion
In this paper, the reason of the speckle noise generation in holographic display is provide by analyzing the hologram generation process and the reconstruction process. Meanwhile, the evaluation criteria for speckle noise in holographic display is introduced. In addition, the speckle noise suppression methods are introduced by considering the hologram generation process and the reconstruction process. Based on the hologram generation process, the discussed methods are divided to the iterative and non-iterative methods. In the reconstruction process, other speckle noise reduction methods are also introduced based on the perspective of light coherence, human visual system and optical system. Finally, we summarize the prospects of each type of method.
Author Contributions
Conceptualization: N-NL and DW; writing-original draft preparation, N-NL, CC, DW, BL, and Q-HW.
Funding
This work is supported by the National Natural Science Foundation of China under Grant Nos. 62020106010, 62011540406 and the National Research Foundation of Korea (2020K2A9A2A06038623).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Dr. Yi-Wei Zheng, Dr. Zhao-Song Li and Dr. Yi-Long Li for revising the manuscript. We would like to thank Nanofabrication facility in Beihang Nano for technique consultation.
References
Barnard, E., Vermeulen, P., and Casasent, D. P. (1989). Optical Correlation CGHs with Modulated Error Diffusion. Appl. Opt. 28, 5358–5362. doi:10.1364/ao.28.005358
Bernardo, M. V., Fonseca, E., Pinheiro, A. M. G., Fiadeiro, P. T., and Pereira, M. (2021). Efficient Coding of Experimental Holograms Using Speckle Denoising. Signal. Processing: Image Commun. 96, 116306. doi:10.1016/j.image.2021.116306
Bolek, J., and Makowski, M. (2019). Non-invasive Correction of Thermally Induced Wavefront Aberrations of Spatial Light Modulator in Holographic Projection. Opt. Express 27 (7), 10193–10207. doi:10.1364/oe.27.010193
Brown, B. R., and Lohmann, A. W. (1966). Complex Spatial Filtering with Binary Masks. Appl. Opt. 5, 967–969. doi:10.1364/ao.5.000967
Brown, B. R., and Lohmann, A. W. (1969). Computer-generated Binary Holograms. IBM J. Res. Dev. 13, 160–168. doi:10.1147/rd.132.0160
Bu, H.-Z., Jiao, S.-M., and Jiao, S.-m. (2021). Review of Computer-Generated Phase-Only Hologram Optimization Algorithm. Chin. J. Liq. Cryst. Disp. 36, 810–826. doi:10.37188/cjlcd.2021-0035
Chakravarthula, P., Tseng, E., Srivastava, T., Fuchs, H., and Heide, F. (2020). Learned Hardware-In-The-Loop Phase Retrieval for Holographic Near-Eye Displays. ACM Trans. Graph. 39, 1–18. doi:10.1145/3414685.3417846
Chakravarthula, P., Zhang, Z., Tursun, O., Didyk, P., Sun, Q., and Fuchs, H. (2021). Gaze-contingent Retinal Speckle Suppression for Perceptually-Matched Foveated Holographic Displays. IEEE Trans. Vis. Comput. Graphics 27, 4194–4203. doi:10.1109/tvcg.2021.3106433
Chang, C., Xia, J., Yang, L., Lei, W., Yang, Z., and Chen, J. (2015). Speckle-suppressed Phase-Only Holographic Three-Dimensional Display Based on Double-Constraint Gerchberg-Saxton Algorithm. Appl. Opt. 54, 6994–7001. doi:10.1364/ao.54.006994
Chen, C., Chang, K., Liu, C., Wang, J., and Wang, Q. (2019). Fast Hologram Generation Using Intermediate Angular-Spectrum Method for High-Quality Compact on-axis Holographic Display. Opt. Express 27, 29401–29414. doi:10.1364/oe.27.029401
Chen, C., Lee, B., Li, N.-N., Chae, M., Wang, D., Wang, Q.-H., et al. (2021). Multi-depth Hologram Generation Using Stochastic Gradient Descent Algorithm with Complex Loss Function. Opt. Express 29, 15089–15103. doi:10.1364/oe.425077
Chen, H.-M., Yang, J.-P., Yen, H.-T., Hsu, Z.-N., Huang, Y., and Wu, S.-T. (2018). Pursuing High Quality Phase-Only Liquid crystal on Silicon (LCoS) Devices. Appl. Sci. 8, 2323–2338. doi:10.3390/app8112323
Chen, L., Tian, S., Zhang, H., Cao, L., and Jin, G. (2021). Phase Hologram Optimization with Bandwidth Constraint Strategy for Speckle-free Optical Reconstruction. Opt. Express 29, 11645–11663. doi:10.1364/oe.422115
Cheung, W. K., Tsang, P., Poon, T. C., and Zhou, C. (2011). Enhanced Method for the Generation of Binary Fresnel Holograms Based on Grid-Cross Downsampling. Chin. Opt. Lett. 9, 120005–120009. doi:10.3788/col201109.120005
Choi, S., Gopakumar, M., Peng, Y., Kim, J., and Wetzstein, G. (2021). Neural 3D Holography: Learning Accurate Wave Propagation Models for 3D Holographic Virtual and Augmented Reality Displays. ACM Trans. Graph. 40, 240. doi:10.1145/3478513.3480542
Choi, S., Kim, J., Peng, Y., and Wetzstein, G. (2021). Optimizing Image Quality for Holographic Near-Eye Displays with Michelson Holography. Optica 8, 143–146. doi:10.1364/optica.410622
Curtis, V.-R., Cairam, N.-W., Xu, J., Sata, A. S., and Pégard, C. N. (2021). “Dynamic Computer Generated Holography for Speckle-free, High Fidelity 3D Displays,” in Proceedings of the 2021 IEEE Virtual Reality and 3D User Interfaces (VR), Lisboa, Portugal, 27 March-1 April 2021, 1–9.
Duan, X., Liu, J., Li, X., Xue, G., Zhao, T., and Duan, J. (2019). Novel Computer-Generated Hologram Encoding Method Based on Partially Temporal Coherent Light. Opt. Express 27, 6851–6862. doi:10.1364/oe.27.006851
Eybposh, M. E., Caira, N. W., Atisa, M., Chakravarthula, P., and Pégard, N. C. (2020). DeepCGH: 3D Computer-Generated Holography Using Deep Learning. Opt. Express 28, 26636–26650. doi:10.1364/oe.399624
Gerchberg, R.-W., and Saxton, W.-O. (1972). A Practical Algorithm for the Determination of Phase from Image and Diffraction Plane Pictures. Optik 35, 237–246.
Hamann, S., Shi, L., Solgaard, O., and Wetzstein, G. (2018). Time-multiplexed Light Field Synthesis via Factored Wigner Distribution Function. Opt. Lett. 43, 599–602. doi:10.1364/ol.43.000599
Horisaki, R., Takagi, R., and Tanida, J. (2018). Deep-learning-generated Holography. Appl. Opt. 57, 3859–3863. doi:10.1364/ao.57.003859
Jang, C., Bang, K., Li, G., and Lee, B. (2018). Holographic Near-Eye Display with Expanded Eye-Box. ACM Trans. Graph. 37, 195. doi:10.1145/3272127.3275069
Jiao, S., Zhang, D., Zhang, C., Gao, Y., Lei, T., and Yuan, X. (2020). Complex-amplitude Holographic Projection with a Digital Micromirror Device (DMD) and Error Diffusion Algorithm. IEEE J. Select. Top. Quan. Electron. 26, 1–8. doi:10.1109/jstqe.2020.2996657
Jun, A., Hirotsuna, M., and Tomio, S. (1995). Speckle-noise Reduction on Kinoform Reconstruction Using a Phase-Only Spatial Light Modulator. Appl. Opt. 34, 3165–3171. doi:10.1364/AO.34.003165
Kuzmenko, A., Iezhov, P., and Kim, J.-T. (2011). “Weighting Iterative Fourier Transform Algorithm for Kinoform Implemented with Phase-Only SLM,” in Digital Holography and Three-Dimensional Imaging. Editors H. Yoshikawa, and M. K. Kim (Washington, D.C., United States: Optical Society of America), DTuC37. doi:10.1364/dh.2011.dtuc37
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. Nature 521, 436–444. doi:10.1038/nature14539
Lee, J., Jeong, J., Cho, J., Yoo, D., Lee, B., and Lee, B. (2020). Deep Neural Network for Multi-Depth Hologram Generation and its Training Strategy. Opt. Express 28, 27137–27154. doi:10.1364/oe.402317
Lee, S., Kim, D., Nam, S.-W., Lee, B., Cho, J., and Lee, B. (2020). Light Source Optimization for Partially Coherent Holographic Displays with Consideration of Speckle Contrast, Resolution, and Depth of Field. Sci. Rep. 10, 18832–18844. doi:10.1038/s41598-020-75947-0
Lee, S., Kim, D., Nam, S.-W., and Lee, B. (2020). Speckle Reduced Holographic Displays Using Tomographic Synthesis. Opt. Lett. 45, 4686–4689. doi:10.1364/ol.399623
Li, N.-N., Wang, D., Li, Y.-L., and Wang, Q.-H. (2020). Method of Curved Composite Hologram Generation with Suppressed Speckle Noise. Opt. Express 28, 34378–34389. doi:10.1364/oe.406265
Lin, S.-F., Gentet, P., Wang, D., Lee, S.-H., Kim, E.-S., and Wang, Q.-H. (2021). Simply Structured Full-Color Holographic Three-Dimensional Display Using Angular-Compensating Holographic Optical Element. Opt. Lasers Eng. 138, 106404. doi:10.1016/j.optlaseng.2020.106404
Liu, J.-P., Wu, M.-H., and Tsang, P. W. M. (2020). 3D Display by Binary Computer-Generated Holograms with Localized Random Down-Sampling and Adaptive Intensity Accumulation. Opt. Express 28, 24526–24537. doi:10.1364/oe.399011
Liu, S.-J., Wang, D., and Wang, Q.-H. (2019). Speckle Noise Suppression Method in Holographic Display Using Time Multiplexing Technique. Opt. Commun. 436, 253–257. doi:10.1016/j.optcom.2018.12.038
Lohmann, A. W., and Paris, D. P. (1967). Binary Fraunhofer Holograms, Generated by Computer. Appl. Opt. 6, 1739–1748. doi:10.1364/ao.6.001739
Lucente, M. E. (1993). Interactive Computation of Holograms Using a Look-Up Table. J. Electron. Imaging 2, 28–34. doi:10.1117/12.133376
Ma, H., Liu, J., Yang, M., Li, X., Xue, G., and Wang, Y. (2017). Influence of Limited Random-phase of Objects on the Image Quality of 3D Holographic Display. Opt. Commun. 385, 153–159. doi:10.1016/j.optcom.2016.10.042
Maimone, A., Georgiou, A., and Kollin, J. S. (2017). Holographic Near-Eye Displays for Virtual and Augmented Reality. ACM Trans. Graph. 36, 1–16. doi:10.1145/3072959.3073624
Masaya, M., and Yuji, S. (2019). “Effect of point Pitch on Speckle Noise in Computer-Generated Hologram Using point-based Method,” in Proceedings Volume 10944, Practical Holography XXXIII: Displays, Materials, and Applications, San Francisco, California, United States, March 2019, 10944. doi:10.1117/12.2509088
Memmolo, P., Bianco, V., Paturzo, M., Javidi, B., Netti, P. A., and Ferraro, P. (2014). Encoding Multiple Holograms for Speckle-Noise Reduction in Optical Display. Opt. Express 22, 25768–25775. doi:10.1364/oe.22.025768
Mendoza-Yero, O., Mínguez-Vega, G., and Lancis, J. (2014). Encoding Complex fields by Using a Phase-Only Optical Element. Opt. Lett. 39, 1740–1743. doi:10.1364/ol.39.001740
Montrésor, S., Memmolo, P., Bianco, V., Ferraro, P., and Picart, P. (2019). Comparative Study of Multi-Look Processing for Phase Map De-noising in Digital Fresnel Holographic Interferometry. J. Opt. Soc. Am. A. Opt. Image Sci. Vis. 36, A59–A66. doi:10.1364/JOSAA.36.000A59
Mori, Y., Fukuoka, T., and Nomura, T. (2014). Speckle Reduction in Holographic Projection by Random Pixel Separation with Time Multiplexing. Appl. Opt. 53, 8182–8188. doi:10.1364/ao.53.008182
Nagahama, Y., Shimobaba, T., Kakue, T., Takaki, Y., and Ito, T. (2019). Image Quality Improvement of Random Phase-free Holograms by Addressing the Cause of Ringing Artifacts. Appl. Opt. 58, 2146–2151. doi:10.1364/ao.58.002146
Nishitsuji, T., Yamamoto, Y., Sugie, T., Akamatsu, T., Hirayama, R., Nakayama, H., et al. (2018). Special-purpose Computer HORN-8 for Phase-type Electro-Holography. Opt. Express 26, 26722–26733. doi:10.1364/oe.26.026722
Park, D.-Y., and Park, J.-H. (2020). Hologram Conversion for Speckle Free Reconstruction Using Light Field Extraction and Deep Learning. Opt. Express 28, 5393–5409. doi:10.1364/oe.384888
Peng, Y., Choi, S., Padmanaban, N., and Wetzstein, G. (2020). Neural Holography with Camera-In-The-Loop Training. ACM Trans. Graph. 39, 1–14. doi:10.1145/3414685.3417802
Qi, Y., Chang, C., and Xia, J. (2016). Speckleless Holographic Display by Complex Modulation Based on Double-phase Method. Opt. Express 24, 30368–30378. doi:10.1364/oe.24.030368
Redding, B., Choma, M. A., and Cao, H. (2012). Speckle-free Laser Imaging Using Random Laser Illumination. Nat. Photon 6, 355–359. doi:10.1038/nphoton.2012.90
Shi, L., Huang, F.-C., Lopes, W., Matusik, W., and Luebke, D. (2017). Near-eye Light Field Holographic Rendering with Spherical Waves for Wide Field of View Interactive 3D Computer Graphics. ACM Trans. Graph. 36, 236. doi:10.1145/3130800.3130832
Shi, L., Li, B., Kim, C., Kellnhofer, P., and Matusik, W. (2021). Towards Real-Time Photorealistic 3D Holography with Deep Neural Networks. Nature 591, 234–239. doi:10.1038/s41586-020-03152-0
Shimobaba, T., and Ito, T. (2015). Random Phase-free Computer-Generated Hologram. Opt. Express 23, 9549–9554. doi:10.1364/oe.23.009549
St. Hilaire, P., Benton, S. A., and Lucente, M. (1992). Synthetic Aperture Holography: a Novel Approach to Three-Dimensional Displays. J. Opt. Soc. Am. A. 9, 1969–1977. doi:10.1364/josaa.9.001969
Tsang, P. W. M., Liu, J.-P., Lam, H., and Poon, T.-C. (2020). Enhancing the Quality of Sampled Phase-Only Hologram (SPOH) Based on Time-Division Comb Filtering. Appl. Sci. 10, 2732–2746. doi:10.3390/app10082732
Tsang, P. W. M., Poon, T.-C., and Jiao, A. S. M. (2013). Embedding Intensity Image in Grid-Cross Down-Sampling (GCD) Binary Holograms Based on Block Truncation Coding. Opt. Commun. 304, 62–70. doi:10.1016/j.optcom.2013.04.019
Wang, D., Li, N.-N., Chang, C.-L., Liu, C., and Wang, Q.-H. (2020). Method of Speckle Noise Suppression for Holographic Zoom Display Based on Layered-Pixel-Scanning Algorithm. IEEE Access 8, 102128–102137. doi:10.1109/access.2020.2999476
Wang, D., Li, N.-N., Liu, C., and Wang, Q.-H. (2019). Holographic Display Method to Suppress Speckle Noise Based on Effective Utilization of Two Spatial Light Modulators. Opt. Express 27, 11617–11625. doi:10.1364/oe.27.011617
Wang, D., Liu, C., Shen, C., Xing, Y., and Wang, Q.-H. (2020). Holographic Capture and Projection System of Real Object Based on Tunable Zoom Lens. PhotoniX 1, 6. doi:10.1186/s43074-020-0004-3
Wang, Z., Lv, G., Feng, Q., Wang, A., and Ming, H. (2020). Enhanced Resolution of Holographic Stereograms by Moving or Diffusing a Virtual Pinhole Array. Opt. Express 28, 22755–22766. doi:10.1364/oe.396639
Wu, J., Liu, K., Sui, X., and Cao, L. (2021). High-speed Computer-Generated Holography Using an Autoencoder-Based Deep Neural Network. Opt. Lett. 46, 2908–2911. doi:10.1364/ol.425485
Wu, L., and Zhang, Z. (2021). Domain Multiplexed Computer-Generated Holography by Embedded Wavevector Filtering Algorithm. PhotoniX 2, 1. doi:10.1186/s43074-020-00023-9
Wu, Y., Wang, J., Chen, C., Liu, C.-J., Jin, F.-M., and Chen, N. (2021). Adaptive Weighted Gerchberg-Saxton Algorithm for Generation of Phase-Only Hologram with Artifacts Suppression. Opt. Express 29, 1412–1427. doi:10.1364/oe.413723
Yamaguchi, M., Ohyama, N., and Honda, T. (1992). Holographic Three-Dimensional Printer: New Method. Appl. Opt. 31, 217–222. doi:10.1364/ao.31.000217
Yanagihara, H., Shimobaba, T., Kakue, T., and Ito, T. (2020). Image Quality Improvement of Holographic 3-D Images Based on a Wavefront Recording Plane Method with a Limiting Diffraction Region. Opt. Express 28, 17853–17867. doi:10.1364/oe.395091
Yoo, D., Jo, Y., Nam, S.-W., Chen, C., and Lee, B. (2021). Optimization of Computer-Generated Holograms Featuring Phase Randomness Control. Opt. Lett. 46, 4769–4772. doi:10.1364/ol.437375
Ysang, P.-W.-M., Jiao, A.-S.-M., and Poon, T.-C. (2014). Fast Conversion of Digital Fresnel Hologram to Phase-Only Hologram Based on Localized Error Diffusion and Redistribution. Opt. Express 22, 5060–5066.
Zhan, T., Xiong, J., Zou, J., and Wu, S.-T. (2020). Multifocal Displays: Review and prospect. PhotoniX 1, 10. doi:10.1186/s43074-020-00010-0
Zhao, R., Huang, L., and Wang, Y. (2020). Recent Advances in Multi-Dimensional Metasurfaces Holographic Technologies. PhotoniX 1, 20. doi:10.1186/s43074-020-00020-y
Zhao, T., Liu, J., Duan, J., Li, X., and Wang, Y. (2019). Image Quality Enhancement via Gradient-Limited Random Phase Addition in Holographic Display. Opt. Commun. 442, 84–89. doi:10.1016/j.optcom.2019.02.026
Keywords: speckle noise, computer-generated holography, holographic display, three-dimensional display, speckle noise suppression method
Citation: Li N-N, Chen C, Lee B, Wang D and Wang Q-H (2022) Speckle Noise Suppression Algorithm of Holographic Display Based on Spatial Light Modulator. Front. Photon. 2:825610. doi: 10.3389/fphot.2021.825610
Received: 30 November 2021; Accepted: 28 December 2021;
Published: 19 January 2022.
Edited by:
Pietro Ferraro, National Research Council (CNR), ItalyReviewed by:
Michal Makowski, Warsaw University of Technology, PolandShuming Jiao, Peng Cheng Laboratory, China
Vittorio Bianco, National Research Council (CNR), Italy
Copyright © 2022 Li, Chen, Lee, Wang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Di Wang, ZGl3YW5nMThAYnVhYS5lZHUuY24=; Qiong-Hua Wang, cWlvbmdodWFAYnVhYS5lZHUuY24=
 Nan-Nan Li
Nan-Nan Li Chun Chen2
Chun Chen2 Di Wang
Di Wang Qiong-Hua Wang
Qiong-Hua Wang