Resolving sub-cycle signatures: A perspective on hallmarks of terahertz metrology

Frequency up-conversion has become amongst the most prevalent techniques for detection of terahertz waves in metrology systems. State-of-the-art up-conversion techniques rely on the coherent transferring of the information encoded in all degrees of freedom of a terahertz wave to either the near-infrared or visible domain, where detectors are readily accessible. This allows for an indirect reconstruction of the terahertz wave. However, unlike most up-conversion methods employed in photonics which are concentrating on narrowband tones (at both terahertz and near-infrared frequencies), a broadband, hence temporally constrained, terahertz transient is sampled on time-scales shorter than its oscillation period. Here, femtosecond laser pules serve as temporal gates. In this perspective, we highlight several hallmarks of terahertz metrology that originate from these sub-cycle measurement capabilities and elaborate why this enables studies in fundamental and applied science, with a particular focus on novel measurement concepts in classical and quantum. We focus on so-far demonstrated detection performance in bulk non-linear crystals. Finally, we discuss current challenges and the most pressing questions ahead.

1 Introduction

Electric field metrology aims to achieve ultimate precision in the characterisation of the spatio-temporal evolution of the electromagnetic field of a wave. This is a very meaningful endeavour since the precise spatio-temporal waveform has direct implications in most of the physical processes that involve light, for example the way and strength light interacts with matter or with other light fields. Light’s properties change as it propagates through a medium in a way that depends on the properties of both the medium and the wave itself. Therefore, ultra-fast phenomena inside materials can be probed by analyzing the properties of custom-tailored light on sub-cycle scales after it has interacted with the medium Raimond et al., 2001.

Characterising the spatio-temporal pattern of a wave is however quite a technical feat: it requires measuring the entire set of degrees of freedom, i.e., amplitude, frequency, phase, polarisation and spatial mode of a wave at once. This is generally possible when dealing with classical states of light. In the quantum limit however, measuring all degrees of freedom of a quantum state of light with arbitrary spatio-temporal precision is prohibited by Heisenberg’s uncertainty principle Loudon, 2000. Here, the measurement of a certain variable with high precision will concomitantly introduce an imprecision in its conjugate variable. This is then manifested through quantum noise that limits the precision of the measurement. Also in this context, sub-cycle spatio-temporal scales are the relevant ones and being able to measure them provides important knowledge about squeezing or anti-squeezing present in the system. This can be in turn leveraged to perform metrology beyond the shot noise limit. Finally, having access to all degrees of freedom on sub-cycle timescales opens up the possibility for single- and few-cycle temporal states to be considered as a viable basis for quantum information processing Brecht et al., 2015.

The examples above provide only a glimpse of the importance of developing sub-cycle metrology tools that can determine all degrees of freedom at once. This has proven extremely challenging across all frequency regimes, and the terahertz makes no exception. More than 20 years of research Dhillon et al., 2017 have resulted in electro-optic sampling being the leading metrology technique. This is a rather unique methodology that can provide, in principle, quantitative reconstruction of the amplitude, phase, polarisation, frequency and spatial mode of a THz waveform on sub-cycle spatio-temporal scales. As a result, sub-cycle quantum metrology has recently emerged as a young and exciting field. It aims to measure sub-cycle signatures down to signal levels that are commensurate with quantum states of light. Since this can be achieved in both the temporal and the spatial domain, this opened up studies about the very nature of these peculiar states. Theoretical proposals were made to probe fundamental hypotheses in special relativity in a table-top experiment using electro-optic sampling Moskalenko et al., 2015; Guedes et al., 2019: realising an Unruh-Dewitt detector Onoe et al., 2022, probing local and non-local correlations of vacuum fields Lindel et al., 2020 or probing the dynamic Casimir force. Experimental studies corroborated these proposals, with direct measurement of the vacuum ground state Riek et al. (2015) and its correlations in space-time Benea-Chelmus et al., 2019, photon statistics of lasers around their threshold Benea-Chelmus et al., 2016, demonstration of Hilbert transforms Sulzer et al., 2020, existence of entanglement outside the lightcone Settembrini et al., 2022 or squeezed temporal states Riek et al., 2017. On the counter side, a very recent theoretical work shows that sub-cycle metrology of terahertz fields may provide information about spatio-temporal properties of dispersive coupled light-matter systems De Liberato., 2019, about the Purcell effect Lindel et al., 2022, or quantum susceptibilities Kizmann et al., 2022.

Despite this initial progress, measuring all degrees of freedom of quantum states of light in the terahertz remains a laborious and challenging task. In this perspective, we discuss—by virtue of contrast—the advantages of electro-optic sampling as opposed to narrowband up-conversion techniques from a fundamental point of view. In the second part 2, we elaborate on the conceptual difference between narrowband up-conversion, which is the most prevalent in photonics, and broadband up-conversion, which gives access to a sub-cycle portion of the terahertz waveform. We corner its unique advantages by proposing five hallmarks of terahertz field metrology, in 3. In the fourth part 4, we discuss challenges and opportunities ahead when connecting the two realms: sub-cycle metrology with the advantages quantum-level sensitivity. A particular focus will lie on existing important challenges of bulk systems and an outlook of important milestones to be addressed ahead.

2 Metrology on sub-THz-cycle scales

Electro-optic sampling relies on the optical up-conversion of a spatio-temporal terahertz wave ${\vec{E}}_{\mathit{THz}}(x,y,z,t)=E_{\mathit{THz}}(x,y,z,t){\vec{e}}_{\mathit{THz}}$ oscillating at frequency Ω. This is achieved by mixing it with a probe beam ${\vec{E}}_p(x,y,z,t)=E_p(x,y,z,t){\vec{e}}_p$ at a frequency ω. It exploits a χ⁽²⁾-driven mechanism, i.e., a coherent process in which a new field ${\vec{E}}^{(2)}(x,y,z,t)=E^{(2)}(x,y,z,t){\vec{e}}_{(2)}$ is generated as a result of a non-linear polarisation ${\vec{P}}^{(2)}(x,y,z,t)={ϵ}_0{\chi }^{(2)}{\vec{E}}_{\mathit{THz}}(x,y,z,t){\vec{E}}_p(x,y,z,t)$ that arises in the material under THz illumination. ${\vec{e}}_{\mathit{THz}}$, ${\vec{e}}_p$ and ${\vec{e}}_{(2)}$ are unitary vectors that designate the polarisation of the source and resulting fields.

χ⁽²⁾ is in general a three-dimensional tensor that describes all possible combinations of mixing between the components of the near-infrared and terahertz fields. As a result, the information about the amplitude, phase, polarisation and frequency of the sampled terahertz radiation is generally preserved in the up-conversion process. One can show that the resulting non-linear field takes the shape of ${\vec{E}}^{(2)}(x,y,z,t)=E_p(x,y,z,t)e^{i\mathrm{\Delta }\varphi }{\vec{e}}_{(2)}$, where $\mathrm{\Delta }\varphi =\frac{1}{2c}{n}^{3}r\omega E_{\mathit{THz}}(x,y,z,t)l$, where n is the refractive index of the non-linear material at the probe frequency, r is the electro-optic coefficient and l is an effective interaction length between the two beams that accounts for phase matching. In a typical metrology experiment, the THz-induced non-linear polarisation field interferes with the probe field, leading to a total field ${\vec{E}}_{\mathit{tot}}(x,y,z,t)$ that is a modulation of the probe beam itself:

${\vec{E}}_{\mathit{tot}}\left(x,y,z,t\right)=E_p\left(x,y,z,t\right){\vec{e}}_p+E^{\left(2\right)}\left(x,y,z,t\right){\vec{e}}_{\left(2\right)}(1)$

Depending on the relative vectorial orientation of the polarisation of the probe field, described by ${\vec{e}}_p$ with the newly generated field, described by ${\vec{e}}_{(2)}$, the original probe field is modulated either in its phase/amplitude (when both contributions have the same polarisation ${\vec{e}}_p\Vert {\vec{e}}_{(2)}$), or in its polarisation (when orthogonally polarized ${\vec{e}}_p\perp {\vec{e}}_{(2)}$). Without loss of generality, here we will restrict our discussion to the case where the two interfering waves are polarised along the same direction.

Two distinct approaches can be followed, depending on the spectral characteristics of the two mixing beams: narrowband or broadband up-conversion. We discuss them graphically in Figure 1 both from a time-domain and from a frequency-domain perspective. In Figure 1A, a narrowband probe is mixed with a narrowband THz tone. Consequently, the up-conversion is temporally extended over many cycles of the THz tone and the resulting probe signal is characterised by a beating period equal to the THz frequency. In the frequency domain, the narrowband THz tone is up-shifted to the near-infrared range and is well resolved from the original probe tone. Hence, in this case we operate in the resolved sideband regime. To retrieve the amplitude and phase information about the up-converted terahertz waveform, the beating between the up-shifted tone and the original probe tone can be used. It needs to be detected at an intensity detector with an electronic bandwidth larger than the terahertz frequency. Consequently, the lack of photodetectors with terahertz bandwidth strongly limits the maximal terahertz frequency that can be detected in this fashion.

FIGURE 1

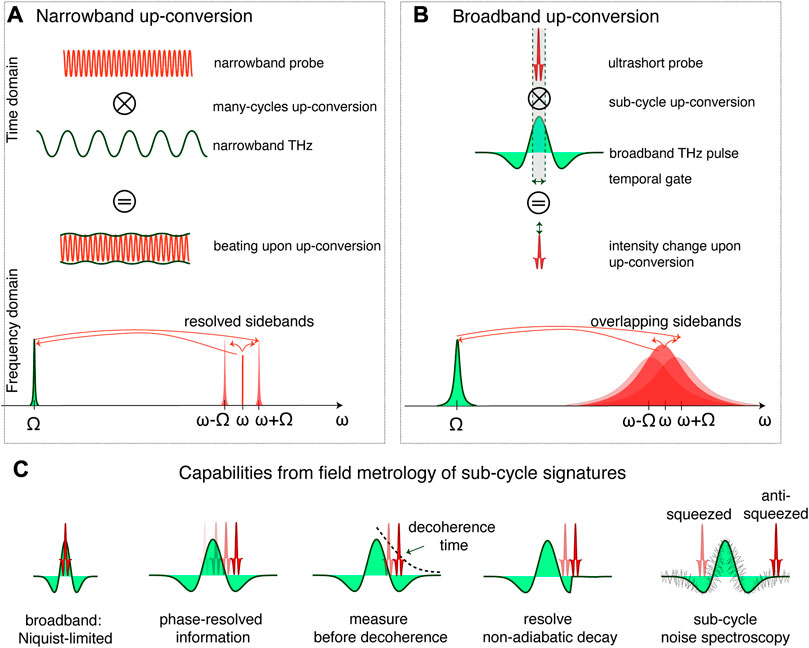
FIGURE 1. Today’s capabilities of terahertz field metrology stem from utilizing broadband up-conversion by mixing a terahertz wave with a femtosecond probe pulse, which has a duration that is typically much shorter than a terahertz cycle. This approach is distinct from narrow-band up-conversion shown in (A), where a narrowband probe beam is mixed with a narrowband THz wave (featured by a linewidth much narrower that its central frequency), thus resulting into a beating modulation of the probe at the THz frequency. In the frequency domain, the up-conversion process leads to the formation of well resolved sidebands. In contrast, broadband up-conversion shown in (B) employs ultrashort pulses to effectively gate the up-conversion process to occur on timescales that are shorter than one cycle of THz oscillation. In the frequency domain, this leads to the formation of sidebands that overlap significantly with the original probe spectrum, leading to a modulation of its either intensity or phase. This metrology technique, called electro-optic sampling, effectively probes only a sub-cycle portion of the terahertz waveform, much like an oscilloscope does to a radio-frequency signal. (C) The access to sub-cycle signatures of a THz waveform leads to several capabilities that have become the hallmarks of terahertz metrology: broadband detection, phase-resolved information, measurement before decoherence, resolution of non-adiabatic decay and sub-cycle noise spectroscopy.

Broadband up-conversion, shown in Figure 1B, stands in contrast to the previously mentioned approach. In this case, the probe beam is an ultrashort pulse, the width of which satisfies $\mathrm{\Delta }{t}_{\mathit{probe}}\ll \frac{T_{\mathit{THz}}}{2}$, where T_THz is the center frequency of the sampled THz waveform. In this situation, the up-conversion process is temporally limited to the extent of the ultrashort probe pulse, which now acts as a temporal gate for the measurement of the terahertz waveform. In the case of the sampling time being well below the Nyquist limit, the electric field of the THz transient may even be assumed to be constant. In this case, one can find that the interference of the newly generated field with the probe of Equation (1) leads to an intensity modulation that can, after accounting for push-pull configuration (differential operation), be generally quantified as

$\frac{\mathrm{\Delta }I}{I}=\frac{1}{\mathrm{c}}{n}^{3}r\omega E_{\mathit{THz}}\left(x,y,z,t\right)l.(2)$

Here E_THz(x, y, z, t) is the sub-cycle portion of the real THz field with which the probe pulse is overlapped in time and space. Consequently, by simply displacing the probe pulse in time or space, one can access other space-time points of the terahertz waveform in a quantitative manner.

An essential feature of electro-optic sampling is that the availability of shot-noise limited intensity detectors in the near-infrared can be paired with ultra-stable femtosecond laser systems, so as to bypass the necessity of shot-noise limited detectors in the terahertz range that would otherwise become compelling. State-of-the-art laser technologies routinely provide ultrashort (i.e., from sub-picosecond down to a few tens of femtoseconds) pulsed beams in the near-infrared, and they are tunable in a relatively large range of wavelengths.

3 Hallmarks of terahertz metrology

Multiple unique capabilities arise from the spatio-temporal resolution to sub-THz-cycle scales provided by the femtosecond pulses in electro-optic sampling, graphically summarized in Figure 1C.

We succinctly summarize these capabilities by proposing five hallmarks that set terahertz field metrology via broadband up-conversion apart from other terahertz detection techniques, typically featuring detection schemes aimed at retrieving the average intensity of the terahertz wave.

1. Broadband detection: sub-THz-cycle metrology is capable of detecting broadband THz radiation, down to single-cycle waveforms. The upper frequency limit is imposed by the Nyquist criterion where $\mathrm{\Delta }{t}_{\mathit{probe}}=\frac{T_{\mathit{THz}}}{2}$. This capability is leveraged in broadband spectroscopy, Neu and Schmuttenmaer, 2018 e.g. of solid-state materials Woerner et al., 2013 to monitor several resonant transitions at once, as well as to measure the broadband radiation generated through a high harmonic generation process. Finally, THz pulses are employed to characterize layered materials, by performing time-of-flight measurements in either a transmission or reflection geometry, which return information about the number, depth and chemical composition of each layer Takayanagi et al., 2009.

2. Phase-resolved information: Electro-optic sampling allows for the recording of the entire THz time-varying waveform, in terms of both amplitude and phase simultaneously Jepsen (2019). This is achieved by scanning the relative delay between the THz and probe pulses, within their temporal window of interaction. In particular, phase information recovery enables for broadband measurements of the complex refractive index van Exter et al., 1989 e.g. of THz-transparent materials, but also of materials that have strong dispersion due to the proximity to phonon resonances.

3. Measurement before decoherence: full characterization of the THz waveform can be performed before loss of phase coherence. This property allows to resolve a decay of e.g., a given material excitation after it has been driven coherently by a waveform in the terahertz Zhang et al., 2014. In addition, this allows for the characterization of incoherent sources e.g., through a measurement of their first order coherence function Benea-Chelmus et al., 2016.

4. Snapshot of non-adiabatic processes: as the temporal resolution provided by the femtosecond pulse is typically in the order of 100 femtoseconds, signatures that happen on much shorter time-scales than one terahertz oscillation cycle can be resolved. This capability has been explored to characterise the response of supercoductors in the non-adiabatic excitation regime Matsunaga et al., 2013 or to characterize abrupt switch-off of light-matter systems Halbhuber et al., 2020; Mornhinweg et al., 2021.

5. Sub-cycle noise spectroscopy: by studying the noise properties of the sampled terahertz transients as a function of space-time, quantum properties of the THz waveforms can be revealed. This property has been instrumental for characterisation of the ground state of light—vacuum field fluctuations Riek et al., 2015, Benea-Chelmus et al., 2019, Settembrini et al., 2022.

4 State of the art detection in bulk crystals, challenges and opportunities ahead

Today, the vast majority of terahertz-compatible metrology techniques rely on bulk non-linear crystals. The THz waveform is co-propagating with an ultrashort probe pulse. Their transverse profile inside the bulk medium is well-approximated by Gaussian beams, yet featuring spot diameters with significantly different sizes, dictated by a wavelength ratio higher than a factor of 100. This implies that the magnitude of the sampled THz waveform is strongly determined by the use of focusing optics. The latter imposes a minimal confinement volume due to the diffraction limit. At the detection crystal, a sub-THz-cycle spatial overlap between probe and THz spots can be realised. This scheme comes with several advantages and shortcomings. On the one hand, the probe pulse power should be chosen sufficiently high so as to maximize the signal-to-noise ratio of the measurements, i.e. by reaching the shot-noise-limited regime, much like in any homodyne detection technique. On the other hand, the sampled THz electric field strength E_THz(x, y, z, t) is mainly enhanced by focusing effect, while the effective interaction length l (between probe and THz beams) is limited by both the focusing condition of the two beams and their phase-matching, the latter being linked to the refractive indices at near-infrared and terahertz frequencies. For this reason, a careful compromise should be achieved in order to optimize the overall detection efficiency in a certain terahertz band, by simultaneously optimizing phase matching and THz focusing at the detection crystal, both being conditions mutually dependent upon each other.

Zinc telluride (ZnTe) is historically the most utilized material at THz frequencies Nahata et al., 1996 as it is naturally phase-matched (in a collinear propagation geometry) with the 800 nm line emitted by Ti:Sapphire lasers. Since the band-gap of ZnTe (2.26 eV) is larger than the energy associated to 800 nm-photons (1.55 eV), it can be optically pumped without introducing a significant free-carrier absorption, while featuring moderate dispersion in a broad optical range. Because of this, ZnTe allows for a remarkably simple implementation of the electro-optic sampling technique, which can be also extended to broadband regimes (ultrashort THz transients), since the large spectral linewidth of the laser pulse ($>$ 15 nm) enables for THz spectral sensitivities potentially spanning over a two decade-wide frequency window. However, ZnTe features a transverse (TO) resonant mode located at 5.32 THz, which causes the crystal to be strongly opaque around the resonant frequency (Reststrahlen band), additionally exhibiting a pronounced dispersion that dramatically worsens the phase-matching with the probe pulses. These two effects combined limit the exploitation ZnTe-based electro-optic sampling to bandwidths not larger than roughly 4 THz. Indeed, the sub-cycle characterisation of vacuum field fluctuations in the frequency band below 3 THz has been experimentally demonstrated using zinc telluride cooled to 4 K as a detection crystal. The extreme low signal-to-noise ratio of 10^–8 was compensated by an extreme stability of nowadays pulsed laser systems, combined with self-referencing protocols to ensure shot-noise limited detection even on time-scales up to minutes or longer. However, the measurement was limited to only one polarisation component of the terahertz quantum field. In the future, (111)-cut zinc telluride could access the full terahertz polarisation state as it evolves in time. The lack of sensitivity at higher frequencies has led to the necessity of exploring diverse large band-gap materials, such as CdTe, GaP, InP, GaSe, and even GaAs. In particular, GaP happens to be naturally phase-matched roughly at the emission wavelength (1030 nm) of Ytterbium lasers Wu and Zhang (1995). Although GaP could be potentially employed with THz transients nearly covering the entire THz range, as its TO resonance is located at ∼11 THz, the relatively narrower bandwidth associated to the 1030-nm-probe beam ultimately limits the electro-optic sampling detection to spectral ranges comparable to the ZnTe counterpart. Nevertheless, pulse-compression approaches, relying on the use of hollow-core fibers, could be implemented in order to shorten Ytterbium laser pulses, down to a nearly single-cycle regime ($<$ 5 fs), thus allowing for the operation of GaP-based electro-optic sampling with spectral sensitivities well-exceeding the 10-THz-upper limit Cui et al., 2018; Piccoli et al., 2019. A special case is represented by GaAs, since it possesses a high non-linearity (d = 47 pm/V), while its absorption coefficient at THz frequencies is among the lowest ($<$ 1 cm⁻¹ below 1.5 THz). Remarkably, its optical group and THz refractive indices nearly match (∼3.43 and ∼3.61, respectively), allowing for the employment of relatively long GaAs samples to perform electro-optic sampling, which benefits time-domain spectroscopy systems in terms of both detection efficiency and spectral resolution. Despite all these advantages, GaAs has been finding little practical applications in current electro-optic sampling-based THz systems, since it is totally opaque at the typical emission wavelength of Ti:Sapphire lasers. Moreover, strong second-order absorption processes prevent from effectively using it with wavelengths belonging to the entire NIR range (including Ytterbium lasers). However, as the development of innovative laser sources (such as compact optical-parametric oscillators and thin-disk lasers) emitting pulsed beams in the Mid-IR range (above 2 μm) is quickly advancing, the adoption of GaAs as electro-optic material is envisioned to allow novel electro-optic sampling schemes, as well as open up new opportunities for THz metrology. Finally, it is worth mentioning the case of GaSe, which exhibits a quite low dispersion (comparable to GaAs) and an even higher non-linear coefficient (d = 54 pm/V) and allows for a fine tuning of the phase-matching bandwidth by exploiting its inherent birefrigence Huber et al., 2000, while being transparent at optical wavelengths ranging across the entire NIR and Mid-IR.

In conclusion, from the standpoint of temporal resolution, electro-optic sampling can nowadays be pushed to the extreme of using few-femtosecond pulses, in order to measure ultrashort transients featuring bandwidth extending up to the mid-infrared and even near-infrared. Looking ahead, several important milestones will need to be addressed in order to make sub-cycle metrology at the quantum level broadly accessible, and hence make full use of the hallmarks we propose. The most pressing ones, currently partially a field of intense research, relate to an increase in sensitivity, up to regimes superior to the conventional shot-noise limited detection in zinc telluride. This is mainly pursued by leveraging on advantages brought by miniaturisation: 1. to engineer the near-field and far-field spatio-temporal distribution of terahertz wave e.g. by using on-chip terahertz cavities or antennas integrated photonic circuits Salamin et al., 2019; Benea-Chelmus et al., 2020 or metasurfaces and 2. to engineer the probe pulse itself by custom-tailored non-linearities inside tailored on-chip waveguides and its further interaction with the local terahertz field. However, we foresee that limitations of the on-chip probe pulse energies need careful consideration, because both signal-to-noise ratio of the field measurement and the efficiency of undesired spurious non-linear processes increases with high probe powers. Furthermore, many of such on-chip detection schemes have not yet been characterised in the terahertz at cryogenic temperatures, which are necessary for operation at zero thermal occupation. On the other side, miniaturisation may provide a way to integrate novel material systems that allow innovative measurement protocols such as e.g. of the magnetic field via the magneto-optical Kerr effect as was recently done in bulk Weiss et al., 2023, exploitation of higher order non-linear processes such as χ⁽³⁾ towards on-chip terahertz field induces second harmonic generation (TFISH) Cook et al., 1999, full polarisation state reconstruction, single-shot terahertz acquisition, use of pre-conditioned probes Virally et al., 2021, development of multi-pulse sensing techniques beyond two individual probe pulses towards correlations beyond the first and second order coherence of the electric field that is possible today.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

IB and AT contributed equally to the manuscript.

Funding

IB acknowledges funding from the Swiss National Science Foundation under the PRIMA grant number 201547.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Benea-Chelmus, I.-C., Bonzon, C., Maissen, C., Scalari, G., Beck, M., and Faist, J. (2016). Subcycle measurement of intensity correlations in the terahertz frequency range. Phys. Rev. A 93, 043812. doi:10.1103/PhysRevA.93.043812

CrossRef Full Text | Google Scholar

Benea-Chelmus, I.-C., Salamin, Y., Settembrini, F. F., Fedoryshyn, Y., Heni, W., Elder, D. L., et al. (2020). Electro-optic interface for ultrasensitive intracavity electric field measurements at microwave and terahertz frequencies. Optica 7, 498–505. doi:10.1364/OPTICA.384160

CrossRef Full Text | Google Scholar

Benea-Chelmus, I.-C., Settembrini, F., Scalari, G., and Faist, J. (2019). Electric field correlation measurements on the electromagnetic vacuum state. Nature 568, 202–206. doi:10.1038/s41586-019-1083-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Brecht, B., Reddy, D. V., Silberhorn, C., and Raymer, M. G. (2015). Photon temporal modes: A complete framework for quantum information science. Phys. Rev. X 5, 041017. doi:10.1103/PhysRevX.5.041017

CrossRef Full Text | Google Scholar

Cook, D. J., Chen, J. X., Morlino, E. A., and Hochstrasser, R. M. (1999). Terahertz-field-induced second-harmonic generation measurements of liquid dynamics. Chem. Phys. Lett. 309, 221–228. doi:10.1016/S0009-2614(99)00668-5

CrossRef Full Text | Google Scholar

Cui, W., Schiff-Kearn, A. W., Zhang, E., Couture, N., Tani, F., Novoa, D., et al. (2018). Broadband and tunable time-resolved thz system using argon-filled hollow-core photonic crystal fiber. Apl. Photonics 3, 111301. doi:10.1063/1.5043270

CrossRef Full Text | Google Scholar

De Liberato, S. (2019). Electro-optical sampling of quantum vacuum fluctuations in dispersive dielectrics.

Google Scholar

Dhillon, S. S., Vitiello, M. S., Linfield, E. H., Davies, A. G., Hoffmann, M. C., Booske, J., et al. (2017). The 2017 terahertz science and technology roadmap. J. Phys. D. Appl. Phys. 50, 043001. doi:10.1088/1361-6463/50/4/043001

CrossRef Full Text | Google Scholar

Guedes, T. L., Kizmann, M., Seletskiy, D. V., Leitenstorfer, A., Burkard, G., and Moskalenko, A. S. (2019). Spectra of ultrabroadband squeezed pulses and the finite-time unruh-davies effect. Phys. Rev. Lett. 122, 053604. doi:10.1103/PhysRevLett.122.053604

PubMed Abstract | CrossRef Full Text | Google Scholar

Halbhuber, M., Mornhinweg, J., Zeller, V., Ciuti, C., Bougeard, D., Huber, R., et al. (2020). Non-adiabatic stripping of a cavity field from electrons in the deep-strong coupling regime. Nat. Photonics 14, 675–679. doi:10.1038/s41566-020-0673-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Huber, R., Brodschelm, A., Tauser, F., and Leitenstorfer, A. (2000). Generation and field-resolved detection of femtosecond electromagnetic pulses tunable up to 41 THz. Appl. Phys. Lett. 76, 3191–3193. doi:10.1063/1.126625

CrossRef Full Text | Google Scholar

Jepsen, P. U. (2019). Phase retrieval in terahertz time-domain measurements: A “how to” tutorial. J. Infrared, Millim. Terahertz Waves 40, 395–411. doi:10.1007/s10762-019-00578-0

CrossRef Full Text | Google Scholar

Kizmann, M., Moskalenko, A. S., Leitenstorfer, A., Burkard, G., and Mukamel, S. (2022). Quantum susceptibilities in time-domain sampling of electric field fluctuations. Laser & Photonics Rev. 16, 2100423. doi:10.1002/lpor.202100423

CrossRef Full Text | Google Scholar

Lindel, F., Bennett, R., and Buhmann, S. Y. (2020). Theory of polaritonic quantum-vacuum detection. Phys. Rev. A 102, 041701. doi:10.1103/PhysRevA.102.041701

CrossRef Full Text | Google Scholar

Lindel, F., Settembrini, F. F., Bennett, R., and Buhmann, S. Y. (2022). Probing the Purcell effect without radiative decay: Lessons in the frequency and time domains. New J. Phys. 24, 013006. doi:10.1088/1367-2630/ac434e

CrossRef Full Text | Google Scholar

Loudon, R. (2000). The Quantum theory of light.

Google Scholar

Matsunaga, R., Hamada, Y. I., Makise, K., Uzawa, Y., Terai, H., Wang, Z., et al. (2013). Higgs amplitude mode in the bcs superconductors nb_1-xti_xN induced by terahertz pulse excitation. Phys. Rev. Lett. 111, 057002. doi:10.1103/PhysRevLett.111.057002

PubMed Abstract | CrossRef Full Text | Google Scholar

Mornhinweg, J., Halbhuber, M., Ciuti, C., Bougeard, D., Huber, R., and Lange, C. (2021). Tailored subcycle nonlinearities of ultrastrong light-matter coupling. Phys. Rev. Lett. 126, 177404. doi:10.1103/PhysRevLett.126.177404

PubMed Abstract | CrossRef Full Text | Google Scholar

Moskalenko, A. S., Riek, C., Seletskiy, D. V., Burkard, G., and Leitenstorfer, A. (2015). Paraxial theory of direct electro-optic sampling of the quantum vacuum. Phys. Rev. Lett. 115, 263601. doi:10.1103/PhysRevLett.115.263601

PubMed Abstract | CrossRef Full Text | Google Scholar

Nahata, A., Weling, A. S., and Heinz, T. F. (1996). A wideband coherent terahertz spectroscopy system using optical rectification and electro-optic sampling. Appl. Phys. Lett. 69, 2321–2323. doi:10.1063/1.117511

CrossRef Full Text | Google Scholar

Neu, J., and Schmuttenmaer, C. A. (2018). Tutorial: An introduction to terahertz time domain spectroscopy (thz-tds). J. Appl. Phys. 124, 231101. doi:10.1063/1.5047659

CrossRef Full Text | Google Scholar

Onoe, S., Guedes, T. L. M., Moskalenko, A. S., Leitenstorfer, A., Burkard, G., and Ralph, T. C. (2022). Realizing a rapidly switched Unruh-DeWitt detector through electro-optic sampling of the electromagnetic vacuum. Phys. Rev. D. 105, 056023. doi:10.1103/PhysRevD.105.056023

CrossRef Full Text | Google Scholar

Piccoli, R., Rovere, A., Jeong, Y.-G., Jia, Y., Zanotto, L., Légaré, F., et al. (2019). Extremely broadband terahertz generation via pulse compression of an Ytterbium laser amplifier. Opt. Express 27, 32659–32665. doi:10.1364/OE.27.032659

PubMed Abstract | CrossRef Full Text | Google Scholar

Raimond, J. M., Brune, M., and Haroche, S. (2001). Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 73, 565–582. doi:10.1103/RevModPhys.73.565

CrossRef Full Text | Google Scholar

Riek, C., Seletskiy, D. V., Moskalenko, A. S., Schmidt, J. F., Krauspe, P., Eckart, S., et al. (2015). Direct sampling of electric-field vacuum fluctuations. Science 350, 420–423. doi:10.1126/science.aac9788

PubMed Abstract | CrossRef Full Text | Google Scholar

Riek, C., Sulzer, P., Seeger, M., Moskalenko, A. S., Burkard, G., Seletskiy, D. V., et al. (2017). Subcycle quantum electrodynamics. Nature 541, 376–379. doi:10.1038/nature21024

PubMed Abstract | CrossRef Full Text | Google Scholar

Salamin, Y., Benea-Chelmus, I.-C., Fedoryshyn, Y., Heni, W., Elder, D. L., Dalton, L. R., et al. (2019). Compact and ultra-efficient broadband plasmonic terahertz field detector. Nat. Commun. 10, 5550. doi:10.1038/s41467-019-13490-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Settembrini, F. F., Lindel, F., Herter, A. M., Buhmann, S. Y., and Faist, J. (2022). Detection of quantum-vacuum field correlations outside the light cone. Nat. Commun. 13, 3383. doi:10.1038/s41467-022-31081-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Sulzer, P., Oguchi, K., Huster, J., Kizmann, M., Guedes, T. L. M., Liehl, A., et al. (2020). Determination of the electric field and its Hilbert transform in femtosecond electro-optic sampling. Phys. Rev. A 101, 033821. doi:10.1103/PhysRevA.101.033821

CrossRef Full Text | Google Scholar

Takayanagi, J., Jinno, H., Ichino, S., Suizu, K., Yamashita, M., Ouchi, T., et al. (2009). High-resolution time-of-flight terahertz tomography using a femtosecond fiber laser. Opt. Express 17, 7533–7539. doi:10.1364/OE.17.007533

PubMed Abstract | CrossRef Full Text | Google Scholar

van Exter, M., Fattinger, C., and Grischkowsky, D. (1989). Terahertz time-domain spectroscopy of water vapor. Opt. Lett. 14, 1128–1130. doi:10.1364/OL.14.001128

PubMed Abstract | CrossRef Full Text | Google Scholar

Virally, S., Cusson, P., and Seletskiy, D. V. (2021). Enhanced electro-optic sampling with quantum probes. Phys. Rev. Lett. 127, 270504. doi:10.1103/PhysRevLett.127.270504

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiss, M. A., Herbst, A., Schlegel, J., Dannegger, T., Evers, M., Donges, A., et al. (2023). Ultrafast spontaneous spin switching in an antiferromagnet. doi:10.48550/ARXIV.2301.02006

CrossRef Full Text | Google Scholar

Woerner, M., Kuehn, W., Bowlan, P., Reimann, K., and Elsaesser, T. (2013). Ultrafast two-dimensional terahertz spectroscopy of elementary excitations in solids. New J. Phys. 15, 025039. doi:10.1088/1367-2630/15/2/025039

CrossRef Full Text | Google Scholar

Wu, Q., and Zhang, X. (1995). Free-space electro-optic sampling of terahertz beams. Appl. Phys. Lett. 67, 3523–3525. doi:10.1063/1.114909

CrossRef Full Text | Google Scholar

Zhang, Q., Arikawa, T., Kato, E., Reno, J. L., Pan, W., Watson, J. D., et al. (2014). Superradiant decay of cyclotron resonance of two-dimensional electron gases. Phys. Rev. Lett. 113, 047601. doi:10.1103/PhysRevLett.113.047601

PubMed Abstract | CrossRef Full Text | Google Scholar