- 1 Behavioural Science Institute, Radboud University Nijmegen, Nijmegen, Netherlands
- 2 Department of Developmental Psychology, University of Groningen, Groningen, Netherlands
- 3 CAP Center for Cognition, Action and Perception, University of Cincinnati, Cincinnati, OH, USA
This study investigates human performance in a cyclic Fitts task at three different scales of observation, either in the presence (difficult condition) or in the absence (easy condition) of a speed–accuracy trade-off. At the fastest scale, the harmonicity of the back and forth movements, which reflects the dissipation of mechanical energy, was measured within the timeframe of single trials. At an intermediate scale, speed and accuracy measures were determined over a trial. The slowest scale pertains to the temporal structure of movement variability, which evolves over multiple trials. In the difficult condition, reliable correlations across each of the measures corroborated a coupling of nested scales of performance. Participants who predominantly emphasized the speed-side of the trade-off (despite the instruction to be both fast and accurate) produced more harmonic movements and clearer 1/f scaling in the produced movement time series, but were less accurate and produced more random variability in the produced movement amplitudes (vice versa for more accurate participants). This implied that speed–accuracy trade-off was accompanied by a trade-off between temporal and spatial streams of 1/f scaling, as confirmed by entropy measures. In the easy condition, however, no trade-offs nor couplings among scales of performance were observed. Together, these results suggest that 1/f scaling is more than just a byproduct of cognition. These findings rather support the claim that interaction-dominant dynamics constitute a coordinative basis for goal-directed behavior.
Introduction
Trade-off phenomena emerge when human performance reaches its limits, and the trade-off between speed and accuracy especially, has played an historic role in the study of cognitive performances. Speed–accuracy trade-offs entail that faster actions are performed less accurately, while more accurate actions are executed more slowly, and have been a topic of study for more than a century (Woodworth, 1899). Nevertheless, the origins of speed–accuracy trade-offs are still debated. This study aims to describe a speed–accuracy trade-off in terms of interacting constraints, which are nested across different timescales of performance.
Our interest in nested constraints is motivated by the fact that well-coordinated behavior consists of dynamic sequences that evolve simultaneously on slower or faster timescales (cf. Pattee, 1973). For instance, in an everyday conversation, a conversant will produce syllables, themselves contained in words, which in turn are contained in sentences. The events that equate pronouncing a syllable (fast), word (slower), or sentence (slowest) unfold on different timescales. The involved timescales of control extend to around 70 muscles that must coordinate to pronounce a single syllable (Turvey, 2007), as well as to the postural sway and eye movements of speakers that become coupled in their conversation (Shockley et al., 2003; Richardson et al., 2007). All these correlated events (e.g., producing an utterance, word, or sentence, leaning forward, or backward, etc.) exist across nested timescales of change, from milliseconds to minutes or possibly hours, although they are coupled, nonetheless, in a highly constrained coordinated activity of speech to enact a conversation.
The example of a conversation aims to show that coordinating listening and speaking means properly sequencing events across a hierarchy of timescales. With these multiple timescales present in any example of behavior, the challenge is to identify the general principles of coordination in systems of such complexity. A good place to start investigating how behavior becomes so precisely ordered spatially and temporally is at the limits of task performance. It is in behavioral regimes where incompatible constraints are imposed on performance where trade-off behaviors emerge, and where the different timescales of changing constraints are likely to reveal themselves in most detail.
In this study, we employ a cyclic precision aiming task that has a long history in psychology (Fitts, 1954), allowing a solid empirical ground on which to begin to describe the nested sources of constraint within a speed–accuracy trade-off. In this task, participants are typically instructed to move a pen or stylus as fast and as accurately as possible back and forth between two visual targets. Arguably one of the most robust models of speed–accuracy in goal-directed movements, Fitts’ law, describes the relation between the duration of accurate movements (MT) and the precision constraints of the task, namely the target size W and the movement amplitude D between the targets; MT = a + b log2 (2D/W).
Note that movement time and accuracy describe performance at the timescale of aggregate single trial outcomes. Consequently, Fitts’ original model made no predictions about the movement trajectories enacted within a trial. Historically, however, the study of speed–accuracy trade-offs has been tied as well to the kinematics of movement trajectories (i.e., changes in displacement, velocity, and acceleration over time or position). Increasing accuracy requirements, for instance, induces systematic changes in movement kinematics (e.g., the deceleration phase lengthens for more narrow targets, time to peak velocity is scaled to movement amplitude, etc.; Adam, 1992). The speed–accuracy trade-off thus yields contingencies that couple the timescale of single trial outcome measures (as expressed by aggregate speed and accuracy measures), to the faster changing kinematics enacted within a single movement.
Here, we further pursue the suggestion that constraints at one timescale interact with and may therefore trade-off against constraints at a slower or faster timescale. This entails contingencies of trade-off phenomena that compose horizontal couplings (within a timescale: i.e., speed versus accuracy) as well as vertical couplings (across timescales: i.e., speed or accuracy versus movement kinematics). The present study tests whether such couplings extend to the temporal structure of observed variability in sources of constraint evolving on timescales slower still than the trial-by-trial scale of average speed or accuracy (Gilden et al., 1995; Slifkin and Newell, 1998; Gilden, 2001; Riley and Turvey, 2002; Van Orden et al., 2003; Hausdorff, 2007).
Figure 1 presents the different levels of analysis included in this study, each of which pertains to a different measurement of performance. The top part of Figure 1 pertains to the fastest timescale of the Fitts task. It shows acceleration profiles that reveal the biomechanical constraints that operate on kinematic parameters within the movement trajectories of a Fitts task performance. The middle part of Figure 1 pertains to an intermediate measurement scale of speed and accuracy measures, which summarize an entire movement outcome and directly reveals the degree of task-compliance. The bottom part of Figure 1 pertains to the slowest changes occurring over multiple trial outcomes across the entire Fitts task session, as it shows two time series with a distinct sequential structure of variability over many trials.
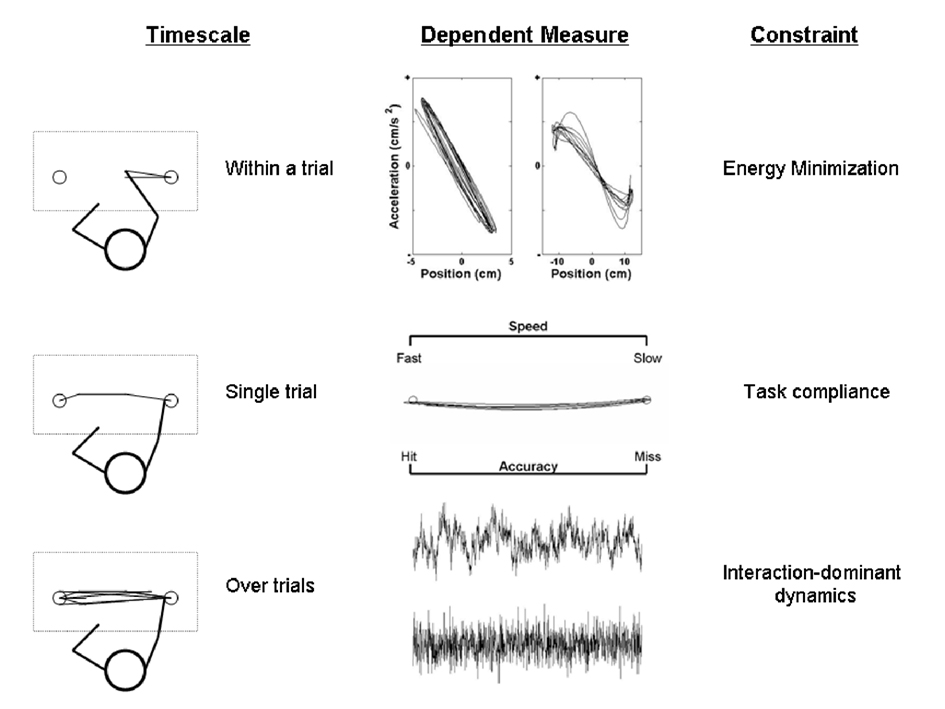
Figure 1. Three possibly interlinked measurement scales are shown. The top part represents an example of performances evolving within the timeframe of a movement (finest scale). The middle part pertains to performances at the level of a movement outcome (intermediate scale). The bottom part concerns dynamics evolving over sequences of multiple trial outcomes (coarsest scales).
By investigating a perceptual-motor task simultaneously at three different scales of observation, we expect linkages within and between these scales. If control is indeed distributed over intertwined timescales, that would challenge the conventional assumption, however, that the locus of human control is encapsulated in discrete components that each solve their own problems along a single common timescale (cf. Simon, 1973). And in fact, there exist good arguments to support the idea that the many free variables of the skeletomuscular system are not controlled individually (Bernstein, 1967; Turvey, 2007). For instance, in natural and artificial self-organizing systems, simple coupling rules at the level of the individual components of the system can result in overall coherent behavior (Prigogine and Stengers, 1984; Bak et al., 1987).
Movement Kinematics
The spatial and temporal details of movement trajectories constitute a rich source of information about the organization of human movement. This fine observational scale of movement analysis contains details which are lost at the coarser scale of a movement outcome as it provides information on how muscles act to generate and degenerate kinetic energy in the moving arm within the timeframe of an entire movement. Kinematic descriptions of movement patterns have a long history in the study of motor control and have substantially fueled the debate on trade-off phenomena. In this study we limit our interest in movement kinematics to a physical description of the dissipation of mechanical energy in rhythmical movements.
Specifically, rhythmical movements can be described precisely in physical terms of a self-sustained oscillation (e.g., Haken et al., 1985; Kay et al., 1987; Kugler and Turvey, 1987; Beek et al., 1995; Kelso, 1995). As an example, consider a mass-spring system without friction. If the system is at rest at the equilibrium position then there is no force acting on the mass. If the mass is displaced from the equilibrium position, a restoring (elastic) force F (potential energy) is exerted by the spring in the form of: F = −kx (Hooke, 1678; known as Hooke’s law), where k is a spring constant, and x is the displacement from the equilibrium position. The negative sign means that the elastic, restoring force always acts in the opposite direction of the displacement. In other words, when the system is displaced from its equilibrium position, mass will start oscillating in a sinusoidal fashion (called simple harmonic motion) because an elastic restoring force which obeys Hooke’s law tends to restore the system toward the center of displacement. This means that velocity is maximal at the center of the movement (equilibrium position) and minimal at the turning points, while acceleration is maximal at the turning points, and minimal at the center. Thus, if rhythmical movements reveal simple harmonic motion, the oscillator energetically self-sustains itself, hence the term self-sustaining oscillator.
Under certain conditions, typically involving low precision constraints, a moving limb in a cyclic Fitts task acts as a linear oscillator and thus displays simple harmonic motion (e.g., Mottet and Bootsma, 1999). Rhythmical movement thus exploits the elastic properties of the neuromuscular system, much like a mass-spring system. This means that when the moving arm, hand, and shoulder are stretched to the left, it pulls back to the right near reversals, because muscular and other tissues function as the spring that elastically stores and releases mechanical energy (Turvey, 1990). In other words, kinetic energy that is lost toward the end of each movement is stored in a potential, elastic form at the natural biomechanical turning points of the limbs to the benefit of the next half-cycle of movement (Guiard, 1993). Unlike the mass-spring example, however, human movement is susceptible to friction and consequently mechanical energy is lost in each movement cycle. A self-sustained linear oscillator must therefore overcome the energy loss due to friction to sustain cyclic motion (see Kugler and Turvey, 1987, for a detailed description).
Figure 2A shows 20 low precision-constrained movement trajectories (targets are 2 cm wide and 8 cm apart) that reveal simple harmonic motion, and hence, obey Hooke’s law. Figure 2C shows that changes in velocity with changes in displacement (called a phase portrait) are circular, typical for a linear oscillator: maximal velocity is reached at the center of the movement where acceleration is minimal (see Figure 2E), and maximum acceleration is reached at movement reversals where velocity is minimal. The smooth cyclic motion requires only a modicum of fresh energy to sustain the trajectory to the next target, thus dissipating little mechanical energy because of the elastic restoring force.
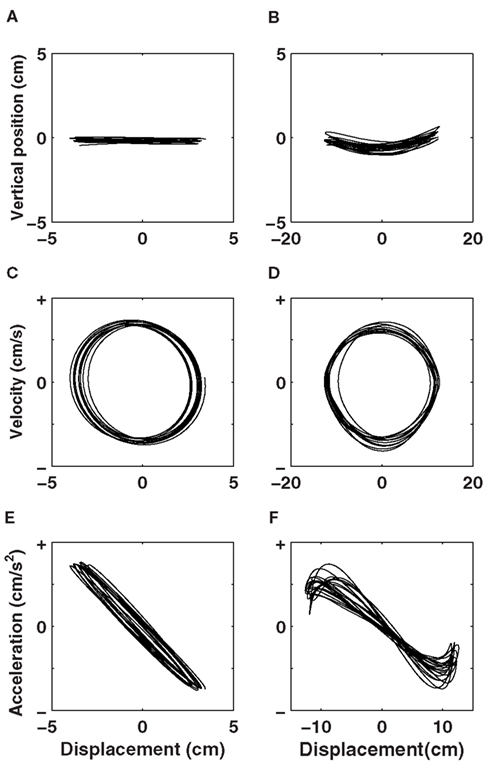
Figure 2. (A) Depicts 20 harmonic half-cycles (the circular targets were 2 cm wide and 8 cm apart) produced by one representative participant during the course of the experiment. (B) Shows 20 inharmonic half-cycles produced by another representative participant in a condition where targets were 0.4 cm wide and 24 cm apart. (C) Harmonic half-cycles reveal a circular phase portrait typical for a linear oscillator, whereas (D) inharmonic half-cycles reveal a damped phase portrait. The respective acceleration (Hooke’s) portraits for the harmonic and inharmonic movements are presented in the respective (E,F). Note the different scale on the x-axes.
Highly precision-constrained movements, in contrast (as shown in Figure 2B; targets are 0.4 cm wide and 24 cm apart) typically require strong deceleration when approaching a target, and thus display inharmonic motion. In physical terms, the self-sustained oscillation becomes dampened as mechanical energy is dissipated by decelerating toward the target (see Figures 2D,F). This means that the mechanical energy that cannot be recovered in potential form (because it is dissipated) needs to be re-inserted each time a participant re-accelerates toward the next target. The relative degree of harmonicity in the kinematics of rhythmical movement thus offers a physical description of the recycling of kinetic energy in potential form, which acts as a biomechanical constraint on speed–accuracy trade-off in cyclic movements.
Long-Range Dynamics
When people perform cyclic movements, there is always cycle-to-cycle variability. The variability of goal-directed behavior may in fact be one of its most prominent characteristics: Individual movement cycles are never exact duplicates of one another. The conventional assumption is that movement variability is a product of unstructured (random, Gaussian) noise, superimposed on a deterministic signal. That is, trial-ordered dynamics are usually conceived as a statistical nuisance, providing minimal, if any, insight into the nature of coordination, apart from the magnitude of white noise (e.g., standard deviation).
Over recent decades, however, it has become clear that movement variability rarely equates with white noise, and that temporal variability is usually structured and reveals specific details of the system dynamics (Slifkin and Newell, 1998; Gilden, 2001; Riley and Turvey, 2002; Stergiou and Decker, 2011; Torre and Balasubramaniam, 2011). In fact, structured variability appears to be the rule rather than the exception, and is often more revealing than aggregate information in terms of unpacking the nature of the system organization (Kello et al., 2007; Kiefer et al., 2009; Ihlen and Vereijken, 2010; Konvalinka et al., 2011; Wallot and Van Orden, 2011a).
Nevertheless, the nature of cognitive dynamics still remains a much debated topic. Some scientists prefer to retain that long-range dynamics are only a byproduct, which is neither detrimental nor particularly useful to inquiry (Wagenmakers et al., 2011). Others have suggested that structured variability is a fundamental, functional feature, playing a crucial role in the coordination of perception and action (Van Orden et al., 2003; Kello et al., 2007; Wijnants et al., 2009). Here we pursue the latter suggestion by investigating the fractal scaling properties and entropy of spatial and temporal long-range dynamics, both in the presence and in the absence of speed–accuracy trade-off.
1/f scaling
1/f Fluctuation presents an intriguing phenomenon that has received a growing interest in biology, psychology, and movement sciences during the last decade. It is a describing property of the trial-by-trial variability of a time series, observed during repeated human performances. Fractal processes like 1/f scaling have the characteristic of self-similarity, which means that similar statistical features are observed across different temporal or spatial scales. The fractal pattern of variation can, for instance, be portrayed in a spectral analysis. This involves transforming a time series into the frequency domain by Fourier analysis, which represents the series as a set of sine waves, each with an associated frequency (how often changes of a particular size occur) and power (the size of changes across measured values). 1/f Scaling of a time series means that changes in power are typically small at the highest frequencies (i.e., extending over few trials), but that those changes are embedded in overarching, lower frequent changes of higher amplitude spanning over many measurements. 1/f Scaling thus composes a nested pattern of response variability across scales; a time series plot of 1/f fluctuations has the same “look and feel” as one zooms in or out to see more fine-grained or coarse-grained features of the fluctuations (e.g., see Wallot and Van Orden, 2011b).
Statistically, a 1/f scaling relation can be expressed as a relation between the size of changes (power), and how often changes of that size occur (frequency), which is inversely proportional on logarithmic scales. Figure 3 presents three types of temporal variability (i.e., noise) of a time series accompanied by their respective power spectra. The top part of the figure represents a data series with random background noise. A data series with random background noise, as traditionally assumed in many statistical analyses, does not yield a relationship among frequency (f) and a particular change of amplitude S(f) in the signal. The middle part of the figure represents a time series that is very close to ideal 1/f scaling, and can be parameterized by an exponent α, as 1/fα, where α is 1 for ideal 1/f scaling. The bottom part of the figure is called Brownian noise and can be described as 1/f2 noise. Brownian noise is also called a random walk, because it can be produced by adding a random increment to each sample to obtain the next. In contrast to white noise, which can be produced by randomly choosing each sample independently, Brownian noise yields persistence or memory in the data series.
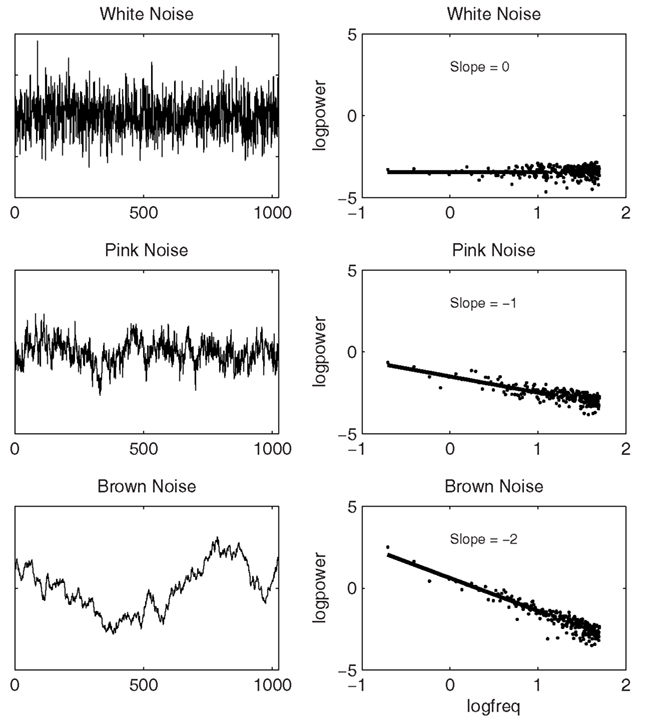
Figure 3. Three different classes of temporal variability, white noise (upper left panel), 1/f scaling (middle left panel), and Brownian noise (lower left panel), and their respective power spectra are shown in the respective panels at the right.
To date, dozens of studies have been published on 1/f scaling in cognitive and motor performance, all demonstrating widespread, perhaps ubiquitous fractal dynamics (e.g., Diniz et al., 2011; Van Orden et al., 2011, are reviews). Typically, repeated human behaviors show a scaling exponent α in the range of 0 and 1, in between random noise and 1/f scaling. Examples of cognitive tasks include mental rotation, lexical decision, and visual search (Gilden, 2001), simple reaction time and word-naming (Van Orden et al., 2003), forearm oscillation (Delignières et al., 2008), synchronization to a metronome (Chen et al., 1997; Ding et al., 2002); implicit associations (Correll, 2008), bi-daily reports of self-esteem (Delignières et al., 2004), and movement times in a Fitts task (Valdez and Amazeen, 2008; Wijnants et al., 2009), among others. But sometimes α varies between 1 and 2 or even beyond, often in continuous processes like postural sway (e.g., Collins and De Luca, 1993), force production (Sosnoff et al., 2009), or galvanic skin response (Wijnants, 2012).
Although 1/f scaling has been observed throughout human physiology and behavior in varying degrees, its origin, and meaning remains unclear (Van Orden et al., 2005; Diniz et al., 2011). One position in the debate is that 1/f scaling is a typical behavior of self-organizing systems, which reflects a fundamental aspect of all physiological and cognitive functions: their emergence in the balance of independent versus interdependent component activities. In recent years, there has been a growing empirical support for the position that 1/f scaling may indeed result from the interaction of many ongoing processes over a multiplicity of interdependent scales, thereby serving as a coordinative basis of cognitive function (e.g., Kello et al., 2007; Wijnants et al., 2009; Kello, 2011; Van Orden et al., 2011). That is, 1/f scaling is usually seen most clearly in well-coordinated behaviors, and less clearly in non-optimal performance or with aging and disease (e.g., Goldberger et al., 2002; West, 2006).
For instance, deviations from 1/f scaling, either toward white noise or toward Brownian motion, have been found with epilepsy (Ramon et al., 2008), heart failure (Goldberger et al., 2002), fetal distress syndrome (Goldberger, 1996), major-depressive disorder (Linkenkaer-Hansen et al., 2005), mania (Bahrami et al., 2005), attention-deficit-hyperactivity-disorder (Gilden and Hancock, 2007), developmental dyslexia (Wijnants, 2012), autism (Lai et al., 2010), Alzheimer’s disease (Abásolo et al., 2006), Huntington’s disease (West, 2006), Parkinson’s disease (Hausdorff, 2007), and slow transit constipation (Yan et al., 2008), among other examples. In each of these studies, healthy controls revealed long-range dynamics reliably closer to 1/f scaling in the respective variables of interest.
These examples have been paralleled by manipulations of task constraints as well. For instance, the presence of 1/f scaling increases as performance becomes more proficient with learning (Wijnants et al., 2009), yet may sometimes decrease as task demands increase (Clayton and Frey, 1997; Correll, 2008; although cf. Kloos and Van Orden, 2010). The presence of 1/f scaling also correlates with the severity of a reading impairment (Wijnants, 2012), depression symptoms (Linkenkaer-Hansen et al., 2005), the success rate of recovery from traumatic brain injury (Burr et al., 2008), the severity of Huntington’s and Parkinson’s symptoms (Van Orden, 2010) and falling risk in elderly (Hausdorff, 2007). In each of the cases more flexibly stable, adaptive, or coordinated behaviors showed clearer 1/f scaling.
These studies raise the suggestion of close linkages between fractal dynamics and coordination in human physiology and cognition, and with these precedent studies in mind we employ 1/f scaling as a performance index of coordination in a Fitts task (cf. Miyazaki et al., 2001; Valdez and Amazeen, 2008) to investigate speed–accuracy trade-off. Far from being a statistical artifact or “just” unexplained variance, fractal patterns may actually be a signature of strongly emergent coordination. If so, one may expect 1/f scaling measures to be sensitive to the task-specific constraints that are in play in a trade-off among performance measures.
Entropy
We complement our analyses of long-range dynamics by assessing the entropy of the data signals, which provides a complementary way of characterizing the presence of temporal structure in a time series. A measure of entropy summarizes the degree of predictability of a time series, which is the likelihood that similar observations (i.e., observations within a specified range of measurement values) are followed by a number of additional observations within that range. Entropy can thus be conceived as a measure of orderliness. The entropy of a system increases as it becomes more disordered or random, and decreases as it becomes more patterned (i.e., shows increased temporal order, as in 1/f scaling). This means that changes in entropy provide a potential window into self-organizing control in complex systems, because self-organization can be considered as a spontaneous tendency of a system toward order and entropy is a measure of the disorder of a system.
In other words, time series containing coherent dynamical structure are expected to yield lower entropy than less predictable (i.e., random) time series. Nonetheless, reduced entropy is far from an exclusive criterion for self-organization. For instance, trivially uniform or periodic signals would yield even lower entropy (i.e., high self-similarity on a fixed scale) than would be expected from the behavior of a self-organizing system that is scale-free. That is, self-organizing systems arguably live near the midpoint of a scale that ranges from independent random variables (i.e., high entropy) to static or periodic variables (i.e., low entropy). Inconveniently, there is neither a clear-cut midpoint nor an absolute scale of entropy in terms of cognitive activities. Therefore, we use entropy here solely as a check of convergence in direction of change with 1/f scaling measures. Although the extent of 1/f scaling should be honest in itself, a measure of entropy provides an additional reliability check of the deviations from randomness that are expected in the performances of low-dimensional, self-organizing systems constrained across multiple scales of degrees of freedom.
Hypothesis
Here, we employ the classic paradigm of precision aiming to investigate speed–accuracy trade-off in goal-directed behavior. We presented participants with a Fitts task and instructed them to move as fast and as accurately as possible back and forth between two circular targets for a prolonged time (1100 half-cycles). The resultant movement coordinates were analyzed at three different measurement scales of performance. The finest scale yields a measurement of the movement kinematics (within-trial). This description of performance is not implied by aggregate single trial outcomes (speed and accuracy) which, in turn, are not implied by the structure of motor variability (1/f scaling and entropy). Changes in long-range dynamics contingent on a trade-off between speed and accuracy would complete an evaluation of performance at the three different measurement scales.
Half of the participants were presented with a difficult Fitts task (D = 24 cm, W = 0.4 cm). This difficult condition was designed to be incompatible with the speed–accuracy task instruction. We expected that in the presence of incompatible task constraints (i.e., performing a highly precision-constrained task simultaneously fast and accurate), participants would predominantly emphasize one of the conflicting task dimensions over the other, because it is known that participants self-define their position along the continuum of speed versus accuracy while being equally instructed to move as fast and as accurately as possible (cf. Adam, 1992; Rinkenauer et al., 2004). We exploited the resultant between-subject variability to evaluate whether these performance modes entail constraints that apply to the other two scales of description.
If levels of performance are coupled across timescales, it is expected that movement kinematics and long-range dynamics will be contingent upon control over the emphasized side of the trade-off. For instance, it is known that faster, less accurate performance better capitalizes on the elastic properties of the body, and thus producing more harmonic kinematics compared with more accurate, but slower performance (e.g., see Figure 5). Equally, there is evidence suggesting that long-range dynamics of human performance are contingent on the emphasized performance mode. For instance, extensive practice of a challenging Fitts task not only leads to faster movement times, but also to clearer 1/f scaling and reduced entropy in a time series of movement times (Wijnants et al., 2009). So, if 1/f scaling indeed serves as a coordinative basis for goal-directed behavior, the straight-forward prediction follows that clearer 1/f scaling, and lower entropy are expected in long-range dynamics pertaining to the emphasized performance outcome (either speed or accuracy).
This would entail functional motor synergies optimizing speed and yielding clearer examples of 1/f scaling and reduced entropy in movement time series (see Figure 4A). At the same time, a faster performance mode entails less control over accuracy, and thus, less clear examples of 1/f scaling and higher entropy are expected in movement amplitude series (see Figure 4B). Conversely, when control comes down on the accuracy side of the trade-off, we may expect clearer examples of 1/f scaling and reduced entropy in movement amplitude series, but more random dynamics in movement time series. This would then amount to a trade-off in long-range dynamics that is contingent on the speed–accuracy trade-off.
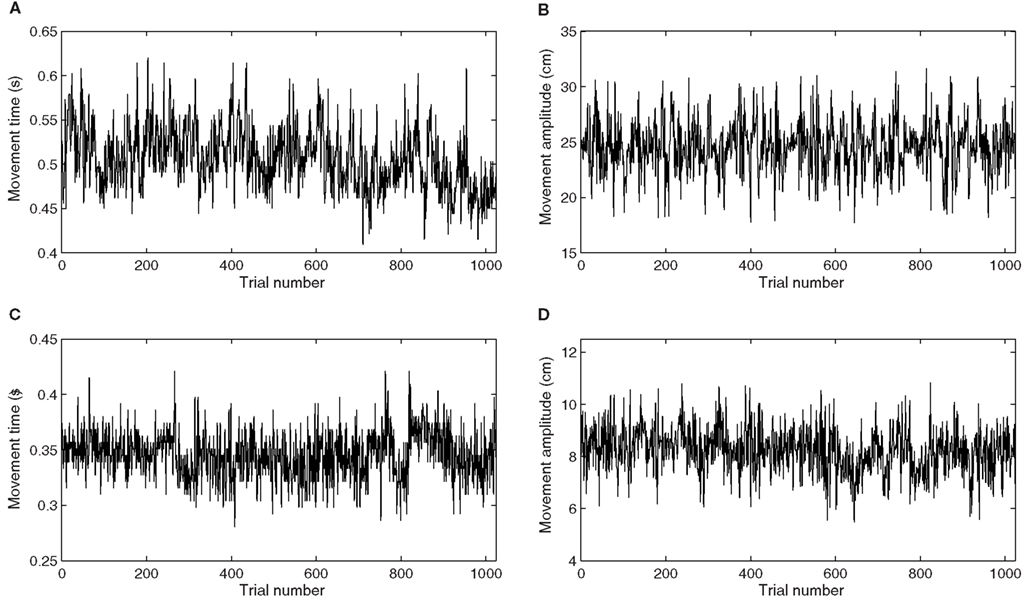
Figure 4. (A,B) Represent example movement time and movement amplitude series in the difficult condition. (C,D) Represent example movement time and movement amplitude series in the easy condition.
The other half of the participants was presented with an easy Fitts task (D = 8 cm, W = 2 cm), designed to be compatible with the speed–accuracy task instruction. The targets were five times as large and three times closer together compared to the difficult condition. This easy condition allowed participants to be simultaneously fast and accurate, rather than requiring them to emphasize one task requirement over the other like in a speed–accuracy trade-off. Thus, we expected participants to assemble functional synergies supporting fast and accurate performance simultaneously. Consequently, we anticipate the trade-off between long-range dynamics of movement time series (see Figure 4C) and movement amplitude series (see Figure 4D), hypothesized in the difficult condition, to be absent in the easy condition because both task requirements can be met simultaneously.
Materials and Methods
Participants
Thirty undergraduate students were randomly assigned to one of the two difficulty conditions. The participants received course credits for participation. All participants had normal or corrected to normal vision and were right-handed. None suffered from any known motor impairment.
Materials
Fitts’ law allowed us to construct material conditions that differed reliably, and to a known degree, in difficulty. An Index of Difficulty (ID, measured in bits/s) has been derived from Fitts’ law, using the ratio between the width W of targets and their distance D. For this study, two levels of difficulty were constructed. The difficult condition used circular targets 0.4 cm wide and 24 cm apart, yielding an ID of 6.9. At this level of task difficulty, participants are generally unable to produce optimal kinematics and remain accurate, as opposed to the easy condition which used circular targets 2 cm wide and only 8 cm apart, yielding an ID of 3 (Guiard, 1993; Mottet and Bootsma, 1999). Movement coordinates were recorded on a WACOM digitizer tablet with a sampling rate of 171 Hz. The input device was an inkless stylus used on a model sheet (A4) placed on top of the digitizer tablet.
Procedure
Participants were seated on a height-adjustable chair and instructed to use their dominant hand to draw lines (hence, not tapping) back and forth between two circular targets, as quickly and accurately as possible. The targets were positioned one on the left and one on the right side of a printed sheet of paper. When 1100 trials were completed a tone signaled the end of the experiment.
Data Analysis
We analyzed the participants’ performances at three different scales of analysis. From each participants’ sequence of 1100 movements we computed an Index of Harmonicity (H) from the movement kinematics, aggregate speed and accuracy measures of single trial outcomes, and long-range dynamics of movement time and movement amplitude series using fractal dimension (FD) and sample entropy statistics (as explained below). Then, within each task condition, the 15 participants were ranked on each of the variables applying non-parametric (Spearman) correlation statistics to assess contingencies in the between-subject variability across these variables. We used Spearman’s rho because we expected monotonic relations, but not necessarily linear ones.
Harmonicity
A measurement called Index of Harmonicity (H; cf. Guiard, 1993) was computed based on the acceleration trace of the back and forth movements. First, the recorded position time series were filtered using a third-order 5 Hz low-pass Butterworth filter. As a second step the position recordings were rescaled so that the point of zero position was exactly in the middle of the two targets. For example in the easy task condition target distance was 8 cm, so the left target was at −4 cm, and the right target at 4 cm.
Then the acceleration time series were computed (in cm/s2), and segmented so that each segment ranged from one zero-crossing in displacement (movement midpoint) to the next zero-crossing and thus contained one movement reversal. Figure 5A shows three example acceleration profiles from four consecutive movements segmented this way. The oscillation midpoints are shown as vertical lines, and time is on the x-axis. Also displacement is shown, but note that acceleration and displacement were normalized to bring them on a comparable scale in the figure. Also note that a segment containing a reversal at the right target (positive displacement) is shown as negative acceleration, and a segment containing a movement reversal at the left target (negative displacement) as positive acceleration.
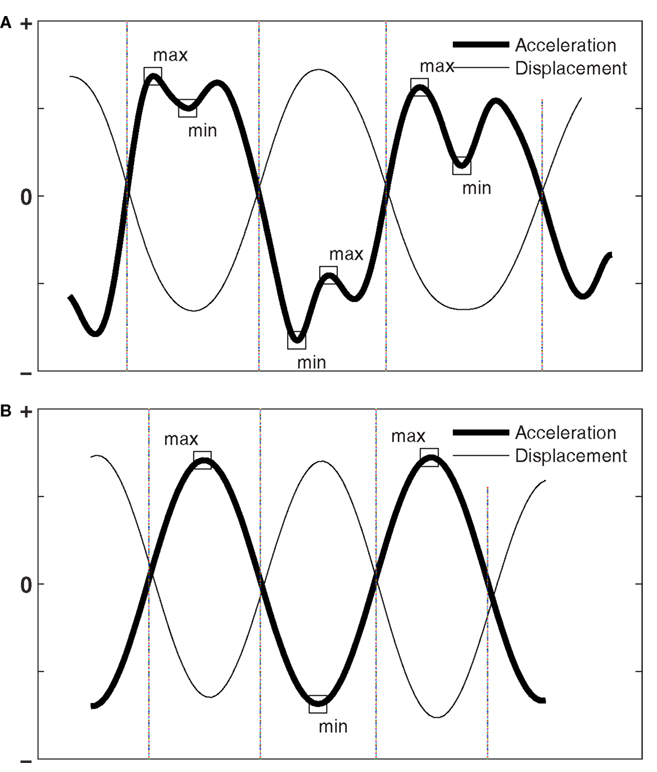
Figure 5. (A) Shows the normalized acceleration and displacement series observed in four half-cycles of movement (difficult condition) divided into three segments, each containing a movement reversal. The minimal and maximal local extrema (LE) in each segment are shown as square markers. H was computed as the ratio of these extrema (see text). If only one local extreme was observed, as in the (B) (easy condition), H is the ratio of that extreme against itself (H = 1).
Next, the local extrema (LE) were identified in the acceleration trace of each segment. The minimal and maximal LE within each segment are shown as square markers in Figure 5. H was computed as the ratio of the maximal LE to the minimal LE of acceleration for positive displacement (i.e., movement to the right; note, negative acceleration), and vice versa as the ratio of minimal LE to maximal LE for negative displacement (i.e., movement to the left; note, positive acceleration). By construction, H ranges between 0 and 1. That is, if acceleration changes sign at a movement reversal (i.e., a corrective movement), H is set to 0, reflecting the full dissipation of mechanical energy. The value of H was computed for every segment, and averaged to yield a global estimate of H.
The extent to which, at movement reversals, terminal braking, and initial re-acceleration fuse, as expressed by H, is of interest because such a fusion reflects the saving of mechanical energy, that is, the recycling of kinetic energy in potential form. For instance, Figure 5A is taken from the difficult task condition and shows that terminal braking is required when approaching the target to comply with the high precision constraint, and consequently mechanical energy is dissipated (cf. Figure 2F). In the next movement, re-acceleration is required to meet up with the speed-constraint. This can be seen as biphasic acceleration segments (Figure 5A) of which H expresses the depth of the well, hence the amount of mechanical energy that is dissipated. The stronger the deceleration (and the consequent re-acceleration) near movement reversals, the more energy is dissipated and the lower the value of H.
In easy task conditions, however, the two peaks in the biphasic acceleration profile tend to merge into a single event (see Figure 5B). The acceleration profile becomes sinusoidal, because the displacement series is perfectly sinusoidal, as in a frictionless mass-spring system. In this case only one LE is detected, and H is the ratio of the LE to itself (i.e., H = 1), evidencing perfectly simple harmonious kinematics (cf., Figure 2E).
Speed and accuracy
For each participant, we computed the average movement time and the percentage of accuracy. Movement time (in seconds) was determined as the difference in the number of sampled points between begin and end points of each movement (zero-crossings in velocity), divided by sample rate (in Hz). Accuracy was determined as the percentage of hits (hits/total number of movements*100).
1/f scaling
The repeated performances of each participant were treated as a time series. That is, the movement time and movement amplitude sequences were kept in the trial-order in which they were collected. The movement amplitudes were computed as the one-dimensional distance between zero-crossings in velocity (cf. Fitts, 1954), see for instance Figures 2C,D. We estimated the FDs of the time series using spectral analysis, standardized dispersion analysis (SDA), and detrended fluctuation analysis (DFA). These methods are complementary in that the strengths of each compensate for the weaknesses of the others. For instance, spectral analysis, while robust in many respects, requires preprocessing of the signal because extreme observations can contaminate the outcome of the analysis (see Holden, 2005). DFA can be applied to non-stationary signals and is not susceptible to most statistical artifacts or long-term trends, but it can falsely classify certain types of signals as fractal (Rangarajan and Ding, 2000). SDA is also highly reliable, but linear and quadratic trends may bias its output. We ensure reliable conclusions by using all three methods together.
With these analyses it is prudent to preprocess the raw data in order to avoid the known pitfalls (Holden, 2005). Therefore, outliers were removed if they lay outside three standard deviations from the mean. Then, linear trends and quadratic trends were removed and the beginning trials of the experiment were truncated until 1,024 observations remained, because spectral analysis and SDA require series lengths that are a power of 2. As a last step, the time series were normalized.
Spectral analysis
Spectral analysis transforms data series from the time domain (e.g., milliseconds) into a frequency domain (Hz), through a Fast-Fourier-Transformation. The procedure finds the best-fitting sum of harmonic sine waves in a data signal, and renders their power (amplitude square) at each fitted frequency on log–log-scales. The total number of estimated frequencies in the Fast-Fourier Transform was 512. The statistic of interest is the slope of the spectral portrait, which captures the relation between amplitudes and frequencies of variation in the data signal. Here, we fitted the spectral slope over the 25% of lowest frequencies (cf. Eke et al., 2002). A zero slope indicates a random signal, a slope of −1 indicates 1/f scaling. Spectral slopes as steep as −2 indicate fractional Brownian motion, the epitome of random walk processes (see Figure 3).
Standardized dispersion analysis
Standardized dispersion analysis investigates the scaling of variability with changes in sample size. That is, variability is measured using the standard deviation (using the population formula, i.e., using N, the number of data points, in the calculation, rather than the usual bias corrected N − 1) of means of progressively larger adjacent samples in a time series. That is, the analysis tracks how dispersion in sample means decreases as progressively larger samples of adjacent data points (bins) are aggregated together in a sample mean. As a first step, the standard deviation is computed for the original data series, which contains 1024 “mean” values of the data points themselves. The second step involves calculating the standard deviation of the 512 means (bins) of each two consecutive measurements (bin size), and so on. We iterated this procedure until only 32 bins were remaining, each of which represents the mean of 32 adjacent samples in the original time series.
The results from SDA can be seen in a plot of the logarithm of the bin size against the logarithm of the standard deviation, as in Figure 6. For random, white noise, it should not matter that adjacent samples are being grouped and regrouped to form samples of different sizes; for white noise, the slope in Figure 6 is close to −0.5 (see Van Orden et al., 2003 for a detailed description). The outcome of SDA is expressed by the FD of a time series, which is given as 1 – the slope of the regression line. Thus, the FD of white noise is 1.5. This can be derived simply from the equation for the standard error of the mean (SE = SD/√N). For a large sample size N, the standard error SE gets close to zero, and thus yields a stable population parameter for white noise. Thus, SE scales as a function of sample size N as 1/√N for a SD of 1 as in our normalized series. On log–log-scales, this can be written as log (SE) = −0.5 log(N). The slope of −0.5 in Figure 6 simply follows from this equation, and leads to a corresponding FD of 1 − (−0.5) = 1.5. A shallower slope (i.e., the 1/f scaling pattern shown in Figure 5 has a slope of around −0.2; i.e., FD equals roughly 1.2), however, indicates correlated activity across timescales, as expressed by the change in a variance statistic due to changes in bin sample sizes. A FD thus expresses whether the variance statistic converges fast enough, as sample size increases, to yield a stable population parameter. If not, then the process that produced the variance would reveal a slope that is less steep than −0.5 (suggesting a FD less than 1.5), which would indicate a lack of characteristic scale or quantity of variance in the series. An in-depth tutorial of both spectral analysis and SDA can be found in Holden (2005).
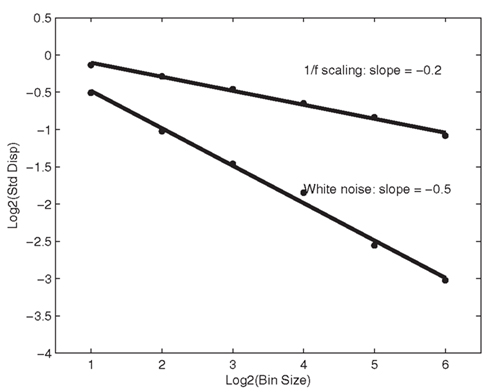
Figure 6. Standardized dispersion is shown as a function of sample-bin size, on log-scales (base 2 was used here). The solid line is the least-squares regression for the six different estimates. Fractal dimension is computed as 1 – the slope. The fractal dimension of white noise equals 1.5, whereas a fractal dimension of 1.2 indicates exact 1/f scaling.
Detrended fluctuation analysis
Detrended Fluctuation Analysis (Peng et al., 1993) is yet another method to reveal the extent of 1/f scaling in behavioral time series, and is especially useful when confronted with non-stationary signals. The first step is to integrate the time series to be analyzed. Next, the integrated time series is divided into bins of equal length, containing n data points. In each bin of length n, a least-squares line is fitted to the data (representing the trend in that bin). And then the time series is detrended by subtracting the local trend in each bin. From the now integrated and detrended time series, the root-mean-square fluctuation (average fluctuation) is calculated. This computation is repeated over various timescales (bin sizes) to characterize the average fluctuation at each timescale. In the present study, DFA was performed on bin sizes ranging between 22 and 29 data points (ranging from a few seconds to minutes of performance). The results from DFA are usually shown in a plot of bin size against fluctuation, as in Figure 7, in which the scaling exponent is given by the slope. For 1/f scaling, fluctuation will increase with bin size, as indicated by a linear relationship on log-scales (yielding a slope of 1). White noise yields a slope of 0.5.
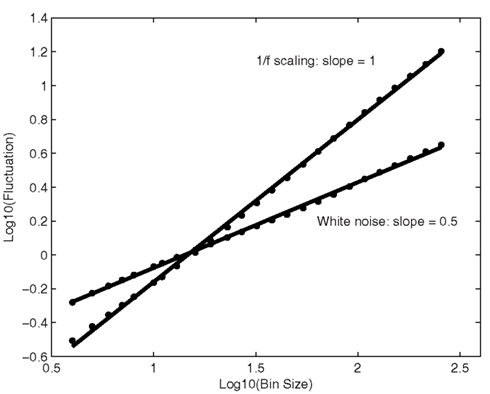
Figure 7. Average fluctuation is depicted as a function of sample-bin size, on log-scales. The solid line is the least-squares regression across timescales. The slope of the regression line equals 0.5 for white noise, and 1 for 1/f scaling.
A common scale of fractal dimension
The reported FD statistics were taken from an average of the FDs across the three estimates (spectral analysis, SDA, and DFA). The outcomes of spectral analyses and DFA were first transformed into a common scale of FD. We assumed that a FD of 1.5 equals white noise, exact 1/f scaling yields a FD of 1.2, and Brownian motion 1.1, and then fitted a curve between these values and the desired corresponding spectral slope (i.e., white noise = 0, pink = −1, and Brownian motion = −2) and DFA exponents (i.e., white noise = 0.5, pink = 1, and Brownian motion = 1.5). This led for spectral analysis to the conversion formula FD = (α2 + 4α + 15)/10, where FD is the fractal dimension, and α the slope of the power spectrum, and for DFA, FD = 0.4β2 − 1.2β + 2, where β is the slope of the log-plot of bin size against fluctuation. For a more in-depth discussion on conversion strategies, see Hasselman (in preparation).
Sample entropy
We supplemented the fractal analyses by estimating the entropy in each data series. Entropy measures have previously been used as a gage of complexity in human performance (e.g., Slifkin and Newell, 1998; Newell et al., 2003; Stergiou and Decker, 2011) and covary with fractal statistics in goal-directed movements (Wijnants et al., 2009). The measure of entropy used here is called Sample Entropy or SampEn. SampEn (m, r, N) is the negative natural logarithm of the conditional probability that a data set of length N, having stayed within a tolerance r for a number m of data points, will continue within that tolerance at the next point, disallowing self-matches. SampEn can thus be considered a measure of self-similarity in a time series and was computed as described by Richman and Moorman (2000).
Sample entropy measures generally range between 0 and 2, where higher values indicate more uniform dispersion of data values (less structured). Our results were robust over a wide range of choices for m and r. In the present analysis, we used parameter values of m = 3 and a tolerance of r = 1 SD, which were both comfortably within that robust range. Sample entropy has the advantage over approximate entropy because it is less biased (i.e., the procedure does not include self-matches), and more robust over a range of input parameters (see Lake et al., 2002).
Results
Descriptive Statistics
The means and standard deviations pertaining to each of the measured variables are presented in Table 1 for both task conditions. As expected, participants in the difficult condition produced slower and less accurate movements than participants in the easy task condition. In the difficult condition, participants also produced less harmonic oscillating behavior, as expected given the conflicting speed–accuracy constraints involved. The FD of movement time and movement amplitude, and the sample entropy of movement time, were lower on average in the easy condition, but not reliably so. The sample entropy of movement amplitude series was higher in the easy condition, which is likely an artifact of the larger movement amplitude tolerance in the easy condition.
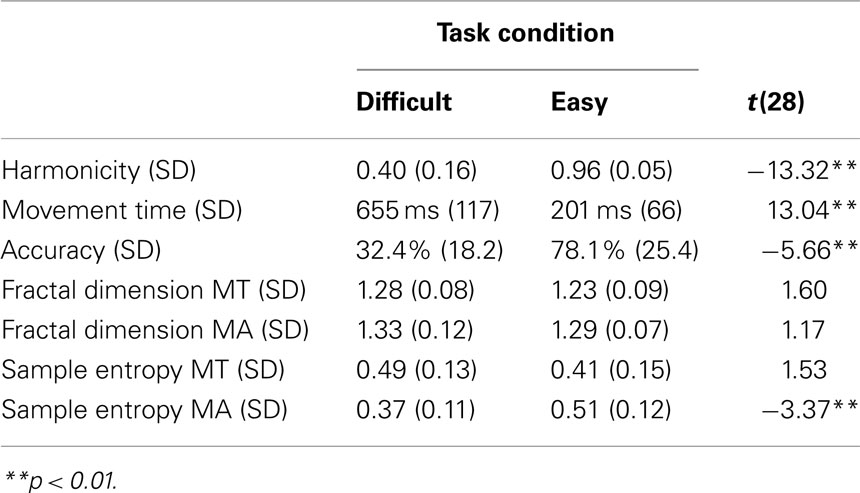
Table 1. Means and standard deviations of the measured variables in the difficult and easy condition.
Non-Parametric Correlations
We used one-tailed Spearman correlations to relate the 15 pairs (individual participant scores) of each combination of the measured variables in both task conditions. This implies separately ranking the individual values within and across their scale of observation. We first discuss the contingencies among variables within each scale of performance, before proceeding to the vertical couplings among the levels themselves.
Within scales of performance
Within the observational level of single movement outcomes, the speed and accuracy measures traded off reliably between-subjects in the difficult condition (movement time and hit rate were positively correlated, ρ = 0.84, p < 0.01). In the easy task condition, however, no speed–accuracy trade-off was observed between-subjects (ρ = −0.10, p = 0.36). Intriguingly, the manipulation of task difficulty had the same effect on the observed long-range dynamics. In the difficult condition, temporal (movement times) and spatial (movement amplitude) sources of 1/f scaling traded off reliably (ρ = −0.64, p < 0.01), as did the entropy values (ρ = −0.84, p < 0.01).
In the easy task condition, however, no trade-offs were observed between spatial and temporal streams of 1/f scaling. To the contrary, the FDs of movement time vs. movement amplitude were positively correlated (ρ = 0.63, p < 0.01), indicating that participants who exploited a wider range of scale-free variability in their temporal performance, also showed clearer fractal-like patterns of variability in their spatial performance. This win–win vs. loose–loose situation was not reliably countered by measures of sample entropy, however (ρ = 0.40, p = 0.07).
Across scales of performance
From the previous paragraph it remains to be answered how our finest scale of observation (movement kinematics) fits into the equation. This question, however, pertains to contingencies across timescales because the harmonicity index primarily reflects the trade-off of energy dissipation of the moving arm against the imposed speed and accuracy constraints, rather than a pure “within-timescale” trade-off.
As expected, the Index of Harmonicity (H) was contingent upon the balance of speed and accuracy in the difficult condition. In the difficult condition, participants who showed shorter movement times produced higher values of H (ρ = −0.90, p < 0.01), and vice versa, slower participants showed less harmonic movements. More surprisingly, H was equally contingent on the observed long-range dynamics (see Table 2). Clearer harmonic motion in participants’ back and forth oscillations went with clearer 1/f scaling in movement times (FD of Movement Time ranged from 1.14 to 1.42), but with less clear 1/f scaling in movement amplitudes (FD of Movement Amplitude ranged from 1.12 to 1.52). Vice versa, less harmonic performances yielded less clear 1/f scaling in movement times, but clearer 1/f scaling in movement amplitude. These fairly strong relations were confirmed by the entropy measures at every turn. In the easy condition, in contrast, none of these relations were reliable.
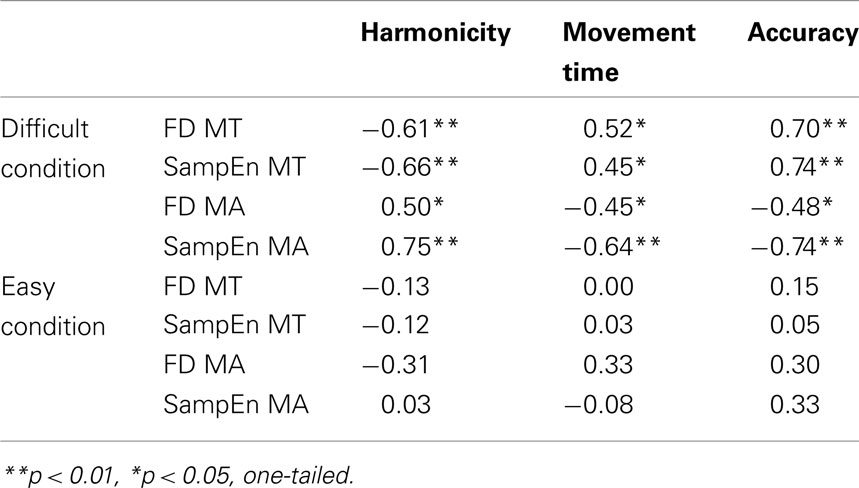
Table 2. For both task conditions, Spearman’s rho is shown for the vertical couplings (across timescales) between the measured variables; harmonicity at the finest timescale, movement time and accuracy at the aggregate level of whole movements, and fractal dimension (FD) and sample entropy (SampEn) of the slower timescales, found in movement time (MT) and movement amplitude (MA) series.
Given the former results, it comes as no surprise that speed and accuracy themselves are closely tied to the long-range dynamics observed in goal-directed behavior. That is, in the difficult condition, faster participants showed more 1/f scaling in the movement time series (the positive relation indicates that low values of Movement Time are associated with low values of FD of Movement Time), and less 1/f scaling in their movement amplitude series (the negative relation indicates that low values of Movement Time are associated with high values of FD of Movement Amplitude), while more accurate participants showed less 1/f scaling in their movement time series (hence, the positive correlation between accuracy and FD Movement Time), but more 1/f scaling in their movement amplitude series (hence, the negative correlation between accuracy and FD Movement Amplitude), as shown in Table 2. Also these relations were confirmed by the sample entropy measures. And most importantly, each of these relations was absent in the easy condition.
Discussion
The present experiment builds upon a long line of research addressing the relation between movement speed and accuracy in goal-directed movements, the kinematics of the movement trajectory itself, and their mutual relation. It was designed to replicate the relation between Fitts’ law (Fitts, 1954) and Hooke’s law (Hooke, 1678) and to extend this coupling to another lawful physical phenomenon: the presence of fractal dynamics in the behavior of complex, biological systems (Mandelbrot, 1982; Bak et al., 1987). Our hypothesis was that control over goal-directed movements is not to be found at a single isolated level within an individual’s functional architecture, but rather in an emergent, dynamic fashion out of the ongoing interaction between processes taking place at multiple scales simultaneously.
We investigated a perceptual-motor task at three different scales of measurement (movement kinematics, movement time and accuracy, and long-range dynamics) to inspect possible linkages within and between these performance scales. Half of the participants were presented with a challenging task condition that was designed to yield incompatible speed–accuracy constraints, so that more accurate participants would be slower performers and faster participants less accurate performers. With the challenging constraints imposed, as expected, faster participants produced more harmonic oscillations than more accurate but slower participants. These measures (harmonicity, revealing details about within-movement kinematics, and movement time and accuracy, revealing the outcomes of whole movements), each at their own scale of observation, were tightly coupled with the long-range dynamics of movement times and movement amplitudes. This third scale of observation pertained to a measurement window ranging from less than a second up to minutes of performance.
In the difficult task condition a close coupling was revealed among measured values probing the different scales of performance. Participants who predominantly emphasized speed, showed more harmonic limb oscillations and clearer 1/f scaling in their produced movement time series (but more random spatial long-range dynamics). More accurate participants, in contrast, showed less harmonicity and clearer 1/f scaling in their produced movement amplitude series (but more random temporal long-range dynamics). A clearer presence of 1/f scaling thus hinges on the task requirement emphasized by the participant. This pattern of couplings among embodied timescales was accompanied by a trade-off between the long-range dynamics of movement time and movement amplitude that was contingent upon the speed–accuracy trade-off. Corresponding sample entropy statistics paralleled the correlations with fractal statistics at every turn.
The observed cross-scale dependencies within an individual’s performance confirmed our initial suspicion that task-specific constraints affect performance measures regardless of the scales of measurement to which they pertain. When faced with incompatible task requirements, the predominant performance mode of the participants (either the speed or the accuracy side of the trade-off) was equally expressed by movement kinematics, average speed and accuracy, and spatial and temporal long-range dynamics. This suggests that near the limits of coordination, human performance has the tendency to only use a narrow set of solutions, specific to the emphasized task requirement, and regardless of measurement scale, more autonomy (a wider set of solutions) is sacrificed to gain control. The source of consistent trade-offs at different measurement scales may simply be that these solutions are distributed across the measurement scales of embodied constraints, rather than within a particular scale.
None of the systematic relations found in the difficult condition were reliable in the contrasted easy condition, however. For instance, the lack of trade-off in the aggregate speed and accuracy measures was absent in the corresponding long-range dynamics (the sign of the trade-off actually conversed in the easy condition). The lack of systematic relations among the different measurement scales in the easy condition may be a consequence of the restriction of range within the measured variables, since harmonicity, speed, and accuracy were all dispersed relatively close to their ceiling values in the easy condition.
It is not unconceivable, however, that, under these less stringent constraints, human performance becomes more flexibly organized as synergies that can be formed over a wider range of degrees of freedom, what Gelfand and Latash (1998) called the principle of abundance. Abundant controllable degrees of freedom make it possible to be fast and accurate at the same time in easy conditions, which would also yield performances close to their ceiling values. For instance, in face of compatible speed–accuracy constraints, harmonious oscillations can energetically self-sustain themselves by exploiting the elasticity of the muscles and the joints. Consequently there is little need for the kinematics to be so tightly constrained by the other requirements of task performance. The cross-scale coupling among these factors is thus hidden by the fluid ease and skill with which performance is enacted. Hence, the fluid accommodation of the task masks the nature of the coupling across scales by which it is accomplished, and in this respect the conflict between task constraints of speed and accuracy provided a means to test this hypothesis.
The observation that a restricted dispersion of measurement values reduces or even masks the relations between long-range dynamics and other performance measures is consistent with other studies (e.g., Torre and Balasubramaniam, 2011; Wijnants et al., 2012). These observations do not imply, however, that every timescale is controlled separately in more manageable task settings. By contrast, it is conceivable that at the limits of a behavior where errors and other qualitative changes can be observed, a complex system simply reveals itself in most detail (e.g., Kelso, 2003). That said, we do not want to rule out the possibility that another set of observables with a less restricted data range could be defined in easy conditions that would still exhibit rich cross-scale relationships.
The close coupling of performance outcomes observed in the difficult condition (either serving the speed or the accuracy side of the trade-off) enabled for improved performance along the emphasized task requirement; at the cost of loosing control over the other, however. The fact that this was paralleled by clearer 1/f scaling in the variable that pertained to that task requirement suggests that interdependent timescales mutually constrain their respective degrees of freedom, rather than that every scale is controlled separately. This illustrates how system components may interact so completely that one can no longer parse their individual contributions in the collective activity of the whole. While performance at each measurement scale may contribute its own potentials and constraints in shaping this collective activity, the activity at each scale is strongly interdependent with the activities at other scales.
Based on traditional approaches in the Fitts paradigm, observing 1/f scaling and consistent changes in its presence may run against standard intuitions, and certainly when it is tied so strongly to other functional variables of a performance, because trial to trial performances are typically assumed to fluctuate randomly from trial to trial. The assumption that movement variability is a product of unstructured, white neuromotor noise superimposed on a deterministic signal traces back to Fitts and was built on the tenets of information theory (Shannon, 1949), which treats variability as random “errors,” which to some extent contaminate an underlying deterministic (average) signal in the information processing stream (Fitts, 1954; Broadbent, 1958). As a consequence, standard approaches to the speed–accuracy trade-off are often limited to an exchange rate for the disparate units of speed and accuracy at their fixed measurement scale (i.e., without making predictions about movement trajectories).
In the 1960s and 1970s of the twentieth century, motor control theorists began to adopt the language of control theory to account for the specificities of the trajectories themselves. As one example, Meyer’s optimal control model (Meyer et al., 1988) captured movement variability as a function of the velocity of sub-movements, thereby extending the relevant scales of analysis in a speed–accuracy trade-off to movement kinematics. Substantial theoretical developments have followed (For a review see, e.g., MacKenzie, 1992; Plamondon and Alimi, 1997; Elliot et al., 2004), leading eventually to the recognition that a trial movement time can be modeled from the kinematics as an emergent property (e.g., Bootsma et al., 1998; Bootsma et al., 2004).
Our main message is that a second round of progress in the Fitts paradigm is apt, which steps beyond identifying causal relations between movement kinematics and movement durations, by accepting the challenges imposed by fractal scaling and spontaneous entropy reduction in well-coordinated performances. Gaging 1/f scaling and entropy extends beyond the usual scales of analysis, and reveals nonetheless cognitive structure that was previously hidden, but equally sustains (and is constrained by) a given task performance and a participants’ emphasis therein. So, while the observed relation between kinematics vs. speed and accuracy is not new, our study clearly builds upon the long history of research in the Fitts paradigm by adding the measurement scale of long-range dynamics. The consistent changes in 1/f scaling in different task performances suggest that it is far too simplistic for kinematic features at their fast timescale, defined by a task condition, to “cause” a corresponding average movement time and movement amplitude at a coarser scale, because basic features of a performance cannot simply be averaged out to obtain unicausal features at longer time scales (i.e., up to long-range dynamics).
That is, far from being a statistical or functional nuisance, a consistent coupling of scales appears to be a signature of strongly emergent coordination (cf., Van Orden et al., 2003; Buzsàki, 2006; Kello et al., 2007; Diniz et al., 2011). Emergent coordination allows slower timescale dynamics to supply specific constraints on the possible changes at faster timescales. Faster timescales in turn can act as intermittent sources of perturbations and change to the slower timescale dynamics (if they are amplified in positive feedback), which amounts to a circular, nested, or downward influences among timescales of constraint. The result is emergent and system-wide control that is economical in the sense that it reduces the number of variables that must be independently specified in the coordination of a given performance (Van Orden et al., 2003; Turvey, 2007; Kello and Van Orden, 2009; Wijnants et al., 2009).
The observation that a constituent part of a performance constrains the efficient functioning of the same system’s other parts through cross-scale contingencies raises the broader question of fractal dynamics in human control. The specific meaning of 1/f scaling that we have hypothesized refers in itself to activity across interlinked timescales. Here we accompanied this statistical regularity with actual empirical cross-scale observables that pertain to intra-individual modes of coordination to satisfy task demands. Previous widespread findings associate change in scaling exponents, in the direction of α = 1 of 1/f scaling, with fluid task performance (e.g., Goldberger et al., 2002; Kello et al., 2007; Werner, 2010; Diniz et al., 2011; Van Orden et al., 2011; Wijnants, 2012). The present findings add to these observations and suggest that control is delegated across interdependent embodied scales that exploit the natural constraints imposed on peripheral muscle systems (i.e., springlike properties) as well as emergent patterns of coordination (i.e., 1/f scaling), to situate task performance within the particular demands of task contexts.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The work reported in this article was supported by NSF grants to Guy Van Orden (BCS #0642716; BCS #0843133; DHB #0728743). The authors certify to have complied with the APA ethical principles regarding research with human participants in the conduct of the research presented in this manuscript.
References
Abásolo, D., Hornero, R., Gómez, C., García, M., and López, M. (2006). Analysis of EEG background activity in Alzheimer’s disease patients with Lempel-Ziv complexity and central tendency measure. Med. Eng. Phys. 28, 315–322.
Adam, J. J. (1992). The effects of objectives and constraints on motor control strategy in reciprocal aiming movements. J. Mot. Behav. 24, 173–185.
Bahrami, B., Seyedsadjadi, R., Babadi, B., and Noroozian, M. (2005). Brain complexity increases in mania. Neuroreport 16, 187–191.
Bak, P., Tang, C., and Wiesenfeld, K. (1987). Self-organized criticality: an explanation of 1/f noise. Phys. Rev. Lett. 59, 381–384.
Beek, P. J., Schmidt, R. C., Morris, A. W., Sim, M.-Y., and Turvey, M. T. (1995). Linear and nonlinear stiffness and friction in biological rhythmic movements. Biol. Cybern. 73, 499–507.
Bootsma, R. J., Fernandez, L., and Mottet, D. (2004). Behind Fitts’ law: kinematic patterns in goal-directed movements. Int. J. Hum. Comput. Stud. 61, 811–821.
Bootsma, R. J., Mottet, D., and Zaal, F. T. J. M. (1998). Trajectory formation and speed-accuracy trade-off in aiming movements. C. R. Acad. Sci. III Sci. Vie 321, 377–383.
Burr, R. L., Kirkness, C. J., and Mitchell, P. H. (2008). Detrended fluctuation analysis of intracranial pressure predicts outcome following traumatic brain injury. IEEE Trans. Biomed. Eng. 55, 2509–2518.
Chen, Y., Ding, M., and Kelso, J. A. S. (1997). Long memory processes (1/fα type) in human coordination. Phys. Rev. Lett. 79, 4501–4504.
Clayton, K., and Frey, B. B. (1997). Studies of mental “noise.” Nonlinear Dynamics Psychol. Life Sci. 1, 173–180.
Collins, J. J., and De Luca, C. J. (1993). Open-loop and closed-loop control of posture: a random-walk analysis of center-of-pressure trajectories. Exp. Brain Res. 95, 308–318.
Correll, J. (2008). 1/f Noise and effort on implicit measures of racial bias. J. Pers. Soc. Psychol. 94, 48–59.
Delignières, D., Fortes, M., and Ninot, G. (2004). The fractal dynamics of self-esteem and physical self. Nonlinear Dynamics Psychol. Life Sci. 8, 479–510.
Delignières, D., Torre, K., and Lemoine, L. (2008). Fractal models for event-based and dynamical timers. Acta Psychol. (Amst.) 127, 382–397.
Diniz, A., Wijnants, M. L., Torre, K., Barreiros, J., Crato, N., Bosman, A. M. T., Hasselman, F., Cox, R. F. A., Van Orden, G., and Delignières, D. (2011). Contemporary theories of 1/f noise in motor control. Hum. Mov. Sci. 30, 889–905.
Ding, M., Chen, Y., and Kelso, J. A. S. (2002). Statistical analysis of timing errors. Brain Cogn. 48, 98–106.
Eke, A., Hermán, P., Kocsis, L., and Kozak, L. R. (2002). Fractal characterization of complexity in temporal physiological signals. Physiol. Meas. 23, 1–38.
Elliot, D., Hansen, S., Mendoza, J., and Tremblay, L. (2004). Learning to optimize speed, accuracy, and energy expenditure: a framework for understanding speed-accuracy relations in goal-directed aiming. J. Mot. Behav. 36, 339–351.
Fitts, P. M. (1954). The information capacity of the human motor system in controlling the amplitude of movement. J. Exp. Psychol. Gen. 47, 381–391.
Gelfand, I. M., and Latash, M. L. (1998). On the problem of adequate language in motor control. Motor Control 2, 306–313.
Gilden, D. L., and Hancock, H. (2007). Response variability in attention deficit disorders. Psychol. Sci. 18, 796–802.
Gilden, D. L., Thornton, T. L., and Mallon, M. W. (1995). 1/f Noise in human cognition. Science 267, 1837–1839.
Goldberger, A. L. (1996). Non-linear dynamics for clinicians: Chaos theory, fractals and complexity at the bedside. Lancet 347, 1312–1314.
Goldberger, A. L., Amaral, L. A. N., Hausdorff, J. M., Ivanov, P. Ch., Peng, C.-K., and Stanley, H. E. (2002). Fractal dynamics in physiology: alterations with disease and aging. Proc. Natl. Acad. Sci. U.S.A. 99, 2466–2472.
Guiard, Y. (1993). On Fitts’and Hooke’s laws: simple harmonic movement in upper-limb cyclical aiming. Acta Psychol. (Amst.) 82, 139–159.
Haken, H., Kelso, J. A. S., and Bunz, H. (1985). A theoretical model of phase transitions in human hand movements. Biol. Cybern. 51, 347–356.
Hausdorff, J. M. (2007). Gait dynamics, fractals and falls: finding meaning in the stride-to-stride fluctuations of human walking. Hum. Mov. Sci. 26, 555–589.
Holden, J. G. (2005). “Gauging the fractal dimension of response times from cognitive tasks,” in Contemporary Nonlinear Methods for Behavioral Scientists: A Webbook Tutorial, eds M. A. Riley, and G. Van Orden 267–318. Available at: http://www.nsf.gov/sbe/bcs/pac/nmbs/nmbs.pdf
Ihlen, E. A. F., and Vereijken, B. (2010). Interaction-dominant dynamics in human cognition: beyond 1/fα fluctuation. J. Exp. Psychol. Gen. 139, 436–463.
Kay, B. A., Saltzman, E. L., Kelso, J. A. S., and Schöner, G. (1987). Space-time behavior of single and bimanual rhythmical movements: data and limit cycle model. J. Exp. Psychol. Hum. Percept. Perform. 13, 178–192.
Kello, C. T. (2011). Intrinsic fluctuations yield pervasive 1/f scaling: comment on Moscoso del Prado Marti’n (2011). Cogn. Sci. 35, 838–841.
Kello, C. T., Beltz, B. C., Holden, J. G., and Van Orden, G. (2007). The emergent coordination of cognitive function. J. Exp. Psychol. Gen. 136, 551–568.
Kello, C. T., and Van Orden, G. (2009). Soft-assembly of sensorimotor function. Nonlinear Dynamics Psychol. Life Sci. 13, 57–78.
Kelso, J. A. S. (1995). Dynamic Patterns: The Self-Organization of Brain and Behavior. Cambridge, MA: MIT Press.
Kelso, J. A. S. (2003). “Cognitive coordination dynamics,” in The Dynamical Systems Approach to Cognition: Concepts and Empirical Paradigms Based on Self-Organization, Embodiment and Coordination Dynamics, eds W. Tschacher, and J. P. Dauwalder (Singapore: World Scientific), 45–71.
Kiefer, A. W., Riley, M. A., Shockley, K., Villard, S., and Van Orden, G. C. (2009). Walking changes the dynamics of cognitive estimates of time intervals. J. Exp. Psychol. Hum. Percept. Perform. 35, 1532–1541.
Kloos, H., and Van Orden, G. (2010). Voluntary behavior in cognitive and motor tasks. Mind Matter 8, 19–43.
Konvalinka, I., Xygalatas, D., Bulbulia, J., Schjødt, U., Jegindø, E. M., Wallot, S., Van Orden, G., and Roepstorff, A. (2011). Synchronized arousal between performers and related spectators in a fire-walking ritual. Proc. Natl. Acad. Sci. U.S.A. 108, 8514–8519.
Kugler, P. N., and Turvey, M. T. (1987). Information, Natural Law, and the Self-Assembly of Rhythmic Movement. Hillsdale, NJ: LEA.
Lai, M. C., Lombardo, M. V., Chakrabarti, B., Sadek, S. A., Pasco, G., Wheelwright, S. J., Bullmore, E. T., Baron-Cohen, S., MRC AIMS Consortium, and Suckling, J. (2010). A Shift to randomness of brain oscillations in people with autism. Biol. Psychiatry 68, 1092–1099.
Lake, D. E., Richman, J. S., Griffin, M. P., and Moorman, J. R. (2002). Sample entropy analysis of neonatal heart rate variability. Am. J. Physiol. Regul. Integr. Comp. Physiol. 283, 789–797.
Linkenkaer-Hansen, K., Monto, S., Rytsälä, H., Suominen, K., Isometsä, E., and Kähkönen, S. (2005). Breakdown of long-range temporal correlations in theta oscillations in patients with major depressive disorder. J. Neurosci. 25, 10131–10137.
MacKenzie, I. S. (1992). Fitts’ law as a research and design tool in human–computer interaction. Hum. Comp. Interact. 7, 91–139.
Meyer, D. E., Abrams, R., Kornblum, S., Wright, C. E., and Smith, J. E. K. (1988). Optimality in human motor performance: ideal control of rapid aimed movements. Psychol. Rev. 95, 340–370.
Miyazaki, M., Kadota, H., Kudo, K., Masani, K., and Ohtsuki, T. (2001). Fractal correlation of initial trajectory dynamics vanishes at the movement endpint in human rapid goal-directed movements. Neurosci. Lett. 3, 173–176.
Mottet, D., and Bootsma, R. J. (1999). The dynamics of goal-directed rhythmical aiming. Biol. Cybern. 80, 235–245.
Newell, K. M., Broderick, M. P., Deutsch, K. M., and Slifkin, A. B. (2003).Task goals and change in dynamical degrees of freedom with motor learning. J. Exp. Psychol. Hum. Percept. Perform. 29, 379–387.
Pattee, H. H. (1973). “The physical basis and origin of hierarchical control theory,” in The Challenge of Complex Systems, ed. H. Pattee (New York: George Braziller), 73–108.
Peng, C. K., Mietus, J., Hausdorff, J. M., Havlin, S., Stanley, H. E., and Goldberger, A. L. (1993). Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 70, 1343–1346.
Plamondon, R., and Alimi, A. M. (1997). Speed/accuracy trade-offs in target-directed movements. Behav. Brain Sci. 20, 279–349.
Prigogine, I., and Stengers, I. (1984). Order Out of Chaos. Man’s New Dialogue with Nature. New York: Bantam Books.
Ramon, C., Holmes, M. D., Freeman, W. J., McElroy, R., and Rezvanian, E. (2008). “Comparative analysis of temporal dynamics of EEG and phase synchronization of EEG to localize epileptic sites from high density scalp EEG interictal recordings,” in Conference Proceedings of the International Conference of IEEE Engineering in Medicine and Biology Society, 4548–4550.
Rangarajan, G., and Ding, M. (2000). Integrated approach to the assessment of long range correlation in time series data. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 61, 4991–5001.
Richardson, D. C., Dale, R., and Kirkham, N. Z. (2007). The art of conversation is coordination: common ground and the coupling of eye movements during dialogue. Psychol. Sci. 18, 407–413.
Richman, J. S., and Moorman, J. R. (2000). Physiological time series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 278, 2039–2049.
Riley, M. A., and Turvey, M. T. (2002). Variability and determinism in elementary behaviors. J. Mot. Behav. 34, 99–125.
Rinkenauer, G., Osman, A., Ulrich, R., Müller-Gethmann, and Mattes, S. (2004). On the locus of speed–accuracy trade-off in reaction time: Inferences from the lateralized readiness potential. J. Exp. Psychol. Gen. 133, 261–282.
Simon, H. A. (1973). “The organization of complex systems,” in Hierarchy Theory: The Challenge of Complex Systems, ed. H. H. Pattee (New York: George Braziller, Inc), 1–27.
Shockley, K., Santana, M. V., and Fowler, C. A. (2003).Mutual interpersonal postural constraints are involved in cooperative conversation. J. Exp. Psychol. Hum. Percept. Perform. 29, 326–32.
Slifkin, A. B., and Newell, K. M. (1998). Is variability in human performance a reflection of system noise? Curr. Dir. Psychol. Sci. 7, 170–177.
Sosnoff, J. J., Valantine, A. D., and Newell, K. M. (2009). The adaptive range of 1/f Isometric force production. J. Exp. Psychol. Hum. Percept. Perform. 35, 439–446.
Stergiou, N., and Decker, L. M. (2011). Human movement variability, nonlinear dynamics, and pathology: is there a connection? Hum. Mov. Sci. 30, 869–888.
Torre, K., and Balasubramaniam, R. (2011). Disentangling stability, variability and adaptability in human performance: focus on the interplay between local variance and serial correlation. J. Exp. Psychol. Hum. Percept. Perform. 37, 539–550.
Valdez, A., and Amazeen, E. (2008). Using 1/f noise to examining planning and control in a discrete aiming task. Exp. Brain Res. 187, 303–319.
Van Orden, G., Holden, J. G., and Turvey, M. T. (2003). Self-organization of cognitive performance. J. Exp. Psychol. Gen. 132, 331–350.
Van Orden, G., Holden, J. G., and Turvey, M. T. (2005). Human cognition and 1/f scaling. J. Exp. Psychol. Gen. 134, 117–123.
Van Orden, G., Kloos, H., and Wallot, S. (2011). “Living in the pink: Intentionality, wellness, and complexity,” in Handbook of the Philosophy of Science, Vol. 10: Philosophy of Complex Systems, ed. C. Hooker (Amsterdam: Elsevier), 639–682.
Wagenmakers, E.-J., van der Maas, H. L. J., and Farrell, S. (2011). Abstract concepts require concrete models: why cognitive scientists have not yet embraced nonlinearly-coupled, dynamical, self-organized critical, synergistic, scale-free, exquisitely context-sensitive, interaction-dominant, multifractal, interdependent brain-body-niche systems. Top. Cogn. Sci. 4, 87–93; discussion 94–102.
Wallot, S., and Van Orden, G. (2011a). Nonlinear analyses of self-paced reading. Ment. Lex. 6, 245–274.
Wallot, S., and Van Orden, G. (2011b). Grounding language in the anticipatory dynamics of the body. Ecol. Psychol. 23, 157–184.
Werner, G. (2010). Fractals in the nervous system: conceptual implications for theoretical neuroscience. Front. Physiol. 1:15. doi:10.3389/fphys.2010.00015
West, B. J. (2006). Where Medicine Went Wrong: Rediscovering the Path to Complexity. Hackensack, NJ: World Scientific.
Wijnants, M. L. (2012). Fractal Coordination in Cognitive Performances. (Doctoral dissertation). Radboud University Nijmegen, Nijmegen.
Wijnants, M. L., Bosman, A. M. T., Hasselman, F., Cox, R. F. A., and Van Orden, G. (2009). 1/f Scaling in movement time changes with practice in precision aiming. Nonlinear Dynamics Psychol. Life Sci. 13, 75–94.
Wijnants, M. L., Hasselman, F., Cox, R. F. A., Bosman, A. M. T., and Van Orden, G. (2012). An interaction-dominant perspective on reading fluency and dyslexia. Ann. Dyslexia. doi:10:1007/S11881-012-0067-3
Keywords: speed–accuracy trade-off, kinematics, 1/f noise, motor control, self-organization
Citation: Wijnants ML, Cox RFA, Hasselman F, Bosman AMT and Van Orden G (2012) A trade-off study revealing nested timescales of constraint. Front. Physio. 3:116. doi: 10.3389/fphys.2012.00116
Received: 21 September 2011; Accepted: 09 April 2012;
Published online: 23 May 2012.
Edited by:
Radhakrishnan Nagarajan, University of Arkansas for Medical Sciences, USAReviewed by:
Damian Stephen, Harvard University, USARathinaswamy Bhavanandhan Govindan, Children’s National Medical Center, USA
Copyright: © 2012 Wijnants, Cox, Hasselman, Bosman and Van Orden. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: M. L. Wijnants, Behavioural Science Institute, Radboud University Nijmegen, P.O. Box 9104, 6500 HE Nijmegen, Netherlands. e-mail:bS53aWpuYW50c0Bwd28ucnUubmw=


