Scale-free and multifractal time dynamics of fMRI signals during rest and task

Scaling temporal dynamics in functional MRI (fMRI) signals have been evidenced for a decade as intrinsic characteristics of ongoing brain activity (Zarahn et al., 1997). Recently, scaling properties were shown to fluctuate across brain networks and to be modulated between rest and task (He, 2011): notably, Hurst exponent, quantifying long memory, decreases under task in activating and deactivating brain regions. In most cases, such results were obtained: First, from univariate (voxelwise or regionwise) analysis, hence focusing on specific cognitive systems such as Resting-State Networks (RSNs) and raising the issue of the specificity of this scale-free dynamics modulation in RSNs. Second, using analysis tools designed to measure a single scaling exponent related to the second order statistics of the data, thus relying on models that either implicitly or explicitly assume Gaussianity and (asymptotic) self-similarity, while fMRI signals may significantly depart from those either of those two assumptions (Ciuciu et al., 2008; Wink et al., 2008). To address these issues, the present contribution elaborates on the analysis of the scaling properties of fMRI temporal dynamics by proposing two significant variations. First, scaling properties are technically investigated using the recently introduced Wavelet Leader-based Multifractal formalism (WLMF; Wendt et al., 2007). This measures a collection of scaling exponents, thus enables a richer and more versatile description of scale invariance (beyond correlation and Gaussianity), referred to as multifractality. Also, it benefits from improved estimation performance compared to tools previously used in the literature. Second, scaling properties are investigated in both RSN and non-RSN structures (e.g., artifacts), at a broader spatial scale than the voxel one, using a multivariate approach, namely the Multi-Subject Dictionary Learning (MSDL) algorithm (Varoquaux et al., 2011) that produces a set of spatial components that appear more sparse than their Independent Component Analysis (ICA) counterpart. These tools are combined and applied to a fMRI dataset comprising 12 subjects with resting-state and activation runs (Sadaghiani et al., 2009). Results stemming from those analysis confirm the already reported task-related decrease of long memory in functional networks, but also show that it occurs in artifacts, thus making this feature not specific to functional networks. Further, results indicate that most fMRI signals appear multifractal at rest except in non-cortical regions. Task-related modulation of multifractality appears only significant in functional networks and thus can be considered as the key property disentangling functional networks from artifacts. These finding are discussed in the light of the recent literature reporting scaling dynamics of EEG microstate sequences at rest and addressing non-stationarity issues in temporally independent fMRI modes.

1. Introduction

Much of what is known about brain function stems from studies in which a task or a stimulus is administered and the resulting changes in neuronal activity and behavior are measured. From the advent of human electroencephalography (EEG) to cognitive activation paradigms in functional Magnetic Resonance Imaging (fMRI), this approach proved very successful to study brain function, and more precisely functional specialization in human brain. It has relied, on one hand, on contrasting signal magnitude between different experimental conditions (Rosen et al., 1998) or task-specific hemodynamic response (HRF) shape (Dale, 1999) and, on other-hand, on statistical methods often framed within linear or bilinear modeling strategies (Friston et al., 1995; Makni et al., 2005, 2008).

Spontaneous modulations of neural activity in Blood Oxygenation Level Dependent (BOLD) fMRI signals however arise without external input or stimulus and thus depict intrinsic brain activity (Damoiseaux et al., 2006). This ongoing activity constitutes a major part of fMRI recordings and is responsible for most of brain energy consumption. It has hence been intensively studied over the last decade using various methods ranging from univariate, i.e., Seed-based linear Correlation Analysis (SCA; Biswal et al., 1995; Greicius et al., 2003), to multivariate methods such as Independent Component Analysis (ICA; Calhoun et al., 2001; Beckmann and Smith, 2004), group-level ICA (Cole et al., 2010; Varoquaux et al., 2010b), or more recent dictionary learning techniques (Varoquaux et al., 2011). All these methods have revealed that interactions between brain regions, also referred to as functional connectivity, occur through these spontaneous modulations and consistently vary between rest and task (Damoiseaux et al., 2006; Fox et al., 2007). Resting-State Network (RSN) extraction from resting-state fMRI time series is thus achieved either by thresholding the correlation matrix computed between voxels or regions (seed-based or univariate approach) or by identifying spatial maps in ICA-based algorithms that closely match RSNs such as somato-sensory systems (visual, motor, auditory), the default mode, and attentional networks (ventral and dorsal; Fox et al., 2007; Smith et al., 2009). For a recent review about the pros and cons of the SCA and ICA approaches to RSN extraction, the reader can refer to Cole et al. (2010). Once RSNs are extracted, their topological properties can be analyzed with respect to small-world or scale-free models (Chialvo, 2004; Eguiluz et al., 2005; Zemanová et al., 2006; Bullmore and Sporns, 2009).

In parallel and alternatively to brain topology, the temporal dynamics of brain activity have also been extensively studied. It is now well accepted that brain activity, irrespective of the imaging technique involved in observation, is always arrhythmic and shows a scaling, or scale invariant or scale-free, time dynamics, which implies that no time scale plays a predominant or specific role. Often, scale invariance or scale-free dynamics is associated with long-range correlation in time (Linkenkaer-Hansen et al., 2001; Stam and de Bruin, 2004; Van de Ville et al., 2010), and accordingly, in the frequency domain, related to a power-law decrease of the power spectrum (Γ( f )∝1/f^β with β > 0) in the limit of small frequencies ( f → 0). Interestingly, it is generally admitted that only low frequencies (<0.1 Hz) convey information related to neural connectivity in fMRI signals (Cordes et al., 2001; Leopold et al., 2003; Achard et al., 2006). Evidence of fractal or scale-free behavior in fMRI signals has been demonstrated for a long while (Zarahn et al., 1997; Bullmore et al., 2001; Bullock et al., 2003) though it was initially regarded as noise. Deeper investigations of the temporal scale-free property in fMRI have demonstrated that this constitutes an intrinsic feature of ongoing brain activity (c.f., e.g., Thurner et al., 2003; Shimizu et al., 2004; Maxim et al., 2005; Ciuciu et al., 2008; Wink et al., 2008; He et al., 2010; He, 2011). First attempts to identify stimulus-induced signal changes from scaling parameters were proposed in Thurner et al. (2003), Shimizu et al. (2004), where a voxel-based fluctuation analysis was applied to high temporal resolution fMRI data. Interestingly, fractal features of voxel time series have enabled to discriminate white matter, cerebrospinal fluid, and active from inactive brain regions during a block paradigm (Shimizu et al., 2004). Further, it was shown that scaling properties can be modulated in neurological disorder (Maxim et al., 2005) or between rest and task (Thurner et al., 2003; Shimizu et al., 2004; Ciuciu et al., 2008; Wink et al., 2008; He, 2011): It was shown that long memory, as quantified by the Hurst exponent, decreases during task in activating and deactivating brain regions. Analyzing scale invariance in temporal dynamics may thus provide new insights into how the brain works by mapping quantitative estimations of parameters with good specificities to cognitive states, task performance (Shimizu et al., 2004; Wink et al., 2008; He et al., 2010; He, 2011).

Small-world and scale-free topology led to model brain as a complex critical system, that is as a large conglomerate of interacting components, with possibly non-linear interactions (Bak and Paczuski, 1995; Chialvo, 2010). Further, these complex systems were then regarded as potential origins for long-range correlation spatio-temporal patterns, as critical systems, i.e., complex systems driven close to their phase transitions, constitute known mechanism yielding scaling time dynamics and generic 1/f power spectral densities (see e.g., Chialvo, 2010). They however so far failed to account for the existence of possibly richer scaling properties (such as, e.g., multifractality). At a general level, scale invariance in time dynamics and scale-free property of brain topology are, in essence, totally independent properties that must not be confused one with the other. Whether or not and how these two scale-free instances are related one to the other in the fMRI context remains a difficult and largely unsolved issue, far beyond the scope of the present contribution, that concentrates instead on performing a thorough analysis of scale invariance temporal dynamics in fMRI signals.

In the existing literature, the analysis of scale invariance in fMRI signals suffers from two limitations: First, it has often been performed at the voxel or region level, thus consisting of a collection of univariate analyses, suffering from the classical bias of voxel selection or region definition. Moreover, although the fluctuation of scale-free dynamics with tissue type has been studied in Shimizu et al. (2004), Wink et al. (2008) to derive that stronger persistency occurs in gray matter and that this background activity might represent neuronal dynamics, no systematic analysis has been undertaken to disentangle the scale-free properties of RSN and non-RSN components, such as artifacts. This investigation can be better handled using multivariate or ICA-like approaches. Second, scale invariance in fMRI signals has mostly been based on spectral analysis and/or Detrended Fluctuation Analysis (c.f., e.g., Thurner et al., 2003; Stam and de Bruin, 2004; He, 2011). This amounts to considering that scaling is associated only with the correlation or the spectrum (hence with the second order statistics) of the data and thus, implicitly and sometimes even explicitly, to assuming Gaussianity and (asymptotic) self-similarity for the data (cf., e.g., Eke et al., 2002) for a survey in the fMRI context). Also, it is now well-known that such technics lack robustness to disentangle stationarity/non-stationarity versus true scaling property issues and do not allow simple extension to account for richer scaling properties such as those observed in multifractal models. It is well accepted that wavelet analysis based analysis of scaling (cf., e.g., Abry et al., 1995, 1998; Bullmore et al., 2001; Veitch and Abry, 2001; Fadili and Bullmore, 2002) yield not only better estimation performance, but also show significant practical robustness, notably to non-stationarity, while paving the way toward the analysis of scaling properties beyond the strict second order (hence beyond Gaussianity and asymptotic self-similarity).

In this context, the present contribution elaborates on earlier works dedicated to the analysis of scale invariance in fMRI temporal dynamics by proposing two significant variations.

First, scale invariance dynamics is not investigated at the voxel or region spatial scale level independently. Instead, group-level resting-state networks are segmented by an exploratory multivariate decomposition approach, namely the MSDL algorithm (Varoquaux et al., 2011), detailed in Section 3: It produces both a set of spatial components and a set of times series, for each component and each subject, that conveys ongoing dynamics in functional networks but also in artifacts. As shown in Varoquaux et al. (2011), the sparsity promoting regularization involved in the MSDL algorithm enables to recover less noisy spatial maps than group-level or canonical ICA (Varoquaux et al., 2010b). This makes their interpretation easier in the context of small group of individuals. This technique is detailed in Section 3.

Second, to enable an in-depth analysis of the scaling properties of the temporal dynamics in fMRI signals, we resort to multifractal analysis, that measures not a single but a collection of scaling exponents, thus enabling a richer and more versatile description of scale invariance (beyond correlation and Gaussianity), referred to as multifractality. It is thus likely to better account for the variety and complexity of potential scaling dynamics, as already suggested in the context of fMRI in, e.g., Ciuciu et al. (2008), Wink et al. (2008). However, in contrast to Wink et al. (2008), and following the track opened in Ciuciu et al. (2008), we use a recent statistical analysis tool, the Wavelet Leader-based Multifractal formalism (WLMF; Wendt et al., 2007). This formalism benefits from better mathematical grounding and shows improved estimation performance compared to tools previously used in the literature. This framework is introduced in Section 4, after a review of the intuition, models, and methodologies underlying the definition and analysis of scaling temporal dynamics, thus, to some extend, continuing, and renewing the surveys provided in (Eke et al., 2002; Ciuciu et al., 2008).

These tools are combined together and applied to two datasets, corresponding to resting-state and activation runs. They are described in Section 2 (see also Sadaghiani et al., 2009). Modulations of scale-free and multifractal properties in space, i.e., between functional and artifactual components but also between rest and task, are statistically assessed at the group-level in Section 5.

In agreement with findings in He (2011), the results reported here confirm that fMRI signals can be modeled as stationary processes, as well as the decrease of the estimated long memory parameter under task. However, this is found to occur everywhere in the brain and not specifically in functional networks. Moreover, evidence for multifractality in resting-state fMRI signals is demonstrated except for non-cortical regions. Task-related modulations of multifractality appear only significant in functional networks and thus become the key property to disentangle functional networks from artifacts. However, in contrast to what happens for the long memory parameter, this modulation is not monotonous across the brain and varies between cortical and non-cortical regions. These results are further discussed in Section 6 in the light of recent findings related to scale-free dynamics of EEG microstate sequences and non-stationarity of functional modes. Conclusions are drawn in Section 7.

2. Data Acquisition and Analysis

2.1. Data Acquisition

Twelve right-handed normal-hearing subjects (two female; ages, 19–30) gave written informed consent before participation in an imaging study on a 3-T MRI whole-body scanner (Tim-Trio; Siemens). The study received ethics committee approval by the authorities responsible for our institution. Anatomical imaging used a T1-weighted magnetization-prepared rapid acquisition gradient-echo sequence [176 slices, repetition time (TR) 2300 ms, echo time (TE) 4.18 ms, field of view (FOV) 256, voxel size 1 mm × 1 mm × 1 mm]. Functional imaging used a T2*-weighted gradient-echo, echo-planar-imaging sequence (25 slices, TR = 1500 ms, TE = 30 ms, FOV 192, voxel size 3 mm × 3 mm × 3 mm). Stimulus presentation and response recording used the Cogent Toolbox (John Romaya, Vision Lab, UCL¹) for Matlab and sound delivery a commercially available MR-compatible system (MR Confon).

The rs-fMRI dataset we consider in this study has already been published in Sadaghiani et al. (2009). Eight hundred-twenty volumes of task-free “resting-state” data (with closed, blind-folded eyes) were acquired before getting experimental runs of 820 volumes each. These experimental runs, which have not been analyzed in Sadaghiani et al. (2009), involve an auditory detection task (run 2, motor response), and make use of a sparse supra-threshold auditory stimulus detection.

The auditory stimulus was a 500-ms noise burst with its frequency band modulated at 2 Hz (from white noise to a narrower band of 0–5 kHz and back to white noise). Inter-stimulus intervals ranged unpredictably from 20 to 40 s, with each specific interval used only once. Subjects were instructed to report as quickly and accurately as possible by a right-hand key press whenever they heard the target sound despite scanner’s background noise. Details about the definition of each subject’s auditory threshold are available in Sadaghiani et al. (2009).

2.2. Data Analysis

We used here statistical parametric mapping (SPM5, Wellcome Department of Imaging Neuroscience, UK². For image preprocessing (realignment, coregistration, normalization to MNI stereotactic space, spatial smoothing with a 5-mm full-width at half-maximum isotropic Gaussian kernel for single-subject and group analyses) and our own software developments for subsequent analyses. More precisely, the MSDL algorithm relies on the scikit-learn Python toolbox³ and the multifractal analysis on the WLBMF Matlab toolbox⁴.

3. Multivariate Decomposition of Resting-State Networks

3.1. Multi-Subject Spatial Decomposition Techniques

The fMRI signal observed in a voxel reflects many different processes, such as cardiac or respiratory noise, movement effects, scanner artifacts, or the BOLD effect that reveals the underlying neural activity of interest. We separate these different contributions making use of a recently introduced multivariate analysis technique that estimates jointly spatial maps and time series characteristic of these different processes (Varoquaux et al., 2011). Formally, this estimation procedure amounts to finding K spatial maps V _s ∈ ℝ^p×K and the corresponding time series U _s ∈ ℝ^n×K, whose linear combination fits well the observed brain signals, Y _s ∈ ℝ^n×p, of length n, measured over p voxels, for subject s:

${\mathit{\text{Y}}}_s={\mathit{\text{U}}}_s{\mathit{\text{V}}}_s^{\text{t}}+{\mathit{\text{E}}}_s,$ (1)

with E _s ∈ ℝ^n×p the subject-level noise, or residuals not explained by the model. Finding ${\mathit{\text{V}}}_s^{\text{t}}$ enables the separation of the contributions of the different process that are mixed at the voxel level, but implies to work on spatial maps rather than on specific voxels. The number of spatial maps, K, is not chosen a priori, but selected by the procedure.

This problem can be seen as a blind source separation task in the presence of noise, and has often been tackled in fMRI using ICA, combined with principal component analysis (PCA) to reject noise (McKeown et al., 1998; Kiviniemi et al., 2003; Beckmann and Smith, 2004). In the multi-subject configuration, estimating the spatial maps on all subjects simultaneously makes it easy to relate the factors estimated across the different subjects. This can be done by concatenating the data across subject, modeling a common distribution (Calhoun et al., 2001), or by extending the data-reduction step performed in the PCA by a second level capturing inter-subject variability (Varoquaux et al., 2010b). More recently, it was proposed that the key to the success of ICA on fMRI data, is to recover sparse spatial maps (Daubechies et al., 2009; Varoquaux et al., 2010a). This hypothesis can be formulated as a sparse prior in model (1), which can then be estimated using sparse PCA or sparse dictionary learning procedures. With regards to our goal in this study, extracting time series specific to the various processes observed, a strong benefit of such procedures is that they can perform data-reduction, i.e., estimation of the residuals not explained by the model, and extraction of the relevant signals in a single step informed by our prior. On the opposite, with ICA-based procedures, the residuals are selected by the PCA step, and not the ICA step.

3.2. Multi-Subject Dictionary Learning Algorithm

In addition, Varoquaux et al. (2011) have adapted the dictionary learning procedures to a multi-subject setting, in a so-called multi-subject dictionary learning (MSDL) framework. On fMRI datasets, the procedure extracts a group-level atlas of spatial signatures of the processes observed, as well as corresponding subject-level maps, accounting for the individual specificities. They show that, with a small spatial smoothness prior added to the sparsity prior on the maps, the extracted patterns correspond to the segmentation of various structures in the signal: functional regions, blood vessels, interstitial spaces, sub-cortical structures… In these settings, the subject-level maps V_s are modeled as generated by group-level maps V ∈ ℝ^p×K with additional inter-subject variability that appears as residual terms, F_s ∈ ℝ^p×K, at the group-level:

$\forall s\in \left\{1,\dots ,S\right\},{\mathit{\text{V}}}_s=\mathit{\text{V}}+{\mathit{\text{F}}}_s.$

The model is estimated by finding the group-level and subject-level maps that maximize the probability of observing the data at hand with the given prior. This procedure is known as a Maximum A Posteriori (MAP) estimate, and boils down to minimizing the negated log-likelihood of the model with an additional penalizing term. If the two sources of unexplained signal, i.e., subject-level residuals E _s and inter-subject variability F _s are modeled as Gaussian random variates, the log-likelihood term is the sum of squares of these errors. The prior term appears as the sum of the sparsity-inducing ℓ₁ norm of V, and the ℓ₂-norm of the gradient of the map, enforcing the smoothness. This prior has been used previously in regression settings under the name of smooth-Lasso (Hebiri and van de Geer, 2011). Estimating the model from the data thus consists of minimizing the following criterion:

$\mathcal{𝒥}\left({\mathit{\text{U}}}_s,{\mathit{\text{V}}}_s,\mathit{\text{V}}\right)=\sum _{s=1}^S\left({∥{\mathit{\text{Y}}}_s-{\mathit{\text{U}}}_s{\mathit{\text{V}}}_s^{\text{t}}∥}^2+\mu {∥{\mathit{\text{V}}}_s-\mathit{\text{V}}∥}^2\right)+\lambda \left({∥\mathit{\text{V}}∥}_1+{\mathit{\text{V}}}^{\text{t}}\mathit{\text{L V}}∕2\right)$

where, ||V ||₁ is the ℓ₁ norm of V, i.e., the sum the absolute values, L is the image Laplacian −V^t LV is the norm of the gradient. λ is a parameter controlling the amount of prior set on the maps, and thus the amount of sparsity, that is set by Cross-Validation (CV). μ is a parameter controlling the amount of inter-subject validation, that is set by comparing intra-subject variance in the observations with inter-subject variance. For more details about the estimation procedure or the parameter setting, we refer the reader to Varoquaux et al. (2011).

3.3. Resting-State MSDL Maps

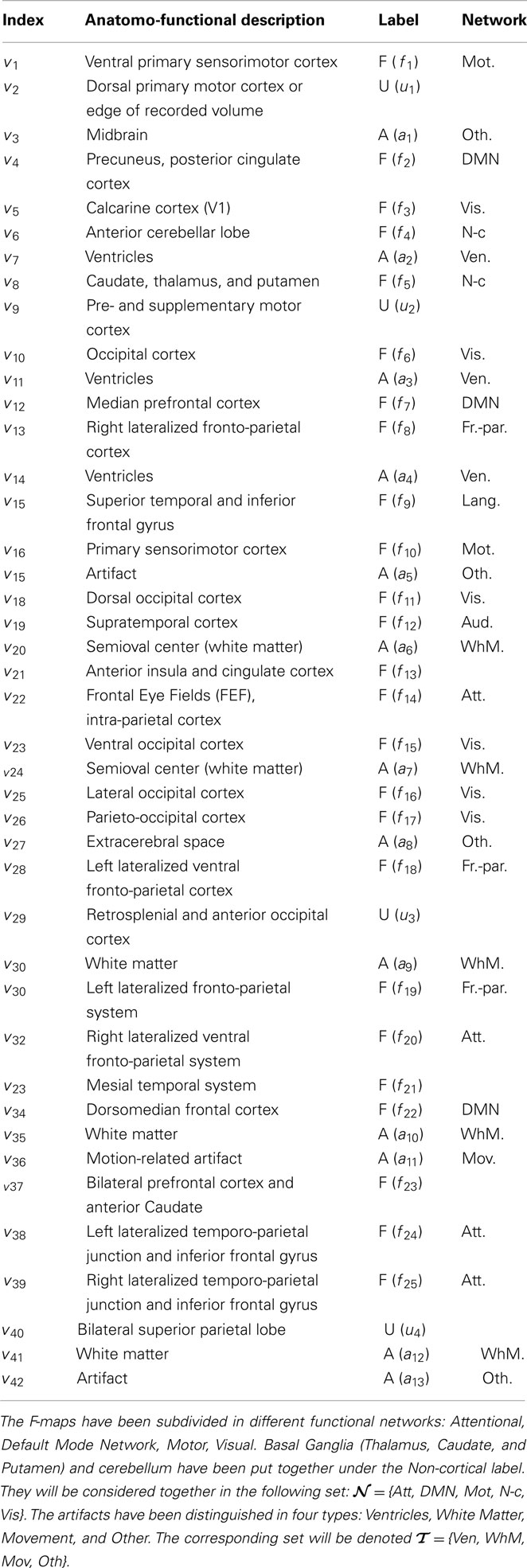
rs-fMRI runs were analyzed for S = 12 subjects, consisting of n = 820 volumes (time points) with a 3-mm isotropic resolution, corresponding to approximately p = 50000 voxels within the brain. The automatic determination rule of the number of maps exposed in Varoquaux et al. (2010a) converges to K = 42. Also, the CV procedure gives us the best CV criterion for λ = 2. The group-level maps V are shown in Figure 1. They have been manually classified in three groups: Functional (F), Artifactual (A), and Undefined (U) maps that appear color-coded in red, blue, and green, respectively. The undefined class appeared necessary to introduce some confidence measure in our classification and disambiguate well-established networks (e.g., dorsal attentional network) from inhomogeneous components mixing artifacts with neuronal regions (e.g., like in v₉). The anatomo-functional description of these group-level maps and their class assignment is given in Table 1. The same rules applied for individual maps V_s. In what follows, we will denote by ℱ, 𝒜 and 𝒰 the index sets of F/A/U-maps, respectively and by Card (ℱ) = 25, Card (𝒜) = 13, and Card (𝒰) = 4 their respective size.

FIGURE 1

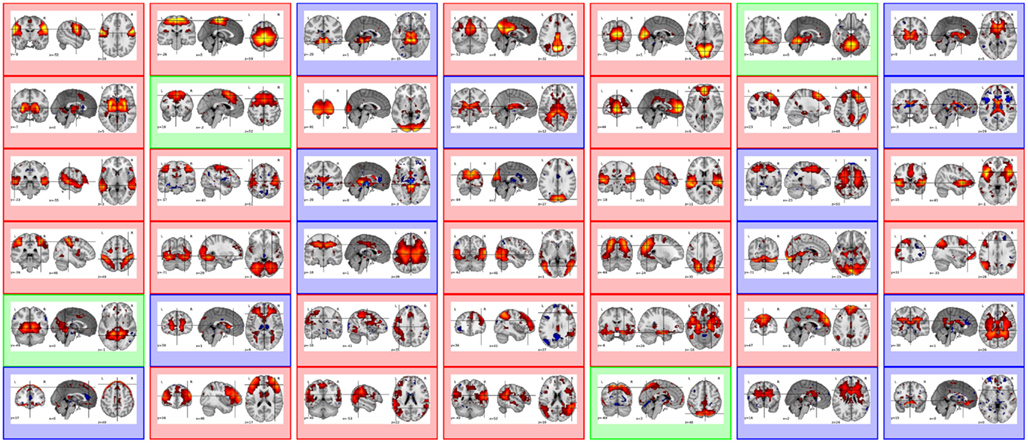
Figure 1. From left to right and top to bottom, group-level MSDL maps V = |v₁|…|v₄₂| inferred from the multi-subject (S = 12) resting-state fMRI dataset (Neurological convention: left is left). Functional (F), Artifactual (A), and Undefined (U) maps appear color-coded boxes in red, blue, and green, respectively. Let us denote ℱ, 𝒜, and 𝒰 the index sets of F/A/U-maps, respectively and Card (ℱ) = 25, Card (𝒜) = 13, and Card (𝒰) = 4 their respective size. Each map v_k consists of loading parameters within the (−1, 1) range where positive and negative values are depicted by the hot and cold parts of the color bar.

TABLE 1

Table 1. Classification of group-level V = |v_{1 |}…|v₄₂| maps according to the F/A/U labeling.

To compare spontaneous and evoked activity, the same spatial decomposition was used on resting-state (run 1, Rest) and task-related data, which were acquired during an auditory detection task (run 2, Task). In practice, this consists of projecting the task-related fMRI data ${\widetilde{\mathit{\text{Y}}}}_s$ onto the inferred spatial maps V _s by minimizing the following least square criterion, ${∥{\widetilde{\mathit{\text{Y}}}}_s-{\mathit{\text{W}}}_s{\mathit{\text{V}}}_s^{\text{t}}∥}^2,$ with respect to W _s. The time series solution admits a closed-form expression: ${\widetilde{\mathit{\text{U}}}}_s={\widetilde{\mathit{\text{Y}}}}_s{\mathit{\text{V}}}_s{\left({\mathit{\text{V}}}_s^{\text{t}}{\mathit{\text{V}}}_s\right)}^{-1}.$ The subsequent scale-free analysis is applied to the two sets of n × K map-level fMRI time series U_S = [u_s,1|…|u_s,K]^t and ${\widetilde{\mathit{\text{U}}}}_s={\left[{\widetilde{\mathit{\text{u}}}}_{s,1}\left|\dots \right|{\widetilde{\mathit{\text{u}}}}_{s,K}\right]}^{\text{t}}$ in a univariate manner, that is to each time series u_s,k and ${\widetilde{\mathit{\text{u}}}}_{s,k}$ for Rest and Task, respectively.

4. Scale-Free: Intuition, Models, and Analyses

4.1. Intuition

In the analysis of evoked brain activity, it is common to seek correlations of BOLD signals with any a priori shape of the hemodynamic response convolved with the experimental paradigm. In the frequency domain, this amounts to seeking response energy concentration in pre-defined spectral bands, as induced for instance by periodic stimulation (e.g., flashing checkerboards). In resting-state fMRI, it is now well admitted that intrinsic brain activity is characterized by scale-free properties (Zarahn et al., 1997; He, 2011). This constitutes a major change in paradigm as it implies that brain activity is not to be analyzed via the amounts of energy it shows within specific and a priori chosen frequency bands, but instead via the fact that all frequencies are jointly contributing in an equivalent manner to its dynamics. Scale-free dynamics are usually described in the spectral domain by a power-law decrease: Let Y(t) denote the signal quantifying brain activity and Γ_Y (f ) its Power Spectral Density (PSD). Scale-free property is classically envisaged as:

${\mathcal{ℳ}}_0:{\Gamma }_Y\left(f\right)\simeq C{\left|f\right|}^{-\beta },\beta \ge 0,$ (2)

with f_m ≤ |f | ≤ f_M, f_M/f_m ≫ 1. Such a power-law behavior over a broad range of frequencies implies that no frequency in that range plays a specific role, or equivalently, that they are all equally important. To analyze brain activity, this power-law relation thus becomes a more important feature than the energy measured at some specific frequencies. For instance, it implies that energy at frequency f₁ can be deduced from energy at frequency f₂ according to He (2011):

${\Gamma }_Y\left(f_2\right)={\Gamma }_Y\left(f_1\right){\left(\left|f_2\right|/\left|f_1\right|\right)}^{-\beta }.$ (3)

In the scale-free framework, one therefore tries to quantify brain activity by considering the scaling exponent β (or variants) as the key descriptor. Let us moreover note that the terminology scale-free is equivalent to scale invariance or simply scaling, encountered in other scientific fields, where this property has also been found to play a central role (c.f., Abry et al., 2002; Ciuciu et al., 2008).

4.2. Scale-free Models

4.2.1. From spectrum to increments

Though appealing, equations (2) and (3) do not provide practitioners with a versatile enough definition of scale-free with respect to real-world data analysis. Indeed, they concentrate only on the second order statistics and hence account neither for the marginal distribution (first order statistics) of the signal Y, nor for its higher order dynamics (or dependence structure). For instance, it does not indicate whether data are jointly Gaussian or depart, weakly, or strongly, from Gaussianity.

To investigate how to enrich Model ℳ₀, let us assume for now that Y consists of a stationary jointly Gaussian process, with PSD as in equation (2). Equivalently, this implies that the covariance function behaves as $C_Y\left(\tau \right)~{\sigma }_Y^2\left(1+C^{\prime }|\tau {|}^{-\alpha }\right),$ for τ_m ≤ τ ≤ τ_M, with α = 1 − β. A simple calculation hence shows that 𝔼(Y(t + τ) − Y(t))² = 𝔼Y(t + τ)² + 𝔼Y(t)² − 2𝔼Y(t + τ)Y(t) = c₂|τ|^−α. The Gaussianity of Y further implies that ∀q > −1:

$\mathbb{E}{\left|Y\left(t+\tau \right)-Y\left(t\right)\right|}^q=c_q{\left|\tau \right|}^{-\frac{q\beta }{2}},{\tau }_m\le \tau \le {\tau }_M.$ (4)

Defining X(t) = ∫t^t Y(s)ds, equation (4) straightforwardly implies that, as long as τ_m ≤ τ₁,τ₂ ≤ τ_M:

${\left\{\frac{X\left(t+{\tau }_1\right)-X\left(t\right)}{{\tau }_1^H}\right\}}_{t\in ℝ}\stackrel{fdd}{=}{\left\{\frac{X\left(t+{\tau }_2\right)-X\left(t\right)}{{\tau }_2^H}\right\}}_{t\in ℝ},$ (5)

with H = (−α/2) = (β + 1)/2, and where $f\underset{¯}{\underset{¯}{d}}d$ means equality of all joint finite dimensional distributions: i.e., $\left(X\left(t+{\tau }_1\right)-X\left(t\right)\right)∕{\tau }_1^H$ and $\left(X\left(t+{\tau }_2\right)-X\left(t\right)\right)∕{\tau }_2^H$ have the same joint distributions. In turn, this implies that ∀q > −1, such that 𝔼|X(t)|^q < ∞:

$\begin{array}{rcll}& \mathbb{E}{\left|X\left(t+\tau \right)-X\left(t\right)\right|}^q=c_q{\left|\tau \right|}^{qH},{\tau }_m\le \tau \le {\tau }_M,or& & \text{(6)}\\ & \mathbb{E}{\left|X\left(t+{\tau }_2\right)-X\left(t\right)\right|}^q=\mathbb{E}{\left|X\left(t+{\tau }_1\right)-X\left(t\right)\right|}^q{\left(\frac{\left|{\tau }_2\right|}{\left|{\tau }_1\right|}\right)}^{qH},& & \text{(7)}\end{array}$

with τ_m ≤ τ_1,τ₂ ≤ τ_M, which are reminiscent of equations (2) and (3).

4.2.2. Self-Similar processes with stationary increments

Equations (6) and (7) turn out to hold not only for jointly Gaussian 1/f-processes but for a much wider and better defined class, that of self-similar processes with stationary increments, referred to as H-sssi processes, and defined as, c.f., Samorodnitsky and Taqqu (1994):

${\mathcal{ℳ}}_1:{\left\{X\left(t\right)\right\}}_{t\in ℝ}\stackrel{fdd}{=}{\left\{a^{H}X\left(t∕a\right)\right\}}_{t\in ℝ},$ (8)

∀a > 0, H ∈ (0, 1). Essentially, it means that X cannot be distinguished (statistically) from any copy, dilated by scale factor a > 0, on condition that the amplitude axis is scaled by a^H. Parameter H is referred to as the self-similarity exponent. A major practical consequence of this definition consists of the fact that equations (6) and (7) hold for all τ (resp., τ₁,τ₂).

The central benefit of such a definition is that it does not require the data to be Gaussian but provides both theoreticians and practitioners with a well-defined model. For analysis, fMRI data can hence be envisaged as the increment process Y(t) = X(t + τ₀) − X(t) of an H-sssi process X (where τ₀ is an arbitrary constant chosen to make sense with respect to physiology and data acquisition set up, e.g., τ₀ = TR). This constitutes a second model to account for scale-free properties in data, that encompasses the simpler 1/f-spectrum first model.

Further, if joint Gaussianity is assumed, the model becomes even more precise as the only Gaussian H-sssi process X is the so-called fractional Brownian motion (fBm), c.f., e.g., Mandelbrot and van Ness (1968), hereafter labeled X(t) ≡ B_H(t). The corresponding increment process Y(t) = G_H(t) = B_H(t + 1) − B_H(t) is termed fractional Gaussian noise (fGn). Additionally, note that it may sometimes constitute a practical and relevant challenging issue to decide whether brain activity is better modeled by the H-sssi process X (hence a non-stationary process) or by its increment process Y (hence a stationary process; c.f., e.g., Ciuciu et al., 2008; He et al., 2010; He, 2011).

4.2.3. Multifractal processes

In a number of situations, it has been actually observed on a variety of real-world data of very different nature (c.f., e.g., Abry et al., 2002 for reviews) that equation (6) holds over a wide range of τs, however, with scaling exponents that depart significantly from the theoretical linear behavior qH:

$\mathbb{E}{\left|X\left(t+\tau \right)-X\left(t\right)\right|}^q=c_q{\left|\tau \right|}^{\zeta \left(q\right)},{\tau }_m\le \tau \le {\tau }_M.$ (9)

The generic behaviors modeled by equation (9) can be considered as a practical or operational, definition of scale-free property. Let us note that, by nature, ζ(q) is necessarily a concave function of q (c.f., e.g., Wendt et al., 2007).

Scaling exponents ζ(q) that are strictly concave rule out the use of H-sssi process as models. Instead, a broader class should be used, referred to as that of multifractal processes. This is however a large and not-well-defined class of processes. For the purposes of this contribution, let us use a particular subclass of multifractal processes defined as fBm subordinated to a multiplicative Compound Poisson cascade:

${\mathcal{ℳ}}_2:X\left(t\right):=B_H\left(A\left(t\right)\right),\text{where}A\left(t\right)={\int }^{t}W\left(s\right)ds,$ (10)

with W(s) a multiplicative Compound Poisson cascade (or martingale), such as those defined in Barral and Mandelbrot (2002). The complete definition of these cascades has been given and studied with details elsewhere and is hence not recalled here (c.f., Bacry et al., 2001; Barral and Mandelbrot, 2002; Chainais et al., 2005). It is enough to emphasize that they rely on the choice of positive random variables whose moments of order q define the ζ(q). The process X thus defined satisfies equation (9) with strictly convex tunable scaling exponents ζ(q), has stationary increments Y, and has distributions that depart from strict jointly Gaussian laws. Such departures, that may however turn subtle and hard to detect in practice, are precisely quantified by the departure of ζ(q) from a linear behavior in q. The ζ(q) therefore convey a rich information about data X, and hence about Y, as they account for the entire dependence structure of the data, hence both to the time dynamic and distributions of data. Their accurate estimation from real-world data therefore naturally constitutes an important practical challenge discussed below.

4.3. Scale-Free Analysis

4.3.1. From spectrum to wavelet analysis

Assuming that data Y have a power-law spectrum behavior as in equation (2), it is natural to rely on spectral estimation to measure β. A classical tool in spectrum analysis is the Welch estimator that consists in splitting data Y into blocks and in averaging the squared Fourier transforms computed independently over each block. For scale-free data, it is hence expected that:

${\widehat{\Gamma }}_Y\left(f\right)=\sum _k{\left|⟨Y,g_{f,k}⟩\right|}^2\simeq C{\left|f\right|}^{-\beta },$ (11)

where the g_f,k = g₀(t − k)e^℩2πft are translated into time and into frequency templates of a reference pattern g₀(t). This relation can be further used to estimate β.

It has been shown that wavelet transforms can achieve better performance both in the analysis of scale-free properties in real-world data, and in the estimation of the corresponding scaling parameters (c.f., Abry et al., 1995, 1998; Veitch and Abry, 2001). The discrete wavelet transform (DWT) coefficients of Y are defined as:

$d_Y\left(j,k\right)={\int }_{ℝ}Y\left(t\right)2^{-j}{\psi }_0\left(2^{-j}t-k\right)dt\equiv ⟨Y,{\psi }_{j,k}⟩,$ (12)

where the ψ_j,k = 2^−jψ₀(2^−jt − k) consists of templates of a reference pattern ψ₀ translated in time and dilated (by a factor a = 2^j). It is referred to as the mother-wavelet: an elementary function, characterized by fast exponential decays in both the time and frequency domains, as well as by a strictly positive integer N_ψ ≥ 1, the number of vanishing moments, defined as $\forall k=0,1,\dots$, N_ψ − 1, ∫t_ℝ t^kψ₀(t)dt ≡ 0, and ∫t_ℝ t^Nψ₀(t)dt ≠ 0. Note the choice of the L¹-norm (as opposed to the more common L²-norm choice) that better matches scaling analysis. For further introduction to wavelet transforms, the reader is referred to, e.g., Mallat (2009).

Defining $S_Y^d\left(j,2\right)=\frac{1}{n_j}{\Sigma }_{k=1}^{n_j}{\left|d_Y\left(j,k\right)\right|}^2$ (with n_j the number of d_X(j,k) available at scale 2^j), one obtains (c.f. Abry et al., 1995):

$\mathbb{E}{S}_Y^d\left(j,2\right)={\int }_{ℝ}{\Gamma }_Y\left(f\right){\left|{\Psi }_0\left(2^{j}f\right)\right|}^{2}df$ (13)

where Ψ₀ denotes the Fourier transform of ψ₀. This indicates that $S_Y^d\left(j,2\right)$ can be read as a wavelet based estimate of the PSD and is hence referred to as the wavelet spectrum. It measures the amount of energy of Y around the frequency f_j = f₀/2^j where f₀ is a constant that depends on the explicit choice of ψ₀ (for the Daubechies wavelet used here, f₀ ≃ 3f_s/4 with f_s the sampling frequency). This correspondence between the Fourier and wavelet spectra is illustrated on fMRI signals in Figure 2. For scale-free processes satisfying equation (2), it implies:

FIGURE 2

Figure 2. (A) Welch (blue curves) vs. Wavelet (black curves) spectra associated with a F-map (f₁₈). Solid and dashed lines correspond to rest and task, respectively. (B) Corresponding multifractal spectra 𝒟(h).

$S_Y^d\left(j,2\right)\equiv \frac{1}{n_j}\sum _{k=1}^{n_j}{\left|⟨Y,{\psi }_{j,k}⟩\right|}^2\simeq C_2{2}^{j\left(\beta -1\right)},a_m\le 2^j\le a_M.$

While this formally looks like equation (11), it has been shown in detail how and why the wavelet spectrum yields better estimates of the scaling exponents β than Welch based-ones, both in terms of estimation performance and robustness to various forms of non-stationarity in data that may be confused with scale-free behaviors (Abry et al., 1995, 1998; Veitch and Abry, 2001). Notably, it was shown how wavelet analysis enables to disentangle non-stationarity, stemming from fMRI environment, from true long memory in brain activity. Also, the wavelet spectrum avoids the potentially difficult issue that consists of deciding a priori whether empirical data are better modeled by Y or X, needed by classical spectrum estimation, that can only be applied to stationary data. In a nutshell, these benefits stem from the use of the change of scale operator to design the analysis tool, that intuitively matches scale-free behavior more naturally than a frequency shift operator.

4.3.2. From 2nd to other statistical orders: wavelet leaders

As discussed in Section 4.2, analyzing in-depth scale-free properties implies investigating not only the spectrum (i.e., the second order statistics of data) but rather the entire dependence structure, i.e., the whole range of available statistical orders q. It had initially been thought that this would amount to extending the definition of $S_Y^d\left(j,2\right)$ to other orders q, $S_Y^d\left(j,q\right)\equiv \frac{1}{n_j}{\sum }_{k=1}^{n_j}{\left|⟨Y,{\psi }_{j,k}⟩\right|}^q.$ It has however recently been shown that this approach, though intuitive and appealingly simple, fails to yield satisfactory estimation of the ζ(q). Notably, wavelet coefficients show little power in enabling practitioners to decide whether ζ(q) is a linear or strictly concave function of q. Instead, it is now well documented that the estimation of the ζ(q) should be based on Wavelet Leaders (Wendt et al., 2007).

Let us now assume that ψ₀ has a compact time support and introduce the global regularity of Y, h_m, defined as: $h_m=\lim {\inf }_{2^j\to 0}\log ({\sup }_k|d_Y(j,k)|)/\log (2^j)$ Therefore, h_m can be estimated by a linear regression of the log of the magnitude of the largest wavelet coefficient at scales 2^j versus the log of the scales 2^j (Wendt et al., 2007). Let γ ≥ 0 be defined as, with ∈ > 0: γ = 0 if h_m > 0, and γ = −h_m + ∈ otherwise. Further, let λ_j,k denote the dyadic interval λ_j,k = [k2^j, (K + 1)2^j), and denote by 3λ_j,k the union of λ_j,k and its 2 closest neighbors, 3λ_j,k = [(k − 1)2^j, (k + 2)2^j). The wavelet leaders $L_Y^{\left(\gamma \right)}$ are defined as $L_Y^{\left(\gamma \right)}\left(j,k\right)={\text{sup}}_{{\lambda }^{\prime }\subset 3{\lambda }_{j,k}}{2}^{\gamma j}\left|d_Y\left({\lambda }^{\prime }\right)\right|$. In practice, $L_Y^{\left(\gamma \right)}\left(j,k\right)$ simply consists of any of the largest coefficients 2^γj|d_Y(λ′)| located at scales finer or equal to 2^j and within a small time neighborhood. It is then necessary to form the so-called wavelet Leader structure functions that reproduce the scale-free properties in Y according to:

$S_Y^L\left(j,q,\gamma \right)\equiv \frac{1}{n_j}\sum _{k=1}^{n_j}{\left(L_Y^{\left(\gamma \right)}\left(j,k\right)\right)}^q\simeq c_q{2}^{j\zeta \left(q,\gamma \right)},$ (14)

Moreover, for a large class of processes, one has: ζ(q,γ) = ζ(q) + γq. For all real-world data analyzed so far with WLMF, this relation is found to hold, by varying γ (c.f. Wendt et al., 2007 for a thorough discussion). This has also been verified empirically for fMRI data. Further, because it can take any concave shape, the function ζ(q,γ) is often written as a polynomial expansion (Arneodo et al., 2002): $\zeta \left(q,\gamma \right)={\Sigma }_{p\ge 1}{c}_p^{\left(\gamma \right)}{q}^p∕p!$. Notably, the second order truncation $\zeta \left(q,\gamma \right)\simeq c_1^{\left(\gamma \right)}q+c_2^{\left(\gamma \right)}{q}^2∕2$ (with $c_2^{\left(\gamma \right)}\le 0$ by concavity) can be regarded as a potentially interesting approximation that captures the crucial information regarding whether the ζ(q,γ) are linear in q (hence indicating H-sssi models) or strictly concave (hence suggesting multiplicative cascade models). Interestingly, the coefficients $c_p^{\left(\gamma \right)}$ entering the polynomial expansion of ζ(q,γ) are not abstract figures but rather turn out to be quantities deeply tied to the scale-free properties of Y, as they are related to the scale dependence of the cumulants of order p ≥ 1, $C_Y^{\left(\gamma \right)}\left(j,p\right)$, of the random variable $ln{L}_Y^{\left(\gamma \right)}\left(j,k\right)$:

$\forall p\ge 1,C^{\left(\gamma \right)}{\left(j,p\right)}_Y=c_{0,p}^{\left(\gamma \right)}+c_p^{\left(\gamma \right)}ln{2}^j.$ (15)

Equations (14) and (15) suggest that the ζ(q,γ) or $c_p^{\left(\gamma \right)}$ can be efficiently estimated from linear regressions: $\widehat{\zeta }\left(q,\gamma \right)={\Sigma }_{j=j_1}^{j_2}{w}_j{log}_2{S}_Y^L\left(j,q,\gamma \right)$ and ${ĉ}_p^{\left(\gamma \right)}={log}_{2}e{\Sigma }_{j=j_1}^{j_2}{w}_j{Ĉ}_Y^L\left(j,p,\gamma \right)$. The weights w_j are chosen to perform ordinary (or non-weighted) least squares estimation (c.f. Veitch and Abry, 2001 for discussion). Further, ζ(q,γ) = ζ(q) + γq obviously implies that $c_1=c_1^{\left(\Gamma \right)}-\gamma$ and ∀p ≥ 2, $\forall p\ge 2,c_p=c_p^{(\Gamma )}.$

This wavelet Leader-based analysis of scale-free properties is intimately and ultimately related to multifractal analysis, the detailed introduction of which is beyond the scope of the present contribution. We restate here only its essence. Multifractal analyses describe globally the fluctuations along time of the local regularity of a signal Y(t). This local regularity is measured by the so-called Hölder exponent h(t), that essentially compares Y around time t₀ against a local power-law behavior: |Y(t) − Y(t₀)| ≤ |t − t₀|^h, |t − t₀| → 0. The variations of h along time are then described globally via the multifractal spectrum, consisting of the collection of Hausdorff dimensions, 𝒟(h), of the sets of points {t,h(t) = h}. In practice, the multifractal spectrum is estimated indirectly via (a Legendre transform of) the function ζ(q). The approximation ζ(q) ≃ c₁ q + c₁ q²/2 translates into 𝒟(h) ≃ 1 − (h − c₁)²/(2|c₂|). For thorough and detailed introductions to multifractal analysis, the reader is referred to, e.g., Wendt et al. (2007). Examples of such multifractal spectra estimated using the WLMF from real fMRI signals are illustrated in Figure 2B. An outcome of the mathematical theory underlying multifractal analysis, of key practical importance and impact, is the following: the function 𝒟(h) theoretically constitutes a rich characterization of the scale-free properties of a signal Y and its complete and entire estimation requires the use, in equation (14), of both positive and negative order qs, concentrated left and right around 0 (Wendt et al., 2007).

5. Multifractal Analysis of MSDL Maps

5.1. Single-Subject Analysis

5.1.1. Scaling range

For analysis, orthonormal minimal-length time support Daubechies’s wavelets were used with N_ψ = 3. Scale-free properties are systematically found to hold within a 4-octave range ((j₁,j₂) = (3,6)), corresponding to a frequency range of [0.008, 0.063] Hz⁵, which is hence consistent with the upper limit 0.1 Hz classically associated with the hemodynamics boundary and scaling in fMRI data (Cordes et al., 2001).

5.1.2. Fourier vs. wavelet spectra

For illustrative purposes, two time series corresponding to a functional map (k = 28, f₁₈ in Table 1), were selected in the rest and task runs from the first subject. In Figure 2A, the Fourier spectrum estimate $\left({log}_2{\widehat{\Gamma }}_{{\mathbf{\text{u}}}_{s,k}}\left(f\right)\right)$ based on Welch’s averaged periodogram and its wavelet spectrum counterpart $\left({log}_2{S}_{{\mathit{\text{u}}}_{s,k}}^d\left(j,2\right)\right)$ are found to closely match, as predicted by equation (13). Interestingly, Figure 2A shows that the β exponent, measured within frequency range [0.008, 0.063] Hz, in equation (2) (i.e., the neg-slope of the log-spectra ${log}_2{\hat{\Gamma }}_{{\mathit{\text{u}}}_{s,k}}\left(f\right)$) decreases with task-related activity in f₁₈. This amounts to observing lower Hurst exponent H = (β − 1)/2 in the task-related dataset: ${\hat{H}}_{{\mathit{\text{f}}}_{18}}^{\text{R}}\simeq 0.66$ and ${\hat{H}}_{{\mathit{\text{f}}}_{18}}^{\text{T}}\simeq 0.5.$ As shown in the following, this decrease of self-similarity is not specific to functional maps and will be observed in artifactual and undefined maps. Following He (2011), the stationarity of fMRI signals is confirmed since we systematically observed ${\hat{H}}_k^{\text{R},\text{T}}<1.$

5.1.3. Multifractal spectrum

For the same time series, MF spectra 𝒟(h), estimated using the WLMF tool described above, are depicted in Figure 2B. The decrease of self-similarity between rest and task is captured by a shift to the left of the position ${\hat{c}}_1$ of the maximum of $D\text{(}h\text{): }\left({\left({\hat{c}}_1\right)}_{f_{18}}^{\text{R}},{\left({\hat{c}}_1\right)}_{f_{18}}^T\right)=\left(0.75,0.5\right)$ It should also be noted that parameter ${\hat{c}}_1$ systematically takes values that are close to those of the Hurst exponent. This is consistent with the theoretical modeling of scale-free property that establishes a clear connection between c₁ and H and predicts c₁ ≃ H (c.f. Wendt et al., 2007). Therefore, in the following, c₁ will be referred to as the self-similarity parameter although this is a slight misnomer. Further, Figure 2B confirms the presence of multifractality in fMRI data as strictly negative c₂ < 0 are almost always observed. Indeed, parameter c₂ quantifies the width of 𝒟(h; as a curvature radius of 𝒟(h) around (${\hat{c}}_1$): ${\hat{c}}_2<0.$ Multifractality is however not specific to a given brain state since we measured $\left({\left({\hat{c}}_2\right)}_{f_{18}}^{\text{R}},{\left({\hat{c}}_2\right)}_{f_{18}}^{\text{T}}\right)=\left(-0.07,-0.06\right).$ In this example, multifractality, as measured by the width of the multifractal spectra, is decreased from rest to task. However, opposite fluctuations will be also observed amongst F-maps.

The sole two self-similarity and multifractality parameters c₁ and c₂ are therefore used from now on as sufficient and relevant descriptors of the scale-free properties of fMRI signals (superscript γ is dropped for the sake of conciseness, while γ has been systematically set to γ = 2).

5.2. Group-Level Analysis

5.2.1. Group-level scale-free properties

Let $c_{i,k}^{j,s}$ denote the ${ĉ}_1$ and ${ĉ}_2$ estimates (index i = 1:2) for differents maps (index k = 1:K), runs (index j = R,T for Rest and Task, respectively) and for different subjects (index s). The map-dependent group-level values have been computed as ${\mu }_{i,k}^j={\Sigma }_{s=1}^S{ĉ}_{i,k}^{j,s}∕S$ and sorted according to their labeling (F/A/U-maps) given in Table 1. Then, global spatial averaging of the means ${\mu }_{i,k}^j$ has been performed so as to derive global F/A/U-average parameter estimates: ${\bar{\mu }}_{i,F}^j={\Sigma }_{k\subset \mathcal{ℱ}}{\mu }_{i,k}^j∕\text{Card(}\mathcal{ℱ}\text{)}$, ${\bar{\mu }}_{i,A}^j$, and ${\bar{\mu }}_{i,U}^j$ are defined equivalently. In the same spirit, group-level multifractal attributes ${\bar{\mu }}_{i,v_{\ell }}^j$ are derived for each functional network v_ℓ ∈ 𝒩 = {Att, DMN, Mot, N-c, Vis} such that ${\bar{\mu }}_{i,n_{\ell }}^j={\Sigma }_{k\in n_{\ell }}{\mu }_{i,k}^j∕\text{Card(}{\mathit{\text{n}}}_{\ell }\text{)}$, ∀ℓ = 1:5, and j = (R,T). We proceed in the same way for analyzing artifact types t_r ∈ 𝒯 = {Ven, WhM, Mov, Oth}, and computing ${\bar{\mu }}_{i,{\mathit{\text{t}}}_r}^j$ for r = 1:4.

As shown in Figure 3[top], the group-averaged values of self-similarity ${\mu }_{1,k}^j$ lie approximately in the same range [0.55, 1], indicating long memory, for all components (F/A/U-maps). An almost systematic decrease of self-similarity is observed in the task-related dataset $\left({\delta }_{1,k}={\mu }_{1,k}^{\text{T}}-{\mu }_{1,k}^{\text{R}}<0\right),$ for k ∈ ℱ∪𝒜∪ 𝒰. This trend is therefore not specific to F-maps. Moreover, the average decrease computed over F-maps is about the same as the one estimated for A and U-maps $({\overline{\delta }}_{1,F}=-0.125,{\overline{\delta }}_{1,A}=-0.11\text{and\hspace{0.17em}}{\overline{\delta }}_{1,U}=-0.13)$. Also, the averaged standard deviations $({\overline{\sigma }}_{1,F}^R,{\overline{\sigma }}_{1,A}^R,\text{and}{\overline{\sigma }}_{1,U}^R)$ computed over the F/A/U-maps, are close to each other $\left({\bar{\sigma }}_{1,F∕A∕U}^{\text{R}}\approx 0.18\right)$ and systematically increase with the task-related activity $\left({\bar{\sigma }}_{1,F∕A∕U}^{\text{T}}>{\bar{\sigma }}_{1,F∕A∕U}^{\text{R}}\right).$

FIGURE 3

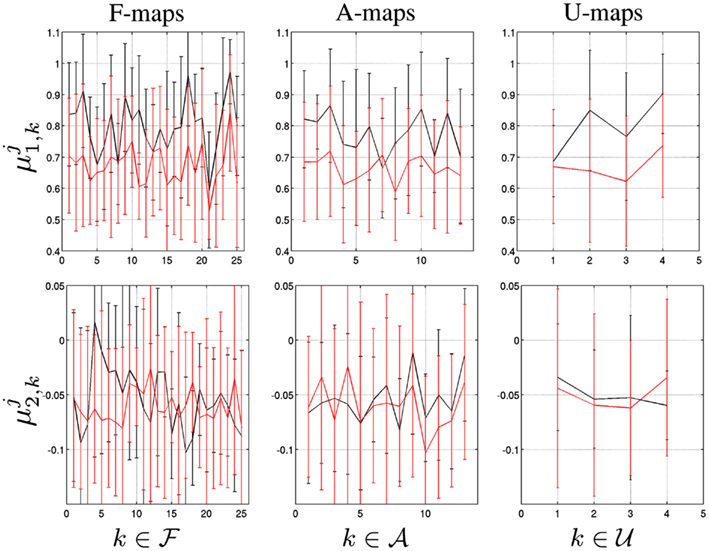
Figure 3. From left to right: Group-averaged map-dependent MF parameters ${\mu }_{\text{1},k}^j$ (top), ${\mu }_{\text{2},k}^j$ (bottom) specific to F/A/U-maps defined in Table 1. Black and red curves code for j = {R} (Rest) and j = {T} (Task).

Figure 3[bottom] illustrates that the group-averaged values of ${\mu }_{2,k}^{\text{R},\text{T}}$ are almost all negative in the F/A/U-maps indicating multifractality in fMRI time series irrespective of the map type or brain state. Between rest to task-related situation minor changes in the A and U-maps are also observed since |δ_2,k| < 0.03 for $k\in \mathcal{𝒰}\cup \mathcal{𝒜}$) while we measured |δ_2,k| < 0.08 for k∈ℱ $\left({\delta }_{2,k}={\mu }_{2,k}^{\text{T}}-{\mu }_{2,k}^{\text{R}}\right).$ Hence, the level of multifractality does not change much between rest and task in irrelevant maps. In contrast, large changes in the multifractal parameters are observed in F-maps, while not systematically in the same direction. For instance, in cerebellum ( f ₄), basal ganglia ( f ₅), DMN ( f ₇) and fronto-parietal network ( f ₈) evoked activity induces a large increase of multifractality (δ_2,k< 0) while in the auditory and attentional systems (e.g., f ₁₂ and f ₂₄, respectively), which are supposed to be involved in the auditory detection task, the converse observation holds, i.e. (δ_2,k> 0. Also, it is worth noticing that the averaged standard deviations computed over the A/U-maps increase when switching from rest to task $\left({\bar{\sigma }}_{2,A}^{\text{R}}=0.06<{\bar{\sigma }}_{2,A}^{\text{T}}=0.09\text{and}{\bar{\sigma }}_{2,U}^{\text{R}}=0.05<{\bar{\sigma }}_{2,U}^{\text{T}}=0.085\right)$ while they remain at the same level in the F-maps: ${\bar{\sigma }}_{2,F}^{\text{R}}\approx {\bar{\sigma }}_{2,F}^{\text{T}}\approx 0.08.$

We computed the grand means of the self-similarity parameters ${\bar{\mu }}_{1,F∕A∕U}^{\text{R},\text{T}}$ over the F/A/U-maps, respectively, and draw the same conclusion at this macroscopic level, as demonstrated in Figures 4A–C: the decrease of self-similarity from rest to task is not specific to functional components and only slightly fluctuates between networks and artifact types. Moreover, we did not observe any significant modification of the grand means of multifractal parameter estimates ${\bar{\mu }}_{2,F∕A∕U}^{\text{R},\text{T}}$ between rest and task, as illustrated in Figure 4D. This motivated deeper investigations at the network and artifact levels, especially concerning the fluctuation of multifractality induced by task. Figure 4E reveals that a major increase of multifractality $({\overline{\mu }}_{2,n_4}^{\text{T}}<{\overline{\mu }}_{2,n_4}^{\text{R}})$ occurred only in the non-cortical regions while no major change appeared in the artifacts $\left({\mu }_{2,t_r}^{-\text{T}}\simeq {\mu }_{2,t_r}^{-\text{R}},\forall r\in 𝓣\right)$ as shown in Figure 4F.

FIGURE 4

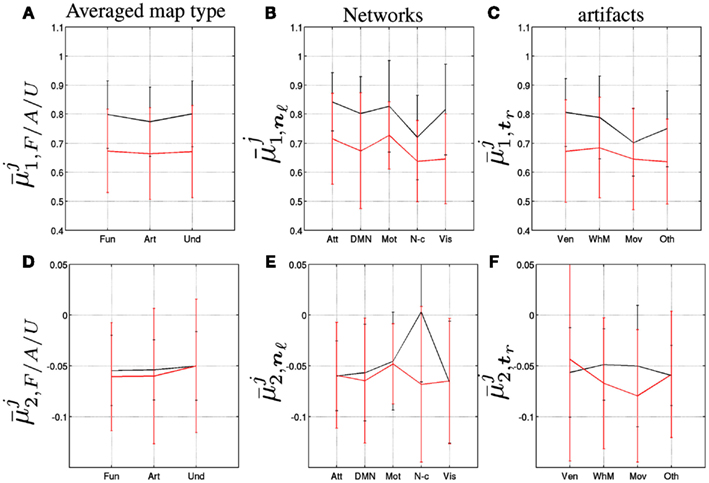
Figure 4. Group-level grand-mean self-similarity parameter ${\bar{\mu }}_{1,k}^j$ averaged over the F/A/U-maps, i.e., k∈ℱ/𝒜/𝒰 (A), the functional networks, k∈𝒩 (B) and the artifact types, k∈𝒯, (C). Group-level grand-mean multifractality parameter ${\overline{\mu }}_{2,k}^j$ averaged over the F/A/U-maps, i.e., k∈𝒻/𝒜/𝒰 (D), the functional networks, k∈𝒩 (E) and the artifact types, k∈𝒯, (F). Black and red curves code for j = R (Rest) and j = T (Task).

5.2.2. One-sample statistical tests

To assess the statistical significance of the multifractal parameters for the rest and task-related datasets at the group-level, we used one-sided tests associated with the following null hypotheses ∀k ∈ ℱ∪𝒜 ∪ 𝒰:

$\left.\begin{array}{ccc}{H}_{0,j}^{\left(1,k\right)}:{\mu }_{1,k}^j\hfill & \le 0.5,\hfill & \left(\text{White}\text{noise}\text{or}\text{SRD}\right)\hfill \\ H_{0,j}^{\left(2,k\right)}:{\mu }_{2,k}^j\hfill & =0.,\hfill & \left(\text{H}-\text{sssi}\text{process}\right).\hfill \\ \hfill \end{array}\right\}$ (16)

We also conducted similar tests at the macroscopic level (k ∈ 𝒩 ∪ 𝒯) by replacing ${\mu }_{i,k}^j$ with ${\overline{\mu }}_{i,k}^j$ in the null hypotheses (16). Because there is no definite proof nor evidence that MF parameter estimates ${ĉ}_{i,k}^{j,s}$ should be normally distributed across subjects, we investigated different statistics (Student-t, Wilcoxon’s signed rank (WSR) statistic). Indeed, other statistics may provide more sensitive results in presence of outliers. To account for multiple comparisons (K tests performed simultaneously) and to ensure correct specificity control (control of false positives), the Bonferroni correction was applied.

Rejecting $H_{0,j}^{(1,k)}$ clearly amounts to localizing brain areas or components eliciting significant long memory or self-similarity. Rejecting $H_{0,j}^{(2,k)}$ enables to discriminate multifractality from self-similarity. Similar tests involving ${\overline{\mu }}_{i,F/A/U}^j,{\overline{\mu }}_{i,n_{\ell }}^j$, and ${\overline{\mu }}_{i,t_r}^j$ in the definition of null hypotheses(16) for (i = 1, 2) were also performed.

Analysis of statistical significance of F-maps regarding $H_{0,R}^{(1),k}$ showed that most components (22/25) rejected this null hypothesis at rest using T-test and thus were significantly self-similar (see blue curves in Figure 5A). The task effect then induced a loss of significance in the vast majority of components as shown in Figure 5B: only four maps ( f ₁₀, f ₁₄, f ₁₈, and f ₂₄) demonstrated a significant level of self-similarity using T-test in the task-related dataset. These maps are related to the motor, fronto-parietal, and attentional (parieto-temporal junction and IPS/FEF) networks. Two out of them are lateralized in the left hemisphere. Statistical analysis of F-maps regarding $H_{0,R}^{(2),k}$ demonstrated that only six components ( f ₁₅, f ₁₇, f ₁₈, f ₂₁, f ₂₃, f ₂₄) rejected this null hypothesis at rest: see red curves in Figure 5A. The task-related modulation tends to reduce the number of significant F-maps: As depicted in Figure 5B, only 3 components survived the T-test ( f ₁₀, f ₁₅, and f ₁₉) in the task-related dataset. Interestingly, f ₁₀ and f ₁₉ are likely to be involved in the auditory detection task and the motor response since they belong to the Motor and Attentional networks. Hence, a significant level of multifractality is observed during task in components that were monofractal at rest. Besides, the level of multifractality remains significant in the ventral occipital cortex ( f ₁₅) irrespective of the brain state and that a few components in the visual ( f ₁₇), fronto-parietal ( f ₁₈), temporal ( f ₂₁), prefrontal ( f ₂₃), and attentional ( f ₂₄) networks became monofractal under the task effect.

FIGURE 5

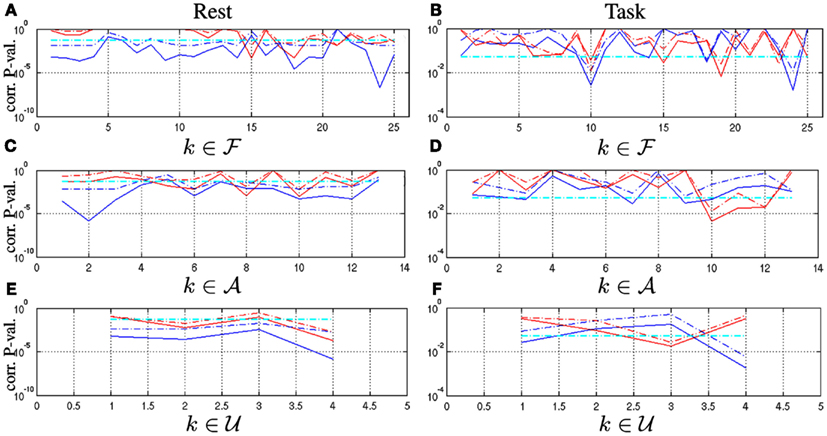
Figure 5. Corrected p-values associated with one-sample Student-t () and WSR () tests performed on resting-state ([A,C,E]) and task-related multifractal parameters ([B,D,F]) for assessing $H_{0,j}^{(1,\cdot )}$ (blue curves) and $H_{0,j}^{(2,\cdot )}$ (red curves) on the functional ([A-B]), artifactual ([C-D]) and undefined maps ([E-F]), respectively. Significance level (α = 0.05) is shown in .

Statistical analysis of A and U-maps regarding $H_{0,j}^{(1),k}$ showed the same behavior when switching from rest to task, namely a strong decrease of the number of significant self-similar components (from 10 to 4 and 4 to 2 for A/U-maps, respectively): see blue curves in Figures 5C–F, respectively. Statistical analysis of A and U-maps regarding $H_{0,j}^{(2),k}$ also demonstrated a reduction of the number of multifractal components in A/U-maps. Two artifactual components (a₁₀ and a₁₂) located in the white matter remained consistently multifractal in both datasets and one undefined component (u₃) became significantly multifractal when switching from rest to task. In all cases, a loss of significance is observed using WSR tests (dash dotted curves) instead of T-tests (solid curves) indicating that there is no outlier in this group and thus that the Gaussian distribution hypothesis is tenable.

Then, we focused on the statistical analysis at different macroscopic scales, first by averaging all F/A and U-maps respectively so as to derive a mean behavior for F/A/U-maps. Finally, we looked at functional networks and artifact types in more details. Blue curves in Figures 6A,B report such results for the rest and task-related datasets, respectively. We still observed a significant level of self-similarity in all averaged groups (blue curves) irrespective of the brain state: ${\overline{H}}_{0,j}^{(1,F/A/U)}$ is systematically rejected for j = (R, T). However, we still noticed a reduction of statistical significance induced by task irrespective of the map type. More interestingly, we found at this macroscopic level that all averaged maps were multifractal at rest whereas only the functional one remained multifractal during task: see red curves in Figures 6A,B. Further, statistical analysis of functional networks defined in Table 1 was conducted to understand which network drives this effect. When comparing p-values in Figures 6C,D on functional networks, we observed that all remained significantly self-similar in both states, while the DMN is close to the significance level α = 0.05 during task (blue curves). Regarding multifractality, only the non-cortical regions appeared monofractal at rest and all networks kept a significant amount of multifractality during task. In contrast, this observation did not hold for artifacts: when looking at Figures 6E,F in detail, the signal related to ventricles became monofractal during task.

FIGURE 6

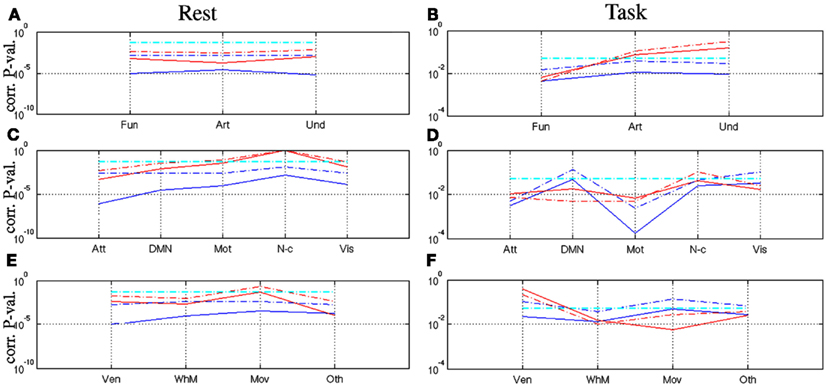
Figure 6. Corrected p-values associated with one-sample Student-t () and WSR () tests performed on resting-state ([A,C,E]) and task-related multifractal parameters ([B,D,F]) for assessing $H_{0,j}^{(1,\cdot )}$ (blue curves) and $H_{0,j}^{(2,\cdot )}$ (red curves) on the the averaged map types ([A-B]), networks 𝒩 ([C-D]) and artifact types 𝒯 ([E-F]), respectively. Significance level (α = 0.05) is shown in .

5.2.3. 2-way repeated measures ANOVA

In order to assess any significant change of self-similarity or multifractality between rest and task, we entered the subject-dependent parameter estimates $\left({ĉ}_{i,k}^{j,s}\right)$ in several 2-way repeated measures ANOVAs involving two factors: brain state (two values: j = R, T) and map type (with varying number of values). These ANOVAs were conducted separately for assessing self-similarity (i = 1) and multifractality (i = 2) changes. First six ANOVAs (three for each parameter) were carried out by considering the F/A/U-maps as the second factor, respectively. This second factor thus took a number of values that depends on the set under study: ℱ, 𝒜, or 𝒰. Results are summarized in Table 2. Regarding the analysis of self-similarity $\left({ĉ}_{1,k}^{j,s}\text{parameters}\right)$, a significant brain state effect appeared in all F/A/U-maps, and a significant map effect in the F and A-sets. Significant interactions were found for the F and U-maps. This confirms that the level of self-similarity is not sufficient to disentangle functional networks from artifactual or undefined maps.

TABLE 2

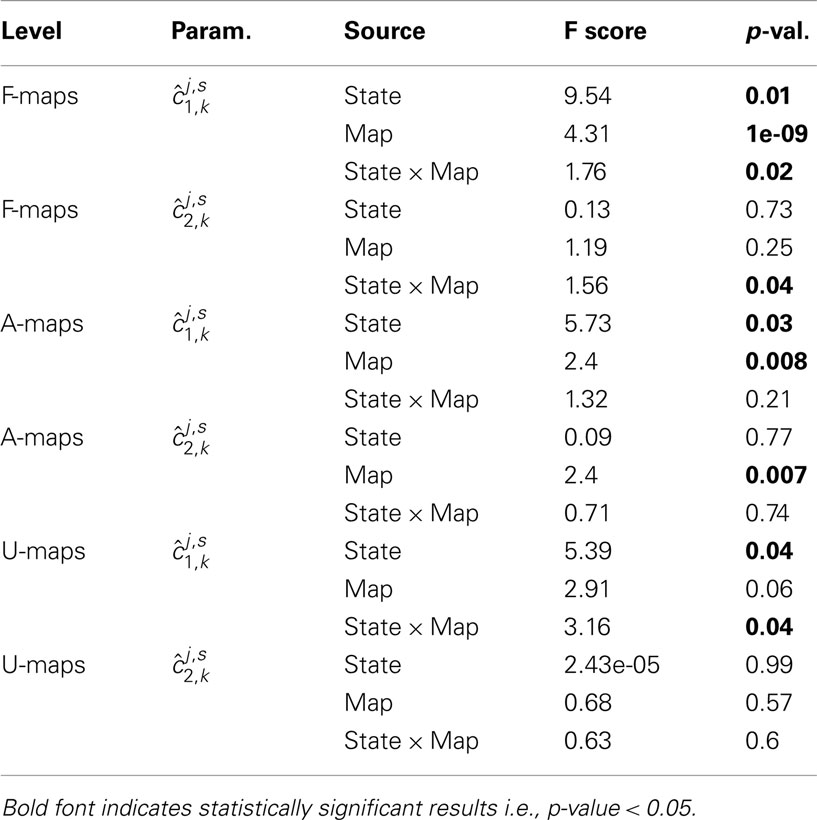
Table 2. 2-way repeated measures ANOVA results based on the ${ĉ}_{i,k}^{j,s}$ parameters for i = {1, 2}, j = (R,T), s = 1:S, and k ∈ ℱ (top), k ∈ 𝒜 (middle), k ∈ 𝒰 (bottom).

As regards ANOVAs based on ${ĉ}_{2,k}^{j,s}$ parameters, a significant interaction for F-maps is found, thus indicating that the averaged change in multifractality between rest and task is significant for functional maps only. In summary, only F-maps exhibited significant interactions for both multifractal attributes.

Akin to the one-sample analyses above, we looked at a larger spatial scale, the functional network, and artifact type levels and performed similar ANOVAs, corresponding results are reported in Table 3. While both functional networks and artifacts demonstrate a significant change in the self-similarity parameter between rest and task, only functional networks made the map type effect significant. More importantly, the key feature for discriminating functional networks from artifacts relied on ANOVAs based on ${ĉ}_{2,k}^{j,s}$ parameters. Indeed, a significant network effect and more importantly a significant interaction between rest and task are observed in functional networks.

TABLE 3

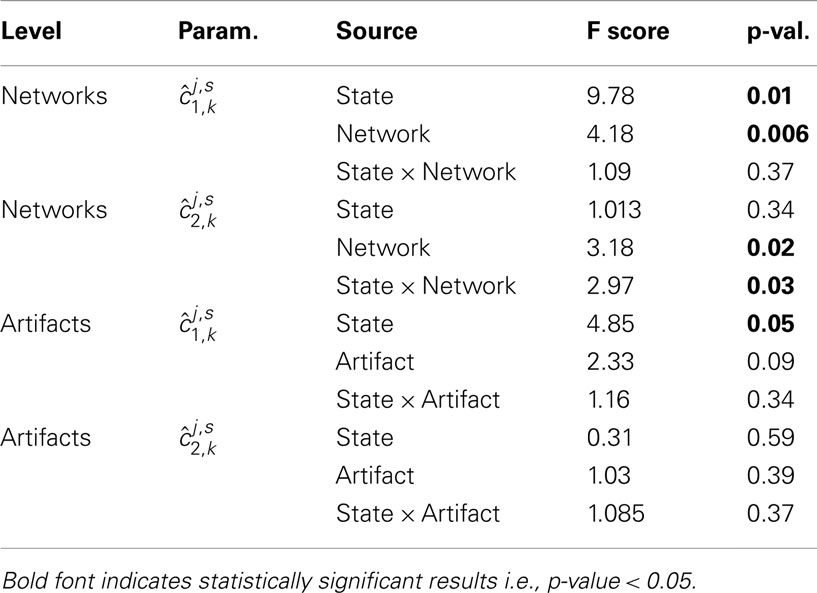
Table 3. 2-way repeated measures ANOVA results based on the ${ĉ}_{i,k}^{j,s}$ parameters for i = {1,2}, j = (R,T), s = 1:S, and k∈𝒩 (top) and k∈𝒯 (bottom).

5.2.4. Two-sample statistical tests

To localize which maps are responsible for statistically significant ANOVA results, we finally performed two-sample T-tests in which we tested the following null hypotheses:

$\left\{\begin{array}{c}\hfill {\tilde{H}}_0^{\left(1,k\right)}:{\mu }_{1,k}^{\text{R}}={\mu }_{1,k}^{\text{T}},\forall k\in \mathcal{ℱ}\cup \mathcal{𝒜}\cup \mathcal{𝒰}\hfill \\ \hfill {\tilde{H}}_0^{\left(2,k\right)}:{\mu }_{2,k}^{\text{R}}={\mu }_{2,k}^{\text{T}},\forall k\in \mathcal{ℱ}\cup \mathcal{𝒜}\cup \mathcal{𝒰}.\hfill \\ \hfill \hfill \end{array}\right.$ (17)

We also conducted similar tests at the macroscopic level (k ∈ 𝒩∪𝒯) by replacing ${\mu }_{i,k}^j$ with ${\bar{\mu }}_{i,k}^j$ in the null hypotheses (17). The fluctuations in self-similarity being systematically in the same direction between rest and task, we performed one-sided tests as regards the ${\mu }_{1,k}^j\text{’s}$ while two-sided tests were considered for the ${\mu }_{2,k}^j\text{’s}$: task-related positive and negative fluctuations of ${\mu }_{2,k}^j$ were actually observed in Subsection 5.2.1. Figures 7A,B shows the uncorrected p-values for the F-maps and networks, respectively. We rejected ${\tilde{H}}_0^{\left(1,k\right)}$ for ( f ₃, f ₄, f ₁₁, f ₁₈, f ₂₅) at a significance level set to α₁ = 0.01 and ${\tilde{H}}_0^{\left(2,k\right)}$ for ( f ₄, f ₇, f ₁₈) at α₂ = 0.05. These components clearly explain significant results reported in Table 2 about the changes in self-similarity and multifractality that occurred in F-maps. Interestingly, among the latter, the null hypothesis was rejected because of a large increase of multifractality in ( f ₄, f ₇). In contrast, a decrease of multifractality was responsible for the rejection of ${\tilde{H}}_0^{\left(2,k\right)}$ in f ₁₈. When setting α₂ = α₁ = 0.01, only f ₁₈ survived this threshold and thus remained the single functional component for which a significant difference of self-similarity and multifractality was found between rest and task. This component clearly drove the significant interaction reported in Table 2 for the change in multifractality in F-maps. Figure 7B also showed that the state effect reported in Table 3 on $\left({ĉ}_{1,k}^{j,s}\right)$ at the network level was driven by the attentional, motor, and visual systems. Last, the significant interaction reported in Table 3 on $\left({ĉ}_{2,k}^{j,s}\right)$ is explained by the non-cortical regions as shown in Figure 7B.

FIGURE 7

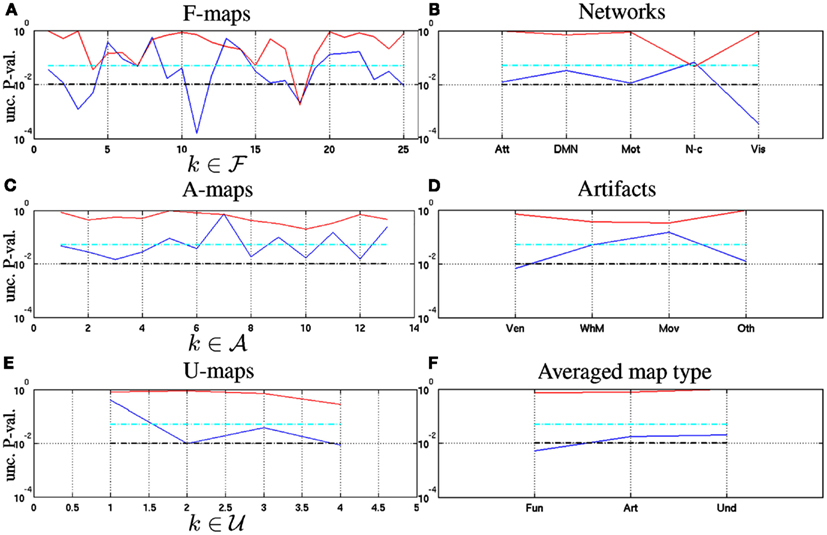
Figure 7. Uncorrected p-values associated with two-samples Student-t test performed between resting-state and task-related multifractal parameters for assessing ${\tilde{H}}_0^{\left(1,\cdot \right)}$ (blue curves) and ${\tilde{H}}_0^{\left(2,\cdot \right)}$ (red curves) on the on the functional (A), artifactual (C) and undefined maps (E), respectively. Similar tests were computed at a broader spatial scale on the functional networks (B), the artifacts (D) and the averaged map types (F), respectively. Significance levels (α₁ = 0.01 and α₂ = 0.05) are shown in - - and , respectively.

Figures 7C,D shows the localization of the state effects reported in Tables 2 and 3 for the changes in self-similarity that occurred in artifacts at the local and global levels. No A-map enabled to reject ${\tilde{H}}_0^{\left(1,k\right)}$ at the α₁ significance level but a majority of A-maps (a_1:4, a₆, a₈, a₁₀, a₁₂) contributed to the significant state effect observed in Table 2. At the global artifact level, the ventricles appear as the main source of the significant state effect reported in Table 3 for the change in self-similarity. Also, no significant difference in multifractality was reported for artifacts whatever the observation level (A-maps or averaged artifacts). Similarly, Figure 7E enables us to show that u ₂ and u ₄ were the main sources of the significant state effect and interactions reported in Table 2 for the change in self-similarity. At the macroscopic level, we finally observed in Figure 7F that only the grand mean of functional maps leads to a significant modulation of self-similarity between rest and task at level α₁.

6. Discussion

6.1. Results Interpretation

This study analyzed in-depth the scale-free properties of fMRI signals, using multifractal methodologies, and their modulations during rest and task both in functional networks and artifactual regions. The underlying goal was to finely characterize which properties are specific to functional networks and which modulation can be expected for these networks from task-related activity. Previous attempts in the literature (Cordes et al., 2001; Leopold et al., 2003; He, 2011) focused on functional networks without comparing results with the behavior of artifacts. The main reason comes from the fact that seed region analyses were only conducted in such studies. Hence, no comparison with vascular or ventricles-related signals was undertaken.

Our results confirmed that fMRI signals are stationary and self-similar but not specifically in functional networks. Also we showed that the amount of self-similarity significantly varies between rest and task not only in functional networks involved in our auditory detection task with a motor response (Attentional, Motor) but also quite surprisingly in the visual system and in some artifacts (ventricles) and undefined maps. This observation led us to investigate the scale-free structure of fMRI signals using richer models, namely multifractal processes, to which the WLMF toolbox is dedicated. Our statistical results demonstrate first that fMRI signals are multifractal, second that interactions between brain state and maps only occurred in F-maps and functional networks and third, that specific F-maps such as in non-cortical regions demonstrated a statistically significant fluctuation between rest and task. This result shows that the concept of multifractality permits to disentangle functional components from artifactual ones, in a robust and significant manner.

However, in contrast to self-similarity that systematically decreases with evoked activity, multifractality decreases in cortical ( f ₁₈) but increases in non-cortical ( f ₄, f ₇). Thus, task-related activity has no systematic impact with respect to increase/decrease of multifractality. Interestingly, we found a statistically non-significant trend toward a decrease of multifractality in regions primarily involved in the task ( f ₁₂, f ₂₄, f ₂₅). However, the group size of this study remains small (12 subjects only) to achieve significant results, mainly because of the between-subject variability and of the difficulty in estimating ${ĉ}_{2,k}^{j,s}$ parameters on short time series.

Further investigations beyond the scope of this paper are necessary to find out any general trend on the direction change of multifractality with evoked activity by cross-correlating multifractal parameters with task-related activity (e.g., group-level Z-scores) and task performance. However, to derive reliable results for multifractality, a larger group of individuals will be considered and a larger number of scans will be acquired while maintaining the same scanning time: To this end, accelerated SENSE imaging will be used together with recent reconstruction algorithms so as to improve temporal resolution (Chaari et al., 2011b).

6.2. Monofractal Scale-Free EEG Microstate Sequences vs. Multifractal Dynamics for RSN

The results obtained in this contribution shows multifractal temporal dynamics in fMRI signals and thus naturally lead to question the potential origins and generative mechanisms for this departure from the more traditional long-range correlation modeling of scale invariance. A natural track to inspect consists of that of the relations between hemodynamic (fMRI) and electrical (EEG) signatures for brain activity at rest. This question has been intensively studied over the last decade (Laufs et al., 2003; Mantini et al., 2007; Britz et al., 2010; Musso et al., 2010; Van de Ville et al., 2010; Yuan et al., 2012), first by measuring cross correlations between fMRI data at rest and EEG-informed regressors derived from the convolution of the EEG power signal in five well-identified frequency bands (δ ∈ (1,4) Hz, þeta ∈ (4,7) Hz, α ∈ (8,12) Hz, β ∈ (13,30) Hz, and γ > 30 Hz) with the canonical HRF. This approach revealed the negative correlation of α-band activity with the attentional network and the positive correlation with β₂-band with the default mode network (precuneus and posterior cingulate cortex; Laufs et al., 2003). Also, Mantini et al. (2007) showed that functional resting-state networks have different EEG signatures which are not specific to a given frequency band but are rather spread over several oscillations regimes (e.g., correlation between α and β power in specific RSN), a consequence of the so-called oscillation hierarchy (Buzsáki, 2006) and the of phase-amplitude cross-frequency coupling (He et al., 2010). However, none of these works enable to explain the low frequency fluctuations (<0.1 Hz) or scale-free dynamics of the fMRI signal at rest, because this phenomenon is much more widespread than oscillations.

Scale-free dynamics of brain electrical activity at rest has recently been studied (Van de Ville et al., 2010) but not directly on raw data. Instead, EEG microscates that correspond to short periods (100 ms) during which the EEG scalp topography remains quasi-stable, have been first segmented. Remarkably, it has been shown that only four different EEG microstate patterns are necessary to describe the ongoing electrical brain activity at rest (Britz et al., 2010) and that these four microscates correlate with well-known RSNs, which were classically identified from fMRI dataset alone using group-level ICA. This demonstrated that the EEG microstate with rapid fluctuations might be considered as the electrophysiological signature of intrinsic functional connectivity patterns. The investigation of scale-free dynamics was thus performed on the EEG microstate sequence to understand how fast the microscates are changing and what kind of correlation structure (short or long-range) they bring (Van de Ville et al., 2010).

The recent finding that EEG microscate sequences reveal purely monofractal dynamics (Van de Ville et al., 2010), irrespective of the data filtering, may lead to conclude that the same monofractal behavior in the fMRI signature of RSN (strongly correlate with these microstates) should be expected, if one assumes a linear and time invariant HRF model for the neurovascular coupling. However, the results obtained in the present contribution can be considered not only as evidence in favor of multifractality in fMRI data, but also as evidence that this multifractal effect is discriminant of cortical versus non-cortical regions and characteristic of functional network with respect to modulation under task.

Several factors may explain this apparent discrepancy. First, an accurate comparison of both sets of result would require a precise match of the range of scales (or frequencies) within which scale invariance is analyzed and corresponding parameters measured. Here, the selected range of frequencies corresponds to ([0.008,0.063]Hz), while the monofractal behavior of EEG microstate sequences was exhibited on a distinct frequency range, i.e. ([0.063, 3.9]Hz) in Van de Ville et al. (2010). Comparison of scaling properties requires that the same frequency range is selected but this constraint is clearly not tenable across modalities like EEG and fMRI given the fMRI sampling rate.

Second, it is indeed very unlikely that a linear and time invariant filtering may create multifractality in fMRI starting from a monofractal electrophysiological signal in EEG. The general issue of the relations between (linear and non-linear) filtering and multifractality were barely studied theoretically so far but interestingly, Abry et al. has shown that simple non-linear filter can turn mono- into multifractality. Hence, another putative origin for the apparent contradiction between our findings and those in Van de Ville et al. (2010) lies in refined descriptions of HRF model by non-linear dynamical systems (e.g., Balloon model; Buxton et al., 1998, 2004). Of course, linear and stationary approximations like the canonical HRF model (Glover, 1999) or non-parametric alternatives (Vincent et al., 2010; Chaari et al., 2011a) have been validated but only on evoked activity and considering inter-stimulus intervals larger than 3 s. For shorter ISIs, non-linear hemodynamics has turned out to be a valid property (Liu and Gao, 2000). In this context, habituation, or repetition suppression effects may occur and induce a sublinear hemodynamic response, which would modify scaling properties (Dehaene-Lambertz et al., 2006; Ciuciu et al., 2009). Hence, by modeling the sequence of EEG transient brain states as a series of short time epochs, this could induce non-linearities in the hemodynamic system that could explain the switch from purely fractal EEG microstates to multifractal signatures in the corresponding RSNs.

Third, instead of segregating EEG microstates in multiple groups based upon the maximal spatial dissimilarity between groups (Britz et al., 2010; Musso et al., 2010), a more recent analysis of joint EEG/fMRI resting-state data has revealed a larger number (thirteen) of EEG microstates that show temporal independence from each other (Yuan et al., 2012). In this latter work, all resting-state networks including visual, motor, auditory, attention, saliency and default mode networks were characterized by a specific electrophysiological signature involving several EEG microstates. This clearly indicates that the original analysis of scale-free dynamics for EEG microscates done in Van de Ville et al. (2010) should be revisited on this larger number of metastable states to disentangle whether multifractality in this larger set of microstates has been discarded due to averaging effects. It is actually clear that the sequence mixing thirteen different microstates may generate richer singularities (abrupt changes between microstates) than the ones relying on four microstates only. Fourth, the temporal signatures of EEG microstates found in Musso et al. (2010), Van de Ville et al. (2010) are correlated in time since the spatial similarity was the key factor to identify them. As a consequence, the microstate sequences is correlated too and might loose some singularities that could be found out in the microstate sequences generated by Yuan et al. (2012). Finally, the presence of multifractality in resting-state (and task-related) MEG data has been evidenced in the sensor space in Zilber et al. (2012). These findings open new research avenues: For instance, it is natural to explore whether the observed multifractal properties can be related multiplicative cascade processes, that is to one of the only practical mechanism known to generate multifractal dynamics, or to investigate whether this cascade takes place at meso or macroscopic scales, as well as to figure out how brain networks could implement such cascade mechanisms. This topic is beyond the scope of the present contribution, however the log-normal statistics of neuronal firing rate could provide us with a first clue to uncover any generative process underlying multifractal dynamics.

6.3. Stationarity vs. Non-Stationarity of the RSN Dynamics

Recent results in resting-state fMRI reveal temporally independent functional modes of spontaneous brain activity (Smith et al., 2012) and postulate the presence of temporally non-stationary modes in part of the default mode network by resorting to high temporal resolution fMRI. While stationarity receives a unique and clear definition, non-stationarity can correspond to a bunch of different situations; for example, non-stationarity might (i) refer to an apparent change over time in the correlation between two regions or (ii) refer to changes in the mean and/or variance in the time course of a functional network.

The wavelet based analysis of scaling proposed here already addresses a number of such situations. The fact that the estimated Hurst coefficient of fMRI time series remains consistently below 1 indicates that fMRI signals at hand here are better modeled as a stationary step process Y rather than as a non-stationary random walk X. Further, wavelet analysis are known to bring robustness against various forms of non-stationarities, such as smooth trends superimposed to data, to mean or variance modulation (c.f. (ii)). The multifractal analysis performed here is thus not impaired by such form of non-stationarities. This leaves open issues such as the presence of oscillations superimposed to scaling. Given that time series are very short, the use of formal stationarity test will lack power and are not likely to reject stationarity. Further, in all the analysis conducted in the present work, no evidence of non-stationarity in the fMRI time series at hand were evidenced. This is in agreement with what has been reported in He (2011) in an fMRI ROI-based analysis. Finally, previous attempts to scale-free analysis of densely sampled fMRI datasets in time (using the EVI sequence; Rabrait et al., 2008) already confirmed the validity of a the stationarity assumption; see Ciuciu et al. (2008).

7. Conclusion

We uncovered multifractal scale-free dynamics of fMRI time series over four octaves (15–125 s) both in functional networks and in artifacts. We then disentangled functional components from artifactual ones in a robust and significant manner by demonstrating that only the former gave rise to significant modulations of the multifractal attributes between rest and task-related activity. Variability in human performance scores also generally exhibits power-law distributions, whose strength (or exponent) is often modulated across conditions and tasks (Holden et al., 2011). This paves the way toward future works devoted to investigating the extent to which behavioral properties are correlated with the change of scale-free dynamics in neuroimaging time series (MEG, fMRI) acquired during multisensory learning (Seitz et al., 2007).

Conflict of Interest Statement

The authors declare that there search was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank the French National Research Agency (ANR) for its financial support to the SCHUBERT (ANR-09-JCJC-0071) young researcher project (2009-13). The authors are also grateful to the anonymous reviewers and the associate editor, Dr. BJ He, for their remarks and criticisms that helped us to improve the manuscript and enlarge the readership. Finally, we would like to warmly thank Dr. V. van Wassenhove for her careful rereading and constructive comments.

Footnotes

1. ^www.vislab.ucl.ac.uk
2. ^www.fil.ion.ucl.ac.uk
3. ^http://scikit-learn.org/stable/
4. ^http://perso.ens-lyon.fr/herwig.wendt/
5. ^The scale and band-specific central frequency are related according to f_j = 3f_e/(42^j).

References

Abry, P., Baraniuk, R., Flandrin, P., Riedi, R., and Veitch, D. (2002). Multiscale network traffic analysis, modeling, and inference using wavelets, multifractals, and cascades. IEEE Signal Process. Mag. 3, 28–46.

CrossRef Full Text

Abry, P., Gonçalvès, P., and Flandrin, P. (1995). Wavelets, Spectrum Estimation and 1/f Processes, Chap. 103. Springer-Verlag, NY: Wavelets and Statistics, Lecture Notes in Statistics.

Abry, P., Veitch, D., and Flandrin, P. (1998). Long-range dependence: revisiting aggregation with wavelets. J. Time Ser. Anal. 19, 253–266.

CrossRef Full Text

Achard, S., Salvador, R., Whitcher, B., Suckling, J., and Bullmore, E. (2006). A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 26, 63–72.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Arneodo, A., Audit, B., Decoster, N., Muzy, J.-F., and Vaillant, C. (2002). “Wavelet-based multifractal formalism: applications to dna sequences, satellite images of the cloud structure and stock market data,” in The Science of Disasters, eds A. Bunde, J. Kropp, and H. J. Schellnhuber (Springer), 27–102.

Bacry, E., Delour, J., and Muzy, J. (2001). Multifractal random walk. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 64, 026103.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bak, P., and Paczuski, M. (1995). Complexity, contingency, and criticality. Proc. Natl. Acad. Sci. U.S.A. 92, 6689–6696.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Barral, J., and Mandelbrot, B. (2002). Multifractal products of cylindrical pulses. Probab. Theor. Relat. Fields 124, 409–430.

CrossRef Full Text

Beckmann, C., and Smith, S. (2004). Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Trans. Med. Imaging 23, 137–152.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Biswal, B., Zerrin Yetkin, F., Haughton, V., and Hyde, J. (1995). Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn. Reson. Med. 34, 537–541.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Britz, J., Van De Ville, D., and Michel, C. M. (2010). BOLD correlates of EEG topography reveal rapid resting-state network dynamics. Neuroimage 52, 1162–1170.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bullmore, E., Long, C., Suckling, J., Fadili, J., Calvert, G., Zelaya, F., Carpenter, T., and Brammer, M. (2001). Colored noise and computational inference in neurophysiological (fMRI) time series analysis: resampling methods in time and wavelet domains. Hum. Brain Mapp. 12, 61–78.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bullmore, E., and Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bullock, T., Mcclune, M., and Enright, J. (2003). Are the electroencephalograms mainly rhythmic? Assessment of periodicity in wide-band time series. Neuroscience 121, 233–252.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buxton, R. B., Uludag, K., Dubowitz, D. J., and Liu, T. T. (2004). Modeling the hemodynamic response to brain activation. 23(Suppl. 1), S220–S233.

Buxton, R. B., Wong, E. C., and Frank, L. R. (1998). Dynamics of blood flow and oxygenation changes during brain activation: the balloon model. Magn. Reson. Med. 39, 855–864.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buzsáki, G. (2006). Rhythms of the Brain. New York: Oxford university Press.

Calhoun, V. D., Adali, T., Pearlson, G. D., and Pekar, J. J. (2001). A method for making group inferences from functional MRI data using independent component analysis. Hum. Brain Mapp. 14, 140–151.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chaari, L., Forbes, F., Vincent, T., Dojat, M., and Ciuciu, P. (2011a). “Variational solution to the joint detection estimation of brain activity in fMRI,” in 14th MICCAI’11, LNCS 6892 (Part II) (Toronto: Springer Verlag), 260–268.

Chaari, L., Pesquet, J.-C., Benazza-Benyahia, A., and Ciuciu, P. (2011b). A wavelet-based regularized reconstruction algorithm for SENSE parallel MRI with applications to neuroimaging. Med. Image Anal. 15, 185–201.

CrossRef Full Text

Chainais, P., Riedi, R., and Abry, P. (2005). On non scale invariant infinitely divisible cascades. IEEE Trans. Inform. Theor. 51, 1063–1083.

CrossRef Full Text

Chialvo, D. R. (2004). Critical brain networks. Physica A 340, 756–765.

CrossRef Full Text

Chialvo, D. R. (2010). Emergent complex neural dynamics. Nat. Phys. 6, 744–750.

CrossRef Full Text

Ciuciu, P., Abry, P., Rabrait, C., and Wendt, H. (2008). Log Wavelet Leaders Cumulant Based Multifractal Analysis of EVI fMRI Time Series: Evidence of Scaling in Ongoing and Evoked Brain Activity. IEEE J. Sel. Top. Signal Process. 2, 929–943.

CrossRef Full Text

Ciuciu, P., Sockeel, S., Vincent, T., and Idier, J. (2009). “Modelling the neurovascular habituation effect on fMRI time series,” in Proceedings of the 34th IEEE International Conference on Acoustic, Speech and Signal Processing, (Taipei: IEEE Conference Publications), 433–436.

Cole, D. M., Smith, S. M., and Beckmann, C. F. (2010). Advances and pitfalls in the analysis and interpretation of resting-state FMRI data. Front. Syst. Neurosci. 4:8.

CrossRef Full Text

Cordes, D., Haughton, V., Arfanakis, K., Carew, J., Turski, P., Moritz, C., Quigley, M., and Meyerand, M. (2001). Frequencies contributing to functional connectivity in the cerebral cortex in “resting-state” data. AJNR Am. J. Neuroradiol. 22, 1326–1333.

Pubmed Abstract | Pubmed Full Text

Dale, A. M. (1999). Optimal experimental design for event-related fMRI. Hum. Brain Mapp. 8, 109–114.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Damoiseaux, J. S., Rombouts, S. A., Barkhof, F., Scheltens, P., Stam, C. J., Smith, S. M., and Beckmann, C. F. (2006). Consistent resting-state networks across healthy subjects. Proc. Natl. Acad. Sci. U.S.A. 103, 13848–13853.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Daubechies, I., Roussos, E., Takerkart, S., Benharrosh, M., Golden, C., D’Ardenne, K., Richter, W., Cohen, J. D., and Haxby, J. (2009). Independent component analysis for brain fmri does not select for independence. Proc. Natl. Acad. Sci. U.S.A. 106, 10415–10422.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dehaene-Lambertz, G., Dehaene, S., Anton, J.-L., Campagne, A., Ciuciu, P., Dehaene, G. P., Denghien, I., Jobert, A., Le Bihan, D., Sigman, M., Pallier, C., and Poline, J.-B. (2006). Functional segregation of cortical language areas by sentence repetition. Hum. Brain Mapp. 27, 360–371.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eguiluz, V. M., Chialvo, D. R., Cecchi, G. A., Baliki, M., and Apkarian, A. V. (2005). Scale-free brain functional networks. Phys. Rev. Lett. 94, 1–4.

CrossRef Full Text

Eke, A., Herman, P., Kocsis, L., and Kozak, L. R. (2002). Fractal characterization of complexity in temporal physiological signals. Physiol. Meas. 23, R1–R38.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fadili, J., and Bullmore, E. (2002). Wavelet-generalized least squares: a new BLU estimator of linear regression models with 1/f errors. Neuroimage 15, 217–232.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fox, M. D., Snyder, A. Z., Vincent, J. L., and Raichle, M. E. (2007). Intrinsic fluctuations within cortical systems account for intertrial variability in human evoked brain responses. Proc. Natl. Acad. Sci. U.S.A. 56, 171–184.

Friston, K., Holmes, A. P., Worlsey, K., Poline, J.-B., Frith, C., and Frackowiak, R. (1995). Statistical parametric maps in functional neuroimaging: a general linear approach. Hum. Brain Mapp. 2, 189–210.

CrossRef Full Text

Glover, G. H. (1999). Deconvolution of impulse response in event-related BOLD fMRI. Neuroimage 9, 416–429.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Greicius, M., Krasnow, B., Reiss, A., and Menon, V. (2003). Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc. Natl. Acad. Sci. U.S.A. 100, 253–258.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

He, B. (2011). Scale-free properties of the functional magnetic resonance imaging signal during rest and task. J. Neurosci. 31, 13786–13795.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

He, B., Zempel, J., Snyder, A., and Raichle, M. (2010). The temporal structures and functional significance of scale-free brain activity. Neuron 66, 353–369.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hebiri, M., and van de Geer, S. (2011). The smooth-lasso and other 1 + 2-penalized methods. Electron. J. Stat. 5, 1184–1226.

CrossRef Full Text

Holden, J. G., Choi, I., Amazeen, P. G., and Van Orden, G. (2011). Fractal 1/f dynamics suggest entanglement of measurement and human performance. J. Exp. Psychol. Hum. Percept. Perform. 37, 935–948.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kiviniemi, V., Kantola, J., Jauhiainen, J., Hyvärinen, A., and Tervonen, O. (2003). Independent component analysis of nondeterministic fMRI signal sources. Neuroimage 19, 253–260.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Laufs, H., Krakow, K., Sterzer, P., Eger, E., Beyerle, A., Salek-Haddadi, A., and Kleinschmidt, A. (2003). Electroencephalographic signatures of attentional and cognitive default modes in spontaneous brain activity fluctuations at rest. Proc. Natl. Acad. Sci. U.S.A. 100, 11053–11058.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Leopold, D., Murayama, Y., and Logothetis, N. (2003). Very slow activity fluctuations in monkey visual cortex: implications for functional brain imaging. Cereb. Cortex 13, 422–433.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Linkenkaer-Hansen, K., Nikouline, V., Palva, J., and Ilmoniemi, R. (2001). Long-range temporal correlations and scaling behavior in human brain oscillations. J. Neurosci. 21, 1370–1377.

Pubmed Abstract | Pubmed Full Text

Liu, H.-L., and Gao, J.-H. (2000). An investigation of the impulse functions for the nonlinear BOLD response in functional MRI. Magn. Reson. Imaging 18, 11053–11058.

CrossRef Full Text

Makni, S., Ciuciu, P., Idier, J., and Poline, J.-B. (2005). Joint detection-estimation of brain activity in functional MRI: a multichannel deconvolution solution. IEEE Trans. Signal Process. 53, 3488–3502.

CrossRef Full Text

Makni, S., Idier, J., Vincent, T., Thirion, B., Dehaene-Lambertz, G., and Ciuciu, P. (2008). A fully Bayesian approach to the parcel-based detection-estimation of brain activity in fMRI. Neuroimage 41, 941–969.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mallat, S. (2009). A Wavelet Tour of Signal Processing: The Sparse Way. Burlington, MA: Academic Press.

Mandelbrot, B., and van Ness, J. (1968). Fractional Brownian motion, fractional noises and applications. SIAM Rev. Soc. Ind. Appl. Math. 10, 422–437.

Mantini, D., Perrucci, M. G., del Gratta, C., Romani, G. L., and Corbetta, M. (2007). Electrophysiological signatures of resting state networks in the human brain. Proc. Natl. Acad. Sci. U.S.A. 104, 13170–13175.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Maxim, V., Sendur, L., Fadili, J., Suckling, J., Gould, R., Howard, R., and Bullmore, E. (2005). Fractional Gaussian noise, functional MRI and Alzheimer’s disease. Neuroimage 25, 141–158.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McKeown, M., Makeig, S., Brown, G., Jung, T., Kindermann, S., Bell, A., and Sejnowski, T. (1998). Analysis of fMRI data by blind separation into independent spatial components. Hum. Brain Mapp. 6, 160–188.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Musso, F., Brinkmeyer, J., Mobascher, A., Warbrick, T., and Winterer, G. (2010). Spontaneous brain activity and EEG microstates. A novel EEG/fMRI analysis approach to explore resting-state networks. Neuroimage 52, 1149–1161.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rabrait, C., Ciuciu, P., Ribès, A., Poupon, C., Leroux, P., Lebon, V., Dehaene-Lambertz, G., Le Bihan, D., and Lethimonnier, F. (2008). High temporal resolution functional MRI using parallel echo volume imaging. J. Magn. Reson. Imaging 27, 744–753.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rosen, B. R., Buckner, R. L., and Dale, A. M. (1998). Event-related functional MRI: past, present and future. Proc. Natl. Acad. Sci. U.S.A. 95, 773–780.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sadaghiani, S., Hesselmann, G., and Kleinschmidt, A. (2009). Distributed and antagonistic contributions of ongoing activity fluctuations to auditory stimulus detection. J. Neurosci. 29, 13410–13417.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Samorodnitsky, G., and Taqqu, M. (1994). Stable Non-Gaussian Random Processes. New York: Chapman and Hall.

Seitz, A., Kim, R., van Wassenhove, V., and Shams, L. (2007). Simultaneous and independent acquisition of multisensory and unisensory associations. Perception 36, 1445–1453.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shimizu, Y., Barth, M., Windischberger, C., Moser, E., and Thurner, S. (2004). Wavelet-based multifractal analysis of fMRI time series. Neuroimage 22, 1195–1202.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M., Mackay, C. E., Filippini, N., Watkins, K. E., Toro, R., Laird, A. R., and Beckmann, C. F. (2009). Correspondence of the brain’s functional architecture during activation and rest. Proc. Natl. Acad. Sci. U.S.A. 106, 13040.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Smith, S. M., Miller, K. L., Moeller, S., Xu, J., Auerbach, E. J., Woolrich, M. W., Beckmann, C. F., Jenkinson, M., Andersson, J., Glasser, M. F., Van Essen, D. C., Feinberg, D. A., Yacoub, E. S., and Ugurbil, K. (2012). Temporally-independent functional modes of spontaneous brain activity. Proc. Natl. Acad. Sci. U.S.A. 109, 3131–3136.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stam, C. J., and de Bruin, E. A. (2004). Scale-free dynamics of global functional connectivity in the human brain. Hum. Brain Mapp. 22, 97–109.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thurner, S., Windischberger, C., Moser, E., Walla, P., and Barth, M. (2003). Scaling laws and persistence in human brain activity. Physica A 326, 511–521.

CrossRef Full Text

Van de Ville, D., Britz, J., and Michel, C. M. (2010). EEG microstate sequences in healthy humans at rest reveal scale-free dynamics. Proc. Natl. Acad. Sci. U.S.A. 107, 18179–18184.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Varoquaux, G., Keller, M., Poline, J., Ciuciu, P., and Thirion, B. (2010a). “ICA-based sparse features recovery from fMRI datasets,” in Proceedings of the 7th IEEE International Symposium on Biomedical Imaging, Rotterdam, 1177–1180.

Varoquaux, G., Sadaghiani, S., Pinel, P., Kleinschmidt, A., Poline, J.-B., and Thirion, B. (2010b). A group model for stable multi-subject ICA on fMRI datasets. Neuroimage 51, 288–299.

CrossRef Full Text

Veitch, D., and Abry, P. (2001). A statistical test for the time constancy of scaling exponents. IEEE Trans. Signal Process. 49, 2325–2334.

CrossRef Full Text

Vincent, T., Risser, L., and Ciuciu, P. (2010). Spatially adaptive mixture modeling for analysis of within-subject fMRI time series. IEEE Trans. Med. Imaging 29, 1059–1074.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wendt, H., Abry, P., and Jaffard, S. (2007). Bootstrap for empirical multifractal analysis. IEEE Signal Process. Mag. 24, 38–48.

CrossRef Full Text

Wink, A.-M., Bullmore, E., Barnes, A., Bernard, F., and Suckling, J. (2008). Monofractal and multifractal dynamics of low frequency endogenous brain oscillations in functional MRI. Hum. Brain Mapp. 29, 791–801.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yuan, H., Zotev, V., Phillips, R., Drevets, W. C., and Bodurka, J. (2012). Spatiotemporal dynamics of the brain at rest – exploring EEG microstates as electrophysiological signatures of BOLD resting state networks. Neuroimage 60, 2062–2072.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zarahn, E., Aguirre, G. K., and D’Esposito, M. (1997). Empirical analysis of BOLD fMRI statistics. I. Spatially unsmoothed data collected under null-hypothesis conditions. Neuroimage 5, 179–197.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zemanová, L., Zhou, C., and Kurths, J. (2006). Structural and functional clusters of complex brain networks. Physica D 224, 202–212.

CrossRef Full Text

Zilber, N., Ciuciu, P., Abry, P., and van Wassenhove, V. (2012). “Modulation of scale-free properties of brain activity in MEG,” in Proceedings of the 9th IEEE International Symposium on Biomedical Imaging, Barcelona, 1531–1534.