- 1Division of Biomedical Engineering, Department of Human Biology, University of Cape Town, Cape Town, South Africa
- 2Department of Surgery, University of California, San Francisco, San Francisco, CA, United States
- 3Bioengineering Science Research Group, Engineering Sciences, Faculty of Engineering and the Environment, University of Southampton, Southampton, United Kingdom
- 4Department of Medicine, Brigham and Women's Hospital, Boston, MA, United States
- 5Cardiovascular Research Foundation, New York, NY, United States
Predictive computation models offer the potential to uncover the mechanisms of treatments whose actions cannot be easily determined by experimental or imaging techniques. This is particularly relevant for investigating left ventricular mechanical assistance, a therapy for end-stage heart failure, which is increasingly used as more than just a bridge-to-transplant therapy. The high incidence of right ventricular failure following left ventricular assistance reflects an undesired consequence of treatment, which has been hypothesized to be related to the mechanical interdependence between the two ventricles. To investigate the implication of this interdependence specifically in the setting of left ventricular assistance device (LVAD) support, we introduce a patient-specific finite-element model of dilated chronic heart failure. The model geometry and material parameters were calibrated using patient-specific clinical data, producing a mechanical surrogate of the failing in vivo heart that models its dynamic strain and stress throughout the cardiac cycle. The model of the heart was coupled to lumped-parameter circulatory systems to simulate realistic ventricular loading conditions. Finally, the impact of ventricular assistance was investigated by incorporating a pump with pressure-flow characteristics of an LVAD (HeartMate II™ operating between 8 and 12 k RPM) in parallel to the left ventricle. This allowed us to investigate the mechanical impact of acute left ventricular assistance at multiple operating-speeds on right ventricular mechanics and septal wall motion. Our findings show that left ventricular assistance reduces myofiber stress in the left ventricle and, to a lesser extent, right ventricle free wall, while increasing leftward septal-shift with increased operating-speeds. These effects were achieved with secondary, potentially negative effects on the interventricular septum which showed that support from LVADs, introduces unnatural bending of the septum and with it, increased localized stress regions. Left ventricular assistance unloads the left ventricle significantly and shifts the right ventricular pressure-volume-loop toward larger volumes and higher pressures; a consequence of left-to-right ventricular interactions and a leftward septal shift. The methods and results described in the present study are a meaningful advancement of computational efforts to investigate heart-failure therapies in silico and illustrate the potential of computational models to aid understanding of complex mechanical and hemodynamic effects of new therapies.
Introduction
In view of the growing number and dismal prognosis of patients with end-stage heart failure, interest in emerging mechanical therapies such as left ventricular assistance devices (LVADs) has intensified. LVADs are used as a bridge to transplant, bridge to decision, destination therapy and, increasingly, as a bridge to recovery. The latter is fueled by the nearly ubiquitous demonstration that left ventricular (LV) unloading provided by LVADs causes reverse remodeling and, in a small percentage of patients, induces myocardial recovery to the point where devices can be explanted (Wohlschlaeger et al., 2005; Birks et al., 2006; Burkhoff et al., 2006; Lampropulos et al., 2014; McIlvennan et al., 2014; Topkara et al., 2016). The introduction of smaller, partial (i.e., low) flow LVADs designed to be implanted at an earlier stage of disease severity has broadened the potential applicability to a currently underserved and large patient population (Mohite et al., 2014; Sabashnikov et al., 2014; Sack et al., 2016).
Among the remaining adverse effects that impact negatively on long-term morbidity and mortality of LVAD patients is right heart failure (Grant et al., 2012; Hayek et al., 2014; Rich et al., 2017). Ten to thirty percent of LVAD patients develop right ventricular (RV) failure (Kavarana et al., 2002; Dang et al., 2006; Kormos et al., 2010; Baumwol et al., 2011; Argiriou et al., 2014) requiring either prolonged use of inotropic therapy or the need for temporary or long-term RV mechanical circulatory support. RV failure is associated with elevated central venous pressure (CVP), which adversely affects renal, hepatic, and gastorintestinal function, and results in LV underfilling that reduces LVAD flow.
LVAD support influences RV function in several ways; some beneficial and some detrimental. On the one hand, LVAD-induced unloading leads directly to a reduction of pulmonary capillary wedge pressure. This pressure accounts for a large part of the mechanical afterload on the RV so its reduction can favorably impact the ability of the RV to eject blood and maintain a normal CVP. On the other hand, LVADs increase systemic blood flow, which can cause a volume overload on the RV. Additionally, LV unloading can have a detrimental effect on RV function due to interventricular interactions (Kavarana et al., 2002; Küçüker et al., 2004; Dang et al., 2006; Maeder et al., 2009). This latter effect is a consequence of the interdependence of RV and LV pressure generation mediated by the interventricular septum. It is well-known that as much as 30% of RV pressure generation is due to LV pressure generation and that the position of the interventricular septum can influence RV function (Slater et al., 1997). Thus, LVADs can impact RV function because the RV and LV are two pumps working functionally in series within the circulation, are anatomically arranged in parallel with each other, and share a common wall.
Although the potential implications of ventricular interactions on RV function during LVAD support are well-appreciated, no study has yet proven, in any setting, that LV unloading and septal shift can actually lead to RV failure. This is because it is physically impossible to separate the hemodynamic effects of the serial and parallel contributions of RV-LV interactions in a patient or even in experimental preclinical studies.
Computational modeling is well-suited to investigate and elucidate the individual contributions of these primary hemodynamic factors. However, research efforts have been impeded by the substantial complexities involved in coupling a simulated circulatory system with geometrically realistic models of the heart. Only recently have computational models had the necessary sophistication to model this coupled behavior (e.g., Kerckhoffs et al., 2007; Lim et al., 2012; Baillargeon et al., 2014; Sack et al., 2016). Consequently, very limited research has been undertaken to explore the effect of LVAD function on ventricular mechanics, and no study has investigated the important issue of right heart failure. Such research has significant practical implications since current guidelines for the care of LVAD patients recommend that LVAD speeds be adjusted to ensure that the interventricular septum is not leftward shifted. This recommendation is based on expert opinion, not on any physiological or clinical evidence.
We previously created a model of a failing LV supported with partial LV assistance in a four-chamber generic heart model (Sack et al., 2016). In the present study we modify this representation to include a biventricular model of a patient with dilated cardiomyopathy. LVAD therapy is then simulated using realistic pressure-flow relations of a commonly used LVAD, allowing us to capture assisted flow for device operation over a broad range of rotational speeds (RPMs). By analyzing the resulting changes in LV pressure generation, total blood flow, myocardial stress, and septal wall motion, we quantified the relative influences of these factors on RV function. The specific purpose of this paper is to describe the mathematical methods and general behavior of this model of the failing heart during different degrees of LVAD-induced LV unloading.
Methods
Our cardiac modeling methods have been described extensively in previous studies (Baillargeon et al., 2014, 2015; Sack et al., 2016). Here, we present a brief overview of these established methods, with an additional focus on recent developments and methods that are critical for the current study.
Patient Data
In vivo cardiac magnetic resonance (MR) data sets were obtained as part of the Aliskiren Study in Post-MI Patients to Reduce Remodeling (ASPIRE) trial (Solomon et al., 2011). Individual patients provided informed consent and anonymized data were sent to a core laboratory for analysis.
Geometric Considerations
For one patient with dilated cardiomyopathy, the MR data sets (1.25 × 1.24 × 10 mm spatial resolution) were imported and processed in Simpleware ScanIP (Synopsys, Mountain View, USA). Geometrically detailed segmentations of the LV and RV were created relying on a combination of well-established techniques, including region growing, level-set thresholding, and morphological smoothing (Vadakkumpadan et al., 2010; Setarehdan and Singh, 2012). The biventricular structure was truncated at the base and illustrations of the image data, segmentation, and Finite Element (FE) mesh construction are presented in Figure 1.
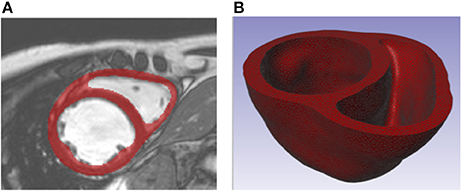
Figure 1. (A) Short axis MR image of patient with dilated chronic heart failure overlaid with the segmentation of the myocardium. (B) Truncated biventricular geometry extracted from segmentation and meshed using tetrahedral elements.
We introduced prolate spheroidal coordinates (Lombaert et al., 2012; Toussaint et al., 2013) into the image-coordinate space aligned with the long axis of the LV. The prolate spheroidal coordinates were used to describe myofiber orientations using a rule-based approach. Based on previous computational studies (Genet et al., 2014), histological studies (Streeter et al., 1969), and diffusion tensor MR studies (Lombaert et al., 2011), we assumed that the myofiber orientation could be represented through a linearly varying helix angle from −60° on the epicardium to +60° on the endocardium. This was assigned to each material point in the model through a custom MATLAB (The MathWorks, Inc., Natick, Massachusetts, United States) script that specifies myofiber orientation by rotating the local circumferential unit vector by the helix angle in the circumferential-longitudinal plane. The same fiber description from endocardium to epicardium was applied to the LV free wall, septal wall, and RV free wall as other studies typically assume (Goktepe et al., 2011; Wenk et al., 2012; Wong and Kuhl, 2014).
While multiple models and explanations of sheet structure exist (Gilbert et al., 2007), for simplicity we define the sheet directions to be normal with epicardial and endocardial surfaces (i.e., normal with the circumferential-longitudinal plane in which the fiber direction resides). This assumption is relatively reasonable when considering the macroscopically visible cleavage planes observed experimentally (LeGrice et al., 2001; Chen et al., 2005) and is in line with other computational studies (Bovendeerd et al., 1994; Goktepe et al., 2011).
Regarding boundary conditions, the base of the biventricular structure (plane of truncation) was fixed in the longitudinal direction. Furthermore, the nodes on the endocardial annulus were constrained by coupling the average translation and rotation of the nodes to a fixed point in space located at the annulus center. This prevents rigid body rotation while allowing the annulus relative motion to inflate and contract during the cardiac cycle.
Constitutive Law and Parameter Estimation
The passive material response of the cardiac tissue uses an anisotropic hyperelastic formulation proposed by Holzapfel and Ogden (Holzapfel and Ogden, 2009). The isochoric and volumetric responses are governed by the strain energy potentials in Equations (1–2)
Equation (1) is defined through eight material parameters a, b, af, bf, as, bs, afs, bfs and four strain invariants I1, I4f, I4s, and I8fs. These strain invariants are derived from the isochoric right Cauchy-Green tensor,
where F is the deformation gradient, J is the determinant of the deformation gradient, J = det(F) and is the isochoric part of the deformation gradient such that
The expression of these strain invariants can now be defined as:
Where f0 and s0 are orthogonal vectors in the fiber and sheet direction in the reference configuration. Equation (2) is defined through J and a penalty term D, which is a multiple of the bulk modulus (D = 2/K). For deformation that perfectly preserves volume, J = 1.
This passive material model, Equations (1–2), ensures that the material exhibits the well-documented exponential and anisotropic response to strain (Demer and Yin, 1983; Hunter et al., 1998; Dokos et al., 2002) while enforcing incompressibility.
The description of our time-varying elastance model of active force development (Guccione and McCulloch, 1993) is specified as:
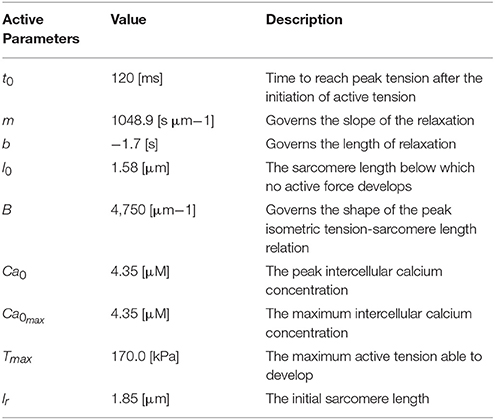
where Tmax, the maximum allowable active tension, is multiplied with a term governing the calcium concentration, and a term governing the timing of contraction. Both terms depend on sarcomere length l, which in turn depends on the strain in the fiber direction. The active tension generated from this representation conforms well with experimental studies (Guccione and McCulloch, 1993) and captures length-dependent effects such as Frank Starling's Law (Holmes et al., 2002; Solaro, 2007). Further detail of the active tension law is provided in the Appendix for the interested reader.
We consider the total Cauchy stress to be an additive contribution of passive and active components. The passive Cauchy stress, σp, is given by σp = 2J−1 F(∂Ψ/∂C)FT. We consider an active contractile stress in the fiber direction, resulting in a total Cauchy stress in the fiber direction, (i.e., myofiber stress) by combining this with to the passive stress state in this direction (σpf):
Biaxial investigations on actively contracting rabbit myocardium revealed significant stress development in the cross-fiber direction that could not be completely attributed to myofiber dispersion or deformation effects (Lin and Yin, 1998). This has motivated computational efforts to consider a proportion of the active stress developed in the myofiber direction to be transferred onto the stress in the sheet direction by a scalar ns ∈ (0, 1), such that the total Cauchy stress in the sheet direction is:
Material Parameter Estimation
Full records of the patient who was used in our heart model were unavailable; therefore, we relied on clinical input to provide representative functional targets for volume and pressures. To this end, the dilated failing heart used in this study was assumed to have an end-diastolic volume (EDV) of 254 ml and an end-systolic volume (ESV) of 224 ml. End-diastolic pressure (EDP) and end-systolic pressure (ESP) were assumed to be 23 and 86 mmHg, respectively. These classify the patient with a severely dilated LV (>200 ml), elevated EDP (>16 mmHg, Paulus et al., 2007 and 23 mmHg, Mielniczuk et al., 2007) and severely reduced ejection fraction (EF = 1− ESV/EDV = 12%) i.e., <35% (McMurray et al., 2012; Mann et al., 2014).
The material parameters a, b, af, bf, as, bs, afs, bfs were found through optimization techniques relying on two stages of determination. Initial values were determined from the calibration of normal myocardium specimen samples to experimental tri-axial shear data of human myocardium (Sommer et al., 2015). Calibration was performed using ABAQUS as the forward solver, whereby in silico cubes of myocardium with dimensions matching those of the study of interest were meshed into a uniform 27 linear hex-element mesh. Shearing was executed by specifying the translational displacement of a specified cube face, while enforcing zero displacement boundary conditions on the opposite cube face. The optimization was performed in MATLAB using a non-linear least-square optimization routine.
To capture patient-specific material parameters of our failing human heart, a second stage of “scaling” was needed. Here, linear (a, af, as, and afs) and exponential (b, bf, bs, bfs) terms were subject to uniform scaling by parameters A and B, a scalar and an exponential multiplier, respectively. These values were found by minimizing the error between the in silico diastolic PV course resulting from loading the LV of the FE model to the analytical Klotz curve (Klotz et al., 2006), starting from the unloaded LV volume V0 until the EDV was reached at the specified end-diastolic pressure (EDP). Material parameters were calibrated using ABAQUS as the forward solver, and an in-house PYTHON script containing the sequential least squares programming (SLSQP) optimization algorithm (Jones et al., 2001). These passive parameters expressed in Equations (1) were identified by minimizing the error between the in silico diastolic PV curve and the analytical Klotz curve.
Once passive parameters were found, the active parameter TMAX was identified by minimizing the error between predicted and specified stroke volume and assuming that 25% of active tension was transferred in the sheet direction (i.e., ns = 0.25). Calibrated material parameters are presented in Table 1.
Coupled Circulatory System and LVAD Support
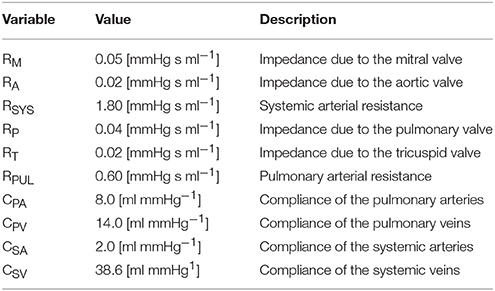
The FE model of the heart was coupled to lumped models of the pulmonary and systemic circulatory systems used in our previous study (Sack et al., 2016). A small modification was introduced to separate the pulmonary circuit into venous and arterial components. Collectively, this captures fluid exchanges between the systemic circuit, the heart and the pulmonary circuit. A schematic diagram outlining the fluid connections between the patient-specific biventricular structure and the lumped circulatory system with the LVAD is presented in Figure 2; all parameters relating to the lumped model are presented in the Appendix in Table A2.
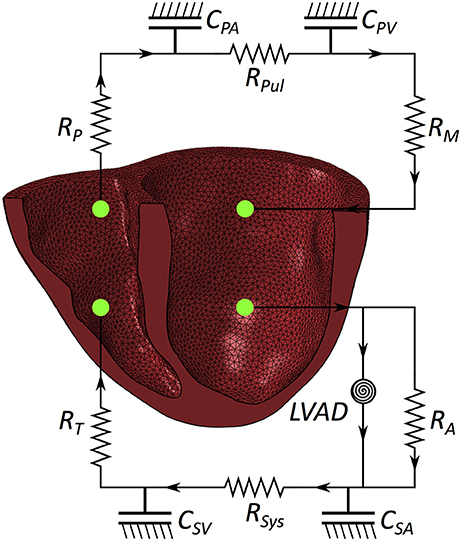
Figure 2. Schematic of the patient-specific biventricular structure coupled with the circulatory system and LVAD. RM is mitral valve resistance, RA is aortic valve resistance, CSA is systemic arterial compliance, RSYS is systemic arterial resistance, CSV is systemic venous compliance, RT is tricuspid valve resistance, RP is pulmonary valve resistance, CPA is pulmonary arterial compliance, RPUL is pulmonary arterial resistance, CPV is pulmonary venous compliance.
Two further changes are present in the model used in this study compared with the model used in our prior study (Sack et al., 2016). First, the mechanical heart is replaced with a patient-specific biventricular structure (as detailed in previous sections).
The second change is that a far more complex and realistic representation of LVAD flow is included. We simulated the effect of a Heartmate II ™ LVAD device operating at device speeds of 8, 9, 10, 11, and 12 k RPM. Each speed has a flow rate profile that is dependent on the pressure difference (dP) between the inflow and outflow cavities to which the pump connects. Experimental datasets specifying flow rates for a range of dP between 0 and 200 mmHg at discrete intervals of 2 mmHg were incorporated in the simulated flow profile for each operating speed. Flow rates were interpolated and extrapolated linearly between discrete values to account for a continuous flow-rate description for any dP the model may encounter. This is illustrated in Figure 3 for three LVAD operating speeds (8, 10, and 12 k RPM).
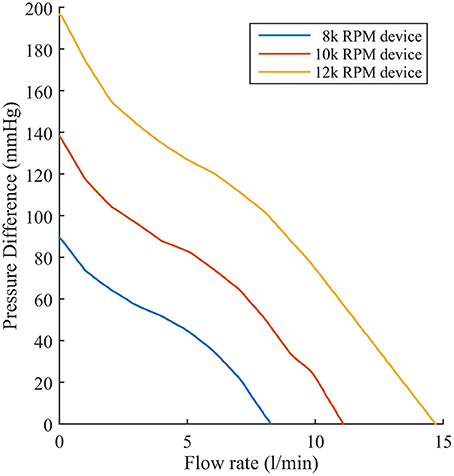
Figure 3. Experimentally recorded flow rates of the Heartmate II™ LVAD operating at 8, 10, and 12 k RPM as a function of pressure difference.
Experimental Design
For this study, cardiac function was simulated for a patient with chronic heart failure. LVAD therapy was introduced by simulating the effect of a HeartMate II operating at speeds ranging from 8–12 k RPM in 1 k RPM increments. Pressure and volume measurements of the ventricular chambers were recorded and compared to quantify ventricular loading and output performance. Myofiber stress was recorded and quantified for each simulation and compared to analyze the efficacy of treatment in the LV and potential harm of treatment to the septal wall and RV. Stress data in this study are expressed as mean ± standard of deviation (SD) unless otherwise stated. The differences between results were evaluated using analysis of variance (ANOVA) with differences considered statistically significant with p < 0.05. Time points in the cardiac cycle, such as end diastole, were defined for the untreated case and compared to the time points in simulations with LVAD support. End diastole and end systole, for each ventricle, were identified from the pressure-volume curves as the points immediately preceding isovolumetric contraction and relaxation respectively.
Results
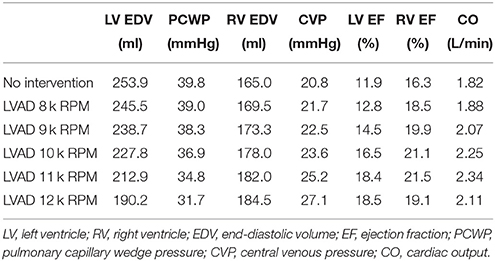
The model of chronic heart failure without LVAD support represents a critical patient with advanced heart failure. The LV is substantially overloaded at end diastole with an EDV of 254 ml, an EDP of 23 mmHg, and an LV EF of 12%. The support introduced through LVAD operation improves these functional metrics: the diastolic loading of the LV decreases and the LV EF increases as the RPM of the device increases (i.e., increased support), as shown in Table 2. These LV benefits occur simultaneously with increases in the RV loading, seen by the rise in RV EDV (Table 2) and EDP which increases from 20.8 mmHg (untreated) to 27.9 mmHg (LVAD operating at 12 k RPM), as the mean central venous pressure rises (Table 2). Although the RV EF initially increases with LVAD operation, it reaches a peak functional value with LVAD support at 11 k RPM, after which it starts to decline.
These functional changes are also captured in pressure-volume loops of each chamber, as shown in Figure 4. These curves illustrate the reduction of LV EDP, which ranged from 17.9 to 0.5 mmHg, with the simulated LVAD operating between 8 and 12 k RPM. As LVAD flow increases, the LV PV-loop becomes more triangular, indicative of the device's effect during the normally isovolumetric periods of the cardiac cycle. As the loop shifted leftward toward lower volumes, it tracked down a single end-diastolic pressure-volume relationship. As the LV was increasingly unloaded by increases in LVAD speed, the RV PV-loops shifted rightward toward higher volumes and pressures. In addition, the systolic portion of the loops also shifts rightward and peak RV pressure also decreases. These shifts are a consequence of the reductions of LV pressure during both diastole and systole. It is noteworthy that LVAD speeds of up to 12 k increased RV EDP, resulted in excessive reductions of LV volume and, in the case of the 12 k RPM simulation, reduced cardiac output: three distinctive characteristics of right heart failure. Additional pressure tracings of the LV, the systemic arteries (analogous of aortic pressure), the RV and the pulmonary arteries are provided in Figure 5 for two heartbeats.
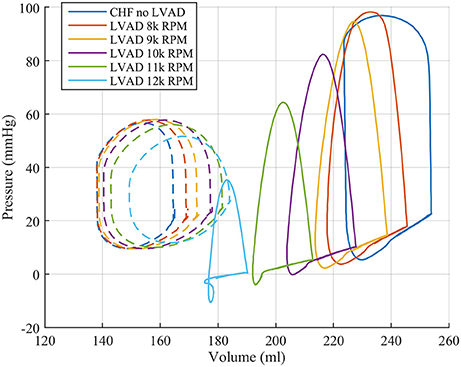
Figure 4. Pressure volume loops for the LV (solid lines) and RV (dashed lines) from the FE model study.
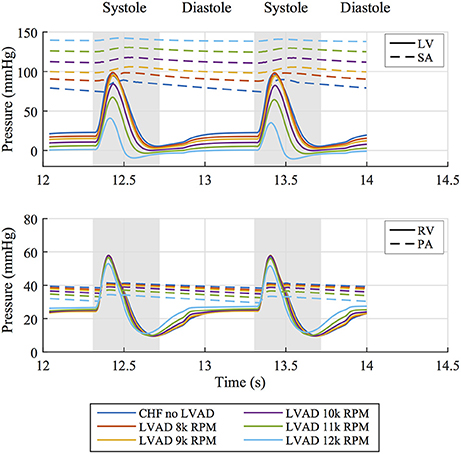
Figure 5. (Top) Pressure tracings of the LV and systemic arterial compliance (SA) over two cardiac cycles for all simulated cases. (Bottom) Pressure tracings of the RV and pulmonary arterial compliance (PA) over two cardiac cycles for all simulated cases.
The interventricular septum is in constant motion throughout the cardiac cycle. We tracked the midpoint motion at the base of the septal wall and quantified the leftward shift of this point in reference to the line through the anterior and posterior LV-septal-RV junctions. This measure of septal shift is positive when the septal wall bulges into the LV cavity, zero when the septal wall forms a straight line and negative when the wall bulges into the RV cavity. A time course of this measure over two heartbeats, shown in Figure 6 alongside the pressure difference between the ventricles, reveals that peak leftward shift occurs during diastolic function and goes from being concave in the unsupported case to convex in the case of simulated LVAD support >10 k RPM. Rightward septal shift coincides with peak systole (and minimum trans-septal pressure) and is driven by the contractile forces with the heart returning the shape to a more “normal” configuration. Septal shift is also shown by plotting displacements in the dynamic beating ventricles of the patient with no intervention and LVAD operating speeds of 8, 10, and 12 k RPM in the Supplementary Animations S1, S2.
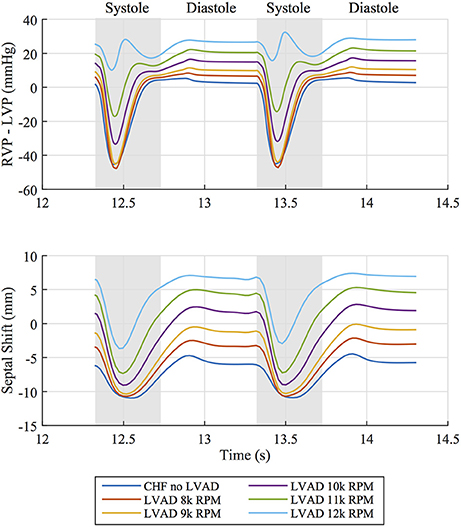
Figure 6. (Top) Pressure difference between right ventricular pressure (RVP) and left ventricular pressure (LVP) over two cardiac cycles for all simulated cases. (Bottom) Corresponding leftward septal shift over the same time period. Diastolic and systolic portions of the cardiac cycle are labeled.
The volumetric-averaged myofiber stress (along the local muscle fiber direction) was calculated at end diastole and end systole, and the mean ± SD are presented in Table 3 for the RV free wall, the septal wall, and LV free wall separately. Compared to the unsupported CHF case, LV mean myofiber stress is reduced by LVAD support by an order of magnitude at end diastole and end systole (p < 0.001). The improvements to RV mean myofiber stress were less substantial, with both end diastole and end systole myofiber stress in the RV remaining relatively unaffected.
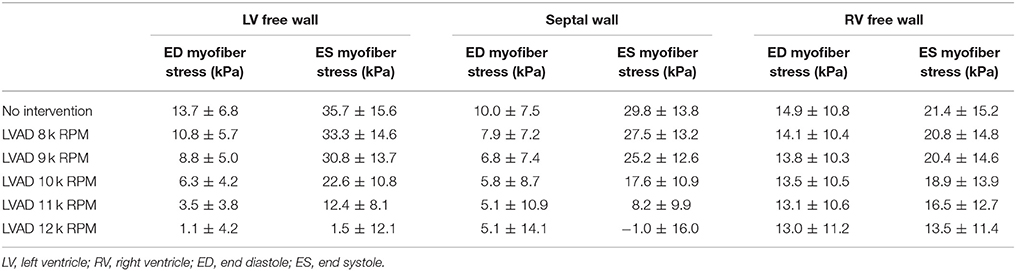
Table 3. LV and RV myofiber stress results (mean ± SD) at end diastole and end systole (p < 0.001 for comparisons within each column).
Myofiber stress distributions and overall geometry are presented in Figure 7 at end diastole to illustrate stresses and the deformed configuration corresponding to maximum volume loading. These stress distributions reveal geometrically relevant stress characteristics that evolve with increased LVAD operation. The large stress values seen on the LV endocardium (excluding the septal wall) due to volumetric loading at end diastole decrease with LVAD support and appear to dissipate with maximum LVAD operation of 12 k RPM. However, a localized region of tensile (i.e., positive) myofiber stress appears and grows with increased LVAD support on the LV side of the septal wall near the base (Figure 7). Additionally, LVAD operation promotes a localized region of compressive (i.e., negative) myofiber stress on the RV side of the septal wall in the same region.
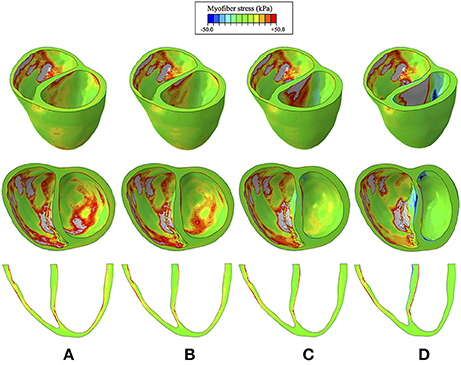
Figure 7. Myofiber stress distributions at end diastole for the cases of (A) CHF with no LVAD support, (B) CHF with LVAD support running at 8 k RPM, (C), CHF with LVAD support running at 10 k RPM, (D) CHF with LVAD support running at 12 k RPM. Top row reveals a predominantly long-axis view of the biventricular structure, the middle row reveals a short-axis view, exposing the ventricular cavities, and the bottom row reveals a long-axis cut plane that bisects the ventricles. Light gray regions correspond to extreme stress values that exceed the threshold of +50 kPa.
A quantitative analysis of myofiber stress distribution in a segmented region of the vulnerable septal wall is presented in Figure 8. Initially (i.e., chronic heart failure with no LVAD support) the myofiber stresses in this region display a mostly Gaussian distribution. At 10 k RPM the myofiber stress distributions in this region begin to display bimodal peaks, which become more exaggerated with increased LVAD support.
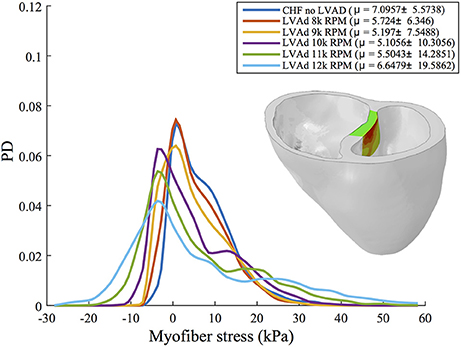
Figure 8. Interpolated histograms of myofiber stress distributions in the region of maximum septal shift (colored region of inlaid illustration) for all simulations of CHF and LVAD operation. Mean ± SD values are given in the legend for each case. Histograms are normalized by probability density (PD), i.e., the area under each distribution sums to 1.
Discussion
We describe a geometrically and physically realistic model of an end-stage failing heart with representative systolic and diastolic myocardial material properties coupled to lumped parameter Windkessel-like models of the pulmonary and systemic circulations. This permitted study of heart mechanics and dynamics under realistic loading conditions i.e., pre-load and afterload of each ventricle. Finally, we simulated the effects of LVAD support by using experimentally recorded pressure-flow characteristics of a commonly used device. The present model represents a significant improvement over our prior modeling efforts (Sack et al., 2016) in that the effects of an LVAD on chronic rather than acute left heart failure were quantified using a patient-specific biventricular geometry and device-specific pressure-flow characteristics, rather than constant flow rates.
This improved model reproduced a wide range of expected, fundamental behaviors of the LV and RV. There were LVAD speed-dependent reductions in LV filling pressure, pressure generation, and a progressive transformation of the PV-loop from trapezoidal shape to triangular shape. This shape transformation is because LVADs are continuous flow pumps that remove volume from the LV throughout the cardiac cycle, thus eliminating isovolumic contraction phases (Morley et al., 2007; Wang et al., 2014). With LVAD-induced LV unloading, the RV PV-loop shifted toward larger volumes and higher pressures, indicating that the RV end-diastolic pressure-volume loop was shifting rightward; this is indicative of increased RV diastolic compliance and is a consequence of RV-LV interactions and a leftward septal shift. RV systolic pressure also decreased, also a consequence of RV-LV interactions. In the case of high LVAD operational speed, a secondary “Figure 8” shaped loop is visible at the end of relaxation and the start of passive filling. This ultimately results from the combined effects of RV-LV interactions, pressure-sensitive LVAD operation and the LV being unloaded at a faster rate than it being filled. The degree of unloading that would cause this would likely initiate ventricular arrhythmias in the clinical environment, so data surrounding this type of phenomena is very rare. LVAD speed-dependent septal shifts were clearly evident in the 3-dimensional images. Those images match changes in echocardiographs obtained from LVAD patients at high LVAD speeds, particular in those with right heart failure. For example, Figure 9A shows a patient with low RPMs and normal, right-shifted interventricular septum (traced out by the red line) compared to Figure 9B showing a patient with markedly left-shifted septum. Note the remarkable similarity of these images to those presented in the lower panels of Figures 7A,D.
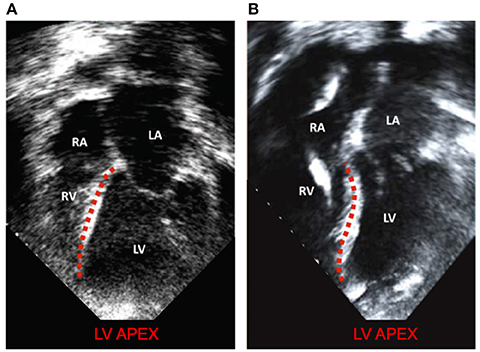
Figure 9. Modified with permission from Topilsky et al. (2011). (A) a patient with low RPMs and normal, right shifted interventricular septum (traced out by the red line) compared to (B) a patient with markedly left-shifted septum (traced out by the red line). LV, left ventricle; RV, right ventricle; LA, left atrium; RA: right atrium.
We found that LVAD support reduced estimates of global LV and, to a lesser extent, septal wall myocardial stresses. However, these improvements were achieved with secondary negative effects on the RV, which experienced a rightward shift toward higher EDPs and larger EDVs with LVAD support, which kept RV stresses high. Additional, potentially negative, effects were seen on the interventricular septum, which showed that LVAD support introduces unnatural bending of the septum with increased localized myofiber stresses. Such deformations are similar to those of a beam undergoing bending deformation, which introduces LVAD speed-dependent regions of tensile stress on the LV side and regions of compressive stress on the RV side of the septal wall (Figure 7). In general, myocardial properties (genetic expression, molecular makeup, structure and function) are modified in response to chronic stresses. However, it is unknown if these abnormal stresses on the myocardium of the septum have any implications for myocardial function as abnormal stresses may relate to the development of right heart failure in the long term.
Over the last few decades, numerical and analytical models of circulatory flow and ventricular assistance have been introduced (e.g., Levin et al., 1995; Vollkron et al., 2002; Morley et al., 2007; Lim et al., 2010). Many of these models represent heart function, without including geometric considerations (often referred to as zero-dimensional models). Despite those limitations, the basic findings derived from such models have generally been in agreement with the present findings. While some research has incorporated functionally realistic ventricular assistance devices, these studies also ignore geometric effects on the heart and, in particular, have not considered ventricular interactions or shifts of septal position (Donahue et al., 2009; Long et al., 2013; Chiu et al., 2014; Selishchev and Telyshev, 2016).
FE modeling enables estimation of regional stress that cannot be measured in patients using alternative techniques. This allows identification of the LVAD speed at which bending and abnormal stresses emerge in the septum. If patient-specific geometries could be incorporated more easily, such modeling could provide interesting metrics with clinical applicability for understanding and perhaps predicting the impact of LVAD speed on septal mechanics.
One goal of developing the present model is to study the degree to which RV-LV interactions and septal shift plays a role in the development of RV failure following LVAD implantation. Many other factors can contribute to the development of RF failure, such as RV myocardial dysfunction, increased pulmonary vascular resistance and volume overload. The impact of those factors, and even RV-LV interactions, are readily ascertained through simpler zero-dimension modeling of the cardiovascular system (HARVI, 2014a,b; Burkhoff et al., 2017). However, it is only through finite element analysis (FEA) that the question of the impact of septal shifts can be determined. For example, although in the present example we demonstrated marked septal shifts at high LVAD speeds accompanied by increased RV EDPs, there were balanced shifts of systolic and diastolic volumes such that cardiac output was mostly preserved, with only minor impact on RV systolic pressure. Thus, in this example, marked septal shift resulted in RV dysfunction and not full-blown failure. However, we have only studied one set of conditions (i.e., one starting RV geometry, one level of myocardial contractility, and one value of pulmonary vascular resistance). A thorough evaluation over a range of conditions and a sensitivity analysis on parameter values is required to fully explore this important question.
Limitations
The model described in the present study is an improvement over prior models, but several limitations exist. First, the model does not contain atria. Since LV filling dynamics are impacted by atrial contraction, this could have an effect on the diastolic portion of the PV-loop and time-course of change of septal motion. Second, the models of the vascular system are adequate to provide the basic aspects of ventricular afterload and yielded realistic PV-loop shapes, but more sophisticated models that incorporate fluid-structure interactions, the valve geometries and wave reflections would be more accurate. Third, a sensitivity analysis was not performed to quantify the relative impact of material parameters to model results. This was viewed as beyond the scope of this research but should be performed (alongside rigorous validation studies) before computational models contribute to clinical decision making. We intend to address this in our future work. Finally, as noted, we studied only one combination of myocardial properties, RV and LV and vascular properties. Every patient is unique and conclusions arrived at are not generalizable.
Summary
We described results of an FEA model based on the anatomy of an end-stage failing heart coupled to systemic and pulmonary vascular systems and an LVAD. We demonstrated the anatomic and hemodynamic impact of increasing LVAD speed on global pump function, regional stress distributions, and septal position. Realistic results were obtained in terms of ventricular deformation and PV loops. We demonstrated the expected findings that RV systolic and diastolic properties are affected by LVAD-induced unloading of the LV, resulting in RV dysfunction at high LVAD operating speeds. Having established the foundation of this model, we are poised to address the important question of whether and under what conditions, septal shift, and reduced LV pressure generation are important mechanisms of the development of RV failure following LVAD implantation. The specific conditions studied in the present model demonstrate that septal shifting alone is not sufficient to induce RV failure. Simulations spanning a wide range of conditions are required to fully address this important question.
Beyond this, the methods are generalizable in the sense that patient-specific geometries and vascular properties can be incorporated into the model, with the ultimate purpose of gaining insights into LVAD effects in vivo. Such an approach has the potential for predicting hemodynamics, such as the degree of unloading achievable, and the risk of developing right heart failure following LVAD implantation. Advances in patient-specific modeling in other fields of cardiology are already having an impact on clinical practice and it is anticipated that new applications will emerge, especially in the field of heart failure. The methods and results described in the present study have potential to meaningfully advance such efforts.
Ethics Statement
Patient cardiac MR data was obtained as part of the Aliskiren Study in Post-MI Patients to Reduce Remodeling (ASPIRE) trial. The study protocol was written by members of the executive committee of the trial and was approved by the ethics committees at each participating site. Individual patients provided written informed consent in accordance with the Declaration of Helsinki and anonymized data were sent to a core laboratory for analysis.
Author Contributions
KS, TF, DB, and JG were involved in the conception and design of study. KS created the computational models. Acquisition of various data critical to model creation was performed by SS and DB. The analysis and interpretation of modeling results was performed by all authors. KS wrote the first draft of the manuscript. DB and JG wrote sections of the manuscript. All authors contributed to manuscript revision, read and approved the submitted version.
Funding
This work was supported by NIH grants R01-HL-077921, R01-HL-118627, and U01-HL-119578. Further financial support was provided by the Oppenheimer Memorial Trust (OMT) and the National Research Foundation (NRF) of South Africa (grant UID 92531). Opinions expressed and conclusions arrived at, are those of the authors and are not necessarily to be attributed to the NRF or OMT.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank Pamela Derish in the Department of Surgery, University of California San Francisco for proofreading the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2018.00520/full#supplementary-material
References
Argiriou, M., Kolokotron, S.-M., Sakellaridis, T., Argiriou, O., Charitos, C., Zarogoulidis, P., et al. (2014). Right heart failure post left ventricular assist device implantation. J. Thoracic. Dis. 6(Suppl. 1), S52–S59. doi: 10.3978/j.issn.2072-1439.2013.10.26
Baillargeon, B., Costa, I., Leach, J. R., Lee, L. C., Genet, M., Toutain, A., et al. (2015). Human cardiac function simulator for the optimal design of a novel annuloplasty ring with a sub-valvular element for correction of ischemic mitral regurgitation. Cardiovasc. Eng. Technol. 6, 105–116. doi: 10.1007/s13239-015-0216-z
Baillargeon, B., Rebelo, N., Fox, D. D., Taylor, R. L., and Kuhl, E. (2014). The living heart project: a robust and integrative simulator for human heart function. Eur. J. Mech. A Solids 48, 38–47. doi: 10.1016/j.euromechsol.2014.04.001
Baumwol, J., Macdonald, P. S., Keogh, A. M., Kotlyar, E., Spratt, P., Jansz, P., et al. (2011). Right heart failure and “failure to thrive” after left ventricular assist device: clinical predictors and outcomes. J. Heart Lung Transplant. 30, 888–895. doi: 10.1016/j.healun.2011.03.006
Birks, E. J., Tansley, P. D., Hardy, J., George, R. S., Bowles, C. T., Burke, M., et al. (2006). Left ventricular assist device and drug therapy for the reversal of heart failure. N. Engl. J. Med. 355, 1873–1884. doi: 10.1056/NEJMoa053063
Bovendeerd, P., Huyghe, J., Arts, T., Van Campen, D., and Reneman, R. (1994). Influence of endocardial-epicardial crossover of muscle fibers on left ventricular wall mechanics. J. Biomech. 27, 941–951. doi: 10.1016/0021-9290(94)90266-6
Burkhoff, D., Dickstein, M., and Schleicher, T. (2017). HARVI - Online. Available online at: http://harvi.online (Cited April 29, 2017).
Burkhoff, D., Klotz, S., and Mancini, D. M. (2006). LVAD-induced reverse remodeling: basic and clinical implications for myocardial recovery. J. Card. Fail. 12, 227–239. doi: 10.1016/j.cardfail.2005.10.012
Chen, J., Liu, W., Zhang, H., Lacy, L., Yang, X., Song, S.-K., et al. (2005). Regional ventricular wall thickening reflects changes in cardiac fiber and sheet structure during contraction: quantification with diffusion tensor MRI. Am. J. Physiol. Heart Circ. Physiol. 289, H1898–H907. doi: 10.1152/ajpheart.00041.2005
Chiu, W.-C., Girdhar, G., Xenos, M., Alemu, Y., Soares, J. S., Einav, S., et al. (2014). Thromboresistance comparison of the HeartMate II ventricular assist device with the device thrombogenicity emulation-optimized HeartAssist 5 VAD. J. Biomech. Eng. 136:021014. doi: 10.1115/1.4026254
Dang, N. C., Topkara, V. K., Mercando, M., Kay, J., Kruger, K. H., Aboodi, M. S., et al. (2006). Right heart failure after left ventricular assist device implantation in patients with chronic congestive heart failure. J. Heart Lung Transplant. 25, 1–6. doi: 10.1016/j.healun.2005.07.008
Demer, L. L., and Yin, F. C. (1983). Passive biaxial mechanical properties of isolated canine myocardium. J. Physiol. 339, 615–630. doi: 10.1113/jphysiol.1983.sp014738
Dokos, S., Smaill, B. H., Young, A. A., and LeGrice, I. J. (2002). Shear properties of passive ventricular myocardium. Am. J. Physiol. Heart Circ. Physiol. 283, H2650–H2659. doi: 10.1152/ajpheart.00111.2002
Donahue, T. H., Dehlin, W., Gillespie, J., Weiss, W., and Rosenberg, G. (2009). Finite element analysis of stresses developed in the blood sac of a left ventricular assist device. Med. Eng. Phys. 31, 454–460. doi: 10.1016/j.medengphy.2008.11.011
Genet, M., Lee, L. C., Nguyen, R., Haraldsson, H., Acevedo-Bolton, G., Zhang, Z., et al. (2014). Distribution of normal human left ventricular myofiber stress at end diastole and end systole: a target for in silico design of heart failure treatments. J. Appl. Physiol. 117, 142–152. doi: 10.1152/japplphysiol.00255.2014
Gilbert, S. H., Benson, A. P., Li, P., and Holden, A. V. (2007). Regional localisation of left ventricular sheet structure: integration with current models of cardiac fibre, sheet and band structure. Eur. J. Cardiothorac. Surg. 32, 231–249. doi: 10.1016/j.ejcts.2007.03.032
Goktepe, S., Acharya, S. N. S., Wong, J., and Kuhl, E. (2011). Computational modeling of passive myocardium. Int. J. Numer. Methods Bio 27, 1–12. doi: 10.1002/cnm.1402
Grant, A. D., Smedira, N. G., Starling, R. C., and Marwick, T. H. (2012). Independent and incremental role of quantitative right ventricular evaluation for the prediction of right ventricular failure after left ventricular assist device implantation. J. Am. Coll. Cardiol. 60, 521–528. doi: 10.1016/j.jacc.2012.02.073
Guccione, J. M., and McCulloch, A. D. (1993). Mechanics of active contraction in cardiac muscle: Part I–constitutive relations for fiber stress that describe deactivation. J. Biomech. Eng. 115, 72–81. doi: 10.1115/1.2895473
HARVI (2014a). Cardiovascular Physiology, and Hemodynamics. Part, I. Basic Physiological Principles [Computer Program]. Available online at: https://itunes.apple.com/gb/app/harvi/id568196279?mt=8
HARVI (2014b). Cardiovascular Physiology, and Hemodynamics. Part, I. I. Advanced Physiological Concepts [computer Program]. Available online at: https://itunes.apple.com/gb/app/harvi/id568196279?mt=8
Hayek, S., Sims, D. B., Markham, D. W., Butler, J., and Kalogeropoulos, A. P. (2014). Assessment of right ventricular function in left ventricular assist device candidates. Circ. Cardiovasc. Imag. 7, 379–389. doi: 10.1161/CIRCIMAGING.113.001127
Holmes, J. W., Hunlich, M., and Hasenfuss, G. (2002). Energetics of the Frank-Starling effect in rabbit myocardium: economy and efficiency depend on muscle length. Am. J. Physiol. Heart Circ. Physiol. 283, H324–H330. doi: 10.1152/ajpheart.00687.2001
Holzapfel, G. A., and Ogden, R. W. (2009). Constitutive modelling of passive myocardium: a structurally based framework for material characterization. Philos. Trans. A Math. Phys. Eng. Sci. 367, 3445–3475. doi: 10.1098/rsta.2009.0091
Hunter, P. J., McCulloch, A. D., and ter Keurs, H. E. (1998). Modelling the mechanical properties of cardiac muscle. Prog. Biophys. Mol. Biol. 69, 289–331. doi: 10.1016/S0079-6107(98)00013-3
Jones, E., Oliphant, T., and Peterson, P. (2001). SciPy: Open Source Scientific Tools for Python. Available online at: http://www.scipy.org
Kavarana, M. N., Pessin-Minsley, M. S., Urtecho, J., Catanese, K. A., Flannery, M., Oz, M. C., et al. (2002). Right ventricular dysfunction and organ failure in left ventricular assist device recipients: a continuing problem. Ann. Thorac. Surg. 73, 745–750. doi: 10.1016/S0003-4975(01)03406-3
Kerckhoffs, R. C., Neal, M. L., Gu, Q., Bassingthwaighte, J. B., Omens, J. H., and McCulloch, A. D. (2007). Coupling of a 3D finite element model of cardiac ventricular mechanics to lumped systems models of the systemic and pulmonic circulation. Ann. Biomed. Eng. 35, 1–18. doi: 10.1007/s10439-006-9212-7
Klotz, S., Hay, I., Dickstein, M. L., Yi, G. H., Wang, J., Maurer, M. S., et al. (2006). Single-beat estimation of end-diastolic pressure-volume relationship: a novel method with potential for noninvasive application. Am. J. Physiol. Heart Circ. Physiol. 291, H403–H412. doi: 10.1152/ajpheart.01240.2005
Kormos, R. L., Teuteberg, J. J., Pagani, F. D., Russell, S. D., John, R., Miller, L. W., et al. (2010). Right ventricular failure in patients with the HeartMate II continuous-flow left ventricular assist device: incidence, risk factors, and effect on outcomes. J. Thorac. Cardiovasc. Surg. 139, 1316–1324. doi: 10.1016/j.jtcvs.2009.11.020
Küçüker, S. A., Stetson, S. J., Becker, K. A., Akgül, A., Loebe, M., Lafuente, J. A., et al. (2004). Evidence of improved right ventricular structure after LVAD support in patients with end-stage cardiomyopathy. J. Heart Lung Transplant. 23, 28–35. doi: 10.1016/S1053-2498(03)00057-3
Lampropulos, J. F., Kim, N., Wang, Y., Desai, M. M., Barreto-Filho, J. A., Dodson, J. A., et al. (2014). Trends in left ventricular assist device use and outcomes among medicare beneficiaries, 2004–2011. Open Heart 1:e000109. doi: 10.1136/openhrt-2014-000109
LeGrice, I., Hunter, P., Young, A., and Small, B. (2001). The architecture of the heart: a data-based model. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 359, 1217–1232. doi: 10.1098/rsta.2001.0827
Levin, H. R., Oz, M. C., Chen, J. M., Packer, M., Rose, E. A., and Burkhoff, D. (1995). Reversal of chronic ventricular dilation in patients with end-stage cardiomyopathy by prolonged mechanical unloading. Circulation 91, 2717–2720. doi: 10.1161/01.CIR.91.11.2717
Lim, E., Dokos, S., Cloherty, S. L., Salamonsen, R. F., Mason, D. G., Reizes, J. A., et al. (2010). Parameter-optimized model of cardiovascular–rotary blood pump interactions. IEEE Trans. Biomed. Eng. 57, 254–266. doi: 10.1109/TBME.2009.2031629
Lim, K. M., Constantino, J., Gurev, V., Zhu, R., Shim, E. B., and Trayanova, N. A. (2012). Comparison of the effects of continuous and pulsatile left ventricular-assist devices on ventricular unloading using a cardiac electromechanics model. J. Physiol. Sci. 62, 11–19. doi: 10.1007/s12576-011-0180-9
Lin, D., and Yin, F. (1998). A multiaxial constitutive law for mammalian left ventricular myocardium in steady-state barium contracture or tetanus. J. Biomech. Eng. 120, 504–517. doi: 10.1115/1.2798021
Lombaert, H., Peyrat, J. M., Croisille, P., Rapacchi, S., Fanton, L., Cheriet, F., et al. (2012). Human atlas of the cardiac fiber architecture: study on a healthy population. IEEE Trans. Med. Imag. 31, 1436–1447. doi: 10.1109/TMI.2012.2192743
Lombaert, H., Peyrat, J-M., Croisille, P., Rapacchi, S., Fanton, L., Clarysse, P., et al. (2011). “Statistical analysis of the human cardiac fiber architecture from DT-MRI,” Functional Imaging and Modeling of the Heart (Springer), 171–179.
Long, C., Marsden, A., and Bazilevs, Y. (2013). Fluid–structure interaction simulation of pulsatile ventricular assist devices. Comput. Mech. 52, 971–981. doi: 10.1007/s00466-013-0858-3
Maeder, M. T., Leet, A., Ross, A., Esmore, D., and Kaye, D. M. (2009). Changes in right ventricular function during continuous-low left ventricular assist device support. J. Heart Lung Transplant. 28, 360–366. doi: 10.1016/j.healun.2009.01.007
Mann, D. L., Zipes, D. P., Libby, P., and Bonow, R. O. (2014). Braunwald's Heart Disease: A Textbook of Cardiovascular Medicine. Amsterdam: Elsevier Health Sciences.
McIlvennan, C. K., Magid, K. H., Ambardekar, A. V., Thompson, J. S., Matlock, D. D., and Allen, L. A. (2014). Clinical outcomes after continuous-flow left ventricular assist device: a systematic review. Circ. Heart Fail. 7, 1003–1013. doi: 10.1161/CIRCHEARTFAILURE.114.001391
McMurray, J. J., Adamopoulos, S., Anker, S. D., Auricchio, A., Böhm, M., Dickstein, K., et al. (2012). ESC Guidelines for the diagnosis and treatment of acute and chronic heart failure 2012. Eur. J. Heart Fail. 14, 803–869. doi: 10.1093/eurjhf/hfs105
Mielniczuk, L. M., Lamas, G. A., Flaker, G. C., Mitchell, G., Smith, S. C., Gersh, B. J., et al. (2007). Left ventricular end-diastolic pressure and risk of subsequent heart failure in patients following an acute myocardial infarction. Congest. Heart Fail. 13, 209–214. doi: 10.1111/j.1527-5299.2007.06624.x
Mohite, P. N., Sabashnikov, A., Simon, A. R., Weymann, A., Patil, N. P., Unsoeld, B., et al. (2014). Does CircuLite Synergy assist device as partial ventricular support have a place in modern management of advanced heart failure? Expert Rev. Med. Devices 12, 49–60. doi: 10.1586/17434440.2015.985208
Morley, D., Litwak, K., Ferber, P., Spence, P., Dowling, R., Meyns, B., et al. (2007). Hemodynamic effects of partial ventricular support in chronic heart failure: results of simulation validated with in vivo data. J. Thorac. Cardiovasc. Surg. 133, 21–28.e4. doi: 10.1016/j.jtcvs.2006.07.037
Paulus, W. J., Tschöpe, C., Sanderson, J. E., Rusconi, C., Flachskampf, F. A., Rademakers, F. E., et al. (2007). How to diagnose diastolic heart failure: a consensus statement on the diagnosis of heart failure with normal left ventricular ejection fraction by the heart failure and echocardiography associations of the European society of cardiology. Eur. Heart J. 28, 2539–2550. doi: 10.1093/eurheartj/ehm037
Rich, J. D., Gosev, I., Patel, C. B., Joseph, S., Katz, J. N., Eckman, P. M., et al. (2017). The incidence, risk factors, and outcomes associated with late right-sided heart failure in patients supported with an axial-flow left ventricular assist device. J. Heart Lung Transplant. 36, 50–58. doi: 10.1016/j.healun.2016.08.010
Sabashnikov, A., Popov, A. F., Bowles, C. T., Mohite, P. N., Weymann, A., Hards, R., et al. (2014). Outcomes after implantation of partial-support left ventricular assist devices in inotropic-dependent patients: do we still need full-support assist devices? J. Thorac. Cardiovasc .Surg. 148, 1115–1121. doi: 10.1016/j.jtcvs.2014.05.063
Sack, K. L., Baillargeon, B., Acevedo-Bolton, G., Genet, M., Rebelo, N., Kuhl, E., et al. (2016). Partial LVAD restores ventricular outputs and normalizes LV but not RV stress distributions in the acutely failing heart in silico. Int. J. Artif. Organs 39, 421–430. doi: 10.5301/ijao.5000520
Selishchev, S. V., and Telyshev, D. V. (2016). Optimisation of the Sputnik-VAD design. Int. J. Artif. Organs 39, 407–414. doi: 10.5301/ijao.5000518
Setarehdan, S. K., and Singh, S. (2012). Advanced Algorithmic Approaches to Medical Image Segmentation: State-of-the-Art Applications in Cardiology, Neurology, Mammography and Pathology. London: Springer Science and Business Media.
Slater, J. P., Lipsitz, E. C., Chen, J. M., Levin, H. R., Oz, M. C., Goldstein, D. J., et al. (1997). Systolic ventricular interaction in normal and diseased explanted human hearts. J. Thor. Cardiovasc. Surg. 113, 1091–1099. doi: 10.1016/S0022-5223(97)70296-4
Solaro, R. J. (2007). Mechanisms of the Frank-Starling law of the heart: the beat goes on. Biophys. J. 93, 4095–4096. doi: 10.1529/biophysj.107.117200
Solomon, S. D., Hee Shin, S., Shah, A., Skali, H., Desai, A., Kober, L., et al. (2011). Effect of the direct renin inhibitor aliskiren on left ventricular remodelling following myocardial infarction with systolic dysfunction. Eur. Heart J. 32, 1227–1234. doi: 10.1093/eurheartj/ehq522
Sommer, G., Schriefl, A. J., Andrä, M., Sacherer, M., Viertler, C., Wolinski, H., et al. (2015). Biomechanical properties and microstructure of human ventricular myocardium. Acta Biomater. 24, 172–192. doi: 10.1016/j.actbio.2015.06.031
Streeter, D. D., Spotnitz, H. M., Patel, D. P., Ross, J., and Sonnenblick, E. H. (1969). Fiber orientation in the canine left ventricle during diastole and systole. Circ. Res. 24, 339–347. doi: 10.1161/01.RES.24.3.339
Topilsky, Y., Hasin, T., Oh, J., Borgeson, D., Boilson, B., Schirger, J., et al. (2011). Echocardiographic variables after left ventricular assist device implantation associated with adverse outcome. Circ. Cardiovasc. Imag. 4, 648–661. doi: 10.1161/CIRCIMAGING.111.965335
Topkara, V. K., Garan, A. R., Fine, B., Godier-Furnémont, A. F., Breskin, A., Cagliostro, B., et al. (2016). Myocardial recovery in patients receiving contemporary left ventricular assist devices clinical perspective. Circ. Heart Fail. 9:e003157. doi: 10.1161/CIRCHEARTFAILURE.116.003157
Toussaint, N., Stoeck, C. T., Schaeffter, T., Kozerke, S., Sermesant, M., and Batchelor, P. G. (2013). In vivo human cardiac fibre architecture estimation using shape-based diffusion tensor processing. Med. Image Anal. 17, 1243–1255. doi: 10.1016/j.media.2013.02.008
Vadakkumpadan, F., Arevalo, H., Prassl, A. J., Chen, J. J., Kickinger, F., Kohl, P., et al. (2010). Image-based models of cardiac structure in health and disease. WIRE Syst. Biol. Med. 2, 489–506. doi: 10.1002/wsbm.76
Vollkron, M., Schima, H., Huber, L., and Wieselthaler, G. (2002). Interaction of the cardiovascular system with an implanted rotary assist device: simulation study with a refined computer model. Artif. Organs 26, 349–359. doi: 10.1046/j.1525-1594.2002.06870.x
Wang, Y., Loghmanpour, N., Vandenberghe, S., Ferreira, A., Keller, B., Gorcsan, J., et al. (2014). Simulation of dilated heart failure with continuous flow circulatory support. PLoS ONE 9:e85234. doi: 10.1371/journal.pone.0085234
Wenk, J. F., Ge, L., Zhang, Z., Soleimani, M., Potter, D. D., Wallace, A. W., et al. (2012). A coupled biventricular finite element and lumped-parameter circulatory system model of heart failure. Comput. Methods Biomech. Biomed. Engin. 16, 807–818. doi: 10.1080/10255842.2011.641121
Wohlschlaeger, J., Schmitz, K. J., Schmid, C., Schmid, K. W., Keul, P., Takeda, A., et al. (2005). Reverse remodeling following insertion of left ventricular assist devices (LVAD): a review of the morphological and molecular changes. Cardiovasc. Res. 68, 376–386. doi: 10.1016/j.cardiores.2005.06.030
Wong, J., and Kuhl, E. (2014). Generating fibre orientation maps in human heart models using Poisson interpolation. Comput. Methods Biomech. Biomed. Eng. 17, 1217–1226. doi: 10.1080/10255842.2012.739167
Appendix
Active Tension Development
The full description of active tension is described by
where
with parameters definitions and values provided in Table A1. This mathematical description of active tension ensures a smooth yet steep transition from zero tension at the start of systole to peak active tension, Tmax, at time t0 and then a smooth decline back to zero for the specified relaxation time tr.
Parameters for Lumped Circulatory Model
All lumped circulatory parameter values are provided in Table A2.
Keywords: heart failure, finite element method, realistic simulation, ventricular function, right ventricle, ventricular assist device, mechanical circulatory support
Citation: Sack KL, Dabiri Y, Franz T, Solomon SD, Burkhoff D and Guccione JM (2018) Investigating the Role of Interventricular Interdependence in Development of Right Heart Dysfunction During LVAD Support: A Patient-Specific Methods-Based Approach. Front. Physiol. 9:520. doi: 10.3389/fphys.2018.00520
Received: 19 December 2017; Accepted: 23 April 2018;
Published: 11 May 2018.
Edited by:
Joseph L. Greenstein, Johns Hopkins University, United StatesReviewed by:
Joost Lumens, Maastricht University, NetherlandsAdarsh Krishnamurthy, Iowa State University, United States
Copyright © 2018 Sack, Dabiri, Franz, Solomon, Burkhoff and Guccione. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Julius M. Guccione, anVsaXVzLmd1Y2Npb25lQHVjc2YuZWR1
 Kevin L. Sack
Kevin L. Sack Yaghoub Dabiri
Yaghoub Dabiri Thomas Franz
Thomas Franz Scott D. Solomon4
Scott D. Solomon4 Julius M. Guccione
Julius M. Guccione