- 1IMB, UMR 5251, University of Bordeaux, Pessac, France
- 2IHU Liryc, Electrophysiology and Heart Modeling Institute, Fondation Bordeaux University, Pessac, France
- 3Department of Biomedical Engineering, King's College London, London, United Kingdom
The mechanisms underlying atrial fibrillation (AF), the most common sustained cardiac rhythm disturbance, remain elusive. Atrial fibrosis plays an important role in the development of AF and rotor dynamics. Both electrical wavelength (WL) and the degree of atrial fibrosis change as AF progresses. However, their combined effect on rotor core location remains unknown. The aim of this study was to analyze the effects of WL change on rotor core location in both fibrotic and non-fibrotic atria. Three patient specific fibrosis distributions (total fibrosis content: 16.6, 22.8, and 19.2%) obtained from clinical imaging data of persistent AF patients were incorporated in a bilayer atrial computational model. Fibrotic effects were modeled as myocyte-fibroblast coupling + conductivity remodeling; structural remodeling; ionic current changes + conductivity remodeling; and combinations of these methods. To change WL, action potential duration (APD) was varied from 120 to 240ms, representing the range of clinically observed AF cycle length, by modifying the inward rectifier potassium current (IK1) conductance between 80 and 140% of the original value. Phase singularities (PSs) were computed to identify rotor core locations. Our results show that IK1 conductance variation resulted in a decrease of APD and WL across the atria. For large WL in the absence of fibrosis, PSs anchored to regions with high APD gradient at the center of the left atrium (LA) anterior wall and near the junctions of the inferior pulmonary veins (PVs) with the LA. Decreasing the WL induced more PSs, whose distribution became less clustered. With fibrosis, PS locations depended on the fibrosis distribution and the fibrosis implementation method. The proportion of PSs in fibrotic areas and along the borders varied with both WL and fibrosis modeling method: for patient one, this was 4.2–14.9% as IK1 varied for the structural remodeling representation, but 12.3–88.4% using the combination of structural remodeling with myocyte-fibroblast coupling. The degree and distribution of fibrosis and the choice of implementation technique had a larger effect on PS locations than the WL variation. Thus, distinguishing the fibrotic mechanisms present in a patient is important for interpreting clinical fibrosis maps to create personalized models.
1. Introduction
Cardiac arrhythmia is a major cause of death, with considerable health and economic impacts. Atrial Fibrillation (AF) is the most common cardiac arrhythmia. It leads to heart failure and stroke (Kannel et al., 1998). The understanding of the pathophysiology of AF remains incomplete despite numerous experimental and clinical studies, as well as several in-silico studies (Wolf et al., 1991; Courtemanche et al., 1998; Labarthe et al., 2014). Currently, because of its easy reproducibility, its inexpensiveness and its non-invasiveness, computational modeling is widely used to investigate the mechanisms underlying AF.
The underlying atrial substrate is essential for AF maintenance (Kostin et al., 2002). For many patients, the success of anti-arrhythmic drug therapy is low. Thus, catheter ablation is used to eliminate arrhythmogenic electrical sources by destroying the underlying tissue substrate (for example by isolating the pulmonary veins or by targeting potential reentrant sources) using localized energy delivery (Earley et al., 2006). However, AF is recurrent in 30–50% of patients (Calkins et al., 2012). The sub-optimal success rate of AF treatment by catheter ablation procedures is confounded by a lack of consensus between clinicians on the precise locations to be targeted (Schotten et al., 2011; Calkins et al., 2012).
AF dynamics are strongly influenced by heterogeneities in the electrophysiological tissue properties (Kottkamp et al., 2016) and the spatial pattern of tissue structural changes, which are patient specific. Cardiac wavelength (WL)—the distance traveled by the depolarization wave during the functional refractory period (Jacquemet et al., 2005)—is shortened by structural and electrical remodeling in tissue with chronic or persistent AF (Krogh-Madsen et al., 2012). Previous studies have shown that modifying WL properties (through action potential duration, APD, variation) affects AF dynamics (Qu et al., 1999). However, Deng et al. (2017) found that with modest changes in electrophysiological properties, reentrant drivers localized to the same areas, at the edges of high fibrotic regions.
Furthermore, myocardial fibrosis affects AF maintenance (Morgan et al., 2016; Cochet et al., 2018). Fibrotic remodeling is multi-factorial, and includes interstitial fibrosis (the deposition of collagen between fiber bundles), replacement fibrosis, gap junctional remodeling due to downregulation of connexin 43, fibroblast coupling and paracrine factors. These factors may initiate and sustain AF by modifying conduction pathways. Previous studies have suggested targeting fibrotic areas during catheter ablation procedures.
In this study, we investigate how WL affects AF driver location using a computational bilayer model of the human atria, incorporating fibrosis distributions based on late gadolinium enhancement (LGE) Magnetic Resonance Imaging (MRI) scans from patients with persistent AF. In comparison with previous studies, we explore a larger range of clinically observed APD, consider multiple techniques for modeling atrial fibrosis, and directly compare with clinical rotor core trajectory data.
2. Methods
2.1. AF Bilayer Model
We used our previously described human biatrial biophysically-detailed bilayer model (Labarthe et al., 2014), with AF simulated as in our former work (Bayer et al., 2016). Briefly, the bilayer model is a finite element model composed of discretely connected 2D layers. The right atrium (RA) consists of an epicardial layer and a layer for the crista terminalis (CT) and the pectinate muscles (PM). The left atrium (LA) comprises endocardial and epicardial layers. Each node on the LA endocardium and RA endocardial structures (the CT and PM) is connected by a discrete resistance to the closest node on the LA or RA epicardial surface, respectively. Interatrial connections include Bachmann's bundle, the rim of the fossa ovalis, and the muscular sheath of the coronary sinus. The mesh contains 363561 nodes with an edge length of approximately 300μm. Atrial action potentials (AP) vary from region to region (Gelband et al., 1972). As in previous work (Bayer et al., 2016; Roney et al., 2018), the Courtemanche-Ramirez-Nattel human atrial ionic model (Courtemanche et al., 1998) was used and ionic channel conductances varied to recreate the observed heterogeneity (Aslanidi et al., 2011; Krueger et al., 2013). This ionic model is sufficient since we are mainly concerned with APD restitution, and not the detailed subcellular processes seen in newer models which carry significantly increased computational costs. We also incorporate heterogeneous coupling, resulting in different conduction velocities (CVs) in different anatomical regions, according to human data (Lemery et al., 2007; Bayer et al., 2016). Furthermore, to simulate chronic AF, the following electrical remodeling was incorporated: a 50% decrease in the conductance of the atrial-specific ultra-rapid potassium current IKur, a 50% decrease in the conductance of the transient outward current Ito, and a 70% decrease in the conductance of the L-type calcium current ICaL (Courtemanche et al., 1999).
2.2. Wavelength Variation
WL is the product of the effective refractory period (ERP) and CV (Jacquemet et al., 2005), which we approximate as APD × CV. Changing the conductance of IK1 alone does not affect CV (Entz and William, 2018; Nobles et al., 2018; Valli et al., 2018). Pandit and Jalife (2013) found that the inward rectifier K+ channel (IK1) has an important role on the spatiotemporal organization of AF drivers across different parts of the heart. Specifically, changes in IK1 conductance lead to variation of rotor (AF driver) frequency and tip meander because of changes in APD and in the resting level of the membrane potential (which in turn affects cardiac excitability). Previous studies have investigated the effects of IK1 conductance on APD (Dhamoon and Jalife, 2005; Pandit et al., 2005; Lee et al., 2016). We multiplied IK1 conductance by 80, 95, 100, 120, and 140 to modify the APD, and thereby the WL. These values were chosen to give tissue AF cycle lengths in the clinically reported range of 120–240 ms (Konings et al., 1994; Ng et al., 2006).
2.3. Patient Fibrosis Data and Fibrosis Modeling
2.3.1. Patient Data
LGE-MRI intensity data from three patients with persistent AF (Cochet et al., 2015) were projected onto the aforementioned computational atrial bilayer model to assign a fibrosis distribution. For each patient, these intensity values were assigned for each point on an endocardial surface mesh as the maximum value through the atrial wall. These distributions of LGE intensity values were then mapped to the atrial bilayer model using an iterative closest point algorithm (Roney et al., 2016; Cochet et al., 2018). Each of the patients gave informed written consent. The ethics committee of the University of Bordeaux approved the study and it complies with the declaration of Helsinki. Figures 1A–C show the distribution maps of LGE intensity, normalized with respect to the highest value for each patient. We considered an identical LGE intensity distribution on the LA epicardium and endocardium. For the RA, we included atrial fibrosis in the epicardial layer of the model, but not on the endocardial structures. To incorporate atrial fibrosis in the models, nodes with normalized LGE intensity greater than 0.7 were defined to be fibrotic. This corresponds to 13.2, 27.2, and 27.5% of the LA tissue being classified as fibrotic, for patients 1, 2, and 3 respectively (16.6, 22.8, and 19.2% of the entire atria). Since previous studies have found phase singularities (PSs) on the border between fibrosis and normal myocardium (Zahid et al., 2016; Cochet et al., 2018), we defined nodes within 0.75mm of the boundary to be in the border region (Figures 1A–F). This distance, representing a region about five elements wide, allowed us to be specific, while respecting clinical resolution. This width is less than an ablation line, which is usually greater than 2 mm (Bhaskaran et al., 2016). Therefore, we ensure that if the ablation strategy follows such a border, the entire width of the border would be ablated. This border region is only considered for post-processing analyses and does not affect the model construction. The border region corresponds to 38.2, 62.4, and 71.9% of the total fibrotic area (normalized LGE intensity greater than 0.7) for patient 1–3, respectively.
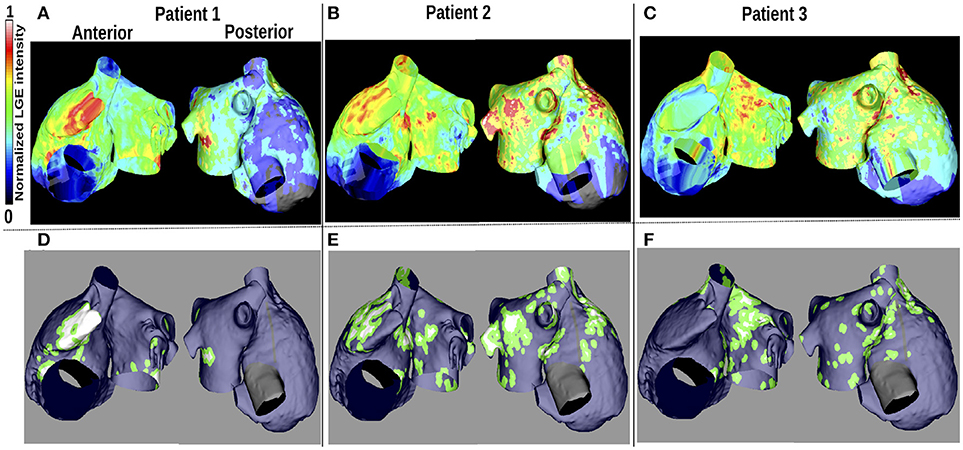
Figure 1. Patient LGE data and fibrosis distribution used for modeling. (A–C): Normalized LGE intensity. (D–F): Fibrotic tissue (white), non-fibrotic areas (blue), and the border between them (green) are shown. The inferior vena cava and line of block regions of the model are electrically inactive and displayed in black in (D–F).
2.3.2. Fibrosis Implementation Methods
Computational modeling studies use different methodologies to model fibrosis (Morgan et al., 2016; Vigmond et al., 2016; Zahid et al., 2016), and previous studies show that the reentry dynamics are affected by the fibrosis implementation method. To study how rotor core position changes when WL is varied in fibrotic atria, we used three different implementation methods: structural remodeling, ionic remodeling and fibroblast coupling, as well as two combinations: structural + ionic changes, and structural changes + fibroblast coupling.
Structural Remodeling
Vigmond et al. (2016) and Roney et al. (2016) give detailed descriptions of this method. It consists of randomly removing elements from the mesh, with a probability depending on the normalized LGE intensity.
Ionic Remodeling
To incorporate ionic remodeling, we rescaled the ionic conductances of the human atrial AF ionic cell model, following Zahid et al. (2016). Specifically, in fibrotic regions, ionic conductances were rescaled as follows: 50% reduction in inward rectifier potassium current (IK1), 50% reduction in L-type calcium current (ICaL), and 40% reduction in the sodium current (INa). To take into account the impact of fibrosis on the intermyocyte coupling, the longitudinal conductivity in the fibrotic regions of the model was reduced by 30%, and then the longitudinal-to-transverse anisotropy ratio was increased to 8:1 to model additional slowing of velocity in the transverse direction.
Fibroblast Coupling
We used the Morgan et al. (2016) model of atrial fibroblasts. Briefly, the interaction between fibroblast and myocyte cells is modeled with a gap junctional conductance of 0.5nS. For each patient, the normalized LGE intensity was divided into six intervals (0−0.27−0.4−0.55−0.69−0.82−1). These intervals correspond to one non-fibrotic region and five different degrees of fibrotic remodeling, ranging from diffuse (1 and 2 fibroblasts per myocyte) to patchy (3 and 4 fibroblasts per myocyte) and dense (5 fibroblasts per myocyte). The myocyte-myocyte longitudinal coupling conductivity was decreased from 100% (in regions with no fibroblast coupling) to 20% of the baseline value (in regions with coupling to 5 fibroblasts per myocyte), following Morgan et al. (2016).
2.4. Simulation Protocol
We used the monodomain formulation and solved it with the Cardiac Arrhythmia Research Package (CARP) simulator (Vigmond et al., 2003). For each case, we first simulated the model for 2 seconds without electrical stimulation, followed by 3.5 s of sinus rhythm with a cycle length of 0.7 seconds (Roney et al., 2016). Five rapid pacing pulses, with a cycle length in the range 112–184 ms, depending on model inducibility, were applied to the upper right pulmonary vein (URPV) to initiate AF. We simulated each model for 2.1 s to allow AF arrhythmia dynamics to stabilize and the final 2.1 seconds were used for analysis for a total simulation time of 9.7 s. All models were inducible.
2.5. Analysis of the Effects of Wavelength Variations on PS Positions
To estimate WL, action potential duration at 90% repolarization (APD90) and CV were calculated over the atrial mesh for each simulation set-up during sinus rhythm. Local CV was computed as the magnitude of conduction velocity. WL was then estimated as the product of APD90 and CV for each node of the mesh.
PSs were located by the intersection of the isopotential line Vm = −20 mV and the line of dVm/dt = 0 (Bishop and Plank, 2012). We plotted and analyzed changes in the percentage (defined as the number of PSs in an area over the total number of PSs in the model) and number of PSs per time unit (each ms) located in each atrial region as IK1 was varied. We analyzed the following atrial regions separately: the PVs [the upper left pulmonary vein (ULPV), the upper right pulmonary vein (URPV), the left lower pulmonary vein (LLPV) and the lower right pulmonary vein (LRPV)], the fossa-ovalis (FO), the superior vena cava (SVC), the LA and the RA. In models with fibrosis, we analyzed the PS content of the fibrotic areas and their borders. To reduce the computation time, parameters were evaluated on a reduced mesh, excluding the electrically inactive regions (the inferior vena cava and the septal line of block), Bachmann's bundle, the crista terminalis, and the pectinate muscles.
3. Results
3.1. Physiological Changes Due to IK1 Variation
APD90, CV, and WL were computed for 5 values of IK1 conductance. For each of these measurements, the maximum values were located in the same atrial region for all of the IK1 values; this was also the case for the minimum values. Maps of these quantities are illustrated in Figure 2. The maximum and minimum APD90 changed when IK1 was varied, as shown in Table 1. As IK1 conductance was increased from 80% to 140% of the control value, APDmin decreased from 139.9 to 120.5 ms and APDmax from 312.9 to 227.1 ms, respectively. The maximum and minimum CV were ~1.1 and ~0.15 m/s, respectively. The CV extrema exhibit little variation as IK1 increased from 80% to 140% of control. The minimum and maximum WL decreased from 35.9 to 28.4 mm, and from 312.4 to 225.6 mm, respectively, when IK1 varied from 80 to 140% of control as shown in Table 1. These WL calculations are local and based on nonuniform propagation; APD and CV are influenced by wavefront curvature, changes in fiber direction, propagation into inexcitable borders, and wavefront collision.
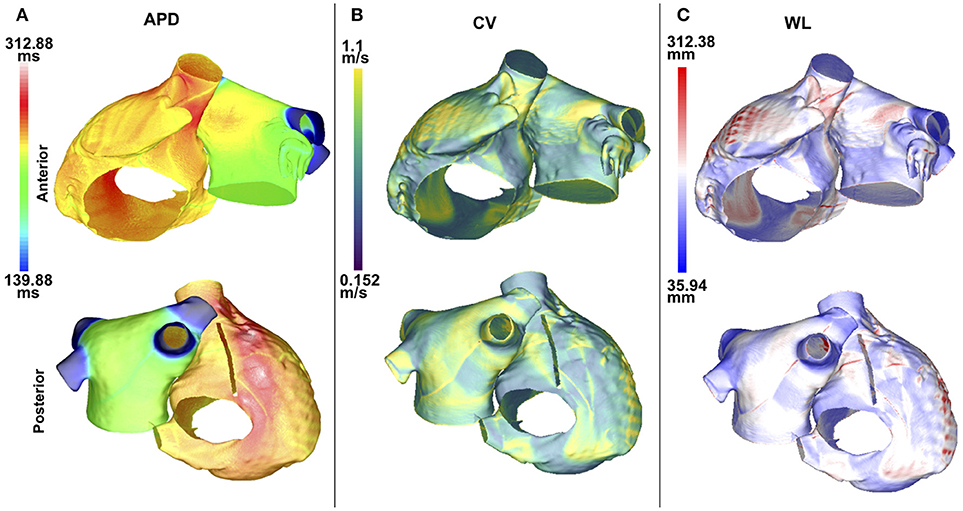
Figure 2. APD, CV, and WL maps are spatially heterogeneous in the control case without fibrosis. Anteroposterior (top row) and posteroanterior (bottom row) views are shown. (A) APD90 map. (B) CV map. (C) WL map. Data are displayed on a reduced mesh for 80%IK1.
The APD90 map is almost uniform on the LA posterior wall. On the LA anterior wall, the APD is higher around Bachmann's bundle than on the rest of the wall. This results in a large gradient of APD around the connection area. The CV and WL are higher on the LA wall area close to the LAA and inferior PV intersections. The highest APD, CV and WL values are seen on the RA posterior wall at the cristae terminalis and pectinate muscles, and near the anterior SVC junction. There are gradients in APD and WL around the intersections of the LA wall with the PVs.
3.2. PS Location With No Fibrosis
Figures 3A–E show changes in PS density as IK1 is varied, and Figure 3F shows a corresponding map indicating the PS locations. For small IK1 values (corresponding to large APD values), rotor organizing centers were more likely to appear on the LA than the RA, in the center of the anterior wall and around the lower PVs intersections, where the APD gradients are high (see Figure 2). As the WL decreased (corresponding to increased IK1), the PS density became less clustered and more widespread over the LA. In addition, PS trajectories covered larger areas of the RA. Concurrently, in the LA, the PS density decreased progressively as WL decreased, and more PS positions appeared.
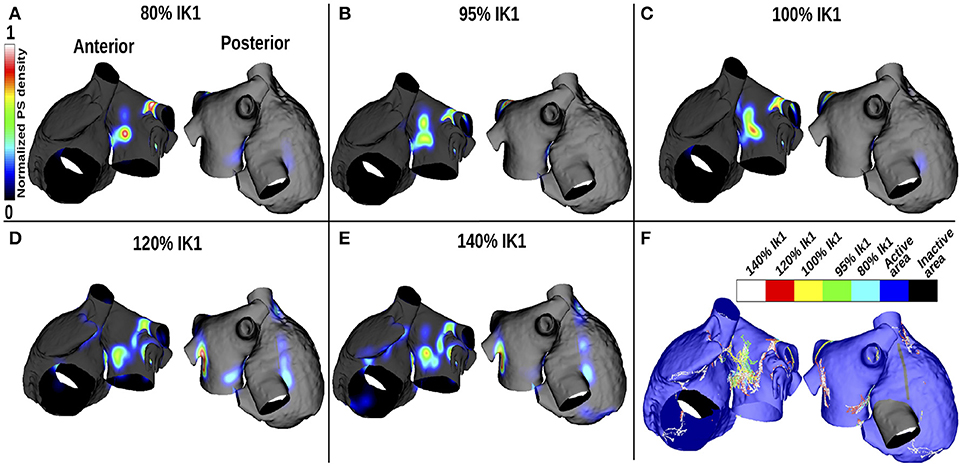
Figure 3. PS density maps change with APD variation for the control case of no atrial fibrosis. Each subfigure shows anteroposterior (left) and posteroanterior (right) views. (A–E) display PS density distributions for 5 IK1 values. (F) Shows PS positions displayed on the same mesh for the different IK1 values.
Figure 4 shows how the number and locations of PSs change in different areas as the IK1 conductance was varied. The percentage of PS positions on the LA decreases from ~90% for large APD values to ~60% for short APD values, while it increases in the RA and PVs from ~5% each to ~22% and ~18%, respectively. The number of PSs increases with IK1 conductance for all regions. There were a greater number of PSs on the LA than on the RA for all IK1 conductance values.
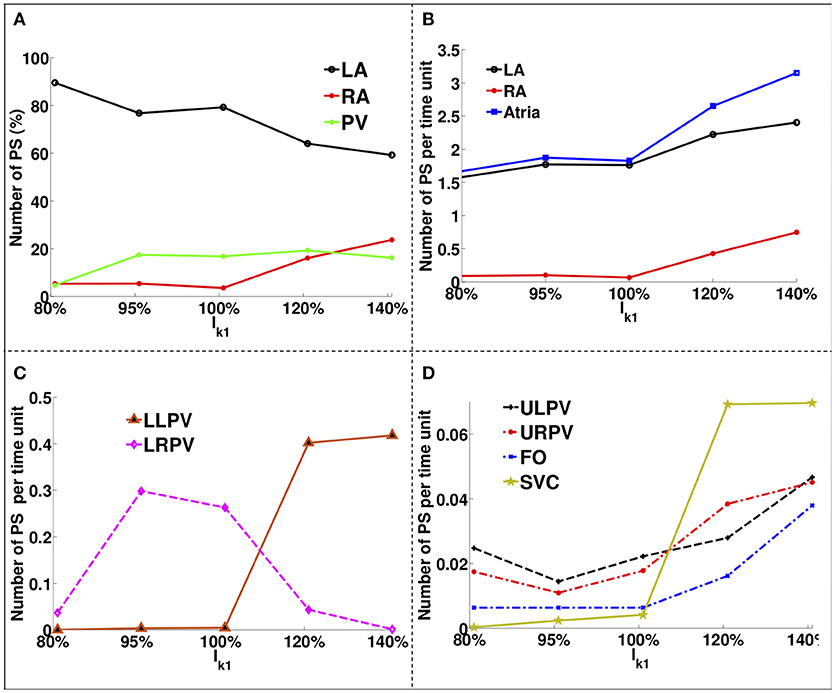
Figure 4. PS location variation as a function of IK1 for atria with no fibrosis. (A) Percentage of PS locations on the LA body, on the RA and on the PVs. (B) Number of PSs per unit time on the entire LA, on the RA and on the whole atria. (C) Number of PSs per time unit on the LLPV and on the LRPV. (D) Number of PSs per unit time on the ULPV, URPV, FO, and SVC.
The LA had ~1.6 PS positions per time unit compared to ~0.1 in the RA for large APD, while for short APD, the LA had ~2.3 compared to ~0.9 in the RA. The lower PVs (Figure 4C) had an order of magnitude more PSs than the upper PVs (Figure 4D). The number of PSs on the FO and SVC increased monotonically with IK1 conductance. For large APD values, there were no PS located on the LLPV or on the SVC, but as APD was decreased, the number of PS on both the LLPV and SVC increased.
3.3. PS Location Analyses for Cases With Fibrosis
Rotor core location depends on both fibrosis distribution and WL. Results are presented in full for one patient; similar results for the other patients are presented in the Supplementary Material.
Figure 5 presents PS location maps for patient 2 as IK1 conductance was varied from 80 to 140% for the five fibrosis implementation methods: structural changes, ionic current remodeling, myocyte-fibroblast coupling, the combination of structural + ionic current remodeling, and the combination of structural changes + myocyte-fibroblast coupling. An area of moderate PS density on the anterior wall of the LA and RA is seen in the clinical data (Figure 5F), and also in each of the simulations. This area of agreement is present for all of the fibrosis implementations. There is an area of high PS density on the posterior wall of the LA in the clinical, as presented in Figure 5F, that is not reproduced in the simulation results.
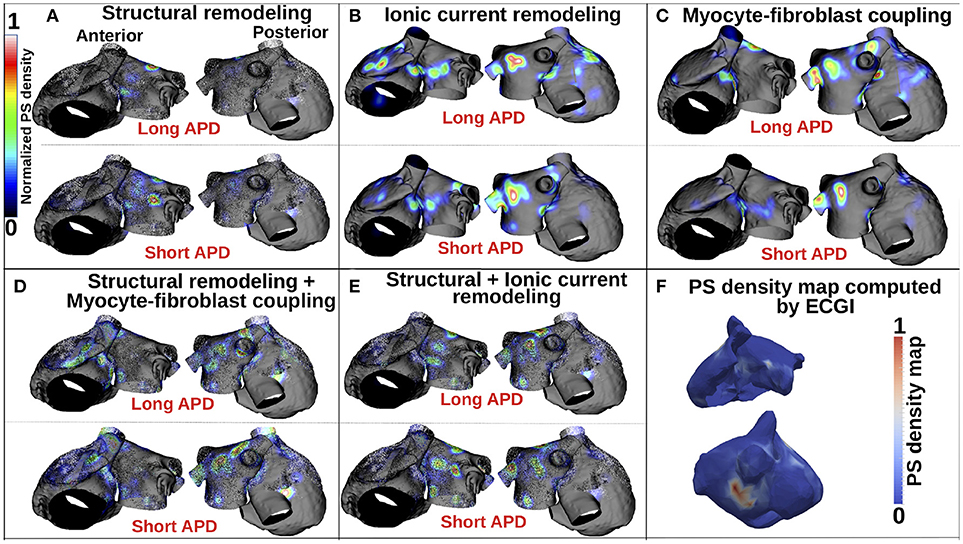
Figure 5. PS density maps depend on both fibrosis implementation method and APD. (A–E) Show PS density maps for the 5 fibrosis implementation methods: structural remodeling, ionic current remodeling, myocyte-fibroblast coupling, structural remodeling + myocyte-fibroblast coupling, and structural + ionic current remodeling, respectively. (F) Clinical PS density map computed using electrocardiographic imaging (ECGi). These data are for patient 2; see Supplementary Figure 1 for patients 1 and 3.
Supplementary Figure 1 presents PS density maps corresponding to long and short APD values for each of the fibrosis modeling methodologies, for each of the patients. In general, there is a good visual correspondence between PS density maps for long and short APDs, and a much larger variation in PS density maps between fibrosis implementation methods. The correlation between PS density maps as APD is varied is greatest for the ionic method (see Supplementary Tables 1–3), and generally lower for the structural remodeling method.
Figure 5A shows that for the structural remodeling method, reentry cores were more likely to be located outside of the fibrotic areas than either inside the fibrotic areas or in the border regions, regardless of APD variation. PSs are also more likely to be in the fibrosis border region than in the fibrosis region itself. Figure 6A quantifies this for structural remodeling in terms of the percentages of PS positions on the border and in the fibrosis area for each patient as APD changes: more than 60% of the PS positions are located outside of the fibrotic area, regardless of the fibrosis distribution.
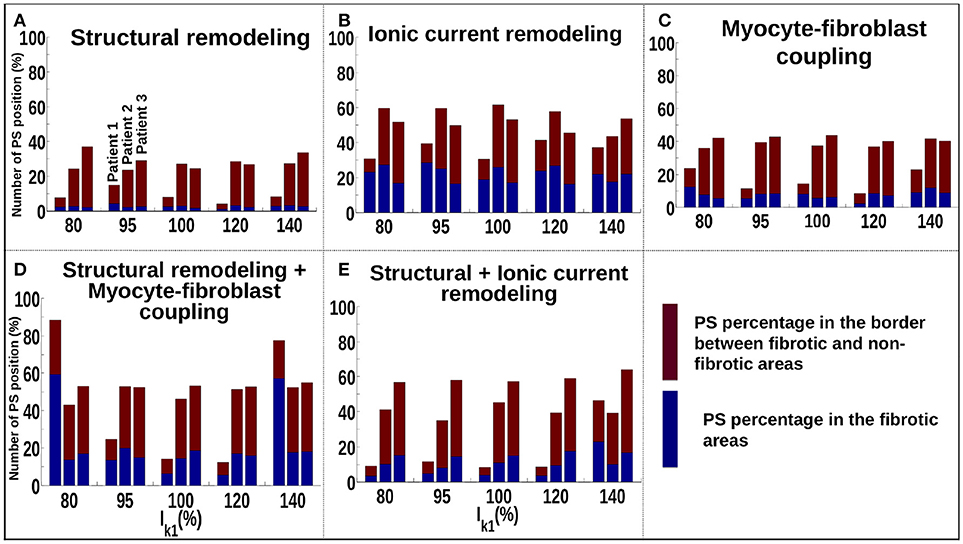
Figure 6. Number of PSs located in the border and in the fibrosis area for patients 1–3 for different fibrosis modeling methodologies, corresponding to: (A) structural remodeling, (B) ionic current remodeling, (C) myocyte-fibroblast coupling, (D) structural remodeling and myocyte-fibroblast coupling, (E) structural and ionic current remodeling.
For the ionic current remodeling method (Figures 5B, 6B), PSs tend to cluster more on the border and in the fibrotic areas than using the structural remodeling methodology or the combination methodologies. With this fibrosis implementation, the number of PS per unit time in the entire atria (Figure 7B) is higher (mean ~3.53 ± 0.84 PS per unit time) than for methodologies incorporating structural remodeling (Figures 7A,D,E; mean values: ~0.95 ± 0.44, ~1.45 ± 1.02, and ~0.92 ± 0.48, respectively). The number of PS is higher and the distribution is less scattered using ionic current remodeling than using methodologies incorporating structural remodeling.
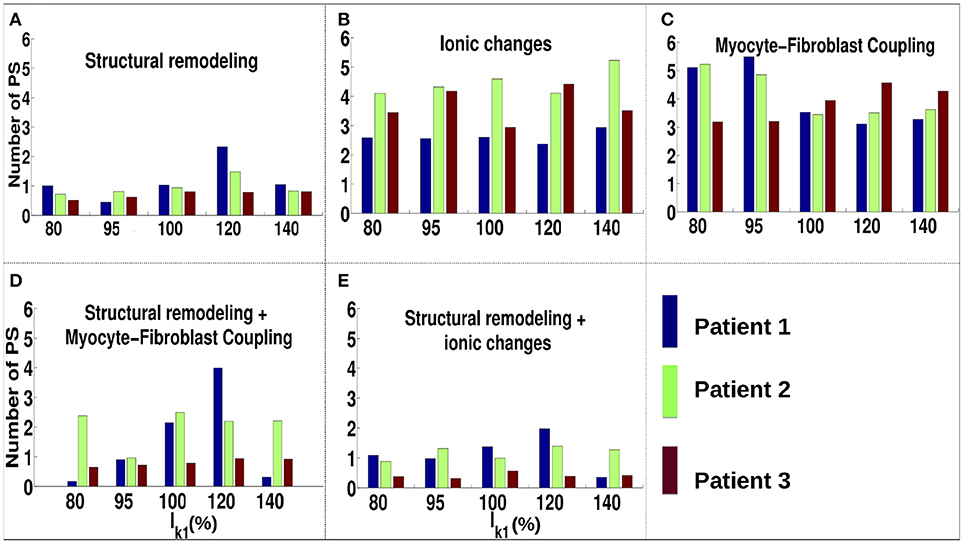
Figure 7. Number of PS per time unit for IK1 conductance scaled by 80–140% for different fibrosis modeling methodologies, corresponding to: (A) structural remodeling, (B) ionic current remodeling, (C) myocyte-fibroblast coupling, (D) structural remodeling and myocyte-fibroblast coupling, (E) structural and ionic current remodeling.
For the myocyte-fibroblast coupling method (Figures 5C, 6C), the proportion of PSs within the fibrotic area and its border is higher than the equivalent measures for structural changes, but lower than for the ionic current remodeling method. The number of PS per time unit in the entire atria (Figure 7C) using the myocyte-fibroblast coupling method is ~4.02 ± 0.80. Thus, it is higher than the number of PSs using implementations including structural remodeling. For the two combination methods (Figures 5D,E, 6D,E), PSs tend to cluster more in the border and the fibrotic areas than using the structural remodeling method alone, but the number of PS per time unit in the entire atria remains low (~1.45 ± 1.02 and ~0.92 ± 0.48 for Figures 7D,E, respectively). The myocyte-fibroblast coupling method and the ionic method result in a larger number of PSs than the structural remodeling or combination methods, and the PS density maps for these methods are more similar to each other than to the structural remodeling method (see Supplementary Figure 1). For each of the fibrosis implementation methods together with the different patient-specific fibrosis distributions, the number of PSs varies non-monotonically as the APD is decreased.
As for the control case without fibrosis, we investigated how the quantity of reentry cores located in different parts of the atria varies with APD. For each patient and each fibrosis implementation method, the variation in the percentage of PS located on all the PVs, on the LA and on the RA are presented in Supplementary Figure 2. The relative distribution of PSs in the LA compared to the RA changes between the fibrosis modeling methodologies. For example, for patient 3, there is a higher number of PSs in the RA compared to the LA for structural remodeling (~62.28 ± 10.57% of PS located on RA vs. ~30.13 ± 11.16% on LA) and also for combining structural remodeling and ionic current changes (RA ~47.24 ± 5.82% vs. LA ~37.99 ± 3.60%). Whereas, there is a higher number in the LA than the RA for the other modeling methodologies (ionic current changes: RA ~28.48 ± 5.97% vs. LA ~52.08 ± 5.48%; fibroblast coupling method alone: RA ~31.50 ± 6.75% vs. LA ~49.11 ± 8.16%; and combining structural remodeling and fibroblast coupling techniques: RA ~28.35 ± 3.45% vs. LA ~50.14 ± 5.64%).
The number of PS per unit time located on the LA, on the RA, around the FO, on the SVC and on each PV are shown in Supplementary Figure 3 for different WLs. These quantities vary with WL. Using the structural remodeling method for fibrosis, patient 1 has ~7.7, ~14.9, ~7.97, ~4.18, and ~8.29% of PS located in fibrosis areas and borders for the 5 increasing values of IK1, respectively (Figure 6A). Combining structural remodeling with myocyte-fibroblast coupling, the number of PS in fibrosis areas and borders are: ~88.41, ~24.69, ~14.20, ~12.34, and ~77.53%, respectively (Figure 6D), demonstrating that the effect of the fibrosis implementation formulation may be greater than the effect of the variation of WL.
4. Discussion
In this study, we used computer modeling to investigate the effects of WL variation on reentry in both fibrotic atria and non-fibrotic atria for three different patient-specific fibrosis distributions, with five known fibrosis implementation methods, on the same atrial mesh to exclude geometrical effects. Our study is unique in that it explores a broader range of APDs, closer to the range seen clinically, as well as investigating the effects of different AF modeling implementations. We further elucidated how structural and electrophysiological remodeling interact to determine rotor core location.
In the case of AF without fibrosis, PSs anchor on the center of the LA anterior wall and near the LA/PV junction for large APD values (Figure 3). These areas have high APD gradients (Figure 2). Decreasing the WL increases the number of PS and the distribution becomes less focused. In the case of fibrotic atria, propagation is constrained by the distribution of fibrosis through the physiological and/or structural changes made to the tissue, depending on the formulation of the implementation method. Previous clinical and computational studies have shown that tissue areas with higher fibrosis density attract more re-entrant activity than other areas (Deng et al., 2017; Cochet et al., 2018), but the trajectories can change, particularly when there are several fibrotic areas close to each other.
There is more variation in the number and location of PSs as IK1 varies in our simulations without fibrosis, demonstrating that the effects of WL will depend on the degree of fibrosis (comparing Figures 4, 7). The fibrosis modeling method has a large effect on the number of PSs in the fibrosis areas and its border. WL has a larger effect on rotor location for the myocyte-fibroblast coupling method and the structural remodeling method than for the other methodologies.
Incorporating atrial fibrosis in the model changed the relationship between WL and number of PSs. Figure 7 shows that there is no consistent relationship between IK1 conductance and the number of PSs for any of the fibrosis implementation methodologies. The number of PSs, and their locality to the fibrotic areas (Figure 6), shows a greater dependence on the fibrosis type than the IK1 conductance. In addition, there are large differences in the proportion of PSs located in regions of fibrosis between fibrosis implementation types. Clinically, there is evidence both for (Cochet et al., 2018) and against (Chrispin et al., 2016) the delocalization of rotational activity with high LGE-intensity. These differences may be because of variations in the type of atrial remodeling. LGE imaging does not have the resolution required to capture microscale fibrotic factors; the effects of which may change as AF progresses.
The structural remodeling method localizes less PSs in areas with high fibrosis intensity, but combining the structural remodeling method with either ionic current remodeling or fibroblast-myocyte coupling forms electrical heterogeneities that better anchor the reentrant drivers. In particular, reentry anchors around areas of fibrosis for the ionic remodeling method due to the longer APD and lower CV with this fibrosis implementation method. Similar results were found in our previous work (Roney et al., 2016), in which differences in the amounts of rotational activity and wavebreak were found between models. Zou et al. (2005) showed that AF initiation, maintenance and dynamics are strongly affected by substrate size. In addition, Panfilov (2006) suggested that the number of fibrillatory sources is proportional to the effective tissue size. In our study, the low presence of PS locations in high fibrosis density zones when modeling structural changes alone may be explained by the large quantity of elements that are removed in these regions, making the effective size of the tissue per unit surface area too small for rotor creation. The effective tissue size per surface unit is also low for cases with structural remodeling combined with ionic remodeling or fibroblast coupling, leading to a low presence of PS locations in high fibrosis density regions. Incorporating ionic remodeling or fibroblast coupling alone to implement fibrosis does not affect the effective tissue size per unit area, and results in a larger quantity of PSs. The higher number of PSs obtained with the fibroblast coupling method compared to the ionic remodeling method may be explained by the way in which the gradient of the physiological parameters is implemented for the two methods. The ionic remodeling method imposes an abrupt decrease in the conductivity at the border between fibrotic and non-fibrotic zones, whereas the fibroblast coupling method has five different levels of conductivity, changing from non-fibrotic to the highly fibrotic zones. This suggests that a more gradual spatial change in conductivity may lead to a larger number of PSs.
Deng et al. (2017) investigated the sensitivity of rotor location to variations in APD and CV, for simulations incorporating fibrosis modeled with modified ionic and conductivity properties. In their simulations, rotors were overwhelmingly located in border regions between fibrotic and healthy tissue regardless of APD and CV values; however, the specific border regions that contained rotors varied depending on the APD and CV parameters. A subset of rotor locations in the modified APD and CV cases were also present in the baseline case (35–80% agreement). The ionic remodeling fibrosis modeling methodology in our study is similar to the methodology used by Deng et al. (2017). We found a higher proportion of PSs in the fibrosis area and its border using this methodology than either the structural remodeling or fibroblast coupling method, and this proportion was high for all IK1 values. For the ionic fibrosis implementation, the number and distribution of PSs was similar for the different IK1 values. As such, our findings for the ionic fibrosis implementation agree with those of Deng et al. (2017) since we also see PSs in the fibrosis border zone, with some sites preserved as well as some different sites emerging as IK1 is varied.
However, in our simulations, there were also a significant proportion of PSs outside of the fibrosis area and border region, particularly around areas with significant APD gradient - for example the LA/PV junction. PS locations were found in areas of long APD (Figure 3), which is consistent with previous studies showing that areas of long APD attract PSs more strongly than inexcitable obstacles (Calvo et al., 2014; Defauw et al., 2014). Our model includes regional heterogeneity between atrial regions, resulting in APD heterogeneities in addition to those from the fibrosis distribution. Further differences in behavior may be attributable to model differences which include our representation of a bilayer mesh with discrete interatrial connections as opposed to a continuous three-dimensional (3D) mesh.
The parameters used for the fibrosis modeling methodologies will affect PS distributions. For the ionic current remodeling method, a threshold intensity must be chosen to assign fibrotic regions, while for the myocyte-fibroblast coupling method, the number of fibroblasts must be chosen. The ionic and fibroblast methods include different degrees of conductivity changes. Matching simulation results with clinical data depends on these parameters. Parameter choice sensitivity was investigated in previous studies (Morgan et al., 2016; Roney et al., 2016; Zahid et al., 2016).
Catheter ablation therapy typically focuses on the LA. Our results show that the proportion of PSs in the RA is typically low for longer APD values; however, this increases as APD decreases (see Figure 4A). This suggests that for shorter WLs, the RA may play a larger role in driving the arrhythmia and RA ablation may be required. In addition, for the control case without fibrosis, the number of PSs and arrhythmia complexity increases as WL is decreased (see Figure 4B). Thus, estimating WL (as the product of AF cycle length and CV) during a procedure may help with therapy planning.
Multiple studies have investigated the effects of ERP, CV and tissue area on the probability that AF sustains. For example, Ravelli and Allessie (1997) found that ERP shortening induced by atrial stretch increased AF vulnerability; Zhuang et al. (2011) report that AF recurrence is more likely in dilated atria because of the increase in size; and Lee et al. (2013) found that both ERP and area affect the probability that AF sustains. Rensma et al. (1988) suggested that ERP and CV alone are poor predictors of susceptibility to reentry, and that the combined measure of WL is a better predictor. Reentry occurs when the path length taken by the wavefront is longer than the WL. WL changes as AF progresses due to increased electrical and structural remodeling. AF susceptibility can then be considered in terms of a critical WL value (Jacquemet et al., 2005), or a fibrillation number, which combines the atrial area and WL into a single measure that is higher in patients with post PV isolation AF inducibility (Hwang et al., 2015). In our study, the number of PSs increases with decreasing WL for simulations without fibrosis, meaning that shorter WL AF simulations are more likely to sustain. However, this was not the case for simulations with fibrosis. Fareh et al. (1998) found that ERP heterogeneity was more important than WL in predicting AF susceptibility, which may be the case for our simulations with fibrosis in which the presence of fibrosis results in conduction and depolarization gradients.
Reentry dynamics depend on both depolarization gradients, with increased PS density in regions of high APD gradient (for example the LA/PV junction), and fibrosis distribution. PS density maps show a closer correspondence with LGE-MRI intensity and are less affected by WL for ionic remodeling and myocyte-fibroblast coupling than for structural remodeling. The effects of fibrosis may outweigh the effects of WL variation in later stages of AF when the fibrosis burden is higher. During the onset of AF, WL and electrophysiology may be more important since electrical remodeling typically occurs before substrate remodeling.
5. Limitations
To investigate the effects of WL and fibrosis in isolation, we used the same atrial geometry for all simulations. However, patient-specific geometry and volume will affect AF dynamics (Cochet et al., 2018). The choice of human atrial cell model affects PS locations (Cherry and Evans, 2008; Wilhelms et al., 2013), but we did not investigate this. We changed WL through variations in ERP, but CV will also affect WL and reentry dynamics (Lim et al., 2017). In addition, we use a 2D bilayer model of the atria, rather than a full 3D model, so we cannot account for the effects of atrial thickness on rotor dynamics (Dutta et al., 2016). We used identical fibrosis distributions for the endocardial and epicardial surfaces of the LA and only included fibrosis on the RA epicardium; however, fibrosis is known to occur in the pectinate muscles (Spach et al., 1988) and the development of atrial fibrosis varies across the atrial thickness (Verheule et al., 2014), starting in the epicardial layer. We normalized LGE intensity to the maximum value for each patient, rather than working with either a number of standard deviations above the blood pool mean or the image intensity ratio for defining fibrotic tissue, which means that the amount of fibrosis included in each model does not necessarily reflect the Utah score for the patient. The choice of LGE-MRI intensity threshold used to define fibrotic and non-fibrotic areas in the image processing and modeling pipeline will affect the resulting AF dynamics, but the optimum value is unknown. For the fibroblast-myocyte coupling model of fibrosis, the fibroblast-myocyte gap-junction conductance value remains experimentally uncertain; in vivo measurements are required to validate fibroblast-myocyte coupling properties used in the simulations.
6. Conclusion
Cardiac WL affects reentry dynamics. Without fibrotic remodeling, increasing the cardiac WL decreased arrhythmia complexity, such that reentrant activities anchored and the number of PSs reduced. WL variation also modified reentry dynamics in fibrotic atria; however, this relationship is more complicated, as it also depends on the fibrosis distribution and fibrosis implementation method. The effects of WL, electrophysiology and APD heterogeneity should be included in computational simulations of AF. With higher fibrosis content, simulated PSs are less affected by WL and more likely to be found close to fibrotic patches. This has implications for model personalization as it suggests that it is important to tune WL for patients with a low degree of fibrotic remodeling, whilst LGE maps alone may be sufficient to predict behavior for patients with significant fibrosis, for which fibrosis implementation method is important.
Author Contributions
MS ran the computational simulations, analyzed data and generated graphs. CR and EV conceived and designed the study and wrote analysis tools for the project. MS, CR, and EV drafted the manuscript. JB provided technical input on the simulation tools. MM and RD analyzed the CardioInsight clinical data. HC segmented the LGE-MRI data.
Funding
The funding for this study was provided by the FRM (Fondation de la Recherche Medicale) grant SPF20160936220. CR acknowledges a Lefoulon-Delalande Foundation fellowship administered by the Institute of France. This study received financial support from the French Government as part of the Investments of the Future program managed by the National Research Agency (ANR), grant reference ANR-10-IAHU-04. EV acknowledges PRACE for awarding access to Marconi at CINECA, Italy, and to ARCHER UK National Supercomputing Service. JB gratefully acknowledges the French National Research Agency for the grant ANR-16-CE19-0009. This work was also supported by the Wellcome/EPSRC Center for Medical Engineering [WT 203148/Z/16/Z].
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2018.01207/full#supplementary-material
References
Aslanidi, O. V., Colman, M. A., Stott, J., Dobrzynski, H., Boyett, M. R., Holden, A. V., et al. (2011). 3d virtual human atria: A computational platform for studying clinical atrial fibrillation. Progr. Biophys. Mol. Biol. 107, 156–168. doi: 10.1016/j.pbiomolbio.2011.06.011
Bayer, J. D., Roney, C. H., Pashaei, A., Jaïs, P., and Vigmond, E. J. (2016). Novel radiofrequency ablation strategies for terminating atrial fibrillation in the left atrium: a simulation study. Front. Physiol. 7:108. doi: 10.3389/fphys.2016.00108
Bhaskaran, A., Chik, W., Pouliopoulos, J., Nalliah, C., Qian, P., Barry, T., et al. (2016). Five seconds of 50–60 w radio frequency atrial ablations were transmural and safe: an in vitro mechanistic assessment and force-controlled in vivo validation. Europace 19, 874–880. doi: 10.1093/europace/euw077
Bishop, M. J., and Plank, G. (2012). The role of fine-scale anatomical structure in the dynamics of reentry in computational models of the rabbit ventricles. J. Physiol. 590, 4515–4535. doi: 10.1113/jphysiol.2012.229062
Calkins, H., Kuck, K. H., Cappato, R., Brugada, J., Camm, A. J., Chen, S.-A., et al. (2012). 2012 HRS/EHRA/ECAS Expert consensus statement on catheter and surgical ablation of atrial fibrillation: recommendations for patient selection, procedural techniques, patient management and follow-up, definitions, endpoints, and research trial design. Heart Rhythm 9, 632–696. doi: 10.1016/j.hrthm.2011.12.016
Calvo, C. J., Deo, M., Zlochiver, S., Millet, J., and Berenfeld, O. (2014). Attraction of rotors to the pulmonary veins in paroxysmal atrial fibrillation: a modeling study. Biophys. J. 106, 1811–1821. doi: 10.1016/j.bpj.2014.02.030
Cherry, E. M., and Evans, S. J. (2008). Properties of two human atrial cell models in tissue: restitution, memory, propagation, and reentry. J. Theor. Biol. 254, 674–690. doi: 10.1016/j.jtbi.2008.06.030
Chrispin, J., Ipek, E. G., Zahid, S., Prakosa, A., Habibi, M., Spragg, D., et al. (2016). Lack of regional association between atrial late gadolinium enhancement on cardiac magnetic resonance and atrial fibrillation rotors. Heart Rhythm 13, 654–660. doi: 10.1016/j.hrthm.2015.11.011
Cochet, H., Dubois, R., Yamashita, S., Al Jefairi, N., Berte, B., Sellal, J.-M., et al. (2018). Relationship between fibrosis detected on late gadolinium-enhanced cardiac magnetic resonance and re-entrant activity assessed with electrocardiographic imaging in human persistent atrial fibrillation. JACC Clin. Electrophysiol. 4, 17–29. doi: 10.1016/j.jacep.2017.07.019
Cochet, H., Mouries, A., Nivet, H., Sacher, F., Derval, N., Denis, A., et al. (2015). Age, atrial fibrillation, and structural heart disease are the main determinants of left atrial fibrosis detected by delayed-enhanced magnetic resonance imaging in a general cardiology population. J. Cardiovasc. Electrophysiol. 26, 484–492. doi: 10.1111/jce.12651
Courtemanche, M., Ramirez, R. J., and Nattel, S. (1998). Ionic mechanisms underlying human atrial action potential properties: insights from a mathematical model. Am. J. Physiol. Heart Circ. Physiol. 275, H301–H321. doi: 10.1152/ajpheart.1998.275.1.H301
Courtemanche, M., Ramirez, R. J., and Nattel, S. (1999). Ionic targets for drug therapy and atrial fibrillation-induced electrical remodeling: insights from a mathematical model. Cardiovasc. Res. 42, 477–489. doi: 10.1016/S0008-6363(99)00034-6
Defauw, A., Vandersickel, N., Dawyndt, P., and Panfilov, A. V. (2014). Small size ionic heterogeneities in the human heart can attract rotors. Am. J. Physiol. Heart Circ. Physiol. 307, H1456–H1468. doi: 10.1152/ajpheart.00410.2014
Deng, D., Murphy, M. J., Hakim, J. B., Franceschi, W. H., Zahid, S., Pashakhanloo, F., et al. (2017). Sensitivity of reentrant driver localization to electrophysiological parameter variability in image-based computational models of persistent atrial fibrillation sustained by a fibrotic substrate. Chaos Interdisc. J. Nonlinear Sci. 27:093932. doi: 10.1063/1.5003340
Dhamoon, A. S., and Jalife, J. (2005). The inward rectifier current (IK1) controls cardiac excitability and is involved in arrhythmogenesis. Heart Rhythm 2, 316–324. doi: 10.1016/j.hrthm.2004.11.012
Dutta, S., Mincholé, A., Zacur, E., Quinn, T. A., Taggart, P., and Rodriguez, B. (2016). Early afterdepolarizations promote transmural reentry in ischemic human ventricles with reduced repolarization reserve. Progr. Biophys. Mol. Biol. 120, 236–248. doi: 10.1016/j.pbiomolbio.2016.01.008
Earley, M. J., Showkathali, R., Alzetani, M., Kistler, P. M., Gupta, D., Abrams, D. J., et al. (2006). Radiofrequency ablation of arrhythmias guided by non-fluoroscopic catheter location: a prospective randomized trial. Eur. Heart J. 27, 1223–1229. doi: 10.1093/eurheartj/ehi834
Entz, I., and William, M. (2018). Effects of Perfusate Solution Composition on the Relationship between Cardiac Conduction Velocity and Gap Junction Coupling. PhD thesis, Virginia Tech.
Fareh, S., Villemaire, C., and Nattel, S. (1998). Importance of refractoriness heterogeneity in the enhanced vulnerability to atrial fibrillation induction caused by tachycardia-induced atrial electrical remodeling. Circulation 98, 2202–2209. doi: 10.1161/01.CIR.98.20.2202
Gelband, H., Bush, H. L., Rosen, M. R., Myerburg, R. J., and Hoffman, B. F. (1972). Electrophysiologic properties of isolated preparations of human atrial myocardium. Circ. Res. 30, 293–300. doi: 10.1161/res.30.3.293
Hwang, M., Park, J., Lee, Y.-S., Park, J. H., Choi, S. H., Shim, E. B., et al. (2015). Fibrillation number based on wavelength and critical mass in patients who underwent radiofrequency catheter ablation for atrial fibrillation. IEEE Trans. Biomed. Eng. 62, 673–679. doi: 10.1109/TBME.2014.2363669
Jacquemet, V., Virag, N., and Kappenberger, L. (2005). Wavelength and vulnerability to atrial fibrillation: insights from a computer model of human atria. EP Europace 7, S83–S92. doi: 10.1016/j.eupc.2005.03.017
Kannel, W. B., Wolf, P. A., Benjamin, E. J., and Levy, D. (1998). Prevalence, incidence, prognosis, and predisposing conditions for atrial fibrillation: population-based estimates 1. Am. J. Cardiol. 82, 2N–9N. doi: 10.1016/S0002-9149(98)00583-9
Konings, K., Kirchhof, C., Smeets, J., Wellens, H., Penn, O. C., and Allessie, M. A. (1994). High-density mapping of electrically induced atrial fibrillation in humans. Circulation 89, 1665–1680. doi: 10.1161/01.CIR.89.4.1665
Kostin, S., Klein, G., Szalay, Z., Hein, S., Bauer, E. P., and Schaper, J. (2002). Structural correlate of atrial fibrillation in human patients. Cardiovasc. Res. 54, 361–379. doi: 10.1016/S0008-6363(02)00273-0
Kottkamp, H., Berg, J., Bender, R., Rieger, A., and Schreiber, D. (2016). Box isolation of fibrotic areas (bifa): a patient-tailored substrate modification approach for ablation of atrial fibrillation. J. Cardiovasc. Electrophysiol. 27, 22–30. doi: 10.1111/jce.12870
Krogh-Madsen, T., Abbott, G. W., and Christini, D. J. (2012). Effects of electrical and structural remodeling on atrial fibrillation maintenance: a simulation study. PLoS Comput. Biol. 8:e1002390. doi: 10.1371/journal.pcbi.1002390
Krueger, M. W., Dorn, A., Keller, D. U., Holmqvist, F., Carlson, J., Platonov, P. G., et al. (2013). in-silico modeling of atrial repolarization in normal and atrial fibrillation remodeled state. Med. Biol. Eng. Comput. 51, 1105–1119. doi: 10.1007/s11517-013-1090-1
Labarthe, S., Bayer, J., Coudière, Y., Henry, J., Cochet, H., Jaïs, P., et al. (2014). A bilayer model of human atria: mathematical background, construction, and assessment. Europace 16, iv21–iv29. doi: 10.1093/europace/euu256
Lee, A. M., Aziz, A., Didesch, J., Clark, K. L., Schuessler, R. B., and Damiano, R. J. (2013). Importance of atrial surface area and refractory period in sustaining atrial fibrillation: testing the critical mass hypothesis. J. Thoracic Cardiovasc. Surg. 146, 593–598. doi: 10.1016/j.jtcvs.2012.04.021
Lee, Y.-S., Hwang, M., Song, J.-S., Li, C., Joung, B., Sobie, E. A., et al. (2016). The contribution of ionic currents to rate-dependent action potential duration and pattern of reentry in a mathematical model of human atrial fibrillation. PLoS ONE 11:e0150779. doi: 10.1371/journal.pone.0150779
Lemery, R., Birnie, D., Tang, A. S., Green, M., Gollob, M., Hendry, M., et al. (2007). Normal atrial activation and voltage during sinus rhythm in the human heart: an endocardial and epicardial mapping study in patients with a history of atrial fibrillation. J. Cardiovasc. Electrophysiol. 18, 402–408. doi: 10.1111/j.1540-8167.2007.00762.x
Lim, B., Hwang, M., Song, J.-S., Ryu, A.-J., Joung, B., Shim, E. B., et al. (2017). Effectiveness of atrial fibrillation rotor ablation is dependent on conduction velocity: an in-silico 3-dimensional modeling study. PLoS ONE 12:e0190398. doi: 10.1371/journal.pone.0190398
Morgan, R., Colman, M. A., Chubb, H., Seemann, G., and Aslanidi, O. V. (2016). Slow conduction in the border zones of patchy fibrosis stabilizes the drivers for atrial fibrillation: insights from multi-scale human atrial modeling. Front. Physiol. 7:474. doi: 10.3389/fphys.2016.00474
Ng, J., Kadish, A. H., and Goldberger, J. J. (2006). Effect of electrogram characteristics on the relationship of dominant frequency to atrial activation rate in atrial fibrillation. Heart Rhythm 3, 1295–1305. doi: 10.1016/j.hrthm.2006.07.027
Nobles, M., Montaigne, D., Sebastian, S., Birnbaumer, L., and Tinker, A. (2018). Differential effects of inhibitory g-protein isoforms on g-protein gated inwardly rectifying k+ currents in adult murine atria. Am. J. Physiol. Cell Physiol. 314, C616–C626. doi: 10.1152/ajpcell.00271.2016
Pandit, S. V., Berenfeld, O., Anumonwo, J. M., Zaritski, R. M., Kneller, J., Nattel, S., et al. (2005). Ionic determinants of functional reentry in a 2-D model of human atrial cells during simulated chronic atrial fibrillation. Biophys. J. 88, 3806–3821. doi: 10.1529/biophysj.105.060459
Pandit, S. V., and Jalife, J. (2013). Rotors and the dynamics of cardiac fibrillation. Circ. Res. 112, 849–862. doi: 10.1161/CIRCRESAHA.111.300158
Panfilov, A. V. (2006). Is heart size a factor in ventricular fibrillation? or how close are rabbit and human hearts? Heart Rhythm 3, 862–864 doi: 10.1016/j.hrthm.2005.12.022
Qu, Z., Weiss, J. N., and Garfinkel, A. (1999). Cardiac electrical restitution properties and stability of reentrant spiral waves: a simulation study. Am. J. Physiol. Heart Circ. Physiol. 276, H269–H283. doi: 10.1152/ajpheart.1999.276.1.H269
Ravelli, F., and Allessie, M. (1997). Effects of atrial dilatation on refractory period and vulnerability to atrial fibrillation in the isolated langendorff-perfused rabbit heart. Circulation 96, 1686–1695. doi: 10.1161/01.CIR.96.5.1686
Rensma, P. L., Allessie, M. A., Lammers, W. J., Bonke, F. I., and Schalij, M. J. (1988). Length of excitation wave and susceptibility to reentrant atrial arrhythmias in normal conscious dogs. Circ. Res. 62, 395–410. doi: 10.1161/01.RES.62.2.395
Roney, C. H., Bayer, J. D., Cochet, H., Meo, M., Dubois, R., Jaïs, P., et al. (2018). Variability in pulmonary vein electrophysiology and fibrosis determines arrhythmia susceptibility and dynamics. PLoS Comput. Biol. 14:e1006166. doi: 10.1371/journal.pcbi.1006166
Roney, C. H., Bayer, J. D., Zahid, S., Meo, M., Boyle, P. M., Trayanova, N. A., et al. (2016). Modelling methodology of atrial fibrosis affects rotor dynamics and electrograms. EP Europace 18(Suppl. 4), iv146–iv155. doi: 10.1093/europace/euw365
Schotten, U., Verheule, S., Kirchhof, P., and Goette, A. (2011). Pathophysiological mechanisms of atrial fibrillation: a translational appraisal. Physiol. Rev. 91, 265–325. doi: 10.1152/physrev.00031.2009
Spach, M. S., Dolber, P. C., and Heidlage, J. F. (1988). Influence of the passive anisotropic properties on directional differences in propagation following modification of the sodium conductance in human atrial muscle. a model of reentry based on anisotropic discontinuous propagation. Circ. Res. 62, 811–832. doi: 10.1161/01.RES.62.4.811
Valli, H., Ahmad, S., Jiang, A. Y., Smyth, R., Jeevaratnam, K., Matthews, H. R., et al. (2018). Cardiomyocyte ionic currents in intact young and aged murine pgc-1β-/- atrial preparations. Mech. Ageing Develop. 169, 1–9. doi: 10.1016/j.mad.2017.11.016
Verheule, S., Eckstein, J., Linz, D., Maesen, B., Bidar, E., Gharaviri, A., et al. (2014). Role of endo-epicardial dissociation of electrical activity and transmural conduction in the development of persistent atrial fibrillation. Progr. Biophys. Mol. Biol. 115, 173–185. doi: 10.1016/j.pbiomolbio.2014.07.007
Vigmond, E., Pashaei, A., Amraoui, S., Cochet, H., and Haïssaguerre, M. (2016). Percolation as a mechanism to explain atrial fractionated electrograms and reentry in a fibrosis model based on imaging data. Heart Rhythm 13, 1536–1543. doi: 10.1016/j.hrthm.2016.03.019
Vigmond, E. J., Hughes, M., Plank, G., and Leon, L. J. (2003). Computational tools for modeling electrical activity in cardiac tissue. J. Electrocardiol. 36, 69–74. doi: 10.1016/j.jelectrocard.2003.09.017
Wilhelms, M., Hettmann, H., Maleckar, M. M. C., Koivumäki, J. T., Dössel, O., and Seemann, G. (2013). Benchmarking electrophysiological models of human atrial myocytes. Front. Physiol. 3:487. doi: 10.3389/fphys.2012.00487
Wolf, P. A., Abbott, R. D., and Kannel, W. B. (1991). Atrial fibrillation as an independent risk factor for stroke: the framingham study. Stroke 22, 983–988. doi: 10.1161/01.STR.22.8.983
Zahid, S., Cochet, H., Boyle, P. M., Schwarz, E. L., Whyte, K. N., Vigmond, E. J., et al. (2016). Patient-derived models link re-entrant driver localization in atrial fibrillation to fibrosis spatial pattern. Cardiovasc. Res. 110, 443–454. doi: 10.1093/cvr/cvw073
Zhuang, J., Wang, Y., Tang, K., Li, X., Peng, W., Liang, C., et al. (2011). Association between left atrial size and atrial fibrillation recurrence after single circumferential pulmonary vein isolation: a systematic review and meta-analysis of observational studies. Europace 14, 638–645. doi: 10.1093/europace/eur364
Keywords: atrial fibrillation, computer simulation, phase singularity mapping, Fibrosis, repolarization heterogeneity
Citation: Saha M, Roney CH, Bayer JD, Meo M, Cochet H, Dubois R and Vigmond EJ (2018) Wavelength and Fibrosis Affect Phase Singularity Locations During Atrial Fibrillation. Front. Physiol. 9:1207. doi: 10.3389/fphys.2018.01207
Received: 30 April 2018; Accepted: 10 August 2018;
Published: 10 September 2018.
Edited by:
Jichao Zhao, University of Auckland, New ZealandReviewed by:
Sanjay Ram Kharche, University of Western Ontario, CanadaWouter-Jan Rappel, University of California, Davis, United States
Copyright © 2018 Saha, Roney, Bayer, Meo, Cochet, Dubois and Vigmond. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Edward J. Vigmond, ZWR3YXJkLnZpZ21vbmRAdS1ib3JkZWF1eC5mcg==
† These authors have contributed equally to this work
 Mirabeau Saha
Mirabeau Saha Caroline H. Roney
Caroline H. Roney Jason D. Bayer
Jason D. Bayer Marianna Meo
Marianna Meo Hubert Cochet1,2
Hubert Cochet1,2 Edward J. Vigmond
Edward J. Vigmond