A Commentary on
Atrial Rotor Dynamics Under Complex Fractional Order Diffusion
by Ugarte, J. P., Tobón, C., Lopes, A. M., and Tenreiro Machado, J. A. (2018). Front. Physiol. 9:975. doi: 10.3389/fphys.2018.00975
Even at healthy states, cardiac tissue conforms one of the most representative cases of a highly heterogeneous and composite biological medium, whose spatial complexity has for long been known to modulate electrical conduction (Frank and Langer, 1974; Spach et al., 1981). How to capture its intricate structural heterogeneity at a tractable cost remains an open challenge in computational physiology and medicine, as traditional approaches such as the monodomain or bidomain equations inherently assume that the tissue behaves as an averaged syncytium with negligible contribution of its composite microstructure.
To overcome some of these limitations, we recently pioneered the use of fractional diffusion for the description of cardiac conduction (Bueno-Orovio et al., 2014b). Our proposed framework took the form
where −(−∇ · D∇V)α/2 is the so-called fractional Laplacian of real order 1 < α ≤ 2. For α = 2, the model clearly recovers the standard monodomain equation, and could equally be extended to the bidomain setting. The well-founded potential theory around the fractional Laplacian allowed us to establish its biophysical interpretation, showing it represents the modulation of the electrical field of a homogeneous conductor by the secondary electrical sources associated with its inhomogeneities. The model further helped elucidating formerly unrelated effects of tissue microstructure on cardiac conduction, including widespread of the action potential foot during depolarization, action potential shortening along the activation pathway, and the modulated dispersion of repolarization. Experimentally, the model has been supported by diffusion spectrum imaging in ex-vivo hearts, indicating fractional diffusion metrics as indices of myocardial microstructure (Bueno-Orovio et al., 2016), as well as by high-resolution optical mapping on cardiac tissue preparations, demonstrating fractional scaling in the propagation of the cardiac wavelength (Loppini et al., 2018).
In the work under comment, Ugarte et al. build and expand on these ideas to present a two-dimensional isotropic fractional diffusion framework of complex order, of the form
with operators and involving pairs of complex-conjugate fractional derivatives defined by
where γ = α + jβ is the complex fractional order, and its complex conjugate. The authors' interpretation of their complex-order model newly builds on potential theory, which connects potential distributions over fractal domains and the complex-order fractional Laplacian. Indeed, the inclusion of the imaginary part β implies that cardiac tissue must satisfy a discrete-scale fractal structure (self-similarity at discrete scales). Whilst such a self-similarity could perhaps be arguable for the main volumetric constituents of cardiac tissue (cardiomyocytes), other components might very well exhibit a fractal structure (e.g., microvasculature). Importantly, such a complex-order fractional framework holds a great potential for consideration of structural remodeling, shall the associated structures (e.g. fibrotic clefts) are proved to have a fractal nature.
However, an important limitation of Ugarte et al. (2018) is that their proposed model is not consistent with the fractional Laplacian in which the authors base their analysis. Taking β = 0 for simplicity, Equations (2), (3) then reduce to
known as a fractional Riesz operator (fractional derivatives independently applied in each spatial coordinate). Conversely, under two-dimensional isotropic conditions, the fractional Laplacian model given by Equation (1) becomes
where for clarity the same notation κα has been used for the equivalent diffusion coefficient. Comparing (4) and (5), it becomes evident that the proposed fractional model is only equivalent to the fractional Laplacian under the standard diffusion case, given by α = 2.
The implications of these subtle but important discrepancies on cardiac conduction are exemplified in Figure 1. Simulations illustrate isotropic conduction for both models under decreasing fractional order α, with ion dynamics described for simplicity by Fenton and Karma (1998). Whereas the fractional Laplacian (Figure 1A) correctly replicates for all α the circular propagation patterns observed on isotropic cardiac monolayers as the simplest yet inhomogeneous in-vitro model of cardiac tissue (Badie and Bursac, 2009; Bian et al., 2014; Molitoris et al., 2016), the fractional Riesz operator (Figure 1B) induces increasingly larger curvature artifacts on wavefront conduction for decreasing α. Such curvature artifacts indeed translate into the results of Ugarte et al. (2018), as evidenced by their square-like spiral wavefronts and rotor trajectories. Given the well-known curvature-related modulation of conduction velocity and therefore wavefront-waveback interactions (Fast and Kléber, 1997; Comtois and Vinet, 1999; Comtois et al., 2005; Kadota et al., 2012), their results on vulnerability to re-entry and associated rotor biomarkers thus must be cautiously interpreted.
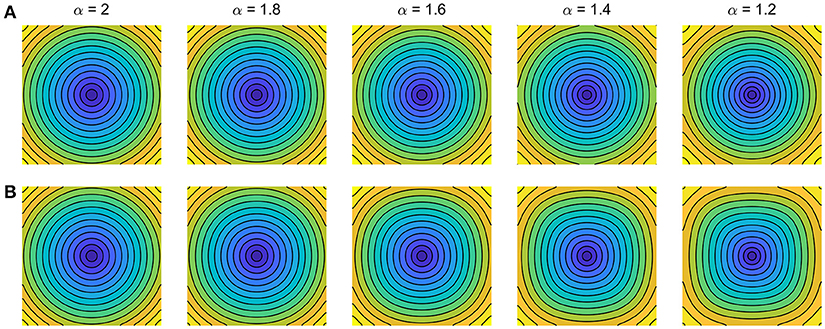
Figure 1. Impact of fractional diffusion operators on cardiac conduction for decreasing order α. Activation maps for central domain stimulation are shown (5 ms separation isochrones). (A) Fractional Laplacian (Bueno-Orovio et al., 2014b). (B) Fractional Riesz operator (Ugarte et al., 2018). Diffusion coefficients were optimized to match standard diffusion conduction velocity at the center of 5 cm fiber strands. Ionic term: Fenton–Karma (modified Beeler–Reuter) dynamics; domain size: 5 × 5 cm; space discretisation: 512 × 512 points; time resolution: 0.025 ms.
It is nevertheless relevant to note that more squared propagation patterns have been reported in both optical mapping (Koura et al., 2002; de Diego et al., 2011) and computational (He and Liu, 2010) studies. This was however under marked anisotropic conduction, not accounted in the isotropic model by Ugarte et al. (2018). In addition, fractional Riesz operators have been also used in modeling electrical propagation (Liu et al., 2013, 2015; Zeng et al., 2014). Such works, more centered in numerical analysis than in gaining physiological insights, might be additionally contributing to spreading the inconsistencies between these two types of fractional diffusion operators. Finally, a too coarse spatial resolution for atrial dynamics compared to previous studies (Wilhelms et al., 2013) could also contribute to partially unresolved re-entrant patterns. Although minimized by the high-order approach on which the authors base their numerical methods (Bueno-Orovio et al., 2014a), allowing considerably larger space steps than traditional stencils, this aspect certainly deserves further consideration.
As previously discussed, the ideas presented in Ugarte et al. (2018) hold a great potential for advancing the field of fractional diffusion applied to cardiac tissue, in order to promote our understanding of the role of tissue microstructure and structural remodeling in modulating wavefront propagation. However, this contribution raises awareness on the definition of suitable fractional diffusion models, exemplifying that simply recovering standard diffusion for a specific value of the considered tissue parameters is not a sufficient condition for realistic cardiac conduction. In this regard, frameworks that are consistent with the fractional Laplacian (Bueno-Orovio et al., 2014b; Cusimano et al., 2015; Cusimano and Gerardo-Giorda, 2018) seem a more suitable modeling approach to correctly capture the characteristic electrotonic loading of cardiac tissue.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
AB-O holds a British Heart Foundation Intermediate Basic Science Research Fellowship (FS/17/22/32644).
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Badie, N., and Bursac, N. (2009). Novel micropatterned cardiac cell cultures with realistic ventricular microstructure. Biophys. J. 96, 3873–3885. doi: 10.1016/j.bpj.2009.02.019
Bian, W., Jackman, C. P., and Bursac, N. (2014). Controlling the structural and functional anisotropy of engineered cardiac tissues. Biofabrication 6:024109. doi: 10.1088/1758-5082/6/2/024109
Bueno-Orovio, A., Kay, D., and Burrage, K. (2014a). Fourier spectral methods for fractional-in-space reaction-diffusion equations. BIT Numer. Math. 54, 937–954. doi: 10.1186/s40064-016-3295-x
Bueno-Orovio, A., Kay, D., Grau, V., Rodriguez, B., and Burrage, K. (2014b). Fractional diffusion models of cardiac electrical propagation: role of structural heterogeneity in dispersion of repolarization. J. R. Soc. Interface 11:20140352. doi: 10.1098/rsif.2014.0352
Bueno-Orovio, A., Teh, I., Schneider, J. E., Burrage, K., and Grau, V. (2016). Anomalous diffusion in cardiac tissue as an index of myocardial microstructure. IEEE Trans. Med. Imaging 35, 2200–2207. doi: 10.1109/TMI.2016.2548503
Comtois, P., Kneller, J., and Nattel, S. (2005). Of circles and spirals: bridging the gap between the leading circle and spiral wave concepts of cardiac reentry. Europace 7, S10–S20. doi: 10.1016/j.eupc.2005.05.011
Comtois, P., and Vinet, A. (1999). Curvature effects on activation speed and repolarization in an ionic model of cardiac myocytes. Phys. Rev. E 60:4619.
Cusimano, N., Bueno-Orovio, A., Turner, I., and Burrage, K. (2015). On the order of the fractional Laplacian in determining the spatio-temporal evolution of a space-fractional model of cardiac electrophysiology. PLoS ONE 10:e0143938. doi: 10.1371/journal.pone.0143938
Cusimano, N., and Gerardo-Giorda, L. (2018). A space-fractional monodomain model for cardiac electrophysiology combining anisotropy and heterogeneity on realistic geometries. J. Comput. Phys. 362, 409–424. doi: 10.1016/j.jcp.2018.02.034
de Diego, C., Chen, F., Xie, Y., Pai, R. K., Slavin, L., Parker, J., et al. (2011). Anisotropic conduction block and reentry in neonatal rat ventricular myocyte monolayers. Am. J. Physiol. Heart Circ. Physiol. 300, H271–H278. doi: 10.1152/ajpheart.00758.2009
Fast, V. G., and Kléber, A. G. (1997). Role of wavefront curvature in propagation of cardiac impulse. Cardiovasc. Res. 33, 258–271. doi: 10.1016/S0008-6363(96)00216-7
Fenton, F., and Karma, A. (1998). Vortex dynamics in three-dimensional continuous myocardium with fiber rotation: filament instability and fibrillation. Chaos 8, 20–47. doi: 10.1063/1.166311
Frank, J. S., and Langer, G. A. (1974). The myocardial interstitium: its structure and its role in ionic exchange. J. Cell Biol. 60, 586–601. doi: 10.1083/jcb.60.3.586
He, Z. Z., and Liu, J. (2010). Effect of cardiac tissue anisotropy on three-dimensional electrical action potential propagation. Mod. Phys. Lett. B. 24, 1847–1853. doi: 10.1142/S0217984910024237
Kadota, S., Kay, M. W., Magome, N., and Agladzea, K. (2012). Curvature-dependent excitation propagation in cultured cardiac tissue. JETP Lett. 94, 824–830. doi: 10.1134/S0021364011230044
Koura, T., Hara, M., Takeuchi, S., Ota, K., Okada, Y., Miyoshi, S., et al. (2002). Anisotropic conduction properties in canine atria analyzed by high-resolution optical mapping: preferential direction of conduction block changes from longitudinal to transverse with increasing age. Circulation 105, 2092–2098. doi: 10.1161/01.CIR.0000015506.36371.0D
Liu, F., Turner, I., Anh, V., Yang, Q., and Burrage, K. (2013). A numerical method for the fractional Fitzhugh–Nagumo monodomain model. ANZIAM J. 54, C608–C629. doi: 10.21914/anziamj.v54i0.6372
Liu, F., Zhuang, P., Turner, I., Anh, V., and Burrage, K. (2015). A semi-alternating direction method for a 2-D fractional FitzHugh–Nagumo monodomain model on an approximate irregular domain. J. Comput. Phys. 293, 252–263. doi: 10.1016/j.jcp.2014.06.001
Loppini, A., Gizzi, A., Cherubini, C., Cherry, E. M., Fenton, F. H., and Filippi, S. (2018). Spatiotemporal correlation uncovers fractional scaling in cardiac tissue. arXiv [preprint] arXiv:1806.04507.
Molitoris, J. M., Paliwal, S., Sekar, R. B., Blake, R., Park, J., Trayanova, N. A., et al. (2016). Precisely parameterized experimental and computational models of tissue organization. Integr. Biol. 8, 230–242. doi: 10.1039/C5IB00270B
Spach, M. S., Miller III, W. T., Geselowitz, D. B., Barr, R. C., Kootsey, J. M., and Johnson, E. A. (1981). The discontinuous nature of propagation in normal canine cardiac muscle. Evidence for recurrent discontinuities of intracellular resistance that affect the membrane currents. Circ. Res. 48, 39–54. doi: 10.1161/01.RES.48.1.39
Ugarte, J. P., Tobón, C., Lopes, A. M., and Tenreiro Machado, J. A. (2018). Atrial rotor dynamics under complex fractional order diffusion. Front. Physiol. 9:975. doi: 10.3389/fphys.2018.00975
Wilhelms, M., Hettmann, H., Maleckar, M. M., Koivumäki, J. T., Dössel, O., and Seemann, G. (2013). Benchmarking electrophysiological models of human atrial myocytes. Front. Physiol. 3:487. doi: 10.3389/fphys.2012.00487
Keywords: cardiac tissue, structural heterogeneity, electrical propagation, fractional diffusion, wavefront curvature
Citation: Bueno-Orovio A (2018) Commentary: Atrial Rotor Dynamics Under Complex Fractional Order Diffusion. Front. Physiol. 9:1386. doi: 10.3389/fphys.2018.01386
Received: 30 August 2018; Accepted: 11 September 2018;
Published: 04 October 2018.
Edited by:
Jichao Zhao, University of Auckland, New ZealandReviewed by:
Juan Pablo Ugarte, Universidad de san Buenaventura, Medellin, ColombiaArun V. Holden, University of Leeds, United Kingdom
Copyright © 2018 Bueno-Orovio. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alfonso Bueno-Orovio, YWxmb25zby5idWVub0Bjcy5veC5hYy51aw==
 Alfonso Bueno-Orovio
Alfonso Bueno-Orovio