- Department of Gastroenterology, Sichuan Academy of Medical Sciences & Sichuan Provincial People's Hospital, Chengdu, China
In recent years, with the development of magnified endoscopic technology, the microstructure of the gastric mucosa surface has been widely studied. However, it is unclear why the crypt opening shape of the fundic gland is different from that of the pyloric gland. We attempted to explain the problem by means of physical concepts, mathematical tools and some pathological perspectives. We first constructed an “L” type tubular structure on the basis of the pathology of the gastric mucosa and some geometric principles and then analyzed the distortion of marginal crypt epithelia after we added cells in the model via the mechanism of continuous regeneration. Finally, we determined that the crypt opening shape of the pyloric gland is derived mathematically from that of the fundic gland with the help of the idea of the Riemann sum. According to the derivation of the Euler force, it is possible that the epithelial-mesenchymal transition (EMT) protects the integrity of the gastric mucosa. Our model suggests that the evolution of the fundic gland and the pyloric gland triggers the EMT via elastic deformation. The basic logic of our model is the principle of least action.
Introduction
Magnified endoscopic technological (Yao, 2014) development in recent years has made observing the microstructure of the gastric mucosa easier than with a scanning electron microscope. Based on extensive clinical studies (Yao, 2014, 2015), structural changes within the gastric mucosal surface are accepted universally as an important reflection of its physiological function and pathological effects in the stomach. As the site through which gastric acid and digestive enzymes exit (Johansson et al., 2000; Phillipson, 2004), the gastric crypt opening plays a vital part in the micro-surface of the stomach. Understanding this process on a microstructural level will help us better understand metaplastic (chronic) atrophic gastritis (Jense and Feldman, 2016) and early gastric cancer (Shimizu et al., 1995).
The traditional view of pathology says that the crypt opening in the stomach should be approximately round or oval. The crypt opening morphology of the fundic gland certainly matches this view based on the magnified endoscopy (ME) photographic data (Yao, 2014; Boeriu et al., 2015; Muto et al., 2015) and scanning electron microscopy (SEM) (Sugimoto and Ogata, 1989), but the gastric crypt opening shows a completely different shape in the gastric antrum (Yao and Oishi, 2001; Niwa et al., 2008; Yao, 2014). If we observe the antral gastric mucosa using ME with narrow-bandimaging (NBI-ME) (Figure 1B), the crypt openings are difficult to see because the rugged intervening section between them that is located side-by-side can cause marginal crypt epithelia (MCE) to cover the crypt openings. Some researchers (Yao, 2014, 2015; Muto et al., 2015) have found that using a combination of two kinds of technology, magnified examination with some assistive technology, and examining the cross-section via microscope can help locate the antral gastric crypt openings. As technology advances, a growing number of studies (Yao, 2014, 2015; Boeriu et al., 2015; Muto et al., 2015) have suggested that gastric crypt openings are approximately linear or have a reticular groove. In addition, the discovery of the light blue crest (Uedo et al., 2006) using NBI-ME indirectly supports this idea.
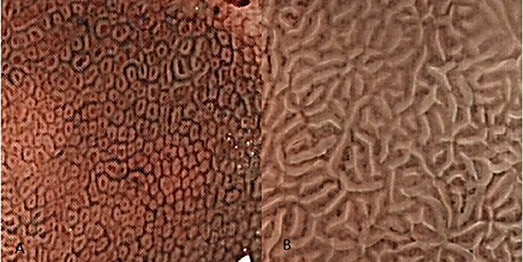
Figure 1. The Crypt opening morphology of the gastric mucosa. These images were taken using magnified endoscopic technology with narrow-band imaging (NBI-ME). (A) The subepithelial capillary network (SECN) looks like a honeycomb in the gastric body, and we can see many approximate round or oval dots in the middle of the honeycombs. These black dots are the crypt openings of fundic glands. (B) Although we cannot see the crypt opening in the gastric antrum mucosa, gastric crypt openings are approximately linear or have a reticular groove based on NBI-ME and pathological examination. These openings are hidden between marginal crypt epithelia (white stripes).
From the above studies, we can conclude that a linear or reticular groove is the morphological feature of crypt openings in the gastric antrum mucosa. Although studies of human gastric mucosa have evolved significantly in just the past decade, some key questions are still difficult to answer. Why is the gastric crypt opening approximately linear or a reticular groove in the gastric antrum mucosa? Why are the micro-surfaces of the multiple white and flat elevated lesions very similar in the gastric antrum mucosa and gastric fundic mucosa? It is possible that ME or pathology cannot answer these questions. Thus, these problems may need to be answered using different methods, such as a constructed elastic mechanics and mathematical modeling.
Model
From a physiological and histological (Rotterdam and Enterline, 1989) perspective, the tubular structure is an important structure in the gastric mucosa. Among the spectrum of gastric diseases, intestinal gastric cancer (IGC) requires a “cascade” of events, and chronic active non-atrophic gastritis can progress over time to invasive carcinoma (Correa, 1992) (Figure S1). IGC has a glandular structure and replaces the full mucosa layer of the surrounding glands (Oyama, 2016). The evolution of IGC implies that the tubular structure is the core structure in the gastric mucosa. Furthermore, there is a high rate of IGC in specific high-risk areas (Crew and Neugut, 2006). Therefore, as a first step (Brannan and Boyce, 2015), we chose the tubular structure to construct our elastic mechanics and mathematical model. Because the gastric body crypt openings are round or oval, we used the fundic gland as our model's starting point. The gastric acid secretions from several glands reach the gastric lumen through only one pit (McDonald et al., 2008; Hoffmann, 2015). We call this system a gastric unit. However, we need to moderate abstract scientific methods to grasp the essence of our main question (i.e., the mechanism of forming the crypt opening of the gastric mucosa) and to ignore many other less important factors in our model, such as the complex, 3D structure of the gastric unit. Therefore, for simplification, let us suppose that a single pit connects a single gland.
“L” Type Tubular Structure
Foveolar cells, chief cells, parietal cells, and other cells comprise the gastric gland. These simple columnar epithelial cells share a common feature: nuclear polarity. The major axis of a normal cell nucleus is always perpendicular to the basement membrane. Considering this fact from the perspective of a 2D plane, a closed curve is a reasonable structure when a liquid needs to be transported and stored in a biological system. Many cross-sectional diagrams of pathological digestive tracts also confirm this view. Therefore, the first step in our model is to find the most suitable geometric shapes of these closed curves. As a complex biological system, the real geometric shapes of these closed curves are influenced by many factors. Differing stiffness of the extracellular matrix can induce morphological differentiation of stem cells (Engler et al., 2006). Epithelial cells feature a distinguishing characteristic, epithelial-mesenchymal transition (EMT) (Kalluri and Weinberg, 2009), and the extracellular matrix (ECM) and glandular cell's mechanical force [produced by E-cadherin (Guilford et al., 1999) and called an ideal state] are undoubtedly the major contributors to the geometric shapes of these closed curves. Thus, the biological system can be written as Equation (1):
Greal is the real geometric shape of these closed curves. Gideal is the ideal geometric shape of these closed curves, and it is influenced by the ECM and time. The value of its function is equal to dGideal, where t is time (Figure S1). EMT suggests that Greal plays a major role in the early evolution of our model. Let us suppose that t approaches 0; then, we obtain Equation (2):
The biological system should be approximately in an ideal state in the initial stage based on the principle of approximation in calculus (Thomas et al., 2004). For a greater understanding of our model, we first need to construct it in an ideal setting. Prior to finding the most suitable geometric shapes of these closed curves, we need to use the principle of least action (Feynman et al., 1970; Xiong, 2015) as the basis for our model because the principle is so universal in nature. That is, we need to show that the tubular structure conforms to the least action principle by modeling crypt opening morphogenesis. The gastric unit needs to deliver gastric acid and pepsin to the gastric mucosa. The 2D plane (i.e., the cross-section) represents the instantaneous state of acid and pepsin secretion compared with the 3D space (Xiong, 2015). Therefore, these closed curves represent an instantaneous state of transportation of the liquid. The least action principle examines these closed curves that sense all geometric shapes and chooses the one with the least action. From a transport efficiency perspective, the larger the closed curve, the higher the gastric gland's transport efficiency. According to isoperimetric inequality, the assumptions for the circumference of the closed curve are fixed in our model, and the most suitable geometric shape of these closed curves is a circle. In short, the circle has the least action in a 2D plane from a transport efficiency perspective. Therefore, we can show the geometric pattern of the cross-sectional diagram in an ideal state (Figure 2A). Now, suppose that we imagine that many similar 2D spaces overlap along a straight line parallel to the gastric mucosal surface. Thus, we can gain many cylinders (Figure 2B). However, from our pathologist's perspective (Montgomery and Voltaggio, 2011), these gastric glands are a coiled and complex structure rather than a simple structure consisting of straight tubes that are perpendicular to the gastric mucosa in 3D space. Therefore, according to the principle of least action, we need to identify what these cylinders' spatial arrangement is in an ideal setting. From an evolutionary perspective, gastric acid secretion may put humans at an evolutionary advantage. We need to produce enough gastric acid to filter microbes in a short time (Beasley et al., 2015).
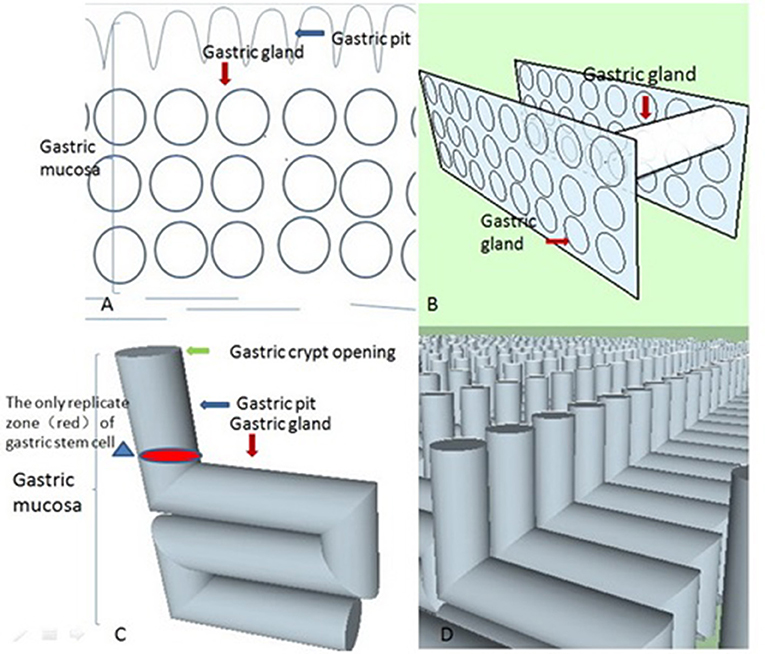
Figure 2. These four conceptual diagrams show the derivation process of these stereoscopic structures of gastric glands in an ideal state based on the principle of least action. (A) According to isoperimetric inequality, we delineated an ideal geometrical morphology of the gastric gland in 2D space. (B) Let us suppose there are many similar 2D spaces (like Figure 2A) overlapping along a straight line that is parallel to the gastric mucosal surface, which gives us many cylinders. From the least action principle, these cylinders are parallel to the gastric mucosal surface. (C) When we unite the geometric shapes of the gastric body's gastric pits with these cylinders, we can obtain an “L” type tubular structure of the gastric gland in the ideal state. (D) The “L” type tubular structure of the gastric gland fills the whole mucosa in the ideal state. Its real state is disorganized and chaotic. The neat rows of these “L” type tubular structures are only easy to observe (the distribution of these structures does not contribute to the final result). A gastric unit consists of several glands that open into a common pit. However, if we apply that definition, our model becomes more complex in what was already a very complex environment. Our aim is to find the mechanism for the formation of the crypt opening of the gastric mucosa, not the stereoscopic structures of the gastric gland. For simplification, we assume that a single pit is connected to a single gland.
We can prove that these cylinders are parallel to the gastric mucosa with the help of some properties of triangles and the fact that the pit tends to be perpendicular to the x-axis with the help of the least action principle (extended mathematical analysis procedure and Figure 3). Therefore, we can produce a model of an “L” type tubular structure (Figure 2).
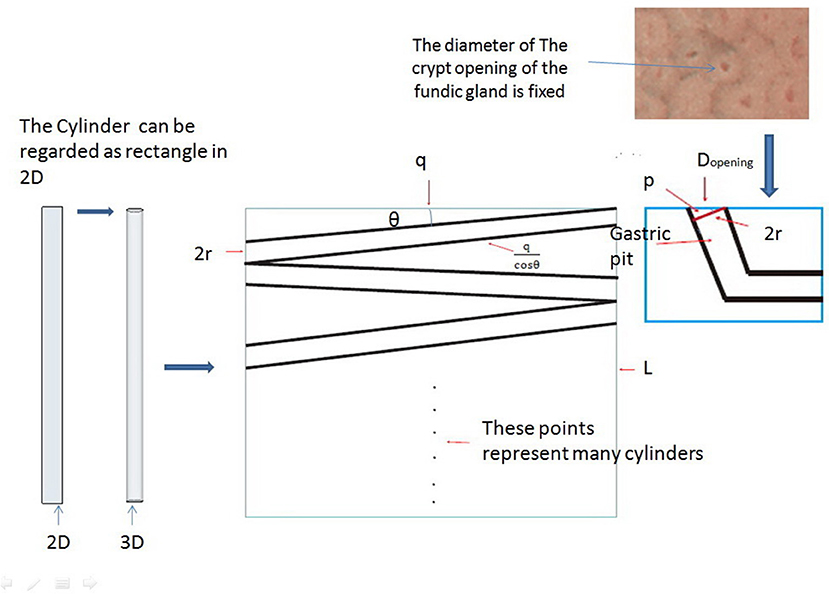
Figure 3. We can think of cylinders as rectangles in a 2D plane. The middle part of the picture shows the rectangle plane distribution at any angle θk (k = 1, 2, 3 … n), and we can demonstrate that these rectangles are parallel to q based on the principle of least action with the help of some properties of triangles and the definition of area.
Multiple Flat White Lesions
We now return to our original question. Thus far, our model has been based on the fundic gland's microstructure. Therefore, the next logical thing to do is to determine the structure of the mucosa surface as the connection between fundic glands and pyloric glands from a pathological perspective. Fortunately, multiple white flat lesions (Uedo et al., 2017) in the gastric corpus may be able to play this role (Figures 1B, 4). If we look closely at multiple white flat lesions, it is safe to assume that the micro-surface structures of the multiple white flat lesions are similar to the antral gastric mucosa. Furthermore, if this assumption is true, then the morphological features of the crypt opening on the multiple white flat lesions are linear or a reticular groove, just as with the antral gastric mucosa.
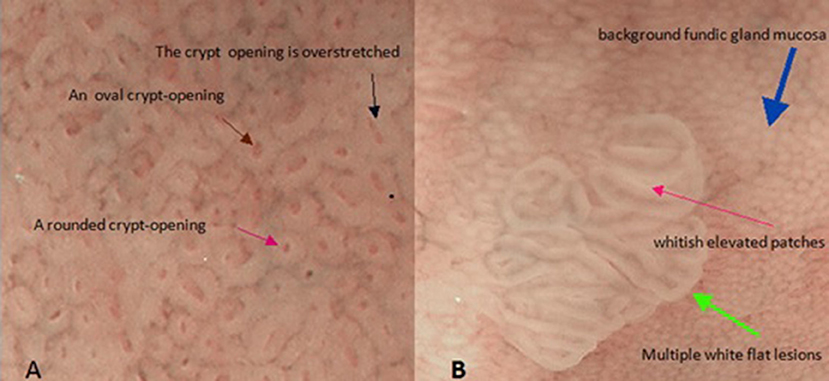
Figure 4. These two pictures show the mucosal surface structure of the fundus of the stomach with the help of magnified endoscopy with narrow-band imaging (NBI-ME). (A) There are some different morphological characteristics of gastric crypt openings. (B) This image shows the morphological characteristics of a flat white lesion. There are huge differences in the epithelial structures between background fundic gland mucosa and multiple white flat lesions.
In addition, as described by Uedo et al. (2017), multiple white flat lesions are hyperplastic lesions. The characteristics of hyperplastic lesions suggest that continuous regeneration (Hoffmann, 2008) via proliferation and differentiation of stem cells is responsible for multiple white flat lesions. Additionally, dysregulated regeneration causes intestinal metaplasia. The appearance of whitish elevated patches in the antrum often represents intestinal metaplasia on magnified narrow-band imaging. The same characteristic is observed on multiple white flat lesions (Uedo et al., 2017). This coincidence allows us to associate continuous regeneration with multiple white flat lesions. Hence, in our model, we need to demonstrate only that the morphological features of the crypt opening on the multiple white flat lesions are linear or a reticular groove based on continuous regeneration.
Results
The Motion of the Epithelium in the Gastric Fundus and Body
Approximately 60 years ago, Leblond et al found that the isthmus and neck are the major sites of gastric stem and progenitor cells (Stevens and Leblond, 1953). However, it is difficult to determine the isthmus and neck's location because the gastric gland is a complex spatial structure. Fortunately, for our model, we can look for some clues about the isthmus and neck's location based on pathology. According to a Japanese experts' view (Oyama, 2016), each cancer cell in poorly differentiated adenocarcinoma spreads laterally at the isthmus and neck of the gland. As shown in the “L” type tubular structure, let us suppose that gastric stem cells are distributed into rings and that only two geometric types of replication zones of gastric stem cells' spatial position are possible: a closed ring in the horizontal orientation and a closed ring in the vertical orientation. If the latter is true, half of the cancer cells move more vertically in pathological sections. Therefore, the latter is far removed from the direction of the poorly differentiated adenocarcinoma's invasion in the cross-sectional diagram (Figure 5). In addition, we already know that several glands share a single pit. According to gland fission's formation mechanism (McDonald et al., 2008), if the replication zone of gastric stem cells' spatial position is in the horizontal orientation, a new gland's development will be blocked by the dense structure of the gastric unit. Thus, it is reasonable that we place the replication zone of gastric stem cells at the bottom of the pit in our model (Figure 2C).
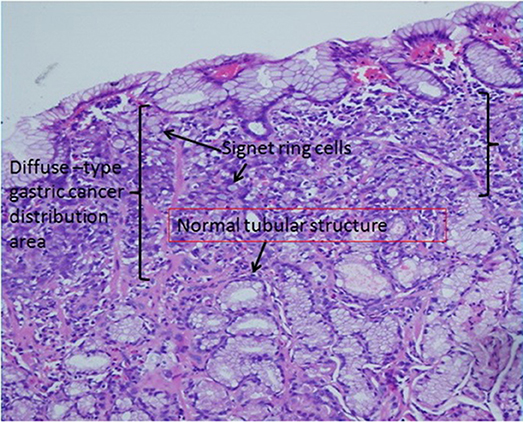
Figure 5. Gastric signet ring cell carcinoma confined to the mucosal layer in the picture. If we carefully observe the diffuse-type gastric cancer distribution area, the lateral length of the distribution area is far longer than the longitudinal length. This characteristic suggests that diffuse-type gastric cancer spreads laterally in the pathological section. In addition, based on our model, we find many normal tubular structures below the diffuse-type gastric cancer distribution area.
Simple columnar epithelial cells belong to every part of the stomach. For our model, in an ideal state, the only mechanical force holding simple columnar epithelial cells together is E-cadherin (Guilford et al., 1999). To better understand the mechanical force that acts on the gastric epithelium, it is important to simplify these cells into roundness based on Saint-Venant's principle and to suppose that cells are arranged in rows and columns (Figure 6A). According to Natalia Guz et al.'s research (Guz et al., 2014), our model can be viewed as an elastic body. We need to know that the elastic body also satisfies the least action principle (Feynman et al., 1970). To minimize energy, the elastic body's internal forces must be in equilibrium. Now suppose we have an epithelial cell on the MCE of a fundic gland. For our model, it is located at the top edge of the vertical cylinder. We called it Ce, and if Ce is in equilibrium, we have:
where Fint is the total internal force acting on Ce. Suppose gastric stem cells are distributed in a ring at the bottom of a pit in our model. For our model, there is a one-to-one correspondence between each gastric stem cell and each column of epithelial cells in the vertical cylinder. Let us denote the two cells on the right and left side of Ce by CR and CL at MCE sites (Figure 6A). At least one epithelial cell is also connected to Ce at the gastric epithelium besides the MCE. We denote it by Cc for our model, and we can use the regeneration mechanism of the mucous epithelia, i.e., continuous regeneration via the differentiation of stem cells (Hoffmann, 2008), in the following way: we consider that a gastric stem cell splits and forms two new gastric epithelial cells only at Ce's column (Figure 6B). For Ce's column, the added cell can generate external force, which acts from a distance on Ce to produce a force per unit volume fext. Owing to elastic strain energy attenuating with distance (Toupin, 1965), let us suppose that Ce will deform more or less under the action of the external force, Fext. Then, we can write Fext as
where V is these cells' average volume.
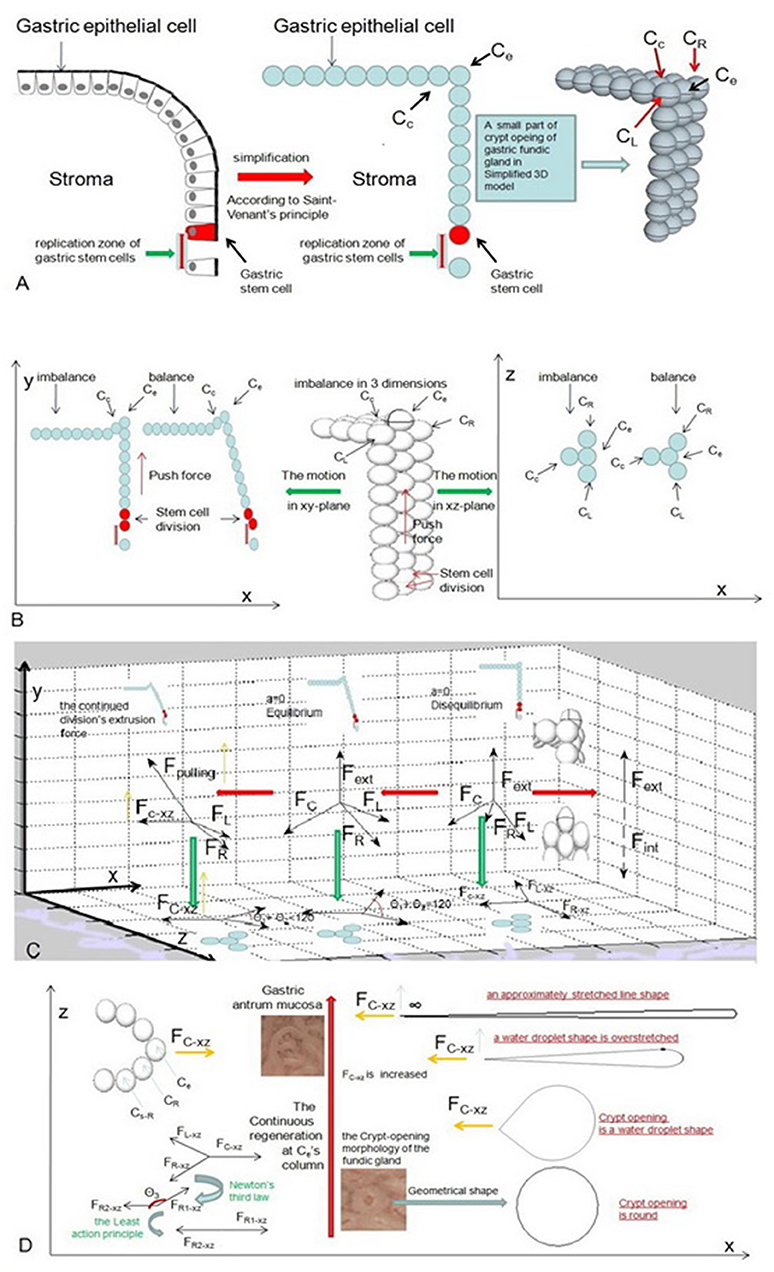
Figure 6. These pictures show the motion of the epithelial cell in an ideal state. (A) We need to simplify these cells into roundness based on Saint-Venant's principle and suppose that cells are arranged in rows and columns. (B) When a gastric stem cell splits and forms two new gastric epithelial cells within Ce's column, these forces act acrossCe and are analyzed at the initial stage. (C) Our model shows the changes in these forces and the changes in the position of Ce for balance. (D) The crypt opening demonstrates an approximately stretched line shape when FC−xz is infinite.
The elastic body must adjust itself to an equilibrium because of the least action principle. Therefore, the internal stresses on it must also adjust themselves to minimize energy (Feynman et al., 1970). Furthermore, Fext should counteract the force Fint from the neighboring cells, which act across Ce. Let us suppose that these cells are not in equilibrium. If they are moving, we have
where ρ is the density of these cells, and a is their acceleration. We can now combine Equations (4) and (5) to yield
When these cells are in equilibrium, there is no acceleration. Then, Equation (5) is written as
In other words, we can change Equation (7) to
These equations tell us how the external force from cell division is related to the sum force Fint from the neighboring cells, which act across Ce. As shown in an earlier chapter, the cell adhesion force (Guilford et al., 1999) is only an internal force of the elastic body in an ideal state. According to the definition of vectors, both Fint and Fext are represented by a directed line segment. Equation (8) suggests that the vector lengths are equal. Now let us put our model into rectangular coordinates. The x-axis is parallel to the mucosal surface, the y-axis is perpendicular to the mucosal surface and the z-axis is perpendicular to the xy-plane:
where s is a curve. Equation (9) through Equation (11) suggest the elastic body is in equilibrium in the x, y, and z directions. There are 3 directions that we can examine to help us understand how Ce reaches equilibrium after a gastric stem cell finishes a division at Ce‘s column.
The Y-Axis
When a gastric stem cell splits and forms two new gastric epithelial cells, only Ce is produced by Ce's column. The y-axis force toward Ce is produced by an extrusion force from Ce‘s column (Figure 6C). The force produces the initial displacement of Ce on the y-axis. The elastic body is not in equilibrium in the initial stage. According to Equations (7) and (8), we have
where ay is a component of acceleration on the y-axis. After Ce is in equilibrium, FR, FL, and FC indicatethat some pulls from Cc, CR, and CL act on Ce. θR−y, θL−y, and θC−y represent the angles between these pulls among Cc, CR, CL and the y-axis.
The Z-Axis
Because CR and CL are located on either side of Ce, it is reasonable that their components are equal on the z-axis. We will not go into detail in our model because they donot impact the distortion of the elastic body.
The X-Axis
Let us suppose that CR, CL, and Ce lie on one line based on the approximation principle. Only one component can generate a pulling force from Cc on the x-axis. We obtain new displacement of Ce on the x-axis. As mentioned previously, the energy of the elastic body must be minimized. Now, we project FR and FL and FC onto the xz-plane, and we can obtain three components of FR, FL, and FC in the xz-plane. For our model, FR−xz, FL−xz, and FC−xz are adapted to represent each of these components. To obtain equilibrium, FR−xz and FL−xz gradually move inward as FC−xz increases until the sum component force of FR−xz and FL−xz on the x-axis is equal to FC−xz. Therefore, we have
where θ1 and θ2 are the angles between FR−xz and FL−xz and the x-axis, respectively.
Suppose that we imagine that the gastric stem cell continues cell division. The number of epithelial cells continues to increase in Ce's column. The continued division can result in an increase in FC−xz. Finally, we have (Figure 6C)
The equation represents these forces' equilibrium state in the xy-plane. However, if cell divisions continue to occur, they could cause an incline at Ce's column due to the displacement of Ce. Therefore, θ1+θ2 reach 0, and FC−xz will continue to increase due to a component of the continued division's extrusion force in the direction of the x-axis (Figure 6C). We call this force Fpulling. As a result, based on the least action principle, the elastic system has to further decrease the value of θ1+θ2 because the sum component force of FR−xz and FL−xz on the x-axis counteracts FC−xz with minimal effort. Now we use Cs−R to represent the first cell behind CR on MCE. According to Newton's third law, we indicate that the counterforce of FR−xz acting on CR as FR1−xz in the xz-plane. A force from the junction between FR1−xz and FR2−xz as θ3 also exists. Finally, we ignored the influence of other junctions between CR and other cells. When our system is in equilibrium, we have
Let us assume that the value of FC−xz tends to be infinite and that cellular junctions among epithelial cells donot break. According to the least action principle, we can write
Therefore, the crypt opening of the fundic gland has a water droplet shape in the xz-plane (Figure 6D). θ1+θ2 approaches zero, and the crypt opening demonstrates an approximately infinitely stretched line shape under magnifying endoscopy (Figure 6D).
Buckling of the Gastric Epithelium
In the previous model, we ignored a problem: the gastric epithelium will break when Fext reaches a certain value. Next, we will address this problem from a classical theory of elastic mechanics, Hooke's law. Now, we observe our model from the xy-plane. Suppose we take a segment of gastric epithelial cells of length l. These cells are again columnar. When cell division occurs within Ce's column, we expect a small bending of the gastric epithelium. There exists a surface of simple columnar epithelial cells that is parallel to the x-axis, and its length is l. Thus, cell components above the surface are compressed, and the cell components below it are stretched. We called the surface a neutral surface (Feynman et al., 1970). Now we set Δl as the longitudinal stretch, y as the height between the neutral surface and normal gastric mucosa, and R as the radius of curvature of the gastric epithelium. Based on geometry, we have (Figure 7)
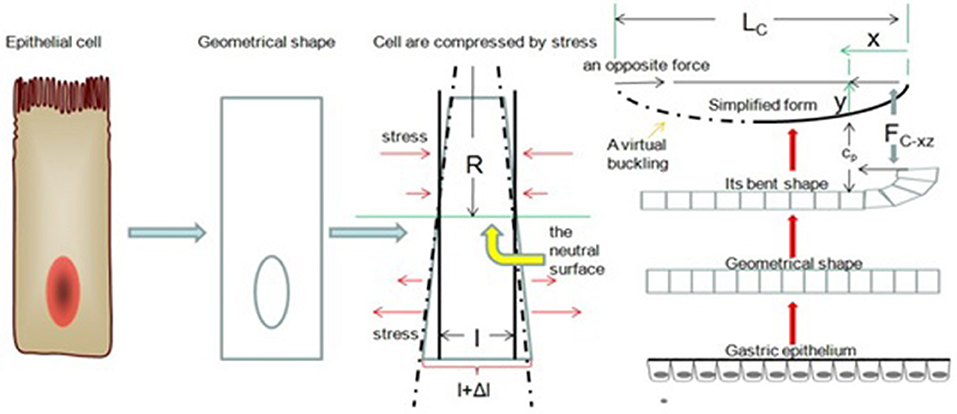
Figure 7. Buckling of the gastric epithelium. The cell components above the neutral surface are compressed, and the cell components below the neutral surface are stretched. When FC−xz is increasing, the gastric epithelium can be simplified as a bending line.
A unit area in a columnar cell Fcell is proportional; therefore, according to Hooke's law (Feynman et al., 1970), the force per longitudinal section (xz-plane)
where E is Young's modulus, and ΔAcell is a longitudinal section (xz-plane) of unit area of a columnar cell, which is the area between a columnar cell's free surface and the neutral surface. For a small bend, the neutral line is near the middle of the cross-section (xz-plane), and y can be approximated as the distance between the neutral surface and an epithelial cell's basal surface. Therefore, we can compute the total bending moment:
where τ is the bending moment. From Equation (18), we have
According to the definition of moment of inertia (Feynman et al., 1970), we have
where l is the moment of inertia. Its principal axis is parallel to the x-axis and through the cell's barycenter. Then, the bending moment is
Suppose that we imagine that an opposite force (equal to FC−xz) is at the other end of the segment of the gastric epithelium in the xy-plane (Figure 7). We call any one cell of the gastric epithelial cells Cp. Therefore, the bending moment τ of Cp is
where yp is the moment arm, the perpendicular distance between Cp and a line along the direction of FC−xz. Using equation (20), we rewrite the equation as
When our model adds a new epithelial cell at Ce' s column, we can see the deformation as a small bend. According to the definition of curvature (Thomas et al., 2004), we can take
where Tcurvature is a unit tangent's vector of the gastric epithelium, and Scurvature Scurvature is the arc length parameter. Then, we have
We can see the right side of the equation is equal to an inverted sine wave equation. Now, we can set the connecting line between the ends to Lc. For convenience, let us assume that the wavelength is equal to Lc and that Lc is twice as long as l
where K is constant. Taking the derivative, we have
Taking the derivative again, we get
Using Equation (25):
We put this equation into Equation (25), and we can see
The force of the equation is more commonly known as the Euler force (Feynman et al., 1970). The equation shows the force is independent of yp for small bending. In other words, if the force is less than the Euler force, it is impossible for the gastric epithelium to break. It is logical to keep FC−xz in the Euler force's vicinity with the help of some mechanisms so that our gastric epithelium does not break during continuous regeneration. Now let us return to the multiple white flat lesions. Based on the research of Uedo et al. (2017), there are two biological structures in its pathological sections: tubular structures and mesenchyme. The former structures are produced by continuous regeneration; we need to understand the source of multiple white flat lesions' mesenchyme. According to renal fibrosis research, renal fibrosis is induced by pressure force (Hoffman et al., 2006; Broadbelt et al., 2007; Chen et al., 2014). For our model, logic suggests that the pressure force is equal to the stress of the deformation of the gastric epithelium. In short, if , EMT will be induced by the stress. When FC−xz is continuously increasing, the continuing EMT minimizes yp and leads to a bend in the gastric epithelium. Let us suppose that the heights of the epithelial cells are elevated until the maximum heights are parallel to the height of Ce (Ce refers to the epithelial cell on the MCE site, it does not fixate on any cell) and that mucosal defects due to EMT are repaired by continuous regeneration. Therefore, Fint is zero on the x-axis. Again, supposing that the number of epithelial cells stays essentially the same, some cells are compressed, and the elastic force of these cells counterbalances FC−xz. As a result, FC−xz is always in the Euler force vicinity, and EMT can prevent gastric epithelium breakage from continuous regeneration. Therefore, we can write
where CR is continuous regeneration. However, Equation (32) contains logical paradoxes. The increasing FC−xz and FC−xz always keep themselves in the Euler force vicinity. Now, we need to solve the equation from a different angle: the viscoelastic behavior of macromolecular materials. According to some studies (Hoffman et al., 2006; Fletcher and Mullins, 2010; Guo et al., 2014) on cell mechanics, let us think of these cells as viscoelastic materials. When these cells are compressed, the elastic forces of the cytoskeletons try to return these cells to their original shape. The elastic forces thus must force the cellular liquid back to the original location. However, the recovery time for this process will occur more slowly than deformation because of the liquid's viscosity. The forces that are produced by continuous regeneration are much larger than the elastic force exerted by the cytoskeletons. A combination of large, stiff proteins; protein complexes; smaller, moveable proteins; siRNA (Hannon and Rossi, 2004);microRNA (Ambros, 2004) and other molecules in the cytoplasm is responsible for the process. Suppose that Ce moves distance Sx along the x-axis after the crypt opening demonstrates an approximately stretched line shape and that the first cell division can trigger EMT. According to Hooke's law, we have
where S1 is the displacement distance of Ce along the x-axis after the first cell's division, and K is a constant. When our system wants to recover its original shape, there is energy loss in the system because the friction between macromolecules and water produces heat loss. It is impossible for Ce to return to its original position based on energy conservation. Therefore, we have
where W1 is the work done along the x-axis after the first cell's division,Fv is the viscous force along the x-axis after the first cell division, and S01 is the actual moved distance of Ce along the return path. Equations (31) and (32) lead us to
Using Equation (33), we get
where n is the number of times a cell divides after the crypt opening has an approximately stretched line shape. In addition, recent studies (Stolberg and McCloskey, 2009; Mou et al., 2017) have suggested that stem cells' differential behaviors are stimulated by stress. Thus, let us add stress to our model. Therefore, the internal stress is caused by stem cell differentiation within Ce'scolumn, which can induce other stem cell differentiation in neighboring columns. The continuous regenerations can trigger EMT at these columns. In the earlier section, it was reasonable to ignore the influences of junctions between CR and other cells on the MCE. Here, it is important to note that our model is in 3D space. For many cross-sections of the gastric pit, the extent of deformations reduces with their distance from MCE along the y-axis based on Saint-Venant's principle (Hibbeler, 2013). Therefore, we can write
where m is the number of cross-sections of the gastric pit, and Sxm is the displacement of the stem cell at the isthmus and neck of the gland along the x-axis.
As mentioned above, the value of FC−xz tends to be infinite in our model. Stem cell differentiation is induced by the stress from FC−xz along the x-axis and MCE's drawing force with the rise in MCE. Because the replication zone of the gastric stem cells is at the bottom of a pit, these stem cells can add cells only near the replication zone of the xz-plane because of continuous regeneration. Therefore, we can rewrite Equation (37) as
Here, AL is the length of these added cells along the x-axis in different xz-planes. The displacement of Ce in the y-direction is less than or equal to the diameter of a cell. Thus, the geometric shape of our model's gastric pit is very similar to the shape of the lateral sulci.
Based on the simulation and analysis of the motion in the epithelium of the fundic gland, multiple white flat lesions are the result of interactions among four types of mechanisms: continuous regeneration, EMT, the viscoelastic properties of the cells and stem cells induced by stress. First, continuous regeneration provides a tensile force to overstretch crypts at the opening of the fundic gland. Second, stress-induced EMT can prevent gastric epithelium breakage along the y-axis. Third, the viscoelastic properties of cells can “remember” the shape of the cells in the xz-plane. Finally, stem cells induced by stress provide enough epithelial cells to relax the overstretched crypt opening. This complex process is repeated until the initial continuous regeneration stops to produce new epithelial cells. The mechanism through which multiple white flat lesions form can also explain why the crypt opening is approximately linear or a reticular groove on the gastric antrum mucosa.
Discussion
Can the evolution between the fundic gland and the pyloric gland trigger EMT?
Many physiological cell functions depend on random macromolecular collisions, such as signaling pathways (Strehl and Rohlf, 2016), replication, and transcription (Krebs, 2013). Although we can explain the mechanism of EMT with the help of pathology and some molecular probes (Kalluri and Weinberg, 2009), some unanswered questions still exist in EMT research. For example, can the evolution between the fundic gland and the pyloric gland trigger EMT? If we want to answer this question from our model, we must know a few of the features inside our cells. Recent studies provide evidence (Ellis and Minton, 2003; Margaret et al., 2005) that our cells have a high concentration of molecules, leading to a crowded environment. The characteristics of our cells suggest at least three effects. (1) Proteins are folded into new states in overcrowded conditions (Dhar et al., 2010). When the new state of the protein cause collision with one another, it usually means that a new chemical reaction occurs in the cell. (2) Protein folding is stabilized in overcrowded conditions (Dhar et al., 2010; McGuffee and Elcock, 2010). (3) According to “random walk” (Xiong, 2015), collision probability is increased between molecular motors and microtubules, which has a vast impact on transportation. In addition, intermolecular forces can be classified into three types of force according to their different physical or chemical origins (Israelachvili, 2011). Owing to the crowded environment in the cell and the entropy rule (Phillips et al., 2009), the intermolecular force has a purely entropic origin, such as pressure (stress) or osmotic force.
Let us return to our model. As previously mentioned, when FC−xz is increased, the cell components above the neutral surface are compressed by the stress, and the cell components below it are stretched by the stress in the opposite direction (Figure 7). The polarized nature of these epithelial cells means that the majority of the cytoplasm is located above the neutral surface. Thus, the density of molecules increases locally above the neutral surface. Regarding diffusion, there is a concentration gradient from the region above the neutral surface to the region below the neutral surface. The viscosity can stop the diffusion of macromolecules. However, our cells use molecular motors to overcome this issue. For example, cytoplasmic dynein and kinesin provide controlled directional movement of macromolecules by means of ATP's chemical energy (Schliwa and Woehlke, 2003) in the cytoplasm. ATP is a small molecule, therefore, Its diffusion is not restricted to the cell's viscosity. Let us suppose that ATP is distributed evenly after deformation and ignore the location of the mitochondria. Molecular motors can carry macromolecules along microtubules. Therefore, the contradiction is that if we donot change the direction of the microtubule, we do not keep the cells in mechanical equilibrium (Phillips et al., 2009) based on the entropy rule. Because of spatial asymmetry and because dynein swivels (Rao and Baas, 2017), the osmotic pressure can force cytoplasmic dynein to rotate in a new direction. As a result, most short mobile microtubules point to the cytoplasm below the neutral surface. When these microtubules are transported to the area below the surface by dynein or they elongate into the area via an assembly of tubulins, the dynamic state of plus-end-out microtubules is broken in the lateral direction because the osmotic pressure forces tubulin' s random motion to move along the longitudinal axis according to a collision probability model (Xiong, 2015). In previous studies, microtubule dynamics have a vast impact on the concentration of E-cadherin at cell junctions (Stehbens et al., 2006; Kitase and Shuler, 2013). Our model suggests that a dynamic change in plus-end-out microtubule spatial position induces a change in the sum adhesive power of E-cadherin. In short, the spatial structure's asymmetry leads to EMT. The spatial structure's asymmetry is rooted in the stress from FC−xz. Certainly, the details of the relationship between E-cadherin and microtubules are not clearly known, and further studies are needed.
In conclusion, when the external force of cell division acts on our model, kinetic energy can be converted back to potential energy by means of the asymmetrical structure. Potential energy is released with the help of elasticity. Viscosity can be overcome by the interaction of macromolecules and micromolecules. In short, our model suggests that the evolution of the fundic gland and the pyloric gland triggers EMT.
Author Contributions
FX conceived the idea. FX designed and analyzed the model. FX wrote the main manuscript text. XL prepared Figures 1, 4, 5. FX prepared Figures 2, 3, 6, 7. FX prepared all supplementary materials. All authors reviewed the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Our work is supported by the Department of Gastroenterology of Sichuan Provincial Hospital.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2018.01388/full#supplementary-material
References
Beasley, D. E., Koltz, A. M., Lambert, J. E., Fierer, N., and Dunn, R. R. (2015). The evolution of stomach acidity and its relevance to the human microbiome. PLoS ONE 10:e0134116. doi: 10.1371/journal.pone.0134116
Boeriu, A., Boeriu, C., Drasovean, S., Pascarenco, O., Mocan, S., Stoian, M., et al. (2015). Narrow-band imaging with magnifying endoscopy for the evaluation of gastrointestinal lesions. World J. Gastrointest. Endosc. 7:10. doi: 10.4253/wjge.v7.i2.110
Brannan, J. R., and Boyce, W. E. (2015). Differential Equations: An Introduction to Modern Methods and Applications Textbook Solutions. Hoboken, NJ: Wiley & Sons.
Broadbelt, N. V., Stahl, P. J., Chen, J., Mizrahi, M., Lal, A., Bozkurt, A., et al. (2007). Early upregulation of iNOS mRNA expression and increase in NO metabolites in pressurized renal epithelial cells. Am. J. Physiol. Renal. Physiol. 293, F1877–1888. doi: 10.1152/ajprenal.00238.2007
Chen, C. H., Cheng, C. Y., Chen, Y. C., Sue, Y. M., Liu, C. T., Cheng, T. H., et al. (2014). MicroRNA-328 inhibits renal tubular cell epithelial-to-mesenchymal transition by targeting the CD44 in pressure-induced renal fibrosis. PLoS ONE 9:e99802. doi: 10.1371/journal.pone.0099802
Correa, P. (1992). Human gastric carcinogenesis: a multistep and multifactorial process—first American Cancer Society award lecture on cancer epidemiology and prevention. Cancer Res. 52, 6735–6740.
Crew, K. D., and Neugut, A. I. (2006). Epidemiology of gastric cancer. World J. Gastroenterol. 12, 23–34. doi: 10.3748/wjg.v12.i3.354
Dhar, A., Samiotakis, A., Ebbinghaus, S., Nienhaus, L., Homouz, D., and Gruebele, M. (2010). Structure, function, and folding of phosphoglycerate kinase are strongly perturbed by macromolecular crowding. Proc. Natl. Acad. Sci. U.S.A. 107, 17586–17591. doi: 10.1073/pnas.1006760107
Ellis, R. J., and Minton, A. P. (2003). Cell biology: join the crowd. Nature 425, 27–28. doi: 10.1038/425027a
Engler, A. J., Sen, S., Sweeney, H. L., and Discher, D. E. (2006). Matrix elasticity directs stem cell lineage specification. Cell 126, 677–689. doi: 10.1016/j.cell.2006.06.044
Feynman, R. P., Leighton, R. B., and Sands, M. (1970). The Feynman Lecture on Physics. London: Addison Wesley Longman.
Fletcher, D. A., and Mullins, R. D. (2010). Cell mechanics and the cytoskeleton. Nature 463, 485–492. doi: 10.1038/nature08908
Guilford, P. J., Hopkins, J. B., Grady, W. M., Markowitz, S. D., Willis, J., Lynch, H., et al. (1999). E-cadherin germline mutations define an inherited cancer syndrome dominated by diffuse gastric cancer. Hum. Mutat. 14, 249–255.
Guo, M., Ehrlicher, A. J., Jensen, M. H., Renz, M., Moore, J. R., Goldman, R. D., et al. (2014). Probing the stochastic, motor-driven properties of the cytoplasm using force spectrum microscopy. Cell 158, 822–832. doi: 10.1016/j.cell.2014.06.051
Guz, N., Dokukin, M., Kalaparthi, V., and Sokolov, I. (2014). If cell mechanics can be described by elastic modulus: study of different models and probes used in indentation experiments. Biophys. J. 107, 564–575. doi: 10.1016/j.bpj.2014.06.033
Hannon, G. J., and Rossi, J. J. (2004). Unlocking the potential of the human genome with RNA interference. Nature 431, 371–378. doi: 10.1038/nature02870
Hoffman, B. D., Massiera, G., Van Citters, K. M., and Crocker, J. C. (2006). The consensus mechanics of cultured mammalian cells. Proc. Natl. Acad. Sci. U.S.A. 103, 10259–10264. doi: 10.1073/pnas.0510348103
Hoffmann, W. (2008). Regeneration of the gastric mucosa and its glands from stem cells. Curr. Med. Chem. 15, 3133–3144. doi: 10.2174/092986708786848587
Hoffmann, W. (2015). Current status on stem cells and cancers of the gastric epithelium. Int. J. Mol. Sci. 16, 19153–19169. doi: 10.3390/ijms160819153
Jense, P. J., and Feldman, M. (2016). Acute and Chronic Gastritis Due to Helicobacter Pylori. Available online at: https://www.uptodate.com/contents/acute-and-chronic-gastritis-due-to-helicobacter-pylori
Johansson, M., Synnerstad, I., and Holm, L. (2000). Acid transport through channels in the mucous layer of rat stomach. Gastroenterology 119, 1297–1304. doi: 10.1053/gast.2000.19455
Kalluri, R., and Weinberg, R. A. (2009). The basics of epithelial-mesenchymal transition. J. Clin. Invest. 119, 1420–1428. doi: 10.1172/JCI39104
Kitase, Y., and Shuler, C. F. (2013). Microtubule disassembly prevents palatal fusion and alters regulation of the E-cadherin/catenin complex. Int. J. Dev. Biol. 57, 55–60. doi: 10.1387/ijdb.120117yk
Margaret, S., and Cheung, D. K. (2005). Molecular crowding enhances native state stability and refolding rates of globular proteins. Proc. Natl. Acad. Sci. U.S.A. 102, 4753–4758. doi: 10.1073/pnas.0409630102
McDonald, S. A., Greaves, L. C., Gutierrez-Gonzalez, L., Rodriguez-Justo, M., Deheragoda, M., Leedham, S. J., et al. (2008). Mechanisms of field cancerization in the human stomach: the expansion and spread of mutated gastric stem cells. Gastroenterology 134, 500–510. doi: 10.1053/j.gastro.2007.11.035
McGuffee, S. R., and Elcock, A. H. (2010). Diffusion, crowding & protein stability in a dynamic molecular model of the bacterial cytoplasm. PLoS Comput. Biol. 6:e1000694. doi: 10.1371/journal.pcbi.1000694
Montgomery, E. A., and Voltaggio, L. (2011). Biopsy Interpretation of the Gastrointestinal Tract Mucosa: Non-Neoplastic (Biopsy Interpretation Series. Vol. 1. Philadelphia, PA: Lippincott Williams & Williams.
Mou, X., Wang, S., Liu, X., Guo, W., Li, J., Qiu, J., et al. (2017). Static pressure-induced neural differentiation of mesenchymal stem cells. Nanoscale 9, 10031–10037. doi: 10.1039/C7NR00744B
Muto, M., Yao, K., and Sano, Y. (2015). Atlas of Endoscopy With Narrow Band Imaging. Japan: Springer Japan.
Niwa, H., Tajiri, H., Nakajima, M., and Yasuda, K. (2008). New Challenges in Gastrointestinal Endoscopy. Tokyo: Springer.
Phillips, R., Kondev, J., Theriot, J., and Garcia, H. (2009). Physical Biology of the Cell. New York, NY: Garland Science.
Phillipson, M. (2004). Acid transport through gastric mucus. Upsala J. Med. Sci. 109, 1–24. doi: 10.3109/2000-1967-106
Rao, A. N., and Baas, P. W. (2017). Polarity sorting of microtubules in the axon. Trends Neurosci. 41, 77–88. doi: 10.1016/j.tins.2017.11.002
Rotterdam, H., and Enterline, H. T. (1989). Pathology of the Stomach and Duodenum. New York, NY: Springer-Verlag
Schliwa, M., and Woehlke, G. (2003). Molecular motors. Nature 422, 759–765. doi: 10.1038/nature01601
Shimizu, S., Tada, M., and Kawai, K. (1995). Early gastric cancer: its surveillance and natural course. Endoscopy 27, 27–31. doi: 10.1055/s-2007-1005628
Stehbens, S. J., Paterson, A. D., Crampton, M. S., Shewan, A. M., Ferguson, C., Akhmanova, A., et al. (2006). Dynamic microtubules regulate the local concentration of E-cadherin at cell-cell contacts. J. Cell. Sci. 119, 1801–1811. doi: 10.1242/jcs.02903
Stevens, C. E., and Leblond, C. P. (1953). Renewal of the mucous cells in the gastric mucosa of the rat. Anat. Rec. 115, 231–245. doi: 10.1002/ar.1091150206
Stolberg, S., and McCloskey, K. E. (2009). Can shear stress direct stem cell fate? Biotechnol. Prog. 25, 10–19. doi: 10.1002/btpr.124
Strehl, R., and Rohlf, K. (2016). Multiparticle collision dynamics for diffusion-influenced signaling pathways. Phys. Biol. 13:046004. doi: 10.1088/1478-3975/13/4/046004
Sugimoto, T., and Ogata, T. (1989). Scanning electron microscopic studies on the subepithelial tissue of the gastrointestinal mucosa of the rat. Arch. Histol. Cytol. 52, 257–265. doi: 10.1679/aohc.52.257
Thomas, G. B., Weir, M. D., Hass, J., and Giordano, F. R. (2004). Thomas' Calculus, 11th Edn. Boston, MA: Addison Wesley.
Toupin, R. A. (1965). Division of Engineering: Saint-venant and a Matter of Principle. New York, NY: The New York Academy of Sciences.
Uedo, N., Ishihara, R., Iishi, H., Yamamoto, S., Yamada, T., Imanaka, K., et al. (2006). A new method of diagnosing gastric intestinal metaplasia: narrow-band imaging with magnifying endoscopy. Endoscopy 8, 819–824. doi: 10.1055/s-2006-944632
Uedo, N., Yamaoka, R., and Yao, K. (2017). Multiple white flat lesions in the gastric corpus are not intestinal metaplasia. Endoscopy 49, 615–616. doi: 10.1055/s-0043-106434
Xiong, F. (2015). A collision probability model of portal vein tumor thrombus formation in hepatocelluar carcinoma. PLoS ONE 10:e0130366. doi: 10.1371/journal.pone.0138165
Yao, K. (2015). Clinical application of magnifying endoscopy with narrow-band imaging in the stomach. Clin. Endosc. 48, 481–490. doi: 10.5946/ce.2015.48.6.481
Keywords: crypt opening, fundic gland, multiple white flat lesions, the Euler force, epithelial-mesenchymal transition
Citation: Xiong F and Liu XG (2018) A Theoretical Model: Elastic Analysis of the Evolution of the Crypt Opening Between the Fundic Gland and the Pyloric Gland. Front. Physiol. 9:1388. doi: 10.3389/fphys.2018.01388
Received: 07 June 2018; Accepted: 12 September 2018;
Published: 02 October 2018.
Edited by:
Stephen J. Pandol, Cedars-Sinai Medical Center, United StatesReviewed by:
Sarbjeet Makkar, Washington University in St. Louis, United StatesMirajul Hoque Kazi, University of Maryland, United States
Copyright © 2018 Xiong and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fei Xiong, ZmVpamkxOTg0MTk4NEBnbWFpbC5jb20=
 Fei Xiong
Fei Xiong Xiao Gang Liu
Xiao Gang Liu