- 1Roy J. Carver Department of Biomedical Engineering, University of Iowa, Iowa City, IA, United States
- 2Department of Anesthesia, University of Iowa, Iowa City, IA, United States
- 3OscillaVent, Inc., Iowa City, IA, United States
- 4Department of Electrical and Computer Engineering, University of Iowa, Iowa City, IA, United States
- 5Department of Radiology, University of Iowa, Iowa City, IA, United States
- 6Department of Radiation Oncology, University of Iowa, Iowa City, IA, United States
- 7Department of Internal Medicine, University of Iowa, Iowa City, IA, United States
Mechanical ventilation strategies that reduce the heterogeneity of regional lung stress and strain may reduce the risk of ventilator-induced lung injury (VILI). In this study, we used registration of four-dimensional computed tomographic (4DCT) images to assess regional lung aeration and deformation in 10 pigs under baseline conditions and following acute lung injury induced with oleic acid. CT images were obtained via dynamic axial imaging (Siemens SOMATOM Force) during conventional pressure-controlled mechanical ventilation (CMV), as well as high-frequency and multi-frequency oscillatory ventilation modalities (HFOV and MFOV, respectively). Our results demonstrate that oscillatory modalities reduce intratidal strain throughout the lung in comparison to conventional ventilation, as well as the spatial gradients of dynamic strain along the dorsal-ventral axis. Harmonic distortion of parenchymal deformation was observed during HFOV with a single discrete sinusoid delivered at the airway opening, suggesting inherent mechanical nonlinearity of the lung tissues. MFOV may therefore provide improved lung-protective ventilation by reducing strain magnitudes and spatial gradients of strain compared to either CMV or HFOV.
Introduction
Ventilator-induced lung injury (VILI) may inadvertently occur in critically ill patients receiving mechanical ventilation, due to the harmful stresses and strains associated with gas flows driven under positive pressure (Slutsky and Ranieri, 2013). Patients with injured, inflamed, and/or edematous lungs, such as those with the acute respiratory distress syndrome (ARDS), are especially at risk for VILI due to increased ventilation heterogeneity (Carrasco Loza et al., 2015). Maintaining normal levels of arterial oxygen and carbon dioxide tensions in patients with ARDS may be extremely difficult using conventional mechanical ventilation (CMV), since increasing the tidal volume or driving pressure to compensate for gas exchange deficiencies may be detrimental to the mechanically over-burdened lung (Acute Respiratory Distress Syndrome Network, 2000; Amato et al., 2015; Gattinoni et al., 2016a). The goal of lung-protective ventilation is to provide life-sustaining gas exchange without exacerbating existing injury within vulnerable parenchymal tissues.
In some instances, high-frequency oscillatory ventilation (HFOV) has been proposed as a rescue treatment for refractory hypoxemia in ARDS, given its theoretically ideal qualities for lung-protection: small tidal volumes that mitigate the risk of dynamic strain injury (i.e., volutrauma), and high mean airway pressures that prevent cyclic recruitment/derecruitment (i.e., atelectrauma) (Sklar et al., 2017). Despite an extensive history of scientific and clinical research over several decades, optimal strategies for HFOV initiation and management remain a subject of controversy (Malhotra and Drazen, 2013; Kneyber and Markhorst, 2016; Nguyen et al., 2016). As it is currently delivered, HFOV may not be an appropriate ventilatory modality in many patients with ARDS for several reasons. First, the use of high mean airway pressures may result in hemodynamic compromise due to impaired venous return and low cardiac output (Meade et al., 2017). In addition, high strain rates within the lung tissues during HFOV may also contribute to VILI, by increasing the mechanical power dissipated across the parenchyma (Gattinoni et al., 2016b; Protti et al., 2016; Herrmann et al., 2019b). Finally, high frequency oscillatory flows are distributed in a heterogeneous and frequency-dependent manner, predisposing overventilated regions to excess mechanical strain, and underventilated regions to derecruitment and atelectasis (Amini and Kaczka, 2013; Herrmann et al., 2016).
Multi-frequency oscillatory ventilation (MFOV) has thus also been proposed as an alternative modality for lung-protective ventilation, by delivering multiple frequencies of oscillatory flow and pressure simultaneously (Kaczka et al., 2015; Herrmann et al., 2019b). MFOV has been shown to improve gas exchange and mechanical function compared to traditional “single-frequency” HFOV (Kaczka et al., 2015; Herrmann et al., 2018). Its postulated mechanism of benefit relies on the frequency-dependence of ventilation distribution and gas transport during conventional and oscillatory modes of ventilation (Herrmann et al., 2018), which can be exploited by using flow waveforms with enhanced harmonic content. Given such frequency-dependence of gas flow throughout the airway tree, mechanically disparate regions of an injured lung may thus selectively filter out “less desirable” frequency components of a broadband oscillatory waveform delivered at the airway opening. The corresponding homogenization of intrapulmonary gas transport with MFOV may then contribute to enhanced gas exchange, and simultaneously distribute the mechanical burden of ventilation more uniformly throughout the lung. Nonetheless, specific experimental evidence to support such a mechanism is lacking, and it remains to be seen whether MFOV improves the regional distribution of parenchymal strain throughout the lung compared to CMV or traditional HFOV.
The purpose of this study was to characterize the distribution of regional intratidal lung deformation during conventional and oscillatory modes of ventilation in pigs under baseline conditions and following acute lung injury with oleic acid. We hypothesized that such variations would be less heterogeneous during MFOV, compared to CMV or traditional single-frequency HFOV. Specifically, we quantified intratidal variations in dynamic regional lung aeration, volumetric strain, and volumetric strain rate during CMV, HFOV, and MFOV using frequency-selective four-dimensional computed tomographic (4DCT) image reconstruction (Herrmann et al., 2017) and registration (Zhao et al., 2016).
Materials and Methods
Animal Preparation
All experimental procedures were approved by the University of Iowa Institute for Animal Care and Use Committee (Protocol Number 5061428). Ten healthy pigs were used in this study, weighing between 9 and 13 kg. Following intramuscular injection of 2.2 mg kg−1 telazol, 1.1 mg kg−1 ketamine, and 1.1 mg kg−1 xylazine, general anesthesia was induced during spontaneous breathing with inhaled isoflurane delivered via nosecone. Each pig was then intubated with a cuffed endotracheal tube (4.5–5.5 mm inner diameter), and mechanically ventilated (Uni-Vent Eagle Model 754, ZOLL Medical Corporation, Chelmsford, MA). Capnography, peripheral oxygen saturation (SpO2), and electrocardiogram waveforms were obtained using a Philips patient monitor equipped with the M3001A measurement module (Philips Healthcare, Andover, MA). Surgical incision into the neck was performed to allow cannulation of the internal jugular vein and carotid artery, as well as relocation of the endotracheal tube into an incision in the trachea just below the larynx. Endotracheal tubes were manually shortened (to final length 12–15 cm depending on tube diameter) prior to tracheostomy, to reduce apparatus deadspace. Anesthesia was maintained using an intravenous infusion of propofol (7–9 mg kg−1 hr−1), and muscular relaxation was achieved using intermittent intravenous boluses of either rocuronium (1–2 mg kg−1) or pancuronium (0.01–0.15 mg kg−1).
Lung injury was induced by slow infusion of 0.08 cm3 kg−1 oleic acid into the internal jugular vein over 15 min. Maturation of injury required ~90 min, and was confirmed by a ratio of arterial oxygen tension to inspired oxygen fraction (PaO2:FiO2) <300 mmHg during ventilation with 5 cmH2O of positive end-expiratory pressure (PEEP). Additional oleic acid (0.04 cm3 kg−1) was administered if PaO2:FiO2 remained >300 mmHg 90 min after the initial dose. If necessary, normal systemic arterial blood pressure (systolic/diastolic ≥ 90/60 mmHg) was maintained with intravenous crystalloid solutions and intermittent doses of phenylephrine (1–2 μg kg−1).
Experimental Protocol
All measurements and ventilation modalities were performed under baseline conditions and following lung injury. Each subject was mechanically ventilated with CMV, HFOV, and MFOV in random order over 30-min intervals, using a FabianHFO hybrid oscillator/ventilator (Acutronic Medical Systems AG, Switzerland). Mean airway pressure () was set to 12 cmH2O for all modalities. During baseline conditions, FiO2 was set to 40%, but was increased to maintain SpO2 ≥ 90% following lung injury. Pressure-controlled CMV was delivered at rates between 20 and 32 min−1 (0.33 to 0.53 Hz), with inspiratory:expiratory ratio of 1:2. Single-frequency HFOV was delivered at 5 Hz, while MFOV was delivered using a combination of 5, 10, 15, and 20 Hz superimposed sinusoids with uniform flow amplitudes (Kaczka et al., 2015). Example ventilator waveforms are provided in Supplementary Figures S-1, S-2, S-3. Sampling frequency for recorded ventilator waveforms was 200 Hz. Ventilator driving pressure or pressure amplitudes were adjusted to obtain arterial CO2 tension (PaCO2) in the target range of 30–60 mmHg. Each 30-min experimental interval was followed by an arterial blood gas analysis and 4DCT scan sequence, without interrupting mechanical ventilation (Herrmann et al., 2017). Between each experimental ventilation interval, a 15-min wash-out period of CMV and a 30-s recruitment maneuver to 35 cmH2O of airway pressure were used to restore a control mechanical and physiological state. After completion of the experimental protocol, subjects were euthanized with an intravenous solution of pentobarbital sodium and phenytoin sodium (1 mL + 0.2 mL kg−1).
Assessment of Gas Exchange and Mechanics
Oxygenation was assessed using the oxygenation index (OI), defined as (Ortiz et al., 1987):
The efficiency of CO2 elimination during each modality was assessed using a ventilatory cost function (VC), defined as (Kaczka et al., 2015):
where Vrms is the root mean-square of the volume waveform V(t) delivered to the airway opening:
T denotes the time duration over which the integration in Equation (3) is performed (i.e., one breath for CMV or one second during HFOV/MFOV), and is the mean of the volume waveform over the interval 0 to T.1 Peak-to-peak range of volume (Vpp) was computed as the difference between the largest and smallest values of time-varying volume:
Dynamic respiratory system elastance (Ers) during pressure-controlled CMV was computed as the quotient of driving pressure (ΔPaw) and tidal volume:
where:
Measurements of respiratory impedance (Zrs) were obtained under baseline conditions and after maturation of lung injury. A pseudorandom waveform consisting of nine sinusoids ranging in frequency from 0.078 to 8.9 Hz was generated by a digital-to-analog converter (NI USB-6356, National Instruments, Austin, TX), low-pass filtered at 12 Hz (858L8B-2, Frequency Devices, Haverhill, MA), and used as the input driving signal to a custom servo-controlled pneumatic pressure oscillator (Kaczka and Lutchen, 2004). Airway pressure was measured with a transducer placed at the proximal end of the endotracheal tube (Celesco LCVR-0050, Canoga Park, CA), while flow was measured using a screen pneumotach (4700A, Hans Rudolph, Shawnee, KS) coupled to a differential pressure transducer (Celesco LCVR-0002, Canoga Park, CA). The airway pressure and flow signals were sampled at 40 Hz over ~90 s during the application of forced oscillations, allowing for three repetitions of the 25.6-s periodic control signal. Each Zrs spectrum and its corresponding coherence function (γ2) was computed using the Welch periodogram technique (Welch, 1967), with rectangular windowing and 80% overlap. The complex values of Zrs were evaluated only at the nine frequencies used in the control signal (Suki and Lutchen, 1992). Corresponding resistance Rrs and reactance Xrs spectra were defined by the real and imaginary parts of Zrs, respectively. The resonant frequency fres was estimated from the zero-crossing of Xrs using spline interpolation. Each Zrs spectrum was then characterized by a 4-element constant-phase model consisting of parameters for Newtonian airway and chest wall resistance (R), airway inertance (Iaw), tissue hysteresivity (η), and tissue elastance (H):
where Ẑrs denotes the model-predicted Zrs and . Model parameters were estimated by constrained nonlinear gradient descent technique (MATLAB, Natick, MA).
Image Acquisition and Processing
CT scans were acquired using a Siemens SOMATOM Force (Siemens Healthineers, Germany) in an axial scanning mode, with 5.76 cm of axial coverage and 0.6 mm slice thickness. Subjects were continuously scanned at 80 kVp tube voltage and 150 mA tube current, with 250 ms scanner rotation period. Each scan lasted a total duration of 30 s, resulting in a radiation exposure of 345 mGy and generating a continuous set of projection images. The 4DCT image sequences were reconstructed by retrospective binning of x-ray projection data according to mechanical ventilation phase using a frequency-selective reconstruction algorithm (Herrmann et al., 2017), yielding between 13 and 21 volumetric images per 4DCT sequence with isotropic 0.6 mm spatial resolution. The corresponding temporal sampling frequencies for 21-phase image sequences were 7 Hz during CMV with fundamental 0.33 Hz, and 105 Hz during HFOV or MFOV with fundamental 5 Hz. Each sequence was periodic in the temporal (i.e., ventilation phase) dimension, such that the choice of “initial” image in the sequence was arbitrary. Each volumetric image in the temporal sequence was labeled In(xn), where n indexes the number of images in the sequence 0 through N − 1, and xn is a vector representing 3-dimensional spatial position. Voxels corresponding to spatial positions within the lungs were identified by a fully automated segmentation algorithm using a deep convolutional neural network (Gerard et al., 2018, 2020), generating a distinct lung mask Mn(xn) for each image phase. The neural network was trained using manually segmented lungs in CT images obtained from multiple datasets of experimental lung injury models, including a subset of images from the current study.
The periodic motion of respiratory structures was estimated using a deformable 4D image registration technique. This procedure produced N 3-dimensional transformation functions denoted as ϕn(X) = xn, where X is a vector representing 3-dimensional spatial position within the reference frame of a phase-averaged image Iavg(X), and xn represents spatial position in image In(xn). Image Iavg(X) was used as the target for groupwise image registration of the images In(xn), n = 0…N − 1. Thus, ϕn(X) = xn is a spatial mapping from the coordinate system of Iavg(X) to that of In(xn), such that a deformed image In → avg(X) was generated with respiratory structures aligned to the target image as:
Figure 1 shows a schematic of the transformations mapping between all images in the periodic sequence and Iavg(X). The transformations ϕn(X) were coupled together using 4-dimensional cubic B-splines and jointly estimated to ensure smoothness across both spatial and temporal dimensions (Metz et al., 2011). The parameters of the transformation function were iteratively adjusted using the Elastix library (Klein et al., 2010) to minimize the sum of squared tissue volume differences (SSTVD) between each In → avg(X) and Iavg(X), such that each deformed image preserved the volume of tissue contained within each voxel (Gorbunova et al., 2008; Yin et al., 2009; Zhao et al., 2016). Thus, changes in CT voxel density due to variations in fractional gas content were adjusted using this similarity cost function. Following registration, ϕn(X) and its inverse mapping were used to align images between arbitrary phases. Deformed images were denoted as In→m(xm), indicating the nth image deformed into the mth spatial reference frame:
For the trivial case of m = n, Equation (9) simplifies to In→n(xn) = In(xn). Conceptually, aligning images from any two phases can be achieved by warping one spatial reference frame to another, passing through the target reference frame X (see Figure 1). Using this approach, all images were warped to align structures with a single, arbitrarily selected reference phase at m = 0. Phasic variations in regional aeration and strain could then be associated with the tissue contained within the region of interest at the reference phase. Figure 2 schematizes the use of a single reference phase to align respiratory structures across several ventilatory phases, thus tracking tissue-correlated changes in aeration and regional volume. Changes in regional aeration were then assessed by the range of voxel intensity values in the deformed image:
while changes in regional volumetric strain were estimated using the Jacobian matrix () of transformation spatial derivatives:
where ∇xm is the spatial gradient operator. Note that is expressed in the mth spatial reference frame and describes the gradient of the “pullback” transformation . This pullback transformation is interpreted as “pulling back” point xn in ventilation phase n to the corresponding point xm in phase m. Regional volume changes relative to the reference phase (i.e., m = 0) were computed by the determinant of :
where Vn(x0) corresponds to the phase-varying volume of a region which, in the reference phase 0, occupies a single voxel centered at position x0. Accordingly, V0(x0) is everywhere equal to the volume of a single voxel δV, determined by the image spatial resolution. Thus, Equation (12) may be simplified to:
Note that when the corresponding region deflates relative to the reference phase, when it expands, and when there is no volume change (i.e., isovolumetric deformation). Figure 3 shows an example image sequence for each ventilation modality in one injured subject, demonstrating phase-varying aeration In → 0(x0) and volume change Vn(x0) for each voxel in a sample region of interest in x0. Animated image sequences for one subject under baseline and injured conditions are also provided (Supplementary Animations S-1, S-2). Phase-varying strain (ε) for each lung region with respect to its respective minimum inflation state was defined as:
Changes in regional volumetric strain were assessed by the range of εn(x0):
Since the minimum value of εn(x0) is zero by definition, Equation (15) may be reduced to:
Similarly, regional volumetric strain rate () was computed by the temporal rate of change in εn(x) using the forward difference scheme:
where δt is the time difference between adjacent phases. The modulo operator is used to indicate the periodicity of ventilatory phase. The value of δt is computed from the ventilatory fundamental frequency (f0) and the number of images in the 4DCT sequence (N):
Finally, changes in regional volumetric strain rate were assessed by the range of :
Note that generally will be positive during inflation of a specified lung region, and negative during the corresponding deflation. Thus, will reflect the sum of the fastest inflation and deflation rates of the region.
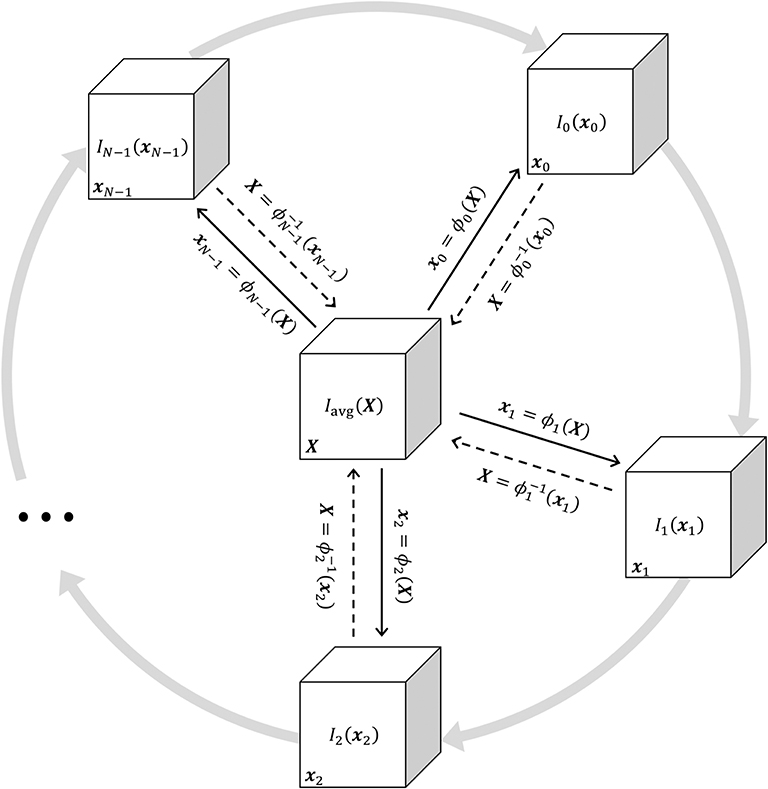
Figure 1. Schematic illustrating the jointly estimated 3D transformations ϕn(X) = xn mapping between all images in the periodic 4DCT image sequence In(xn) and the target average image Iavg(X). Solid black arrows indicate the transformation from the target reference frame X to the general reference frame xn. Dashed black arrows indicate the inverse transformation. Gray arrows represent the periodic sequence of N ventilatory phases indexed from 0 to N − 1. Any In(xn) may be deformed to achieve structural alignment with any other Im(xm) by applying a sequence of two transformations , warping xm through X.
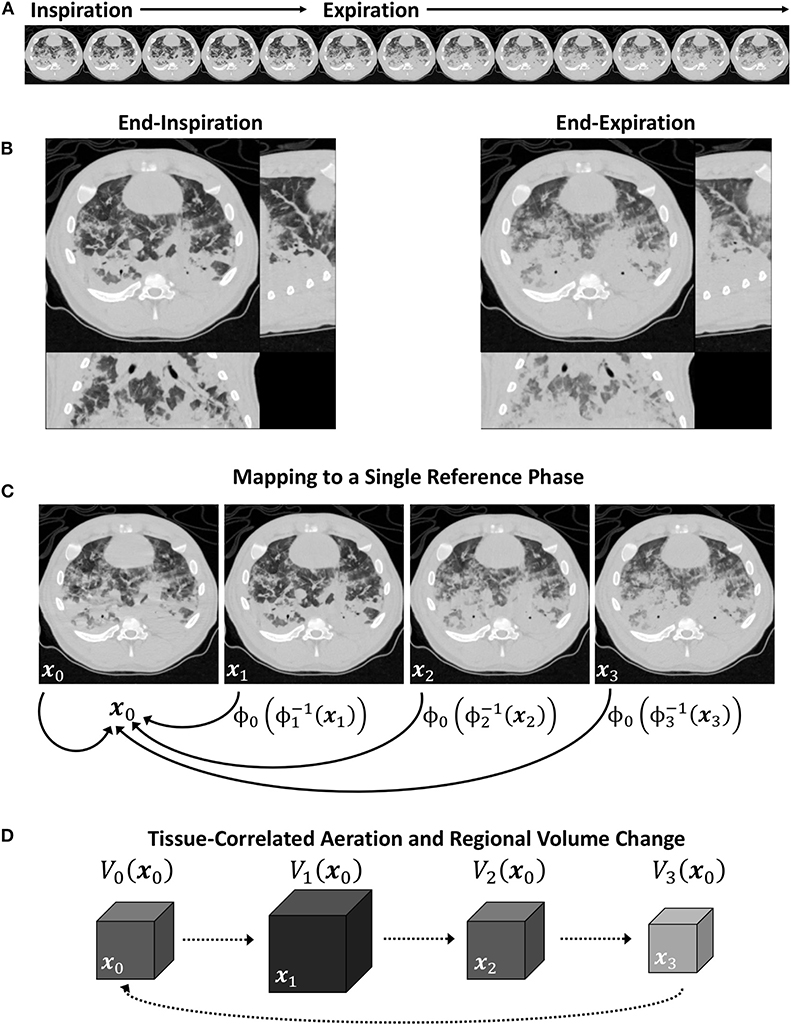
Figure 2. Schematic of a periodic 4DCT image sequence during conventional mechanical ventilation (A), with inspiratory and expiratory phases (B). Image registration is used to map each image in the sequence to a single reference phase (C), after which intratidal variations in aeration and regional volume may be associated to specific regions of lung tissue (D).
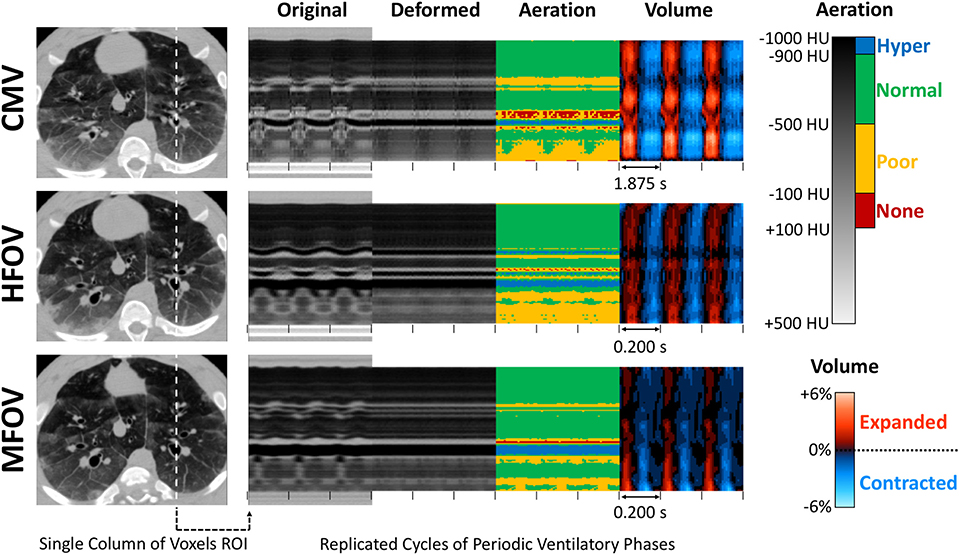
Figure 3. Four-dimensional image registration was used to deform images such that respiratory structures were aligned to a single reference phase. After registration, regional aeration and volume change throughout the lung were assessed by the variations in deformed image voxel value and determinant of the Jacobian matrix of the deformation. This technique was applied during conventional mechanical ventilation (CMV), high-frequency oscillatory ventilation (HFOV), and multi-frequency oscillatory ventilation (MFOV). Ventilatory cycle duration is indicated by spacing between tick marks. In this example, each ventilatory cycle corresponds to a sequence of images representing 21 distinct ventilatory phases. Note that multiple cycles of each ventilation waveform are shown for clarity, however all cycles are identical replicates. See also Supplementary Animations S-1, S-2.
Voxels within 6.0 mm of the image boundaries along the rostral-caudal axis were excluded from the mask for the purposes of image analysis, due to potential registration artifacts caused by motion of lung tissue into or out of the axial field of view. Regional aeration (ΔI), strain (Δε), and strain rate () were compared across subjects, lung conditions, and ventilation modalities by their mean value throughout the lung mask, coefficient of variation, and spatial gradients in the right-left, dorsal-ventral, and rostral-caudal directions. Spatial gradients for each variable were determined from the slopes computed by linear regression with respect to position along each of the principal anatomic axes. Spatial gradients were examined unnormalized and normalized by the spatial mean, in each case comparing both signed values of the gradient (i.e., positive and negative) and gradient magnitude (i.e., absolute value).
Given the harmonic nature of MFOV, the individual frequency components of In, εn, and were assessed using the Discrete Fourier Transform (DFT), to relate these periodic time-varying properties at each spatial position into harmonic amplitude and phase components. The regional heterogeneity of volumetric strain (Δε) was assessed using octree and supervoxel decomposition, each of which recursively subdivide regions-of-interest (ROIs) within the lung mask. Both decomposition methods were initialized with a single ROI containing the entire lung mask. At each recursive step, the designated ROI was subdivided into multiple new ROIs if the standard deviation of the contained voxel intensity was greater than a fixed threshold, set to a standard deviation of mean-normalized Δε ≥ 0.3.2 Octree decomposition, a three-dimensional extension of quadtree decomposition, was used to partition each ROI into eight octants according to bisecting coronal, sagittal, and transverse planes (Perchiazzi et al., 2014). Supervoxel decomposition was used to partition each ROI into two new ROIs by a weighted k-means clustering of voxels according to intensity similarity and spatial proximity (Conze et al., 2017). Recursive subdivision was continued until all ROIs either contained below-threshold values of standard deviation, or were <0.2% of the lung mask. Regional heterogeneity of Δε was then quantified by the mean ROI volume () as a fraction of the lung mask.
Statistics
Non-parametric Kruskal-Wallis rank sum tests were performed for each outcome, testing for main effects of lung condition (i.e., baseline, injured) and ventilation modality (i.e., CMV, HFOV, MFOV) at the 0.05 significance level. The effect of ventilation modality was tested separately under baseline and injured conditions. For outcomes with a significant main effect of ventilation modality, differences among modalities were identified by a Dunn post hoc comparison with adjustment for rank ties and further adjustment by the Benjamini-Hochberg procedure for reduced false discovery rate. A web-based tool was used for statistical calculations (Vasavada, 2016).
Results
Figure 4 shows a summary of the respiratory impedance spectra Zrs across all subjects measured under baseline and injured conditions, while Table 1 provides a summary of the constant phase model applied to Zrs. Under baseline conditions, average model-based tissue elastance H was 121 cmH2O L−1 at 1 rad s−1 (0.16 Hz) with a coefficient of variation of 0.31. The increase in H after oleic acid injury was highly variable, resulting in a mean of 435 cmH2O L−1 at 1 rad s−1 with a coefficient of variation of 0.94. By comparison, measurement of dynamic elastance (Ers) during CMV (Equation 5) was 148.9 ± 26.9 cmH2O L−1 and 257.5 ± 64.2 cmH2O L−1 under baseline and injured conditions, respectively. Resonant frequency (fres) increased after lung injury, in some cases above the measurement range allowed by the sampling parameters. Table 2 contains a summary of all significant effects identified by non-parametric Kruskal-Wallis tests, as well as post hoc comparisons as appropriate. These results are described further in the context of specific figures below.
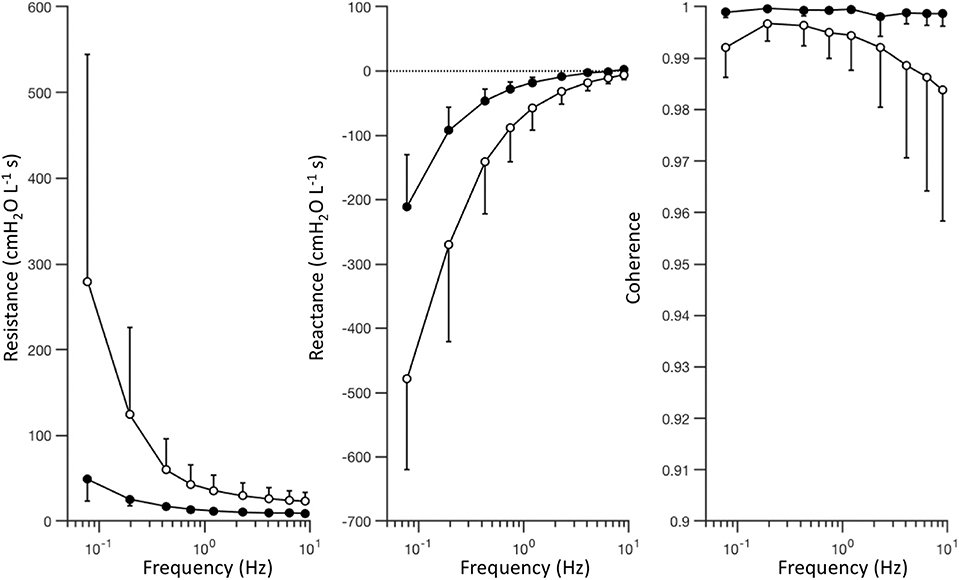
Figure 4. Respiratory impedance measured under baseline (black) and injured (white) conditions, represented by the mean value (circles) and standard deviation (error bars) at each frequency, across subjects. The complex-valued impedance spectrum is represented by its real part or in-phase component (i.e., resistance), and its imaginary part or out-of-phase component (i.e., reactance). Coherence provides an estimate of signal quality and linearity of the measured relationship between pressure and flow oscillations.
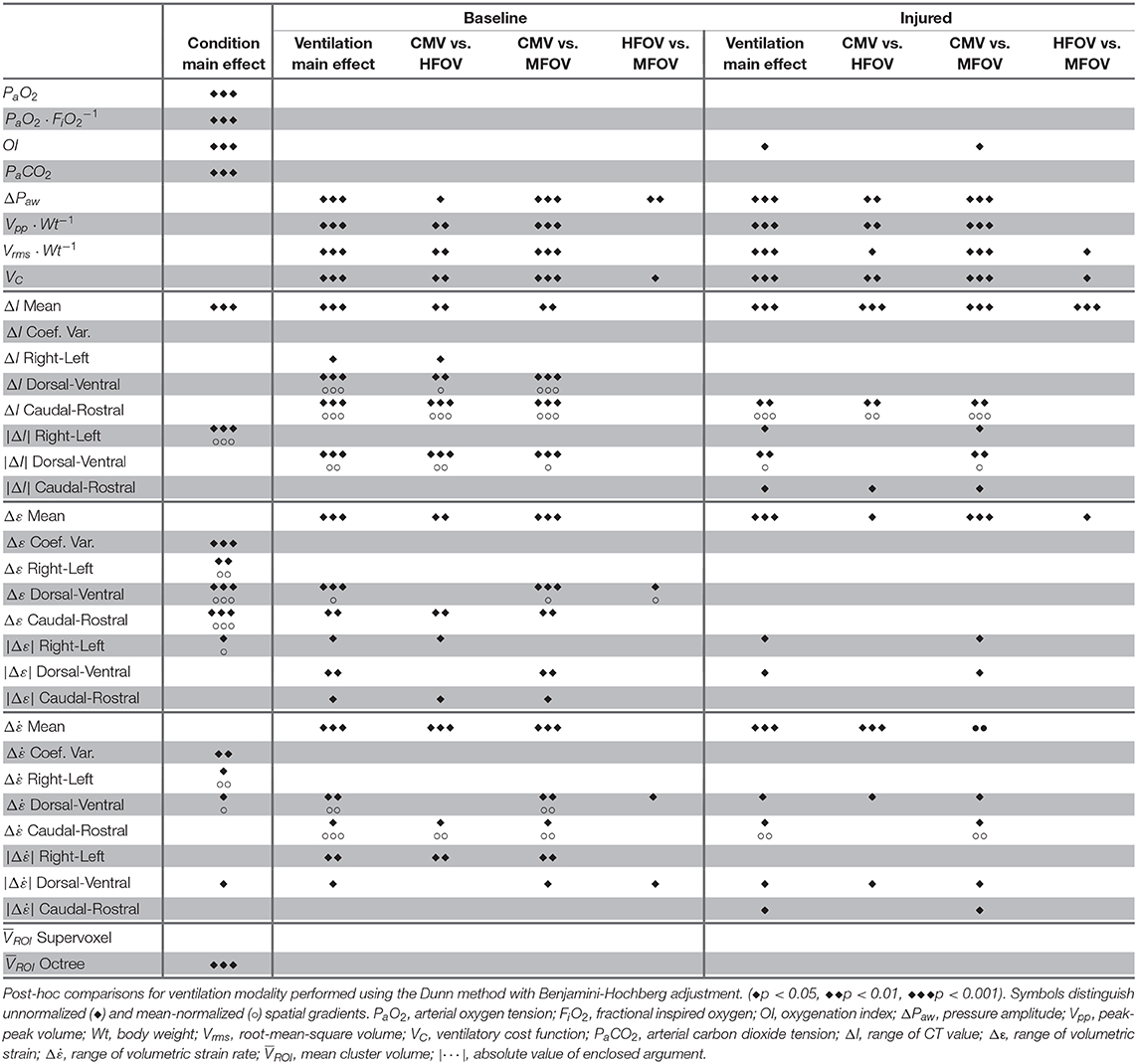
Table 2. Statistically significant effects determined by Kruskal-Wallis rank sum test for main effects of lung condition (i.e., baseline, injured) and ventilation modality (i.e., CMV, HFOV, MFOV).
Figure 5 shows gas exchange outcomes related to mechanical ventilation, including oxygenation index () and ventilatory cost function (). A significant main effect of lung condition (baseline vs. injured) was found for PaO2, , OI, and PaCO2 (p < 0.001). A significant main effect of ventilation modality was found in ΔPaw, , , and VC (p < 0.001) for both lung conditions, as well as in OI for the injured condition (p < 0.05). In particular, median OI increased by 300% for injured subjects compared to baseline (p < 0.001), but was 48% lower for injured subjects during MFOV compared to CMV (p < 0.05). MFOV and HFOV were associated with lower median VC for both baseline and injured conditions compared to CMV (HFOV 84% lower than CMV, p < 0.01; MFOV 93% lower than CMV, p < 0.001). Pairwise comparison of VC for MFOV against HFOV also achieved a statistically significant difference, with 60% lower median VC for MFOV compared to HFOV (p < 0.05). Median was 41% lower for MFOV vs. HFOV (p = 0.0505 baseline; p < 0.05 injured) and 75% lower for MFOV vs. CMV (p < 0.001).
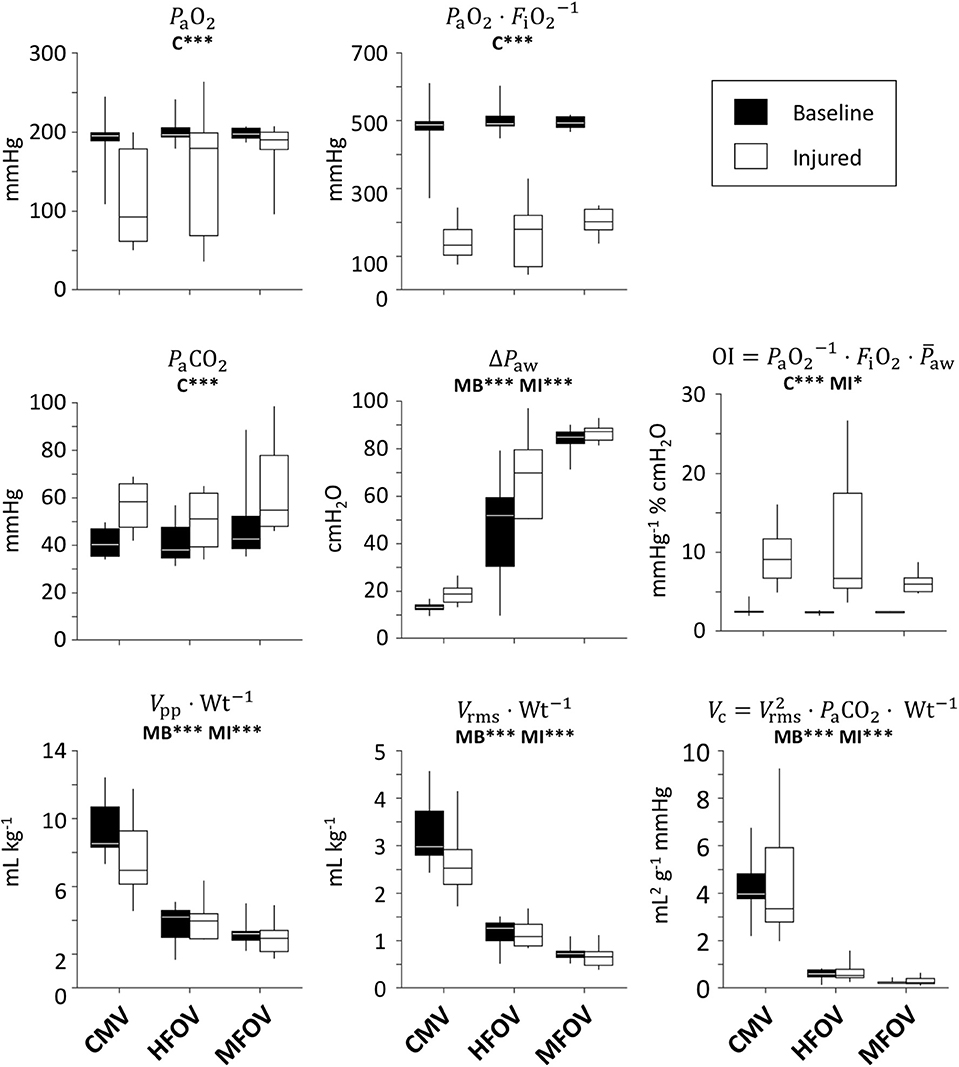
Figure 5. Gas exchange outcomes, represented by box plots showing minimum, maximum, and quartiles across subjects under baseline (black) and injured (white) conditions, during conventional mechanical ventilation (CMV), high-frequency oscillatory ventilation (HFOV), and multi-frequency oscillatory ventilation (MFOV). Asterisks indicate significance levels (*p < 0.05, ***p < 0.001) for main effects (C = lung condition, MB = modality for baseline condition, MI = modality for injured condition). See Table 2 for additional clarification. PaO2 = arterial oxygen tension; FiO2 = fractional inspired oxygen; PaCO2 = arterial carbon dioxide tension; ΔPaw = airway pressure amplitude; Vpp = peak-to-peak volume range; Wt = body weight; Vrms = root-mean-square volume.
Figure 6 shows registration-based estimates of regional ventilation, as intratidal changes in voxel aeration (ΔI), volumetric strain (Δε), and volumetric strain rate (. A significant main effect of condition (baseline vs. injured) was found for ΔI spatial mean (p < 0.001), Δε coefficient of variation (p < 0.001) and coefficient of variation (p < 0.01). A significant main effect of ventilation modality was found for the spatial means of all three variables—ΔI, Δε, and –in both baseline and injured lung conditions (p < 0.001). In particular, MFOV and HFOV both produced smaller ΔI, smaller Δε, and larger compared to CMV under baseline and injured conditions (p < 0.05). For the injured condition, MFOV resulted in significantly lower ΔI and Δε compared to HFOV (p < 0.05), but no difference for (p = 0.20).
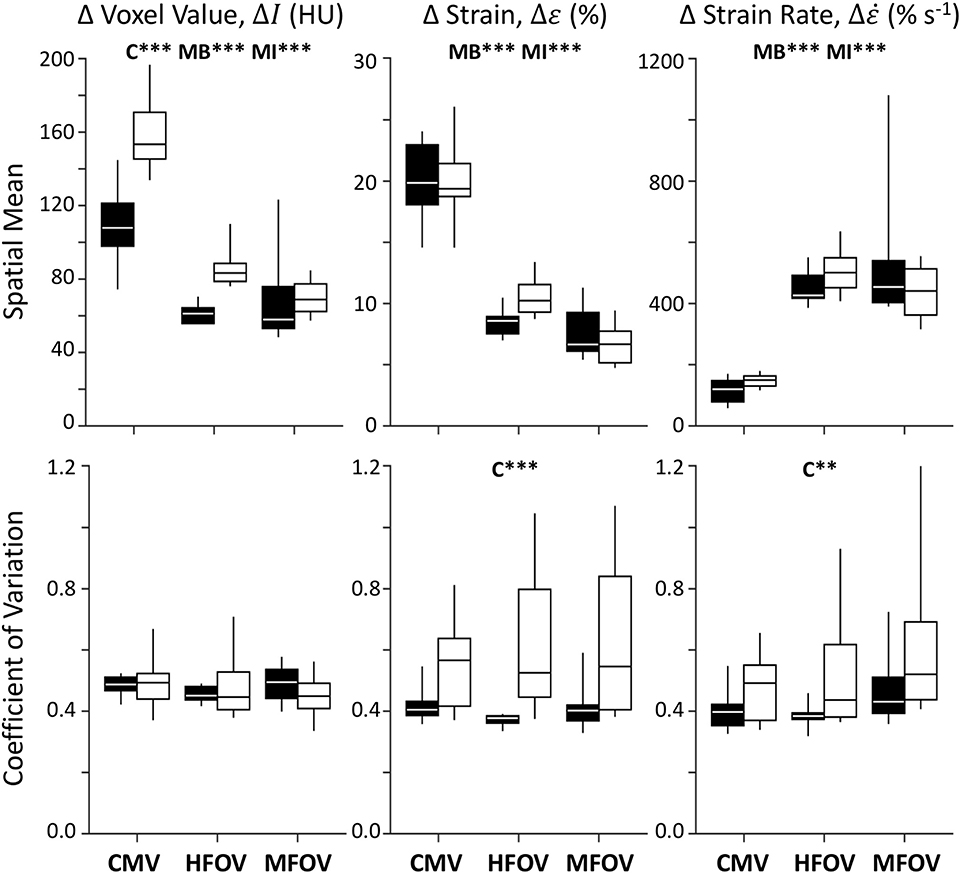
Figure 6. Summary of image registration-based regional ventilation measures for intratidal changes in aeration (ΔI), volumetric strain (Δε), and volumetric strain rate (). Mean and coefficient of variation throughout the lung mask are shown for each variable, represented by box plots showing minimum, maximum, and quartiles across subjects under baseline (black) and injured (white) conditions, during conventional mechanical ventilation (CMV), high-frequency oscillatory ventilation (HFOV), and multi-frequency oscillatory ventilation (MFOV). Asterisks indicate significance levels (**p < 0.01, ***p < 0.001) for main effects (C = lung condition, MB = modality for baseline condition, MI = modality for injured condition). See Table 2 for additional clarification.
Figure 7 shows unnormalized spatial gradients of ΔI, Δε, and in the right-left, dorsal-ventral, and caudal-rostral axes. The largest spatial gradient magnitudes observed occurred along the dorsal-ventral axis. In particular, the injured lung condition was associated with significantly more positive dorsal-ventral gradients of Δε (p < 0.001) and (p < 0.05). Ventilation modality had a significant effect on all dorsal-ventral gradients under baseline conditions (ΔI, p < 0.001; Δε, p < 0.001; , p < 0.01), with MFOV producing the least negative dorsal-ventral gradients of ΔI and Δε, but the most positive dorsal-ventral gradients of . Although modality was not a significant predictor of variability in the actual value (positive or negative) of any dorsal-ventral gradient for injured subjects, it was a significant main effect for the magnitudes of all dorsal-ventral gradients (ΔI, p < 0.001; Δε, p < 0.01; , p < 0.05). In general HFOV and MFOV reduced the dorsal-ventral gradient magnitudes of ΔI and Δε under both baseline and injured conditions, while increasing the corresponding gradient. Figure 8 shows corresponding mean-normalized spatial gradients. In general, normalizing each spatial gradients by the respective spatial mean accounted for much of the variability observed in the unnormalized spatial gradients (Figure 7) with respect to varying ventilation modality. This is also evidenced by the loss of significant differences between ventilation modalities for the corresponding spatial gradients as indicated in Table 2.
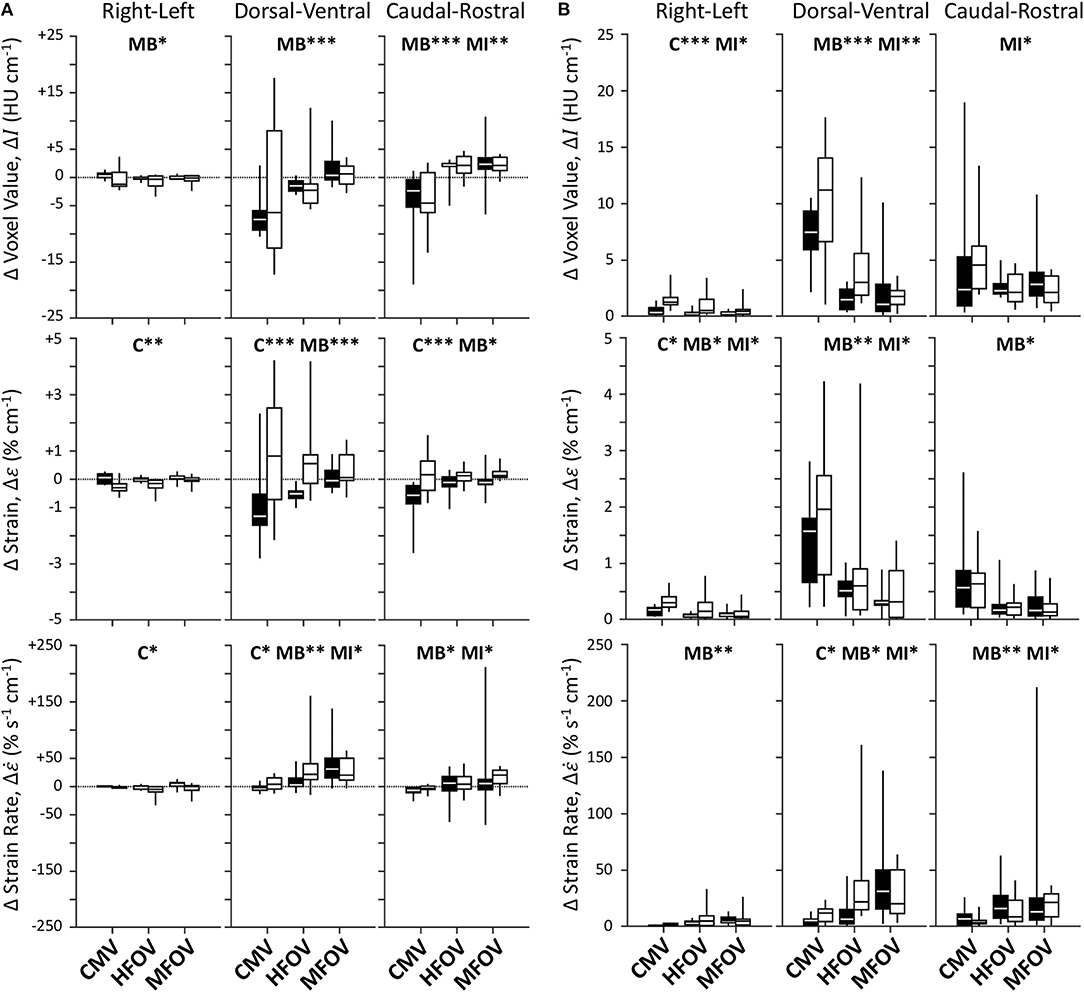
Figure 7. Unnormalized spatial gradient values (A) and magnitudes (B) for image registration-based regional ventilation measures of intratidal changes in aeration (ΔI), volumetric strain (Δε), and volumetric strain rate (). Linear spatial gradients in each of the three principal anatomic directions throughout the lung mask are shown for each variable, represented by box plots showing minimum, maximum, and quartiles across subjects under baseline (black) and injured (white) conditions, during conventional mechanical ventilation (CMV), high-frequency oscillatory ventilation (HFOV), and multi-frequency oscillatory ventilation (MFOV). Asterisks indicate significance levels (*p < 0.05, **p < 0.01, ***p < 0.001) for main effects (C = lung condition, MB = modality for baseline condition, MI = modality for injured condition). See Table 2 for additional clarification.
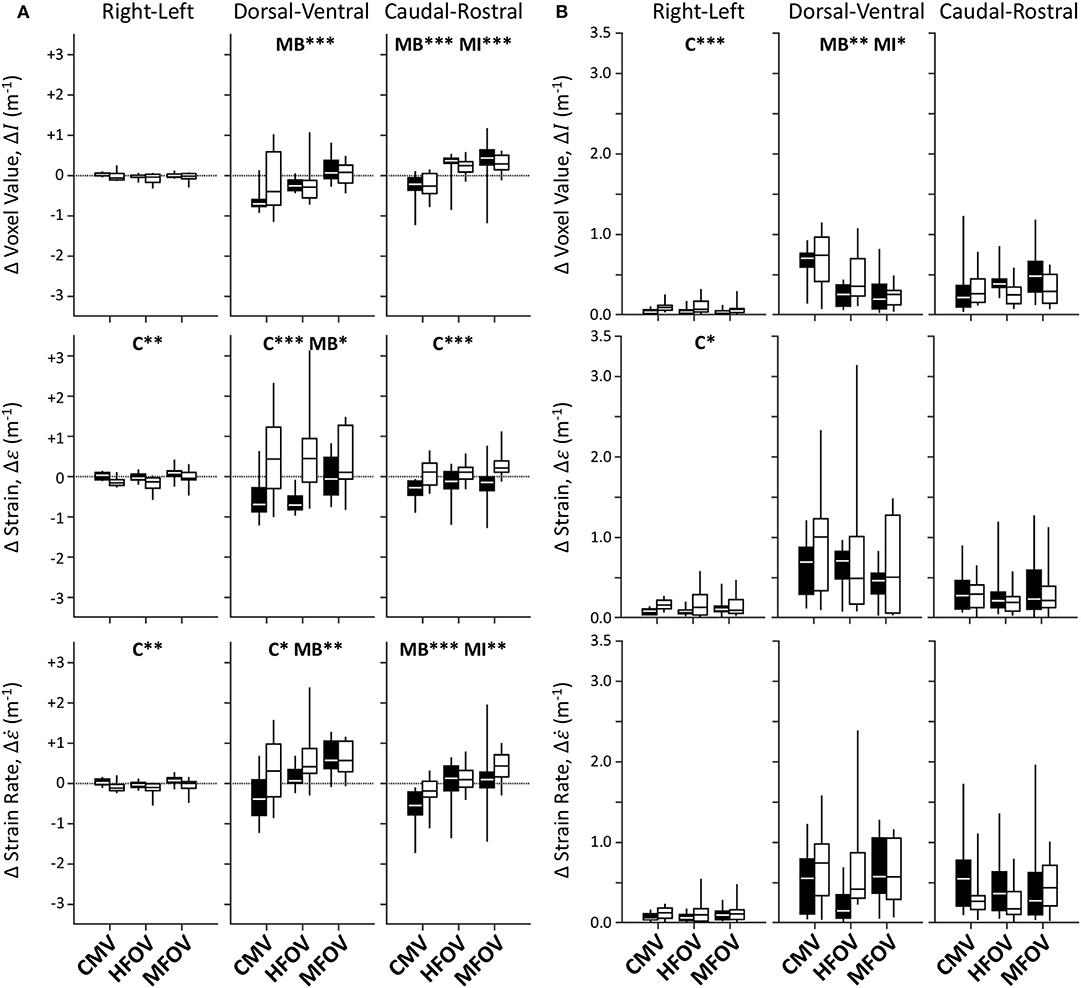
Figure 8. Mean-normalized spatial gradient values (A) and magnitudes (B) for image registration-based regional ventilation measures of intratidal changes in aeration (ΔI), volumetric strain (Δε), and volumetric strain rate (). Linear spatial gradients in each of the three principal anatomic directions throughout the lung mask are shown for each variable, represented by box plots showing minimum, maximum, and quartiles across subjects under baseline (black) and injured (white) conditions, during conventional mechanical ventilation (CMV), high-frequency oscillatory ventilation (HFOV), and multi-frequency oscillatory ventilation (MFOV). Asterisks indicate significance levels (*p < 0.05, **p < 0.01, ***p < 0.001) for main effects (C = lung condition, MB = modality for baseline condition, MI = modality for injured condition). See Table 2 for additional clarification.
Figure 9 shows an example of regions-of-interest defined by recursive supervoxel and octree decomposition performed on mean-normalized Δε in one subject. Clustered regions are illustrated using contours and filled regions in two-dimensional views of a slice, as well as translucent surface renderings in three-dimensional projections. Note that supervoxel decomposition produces larger contiguous ROIs, despite using the same decision criteria for recursive cluster subdivision. Figure 9 also provides a summary of mean cluster size () across subjects, condition, and ventilation modality. A significant effect of lung condition was found for the octree technique (p < 0.001), with 32% smaller median in injured lungs.
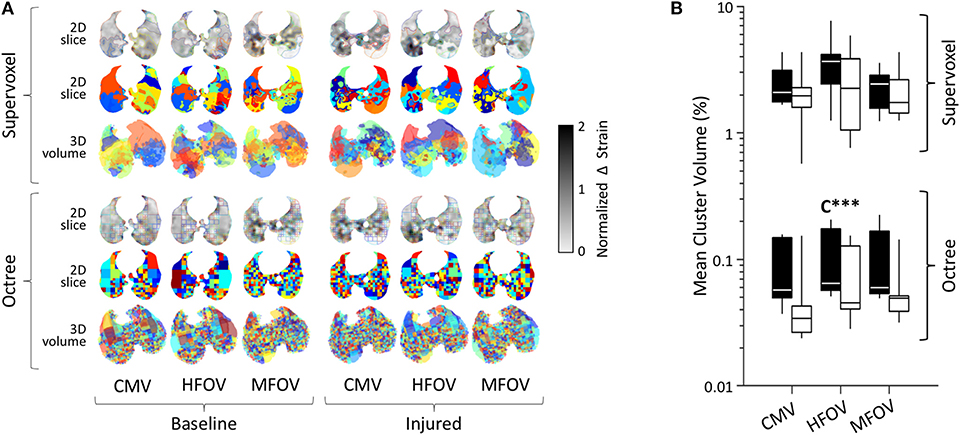
Figure 9. Regional patchiness of intratidal variations in volumetric strain (Δε) during conventional mechanical ventilation (CMV), high-frequency oscillatory ventilation (HFOV), and multi-frequency oscillatory ventilation (MFOV). Regional patchiness was assessed by the size, number, and distribution of regions-of-interest or clusters (randomized colors) obtained by recursive supervoxel or octree decomposition. Examples from a representative subject (A), and cluster volumes as a fraction of the lung mask (B) represented by box plots showing minimum, maximum, and quartiles across subjects under baseline (black) and injured (white) conditions. Asterisks indicate significance levels (***p < 0.001) for main effects (C = lung condition).
Figure 10 shows example distributions of strain amplitude and phase at the first four harmonics for CMV, HFOV, or MFOV, computed using the discrete Fourier transform of time-varying Jacobian determinants in aligned images. Figure 11 provides a summary of the harmonic strain amplitudes during HFOV and MFOV across all subjects, correlated with corresponding amplitudes of the ventilator volume waveform V(t). The oscillatory waveforms were a 5 Hz sinusoid (HFOV) and a combination of 5, 10, 15, and 20 Hz sinusoids with uniform flow amplitudes (MFOV). The relative amplitude distributions in the flow waveforms delivered by the ventilator were largely preserved throughout the lung, according to the registration-based metrics (r2 = 0.78). However, harmonic distortion measurements during HFOV indicated nearly 20% of the spectral power in regional strain was concentrated in the higher-order harmonics of the 5 Hz waveform (i.e., 10, 15, 20 Hz), whereas the ventilator volume waveform exhibited only 5% harmonic distortion (Zhang et al., 1995; Amini et al., 2017).
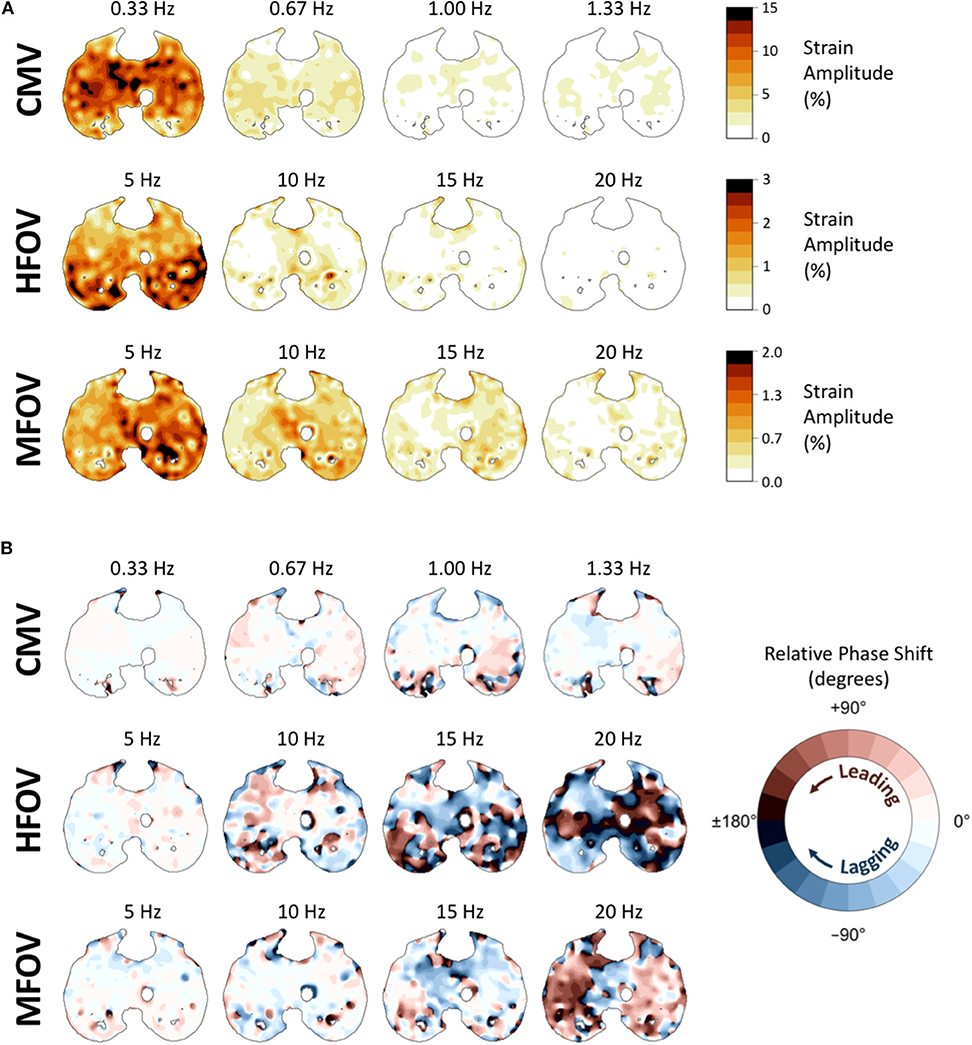
Figure 10. Frequency-domain representations of tissue-correlated regional strain amplitude (A) and phase variations (B) in one subject during conventional mechanical ventilation (CMV), high-frequency oscillatory ventilation (HFOV), and multi-frequency oscillatory ventilation (MFOV). For each ventilation modality, strain amplitudes and phases were obtained from the discrete Fourier transform of time-varying Jacobian determinants within each voxel, using transformations mapped to a single reference image. In each cross-section of the reference image, voxel color in (A) indicates the strain amplitude at that frequency, corresponding to the amplitude of volumetric strain relative to the minimum volume of that particular voxel. Voxel color in (B) indicates the amount of phase shift (leading or lagging) relative to the median phase of all lung voxels at the specified frequency.
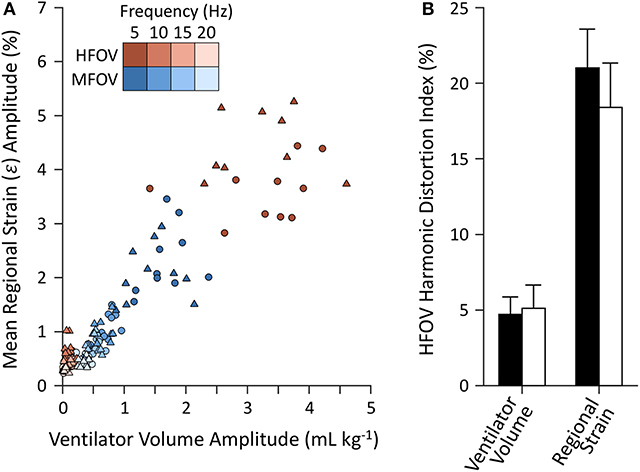
Figure 11. Harmonic amplitudes (A) from imaging-based regional strain measurements and corresponding amplitudes from the ventilator volume waveform measured at the airway opening under baseline (circles) and injured (triangles) conditions. Harmonic distortion index (B) mean and standard deviation for each set of measurements, grouped by baseline (black) and injured (white) lung conditions.
Discussion
In this study, we demonstrated that oscillatory ventilation improves the average regional lung strain, as well as the spatial gradients of lung strain, compared to a conventional pressure-controlled modality in pigs with heterogeneous lung injury. This study revealed a mechanism by which enhanced harmonic content in MFOV waveforms may improve gas exchange compared to either CMV or single-frequency HFOV waveforms.
The increase in respiratory system elastance following lung injury (i.e., 183% increase in Ers and 355% increase in H) is consistent with substantial lung derecruitment and/or surfactant dysfunction. Consequently, increased driving pressure was required to maintain eucapnia at comparable respiratory rates. Despite similar and ventilatory cost function (VC), the driving pressure (ΔPaw) after lung injury increased to 18.7 cmH2O, compared to 13.0 cmH2O at baseline (Figure 5). Increased ΔPaw during CMV after injury exceeded the 15 cmH2O threshold identified by Amato et al. (2015), above which the mortality odds ratio was greater than unity in patients with ARDS. The use of ΔPaw > 15 cmH2O suggests substantial potential for VILI despite average measured of 7.5 mL kg−1 (Figure 5). However, such heuristics are only applicable during CMV, for which Paw fluctuations are well-correlated with lung strain. During oscillatory modes of ventilation, ΔPaw as computed from Equation (6) does not represent elastic pressures distending peripheral alveoli, but also includes substantial pressure losses due to resistive and inertial loads imposed by the endotracheal tube and conducting airways, especially with increasing frequency. The fact that ΔPaw was greater during MFOV than HFOV indicates that larger pressure amplitudes were required to overcome the increased resistive and inertial losses at frequencies up to 20 Hz compared to 5 Hz, but does not indicate that these larger airway pressures were transmitted to distal alveoli (Pillow et al., 2002). We found that the spatial mean of strain throughout the entire lung during CMV was unchanged after injury, despite increased ΔPaw and ΔI spatial mean (Figure 6). Some evidence to reconcile this discrepancy is apparent in the greatly increased coefficient of variation for Δε (Figure 6). Upon closer examination of the regional strain distributions in injured lungs, Δε was nearly zero in consolidated regions of the lung with I >-100 HU. By contrast, Δε was increased by 25% in normally aerated regions (i.e., −900 HU < I < −500 HU) relative to the average throughout the entire lung mask. Thus, the increased ΔPaw required to deliver similar (Figure 5) resulted in concentrated strains within the recruited lung. This finding is consistent with the concept of the “baby lung,” which describes reduced functional recruited volume in ARDS (Gattinoni and Pesenti, 2005; Gattinoni et al., 2016a).
Spatial gradients of intratidal strain also provide some insight into the redistribution of mechanical flows after lung injury. As expected, the magnitudes of right-left gradients were small relative to those of the dorsal-ventral and caudal-rostral gradients (Figure 7). Most noticeably, lung injury was associated with dramatic changes in dorsal-ventral Δε gradients. Ventilation in healthy subjects during CMV tended to distribute toward the dorsal and caudal lung regions. However, varying degrees of lung injury resulted in consolidation or derecruitment of the dependent lung, such that dorsal-ventral Δε gradients were reduced (or even reversed) depending on the extent of edema, particularly for CMV and HFOV. Interestingly, intratidal changes in aeration tended to preserve the dorsal-ventral ΔI gradient before and after injury, despite the positive shift observed in dorsal-ventral Δε gradients. It should be noted that actual spatial distributions of ΔI and Δε are likely not well-described by linear functions of spatial position following lung injury, and may even be non-monotonic (Johnson et al., 2017). For example, negative dorsal-ventral gradients may be possible in the recruited lung, but counteracted by zero ventilation in the derecruited dependent lung such that the resulting overall linear gradient may be negative, zero, or even positive. Nonetheless compared to either CMV of HFOV, MFOV reduced the magnitude of spatial gradients in ventilation regardless of the lung condition. Other strategies for improving ventilation distribution and eliminating large dorsal-ventral gradients include prone position ventilation (Scholten et al., 2017; Xin et al., 2018), which was not used in this study. Prone posture serves to eliminate large-scale gravitational gradients in lung expansion (Hoffman, 1985), but would not be expected to affect the local, region-to-region mechanical differences which MFOV targets. Finally, both HFOV and MFOV were associated with more positive caudal-rostral ΔI gradients compared to CMV, regardless of injured condition (p < 0.001). CMV-associated findings indicate that in contrast to oscillatory modalities, CMV preferentially ventilates the basal regions of the lungs, consistent with a previous positron emission tomography study (Venegas et al., 1993).
Much of the variability in spatial gradient magnitudes across different ventilation modalities was due to changes in the spatial means. By contrast, the normalized gradients (i.e., the spatial gradients divided by the spatial mean) exhibited fewer significant differences across modalities (Figure 8, Table 2). This finding indicates that, at least for the particular frequencies and waveforms used in this study, the relative spatial gradients were not substantially altered by modality. This may be due in part to the predominance of the 5 Hz component in both HFOV and MFOV waveforms, which was below the resonant frequency in almost every case (Table 1), and therefore below a threshold frequency for developing regional ventilation heterogeneity due to resonant amplification (Herrmann et al., 2019a). Our results then indicate that broadband MFOV waveforms, while producing the same relative ventilation heterogeneity as HFOV, still reduce the average strain and magnitude of strain gradients that are associated with risk for VILI.
Based on our supervoxel and octree analysis, regional strain heterogeneity did not differ greatly across ventilation modality, although the injured lungs did require smaller sizes to describe the spatial clustering of Δε compared to the baseline conditions (Figure 9). Lung injury may thus result in increased small-scale strain heterogeneity (Kaczka et al., 2011; Perchiazzi et al., 2014). It should be noted that our estimates of regional strain derived from image registration are inherently smooth due to the use of B-splines to define the spatiotemporal deformations. The discrepancy between the supervoxel- and octree-based results may also be due in part to the discrete anatomic structure of lungs, which consist of an assumed continuum of spongy parenchymal tissues penetrated by branching networks of airways and vessels. Airways and vessels are not expected to undergo large volumetric strains during mechanical ventilation, and therefore give rise to irregularities in the spatial field of Δε. Such irregularities may be approximately contoured by supervoxel boundaries, which are not rigidly constrained. By contrast, octree decomposition is strictly planar, and therefore may require greater degrees of recursive subdivision to isolate such irregular spatial distributions of Δε (Perchiazzi et al., 2014). The supervoxel decomposition incorporates spatial proximity as well as image intensity, such that reducing the spatial proximity weighting may facilitate the identification of larger clusters albeit with irregular boundaries. Therefore, it is possible that our findings would be altered if smaller airways and blood vessels were further segmented from the lung parenchyma prior to cluster analysis, or if a different spatial proximity weighting was used for the supervoxel decomposition.
Separation of the harmonic content of regional ventilation illustrates a potential influence of nonlinear mechanics during HFOV at 5 Hz (Figure 11). For example, image registration resulted in estimation of amplitudes at 10, 15, and 20 Hz of roughly one third those at 5 Hz, despite the ventilator waveform consisting of only 5 Hz oscillation (Supplementary Figure S-4). By contrast, amplitudes during MFOV approximated the input distribution of uniform amplitude flow at all four harmonics (Supplementary Figure S-4). Intrapulmonary harmonic distortion of distributed flows during HFOV (with only a single frequency) may result from the use of larger-amplitude flows exacerbating inherent mechanical nonlinearities, but may also result from the complex interaction of mechanically-interdependent lung tissues (Suki and Bates, 1991; Suki et al., 1991). During MFOV, the use of small-amplitude flows may contribute to relatively linear mechanical behavior of the lung tissues. It is also possible that the observed nonlinearity may be due in part to imaging artifact and errors in image registration resulting in misidentified high-frequency, small-amplitude motion. Assuming that our registration results are accurate however, the amplitudes measured at the higher harmonics during HFOV are surprisingly large, almost comparable to those intentionally delivered during MFOV. It is plausible that the mechanisms by which MFOV may enhance gas transport already occur, at least to some extent, within the lung periphery during HFOV. However, MFOV may induce these higher harmonics directly, without incurring the overhead of generating high flow rates at the fundamental frequency. The consequences of such overhead may include, for example, increased spatial gradients of strain and strain rate due to gravitational dependence (Figure 7).
Limitations
MFOV may improve ventilation distribution and the efficiency gas exchange efficacy (Kaczka et al., 2015; Herrmann et al., 2018, 2019b). However, given the technical limitations of the mechanical ventilator as well as our dynamic CT image reconstruction technique which assumed strict periodicity of motion (Herrmann et al., 2017), the MFOV waveform used in this study comprised only harmonic components of the fundamental frequency. Cardiogenic motion was not synchronized with respiratory motion and therefore presents a source of artifact in the reconstructed 4DCT images of respiratory motion, depending on the relative periodicity between the ventilator frequency and the heart rate. Such artifact may manifest as rapid oscillations in CT density (Herrmann et al., 2017), which may influence registration-based estimates of strain rate, especially in regions adjacent to the mediastinum.
In addition, the interpretation of regional strain in the proximity of recruitment/derecruitment is challenging for several reasons. Standard image registration techniques (e.g., using a similarity cost function defined as the sum of squared intensity differences) assume a uniform intensity transform to predict voxel-wise correspondence, but cannot account for local changes in intensity associated with changing gas fraction. Consequently, these approaches may result in the prediction of non-physical deformations, such as contraction of nonaerated lung regions. The sum of squared tissue volume differences (SSTVD) similarity cost function used in this study addresses this problem using a non-uniform intensity transform that accounts for local variations in CT intensity that are due to changing proportions of gas-to-tissue content in each lung region during breathing or ventilation (Zhao et al., 2016). Another challenge to registration of injured lungs is the lack of contrast or structural landmarks in consolidated regions, which renders validation of estimated voxel-wise correspondence nearly impossible, especially when large changes in recruitment occur between two images. In this study, high temporal resolution imaging (7–105 Hz) was used to minimize the time between adjacent ventilation phases, which resulted in small deformations and small changes in recruitment between adjacent images being registered. Linear elastic regularization produces plausible predictions of voxel-wise correspondence in regions with little contrast, assuming the lung parenchyma deforms as a linear elastic material. An important limitation of most registration techniques is the assumption of smoothly varying deformation, which may not accurately reflect discontinuous motion at distinct structural boundaries between aerated and nonaerated lung tissue. Due to the limited spatial resolution in this study (0.6 mm), each voxel may contain up to dozens of alveoli. Thus, it is difficult, if not impossible, to distinguish the underlying cause of observed changes in aeration (Cereda et al., 2019). For example, the same change in aeration of a single voxel may represent uniform deflation of its alveoli, complete derecruitment of only a portion of alveoli, or any combination thereof. Thus, prediction of recruitment/derecruitment on the basis of voxel aeration is speculative.
Finally, while our study focused on regional distributions of aeration, strain, and strain rate as the primary indicators of ventilation and VILI, the exact relationship between these mechanical variables and VILI is difficult to ascertain. VILI is a complicated process associated with a diverse range of mechanical stimuli (Hussein et al., 2013; Carrasco Loza et al., 2015; Güldner et al., 2016; Smith et al., 2017; Tonetti et al., 2017). So-called “mechanical power” (i.e., the rate of energy dissipation across parenchymal tissues) may provide a better prediction of VILI compared to either strain or strain rate alone (Gattinoni et al., 2016b; Serpa Neto et al., 2018). However, measurement of regional mechanical power is not practical, given the requirement of regional gas pressure within the lung for its estimation. Alternatively, VILI may also be assessed using fluoro-deoxyglucose (FDG) uptake (Wellman et al., 2014), serum or alveolar inflammatory cytokines (Liu et al., 2013), protein content in bronchoalveolar lavage fluid (Smith et al., 2017), and histopathology. All of these quantitative measurements of lung injury require extensive durations of mechanical ventilation prior to measurement, some of which may only be obtained post mortem.
Conclusion
In an oleic acid model of porcine ARDS, high-frequency and multi-frequency oscillatory ventilation resulted in improved gas exchange efficiency and reduced regional lung strain compared to conventional mechanical ventilation. MFOV also reduced spatial gradients in lung strain compared to CMV or HFOV, resulting in a more uniform overall distribution of lung strain. By contrast, mean-normalized spatial gradients exhibited less dependence on ventilation modality, indicating that the use of higher harmonic frequencies in MFOV does not substantially alter relative ventilation heterogeneity. Thus, the reduced spatial strain gradients observed with MFOV, compared to HFOV or CMV, may be explained by reductions in the average parenchymal strain. In summary, MFOV supports gas exchange with reduced lung strain, and may provide additional benefit over HFOV by reducing ventilation heterogeneity associated with spatial gradients in absolute strain, and by reducing the strain associated with conventional ventilation or single-frequency oscillation.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Ethics Statement
The animal study was reviewed and approved by University of Iowa Institute for Animal Care and Use Committee (Protocol Number 5061428).
Author Contributions
JH and DK conceived the study, collected the data, and wrote the manuscript. JH, SG, WS, MH, JR, GC, EH, and DK analyzed the data and revised the manuscript.
Funding
This work was supported by the Office of the Assistant Secretary of Defense for Health Affairs, through the Peer Reviewed Medical Research Program under Award No. W81XWH-16-1-0434. Opinions, interpretations, conclusions, and recommendations are those of the authors and are not necessarily endorsed by the Department of Defense. This study was also supported by the Department of Anesthesia at the University of Iowa Hospital and Clinics, and by National Institutes of Health awards R41 HL140640, R01 CA166703, and R01 HL142625. This work utilized a CT scanner that was purchased with funding from National Institutes of Health Shared Instrumentation Grant 1S10OD018526. This research was supported in part through high-performance computing resources provided by The University of Iowa, Iowa City, Iowa.
Conflict of Interest
JH and DK are co-founders and shareholders of OscillaVent, Inc. JR and EH are co-founders and shareholders of VIDA Diagnostics, Inc.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Andrea Fonseca da Cruz, Bakir Hajdarevic, Eli Schmidt, Chelsea Sloan, and Kelly M. Stark assisted with performing the experimental protocol. Melissa Saylor, Jarron Atha, and Shayna Hogue assisted with computed tomographic imaging. Ahmed Halaweish, Mathew K. Fuld, and Siemens Healthineers (Forchheim, Germany) provided technical assistance for image reconstruction. Andrea Fonseca da Cruz, Eli Schmidt, Charles A. Mascardo, and Ethan L. Chen assisted with manual image segmentation. ZOLL Medical Corporation generously loaned a portable ventilator for use in animal experiments. The authors are deeply grateful for all of their contributions to this investigation.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2020.00014/full#supplementary-material
Footnotes
1. ^The use of Vrms enables comparison between single-frequency modalities, which are typically described by a single tidal volume, and MFOV, which is described by a distinct volume amplitude at each frequency (Kaczka et al., 2015).
2. ^This threshold value was empirically chosen to be lower than the values of the regional strain coefficient of variation observed across all subjects, to ensure that the recursive subdivision would not be terminated trivially at the level of the entire lung mask, yet high enough to avoid termination at the level of individual voxels. The same threshold was used for all normalized images.
References
Acute Respiratory Distress Syndrome Network (2000). Ventilation with lower tidal volumes as compared with traditional tidal volumes for acute lung injury and the acute respiratory distress syndrome. The Acute Respiratory Distress Syndrome Network. N. Engl. J. Med. 342, 1301–1308. doi: 10.1056/NEJM200005043421801
Amato, M. B., Meade, M. O., Slutsky, A. S., Brochard, L., Costa, E. L., Schoenfeld, D. A., et al. (2015). Driving pressure and survival in the acute respiratory distress syndrome. N. Engl. J. Med. 372, 747–755. doi: 10.1056/NEJMsa1410639
Amini, R., Herrmann, J., and Kaczka, D. W. (2017). Intratidal overdistention and derecruitment in the injured lung: a simulation study. IEEE Trans. Biomed. Eng. 64, 681–689. doi: 10.1109/TBME.2016.2572678
Amini, R., and Kaczka, D. W. (2013). Impact of ventilation frequency and parenchymal stiffness on flow and pressure distribution in a canine lung model. Ann. Biomed. Eng. 41, 2699–2711. doi: 10.1007/s10439-013-0866-7
Carrasco Loza, R., Villamizar Rodríguez, G., and Medel Fernández, N. (2015). Ventilator-induced lung injury (VILI) in acute respiratory distress syndrome (ARDS): volutrauma and molecular effects. Open Respir. Med. J. 9, 112–119. doi: 10.2174/1874306401509010112
Cereda, M., Xin, Y., Goffi, A., Herrmann, J., Kaczka, D. W., Kavanagh, B. P., et al. (2019). Imaging the injured lung: Mechanisms of action and clinical use. Anesthesiology. 131, 716–749. doi: 10.1097/ALN.0000000000002583
Conze, P. H., Noblet, V., Rousseau, F., Heitz, F., de Blasi, V., Memeo, R., et al. (2017). Scale-adaptive supervoxel-based random forests for liver tumor segmentation in dynamic contrast-enhanced CT scans. Int. J. Comput. Assist. Radiol. Surg. 12, 223–233. doi: 10.1007/s11548-016-1493-1
Gattinoni, L., Marini, J. J., Pesenti, A., Quintel, M., Mancebo, J., and Brochard, L. (2016a). The “baby lung” became an adult. Intensive Care Med. 42, 663–673. doi: 10.1007/s00134-015-4200-8
Gattinoni, L., and Pesenti, A. (2005). The concept of “baby lung”. Intensive Care Med. 31, 776–784. doi: 10.1007/s00134-005-2627-z
Gattinoni, L., Tonetti, T., Cressoni, M., Cadringher, P., Herrmann, P., Moerer, O., et al. (2016b). Ventilator-related causes of lung injury: the mechanical power. Intensive Care Med. 42, 1567–1575. doi: 10.1007/s00134-016-4505-2
Gerard, S. E., Herrmann, J., Kaczka, D. W., Musch, G., Fernandez-Bustamante, A., and Reinhardt, J. M. (2020). Multi-resolution convolutional neural networks for fully automated segmentation of acutely injured lungs in multiple species. Med. Image Anal. 60:101592. doi: 10.1016/j.media.2019.101592
Gerard, S. E., Herrmann, J., Kaczka, D. W., and Reinhardt, J. M. (2018). “Transfer learning for segmentation of injured lungs using coarse-to-fine convolutional neural networks,” in Image Analysis for Moving Organ, Breast, and Thoracic Images (Granada: Springer International Publishing), 191–201.
Gorbunova, V., Lol, P., Ashraf, H., Dirksen, A., Nielsen, M., and de Bruijne, M. (2008). Weight preserving image registration for monitoring disease progression in lung CT. Med. Image Comput. Comput. Interv. 11, 863–870. doi: 10.1007/978-3-540-85990-1_104
Güldner, A., Braune, A., Ball, L., Silva, P. L., Samary, C., Insorsi, A., et al. (2016). Comparative effects of volutrauma and atelectrauma on lung inflammation in experimental acute respiratory distress syndrome. Crit. Care Med. 44, 1–12. doi: 10.1097/CCM.0000000000001721
Herrmann, J., Hoffman, E. A., and Kaczka, D. W. (2017). Frequency-selective computed tomography: applications during periodic thoracic motion. IEEE Trans. Med. Imaging 36, 1722–1732. doi: 10.1109/TMI.2017.2694887
Herrmann, J., Lilitwat, W., Tawhai, M. H., and Kaczka, D. W. (2019a). High-frequency oscillatory ventilation and ventilator-induced lung injury: size does matter. Crit. Care Med. 48, e66–e73. doi: 10.1097/CCM.0000000000004073
Herrmann, J., Tawhai, M. H., and Kaczka, D. W. (2016). Regional gas transport in the heterogeneous lung during oscillatory ventilation. J. Appl. Physiol. 121, 1306–1318. doi: 10.1152/japplphysiol.00097.2016
Herrmann, J., Tawhai, M. H., and Kaczka, D. W. (2018). Parenchymal strain heterogeneity during oscillatory ventilation: why two frequencies are better than one. J. Appl. Physiol. 124, 653–663. doi: 10.1152/japplphysiol.00615.2017
Herrmann, J., Tawhai, M. H., and Kaczka, D. W. (2019b). Strain, strain rate, and mechanical power: an optimization comparison for oscillatory ventilation. Int. j. Numer. Method. Biomed. Eng. 35:e3238. doi: 10.1002/cnm.3238
Hoffman, E. A. (1985). Effect of body orientation on regional lung expansion: a computed tomographic approach. J. Appl. Physiol. 59, 468–480. doi: 10.1152/jappl.1985.59.2.468
Hussein, O., Walters, B., Stroetz, R., Valencia, P., McCall, D., and Hubmayr, R. D. (2013). Biophysical determinants of alveolar epithelial plasma membrane wounding associated with mechanical ventilation. Am. J. Physiol. Lung Cell. Mol. Physiol. 305, L478–L484. doi: 10.1152/ajplung.00437.2012
Johnson, N. J., Luks, A. M., and Glenny, R. W. (2017). Gas exchange in the prone posture. Respir. Care 62, 1097–1110. doi: 10.4187/respcare.05512
Kaczka, D. W., Cao, K., Christensen, G. E., Bates, J. H., and Simon, B. A. (2011). Analysis of regional mechanics in canine lung injury using forced oscillations and 3D image registration. Ann. Biomed. Eng. 39, 1112–1124. doi: 10.1007/s10439-010-0214-0
Kaczka, D. W., Herrmann, J., Zonneveld, C. E., Tingay, D. G., Lavizzari, A., Noble, P. B., et al. (2015). Multifrequency oscillatory ventilation in the premature lung: effects on gas exchange, mechanics, and ventilation distribution. Anesthesiology 123, 1394–1403. doi: 10.1097/ALN.0000000000000898
Kaczka, D. W., and Lutchen, K. R. (2004). Servo-controlled pneumatic pressure oscillator for respiratory impedance measurements and high-frequency ventilation. Ann. Biomed. Eng. 32, 596–608. doi: 10.1023/b:abme.0000019179.87974.7d
Klein, S., Staring, M., Murphy, K., Viergever, M. A., and Pluim, J. P. (2010). Elastix: a toolbox for intensity-based medical image registration. IEEE Trans. Med. Imaging 29, 196–205. doi: 10.1109/TMI.2009.2035616
Kneyber, M. C. J., and Markhorst, D. G. (2016). Do we really know how to use high-frequency oscillatory ventilation in critically ill children? Am. J. Respir. Crit. Care Med. 193, 1067–1068. doi: 10.1164/rccm.201512-2418LE
Liu, S., Yi, Y., Wang, M., Chen, Q., Huang, Y., Liu, L., et al. (2013). Higher frequency ventilation attenuates lung injury during high-frequency oscillatory ventilation in sheep models of acute respiratory distress syndrome. Anesthesiology 119, 398–411. doi: 10.1097/ALN.0b013e31829419a6
Malhotra, A., and Drazen, J. M. (2013). High-frequency oscillatory ventilation on shaky ground. N. Engl. J. Med. 368, 863–865. doi: 10.1056/NEJMe1300103
Meade, M. O., Young, D., Hanna, S., Zhou, Q., Bachman, T. E., Bollen, C., et al. (2017). Severity of hypoxemia and effect of high-frequency oscillatory ventilation in acute respiratory distress syndrome. Am. J. Respir. Crit. Care Med. 196, 727–733. doi: 10.1164/rccm.201609-1938OC
Metz, C. T., Klein, S., Schaap, M., van Walsum, T., and Niessen, W. J. (2011). Nonrigid registration of dynamic medical imaging data using nD+t B-splines and a groupwise optimization approach. Med. Image Anal. 15, 238–249. doi: 10.1016/j.media.2010.10.003
Nguyen, A. P., Schmidt, U. H., and MacIntyre, N. R. (2016). Should high-frequency ventilation in the adult be abandoned? Respir. Care 61, 791–800. doi: 10.4187/respcare.04584
Ortiz, R. M., Cilley, R. E., and Bartlett, R. H. (1987). Extracorporeal membrane oxygenation in pediatric respiratory failure. Pediatr. Clin. North Am. 34, 39–46. doi: 10.1016/S0031-3955(16)36179-X
Perchiazzi, G., Rylander, C., Derosa, S., Pellegrini, M., Pitagora, L., Polieri, D., et al. (2014). Regional distribution of lung compliance by image analysis of computed tomograms. Respir. Physiol. Neurobiol. 201, 60–70. doi: 10.1016/j.resp.2014.07.001
Pillow, J. J., Sly, P. D., Hantos, Z., and Bates, J. H. (2002). Dependence of intrapulmonary pressure amplitudes on respiratory mechanics during high-frequency oscillatory ventilation in preterm lambs. Pediatr. Res. 52, 538–544. doi: 10.1203/00006450-200210000-00013
Protti, A., Maraffi, T., Milesi, M., Votta, E., Santini, A., Pugni, P., et al. (2016). Role of strain rate in the pathogenesis of ventilator-induced lung edema. Crit. Care Med. 44, e838–e845. doi: 10.1097/CCM.0000000000001718
Scholten, E. L., Beitler, J. R., Prisk, G. K., and Malhotra, A. (2017). Treatment of ARDS with prone positioning. Chest 151, 215–224. doi: 10.1016/j.chest.2016.06.032
Serpa Neto, A., Deliberato, R. O., Johnson, A. E. W., Bos, L. D., Amorim, P., Pereira, S. M., et al. (2018). Mechanical power of ventilation is associated with mortality in critically ill patients: An analysis of patients in two observational cohorts. Intensive Care Med. 44, 1914–1922. doi: 10.1007/s00134-018-5375-6
Sklar, M. C., Fan, E., and Goligher, E. C. (2017). High-frequency oscillatory ventilation in adults with ARDS: past, present, and future. Chest 152, 1306–1317. doi: 10.1016/j.chest.2017.06.025
Slutsky, A. S., and Ranieri, V. M. (2013). Ventilator-induced lung injury. N. Engl. J. Med. 369, 2126–2136. doi: 10.1056/NEJMra1208707
Smith, B. J., Bartolak-Suki, E., Suki, B., Roy, G. S., Hamlington, K. L., Charlebois, C. M., et al. (2017). Linking ventilator injury-induced leak across the blood-gas barrier to derangements in murine lung function. Front. Physiol. 8:466. doi: 10.3389/fphys.2017.00466
Suki, B., and Bates, J. H. (1991). A nonlinear viscoelastic model of lung tissue mechanics. J. Appl. Physiol. 71, 826–833. doi: 10.1152/jappl.1991.71.3.826
Suki, B., Hantos, Z., Daróczy, B., Alkaysi, G., and Nagy, S. (1991). Nonlinearity and harmonic distortion of dog lungs measured by low-frequency forced oscillations. J. Appl. Physiol. 71, 69–75. doi: 10.1152/jappl.1991.71.1.69
Suki, B., and Lutchen, K. R. (1992). Pseudorandom signals to estimate apparent transfer and coherence functions of nonlinear systems: applications to respiratory mechanics. IEEE Trans. Biomed. Eng. 39, 1142–1151. doi: 10.1109/10.168693
Tonetti, T., Vasques, F., Rapetti, F., Maiolo, G., Collino, F., Romitti, F., et al. (2017). Driving pressure and mechanical power: new targets for VILI prevention. Ann. Transl. Med. 5:286. doi: 10.21037/atm.2017.07.08
Vasavada, N. (2016). Kruskal-Wallis rank sum test calculator. Available online at: https://astatsa.com/KruskalWallisTest/ (accessed September 18, 2019).
Venegas, J. G., Tsuzaki, K., Fox, B. J., Simon, B. A., and Hales, C. A. (1993). Regional coupling between chest wall and lung expansion during HFV: a positron imaging study. J. Appl. Physiol. 74, 2242–2252. doi: 10.1152/jappl.1993.74.5.2242
Welch, P. (1967). The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans Audio Electroacoust 15, 70–73. doi: 10.1109/TAU.1967.1161901
Wellman, T. J., Winkler, T., Costa, E. L., Musch, G., Harris, R. S., Zheng, H., et al. (2014). Effect of local tidal lung strain on inflammation in normal and lipopolysaccharide-exposed sheep. Crit. Care Med. 42, e491–500. doi: 10.1097/CCM.0000000000000346
Xin, Y., Cereda, M., Hamedani, H., Pourfathi, M., Siddiqui, S., Meeder, N., et al. (2018). Unstable inflation causing injury insight from prone position and paired computed tomography scans. Am. J. Respir. Crit. Care Med. 198, 197–207. doi: 10.1164/rccm.201708-1728OC
Yin, Y., Hoffman, E. A., and Lin, C.-L. (2009). Mass preserving nonrigid registration of CT lung images using cubic B-spline. Med. Phys. 36, 4213–4222. doi: 10.1118/1.3193526
Zhang, Q., Suki, B., and Lutchen, K. R. (1995). Harmonic distortion from nonlinear systems with broadband inputs: applications to lung mechanics. Ann. Biomed. Eng. 23, 672–681. doi: 10.1007/bf02584464
Zhao, B., Christensen, G. E., Hyun Song, J., Pan, Y., Gerard, S. E., Reinhardt, J. M., et al. (2016). “Tissue-volume preserving deformable image registration for 4DCT pulmonary images,” in IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW) (Las Vegas, NV), 41–49.
Nomenclature
Keywords: mechanical ventilation, ventilator-induced lung injury, respiratory mechanics, high-frequency oscillatory ventilation, multi-frequency oscillatory ventilation, computed tomography, image registration
Citation: Herrmann J, Gerard SE, Shao W, Hawley ML, Reinhardt JM, Christensen GE, Hoffman EA and Kaczka DW (2020) Quantifying Regional Lung Deformation Using Four-Dimensional Computed Tomography: A Comparison of Conventional and Oscillatory Ventilation. Front. Physiol. 11:14. doi: 10.3389/fphys.2020.00014
Received: 16 October 2019; Accepted: 13 January 2020;
Published: 20 February 2020.
Edited by:
Bradford Julian Smith, University of Colorado Denver, United StatesReviewed by:
Sam Bayat, University of Picardie Jules Verne, FranceNorihiro Shinozuka, Chibaken Saiseikai Narashino Hospital, Japan
Copyright © 2020 Herrmann, Gerard, Shao, Hawley, Reinhardt, Christensen, Hoffman and Kaczka. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David W. Kaczka, ZGF2aWQta2FjemthQHVpb3dhLmVkdQ==
 Jacob Herrmann
Jacob Herrmann Sarah E. Gerard1
Sarah E. Gerard1 Wei Shao
Wei Shao Joseph M. Reinhardt
Joseph M. Reinhardt David W. Kaczka
David W. Kaczka