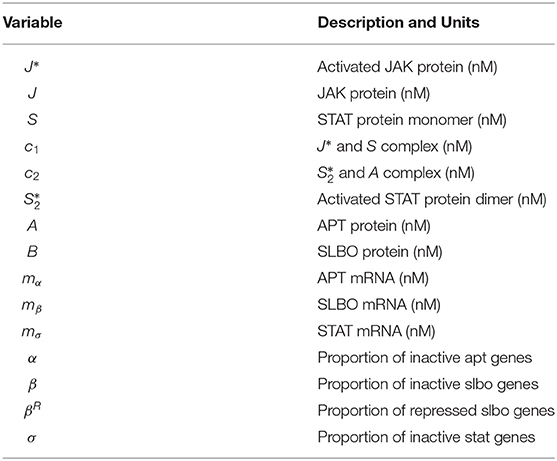
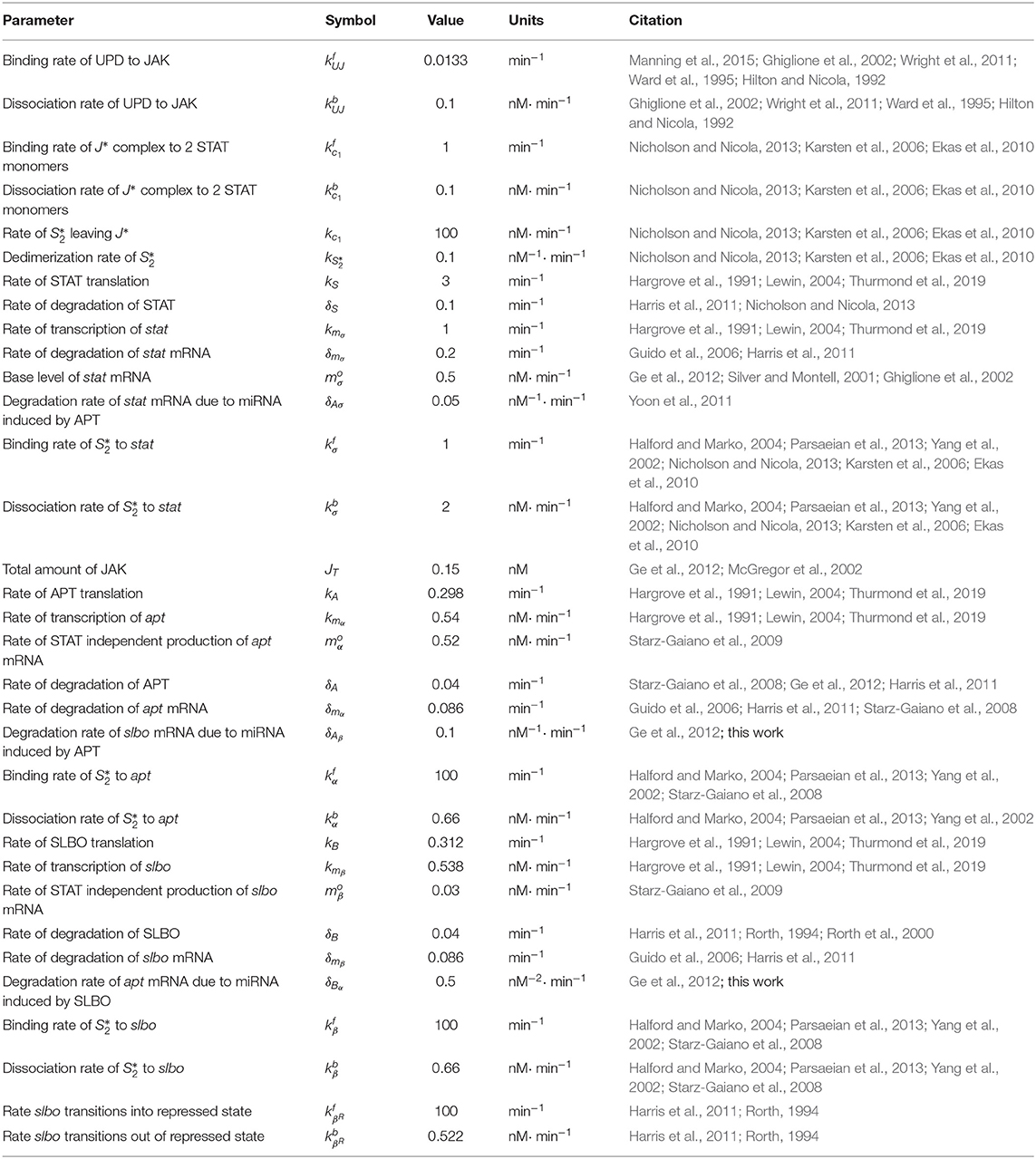
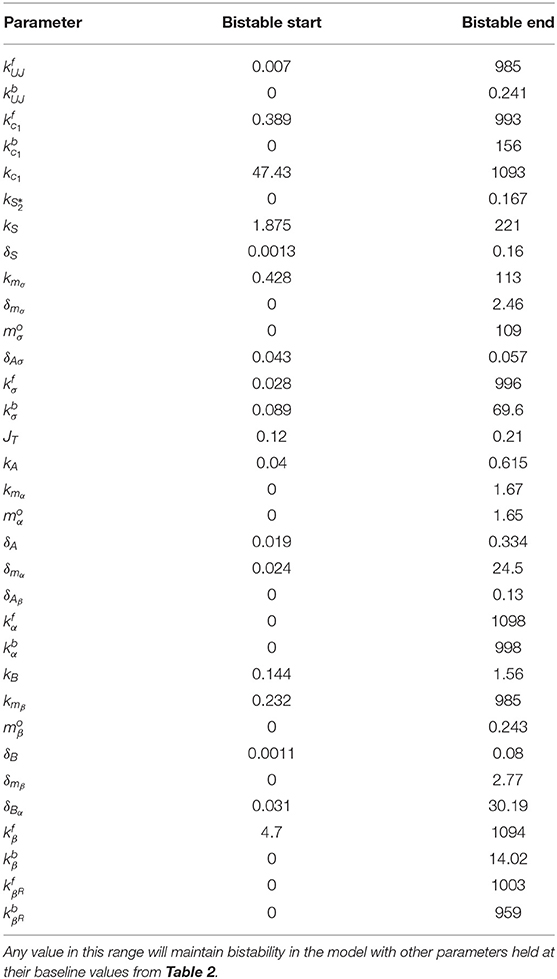
- 1Department of Mathematics and Statistics, University of Maryland Baltimore County, Baltimore, MD, United States
- 2Department of Biological Sciences, University of Maryland Baltimore County, Baltimore, MD, United States
Cell migration is a key component in development, homeostasis, immune function, and pathology. It is important to understand the molecular activity that allows some cells to migrate. Drosophila melanogaster is a useful model system because its genes are largely conserved with humans and it is straightforward to study biologically. The well-conserved transcriptional regulator Signal Transducer and Activator of Transcription (STAT) promotes cell migration, but its signaling is modulated by downstream targets Apontic (APT) and Slow Border Cells (SLBO). Inhibition of STAT activity by APT and cross-repression of APT and SLBO determines whether an epithelial cell in the Drosophila egg chamber becomes motile or remains stationary. Through mathematical modeling and analysis, we examine how the interaction of STAT, APT, and SLBO creates bistability in the Janus Kinase (JAK)/STAT signaling pathway. In this paper, we update and analyze earlier models to represent mechanistically the processes of the JAK/STAT pathway. We utilize parameter, bifurcation, and phase portrait analyses, and make reductions to the system to produce a minimal three-variable quantitative model. We analyze the manifold between migratory and stationary steady states in this minimal model and show that when the initial conditions of our model are near this manifold, cell migration can be delayed.
1. Introduction
The acquisition of cellular migration plays a critical role in both normal and pathological development. A better understanding of the processes cells undergo as they transition from a stationary state to a migratory state is thus of broad interest. Studying the mechanics of how cohorts of cells move together introduces additional complexities, and existing models of collectively migrating cells differ greatly (Peercy and Starz-Gaiano, 2020; Stuelten et al., 2018; Aman and Piotrowski, 2010; Saadin and Starz-Gaiano, 2016; Olson and Nechiporuk, 2018; Leonard and Taneyhill, 2020; Friedl and Mayor, 2017). To study cell migration, some scientists turn to an experimental model system amenable to both genetic analysis and live imaging. In Drosophila melanogaster during oogenesis, a set of cells called border cells develop within a layer of follicle cells and later become migratory, leaving the nearby epithelial cells behind as they move to the oocyte (Montell et al., 2012; Saadin and Starz-Gaiano, 2016). Experimentalists have discovered much of the molecular regulation that governs this process and what causes some border cells to become motile while others remain stationary, including the primary biochemical and molecular pathways. We are interested in advancing a mathematical model of these pathways, which could have implications on acquisition of cell motility in animals in general.
The Janus Kinase/Signal Transducer and Activator of Transcription (JAK/STAT) signaling pathway has been shown by previous studies to be crucial in the motility of border cells, as well as in stem cells and immune response (Montell et al., 2012; Arbouzova and Zeidler, 2006; Trivedi and Starz-Gaiano, 2018; Amoyel and Bach, 2012; Amoyel et al., 2014). The JAK/STAT pathway is well-conserved from fruit flies to humans. Anterior polar cells in the Drosophila egg chamber (see Figures 1, 2A) secrete the cytokine Unpaired (UPD), which acts as the ligand for the transmembrane Domeless receptor in neighboring follicle cells. UPD is predicted to form a gradient across the adjacent cells (Van De Bor et al., 2011; Xi et al., 2003; Starz-Gaiano et al., 2008). The binding of UPD to Domeless activates JAK, leading to the phosphorylation of the activated JAK/receptor complex. The activated complex then recruits and phosphorylates STAT. The phosphorylated STAT dimerizes, moves to the nucleus, and acts as a transcription factor for specific target genes.
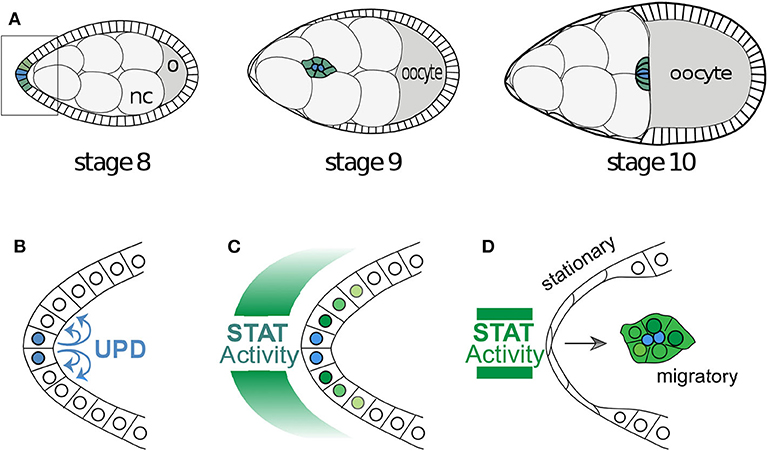
Figure 1. Egg development and the migration of border cells. (A) A cartoon of the development of a Drosophila egg chamber and the movement of the border cells between the nurse cells (nc). The outer edge of the egg chamber is made up of epithelial follicle cells and the box outlines the cells in (B). (B) The signaling molecule Unpaired is secreted from the polar cells and (C) induces a gradient of STAT activity across the anterior epithelium. Often the follicle cells very close to the polar cells assume the identity of border cells and (D) become motile and migrate as a cluster toward the oocyte. The cells with below-threshold levels of STAT activity shut the signaling off in a switch like manner.
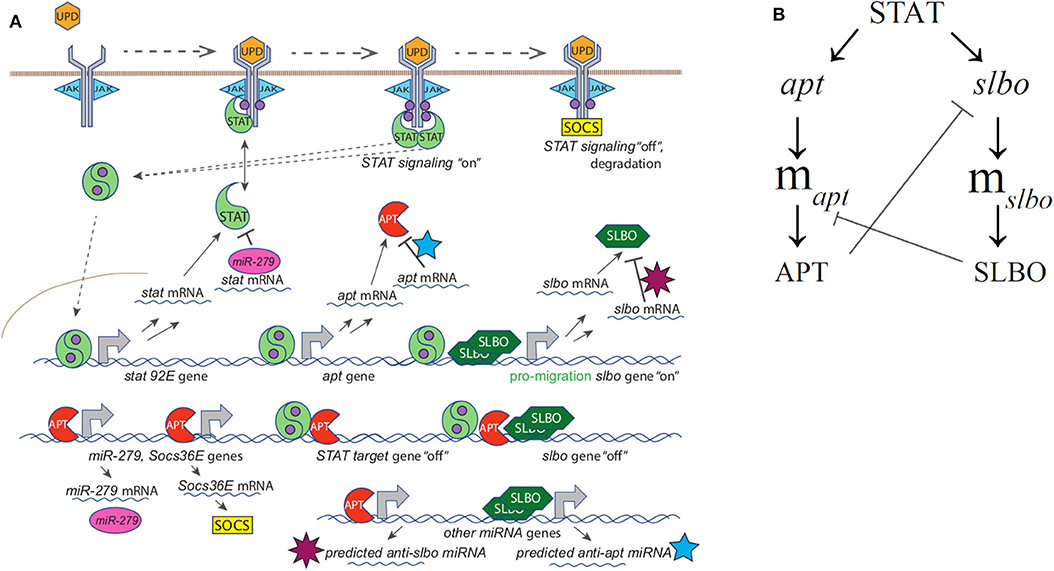
Figure 2. (A) Full mechanistic diagram of JAK/STAT pathway (B) Cross-repression system of APT and SLBO. STAT activates apt and slbo transcription leading to the production of apt and slbo mRNA and translation into APT and SLBO proteins. SLBO represses apt translation while APT suppresses slbo transcription and function. High APT levels make the cell stationary and high SLBO levels make the cell motile. However, which state dominates cannot be determined from this qualitative diagram alone.
A key target of STAT is the C/EBP transcription factor Slow Border Cells (Slbo) (Montell et al., 1992; Starz-Gaiano et al., 2008). Cells specified by high levels of SLBO to become the border cells respond to chemoattractants that activate two receptor tyrosine kinases (RTKs), which turn on signaling cascades that promote directional movement (Montell et al., 2012; Stuelten et al., 2018; Saadin and Starz-Gaiano, 2016; Friedl and Mayor, 2017). Downstream of the RTKs, guided motility is governed in border cells largely through regulation of the actinomyosin cytoskeleton via the Rho GTPase, Rac, and myosin phosphorylation states, with coordinated changes in cell-cell adhesion mediated by E-cadherin (Stuelten et al., 2018; Saadin and Starz-Gaiano, 2016; Montell et al., 2012; Chen et al., 2020). The follicle cells receiving sufficiently high levels of UPD—not necessarily just those in closer proximity to the polar cells depending on the extracellular geometry (Manning et al., 2015)—turn on a higher level of STAT activity and become motile border cells while nearby cells with lower levels do not. Interestingly, high STAT activity in ovarian follicle cell is sufficient to induce motility in usually stationary lateral follicle cells (Silver and Montell, 2001).
We focus on the protein products from two genes activated by STAT: Apontic (APT) and SLBO. SLBO promotes migratory behavior and an insufficient amount of SLBO prevents motility (Montell et al., 1992). APT protein is a transcription factor that downregulates the function of JAK/STAT and SLBO, and thus inhibits migration (Starz-Gaiano et al., 2008). APT acts as a feedback inhibitor on the JAK/STAT pathway, and this process is mediated by APT's activation of a microRNA that reduces STAT protein and activity (Yoon et al., 2011). APT also activates expression of Socs36E, which downregulates STAT signaling via a degradation pathway (Monahan and Starz-Gaiano, 2015). APT and SLBO exhibit cross-repressional behavior (Starz-Gaiano et al., 2008, 2009). APT directly represses slbo transcription while SLBO only decreases the level of expression of APT protein. The dominating protein in a given cell determines the cell fate: stationary or motile. This creates what appears to be a bistable system, as cells that receive intermediate amounts of STAT have the potential to reach either fate (Starz-Gaiano et al., 2009; Rorth, 1994). While it is reasonable based on the non-linearities in the system to model this cell fate regulation as bistability, in vivo experiments to support this are challenging and we are not aware of any particular experiments that have been done to confirm bistability. By identifying the conditions under which bistability occurs, modeling can help to design experimental protocols to confirm bistability.
We base our model on the mechanistic model built by Ge et al. (2012). Focusing on the cross-repression system of APT and SLBO, they built a mathematical model using elementary interactions to identify which components of the system are sufficient for bistability. Depending on the strength of the UPD signal and thus the level of STAT activity, each border cell can become motile (SLBO dominates) or remain stationary (APT dominates). Cells with an intermediate level of STAT activity may fall above or below the threshold necessary for mobility.
Ge and Stonko created a 15-variable model including many mechanisms of STAT regulation (see Figure 2A) as well as the cross-repression system of APT and SLBO (see Figure 2B) with sufficient elements, specifically cooperativity in SLBO repressing apt mRNA translation, to cause bistability. We do not know the mechanism for this, but we suspect SLBO activates expression of a microRNA that mediates the effect. Ge et al. (2012) identified several miRNAs in the Drosophila genome that have upstream binding sites for SLBO activation and seed sequences that would target the apt mRNA 3′ untranslated regions.
To describe briefly the full model, in Equations (1) and (2) JAK (J) is altered to an enzymatically active state, J*, in the presence of UPD (U). Further in Equation (1) J* enzymatically activates two STAT monomers (S) to create the activated STAT dimer () shown for STAT variables and complexes in Equations (3)–(6) with c1 denoting the complex between activated JAK (J*) and STAT (S). Equation (5) represents APT sequestering in c2. In Equations (7) and (8) APT (A) and SLBO (B) are produced from their mRNA and degraded, while A binding with is accounted for. The mRNA production of stat (mσ), apt (mα), and slbo (mβ), is shown in Equations (7)–(9) based on a constant basal production and transcribing or probabilistic fraction based on non-transcribing stat (σ), apt (α), and slbo (β) respectively, along with degradation. In Equation (9) B cooperatively enhances mα degradation, while in Equations (10) and (11) A enhances mσ and mβ degradation. The gene state dynamics are shown in Equations (12)–(15), with inducing transcription of σ, α, and β, while binding with A puts slbo into a repressed state (βR). Model variables for Equations (1)–(15) from Ge et al. (2012) are in Table 1.
The 15-variable model is:
In this paper we analyze and adapt the Ge and Stonko model so that a minimal reduction retains the dynamics of the detailed model. In section 2 we describe the methods we use to establish parameters and for bifurcation analysis. In section 3 we develop the minimal reduced model. In section 4 we analyze bifurcation results, identify the critical stable manifold separating the migratory and stationary steady states, validate experimental results, and compare our model to previous models. We apply this model in the interesting case of controlling microRNA-mediated degradation of stat mRNA via APT and show that delays in STAT activation, even to the point of activation failure within a biophysical time span, are possible due to the proximity of the critical UPD level to a limit point bifurcation. We conclude with possible experimentation that could test and improve our model.
2. Materials and Methods
In this section, we describe the methods used to analyze our minimal reduced model developed below. We use bifurcation and parameter analysis and identify the stable manifold between the stationary and motile steady states.
2.1. Time Course and Bifurcation Analysis
We use XPPAUT (Ermentrout, 2002) to create time course simulations and bifurcation diagrams and to analyze the bistability of the reduced model. We use the stiff integration method to solve our system of ODEs. A bifurcation occurs when a small change in parameter values results in a qualitative change in a system. Bifurcation analysis allows us to identify limit points treating UPD as a parameter, and helps to identify the separatrix between our steady states.
2.2. Establishing Parameters
In order to establish a more biophysically realistic model for this study, we researched existing literature to find data to establish parameter values. For some parameters we were able to find data specific to the JAK/STAT pathway or Drosophila. For other parameters, related pathways were used to obtain data relevant to this model.
We were able to identify published values for general translation and transcription rates and applied the established rates to the lengths of JAK (encoded by hopscotch), STAT (encoded by Stat92E), APT, and SLBO genes and proteins (Hargrove et al., 1991; Lewin, 2004). The lengths are found in the fly genome database, Flybase (Thurmond et al., 2019). Protein and mRNA degradation rates have a wide range of average values so JAK, STAT, APT, and SLBO are assumed to conform to this range (Guido et al., 2006; Harris et al., 2011; Nicholson and Nicola, 2013). The protein to DNA binding and dissociation rates of JAK and STAT have been identified in general but not specifically for APT and SLBO (Halford and Marko, 2004; Parsaeian et al., 2013; Yang et al., 2002; Nicholson and Nicola, 2013).
Many signaling pathways, including the JAK/STAT pathway, are regulated by microRNAs (miRNAs) (Lui et al., 2015; Yoon et al., 2011). Ge et al. (2012) identified several microRNAs annotated in the genome (Thurmond et al., 2019; Betel et al., 2007) that have seed sequences corresponding to apt and slbo, suggesting they are also regulated by this mechanism. This regulation can occur through mRNA degradation, translational inhibition, or other means, making the parameters corresponding to miRNA kinetics difficult to assign. Ge and Stonko addressed this by condensing the various processes by which miRNA can affect mRNA into one degradation rate. We identified a parameter value for this combined effect through information from the model established in Yoon et al. (2011). The rate that slbo transitions in and out of its repressed state was also hard to identify due to lack of data, so we utilized the rate given in Ge and Stonko which was adapted from the rate for a different repressor in Harris et al. (2011) and information from Rorth (1994). The base levels of STAT and the total amount of JAK present in border cells were estimated from Yoon et al. (2011); Starz-Gaiano et al. (2008), and McGregor et al. (2002). Lastly, for the rates of STAT independent mRNA production, we again used the original parameter values from Starz-Gaiano et al. (2009). For slbo, this rate is most likely negligible. However, apt can be activated by means other than STAT. The protein Eyes Absent (EYA) can also activate transcription of apt (Starz-Gaiano et al., 2009).
2.3. Manifolds Separating Cell Fate Basins of Attraction
One goal in developing the three-variable model was to be able to fully understand the manifold that separates the steady states in the model. For a level of UPD in the bistable region, cells can either become motile or remain stationary depending on the initial conditions of the system.
We visually identified the manifolds by labeling initial conditions according to the steady state to which they converge. This allows us to see the basins of attraction for each steady state. These two stable steady states, one where SLBO dominates and the cell becomes motile and one where APT dominates and the cell remains stationary, are listed in the appendix with values for each variable. In our three-dimensional system we are able to approximate the manifold by fitting a surface to the boundary between the basins of attraction.
A graphical representation of the boundary manifold was achieved by creating a 3-d grid of initial conditions and determining to which steady state each converged within 500 min, a time deemed reasonable from experimental data. Any initial conditions that did not converge by this time were identified as lying near the manifold. We then used the MATLAB curve fitting toolbox to fit a surface to these points, creating an approximation of the manifold between the steady states.
3. Developing the Reduced Model
We began by reducing the fixed STAT cross-repression system of APT and SLBO (Equations, 7–10, 12–14) to a two-variable model. In the process of researching biophysically realistic parameters we discovered that the binding rate of STAT to target genes appears to be several orders of magnitude faster than any other process in the system, as seen in Table 2 (Halford and Marko, 2004; Parsaeian et al., 2013; Yang et al., 2002; Nicholson and Nicola, 2013; Karsten et al., 2006; Ekas et al., 2010). For example, , , and are at least three orders of magnitude faster than the translation and transcription kinetics. Additionally, α, β, and βR reach equilibrium significantly faster than the other variables. We used time-scale analysis to reduce the system. We made a quasi-steady state approximation for α, β, and βR and set those derivatives equal to zero. This allowed us to solve Equations (12), (13), and (14) for α* = 1−α and β* = 1−β−βR in terms of APT protein and STAT dimer:
Our parameter values indicate that the mRNA processes occur at least twice as fast as the protein processes. This makes a quasi-steady state approximation for mα and mβ plausible. Thus, we have a two-variable model where only APT and SLBO are dynamic.
The two-variable model is:
After establishing the cross-repressional system of APT and SLBO, we reintroduced STAT dynamics to the model. Now we reduce the STAT activation system (Equations 1–6, 11, 15) through a number of assumptions.
First, we ignored the theoretical APT-STAT complex (c2) as its effects of APT sequestering STAT do not affect the steady state structure of the model, which we proved analytically. Then we used the Michaelis-Menten approximation for the activated JAK (J*) conversion of two STAT molecules to an activated STAT dimer (). This eliminates the JAK-STAT complex (c1) and condenses the conversion. We assumed conservation of JAK to eliminate unactivated JAK (J) by defining a constant total JAK as . We also assumed that UPD (U) activation of JAK and STAT activation are fast so J* and can be solved for by quasi-steady state approximations. Lastly, similar to the reduction made for apt and slbo, the inactive stat gene state (σ) and stat mRNA (mσ) were solved by quasi-steady state approximations. These assumptions gave us the following additional approximations:
Thus, producing our minimal three-variable model in APT, SLBO, and STAT:
4. Results
4.1. Bifurcation Analysis
Time courses of STAT, APT, and SLBO show the difference between the motile and stationary steady states in Figures 3A,B. Figures 3C,D shows the comparable results for the original 15-variable model. The two models converge to slightly different steady state values. This is due to the methods used to reduce the STAT dynamics in the 3-variable model. Exact steady state values can be found in the Supplementary Materials.
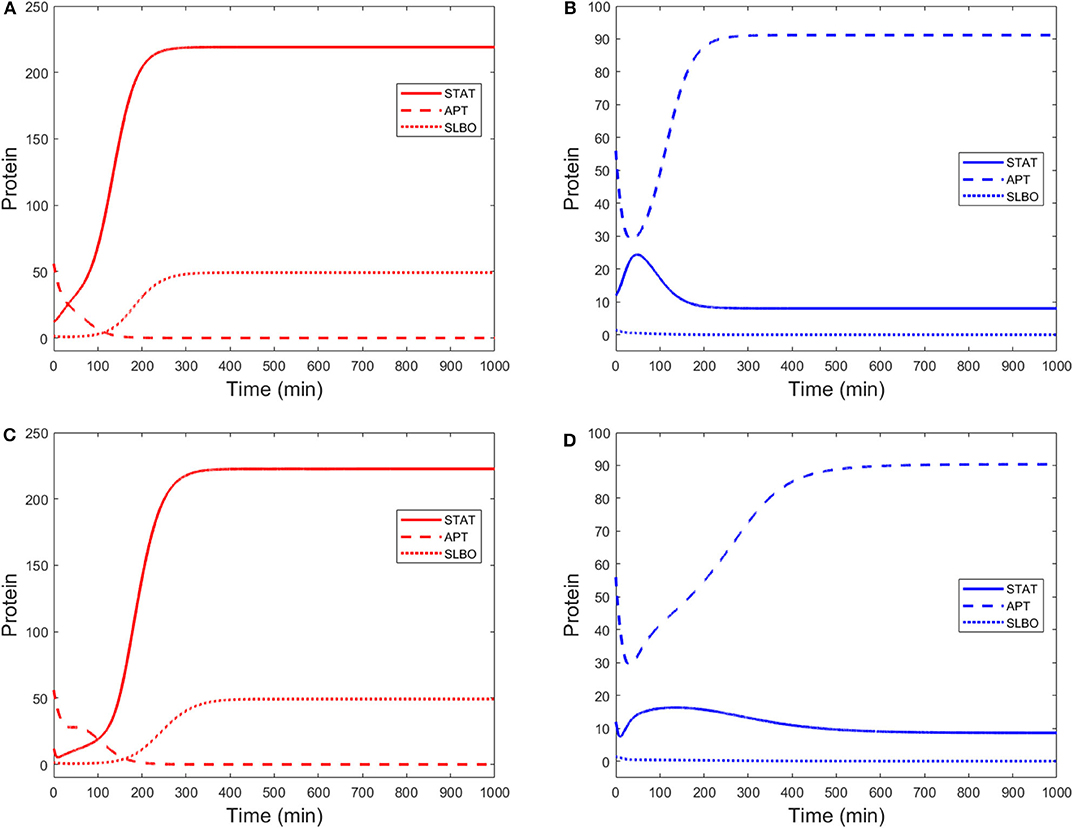
Figure 3. Time courses of STAT, APT, and SLBO with initial conditions STAT = 12, APT = 56, SLBO = 1.5 in the 3-variable model for (A) motile steady state (UPD = 4) and (B) stationary steady state (UPD = 1) and the 15-variable model for (C) motile steady state (UPD = 4) and (D) stationary steady state (UPD = 1).
A bifurcation diagram of APT against UPD revealed a non-trivial state when U = 0 with a high level of APT, as seen in Figure 4A. This can be interpreted as the system being predisposed to the stationary cell fate until UPD and thus STAT is high enough, at UPD >11.24 nM. As UPD approaches 0 on the upper branch, APT stops at a value of 44.73 nM. Since APT is also positively affected by STAT via UPD, very low UPD will decrease the steady state levels of APT but not to zero, leaving the stationary state the only steady state at very low UPD. Here the system encounters a limit point bifurcation and with a higher UPD level would transition to low APT and a motile cell fate.
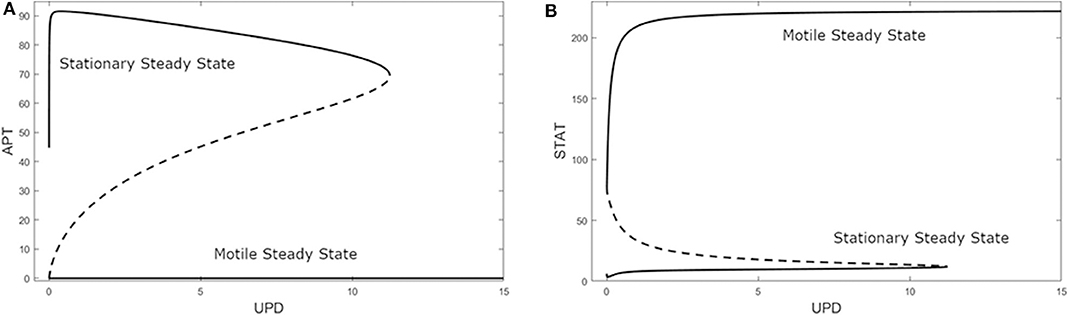
Figure 4. Bifurcation diagrams of (A) APT and (B) STAT against UPD in the three-variable model. A solid line indicates a stable steady state, a dashed line indicates an unstable steady state. Limit point bifurcations (where the sold and dashed lines meet) create “knees” where the model jumps from one steady state to the other. At U = 0 APT dominates.
Additionally, with the same parameters as Figure 4A, the STAT bifurcation (Figure 4B) shows that if UPD begins at a high level in a cell, the cell will remain in the motile state even as UPD decreases to a very low level. This can be seen in experiments that dissociate polar cells and border cells. The border cells continue to migrate until their UPD level presumably drops below the threshold level, i.e., as they get too far away from the polar cells (Starz-Gaiano et al., 2008; Cai et al., 2014). This threshold also exists in the opposite direction—as the level of UPD increases in an epithelial cell, it becomes a migratory border cell once the threshold is reached (Manning et al., 2015).
The bistability in the model depends on two mechanisms. We show that the predominate non-linearity is in SLBO cooperative repression of apt mRNA translation. We also show the repressed state for the slbo gene induced by APT contributes to bistability (Starz-Gaiano et al., 2008). Bifurcation diagrams for STAT, APT, and SLBO with each combination of these criteria are presented as Figures S1–S3. As quadratic non-linearity in SLBO is made linear and the ability to reach the slbo gene repressed state is eliminated, the stationary basin of attraction becomes smaller until bistability is lost.
4.2. Parameter Values
Throughout the research on parameter values, the goal was to develop a range of realistic parameters to test in our model. There are two reasons why a range of values is desirable. First, from the biological point of view, many biological processes do not occur at a constant rate. Second, heterogeneity in cellular parameters will likely lead to some parameter variety. A range of average values is thus both more appropriate and more consistent with experimental data. We were able to test the robustness of the dynamics over the ranges of parameters to see if the model behavior matches experimentally observed outcomes.
The parameter values established through research from a variety of experimental systems and testing for bistability are shown in Table 2. The range of values identified for each parameter demonstrates a robust region of bistability. This adds confidence in the decision to use some parameter values that were established from a range of possible values.
Figure 5 shows the percent change on a log10 scale in each parameter that maintains bistability. The exact range for each parameter is listed in Table 3. The most sensitive parameter is δAσ. This makes sense biologically, as δAσ controls APT induced miRNA degradation of stat. Changing this rate directly affects whether a presumptive border cell produces enough STAT activity to pass the threshold needed for motility given a particular amount of UPD. APT has multiple levels of control on STAT, but this may be the most sensitive because there are multiple other regulators at the protein level. We explore the effects of this parameter on the outcome of the system below. The range of possible values for each parameter supports the robustness of the JAK/STAT pathway as a bistable system.
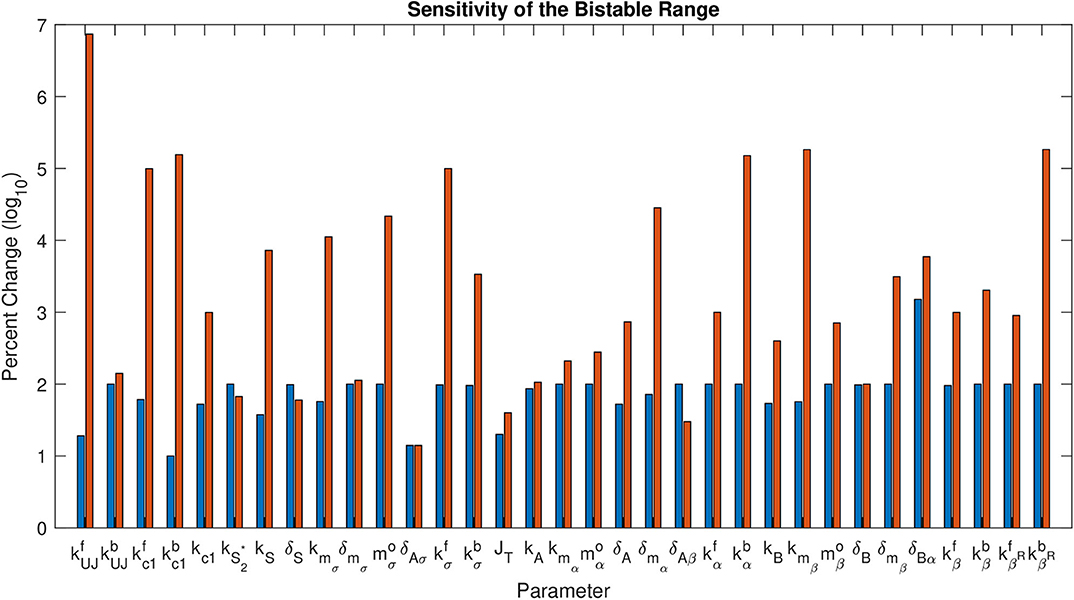
Figure 5. Sensitivity of the Bistable Range. This shows log10 of percent change in each parameter that maintains bistability. The first bar (blue) for each parameter is the negative change, the second (red) is the positive change.
4.3. Manifolds in Three-Variable Model
We found that our three-variable minimal model retains the bistability and dynamics of the 15-variable model. Therefore, we use the three-dimensional manifolds in this model to better understand the behavior of the full model.
The stable manifold appears to be near-planar in the STAT-APT-SLBO phase space. The UPD value determines the position of the plane, with the manifold shifting from the STAT-SLBO plane to the STAT-APT plane as UPD increases, thus increasing STAT and SLBO production. Figure 6 shows how the manifold shifts as UPD increases from 0.0133 to 4, values that cover much of the bistable range of UPD.
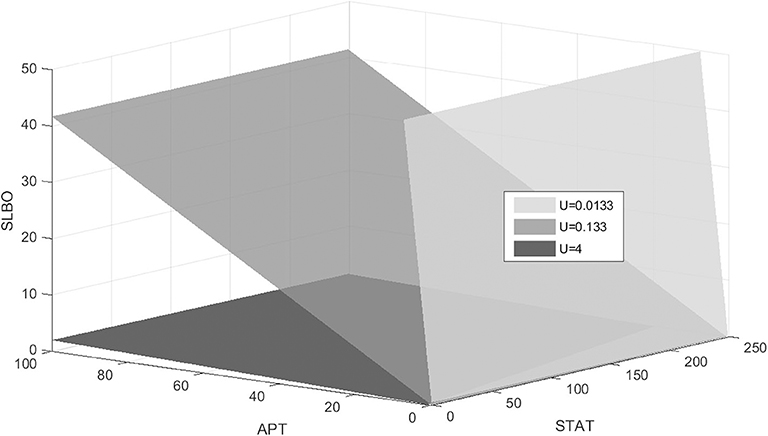
Figure 6. Stable manifold when UPD = 0.0133, UPD = 0.133, and UPD = 4. As UPD increases, the manifold shifts from the STAT-SLBO plane to the STAT-APT plane.
To visualize the dynamics for each of the three values of UPD in the bistable region used in Figure 6, we plot trajectories to demonstrate how the manifold affects the outcomes of different initial conditions. Initial conditions that lie just below the manifold are attracted to the stable manifold near the unstable steady state and then repelled toward the stationary steady state. Initial conditions that lie just above the manifold behave similarly but converge to the motile steady state. Figure 7 depicts this behavior, with initial conditions that progress to the stationary steady state and the corresponding trajectories in blue and initial conditions that progress to the motile steady state and the corresponding trajectories in red. Three initial conditions and trajectories for each steady state are plotted. The motile steady state is in red, the stationary steady state is in blue, and the unstable steady state is in black. The unstable steady state lies on the 2D stable manifold.
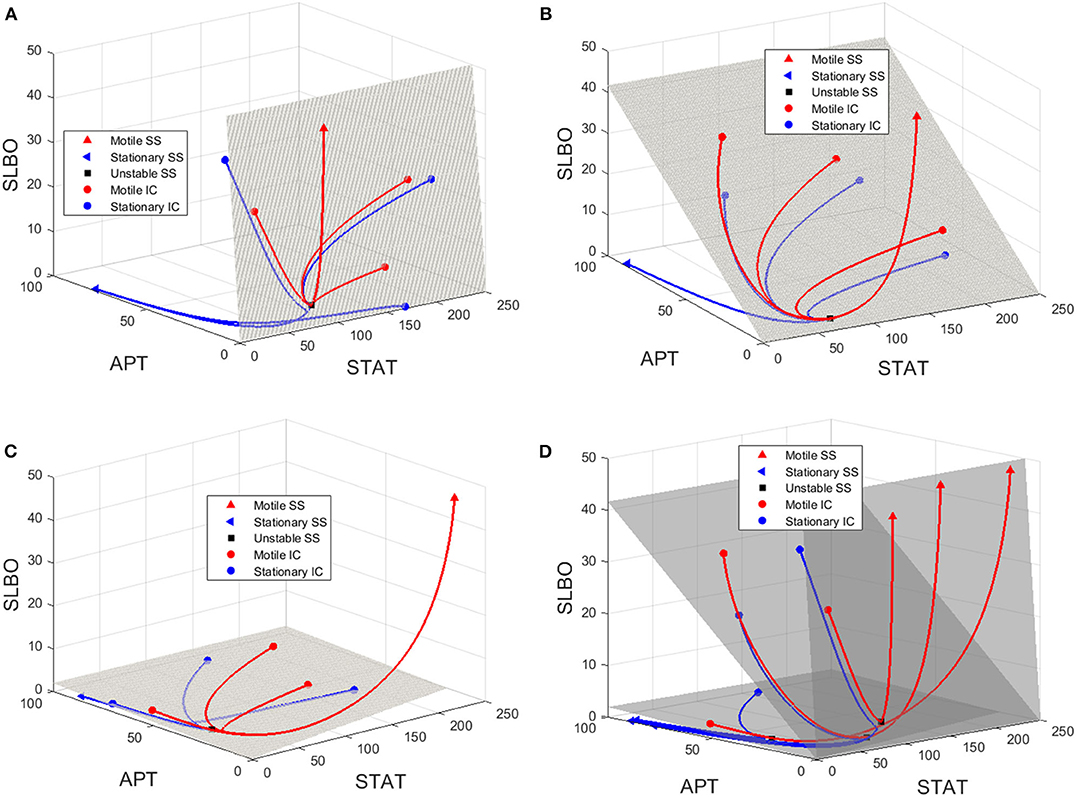
Figure 7. Manifolds and trajectories for three values of UPD. Stationary initial conditions and trajectories are in blue and motile initial conditions and trajectories are in red. The motile steady state is in red, the stationary steady state is in blue, and the unstable steady state is in black. (A) Manifold and trajectories for UPD = 0.0133. (B) Manifold and trajectories for UPD = 0.133. (C) Manifold and trajectories for UPD = 4. Movies showing a 3D rotation of each space and time series of each trajectory are available in the Figures S4-S8. (D) A-C combined to show how the motile basin of attraction expands as UPD increases and the manifold shifts.
When UPD is low, such as in Figure 7A, initial conditions in most of the phase space will result in the stationary steady state. When UPD is high, such as in Figure 7C, initial conditions in most of the phase space will result in the motile steady state.
Figure 7D combines Figures 7A–C to show how the shifting manifold affects the system. As the value of UPD increases and the manifold moves below additional initial conditions, the motile basin of attraction expands and the motile and stationary steady states shift slightly. Movies showing a 3D rotation of each space and time series of each trajectory are available in the Figures S4–S8.
4.4. Delay From miRNA
The rate at which APT-induced miRNAs lead to degradation of stat mRNA is controlled in the model by the parameter δAσ. Figure 8A shows time courses of S in the three-variable model with UPD = 4 for different values of δAσ. We established a typical value of δAσ = 0.05 that allows S to equilibrate around 200 min, which is consistent with the time it takes for border cells to respond to UPD (Starz-Gaiano et al., 2008; Manning et al., 2015). The STAT level when δAσ = 0.05 is well above the threshold needed for the cell to become motile. An increase to δAσ = 0.17382 delays STAT convergence by a significant amount of time, about 600 min. If we increase δAσ to just 0.18, S never elevates within 1,000 min. Thus, the cell remains stationary. Each time course in Figure 8 represents a different outcome of the JAK/STAT pathway: , where SLBO dominates (δAσ = 0.05); , where APT dominates (δAσ = 0.18); and , where the transition to motility is delayed (δAσ = 0.17382). The mechanisms of how APT-activated miRNAs affect STAT are still being analyzed, but initial findings support the idea that changes in miRNA activity can cause delays similar to those seen in our model (Yoon et al., 2011; Luo and Sehgal., 2012; Monahan and Starz-Gaiano, 2016; Sun et al., 2015). Delays in STAT activation and failure of activation are possible within a realistic time frame.
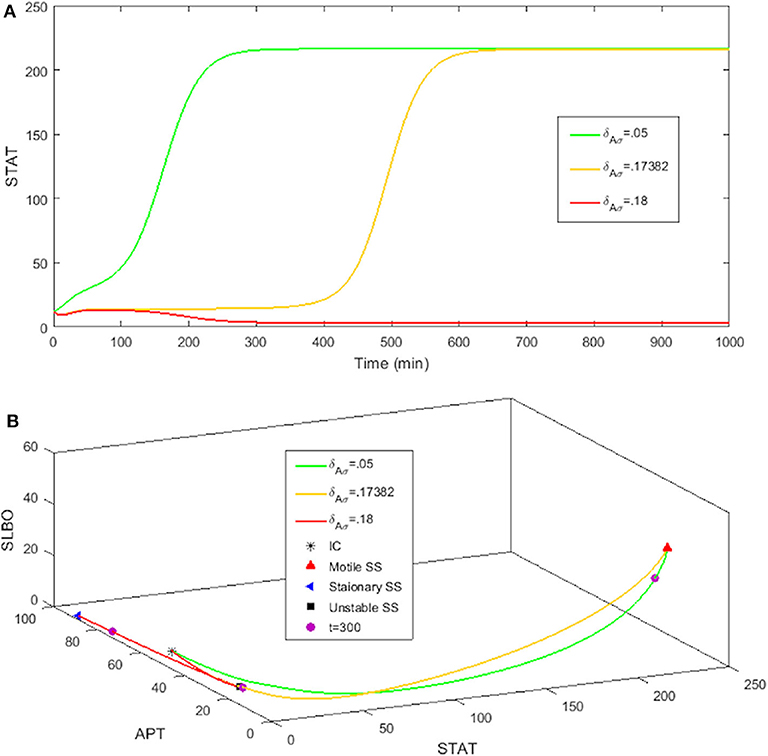
Figure 8. Three levels of miRNA controlled by δAσ: δAσ = 0.05, δAσ = 0.18, δAσ = 0.17382 with initial conditions STAT = 12, APT = 56, SLBO = 1.5, and UPD = 4. (A) Time courses of STAT. As δAσ increases STAT activation is delayed. (B) 3D plot of the three cell fates in (A). The motile steady state is in red, the stationary steady state is in blue, and the unstable steady state is in black. t = 300 on each trajectory is marked in purple.
For basal levels of δAσ the system has normal STAT activation. However, as δAσ is increased the manifold separating the and basins of attraction gets close to the initial condition, slowing the rise time to activation. If δAσ is raised enough the manifold crosses the initial condition and the trajectory is attracted to the fate. Figure 8B further illustrates this delay. The 3D plot shows that at t = 300 the cell fate still has very low STAT and SLBO production. At the same time the and cell fates have almost converged to their respective steady states. This change in outcome for one initial condition occurs because the increase in δAσ causes the manifold to shift just above the initial condition. This can be seen in Figure 9, where the initial condition lies between the manifold and the manifold.
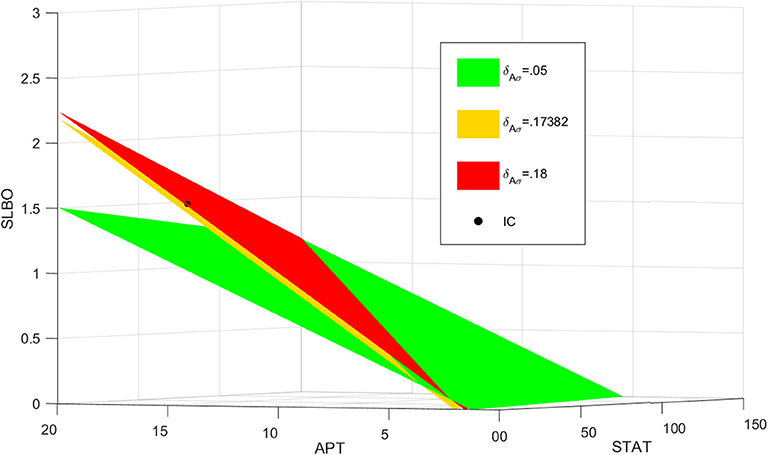
Figure 9. Manifolds for , , . As δAσ increases, the manifold shifts above the initial condition in black.
4.5. Experimental Tests
We tested our models to confirm if they reproduced certain behaviors identified in various experiments. It has been shown that if STAT activity is blocked by stage 9 of cell migration, the level of APT protein drops by about half (Starz-Gaiano et al., 2008, 2009; Yoon et al., 2011; Monahan and Starz-Gaiano, 2015). It is also known that increasing the initial condition of APT should decrease the level of STAT protein and activity (Starz-Gaiano et al., 2008). These behaviors should be achievable by our models.
The three-variable model (Equations 29–31) reproduces the experimental behavior of APT when STAT is knocked down, as shown in Figure 10A. STAT initially converges to a value of about 4. Setting kS = 0 causes STAT to be constantly zero. This causes APT to converge to an equilibrium roughly half that of the stationary steady state. APT acts as an inhibitor to STAT activity, so for higher APT initial conditions we should see lower levels of STAT. This also occurs in the three-variable model (Figure 10B).
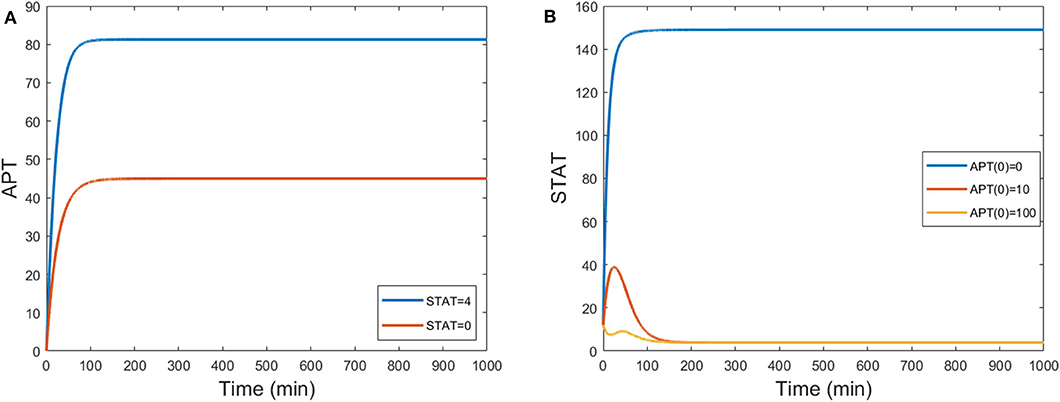
Figure 10. (A) Time courses of APT show levels decrease by half when STAT is knocked down from a steady state value of around 4 to one of 0 by setting kS = 0. (B) Time courses of STAT for different initial conditions of APT. When UPD = 0.1, STAT steady state levels decrease for high initial conditions of APT. S(0) = 12 and B(0) = 1.5.
4.6. Comparison to Previous Models
Previous mathematical models of the JAK/STAT pathway in Drosophila have focused on matching the qualitative behavior of the system. We compare our mechanistic model to the models developed in Starz-Gaiano et al. (2008) and Yoon et al. (2011) in Table 4. We rewrite our equations and use composite parameters to allow for easier comparison. The names of variables for STAT and SLBO differ across the models.
Our model and the earlier models share the same basic structure. The equations for STAT, APT, and SLBO all have a production term and a degradation term. The production terms include the cross-reactions of the proteins. However, our model describes these interactions in more detail, accounting for more of the known molecular interactions and biochemical production/degradation rates. For example, our STAT equation includes the feedback inhibition from APT. Our model also includes STAT independent production rates for both APT and SLBO, while the earlier models only include this for APT. By including the details of these molecular interactions, we gain the ability to mathematically examine the bistability of the JAK/STAT pathway.
Dynamic UPD is a feature of earlier models. Earlier models also include that levels of active STAT are positively regulated by production of UPD. Our model can be combined with the UPD dynamics developed in Manning et al. (2015). They used a partial differential equation to model the change in UPD concentration over time in three-dimensional extracellular space (Manning et al., 2015). This more detailed version of UPD dynamics includes the spatial element of how UPD diffuses from the polar cells into the border cells. It also helps to explain how border cells farther from the polar cells, which receive less UPD, can be delayed in becoming motile. Additionally, modeling in Peercy and Starz-Gaiano (2020) gives details of how the geometry of the egg chamber influences cell fate and migration dynamics. They also examine models of velocity and migratory cohort size as well as how clusters of border cells function to guide directional movement. Together our mechanistic model, the spatial dynamics of UPD from Manning et al. (2015), and models of collective migration from Peercy and Starz-Gaiano (2020) help us gain a better understanding of the threshold for motility in border cells.
5. Discussion
We reduced the mechanistic Ge and Stonko model in stages to arrive at our minimal three-variable model. This final model allows us to better understand bistability in the JAK/STAT pathway. Our minimal model retains the parameters from the more complex model, allowing easier analysis but retaining critical properties. We discovered that non-linearity in SLBO repression of apt mRNA translation (Equation 9), and to a lesser extent APT repression of the slbo gene is required for bistability. The model displays the bistability of the stationary and motile cell states expected from experimental data for medium saturation of STAT activity. It has been shown that modulating UPD expression affects the number of migratory cells (Manning et al., 2015; Van De Bor et al., 2011; Silver and Montell, 2001; Xi et al., 2003; Grammont and Irvine, 2002). If UPD is low there are no migratory cells and if UPD is high there are many. This can induce normally stationary cells far away from the anterior to become motile (Manning et al., 2015).
We established parameters that showed bistability was obtainable under realistic conditions. Every parameter in the 15-variable model was found to have a wide range of values that guaranteed bistability. The robustness with respect to parameter values also suggests the biophysical utility of the model. Cell migration is an essential biological process, so the JAK/STAT pathway necessitates robustness under a range of parameter values, which the model supports. It makes sense that the JAK/STAT pathway would be able to operate successfully under a range of parameter values.
Ge and Stonko assumed that a key aspect necessary for bistability in APT and SLBO is cooperativity in SLBO repressing apt mRNA. In our dynamic STAT model, we found that the feedback inhibition of APT on STAT is necessary for bistability in STAT activity coming from the bistability between APT and SLBO. We also found that the initial amount of APT present in a cell is a major factor in whether or not the cell will become motile through affecting the level of STAT activity. Our minimal reduced model also reproduces behavior seen in experiments, such as declines in APT expression when STAT is knocked down and how initial levels of APT affect final levels of STAT (Starz-Gaiano et al., 2008).
We also showed that delays in STAT activation and failure of activation are possible within a realistic time frame. By controlling the degree of feedback inhibition of APT on STAT we can induce a delay in the transition to cell motility or cause the cell to remain stationary. This result is due to the proximity of the UPD level to a limit point bifurcation.
Assumptions made in the development of this model lead to some limitations. Specific parameter values for the exact reactions occurring in the egg chamber are not known, so we performed sensitivity analysis to show the robustness in parameter values. The STAT dynamics were reduced under a number of assumptions. One was the decision to ignore the c2 equation, which allows APT to act as a buffer on STAT. Since the action of APT on STAT is known to function by preventing activation through miRNAs (Yoon et al., 2011) as well as limiting active protein present (Monahan and Starz-Gaiano, 2015, 2016), this assumption might oversimplify the larger system. Additionally, the quasi-steady state assumptions made in reducing STAT dynamics may also oversimplify the model.
Further study into the various methods by which APT inhibits STAT would enable us to improve how the model captures this interaction. Experiments that change the level of APT or STAT may give more information about how the delay in specification affects the migration of the cell cluster. Experimenting with apt mutants could tell us more about how the bistability we show in cell specification ultimately affects cluster migration and the further development of the egg chamber. When STAT is abnormally high more intermediate border cells trail behind the polar cells (Silver and Montell, 2001; Silver et al., 2005; Monahan and Starz-Gaiano, 2015; Starz-Gaiano et al., 2008). Socs36E limits STAT signaling and higher Socs36E reduces motile cell number. Both of these cases may suggest how a delay in cell specification affects cell migration.
It may also be important to consider how APT and SLBO may interact through miRNAs. Currently there is little data beyond the existence of these miRNAs (Ge et al., 2012). miRNA interactions directly affect bistability in the model, so greater detail could improve the model. Experiments that control the level of UPD secreted could identify how quickly the signal enters border cells and the levels of UPD which correspond with the activated STAT threshold to induce motility. To further gauge the STAT levels it would also be valuable to know the level of APT present in border cells through activation by EYA, prior to STAT activation and upregulation by STAT.
The JAK/STAT signaling pathway is known to be well-conserved. Specifically, it seems to be comparable in Drosophila and in humans (Trivedi and Starz-Gaiano, 2018; Arbouzova and Zeidler, 2006; Amoyel and Bach, 2012; Amoyel et al., 2014). Thus, as the model we have developed helps to explain cell motility in Drosophila, it may prove useful to our understanding of the process in humans. The “decision” for tumor cells to become motile is often a turning point for cancer progression. Additionally, STAT signaling is also well-known for controlling stem cell division decisions. Thus, the decisiveness of STAT-based signaling may have a variety of roles in different cell types, but the model and its bistability shown in this paper may help to explain how this STAT signaling operates in different situations.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
BP and MS-G contributed conception and methodology, and reviewed and edited the manuscript. AB was the main writer the manuscript, and developed the reduced model, performed analysis, and ran simulations. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work was supported in part by National Science Foundation grant IOS-1656550 to MS-G. AB was funded in part by a summer research grant from the Dean of the College of Natural and Mathematical Sciences at UMBC.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to acknowledge the previous work done within the NSF-funded UBM program at UMBC that forms the basis of this research.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2020.00803/full#supplementary-material
References
Aman, A., and Piotrowski, T. (2010). Cell migration during morphogenesis. Dev. Biol. 341, 20–33. doi: 10.1016/j.ydbio.2009.11.014
Amoyel, M., Anderson, A. M., and Bach, E. A. (2014). JAK/STAT pathway dysregulation in tumors: a Drosophila perspective. Semin. Cell Dev. Biol. 28, 96–103. doi: 10.1016/j.semcdb.2014.03.023
Amoyel, M., and Bach, E. A. (2012). Functions of the Drosophila JAK-STAT pathway: lessons from stem cells. Jak Stat 1, 176–183. doi: 10.4161/jkst.21621
Arbouzova, N. I., and Zeidler, M. P. (2006). JAK/STAT signalling in Drosophila: insights into conserved regulatory and cellular functions. Development 133, 2605–2616. doi: 10.1242/dev.02411
Betel, D., Wilson, M., Gabow, A., Marks, D. S., and Sander, C. (2007). The microRNA.org resource: targets and expression. Nucleic. Acids. Res. 36, 149–153. doi: 10.1093/nar/gkm995
Cai, D., Chen, S.-C., Prasad, M., He, L., Wang, X., Choesmel-Cadamuro, V., et al. (2014). Mechanical feedback through E-cadherin promotes direction sensing during collective cell migration. Cell 157, 1146–159. doi: 10.1016/j.cell.2014.03.045
Chen, Y., Kotian, N., Aranjuez, G., Chen, L., Messer, C. L., Burtscher, A., et al. (2020). Protein phosphatase 1 activity controls a balance between collective and single cell modes of migration. Elife 9:e52979. doi: 10.7554/eLife.52979.sa2
Ekas, L. A., Cardozo, T. J., Flaherty, M. S., McMillan, E. A., Gonsalves, F. C., and Bach, E. A. (2010). Characterization of a dominant-active stat that promotes tumorigenesis in Drosophila. Dev. Biol. 344, 621–636. doi: 10.1016/j.ydbio.2010.05.497
Ermentrout, B. (2002). Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students. Philadelphia, PA: Society for Industrial and Applied Mathematics.
Friedl, P., and Mayor, R. (2017). Tuning collective cell migration by cell–cell junction regulation. Cold Spring Harbor Perspect. Biol. 9:a029199. doi: 10.1101/cshperspect.a029199
Ge, X., Stonko, D., Peercy, B., and Starz-Gaiano, M. (2012). Modelling a cellular response to a gradient. UMBC Rev. 13, 92–113.
Ghiglione, C., Devergne, O., Georgenthum, E., Carballès, F., Médioni, C., Cerezo, D., et al. (2002). The Drosophila cytokine receptor Domeless controls border cell migration and epithelial polarization during oogenesis. Development 129, 5437–5447. doi: 10.1242/dev.00116
Grammont, M., and Irvine, K. D. (2002). Organizer activity of the polar cells during Drosophila oogenesis. Development 129, 5131–5140. Available online at: https://dev.biologists.org/content/129/22/5131
Guido, N. J., Wang, X., Adalsteinsson, D., McMillen, D., Hasty, J., Cantor, C. R., et al. (2006). A bottom-up approach to gene regulation. Nature 439, 856–860. doi: 10.1038/nature04473
Halford, S. E., and Marko, J. F. (2004). How do site-specific DNA-binding proteins find their targets? Nucleic Acids Res. 32, 3040–3052. doi: 10.1093/nar/gkh624
Hargrove, J. L., Hulsey, M. G., and Beale, E. G. (1991). The kinetics of mammalian gene expression. Bioessays 13, 667–674. doi: 10.1002/bies.950131209
Harris, R. E., Pargett, M., Sutcliffe, C., Umulis, D., and Ashe, H. L. (2011). Brat promotes stem cell differentiation via control of a bistable switch that restricts BMP signaling. Dev. Cell 20, 72–83. doi: 10.1016/j.devcel.2010.11.019
Hilton, D., and Nicola, N. (1992). Kinetic analyses of the binding of leukemia inhibitory factor to receptor on cells and membranes and in detergent solution. J. Biol. Chem. 267, 10238–10247.
Karsten, P., Plischke, I., Perrimon, N., and Zeidler, M. P. (2006). Mutational analysis reveals separable DNA binding and trans-activation of Drosophila STAT92E. Cell. Signal. 18, 819–829. doi: 10.1016/j.cellsig.2005.07.006
Leonard, C. E., and Taneyhill, L. A. (2020). The road best traveled: neural crest migration upon the extracellular matrix. Semin. Cell Dev. Biol. 100, 177–185. doi: 10.1016/j.semcdb.2019.10.013
Lui, P.-Y., Jin, D.-Y., and Stevenson, N. J. (2015). MicroRNA: master controllers of intracellular signaling pathways. Cell. Mol. Life Sci. 72, 3531–3542. doi: 10.1007/s00018-015-1940-0
Luo, W., and Sehgal, A. (2012). Regulation of circadian behavioral output via a MicroRNA-JAK/STAT circuit. Cell 148, 765–779. doi: 10.1016/j.cell.2011.12.024
Manning, L. A., Weideman, A. M., Peercy, B. E., and Starz-Gaiano, M. (2015). Tissue landscape alters adjacent cell fates during Drosophila egg development. Nat. Commun. 6:7356. doi: 10.1038/ncomms8356
McGregor, J. R., Xi, R., and Harrison, D. A. (2002). JAK signaling is somatically required for follicle cell differentiation in Drosophila. Development 129, 705–717. Available online at: https://dev.biologists.org/content/129/3/705
Monahan, A., and Starz-Gaiano, M. (2016). Apontic regulates somatic stem cell numbers in Drosophila testes. BMC Dev. Biol. 16:5. doi: 10.1186/s12861-016-0103-3
Monahan, A. J., and Starz-Gaiano, M. (2015). Socs36E limits STAT signaling via Cullin2 and a SOCS-box independent mechanism in the Drosophila egg chamber. Mech. Dev. 138(Pt 3), 313–327. doi: 10.1016/j.mod.2015.08.003
Montell, D. J., Rorth, P., and Spradling, A. C. (1992). Slow border cells, a locus required for a developmentally regulated cell migration during oogenesis, encodes Drosophila C/EBP. Cell 71, 51–62. doi: 10.1016/0092-8674(92)90265-E
Montell, D. J., Yoon, W. H., and Starz-Gaiano, M. (2012). Group choreography: mechanisms orchestrating the collective movement of border cells. Nat. Rev. Mol. Cell Biol. 13, 631–645. doi: 10.1038/nrm3433
Nicholson, S. E., and Nicola, N. A., (eds.). (2013). JAK-STAT Signalling: Methods and Protocols, Volume 967 of Methods in Molecular Biology. New York, NY: Humana Press.
Olson, H. M., and Nechiporuk, A. V. (2018). Using zebrafish to study collective cell migration in development and disease. Front. Cell Dev. Biol. 6:83. doi: 10.3389/fcell.2018.00083
Parsaeian, A., de la Cruz, M. O., and Marko, J. F. (2013). Binding-rebinding dynamics of proteins interacting non-specifically with a long DNA molecule. Phys. Rev. E Stat Nonlinear Soft Matter Phys. 4:040703. doi: 10.1103/PhysRevE.88.040703
Peercy, B. E., and Starz-Gaiano, M. (2020). Clustered cell migration: modeling the model system of Drosophila border cells. Semin. Cell Dev. Biol. 100, 167–176. doi: 10.1016/j.semcdb.2019.11.010
Rorth, P. (1994). Specification of C/EBP function during Drosophila development by the bZIP basic region. Science 266, 1878–1881. doi: 10.1126/science.7997882
Rorth, P., Szabo, K., and Texido, G. (2000). The level of C/EBP protein is critical for cell migration during Drosophila oogenesis and is tightly controlled by regulated degradation. Mol. Cell 6, 23–30. doi: 10.1016/S1097-2765(05)00008-0
Saadin, A., and Starz-Gaiano, M. (2016). Circuitous genetic regulation governs a straightforward cell migration. Trends Genet. 32, 660–673. doi: 10.1016/j.tig.2016.08.001
Silver, D. L., Geisbrecht, E. R., and Montell, D. J. (2005). Requirement for JAK/STAT signaling throughout border cell migration in Drosophila. Development 132, 3483–3492. doi: 10.1242/dev.01910
Silver, D. L., and Montell, D. J. (2001). Paracrine signaling through the JAK/STAT pathway activates invasive behavior of ovarian epithelial cells in Drosophila. Cell 107, 831–841. doi: 10.1016/S0092-8674(01)00607-9
Starz-Gaiano, M., Melani, M., Meinhardt, H., and Montell, D. (2009). Interpretation of the UPD/JAK/STAT morphogen gradient in Drosophila follicle cells. Cell Cycle 8, 2917–2925. doi: 10.4161/cc.8.18.9547
Starz-Gaiano, M., Melani, M., Wang, X., Meinhardt, H., and Montell, D. J. (2008). Feedback inhibition of JAK/STAT signaling by apontic is required to limit an invasive cell population. Dev. Cell 14, 726–738. doi: 10.1016/j.devcel.2008.03.005
Stuelten, C. H., Parent, C. A., and Montell, D. J. (2018). Cell motility in cancer invasion and metastasis: insights from simple model organisms. Nat. Rev. Cancer 18, 296–312. doi: 10.1038/nrc.2018.15
Sun, K., Jee, D., de Navas, L. F., Duan, H., and Lai, E. C. (2015). Multiple in vivo biological processes are mediated by functionally redundant activities of Drosophila mir-279 and mir-996. PLoS Genet. 11:e1005245. doi: 10.1371/journal.pgen.1005245
Thurmond, J., Goodman, J., Strelets, V., Attrill, H., Gramates, L., Marygold, S., et al. (2019). Flybase 2.0: the next generation. Nucleic Acids Res. 47, D759–D765. doi: 10.1093/nar/gky1003
Trivedi, S., and Starz-Gaiano, M. (2018). Drosophila Jak/STAT signaling: regulation and relevance in human cancer and metastasis. Int. J. Mol. Sci. 19:4056. doi: 10.3390/ijms19124056
Van De Bor, V., Zimniak, G., Cerezo, D., Schaub, S., and Noselli, S. (2011). Asymmetric localisation of cytokine mRNA is essential for JAK/STAT activation during cell invasiveness. Development 138, 1383–1393. doi: 10.1242/dev.056184
Ward, L., Howlett, G., and Hammacher, A. (1995). Use of a biosensor with surface plasmon resonance detection for the determination of binding constants: measurement of interleukin-6 binding to the soluble interleukin-6 receptor. Biochemistry 34, 2901–2907. doi: 10.1021/bi00009a021
Wright, V. M., Vogt, K. L., Smythe, E., and Zeidler, M. P. (2011). Differential activities of the Drosophila JAK/STAT pathway ligands Upd, Upd2 and Upd3. Cell. Signal. 23, 920–927. doi: 10.1016/j.cellsig.2011.01.020
Xi, R., McGregor, J. R., and Harrison, D. A. (2003). A gradient of JAK pathway activity patterns the anterior-posterior axis of the follicular epithelium. Dev. Cell 4, 167–177. doi: 10.1016/S1534-5807(02)00412-4
Yang, E., Henriksen, M. A., Schaefer, O., Zakharova, N., and Darnell, J. E. (2002). Dissociation time from DNA determines transcriptional function in a STAT1 linker mutant. J. Biol. Chem. 277, 13455–13462. doi: 10.1074/jbc.M112038200
Keywords: JAK/STAT, Drosophila melanogaster, border cell migration, mathematical model, bistability
Citation: Berez A, Peercy BE and Starz-Gaiano M (2020) Development and Analysis of a Quantitative Mathematical Model of Bistability in the Cross Repression System Between APT and SLBO Within the JAK/STAT Signaling Pathway. Front. Physiol. 11:803. doi: 10.3389/fphys.2020.00803
Received: 31 March 2020; Accepted: 17 June 2020;
Published: 28 July 2020.
Edited by:
Denis Tsygankov, Georgia Institute of Technology, United StatesReviewed by:
Didier Gonze, Université libre de Bruxelles, BelgiumNathan Weinstein, Universidad Nacional Autnoma de Mexico, Mexico
Copyright © 2020 Berez, Peercy and Starz-Gaiano. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bradford E. Peercy, YnBlZXJjeUB1bWJjLmVkdQ==
 Alyssa Berez
Alyssa Berez Bradford E. Peercy
Bradford E. Peercy Michelle Starz-Gaiano
Michelle Starz-Gaiano