- 1Science Directorate, NASA Langley Research Center, Hampton, VA, United States
- 2Department of Hydrology and Atmospheric Sciences, The University of Arizona, Tucson, AZ, United States
- 3NASA Ames Research Center, Moffett Field, CA, United States
- 4Department of Atmospheric Sciences, University of Washington, Seattle, WA, United States
- 5The Department of Atmospheric Sciences, Texas A&M, College Station, TX, United States
- 6Ball Aerospace & Technologies Corp., Boulder, CO, United States
- 7Department of Physics, Stevens Institute of Technology, Hoboken, NJ, United States
Lidar multiple scattering measurements provide the probability distribution of the distance laser light travels inside snow. Based on an analytic two-stream radiative transfer solution, the present study demonstrates why/how these lidar measurements can be used to derive snow depth and snow density. In particular, for a laser wavelength with little snow absorption, an analytical radiative transfer solution is leveraged to prove that the physical snow depth is half of the average distance photons travel inside snow and that the relationship linking lidar measurements and the extinction coefficient of the snow is valid. Theoretical formulas that link lidar measurements to the extinction coefficient and the effective grain size of snow are provided. Snow density can also be derived from the multi-wavelength lidar measurements of the snow extinction coefficient and snow effective grain size. Alternatively, lidars can provide the most direct snow density measurements and the effective discrimination between snow and trees by adding vibrational Raman scattering channels.
1 Introduction
In recent studies (Hu et al., 2022; Lu et al., 2022), a simple relationship,
Analyzing the snow bidirectional reflectance of a simple two-stream radiative transfer solution, the objective of this paper is to derive a simple, analytical relationship between snow depth and the average distance photons travel inside snow, to derive the expression for the snow extinction coefficient as an analytical function of
2
When a space-based lidar receiver’s ground footprint size is a few meters larger than the laser spot size, the reflectance of the laser beam by a layer of snow is equivalent to the bidirectional reflectance of sunlight due to reciprocity. This is because snow extinction coefficients are greater than 100 1/m and thus the lidar receiver collects all the multiple scattering of the laser light. Light propagation in the snow can be described by the following one-dimensional radiative transfer equation,
where I is radiance, µ the cosine of viewing zenith angle, τ the optical depth, ω the single-scattering albedo,
The diffuse component of the radiance can be computed with a simple two-stream solution and a modified Eddington approximation that discretizes the differential-integral equation as follows:
In the above equations,
This modified Eddington approximation is optimized for calculating nadir-viewing azimuth independent diffuse radiance measurements of snow in order to properly capture its dependence on absorption, which is view angle and solar zenith angle dependent. Thus, for this modified Eddington approximation of diffuse radiance calculation, the source terms is different from the standard Eddington approximation for hemispheric radiative flux calculations, and
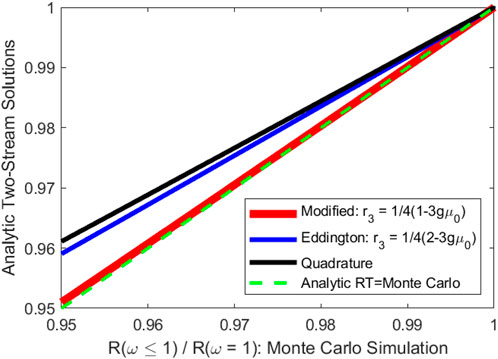
FIGURE 1. Comparisons of absorptions in space-based lidar measurements of weak absorbing snow-like media computed from Monte Carlo simulations of lidar measurements (X-axis) and that from bidirectional reflectance calculated with the modified Eddington approximation (red line), and that from the hemispheric fluxes calculated from the standard Eddington approximation (blue line) and the quadrature method (black line).
The eigenvalues of the above two equations are
The bidirectional reflectance at the top of the layer (Meador and Weaver, 1980) is
Here,
For nadir-pointing lidar (
This equation is similar but not identical to Eq. (7.87) in Stamnes et al. (2017) for g = 0 (isotropic scattering).
For a snow measurement lidar with its receiver footprint diameter a few meters greater than that of the laser spot, the lidar receiver can capture nearly all multiple scattering signals in the 180-degree backscatter direction. Increasing the footprint size will not change the lidar measurements. Thus, the lidar measurements of snow can be considered as 1) a laser beam with a divergence angle equivalent to the field-of-view angle of a passive sensor pointing at nadir; 2) a receiver as far as the Sun at solar zenith angle = 0° with a footprint near infinity. Due to reciprocity, the bidirectional reflectance,
Here, L is the distance of photons traveled within the medium.
In previous studies (Hu et al., 2022; Lu et al., 2022), a simple relationship between the snow depth, H, and the averaged distance of photons traveling inside the non-absorbing medium, <L>, is
Here, I(
where
Similarly, we can also use the higher order Taylor expansion,
Here,
For the limit of an extremely weakly absorbing optically thick medium where
Using Eq. 5 and the above relation, we can rewrite R as
Thus, when the absorption optical depth
From Eq. 12,
A Appendix A provides a different derivation of Eq. 17. It is important to note that the above equation is valid for weakly absorbing or non-absorbing media, of which
3 Snow density measurements from Raman lidar
At the top of the snow, the Raman scattering of snow is proportional to snow density. Thus, lidar can provide the most direct measurements of snow density by adding vibrational Raman channels (around 3,300 cm−1 away from the laser frequency). The concept of Raman scattering for snow density measurement is similar to the ice water content measurements estimates from the Raman scattering of ice clouds (e.g., Wang et al., 2004). Assuming the Raman backscatter cross section of each ice molecule in snow as
where
Another benefit of the Raman backscatter measurements is the effective discrimination between snow and trees. Raman signals of trees are significantly weaker compared with snow. Depending on the tree types, Raman shifts of trees in general are between 100 cm−1 and 2,000 cm−1 (e.g., Sevetlidis and Pavlidis, 2019), depending on the tree types, which differ significantly from that of snow (3,200 cm−1 to 3,500 cm−1).
4 Snow grain size and snow density measurements from backscatter lidar
4.1 Snow density can be derived from extinction coefficient and snow grain size
Similar to previous studies (e.g., Barkstrom, 1972; Bohren and Barkstrom, 1974), snow particles are assumed to be spherical. The diffraction truncated extinction coefficient is
Here,
Snow density,
4.2 Lidar measurements of extinction coefficients of snow
The extinction coefficient,
Previous random-walk studies (Blanco and Fournier, 2006; Hu et al., 2022) suggest that there is a simple relationship between the second moment of the snow entry-to-exit path length distribution,
The diffuse extinction coefficient,
Here, we prove that this equation can also be derived from the two-stream solution, with higher order Taylor expansion of the exponential terms,
Eq. 14 can be rewritten as
The right-hand side of the above equation equals
4.3 Lidar measurements of snow grain size and snow density
Snow grain size, d, can be derived from lidar measurements of snow bidirectional reflectance, which is the integrated lidar backscattering of the snow layer. As discussed earlier, lidar can directly measure the snow bidirectional reflectance,
Snow grain size can be estimated from multi-wavelength lidar measurements of snow bidirectional reflectance, using the relationship between snow grain size and snow bidirectional reflectance from the two-stream solution.
First, snow grain size, d, can be measured by a lidar with an infrared wavelength laser (e.g., 1,064 nm or 1,030 nm), for which the absorption is significantly higher than in the visible range. The derivation of the simple relationship between the snow bidirectional reflectance and snow grain size is as follows:
The absorption coefficient of snow particles can be estimated using a simple ray tracing technique (Barkstrom, 1972; Bohren and Barkstrom, 1974),
Here, N is the number density of snow particles. The absorption coefficient of ice,
The asymmetry factor of the single scattering phase function of snow particles, after removing the diffraction peak, can be assumed to be 0.874 (Bohren and Barkstrom, 1974),
For an infrared wavelength (around 1,064 nm) lidar pointing near nadir (
Thus, the bidirectional reflectance at the top of the layer is
Here, A is dependent on the asymmetry factor,
Spherical particles absorb more strongly than real snow particles, which are non-spherical (Dang et al., 2016). For non-spherical particles with
Snow density (in unit kg/m3) can be derived from the lower moments of multiple scattering entry-to-exit distance distribution of a conservative medium (532 nm lidar measurements with corrections for absorption) and from the lidar measurements of 1,064 nm bidirectional reflectance (layer integrated backscatter of snow),
5 Summary and discussion
When the absorption coefficient of snow approaches zero, the reduction of snow bidirectional reflectance due to absorption equals the absorption coefficient multiplied by the average path-length, i.e., the distance traveled by photons during temporal intervals between their entry to and exit from the snow measured by lidar, <L>. Using a simple two-stream radiative transfer equation, this study demonstrates that, when the absorption coefficient approaches zero, the reduction of snow bidirectional reflectance due to absorption is proportional to twice the absorption optical depth of the snow layer, which equals the absorption coefficient multiplied by twice the snow depth H. This solution holds for all scattering phase functions and extinction coefficients. Thus, the two-stream solution suggests that <L> =2H, confirming the finding of Hu et al. (2022) based on Monte Carlo simulations.
Lidar also measures the extinction coefficient of snow accurately using the second moment of the distribution of the photon path-lengths within the snow. The relationship between extinction coefficient,
Using the two-stream radiative transfer theory, we also demonstrate that snow grain size can be derived from the lidar measurements of snow bidirectional reflectance, which is equivalent to the integrated lidar backscattering of the snow layer. Snow density, which is a function of the snow extinction coefficient and snow grain size, can be measured by the multi-wavelength lidar measurements of snow. The snow grains are simplified as equivalent spheres in the two-stream radiative transfer studies. As the microstructure of snow is complicated (e.g., Ding and Tsang, 2010; Xiong and Shi, 2013), our simplification may introduce uncertainties in the snow density estimates. Alternatively, snow density can be measured effectively by adding vibrational Raman scattering channels to the lidar measurements. Raman scattering measurements also enable the discrimination between snow and trees.
In order to obtain the above analytical solutions, it is assumed in the derivations that snowpack consists of snow particles of uniform diameter. For physical reasons (e.g., Dawson et al., 2017), snow density should increase with depth in general. Future efforts are needed to address two questions. First, does the derived snow density represent the average density of snowpack? Second, could we use the same functional form (e.g., Eq. 35) but with different coefficients to represent the average density of snowpack or the density of the top snow layer? For the former, snow water equivalent (SWE) can be directly obtained from snow depth multiplied by the average snow density. For the latter, we recognize that the snow density of the top layer is most uncertain, as the density of lower layers can be estimated based on physical processes in the snowpack. For instance, if the top snow layer density can be retrieved, we could use the snow density model in Dawson et al. (2017) driven by daily temperature and precipitation to obtain the snow density for different snow layers (up to 10 layers). Then the average snow density can be obtained to compute SWE. In this way, a multi-wavelength lidar would be able to retrieve snow depth, snow density, and SWE, providing an innovative approach for one of the seven observables for the Earth System Explorers satellite mission competition, as recommended by the 2017–2027 Decadal Survey for Earth Science and Applications from Space (National Academies, 2018).
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
YoH worked together with all the co-authors to develop the measurement concept. All authors contributed to the article and approved the submitted version.
Funding
The Funding for the lead author was provided by NASA’s ESTO and R&A programs.
Acknowledgments
The authors wish to thank the NASA ICESat-2 program, NASA Remote Sensing Theory program, and NASA ESTO’s IIP program for supporting this research.
Conflict of interest
Author CW was employed by Ball Aerospace & Technologies Corp.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Barkstrom, B. R. (1972). Some effects of multiple scattering on the distribution of solar radiation in snow and ice. J. Glaciol. 11 (63), 357–368. doi:10.1017/s0022143000022334
Blanco, S., and Fournier, R. (2006). Short-path statistics and the diffusion approximation. Phys. Rev. Lett. 97 (23), 230604. doi:10.1103/physrevlett.97.230604
Bohren, C. F., and Barkstrom, B. R. (1974). Theory of the optical properties of snow. J. Geophys. Res. 79 (30), 4527–4535. doi:10.1029/jc079i030p04527
Bohren, C. F., and Beschta, R. L. (1979). Snowpack albedo and snow density. Cold Regions Sci. Technol. 1 (1), 47–50. doi:10.1016/0165-232x(79)90018-1
Dang, C., Fu, Q., and Warren, S. G. (2016). Effect of snow grain shape on snow albedo. J. Atmos. Sci. 73 (9), 3573–3583. doi:10.1175/jas-d-15-0276.1
Dawson, N., Broxton, P., and Zeng, X. (2017). A new snow density parameterization for land data initialization. J. Hydrometeorol. 18, 197–207. doi:10.1175/JHM-D-16-0166.1
Ding, K., Xu, X., and Tsang, L. (2010). Electromagnetic scattering by bicontinuous random microstructures with discrete permittivities. IEEE Trans. Geosci. Remote Sens. 48, 3139–3151. doi:10.1109/tgrs.2010.2043953
Hu, Y., Lu, X., Zeng, X., Stamnes, S. A., Neuman, T. A., Kurtz, N. T., et al. (2022). Deriving snow depth from ICESat-2 lidar multiple scattering measurements. Front. Remote Sens. 3, 855159. doi:10.3389/frsen.2022.855159
Lu, X., Hu, Y., Zeng, X., Stamnes, S. A., Neuman, T. A., Kurtz, N. T., et al. (2022). Deriving snow depth from ICESat-2 lidar multiple scattering measurements: uncertainty analyses. Front. Remote Sens. 3, 891481. doi:10.3389/frsen.2022.891481
Meador, W. E., and Weaver, W. R. (1980). Two-stream approximations to radiative transfer in planetary atmospheres: A unified description of existing methods and a new improvement. J. Atmos. Sci. 37 (3), 630–643. doi:10.1175/1520-0469(1980)037<0630:tsatrt>2.0.co;2
National Academies (2018). Thriving on our changing planet: A decadal strategy for Earth observation from space. Washington, DC, USA: National Academies Press, 716. doi:10.17226/24938
Pershin, S. M., Lednev, V. N., Klinkov, V. K., Yulmetov, R. N., and Bunkin, A. F. (2014). Ice thickness measurements by Raman scattering. Opt. Lett. 39 (9), 2573–2575. doi:10.1364/ol.39.002573
Reichardt, J., Knist, C., Kouremeti, N., Kitchin, W., and Plakhotnik, T. (2022). Accurate absolute measurements of liquid water content (LWC) and ice water content (IWC) of clouds and precipitation with spectrometric water Raman lidar. J. Atmos. Ocean. Technol. 39 (2), 163–180. doi:10.1175/jtech-d-21-0077.1
Sevetlidis, V., and Pavlidis, G. (2019). Effective Raman spectra identification with tree-based methods. J. Cult. Herit. 37, 121–128. doi:10.1016/j.culher.2018.10.016
Stamnes, K., Thomas, G., and Stamnes, J. (2017). Radiative transfer in the atmosphere and ocean. Cambridge: Cambridge University Press. doi:10.1017/9781316148549
Wang, Z., Whiteman, D. N., Demoz, B. B., and Veselovskii, I. (2004). A new way to measure cirrus cloud ice water content by using ice Raman scatter with Raman lidar. Geophys. Res. Lett. 31 (15), L15101. doi:10.1029/2004gl020004
Xiong, C., and Shi, J. (2013). Simulating polarized light scattering in terrestrial snow based on bicontinuous random medium and Monte Carlo ray tracing. J. Quantitative Spectrosc. Radiat. Transf. 133, 177–189. doi:10.1016/j.jqsrt.2013.07.026
Appendix A
The relationship
thus,
As
Keywords: snow depth, snow density, snow grain size, lidar, path length distribution, multiple scattering
Citation: Hu Y, Lu X, Zeng X, Gatebe C, Fu Q, Yang P, Weimer C, Stamnes S, Baize R, Omar A, Creary G, Ashraf A, Stamnes K and Huang Y (2023) Linking lidar multiple scattering profiles to snow depth and snow density: an analytical radiative transfer analysis and the implications for remote sensing of snow. Front. Remote Sens. 4:1202234. doi: 10.3389/frsen.2023.1202234
Received: 07 April 2023; Accepted: 04 August 2023;
Published: 04 September 2023.
Edited by:
Xiaoguang Xu, University of Maryland, Baltimore County, United StatesReviewed by:
Lingmei Jiang, Beijing Normal University, ChinaAnin Puthukkudy, University of Maryland, Baltimore County, United States
Copyright © 2023 United States Government as represented by the Administrator of the National Aeronautics and Space Administration and Xubin Zeng, Qiang Fu, Ping Yang, Carl Weimer, Knut Stamnes, and Yuping Huang. At least a portion of this work is authored by Yongxiang Hu, Xiaomei Lu, Charles Gatebe, Snorre Stamnes, Rosemary Baize, Ali Omar, Garfield Creary, and Anum Ashraf on behalf of the U.S government and, as regards Dr. Hu, Dr. Lu, Dr. Gatebe, Dr. Stamnes, Dr. Baize, Dr. Omar, Dr. Creary, and Dr. Ashraf, U.S. copyright protection does not attach to separable portions of a Work authored solely by U.S. Government employees as part of their official duties. The U.S. Government is the owner of foreign copyrights in such separable portions of the Work and is a joint owner (with any non-U.S. Government author) of U.S. and foreign copyrights that may be asserted in inseparable portions the Work. The U.S. Government retains the right to use, reproduce, distribute, create derivative works, perform, and display portions of the Work authored solely or co-authored by a U.S. Government employee. Non-U.S copyrights also apply. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yongxiang Hu, eW9uZ3hpYW5nLmh1LTFAbmFzYS5nb3Y=
 Yongxiang Hu
Yongxiang Hu Xiaomei Lu
Xiaomei Lu Xubin Zeng
Xubin Zeng Charles Gatebe
Charles Gatebe Qiang Fu4
Qiang Fu4 Carl Weimer
Carl Weimer Snorre Stamnes
Snorre Stamnes Knut Stamnes
Knut Stamnes