Numerical modelling of elasto-plastic friction in bow–string interaction with guaranteed passivity

In order to simulate the function of bowed string instruments, it is necessary to model the frictional interaction between the bow hair and the vibrating string. This is possible using an elasto-plastic friction model, which has previously succeeded in reproducing experimental data captured on a monochord setup. In this study, this elasto-plastic model is refined to guarantee passivity, and a stable numerical scheme is derived that inherits the energy balance of the underlying continuous model. The approach presented considers a finite-width bow, thus spreading the bow–string interaction over an area. The compliance of the bow hair and the torsional motion of the string are also taken into account. A sound example and animations of the string motion are provided to demonstrate the behavior of the model.

1 Introduction

In order to simulate bow–string interaction, it is crucial to accurately model the friction between string and bow. Several friction models—both static and dynamic—have been developed in recent decades. The static models were obtained after measuring the coefficient of friction either in a steady-state (see friction curve model suggested by Smith and Woodhouse (1999)) or in a transient part of the waveform (see friction curve model suggested by Galluzzo, 2004). Among existing dynamic friction models used to simulate string vibrations are an elasto-plastic friction model developed by Dupont et al. (2002) and first applied in bow–string simulations by Serafin et al. (2003) and a thermal model introduced by Woodhouse (2003) where the temperature of rosin is considered; it is implemented using digital waveguides in Maestre et al. (2014). Regardless of the modeling choice, it is essential to use a guaranteed-passive model along with a discretization method that preserves the energy-conservation properties of the continuous system (e.g., Chabassier and Joly, 2010; Bilbao et al., 2015; Desvages, 2018; Ducceschi and Bilbao, 2022; van Walstijn et al., 2024).

This study examines the application of the elasto-plastic friction model by Dupont et al. (2000) and Dupont et al. (2002) to numerical modeling of bow–string interaction. Their formulation is a refinement of the LuGre friction model (de Wit et al., 2024) which encountered drift at low sliding velocities. The idea behind the model is that two sliding surfaces are irregular at the microscopic level; their interaction is modelled as a bundle of elastic bristles, with each bristle contributing to the overall frictional force. This model has already been applied to bowed strings: it was implemented using a finite difference method in Willemsen et al. (2019), where it was applied to point-bowing a stiff string, and in Matusiak and Chatziioannou (2024), where it was applied to a finite-width bow model. A comparison between this elasto-plastic model and the thermal friction model introduced in Smith and Woodhouse (1999) was conducted in Serafin (2004) using both a digital waveguide implementation and a finite difference method locally under the bow. That study focused on highlighting the differences and similarities between these two dynamic friction models. It was demonstrated in Matusiak and Chatziioannou (2024) that, given the right set of parameters, the elasto-plastic friction model is able to reconstruct the steady-state as well as the transient of a measured waveform.

Although the elasto-plastic friction model has been successfully implemented in the above studies, the passivity of the model has not been thoroughly investigated. This is important in order to guarantee the stability of numerical simulations. In a recent study by Falaize and Roze (2024) on nonlinear interaction modelling, the Dupont model was incorporated in a Port-Hamiltonian formulation, which—besides the part related to the elastic bristles—can be shown to be passive. Passivity, however, is not guaranteed for the coupled bow–string interaction model, since the dissipation term associated with the bristle displacement can become negative for certain parameter values.

In this study, we re-examine this issue and propose a refined model which is shown to be passive for any model parameters. Such a refinement can also demonstrate the existence and uniqueness of solutions to the underlying differential equations. Furthermore, in order to numerically implement the model in a stable manner, an energy preserving discretization scheme is derived. This is an improvement on the implementation proposed in Willemsen (2021), where the numerical bristle energy was not guaranteed to be non-negative.

The paper is structured as follows. In Section 2, the elasto-plastic model is introduced in the context of a lumped bowed mass, and energy analysis is performed in the continuous domain to reveal the lack of passivity of the original elasto-plastic model. Section 3 presents a refined version of the model that preserves passivity and guarantees the uniqueness of the solution. Section 4 is concerned with the numerical formulation of the bowed mass model; discretization using the finite difference method and energy analysis in the discrete setting are performed, followed by numerical experiments and comparison of the two models. In Section 5, the friction model is applied to the problem of bowing a string with a bow of finite width. Transverse and torsional waves on the string are accounted for. Section 6 presents the numerical model for the bow–string interaction, including analysis of the discrete energy, and some concluding remarks are given in Section 7.

2 Elasto-plastic friction model

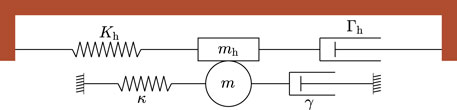
It is helpful to first present the problem in its simpler form, which involves modelling the bowing of a lumped mass connected to a stiff spring. This represents a specific case of the bowed string model, restricted solely to the transverse movement of a string that is bowed at a single contact point and considering only its fundamental mode of vibration (see Appendix).

Consider a bowed mass $m$ undergoing a tangential friction force $F$ (Figure 1). The mass is excited by a bow moving with velocity $v_{\text{b}}$ which is modeled as a harmonic oscillator with bow hair mass $m_{\text{h}}$, stiffness $K_{\text{h}}$ [kg/s²], and damping ${\mathrm{\Gamma }}_{\text{h}}$ [kg/s]. The bow hair displacement relative to the rigid bow is denoted by $\eta =\eta (t)$. The motion of the two masses can be then described by

$m\ddot{u}=-\kappa u-\gamma \dot{u}-F,(1)$

$m_{\text{h}}\ddot{\eta }=-K_{\text{h}}\eta -{\mathrm{\Gamma }}_{\text{h}}\dot{\eta }-F,(2)$

$v=\dot{u}-\left(v_{\text{b}}-\dot{\eta }\right),(3)$

where $u=u(t)$ denotes the displacement of the mass attached to a spring of stiffness $\kappa$ [kg/s²] and damping $\gamma$ [kg/s]. The relative velocity $v$ between bow and mass is given by Equation 3.

Figure 1

Figure 1. Sketch of the bowed lumped mass system.

Following Dupont et al. (2002), an elasto-plastic model is used to simulate the tangential friction force. This model assumes that the two surfaces—in this case the bow hair and the mass—are irregular at the microscopic level, and their contact is modelled through an ensemble of elastic bristles, each contributing to the total friction load. The bristles are modelled as damped stiff springs, and when the strain exceeds a certain breakaway threshold, the bristles break, and the two surfaces begin to slide. Denoting by $z$, the average bristle deflection, and by $v$, the relative velocity between the string and the bow, the model is described as follows.

$F={\sigma }_{0}z+{\sigma }_1\dot{z},(4)$

$\dot{z}=v\left[1-\alpha \left(z,v\right)\frac{z}{z_{\text{ss}}\left(v\right)}\right],(5)$

where ${\sigma }_0$ in [kg/s²] and ${\sigma }_1$ in [kg/s] are bristle stiffness and damping, respectively. The change of rate with which the bristles stretch or contract is related to the relative velocity through the adhesion map $\alpha$, defined as

$\alpha \left(z,v\right)=\left\{\begin{array}{cc}0,\hfill & vz\le 0\hfill \\ {\alpha }_{\text{m}}\left(z,v\right),\hfill & vz>0,\hfill \end{array}\right.(6)$

where

${\alpha }_{\text{m}}\left(z,v\right)=\left\{\begin{array}{cc}0,\hfill & |z|\le z_{\text{ba}}\hfill \\ {\bar{\alpha }}_{\text{m}}\left(v,z\right),\hfill & z_{\text{ba}}<|z|<|z_{\text{ss}}\left(v\right)|\hfill \\ 1,\hfill & |z|\ge |z_{\text{ss}}\left(v\right)|,\hfill \end{array}\right.(7)$

and where $z_{\text{ba}}\le {\mu }_{\text{C}}{f}_{\text{N}}/{\sigma }_0$ is the breakaway displacement

${\bar{\alpha }}_{\text{m}}\left(z,v\right)=\frac{1}{2}\left[\sin \left(\pi \theta \left(z,v\right)\right)+1\right],\theta \left(z,v\right)=\frac{|z|-\frac{1}{2}\left(|z_{\text{ss}}\left(v\right)|+z_{\text{ba}}\right)}{|z_{\text{ss}}\left(v\right)|-z_{\text{ba}}},(8)$

and $z_{\text{ss}}$ is the steady-state displacement for constant velocities

$z_{\text{ss}}\left(v\right)=\left\{\begin{array}{cc}\frac{f_{\text{N}}}{{\sigma }_0}\left({\mu }_{\text{C}}+\left({\mu }_{\text{S}}-{\mu }_{\text{C}}\right)e^{-|v/v_{\text{S}}{|}^p}\right),\hfill & v\ge 0\hfill \\ -\frac{f_{\text{N}}}{{\sigma }_0}\left({\mu }_{\text{C}}+\left({\mu }_{\text{S}}-{\mu }_{\text{C}}\right)e^{-|v/v_{\text{S}}{|}^p}\right),\hfill & v<0,\hfill \end{array}\right.(9)$

with $v_{\text{S}}>0$ and $p\ge 1$. When $p=2$, $v_{\text{S}}$ is referred to as “Stribeck velocity.” In the numerical experiments in Sections 4.4 and 6.4, $p=2$ is used. Here, ${\mu }_{\text{S}}$ and ${\mu }_{\text{C}}$ denote static and dynamic friction coefficients, respectively, and $f_{\text{N}}$ is the normal force applied by the bow. For small bristle displacements, when $|z|\le z_{\text{ba}}$, $\alpha (v,z)=0$, and consequently $\dot{z}=v$, a purely elastic and reversible regime is entered, referred to as “pre-sliding” (sticking). For larger displacements—that is, when $z_{\text{ba}}<|z|<|z_{\text{ss}}(v)|$—some bristles start to break, and a mixed elasto-plastic sliding occurs. Finally, for $|z|\ge |z_{\text{ss}}(v)|$, all bristles break, and a purely plastic regime is achieved—the string slips under the bow. In that situation, $\alpha (z,v)=1$. This model for a friction force was first developed in Dupont et al. (2000) and used for simulating friction in various industrial applications.

2.1 Energy balance

In order to investigate the passivity of the model given by Equations 1–5, the energy balance of the system is considered.

Multiplying Equation 1 with $\dot{u}$, Equation 2 with $\dot{\eta }$, and Equation 5 with ${\sigma }_{0}z$, summing up and using the relation in Equation 3 yields the energy balance

$\underset{{\dot{\mathcal{H}}}_{\text{r}}}{\underbrace{m\ddot{u}\dot{u}+\kappa u\dot{u}}}+\underset{{\dot{\mathcal{H}}}_{\text{h}}}{\underbrace{m_{\text{h}}\ddot{\eta }\dot{\eta }+K_{\text{h}}\eta \dot{\eta }}}+\underset{{\dot{\mathcal{H}}}_{\text{b}}}{\underbrace{{\sigma }_{0}z\dot{z}}}=-\underset{\mathcal{P}}{\underbrace{v_{\text{b}}F}}-\underset{{\mathcal{Q}}_{\text{r}}}{\underbrace{\gamma {\dot{u}}^2}}-\underset{{\mathcal{Q}}_{\text{h}}}{\underbrace{{\mathrm{\Gamma }}_{\text{h}}{\dot{\eta }}^2}}-\underset{{\mathcal{Q}}_{\text{b}}}{\underbrace{\left({\sigma }_1{v}^2+\alpha \left(z,v\right)\frac{vz}{z_{\text{ss}}\left(v\right)}\left({\sigma }_{0}z-{\sigma }_{1}v\right)\right)}},$

where

$\begin{array}{cccc}\hfill {\mathcal{H}}_{\text{r}}& =\frac{m}{2}{\dot{u}}^2+\frac{\kappa }{2}{u}^2\ge 0\hfill & \hfill & \mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{s}\mathrm{c}\mathrm{i}\mathrm{l}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{r}\left(\mathrm{k}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{\&}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\right)\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y},\hfill \\ \hfill {\mathcal{H}}_{\text{h}}& =\frac{m_{\text{h}}}{2}{\dot{\eta }}^2+\frac{K_{\text{h}}}{2}{\eta }^2\ge 0\hfill & \hfill & \mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{b}\mathrm{o}\mathrm{w}\mathrm{h}\mathrm{a}\mathrm{i}\mathrm{r}\left(\mathrm{k}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{\&}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\right)\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}\mathrm{a}\mathrm{n}\mathrm{d}\hfill \\ \hfill {\mathcal{H}}_{\text{b}}& =\frac{{\sigma }_0}{2}{z}^2\ge 0\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{b}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{l}\mathrm{e}\mathrm{s}.\hfill \end{array}$

$\mathcal{P}$ is the power supplied by the bow via the friction force, and ${\mathcal{Q}}_{\text{r}}$, ${\mathcal{Q}}_{\text{h}}$, and ${\mathcal{Q}}_{\text{b}}$ are dissipation terms, corresponding to the oscillator, the bow hair, and the bristles, respectively. This leads to the following conservation law:

${\mathcal{H}}_{\text{r}}+{\mathcal{H}}_{\text{h}}+{\mathcal{H}}_{\text{b}}+\int \left(\mathcal{P}+{\mathcal{Q}}_{\text{r}}+{\mathcal{Q}}_{\text{h}}+{\mathcal{Q}}_{\text{b}}\right)dt=\mathcal{H}\left(0\right),(10)$

where $\mathcal{H}(0)$ is the initial system energy (if any). ${\mathcal{Q}}_{\text{r}}$ and ${\mathcal{Q}}_{\text{h}}$ are trivially non-negative, and ${\mathcal{Q}}_{\text{b}}$ is non-negative whenever $\alpha \ne 1$. For $\alpha =1$, and for high—relative to ${\sigma }_0$—values of ${\sigma }_1$, ${\mathcal{Q}}_{\text{b}}$ can become negative, which violates passivity and is unphysical (Dupont et al., 2000). Therefore, without a certain condition on the relationship between the stiffness and damping coefficients, passivity cannot be ensured. Following Olsson (1996), who analyzed a simpler version of the Dupont model—the so-called LuGre friction model (de Wit et al., 2024)—Willemsen (2021) derived a condition on ${\sigma }_1$ to guarantee passivity for the elasto-plastic friction model. The condition reads:

${\sigma }_1\le \frac{4{\sigma }_0{z}_{\text{ss}}\left(v\right)}{|v|}.(11)$

However, without knowing the maximal relative velocity, $v$, it is not possible to set the value for ${\sigma }_1$. In Section 3, a different condition on the bristle damping term is proposed that is less restrictive and does not require any knowledge of the limits of $v$.

Falaize and Roze (2024) employed the elasto-plastic friction model in the framework of port-Hamiltonian systems and arrived at the same dissipation term— ${\mathcal{Q}}_{\text{b}}$. For certain parameter choices, the dissipation matrix defined in Falaize and Roze (2024) is semi positive-definite, but for that property to generally hold, a refinement of ${\sigma }_1$ is needed.

2.2 Boundedness of the bristle displacement

Boundedness of bristle displacement was first shown in Olsson (1996) for a LuGre friction model, and subsequently in Dupont et al. (2000) for an elasto-plastic model, by defining a positive definite Lyapunov function and an invariant set of solutions. Here a slightly different approach is presented.

The bristle displacement $z(t)$ can be thought of as a parametric curved defined by $z(t)$ and $v(t)$ whose rate of change is

$\dot{z}\left(t\right)=v\left(t\right)\left[1-\alpha \left(z\left(t\right),v\left(t\right)\right)\frac{z\left(t\right)}{z_{\text{ss}}\left(v\left(t\right)\right)}\right],(12)$

and

$\text{sign}\left(\dot{z}\left(t\right)\right)=\left\{\begin{array}{cc}-1,\hfill & z\left(t\right)>z_{\text{ss}}\left(v\left(t\right)\right)\hfill \\ 0,\hfill & z\left(t\right)=z_{\text{ss}}\left(v\left(t\right)\right)\text{or}v\left(t\right)=0.\hfill \\ 1,\hfill & z\left(t\right)<z_{\text{ss}}\left(v\left(t\right)\right)\hfill \end{array}\right.(13)$

This means that for $v(t)>0$, if $z(t)$ reaches the maximal value of $z_{\text{ss}}(v(t))$ which is $z_{\text{ss}}(0)=\frac{{\mu }_{\text{S}}{f}_{\text{N}}}{{\sigma }_0}$, it cannot rise any further but has to either decrease or stay constant. Similarly, for $v(t)<0$, if $z(t)$ reaches the minimal value of $z_{\text{ss}}(v(t))$, which equals ${\lim }_{v\to 0^{-}}{z}_{\text{ss}}(v(t))=-\frac{{\mu }_{\text{S}}{f}_{\text{N}}}{{\sigma }_0}$, it cannot decrease any further but has to either rise or stay constant. Therefore, $|z(t)|\le \frac{{\mu }_{\text{S}}{f}_{\text{N}}}{{\sigma }_0}$ (see Figure 2 for visualization). The boundedness of $z$ by itself does not, however, imply stability.

Figure 2

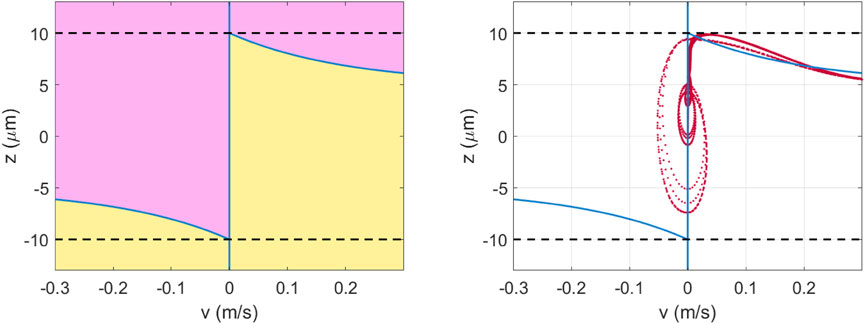
Figure 2. Behavior of the bristle displacement $z(t)$. Left: pink color indicates regions where $z(t)$ is decreasing $(\text{sign}(\dot{z}(t))=-1)$ and yellow is where $z(t)$ is increasing $(\text{sign}(\dot{z}(t))=1)$. Blue line is the region where $\dot{z}(t)=0$, and the black dashed line denotes the maximum and minimum value of $z_{\text{ss}}$. Right: Example trajectory in the $v-z$ plane for model parameters as in Table 1.

3 Refined elasto-plastic model

This section presents a refined version of the elasto-plastic friction model that addresses the passivity of the system. Consider a mass $m$ bowed with velocity $v_{\text{b}}$ as described in Section 2, by Equations 1–5, where bristle damping ${\sigma }_1$ is not constant but varies with $v$ and $f_{\text{N}}$ as follows:

${\sigma }_1\left(v\right)=\frac{{\mu }_{\text{C}}{f}_{\text{N}}}{\sqrt{v^2+{ϵ}^2}},ϵ=\frac{{\mu }_{\text{C}}{f}_{\text{N}}}{{\bar{\sigma }}_1},(14)$

such that $0\le {\sigma }_1(v)\le {\bar{\sigma }}_1$ and ${\sigma }_1(0)={\bar{\sigma }}_1$.

A similar velocity-dependent damping term ${\sigma }_1(v)={\bar{\sigma }}_1{e}^{-(v/v_{\text{d}}^2)}$ was introduced by Olsson (1996) for the LuGre model, motivated by the need to reproduce certain friction phenomena. Provided that the additional free parameter $v_{\text{d}}$ chosen is sufficiently small, the condition in Equation 11 is satisfied, in turn guaranteeing passivity of the LuGre model. This dependency on an external parameter is avoided in the refinement proposed here (Equation 14). Furthermore, for large $v$ values, ${\sigma }_1$ stays closer to the original constant ${\bar{\sigma }}_1$ than with the exponential formula of Olsson.

3.1 Energy balance

With ${\sigma }_1$ now being a function of the relative velocity $v$, the passivity of the system in Equations 1–5 is guaranteed.

Proposition 1: Let $F$ be a friction force as defined in Equation 4 with bristle damping ${\sigma }_1$ defined in Equation 14. Then, the system in Equations 1–5 is passive.

Proof: All terms in the energy balance (Section 2.1) are trivially non-negative, apart from ${\mathcal{Q}}_{\text{b}}$. For $\alpha (v,z)<1$, ${\mathcal{Q}}_{\text{b}}$ is always non-negative. Therefore, only the case when $\alpha (z,v)=1$, which happens when $\text{sign}(z)=\text{sign}(v)$ and $|z|\ge |z_{\text{ss}}(v)|$, is considered here. In that case, we have

$\begin{array}{ll}\hfill {\mathcal{Q}}_{\text{b}}& ={\sigma }_1\left(v\right)v^2+\frac{|z||v|}{|z_{\text{ss}}\left(v\right)|}\left({\sigma }_0|z|-{\sigma }_1\left(v\right)|v|\right)\ge {\sigma }_1\left(v\right)v^2+\frac{|z||v|}{|z_{\text{ss}}\left(v\right)|}\left({\sigma }_0|z_{\text{ss}}\left(v\right)|-{\sigma }_1\left(v\right)|v|\right)\hfill \\ \hfill & \ge {\sigma }_1\left(v\right)v^2+\frac{|z||v|}{|z_{\text{ss}}\left(v\right)|}\left({\mu }_{\text{C}}{f}_{\text{N}}-{\sigma }_1\left(v\right)|v|\right)={\sigma }_1\left(v\right)v^2+\frac{|z||v|}{|z_{\text{ss}}\left(v\right)|}{\mu }_{\text{C}}{f}_{\text{N}}\left[1-\frac{|v|}{\sqrt{v^2+{ϵ}^2}}\right]>0.\hfill \end{array}$

3.2 Existence and uniqueness of the solution

The passivity of the system can be shown to guarantee the existence and uniqueness of the solution. By introducing a variable $\varphi$, the bowed mass system of Equations 1–5 together with Equation 14 can be written as an autonomous system of equations.

$\dot{u}=\varphi ,(15)$

$\dot{\eta }=v+v_{\text{b}}-\varphi ,(16)$

$\dot{\varphi }=\frac{1}{m}\left[-\kappa u-\gamma \varphi -{\sigma }_{0}z-{\sigma }_1\left(v\right)v\left[1-\alpha \left(z,v\right)\frac{z}{z_{\text{ss}}\left(v\right)}\right]\right],(17)$

$\dot{v}=\frac{-\kappa u-\gamma \varphi }{m}+\frac{-K_{\text{h}}\eta -{\mathrm{\Gamma }}_{\text{h}}\left(v+v_{\text{b}}-\varphi \right)}{m_{\text{h}}}-\frac{m+m_{\text{h}}}{m\cdot m_{\text{h}}}\left[{\sigma }_{0}z+{\sigma }_1\left(v\right)v\left[1-\alpha \left(z,v\right)\frac{z}{z_{\text{ss}}\left(v\right)}\right]\right],(18)$

$\dot{z}=v\left[1-\alpha \left(z,v\right)\frac{z}{z_{\text{ss}}\left(v\right)}\right].(19)$

Let $\mathbf{x}=(u,\eta ,\varphi ,v,z)$, then the above can be written as

$\dot{\mathbf{x}}=\mathbf{S}\left(\mathbf{x}\right),(20)$

where $\mathbf{S}=(s_{\text{u}},s_{\eta },s_{\varphi },s_{\text{v}},s_{\text{z}})$ with the functions $s$ corresponding to Equations 15–19. Given initial conditions $\mathbf{x}(t_0)=(u_0,{\eta }_0,{\varphi }_0,v_0,z_0)$, existence and uniqueness of the solution to Equation 20 is guaranteed whenever $\mathbf{S}(\mathbf{x})$ is Lipschitz continuous (Barreira and Valls, 2012).

Definition 1:. A vector-valued function $\mathbf{S}(\mathbf{x})$ is Lipschitz continuous if there exists an $L\ge 0$, called the “Lipschitz constant,” such that for all $\mathbf{x},\mathbf{y}$ in the domain of $\mathcal{S}$

$|\mathbf{S}\left(\mathbf{x}\right)-\mathbf{S}\left(\mathbf{y}\right)|\le L|\mathbf{x}-\mathbf{y}|.(21)$

If $\mathbf{S}(\mathbf{x})=(s_1(\mathbf{x}),\dots ,s_K(\mathbf{x}))$, then the norm of $\mathbf{S}(\mathbf{x})$ is defined as

$|\mathbf{S}\left(\mathbf{x}\right){|}^2={\displaystyle \sum _{i=1}^K}|s_i\left(\mathbf{x}\right){|}^2.$

The norm of $\mathbf{x}$ is similarly defined.

Proposition 2: Consider a bowed mass $m$ described by Equations 1–5 with bristle damping given by Equation 14. Then, for given initial conditions, there exists a solution to the bowed mass system that is unique.

Proof: By the Picard–Lindelöf theorem (Barreira and Valls, 2012), a system of ordinary differential equations $\mathbf{S}$ has a global unique solution if $\mathbf{S}$ is Lipschitz continuous with respect to $\mathbf{x}$ with a Lipschitz constant not depending on $\mathbf{x}$. This is equivalent to all the functions $s_{\text{u}},\dots ,s_{\text{z}}$ being Lipschitz continuous with respect to each variable $u$, $\eta$, $\varphi$, $v$, and $z$.

By passivity, all the variables are bounded. Lipschitz continuity of $s_{\text{u}}$ and $s_{\eta }$ is trivial. Similarly, Lipschitz continuity with respect to $u$, $\eta$, and $\varphi$ is trivially satisfied for all the functions $s_{\text{u}},s_{\eta },s_{\varphi },s_{\text{v}},s_{\text{z}}$. Moreover, it is straightforward to verify that ${\sigma }_1(v)$ defined in Equation 14 is Lipschitz continuous. It remains to show that

$\tilde{g}\left(z,v\right)=\alpha \left(z,v\right)\frac{zv}{z_{\text{ss}}\left(v\right)}(22)$

is Lipschitz continuous.

(i) Let $v$ be fixed. Then, for $z_1,z_2$,

$\begin{array}{ll}\hfill \left|\tilde{g}\left(z_1,v\right)-\tilde{g}\left(z_2,v\right)\right|& \le \frac{|v|}{|z_{\text{ss}}\left(v\right)|}\left(|\alpha \left(z_1,v\right)||z_1-z_2|+|z_2||\alpha \left(z_1,v\right)-\hspace{0.17em}\alpha \left(z_2,v\right)|\right)\hfill \\ \hfill & \le \frac{|v|}{|z_{\text{ss}}\left(v\right)|}\left(|z_1-z_2|+\frac{\pi }{2}\frac{{\mu }_{\text{S}}{f}_{\text{N}}}{{\sigma }_0}\left|\theta \left(z_1,v\right)-\theta \left(z_2,v\right)\right|\right),\hfill \end{array}$

where the last inequality follows from the Lipschitz continuity of the $\sin$ function with Lipschitz constant equal to 1, with $|\sin (\frac{\pi }{2}\theta (z_1,v))-\sin (\frac{\pi }{2}\theta (z_2,v))|\le \frac{\pi }{2}|\theta (z_1,v)-\theta (z_2,v)|$. The function $\theta$ is also Lipschitz continuous with respect to $z$,

$\left|\theta \left(z_1,v\right)-\theta \left(z_2,v\right)\right|=\frac{||z_1|-|z_2||}{|z_{\text{ss}}\left(v\right)|-z_{\text{ba}}}\le \frac{|z_1-z_2|}{|z_{\text{ss}}\left(v\right)|-z_{\text{ba}}}\le \frac{{\sigma }_0}{{\mu }_{\text{C}}{f}_{\text{N}}-{\sigma }_0{z}_{\text{ba}}}|z_1-z_2|.$

Let $v$ be bounded by $B_{\text{v}}$, then

$\left|\tilde{g}\left(z_1,v\right)-\tilde{g}\left(z_2,v\right)\right|\le \underset{L_{\text{z}}}{\underbrace{\left[\frac{B_{\text{v}}{\sigma }_0}{{\mu }_{\text{C}}{f}_{\text{N}}}+\frac{\pi B_{\text{v}}{\sigma }_0{\mu }_{\text{S}}}{{\mu }_{\text{C}}\left({\mu }_{\text{C}}{f}_{\text{N}}-{\sigma }_0{z}_{\text{ba}}\right)}\right]}}|z_1-z_2|.$

Hence, $\tilde{g}(z,v)$ is Lipschitz continuous with respect to $z$ with Lipschitz constant $L_{\text{z}}$.

(ii) Now, let $z$ be fixed and $z>0$. Then

$\tilde{g}\left(z,v\right)=\left\{\begin{array}{cc}0,\hfill & v\le 0\hfill \\ \alpha \left(z,v\right)\frac{zv}{z_{\text{ss}}\left(v\right)},\hfill & v\ge 0\hfill \end{array}\right.$

is continuous and everywhere differentiable except for $v=0$, with

$\frac{\partial \tilde{g}}{\partial v}=\left\{\begin{array}{cc}0,\hfill & v<0\hfill \\ \frac{\partial \alpha }{\partial v}\frac{zv}{z_{\text{ss}}}+\alpha \frac{z{z}_{\text{ss}}-zv{\dot{z}}_{\text{ss}}}{z_{\text{ss}}^2},\hfill & v>0,\hfill \end{array}\right.$

and

$\frac{\partial \alpha }{\partial v}=\frac{\pi }{2}\cos \left(\pi \theta \right)\frac{{\dot{z}}_{\text{ss}}\left(z_{\text{ba}}-|z|\right)}{{\left(z_{\text{ss}}-z_{\text{ba}}\right)}^2}.$

The partial derivative of $\tilde{g}$ with respect to $v$ is bounded and positive, since all the elements are bounded and positive. Therefore, by the mean value theorem for $v_1,v_2>0$

$\left|\tilde{g}\left(z,v_1\right)-\tilde{g}\left(z,v_2\right)\right|\le L_{\text{v}}^1|v_1-v_2|,L_{\text{v}}^1=\max \left\{\frac{\partial \tilde{g}}{\partial v}\right\},(23)$

and $\tilde{g}$ is Lipschitz continuous for $v>0$, with Lipschitz constant $L_{\text{v}}^{(1)}$, and trivially for $v<0$, with any $L_{\text{v}}^{(2)}\ge 0$ as a Lipschitz constant. Now let $v_1>0$ and $v_2\le 0$, then

$\frac{\left|\tilde{g}\left(z,v_1\right)-\tilde{g}\left(z,v_2\right)\right|}{|v_1-v_2|}=\frac{\left|\tilde{g}\left(z,v_1\right)\right|}{|v_1-v_2|}\le \frac{\left|\tilde{g}\left(z,v_1\right)\right|}{|v_1|}=\frac{|z|}{|z_{\text{ss}}\left(v_1\right)|}\le \frac{{\mu }_{\text{S}}}{{\mu }_{\text{C}}}.$

Let $L_{\text{v}}^{(3)}={\mu }_{\text{S}}/{\mu }_{\text{C}}$. Hence, $\tilde{g}$ is Lipschitz continuous with respect to $v$ with Lipschitz constant $L_{\text{v}}=\max \{L_{\text{v}}^{(1)},L_{\text{v}}^{(2)},L_{\text{v}}^{(3)}\}$. A similar proof holds for $z<0$.

Therefore, $\mathbf{S}$ is Lipschitz continuous with respect to $\mathbf{x}$, and a unique solution to Equation 20 is guaranteed.

The original Dupont model was not shown to be passive, as there was no guarantee that $v$ is bounded. In that case, the system in Equations 1–5 has a unique solution only locally.

4 Numerical formulation

In the present section, a finite difference numerical scheme is utilized to discretize the system in Equations 1–5. The proposed discretization is energy conserving.

4.1 Numerical preliminaries

The approximations to $u(t)$ at points $n{\mathrm{\Delta }}_t$ are denoted as $u^n$, where ${\mathrm{\Delta }}_t$ is the time step. The variable $z$ is approximated at an interleaved grid—that is, $z^{n+\frac{1}{2}}$ denotes the approximation to $z(t)$ at time $t=(n+\frac{1}{2}){\mathrm{\Delta }}_t$. The following centered, second-order accurate discretization operators are defined:

$\begin{array}{ll}\hfill {\delta }_{t○}{u}^n& =\frac{u^{n+\frac{1}{2}}-u^{n-\frac{1}{2}}}{{\mathrm{\Delta }}_t}=\dot{u}\left(n{\mathrm{\Delta }}_t\right)+\mathcal{O}\left({\mathrm{\Delta }}_t^2\right),{\delta }_{t\cdot }{u}^n=\frac{u^{n+1}-u^{n-1}}{2{\mathrm{\Delta }}_t}=\dot{u}\left(n{\mathrm{\Delta }}_t\right)+\mathcal{O}\left({\mathrm{\Delta }}_t^2\right),\hfill \\ \hfill {\mu }_{t○}{u}^n& =\frac{u^{n+\frac{1}{2}}+u^{n-\frac{1}{2}}}{2}=u\left(n{\mathrm{\Delta }}_t\right)+\mathcal{O}\left({\mathrm{\Delta }}_t^2\right),{\mu }_{t\cdot }{u}^n=\frac{u^{n+1}+u^{n-1}}{2}=u\left(n{\mathrm{\Delta }}_t\right)+\mathcal{O}\left({\mathrm{\Delta }}_t^2\right).\hfill \end{array}$

In addition, one may define non-centered, first-order accurate discretization operators

$\begin{array}{ll}\hfill {\delta }_{t-}{u}^n& =\frac{u^n-u^{n-1}}{{\mathrm{\Delta }}_t}=\dot{u}\left(n{\mathrm{\Delta }}_t\right)+\mathcal{O}\left({\mathrm{\Delta }}_t\right),{\delta }_{t+}{u}^n=\frac{u^{n+1}-u^n}{{\mathrm{\Delta }}_t}=\dot{u}\left(n{\mathrm{\Delta }}_t\right)+\mathcal{O}\left({\mathrm{\Delta }}_t\right),\hfill \\ \hfill {\mu }_{t-}{u}^n& =\frac{u^n+u^{n-1}}{2}=u\left(n{\mathrm{\Delta }}_t\right)+\mathcal{O}\left({\mathrm{\Delta }}_t\right),{\mu }_{t+}{u}^n=\frac{u^{n+1}+u^n}{2}=u\left(n{\mathrm{\Delta }}_t\right)+\mathcal{O}\left({\mathrm{\Delta }}_t\right).\hfill \end{array}$

The composition of first-order accurate operators results in second-order accurate operators,

$\begin{array}{ll}\hfill {\delta }_{tt}{u}^n& ={\delta }_{t+}{\delta }_{t-}{u}^n=\frac{u^{n+1}-2u^n+u^{n-1}}{{\mathrm{\Delta }}_t^2}=\ddot{u}\left(n{\mathrm{\Delta }}_t\right)+\mathcal{O}\left({\mathrm{\Delta }}_t^2\right),\hfill \\ \hfill {\mu }_{tt}{u}^n& ={\mu }_{t+}{\mu }_{t-}{u}^n=\frac{u^{n+1}+2u^n+u^{n-1}}{4}=u\left(n{\mathrm{\Delta }}_t\right)+\mathcal{O}\left({\mathrm{\Delta }}_t^2\right),\hfill \end{array}$

and several useful identities can be constructed, including

$\begin{array}{ll}\hfill {\delta }_{t\cdot }{u}^n{\delta }_{tt}{u}^n& ={\delta }_{t+}\left\{\frac{1}{2}{\left({\delta }_{t-}{u}^n\right)}^2\right\},{\delta }_{t\cdot }{u}^n{\mu }_{tt}{u}^n={\delta }_{t+}\left\{\frac{1}{2}{\left({\mu }_{t-}{u}^n\right)}^2\right\},\hfill \\ \hfill {\delta }_{t\cdot }{u}^n{u}^n& ={\delta }_{t+}\left\{\frac{1}{2}{u}^n{u}^{n-1}\right\},{\delta }_{t○}{z}^n{\mu }_{t○}{z}^n={\delta }_{t+}\left\{\frac{1}{2}{\left((z^{n-\frac{1}{2}}\right)}^2\right\}.\hfill \end{array}$

4.2 Discretization

For simplicity of notation, let

$g\left(z,v\right)=v\left[1-\alpha \left(z,v\right)\frac{z}{z_{\text{ss}}\left(v\right)}\right].(24)$

The system of Equations 1–5 is discretized as follows:

$m{\delta }_{tt}{u}^n=-\kappa u^n-\gamma {\delta }_{t\cdot }{u}^n-F^n,(25)$

$m_{\text{h}}{\delta }_{tt}{\eta }^n=-K_{\text{h}}{\mu }_{tt}{\eta }^n-{\mathrm{\Gamma }}_{\text{h}}{\delta }_{t\cdot }{\eta }^n-F^n,(26)$

$v^n={\delta }_{t\cdot }{u}^n-v_{\text{b}}^n+{\delta }_{t\cdot }{\eta }^n,(27)$

$F^n={\sigma }_0{\mu }_{t○}{z}^n+{\sigma }_1\left(v^n\right){\delta }_{t○}{z}^n,(28)$

${\delta }_{t○}{z}^n=g\left({\mu }_{t○}{z}^n,v^n\right).(29)$

In the case of the original Dupont model, ${\sigma }_1(v^n)={\bar{\sigma }}_1$. In order to ensure numerical stability for the lumped mass model (Equation 25), the following stability condition is obtained using frequency domain analysis (Bilbao, 2009):

${\mathrm{\Delta }}_t<2{\left(m/\kappa \right)}^{1/2}.$

This discretization choice for the equation of motion of the lumped mass is motivated by the discretization that is carried out for the string model in the distributed case in Section 6. On the other hand, the stiffness term for the bow hair in Equation 26 is discretized using an averaging operator in order to avoid introducing a further stability condition.

For simpler notation, let $r^n={\mu }_{t○}{z}^n$. Using the discretization operators, one can establish identities

${\delta }_{tt}{u}^n=\frac{2}{{\mathrm{\Delta }}_t}\left({\delta }_{t\cdot }{u}^n-{\delta }_{t-}{u}^n\right),{\delta }_{t○}{z}^n=\frac{2}{{\mathrm{\Delta }}_t}\left(r^n-z^{n-\frac{1}{2}}\right),{\mu }_{tt}{u}^n=\frac{{\mathrm{\Delta }}_t}{2}\left({\delta }_{t\cdot }{u}^n-{\delta }_{t-}{u}^n\right)+u^n.(30)$

Substituting into Equations 25, 26, and 28, one obtains

$\begin{array}{ll}\hfill \left(m\frac{2}{{\mathrm{\Delta }}_t}+\gamma \right){\delta }_{t\cdot }{u}^n& =-\kappa u^n+m\frac{2}{{\mathrm{\Delta }}_t}{\delta }_{t-}{u}^n-{\sigma }_0{r}^n-{\sigma }_1\left(v^n\right)\frac{2}{{\mathrm{\Delta }}_t}\left(r^n-z^{n-\frac{1}{2}}\right),\hfill \\ \hfill \left(m_{\text{h}}\frac{2}{{\mathrm{\Delta }}_t}+K_{\text{h}}\frac{{\mathrm{\Delta }}_t}{2}+{\mathrm{\Gamma }}_{\text{h}}\right){\delta }_{t\cdot }{\eta }^n& =-K_{\text{h}}{\eta }^n+\left(m_{\text{h}}\frac{2}{{\mathrm{\Delta }}_t}+K_{\text{h}}\frac{{\mathrm{\Delta }}_t}{2}\right){\delta }_{t-}{\eta }^n-{\sigma }_0{r}^n-{\sigma }_1\left(v^n\right)\frac{2}{{\mathrm{\Delta }}_t}\left(r^n-z^{n-\frac{1}{2}}\right).\hfill \end{array}$

Considering $u^n$, $u^{n-1}$, ${\eta }^n$, ${\eta }^{n-1}$, and $z^{n-\frac{1}{2}}$ to be known, let $p^n={\delta }_{t-}{u}^n$ and $s^n={\delta }_{t-}{\eta }^n$. Using Equation 27, $r^n$ can be expressed as a function of $v^n$

$r^n=-A\left(v^n\right)v^n+B\left(v^n\right),(31)$

where

$\begin{array}{ll}\hfill A\left(v^n\right)& =\frac{\left(m\frac{2}{{\mathrm{\Delta }}_t}+\gamma \right)\left(m_{\text{h}}\frac{2}{{\mathrm{\Delta }}_t}+K_{\text{h}}\frac{{\mathrm{\Delta }}_t}{2}+{\mathrm{\Gamma }}_{\text{h}}\right)}{\frac{2}{{\mathrm{\Delta }}_t}\left(m+m_{\text{h}}\right)+K_{\text{h}}\frac{{\mathrm{\Delta }}_t}{2}+\gamma +{\mathrm{\Gamma }}_{\text{h}}}{\left({\sigma }_0+\frac{2}{{\mathrm{\Delta }}_t}{\sigma }_1\left(v^n\right)\right)}^{-1},\hfill \\ \hfill B\left(v^n\right)& =A\left(v^n\right)\left[\frac{-\kappa u^n+m\frac{2}{{\mathrm{\Delta }}_t}{p}^n}{m\frac{2}{{\mathrm{\Delta }}_t}+\gamma }+\frac{-K_{\text{h}}{\eta }^n+\left(m_{\text{h}}\frac{2}{{\mathrm{\Delta }}_t}+K_{\text{h}}\frac{{\mathrm{\Delta }}_t}{2}\right)s^n}{m_{\text{h}}\frac{2}{{\mathrm{\Delta }}_t}+K_{\text{h}}\frac{{\mathrm{\Delta }}_t}{2}+{\mathrm{\Gamma }}_{\text{h}}}-v_{\text{b}}^n\right]+\frac{\frac{2}{{\mathrm{\Delta }}_t}{\sigma }_1\left(v^n\right)z^{n-\frac{1}{2}}}{{\sigma }_0+\frac{2}{{\mathrm{\Delta }}_t}{\sigma }_1\left(v^n\right)}.\hfill \end{array}$

For the original Dupont model, $A(v^n)$ and $B(v^n)$ are independent of $v^n$, and $r^n$ is linearly related to $v^n$. Substituting Equation 31 into Equation 29 and using the middle identity in Equation 30 yields a nonlinear equation in the unknown $v^n$,

$\frac{2}{{\mathrm{\Delta }}_t}\left[B\left(v^n\right)-A\left(v^n\right)v^n-z^{n-\frac{1}{2}}\right]=g\left(B\left(v^n\right)-A\left(v^n\right)v^n,v^n\right).$

An iterative solver, such as the Newton–Raphson method, can be applied to

$G\left(v^n\right)=g\left(B\left(v^n\right)-A\left(v^n\right)v^n,v^n\right)-\frac{2}{{\mathrm{\Delta }}_t}\left[B\left(v^n\right)-A\left(v^n\right)v^n-z^{n-\frac{1}{2}}\right],(32)$

in order to solve for $v^n$ such that $G(v^n)=0$. Once $v^n$ is known, the friction force $F^n$ can be calculated and the variables $u^{n+1}$, ${\eta }^{n+1}$, and $z^{n+\frac{1}{2}}$ can be updated as follows:

$\begin{array}{ll}\hfill F^n& =\left(B\left(v^n\right)-A\left(v^n\right)v^n\right){\sigma }_0+{\sigma }_1\left(v^n\right)\frac{2}{{\mathrm{\Delta }}_t}\left(B\left(v^n\right)-A\left(v^n\right)v^n-z^{n-\frac{1}{2}}\right),\hfill \\ \hfill z^{n+\frac{1}{2}}& =2\left(B\left(v^n\right)-A\left(v^n\right)v^n\right)-z^{n-\frac{1}{2}},\hfill \\ \hfill {\eta }^{n+1}& =\frac{2{\mathrm{\Delta }}_t}{m_{\text{h}}\frac{2}{{\mathrm{\Delta }}_t}+K_{\text{h}}\frac{{\mathrm{\Delta }}_t}{2}+{\mathrm{\Gamma }}_{\text{h}}}\left[-K_{\text{h}}{\eta }^n+\left(m_{\text{h}}\frac{2}{{\mathrm{\Delta }}_t}+K_{\text{h}}\frac{{\mathrm{\Delta }}_t}{2}\right)s^n+\frac{m_{\text{h}}\frac{2}{{\mathrm{\Delta }}_t}+K_{\text{h}}\frac{{\mathrm{\Delta }}_t}{2}+{\mathrm{\Gamma }}_{\text{h}}}{2{\mathrm{\Delta }}_t}{\eta }^{n-1}-F^n\right],\hfill \\ \hfill u^{n+1}& =u^{n-1}+2{\mathrm{\Delta }}_t\left[v^n+v_{\text{b}}^n-\frac{{\eta }^{n+1}-{\eta }^{n-1}}{2{\mathrm{\Delta }}_t}\right].\hfill \end{array}$

The solution of the nonlinear equation $G(v^n)=0$, for $G(v^n)$ as defined in Equation 32 plays a key role in the algorithm described above. It was shown in Section 3 that in the continuous case, the refined elasto-plastic model has a unique solution. However, this property is not immediately transferable to the numerical case. It remains an open problem to find a threshold on the time step ${\mathrm{\Delta }}_t$ that would guarantee a unique solution.

4.3 Numerical energy balance

The stability of the numerical scheme is analyzed by investigating whether the discrete energy balance preserves the passivity of the underlying continuous system.

Multiplying Equation 25 with ${\delta }_{t\cdot }{u}^n$, Equation 26 with ${\delta }_{t\cdot }{\eta }^n$, and Equation 29 with ${\sigma }_0{\mu }_{t○}{z}^n$ yields

$\begin{array}{ll}\hfill \underset{{\delta }_{t+}{\mathcal{H}}_{\text{r}}^n}{\underbrace{m{\delta }_{t\cdot }{u}^n{\delta }_{tt}{u}^n+\kappa \left({\delta }_{t\cdot }{u}^n\right)u^n}}& =-{\delta }_{t\cdot }{u}^n{F}^n-\underset{{\mathcal{Q}}_{\text{r}}^n}{\underbrace{\gamma {\left({\delta }_{t\cdot }{u}^n\right)}^2}},\hfill \\ \hfill \underset{{\delta }_{t+}{\mathcal{H}}_{\text{h}}^n}{\underbrace{m_{\text{h}}{\delta }_{t\cdot }{\eta }^n{\delta }_{tt}{\eta }^n+K_{\text{h}}{\delta }_{t\cdot }{\eta }^n{\mu }_{tt}{\eta }^n}}& =-{\delta }_{t\cdot }{\eta }^n{F}^n-\underset{{\mathcal{Q}}_{\text{h}}^n}{\underbrace{{\mathrm{\Gamma }}_{\text{h}}{\left({\delta }_{t\cdot }{\eta }^n\right)}^2}},\hfill \\ \hfill \underset{{\delta }_{t+}{\mathcal{H}}_{\text{b}}^n}{\underbrace{{\sigma }_0{\mu }_{t○}{z}^n{\delta }_{t○}{z}^n}}& ={\sigma }_0{\mu }_{t○}{z}^{n}g\left({\mu }_{t○}{z}^n,v^n\right).\hfill \end{array}$

Summing up the above and using relation Equation 27 yields

${\delta }_{t+}\left\{{\mathcal{H}}_{\text{r}}^n+{\mathcal{H}}_{\text{h}}^n+{\mathcal{H}}_{\text{b}}^n\right\}=-{\mathcal{P}}^n-{\mathcal{Q}}_{\text{r}}^n-{\mathcal{Q}}_{\text{h}}^n-{\mathcal{Q}}_{\text{b}}^n,(33)$

where

$\begin{array}{ll}\hfill {\mathcal{H}}_{\text{r}}^n& =\frac{m}{2}{\left({\delta }_{t-}{u}^n\right)}^2+\frac{\kappa }{2}\left(u^n{u}^{n-1}\right)\ge 0,\hfill \\ \hfill {\mathcal{H}}_{\text{h}}^n& =\frac{m_{\text{h}}}{2}{\left({\delta }_{t-}{\eta }^n\right)}^2+\frac{K_{\text{h}}}{2}{\left({\mu }_{t-}{\eta }^n\right)}^2\ge 0,\hfill \\ \hfill {\mathcal{H}}_{\text{b}}^n& =\frac{{\sigma }_0}{2}{\left(z^{n-\frac{1}{2}}\right)}^2\ge 0,\hfill \\ \hfill {\mathcal{P}}^n& =v_{\text{b}}^n{F}^n,\hfill \\ \hfill {\mathcal{Q}}_{\text{b}}^n& ={\sigma }_0{\left(v^n\right)}^2{\mu }_{t○}{z}^n+g\left({\mu }_{t○}{z}^n,v^n\right)\left({\sigma }_1{v}^n-{\sigma }_0{\mu }_{t○}{z}^n\right)\ge 0,\hfill \end{array}(34)$

$\mathcal{P}$ is externally supplied power and ${\mathcal{Q}}_{\text{r}}$, ${\mathcal{Q}}_{\text{h}}$, and ${\mathcal{Q}}_{\text{b}}$ are dissipation terms with ${\mathcal{Q}}_{\text{r}}$ and ${\mathcal{Q}}_{\text{h}}$ trivially non-negative. The proof of passivity in the numerical formulation goes line by line as in the continuous case, with $z$ being substituted by ${\mu }_{t○}{z}^n$ and $v$ by $v^n$.

The energy balance in Equation 33 induces the following discrete conservation law (Chatziioannou and van Walstijn, 2015):

${\mathcal{E}}^n={\mathcal{H}}^{n+1}+{\mathrm{\Delta }}_t{\displaystyle \sum _{i=0}^n}\left({\mathcal{P}}^i+{\mathcal{Q}}_{\text{r}}^i+{\mathcal{Q}}_{\text{h}}^i+{\mathcal{Q}}_{\text{b}}^i\right)={\mathcal{H}}^0,(35)$

where ${\mathcal{H}}^n={\mathcal{H}}_{\text{r}}^n+{\mathcal{H}}_{\text{h}}^n+{\mathcal{H}}_{\text{b}}^n$. This is the discrete equivalent of Equation 10. The conservation of this quantity, subject to machine precision, can be assessed by monitoring the energy conservation error $e^n={\mathcal{E}}^n-{\mathcal{H}}^0$.

4.4 Numerical experiments

To demonstrate the behavior of the model, simulation results are shown in Figure 3. For these simulations, the bow accelerates from 0 at 3.439 m/s² until it reaches the steady-state value $v_{\mathrm{b}}$ (given in Table 1) and then remains constant. The model parameters (Table 1) are set to values found in Matusiak and Chatziioannou (2024) and Pitteroff and Woodhouse (1998a) considering this lumped model hypothesis. The values were obtained for the fundamental mode of a vibrating string (Table 2) according to Equations 64–66 in the Appendix. The energy conservation error $e^n$ (where, in this case ${\mathcal{H}}^0=0$) is also shown in Figure 3.

Figure 3

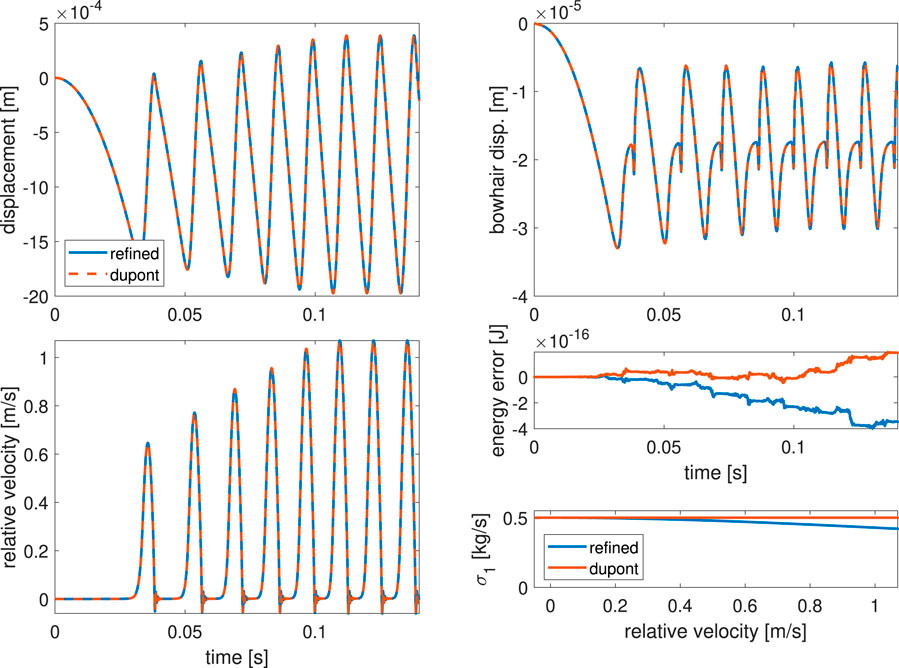
Figure 3. Comparison of the original (orange) and refined (blue) elasto-plastic friction model applied to simulating a bowed lumped mass. Model parameters are given in Table 1. Plotted signals are the mass displacement, bow hair displacement, relative velocity, and energy error, as defined in Equation 35. Bottom right plot shows the deviation of the bristle damping coefficient, in the case of the refined model, from the constant value ${\bar{\sigma }}_1$.

Table 1

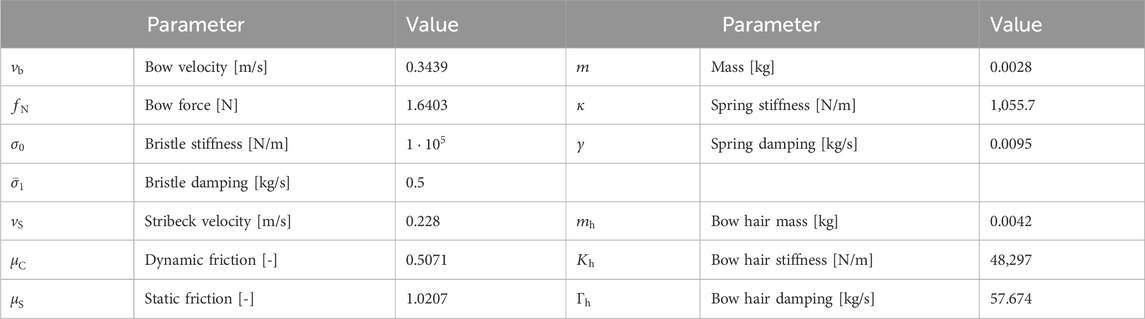
Table 1. Table with parameter values used to generate signals in Figure 3.

Table 2

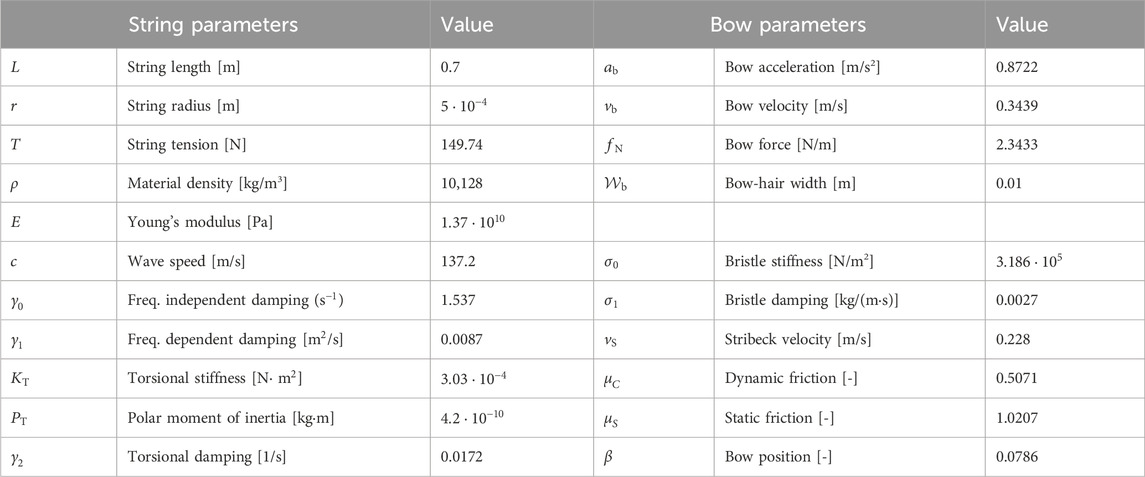
Table 2. Table with parameter values used to generate the signals in Figure 7. Bow-hair mass, stiffness, and damping are as in the lumped case (see Table 1), divided by the width of the bow hair.

For this parameter set, the refined model generates signals that are nearly identical to those generated by the original Dupont model. The latter has been used to simulate a string bowed by a finite-width bow and was validated against experimental measurements for the case of a monochord played by a bow (Matusiak and Chatziioannou, 2024). Therefore, it is possible to deduce that the refined model can also reliably resynthesize measured signals.

The difference between the two models comes into play when the Dupont model violates the passivity condition (Equation 34); the two models then behave quite differently (Figure 4). To generate this figure, the bristle stiffness ${\sigma }_0$ was reduced to 500 N/m, the bristle damping ${\sigma }_1$ was increased to 3 kg/s, and the bow force $f_{\text{N}}$ was increased to 0.25 N. It can be observed that, in the case of the Dupont model, the total energy loss may become negative, which violates passivity. This results in the friction force not closely following the underlying steady state friction curve. By allowing the bristle damping to vary (bottom left of Figure 4), passivity is guaranteed and the friction force trajectory remains close to the steady-state curve.

Figure 4

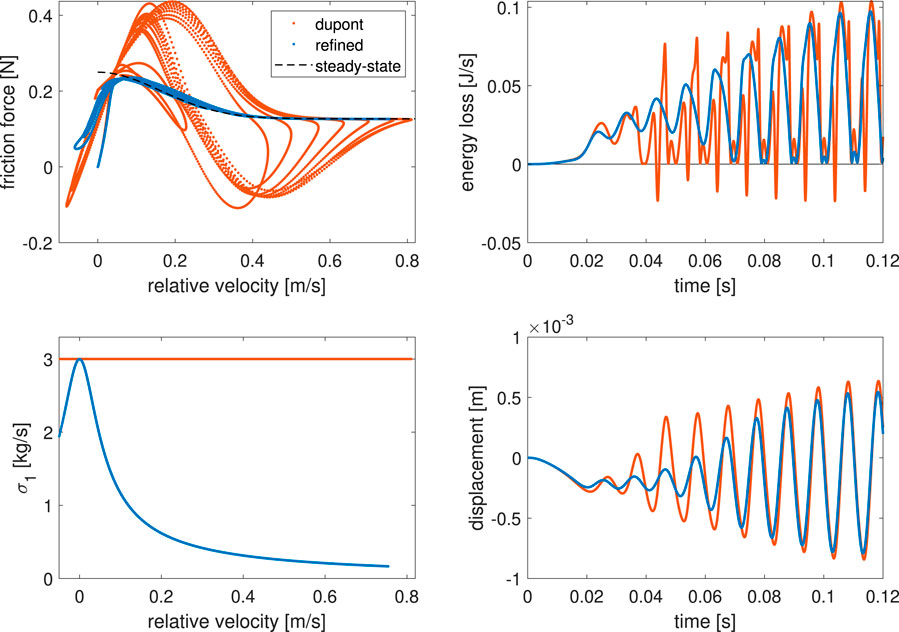
Figure 4. Comparison of the behavior of the original (orange) and refined (blue) elasto-plastic friction models when the passivity condition of the original model is violated. The total energy loss of the original model becomes negative, violating passivity, and the friction force deviates significantly from the underlying theoretical steady-state friction curve.

As discussed in Section 4.2, a further issue with this modeling approach is whether the system possesses a unique solution. This can only be shown for the refined model in the continuous case. For the discrete case, the uniqueness of the solution could only be demonstrated empirically. The nonlinear function $G(v)$ in Equation 32 is plotted in Figure 5 for both the refined and the Dupont model for increasing sampling rates. Model parameters are as in Table 1, except for ${\bar{\sigma }}_1=100$ kg/s. The nonlinear function is plotted for time instance $t=0.0299$ s. It can be observed that while, for the refined model, $G(v)$ has a single root, this is not the case for the original model. Furthermore, the existence of multiple roots in the latter case cannot be avoided by increasing the sampling rate (i.e., oversampling towards the continuous case does not alleviate this issue). While a strict upper bound for ${\mathrm{\Delta }}_t$ guaranteeing uniqueness is not yet available for the refined model, it has been empirically observed, for a large set of parameter values, that a unique solution exists even for sampling rates lower than the audio sampling rate ($f_{\text{s}}=44100$ Hz).

Figure 5

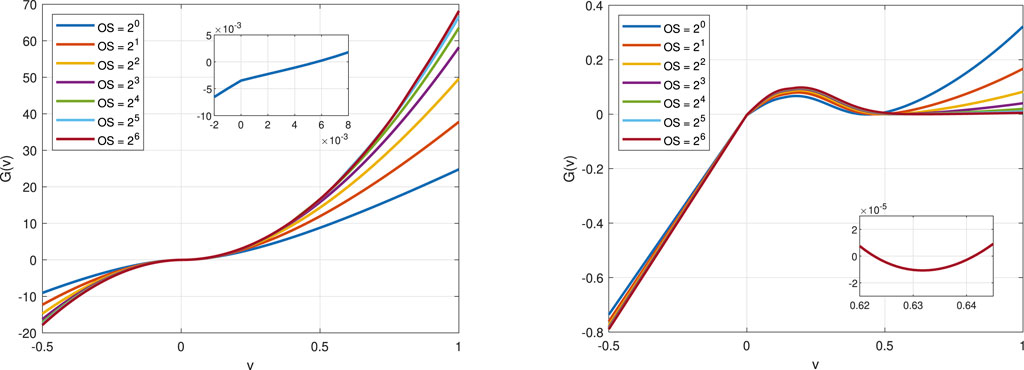
Figure 5. Nonlinear function $G(v)$ for the refined model (left) and the original Dupont model (right). OS is an oversampling factor, with sampling rate $f_{\text{s}}=\mathrm{O}\mathrm{S}\cdot \overline{f_{\text{s}}}$ and $\overline{f_{\text{s}}}=44100$ Hz.

Furthermore, it is possible to observe that for both models, the derivative of $G(v)$ may become equal (or approximately equal) to 0 for certain values of $v$. While this may hinder the convergence of the Newton–Raphson method, there are alternative approaches that may be used to approximate the root of $G(v)$ (e.g., Deuflhard, 2011; Hueso et al., 2009).

Finally, the convergence of the refined model is illustrated in Figure 6. A global error is defined, assuming a reference signal $\widehat{u}$ that is obtained with 1024 times oversampling, as

$e_{\text{g}}=\frac{\sum {\left(u-\widehat{u}\right)}^2}{\sqrt{\sum {\left(\widehat{u}\right)}^2}}(36)$

Figure 6

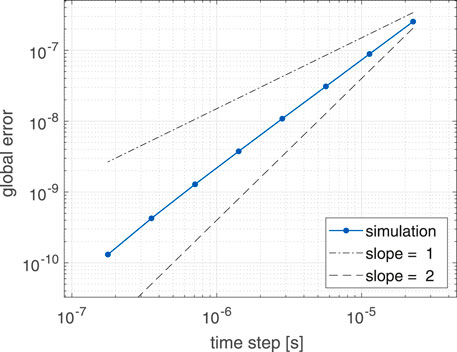
Figure 6. Error of the refined model for different time steps, as defined in Equation 36. Dashed line indicates second-order convergence, while dash-dotted line indicates first order convergence. Model parameters are taken from Table 1.

5 Distributed system

The insights obtained while studying the bowed-mass system are now applied to a distributed system—a string bowed with a finite width bow. In the following, let $u(x,t)$ and $\tilde{u}(x,t)$ be real-valued functions defined over an interval $[0,L]$ and for time $t\ge 0$, with an inner product and a norm defined as

$⟨u,\tilde{u}⟩={\int }_0^{L}u\left(x,t\right)\tilde{u}\left(x,t\right)dx,\Vert u{\Vert }^2=⟨u,u⟩.$

Using the subscripts $x$ and $t$ to denote differentiation with respect to space $({\partial }_x)$ and time $({\partial }_t)$, respectively, the following identities hold.

$⟨{\partial }_{t}u,u⟩=\frac{d}{dt}\left\{\frac{1}{2}\Vert u{\Vert }^2\right\},(37)$

$⟨u,{\partial }_x\tilde{u}⟩=-⟨{\partial }_{x}u,\tilde{u}⟩+u\left(L,t\right)\tilde{u}\left(L,t\right)-u\left(0,t\right)\tilde{u}\left(0,t\right),(38)$

where $\frac{d}{dt}$ is the total derivative with respect to time.

5.1 String model

The governing equations for the motion of a string excited by a bow are the equations describing transverse (Equation 39) and torsional (Equation 40) waves. They are coupled through the distributed friction force $f$ ([N/m]), and this force in turn is linked to the bow hair displacement $\eta$ (Equation 41). The bow hair is modeled as a harmonic oscillator (Pitteroff and Woodhouse, 1998a). The friction force is modelled according to the elasto-plastic friction model. The partial differential equations describing the motion of the bowed string are (Bilbao, 2009; Pitteroff and Woodhouse, 1998b):

$\rho A{\partial }_t^{2}u=T{\partial }_x^{2}u-EI{\partial }_x^{4}u-2{\gamma }_0\rho A{\partial }_{t}u+2{\gamma }_1\rho A{\partial }_t{\partial }_x^{2}u-f,(39)$

$P_{\text{T}}{\partial }_t^{2}w=K_{\text{T}}{\partial }_x^{2}w-2{\gamma }_2{P}_{\text{T}}{\partial }_{t}w+rf,(40)$

$D_{\text{h}}{\partial }_t^2\eta =-K_{\text{h}}\eta -{\mathrm{\Gamma }}_{\text{h}}{\partial }_t\eta -f,(41)$

where $\rho$ is the material density, $A=\pi r^2$ is the cross-sectional area of the string with radius $r$, $T$ is the tension of the string, $E$ is Young’s modulus, $I=\pi r^4/4$ are the area moment of inertia, and ${\gamma }_0$ and ${\gamma }_1$ represent frequency independent and frequency dependent damping. In addition, $P_{\text{T}}$ denotes the polar moment of inertia, $K_{\text{T}}$ torsional stiffness, and ${\gamma }_2$ is a torsional damping coefficient. The bow stick is regarded as a rigid frame moving at a given velocity $v_{\text{b}}$ and supporting a ribbon of compliant bow-hair of density $D_{\text{h}}$ ([kg/m]) with distributed spring and damping constants $K_{\text{h}}$ and ${\mathrm{\Gamma }}_{\text{h}}$, respectively. The relative bow–string velocity is then expressed as

$v=\left({\partial }_{t}u-r{\delta }_{t}w\right)-\left(v_{\text{b}}-{\partial }_t\eta \right).(42)$

This model simplifies string damping and omits body coupling. This simplified approach is favored in this case, as including these additional factors would not enhance the presentation of the friction model.

Assuming simply supported ends, the boundary conditions for the transverse movement of the string are

$u\left(x,t\right){|}_{x=0,L}=0,{\partial }_x^{2}u{|}_{x=0,L}=0,(43)$

and for the torsional movement we assume fixed boundary conditions

$w\left(x,t\right){|}_{x=0,L}=0.(44)$

A fourth equation, needed to close the system, describing the friction force $f$ is

$f\left(z,v\right)={\sigma }_{0}z+{\sigma }_1\left(v\right){\partial }_{t}z,(45)$

where ${\sigma }_0$ and ${\sigma }_1$ are now distributed stiffness and distributed damping, respectively, and ${\partial }_{t}z$ is the time derivative of $z$. It is related to $v$ through

${\partial }_{t}z=v\left[1-\alpha \left(z,v\right)\frac{z}{z_{\text{ss}}\left(v\right)}\right],(46)$

where the adhesion map $\alpha$ is defined in Equation 6 and $z_{\text{ss}}$ is a steady-state displacement function given by the Stribeck curve (Equation 9). The damping term ${\sigma }_1(v)$ is defined in Equation 14.

5.2 Energy analysis

The time derivative of the total energy of the combined transverse and torsional movement of the string, bow hair, and bristle energy may be derived by taking an inner product of Equations 39, 40, 41, and 46 with ${\partial }_{t}u$, ${\partial }_{t}w$, ${\partial }_t\eta$, and ${\sigma }_{0}z$, respectively, and summing the results. Utilizing Equation 37 and the identity in Equation 38 repeatedly, the energy balance follows:

${\left.\frac{d\mathcal{H}}{dt}=-\mathcal{Q}-\mathcal{P}+\mathcal{B}\right|}_0^L,(47)$

where

$\begin{array}{ll}\hfill \mathcal{H}& ={\mathcal{H}}_{\text{r}}+{\mathcal{H}}_{\text{w}}+{\mathcal{H}}_{\text{h}}+{\mathcal{H}}_{\text{b}},\hfill \\ \hfill \mathcal{Q}& ={\mathcal{Q}}_{\text{r}}+{\mathcal{Q}}_{\text{w}}+{\mathcal{Q}}_{\text{h}}+{\mathcal{Q}}_{\text{b}},\hfill \\ \hfill \mathcal{B}& ={\mathcal{B}}_{\text{r}}+{\mathcal{B}}_{\text{w}},\hfill \end{array}$

and $\mathcal{P}(t)=⟨v_{\text{b}},f⟩$ is the power supplied by the bow. The string energy coming from the transverse and torsional motions, ${\mathcal{H}}_{\text{r}}$ and ${\mathcal{H}}_{\text{w}}$, respectively, bow hair energy ${\mathcal{H}}_{\text{h}}$, and bristle energy ${\mathcal{H}}_{\text{b}}$ are given by

$\begin{array}{ll}\hfill {\mathcal{H}}_{\text{r}}\left(t\right)& =\frac{\rho A}{2}\Vert {\partial }_{t}u{\Vert }_2^2+\frac{T}{2}\Vert {\partial }_{x}u{\Vert }_2^2+\frac{EI}{2}\Vert {\partial }_x^{2}u{\Vert }_2^2\ge 0,\hfill \\ \hfill {\mathcal{H}}_{\text{w}}\left(t\right)& =\frac{P_{\text{T}}}{2}\Vert {\partial }_{t}w{\Vert }_2^2+\frac{K_{\text{T}}}{2}\Vert {\partial }_{x}w{\Vert }_2^2\ge 0,\hfill \\ \hfill {\mathcal{H}}_{\text{h}}\left(t\right)& =\frac{D_{\text{h}}}{2}\Vert {\partial }_t\eta {\Vert }_2^2+\frac{K_{\text{h}}}{2}\Vert \eta {\Vert }_2^2\ge 0,\hfill \\ \hfill {\mathcal{H}}_{\text{b}}\left(t\right)& =\frac{{\sigma }_0}{2}\Vert z{\Vert }_2^2\ge 0.\hfill \end{array}$

The dissipated energies in the string (${\mathcal{Q}}_r$ and ${\mathcal{Q}}_w$), bow hair $({\mathcal{Q}}_h)$, and bristles $({\mathcal{Q}}_b)$ are given by

$\begin{array}{ll}\hfill {\mathcal{Q}}_{\text{r}}\left(t\right)& =2{\gamma }_0\rho A\Vert {\partial }_{t}u{\Vert }_2^2+2{\gamma }_1\rho A\Vert {\partial }_x{\partial }_{t}u{\Vert }_2^2\ge 0,\hfill \\ \hfill {\mathcal{Q}}_{\text{w}}\left(t\right)& =2{\gamma }_2{P}_{\text{T}}\Vert {\partial }_{t}w{\Vert }_2^2\ge 0,\hfill \\ \hfill {\mathcal{Q}}_{\text{h}}\left(t\right)& ={\mathrm{\Gamma }}_{\text{h}}\Vert {\partial }_t\eta {\Vert }_2^2\ge 0,\hfill \\ \hfill {\mathcal{Q}}_{\text{b}}\left(t\right)& =⟨{\sigma }_1\left(v\right)v,v⟩+⟨{\sigma }_{0}z-{\sigma }_1\left(v\right)v,\alpha \left(z,v\right)\frac{zv}{z_{\text{ss}}\left(v\right)}⟩,\hfill \end{array}$

and the boundary terms are

$\begin{array}{ll}\hfill {\mathcal{B}}_{\text{r}}\left(t\right)& =T{\partial }_{t}u{\partial }_{x}u-EI{\partial }_{t}u{\partial }_x^{3}u+EI{\partial }_t{\partial }_{x}u{\partial }_x^{2}u+2{\gamma }_1\rho A{\partial }_{t}u{\partial }_t{\partial }_{x}u,\hfill \\ \hfill {\mathcal{B}}_{\text{w}}\left(t\right)& =K_{\text{T}}{\partial }_{t}w{\partial }_{x}w.\hfill \end{array}$

Under simply supported boundary conditions, ${\mathcal{B}}_{\text{r}}$ vanishes. Similarly, ${\mathcal{B}}_{\text{w}}$ vanishes due to fixed boundary conditions for the torsional movement of the string.

Given that $\mathcal{H}\ge 0$, the passivity of the system may be assessed by observing the dissipated energy expressions. More precisely, passivity is guaranteed if ${\mathcal{Q}}_{\text{b}}\ge 0$. Let ${\mathcal{W}}_{\text{b}}$ be the width of the bow, then

${\mathcal{Q}}_{\text{b}}\left(t\right)={\int }_{{\mathcal{W}}_{\text{b}}}\left({\sigma }_1\left(v\right)v^2+\alpha \left(z,v\right)\frac{vz}{z_{\text{ss}}\left(v\right)}\left({\sigma }_{0}z-{\sigma }_1\left(v\right)v\right)\right)dt\ge 0$

since, by Proposition 1, the expression under the integral is positive if ${\sigma }_1(v)$ is defined as in Equation 14. Therefore, the refined elasto-plastic friction model results in a passive system, also for this distributed system.

6 Distributed system—Numerical formulation

6.1 Operators and identities

Let $u(x,t)$ be a function defined over an interval $[0,L]$ and for $t\ge 0$. Let $d_{\text{N}}=\{l{\mathrm{\Delta }}_x:l=0,\dots ,N\}$ be a $N+1$ discrete spatial domain corresponding to $[0,L]$, with ${\mathrm{\Delta }}_x=L/N$. The approximations to $u(x,t)$ at points $(l{\mathrm{\Delta }}_x,n{\mathrm{\Delta }}_t)$ are denoted as $u_l^n$. Let ${\mathbf{u}}^n={[u_0^n,\dots ,u_N^n]}^T$. For two vectors ${\mathbf{u}}^n$ and ${\tilde{\mathbf{u}}}^n$, the discrete inner product and norm on $d_{\text{N}}$ are defined as

${⟨{\mathbf{u}}^n,{\tilde{\mathbf{u}}}^n⟩}_{d_{\text{N}}}={\mathrm{\Delta }}_x{\displaystyle \sum _{l=0}^N}{u}_l^n{\tilde{u}}_l^n,\hspace{1em}\Vert {\mathbf{u}}^n{\Vert }_{d_{\text{N}}}^2={⟨{\mathbf{u}}^n,{\mathbf{u}}^n⟩}_{d_{\text{N}}}.$

Other domains that differ from $d_{\text{N}}$ by removing endpoints and will later be used are

$d_{\bar{\mathrm{N}}}=\left\{l{\mathrm{\Delta }}_x:l=1,\dots ,N\right\},d_{\underline{\mathrm{N}}}=\left\{l{\mathrm{\Delta }}_x:l=0,\dots ,N-1\right\},d_{\underline{\bar{\mathrm{N}}}}=\left\{l{\mathrm{\Delta }}_x:l=1,\dots ,N-1\right\}.(48)$

The time difference and averaging operators introduced in Sections 4.1, 4.2 are valid in their implementation to grid functions. Similarly, as in the continuous case, the following identities hold:

$\begin{array}{ll}\hfill {⟨{\delta }_{t\cdot }{\mathbf{u}}^n,{\mathbf{u}}^n⟩}_{d_{\text{N}}}& ={\delta }_{t+}\left\{\frac{1}{2}{⟨{\mathbf{u}}^n,{\mathbf{u}}^{n-1}⟩}_{d_{\text{N}}}\right\},\hfill \\ \hfill {⟨{\delta }_{t\cdot }{\mathbf{u}}^n,{\delta }_{tt}{\mathbf{u}}^n⟩}_{d_{\text{N}}}& ={\delta }_{t+}\left\{\frac{1}{2}\Vert {\delta }_{t-}{\mathbf{u}}^n{\Vert }_{d_{\text{N}}}^2\right\}.\hfill \end{array}$

Spatial forward, backward, and central discretization operators are defined as

${\delta }_{x+}{u}_l^n=\frac{u_{l+1}^n-u_l^n}{{\mathrm{\Delta }}_x},{\delta }_{x-}{u}_l^n=\frac{u_l^n-u_{l-1}^n}{{\mathrm{\Delta }}_x},{\delta }_{x\cdot }{u}_l^n=\frac{u_{l+1}^n-u_{l-1}^n}{2{\mathrm{\Delta }}_x},(49)$

and can be used to obtain approximations to higher-order partial differential operators:

${\delta }_{xx}={\delta }_{x-}{\delta }_{x+},\hspace{1em}{\delta }_{\mathit{xxxx}}={\delta }_{xx}{\delta }_{xx}.$

Like in the continuous case, the following relation can be derived:

${⟨{\mathbf{u}}^n,{\delta }_{xx}{\tilde{\mathbf{u}}}^n⟩}_{d_{\text{N}}}=-{⟨{\delta }_{x+}{\mathbf{u}}^n,{\delta }_{x+}{\tilde{\mathbf{u}}}^n⟩}_{d_{\underline{\mathrm{N}}}}+u_N^n{\delta }_{x+}{\tilde{u}}_N^n-u_0^n{\delta }_{x+}{\tilde{u}}_0^n.$

6.2 Discretization

Finite-difference schemes for the string in isolation and the bowed string have been described in studies such as Bilbao (2009) and Pitteroff and Woodhouse (1998b). In order to fix the notation, let $x_{\text{B}}^{\text{L}}$ and $x_{\text{B}}^{\text{R}}$ be the positions on the string of the inner and outer bow edges, respectively, with the center of the bow lying at $x_{\text{B}}$. Let $M$ be a desired number of grid points under the bow, denoted by $x_m$.

The model is discretized in time and space with functions $u_l^n$ that are approximations of $u(x,t)$ at points $(l{\mathrm{\Delta }}_x,n{\mathrm{\Delta }}_t)$. Discretization in time is performed with $t=n{\mathrm{\Delta }}_t$, where ${\mathrm{\Delta }}_t=1/f_{\text{s}}$ (in $s$) with $f_{\text{s}}$ the sampling rate (in Hz) and $n\in \mathbb{N}$, and in space with $x=l{\mathrm{\Delta }}_x$, where the grid spacing ${\mathrm{\Delta }}_x$ (in $m$) for the transverse movement of the string must satisfy the following stability condition (Bilbao, 2009):

${\mathrm{\Delta }}_x\ge \sqrt{\frac{\tau +\sqrt{{\tau }^2+16{\kappa }^2{\mathrm{\Delta }}_t^2}}{2}},(50)$

where $\tau =c^2{\mathrm{\Delta }}_t^2+4{\gamma }_1{\mathrm{\Delta }}_t$ with $c=\sqrt{T/\rho A}$ are the wave speed and $\kappa =\sqrt{EI/\rho A}$ is a stiffness coefficient. The grid points are $d_{\text{N}}=\{l{\mathrm{\Delta }}_x:l=0,\dots ,N\}$, where $N=\lfloor L/{\mathrm{\Delta }}_x\rfloor$; hence, the total number of grid points is $N+1$. For the torsional movement of the string, the discretization in time is performed as for the transverse motion while in space with $x=l{\mathrm{\Delta }}_x^{\text{T}}$, where the grid spacing ${\mathrm{\Delta }}_x^{\text{T}}$ (in $m$) for the torsional movement of the string must satisfy (Bilbao, 2009):

${\mathrm{\Delta }}_x^{\text{T}}\ge c_{\text{T}}{\mathrm{\Delta }}_t,(51)$

where $c_{\text{T}}=\sqrt{K_{\text{T}}/P_{\text{T}}}$ is the torsional wave speed. The grid points are $d_{{\mathrm{N}}_{\mathrm{T}}}=\{l{\mathrm{\Delta }}_x^{\text{T}}:l=0,\dots ,N_{\text{T}}\}$, where $N_{\text{T}}=\lfloor L/{\mathrm{\Delta }}_x^{\text{T}}\rfloor$; hence the total number of grid points is $N_{\text{T}}+1$. Torsional waves travel much faster than transverse waves; therefore, the number of grid points $N_{\text{T}}$ is much smaller than $N$. The spatial discretization operators associated with grid $d_{{\mathrm{N}}_{\mathrm{T}}}$ will be denoted with an upper $T$ superscript—for example, ${\delta }_{x+}^{\text{T}}{w}_l^n=\frac{w_{l+1}^n-w_l^n}{{\mathrm{\Delta }}_x^{\text{T}}}$.

For a point $x_m$ under the bow, the interpolation vectors ${\mathbf{i}}^{x_m}$ and ${\mathbf{i}}_{\text{T}}^{x_m}$ interpolate the string displacement at position $x_m$ for the transverse and torsional motion, respectively. ${\mathbf{i}}^{x_m}$ is a row vector of size $N+1$ that multiplies the column vector ${\mathbf{u}}^n={[u_0^n,\dots ,u_N^n]}^T$, and ${\mathbf{i}}_{\text{T}}^{x_m}$ is a row vector of size $N_{\text{T}}+1$ that multiplies the column vector ${\mathbf{w}}^n={[w_0^n,\dots ,w_{N_{\text{T}}}^n]}^T$. The simplest interpolation is the one of $0^{\text{th}}$-order where ${\mathbf{i}}_l^{x_m}=1$ for $l=\lfloor x_m/{\mathrm{\Delta }}_x\rfloor$, and ${\mathbf{i}}_{\text{T},l}^{x_m}=1$ for $l=\lfloor x_m/{\mathrm{\Delta }}_x^T\rfloor$, respectively, and zeros elsewhere. For the definition of higher orders of interpolation vectors, see Bilbao (2009). On the other hand, a spreading vector ${\mathbf{j}}^{x_m}$ is a column vector that distributes the friction force around the bowing point $x_m$ on the grid $l{\mathrm{\Delta }}_x$. Similarly, ${\mathbf{j}}_{\text{T}}^{x_m}$ is a spreading vector that distributes the friction force around the bowing point $x_m$ on the grid $l{\mathrm{\Delta }}_x^{\text{T}}$. The spreading and interpolation vectors are related through

${\mathbf{j}}^{x_m}=\frac{1}{{\mathrm{\Delta }}_x}{\left[{\mathbf{i}}^{x_m}\right]}^T,{\mathbf{j}}_{\text{T}}^{x_m}=\frac{1}{{\mathrm{\Delta }}_x^{\text{T}}}{\left[{\mathbf{i}}_{\text{T}}^{x_m}\right]}^T.$

To simplify the notation, we first divide Equation 39 by $\rho A$, then discretize it to obtain

${\delta }_{tt}{\mathbf{u}}^n=c^2{\delta }_{xx}{\mathbf{u}}^n-{\kappa }^2{\delta }_{\mathit{xxxx}}{\mathbf{u}}^n-2{\gamma }_0{\delta }_{t\cdot }{\mathbf{u}}^n+2{\gamma }_1{\delta }_{t-}{\delta }_{xx}{\mathbf{u}}^n-{\left(M\rho A\right)}^{-1}\mathcal{J}{\mathbf{f}}^n,(52)$

where $\mathcal{J}=[{\mathbf{j}}^{x_1}|\dots |{\mathbf{j}}^{x_M}]$ is an $(N+1)\times M$ matrix with $m$^th column being ${\mathbf{j}}^{x_m}$, $m=1,\dots ,M$, and ${\mathbf{f}}^n={[f_1^n,\dots ,f_M^n]}^T$ is a column vector with $M$ rows where each row describes the friction for a point $x_m$ of the string that is in contact with the bow. The friction force is discretized using an interleaved grid, with

$f_m^n=f\left({\mu }_{t○}{z}_m^n,v_m^n\right),\text{where}f\left({\mu }_{t○}{z}_m^n,v_m^n\right)={\sigma }_0{\mu }_{t○}{z}_m^n+{\sigma }_1\left(v_m^n\right)g\left({\mu }_{t○}{z}_m^n,v_m^n\right),$

with

$g\left({\mu }_{t○}{z}_m^n,v_m^n\right)=v_m^n\left[1-\alpha \left({\mu }_{t○}{z}_m^n,v_m^n\right)\frac{{\mu }_{t○}{z}_m^n}{z_{\text{ss}}\left(v_m^n\right)}\right],$

for $m=1,\dots ,M$. For simplicity of notation, let ${\mathbf{g}}^n$ denote the $M\times 1$ column vector with entries $g_m^n$

$g_m^n=g\left({\mu }_{t○}{z}_m^n,v_m^n\right),$

then

${\delta }_{t○}{\mathbf{z}}^n={\mathbf{g}}^n.(53)$

Assuming simply supported ends, the boundary conditions imply

$u_0^n=u_N^n=0,u_{-1}^n=-u_1^n,u_{N+1}^n=-u_{N-1}^n,(54)$

for all $n\in \mathbb{N}$.

Similarly, by dividing Equation 40 by $P_{\text{T}}$, it is discretized as follows:

${\delta }_{tt}^{\text{T}}{\mathbf{w}}^n=c_{\text{T}}^2{\delta }_{xx}^{\text{T}}{\mathbf{w}}^n-2{\gamma }_2{\delta }_{t\cdot }{\mathbf{w}}^n+\frac{r}{M{P}_{\text{T}}}{\mathcal{J}}_{\text{T}}{\mathbf{f}}^n,(55)$

where ${\mathcal{J}}_{\text{T}}=[{\mathbf{j}}_{\text{T}}^{x_1}|\dots |{\mathbf{j}}_{\text{T}}^{x_M}]$ is an $(N_{\text{T}}+1)\times M$ matrix with the $m$^th column being ${\mathbf{j}}_{\text{T}}^{x_m}$, $m=1,\dots ,M$. Assuming fixed ends, the boundary conditions imply

$w_0^n=w_{N_{\text{T}}}^n=0,(56)$

for all $n\in \mathbb{N}$.

Discretization of the equation governing bow hair displacement is performed as in the lumped case:

$D_{\text{h}}{\delta }_{tt}{\mathit{\eta }}^n=-K_{\text{h}}{\mu }_{tt}{\mathit{\eta }}^n-{\mathrm{\Gamma }}_{\text{h}}{\delta }_{t\cdot }{\mathit{\eta }}^n-\frac{1}{M}{\mathbf{f}}^n,(57)$

where ${\mathit{\eta }}^n={[{\eta }_1^n,\dots ,{\eta }_M^n]}^T$. Here, for each point $x_m$ under the bow, the bow hair compliance is computed. Then, if the bow velocity at time $n{\mathrm{\Delta }}_t$ is $v_{\text{b}}^n$, the relative velocities at points of the string in contact with the bow are discretized as

${\mathbf{v}}^n=\left(\mathcal{I}{\delta }_{t\cdot }{\mathbf{u}}^n-r{\mathcal{I}}_{\text{T}}{\delta }_{t\cdot }{\mathbf{w}}^n\right)-\left(v_{\text{b}}^n-{\delta }_{t\cdot }{\mathit{\eta }}^n\right),(58)$

where $\mathcal{I}=[{\mathbf{i}}^{x_1};\dots ;{\mathbf{i}}^{x_M}]$, ${\mathcal{I}}_{\text{T}}=\frac{{\mathrm{\Delta }}_x}{{\mathrm{\Delta }}_x^{\text{T}}}{[{\mathbf{i}}_{\text{T}}^{x_1};\dots ;{\mathbf{i}}_{\text{T}}^{x_M}]}^T$ are $M\times (N+1)$ and $M\times (N_{\text{T}}+1)$ matrices with the $m$^th row being ${\mathbf{i}}^{x_m}$ and ${\mathbf{i}}_{\text{T}}^{x_m}$, respectively, for $m=1,\dots ,M$. Let ${\mathcal{E}}_{\text{M}}$ be an $M$ by $M$ identity matrix and

$\mathcal{L}=\frac{{\xi }_{\text{S}}}{M\rho A}\mathcal{I}\mathcal{J}+\frac{r^2{\xi }_{\text{T}}}{M{P}_{\text{T}}}{\mathcal{I}}_{\text{T}}{\mathcal{J}}_{\text{T}}+\frac{{\xi }_{\text{H}}}{M}{\mathcal{E}}_{\text{M}},$

where ${\xi }_{\text{S}}={(\frac{2}{{\mathrm{\Delta }}_t}+2{\gamma }_0)}^{-1}$, ${\xi }_{\text{T}}={(\frac{2}{{\mathrm{\Delta }}_t}+2{\gamma }_2)}^{-1}$, and ${\xi }_{\text{H}}={(\frac{2}{{\mathrm{\Delta }}_t}{D}_{\text{h}}+\frac{{\mathrm{\Delta }}_t}{2}{K}_{\text{h}}+{\mathrm{\Gamma }}_{\text{h}})}^{-1}$. Utilizing the expression in Equation 30 for the discrete operators ${\delta }_{tt}$ and ${\mu }_{t○}$, Equation 58 becomes

${\mathbf{v}}^n+v_{\text{b}}^n=-\mathcal{L}\cdot {\mathbf{f}}^n+{\mathbf{s}}^n,(59)$

where ${\mathbf{s}}^n$ is an $M\times 1$ column vector with entries $s_m^n={\xi }_{\text{S}}{a}_m^n-{\xi }_{\text{T}}{b}_m^n+{\xi }_{\text{H}}{c}_m^n$, where

$\begin{array}{ll}\hfill a_m^n& ={\mathbf{i}}^{x_m}\left[c^2{\delta }_{xx}{\mathbf{u}}^n-{\kappa }^2{\delta }_{\mathit{xxxx}}{\mathbf{u}}^n+2{\gamma }_1{\delta }_{t-}{\delta }_{xx}{\mathbf{u}}^n+\frac{2}{{\mathrm{\Delta }}_t}{\delta }_{t-}{\mathbf{u}}^n\right],\hfill \\ \hfill b_m^n& =\frac{{\mathrm{\Delta }}_x}{{\mathrm{\Delta }}_x^{\text{T}}}{\mathbf{i}}_{\text{T}}^{x_m}\left[r{c}_T^2{\delta }_{xx}^{\text{T}}{\mathbf{w}}^n+\frac{2r}{{\mathrm{\Delta }}_t}{\delta }_{t-}{\mathbf{w}}^n\right],\hfill \\ \hfill c_m^n& =\left[\frac{{\mathrm{\Delta }}_t}{2}{K}_{\text{h}}+\frac{2}{{\mathrm{\Delta }}_t}{D}_{\text{h}}\right]\frac{{\eta }_m^n-{\eta }_m^{n-1}}{{\mathrm{\Delta }}_t}-K_{\text{h}}{\eta }_m^n.\hfill \end{array}$

In order to update the system variables, the vectors ${\mathbf{v}}^n$ and ${\mu }_{t○}{\mathbf{z}}^n$ must first be computed. A system of $2M$ equations is formed using Equation 59 and relation in Equation 53 together with ${\delta }_{t○}{\mathbf{z}}^n=\frac{2}{{\mathrm{\Delta }}_t}\left({\mu }_{t○}{\mathbf{z}}^n-{\mathbf{z}}^{n-\frac{1}{2}}\right)$.

${\mathbf{v}}^n+\mathcal{L}{\mathbf{f}}^n-{\mathbf{s}}^n+v_{\text{b}}^n=0,(60)$

${\mathbf{g}}^n-\frac{2}{{\mathrm{\Delta }}_t}\left({\mu }_{t○}{\mathbf{z}}^n-{\mathbf{z}}^{n-\frac{1}{2}}\right)=0.(61)$

The system can then be solved for ${\mathbf{v}}^n$ and ${\mu }_{t○}{\mathbf{z}}^n$ using an iterative solver. Once ${\mathbf{v}}^n$ and ${\mu }_{t○}{\mathbf{z}}^n$ are known, ${\mathbf{u}}^{n+1}$, ${\mathbf{w}}^{n+1}$, and ${\mathit{\eta }}^{n+1}$ can be updated. First, the variables related to the friction force and the friction force itself are computed,

$\begin{array}{ll}\hfill {\mathbf{z}}^{n+\frac{1}{2}}& =2{\mu }_{t○}{\mathbf{z}}^n-{\mathbf{z}}^{n-\frac{1}{2}},\hfill \\ \hfill {\mathbf{g}}^n& =\frac{{\mathbf{z}}^{n+\frac{1}{2}}-{\mathbf{z}}^{n-\frac{1}{2}}}{{\mathrm{\Delta }}_t},\hfill \\ \hfill {\mathbf{f}}^n& ={\sigma }_0{\mu }_{t○}{\mathbf{z}}^n+{\mathrm{\Xi }}_1^n{\mathbf{g}}^n,\hfill \end{array}$

where ${\mathrm{\Xi }}_1^n$ is an $M\times M$ diagonal matrix with diagonal terms being ${\{{\sigma }_1(v_m^n)\}}_{m=1}^M$. Then, the string and bow hair variables are updated as

$\begin{array}{ll}\hfill {\mathbf{u}}^{n+1}& =\frac{2}{{\mathrm{\Delta }}_t}{\xi }_{\text{S}}\left[\mathcal{A}{\mathbf{u}}^n+\mathcal{B}{\mathbf{u}}^{n-1}\right]-\frac{2{\mathrm{\Delta }}_t{\xi }_{\text{S}}}{M\rho A}\mathcal{J}{\mathbf{f}}^n,\hfill \\ \hfill {\mathbf{w}}^{n+1}& =\frac{2}{{\mathrm{\Delta }}_t}{\xi }_{\text{T}}\left[\mathcal{C}{\mathbf{w}}^n-\left(1-{\gamma }_2{\mathrm{\Delta }}_t\right){\mathbf{w}}^{n-1}\right]+r\frac{2{\mathrm{\Delta }}_t{\xi }_{\text{T}}}{M{P}_{\text{T}}}{\mathcal{J}}_{\text{T}}{\mathbf{f}}^n,\hfill \\ \hfill {\mathit{\eta }}^{n+1}& =\mathcal{D}\left[\frac{2D_{\text{h}}}{{\mathrm{\Delta }}_t^2}-\frac{K_{\text{h}}}{2}\right]{\mathit{\eta }}^n-\mathcal{D}\left[\frac{D_{\text{h}}}{{\mathrm{\Delta }}_t^2}+\frac{K_{\text{h}}}{4}-\frac{{\mathrm{\Gamma }}_{\text{h}}}{2{\mathrm{\Delta }}_t}\right]{\mathit{\eta }}^{n-1}-\frac{\mathcal{D}}{M}{\mathbf{f}}^n,\hfill \end{array}$

where

$\begin{array}{ll}\hfill \mathcal{A}& =2\mathcal{E}+\left(2{\gamma }_1{\mathrm{\Delta }}_t+c^2{\mathrm{\Delta }}_t^2\right){\delta }_{xx}-{\kappa }^2{\mathrm{\Delta }}_t^2{\delta }_{\mathit{xxxx}},\hfill \\ \hfill \mathcal{B}& =\left({\gamma }_0{\mathrm{\Delta }}_t-1\right)\mathcal{E}-2{\gamma }_1{\mathrm{\Delta }}_t{\delta }_{xx},\hfill \\ \hfill \mathcal{C}& =2{\mathcal{E}}_{\text{T}}+c_{\text{T}}^2{\mathrm{\Delta }}_t^2{\delta }_{xx}^{\text{T}},\hfill \\ \hfill \mathcal{D}& ={\left[\frac{D_{\text{h}}}{{\mathrm{\Delta }}_t^2}+\frac{K_{\text{h}}}{4}+\frac{{\mathrm{\Gamma }}_{\text{h}}}{2{\mathrm{\Delta }}_t}\right]}^{-1},\hfill \end{array}$

with $\mathcal{E}$ an $(N+1)\times (N+1)$ identity matrix and ${\mathcal{E}}_{\text{T}}$ an $(N_{\text{T}}+1)\times (N_{\text{T}}+1)$ identity matrix.

Note that Equations 60 and 61 can be reduced to solving just one equation, as was performed in the case of the bowed lumped mass. Using Equation 60 and writing the friction force in terms of ${\mu }_{t○}{\mathbf{z}}^n$ as

${\mathbf{f}}^n={\sigma }_0{\mu }_{t○}{\mathbf{z}}^n+\frac{2}{{\mathrm{\Delta }}_t}{\mathrm{\Xi }}_1^n\left({\mu }_{t○}{\mathbf{z}}^n-{\mathbf{z}}^{n-\frac{1}{2}}\right),$

the bristle displacement can be expressed as

${\mu }_{t○}{\mathbf{z}}^n=-{\mathrm{\Xi }}^n\left[{\mathcal{L}}^{-1}\left({\mathbf{v}}^n+v_{\text{b}}^n\right)+{\mathcal{L}}^{-1}{\mathbf{s}}^n+\frac{2}{{\mathrm{\Delta }}_t}{\mathrm{\Xi }}_1^n{\mathbf{z}}^{n-\frac{1}{2}}\right],(62)$

where ${\mathrm{\Xi }}^n$ is an $M\times M$ diagonal matrix with entries ${({\sigma }_0+\frac{2}{{\mathrm{\Delta }}_t}{\sigma }_1(v_m^n))}^{-1}$, $m=1,\dots ,M$ on the diagonal. Plugging (62) into (61) and ${\mathbf{g}}^n$, only Equation 61 must be solved for ${\mathbf{v}}^n$. ${\mathbf{z}}^{n+1/2}$ can then be computed from Equation 62. This approach increases computational efficiency for point bowing when $M=1$, but with more points under the bow it involves matrix inversion, which is computationally expensive.

6.3 Numerical energy and stability condition

An energy balance for the discretized scheme follows from a discrete inner product of Equation 52 with ${\delta }_{t\cdot }{\mathbf{u}}^n$, an inner product of Equation 55 with ${\delta }_{t\cdot }{\mathbf{w}}^n$, an inner product of Equation 57 with ${\delta }_{t\cdot }{\mathit{\eta }}^n$, and an inner product of $\frac{{\sigma }_0}{M}{\mu }_{t○}{\mathbf{z}}^n$ with ${\delta }_{t○}{\mathbf{z}}^n$. Using summation by parts identities as well as boundary conditions leads to

${\delta }_{t+}{\mathcal{H}}^n=-{\mathcal{Q}}^n-{\mathcal{P}}^n+{\mathcal{B}}^n,(63)$

where $\mathcal{H}$, the total numerical energy, is defined as $\mathcal{H}={\mathcal{H}}_{\text{r}}+{\mathcal{H}}_{\text{w}}+{\mathcal{H}}_{\text{h}}+{\mathcal{H}}_{\text{b}}$ and, assuming that the stability conditions in Equations 50 and 51 are satisfied,

$\begin{array}{ll}\hfill {\mathcal{H}}_{\text{r}}^n& =\frac{\rho A}{2}{‖{\delta }_{t-}{\mathbf{u}}^n‖}_{d_{\text{N}}}^2+\frac{T}{2}{⟨{\delta }_{x+}{\mathbf{u}}^n,{\delta }_{x+}{\mathbf{u}}^{n-1}⟩}_{d_{\underline{\mathrm{N}}}}+\frac{EI}{2}{⟨{\delta }_{xx}{\mathbf{u}}^n,{\delta }_{xx}{\mathbf{u}}^{n-1}⟩}_{d_{\overline{\underline{\mathrm{N}}}}}\ge 0,\hfill \\ \hfill {\mathcal{H}}_{\text{w}}^n& =\frac{P_{\text{T}}}{2}\frac{{\mathrm{\Delta }}_x}{{\mathrm{\Delta }}_x^{\text{T}}}{‖{\delta }_{t-}{\mathbf{w}}^n‖}_{d_{{\mathrm{N}}_{\mathrm{T}}}}^2+\frac{K_{\text{T}}}{2}\frac{{\mathrm{\Delta }}_x}{{\mathrm{\Delta }}_x^{\text{T}}}{⟨{\delta }_{x+}^{\text{T}}{\mathbf{w}}^n,{\delta }_{x+}^{\text{T}}{\mathbf{w}}^{n-1}⟩}_{d_{\underline{{\mathrm{N}}_{\mathrm{T}}}}}\ge 0,\hfill \\ \hfill {\mathcal{H}}_{\text{h}}^n& =\frac{D_{\text{h}}}{2}{\left[{\delta }_{t-}{\mathit{\eta }}^n\right]}^T{\delta }_{t-}{\mathit{\eta }}^n+\frac{K_{\text{h}}}{2}{\left[{\mu }_{t-}{\mathit{\eta }}^n\right]}^T{\mu }_{t-}{\mathit{\eta }}^n\ge 0,\hfill \\ \hfill {\mathcal{H}}_{\text{b}}^n& =\frac{1}{M}\frac{{\sigma }_0}{2}{\left[{\mathbf{z}}^{n-\frac{1}{2}}\right]}^T{\mathbf{z}}^{n-\frac{1}{2}}\ge 0.\hfill \end{array}$

The total energy lost due to damping is defined as $\mathcal{Q}={\mathcal{Q}}_{\text{r}}+{\mathcal{Q}}_{\text{w}}+{\mathcal{Q}}_{\text{h}}+{\mathcal{Q}}_{\text{b}}$ with

$\begin{array}{ll}\hfill {\mathcal{Q}}_{\text{r}}^n& =2{\gamma }_0\rho A{‖{\delta }_{t\cdot }{\mathbf{u}}^n‖}_{d_{\text{N}}}^2-2{\gamma }_1\rho A{⟨{\delta }_{t\cdot }{\mathbf{u}}^n,{\delta }_{t-}{\delta }_{xx}{\mathbf{u}}^n⟩}_{d_N}\ge 0,\hfill \\ \hfill {\mathcal{Q}}_{\text{w}}^n& =2{\gamma }_2{P}_{\text{T}}\frac{{\mathrm{\Delta }}_x}{{\mathrm{\Delta }}_x^{\text{T}}}{‖{\delta }_{t\cdot }{\mathbf{w}}^n‖}_{d_{{\mathrm{N}}_{\mathrm{T}}}}^2\ge 0,\hfill \\ \hfill {\mathcal{Q}}_{\text{h}}^n& ={\mathrm{\Gamma }}_{\text{h}}{\left[{\delta }_{t\cdot }{\mathit{\eta }}^n\right]}^T{\delta }_{t\cdot }{\mathit{\eta }}^n\ge 0,\hfill \\ \hfill {\mathcal{Q}}_{\text{b}}^n& =\frac{1}{M}{\mathrm{\Xi }}_1^n{\left[{\mathbf{v}}^n\right]}^T{\mathbf{v}}^n+{\sigma }_0{\left[{\mu }_{t○}{\mathbf{z}}^n\right]}^T{\mathbf{o}}^n-{\mathrm{\Xi }}_1^n{\left[{\mathbf{v}}^n\right]}^T{\mathbf{o}}^n\ge 0,\hfill \end{array}$

where ${\mathbf{o}}^n$ is a vector with entries $o_m^n=\alpha ({\mu }_{t○}{z}_m^n,v_m^n)\frac{{\mu }_{t○}{z}_m^n}{z_{\text{ss}}(v_m^n)}$ for $m=1,\dots ,M$. The non-negativity of the dissipation term ${\mathcal{Q}}_{\text{b}}^n$ can be shown similarly to the lumped case. The energy supplied by the bow $\mathcal{P}$ and boundary terms $\mathcal{B}={\mathcal{B}}_{\text{r}}+{\mathcal{B}}_{\text{w}}$ is

$\begin{array}{ll}\hfill {\mathcal{P}}^n& =\frac{1}{M}{v}_{\text{b}}^n{\displaystyle \sum _{m=1}^M}{f}_m^n,\hfill \\ \hfill {\mathcal{B}}_{\text{r}}^n& =T\left({\delta }_{t\cdot }{u}_N^n{\delta }_{x+}{u}_N^n-{\delta }_{t\cdot }{u}_0^n{\delta }_{x+}{u}_0^n\right)+EI\left({\delta }_{t\cdot }{u}_N^n{\delta }_{x+}{\delta }_{xx}{u}_N^n-{\delta }_{t\cdot }{u}_0^n{\delta }_{x+}{\delta }_{xx}{u}_0^n\right)\hfill \\ \hfill & -EI\left({\delta }_{t\cdot }{\delta }_{x+}{u}_N^n{\delta }_{xx}{u}_N^n-{\delta }_{t\cdot }{\delta }_{x+}{u}_0^n{\delta }_{xx}{u}_0^n\right),\hfill \\ \hfill {\mathcal{B}}_{\text{w}}^n& =K_{\text{T}}\left({\delta }_{t\cdot }{w}_N^n{\delta }_{x+}^{\text{T}}{w}_N^n-{\delta }_{t\cdot }{w}_0^n{\delta }_{x+}^{\text{T}}{w}_0^n\right).\hfill \end{array}$

For simply supported and fixed boundary conditions, the boundary term $\mathcal{B}$ vanishes.

The bowed string model is passive, and the argument follows that in the continuous case, where the integral becomes the sum:

${\mathcal{Q}}_{\text{b}}^n=\frac{1}{M}{\displaystyle \sum _{m=1}^M}\left[{\sigma }_1\left(v_m^n\right){\left(v_m^n\right)}^2+\alpha \left({\mu }_{t○}{z}_m^n,v_m^n\right)\frac{v_m^n{\mu }_{t○}{z}_m^n}{z_{\text{ss}}\left(v_m^n\right)}\left({\sigma }_0{\mu }_{t○}{z}_m^n-{\sigma }_1\left(v_m^n\right)v_m^n\right)\right]\ge 0.$

Non-negativity of ${\mathcal{Q}}_{\text{b}}^n$ is guaranteed, since all terms inside the sum are positive, as was the case for the lumped model.

6.4 Numerical experiments

Simulated signals using the refined bow–string interaction model are shown in Figure 7. In this case, the bow starts in contact with the string, and the force is kept constant while the bow is accelerated from rest with a chosen acceleration value until the steady-state bow velocity $v_{\mathrm{b}}$ is reached. The physical model parameters used to generate these signals are given in Table 2.

Figure 7

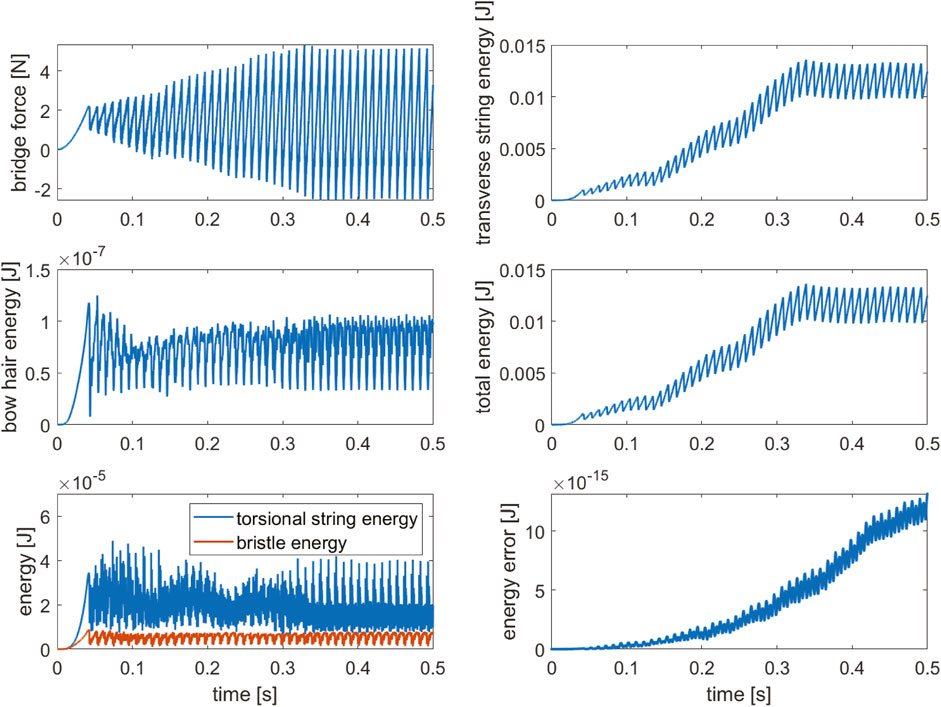
Figure 7. Simulated bridge force using the refined elasto-plastic model, along with various energy components. Total energy is the sum of the transverse and torsional energies of the string as well as the bristle and bow hair energies. The energy error is shown on the bottom right. Model parameter values are given in Table 2.

The original Dupont friction model was recently applied to the distributed case of bowing a string in Matusiak and Chatziioannou (2024). The performance of the original elasto-plastic model was evaluated by simulating a Guettler diagram and comparing it to a Guettler diagram obtained from measurements (Lampis et al., 2024). A Guettler diagram is generated by choosing a fixed location on the string and bowing from rest with an accelerating bow. The bow force while bowing is kept constant. Bowing is then repeated for different accelerations and bow forces that are incremented in small steps. The number of periods required to reach Helmholtz motion is visualized via the color of each pixel (Figure 8). White corresponds to 0 periods (perfect transient) and black to 20 periods, with intermediate transient lengths resulting in different grayscale values. Guettler (2002) proposed such a diagram as a measure of assessing the playability of a bowed string by measuring the length of the transient necessary to arrive at Helmholz motion.

Figure 8

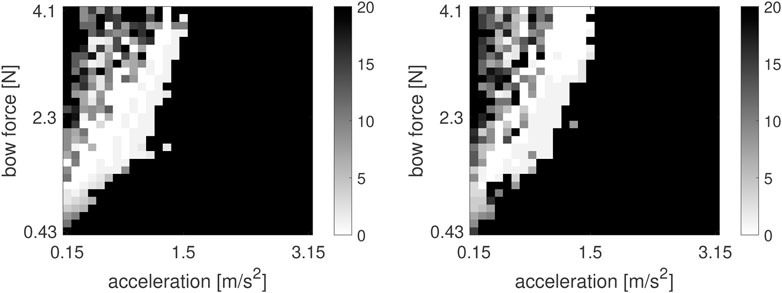
Figure 8. Guettler diagrams using Dupont (left) and refined models (right) with string parameters as in Table 2. The color bar refers to the number of periods required for Helmholtz motion to be achieved (transient length).

The refined model was utilized to simulate a Guettler diagram with the same parameters as in Matusiak and Chatziioannou (2024). The two diagrams are shown in Figure 8 for comparison. The chaotic nature of the frictional interaction manifests itself via the patchiness of the playability regions. Neighboring pixels may correspond to largely different transient durations, indicating sensitivity to small changes in bow force and acceleration. Therefore, the diagrams slightly differ due to the small underlying numerical differences of the two models. Qualitative observations regarding the playability of the system are nevertheless the same for both models.

6.5 Supplementary material

A sound example of the synthesis of a fast sautillé passage is included in the supplementary material. Simulation of this bow stroke style exposes the transient behavior of the proposed bow–string model and offers the reader a preliminary aural impression of it. For synthesis of the G2 notes, the bow velocity and force were varied periodically over time according to patterns similar to those observed in Demoucron (2008). Convolution with a measured cello impulse response was applied to the bridge force signal to render a more realistic audio signal.

Furthermore, animations of the string motion are provided for the case shown in Figure 7, where Helmholtz motion is achieved, as well as for a case where the bow force is reduced by 50% ($f_{\text{N}}=1.17$ N), resulting in a double-slip pattern. The matlab code for the bowed-string simulations is available at doi:10.5281/zenodo.15341818.

7 Conclusion

An elasto-plastic friction model has been investigated from the point of view of energy conservation in the continuous domain and discretized using a finite difference scheme. The model was first analyzed in the setting of a bowed lumped mass. A refinement of the model has been suggested that guarantees passivity for elasto-plastic friction with the Stribeck effect and simultaneously leads to the existence and uniqueness of the solution. A numerical scheme has been derived that respects the energy balance of the underlying continuous model, thus leading to a guaranteed passive model and hence to stable simulations.

Based on this refined version of the elasto-plastic model, simulations of a bowed string were revisited, including bow compliance, string torsion, and a finite bow width. While results are similar to those previously obtained using the original Dupont model, the refined model presented is proven to be guaranteed passive, as is the case for the lumped system.

The main limitation of the proposed implicit scheme is that the Jacobian of the nonlinear function to be solved iteratively at each time step can become singular, which—even when applying deliberately modified versions of the iterative solver (e.g., Hueso et al. 2009)—can lead to the necessity of a huge number of iterations. In practice, this often necessitates heavy oversampling, especially when driving the model with articulation parameters (e.g., bowing force) that vary across over time. A logical future research direction is therefore to develop numerical schemes that sidestep the need for an iterative solver, as has been achieved recently for numerical simulation of various other nonlinear phenomena in musical instruments, including collisions (e.g., van Walstijn et al., 2024).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

EM: conceptualization, investigation, methodology, software, and writing – original draft. VC: funding acquisition, investigation, project administration, validation, and writing – review and editing. MV: investigation, validation, and writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded in whole or in part by the Austrian Science Fund (FWF) [10.55776/P34852]. For open access purposes, the authors have applied a CC BY public copyright license to any author-accepted manuscript version arising from this submission.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsip.2025.1525044/full#supplementary-material

References

Barreira, L., and Valls, C. (2012). Ordinary differential equations: qualitative theory. America, American Mathematical Society.

Google Scholar

Bilbao, S. (2009). Numerical sound synthesis. J. Wiley and Sons. doi:10.1002/9780470749012

CrossRef Full Text | Google Scholar

Bilbao, S., Torin, A., and Chatziioannou, V. (2015). Numerical modeling of collisions in musical instruments. Acta Acust. United Acust. 101, 155–173. doi:10.3813/AAA.918813

CrossRef Full Text | Google Scholar

Chabassier, J., and Joly, P. (2010). Energy preserving schemes for nonlinear Hamiltonian systems of wave equations: application to the vibrating piano string. Comput. Methods Appl. Mech. Eng. 199, 2779–2795. doi:10.1016/j.cma.2010.04.013

CrossRef Full Text | Google Scholar

Chatziioannou, V., and van Walstijn, M. (2015). “Discrete-time conserved quantities for damped oscillators,” in Proceedings of the third Vienna talk on music acoustics (Vienna, AT: Department of Music Acoustics - Wiener Klangstil), 135–139.

Google Scholar

Demoucron, M. (2008). On the control of virtual violins physical modelling and control of bowed string instruments (Stockholm: Royal Institute of Technology). Ph.D. thesis.

Google Scholar

Desvages, C. (2018). Physical modelling of the bowed string and applications to sound synthesis (The University of Edinburgh). Ph.D. thesis.

Google Scholar

Deuflhard, P. (2011). Newton methods for nonlinear problems: affine invariance and adaptive algorithms. Springer Sci. and Bus. Media 35.

Google Scholar

de Wit, C., Olsson, H., Åström, K., and Lischinsky, P. (2024). A new model for control of systems with friction. IEEE Trans. Autom. Control 40, 419–425. doi:10.1109/9.376053

CrossRef Full Text | Google Scholar

Ducceschi, M., and Bilbao, S. (2022). Simulation of the geometrically exact nonlinear string via energy quadratisation. J. Sound Vib. 534, 117021. doi:10.1016/j.jsv.2022.117021

CrossRef Full Text | Google Scholar

Dupont, P., Armstrong, B., and Hayward, V. (2000). Elasto-plastic friction model: contact compliance and stiction. Proc. 2000 Acc. IEEE Chic., 1072–1077 vol.2. doi:10.1109/ACC.2000.876665

CrossRef Full Text | Google Scholar

Dupont, P., Hayward, V., Armstrong, B., and Altpeter, F. (2002). Single state elasto-plastic friction models. IEEE Trans. Autom. Control 47, 787–792. doi:10.1109/TAC.2002.1000274

CrossRef Full Text | Google Scholar

Falaize, A., and Roze, D. (2024). Generic passive-guaranteed nonlinear interaction model and structure-preserving spatial discretization procedure with applications in musical acoustics. Nonlinear Dyn. 112, 3249–3275. doi:10.1007/s11071-024-10438-9

CrossRef Full Text | Google Scholar

Galluzzo, P. (2004). On the playability of stringed instruments. Ph.D. thesis. doi:10.17863/CAM.14046

CrossRef Full Text | Google Scholar

Guettler, K. (2002). On the creation of the helmholtz motion in bowed strings. Acta Acust. united Acust. 88, 970–985.

Google Scholar

Hueso, J., Martínez, E., and Torregrosa, J. (2009). Modified Newton’s method for systems of nonlinear equations with singular Jacobian. J. Comput. Appl. Math. 224, 77–83. doi:10.1016/j.cam.2008.04.013

CrossRef Full Text | Google Scholar

Lampis, A., Mayer, A., and Chatziioannou, V. (2024). Assessing playability limits of bowed-string transients using experimental measurements. Acta Acust. 8, 44. doi:10.1051/aacus/2024034

CrossRef Full Text | Google Scholar

Maestre, E., Spa, C., and Smith, J. (2014). A bowed string physical model including finite-width thermal friction and hair dynamics. ICMC.

Google Scholar

Matusiak, E., and Chatziioannou, V. (2024). Elasto-plastic friction modeling toward reconstructing measured bowed-string transients. J. Acoust. Soc. Am. 156, 1135–1147. doi:10.1121/10.0028228

PubMed Abstract | CrossRef Full Text | Google Scholar

Olsson, H. (1996). Control systems with friction (Lund Institute of Technology LTH). Ph.D. thesis.

Google Scholar

Pitteroff, R., and Woodhouse, J. (1998a). Mechanics of the contact area between a violin bow and a string. Part I: reflection and transmission behaviour. Acta Acust. United Acust. 84, 543–562.

Google Scholar

Pitteroff, R., and Woodhouse, J. (1998b). Mechanics of the contact area between a violin bow and a string. Part II: simulating the bowed string. Acta Acust. United Acust. 84, 744–757.

Google Scholar

Serafin, S. (2004). The sound of friction: real-time models, playability and musical applications (Stanford: Stanford University). Ph.D. thesis.

Google Scholar

Serafin, S., Avanzini, F., and Rocchesso, D. (2003). “Bowed string simulations using an elasto-plastic friction model,” in Proceedings of the Stockholm Music Accoustics Conference, USA, 14–15 June 2023.

Google Scholar

Smith, J., and Woodhouse, J. (1999). The tribology of rosin. J. Mech. Phys. Solids 48, 1633–1681. doi:10.1016/S0022-5096(99)00067-8

CrossRef Full Text | Google Scholar

van Walstijn, M., Chatziioannou, V., and Bhanuprakash, A. (2024). Implicit and explicit schemes for energy-stable simulation of string vibrations with collisions: refinement, analysis, and comparison. J. Sound Vib. 569, 117968. doi:10.1016/j.jsv.2023.117968

CrossRef Full Text | Google Scholar

Willemsen, S. (2021). “Real-time simulation of musical instruments using finite-difference time-domain methods,”.Aalb. Univ. Ph.D. thesis. doi:10.54337/aau451025772

CrossRef Full Text | Google Scholar

Willemsen, S., Bilbao, S., and Serafin, S. (2019). Real-time implementation of an elasto-plastic friction model applied to stiff strings using finite-difference schemes. Proceedings of the International Conference on Digital Audio Effects, USA, 8-10 Sept. 2021, 40–46.

Google Scholar

Woodhouse, J. (2003). Bowed string simulation using a thermal friction model. Acta Acustica united Acustica 89, 355–368. doi:10.25144/18216

CrossRef Full Text | Google Scholar

Appendix

The modal expansion for the displacement of the string, assuming simply supported boundary conditions, is

$u\left(x,t\right)={\displaystyle \sum _{i=1}^{N_{\text{M}}}}{q}_i\left(t\right){\psi }_i\left(x\right),\text{where}{\psi }_i\left(x\right)=\sin \left(\frac{i\pi }{L}x\right),$

where $N_{\text{M}}$ is the number of modes, and it is normally set according to the relevant frequency range. To isolate a single mode of vibration, $u(x,t)$ is substituted into the equation governing the transverse motion of the string,

$\rho A{\partial }_t^{2}u=T{\partial }_x^{2}u-EI{\partial }_x^{4}u-2{\gamma }_0\rho A{\partial }_{t}u+2{\gamma }_1\rho A{\partial }_t{\partial }_x^{2}u,$

and an inner product with ${\psi }_n$ is taken. Since $⟨{\psi }_i,{\psi }_n⟩=\frac{L}{2}{\delta }_{i,n}$, we obtain

$m{\ddot{q}}_n=-{\kappa }_n{q}_n-{\stackrel{\sim }{\gamma }}_n{\dot{q}}_n,$

where

$m=\frac{\rho AL}{2},(64)$

${\kappa }_n=\frac{{\left(n\pi \right)}^2}{2L}\left[T+EI{\left(\frac{n\pi }{L}\right)}^2\right],(65)$

${\stackrel{\sim }{\gamma }}_n=\rho AL\left[{\gamma }_0+{\gamma }_1{\left(\frac{n\pi }{L}\right)}^2\right].(66)$

Therefore, by setting $N_{\text{M}}=1$, the dynamics of the system reduce to a damped harmonic oscillator.