Autonomous Crosslink Radionavigation for a Lunar CubeSat Mission

Introduction

There has been an increasing interest in small satellites for lunar missions lately, forming almost 40% of all planned deep space small satellite missions (Turan et al., 2022a). In these missions, the baseline option for orbit determination is, in general, ground-based radiometric navigation. However, ground-based tracking could be expensive and limited considering crowded ground networks. In addition, small satellite missions are expected to be low-cost and there are also limitations from small satellite themselves such as on-board power for communication. Autonomous navigation, on the other hand, could be a possible approach for these lunar missions. Until now, various autonomous navigation methods have been proposed and implemented. One of them, called LiAISON, uses solely satellite-to-satellite observations, such as range or range-rate, to estimate the absolute states of the involved satellites when at least one of them has an orbit with unique size, shape, and orientation (Hill, 2007; Hill and Born, 2007; Hill and Born, 2008). The characteristics of the acceleration function determine whether inter-satellite range or range-rate measurements can be used alone to estimate the absolute and relative Spacecraft (S/C) states. Considering the asymmetric gravity field in the cislunar vicinity, it is possible to build such an autonomous navigation system. Up to now, various studies have presented the capabilities of LiAISON over the past decade in lunar and deep space mission studies (Leonard et al., 2012; Leonard, 2015; Fujimoto et al., 2016; Wang et al., 2019; Turan et al., 2022b).

This navigation method will be tested via the link between Lunar Reconnaissance Orbiter (LRO) and the CAPSTONE CubeSat soon (Cheetham, 2020). However, many more missions targeted to the EML2 could benefit from such technique. One of these, Lunar Meteoroid Impact Observer (LUMIO) is a CubeSat at EML2 designed to observe, quantify, and characterize the meteoroid impacts by detecting their flashes on the Lunar farside, to provide global information on the Lunar Meteoroid Environment (Speretta et al., 2018; Topputo et al., 2021; Cervone et al., 2022; Speretta et al., 2022). The baseline navigation strategy, as for almost all small satellites targeting this orbit, is ground-based radiometric. Beside this, LUMIO also includes an inter-satellite link to a larger Lunar orbiter for telecommand purposes but not for navigation. Having an inter-satellite link provides an opportunity to investigate the performances of autonomous navigation via crosslink radiometric measurements, potentially extending the mission possibilities with this new technique.

This study presents the autonomous navigation performances of the selected mission scenario: LUMIO, via the link between Lunar Pathfinder (LPF) and the LUMIO CubeSat. A simulation-based analysis will determine the achievable orbit determination accuracy considering realistic radio frequency measurement errors derived from the Phase-A study inter-satellite link design, which was not designed to perform navigation. In the following sections, at first, the selected mission scenario is presented and then, dynamical models are provided. Orbit determination models are introduced including the observability analysis. Thereafter, the navigation simulation setup and results are presented. Finally, conclusions are drawn.

A Lunar CubeSat Scenario

For this study, the LUMIO mission has been selected. It features a 12U CubeSat in a halo orbit at the EML2 to observe, quantify, and characterize meteoroid impacts on the Lunar farside by detecting their flashes (Topputo et al., 2021; Cervone et al., 2022). The mission aims at determining the spatial and temporal characteristics of meteoroids impacting the Lunar surface to characterize their flux. The operative orbit for LUMIO has been selected as a quasi-periodic halo orbit with a Jacobi constant C_j = 3.09 (Cervone et al., 2022). The LUMIO Phase-A study has been completed in March 2021 when the mission’s Phase-B is supposed to start (Speretta et al., 2022).

The radiometric navigation system uses existing hardware of the communication system featuring a combination of Inter-Satellite Link (ISL) and Direct-to-Earth Link (DTE) links. The latter has been designed to provide payload data downlink, ranging and tracking in nominal conditions. Based on the orbit determination (OD) analysis given in (Speretta et al., 2021), ground-based radiometric navigation via Cebreros, ESTRACK or the Sardinia Deep Space Antenna for 3 h per track following a 7 + 7 + 14 days scheme meets the OD requirements of 1 km and 1 cm/s position and velocity accuracy, respectively. In this study the same OD requirements have been considered for an autonomous navigation scenario. The ISL, on the other hand, has been designed to provide a redundant commanding link without involving a dedicated deep-space class ground station but reusing commercial resources. Such link provides optimal performances in terms of visibility, despite the fact that data rates are quite limited. The SSTL LPF spacecraft has been considered as relay satellite. Depending on the relative distance, between a minimum of 31 ,000 km and a maximum of 89 ,000 km, data rates are expected in the order of 0.5–4  kbps based on S-band, 9  dBW Equivalent Isotropic Radiated Power (EIRP) link (also including a 3 dB safety margin (Speretta et al., 2022)).

Autonomous Radiometric Navigation

This study investigates the LiAISON orbit determination performances for the LUMIO mission: autonomous orbit determination requires absolute position and velocity estimates without any ground-based observation. This requires that the S/C states, obtained from inter-satellite observations, must be observable. In the two body problem, relative range or range-rate measurements do not provide full state estimation due to the rank deficiency: absolute orientations of the orbital planes are not observable, which is related to the symmetrical gravity field. In other words, there is no unique orbital configurations in a symmetrical gravity field resulting from the acceleration function. However, in an asymmetrical gravity field, spacecraft-to-spacecraft tracking provides absolute state estimation. The LiAISON orbit determination method uses solely inter-satellite measurements to estimate absolute S/C states of the involved S/C when at least one of them has an orbit with a unique size, shape and orientation (Hill, 2007; Hill and Born, 2007; Hill and Born, 2008). Basically, if one of the S/C has an unique orbit, it is possible to estimate absolute states of all involved spacecrafts. This study derives inter-satellite observations, namely range and range-rate, from radio frequency measurements.

Inter-satellite radiometric measurements can be collected with various methods. Range observations, for example, can be collected via phase or time-based measurements: the phase shift on a ranging signal at the receiver with respect to a transmitter provides an accurate ranging solution (in the order of 1 m). This still requires the phase ambiguity to be solved in case the ranging signal period exceeds the round-trip light time. There are lots of common standards used for this purpose such as pseudo noise/sequential tone-based ranging (Turan et al., 2022a). However, small satellites, in general, have limited on-board power available for data transfer. If a small satellite requires ranging for its navigation, such signal reduces the power available for telemetry in case both signals are modulated at the same time window. On the other hand, timing exchange between satellites provides also a ranging solution. Basically, in order to deal with on-board power limitations, time-derived ranging methods are a possible options for small satellites. These methods are not quite accurate (in the order of 150 m at 10  kbps) but they can provide sufficient ranging solutions to meet the navigation requirements. Because time-derived ranging methods are data-rate dependent, high-data transfer between satellites is beneficial. Another measurement type is range-rate and this can be derived from the Doppler shift between satellites but, again, this measurement type suffers from on-board limitations. In this study, high and low measurement ranging errors derived from the conventional (radiometric) and time-derived ranging methods are considered for the selected mission scenario.

Orbit Determination Models

This section presents the orbit determination models used in this study. Dynamical, measurement and estimation models are given in the following subsections.

Dynamical Model

The dynamical model used in this study is formulated as Circular Restricted Three-body Problem (CRTBP). This is simple but accurate enough for this type of application, considering the mission required position accuracy. In (Hill, 2007), the LiAISON OD performances remain in the same order of magnitude for various force models. In addition to CRTBP, in the end, high-fidelity dynamic simulation models results will also be given for the selected measurement configuration to have a more realistic analysis and to compare results obtained from CRTBP dynamics.

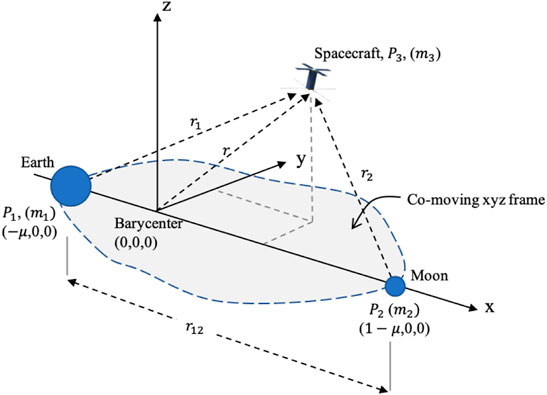
The CRTBP assumes there are two massive bodies, Earth (P₁) with mass m₁ and Moon (P₂) with mass m₂ in this case, moving under their mutual gravitation in a circular orbit around each other with a radius r₁₂, (Curtis, 2020). Considering a non-inertial, co-moving reference frame (see Figure 1) with its origin at the barycenter of the two bodies, the positive x − axis points from the barycenter to P₂. The positive y − axis is parallel to the velocity vector of P₂ and the z − axis is perpendicular to the orbital plane.

FIGURE 1

FIGURE 1. Circular Restricted Three-body Problem: Earth-Moon co-moving reference frame.

Considering a third body of mass m₃ with m₃ ≪ m₁ and m₃ ≪ m₂, it cannot impact the motion of primary bodies, P₁ and P₂. The equations of motion for the CRTBP are (Hill, 2007):

$\ddot{x}-2\dot{y}=x-\left(1-\mu \right)\frac{x+\mu }{r_1^3}-\mu \frac{x+\mu -1}{r_2^3}(1)$

$\ddot{y}+2\dot{x}=\left(1-\frac{1-\mu }{r_1^3}-\frac{\mu }{r_2^3}\right)y(2)$

$\ddot{z}=\left(\frac{\mu -1}{r_1^3}-\frac{\mu }{r_2^3}\right)z(3)$

where $r_1=\sqrt{{(x+\mu )}^2+y^2+z^2}$ and $r_2=\sqrt{{(x+\mu -1)}^2+y^2+z^2}$. For the Earth-Moon system, the gravitational parameter μ is 0.01215, the normalized length l* = r₁₂ = 384 747.96 km, and the normalized time $t^{*}=\sqrt{l^{{*}^3}/G(m_1+m_2)}=$ 4.343 days, respectively. In the study, the Lunar orbiter’s initial states are expressed in the Moon-Centered Inertial (MCI) frame, a coordinate transformation is needed to convert states from the inertial frame to the non-dimensional Earth-Moon barycentric frame. In general, each S/C state vector can be transformed between the inertial frame and the rotating frame as follows (Haapala, 2010):

$X_{inertial}=T{X}_{rot}(4)$

where

$T=\left[\begin{array}{cc}\hfill L\hfill & \hfill 0_{3\times 3}\hfill \\ \hfill \dot{L}\hfill & \hfill L\hfill \end{array}\right],L=\left[\begin{array}{ccc}\hfill \cos \left(t\right)\hfill & \hfill -\sin \left(t\right)\hfill & \hfill 0\hfill \\ \hfill \sin \left(t\right)\hfill & \hfill \cos \left(t\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right](5)$

where X_rot represents the non-dimensional Earth-Moon barycentric coordinates, X_inert represents the inertial states centered on the barycenter (The S/C states can be non-dimensionalized via l* and t*). It is assumed that two frames coincide at the initial time t₀ = 0. A rotating position vector of the S/C in the Moon-centered frame can be found via adding the position of the barycenter with respect to the body (the same procedure applies to the Earth-centered frame) (Hill, 2007). Based on these, S/C states can be transformed from the body centered inertial frame to the Earth-Moon barycentric rotating frame and vice versa.

In high-fidelity dynamical simulations, in addition to gravitational acceleration due to Earth and Moon (treated as point masses in the Earth-Centered Inertial (ECI) J2000 frame), the gravitational acceleration due to Sun treated as a point mass and acceleration due to Solar Radiation Pressure (SRP) with a spherical model have been used. In addition, dynamical model errors are not considered in this study.

Measurement Model

In this study, the autonomous navigation method uses solely inter-satellite measurements and the observables are collected via radiometric measurements. The first radiometric data type used is range, which can be derived from either conventional ranging methods or data-aided ranging. A conventional ranging method using is pseudo-random noise has been selected and, considering a non-coherent transponder with a pseudo-noise square wave shaped ranging signal, and a chip tracking loop, the following one-way ranging error (1σ) would be expected (CCSDS, 2014):

${\sigma }_{{\rho }_{PN}}=\frac{c}{8f_{rc}}\sqrt{\frac{B_L}{\left(P_{RC}/N_0\right)}}(6)$

and the range bias due to a chip rate mismatch:

${\rho }_{\text{bias}}=\frac{c\mathrm{\Delta }{f}_{chip}T}{4f_{chip}}(7)$

with c the speed of light, f_rc the frequency of the ranging clock component, B_L one-sided loop noise bandwidth, P_RC power of the ranging clock component, T integration time, N₀ one-side noise power spectral density, Δf_chip the difference in frequency between the received chip rate and the local chip rate.

The round-trip light time can also be measured via time transfer between satellites. This process requires four successive time stamps to be obtained which represent the time of transmission and reception of both S/C (see Figure 2). If the timing is measured in units of telemetry/telecommand symbols, instead of directly in seconds, the performance of time-derived ranging (one-way) would be:

${\sigma }_{{\rho }_{TD}}=\frac{4c{T}_{sd}^2}{\pi T_l{E}_S/N_0}(8)$

where T_sd is the symbol duration, T_l the correlator integration time and E_S/N₀ the symbol-to-noise ratio. Note that both Eqs 6, 8 represent one-way ranging performance and this requires calculations for both uplink and downlink.

FIGURE 2

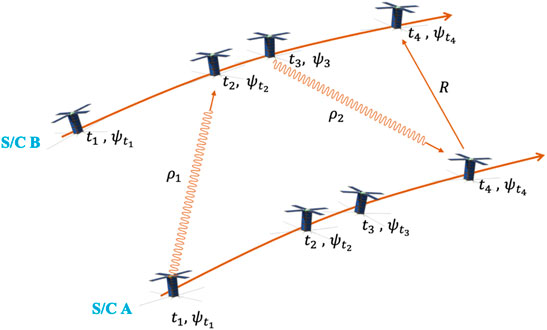
FIGURE 2. Time exchange between satellites for the purpose of time-derived ranging. t_i represents time, ψ_i represents onboard clock states at t_i.

The measurement error for two-way Doppler due to thermal noise, influencing range-rate observations, can be given as follows (DSN, 2018):

${\sigma }_V=\frac{c}{2\sqrt{2}\pi f_{c}T}\sqrt{\frac{1}{{\rho }_L}+\frac{G^2{B}_L}{\left(P_C/N_0\right)}}(9)$

where f_c the downlink carrier frequency, P_C/N₀ uplink carrier power to noise spectral density ratio, ρ_L the downlink carrier loop signal-to-noise ratio, G the turn-around ratio. Doppler data noise can be expressed by the phase noise, σ_φ, in radians and converted to range-rate noise as follows (Montenbruck and Gill, 2000):

${\sigma }_{\dot{\rho }}=\frac{\sqrt{2}c}{2G{f}_t{t}_c}\frac{{\sigma }_{\phi }}{2\pi }(10)$

In this study, the formation includes two S/C, a lunar orbiter, LPF, and EML2 Halo orbiter, LUMIO. The state vector being estimated consists of the position and velocity components of both S/C is as follows:

$\mathbf{X}={\left[\begin{array}{c}\hfill x_1{y}_1{z}_1{\dot{x}}_1{\dot{y}}_1{\dot{z}}_1{x}_2{y}_2{z}_2{\dot{x}}_2{\dot{y}}_2{\dot{z}}_2\hfill \end{array}\right]}^T(11)$

The measurement model in this paper, referred as the pseudo-range, involves the geometric range, the overall clock bias, and other error sources. The two-way ranging measurement concept can be seen in Figure 2. The geometric range is given as follows:

$R=\frac{1}{2}c\left(t_4-t_1\right)+\mathrm{\Delta }\rho (12)$

where Δρ is the S/C position change projection along the Line-of-Sight (LOS) direction. By ignoring the light-time correction, and by assuming the speed of light is greater than the S/C relative velocity, c ≫ v, the geometric range can be modeled as

$R=\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2+{\left(z_1-z_2\right)}^2}(13)$

where x_i, y_i and z_i represents the position components of S/C, i = 1, 2 states and the pseudo range observations can be given as

$\rho =R+c\left({\psi }_{t_4}-{\psi }_{t_1}\right)+c\left({\mathrm{\Delta }}_{tx}+{\mathrm{\Delta }}_{rx}\right)+c{\mathrm{\Delta }}_{trx}+{\rho }_{\text{noise}}(14)$

$\rho =\sqrt{\left({\mathbf{r}}_1-{\mathbf{r}}_2\right)\cdot \left({\mathbf{r}}_1-{\mathbf{r}}_2\right)}+{\rho }_{\text{bias}}+{\rho }_{\text{noise}}(15)$

where ${\psi }_{t_4}$ and ${\psi }_{t_1}$ are the clock states at t₄ and t₁ respectively. The transponder transmit and receive line delays are Δ_tx and Δ_rx, respectively and Δ_trx is the line delay on the S/C transponding the ranging signal. All these terms are combined as ρ_bias and ρ_noise representing the un-modelled statistical error sources.

The range rate measurements, $\dot{\rho }$, can be modeled as:

$\dot{\rho }=\frac{\mathit{\rho }\cdot \dot{\mathit{\rho }}}{\rho }(16)$

$\dot{\rho }=\frac{\left(x_1-x_2\right)\left({\dot{x}}_1-{\dot{x}}_2\right)+\left(y_1-y_2\right)\left({\dot{y}}_1-{\dot{y}}_2\right)+\left(z_1-z_2\right)\left({\dot{z}}_1-{\dot{z}}_2\right)}{\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2+{\left(z_1-z_2\right)}^2}}+{\dot{\rho }}_{\text{bias}}+{\dot{\rho }}_{\text{noise}}(17)$

ρ_noise and ${\dot{\rho }}_{\text{noise}}$ are calculated based on equations given in 6, 8, and 9. This study didn’t consider clock drift and aging in the measurement model due to the short simulation duration.

Estimation Model

In this study, an Extended Kalman Filter (EKF) is adopted as a common method used in real-time navigation. The EKF consists of a prediction and a correction step: in the former, predicted state and error covariance $\bar{P}$ are (Schutz et al., 2004):

$\dot{\mathbf{X}}=\mathit{F}\left(\mathbf{X},t\right),\mathbf{X}\left(t_{k-1}\right)={\widehat{\mathbf{X}}}_{k-1}(18)$

${\bar{\mathit{P}}}_k=\mathbf{\Phi }\left(t_k,t_{k-1}\right){\mathit{P}}_{k-1}{\mathbf{\Phi }}^T\left(t_k,t_{k-1}\right)+\mathit{Q}(19)$

where Φ(t_k, t_k−1) is the state transition matrix from t_k−1 to t_k and Q is the process noise matrix. The correction step is:

${\mathit{K}}_k={\bar{\mathit{P}}}_k{\tilde{\mathit{H}}}_k^T{\left[{\tilde{\mathit{H}}}_k{\bar{\mathit{P}}}_k{\tilde{\mathit{H}}}_k^T+{\mathit{W}}_k\right]}^{-1}(20)$

${\widehat{\mathbf{X}}}_k={\mathbf{X}}_k+{\mathit{K}}_k\left[{\mathbf{y}}_k-{\tilde{\mathit{H}}}_k{\mathbf{X}}_k\right](21)$

${\mathit{P}}_k=\left[\mathit{I}-{\mathit{K}}_k{\tilde{\mathit{H}}}_k\right]{\bar{\mathit{P}}}_k(22)$

where $\widehat{\mathbf{X}}$ is the state estimate, K is the Kalman gain, $\tilde{\mathit{H}}$ is the measurement sensitivity, P is the error covariance estimate, and W is the state noise compensation matrix.

In this study, the state noise compensation is introduced by Q which can be constructed for each S/C as follows (Hill and Born, 2008):

$Q_m=\left[\begin{array}{cccccc}\hfill \frac{\mathrm{\Delta }{t}^4{\sigma }_i^2}{3}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\mathrm{\Delta }{t}^3{\sigma }_i^2}{2}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{\mathrm{\Delta }{t}^4{\sigma }_i^2}{3}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\mathrm{\Delta }{t}^3{\sigma }_i^2}{2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\mathrm{\Delta }{t}^4{\sigma }_i^2}{3}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\mathrm{\Delta }{t}^3{\sigma }_i^2}{2}\hfill \\ \hfill \frac{\mathrm{\Delta }{t}^3{\sigma }_i^2}{2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \mathrm{\Delta }{t}^2{\sigma }_i^2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{\mathrm{\Delta }{t}^3{\sigma }_i^2}{2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \mathrm{\Delta }{t}^2{\sigma }_i^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\mathrm{\Delta }{t}^3{\sigma }_i^2}{2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \mathrm{\Delta }{t}^2{\sigma }_i^2\hfill \end{array}\right],m=\mathrm{1,2}(23)$

The measurement bias is expected to affect the navigation system performances: in general, this can either be neglected or estimated by including dynamic or measurement model parameters into the state vector. Another approach would be to assume its a priori estimate and associated covariance matrix are known. In this study, all three cases (neglected bias, estimated bias and considered bias) were investigated. In case of bias estimation, the estimated state vector must be expanded with a bias component, ρ_bias. This requires $\tilde{\mathit{H}}$ and Φ to expand as follows:

$\tilde{\mathit{H}}=\left[\begin{array}{ccccc}\hfill \frac{\partial \mathit{\rho }}{\partial {\mathbf{r}}_{\mathbf{1}}}\hfill & \hfill \frac{\partial \mathit{\rho }}{\partial {\mathbf{v}}_{\mathbf{1}}}\hfill & \hfill \frac{\partial \mathit{\rho }}{\partial {\mathbf{r}}_{\mathbf{2}}}\hfill & \hfill \frac{\partial \mathit{\rho }}{\partial {\mathbf{v}}_{\mathbf{2}}}\hfill & \hfill 1\hfill \end{array}\right]\mathbf{\Phi }\left(t_k,t_{k-1}\right)=\left[\begin{array}{cc}\hfill {\mathbf{\Phi }}_{\mathbf{Y}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right](24)$

In a similar way, the clock drift can be estimated by expanding $\tilde{\mathit{H}}$ and Φ with (t − t₀) representing the step size and 1 representing unchanged clock parameter during the time update process, respectively. However, expanding them into the state vector may affect the performances by reducing observability of the navigation system. That’s why this study also investigated the considered bias case by implementing a sequential consider filter (known as Consider-Kalman Filter (CKF), Schmidt-Kalman filter (SKF)). Here, the specific time invariant measurement bias case is studied assuming that consider parameter, b_k, is constant for all k and the bias covariance matrix, B_k, is time invariant. CKF is slightly different than EKF and requires to implement the following equation into the time update:

${\bar{\mathit{C}}}_k=\mathbf{\Phi }\left(t_k,t_{k-1}\right){\mathit{C}}_{k-1}(25)$

and changes in measurement update:

${\mathit{K}}_k=\left({\bar{\mathit{P}}}_k{\tilde{\mathit{H}}}_k^T+{\bar{\mathit{C}}}_k{\mathit{N}}_k^T\right){\mathbf{\Omega }}_k^{-1}(26)$

${\widehat{\mathbf{X}}}_k={\mathbf{X}}_k+{\mathit{K}}_k\left[{\mathbf{y}}_k-{\tilde{\mathit{H}}}_k{\mathbf{X}}_k-{\mathbf{N}}_k{\mathbf{b}}_0\right](27)$

${\mathit{P}}_k=\left[\mathit{I}-{\mathit{K}}_k{\tilde{\mathit{H}}}_k\right]{\bar{\mathit{P}}}_k-{\mathit{K}}_k{\mathbf{\Omega }}_k{\bar{\mathit{C}}}_k^T(28)$

${\mathit{C}}_k={\bar{\mathit{C}}}_k-{\mathit{K}}_k\left({\mathit{H}}_k{\bar{\mathit{C}}}_k+{\mathit{N}}_k{\mathbf{B}}_0\right)(29)$

where

${\mathbf{\Omega }}_k={\tilde{\mathit{H}}}_k{\bar{\mathit{P}}}_k{\tilde{\mathit{H}}}_k^T+{\mathit{N}}_k{\bar{\mathit{C}}}_k^T{\tilde{\mathit{H}}}_k^T+{\tilde{\mathit{H}}}_k{\bar{\mathit{C}}}_k{\mathit{N}}_k^T+{\mathit{N}}_k{\mathbf{B}}_0{\mathit{N}}_k^T+{\mathbf{W}}_k(30)$

where C_k is the cross-covariance matrix, B₀ is the bias covariance, b₀ a priori the measurement biases estimate, and N_k the measurement bias vector sensitivity matrix. Note that the CKF turns into EKF in case of zero bias.

Observability

The observability analysis is used to relate OD performance and observation data: in this study, the degree of the system observability is used to evaluate the estimation performances. For this purpose, the observability Gramian is used as follows:

$\mathit{N}=\sum _{k=1}^l\mathbf{\Phi }{\left(t_k,t_0\right)}^T{\tilde{\mathit{H}}}_k^T{\tilde{\mathit{H}}}_k\mathbf{\Phi }\left(t_k,t_0\right)(31)$

The observability can be assessed via Singular Value Decomposition (SVD) of the observability Gramian. In general, two metrics are used for this purpose: the condition number, which is the ratio of the largest singular value to the smallest one, and unobservability index, which is the reciprocal of the smallest local singular value. Most and least observable states can also be derived from unitary matrices via SVD.

Navigation Simulations

This section presents the orbit determination results for the selected mission scenario. The simulation setup is given first and results are given thereafter in the corresponding subsections.

Simulation Setup

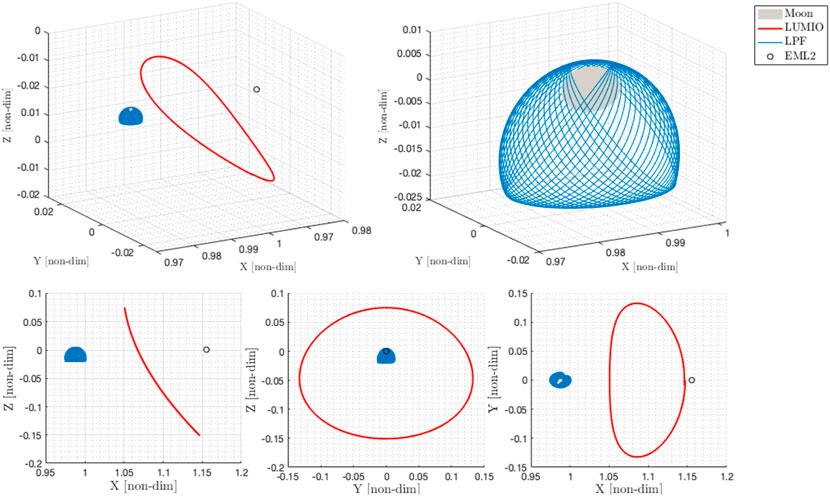
The selected mission scenario consists of two S/C, the LPF and LUMIO, at the Elliptical Lunar Frozen orbit and EML2 Halo orbit (Cervone et al., 2022; Scotti et al., 2022). The simulation duration is set to be 14 days. For the N-body orbital dynamics based analysis, the simulation start time and duration are set to be 18 April 2024, 21:00:00 UTC. The initial states of LPF expressed in MCI are listed in Table 1. LUMIO has a quasi-halo orbit at EML2 with a Jacobi energy of C_j = 3.09. For this study, due to the duration of the simulation, a similar southern Halo orbit (with the same Jacobi energy) has been used in CRTBP. The initial conditions can be found in Table 2 including the LPF converted states from MCI to the non-dimensional Earth-Moon barycentric frame. Corresponding trajectories of both S/C for 14 days can be seen in Figure 3.

TABLE 1

TABLE 1. LPF initial states expressed in MCI (Scotti et al., 2022).

TABLE 2

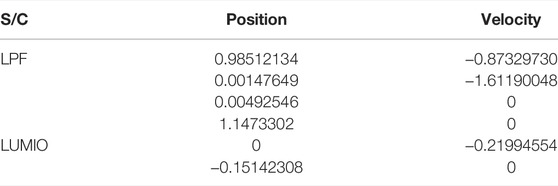
TABLE 2. Initial states used in the simulations (expressed in non-dimensional Earth-Moon barycentric frame).

FIGURE 3

FIGURE 3. Trajectories of both S/C for 14 days in the non-dimensional Earth-Moon barycentric frame.

In the mission scenario, two-different measurement error cases have been simulated which were representing the high-accuracy conventional pseudo-noise ranging method and the time-derived ranging method. Inter-satellite ranging is relaying on the communication system and the link budget for LUMIO is presented in Table 3. Inter-satellite range measurement parameters for both conventional and time-derived methods are given in Table 3. In this table, different from the existing link budget, the uplink data-rate and thus symbol duration is increased in consideration of a higher gain antenna configuration or higher transmit power. This is reasonable because the existing S/C configuration did not take into account the inter-satellite link based autonomous navigation (the existing configuration would give 2,700 m 1σ ranging accuracy which is not sufficient for the mission). This configuration would also fit similar small satellites. Based on these assumptions, range and range-rate measurement performances can be seen in Table 3.

TABLE 3

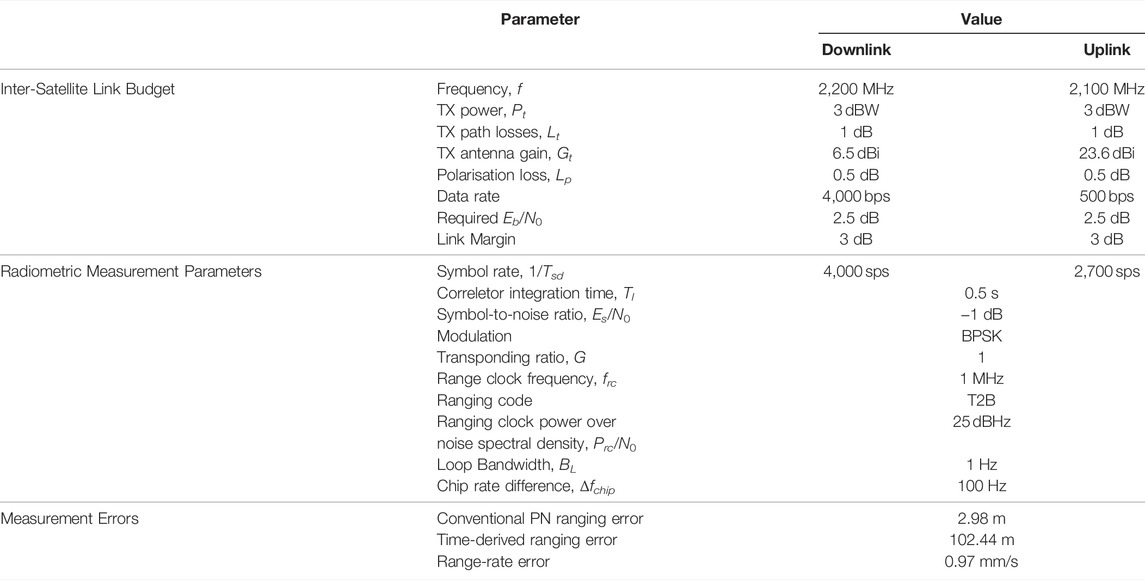
TABLE 3. Assumptions for LUMIO (the link budget is given based on the maximum inter-satellite distance (Speretta et al., 2022). Range measurement parameters are for conventional and time-derived methods and measurement errors are 1σ, two-way).

During the simulations, in each kth time step, the Root Mean Square (RMS) error for the Nth case of the Monte Carlo simulation has been calculated by using following

${RMSE}_k=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(x_{i,k}-{\widehat{x}}_{i,k}\right)}^2}(32)$

where x_i,k and ${\widehat{x}}_{i,k}$ are ith component of state vector and its estimate respectively. Parameters used in simulations can be found in Table 4. Regarding filter uncertainty and initial errors, a more detailed analysis has been done during the LUMIO Phase-A design study, previously. A ground-based tracking for 7 h between 18 April 2021 14:00:00 and 21:00:00 UTC from the Sardinia Deep Space Antenna based on range and range-rate measurements (measurement errors of 1 m range and 0.33 mm/s range-rate with a measurement bias of 2.5 m) would give 0.11 km and 0.95 cm/s position and velocity errors with 1σ uncertainty of 1.65  km and 4.7 cm/s, respectively (Estimation time Epoch: 18 April 2021 21:00:00 UTC with Batch-Least squares). Basically, this single tracking session estimation can be used to initialize the autonomous navigation system on-board. A ground-based state estimation has not been done for LPF. However, it is assumed that ground-based state estimation results for LPF are the same order of magnitude. In brief, initial parameters given in Table 4 are sensible.

TABLE 4

TABLE 4. Parameters used in simulations.

As already mentioned, OD requirement of the EML2 orbiter is 1 km for position and 1 cm/s for velocity, respectively. This has been taken as baseline goal for this study. The trajectory used in the study is also considered as a true reference, so there is no error in the dynamics. In addition to CRTBP dynamical models, the N-body orbital dynamics simulations are also performed. In such model (based on the JPL DE405 ephemeris model), Earth, Moon, and Sun are treated as point masses. Regarding the SRP model, SRP areas are set to 3 and 0.41  m², and reflectivities are set to 1.8 and 1.08, for LPF and LUMIO, respectively (Sirani, 2021; Scotti et al., 2022). The other settings for the high-fidelity analysis are the same.

Results

This section presents the performance of radiometric autonomous navigation for the selected mission scenario. The effects of measurement accuracy, precision, data type and navigation filter on the OD performance have been investigated.

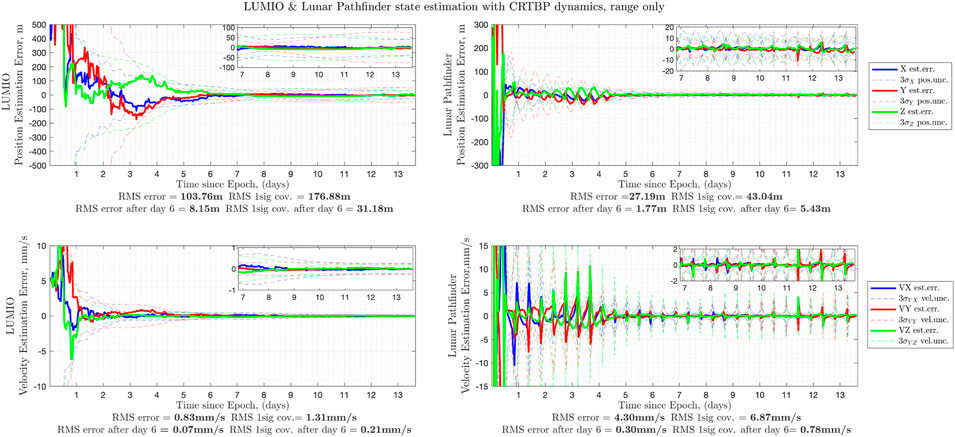
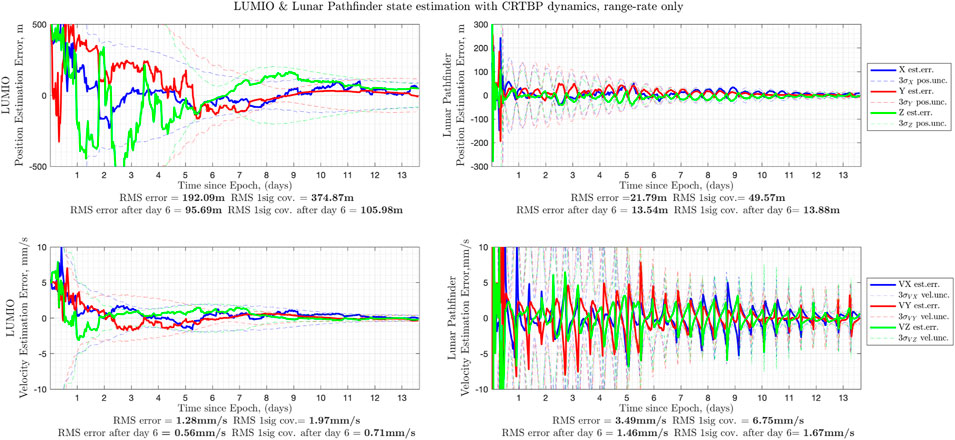
At first, the baseline case has been presented to show the autonomous navigation method works in the lunar vicinity. This case is based on the inter-satellite ranging derived from the conventional Pseudo-Noise (PN) method. Based on the settings given in the previous section, the navigation filter estimates the true states of LUMIO in the order of 100 m for position and 1 mm/s for velocity, respectively. LPF states are estimated within the order of 10 m position and 1 cm/s velocity, respectively. Estimation results can be seen in Figure 4 including RMS error and covariance values. As it can be seen, the filter converged after day 6. This is due to the fact that halo orbit has a period of 14 days and the half-orbit is sufficient to fit for the EML2 orbiter. Fluctuations in the LPF state estimation are related to the relative geometry between S/C. The position estimation converges when LPF approaches the periselene, and diverges when LPF approaches the aposelene. It is beneficial for LPF position estimation to be performed when the LPF is in the high velocity region. In case range-rate measurements are used, instead of range, the filter estimates are not improved (see Figure 5). Monte-Carlo simulation results can be seen in Table 5.

FIGURE 4

FIGURE 4. State estimation results based on range-only measurements.

FIGURE 5

FIGURE 5. State estimation results based on range-rate-only measurements.

TABLE 5

TABLE 5. 100-execution Monte-Carlo simulation results (values in parenthesis represents the results after day 6, and values are averaged over two S/C).

As part of the analysis, it was determined that the most observable states are in order: z₂, $x_1,y_2,x_2,{\dot{y}}_1,z_1,y_1,{\dot{x}}_1,{\dot{z}}_1,{\dot{y}}_2,{\dot{x}}_2,{\dot{z}}_2.$ (subindex 1 for LUMIO and 2 for LPF). Basically, the most and least observable states are the position and velocity components of LPF, respectively. The condition numbers are 2.521×10¹² and 4.324×10¹² for range-only and range-rate only case, respectively. This shows that s range-only system has a higher observability than a range-rate only system. However, the range-rate only case provides higher information to the filter on the least observable state: $\dot{z}$ via the lower unobservability index (0.5829 for range-rate only, and 4.595×10³ for range-only). The range-only system also converges faster than the range-rate only system. Overall, range measurements provide better state estimation due to relative geometry and lower measurement error. For this reason, the coming part of the paper continues with range-only measurements.

The observation effectiveness for the mission scenario has also been investigated. This introduces how much information each measurement provides to the filter. In this case, observation effectiveness on the positional components are given in Figure 6. As it can be seen, effectiveness is increasing as measurements provide valuable information to the filter, e.g., for almost early 6 days to the position estimation of LUMIO states. However, fluctuations can be seen for the LPF plot which is related to the relative geometry between S/C and after a certain time the effectiveness doesn’t increase anymore. Basically, optimal tracking windows can be planned based on these peak and dip periods.

FIGURE 6

FIGURE 6. Observation effectiveness for both S/C positional states.

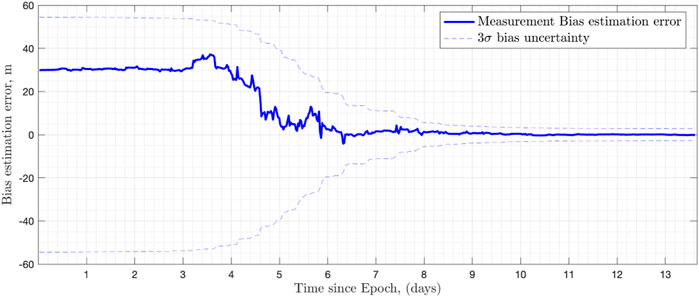
In the previous case, the measurement bias has not been included into the simulation to show directly the relation between the data types. However, it is well known, measurement bias affects the navigation system performances and it is important to know how they degrade with a systematic bias. For this purpose, a measurement bias of 10 m has been implemented and the same scenario has been re-run with three different cases: considered-bias, estimated-bias, and neglected-bias. In the estimated bias case, estimated state-vector has been expanded with a bias term. As it can be seen from Figure 7, measurement bias can be estimated along with dynamical states. For all three cases, Monte-Carlo results are visible in Figure 8. Basically, considered-bias and estimated-bias provides similar performances. However, neglecting the bias increases the state estimation errors.

FIGURE 7

FIGURE 7. Bias estimation error.

FIGURE 8

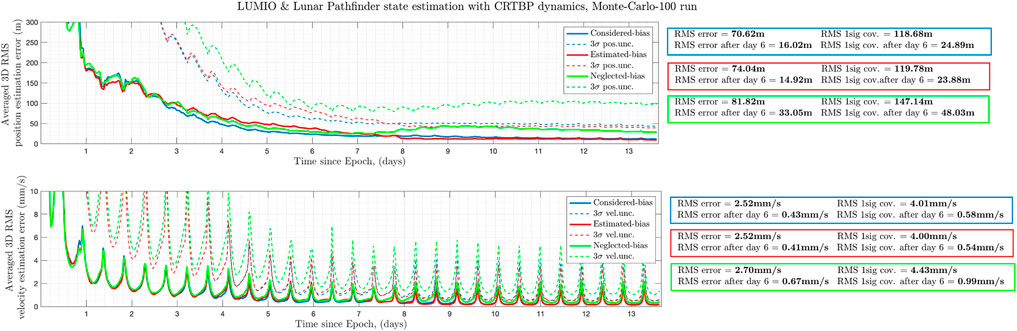
FIGURE 8. Comparison of three different approaches for bias (considered-bias, estimated-bias, and neglected-bias). Values are averaged over two S/C.

In addition to the conventional PN ranging, time-derived ranging based simulations have been performed. As already mentioned, modulating the ranging signal reduces the power available for telemetry and thus supported data rates. Considering the link budget, it is not quite easy to perform ranging sessions and telemetry sessions during the same time window. However, time-derived ranging uses telemetry/telecommand signals to estimate the distance between S/C without using any additional hardware. This ranging method requires only insertion of the S/C clock states into the telemetry and telecommand data frames. Basically, four successive timestamps (reception and transmission time for both S/C) are sufficient to calculate the signal round trip light time and time offset. In addition, this method provides a ranging solution along with data-transfer between S/C which means there is no need to plan additional ranging sessions and can be used anytime via any type of data transfer between S/C. However, this method is not as accurate and this would affect the autonomous navigation performances. In brief, this method would simplify the communication system design and reduce the on-board power required, making this method a perfect candidate for this mission. The time-derived ranging method simulation results are given in Figure 9. As it can be noticed, the filter can estimates the true states of LUMIO in the order of 140 m for position and 1 mm/s velocity, respectively. Errors are almost 4 times higher than the conventional ranging method in simulation. However, this still meets the mission navigation requirements (1 km). This shows, from the navigation performance perspective, that collecting measurements at different time intervals (and thus orbit geometry) has more importance than the absolute measurement errors. As a side note, even in the high measurement error case (time-derived ranging), the system is observable enough to estimate the systematic bias. This only requires more time than in the PN case.

FIGURE 9

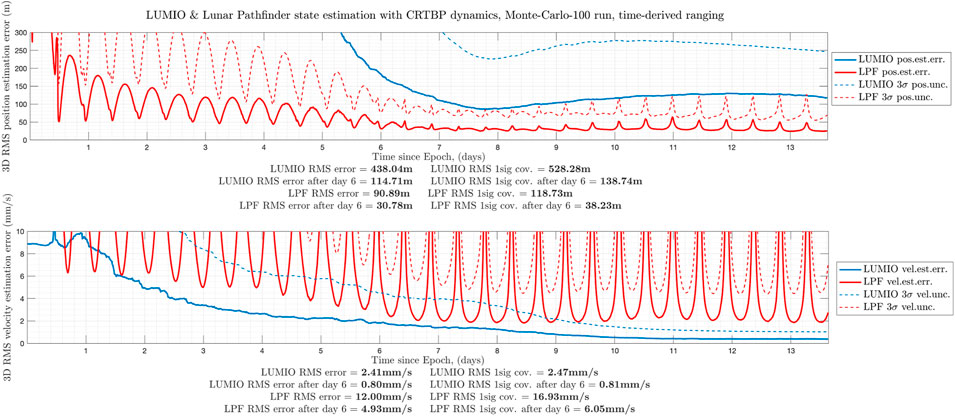
FIGURE 9. State estimation results based on the time-derived ranging method (Monte-Carlo simulation 100-execution.

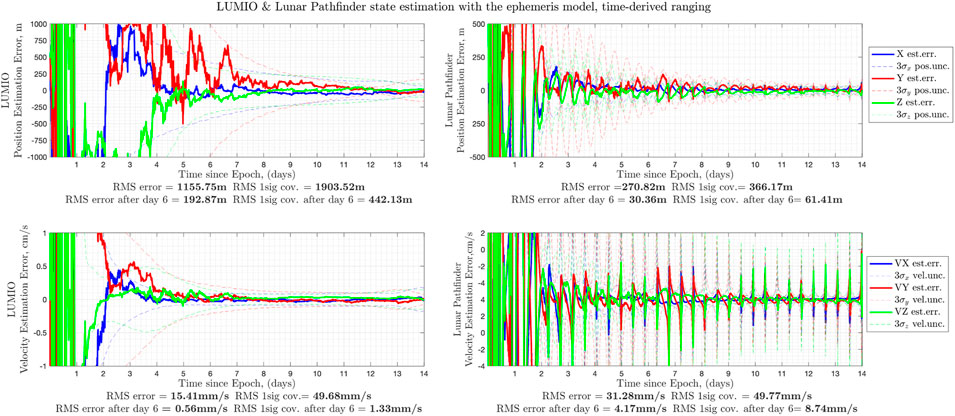
In the last simulation of the paper, the ephemeris model based simulation results are given. This shows the effects of additional perturbations in the system on the navigation performances. Based on the ephemeris model (including SRP and the gravitational acceleration due to Sun), the estimation results are shown in Figure 10: position and velocity estimation uncertainty increased up to three times in this case with respect to the CRTBP case. However, the LUMIO estimation errors are lower than 500 m 1σ for position and 2 mm/s for velocity, respectively, and for LPF, 1σ uncertainties are less than 100 m for position and 1 cm/s velocity. This would meet the OD requirements of 1 km position and 1 cm/s velocity, respectively.

FIGURE 10

FIGURE 10. State estimation results based on the ephemeris model with time-derived ranging method.

Conclusion

This study showed that the LiAISON orbit determination technique could be a possible navigation approach for a proposed mission, LUMIO, based on the existing inter-satellite link between LPF and the LUMIO CubeSat without using any ground based measurements. Simulation results show that the navigation filter estimates the true states of LUMIO in the order of 500 m for position, and 2 mm/s for velocity, respectively. LPF states can be estimated in the order of 100 m for position and 1 cm/s velocity, respectively. Considering the range-only case with 1σ error of 2.98 m provides better states estimation than the range-rate only case with 1σ measurement error of 0.97 mm/s. The observability analysis showed that the system is observable and found that LPF’s position and velocity components are the most and the least observable states, respectively. The best tracking windows are also presented by means of the observation effectiveness analysis. It has been showed that bias would affect the performances, and it can be estimated along with the dynamical states, thanks to the high observability. In addition, the time-derived ranging method provides sufficient information to the filter in order to meet the navigation requirements. In these simulations, only the initial phase of the operative orbit has been considered. Basically, after one orbital period, it is quite expected to improve the estimation due to relative position change between S/C. This would bring additional information to the filter and decrease the uncertainty. This study considered only the first 14 days of the mission. Even though this is sufficient to see the expected performances, further work would be needed to investigate what would happen for the full operative mission lifetime (1-year). This study also didn’t consider the dynamic model errors and the effects of clock drift on the performances and they are considered as topics for future research.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

CCSDS (2014). Pseudo-noise (Pn) Ranging Systems.

Google Scholar

Cervone, A., Topputo, F., Speretta, S., Menicucci, A., Turan, E., and Di Lizia, P. (2022). LUMIO: A CubeSat for Observing and Characterizing Micro-meteoroid Impacts on the Lunar Far Side. Acta Astronaut. 195, 309–317. doi:10.1016/j.actaastro.2022.03.032

CrossRef Full Text | Google Scholar

Cheetham, B. (2020). “Cislunar Autonomous Positioning System Technology Operations and Navigation Experiment (CAPSTONE),” in ASCEND 2020 (American Institute of Aeronautics and Astronautics). doi:10.2514/6.2020-4140

CrossRef Full Text | Google Scholar

Curtis, H. (2020). Orbital Mechanics for Engineering Students. Oxford: Elsevier.

Google Scholar

DSN (2018). DSN Telecommunications Link Design Handbook. Tech. rep. Pasadena, CA: Jet Propulsion Laboratory California Institute of Technology.

Google Scholar

Fujimoto, K., Stacey, N., and Turner, J. M. (2016). “Stereoscopic Image Velocimetry as a Measurement Type for Autonomous Asteroid Gravimetry,” in AIAA/AAS Astrodynamics Specialist Conference (American Institute of Aeronautics and Astronautics). doi:10.2514/6.2016-5566

CrossRef Full Text | Google Scholar

Haapala, A. F. (2010). Trajectory Design Using Periapse Maps and Invariant Manifolds. Master’s thesis. West Lafayette, IN: Purdue University.

Google Scholar

Hill, A. K. (2007). Autonomous Navigation in Libration Point Orbits. Ph.D. thesis. Boulder, CO: University of Colorado.

Google Scholar

Hill, K. A., and Born, G. H. (2008). Autonomous Orbit Determination from Lunar Halo Orbits Using Crosslink Range. J. Spacecr. Rockets 45, 548–553. doi:10.2514/1.32316

CrossRef Full Text | Google Scholar

Hill, K., and Born, G. H. (2007). Autonomous Interplanetary Orbit Determination Using Satellite-To-Satellite Tracking. J. Guid. Control, Dyn. 30, 679–686. doi:10.2514/1.24574

CrossRef Full Text | Google Scholar

Leonard, J., Jones, B., Villalba, E., and Born, G. (2012). “Absolute Orbit Determination and Gravity Field Recovery for 433 Eros Using Satellite-To-Satellite Tracking,” in AIAA/AAS Astrodynamics Specialist Conference (American Institute of Aeronautics and Astronautics). doi:10.2514/6.2012-4877

CrossRef Full Text | Google Scholar

Leonard, J. M. (2015). Supporting Crewed Missions Using LiAISON Navigation in the Earth-Moon System. Ph.D. thesis. Boulder, CO: University of Colorado.

Google Scholar

Montenbruck, O., and Gill, E. (2000). Satellite Orbits. Berlin Heidelberg: Springer. doi:10.1007/978-3-642-58351-3

CrossRef Full Text | Google Scholar

Schutz, B., Tapley, B., and Born, G. H. (2004). Statistical Orbit Determination. Elsevier.

Google Scholar

Scotti, M., Botteron, C., Rico, M., Basile, F., Massaras, V., Kieniewicz, B., et al. (2022). “Navimoon – Ultra-high Sensitivity Gnss Receiver for Lunar Navigation,” in NAVITEC 2022. 1.

Google Scholar

Sirani, S. (2021). LUMIO Orbit Refinement in High Fidelity Model. Master’s thesis. Milano, Italy: Politecnico di Milano.

Google Scholar

Speretta, S., Cervone, A., Menicucci, A., Turan, E., Bertels, E., Bosman, B., et al. (2021). Designing the Radio Link for a Lunar Cubesat: the Lumio Case. IAC 2021, 1.

Google Scholar

Speretta, S., Topputo, F., Biggs, J., Lizia, P. D., Massari, M., Mani, K., et al. (2018). “LUMIO: Achieving Autonomous Operations for Lunar Exploration with a CubeSat,” in 2018 SpaceOps Conference (American Institute of Aeronautics and Astronautics). doi:10.2514/6.2018-2599

CrossRef Full Text | Google Scholar

Speretta, S., Turan, E., Cervone, A., Menicucci, A., Topputo, F., Franzese, V., et al. (2022). “Lumio: A Cubesat to Monitor Micro-meteroid Impacts on the Lunar Farside,” in 2022 IEEE Aerospace Conference, 1–8.

Google Scholar

Topputo, F., Merisio, G., Giordano, G., Franzese, V., Cervone, A., Speretta, S., et al. (2021). “Current Status of Lumio Mission: Characterizing Lunar Meteoroid Impacts with a Cubesat,” in 72th International Astronautical Congress. 1.

Google Scholar

Turan, E., Speretta, S., and Gill, E. (2022). Autonomous Navigation for Deep Space Small Satellites: Scientific and Technological Advances. Acta Astronaut. 193, 56–74. doi:10.1016/j.actaastro.2021.12.030

CrossRef Full Text | Google Scholar

Turan, E., Speretta, S., and Gill, E. (2022). “Autonomous Navigation Performance of Cislunar Orbits Considering High Crosslink Measurement Errors,” in 2022 IEEE Aerospace Conference, 1–11.

Google Scholar

Wang, W., Shu, L., Liu, J., and Gao, Y. (2019). Joint Navigation Performance of Distant Retrograde Orbits and Cislunar Orbits via LiAISON Considering Dynamic and Clock Model Errors. Navigation 66, 781–802. doi:10.1002/navi.340

CrossRef Full Text | Google Scholar