Historical Contingency in Microbial Resilience to Hydrologic Perturbations

Development of reliable biogeochemical models requires a mechanistic consideration of microbial interactions with hydrology. Microbial response to and its recovery after hydrologic perturbations (i.e., resilience) is a critical component to understand in this regard, but generally difficult to predict because the impacts of future events can be dependent on the history of perturbations (i.e., historical contingency). Fundamental issues underlying this phenomenon include how microbial resilience to hydrologic perturbations is influenced by historical contingency and how their relationships vary depending on the characteristics of microbial functions. To answer these questions, we considered a simple microbial community composed of two species that redundantly consume a common substrate but specialize in producing distinct products and developed a continuous flow reactor model where the two species grow with trade-offs along the flow rate. Simulations of this model revealed that (1) the history of hydrologic perturbations can lead to the shifts in microbial populations, which consequently affect the community's functional dynamics, and (2) while historical contingency in resilience was consistently predicted for all microbial functions, it was more pronounced for specialized functions, compared to the redundant function. As a signature of historical contingency, our model also predicted the emergence of hysteresis in the transitions across conditions, a critical aspect that can affect transient formation of intermediate compounds in biogeochemistry. This work presents microbial growth traits and their functional redundancy or specialization as fundamental factors that control historical contingencies in resilience.

Introduction

Interactions between hydrologic and microbial processes control the cycling of dissolved organic matter and other chemical substrates (Covino et al., 2018) in biogeochemical hotspots such as river corridors (Singer et al., 2016; Graham et al., 2019). Predictive biogeochemical modeling therefore necessitates development of reliable models of the dynamics of microbial populations and their interactions with hydrology. For this purpose, it is important to understand how hydrologic inputs alter microbial diversity, abundances, interactions, spatial organization, and functions. While specific microbial phenotypes of interest are assumed to be definable based on known gene functions and environmental conditions (Jansson and Hofmockel, 2018), their dynamics often exhibit non-intuitive, complex dynamics under the influence of the history of perturbations, a phenomenon known as historical contingency (also termed ecological memory or legacy effect) (Fukami, 2015; Ogle et al., 2015; Vass and Langenheder, 2017). Despite its critical impact, we do not know much about how microbial functional responses to hydrologic perturbations are controlled by historical contingencies and how to account for these effects in microbial models (Hawkes and Keitt, 2015).

Historical contingencies of environmental microbial systems have been frequently observed in diverse contexts (Bouskill et al., 2013; Peralta et al., 2013, 2014). For example, microbial enzyme activity and respiration in soil that increased with moisture were shown to be constrained by previous climate such as precipitation history (Averill et al., 2016; Hawkes et al., 2017). As another example, soil systems showed an enhanced protection of plants against a pathogen through the induced presence of disease-suppressive microbes by pre-exposure to the same pathogen in the past, just like an adaptive human immune system (Raaijmakers and Mazzola, 2016). In a recent study, it was shown that different land use significantly affected the transfer of soil organic carbon and bacterial diversity and functions in surface water runoff (Le et al., 2020). Historical contingencies related to hydrologic perturbations were reported by Goldman et al. (2017) where the biogeochemical response (i.e., CO₂ flux) of parafluvial hyporheic zone sediments to re-inundation was contingent on hydrologic history. Goldman et al. (2017) interpreted lower and higher CO₂ fluxes in sediment samples as being caused by relative dominance of fungal and bacterial species, respectively. All examples here indicate the importance of accounting for the role of microbial species controlling historical contingencies for predictive biogeochemical modeling. While a current trend is to increasingly incorporate microbial physiology and processes into biogeochemical models (Wieder et al., 2013; Wang et al., 2017), accounting for historical contingencies still remains a challenge due to the lack of understanding of controlling aspects in microbial systems, severely limiting our ability to reliably predict biogeochemical function (Widder et al., 2016).

As a critical step toward addressing this challenge, we designed an in silico study to examine historical effects on microbial responses to hydrological perturbations. Inspired by the field observations of Goldman et al. (2017) that linked biogeochemical historical contingency with the shifts in microbial populations in a community, we formulated a mathematical model of a microbial consortium composed of two competing microbial species growing with different growth traits in a continuous flow reactor. In the model, one species grows more effectively in lower flow rates and the other species in higher flow conditions so that they hold microbial growth traits as observed in Goldman et al. (2017). We used this model to test the hypothesis that trade-offs in individual growth strategies underlie historical contingencies observed at the community level

In this work, we explored how hydrologic history and population dynamics lead to historical contingency of resilience, whereby microbial responses to future perturbations are dependent on past perturbations (Holling, 1996; Allison and Martiny, 2008; Shade et al., 2012; Song et al., 2015; Martiny et al., 2017). Our model revealed that historical contingencies in resilience can be more pronounced for specialized functions associated with individual species, compared to community functions to which member species commonly contribute, indicating the distribution of growth traits among member species plays a controlling role. The model also predicted the sophisticated dynamics of microbial communities including hysteresis (as an outcome of historical contingency), and endogenous dynamics (i.e., the continued changes in microbial populations in the absence of environmental variation). Beyond highlighting the importance of representing the dynamics of individual species for predictive microbial community modeling, this work provides a specific model structure for parameterization in the context of resilience and historical contingency toward predictive ecological and biogeochemical modeling.

Methods

Design of the Study

Before providing the details on model development and specific metrics used for quantifying the effect of hydrologic perturbations on microbial function in the context of historical contingencies, we here provide a brief overview of the design of our study. Our major goal is to examine how the history of hydrologic perturbations will drive the composition and functions in microbial communities depending on the microbial growth traits and their trade-offs; how this effect will be shown differently for redundant vs. specialized functions among member species. For this purpose, we formulate a mathematical model of a continuous-flow stirred-tank (i.e., well-mixed) reactor where two species competitively grow on the shared nutrient (S) and produce distinct products (P₁ by species 1 and P₂ by species 2). This setting enables assessing the impact of past hydrologic perturbations on microbial functions (i.e., historical contingencies of resilience) based on the following two categories: (1) consumption of S, which represents a function commonly performed among two species and (2) production of P₁ and P₂, which exemplify unshared functions uniquely associated with individual species. To account for growth traits observed in Goldman et al. (2017), we design the kinetics of microbial growth such that species 1 grows faster in lower flow rates, while species 2 grows faster in higher flow rates. This allows us to examine the effect of the trade-off in growth along the flow rate as a key mechanism for the resilience of community functions, particularly those redundantly shared among member species (i.e., the consumption of S). Using the resulting model, we assess resilience based the time-to-recovery after perturbations. For generalizable analysis across scales, we provide the final model equations in dimensionless form. In the following, we begin model description with theories for the co-existence of competing microbial species, which is a pre-requisite in building a microbial community model.

Mechanism for the Coexistence of Competing Species

Implementation of species co-existence in a community model requires a special consideration because simple kinetics will end up with the dominance by a fast grower due to the competitive exclusion principle, a classical ecological theory asserting that only one species can survive the competition (Hardin, 1960). As one of the simplest mechanisms enabling the coexistence of competing organisms in a continuous flow reactor setting considered in this work, we chose density-dependent growth (including flocculation or crowding effect) (De Leenheer et al., 2006; Haegeman and Rapaport, 2008), while several other plausible mechanisms are also available, including: spatial heterogeneity (Stephanopoulos and Fredrickson, 1979), externally imposed temporal fluctuations (Stephanopoulos et al., 1979; Smith, 1981), endogenously induced temporal fluctuations through a specific type of interactions (Hsu et al., 1978; Butler et al., 1983), dormancy (Lennon and Jones, 2011), nutrient storage (Revilla and Weissing, 2008), exchange of metabolic by-products (Hesseler et al., 2006), and time delay in the nutrient uptake and growth (Freedman et al., 1989). Density-dependent growth is a reasonable representation of the growth of microorganisms in natural environments that often form biofilms in sediments and soils where the growth of inside species is limited due to lower availability of nutrients along the depth, indicating that the overall specific growth can be suppressed by crowding as the density increases (Roughgarden, 1971). Even in the case where no biofilm is formed, the density-dependent growth mechanism is still valid in situations where species do not effectively distribute in space because cells surrounded by others will have the same difficulty in accessing nutrients as the local population density increases.

Microbial Growth Kinetics

Based on the density-dependent growth mechanism, we modeled specific growth rates of species i (μ_i), which are split into nutrient- and density-dependent terms, i.e., ${\mu }_i^{\prime }(s)$ and ρ_i(x₁, x₂) as follows:

$\begin{array}{ll}{\mu }_i(s,x_1,x_2)={\mu }_i^{\prime }(s){\rho }_i(x_1,x_2),i=1,2& (1)\end{array}$

where

$\begin{array}{ll}{\mu }_i^{\prime }(s)=\frac{k_{i}s}{K_i+s}& (2)\end{array}$

and

$\begin{array}{ll}{\rho }_i(x_1,x_2)=\{\begin{array}{l}\exp \left(-a{x}_1\right)\left(1-\frac{x_1+x_2}{C}\right),i=1\hfill \\ 1-\frac{x_1+x_2}{C},i=2\hfill \end{array}& (3)\end{array}$

As shown in Equation (3), we imposed environmental constraints (such as limited space and resources) on both organisms to limit the total population of the community below a given carrying capacity (C). Species 1 was chosen to have faster growth kinetics in this work, i.e., ${\mu }_1^{\prime }(s)>{\mu }_2^{\prime }(s)$. Therefore, we additionally considered the exponential term in ρ₁(x₁, x₂) so that μ₁ is suppressed as the population density increases because otherwise co-existence becomes impossible due to the dominance of species 1.

Reaction Stoichiometries and Mass Balances

We considered two reactions (R₁ and R₂), respectively driven by species 1 and 2 (X₁ and X₂) such that they compete for the shared substrate (S) to produce distinct products (P₁ and P₂):

$\begin{array}{ll}\begin{array}{c}{\text{R}}_1:Y_{S_1}\text{S}\to {\text{X}}_1+Y_{P_1}{\text{P}}_1\\ {\text{R}}_2:Y_{S_2}\text{S}\to {\text{X}}_2+Y_{P_2}{\text{P}}_2\end{array}& (4)\end{array}$

where stoichiometric coefficients Y_Si and Y_Pi(i = 1,2) denote how many quantities of S and P_i are consumed or produced whenever a unit mass of biomass is produced through R_i. Specific values of Y_Si and Y_Pi depend on the chemical formulae of S, X_i and P_i, as well as their mass units (i.e., mole or gram). For simplicity, we set all stoichiometric coefficients with unity values i.e.,

$\begin{array}{ll}\begin{array}{c}{\text{R}}_1:\text{S}\to {\text{X}}_1+{\text{P}}_1\\ {\text{R}}_2:\text{S}\to {\text{X}}_2+{\text{P}}_2\end{array}& (5)\end{array}$

Note that the resulting reaction stoichiometries above equate the production rates of P₁ and P₂ with the growth rates of X₁ and X₂, respectively.

To mimic microbial growth in river corridor sediments, we considered a continuous-flow well-mixed reactor where the substrate is fed through water flow into the sediment as illustrated in Figure 1A. A continuous flow reactor configuration has been frequently used in the literature as a model system for addressing ecological questions [e.g., Kraft et al. (2014)] and provides advantages over batch cultures in studying mixed populations (Veldkamp and Jannasch, 1972). Under well-mixed conditions, dynamic mass balances for microbial populations, substrate, and products can be written as follows:

$\begin{array}{ll}\frac{d{x}_i}{dt}={\mu }_i(s,x_1,x_2)x_i-k_d{x}_i,i=1,2& (6)\end{array}$

$\begin{array}{ll}\frac{ds}{dt}=-{\mu }_1(s,x_1,x_2)x_1-{\mu }_2(s,x_1,x_2)x_2+D(s_{in}-s)& (7)\end{array}$

$\begin{array}{ll}\frac{d{p}_i}{dt}={\mu }_i(s,x_1,x_2)x_i-D{p}_i,i=1,2& (8)\end{array}$

where x_i denote the population size of X_i, s and p_i are the concentrations of S and P_i, t is the time, μ_i denotes the specific growth rate (1/time) of X_i (mass/volume), k_d is the specific death rate (1/time) fixed as constant, D is the dilution rate (1/time), and the subscript in represents the quantities associated with the inlet feed flow, respectively. As implied by the same notation of k_d for species 1 and 2, we assumed no difference in the specific death rate between the two organisms.

FIGURE 1

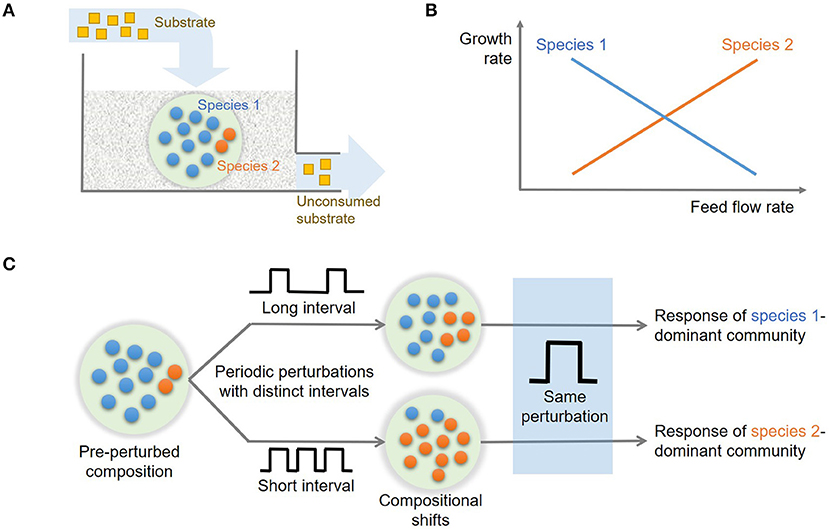
Figure 1. Conceptual model to investigate historical contingencies in microbial response to hydrologic perturbations: (A) a continuous flow reactor configuration for competitive growth of two microbial species on a shared substrate in a homogeneous environment, (B) trade-offs in microbial growth along the flow rate gradient, and (C) expected compositional changes driven by the history of hydrologic perturbations.

Non-dimensionalization

For scale independence, we non-dimensionalized the equations as follows:

$\begin{array}{l}\frac{dx}{d\tau }=f\left(x,y,z\right)x-\lambda x\\ \frac{dy}{d\tau }=g\left(x,y,z\right)y-\lambda y& (9)\end{array}$

$\begin{array}{ll}\frac{dz}{d\tau }=-f\left(x,y,z\right)x-g\left(x,y,z\right)y+\delta \left(1-z\right)& (10)\end{array}$

$\begin{array}{ll}\frac{dp}{d\tau }=f\left(x,y,z\right)x-\delta p& (11)\end{array}$

$\begin{array}{ll}\frac{dq}{d\tau }=g\left(x,y,z\right)y-\delta q& (12)\end{array}$

where

$\begin{array}{ll}\begin{array}{c}f\left(x,y,z\right)=\frac{k_{x}z}{K_x+z}{e}^{-\alpha x}\left(1-\frac{x+y}{\kappa }\right)\hfill \\ g\left(x,y,z\right)=\frac{k_{y}z}{K_y+z}\left(1-\frac{x+y}{\kappa }\right)\hfill \end{array}& (13)\end{array}$

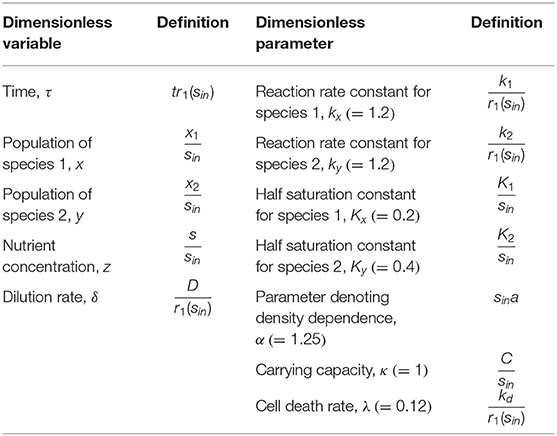
Definitions of dimensionless variables and parameters used in the above equations were provided in Table 1. The values of kinetic parameters k_x, K_x, k_y, and K_y in Equation (13) were derived from the flocculation model by Haegeman and Rapaport (2008). Nutrient concentration in the feed flow in the last term of Equation (10) was set to 1 due to the normalization with respect to itself.

TABLE 1

Table 1. Definitions of dimensionless variables and parameters contained in the model.

Metrics for Resilience

We imposed hydrologic perturbation by fluctuating the dilution rate following a rectangle-shaped wave. Based on the concept of engineering resilience (Holling, 1996; Song et al., 2015), we used “time-to-recovery” as a measure of resilience, i.e., how quickly a chosen system variable or function recovers the pre-perturbed state, while other metrics could also be considered (Hillebrand et al., 2018). Key variables and functions of interest in this work include: microbial and chemical compositions (i.e., x, y, and z) and their associated functions such as consumption rate of z (i.e., r_z ≡ −fx − gy) and production rates of p (i.e., r_p ≡ fx) and q (i.e., r_q ≡ gy). These rates represent redundant (r_z) and unique functions (r_p and r_q) among member species.

In quantifying the resilience of a chosen variable or function among those mentioned above, we ensured the system to be exposed to a cyclic perturbation of dilution rate for a sufficient time period; when the system reached a sustained oscillation, we stopped imposing perturbation and started to measure time-to-recovery. We used two different metrics for the time-to-recovery as defined below:

• Hitting time is when the variable or function hits the pre-perturbed level for the first time. We measured this as the first time when the variable hits an upper or lower boundary of the band around the pre-perturbed level. The bandwidth was defined by the 2 and 5% values above and below the pre-perturbed level.

• Settling time is the time required for the variable or function to finally reach and remain within a given band of the pre-perturbed level. This quantity needs to be distinguished from hitting time when the system recovery takes place in an oscillatory way so that it may touch the boundaries of the band more than one time. In this case, the first and last times that the nutrient profile crosses the boundaries of the band correspond to hitting and settling times, respectively. If there are no oscillations during the post-perturbation period, hitting and settling times are identical. In measuring the settling time, we considered 2 and 5% bandwidths as defined above.

Results

Using a model of microbial community growing in a homogenous continuous flow reactor (Figure 1A), we test the following hypotheses: (H1) distinct growth traits and their trade-offs along the flow rate gradient (Figure 1B) leads to the shifts in the community composition subject to hydrologic perturbations with different intervals, (H2) the resulting microbial communities dominated by species 1 or 2 will show distinct responses to future perturbations (Figure 1C), and (H3) the extent of historical contingencies in microbial functions depend on their redundancy or specialization, i.e., whether a given functions is performed in common among multiple species or uniquely associated with specific organisms.

Trade-Off in Microbial Growth Traits in Steady State

We examined how state variables including species abundances (x and y) and substrate concentration (z) vary along the dilution rate (δ) (Figure 2A), which are dimensionless variables of x₁, x₂, s, and D (Methods). The values of x, y, and z in Figure 2A denote their steady-state values that change as a function of δ. For very low dilution rates (i.e., δ ≤ 0.05), species 2 (y) could not survive the competition with species 1 (x). In this regime, x linearly increased with δ as the supply of substrate accordingly increased. For higher dilution rates above the threshold, two species coexisted with the opposite dependence of their growth rates on the dilution rate, i.e., x decreased with δ, while y increased, so that their population curves intersect at δ ≈ 0.1. This shows that species 1 is more competitive in lower flow rate conditions, while species 2 can grow faster in the higher flow rate regime, confirming that the parameter setting in our model leads to the expected microbial growth traits as indicated in Methods (also see Figure 1B)

FIGURE 2

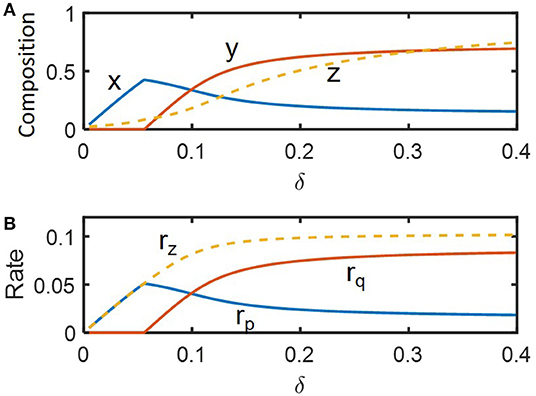
Figure 2. The changes in key variables and functions in steady state as a function of flow rate (δ): (A) species abundances (x and y) and substrate concentration (z), and (B) consumption rate of the shared substrate (r_z) and production rates of distinct products (r_p and r_q).

Similar trends were observed for community functions such as consumption rate of the shared substrate (r_z) and production rates of distinct products (r_p and r_q) (Figure 2B). As the conversion rate of z (r_z) includes the contribution from both species that competitively consume the shared substrate, the function r_z showed milder changes over δ ≥ 0.05, compared to specialized functions (r_p and r_q) that are uniquely associated with only one species. As will be discussed more in the follow-up section, the trade-off in growth traits of the two species provides a mechanistic basis for enhanced resilience of the community. We used the steady state profiles in Figure 2 as a guide map to identify distinct operating zones where the system shows qualitatively different dynamics.

Compositional and Functional Responses to Hydrologic Perturbations

We performed dynamic simulations to examine how microbial communities respond to hydrologic perturbations. Disturbances were imposed by periodically changing the dilution rate (δ) between pre-chosen nominal (i.e., pre-perturbed) (δ_norm = 0.09) and inundated conditions (0.19) (following a rectangular shape in time). For illustration, we simulated compositional and functional responses to the two specific cycles of perturbations with the inundation intervals of 3.5 and 9.5 imposed over 0 ≤ τ ≤ 200 (Figure 3). Among the three state variables denoting microbial and chemical compositions (x, y, and z), z showed the most significant fluctuation in time because the substrate was being fed into the reactor while microorganisms were not. As species 1 is a faster grower at the nominal flow rate (δ = 0.09) and species 2 grows faster following inundation (δ = 0.19) (Figure 2), the abundances of species 1 and 2, respectively decreased and increased under periodic inundation (Figures 3A,B). That is, in the case of the shorter inundation interval (i.e., 3.5), species dominance was switched over from x to y (Figure 3A), while the original composition was recovered after periodic perturbation was stopped. This result supported our hypothesis on the effect of hydrological perturbations on microbial populations (H1). Similar trends were observed for functional responses including production rates of products (r_p and r_q) and consumption rate of the shared substrate (r_z). Temporal fluctuations of r_p and r_q were more significant than those of their populations (x and y) because r_p and r_q are functions of substrate concentration as well as species abundances.

FIGURE 3

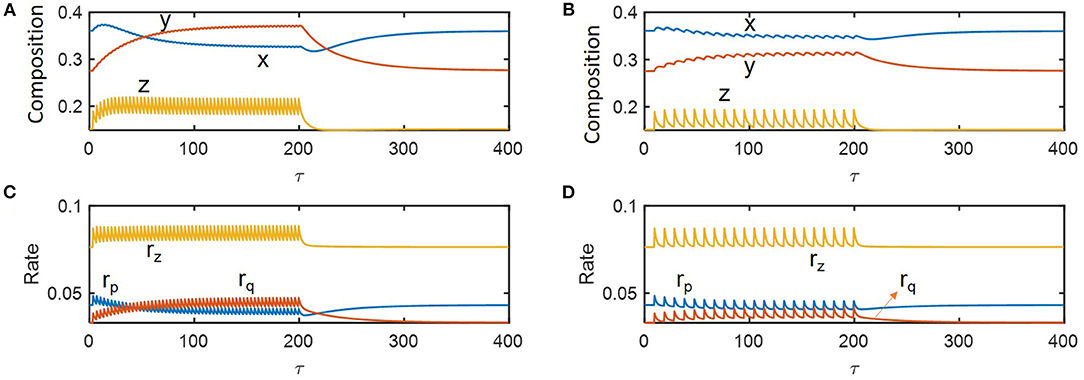
Figure 3. Microbial response to periodic change of the inlet flow (δ) between 0.09 and 0.19: (A,C) perturbation interval of 3.5, and (B,D) perturbation interval of 9.5. The periodic perturbation was imposed over 0 ≤ τ ≤ 200 and released afterwards.

Even in this simple simulation setting, we found several interesting dynamics: (1) species 1 (x) showed inverse responses (i.e., the initial change in its abundance in a direction opposite to the final outcome) when periodic inundation was stopped at τ = 200, while such over- or under-shooting was suppressed for species 2 and substrate concentration; (2) the deviation of r_z during periodic perturbation was the least significant among others (when evaluated based on the minimum values of fluctuation); and (3) the recovery of r_z was the fastest among others. The result (1) indicates that species 1 with relatively fast dynamics and high momentum can show complex dynamics (such as inverse response). The results (2) and (3) partially supported the hypotheses H2 and H3 by showing the highest resilience for r_z, which may be ascribable to the functional compensation from member species with growth trade-off. In the next section, these two hypotheses are more rigorously addressed based on the quantification of time-to-recovery in response to perturbations.

Historical Contingencies in Resilience

We performed a more thorough analysis of how resilience is influenced by historical contingencies. Based on the concept of engineering resilience, i.e., the rate of return to the pre-perturbed state (Holling, 1996; Allison and Martiny, 2008; Shade et al., 2012; Song et al., 2015; Martiny et al., 2017), we evaluated the system's resilience based on time-to-recovery such as hitting and settling times with 2 and 5% criteria as defined in Methods. For δ_norm = 0.09 (as previously considered), we examined how state variables and their recovery times change as a function of inundation interval (Figures 4A–C). In support of the hypothesis H1, state variables including microbial (x, y) and chemical compositions (z) changed as a function of dilution rate. This change was significant in the regime where inundation intervals were small (i.e., when perturbation frequencies were high) (Figure 4A), while the time-to-compositional recovery did not show such a sharp increase over the corresponding regime (Figure 4B). For x and z, the hitting time (solid line) was not always the same as the settling time (open circle), meaning that these variables first entered the area within 2 or 5% range of the nominal (i.e., pre-perturbed) values and later escaped them prior to ultimately returning to pre-perturbation conditions (Figures 4B,C). The time-to-recovery for z was shorter than those for x and y as indicated by the result in the previous section.

FIGURE 4

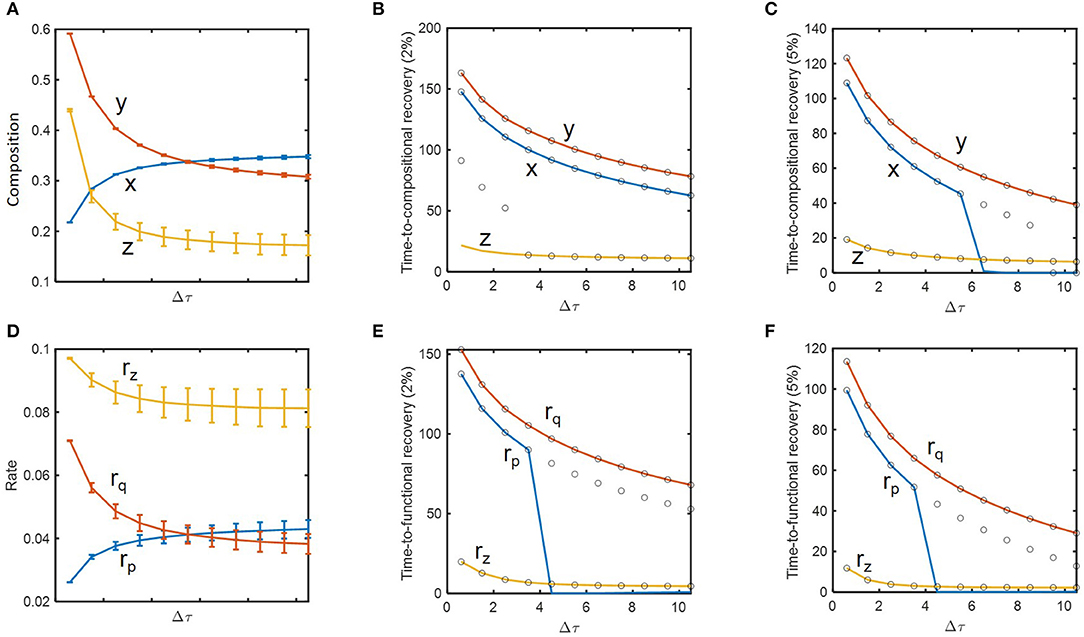
Figure 4. The impact of perturbation interval (Δτ) on species abundances, substrate concentration, microbial functions, and their time-to-recoveries: (A) microbial (x and y) and chemical compositions (z), (B) time-to-compositional recovery calculated by the 2% criterion, (C) time-to-compositional recovery calculated by the 5% criterion, (D) consumption rate of the shared substrate (r_z) and production rates of distinct products (r_p and r_q), (E) time-to-functional recovery calculated by the 2% criterion, (F) time-to-functional recovery calculated by the 5% criterion. In (B,C,E, and F), solid lines and open circles denote hitting and settling times, respectively.

Many of these trends observed from compositional variables (x, y, and z) were reproduced for functional variables (r_p, r_q, and r_z) (Figures 4D–F). As a notable difference, however, r_z showed suppressed changes compared to z due to the functional compensation from member species as explained earlier. Consequently, the time-to-functional recovery for r_z not only was significantly lower than those for r_x and r_y, but also showed a milder dependence on inundation interval (Figures 4E,F). These results provide a clear support for H2 and H3.

Hysteresis in Transition Across Two Distinct Perturbation Cycles

As shown in Figures 5A,B, we simulated sustained oscillations of compositional (x, y, and z) and functional variables (r_p, r_q, and r_z) at two different inundation intervals (5 and 15) to see how the transitions occur between them. Consideration of these two intervals (wider than those considered the previous case) was to ensure the dramatic differences in the fluctuation patterns so that one can see transition trajectories more clearly. We initially imposed the periodic perturbation with the interval of 5 and when sustained oscillation was reached (i.e., at τ = 200), switched to the interval of 15 – this process was repeated afterwards. Phase diagrams in Figures 5C–E showed the existence of hysteresis in the transition between the two periodically perturbed conditions with distinct intervals. The transition between the two limit cycles formed by periodic perturbations with intervals of 5 and 15 occurred through different trajectories. The hysteresis was most effectively shown for the phase diagram of the two compositional variables (x and y) (Figure 5C).

FIGURE 5

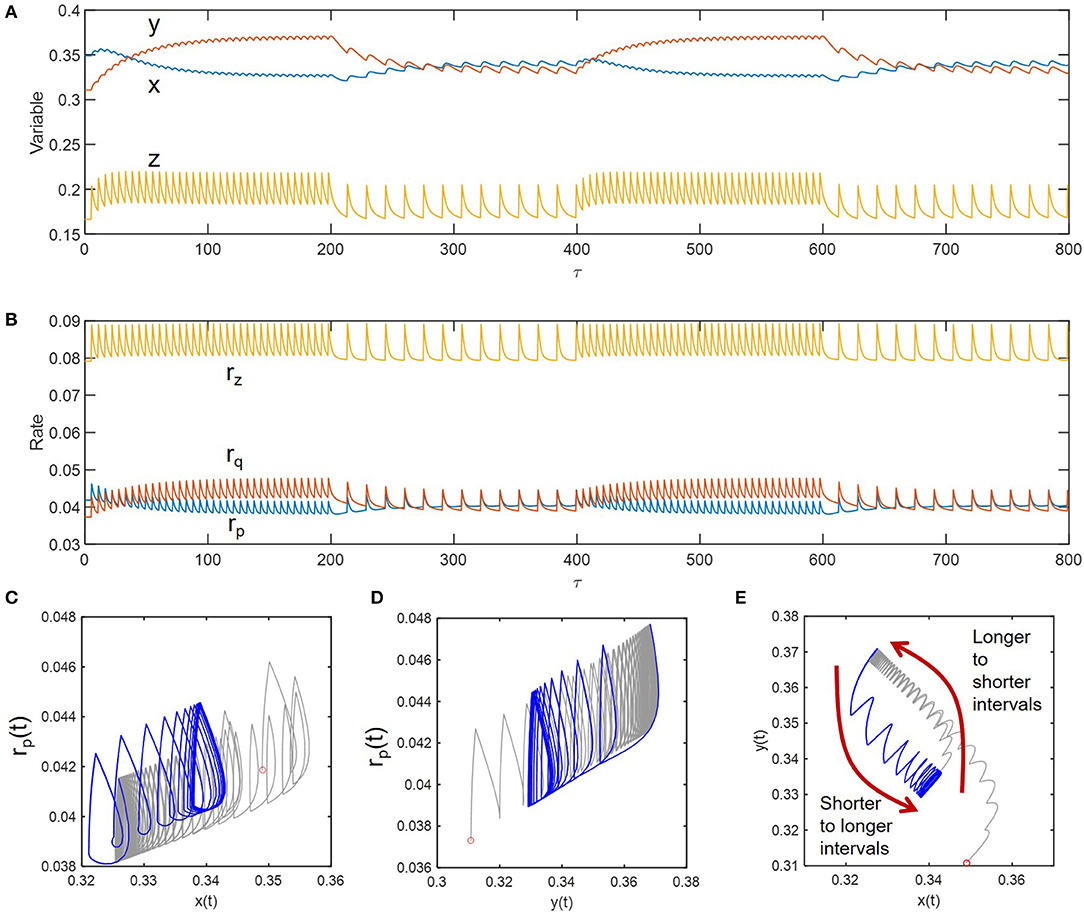
Figure 5. Hysteresis in dynamic transitions between the two distinctively perturbed conditions with the intervals of 5 and 15: (A) compositional fluctuations, (B) functional fluctuations, and (C–E) phase diagrams. Curves in gray and blue, respectively denote the transitions from longer to shorter intervals and from shorter to longer intervals.

Discussion

A growing body of data indicate critical effects of historical contingency in biogeochemistry and microbial ecology, but theoretical frameworks that can predict the sophisticated behavior of environmental systems are still lacking. In this study, we formulated a mathematical model of a minimal complexity to reveal how historical contingencies in resilience to hydrologic perturbations are driven by microbial growth traits and their trade-offs. Our model enabled us to reveal important aspects of resilience and its historical contingencies as summarized below.

Historical contingency in the resilience of microbial systems was significantly affected by the degree of functional redundancy or specialization. Redundant functions commonly performed by multiple species (such as the consumption rate of the shared substrate in this work) were more readily recovered from perturbations, while specialized functions associated with individual species (such as the production rates of distinct products by species 1 and 2) showed slower recovery. Consequently, historical contingencies in resilience were more pronounced for specialized functions partitioned only into specific species. The enhanced resilience for redundant functions performed by majority of species is ascribable to their compensating roles in contributing to a total biomass stock that is more robust to disturbances than individual species. Related to this, we also found that the compositional recovery of microbial populations was prolonged even after a certain community function (e.g., the substrate consumption rate) became stable. While this endogenous dynamics was discussed as an intrinsic characteristic of compositionally complex natural communities (Konopka et al., 2015; Song et al., 2015), our model demonstrated that even structurally simple communities can develop those subtle dynamics in the process of stabilizing microbial functions against perturbations. Our work therefore provides a minimal structure of model for studying a mechanistic linkage between endogenous dynamics, functional redundancy, resilience, and historical contingency.

As an outcome of historical contingency, we also observed hysteresis, whereby the system takes different routes in transitioning across conditions. Hysteresis of biological systems has been typically reported based on forward and backward trajectories of state variables between multiple steady states (Kim et al., 2012; Gedeon et al., 2018), but the hysteresis in this work is defined in a more dynamic context, i.e., as being characterized by distinct transient paths between two sustained oscillations maintained across different inundation intervals. As a signature of historical contingency, a predictive understanding of hysteresis is critically important because it can lead to the unexpected formation of intermediate chemical compounds during the transitions when microbial communities undergo the dynamic shifts in their composition and functions through different trajectories. The lack of understanding of hysteric behaviors in microbial communities therefore may cause a significant error in model predictions, particularly for those associated with specific organisms, the populations of which undergo a more significant dynamic variation than the total community biomass.

Our work offers a direction toward building more mechanistic biogeochemical models. Stronger historical contingencies of specialized functions as predicted by the model highlights the importance of representing distinct traits of individual species for predictive modeling – because the lumped description based on community-level properties such as the total biomass and/or carbon use efficiency cannot predict complex aspects of biogeochemical function such as resilience and historical contingency driven by the interplay between distinct microbial species. In this regard, model extension though linking conceptualized microbial functions with specific biogeochemical pathways would be an important next step. Two reaction pathways driven by species 1 and 2 considered in our model can be translated as specific biogeochemical pathways, for example, such as denitrification and anammox, i.e., once ${\mathrm{\text{NO}}}_3^{-}$ is converted to ${\mathrm{\text{NO}}}_2^{-}$ (as the first step of denitrification), the subsequent reaction paths bifurcated afterwards are driven by distinct microbial functional groups. Therefore, this type of model that has both redundant (i.e., conversion of ${\mathrm{\text{NO}}}_3^{-}$ to ${\mathrm{\text{NO}}}_2^{-}$) and specialized functions (i.e., conversion afterwards through two pathways) would be suitable for investigating function-specific resilience and historical contingencies as demonstrated in our study. For this direction, trait-based modeling approaches that appropriately combine the concepts of functional guilds and functional enzymes should be considered as an appropriate modeling framework (Allison, 2012; Bouskill et al., 2012; Song et al., 2014, 2017). We expect that accounting for individual growth rates, and species-associated specific biogeochemical traits will significantly improve predictive capabilities for multi-scale hydrobiogeochemical models.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/hyunseobsong/history.

Author Contributions

H-SS developed the modeling concept and performed simulations. H-SS drafted out the article, which was edited by JS and EG. All authors contributed to the design of the research, read and approved the final manuscript.

Funding

This research was supported by the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research, Environmental System Science (ESS) program through subcontract to the River Corridor Scientific Focus Area project at Pacific Northwest National Laboratory.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Allison, S. D. (2012). A trait-based approach for modelling microbial litter decomposition. Ecol. Lett. 15, 1058–1070. doi: 10.1111/j.1461-0248.2012.01807.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Allison, S. D., and Martiny, J. B. H. (2008). Resistance, resilience, and redundancy in microbial communities. Proc. Natl. Acad. Sci. U. S. A. 105, 11512–11519. doi: 10.1073/pnas.0801925105

PubMed Abstract | CrossRef Full Text | Google Scholar

Averill, C., Waring, B. G., and Hawkes, C. V. (2016). Historical precipitation predictably alters the shape and magnitude of microbial functional response to soil moisture. Glob. Chang. Biol. 22, 1957–1964. doi: 10.1111/gcb.13219

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouskill, N. J., Lim, H. C., Borglin, S., Salve, R., Wood, T. E., Silver, W. L., et al. (2013). Pre-exposure to drought increases the resistance of tropical forest soil bacterial communities to extended drought. Isme J. 7, 384–394. doi: 10.1038/ismej.2012.113

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouskill, N. J., Tang, J., Riley, W. J., and Brodie, E. L. (2012). Trait-based representation of biological nitr fication: model development testing, and predicted community composition. Front. Microbiol. 3:364. doi: 10.3389/fmicb.2012.00364

PubMed Abstract | CrossRef Full Text | Google Scholar

Butler, G. J., Hsu, S. B., and Waltman, P. (1983). Coexistence of competing predators in a chemostat. J. Math. Biol. 17, 133–151. doi: 10.1007/BF00305755

CrossRef Full Text | Google Scholar

Covino, T., Golden, H. E., Li, H. Y., and Tang, J. Y. (2018). Aquatic carbon-nutrient dynamics as emergent properties of hydrological, biogeochemical, and ecological interactions: scientific advances. Water Resour. Res. 54, 7138–7142. doi: 10.1029/2018WR023588

PubMed Abstract | CrossRef Full Text | Google Scholar

De Leenheer, P., Angeli, D., and Sontag, E. D. (2006). Crowding effects promote coexistence in the chemostat. J. Math. Anal. Appl. 319, 48–60. doi: 10.1016/j.jmaa.2006.02.036

CrossRef Full Text | Google Scholar

Freedman, H. I., So, J. W. H., and Waltman, P. (1989). Coexistence in a model of competition in the chemostat incorporating discrete delays. SIAM J. Appl. Math. 49, 859–870. doi: 10.1137/0149050

CrossRef Full Text | Google Scholar

Fukami, T. (2015). Historical contingency in community assembly: integrating niches, species pools, and priority effects. Annu. Rev. Ecol. Evol. Syst. 46, 1–23. doi: 10.1146/annurev-ecolsys-110411-160340

CrossRef Full Text | Google Scholar

Gedeon, T., Cummins, B., Harker, S., and Mischaikow, K. (2018). Identifying robust hysteresis in networks. PLoS Comput. Biol. 14:e1006121. doi: 10.1371/journal.pcbi.1006121

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldman, A. E., Graham, E. B., Crump, A. R., Kennedy, D. W., Romero, E. B., Anderson, C. G., et al. (2017). Biogeochemical cycling at the aquatic-terrestrial interface is linked to parafluvial hyporheic zone inundation history. Biogeosciences 14, 4229–4241. doi: 10.5194/bg-14-4229-2017

CrossRef Full Text | Google Scholar

Graham, E. B., Stegen, J. C., Huang, M. Y., Chen, X. Y., and Scheibe, T. D. (2019). Subsurface biogeochemistry is a missing link between ecology and hydrology in dam-impacted river corridors. Sci. Total Environ. 657, 435–445. doi: 10.1016/j.scitotenv.2018.11.414

PubMed Abstract | CrossRef Full Text | Google Scholar

Haegeman, B., and Rapaport, A. (2008). How flocculation can explain coexistence in the chemostat. J. Biol. Dyn. 2, 1–13. doi: 10.1080/17513750801942537

CrossRef Full Text | Google Scholar

Hardin, G. (1960). The competitive exclusion principle. Science 131, 1292–1297. doi: 10.1126/science.131.3409.1292

CrossRef Full Text | Google Scholar

Hawkes, C. V., and Keitt, T. H. (2015). Resilience vs. historical contingency in microbial responses to environmental change. Ecol. Lett. 18, 612–625. doi: 10.1111/ele.12451

PubMed Abstract | CrossRef Full Text | Google Scholar

Hawkes, C. V., Waring, B. G., Rocca, J. D., and Kivlin, S. N. (2017). Historical climate controls soil respiration responses to current soil moisture. Proc. Natl. Acad. Sci. U. S. A. 114, 6322–6327. doi: 10.1073/pnas.1620811114

PubMed Abstract | CrossRef Full Text | Google Scholar

Hesseler, J., Schmidt, J. K., Reichl, U., and Flockerzi, D. (2006). Coexistence in the chemostat as a result of metabolic by-products. J. Math. Biol. 53, 556–584. doi: 10.1007/s00285-006-0012-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Hillebrand, H., Langenheder, S., Lebret, K., Lindstrom, E., Ostman, O., and Striebel, M. (2018). Decomposing multiple dimensions of stability in global change experiments. Ecol. Lett. 21, 21–30. doi: 10.1111/ele.12867

PubMed Abstract | CrossRef Full Text | Google Scholar

Holling, C. S. (1996). Engineering resilience vs. ecological resilience. Eng. Ecol. Const. 31:32.

Google Scholar

Hsu, S. B., Hubbell, S. P., and Waltman, P. (1978). Competing predators. SIAM J. Appl. Math. 35, 617–625. doi: 10.1137/0135051

CrossRef Full Text | Google Scholar

Jansson, J. K., and Hofmockel, K. S. (2018). The soil microbiome - from metagenomics to metaphenomics. Curr. Opin. Microbiol. 43, 162–168. doi: 10.1016/j.mib.2018.01.013

CrossRef Full Text | Google Scholar

Kim, J. I., Song, H. S., Sunkara, S. R., Lali, A., and Ramkrishna, D. (2012). Exacting predictions by cybernetic model confirmed experimentally: steady state multiplicity in the chemostat. Biotechnol. Prog. 28, 1160–1166. doi: 10.1002/btpr.1583

PubMed Abstract | CrossRef Full Text | Google Scholar

Konopka, A., Lindemann, S., and Fredrickson, J. (2015). Dynamics in microbial communities: unraveling mechanisms to identify principles. Isme J. 9, 1488–1495. doi: 10.1038/ismej.2014.251

PubMed Abstract | CrossRef Full Text | Google Scholar

Kraft, B., Tegetmeyer, H. E., Meier, D., Geelhoed, J. S., and Strous, M. (2014). Rapid succession of uncultured marine bacterial and archaeal populations in a denitrifying continuous culture. Environ. Microbiol. 16, 3275–3286. doi: 10.1111/1462-2920.12552

PubMed Abstract | CrossRef Full Text | Google Scholar

Le, H. T., Rochelle-Newall, E., Ribolzi, O., Janeau, J. L., Huon, S., Latsachack, K., et al. (2020). Land use strongly influences soil organic carbon and bacterial community export in runoff in tropical uplands. Land Degr. Dev. 31, 118–132. doi: 10.1002/ldr.3433

CrossRef Full Text | Google Scholar

Lennon, J. T., and Jones, S. E. (2011). Microbial seed banks: the ecological and evolutionary implications of dormancy. Nat. Rev. Microbiol. 9, 119–130. doi: 10.1038/nrmicro2504

PubMed Abstract | CrossRef Full Text | Google Scholar

Martiny, J. B. H., Martiny, A. C., Weihe, C., Lu, Y., Berlemont, R., Brodie, E. L., et al. (2017). Microbial legacies alter decomposition in response to simulated global change. Isme J. 11, 490–499. doi: 10.1038/ismej.2016.122

PubMed Abstract | CrossRef Full Text | Google Scholar

Ogle, K., Barber, J. J., Barron-Gafford, G. A., Bentley, L. P., Young, J. M., Huxman, T. E., et al. (2015). Quantifying ecological memory in plant and ecosystem processes. Ecol. Lett. 18, 221–235. doi: 10.1111/ele.12399

PubMed Abstract | CrossRef Full Text | Google Scholar

Peralta, A. L., Ludmer, S., and Kent, A. D. (2013). Hydrologic history influences microbial community composition and nitrogen cycling under experimental drying/wetting treatments. Soil Biol. Biochem. 66, 29–37. doi: 10.1016/j.soilbio.2013.06.019

CrossRef Full Text | Google Scholar

Peralta, A. L., Ludmer, S., Matthews, J. W., and Kent, A. D. (2014). Bacterial community response to changes in soil redox potential along a moisture gradient in restored wetlands. Ecol. Eng. 73, 246–253. doi: 10.1016/j.ecoleng.2014.09.047

CrossRef Full Text | Google Scholar

Raaijmakers, J. M., and Mazzola, M. (2016). Soil immune responses soil microbiomes may be harnessed for plant health. Science 352, 1392–1393. doi: 10.1126/science.aaf3252

CrossRef Full Text | Google Scholar

Revilla, T., and Weissing, F. J. (2008). Nonequilibrium coexistence in a competition model with nutrient storage. Ecology 89, 865–877. doi: 10.1890/07-1103.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Roughgarden, J. (1971). Density-dependent natural selection. Ecology 52, 453–468. doi: 10.2307/1937628

CrossRef Full Text | Google Scholar

Shade, A., Peter, H., Allison, S. D., Baho, D. L., Berga, M., Burgmann, H., et al. (2012). Fundamentals of microbial community resistance and resilience. Front. Microbiol. 3:417. doi: 10.3389/fmicb.2012.00417

PubMed Abstract | CrossRef Full Text | Google Scholar

Singer, M. B., Harrison, L. R., Donovan, P. M., Blum, J. D., and Marvin-Dipasquale, M. (2016). Hydrologic indicators of hot spots and hot moments of mercury methylation potential along river corridors. Sci. Total Environ. 568, 697–711. doi: 10.1016/j.scitotenv.2016.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, H. L. (1981). Competitive coexistence in an oscillating chemostat. SIAM J. Appl. Math. 40, 498–522. doi: 10.1137/0140042

CrossRef Full Text | Google Scholar

Song, H.-S., Cannon, W. R., Beliaev, A. S., and Konopka, A. (2014). Mathematical modeling of microbial community dynamics: a methodological review. Processes 2, 711–752. doi: 10.3390/pr2040711

CrossRef Full Text | Google Scholar

Song, H. S., Renslow, R. S., Fredrickson, J. K., and Lindemann, S. R. (2015). Integrating ecological and engineering concepts of resilience in microbial communities. Front. Microbiol. 6:1298. doi: 10.3389/fmicb.2015.01298

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, H. S., Thomas, D. G., Stegen, J. C., Li, M. J., Liu, C. X., Song, X. H., et al. (2017). Regulation-structured dynamic metabolic model provides a potential mechanism for delayed enzyme response in denitrification process. Front. Microbiol. 8:1866. doi: 10.3389/fmicb.2017.01866

PubMed Abstract | CrossRef Full Text | Google Scholar

Stephanopoulos, G., and Fredrickson, A. G. (1979). Effect of spatial inhomogeneities on the coexistence of competing microbial-populations. Biotechnol. Bioeng. 21, 1491–1498. doi: 10.1002/bit.260210817

CrossRef Full Text | Google Scholar

Stephanopoulos, G., Fredrickson, A. G., and Aris, R. (1979). The growth of competing microbial-populations in a cstr with periodically varying inputs. Aiche J. 25, 863–872. doi: 10.1002/aic.690250515

CrossRef Full Text | Google Scholar

Vass, M., and Langenheder, S. (2017). The legacy of the past: effects of historical processes on microbial metacommunities. Aquat. Microb. Ecol. 79, 13–19. doi: 10.3354/ame01816

CrossRef Full Text | Google Scholar

Veldkamp, H., and Jannasch, H. W. (1972). Mixed culture studies with the chemostat. J. Appl. Chem. Biotechnol. 22, 105–123. doi: 10.1002/jctb.5020220113

CrossRef Full Text | Google Scholar

Wang, K. F., Peng, C. H., Zhu, Q. A., Zhou, X. L., Wang, M., Zhang, K. R., et al. (2017). Modeling global soil carbon and soil microbial carbon by integrating microbial processes into the ecosystem process model TRIPLEX-GHG. J. Adv. Model. Earth Syst. 9, 2368–2384. doi: 10.1002/2017MS000920

CrossRef Full Text | Google Scholar

Widder, S., Allen, R. J., Pfeiffer, T., Curtis, T. P., Wiuf, C., Sloan, W. T., et al. (2016). Challenges in microbial ecology: building predictive understanding of community function and dynamics. Isme J. 10, 2557–2568. doi: 10.1038/ismej.2016.45

PubMed Abstract | CrossRef Full Text | Google Scholar

Wieder, W. R., Bonan, G. B., and Allison, S. D. (2013). Global soil carbon projections are improved by modelling microbial processes. Nat. Clim. Chang. 3, 909–912. doi: 10.1038/nclimate1951

CrossRef Full Text | Google Scholar