- 1Department of Biomedical Engineering, Yale University, New Haven, CT, United States
- 2School of Mathematical Sciences, University of Nottingham, Nottingham, United Kingdom
Healthy lung function depends on a complex system of interactions which regulate the mechanical and biochemical environment of individual cells to the whole organ. Perturbations from these regulated processes give rise to significant lung dysfunction such as chronic inflammation, airway hyperresponsiveness and airway remodelling characteristic of asthma. Importantly, there is ongoing mechanobiological feedback where mechanical factors including airway stiffness and oscillatory loading have considerable influence over cell behavior. The recently proposed area of mechanopharmacology recognises these interactions and aims to highlight the need to consider mechanobiology when identifying and assessing pharmacological targets. However, these multiscale interactions can be difficult to study experimentally due to the need for measurements across a wide range of spatial and temporal scales. On the other hand, integrative multiscale mathematical models have begun to show success in simulating the interactions between different mechanobiological mechanisms or cell/tissue-types across multiple scales. When appropriately informed by experimental data, these models have the potential to serve as extremely useful predictive tools, where physical mechanisms and emergent behaviours can be probed or hypothesised and, more importantly, exploited to propose new mechanopharmacological therapies for asthma and other respiratory diseases. In this review, we first demonstrate via an exemplar, how a multiscale mathematical model of acute bronchoconstriction in an airway could be exploited to propose new mechanopharmacological therapies. We then review current mathematical modelling approaches in respiratory disease and highlight hypotheses generated by such models that could have significant implications for therapies in asthma, but that have not yet been the subject of experimental attention or investigation. Finally we highlight modelling approaches that have shown promise in other biological systems that could be brought to bear in developing mathematical models for optimisation of mechanopharmacological therapies in asthma, with discussion of how they could complement and accelerate current experimental approaches.
1 Introduction
Asthma is a chronic lung disease affecting over 300 million people globally. Severe asthmatics suffer exacerbations requiring frequent hospitalisation and so contribute a significant burden to national health services. Although new therapies such as bronchial thermoplasty appear to provide a “cure” to severe asthmatics, in most cases it is only the symptoms that are treated. Asthma is characterised by inflammation, airway hyperresponsiveness (AHR) and airway remodelling. Inhalation of an allergen, such as pollen or dustmite, triggers an immune response causing infiltration of white blood cells (e.g., eosinophils) from neighbouring blood vessels into the airway. A normal response would see these cells return to the circulation but in asthma they remain elevated, causing inflammation of the airways. The eosinophils interact with resident cells (e.g., mast cells) in the airway and secrete a contractile agonist that causes airway smooth muscle cells in the wall to contract. Hyperresponsiveness refers to the rapid contraction of smooth muscle to lower doses of agonist in asthmatics than in non-asthmatics. Corresponding structural changes in the airway occur over longer timescales (airway remodelling), which include significantly increased smooth muscle mass along with increases in other cell types and extracellular matrix that support the smooth muscle, causing the airway to thicken with the capacity to worsen bronchoconstriction. There is increasing evidence that these three hallmarks are linked through both mechanical and biochemical factors. In parallel and in more general settings, the influence of mechanical factors on cell behavior and how this can affect pharmacological treatments is beginning to gain recognition, leading to the proposed area of mechanopharmacology (Liao et al., 2006; Krishnan et al., 2016); in this arena the role of mechanics and mechanobiology is acknowledged as a key factor to take into account when identifying and assessing the efficacy of pharmacological interventions. Additionally, mechanopharmacology includes consideration of combined or synergistic effects of mechanical and pharmacological interventions, as proposed in the study of Wang et al. (2019), in which tissue-level force oscillations are combined with a treatment that targets intracellular signalling and cytoskeletal stiffness via Rho kinase (ROCK). Given the multiple spatial and temporal scales associated with the underlying biochemical signals and tissue mechanics in asthma, along with interactions between multiple cell and tissue types, integrative multiscale mathematical models are increasingly useful tools for understanding links between inflammation, hyperresponsiveness and remodelling as well as synergies between mechanics and pharmacology. Such models together with novel biomechanics-based high throughput drug-screening technologies (e.g., (Park et al., 2015)) or organ-on-a-chip technologies (e.g., (Huh et al., 2010)) that can mimic physiological mechanical environments (including substrate stiffness, dynamic loading conditions), provide great potential for aiding the design or optimisation of new mechanopharmacological therapies.
In this review we will first consider an exemplar multiscale model (Figure 1) to illustrate how an understanding of cell–tissue interactions could be exploited to propose a potential mechanopharmacological therapy in asthma and acute bronchoconstriction. Noting that there is evidence that mechanotransduction and mechanobiology at the cell-level play important roles in emergent tissue and whole airway mechanics in longer time-scale processes, we then examine how mechanics play a role in linking inflammation to responsiveness and airway remodelling; integrative approaches are clearly necessary to understand these complex interactions at multiple timescales. We therefore also review the significant modelling efforts in respiratory cell and tissue mechanics in multiple respiratory disease settings, illustrating the role of mechanics in the multiscale processes described above. We emphasise that the focus is on recent work, rather than a complete background. Interested readers are referred to recent more extensive reviews for lung tissue mechanics and multiscale models of fibrosis (Burrowes et al., 2019; Leonard-Duke et al., 2020).
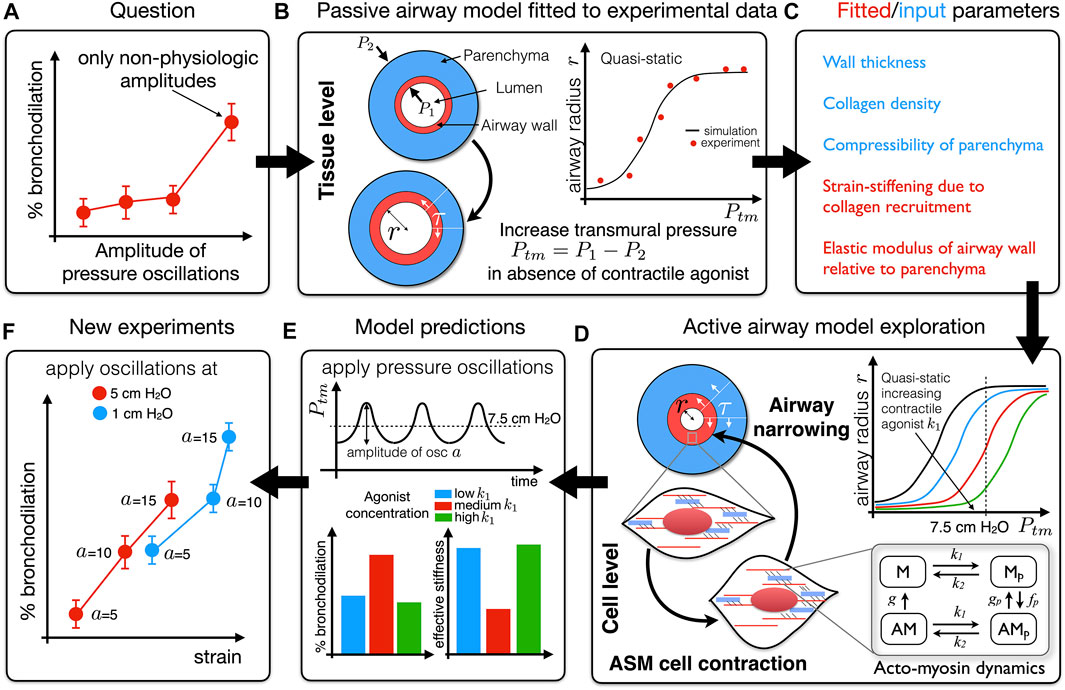
FIGURE 1. Schematic of an iterative process by which experimental data previously informed a mathematical model, exploration of which generated a hypothesis that could be tested experimentally. (A) The question: why is stretch-modulated reduction in contractile force at cell/tissue level not recapitulated in intact airways unless pressure oscillation amplitudes are unphysiologically high (LaPrad et al., 2010)? To address this question we developed a mathematical model of an airway that accounts for force generation via airway smooth muscle fibres and strain-stiffening via collagen fibres embedded in a non-linearly elastic axisymmetric airway wall. (B) In the absence of contractile agonist (passive airway) the quasi-static model is effectively of the form Ptm = P1 − P2 = f (r; p); for each applied transmural pressure (Ptm), the elastic model allows us to predict the corresponding airway radius (r) for a set of parameters p in the form of a “pressure-radius” curve. We use quasi-static experimental data to infer mechanical properties as indicated in (C). (D) The generation of contractile force at the cell-level is modelled via the Huxley-Hai-Murphy model and coupled to the elastic model in (B). This allows us to investigate the effect of contractile agonist on the quasi-static pressure-radius curves. (E) Application of time-dependent pressure oscillations (amplitude a) about a particular transmural pressure allows dynamic changes in the contractile force to be predicted. This reveals that the amount of bronchodilation that can be achieved depends on the effective stiffness of the airway at that transmural pressure (reciprocal of the slope of the pressure-radius curves in panel (D); dr/dPtm(7.5)); the lower the effective stiffness the greater the ability of the oscillations to dilate the airway. We thus hypothesised that higher effective stiffness of an airway limits the strain that can be transmitted to the contractile machinery and so applying pressure oscillations at a more compliant part of the pressure-radius curve will generate greater bronchodilation (B−E) (Hiorns et al., 2014)). (F) In new experiments, pressure oscillations applied to intact airways at different Ptm and amplitudes a confirm this hypothesis (Harvey et al., 2013).
Given the importance of mechanical factors it is somewhat surprising that these have not yet been exploited in combination with pharmacological therapies. It therefore seems timely to consider mathematical models aimed at mechanopharmacological therapies in asthma in both: 1) acute situations, by understanding the role of deep inspirations (DIs) and breathing patterns on bronchodilation, and 2) chronic cases of airway remodelling where the combined role of mechanical stress and subcellular signalling govern adverse changes in tissue properties. Hence we will draw on exemplars to highlight how mechanopharmacology could be considered as a new focus for mathematical modelling in asthma to identify new targets e.g. how mechanical forces might influence the efficacy of a given drug or activate particular growth factors. We note however that:
(i) much more joint modelling and experimental work is needed. In this review we therefore highlight some hypotheses generated by models that remain to be tested experimentally and how these could advance this field, as well as key experimental questions and frameworks where existing modelling techniques could guide mechanistic understanding;
(ii) although this review focuses on subcellular, cellular, tissue, and airway-level models a significant amount of work has been done on networks of branching airways at the organ-level considering ventilation heterogeneity (Venegas et al., 2005; Tgavalekos et al., 2007; Winkler and Venegas, 2007; Bhatawadekar et al., 2015; Donovan, 2016; Leary et al., 2016; Donovan, 2017), multi-breath washout and forced oscillatory technique (Berger et al., 2016; Foy et al., 2019), through to the effects of bronchial thermoplasty (Donovan et al., 2020). The challenge, which will be discussed later, is in upscaling from detailed tissue- and airway-level models, that include cell-level details, to these types of macroscale models;
(iii) the impact of mathematical modelling in respiratory research lags other biomedical areas and so we also highlight research areas where joint experimental–theoretical approaches have borne fruit (e.g., cardiovascular research) and discuss some associated methods from which we could learn.
Box 1 Key terms and definitions referred to in this review.
Airway hyperresponsiveness: greater reduction in airway calibre to low concentration of contractile agonist that occurs in asthmatics compared to non-asthmatics evidenced by leftward shift in dose-response curves (airway calibre as function of agonist concentration).
Airway remodelling: structural changes in the airway wall resulting from increased airway smooth muscle, extracellular matrix, epithelial and goblet cells, thus causing increased wall thickness or decreased luminal area.
Bronchoconstriction: a rapid contraction of airway smooth muscle resulting in airway narrowing.
Crossbridge cycling: repeated binding (and unbinding) of myosin crossbridges with actin binding sites within the airway smooth muscle cell resulting in a relative motion of actin and myosin filaments and thus shortening/contraction of the cell.
Deep inspiration (DI): a deep breath that induces a substantial mechanical perturbation compared to normal (tidal) breathing. DIs have a potent, long-lasting bronchodilatory effect in non-asthmatics but only a transient effect in asthmatics.
Mechanobiology: the study of how cells sense and respond to mechanical cues.
Mechanopharmacology: the consideration of mechanobiological factors when evaluating therapeutic strategies, such as potential interactions or synergies between mechanical and pharmacological perturbations.
2 Deep inspiration and tidal breathing in asthma: An exemplar
During an asthma attack, release of contractile agonist at the cell level causes crossbridges from myosin filaments within the cell to attach and detach from binding sites on actin filaments. This crossbridge cycling causes filaments to slide past each other which in turn causes the cell to shorten along the smooth muscle fibre. This results in contraction of the airways and thus in shortness of breath and wheezing. Tidal breathing and deep inspirations (DIs) at the organ level transmits strain to the airways, the muscle fibres and thus to the cell and the contractile machinery. This perturbs the cycling dynamics, resulting in an interplay between subcellular and organ level processes. In particular, DIs have a potent bronchodilatory effect in normal subjects but only a transient one in asthmatics.
In order to understand why bronchodilatory effects of DIs are attenuated in asthmatics, a number of experimental investigations focus on the effect of cyclic strain on the cell, airway and organ. In particular it is well established that increasing the amplitude of oscillation applied to tissue strips causes a proportionate decrease in mean contractile force compared with application of isometric force (Fredberg et al., 1997; Wang et al., 2000; Bates et al., 2009). Dilation of constricted airways in precision-cut lung-slices (PCLS) on application of oscillations to surrounding parenchymal tissue also appear to indicate that such “breathing-like” oscillations are capable of reducing contractile force (Lavoie et al., 2012). The drop in force is attributed to perturbation of acto-myosin crossbridge binding. While this explained the effect of mechanical stretching on contractile force in isolated smooth muscle, results from other experimental investigations showed that when pressure oscillations are applied to whole airways the airways could not be dilated to the extent predicted by tissue and cell experiments unless the amplitude of the oscillations was extremely high (and not physiologically realistic) (LaPrad et al., 2010; LaPrad and Lutchen, 2011). A key question is: why are not the results from the cell and tissue levels recapitulated at the level of the intact airway (Figure 1A)? Furthermore, how does airway smooth muscle (ASM) force generation manifest at the tissue/airway-level, and in particular how do the dynamic effects of breathing differ between observations in ex vivo experimental assays and in vivo?
To answer these questions we previously developed and validated a multiscale mathematical model that couples models of dynamic force generation via crossbridge mechanics of airway smooth muscle at the subcellular level to an airway modelled as an axisymmetric hyperelastic cylinder under plane strain accounting for strain-stiffening properties of collagen-dominated extracellular matrix (Hiorns et al., 2014) (Figures 1B–D). Application of a time-dependent transmural pressure mimics the effect of breathing (Figure 1E). Most notably, this work shows that although length oscillations may cause a rapid drop in contractile force generated by ASM cells in tissue strips (the most common ex vivo experimental preparation), the additional variable of an operating transmural pressure from which strain oscillations are applied plays an important role in determining the effective stiffness of the intact airway (the slope of the pressure-radius curve which is a non-monotonic function of transmural pressure) and thereby the effectiveness with which strain is transmitted to the ASM cells. Thus, whether or not significant bronchodilation occurs, depends on the transmural pressure at which “breathing-like” oscillations are applied (Hiorns et al., 2014). Essentially, lower effective airway stiffness means greater strain is transmitted to the smooth muscle cells. Harvey et al. (2013) confirmed our theoretical finding by showing experimentally that oscillations applied at lower transmural pressure (i.e., at a more compliant part of the pressure-radius curve) generates greater bronchodilation at more physiologic amplitudes (Figure 1F). It seems that the key to improving lung function in asthmatics would be to make their airways more compliant so that the bronchodilatory effects of DI can be restored. Can inhalation therapies be improved by exploiting these mechanics-based results, e.g., does breathing out first (rather than a DI) get the airways to a more compliant part of the pressure-radius curve? Can this be combined with a bronchodilator to optimize dilation? Appropriately validated multiscale mathematical models of the type described above can play an important role in addressing such questions and thereby enable the design and optimisation of mechanopharmacological therapies.
Furthermore, we showed that the effective stiffness of the airway wall differs significantly in dynamic compared to quasi-static conditions. This then led to an exploration of how dynamic stresses in an intact asthmatic airway differ from those in excised tissue strips (Hiorns et al., 2016). We show that airway geometry, and the interplay between dynamic active and passive forces, give rise to large stress and compliance heterogeneities across the broncho-constricted intact airway wall, that are absent in tissue-strips with identical properties. The study thus demonstrates how findings from a computational model can improve experimental design, suggesting a strategy by which the mechanical environment of smooth muscle cells can be replicated ex vivo; in particular we propose that if the tissue strip experiments are to represent the airway wall, then loading to the strip should utilise auxotonic loading characteristics at the outer wall as predicted by the finite thickness airway model not models based on the thin-walled Laplace approximation. The above work also suggests that integrative studies need to consider how feedback from resulting stress environments might affect ASM cell response over longer periods of time and how these stress environments might drive structural changes (such as activation of growth factors, ASM hypertrophy or hyperplasia and collagen deposition) and hence perturbations away from homoeostasis into pathology. This work has thus highlighted the need for combining multiple interactions, occurring at different spatio-temporal scales, governing bronchoconstriction in asthma, and illustrates the potential for exploiting mechanopharmacology as a potential route to developing new or more effective therapies.
3 Existing modelling approaches
Having considered the above example in some detail, we now review, more generally, modelling efforts in respiratory cell and tissue mechanics in multiple respiratory disease settings, illustrating the role of mechanics in the multiscale processes described above. Modelling efforts have targeted wide-ranging questions across multiple scales, using discrete, continuum, or hybrid approaches. Some primary focus areas discussed in these sections are summarised schematically (Figure 2).
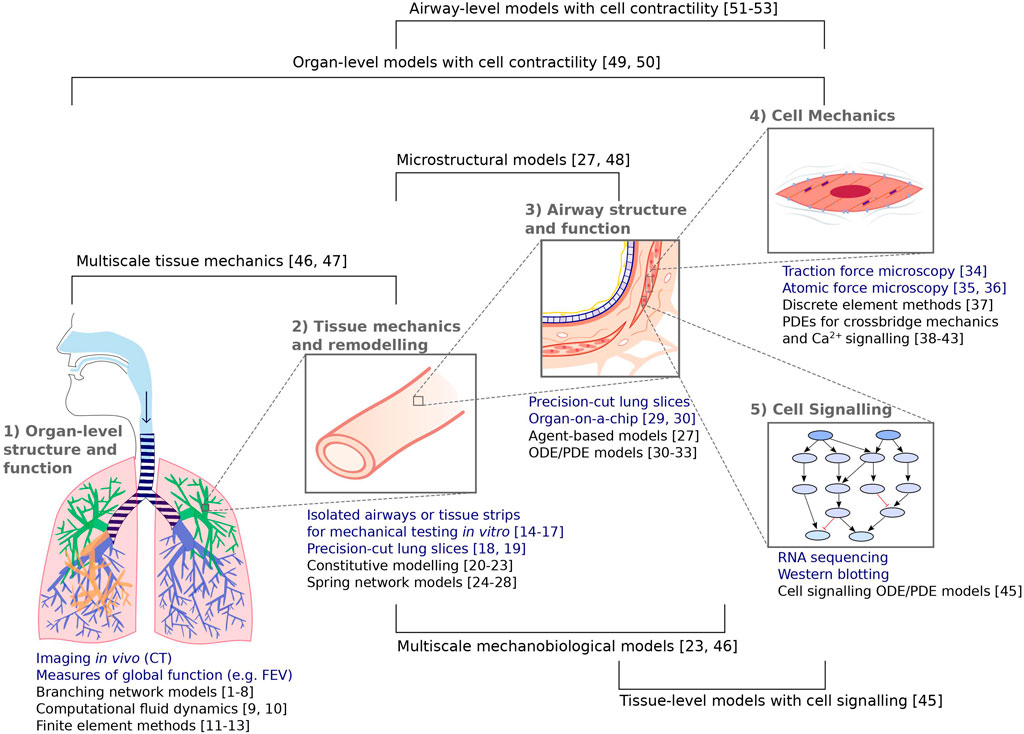
FIGURE 2. Summary of the experimental (blue) and complementary modelling (black) techniques discussed in these sections, spanning from organ-level structure and function to subcellular mechanics and signalling events. Numbers correspond to the following references: [1–8] Venegas et al., 2005; Tgavalekos et al., 2007; Winkler and Venegas, 2007; Bhatawadekar et al., 2015; Donovan, 2016; Leary et al., 2006; Donovan 2017; Foy et al., 2019. [9, 10] Choi et al., 2019; Yoon et al., 2020 [11–13] Berger et al., 2016; Tawhai et al., 2004; Werner et al., 2009 [14–17] Fredberg et al., 1997; Wang et al., 2000; Bates et al., 2009; LaPrad et al., 2010 [18, 19] Lavoie et al., 2012; Pybus et al., 2021b [20–23] Fung, 1974; Eskandari et al., 2019; Birzle et al., 2019; Hill et al., 2018 [24–28] Mead et al., 1970, Cavalcante et al., 2005; Iravani et al., 2020; Wellman et al., 2018; Oliveira et al., 2014 [29, 30] Huh et al., 2010; Kilic et al., 2019 [31–33] Chernyavsky et al., 2014; Chernyavsky et al., 2018; Pybus et al., 2021a [34] Lin et al., 2018 [35, 36] Sun et al., 2005; Smith et al., 2005 [37] Vargas et al., 2020 [38–43] Hai and Murphy, 1998; Mijailovich et al., 2000; Wang et al., 2008; Wang et al., 2010; Croisier et al., 2013; Croisier et al., 2015 [44] Irons et al., 2018 [45] Hao et al., 2015 [46, 47] Pascoe et al., 2020; Donovan et al., 2020 [27, 48] Wellman et al., 2018; Concha and Hurtado, 2020 [49, 50] Politi et al., 2010; Lauzon et al., 2012 [51–53] Hiorns et al., 2014; Hiorns et al., 2016; Brook 2014.
3.1 Organ-level structure and function
Clinical measurements for quantifying lung structure and function primarily occur at the organ scale, for example computed tomography (CT) scans, forced expiratory volume in one second (FEV1), and forced vital capacity (FVC). The metrics for function are highly dependent on the mechanical properties of the lung, including airway stiffness, airway resistance, and the elastic recoil of the lung. Computational models at the level of the whole lung therefore focus on quantifying mechanics in addition to airflow, typically with finite element (FE) methods as well as computational fluid dynamics (CFD) approaches. In the context of asthma, 1D CFD models taking into account structural information from CT scans, airway resistance, and lung compliance, have been used to understand differences in flow and pressure distributions between asthmatic and non-asthmatic subjects (Choi et al., 2019; Yoon et al., 2020). These models capture hysteresis in pressure–volume curves, showing increased hysteresis (and thereby workload) in the asthmatic group. To understand organ-scale deformations, FE models are often used and built around patient-specific geometric data from CT scans (Tawhai et al., 2004; Werner et al., 2009), where the model-predicted deformations rely on a previously developed understanding of the mechanical properties of the tissue.
3.2 Tissue mechanics and remodelling
An early priority for developing computational models was to accurately characterise lung mechanics at the tissue level by finding constitutive relations to appropriately describe experimental stress–strain relationships from loaded tissue strips, isolated airways, or precision-cut lung-slices (PCLS) (Fung, 1974; Birzle et al., 2019; Eskandari et al., 2019). Towards more microstructurally motivated models, it can be desirable to consider the contributions and distinct material properties of different components of the tissue, for example, collagen, elastin, airway smooth muscle cells, and proteoglycans (PGs). In a recent example, a nonlinear continuum mechanics model considering distinct contributions of collagen and elastin was tuned to experimental data from uniaxially loaded PCLS with collagenase and elastase treatments, in which collagen and elastin were digested individually and in combination, allowing their contributions to be quantified (Birzle et al., 2019). Alternatively, discrete methods such as spring network models have also been used to similarly reproduce experimental stress–strain curves (Mead et al., 1970; Cavalcante et al., 2005). Collagen, elastin, PGs, and viscoelastic matrix were considered within a 2D spring network model for parenchymal tissue and, under uniaxial loading, the model was able to generate stress–strain behaviour and hysteresis loops characteristic of experimental curves (Iravani et al., 2020).
The inclusion of more explicit microstructural detail within continuum models is supported via multiscale methods such as two-scale asymptotic homogenisation. A recent model for a poroelastic material at the tissue-level, upscaled from a solid and fluid phase at the microscale, is based on realistic microstructural geometries from micro CT images of lung parenchyma and offers coarse-grained simulations with computational efficiency (Concha and E Hurtado, 2020). In addition to microscale structure, microscale mechanics have also been shown to be important in the modelling of airways. In the case of bronchoconstriction in asthma, airway-level mechanics and deformation are coupled bidirectionally to the force-generating actin–myosin crossbridge dynamics within airway smooth muscle (ASM) cells as considered in multiscale continuum models (Politi et al., 2010; Lauzon et al., 2012; Hiorns et al., 2014). In general the bidirectional coupling in such models cannot easily be modelled entirely via constitutive relationships; dynamic cell-level processes are currently explicitly accounted for which increases computational cost and new approaches for upscaling may be needed (see e.g. (Donovan, 2020)).
In the examples above the relevant constitutive relationships and tissue mechanics are effectively snapshots in time. Disease progression affects tissue structure and function over longer timescales, and hence we next consider modelling that accounts for the effect of such changes on lung mechanics.
3.3 Changes in lung mechanics with time and disease progression
In many cases, disease progression is characterised by adverse changes in tissue structure and function over time. Once reliable frameworks for simulating lung and airway mechanics are in place, it is necessary to be able to model these long-term changes, occuring via tissue remodelling. Although the manifestations of airway remodelling—changes in collagen and airway smooth muscle cell mass, changes in airway wall area and luminal area—are observed at the tissue-level, the underlying regulation occurs at cellular and subcellular levels via complex cell signalling and mechanobiological cues (Noble et al., 2014). To balance model complexity and efficiency, the decision to consider cellular processes explicitly will depend on the question of interest and the available data. For example, to model observed spatial patterning of airway remodelling in human asthmatic airway samples, it was sufficient to hypothesise a linear relationship between remodelling and the extent of bronchoconstriction (when present), representing mechanosensitive cellular regulation but not considering pathways explicitly. This was simulated within a broader modelling framework for the whole lung, taking into account airway tree geometry, connectivity, ASM area and tone (Pascoe et al., 2020). Phenomenological relations like this can be hypothesised, tested, and verified in a specific context, making the models useful for further predictions. However, in order to understand the specific biological mechanisms behind bronchoconstriction-induced remodelling and possible pharmacological interventions, more detail would be needed about mechanobiological processes at the cellular and subcellular scales.
3.4 Airway structure and function
A cell-scale process of importance in asthma biology is that of phenotypic changes to ASM (Amrani and Panettieri, 2003; Wright et al., 2013); the current thinking is that most ASM in vivo likely exists in a contractile phenotype and that only small subpopulations transform to a synthetic or proliferative phenotype. On the other hand, in culture most of ASM quickly switches to a proliferative phenotype and small subpopulations can be driven back to contractile phenotype through serum deprivation (Halayko et al., 1999). An example of an early model that focuses on the role of phenotypic switching between proliferative and contractile ASM in airway remodelling is that of Chernyavsky et al. (2014) who use a relatively simple system of ordinary differential equations (ODEs) to investigate long term changes in ASM mass and phenotype in both deterministic and stochastic settings. A more detailed study is that of Hill et al. (2018), in which a multiphase mechanochemical, morphoelastic model is developed that combines the cardinal features of asthma (inflammation, hyperresponsiveness and remodelling) into a single integrative model. This model couples the mechanical state of asthmatic airways to (simplified) mechanobiological processes described by ODEs: inflammation due to prescribed allergen challenges mediates collagen deposition and phenotypic changes of smooth muscle cells from a contractile to proliferative phenotype. Tissue-level mechanics are considered via a multiphase model for a bilayered, cylindrical airway with constitutive relations prescribed separately for collagen and smooth muscle cells and the model captures feedback between contractility and inflammation. Parameter studies are carried out to simulate different asthmatic phenotypes (with parameters including the frequency of challenge events and clearance rate for inflammation). It provides a framework with which to test the hypothesis that while airway remodelling is initiated by inflammatory mediators, it is perpetuated by mechanical factors. The parameter study shows that persistent contractile tone observed in asthmatics could be a direct effect of the ASM cell’s response to its mechanical environment, and identifies mechanisms that may contribute to the existence of different asthma phenotypes and predisposition to fatal bronchospasms. In parallel with this model development, Tatler et al. (2022) ran a set of model-informed experiments in the ovalbumin chronic mouse model of asthma to quantify accurately the temporal changes in airway constituents in response to inflammatory challenges. This resulted in the development of a computational tool for the extraction of large amounts of quantitative data of airway structure and composition from tissue histomorphological lung slice images, that bridges the experimental and theoretical approaches of both studies (Hill et al., 2018; Tatler et al., 2022). In addition to inflammation, mechanical stress regulates airway remodelling via other mechanosensitive cell signalling pathways and via the direct activation of growth factors such as TGFβ. The relevant stresses in the context of experimental precision-cut lung-slice assays have been simulated in a tissue-level biomechanical model using finite element methods and in a reduced model using asymptotic reductions (Pybus et al., 2021a). This framework forms an efficient and appropriate model for incorporating models of growth factor involvement (such as TGFβ activation), the associated remodelling, and feedback to the tissue-level mechanics. Further modelling studies informed by experimental measurements of protein levels and gene expression are under way (in other contexts; see later) and are much needed in understanding airway remodelling.
While the examples above are associated with structural changes due to disease progression, mathematical models also have a role to play in understanding the effect of bronchial thermoplasty (a therapy involving ablation of ASM cells through radio-frequency heating) where the process is effectively considered to be a “reverse” of airway remodelling via targeted reduction of ASM mass. Theoretical models of bronchial thermoplasty have been informed by experimental in vitro data and validated by data from patients in a bronchial thermoplasty clinical trial (Chernyavsky et al., 2018). The significant finding from this study (that couples Joule heating due to the applied electrical current with bioheat transfer in the airway wall and surrounding parenchymal tissue) is that the acute post-heating phase of the procedure only results in a small fraction of the airway wall being heated to the threshold temperature required for ASM cell necrosis. Taken together with results from the corresponding in vitro study the authors propose that another mechanism must also contribute to the loss of ASM mass at the extent that has been reported by other investigators, over the longer term. This and other studies (Donovan et al., 2018) have generated some discussion in the literature (Brook et al., 2019). The new questions that have arisen from these studies have instigated the development of a new model that could explain longer term ASM loss and provide a possible explanation for why only some patients may benefit from the therapy (Pybus et al., 2021b).
In this section we considered models that account for structural changes at the tissue and airway level in asthma and how these give rise to modified tissue mechanics and therefore modified function. Such models still require upscaling into network models of the branching airway tree to understand the effect of airway remodelling on the whole organ with the associated exacerbation of existing heterogeneities (e.g., (Donovan and Noble, 2021)). Additionally we note that current approaches assume particular phenomenological constitutive relationships but further work is needed to understand how cell-level changes can modify these constitutive relationships.
3.5 Cell mechanics and signalling: understanding the drivers of change
We now consider models that account for more detailed mechanobiological drivers of remodelling in the lungs. In the context of idiopathic pulmonary fibrosis (IPF), a discrete approach was taken to studying spatial patterns in remodelling by considering a 2D spring network for lung tissue mechanics coupled to an agent-based model for the effects of fibroblast cell signalling; namely, their stiffness-dependent activation and deposition of collagen which leads to further local stiffening (Wellman et al., 2018). This positive feedback loop generated spatial patterns (subpleural honeycombing) consistent with CT images of the lungs of IPF patients, supporting the idea that positive feedback is a key driver of this patterning. Here, the positive feedback was provided by tissue stiffening near the already stiffer pleura via the hypothesised fibroblast rules in the agent-based model, which are therefore demonstrated to be plausible mechanisms. However, this does not rule out other causes that do not feature in the model. Additional hypotheses could similarly be tested in agent-based models to see which are viable (i.e., which are able to produce the observed behaviour) or which should be ruled out, with the viable hypotheses then further explored experimentally. Also in the context of IPF, a continuum model using reaction–diffusion partial differential equations (PDEs) for different cell types (monocytes, M1 and M2 macrophages, alveolar epithelial cells, fibroblasts) and key extracellular proteins and cytokines (MCP-1, TGFβ, PDGF, TNFα, IL-13, MMP, TIMP) has been presented (Hao et al., 2015), although not yet coupled to the mechanical state or response of the tissue. These types of models provide steps towards a more detailed understanding of pro-fibrotic cell signalling but they require many kinetic parameters to be determined, especially in this case when diffusion and chemotaxis were considered. Although it is not explored in this paper, the spatial modelling framework has potential for further studying patterning in fibrosis, which has been shown to be important due to differing effects of heterogeneous vs. homogeneous fibrosis on the bulk modulus of the tissue (Oliveira et al., 2014). Models accounting for mechanotransductive signalling pathways in more detail will be essential for understanding the complexities of airway remodelling, which is stimulated by both mechanical and biochemical cues.
In addition to being incorporated into multiscale models, cell-level mechanics have been modelled in more detail separately. Actin–myosin crossbridge dynamics are critical to contractile force-generation by ASM and therefore observed airway-level contractile behaviour. These are described by a well-established Huxley-Hai-Murphy (HHM) PDE model accounting for crossbridge cycling via local attachment and detachment rates and myosin phosphorylation and dephosphorylation (Hai and Murphy, 1988; Mijailovich et al., 2000). An extension of this model includes explicit calcium dependence for myosin light chain kinase activation (Wang et al., 2008). Accounting for disconnectivity and reorganisation of the contractile units (Brook, 2014) provides closer agreement with the “banana-shaped” force-length loops measured in tissue strip experiments (Fredberg et al., 1997; Bates et al., 2009) but requires increased computational time.
There is increasing evidence that the ECM plays an important regulatory role in maintaining ASM and that hyperresponsiveness may result from changes to structural ECM in asthmatic airways (Parameswaran et al., 2006; An et al., 2009; Polio et al., 2019). Additionally cell-level mechanical processes, including cell–matrix and cell–cell adhesion via integrins and cadherins, are mechanosensitive and also coupled bidirectionally to tissue deformation and stiffness. These are beginning to be considered in modelling efforts (Irons et al., 2018; Vargas et al., 2020), where complementary experimental approaches include atomic force microscopy for studying cell adhesion strength, stiffness, and surface topography (Smith et al., 2005; Sun et al., 2005), and traction force microscopy for studying local displacements of extracellular matrix (ECM) during ASM cell contraction (Lin et al., 2018). In particular, Irons et al. (2018) show that bistability in adhesion strength emerges from mechanical cooperativity between the multiple scales involved in the cell-matrix interactions in airways. The model was used to investigate the effect of perturbations mimicking DIs (as described in the exemplar above) where, because of the bistability, a DI applied to the high adhesion state could either induce a permanent switch to a lower adhesion state or allow a return of the system to the high adhesion state. These findings provide a candidate mechanism for the hitherto unexplained transient bronchodilatory effect of a DI observed in asthmatics compared to a more sustained effect in normal subjects. To validate this bistability, a joint experimental–theoretical study was designed incorporating atomic force microscopy (AFM) experiments to study the integrin response to external oscillatory loading of varying amplitudes applied to live smooth muscle cells and to model the corresponding cell–ECM interactions (Irons et al., 2020). Experimentally a transition was observed between states of firm adhesion and of complete detachment as the amplitude of oscillatory loading increased, as well as switching behaviour (which can indicate bistability in stochastic systems) between the two adhesion states during single timecourses at intermediate amplitudes. The model revealed two adhesion states qualitatively similar to the experimentally observed states, with a region of bistability where both the firm adhesion and detachment states can occur depending on the initial adhesion state. The model results provide a potential physical explanation for the experimental results and more importantly, taken together, suggest a means by which transient mechanical stimuli can induce long-term changes in adhesion dynamics, and thereby the ability of the cell to transmit force. While it still remains to be tested whether this region of bistability occurs in the physiologic range—the cell-level strain resulting from an organ-level deformation is yet to be determined—its occurrence is influenced by cell and ECM stiffness, thus structural changes in ECM could have multiple functional consequences for contractile force transmission in asthma.
When considering inter- or intra-cellular signalling, mechanobiological models are often based on experimental observations from cell culture or co-culture experiments where single or multiple cell types are seeded onto a substrate (e.g., collagen gels) and their response to substrate stiffness, mechanical loading, or biochemical stimuli are studied in vitro. Changes in specific proteins or gene expression can be quantified by Western blotting and quantitative polymerase chain reaction (qPCR) or RNA sequencing, respectively, giving insight into mechanosensitive signalling pathways responsible for changes in cell behaviour such as proliferation or contractility. An example of a recent in vitro experimental framework that considers mechanical loading is the so-called ‘bronchial chip’ developed to simultaneously study airway epithelial and smooth muscle cells when epithelial cells are subject to a compressive stress mimicking bronchospasm (Kilic et al., 2019). The ASM cells were observed to rapidly contract before relaxing at later times, mediated by paracrine signalling from the epithelial cells in which there is both positive and negative feedback between the 2 cell types at different timescales. A simple ODE model for the production of spasmogens and relaxants was fit to the data, and potential mediators were identified by measuring secreted factors and changes in epithelial cell gene expression. This could inform more detailed mathematical models in future, for example one in which specific signalling pathways are considered. Further demonstrating the close coupling of mechanics and cell signalling, Wang et al. (2019) showed via an experimental study the synergistic effects of force oscillations, applied to isolated airway smooth muscle strips, and pharmacological inhibition of Rho kinase (ROCK), a key intracellular signaling molecule, on the reduction of contractile force generation. The proposed combination as a so-called mechanopharmacological treatment opens interesting questions and opportunities for future mechanobiological computational models that couple cell-and tissue-scale processes, in which such mechanisms can be considered and strategies for optimising bronchodilation can be determined in silico.
Acto-myosin dynamics are primarily driven by release of calcium from intracellular stores into the ASM cell cytosol. There is a long history of incorporating calcium dynamics into models of acute smooth muscle contractile response to agonists. In particular the combination of simultaneous calcium signals with tissue level deformation in PCLS have provided the means to develop multiscale models that directly link subcellular calcium signalling to airway narrowing in particular. Wang et al. (2008), Wang et al. (2010) demonstrate that calcium oscillations (rather than uniformly elevated cytosolic calcium concentration) play an important role in ASM force generation. Recent models include the study of Croisier et al. (2013) to account for store-operated Ca2+ entry into ASM cells and its effect on Ca2+ oscillations. Building on this model, and using data from PCLS, Croisier et al. (2015) then showed how sensitization of the Ryanodine receptor (RyR) could result in abnormal Ca2+ signaling. This work provides both theoretical and experimental evidence for a possible underlying mechanism that might drive normal airway smooth muscle into a hyperresponsive phenotype and generated new hypotheses that began to be tested in Sanderson’s group (e.g. (Chen and Sanderson, 2017)).
4 Model-generated hypotheses
In Table 1 we highlight model-generated hypotheses that remain to be tested experimentally, focussing on areas with potential mechanopharmacological relevance.
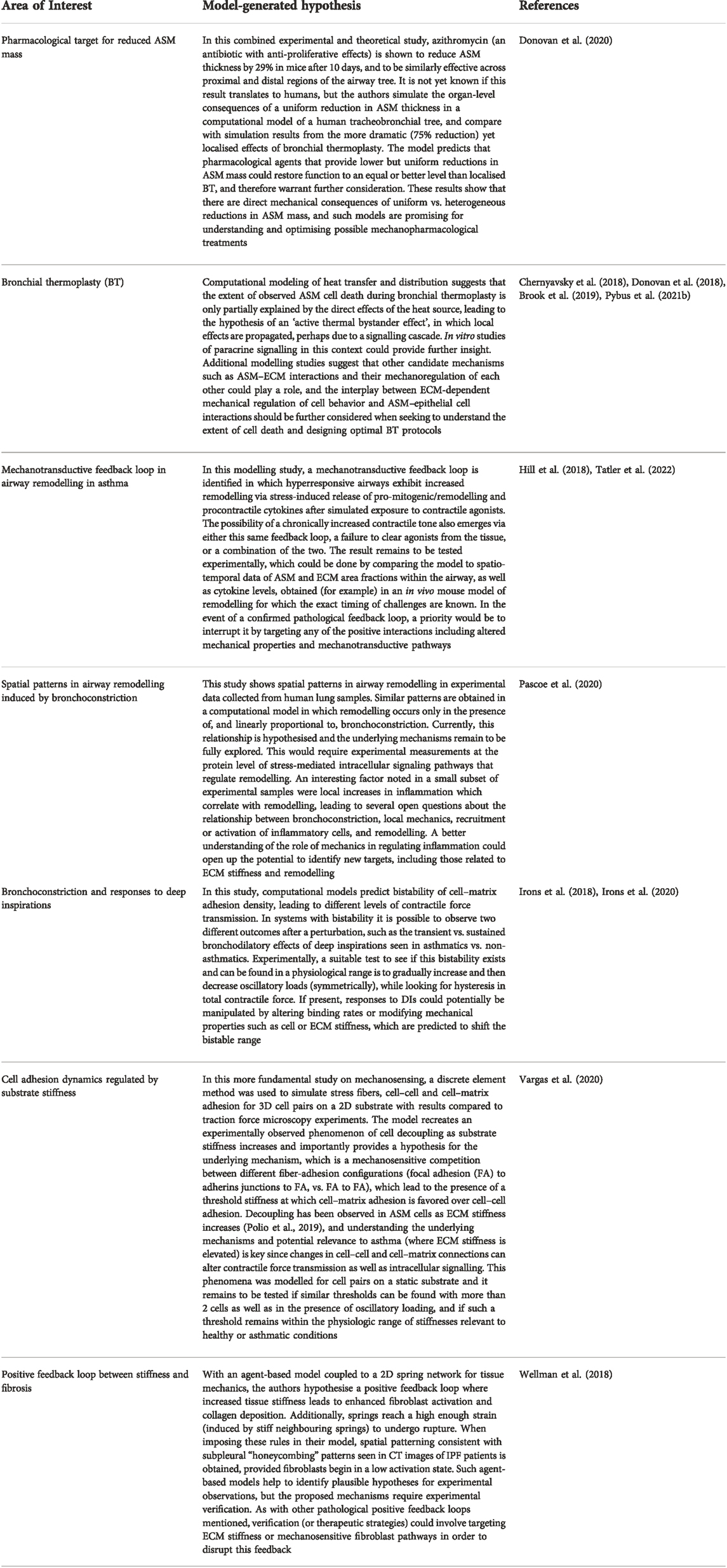
TABLE 1. Examples of hypotheses generated by mathematical modelling studies that are yet to be fully explored experimentally, where mechanics plays a fundamental role.
5 Modelling approaches from other biological systems
5.1 Coupling cell signalling models to models of tissue remodelling
Detailed intracellular signalling in current airway models is mainly limited to cytosolic and store-operated calcium signalling associated with activation of acute ASM contractile responses. Activation of pro-remodelling growth factors are currently modelled using phenomenological relationships inferred from experimental studies which only account for downstream effects of the more complicated mechanosensitive signalling networks involved. While these are good starting points, depending on the questions being addressed (e.g., involvement of pharmacology), more detailed models may be required. Tissue remodelling regulated by mechanosensitive signalling at the cellular level has been modelled in a variety of other biological systems including the skin, heart, and vasculature. We briefly highlight some multiscale modelling approaches taken for coupling tissue mechanics to cell signalling, from which the methods could serve as alternatives or exemplars to build from when considering multiscale modelling approaches for airway remodelling. Methods from arterial remodelling in particular contain many parallels; both airways and arteries are multilayered cylindrical structures with mechanical contributions from collagen and smooth muscle cells (SMCs). SMCs in both cases regulate passive and active contractile tone, and SMCs and fibroblasts regulate collagen turnover and tissue remodelling.
One multiscale tissue remodelling approach has been to couple finite element models for tissue mechanics to agent-based models for cell behavior. For example, in cardiac remodelling there is significant interest in scar formation via collagen deposition after myocardial infarction, and such approaches have been used to study the relation between local tissue mechanics and mechanosensitive fibroblast regulation of collagen (Rouillard and Holmes, 2014). In these models, disparate spatial scales require care to be taken over FEM mesh and ABM grid sizes (Lee et al., 2019). Finite element models can also be coupled to continuous systems of ODEs or PDEs at the cell level, as done in the context of wound healing in skin (Tepole, 2017). Here, PDEs capture transport and interactions between various growth factors and cell types, which influence cell proliferation, collagen deposition and fiber alignment, among other processes. Such reaction kinetics approaches at the cell level have also been used within multiscale models of arterial remodeling (Aparício et al., 2016; Marino et al., 2017), where here both models make use of an axisymmetric cylindrical geometry to simplify the tissue-level mechanics which do not require finite element methods. A major remaining challenge—especially as the number of modelled interactions increases—is the determination of kinetic parameters, which requires extensive timecourse data at the cell level.
In an alternative approach to reaction kinetics that more easily supports larger scale cell signalling networks, activation and inhibition interactions between network species can be written as a set of logic statements, with multivariable interactions implemented by using “AND” and “OR” logical operators. Traditionally, these logic statements would be implemented within a discrete Boolean update scheme where each network species either takes the value 0 or 1, representing an inactive or active state (Morris et al., 2010). Activation or inhibition reactions are then governed by Heaviside step functions and truth tables. Due to the limitations of a discrete approach, however, continuum logic-based methods have now been developed where network species can take any value in the [0, 1] range, where normalised Hill functions are used instead of step functions to model activation and inhibition, and where the logical “AND” and “OR” operators are interpolated between the values in truth tables to also be continuous functions (Wittmann et al., 2009; Kraeutler et al., 2010). One such method was initially proposed and validated against a reaction kinetics model for cardiac β-adrenergic signalling (Kraeutler et al., 2010), with a key advantage including a significantly reduced parameter set yet consistent predictive results. This method has since been used to study large scale intracellular signalling networks across different systems and cell types, with examples including cardiac fibroblasts (Zeigler et al., 2016), vascular smooth muscle cells and fibroblasts (Irons and Humphrey, 2020; Wang et al., 2020; Estrada et al., 2021), dermal fibroblasts (Cursons et al., 2015), brain endothelial cells (Gorick et al., 2022), and macrophages (Liu et al., 2021). Recently, using the cardiac fibroblast model, an in silico screen was carried out for 121 FDA-approved drugs to predict and understand the signaling mechanisms behind observed effects of pharmacological interventions (Zeigler et al., 2021). The flexibility to systematically introduce network perturbations that simulate external interventions make this an appealing framework for initial identification or shortlisting of pharmacological targets. In addition, these types of logic-based signalling networks can incorporate changes in mechanical stimuli and have recently been used within multiscale models, e.g., within a hybrid multiscale agent-based model for cardiac fibrosis (Rikard et al., 2019) and a continuum constrained mixture model for arterial growth and remodelling (Irons et al., 2021) in which pathways behind stress-mediated remodelling and feedback to and from tissue-level mechanics are considered. Similar mechanosensitive pathways are critical to airway remodelling, and multiscale models that consider coupling between airway remodelling, mechanics and detailed intracellular signalling pathways will provide important insight into inflammation- and bronchoconstriction-induced remodelling.
5.2 Data-driven modelling and machine learning
While an important aspect of the models developed above is the validation of model predictions via experimentally-obtained data, another equally important aspect of generating real impact in the development of therapies, is for the models to be informed by experimental data. Many models require assumptions to be made about the underlying biological mechanisms or constitutive mechanical laws for biological tissue; traditionally these assumptions are incorporated through phenomenological relationships based on experimental findings. More recently, however, data-driven modelling approaches are beginning to play an important role in addressing some of the challenges associated with accurately informing models such as sparsity of biological data, multiple candidate mathematical models and computationally expensive numerical simulations. Such approaches use deep learning neural networks to both solve systems of equations (data-driven solution) and identify or discover specific forms for the terms in systems of ODEs or PDEs that may not be easily postulated a priori, but can be “learned” through appropriate use of experimental data (data-driven discovery of PDEs) (Rudy et al., 2017; Raissi et al., 2019). From the point of view of developing mathematical models for biological applications, the most powerful aspect of these approaches is that the governing system of equations are mechanistic so that each term can still be related to specific biological or physical mechanisms. A specific exemplar is the work of Lagergren et al. (2020) who, in an extension of the physics-informed neural networks described by Raissi et al. (2019), provide a data-driven methodology which is demonstrated using a case study of scratch assay experiments. The authors assume a set of governing reaction–diffusion equations in which the exact nonlinear forms of diffusivity and growth are not known. Using spatio-temporal data and cell density from the scratch-assay experiments (with space and time as inputs and cell density as an output to/from a deep neural network) they first approximate the solution of the governing dynamical system. The nonlinear forms of the diffusivity and growth terms in the dynamical system are then learned. Automatic differentiation is used on compositions of the different neural network models (i.e., cell density, diffusivity, and growth) to construct the PDE that describes the governing dynamical system. The governing system is used in an objective function associated with the full neural network to jointly learn and satisfy the governing PDE while minimizing the error between the network outputs and noisy observations. Such approaches could play an important role in identifying mathematical forms for hitherto unknown biological mechanisms, or where it is well known that in vitro data (and corresponding phenomenological relationships) may not accurately reflect in vitro behaviour. A specific example from our work that will benefit from the approach described above is in linking extensive spatio-temporal data from an in vivo mouse model of remodelling (Tatler et al., 2022) to mathematical models of remodelling (Hill et al., 2018) in which specific mathematical forms for the candidate mechanisms could be learned. The reader is directed to (Alber et al., 2019) for further reviews of machine learning in multiscale models.
5.3 Methods for transferring information across scales
Although detailed multiscale models of single airways linking multiple cell types to tissue level behaviour provides important insight into airway mechanics, whole-lung behaviour cannot be easily inferred from isolated airways. Inter-airway interactions as a result of being part of a branching network, as well as interdependence between airways and lung parenchyma need to be considered. For a comprehensive review of such models the reader is directed to Rampadarath and Donovan (Rampadarath and Donovan, 2021). Here we briefly focus on branching network models which need to account for the nonlinear, viscoelastic airway mechanics of bronchoconstriction, to understand, for instance, ventilation heterogeneities observed in hyperpolarised gas imaging studies. These models typically assume Poiseuille flow in individual airways with some correction (e.g., the earliest models of Pedley et al. (1971)) and the tissue mechanics require constitutive relationships of the non-linear pressure-radius or pressure-area relationships to characterise each airway within the network; most studies rely on the empirical observations of Lambert et al. (1982). These measurements and extrapolated relationships provide a reasonable description of passive purely elastic airway mechanics but the resulting branching network models are governed by a large system of differential algebraic equations that can be computationally costly to solve. Depending on the questions being addressed (e.g., heterogeneity of bronchoconstriction) the effect of contractile agonist on the ASM requires additional relationships as measured by LaPrad et al. (2010) and Harvey et al. (2013) but the relationships for each airway in the branching network may vary depending on airway size, agonist concentration, timescale of tidal oscillations or degree of airway remodelling as predicted by Hiorns et al. (2014), Hiorns et al. (2016) and Hill et al. (2018). To incorporate such changes we need appropriate methods for upscaling from individual airways, that exhibit potentially different mechanical characteristics, to branching network models in a computationally efficient way. Not every detail at the individual airway level is needed in the higher scale model and simplifications can be made at the outset; what those simplifications should be will depend on the specific question being addressed. Recently graph-theoretic perspectives have proven useful in characterizing transport in various examples of biological networks. Whitfield et al. (2020) use concepts from spectral graph theory to demonstrate that the resistive properties of realistic tree networks are characterized by a tree-specific operator called the Maury matrix, first introduced in (Maury, 2013) which provides a complete description of linear resistance relations on the network. They demonstrate how ventilation heterogeneity can be evaluated for four realistic airway network models (based on CT imaging) and how the Maury operator efficiently captures spatial patterns of ventilation heterogeneity, providing a new method for dimensionality reduction in these systems. The main limitations to this approach, however, is that it is restricted to fixed linear resistance relations. Future work should consider how the efficiency of such approaches can be exploited to effectively characterise other properties of the network such as dynamic airway compliance, resistance and viscoelasticity.
At the airway scale, we noted above that current phenomenological descriptions for constitutive relationships for the underlying biological tissue cannot easily account for ASM cells actively generating contractile force, or rapid remodelling of the cell cytoskeleton that is thought to occur on short timescales; again methods for determining constitutive relationships are needed. Recent examples for doing this in other biological applications come from bottom-up models of individual cells allowing for key cellular processes of proliferation, adhesion, and short- and long-range signalling to be included (Osborne et al., 2017). Popular approaches for modelling tightly-packed cells are the off-lattice vertex-based models in which each cell is typically modelled as a polygon (each side modelled as a spring) to represent the cell membrane with multicellular tissue effectively modelled as a network of elastic springs. Each cell vertex moves according to a balance of forces due to limited compressibility, cytoskeletal contractility and cell-cell adhesion with additional rules governing cell neighbour rearrangements, proliferation and apoptosis. These types of models have generally been applied to epithelial tissues (e.g., (Nestor-Bergmann et al., 2018)). Preliminary studies suggest that this approach appears to be the most promising avenue for modelling multicellular arrangements of ASM cells in which intracellular contractile apparatus can be introduced and changes in phenotype can be incorporated through modifications to their contractile machinery and therefore ability to respond to contractile stimuli and also through cell shape (to represent spindle-shaped contractile cells versus more rhomboid proliferative phenotype). Tissues built up from individual-based cell models can then be used to represent confluent cell layers in traction force microscopy experiments providing validation of the underlying model, and from which stress–strain relationships emerge (on simulated application of load) that account for the cellular processes of contraction and phenotypic switching.
One of the greatest contributors to computational cost in simulating the cell- or tissue-level models discussed above is that of solving the HHM model to determine distributions of bound cross-bridges and thereby the force generated by ASM cells via acto-myosin crossbridge interactions. Isolated finite-thickness airway models that use the HHM model suffers from significant computational cost (e.g., (Hiorns et al., 2014; Hiorns et al., 2016)); furthermore the cost becomes prohibitive for whole lung branching networks. To provide computationally efficient ways of coupling muscle cell contraction to tissue behaviour, simplified models, first proposed by Zahalak (Zahalak, 1981) for the Huxley model for striated muscle, have been developed for ASM and corresponding HHM models by Rampadarath and Donovan (Rampadarath and Donovan, 2018). The idea behind this is that an ansatz is made regarding the form of probability distribution functions (PDFs) of the cross-bridge distributions, enabling the reduction of the governing PDEs to a system of ODEs in terms of the distribution-moments of the PDF. The idea is further extended to generalised distribution-moment approximations in (Donovan, 2020) and provides potentially viable alternatives to the full HHM model for incorporating ASM activity into branching network models. Other possibilities are the development of Gaussian process emulators used successfully in cardiovascular fluid dynamics (Melis et al., 2017), the pulmonary circulatory system (Noè et al., 2016) and ventricular mechanics (Di Achille et al., 2018). Essentially the computationally expensive mathematical model is replaced with a computationally cheap statistical surrogate model (the emulator) obtained via numerical simulations of the underlying partial differential equations covering as much of the parameter space as possible combined with multivariate smooth interpolation between solutions using methods from non-parametric Bayesian statistics based on Gaussian processes. As far as we are aware such approaches have not been used in the context of cell–tissue interactions in airways but could be a promising avenue allowing for more accurate representation of the underlying biophysical mechanisms.
6 Conclusion and outlook
The dependence of ASM cell responses on airway mechanical environment and loading conditions is now well-established in acute events such as agonist-induced bronchoconstriction and over longer timescales in airway remodelling. Mechanopharmacology and the importance of considering such mechanobiological effects when identifying and optimising pharmacological interventions has been acknowledged in clinical and experimental communities, and should be of high priority in asthma where the interplay between mechanics and cellular processes—including active contraction generated by crossbridge cycling within ASM cells as well as pro-remodelling and pro-inflammatory biochemical signalling cascades—are so closely coupled. One key example of a mechanopharmacological strategy noted above is the study by Wang et al. (2019), in which relaxation of ASM was observed in tissue strips with synergistic effects between the application of force oscillations and low dose β2 agonists and/or a ROCK inhibitor, which reduce contractility and cytoskeletal stiffness respectively. It is thus proposed that either of these interventions would allow for the beneficial effects of pressure oscillations to be obtainable with lower amplitude oscillations. This observation also indicates that expected effects of these pharmacological agents when measured under static conditions may not translate well to the in vivo setting, due to the expected synergy when combined with oscillatory loading. So far, the proposed area of mechanopharmacology has focused on encouraging the use of experimental systems where physiological loads can be applied, and in developing high-throughput methods for such systems (Krishnan et al., 2016). In this review, we aim to have highlighted the potential for using mathematical models to complement this approach in asthma, where numerous modelling frameworks currently exist across scales that consider various aspects of lung and airway mechanics. Although model extensions and integration are still required, there is considerable opportunity to then design or optimise new mechanopharmacological therapies, where in silico exploration can yield improved mechanistic insights into these multiscale processes as well as reducing the experimental burden.
We highlighted some model generated hypotheses that remain to be experimentally validated (Table 1), but it is also worth highlighting some specific experimental approaches that could benefit from complementary modelling frameworks for the development of predictive models. Park et al. (2015) demonstrated how high-throughput drug screening can be improved by ensuring assays being used most closely mimic the biomechanical (micro)environment. The assay they developed uses human cells of patient- and disease-dependent phenotype, and embed mechanical measurements of cell contractility, providing a rich source of data for use in appropriate mathematical models. Other important experimental approaches that maintain a mechanical environment that is as close as possible to that of the airway in vivo are those involving precision-cut lung-slices. These approaches date back to the studies of Dandurand et al. (1993) and Martin et al. (1996) in which the effect of cell contractility on airway narrowing could be directly measured, while the study of Bergner and Sanderson (Bergner and Sanderson, 2002) established the concurrent imaging of intracellular calcium concentration. More recently the effect of immune responses have been studied using PCLS (Henjakovic et al., 2008) as well as longer term changes such as alveologenesis (Akram et al., 2019). Interested readers are directed to the comprehensive reviews of Sanderson (Sanderson, 2011) and Liu et al. (2019). These ex vivo assays not only maintain a similar mechanical environment to the airway in vivo (e.g., a more realistic airway geometry embedded in parenchyma, compared with isolated tissue strips), the ECM and other cell types that interact with ASM cells such as epithelial cells and mast cells are still present, which continue to interact during the experiment. The combination of PCLS with the ability to externally load the lung slice as demonstrated by Lavoie et al. (2012), and the use of tissue traction microscopy to quantify contractile forces in PCLS (Ram-Mohan et al., 2020) opens up further avenues for exploring the interaction of cell- and tissue-mechanics with cell signalling in integrative mathematical models (e.g., (Wang et al., 2008; Brook et al., 2010; Maarsingh et al., 2019; Pybus et al., 2021a)). Organ-on-a-chip (Huh et al., 2010; Huh, 2015) and development of 3D organoid technologies (Güney et al., 2021) also allow inclusion of multiple cell types and ECM as well as application of physiological loading conditions. For instance in the combined experimental/modelling study of Kilic et al. (2019), bronchial-chip results indicate positive feedback between ASM contraction and compressive stress on epithelium. They were able to fit a minimal ODE model (consisting of the three variables—contraction level, spasmogen and relaxant—with competing positive and negative feedback loops) to the experimental data. The authors demonstrate the development of persistent contraction over shorter time scales in a similar mechanism to one that emerged out of the longer-term remodelling study of Hill et al. (2018). Additionally the Kilic et al. model suggests that exposure of ASM to beta-blockers could lead to longer term beneficial effects of endogenous bronchodilators such as PGE2 (while acknowledging the primary effect of acute bronchoconstriction). More detailed cell signalling models exploring the effects of modulated inflammatory response and mucous metaplasia could be of particular benefit here. The mechanopharmacological bioassays described above complemented with multiscale models that account for both mechanics and the relevant pharmacodynamics could be combined to achieve the broader goals of drug efficacy and trial success.
Current therapies in asthma focus almost exclusively on targeting inflammation and reducing ASM force (as discussed above). However, even when inflammation is controlled, asthmatic airways remain hyperresponsive suggesting that alternative mechanisms may play a role in maintaining this state. Some candidate mechanisms emerge from integrative studies cited above, but remain to be experimentally confirmed. An important mechanical component that hitherto has received less attention than ASM is the role of ECM and ASM–ECM interactions (although accounted for in simplified ways in some of the above cited studies). There is increasing evidence for a synergistic relationship between ASM and ECM over long timescales (see (Parameswaran et al., 2006) for a complete review); briefly, ASM cells in the synthetic phenotype can deposit ECM proteins, are involved in the downregulation of MMPs and upregulation of TIMPs which modifies the ECM, and ECM proteins in turn play a role in regulating ASM proliferation, migration and contraction (e.g., (Naveed et al., 2017) and references therein). These regulatory mechanisms (or aberrations thereof) are likely to play an important role in airway remodelling. On shorter timescales Stasiak et al. (2020) show that ECM regulates agonist-induced calcium oscillations in ASM cells; calcium responses in healthy donor ASM cells and stiffened underlying ECM were consistent with responses that would be expected with significantly higher agonist dose. Similarly, interactions between the ASM and a stiffer ECM environment have been shown to lead to increased ASM contractility (Polio et al., 2019) and enough to lead to hyperresponsiveness (Jamieson et al., 2021). All of the above are characteristic features of asthma, suggesting that detailed models of both acute bronchoconstriction and long-term remodelling designed to investigate mechanopharmacological therapies will benefit from the inclusion of the mechanics and regulatory aspects of ECM in airways.
Finally, we discussed methods and modelling frameworks from other contexts where progress has been made. One focus was on models where long term tissue remodelling is driven by (and affects) cell signalling. Detail about specific signalling pathways is lacking in the existing mathematical models of airway remodelling, although there is again much opportunity to expand in this area and to make use of the recent rapid growth of genomic and proteomic data. Models incorporating detailed mechanosensitive cell signalling pathways will be essential for many mechanopharmacological studies, since pharmacological interventions operate at the level of specific intracellular signalling proteins and/or cell surface receptors, alone or in combination. Incorporating these pathways into larger scale modelling frameworks will eventually allow for exploration of many important factors relevant to heterogeneity of response within the lung, the variable responses of heterogeneous populations, including patient-specific geometries or the roles of aging (i.e., associated with modified airway stiffnesses). With the growing availability of large scale datasets and increasing computing power, data-driven approaches could play a more important role in both informing model development as well as in the inference of parameters and underlying non-linear relationships, which are needed to improve the predictive power of such models.
In order to accelerate our understanding of respiratory health and disease and to propose new therapies, we must consolidate rapid and exciting developments in the theoretical and experimental communities, and promote increased interaction and integration of information not only across scales, but also across disciplines.
Author contributions
Both authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
BSB acknowledges funding from the EPSRC Healthcare Technologies NetworkPlus grant (EP/W000490/1) “Integrating data-driven BIOphysical models into REspiratory MEdicine” (BIOREME) and open access publication from the University of Nottingham. This work was supported by the Engineering and Physical Sciences Research Council (grant number EP/W000490/1): EPSRC Healthcare Technologies NetworkPlus “Integrating data-driven BIOphysical models into REspiratory MEdicine” (BIOREME).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akram, K. M., Yates, L. L., Mongey, R., Rothery, S., Gaboriau, D. C. A., Sanderson, J., et al. (2019). Live imaging of alveologenesis in precision-cut lung slices reveals dynamic epithelial cell behaviour. Nat. Commun. 10 (1), 1178. doi:10.1038/s41467-019-09067-3
Alber, M., Buganza Tepole, A., Cannon, W. R., De, S., Dura-Bernal, S., Garikipati, K., et al. (2019). Integrating machine learning and multiscale modeling, perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. NPJ Digit. Med. 2 (1), 115. doi:10.1038/s41746-019-0193-y
Amrani, Y., and Panettieri, R. A. (2003). Airway smooth muscle: Contraction and beyond. Int. J. Biochem. Cell. Biol. 35 (3), 272–276. doi:10.1016/s1357-2725(02)00259-5
An, S. S., Kim, J., Ahn, K., Trepat, X., Drake, K. J., Kumar, S., et al. (2009). Cell stiffness, contractile stress and the role of extracellular matrix. Biochem. Biophys. Res. Commun. 382 (4), 697–703. doi:10.1016/j.bbrc.2009.03.118
Aparício, P., Thompson, M. S., and Watton, P. N. (2016). A novel chemo-mechano-biological model of arterial tissue growth and remodelling. J. Biomech. 49 (12), 2321–2330. doi:10.1016/j.jbiomech.2016.04.037
Bates, J. H. T., Bullimore, S. R., Politi, A. Z., Sneyd, J., Anafi, R. C., and Lauzon, A.-M. (2009). Transient oscillatory force-length behavior of activated airway smooth muscle. Am. J. Physiol. Lung Cell. Mol. Physiol. 297 (2), L362–L372. doi:10.1152/ajplung.00095.2009
Berger, L., Bordas, R., Burrowes, K., Grau, V., Tavener, S., and Kay, D. (2016). A poroelastic model coupled to a fluid network with applications in lung modelling. Int. J. Numer. Method. Biomed. Eng. 32 (1), e02731. doi:10.1002/cnm.2731
Bergner, A., and Sanderson, M. J. (2002). Acetylcholine-induced calcium signaling and contraction of airway smooth muscle cells in lung slices. J. Gen. Physiol. 119 (2), 187–198. doi:10.1085/jgp.119.2.187
Bhatawadekar, S. A., Leary, D., and Maksym, G. N. (2015). Modelling resistance and reactance with heterogeneous airway narrowing in mild to severe asthma. Can. J. Physiol. Pharmacol. 93 (3), 207–214. PMID: 25730711. doi:10.1139/cjpp-2014-0436
Birzle, A. M., Hobrack, S. M. K., Martin, C., Uhlig, S., and Wall, W. A. (2019). Constituent-specific material behavior of soft biological tissue: Experimental quantification and numerical identification for lung parenchyma. Biomech. Model. Mechanobiol. 18 (5), 1383–1400. doi:10.1007/s10237-019-01151-3
Brook, B. S., Chernyavsky, I. L., Russell, R. J., Saunders, R. M., and Brightling, C. E. (2019). Comment on “unraveling a clinical paradox: Why does bronchial thermoplasty work in asthma?”. Am. J. Respir. Cell. Mol. Biol. 61 (5), 660–661. PMID: 31674824. doi:10.1165/rcmb.2019-0095LE
Brook, B. S. (2014). Emergence of airway smooth muscle mechanical behaviour through dynamic reorganisation of contractile units and force transmission pathways. J. Appl. Physiology 116 (8), 980–997. doi:10.1152/japplphysiol.01209.2013
Brook, B. S., Peel, S. E., Hall, I. P., Politi, A. Z., Sneyd, J., Bai, Y., et al. (2010). A biomechanical model of agonist-initiated contraction in the asthmatic airway. Respir. Physiol. Neurobiol. 170 (1), 44–58. doi:10.1016/j.resp.2009.11.006
Burrowes, K. S., Iravani, A., and Kang, W. (2019). Integrated lung tissue mechanics one piece at a time: Computational modeling across the scales of biology. Clin. Biomech. 66, 20–31. doi:10.1016/j.clinbiomech.2018.01.002
Cavalcante, F. S. A., Ito, S., Brewer, K., Sakai, H., Alencar, A. M., Almeida, M. P., et al. (2005). Mechanical interactions between collagen and proteoglycans: Implications for the stability of lung tissue. J. Appl. Physiol. 98 (2), 672–679. doi:10.1152/japplphysiol.00619.2004
Chen, J., and Sanderson, M. J. (2017). Store-operated calcium entry is required for sustained contraction and ca2+ oscillations of airway smooth muscle. J. Physiol. 595 (10), 3203–3218. doi:10.1113/JP272694
Chernyavsky, I. L., Crosier, H., Chapman, L. A. C., Kimpton, L. S., Hiorns, J. E., Brook, B. S., et al. (2014). The role of inflammation resolution speed in airway smooth muscle mass accumulation in asthma: Insight from a theoretical model. PLOS ONE 9 (3), e90162. doi:10.1371/journal.pone.0090162
Chernyavsky, I. L., Russell, R. J., Saunders, R. M., Morris, G. E., Berair, R., Singapuri, A., et al. (2018). In vitro, in silico and in vivo study challenges the impact of bronchial thermoplasty on acute airway smooth muscle mass loss. Eur. Respir. J. 51 (5), 1701680. doi:10.1183/13993003.01680-2017
Choi, S., Yoon, S., Jeon, J., Zou, C., Choi, J., Tawhai, M. H., et al. (2019). 1d network simulations for evaluating regional flow and pressure distributions in healthy and asthmatic human lungs. J. Appl. Physiol. 127 (1), 122–133. doi:10.1152/japplphysiol.00016.2019
Concha, F., and E Hurtado, D. (2020). Upscaling the poroelastic behavior of the lung parenchyma: A finite-deformation micromechanical model. J. Mech. Phys. Solids 145, 104147. doi:10.1016/j.jmps.2020.104147
Croisier, H., Tan, X., Chen, J., Sneyd, J., Sanderson, M. J., and Brook, B. S. (2015). Ryanodine receptor sensitization results in abnormal calcium signaling in airway smooth muscle cells. Am. J. Respir. Cell. Mol. Biol. 53 (5), 703–711. doi:10.1165/rcmb.2014-0386OC
Croisier, H., Tan, X., Perez-Zoghbi, J. F., Sanderson, M. J., Sneyd, J., and Brook, B. S. (2013). Activation of store-operated calcium entry in airway smooth muscle cells: Insight from a mathematical model. PloS one 8 (7), e69598. doi:10.1371/journal.pone.0069598
Cursons, J., Gao, J., Hurley, D. G., Dunbar, P. R., Jacobs, M. D., Crampin, E. J., et al. (2015). Regulation of ERK-MAPK signaling in human epidermis. BMC Syst. Biol. 9 (1), 41. doi:10.1186/s12918-015-0187-6
Dandurand, R. J., Wang, C. G., Phillips, N. C., and Eidelman, D. H. (1993). Responsiveness of individual airways to methacholine in adult rat lung explants. J. Appl. Physiol. 75 (1), 364–372. doi:10.1152/jappl.1993.75.1.364
Di Achille, P., Harouni, A., Khamzin, S., Solovyova, O., Rice, J. J., and Gurev, V. (2018). Gaussian process regressions for inverse problems and parameter searches in models of ventricular mechanics. Front. Physiol. 9, 1002. doi:10.3389/fphys.2018.01002
Donovan, G. M. (2016). Clustered ventilation defects and bilinear respiratory reactance in asthma. J. Theor. Biol. 406, 166–175. doi:10.1016/j.jtbi.2016.06.035
Donovan, G., and Noble, P. B. (2021). Small airways vs large airways in asthma: Time for a new perspective. J. Appl. Physiol. 131, 1839–1841. doi:10.1152/japplphysiol.00403.2021
Donovan, G. M., Elliot, J. G., Green, F. H. Y., James, A. L., and Noble, P. B. (2018). Unraveling a clinical paradox: Why does bronchial thermoplasty work in asthma? Am. J. Respir. Cell. Mol. Biol. 59 (3), 355–362. PMID: 29668295. doi:10.1165/rcmb.2018-0011OC
Donovan, G. M. (2020). Generalized distribution-moment approximation for kinetic theories of muscular contraction. Math. Biosci. 329, 108455. doi:10.1016/j.mbs.2020.108455
Donovan, G. M. (2017). Inter-airway structural heterogeneity interacts with dynamic heterogeneity to determine lung function and flow patterns in both asthmatic and control simulated lungs. J. Theor. Biol. 435, 98–105. doi:10.1016/j.jtbi.2017.08.024
Donovan, G. M., Wang, K. C. W., Shamsuddin, D., Mann, T. S., Henry, P. J., Larcombe, A. N., et al. (2020). Pharmacological ablation of the airway smooth muscle layer; mathematical predictions of functional improvement in asthma. Physiol. Rep. 8 (11), e14451. doi:10.14814/phy2.14451
Eskandari, M., Nordgren, T. M., and O’Connell, G. D. (2019). Mechanics of pulmonary airways: Linking structure to function through constitutive modeling, biochemistry, and histology. Acta Biomater. 97, 513–523. doi:10.1016/j.actbio.2019.07.020
Estrada, A. C., Irons, L., Rego, B. V., Li, G., Tellides, G., and Humphrey, J. D. (2021). Roles of mTOR in thoracic aortopathy understood by complex intracellular signaling interactions. PLoS Comput. Biol. 12 (17), e1009683. doi:10.1371/journal.pcbi.1009683
Foy, B. H., Soares, M., Bordas, R., Richardson, M., Bell, A., Singapuri, A., et al. (2019). Lung computational models and the role of the small airways in asthma. Am. J. Respir. Crit. Care Med. 200 (8), 982–991. PMID: 31106566. doi:10.1164/rccm.201812-2322OC
Fredberg, J. J., Inouye, D., Miller, B., Nathan, M., Jafari, S., Raboudi, S. H., et al. (1997). Airway smooth muscle, tidal stretches, and dynamically determined contractile states. Am. J. Respir. Crit. Care Med. 156 (6), 1752–1759. doi:10.1164/ajrccm.156.6.9611016
Fung, Y.-C. (1974). A theory of elasticity of the lung. J. Appl. Mech. 41 (1), 8–14. doi:10.1115/1.3423281
Gorick, C. M., Saucerman, J. J., and Price, R. J. (2022). Computational model of brain endothelial cell signaling pathways predicts therapeutic targets for cerebral pathologies. J. Mol. Cell. Cardiol. 164, 17–28. doi:10.1016/j.yjmcc.2021.11.005
Güney, T. G., Herranz, A. M., Mumby, S., Dunlop, I. E., and Adcock, I. M. (2021). Epithelial–stromal cell interactions and extracellular matrix mechanics drive the formation of airway-mimetic tubular morphology in lung organoids. Iscience 24 (9), 103061. doi:10.1016/j.isci.2021.103061
Huh, D. (2015). A human breathing lung-on-a-chip. Ann. Am. Thorac. Soc. 12, S42–S44. doi:10.1513/annalsats.201410-442mg
Hai, C.-M., and Murphy, R. A. (1988). Cross-bridge phosphorylation and regulation of latch state in smooth muscle. Am. J. Physiol. 254 (1), C99–C106. doi:10.1152/ajpcell.1988.254.1.C99
Halayko, A. J., Camoretti-Mercado, B., Forsythe, S. M., Vieira, J. E., Mitchell, R. W., Wylam, M. E., et al. (1999). Divergent differentiation paths in airway smooth muscle culture: Induction of functionally contractile myocytes. Am. J. Physiol. 276 (1), L197–L206. doi:10.1152/ajplung.1999.276.1.L197
Hao, W., Marsh, C., and Friedman, A. (2015). A mathematical model of idiopathic pulmonary fibrosis. PLoS One 10 (9), e0135097. doi:10.1371/journal.pone.0135097
Harvey, B. C., Parameswaran, H., and Lutchen, K. R. (2013). Can tidal breathing with deep inspirations of intact airways create sustained bronchoprotection or bronchodilation? J. Appl. Physiol. 115, 436–445. doi:10.1152/japplphysiol.00009.2013
Henjakovic, M., Sewald, K., Switalla, S., Kaiser, D., Müller, M., Veres, T. Z., et al. (2008). Ex vivo testing of immune responses in precision-cut lung slices. Toxicol. Appl. Pharmacol. 231 (1), 68–76. doi:10.1016/j.taap.2008.04.003
Hill, M. R., Philp, C. J., Billington, C. K., Tatler, A. L., Johnson, S. R., O’Dea, R. D., et al. (2018). A theoretical model of inflammation-and mechanotransduction-driven asthmatic airway remodelling. Biomech. Model. Mechanobiol. 17 (5), 1451–1470. doi:10.1007/s10237-018-1037-4
Hiorns, J. E., Jensen, O. E., and Brook, B. S. (2014). Nonlinear compliance modulates dynamic bronchoconstriction in a multiscale airway model. Biophys. J. 107 (12), 3030–3042. doi:10.1016/j.bpj.2014.10.067
Hiorns, J. E., Jensen, O. E., and Brook, B. S. (2016). Static and dynamic stress heterogeneity in a multiscale model of the asthmatic airway wall. J. Appl. Physiol. 121 (1), 233–247. doi:10.1152/japplphysiol.00715.2015
Huh, D., Matthews, B. D., Mammoto, A., Montoya-Zavala, M., Hsin, H. Y., and Ingber, D. E. (2010). Reconstituting organ-level lung functions on a chip. Science 328 (5986), 1662–1668. doi:10.1126/science.1188302
Iravani, A., Thambyah, A., and Burrowes, K. S. (2020). A viscoelastic two-dimensional network model of the lung extracellular matrix. Biomech. Model. Mechanobiol. 19, 2241–2253. doi:10.1007/s10237-020-01336-1
Irons, L., Huang, H., Owen, M. R., O’Dea, R. D., Meininger, G. A., and Brook, B. S. (2020). Switching behaviour in vascular smooth muscle cell–matrix adhesion during oscillatory loading. J. Theor. Biol. 502, 110387. doi:10.1016/j.jtbi.2020.110387
Irons, L., and Humphrey, J. D. (2020). Cell signaling model for arterial mechanobiology. PLoS Comput. Biol. 16 (8), e1008161. doi:10.1371/journal.pcbi.1008161
Irons, L., Latorre, M., and D Humphrey, J. (2021). From transcript to tissue: Multiscale modeling from cell signaling to matrix remodeling. Ann. Biomed. Eng. 49, 1701–1715. doi:10.1007/s10439-020-02713-8
Irons, L., Owen, M. R., O’Dea, R. D., and Brook, B. S. (2018). Effect of loading history on airway smooth muscle cell-matrix adhesions. Biophys. J. 114 (11), 2679–2690. doi:10.1016/j.bpj.2018.04.026
Jamieson, R. R., Stasiak, S. E., Polio, S. R., Augspurg, R. D., McCormick, C. A., Ruberti, J. W., et al. (2021). Stiffening of the extracellular matrix is a sufficient condition for airway hyperreactivity. J. Appl. Physiol. 130 (6), 1635–1645. doi:10.1152/japplphysiol.00554.2020
Kilic, O., Yoon, A., Shah, S. R., Yong, H. M., Ruiz-Valls, A., Chang, H., et al. (2019). A microphysiological model of the bronchial airways reveals the interplay of mechanical and biochemical signals in bronchospasm. Nat. Biomed. Eng. 3 (7), 532–544. doi:10.1038/s41551-019-0366-7
Kraeutler, M. J., Soltis, A. R., and Saucerman, J. J. (2010). Modeling cardiac β-adrenergic signaling with normalized-hill differential equations: Comparison with a biochemical model. BMC Syst. Biol. 4 (1), 157. doi:10.1186/1752-0509-4-157
Krishnan, R., Park, J.-A., Seow, C. Y., Lee, P. V. S., and Stewart, A. G. (2016). Cellular biomechanics in drug screening and evaluation: Mechanopharmacology. Trends Pharmacol. Sci. 37 (2), 87–100. doi:10.1016/j.tips.2015.10.005
Lagergren, J. H., Nardini, J. T., Baker, R. E., Simpson, M. J., and Flores, K. B. (2020). Biologically-informed neural networks guide mechanistic modeling from sparse experimental data. PLoS Comput. Biol. 16 (12), e1008462. doi:10.1371/journal.pcbi.1008462
Lambert, R. K., Wilson, T. A., Hyatt, R. E., and Rodarte, J. R. (1982). A computational model for expiratory flow. J. Appl. Physiol. Respir. Environ. Exerc. Physiol. 52 (1), 44–56. doi:10.1152/jappl.1982.52.1.44
LaPrad, A. S., and Lutchen, K. R. (2011). The dissolution of intact airway responsiveness from breathing fluctuations: What went wrong? J. Appl. Physiol. 110 (6), 1506–1507. doi:10.1152/japplphysiol.00356.2011
LaPrad, A. S., Szabo, T. L., Suki, B., and Lutchen, K. R. (2010). Tidal stretches do not modulate responsiveness of intact airways in vitro. J. Appl. Physiol. 109 (2), 295–304. doi:10.1152/japplphysiol.00107.2010
Lauzon, A.-M., Bates, J. H. T., Donovan, G., Tawhai, M., Sneyd, J., and Sanderson, M. (2012). A multi-scale approach to airway hyperresponsiveness: From molecule to organ. Front. Physiol. 3, 191. doi:10.3389/fphys.2012.00191
Lavoie, T. L., Krishnan, R., Siegel, H. R., Maston, E. D., Fredberg, J. J., Solway, J., et al. (2012). Dilatation of the constricted human airway by tidal expansion of lung parenchyma. Am. J. Respir. Crit. Care Med. 186 (3), 225–232. doi:10.1164/rccm.201202-0368OC
Leary, D., Svenningsen, S., Guo, F., Bhatawadekar, S., Parraga, G., and Maksym, G. N. (2016). Hyperpolarized 3he magnetic resonance imaging ventilation defects in asthma: Relationship to airway mechanics. Physiol. Rep. 4 (7), e12761. doi:10.14814/phy2.12761
Lee, J.-J., Talman, L., Peirce, S. M., and Holmes, J. W. (2019). Spatial scaling in multiscale models: Methods for coupling agent-based and finite-element models of wound healing. Biomech. Model. Mechanobiol. 18 (5), 1297–1309. doi:10.1007/s10237-019-01145-1
Leonard-Duke, J., Evans, S., Hannan, R. T., Barker, T. H., Bates, J. H. T., Bonham, C. A., et al. (2020). Multi-scale models of lung fibrosis. Matrix Biol. 91, 35–50. doi:10.1016/j.matbio.2020.04.003
Liao, F., Li, M., Han, D., Cao, J., and Chen, K. (2006). Biomechanopharmacology: A new borderline discipline. Trends Pharmacol. Sci. 27 (6), 287–289. doi:10.1016/j.tips.2006.04.001
Lin, F., Zhang, H., Huang, J., and Xiong, C. (2018). Contractility of airway smooth muscle cell in response to zinc oxide nanoparticles by traction force microscopy. Ann. Biomed. Eng. 46 (12), 2000–2011. doi:10.1007/s10439-018-2098-3
Liu, G., Betts, C., Cunoosamy, D. M., Åberg, P. M., Hornberg, J. J., Sivars, K. B., et al. (2019). Use of precision cut lung slices as a translational model for the study of lung biology. Respir. Res. 20 (1), 162. doi:10.1186/s12931-019-1131-x
Liu, X., Zhang, J., Zeigler, A. C., Nelson, A. R., Lindsey, M. L., and Saucerman, J. J. (2021). Network analysis reveals a distinct axis of macrophage activation in response to conflicting inflammatory cues. J. Immunol. 206 (4), 883–891. doi:10.4049/jimmunol.1901444
Maarsingh, H., Bidan, C. M., Brook, B. S., Zuidhof, A. B., Elzinga, C. R. S., Smit, M., et al. (2019). Small airway hyperresponsiveness in copd: Relationship between structure and function in lung slices. Am. J. Physiol. Lung Cell. Mol. Physiol. 316 (3), L537–L546. doi:10.1152/ajplung.00325.2018
Marino, M., Pontrelli, G., Vairo, G., and Wriggers, P. (2017). A chemo-mechano-biological formulation for the effects of biochemical alterations on arterial mechanics: The role of molecular transport and multiscale tissue remodelling. J. R. Soc. Interface 14 (136), 20170615. doi:10.1098/rsif.2017.0615
Martin, C., Uhlig, S., and Ullrich, V. (1996). Videomicroscopy of methacholine-induced contraction of individual airways in precision-cut lung slices. Eur. Respir. J. 9 (12), 2479–2487. doi:10.1183/09031936.96.09122479
Mead, J., Takishima, T., and Leith, D. (1970). Stress distribution in lungs: A model of pulmonary elasticity. J. Appl. Physiol. 28 (5), 596–608. doi:10.1152/jappl.1970.28.5.596
Melis, A., Clayton, R. H., and Marzo, A. (2017). Bayesian sensitivity analysis of a 1d vascular model with Gaussian process emulators. Int. J. Numer. Method. Biomed. Eng. 33 (12), e2882. doi:10.1002/cnm.2882
Mijailovich, S. M., Butler, J. P., and Fredberg, J. J. (2000). Perturbed equilibria of myosin binding in airway smooth muscle: Bond-length distributions, mechanics, and atp metabolism. Biophys. J. 79 (5), 2667–2681. doi:10.1016/S0006-3495(00)76505-2
Morris, M. K., Saez-Rodriguez, J., Sorger, P. K., and Lauffenburger, D. A. (2010). Logic-based models for the analysis of cell signaling networks. Biochemistry 49 (15), 3216–3224. doi:10.1021/bi902202q
Naveed, S., Clements, D., Jackson, D. J., Philp, C., Billington, C. K., Soomro, I., et al. (2017). Matrix metalloproteinase-1 activation contributes to airway smooth muscle growth and asthma severity. Am. J. Respir. Crit. Care Med. 195 (8), 1000–1009. doi:10.1164/rccm.201604-0822OC
Nestor-Bergmann, A., Goddard, G., Woolner, S., and Jensen, O. E. (2018). Relating cell shape and mechanical stress in a spatially disordered epithelium using a vertex-based model. Math. Med. Biol. 35, 1–27. doi:10.1093/imammb/dqx008
Noble, P. B., Pascoe, C. D., Lan, B., Ito, S., Kistemaker, L. E. M., Tatler, A. L., et al. (2014). Airway smooth muscle in asthma: Linking contraction and mechanotransduction to disease pathogenesis and remodelling. Pulm. Pharmacol. Ther. 29 (2), 96–107. doi:10.1016/j.pupt.2014.07.005
Noè, U., Chen, W., Filippone, M., Hill, N., and Husmeier, D. (2016). “Inference in a partial differential equations model of pulmonary arterial and venous blood circulation using statistical emulation,” in International meeting on computational intelligence methods for bioinformatics and biostatistics (Milan: Springer), 184–198.
Oliveira, C. L. N., Bates, J. H. T., and Suki, B. (2014). A network model of correlated growth of tissue stiffening in pulmonary fibrosis. New J. Phys. 16 (6), 065022. doi:10.1088/1367-2630/16/6/065022
Osborne, J. M., Fletcher, A. G., Pitt-Francis, J. M., Maini, P. K., and Gavaghan, D. J. (2017). Comparing individual-based approaches to modelling the self-organization of multicellular tissues. PLoS Comput. Biol. 13 (2), e1005387. doi:10.1371/journal.pcbi.1005387
Parameswaran, K., Willems-Widyastuti, A., Alagappan, V. K. T., Radford, K., Kranenburg, A. R., and Sharma, H. S. (2006). Role of extracellular matrix and its regulators in human airway smooth muscle biology. Cell. biochem. Biophys. 44 (1), 139–146. doi:10.1385/CBB:44:1:139
Park, C. Y., Zhou, E. H., Tambe, D., Chen, B., Lavoie, T., Dowell, M., et al. (2015). High-throughput screening for modulators of cellular contractile force. Integr. Biol. 7 (10), 1318–1324. doi:10.1039/c5ib00054h
Pascoe, C. D., Green, F. H. Y., Elliot, J. G., James, A. L., Noble, P. B., and Donovan, G. M. (2020). Airway remodelling with spatial correlations: Implications for asthma pathogenesis. Respir. Physiol. Neurobiol. 279, 103469. doi:10.1016/j.resp.2020.103469
Pedley, T. J., Schroter, R. C., and Sudlow, M. F. (1971). Flow and pressure drop in systems of repeatedly branching tubes. J. Fluid Mech. 46 (2), 365–383. doi:10.1017/s0022112071000594
Polio, S. R., Stasiak, S. E., Jamieson, R. R., Balestrini, J. L., Krishnan, R., and Parameswaran, H. (2019). Extracellular matrix stiffness regulates human airway smooth muscle contraction by altering the cell-cell coupling. Sci. Rep. 9 (1), 9564. doi:10.1038/s41598-019-45716-9
Politi, A. Z., Donovan, G. M., Tawhai, M. H., Sanderson, M. J., Lauzon, A.-M., Bates, J. H. T., et al. (2010). A multiscale, spatially distributed model of asthmatic airway hyper-responsiveness. J. Theor. Biol. 266 (4), 614–624. doi:10.1016/j.jtbi.2010.07.032
Pybus, H. J., O’Dea, R. D., and Brook, B. S. (2021b). A dynamical model of TGF-β activation in asthmatic airways. bioRxiv. doi:10.1101/2021.03.28.437380
Pybus, H. J., Tatler, A. L., Edgar, L. T., O’Dea, R. D., and Brook, B. S. (2021a). Reduced biomechanical models for precision-cut lung-slice stretching experiments. J. Math. Biol. 82 (5), 35–41. doi:10.1007/s00285-021-01578-2
Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707. doi:10.1016/j.jcp.2018.10.045
Ram-Mohan, S., Bai, Y., Schaible, N., Ehrlicher, A. J., Cook, D. P., Suki, B., et al. (2020). Tissue traction microscopy to quantify muscle contraction within precision-cut lung slices. Am. J. Physiol. Lung Cell. Mol. Physiol. 318 (2), L323–L330. doi:10.1152/ajplung.00297.2019
Rampadarath, A. K., and Donovan, G. M. (2018). A distribution-moment approximation for coupled dynamics of the airway wall and airway smooth muscle. Biophysical J. 114 (2), 493–501. doi:10.1016/j.bpj.2017.11.020
Rampadarath, A. K., and Donovan, G. M. (2021). Mathematical modelling of lung function – what have we learnt and where to next? Curr. Opin. Physiology 21 (17–22), 17–22. doi:10.1016/j.cophys.2021.03.004
Rikard, S. M., Athey, T. L., Nelson, A., Christiansen, S. L. M., Lee, J.-J., Holmes, J. W., et al. (2019). Multiscale coupling of an agent-based model of tissue fibrosis and a logic-based model of intracellular signaling. Front. Physiol. 10, 1481. doi:10.3389/fphys.2019.01481
Rouillard, A. D., and Holmes, J. W. (2014). Coupled agent-based and finite-element models for predicting scar structure following myocardial infarction. Prog. Biophys. Mol. Biol. 115 (2-3), 235–243. doi:10.1016/j.pbiomolbio.2014.06.010
Rudy, S. H., Brunton, S. L., Proctor, J. L., and Kutz, J. N. (2017). Data-driven discovery of partial differential equations. Sci. Adv. 3 (4), e1602614. doi:10.1126/sciadv.1602614
Sanderson, M. J. (2011). Exploring lung physiology in health and disease with lung slices. Pulm. Pharmacol. Ther. 24 (5), 452–465. doi:10.1016/j.pupt.2011.05.001
Smith, B. A., Tolloczko, B., Martin, J. G., and Grütter, P. (2005). Probing the viscoelastic behavior of cultured airway smooth muscle cells with atomic force microscopy: Stiffening induced by contractile agonist. Biophys. J. 88 (4), 2994–3007. doi:10.1529/biophysj.104.046649
Stasiak, S. E., Jamieson, R. R., Bouffard, J., Cram, E. J., and Parameswaran, H. (2020). Intercellular communication controls agonist-induced calcium oscillations independently of gap junctions in smooth muscle cells. Sci. Adv. 6 (32), eaba1149. doi:10.1126/sciadv.aba1149
Sun, Z., Martinez-Lemus, L. A., Trache, A., Trzeciakowski, J. P., Davis, G. E., Pohl, U., et al. (2005). Mechanical properties of the interaction between fibronectin and α5β1-integrin on vascular smooth muscle cells studied using atomic force microscopy. Am. J. Physiol. Heart Circ. Physiol. 289 (6), H2526–H2535. doi:10.1152/ajpheart.00658.2004
Tatler, A. L., Philp, C. J., Hill, M. R., Cox, S., Bullock, A., Habgood, A., et al. (2022). Differential remodelling in small and large murine airways revealed by novel whole lung airway analysis. bioRxiv. doi:10.1101/2022.01.15.476324
Tawhai, M. H., Hunter, P., Tschirren, J., Reinhardt, J., McLennan, G., and Hoffman, E. A. (2004). Ct-based geometry analysis and finite element models of the human and ovine bronchial tree. J. Appl. Physiol. 97 (6), 2310–2321. doi:10.1152/japplphysiol.00520.2004
Tepole, A. B. (2017). Computational systems mechanobiology of wound healing. Comput. Methods Appl. Mech. Eng. 314, 46–70. doi:10.1016/j.cma.2016.04.034
Tgavalekos, N. T., Musch, G., Harris, R. S., Vidal Melo, M. F., Winkler, T., Schroeder, T., et al. (2007). Relationship between airway narrowing, patchy ventilation and lung mechanics in asthmatics. Eur. Respir. J. 29 (6), 1174–1181. doi:10.1183/09031936.00113606
Vargas, D. A., Heck, T., Smeets, B., Ramon, H., Parameswaran, H., and Van Oosterwyck, H. (2020). Intercellular adhesion stiffness moderates cell decoupling as a function of substrate stiffness. Biophys. J. 119 (2), 243–257. doi:10.1016/j.bpj.2020.05.036
Venegas, J. G., Winkler, T., Musch, G., Vidal Melo, M. F., Layfield, D., Tgavalekos, N., et al. (2005). Self-organized patchiness in asthma as a prelude to catastrophic shifts. Nature 434 (7034), 777–782. doi:10.1038/nature03490
Whitfield, C. A., Latimer, P., Horsley, A., Wild, J. M., Collier, G. J., and Jensen, O. E. (2020). Spectral graph theory efficiently characterizes ventilation heterogeneity in lung airway networks. J. R. Soc. Interface 17 (168), 20200253. doi:10.1098/rsif.2020.0253
Wang, A., Cao, S., Aboelkassem, Y., and Valdez-Jasso, D. (2020). Quantification of uncertainty in a new network model of pulmonary arterial adventitial fibroblast pro-fibrotic signalling. Philos. Trans. A Math. Phys. Eng. Sci. 378 (2173), 20190338. doi:10.1098/rsta.2019.0338
Wang, I., Bai, Y., Sanderson, M. J., and Sneyd, J. (2010). A mathematical analysis of agonist- and KCl-induced Ca2+ oscillations in mouse airway smooth muscle cells. Biophys. J. 98, 1170–1181. doi:10.1016/j.bpj.2009.12.4273
Wang, I., Politi, A. Z., Tania, N., Bai, Y., Sanderson, M. J., and Sneyd, J. (2008). A mathematical model of airway and pulmonary arteriole smooth muscle. Biophys. J. 94 (6), 2053–2064. doi:10.1529/biophysj.107.113977
Wang, L., Chitano, P., Paré, P. D., and Seow, C. Y. (2019). Mechanopharmacology and synergistic relaxation of airway smooth muscle. J. Eng. Sci. Med. Diagn. Ther. 2 (1), 0110041–0110047. doi:10.1115/1.4042477
Wang, L., Paré, P. D., and Seow, C. Y. (2000). Effects of length oscillation on the subsequent force development in swine tracheal smooth muscle. J. Appl. Physiol. 88 (6), 2246–2250. doi:10.1152/jappl.2000.88.6.2246
Wellman, T. J., Mondoñedo, J. R., Davis, G. S., Bates, J. H. T., and Suki, B. (2018). Topographic distribution of idiopathic pulmonary fibrosis: A hybrid physics-and agent-based model. Physiol. Meas. 39 (6), 064007. doi:10.1088/1361-6579/aaca86
Werner, R., Ehrhardt, J., Schmidt, R., and Handels, H. (2009). Patient-specific finite element modeling of respiratory lung motion using 4d ct image data. Med. Phys. 36 (5), 1500–1511. doi:10.1118/1.3101820
Winkler, T., and Venegas, J. G. (2007). Complex airway behavior and paradoxical responses to bronchoprovocation. J. Appl. Physiol. 103 (2), 655–663. PMID: 17478609. doi:10.1152/japplphysiol.00041.2007
Wittmann, D. M., Krumsiek, J., Saez-Rodriguez, J., Lauffenburger, D. A., Klamt, S., and Theis, F. J. (2009). Transforming boolean models to continuous models: Methodology and application to t-cell receptor signaling. BMC Syst. Biol. 3 (1), 98–21. doi:10.1186/1752-0509-3-98
Wright, D. B., Trian, T., Siddiqui, S., Pascoe, C. D., Johnson, J. R., Dekkers, B. G. J., et al. (2013). Phenotype modulation of airway smooth muscle in asthma. Pulm. Pharmacol. Ther. 26 (1), 42–49. Smooth Muscle in Lung Disease – 7th International Young Investigators Meeting on Airway Smooth Muscle. doi:10.1016/j.pupt.2012.08.005
Yoon, S., Tam, T. M., Rajaraman, P. K., Lin, C.-L., Tawhai, M., Hoffman, E. A., et al. (2020). An integrated 1d breathing lung simulation with relative hysteresis of airway structure and regional pressure for healthy and asthmatic human lungs. J. Appl. Physiol. 129 (4), 732–747. doi:10.1152/japplphysiol.00176.2020
Zahalak, G. I. (1981). A distribution-moment approximation for kinetic theories of muscular contraction. Math. Biosci. 55 (1-2), 89–114. doi:10.1016/0025-5564(81)90014-6
Zeigler, A. C., Chandrabhatla, A. S., Christiansen, S. L., Nelson, A. R., Holmes, J. W., and Saucerman, J. J. (2021). Network model-based screen for fda-approved drugs affecting cardiac fibrosis. CPT. Pharmacometrics Syst. Pharmacol. 10 (4), 377–388. doi:10.1002/psp4.12599
Keywords: multiscale models, mechanobiology, biomechanics, hyperresponsiveness, remodelling
Citation: Irons L and Brook BS (2022) The role of mathematical models in designing mechanopharmacological therapies for asthma. Front. Syst. Biol. 2:929426. doi: 10.3389/fsysb.2022.929426
Received: 26 April 2022; Accepted: 07 September 2022;
Published: 06 October 2022.
Edited by:
Helen Byrne, Larner College of Medicine, University of Oxford, United KingdomReviewed by:
Ruisheng Wang, Harvard Medical School, United StatesLongwei Liu, University of California, San Diego, United States
Copyright © 2022 Irons and Brook. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bindi S. Brook, YmluZGkuYnJvb2tAbm90dGluZ2hhbS5hYy51aw==,
†ORCID: Bindi S. Brook, orcid.org/0000-0001-9883-4131
 Linda Irons
Linda Irons Bindi S. Brook
Bindi S. Brook