- 1Department of Biomedical Engineering, Duke University, Durham, NC, United States
- 2Computational Sciences and Engineering Division, Oak Ridge National Laboratory, Oak Ridge, TN, United States
- 3Department of Medicine/Cardiology, University of Colorado AMC, Aurora, CO, United States
- 4School of Biological and Health Systems Engineering, Arizona State University, Tempe, AZ, United States
- 5Department of Petroleum Engineering, Santa Catarina State University, Balneário Camboriú, Brazil
- 6Department of Medicine, Duke University, Durham, NC, United States
- 7Division of Cardiovascular Medicine, University of San Diego, San Diego, CA, United States
- 8Department of Biomedical Engineering, Georgia Tech, Atlanta, GA, United States
- 9Division of Cardiovascular Medicine, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, United States
Background and objective: Coronary artery disease (CAD) is highly prevalent and associated with adverse events. Challenges have emerged in the treatment of intermediate coronary artery stenoses. These lesions are often interrogated with fractional flow reserve (FFR) testing to determine if a stenosis is likely to be causative for ischemia in a cardiac territory. This invasive test requires insertion of a pressure wire into a coronary vessel. Recently computational fluid dynamics (CFD) has been used to noninvasively assess fractional flow reserve in vessels reconstructed from medical imaging data. However, many of these simulations are unable to provide additional information about intravascular hemodynamics, including velocity, endothelial shear stress (ESS), and vorticity. We hypothesized that vorticity, which has demonstrated utility in the assessment of ventricular and aortic diseases, would also be an important hemodynamic factor in CAD.
Methods: Three-dimensional (3D), patient-specific coronary artery geometries that included all vessels >1 mm in diameter were created from angiography data obtained from 10 patients who underwent diagnostic angiography and FFR testing (n = 9). A massively parallel CFD solver (HARVEY) was used to calculate coronary hemodynamic parameters including pressure, velocity, ESS, and vorticity. These simulations were validated by comparing velocity flow fields from simulation to both velocities derived from in vitro particle image velocimetry and to invasively acquired pressure wire-based data from clinical testing.
Results: There was strong agreement between findings from CFD simulations and particle image velocimetry experimental testing (p < 0.01). CFD-FFR was also highly correlated with invasively measured FFR (ρ = 0.77, p = 0.01) with an average error of 5.9 ± 0.1%. CFD-FFR also had a strong inverse correlation with the vorticity (ρ = -0.86, p = 0.001). Simulations to determine the effect of the coronary stenosis on intravascular hemodynamics demonstrated significant differences in velocity and vorticity (both p < 0.05). Further evaluation of an angiographically normal appearing non-FFR coronary vessel in patients with CAD also demonstrated differences in vorticity when compared with FFR vessels (p < 0.05).
Conclusion: The use of highly accurate 3D CFD-derived intravascular hemodynamics provides additional information beyond pressure measurements that can be used to calculate FFR. Vorticity is one parameter that is modified by a coronary stenosis and appears to be abnormal in angiographically normal vessels in patients with CAD, highlighting a possible use-case in preventative screening for early coronary disease.
1 Introduction
Coronary heart disease is highly prevalent in the United States, and it is estimated that 720,000 individuals will suffer their first cardiac event while recurrent events will occur in approximately 335,000 individuals (Virani et al., 2020). In 2014, there were more than one million inpatient cardiac catheterizations to diagnose coronary artery disease with an associated 371,000 coronary artery bypass grafting surgeries and 480,000 percutaneous coronary interventions (Virani et al., 2020). The decision to revascularize coronary arteries in symptomatic patients is based, in part, on their clinical presentation, medical therapy, and severity of coronary artery stenoses detected at coronary angiography. Coronary stenoses that are ≥70% by visual estimate are considered severe and warrant revascularization (Lawton et al., 2022). In contrast, coronary stenoses that are between 40% and <70% are considered intermediate and typically require additional study to determine if they are physiologically significant and require revascularization (Lawton et al., 2022).
Fractional flow reserve (FFR) is a method used to assess the significance of an intermediate coronary stenosis. FFR is defined as the ratio of the pressure distal to a stenosis (Pd) to the aortic pressure (Pa) at maximal hyperemia (maximal vasodilation of the microvasculature). FFR as a tool to guide PCI has been studied in the Fractional Flow-Reserve-Guided PCI versus Medical Therapy in Stable Coronary Disease (FAME 2) trial. This randomized controlled trial compared FFR guided PCI with optimal medical therapy and reported that patients with an abnormal FFR had a significant benefit with PCI (De Bruyne et al., 2012).
Computational fluid dynamics (CFD) models coronary blood flow with high resolution and broad parameterization (Taylor et al., 2013; Vardhan et al., 2019; Vardhan et al., 2021). CFD simulations can be used to provide a detailed description of a patient’s coronary blood flow and interaction with a coronary stenosis or the blood vessel wall (Taylor et al., 2013). These simulations can be used to determine velocity, pressure, shear stress, and vorticity throughout the entire coronary tree. CFD-derived pressure has been used to calculate the FFR using patient-specific geometries constructed from coronary computed tomography angiography scans or coronary angiograms (Papafaklis et al., 2014; Kornowski et al., 2016; Morris et al., 2017; Zhang et al., 2021; Gao et al., 2022), but other CFD-derived hemodynamic markers, such as vorticity, have largely been ignored. Mathematically, vorticity describes the tendency of fluid to rotate along a central luminal axis and is a descriptor of locally disturbed flow. Regions of high vorticity and flow recirculation can be found in the concave regions of stenosis, while at peak systole, vorticity can result in secondary vortex formations on opposing sense on the arterial wall (Amir et al., 2022). Vorticity is associated with an increase in fluid energy loss leading to a decrease in energy available to deliver blood to the microcirculation (Wu et al., 2007).
Recent clinical works suggest that vorticity and energy loss are correlated with right ventricular dysfunction and exercise capacity in repaired Tetralogy of Fallot patients (Garcia et al., 2013; Loke et al., 2021). Other such investigations identified flow vorticity as an important factor resulting in mean pressure gradient discrepancies between cardiovascular magnetic resonance and transthoracic Doppler-echocardiography (Garcia et al., 2013). Thus, several CFD studies have attempted to understand the role of vortex formation and recirculation in arterial stenoses to investigate hemodynamics resulting in thrombus formation and to understand influence of turbulence in eccentric lesions (Katritsis et al., 2010; Melih et al., 2013; Rigatelli et al., 2019). One study examined vorticity in coronary arteries with intermediate stenoses found that vorticity was associated with the severity of the stenosis and the flow rate (Chu et al., 2018).
In the current study, we hypothesized that vorticity at the site of the minimal luminal diameter would provide additional hemodynamic information beyond FFR to describe perturbations in coronary flow at the site of a stenosis. We examined vorticity as well as pressure, velocity, and shear stress at the site of the minimal luminal diameter using patient-specific 3D geometries of the coronary tree derived from coronary angiograms and a fluid solver capable of ultrahigh-resolution (Vardhan et al., 2019; Vardhan et al., 2021).
2 Methods
2.1 Study population
The study was performed with approval from the Mass General Brigham Human Research Committee Institutional Review Board (protocol #2015P001084). This was a retrospective study that involved data collection only and informed consent was not required. The study included 10 patients who underwent clinically indicated coronary angiography at Brigham and Women’s Hospital, Boston MA. Nine patients had at least one intermediate stenosis in an epicardial coronary artery that required invasive fractional flow reserve (FFR) testing to determine the functional significance of that stenosis. The 10th patient had angiographically normal coronary arteries and was utilized as a control for the study. This control patient had coronary angiography performed for a clinically indicated reason, which was pre-operative assessment of the coronary arteries in a patient that was going to undergo cardiothoracic surgery for valvular heart disease.
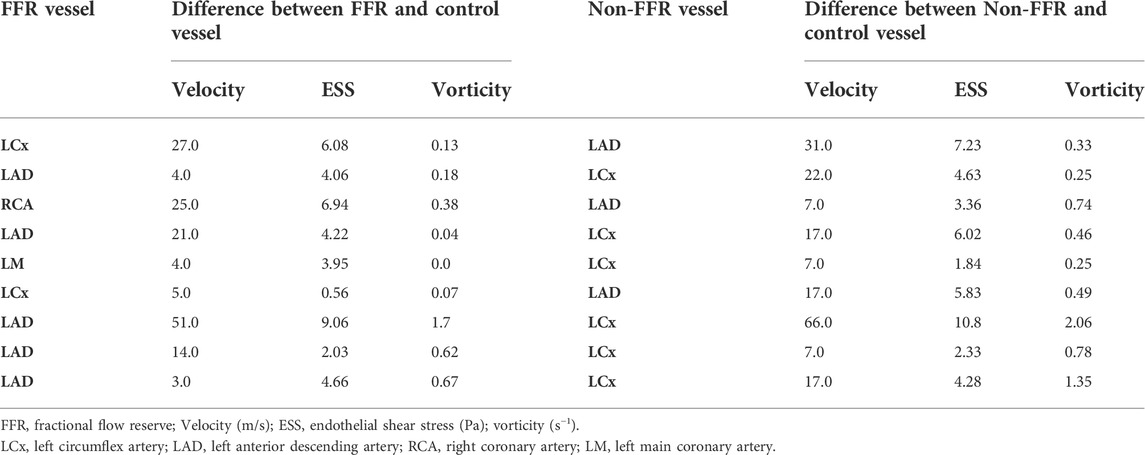
Coronary angiography was performed using single plane angiography with a minimum of 4 standard orthogonal views of the left coronary artery (LCA) and 2 standard orthogonal views of the right coronary artery (RCA). FFR was measured using a coronary pressure wire (PressureWire X, St. Jude Medical) and intravenous administration of adenosine (140 ug/kg/min) was used to induce maximal hyperemia. FFR was computed as the ratio of pressure measured distal (Pd) and proximal (Pa) to the stenosis of interest. Angiograms were reviewed by an experienced interventional cardiologist (JAL) and coronary dominance, lesion location, and pressure wire location at the time of testing were recorded. In addition, the patient’s blood pressure and heart rate at rest and at maximal hyperemia, hematocrit, and cardiac output from right heart catheterization at the time of angiography or echocardiogram were recorded.
2.2 Generation of 3D coronary geometries from 2D coronary angiograms
Coronary angiograms were used to reconstruct patient-specific 3D geometries using a 3D reconstruction algorithm (Chen and Carroll 2000; Green et al., 2005). Briefly, the algorithm extracts the vessel centerline and cross-sectional diameter to create a “coronary skeleton” from two angiograms separated by angles >45°. All 3D arterial geometries were obtained at end-diastole (90% of the cardiac cycle) and were exported in standard stereolithography (STL) mesh format for CFD analysis. Morphological and anatomical validity of all 3D reconstructions were verified by an experienced interventional cardiologist (JAL).
2.3 Patient-specific
CFD simulations CFD simulations were conducted using HARVEY, a massively parallel hemodynamic simulator which implements the lattice Boltzmann method (LBM) (Randles et al., 2013). The LBM is an alternate solver for the traditional Navier-Stokes equations which govern fluid flow (Kruger et al., 2017). In the LBM the probability distribution function fi (x, t) represents the population of particles located at lattice point, x, at time, t, with discrete velocity, ci, moving around a fixed Cartesian grid. f i (x + ciδt, t + δt) − fi (x, t) = −Ω(fi (x, t) – f eq (x, t)). HARVEY discretizes the velocity space using the standard D3Q19 lattice in 3D space and uses the single relaxation time Bhatnagar-Gross-Krook (BGK) collision kernel Ω. Blood vessels were simulated as rigid vessel walls by implementing the no-slip boundary condition using the halfway bounce-back method, while finite difference boundary conditions were used at the inlets and outlets (Latt et al., 2008). The macroscopic variables density ρ and velocity u were computed as the first two moments of the probability distribution function:
For simulations, coronary blood flow was simulated with the assumption that blood is an incompressible Newtonian fluid and that the coronary vessels have rigid walls (Taylor et al., 2013; Eslami et al., 2019; Eslami et al., 2021). Each simulation utilized patient-specific clinical variables to tailor the relevant inlet and outlet boundary conditions, summarized in Table 1 (Vardhan et al., 2019; Vardhan et al., 2021). A pulsatile waveform at the inlet was imposed for each patient using a Poiseuille profile. The inlet waveform flow parameters were determined by calculating the resting total coronary flow rate for each patient using coronary dominance to determine the fraction of cardiac output delivered to the coronary vessels (Table 1). At the outlet, a one element Windkessel model was imposed by computing the vessel microcirculatory resistance (Grinberg and Karniadakis 2008; Taylor et al., 2013). The coronary resistance Ri was computed as the ratio of mean arterial pressure Pi and total coronary flow rate Qi tuned to each arterial outlet using the following equation (Grinberg and Karniadakis 2008; Taylor et al., 2013).
To model maximal hyperemia, coronary flow velocity and microresistance were changed based on the methods described in (Wilson et al., 1990; Taylor et al., 2013). Distal resistance has a strong influence on the modeling of patient-specific arterial hemodynamics (Anselmi et al., 2021). Therefore, for each arterial tree we carefully compute the distal resistance of every outlet based on the vessel diameter, mean flow and mean aortic pressure derived from the clinical measurements of that patient (Table 1). Further details of our approach and the influence of resistance computed by this approach on pressure gradient and other hemodynamic variables, for example ESS and velocity, is discussed elsewhere (Vardhan et al., 2021).
The hemodynamic variables endothelial shear stress (ESS) and vorticity were computed for each vessel of interest. The ESS vector τi was computed using the equation (Matyka et al., 2013):
where
where
As disturbed hemodynamics seldom remain isolated to a single region or vessel in the coronary arterial tree, we evaluated velocity, ESS and vorticity in stenotic coronary vessels and compared these values to the same parameters measured in non-stenotic vessels within the same patient with coronary disease in order to understand the span of parameter variability throughout patient’s coronary arterial trees. For patients with coronary lesions in the left circumflex artery (LCX) or RCA, the left anterior descending (LAD) artery was used for comparison. And for patients with LAD lesions, the LCX was used as the comparator vessel.
2.4 Validating CFD simulation-derived 3D coronary flow profiles using particle image velocimetry
Particle image velocimetry (PIV) was utilized to validate the CFD model in the moderate Reynolds flow regime found in coronary arteries (Re 450–550) using a 3D-printed coronary artery phantom. A 3D geometry was constructed from two orthogonal RCA angiograms and the STL file was used to 3D print an optically clear urethane RCA model with a patent central lumen that was used with a standard PIV setup to acquire flow patterns (Figures 1A,B). CFD simulations were run with the same RCA geometry for comparison. Aqueous sodium iodide solution configured to match the refractive index of the 3D printed model (n = 1.49) was used to mimic blood flow. A steady physiological flow rate of 7.5 ml/s, kinematic viscosity of 2.418 cSt, and density 1,493 kg/m33 were used to determine the velocity field. In the PIV setup, steady flow velocities were acquired at the longitudinal center-plane of the physical model. Further details of the PIV setup, including seeding with fluorescent particles, can be found in (Chaudhury et al., 2016).

FIGURE 1. Setup for particle image velocimetry experiment with right coronary artery. (A) The experimental setup for particle image velocimetry bench testing is shown. (B) A close-up view of the 3D printed right coronary artery showing the bifurcation with a right ventricular marginal branch. A stereolithography file was created from a 3D reconstruction of a patient’s right coronary artery from angiograms. This file was used to 3D print a model with a patent lumen for benchtop testing.
2.5 Statistical analysis
Normal distribution of the data was evaluated using the Kolmogorov-Smirnov test. Comparisons between continuous variables were done using two-tailed t-tests or paired t-tests. Non-parametric data was analyzed using the Mann-Whitney test or Wilcoxon matched-pairs signed rank test. Bland Altman analyses were performed to determine agreement between CFD-computed and invasively measured FFR. Linear regression was used to determine the correlation between invasive FFR measurements and CFD parameters (vorticity, velocity, and ESS). Pearson correlation coefficients were calculated to determine the strength of the correlation between FFR and CFD generated parameters. Data for continuous variables are reported as mean ± standard deviation. A value of p < 0.05 was considered significant. Data were analyzed using Stata 15/SE 15.1 (StataCorp LLC, College Station, TX, United States) and Prism 9.0 (GraphPad, San Diego, CA, United States.
3 Results
3.1 Validating CFD simulations in coronary arteries using PIV
In order to validate our CFD simulations of coronary arteries, a model of a RCA was reconstructed from a patient’s coronary angiogram for PIV testing. The subsequent STL file was used to 3D print a physical model of the vessel with a patent lumen. Bench top PIV flow studies and CFD simulation were then performed using the same coronary artery geometry. The magnitude of the velocity, v, profile across the diameter of the RCA at the level of a bifurcation with a right ventricular marginal branch from the bench top PIV experiment was compared with velocity from the CFD simulation (Figures 2A–C). This site was selected because it is where the velocity was expected to be the least uniform. The mean squared error differences between the PIV and the CFD velocity profiles in the RCA (Figure 2D) and in the side branch (Figure 2E) were significant (p < 0.001) suggesting that the CFD simulation accurately recapitulated what was observed with the PIV experiment. Notably, there was agreement between the profiles towards the center of the vessel where there were higher velocities. Therefore, these results indicate that our CFD methodology resolves the experimental flow pattern and accurately computes velocities in a patient-specific complex coronary artery geometry. Furthermore, since vorticity and ESS are calculated based on the curl of the velocity vector or the velocity, respectively, the results from the PIV experiment supported the accuracy of using our CFD pipeline to compute both vorticity and ESS.
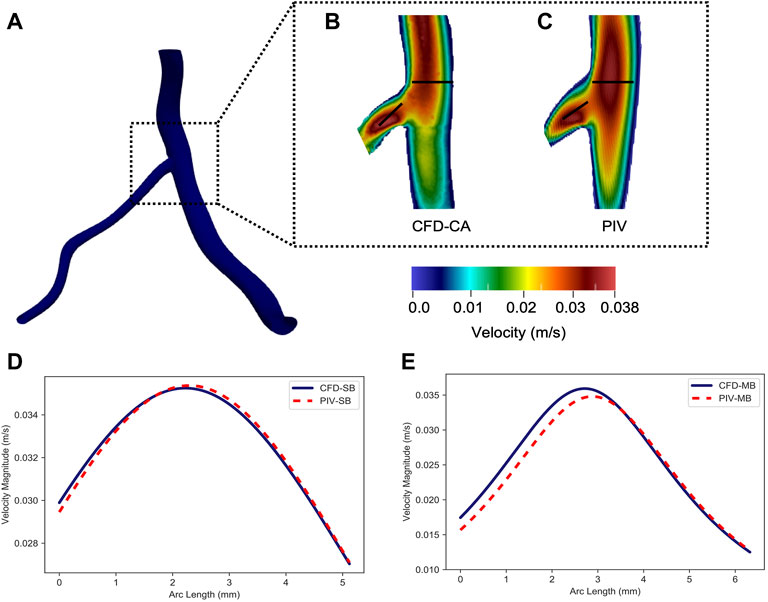
FIGURE 2. Comparison between computational fluid dynamics and particle image velocimetry results. (A) The longitudinal centerplane in the right coronary artery showing the bifurcation with the right ventricular marginal branch. The velocity profile along the right coronary artery and the side branch from (B) computational fluid dynamics simulations of the coronary artery (CFD-CA) and (C) particle image velocimetry testing. The velocity profile obtained by CFD-CA and particle image velocimetry testing was compared in the (D) right coronary artery and (E) the right ventricular marginal side branch.
3.2 Patient-specific CFD simulations correlate with invasively measured FFR
Next, we compared CFD-computed FFR using patient-specific coronary artery geometries with invasive FFR measurements obtained in the cardiac catheterization laboratory, which is considered the ground truth. The patients (n = 9) included in the study were representative of individuals undergoing diagnostic cardiac catheterization. The mean age of the patients was 69.0 ± 7.7 years, 56% were male, 100% had hypertension and hypercholesterolemia, and 44% of the participants were current or former smokers. A total of 67% of patients had a prior myocardial infarction, 33% had a prior percutaneous coronary intervention, and only one patient had a prior coronary artery bypass grafting surgery. Similarly, a total of 22% had a history of congestive heart failure, 11% had peripheral arterial disease, and 44% had chronic kidney disease. The mean left ventricular ejection fraction was 54.5 ± 12.4% and the mean cardiac output was 4.2 ± 0.9 L/min. On the day of catheterization, the mean arterial blood pressure and heart rate were 93.9 ± 9.8 mmHg and 74.9 ± 21.8 bpm, respectively, and 89% of individuals were in normal sinus rhythm. Coronary angiography demonstrated that 56% of the coronary anatomies were right dominant, 33% were left dominant, and 11% were co-dominant.
Comparison between CFD-computed FFR and invasively measured FFR revealed that there was an average error of 5.9 ± 0.1% as well as a strong and significant correlation (p = 0.77, p = 0.01). Bland-Altman analysis estimated the mean difference between the CFD-computed FFR and invasive FFR was 0.04 ± 0.05, suggesting that CFD simulations led to a marginal overestimation of FFR. The Bland-Altman 95% CI agreement values were -0.02 and 0.13 demonstrating further that all values of CFD-computed FFR were within the 95% limits of agreement as compared to invasively measured FFR (Figure 3A). Therefore, patient-specific 3D CFD simulations using our pipeline to measure FFR demonstrated a high degree of accuracy.
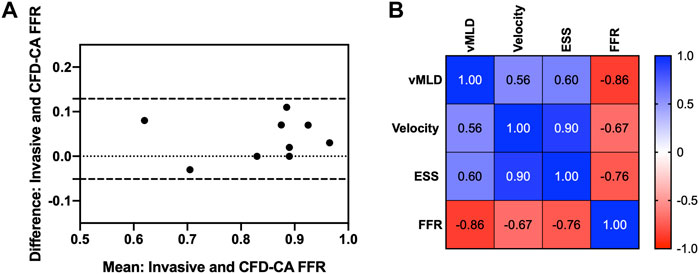
FIGURE 3. Computational fluid dynamics fractional flow reserve and intracoronary hemodynamics. (A) Bland-Altman plot showing agreement between fractional flow reserve determined by computational fluid dynamics versus invasively measured using a pressure wire. (B) Correlations between fractional flow reserve and intracoronary hemodynamics. FFR, fractional flow reserve; vMLD, vorticity at the minimum luminal diameter; ESS, endothelial shear stress.
3.3 Evaluating intracoronary hemodynamic disturbances using vorticity
Next, ESS and vorticity were examined in the coronary arteries containing the stenosis that underwent FFR testing and the adjacent coronary vessel. Figure 4 shows the velocity, ESS, and vorticity maps overlaid on the patient coronary artery reconstructions for each of the nine patients. First, we performed correlation analyses to understand the relationship between vorticity at the vessel minimal luminal diameter and CFD-FRR, ESS and velocity at maximal hyperemia. Vorticity was strongly and inversely correlated with CFD-FFR (p = -0.86, p = 0.001), and positively correlated with ESS (p = 0.6, p = 0.08) and hyperemic velocity (p = 0.56, p = 0.11) (Figure 3B).

FIGURE 4. Personalized computational fluid dynamics simulations map intracoronary hemodynamics. Personalized computational fluid dynamics (CFD) simulations were performed using 3D reconstructions of coronary angiograms for each of the patients and HARVEY. A frame from the coronary angiogram is shown with the corresponding personalized CFD model. Results from CFD simulations are used to map velocity, ESS, and vorticity to the coronary artery (left to right).
Perturbations in coronary hemodynamics are seldom isolated to a single region or vessel in the coronary arterial tree. ESS and vorticity were then determined in the coronary artery containing the stenosis that was examined with FFR and compared these values to what was found in the adjacent main coronary vessel that did not have a stenosis. Table 2 summarizes the velocity, ESS, and vorticity in the FFR vessel and at the same location in the adjacent main coronary vessel. Among these parameters, there was a significant difference in the intracoronary hemodynamics between the stenotic and non-stenotic vessels: velocity (mean difference = 22.2 ± 22.4 m/s, p = 0.02), ESS (mean difference = 4.2 ± 4.3 Pa, p = 0.02), and vorticity (mean difference = 0.25 ± 0.24 s−1, p = 0.01). Thus, there are significant differences in velocity, ESS, and vorticity in coronary arteries with and without stenoses in the same patient.
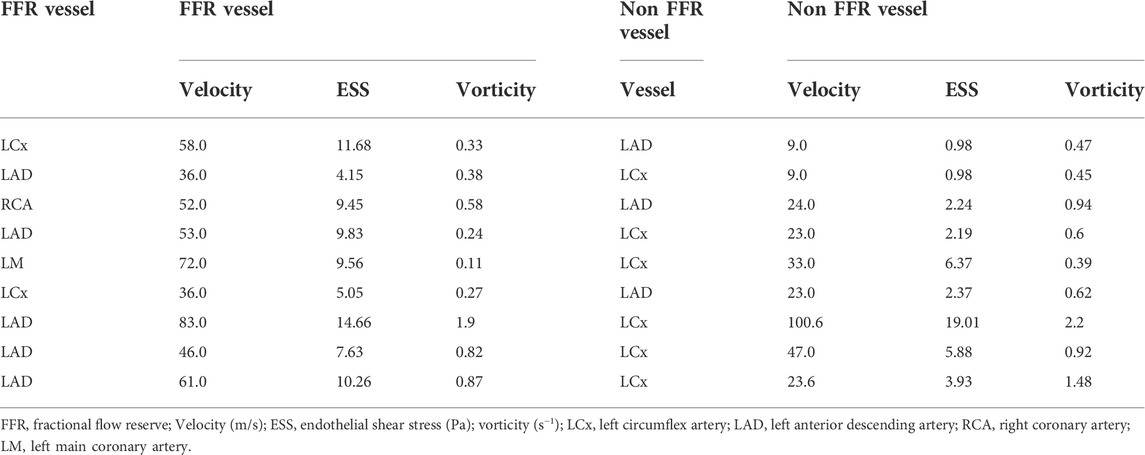
TABLE 2. Comparing hemodynamics in a the FFR vessel with coronary disease and angiographically normal appearing non-FFR vessel in the same patient.
Next, to assess the contribution of the intracoronary stenosis to velocity, ESS, and vorticity, intravascular hemodynamics were compared in the presence and the absence of the intravascular stenosis. To simulate the absence of the stenosis in the coronary vessel of patients diagnosed with coronary disease, we first computed the difference between velocity, ESS, and vorticity between the coronary vessel with a stenosis and the same vessel from a control subject who had no evidence of coronary disease in any vessel at coronary angiography (Table 3). We then examined this difference in intravascular hemodynamics from control patient between the angiographically normal appearing non-FFR vessel (Table 3, left) compared to FFR vessel (Table 3, right) of patients with a diagnosis of coronary disease. Therefore, in Tables 2 and 3 the “control vessel” is the same vessel as the vessel studied in the healthy patient, and the “non-FFR vessel” is another coronary vessel, as discussed in Section 2.3, of the same diseased patient (ni, i = 1–9).
While there was no difference in velocity (33.0 ± 29.0 vs 55.2 ± 15.5 m/s, p = 0.69) or ESS (4.9 ± 5.6 vs 9.1 ± 3.2 Pa, p = 0.57), vorticity remained significantly different (0.9 ± 0.6 vs 0.6 ± 0.5 s−1, p = 0.011). The statistical significance was determined using the Wilcoxon matched-pair signed rank test. Albeit such hemodynamic differences can be anticipated because we are examining different vessels, it is interesting to note that in patients diagnosed with coronary diseases, angiographically normal vessels, non-FFR vessels, can also have impaired flow disturbances quantified by computing the difference of ESS and vorticity from a control patient when compared to corresponding FFR vessel.
4 Discussion
In the current study, we used 3D CFD to assess intracoronary hemodynamics using geometries derived from 2D coronary angiograms from patients undergoing diagnostic coronary angiography. We demonstrated that our CFD pipeline was highly accurate by performing CFD simulations and PIV experiments with the same RCA geometry and found good agreement between the results at the bifurcation, a region that is known to have complex intravascular hemodynamics (Giannoglou et al., 2010). We further demonstrated the accuracy of our pipeline by comparing FFR values of intermediate coronary artery stenoses determined by CFD with invasive pressure wire-based measurements made in the cardiac catheterization laboratory. CFD-derived FFR demonstrated excellent concordance with invasively measured values with an error of 5.9 ± 0.1%, which is similar to the intrinsic sampling reproducibility of catheter based FFR (Berry et al., 2013). Our 3D CFD simulations also allowed us to further phenotype intracoronary hemodynamics by calculating velocity, ESS, and vorticity, in addition to pressure, over the entire coronary tree. Our analysis of these hemodynamic variables revealed several interesting findings. First, velocity, ESS, and vorticity at the site of the stenosis were significantly different when compared to the hemodynamics in another main coronary vessel in the same patient that was angiographically normal. Second, we were able to assess the contribution of the stenosis to perturbations in intravascular hemodynamics and found that the stenosis was associated with differences in intravascular velocity and vorticity. When we simulated absence of the stenosis, only velocity and vorticity were different suggesting that there were other contributors to ESS in our system. Third, we also found that vorticity was significantly different in angiographically normal appearing non-FFR vessels in patients with coronary disease compared to what was observed in corresponding FFR vessel. Taken together, these findings demonstrate that our fluid solver pipeline is highly accurate, and that vorticity may emerge as a potential phenomarker in patients with coronary artery disease.
3D CFD simulations of coronary blood flow using patient-specific coronary artery geometries generates several parameters that describe important components of flow in the vessels. These parameters (pressure, velocity, ESS, and vorticity) provide numerous degrees of freedom, as compared to currently available reduced order CFD methods, and may be able to resolve nuanced disruptions in coronary arterial blood flow. Several works have previously explored the role of ESS, a proatherogenic risk factor, to understand intracoronary hemodynamic patterns that can play role in the plaque formation (Rikhtegar et al., 2012; Szabó et al., 2021; Tufaro et al., 2022). Low fluid velocity and the resulting low ESS on the vessel wall have been reported to be directly related to vessel wall thickening and plaque development (Rikhtegar et al., 2012; Szabó et al., 2021; Tufaro et al., 2022). Such hemodynamic risk factors can provide valuable information for physiologic lesion assessment in patients diagnosed with coronary disease. In this work we specifically explored the role of vorticity in the assessment of CAD. We found a strong inverse correlation between FFR and vorticity in our patient-specific simulations, which is in agreement with prior reports investigating FFR and vorticity as phenomenon related to fluid energy loss in idealized coronary arterial models (Chu et al., 2018).
To date, there has been limited forays into understanding the role of vorticity in coronary artery disease. One study that examined vorticity in virtual vessel models with varying degrees of stenosis and in 3D coronary artery reconstructions from coronary angiograms reported that a disturbed vorticity index, changes in vorticity at the site of the stenosis, was present and correlated with FFR (Chu et al., 2018). This supports our findings; however, the prior study had several issues that may affect the results. The coronary reconstructions studied were truncated and did not include the entire coronary tree. We have shown previously that this affects intracoronary hemodynamics with a 10–20-fold difference in velocity and time-averaged wall shear stress (Vardhan et al., 2019). They also focused on the disturbed vorticity index as opposed to absolute vorticity, which we were able to do with our simulation results.
Within the framework of our CFD pipeline, vorticity can be calculated over the entire coronary arterial tree. Given that vorticity demonstrates a strong inverse relationship with FFR, our CFD method allows for the addition of vorticity to FFR to assess CAD lesions throughout the entire coronary tree without requiring invasive pressure wire assessment of individual CAD lesions. Further, given that clinically meaningful FFR thresholds have been developed, this study lays the groundwork for the development of vorticity thresholds. For example, the Fractional Flow Reserve versus Angiography for Guiding PCI (FAME) study used an FFR threshold of .0.8 to define physiologically significant coronary lesions and showed that a FFR-guided PCI strategy resulted in deferral of PCI in almost 33% of the lesions and better 1-year clinical outcomes compared to angiography alone (Tonino et al., 2009). In our simulations, vorticity was inversely correlated with FFR and has the potential to add information. Whether a combine FFR-vorticity metric has the potential to provide diagnostic information regarding a stenosis remains to be determined.
Critical coronary arterial stenosis is known to manifest as an end-stage complication of atherosclerotic plaque development and progression (Malakar et al., 2019). Biochemical studies demonstrate that many pathobiological changes have occurred in vessels by the time CAD lesions are angiographically apparent. The results from our study are intriguing in that we found hemodynamic alterations, and disturbances in vorticity in particular, in angiographically normal vessels from patients with coronary artery disease in another vessel. This suggests that coronary blood flow alterations may be present in coronary arteries that have not yet developed angiographically apparent lesions. Whether vorticity has utility as a screening tool to identify vessels at risk of developing coronary disease remains to be determined.
There are several limitations to our study that may preclude generalizability of the findings. First, the 3D geometries were created using 2D coronary angiograms and rely on luminography that may not provide the same in-depth detail about the composition of a coronary stenosis achieved with intravascular ultrasound imaging or optical coherence tomography intravascular imaging. To date, there are no studies that have compared CFD results from all three imaging modalities for CFD simulations and use of 2D coronary angiograms for reconstructions has been established by us and others (Papafaklis et al., 2014; Kornowski et al., 2016; Vardhan et al., 2019; Vardhan et al., 2021). Our CFD method also assumes rigid arterial walls and Newtonian flow. These are two common assumptions in CFD simulations and have been shown to be valid at the shear rates and degree of myocardial contractility observed in coronary vessels (Taylor et al., 2013; Eslami et al., 2020). Another limitation of this work is that the computational simulations were performed offline because the time step in LBM-based solvers is limited by the Courant–Friedrichs–Lewy number resulting in long runtime (Fakhari and Lee 2015). Fortunately, with efficient parallelization of the LBM paired with increased computing power, the overall simulation time can be reduced significantly (Randles et al., 2013). Our patient sample size was small as this was a proof-of-concept study and it is plausible that with a higher sample size other findings will emerge. Therefore, it will be critical to pursue the findings of this study in a larger multicenter clinical investigation to establish robust significance of the performance of vorticity in patients with established coronary artery disease.
Overall, this study establishes that intracoronary hemodynamic profiling, through the use of well validated 3D CFD methodology, can accurately determine a clinically actionable metric, FFR, and provide additional information to describe flow profiles around a stenosis and in a vessel. Vorticity at the site of a stenosis was found to correlate well with invasive diagnostics and therefore holds promise as a phenomarkers to be examined using a less invasive assessment of coronary blood flow and function. Furthermore, vorticity in angiographically normal appearing vessels in patients with CAD elsewhere is significantly different as compared to patients without CAD. Future studies are therefore warranted to investigate the full utility of vorticity in the screening for the development of or progression of CAD. Future studies with larger sample sizes to determine the functional significance of vorticity are warranted.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Ethics statement
The protocol was approved by the Mass General Brigham Institutional Review Board and performed under relevant guidelines and regulations per the approved IRB protocol. Informed consent was not required because the study is retrospective and only used de-identified and anonymized datasets.
Author contributions
MV, JG, AK, SC, JL, and AR contributed to the conception and design of the study. SC completed reconstructions. MV, LH, JG, and AR developed the simulation methods. MV performed the simulations and statistical analysis. PN, WW, and DF completed the in vitro experiments. MV wrote the first draft of the manuscript. JK, JL, and AR wrote sections of the manuscript.
Funding
This work was supported by the Coulter Foundation (AR, MV, LH, JG, SC), American Heart Association Predoctoral Fellowship 20PRE35211158 (MV); American Heart Association AIM 19AIML34980000, NHLBI U01 HL125215 (JL); and NSF 1943036 and NIH U01CA253511 (AR). The content does not necessarily represent the official views of the NIH or NSF. This manuscript has been authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Amir, M., Usmani Abdullah, Y., Varshney, M., Fahad, A. S., Khan Saleem, A., Islam, N., et al. (2022). Analysing Spatio-temporal flow hemodynamics in an artery manifesting stenosis. Int. J. Mech. Sci. 218, 107072. doi:10.1016/j.ijmecsci.2022.107072
Anselmi, A., Corbineau, H., Verhoye, J.-P., and Drochon, A. (2021). Impact of revascularization on the distal to proximal pressure ratio in case of multiple coronary stenoses. J. Biomed. Sci. Eng. 14, 142–175. doi:10.4236/jbise.2021.143014
Berry, C., van 't Veer, M., Witt, N., Kala, P., Bocek, O., Pyxaras, S. A., et al. (2013). VERIFY (VERification of instantaneous wave-free ratio and fractional flow reserve for the assessment of coronary artery stenosis severity in EverydaY practice): A multicenter study in consecutive patients. J. Am. Coll. Cardiol. 61 (13), 1421–1427. doi:10.1016/j.jacc.2012.09.065
Chaudhury, R. A., Atlasman, V., Pathangey, G., Pracht, N., Adrian, R. J., and Frakes, D. H. (2016). A high performance pulsatile pump for aortic flow experiments in 3-dimensional models. Cardiovasc. Eng. Technol. 7 (2), 148–158. doi:10.1007/s13239-016-0260-3
Chen, S. J., and Carroll, J. D. (2000). 3-D reconstruction of coronary arterial tree to optimize angiographic visualization. IEEE Trans. Med. Imaging 19 (4), 318–336. doi:10.1109/42.848183
Chu, M., von Birgelen, C., Li, Y., Westra, J., Yang, J., Holm, N. R., et al. (2018). Quantification of disturbed coronary flow by disturbed vorticity index and relation with fractional flow reserve. Atherosclerosis 273, 136–144. doi:10.1016/j.atherosclerosis.2018.02.023
De Bruyne, B., Pijls, N. H., Kalesan, B., Barbato, E., Tonino, P. A., Piroth, Z., et al. (2012). Fractional flow reserve-guided PCI versus medical therapy in stable coronary disease. N. Engl. J. Med. 367 (11), 991–1001. doi:10.1056/NEJMoa1205361
Eslami, P., Hartman, E. M. J., Albaghadai, M., Karady, J., Jin, Z., Thondapu, V., et al. (2021). Validation of wall shear stress assessment in non-invasive coronary cta versus invasive imaging: A patient-specific computational study. Ann. Biomed. Eng. 49 (4), 1151–1168. doi:10.1007/s10439-020-02631-9
Eslami, P., Seo, J. H., Lardo, A. C., Chen, M. Y., and Mittal, R. (2019). Flow dynamics in the aortic arch and its effect on the arterial input function in cardiac computed tomography. J. Biomech. Eng. 141 (10), 1045011–1045018. doi:10.1115/1.4043076
Eslami, P., Tran, J., Jin, Z., Karady, J., Sotoodeh, R., Lu, M. T., et al. (2020). Effect of wall elasticity on hemodynamics and wall shear stress in patient-specific simulations in the coronary arteries. J. Biomech. Eng. 142 (2), 024503. doi:10.1115/1.4043722
Fakhari, A., and Lee, T. (2015). Numerics of the lattice Boltzmann method on nonuniform grids: Standard LBM and finite-difference LBM. Comput. Fluids 107, 205–213. doi:10.1016/j.compfluid.2014.11.013
Feiger, B., Vardhan, M., Gounley, J., Mortensen, M., Nair, P., Chaudhury, R., et al. (2019). Suitability of lattice Boltzmann inlet and outlet boundary conditions for simulating flow in image-derived vasculature. Int. J. Numer. Method. Biomed. Eng. 35 (6), e3198. doi:10.1002/cnm.3198
Gao, Y., Zhao, N., Song, L., Hu, H., Jiang, T., Chen, W., et al. (2022). Diagnostic performance of CT FFR with a new parameter optimized computational fluid dynamics algorithm from the CT-FFR-China trial: Characteristic analysis of gray zone lesions and misdiagnosed lesions. Front. Cardiovasc. Med. 9, 819460. doi:10.3389/fcvm.2022.819460
Garcia, J., Capoulade, R., Le Ven, F., Gaillard, E., Kadem, L., Pibarot, P., et al. (2013). Discrepancies between cardiovascular magnetic resonance and Doppler echocardiography in the measurement of transvalvular gradient in aortic stenosis: The effect of flow vorticity. J. Cardiovasc. Magn. Reson. 15, 84. doi:10.1186/1532-429X-15-84
Giannoglou, G. D., Antoniadis, A. P., Koskinas, K. C., and Chatzizisis, Y. S. (2010). Flow and atherosclerosis in coronary bifurcations. EuroIntervention 6, J16–J23. doi:10.4244/EIJV6SUPJA4
Green, N. E., Chen, S. Y., Hansgen, A. R., Messenger, J. C., Groves, B. M., and Carroll, J. D. (2005). Angiographic views used for percutaneous coronary interventions: A three-dimensional analysis of physician-determined vs. computer-generated views. Catheter. Cardiovasc. Interv. 64 (4), 451–459. doi:10.1002/ccd.20331
Grinberg, L., and Karniadakis, G. E. (2008). Outflow boundary conditions for arterial networks with multiple outlets. Ann. Biomed. Eng. 36 (9), 1496–1514. doi:10.1007/s10439-008-9527-7
Guleren, M. (2013). Numerical flow analysis of coronary arteries through concentric and eccentric stenosed geometries. J. Biomech. 46 (6), 1043–1052. doi:10.1016/j.jbiomech.2013.02.001
Katritsis, D. G., Theodorakakos, A., Pantos, I., Andriotis, A., Efstathopoulos, E. P., Siontis, G., et al. (2010). vortex formation and recirculation zones in left anterior descending artery stenoses: Computational fluid dynamics analysis. Phys. Med. Biol. 55 (5), 1395–1411. doi:10.1088/0031-9155/55/5/009
Kornowski, R., Lavi, I., Pellicano, M., Xaplanteris, P., Vaknin-Assa, H., Assali, A., et al. (2016). Fractional flow reserve derived from routine coronary angiograms. J. Am. Coll. Cardiol. 68 (20), 2235–2237. doi:10.1016/j.jacc.2016.08.051
Kruger, T., Kusumaatmaja, H., Kuzmin, A., Shardt, O., Silva, G., and Viggen, E. M. (2017). The lattice Boltzmann method. Springer Int. Publ. 10 (978-3), 4–15.
Latt, J., Chopard, B., Malaspinas, O., Deville, M., and Michler, A. (2008). Straight velocity boundaries in the lattice Boltzmann method. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 77, 056703. doi:10.1103/PhysRevE.77.056703
Lawton, J. S., Tamis-Holland, J. E., Bangalore, S., Bates, E. R., Beckie, T. M., Bischoff, J. M., et al. (2022). 2021 ACC/AHA/SCAI guideline for coronary artery revascularization: A report of the American College of cardiology/American heart association joint committee on clinical practice guidelines. Circulation 145 (3), e18–e114. doi:10.1161/CIR.0000000000001038
Malakar, A. K., Choudhury, D., Halder, B., Paul, P., Uddin, A., and Chakraborty, S. (2019). A review on coronary artery disease, its risk factors, and therapeutics. J. Cell. Physiol. 234 (10), 16812–16823. doi:10.1002/jcp.28350
Matyka, M., Koza, K., and Miroslaw, L. (2013). Wall orientation and shear stress in the lattice Boltzmann model. Comput. Fluids 73, 115–123. doi:10.1016/j.compfluid.2012.12.018
Morris, P. D., Silva Soto, D. A., Feher, J. F. A., Rafiroiu, D., Lungu, A., Varma, S., et al. (2017). Fast virtual fractional flow reserve based upon steady-state computational fluid dynamics analysis: Results from the VIRTU-fast study. JACC. Basic Transl. Sci. 2 (4), 434–446. doi:10.1016/j.jacbts.2017.04.003
Papafaklis, M. I., Muramatsu, T., Ishibashi, Y., Lakkas, L. S., Nakatani, S., Bourantas, C. V., et al. (2014). Fast virtual functional assessment of intermediate coronary lesions using routine angiographic data and blood flow simulation in humans: Comparison with pressure wire - fractional flow reserve. EuroIntervention 10 (5), 574–583. doi:10.4244/EIJY14M07_01
Randles, A. P., Kale, V., Hammond, J., Gropp, W., and Kaxiras, E. (2013). “Performance analysis of the lattice Boltzmann model beyond Navier-Stokes,” in IEEE 2013 IEEE 27th International Symposium.
Rigatelli, G., Zuin, M., Ngo, T. T., Nguyen, H. T., Nanjundappa, A., Talarico, E., et al. (2019). Intracoronary cavitation as a cause of plaque rupture and thrombosis propagation in patients with acute myocardial infarction: A computational study. J. Transl. Int. Med. 7 (2), 69–75. doi:10.2478/jtim-2019-0014
Rikhtegar, F., Knight, J. A., Olgac, U., Saur, S. C., Poulikakos, D., Marshall, W., et al. (2012). Choosing the optimal wall shear parameter for the prediction of plaque location-A patient-specific computational study in human left coronary arteries. Atherosclerosis 221 (2), 432–437. doi:10.1016/j.atherosclerosis.2012.01.018
Szabó, G. T., Üveges, Á., Tar, B., Ágoston, A., Dorj, A., Jenei, C., et al. (2021). The holistic coronary physiology display: Calculation of the flow separation index in vessel-specific individual flow range during fractional flow reserve measurement using 3D coronary reconstruction. J. Clin. Med. 10 (9), 1910. doi:10.3390/jcm10091910
Taylor, C. A., Fonte, T. A., and Min, J. K. (2013). Computational fluid dynamics applied to cardiac computed tomography for noninvasive quantification of fractional flow reserve: Scientific basis. J. Am. Coll. Cardiol. 61 (22), 2233–2241. doi:10.1016/j.jacc.2012.11.083
Tonino, P. A., De Bruyne, B., Pijls, N. H., Siebert, U., Ikeno, F., van' t Veer, M., et al. (2009). Fractional flow reserve versus angiography for guiding percutaneous coronary intervention. N. Engl. J. Med. 360 (3), 213–224. doi:10.1056/NEJMoa0807611
Tufaro, V., Torii, R., Erdogan, E., Kitslaar, P., Koo, B. K., Rakhit, R., et al. (2022). An automated software for real-time quantification of wall shear stress distribution in quantitative coronary angiography data. Int. J. Cardiol. 357, 14–19. doi:10.1016/j.ijcard.2022.03.022
Vardhan, M., Gounley, J., Chen, S. J., Chi, E. C., Kahn, A. M., Leopold, J. A., et al. (2021). The importance of side branches in modeling 3D hemodynamics from angiograms for patients with coronary artery disease. Sci. Rep. 11 (1), 8854. doi:10.1038/s41598-019-45342-5
Vardhan, M., Gounley, J., Chen, S. J., Kahn, A. M., Leopold, J. A., and Randles, A. (2019). The importance of side branches in modeling 3D hemodynamics from angiograms for patients with coronary artery disease. Sci. Rep. 9 (1), 8854. doi:10.1038/s41598-019-45342-5
Virani, S. S., Alonso, A., Benjamin, E. J., Bittencourt, M. S., Callaway, C. W., Carson, A. P., et al. (2020). Heart disease and stroke statistics-2020 update: A report from the American heart association. Circulation 141 (9), e139–e596. doi:10.1161/CIR.0000000000000757
Wilson, R. F., Wyche, K., Christensen, B. V., Zimmer, S., and Laxson, D. D. (1990). Effects of adenosine on human coronary arterial circulation. Circulation 82 (5), 1595–1606. doi:10.1161/01.cir.82.5.1595
Wu, J. Z., Ma, H. Y., and Zhou, M. D. (2007). Vorticity and vortex hemodynamics. Springer Science & Business Media.
Yue-Hin Loke, Francesco Capuano, Cleveland, Vincent, Mandell, Jason G., Elias, Balaras, Olivieri, Laura J., and Olivieri, L. J. (2021). Moving beyond size: Vorticity and energy loss are correlated with right ventricular dysfunction and exercise intolerance in repaired Tetralogy of Fallot. J. Cardiovasc. Magn. Reson. 23, 98. doi:10.1186/s12968-021-00789-2
Keywords: vorticity, shear stress, coronary artery disease, computational fluid dynamics, fractional flow reserve
Citation: Vardhan M, Gounley J, Chen SJ, Nair P, Wei W, Hegele L, Kusner J, Kahn AM, Frakes D, Leopold JA and Randles A (2022) Evaluation of intracoronary hemodynamics identifies perturbations in vorticity. Front. Syst. Biol. 2:930396. doi: 10.3389/fsysb.2022.930396
Received: 27 April 2022; Accepted: 04 October 2022;
Published: 09 November 2022.
Edited by:
Bairong Shen, Sichuan University, ChinaReviewed by:
Zsolt Kőszegi, University of Debrecen, HungaryAgnes Drochon, Université de Bordeaux, France
Copyright © 2022 Vardhan, Gounley, Chen, Nair, Wei, Hegele, Kusner, Kahn, Frakes, Leopold and Randles. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Amanda Randles, YW1hbmRhLnJhbmRsZXNAZHVrZS5lZHU=
†These authors share senior authorship
 Madhurima Vardhan
Madhurima Vardhan John Gounley
John Gounley S. James Chen3
S. James Chen3 Wei Wei
Wei Wei Luiz Hegele
Luiz Hegele Jonathan Kusner
Jonathan Kusner Andrew M. Kahn
Andrew M. Kahn Jane A. Leopold
Jane A. Leopold Amanda Randles
Amanda Randles