Perspective: Systems biology beyond biology

The past decades have witnessed an astounding rise of the nascent field of systems biology. By and large unknown or ignored for a long time, the field rapidly moved into the limelight and is now in the process of becoming a widely recognized and respected component of mainstream biology. Of course, much remains to be explored and accomplished in systems biology within its parent domain of biology, but the time seems ripe for expansions beyond this domain. The goal of such an expansion should not be the creation of new strongholds or academic silos outside biology, but the true integration of biological systems thinking into educational programs of other disciplines. The expansion should naturally start with closely related fields like biophysics, biochemistry, bioinformatics, and bioengineering, but should continue further into other areas invested in the study of life, such as medicine, epidemiology, and public health, as well as applied mathematics and computer science. This perspective sketches out how systems biological thinking might enrich the training of a new generation of scientists in different fields of scientific endeavor.

Introduction

Nothing in the living world happens in a vacuum. No life processes proceed in isolation. Every event affects others, and every event is affected by others. Life is the consequence of complex, dynamic systems consisting of uncounted parts and processes that are highly regulated. Understanding the inner workings of life and effectively manipulating and improving them, whether through medicine, biomedical engineering, drug development or environmental stewardship, necessitates tools and procedures for analyzing these systems. These tools and procedures are at the core of systems biology.

It is difficult to pinpoint the roots and origins of systems biology. A holistic view of the human body was the centerpiece of Greek, Roman and East Asian medicine, and physicians and philosophers like Hippocrates attributed health and disease to the balance or imbalance of bodily juices, called humors. In the Western world, this holistic view of the body continued into the 19th and 20th Centuries, with leading physiologists considering the body as governed by systems, such as the nervous system, the gastro-intestinal system, and the cardiovascular system. During the second half of the 20th century, this type of thinking became almost entirely replaced by the concept of reductionism (Savageau, 1991a; Brigandt and Love, 2017): To understand the proper functioning of the body, one had to understand the functionality of each of its components: their tissues, cells and, ultimately, the inventory of intracellular molecular building blocks.

This reductionist approach has been enormously successful, and our knowledge regarding biological phenomena has grown with amazing force and speed. Yet, simultaneously with unprecedented successes, science slowly came to realize that even complete knowledge of the molecular inventory would not be sufficient to explain the functionality of life: The parts alone seldom reveal the function of a complex system. It is now widely accepted that means of reconstructing integrated systems from their component parts and processes are required if we are to understand biological phenomena and manipulate them in a rational, targeted manner (Savageau, 1991b).

Systems biology resulted from this realization as a novel manifestation of old concepts. Embracing Claude Bernard’s early ideas of control processes governing life (Bernard, 1865; Noble, 2008), and more so the tenets of dynamical systems analysis, as elegantly proposed by Ludwig von Bertalanffy from the 1920s to 1960s (von Bertalanffy, 1927; von Bertalanffy, 1940; von Bertalanffy, 1968), a few researchers began to develop approaches that would allow representing and analyzing nonlinear models of, in principle, arbitrarily complex systems. In 1968, the term “systems biology” was coined in the context of a conference (Mesarović, 1968). It had become evident to insiders—and now it came out in the open—that the necessary approaches had to be computational to realize the ideas and potential of systems biology. Specifically, these approaches would have to address biological phenomena as complex, hierarchical, adaptive, dynamic systems. They had to be able to deal with change and complicated nonlinearities and thereby facilitate the functional integration of small models (“modules”) into increasingly larger, well-organized ensembles of models in complex contexts. It was beyond doubt that these approaches required the use of mathematics and computation (Melham, 2013; Motta and Pappalardo, 2013; Cvijovic et al., 2016; MacLeod, 2021). Initially, the scientific community at large was reluctant to accept the proposal to use computational methods and control theory to understand living systems, because “biology was too complicated to use math.” However, the tide changed with the new millennium, and the change was irrevocable.

Four aspects can be identified as drivers behind this gradual acceptance of the new dawn of biological systems science with modern technologies. The first two were the imminent completion of the draft human genome project and the emerging and quickly growing availability of high-throughput methods that generated very large molecular datasets of unprecedented magnitude. The third was the explosion in computational power that became accessible to almost anyone in the world. Finally, the fourth aspect was a strong push by influential researchers like Leroy Hood (Ideker et al., 2001; Hood et al., 2004) and Hiroaki Kitano (Kitano, 2002), who were able to convince the community of the importance of systems biology. Since these early days of the new systems biology, its practitioners have done a remarkable job propelling biological systems thinking into the limelight, both through impressive research advances and successful marketing at scientific conferences, and in books, reviews, and tutorials.

Systems biology is about integration of phenomena into functional contexts, both experimentally and computationally. While this integration is increasingly pursued within biology, the time now seems right for systems biology to integrate its core concepts into other pertinent disciplines. Three key aspects of this type of new biological thinking should be propagated, namely:

• The simultaneous consideration of many interdependent components, complementing approaches inspired by reductionism that focus on one core aspect at a time.

• The appreciation of the importance and ubiquity of dynamics. Very few biological constituents remain static for long.

• The universal role and interactivity of regulation. It had been known for a long time that many processes are regulated, for instance, through feedback inhibition, but it has now become clear that often-complicated regulatory networks govern the proper functioning of all cellular and organismal systems.

Due to its transdisciplinary nature, systems biology poses challenges to education, and various modes of education have been proposed over the years (Ideker, 2004; Aderem, 2005; Kumar, 2005; Braillard and Kampourakis, 2013; Cvijovic et al., 2016; Momsen et al., 2022). It is laudable that many universities around the world have implemented programs in systems biology. Examples include Harvard’s Ph.D. Program in Systems, Synthetic, and Quantitative Biology and the Quantitative Biosciences Program at Georgia Tech, as well as similar programs at Stanford, MIT, and universities in Edinburgh, Gothenburg, London, Maastricht, Oxford, Vienna, and Vilnius, to name but a few. These programs teach students that dynamics, multi-level integration, complexity, adaptation, and emergence are important drivers of biological functionality.

This type of thinking, which is fundamental to systems biology, should be exported to other fields and integrated into their core tenets. It is not suggested that other fields would have to change dramatically what they do, but their students should be taught to recognize that everything occurs within a context, that many or all components of systems affect each other, that the components themselves, as well as their interactions, change over time, and that mathematics is needed to address these issues effectively and reliably.

Biological systems thinking may be incorporated into an educational curriculum in a number of ways, quasi on a sliding scale of extent (Voit and Kemp, 2011). The extreme of lowest effort may be the explicit mention and conceptual discussion of this new approach to biological investigation, maybe toward the end of an introductory class, and ideally with a few illustration examples and conceptual references. Even this act of brief introduction can be rather influential, as students are made aware of the existence of a complement to the traditional ways of “doing” science, especially if their program of study offers an elective course on the subject. A slightly higher involvement is a dedicated lecture, module or even section within an introductory course on one or a few key topics of systems biology, ideally with hands-on exercises. Of course, it is possible to offer an entire course, a minor, a programmatic area of emphasis and, at the other extreme of effort, a comprehensive program, such as a Ph.D. program in systems biology or systems medicine, as indicated before. Some illustrations are provided in the next section.

While an entire program of course results in a new cadre of specialists, it is not always desirable to create additional strongholds outside biology. Rather, the community should strive to infuse and integrate key concepts of biological systems thinking meaningfully into other disciplines. Especially if the dominant paradigm of this field is of a reductionist nature, it would be beneficial to the students to experience a complementing view of connectivity, dynamics and regulation, accompanied by a substantive discussion that the unaided human mind has insurmountable problems comprehending these aspects intuitively, but that mathematics and computational modeling have at least the potential of capturing all governing features of these aspects.

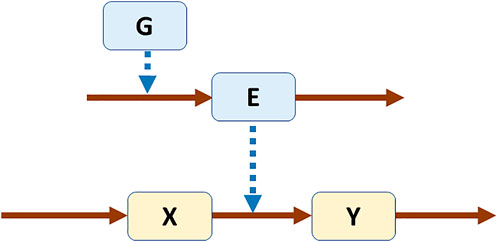
As a simple example, one may compare linear pathways without or with feedback (Figure 1) (Voit, 2017). In a biological setting, X, Y, and Z could be metabolites and E an enzyme catalyzing the conversion of X into Y. In Panel A, the pathway is not regulated, while in Panel B the end product Z triggers the production of a transcription factor TF, which leads to the expression of gene G, which in turn codes for enzyme E. The same system structure would have different interpretations in other disciplines, but they should be easy to construct because direct or indirect feedback is ubiquitous.

FIGURE 1

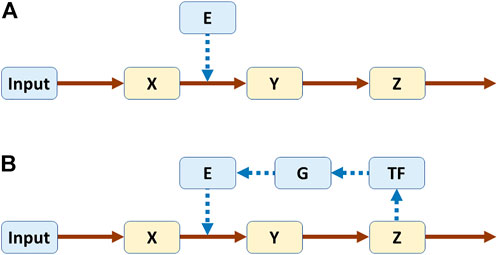
FIGURE 1. Linear pathways without (A) and with (B) feedback. Both systems were modeled in power-law format (Voit, 2017). Equations for pathway (A) $\dot{\mathit{X}}=\mathit{I}\mathit{n}\mathit{p}\mathit{u}\mathit{t}-\mathit{E}\cdot {\mathit{X}}^{0.5}$, $\dot{\mathit{Y}}=\mathit{E}\cdot {\mathit{X}}^{0.5}-{\mathit{Y}}^{0.5}$, $\dot{\mathit{Z}}={\mathit{Y}}^{0.5}-{\mathit{Z}}^{0.5}$ For pathway B, the following equations were added: $\mathit{T}\dot{\mathit{F}}={\mathit{Z}}^{\mathit{p}}-{\mathit{T}\mathit{F}}^{0.5}$, $\dot{\mathit{G}}={\mathit{T}\mathit{F}}^{0.5}-{\mathit{G}}^{0.5}$, $\dot{\mathit{E}}={\mathit{G}}^{0.5}-{\mathit{E}}^{0.5}$ Variation in the value of parameter p in the equation of TF leads to distinct results (cf. Figure 2). Further details are provided in the Appendix.

One might ask the students what they would expect to happen if the independent variable Input is slightly decreased. The answer is easily and correctly found in the unregulated pathway: First X decreases, then Y, then Z. A simple simulation confirms the hypothesis (Figure 2A). In the case of the regulated pathway, the answer is more complicated, and simple arguments like “If this goes down then that goes down” do not yield a reliable answer. In fact, depending on the strength with which Z triggers TF, captured in the parameter p, the outcome is very similar to the unregulated pathway (p = 0.01; result not shown), leads to damped (p = 0.4; Figure 2B) or stable limit-cycle oscillations (p = 0.56, Figure 2C), or cause Y and Z to disappear entirely (p = 0.6, Figure 2D). Thus, the results cannot be reliably intuited as they depend qualitatively on subtle numerical changes in a parameter. Expressed differently, one may be able to figure out the responses of very simple dynamical systems, but as soon as they become more complicated, mathematics and computing are unavoidable. The default for such an analysis is often a model in the form of differential equations, but it is also possible to use discrete approaches (Robeva, 2015) or agent-based models (Railsback and Grimm, 2019; Garcia, 2021).

FIGURE 2

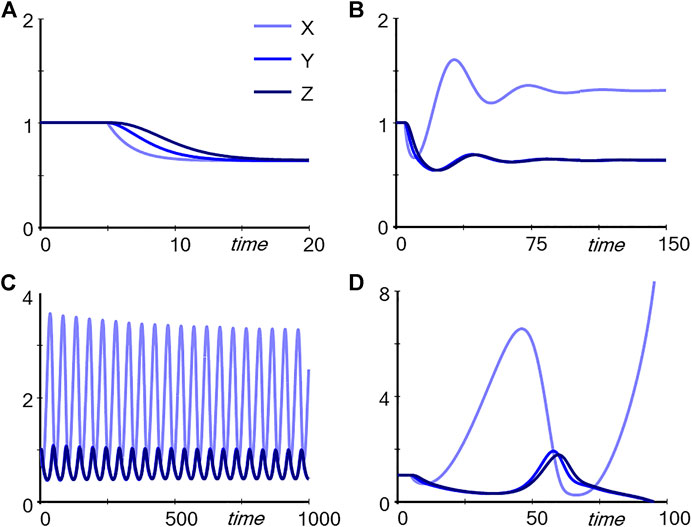
FIGURE 2. Simulation results for the pathways in Figure 1. The system was started at the steady state (all variables at 1). At time 5, Input was reduced from one to 0.8. Panel (A) Trajectories corresponding to Panel A in Figure 1. Panels (B–D): Trajectories corresponding to Panel B in Figure 1 with p = 0.4, p = 0.56, and p = 0.6, respectively.

A role model for low-level integration into other fields may be biostatistics or, more precisely, statistical thinking (ideally without its wide-spread fear factor). Merely a few decades ago, statistics was a dreaded add-on to biomedical investigations. Since then, this situation has slowly, but drastically changed. By now, every biologist and research clinician has been trained to develop a mindset of control experiments, sample sizes and significance testing, even if the actual statistical planning and analysis for complicated biomedical studies is still often done by experts, which is perfectly fine. Similarly, systems thinking should become a natural part of the mindset of all practitioners of biomedical fields, even if formal analyses are mostly done by experts.

Thus, it appears to be beneficial—as well as timely—to include a modicum of systems thinking into the curricula of scientific disciplines that are tangential to biology. Many options exist for specific implementations, as discussed before; the next section describes vignettes of possible realizations of these ideas. The goal of these efforts should be to make students of these disciplines aware of the power and potential of dynamical systems thinking, as it is practiced in systems biology.

One should note that there are different levels of understanding, ranging from recognizing features of complexity to grasping the core principles of analysis to mastering techniques (Savageau, 1991a; Savageau, 1991b). An analogy might be an airplane, where average passengers have a vague notion of jets, pilots are familiar with the plane’s components, but aeronautical engineers know enough to explain the design of the plane and possibly improve it. Similarly, the outcome of different teaching modalities will lead to different levels of mastery.

The main challenge to including systems thinking into educational programs of other disciplines is that all curricula are notoriously “full” and that infusing additional concepts requires reductions somewhere else (Voit and Kemp, 2011). Other challenges include aspects of fundamental human nature, such as hesitance accepting novelty and defensive reactions like “So, you tell me, what I am doing is outdated?” In the case of medical training, an unfortunate attitude is “I need to know how to treat my patients; details of molecular complexity are important but have lower priority.” These challenges often create strong resistance toward changing a curriculum.

Examples of the integration of biological systems thinking into other disciplines

Many examples of computational modeling dot the educational landscape of science. In this section, I offer vignettes from my own experience that are somewhat representative and highlight different means of integrating biological systems thinking into other disciplines. They might serve as role models for similar efforts in other disciplines.

A single class within an introductory course

Earlier this year, I accepted an invitation from Emory University to talk about the role of systems biology in medicine and public health within an introductory course entitled Introduction to Predictive Health and Society. According to the course catalog, this course “introduces the evidence base for the science of health and emphasizes STEM (Science, Technology, Engineering and Mathematics) educational translations to the population, clinic and individual levels. Innovative efforts are needed to drive changes in health care from a reactive, disease-focused system to a proactive health-focused one.” The class was attended by over 150 undergraduate students from a variety of programs, who were still deciding on the exact directions of their future careers. The course thus offered an opportunity to engage in a discussion with “unspoiled” inquisitive minds from a spectrum of health-related fields. I started my presentation with the fact that the health care systems in the Western world are rapidly becoming more expensive and will soon be unaffordable if no course corrections are made. One change could come from personalized treatments and predictable health trajectories, which could reduce costs for treatments that are unnecessary or unlikely to succeed, based on an individual’s physiological predisposition and health history. We discussed the enormous complexity of living organisms as the overriding challenge toward personalized medicine and predictive health, as well as the need of approaching this complexity with systems-based methods. No mathematical or computational details were discussed, but it became evident to the students that the many components of living systems, their nonlinear and threshold-like behaviors and the crucial ubiquity of regulation leave the human mind overwhelmed and offer no true alternatives to computational approaches. No student left the class as a systems biologist, but it is well possible that a seed of curiosity was planted in some of these future scientists and clinicians. Several times before, I taught a similar class, with the same philosophy, in Emory’s Exposome program.

A small hands-on learning module

At Spelman College, we developed a hands-on, stand-alone computational module on homeostasis that introduced students to the compensatory action of the human body if the blood oxygen level is too low. The module was mostly taken by first-year biology majors, but also by students with an interest in pursuing health careers. The course had already addressed cellular respiration, the role of red blood cells (RBCs) and the transport of oxygen (O₂). Thus, the regulation of RBC production and blood oxygenation, mediated by the hormone erythropoietin (Epo), implicitly or explicitly revisited earlier core concepts and was therefore particularly well suited for illustrating the power of transdisciplinary learning. The students had math training at the high school level, but not taken college mathematics or computing. For a detailed account of this module and its context, see (Ayalew et al., 2020).

Because the physiological details of RBC regulation are somewhat convoluted, we found it helpful first to introduce the students to differential equation modeling by considering fluctuations in the water level of a lake. The students readily realized that many processes affect the amount of water in a lake, including inflow from tributaries, rain, and run-off from fields on the one hand and efflux, water use and evaporation on the other. This intuitive understanding was systematically converted into an ordinary differential equation (ODE) in mass action format augmented for inhibition, with positive and negative terms corresponding to influxes and effluxes, respectively. Once the students understood this example, they worked in small groups on transferring their insights into a representation of the dynamics of RBCs. It was discussed that simplifications were necessary and acceptable for a general understanding. Similarly, and with the help of the instructor, equations for O₂ and Epo were established, discussed, and fine-tuned. In the process, the students became somewhat familiar with the notion of modeling, simplification and abstraction, and translating a biological phenomenon into the form of a computable structure that quantitatively captured their conceptual thinking. In the second phase of the module, the students were provided with fully functional Python code of the model. They quickly saw that the code directly aligned with the previously developed equations. Once they had a reasonable grasp of the code, they were presented with different scenarios, such as blood loss, sickle cell anemia, or operation in high altitudes, and tasked to identify which aspects of the model were affected. Their predictions were tested once corresponding changes had been made to the Python code.

To demonstrate the transdisciplinary nature of systems biology, the students focus in subsequent semesters on the same problem space in math and computer science courses, but with different, discipline-based emphases. In an introductory mathematics course, for example, the module can be used to illustrate the conceptual meaning of a derivative as a rate of change, the behavior of different functions in the ODEs (mass action, power-laws with different positive and negative exponents, other functions), modeling alternatives like discrete recursive models, as well as questions regarding the homeostatic state as a fixed point. A higher-level math or computing course could use the module again to discuss linearization, computation of the Jacobian, analyses of eigenvalues, steady–state stability and sensitivity, and different types of oscillations. It is also possible to provide students with synthetic or actual data, from which they could learn how to estimate parameter values for the model.

Semester-long courses

While modules can be very effective in making students aware of the conceptual nature of biological systems, semester-long courses offer the option of truly discussing concepts, methods, and model implementations. Several influential biomedical engineering curricula have already embraced this option, including MIT, the University of Virginia, and Georgia Tech, but many programs have not yet followed their lead. While some undergraduates may at first not see the relevance of such a course, it is easy to explain that, as biomedical engineers, they will ultimately want to manipulate—and then optimize—biomedical systems, but that this task really requires knowledge of how these systems are connected and regulated, and how they change over time.

At Georgia Tech, we also implemented an introductory, hands-on course for graduate students, which every year focuses on a different disease and teaches students how to identify aspects of the disease that are suitable for model analyses, develop models, and draw novel conclusions from simulations and other model analyses. The main goal of the course is not to turn students into master modelers, but to develop a feel for how systems biology might be applicable in their own studies (Voit et al., 2012). Programmatically, this course leads to specialty courses for an enrichment area in biomedical systems, which also offers the opportunity to work on a dissertation focusing on biomedical systems.

Disciplines suitable for inclusion of biological systems thinking

Admittedly painted with a very broad brush, disciplines that would benefit from an infusion of biological systems thinking include the following:

• Bioinformatics, which typically focuses on the analysis of large datasets with the goal of understanding static networks in genomics and transcriptomics, proteomics and metabolomics, but by and large ignores the dynamic changes occurring in all biological systems. Expressed differently, by embracing dynamics, bioinformatics could naturally weave snapshots (data) into stories (e.g., progression of disease).

• Bioengineering, whose declared task it is to manipulate biomedical systems in a targeted manner. Despite the genuine importance of systems, the field has only slowly begun to embrace the enormous complexity of natural systems in its curricula. It appears that a solid grounding in systems biology would be particularly beneficial in sub-disciplines like pharmaceutical engineering, which targets the development and manufacture of medications, which are obviously interacting directly with physiological and metabolic systems.

• Epidemiology, which interprets large disease databases in terms of associations between environmental factors, genetic and other biomarkers, and lifetime choices of specific populations on the one hand, and their risk and prevalence with respect to specific diseases on the other. Due to the statistical nature of typical epidemiological approaches, it is often difficult to distinguish association from causality, that is, symptoms from causes. Systems approaches could fill this gap, at least partially, by developing explanatory, mechanistic models.

• Medicine, which is necessarily taught with a priority on addressing specific health problems, at the cost of not diving very deep into the complexity of the underlying disease physiology and the multiple interdependencies among organismal subsystems. This very practical approach is understandable but also unfortunate, as physiology and its aberrations into disease are clearly driven by uncounted control systems, which would suggest at least some inclusion of the concepts of control theory into the curriculum (Kemp et al., 2017). One should mention the recent emergence of the nascent field of systems medicine (Wolkenhauer, 2020), which truly embraces the concepts of systems biology, applied to human health and disease. The field at present focuses mainly on research, although some graduate programs have been created (e.g., (S.M. SBMI, 2022; S.M. Semm, 2022; S.M. Vilcek, 2022)). While laudable, systems medicine so far appears to operate largely in parallel to mainstream medicine, and it appears that formal systems analysis plays only a minor role in the education of medical students in traditional programs. One should also mention ideas of personalized medicine and its goal of customizing treatments toward the predisposition, health history and other personal features of an individual (Jain, 2002; Chan and Ginsburg, 2011). A good understanding of individualized medicine would also lead to improved predictions of personal health trajectories and prognoses of future health issues. To make personalized medicine cost-effective, advances in molecular systems biology need to be propagated to higher levels of biological organization that focus on organs, organ system, and whole organisms by means of computational approaches (Hood, 2003). This propagation has the potential of leading to new, individualized medical therapeutics based on medical informatics, modeling, and targeted computer simulations. To achieve such goals, medical education could pivot toward accepting new training objectives that involve a transition from reductionist problem solving toward systemic and predictive modeling approaches, which traditionally have been associated with education in engineering

• Sociology, which focuses on society, human interactions, and aspects of culture that affect daily life. Most methods targeting these complex interactions are currently empirical, although a small subfield of computational sociology has begun to emerge that uses statistical methods and artificial intelligence (Edelmann et al., 2020). It is quite evident that biological systems thinking could provide a beneficial complement.

• Mathematics falls into a slightly different category, as mathematical models are at the core of computational systems biology. Nonetheless, an inclusion of biological systems thinking into an applied mathematics curriculum could be beneficial, as it would offer an almost unlimited number of interesting and practically important applications, some of which would require sophisticated mathematical analysis.

• Computer science and the new subfield of data science, like mathematics, fall into a different category since computational systems biology uses computing on a daily basis and often relies on methods of machine learning for data management. Acute problems of systems biology could inspire the creation of novel tools, as it has happened with neural networks and genetic algorithms. For instance, it would be beneficial if computer science would address effective data interpretation and visualization not just for large static networks but also for dynamically changing systems. Furthermore, fundamental questions could be addressed, for instance, regarding the complementary and mutually beneficial nature of data science and computational modeling (Voit, 2019). It is sometimes alleged that the accumulation and statistical analysis of sufficiently many data could make modeling superfluous: “With enough data, the numbers speak for themselves, correlation replaces causation, and science can advance even without coherent models or unified theories” (Anderson, 2008). However, this supposition is faulty for different reasons. As Succi and Coveney (Succi and Coveney, 2019) point out, there are fundamental differences between the law of large numbers, on which machine learning is based, and the mathematical reality of complex biological systems that are often governed by nonlinearities, non-locality of effects, fractal aspects, and high dimensionality, which fundamentally violate the statistical assumptions implicitly underlying big data analysis. Succi and Coveney go as far as stating that too many data are just as bad as insufficient data.

Informing the public

Education in systems biology should not end with undergraduate or graduate students. To gain wide acceptance, it is ultimately imperative to inform the public in a manner that convincingly highlights the progress, potential, challenges, and future of the field. This publicity is needed to secure long-term funding within a very competitive arena.

The recent years have witnessed an enormous increase in books on systems biology, but most were written for specialists and maybe graduate students, but not general readers at the educational level of the general public or of high school students who might become fascinated enough to pursue a career using biological systems thinking; exceptions are (Voit, 2016; Voit, 2020). Even books labeled as “introductory” often require a good dose of background math, which precludes the casual reading rightfully expected by the lay population (e.g., (Choi, 2007; Ingalls, 2013; Sauro, 2014; Klipp et al., 2016; Voit, 2017; Alon, 2019; Raman, 2021)). Confounding the challenge, the effort of keeping the interested public up to date requires repeated, long-term commitment by the scientific community, where educational aspects are often undervalued, especially if they address audiences outside academia. Nonetheless, well-selling books like Chaos by James Gleick (Gleick, 1997) or Linked: The New Science of Networks by Albert-László Barabási (Barabási, 2002) demonstrate that it is possible to get the public excited about a new scientific field, even if it is complicated. It should thus be a goal for the community of systems biologists to gain public acceptance and maybe become included in lists like 24 Best Biology Books for Beginners (Best Books, 2022).

Conclusion

There is no doubt that systems biology has made admirable strides within the biological community. The time seems ripe now to expand beyond the boundaries of biology into tangential disciplines like bioinformatics, bioengineering, medicine, epidemiology, public health, and sociology. This expansion will require a persistent, gradual change in the mindset of practitioners designing curricula toward complexity and dynamics. While new programs are welcomed, it might be more effective to spread the word through small inroads in the form of individual classes, modules, and semester-long courses.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was supported in part by the following grant: NIH-2P30ES019776-05 (PI: Carmen Marsit). The funding agency is not responsible for the content of this article.

Acknowledgments

Many thanks for constructive feedback go to Jacob Davis, Carla Kumbale, Daniel Olivença, and Ann Voit.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aderem, A. (2005). Systems biology: Its practice and challenges. Cell 121, 511–513. doi:10.1016/j.cell.2005.04.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Alon, U. (2019). An introduction to systems biology. 2nd edition. Boca Raton: Chapman and Hall/CRC.

Google Scholar

Anderson, C. (2008). The end of theory: The data deluge makes the scientific method obsolete. Science. Wired. Available at: https://www.wired.com/2008/06/pb-theory/.

Google Scholar

Ayalew, M., Hylton, D., Sistrunk, J., Melton, J., Johnsson, K., and Voit, E. O. (2020). Integration of biology, mathematics and computing in the classroom through the creation and repeated use of transdisciplinary modules. Primus 32, 367–385. doi:10.1080/10511970.2020.1861140

PubMed Abstract | CrossRef Full Text | Google Scholar

Barabási, A.-L. (2002). Linked: The new science of networks. New York NY: Perseus Publishing.

Google Scholar

Bernard, C. (1865). Introduction à L'étude de la Médecine Expérimentale. Paris: J.B. Baillière et fils.

Google Scholar

Best Books (2022). 19 best biology books for Beginners. Available at: https://bookauthority.org/books/beginner-biology-books (Accessed 2022.

Google Scholar

Braillard, P. A. (2013). “Systems biology and education,” in The philosophy of biology. Editor K. Kampourakis (Dordrecht: Springer), 549–575.

CrossRef Full Text | Google Scholar

Brigandt, I., and Love, A. (2017). Reductionism in biology. Stanford Encyclopedia of Philosophy. Available at: https://plato.stanford.edu/entries/reduction-biology/.

Google Scholar

Chan, I. S., and Ginsburg, G. S. (2011). Personalized medicine: Progress and promise. Annu. Rev. Genomics Hum. Genet. 12, 217–244. doi:10.1146/annurev-genom-082410-101446

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, S. E. (2007). Introduction to systems biology. Totowas, NJ: Humana Press.

Google Scholar

Cvijovic, M., Höfer, T., Aćimović, J., Alberghina, L., Almaas, E., Besozzi, D., et al. (2016). Strategies for structuring interdisciplinary education in systems biology: An European perspective. npj Syst. Biol. Appl. 2, 16011. doi:10.1038/npjsba.2016.11

PubMed Abstract | CrossRef Full Text | Google Scholar

Edelmann, A., Wolff, T., Montagne, D., and Bail, C. A. (2020). Computational social science and sociology. Annu. Rev. Sociol. 46, 61–81. doi:10.1146/annurev-soc-121919-054621

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia, J. M. (2021). Agent-Based Modeling and Simulation I: Practical guide to the analysis of complex systems. Ventana Systems Inc.

Google Scholar

Gleick, J. (1997). Chaos: Making a new science. London, U.K.: Penguin Books.

Google Scholar

Hood, L., Heath, J., Phelps, M., and Lin, B. (2004). Systems biology and new technologies enable predictive and preventative medicine. Science 306, 640–643. doi:10.1126/science.1104635

PubMed Abstract | CrossRef Full Text | Google Scholar

Hood, L. (2003). Systems biology: Integrating technology, biology, and computation. Mech. Ageing Dev. 124, 9–16. doi:10.1016/s0047-6374(02)00164-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ideker, T., Galitski, T., and Hood, L. (2001). A new approach to decoding life: Systems biology. Annu. Rev. Genomics Hum. Genet. 2, 343–372. doi:10.1146/annurev.genom.2.1.343

PubMed Abstract | CrossRef Full Text | Google Scholar

Ideker, T. (2004). Systems biology 101—What you need to know. Nat. Biotechnol. 22, 473–475. doi:10.1038/nbt0404-473

PubMed Abstract | CrossRef Full Text | Google Scholar

Ingalls, B. P. (2013). Mathematical modeling in systems biology: An introduction. Cambridge, MA: MIT Press.

Google Scholar

Jain, K. K. (2002). Personalized medicine. Curr. Opin. Mol. Ther. 4, 548–558.

PubMed Abstract | Google Scholar

Kemp, M. L., Lee, R. C., and Voit, E. O. (2017). Perspective: The fundamental value of engineering pedagogy for realizing personalized medicine. Regen. Eng. Transl. Med. 3, 233–238. doi:10.1007/s40883-017-0039-6

CrossRef Full Text | Google Scholar

Kitano, H. (2002). Computational systems biology. Nature 420, 206–210. doi:10.1038/nature01254

PubMed Abstract | CrossRef Full Text | Google Scholar

Klipp, E., Liebermeister, W., Wierling, C., and Kowald, A. (2016). Systems biology: A textbook. 2nd edition. Weinheim, Germany: Wiley-Blackwell.

Google Scholar

Kumar, A. (2005). Teaching systems biology: An active-learning approach. Cell Biol. Educ. 4, 323–329. doi:10.1187/cbe.04-12-0057

PubMed Abstract | CrossRef Full Text | Google Scholar

MacLeod, M. (2021). The applicability of mathematics in computational systems biology and its experimental relations. Euro. Jnl. Phil. Sci. 11, 84. doi:10.1007/s13194-021-00403-3

CrossRef Full Text | Google Scholar

Melham, T. (2013). Modelling, abstraction, and computation in systems biology: A view from computer science. Prog. Biophys. Mol. Biol. 111, 129–136. doi:10.1016/j.pbiomolbio.2012.08.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Mesarović, M. D. (1968). Systems theory and biology. Proceedings of the III systems symposium at case Institute of Technology. NewYork, NY: Springer-Verlag.

Google Scholar

Momsen, J., Speth, E. B., Wyse, S., and Long, T. (2022). Using systems and systems thinking to unify biology education. CBE Life Sci. Educ. 21, es3. doi:10.1187/cbe.21-05-0118

PubMed Abstract | CrossRef Full Text | Google Scholar

Motta, S., and Pappalardo, F. (2013). Mathematical modeling of biological systems. Brief. Bioinform. 14, 411–422. doi:10.1093/bib/bbs061

PubMed Abstract | CrossRef Full Text | Google Scholar

Noble, D. (2008). Claude Bernard, the first systems biologist, and the future of physiology. Exp. Physiol. 93, 16–26. doi:10.1113/expphysiol.2007.038695

PubMed Abstract | CrossRef Full Text | Google Scholar

Railsback, S. F., and Grimm, V. (2019). Agent-based and individual-based modeling: A practical introduction. 2nd. Ed. Princeton, NJ: Princeton Univ. Press.

Google Scholar

Raman, K. E. (2021). An introduction to computational systems biology: Systems-level modelling of cellular networks. Boca Raton: Chapman & Hall/CRC Press.

Google Scholar

Robeva, R. E. (2015). Algebraic and discrete mathematical methods for modern biology. Londonm, UK: Academic Press.

Google Scholar

Sauro, H. (2014). Systems biology: Introduction to pathway modeling. Ambrosius Publishing.

Google Scholar

Savageau, M. A. (1976). Biochemical systems analysis: A study of function and design in molecular biology. Reading, Mass: Addison-Wesley Pub. Co. Advanced Book Program.

Google Scholar

Savageau, M. A. (1991). Reconstructionist molecular biology. New Biol. 3, 190–197.

PubMed Abstract | Google Scholar

Savageau, M. A. (1991). The challenge of reconstruction. New Biol. 3, 101–102.

PubMed Abstract | Google Scholar

S.M. SBMI (2022). Bioinformatics and systems medicine. Available at: https://sbmi.uth.edu/prospective-students/bism.htm (Accessed 2022.

Google Scholar

S.M. Semm (2022). PhD PROGRAM IN SYSTEMS MEDICINE. Available at: https://www.semm.it/education/phd-program-systems-medicine (Accessed 2022.

Google Scholar

S.M. Vilcek (2022). Systems & computational biomedicine PhD training program. Available at: https://med.nyu.edu/research/vilcek-institute-graduate-biomedical-sciences/phd-program/phd-training-programs/systems-computational-biomedicine (Accessed 2022.

Google Scholar

Succi, S., and Coveney, P. V. (2019). Big data: The end of the scientific method? Philos. Trans. A Math. Phys. Eng. Sci. 377, 20180145. doi:10.1098/rsta.2018.0145

PubMed Abstract | CrossRef Full Text | Google Scholar

Voit, E. O. (2017). A first course in systems biology. 2nd Ed. New York, NY: Garland Science.

Google Scholar

Voit, E. O., and Kemp, M. L. (2011). So, you want to be a systems biologist? Determinants for creating graduate curricula in systems biology. IET Syst. Biol. 5, 70–79. doi:10.1049/iet-syb.2009.0071

PubMed Abstract | CrossRef Full Text | Google Scholar

Voit, E. O., Newstetter, W. C., and Kemp, M. L. (2012). A feel for systems. Mol. Syst. Biol. 8, 609. doi:10.1038/msb.2012.41

PubMed Abstract | CrossRef Full Text | Google Scholar

Voit, E. O. (2019). Perspective: Dimensions of the scientific method. PLoS Comp. Biol. 19. doi:10.1371/journal.pcbi.1007279

PubMed Abstract | CrossRef Full Text | Google Scholar

Voit, E. O. (2020). Systems biology. Oxford, U.K.: Oxford University Press.

Google Scholar

Voit, E. O. (2016). The inner workings of life. Vignettes in systems biology. Cambridge, U.K.: Cambridge University Press.

Google Scholar

von Bertalanffy, L. (1940). Der Organismus als physikalisches System betrachtet. Naturwissenschaften 28, 521–531. doi:10.1007/bf01497764

CrossRef Full Text | Google Scholar

von Bertalanffy, L. (1968). General systems theory: Foundations, development, applications. New York, NY: George Braziller.

Google Scholar

von Bertalanffy, L. (1927). Studien über theoretische Biologie. Biol. Zentralblatt 47, 653–662.

Google Scholar

Wolkenhauer, O. (2020). Systems medicine: Integrative, qualitative and computational approaches. Cambridge, MA: Academic Press.

Google Scholar

Appendix: Details of the model used for Figures 1, 2

The model was constructed within the framework of Biochemical Systems Theory (BST) (Savageau, 1976), but it would also be possible to choose other nonlinear functions, such as Michaelis-Menten rate laws. In order to demonstrate limit cycle behavior, the model needs to contain enough nonlinearity though. The powers of 0.5 are often used in BST as defaults for biochemical and physiological processes. One should note two different types of arrows in Figure 1: solid for precursor-product steps and dotted for modulating effects. Consider, as an example, the equation for the enzyme, E, which does not include the substrate, X, of the reaction. It reads $\dot{E}=G^{0.5}-E^{0.5}$. The reason is that the enzyme concentration in a biochemical reaction is traditionally considered constant, because the enzyme is “recycled” in the product-forming step and the substrate does not continue to a loss of E. Instead, the dynamics addressed in the equation for E pertains exclusively to the production of new enzyme, ultimately coming from increased gene expression on the one hand and destruction of the enzyme, e.g., by proteases on the other. A more detailed diagram for this part of the pathway is given in Figure A1. The text uses a simpler diagram as not to appear overly complicated.

FIGURE A1

FIGURE A1. More detailed representation of the dynamics of enzyme E.

In the Matlab code below, the variables in the figures are coded as (X0, …, X6) = (Input, X, Y, Z, TF, G, E). The code addresses specifically the situation in Figure 2C.

function [] = feedback()

t0 = 0;

tf = 1000;

X0 = 0.8;

p = 0.56;

x0 = [1, 1, 1, 1, 1, 1];

[t,X] = ode45(@(t,x)Feedback(t,x,X0,p),(t0: 0.1 : tf),x0);

figure

plot(t,X);

legend('X1','X2','X3','X4','X5','X6'); title(sprintf('X0 = 0.8 , p = 0.56',X0,p));

end

function dx = Feedback(t,x,X0,p)

dx = [X0 - x(6) * x(1) ^ 0.5

x(6) * x(1) ^ 0.5 - x(2) ^ 0.5

x(2) ^ 0.5 - x(3) ^ 0.5

x(3) ^ p - x(4) ^ 0.5

x(4) ^ 0.5 - x(5) ^ 0.5

x(5) ^ 0.5 - x(6) ^ 0.5];

end