1
Department of Neurobiology, The Hebrew University, Jerusalem, Israel
2
The Interdisciplinary Center for Neural Computation, The Hebrew University, Jerusalem, Israel
3
Division of Biology, California Institute of Technology, Pasadena, CA, USA
4
Division of Engineering and Applied Science, California Institute of Technology, Pasadena, CA, USA
Membrane ion channels and synapses are among the most important computational elements of nerve cells. Both have stochastic components that are reflected in random fluctuations of the membrane potential. We measured the spectral characteristics of membrane voltage noise in vitro at the soma and the apical dendrite of layer 4/5 (L4/5) neocortical neurons of rats near the resting potential. We found a remarkable similarity between the voltage noise power spectra at the soma and the dendrites, despite a marked difference in their respective input impedances. At both sites, the noise levels and the input impedance are voltage dependent; in the soma, the noise level increased from σ = 0.33 ± 0.28 mV at 10 mV hyperpolarization from the resting potential to σ = 0.59 ± 0.3 at a depolarization of 10 mV. At the dendrite, the noise increased from σ = 0.34 ± 0.28 to σ = 0.56 ± 0.30 mV, respectively. TTX reduced both the input impedance and the voltage noise, and eliminated their voltage dependence at both locations. We describe a detailed compartmental model of a L4/5 neuron with simplified electrical properties that successfully reproduces the difference in input impedance between dendrites and soma and demonstrates that spatially uniform conductance-base noise sources leads to an apparent isopotential structure which exhibits a uniform power spectra of voltage noise at all locations. We speculate that a homogeneous distribution of noise sources insures that variability in synaptic amplitude as well as timing of action potentials is location invariant.
There is a general consensus that behavioral events are an expression of a change in either the rate or the pattern of firing of neuronal populations. However, there is a longstanding debate as to which aspects of this change in activity are used by the system to encode information (Kruger and Becker, 1991
). The firing rate and firing pattern of neurons are affected by stochastic processes and therefore, firing is distorted by random-like activity considered to be “noise”. Hence, irrespective of the way the neuronal system encodes information, noise plays a major role, by either disrupting or enhancing information processing in the nervous system (Anderson et al., 2000
; Averbeck and Lee, 2006
; Schneidman et al., 1998
). Therefore, a quantitative understanding of neuronal noise as well as a qualitative understanding of its origins are both crucial to assessing the constraints under which the neural code operates (White et al., 2000
).
For example, noise can enhance the computational capability of neurons by increasing their ability to detect weak signals that otherwise would not reach threshold, a process known as “stochastic resonance” (Rudolph and Destexhe, 2001
; Stacey and Durand, 2000
, 2001
; Wiesenfeld and Moss, 1995
). It has been suggested (Anderson et al., 2000
; Suarez and Koch, 1989
), that noise in primary visual cortex neurons enables them to maintain orientation tuning independent of image contrast. However, noise can also hinder the ability of a neuron to generate a reproducible response to incoming stimuli, thus potentially limiting its computational power. The irreproducibility of spike trains over repetitions of the exact same stimulus has been quantified in several works (de Ruyter van Steveninck et al., 1997
; London et al., 2002
; Mainen and Sejnowski, 1995
; Nowak et al., 1997
; Schneidman et al., 1998
; Victor and Purpura, 1996
) showing how sub-threshold noise limits the information capacity of a neuron’s output spike train.
In a previous paper (Jacobson et al., 2005
), we described the voltage noise in the soma of layer 4/5 (L4/5) pyramidal neurons of the rat somatosensory cortex recorded in vitro. We showed that noise due to stochastic opening/closing of membrane ion channels is significant in the sub-threshold voltage regime and that it increases in a non-linear fashion with depolarization. This increase is due to a paradoxical increase in the cell’s impedance, due to the voltage-dependent Na+ conductance.
In the present study, we compared the spectral characteristics of noise in the soma and the dendrite. To our surprise, we found that despite significantly higher input impedance in the dendrites throughout the whole tested frequency range, their noise level was similar to that measured at the soma. Using a compartmental neuron model, we show that the homogeneous distribution of noise sources can account for this “paradoxical” behavior. The functional significance of this finding is discussed.
Slice preparation, recording and analysis methods were similar to those used in our previous study (Jacobson et al., 2005
) and will be described briefly.
Ethical Approval
All procedures used in the study adhere to guidelines approved by the Hebrew University of Jerusalem Animal Care Committee and comply with NIH guidelines.
Experimental Procedures
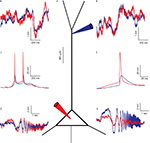
Sprague-Dawley rats (PN 12-22) were anesthetized with an IP injection of pentobarbital and decapitated, and their brains were quickly removed. Para-sagittal brain slices of the neo-cortex (300 μm) were cut. Recordings were made in Ringer solution containing (in mM) 124 NaCl, 3 KCl, 2.4 CaCl2, 1.15 NaH2PO4, 1.3 MgSO4, 26 NaHCO3 and 10 D-glucose, while saturated with 95% O2–5% CO2 at room temperature. In some experiments Na+ channels were blocked using 1 μM TTX (Alomone Labs). Patch pipettes were filled with a solution containing (in mM): 140 potassium gluconate, 4 NaCl, 0.5 CaCl2, 5 Mg-ATP, 5 EGTA, 10 HEPES. Pipette solution was at pH 7.2, and the pipette resistance was 4–6 MΩ for somatic recordings and 10–14 MΩ for dendritic recordings. Pyramidal L4/5 cells were visually identified in all recordings, dendritic and soma-dendritic dual recordings were performed at distances of 70–325 μm from the soma (average distance 150 ± 51 μm). A typical arrangement of two recording electrodes is shown in Figure 1
A. Figure 1
B–G shows recordings from a neuron in which the dendritic electrode is located at a distance of 250 μm from the soma. At this location, a spontaneous action potential reaches only 33% (blue traces in Figure 1
C,F) of the amplitude of the AP measured at the soma (red traces in Figure 1
C,F). Voltage traces were recorded at three holding potentials: resting potential, 10 mV hyperpolarization and 10 mV depolarization, for a duration of 2 min. The holding potential was altered by injecting a DC current simultaneously into the soma and dendrite.
Figure 1. Simultaneous recording from the soma and dendrite of a L4/5 pyramidal neuron in vitro. (A) Schematic drawing of a pyramidal cell with the two patch pipettes located at the soma (red) and at a distance of 250 μm in the apical dendrite (blue). (B,E) Voltage noise recorded simultaneously from the soma (red) and dendrite (blue). Note that the noise is not identical at both locations, higher at times at the soma and at other times in the dendrite. (C) Superposition of two simultaneously recorded spontaneous action potentials recorded in the soma (red) and dendrite (blue). Note the attenuation of spike amplitude between the two recording sites. The difference in spike amplitude and shape confirms that the recording electrodes were electrotonically separate. (F) Magnification of the first spike in (C). (D,G) Voltage response at the soma (red) and dendrite (blue) to a ZAP current (see Materials and Methods) injected in the soma (D) and in the dendrite (G). All measurements were made from the same cell.
Data Acquisition
Recordings were made using an AxoClamp 2A (Axon Instruments, Union City, CA, USA) amplifier and were sampled by a National Instruments board (PCI-MIO-16XE) at rates of either 5 or 10 kHz. The same board was used for converting 500 Hz digital signals (chirps, see below) into analog current signals injected into the cell. The experimental system was controlled by a custom-built interface written in the LabVIEW environment (V5.1 and 6, National Instruments, Austin, TX, USA). For each experimental condition, data were collected for a duration of 2 min.
Data Analysis
All data were analyzed offline using MATLAB (The MathWorks, Natick, MA, USA). Voltage traces were analyzed individually for each holding potential after band-pass filtering (0.2–100 Hz). Power spectral density was estimated using the Welch averaged modified periodogram method, using a discrete prolate spheroidal sequence window (NW = 3) of length 5 s, yielding a resolution of 0.2 Hz. Prior to all analyses, spikes were removed from the data (from 150 ms prior to the spike to 250 ms after the spike) and replaced by a line connecting the end points of the removed segment. In this manner, we removed at the most 3% of the voltage trajectory. The power spectrum integral was used to estimate the voltage noise amplitude, σ(v). To avoid spectral peaks at 50 Hz we summed the integral between 0.2–49 Hz and 55–100 Hz. The cut-off frequency was estimated by visual inspection for each of the 38 somas and 38 dendrites separately and then averaged. The fall-off slope of the power spectrum was estimated by averaging the slopes of linear curves fitted to each power spectrum of the 38 somas and dendrites between the cut-off frequency and 100 Hz.
The input impedance |Zin(f )| was obtained by injecting a logarithmic current chirp, ZAP (0.1–100 Hz, duration 5 s) of minimal amplitude (typically 10–20 pA) into the cell and measuring the average voltage response to 10–50 injections, depending on the variability of the traces (Figure 1
D,G). At each of the three holding potentials, a ZAP was injected separately at the soma (Figure 1
D) and at the dendrite (Figure 1
G) and the voltage response was recorded at both locations. The input impedance was obtained by calculating the ratio of voltage and current Fourier transforms at the injection site. Input resistance was estimated from the average input impedance at low (0.2–2 Hz) frequencies.
In prolonged whole cell recordings, electrode impedance increased due to blockage of its tip by the cell membrane debris. Therefore the bridge of the amplifier was constantly balanced in order to faithfully estimate the cell’s input impedance. Since the input impedance is estimated from the cell’s response to ZAP current injection, the traditional methods of rebalancing the bridge did not work in this case. To find a method that would adequately balance the amplifier we devised the following model: the cell is a parallel RC circuit (R in Ω, C in Farad), and the electrode is a resistor (Re, in Ω) connected serially to the cell’s interior. A parallel capacitor (Ce, in Farad) represents the electrode’s capacitance and ω (in radians).
The input impedance of this circuit is:
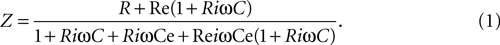
At low frequencies, the impedance of the circuit, Z (in Ω) is the sum of the resistances of the cell and the electrode:

At high frequencies, the impedance of the circuit is affected primarily by the capacitance of the electrode:

The electrode’s impedance is frequency dependent. However, with a 10-MΩ electrode the impedance over a range of 100 Hz changes by 80 Ω. Moreover even with 100 MΩ electrode we still have a frequency dependent change of only 80 Ω. Therefore, we assumed that the error induced by changes in the electrode resistance were frequency-independent. Since the cell’s resistance does not affect the high frequency (100 Hz) response (Eq. 3), we used it to compensate for the change in the electrode resistance.
Current power spectrum was calculated as follows:

Significance analyses were carried out using two different tests. For data recorded from the same cell, we used a paired non-parametric test, the Wilcoxon signed rank test. When data from different cells were compared, we used a t-test. In order to determine whether the impedance of the dendrite was higher than that of the soma at the population level, we divided the frequency axis into 470 equal-sized bins of 0.2 Hz. At each frequency, we compared the impedances of soma and the dendrite using a tailed t-test. We then calculated the percentage of frequencies for which the impedance of the dendrite was significantly higher than that of the soma. In order to determine whether the noise was similar in the soma and dendrite at the population level, we carried out the same calculation as for the impedance. However, the comparison was made using a two-tailed t-test. Frequencies that did not show a significant difference (p > 0.05) were summed and divided by 470.
All calculations and analysis were carried out in the same manner for both experimental and simulated data.
Model and Simulations
All simulations were implemented using NEURON 6.03 (www.neuron.yale.edu). We used a detailed compartmental model of a reconstructed layer 5 pyramidal cell from the somatosensory cortex of rats (kindly provided by Arnd Roth, see Figure 4
A). Passive properties were as follows: Intracellular resistivity, Ri = 350 Ωcm (Major et al., 1994
), specific membrane resistivity Rm = 50 KΩcm2, membrane capacitance, Cm = 1 μF/cm2, resting potential, Vrest = −65 mV. Dendritic spines were accounted for by a twofold increase in Cm and corresponding decreases in Rm. Dendrites were divided into a total of 267 compartments each of maximal length of 24 μm.
Noise sources were modeled as local conductance change simulated as the sum of two exponents with τrise = 0.4 ms, τdecay = 2 ms, g_noise = 100 pS and a reversal potential, Erev = 0. We equipped each compartment with a single noise source working at an average of 2 Hz at random times chosen from an exponential distribution, totaling 267 homogeneously distributed noise sources on the dendritic tree of the modeled neuron (Figure 4
).
The integration time step was t = 25 μs. A voltage-dependent persistent Na+ current (INap) was incorporated in the soma in some of the simulations (indicated in the text). The current was modeled as follows (Poirazi et al., 2003
), INap = gNap · m3 · (V − ENa) where m = 1/(1 + e−(V + 50.4)/4.5), ENa = 50 mV, gNap = 1.5 pS/μm2.
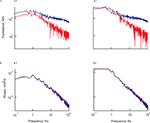
In order to characterize the differences in noise level between the soma and the apical dendrite, we simultaneously measured the impedance (n = 18) and the noise level (n = 38) at these locations (Figure 1
). Representative results are shown in Figure 2
. The impedance (Figure 2
A1), which showed the most reproducible and significant difference, was higher at the dendrites (blue) than at the soma (red). This difference increased at high frequencies, suggesting that at higher frequencies the dendrites respond better to current injection than does the soma. In fact, this difference in response to high frequencies is expected from passive cable theory (Jack et al., 1975
; Tuckwell, 1988
). The soma is a more isopotential structure, whereas the dendrites resemble an electrically distributed cable structure. In an isopotential structure, the temporal response is determined by the membrane time constant, whereas in a cable the longitudinal spread of current accelerates the voltage decay (“the equalizing time constants” – Rall, 1969
; Koch, 1998
). As previously shown (Jacobson et al., 2005
), at the soma the impedance is voltage dependent, and increases with depolarization. Similar behavior was observed at the dendritic level. The voltage dependence of the impedance can be appreciated by comparing the impedance measured at the resting potential (Figure 2
A1) and at 9 mV depolarization (Figure 2
A2). The impedance at both soma and dendrite increased with depolarization but the increase at the soma was larger and, as a result, the impedance at low frequencies in the soma was similar to that of the dendrites (Figure 2
A2).
Figure 2. The similarity in voltage noise spectra in soma and dendrites is inconsistent with the difference in corresponding input impedance. Impedance (A1,A2) and noise spectra (B1,B2) calculated at the soma (red) and the dendrite (blue) on a log-log scale. Left hand side panels (A1,B1) are measured at the resting potential and right hand side panels (A2,B2) are measured for a depolarization of 9 mV. The impedance was estimated from the average response to 20 consecutive ZAP current injections. Note the difference in slope between soma and dendrite. The power spectra were calculated from 2 min long continuous recording after clipping the spikes. Note the similarity in the power spectra of the voltage noise at the two recording sites. All data were obtained from the same cell.
Surprisingly, despite the different impedances at these two sites, the power-spectrum of the voltage noise at the soma and the dendrites was remarkably similar (Figure 2
B1; note the two overlapping curves). As with the impedance, the noise level at both locations was also voltage dependent. Surprisingly, the noise level at both locations increased by the same amount with depolarization and therefore, as in the resting conditions, the two curves completely overlap (Figure 2
B2). Thus, a moderate but significant membrane depolarization, which increased both the somatic impedance and the noise level (Jacobson et al., 2005
), failed to unravel a difference in noise level between the soma and the dendrite (Figure 2
B2).
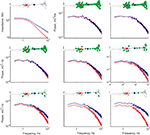
The robustness of these observations was confirmed by analyzing the average results obtained from 38 paired recordings. In Figure 3
A the impedance (z-axis) at three different membrane potentials was averaged and plotted as a function of frequency (x-axis) and voltage (y-axis). The impedance in the dendrites (blue surface) was higher than that of the soma (red surface) throughout most of the parameter space. Population statistics show that the higher dendritic impedances occurred in more than 94% of the frequencies at all three holding potentials (see Materials and Methods).
Figure 3. The similarity of voltage noise spectra in soma and dendrites is corroborated by averaging the results across cells. (A) Average impedance (MΩ) calculated from simultaneous recordings at the soma and the dendrite (n = 18). (B) Average voltage noise power spectrum mV2/Hz of 38 soma and dendrite pair recordings.(C) Average current power spectrum (pA2/Hz) calculated by dividing the average voltage power spectrum in (B) by the square of the average impedance in (A). In all panels red and blue surfaces are for soma and dendrite respectively, x-axis – holding potential (mV); y-axis – log frequency (Hz).
The 3D curves depicted in Figure 3
B show the noise power spectra at three different voltages. The remarkable overlap of the two surface curves strongly suggests that the voltage noise at both locations displays similar properties. Population statistics show that in 94% of the frequency spectrum, the noise level in the dendrites was statistically indistinguishable from that of the soma. As with the impedance, significant voltage dependence was evident at both locations. At the soma, the amplitude of the noise increased from 0.33 ± 0.28 mV to 0.59 ± 0.3 mV upon depolarization of the cells from −69.7 ± 4.1 mV to −52.4 ± 4.8 mV. The amplitude of noise in the dendrite increased from 0.34 ± 0.28 mV to 0.56 ± 0.3 mV following depolarization from −69.4 ± 3.7 mV to −52.2 ± 4.4 mV. At both recording sites, on average, the cut-off frequency of the noise spectra was 1.4 Hz at the resting potential (average = −60.7 ± 4.1 mV and −60.6 ± 3.8 mV for soma and dendrite, respectively, n = 38 pairs) whereas the fall-off slope was −2.4 ± 0.3 and −2.3 ± 0.3 log(mV2)/log(Hz) for soma and dendrite respectively (Figure 3
B; note the two overlapping curves).
The remarkable similarity of the voltage noise spectra in the dendrites and the soma, which extended throughout the measured frequencies and voltages, seems rather paradoxical. One would expect that a site with larger impedance would exhibit larger voltage noise. Thus, a similar voltage noise generated in locations that differ in their impedance implies that either the current that generates the noise is precisely tuned to compensate for the difference in impedance at these locations or that something in the structure or the distribution of noise sources insures a uniform voltage noise.
This hypothetical fine-tuned current noise was estimated by dividing the voltage noise at a given site by the impedance at this site (see Materials and Methods). The results are shown in Figure 3
C. The calculated current noise at the soma (Figure 3
C, red surface) was higher than that calculated at the dendrites (blue surface) and this difference persisted throughout the entire frequency range. The difference in the calculated current noise (Figure 3
C) reflects the difference in impedance; namely, at low frequencies the current noise at the soma was similar to that of the dendrites whereas at high frequencies the current noise in the soma was larger than that of the dendrites.
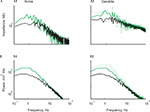
Such fine-tuning of the current sources to exactly compensate for the difference in input impedance due to the dendritic structure is rather unlikely. In order to better understand this situation, we constructed a compartmental model of a L5 reconstructed cortical neuron (see Materials and Methods) in order to examine alternative possibilities. As shown in Figure 4
A, the structure of the neuron by itself accounts for the difference in the impedance between soma and dendrite (the location of the two recording sites is marked in the insets by the filled circles; distance between points are 475 μm. We then homogeneously distributed a large number (267) of localized identical conductance changes in noise sources over the dendritic tree (green circles in Figure 4
B, inset) and activated them at random times (chosen from an exponential distribution with a mean of 2 Hz). Figure 4
B shows that the voltage noise measured at the soma (red curve) is identical to that measured 475 μm into the apical dendrite (blue curve).
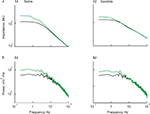
Figure 4. A passive model of a L5 neuron exhibits a difference in input impedance at soma and dendrite yet shows similar voltage noise spectra at these sites when identical noise sources are uniformly distributed over the tree. Insets depict the neuron model with the recording sites depicted as a red circle (soma) and a blue circle (dendrite). The location(s) of the noise sources are depicted by the green dots. (A) Impedance measured at the soma (red) and 475 μm in the apical dendrite (blue). (B–I) The noise spectra calculated at the two recording sites having different values of uniformly distributed, densities of identical noise sources. Total number of noise sources: (A) 0; (B) 267 (C) 137; (D) 67; (E) 32; (F) 16; (G) 8; (H) 4; (I) 1. The decrease in noise source density (B–I) is compensated for by a corresponding increase in input frequency for each noise source.
This surprising result strongly suggests that it is not the current that is fine-tuned to compensate for difference in input impedance. Rather, the spatial uniformity of membrane properties including the noise source density are responsible for the similarity of the noise spectra at the soma and in the dendrites. Thus, concentrating the 267 noise sources at a single location – while keeping the overall charge injected via these noise sources the same – should lead to a progressively more distinct voltage noise profile. This is indeed the case. Figure 4
B shows the starting point, when all 267 synaptic noise sources were spread around both basal and apical dendrites. Then, we gradually (from C to I) reduced the density of the noise sources, maintaining the total charge and the uniform distribution. As clearly shown in Figure 4
C–I, the difference in the noise power spectra increased monotonically with the decrease in noise source density. These differences in voltage noise for the low noise source densities are, as expected, correlated with the difference in local input impedance. Specifically, the power spectrum of the voltage in the dendrite is larger than that of the soma, and the fall-off of the power spectra with frequency is more moderate in the dendrite (Figure 4
G).
In summary, we show that with a spatially uniform distribution of identical noise sources, the voltage noise at the soma has similar characteristics to that of the dendrites at all frequencies, whereas the input impedance displays a significant structural-dependent difference. These observations suggest that the voltage noise measured in this study reflects a homogeneous current noise source, which is most likely distributed throughout the dendritic tree (see Discussion).
In somatic recordings, the voltage dependence of impedance and voltage noise was due to the “apparent resistance” caused by the sodium conductance and was abolished by TTX (Jacobson et al., 2005
). In order to study the effect of TTX on the noise in dendrites, we recorded from the apical trunk of 13 dendrites of pyramidal cells of L4/5 at an average distance of 105 ± 43 μm from the soma. Figure 5
shows a simultaneous recording at the soma (left) and dendrite (right) before (green) and after (black) addition of TTX. The voltage noise in the cell depicted in the figure decreases from 1.22 to 0.55 mV in the soma (Figure 5
B1) and from 1.21 to 0.55 mV in the dendrite (Figure 5
B2). The input resistance decreased from 199 to 114 MΩ in the soma (Figure 5
A1) and from 202 to 96 MΩ in the dendrite (Figure 5
A2). In general, as in the soma (Figure 5
A1), (Jacobson et al., 2005
), TTX in the dendrites reduced the impedance (Figure 5
A2) and the voltage noise (Figure 5
B2), and eliminated their voltage dependence (compare dashed and solid lines in Figure 5
A2,B2) as has been previously shown for the soma (Jacobson et al., 2005
).
Figure 5. TTX decreased noise and impedance in both soma and dendrite. The impedance (A) and noise spectra (B) at the soma (left panels) and the dendrite (right panels). In all panels the results obtained are shown before (green) and following (black) addition of TTX to the bath solution. (A1) impedance at the soma at resting potential. (A2) Impedance at the dendrite at resting potential (solid lines) and at a depolarization of 9 mV (dashed lines). (B1) Noise power spectrum at the soma at resting potential. (B2) Noise power spectrum at the dendrite at resting potential (solid lines) and at a depolarization of 9 mV (dashed lines). Note the decrease in noise level and impedance at low frequencies following TTX. Also note that the voltage dependence of both impedance and noise in the dendrite is abolished by addition of TTX.
In order to reproduce the observed voltage dependence of voltage noise and impedance in the model, we added persistent voltage dependent Na+ current to the soma compartment (Astman et al., 2006
) (see Materials and Methods). As shown in Figure 6
, the model reproduced, qualitatively and quantitatively, the experimental observations. This included the difference in impedance (Figure 6
A1,A2), its dependence on the persistent Na+ current (Figure 6
A1,A2) and the similarity of the voltage noise spectra in dendrites and soma (Figure 6
B1,B2, compare green curves with green curves). This implies that a homogeneous distribution of noise sources and the addition of a persistent current in the soma are sufficient to account for the experimental observations (see Discussion).
Figure 6. The experimental dependence of impedance and voltage noise on the membrane potential can be accounted for by the presence of persistent sodium current near the soma. The impedance (A) and noise spectra (B) at the soma (left panels) and the dendrite (right panels). The results obtained with (green) and without (black) persistent Na+ channels at the soma. Note the decrease in noise level and impedance at low frequencies without persistent Na+ channels. (Compare with Figure 5
).
We compared the input impedance and the voltage noise of L4/5 pyramidal neurons at the soma and in the apical dendrites at a distance of up to 325 μm. We found that the power spectrum of the voltage noise is essentially identical at the two sites whereas the input impedance is significantly larger in the dendrite at all measured frequencies. Both the voltage noise and the input impedance were TTX sensitive and increased with depolarization.
Input Impedance
The input impedance at the dendrites was higher than that measured at the soma and this difference increased with frequency. At low frequencies (i.e., below 10 Hz), the larger impedance of the dendrites reflected their morphological differences from the soma (i.e., smaller diameter). At high frequencies (i.e., above 10 Hz), the isopotential nature of the soma dominated the shape of the impedance curve, whereas in the dendrite, the cable structure dominated the shape of the impedance curve (Jack et al., 1975
; Tuckwell, 1988
). The voltage dependence of the impedance is the consequence of an “apparent resistance” (Jacobson et al., 2005
), caused by the presence of persistent Na+ current that resides near the soma (Astman et al., 2006
; Jacobson et al., 2005
). Depolarization activates this current, leading to a further depolarization. Consequently, as this current is not present in the dendrite, the difference in impedance between soma and apical dendrite decreases upon depolarization. TTX affects the impedance by blocking the persistent Na+ current and abolishing its resultant voltage dependence. The effect of TTX is more significant at the soma than at the dendrite due to the peri-somatic location of the persistent Na+ current.
Voltage Noise
Despite the prominent difference in impedance reflecting the electrotonic distinction between the soma and the dendritic compartments (see also Berger et al., 2003
), the power spectrum of voltage noise at the somatic and dendritic sites was similar. Noise increased with depolarization, as expected from Ohm’s law following the increase in impedance, implying that the Na+ current acts as a voltage-dependent amplifier. TTX abolished the voltage dependence of the voltage noise at both the cell body and the apical dendrite. The surprising result was the striking similarity of the voltage noise spectra at the dendrite and the soma. This similarity is particularly puzzling because the impedance at the dendrites differs significantly from that at the soma. A simple calculation leads to the erroneous conclusion that the current that generates the noise at the dendrites is significantly smaller than the somatic current. Such a conclusion entails an unrealistic hypothetical compensatory mechanism that adjusts the local current noise to the impedance at each and every location and throughout the entire range of frequencies. Another possibility is that the structure of the neuron and the distribution of the noise sources lead to a very similar noise level. In fact, our model L5 pyramidal neuron with spatially uniform identical noise sources predicts that under these conditions the voltage noise at the dendritic location is similar to that in the soma, despite the fundamental differences in their respective impedance values.
In order to understand this observation one must realize that in an electrically distributed structure, the homogeneous and dense distribution of the current sources generates a condition whereby the longitudinal (axial) current is eliminated. Under such uniform input conditions, the structure becomes essentially isopotential. This occurs if the electrotonic distance between the noise sources is rather small (a rough calculation, data not shown, shown that it should not exceed 0.25 λ). With increased distance between the noise sources, axial current flows between the different locations and the apparent isopotentiality diminishes. This will lead to a difference in the power spectra of the voltage noise at different locations. In fact, when measuring the input impedance via a localized (rather than distributed) current injection, voltage gradient (and longitudinal current) do exist, and differences in the intensity of this current are the source of differences in impedance at different dendritic/somatic locations. It is likely, therefore, that a homogeneous distribution of noise sources can account for the similarity in noise power spectra between soma and dendrite that we found experimentally. This, however, conflicts with what we know about the distribution of noise sources. For example, it is commonly accepted that inhibitory synapses reside near the soma while excitatory synapses are more abundant at distal regions of the dendritic tree. This, by itself, will generate a non-homogeneous distribution of one type of noise source - the synaptic input. However, in our slice preparation the contribution of synaptic inputs to the noise spectrum is rather limited due to the low rate of activity, particularly of the inhibitory synapses. Another possible source of noise is the ionic channels, of which only two types of potassium channels are non-uniformly distributed along the dendrites (Berger et al., 2001
; Frick et al., 2004
; Kole et al., 2006
; Korngreen and Sakmann, 2000
; Schaefer et al., 2007
; Williams and Stuart, 2000
). However, the relative contribution of these two ion channel types to the overall noise is small, especially since these channels are not very active near the resting potential. We thus conclude that in at the range of voltage perturbation studied (rest ± 10 mV), the effective noise sources due to ion channels are most likely homogeneously distributed in L5 dendrites.
Functional Implications
When considering the functional implication of uniform noise along the somato-dendritic axis, one should bear in mind that voltage noise induces variability in two important signals. First, the integration of the synaptic potential with the background voltage noise induces variable synaptic amplitude. Second, background noise will cause uncertainty (temporal jitter) in the back propagating action potential (BPAP).
Consequently, when the noise sources are distributed homogeneously, the variability of the synaptic signal in the soma is independent of the location of the synaptic input. In a neuron with non-homogeneously distributed noise sources, synaptic potentials arriving from “noisier” locations will be expressed at the soma with reduced variability due to the saturating effect of the synaptic driving force at its (noisier) site of origin. For example, when a synaptic input, summating with a large voltage noise, reaches the synaptic reversal potential, it will have reduced voltage variability. This implies that a homogeneous distribution of noise sources may serve as a means for the neuron to give similar variability to inputs that originate at different locations.
Similarly, a homogeneous distribution of noise sources will ensure that the jittering in spike initiation (at the axon) (Mainen and Sejnowski, 1995
) is independent of the input location. This is of particular importance due to the possible impact of jitter on synaptic plasticity. It has been postulated that the BPAP is an important signal for the induction of synaptic plasticity, the spike-timing-dependent-plasticity (Magee and Johnston, 1997
; Markram et al., 1997
). Therefore, the precise time of arrival of the BPAP at the location of the synaptic input (Letzkus et al., 2006
) will determine the extent and polarity (Sjostrom and Hausser, 2006
) of any change in synaptic strength. In dendrites with a non-homogeneous distribution of noise sources, jittering is expected in the conductance of the BPAP. At “noisier” locations, an increase in the “conduction jitter” will generate variable temporal interactions of the BPAP with the synaptic input. In fact, this increased variability will be maintained throughout all the area distal to the “noisier” location. This will decrease, or may even eliminate, the plastic changes of the synapse. A homogeneous distribution of noise sources may serve as a means for the neuron to ensure that the temporal jitter of the BPAP (and thus the reliability of plastic changes) will be independent of the location of the synapse that undergoes plasticity.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was supported by the National Institute of Mental Health, by the National Science Foundation and by Israeli Science Academy.