- 1 Department of Cellular and Molecular Physiological and Pharmacological Sciences, University of Pavia and CNISM, Italy
- 2 Theoretical Neurobiology, University of Antwerp, Belgium
- 3 Computational Neuroscience Unit, Okinawa Institute of Science and Technology, Japan
The Golgi cells are inhibitory interneurons of the cerebellar granular layer, which respond to afferent stimulation in vivo with a burst-pause sequence interrupting their irregular background low-frequency firing (Vos et al., 1999a . Eur. J. Neurosci. 11, 2621–2634). However, Golgi cells in vitro are regular pacemakers (Forti et al., 2006 . J. Physiol. 574, 711–729), raising the question how their ionic mechanisms could impact on responses during physiological activity. Using patch-clamp recordings in cerebellar slices we show that the pacemaker cycle can be suddenly reset by spikes, making the cell highly sensitive to input variations. Moreover, the neuron resonates around the pacemaker frequency, making it specifically sensitive to patterned stimulation in the theta-frequency band. Computational analysis based on a model developed to reproduce Golgi cell pacemaking (Solinas et al., 2008 Front. Neurosci., 2:2) predicted that phase-reset required spike-triggered activation of SK channels and that resonance was sustained by a slow voltage-dependent potassium current and amplified by a persistent sodium current. Adding balanced synaptic noise to mimic the irregular discharge observed in vivo, we found that pacemaking converts into spontaneous irregular discharge, that phase-reset plays an important role in generating the burst-pause pattern evoked by sensory stimulation, and that repetitive stimulation at theta-frequency enhances the time-precision of spike coding in the burst. These results suggest that Golgi cell intrinsic properties exert a profound impact on time-dependent signal processing in the cerebellar granular layer.
Introduction
Activity in large neuronal networks is characterized by precisely timed responses imposed on a continuous background discharge. Single neurons, in addition to responding to synaptic inputs, contribute to set up the ensemble network activity itself, which can transiently organize into regular and coherent oscillations (Buzsaki, 2006 ). Although the ionic foundations of neuronal electroresponsiveness have been established (Hutcheon and Yarom, 2000 ; Koch, 1999 ; Llinás, 1988 ; Yamada et al., 1998 ), there is little insight in how neurons, through their intrinsic ionic mechanisms, switch from background activity to stimulus-driven responses and are entrained into collective network behaviors. In this respect, it is relevant that some neurons are endowed with ionic channels causing intrinsic oscillations and resonance tuning of their responses toward specific activity frequencies (Llinás, 1988 ).
An interesting case is the Golgi cell (Golgi, 1883 ), an inhibitory interneuron regulating information flow in the granular layer circuit of cerebellum (Eccles et al., 1967 ; Marr, 1969 ). In the anesthetized rat, Golgi cells beat irregularly at theta-frequency and, as a punctuate sensory stimulus arrives, respond with millisecond precision generating short high-frequency bursts (1–4 spikes at 200–300 Hz) followed by a silent pause (Holtzman et al., 2006a ; Holtzman et al., 2006b ; Vos et al., 1999a ). In the awake restrained cat, Golgi cells also discharge tonically and can be entrained by locomotor activity (Edgley and Lidierth, 1987 ). Since large portions of the granular layer circuit can switch between theta-frequency oscillations and asynchronous discharge in relation to the attentive state (Pellerin and Lamarre, 1997 , in the monkey; Hartmann and Bower, 1998 ; Hartmann and Bower, 2001 , in the rat), Golgi cells may be endowed with specific mechanisms allowing them to follow (and potentially influence) the network activity pattern (Maex and De Schutter, 1998 ; Maex and De Schutter, 2005 ; Vos et al., 1999b ).
The Golgi cell shows regular pacemaker activity in acute cerebellar slices (Forti et al., 2006 , see also Dieudonné, 1998 ). Computational modeling predicted the existence of subthreshold low-frequency oscillations tightly coupled to spikes, which, in turn, stabilized the pacemaker cycle through a repeated phase-reset caused by the activation of a Ca2+-dependent K+ current (Solinas et al., 2007). Here we show that the pacemaker cycle can be suddenly reset by spikes, making the cell highly sensitive to input variations. In addition resonance raises the sensitivity to patterned stimulation in the theta-frequency band. Resonance was predicted to arise from a specific slow K+ current and to be amplified by a persistent Na+ current. Simulations carried out in the presence of balanced synaptic noise provided insights in the effects of these mechanisms on in vivo firing, suggesting that the intrinsic excitable properties of Golgi cells could profoundly influence the temporal dynamics of granular layer activity and cerebellar computations.
Materials and Methods
Patch-clamp recordings and experimental procedures
Golgi cell recordings were obtained from 220 µm thick sagittal or parasagittal slices cut from the cerebellar vermis of 16- to 21-day-old Wistar rats. Slice preparation, whole-cell (WC) and loose cell attached (LCA) patch-clamp recordings were performed at 23°C. Experimental procedures conformed to approved protocols for animal experimentation and are detailed in a previous paper (Forti et al., 2006 ). All recordings were performed in the presence of synaptic receptor blockers in the extracellular medium. Antidromic stimulation was obtained by placing an electrode (a glass pipette filled with standard Krebs solution) in the granular layer and delivering brief (100 µs) voltage pulses (5–10 V). These were either isolated or organized in four impulse trains at 50 Hz repeated every 10 seconds. In vivo recordings shown in Figure 6 B have been kindly provided by Tahon et al., (2005) .
The response of Golgi cells to repetitive low frequency stimuli was elicited by applying sequences of 40 ms long current steps in the whole-cell recording (WCR) configuration. Before applying stimuli, the cell was maintained in the rhythmic firing regime (3 ± 1.7 Hz, n = 3) by steady current injection. The current steps ranged from 600 to 800 pA yielding response frequencies as high as 110–130 Hz. Stimuli were organized in two different patterns. The first pattern had pulse repetition frequencies rising from 0.3 to 15 Hz in 1-Hz steps and each step was repeated 10 times before changing frequency. The second pattern was simply the reverse sequence. The recorded membrane potential traces were processed in order to measure the delay of the first spike and the initial firing rate, i.e., the inverse of the first interspike interval (ISI). Since input–output relationships for the initial firing rate and for the inverse of the first-spike latency were similar for both increasing and decreasing inter-pulse intervals, data from both protocols were pooled.
Subthreshold resonance (reported only for the model) was determined by injecting a small sinusoidal current with frequency varying as A · sin(B · t2) + C, where A and B were constant values chosen to determine the amplitude and oscillation speed (Hz∕s) of the injected current and C regulated the level of tonic current injection (impedance amplitude protocol, ZAP: Gutfreund et al., 1995 ; Puil et al., 1986 ). The power spectrum density of both the injected current and the resulting membrane potential were calculated. The square root of the ratio of the power spectra of potential and current gave the model impedance as a function of the oscillation frequency.
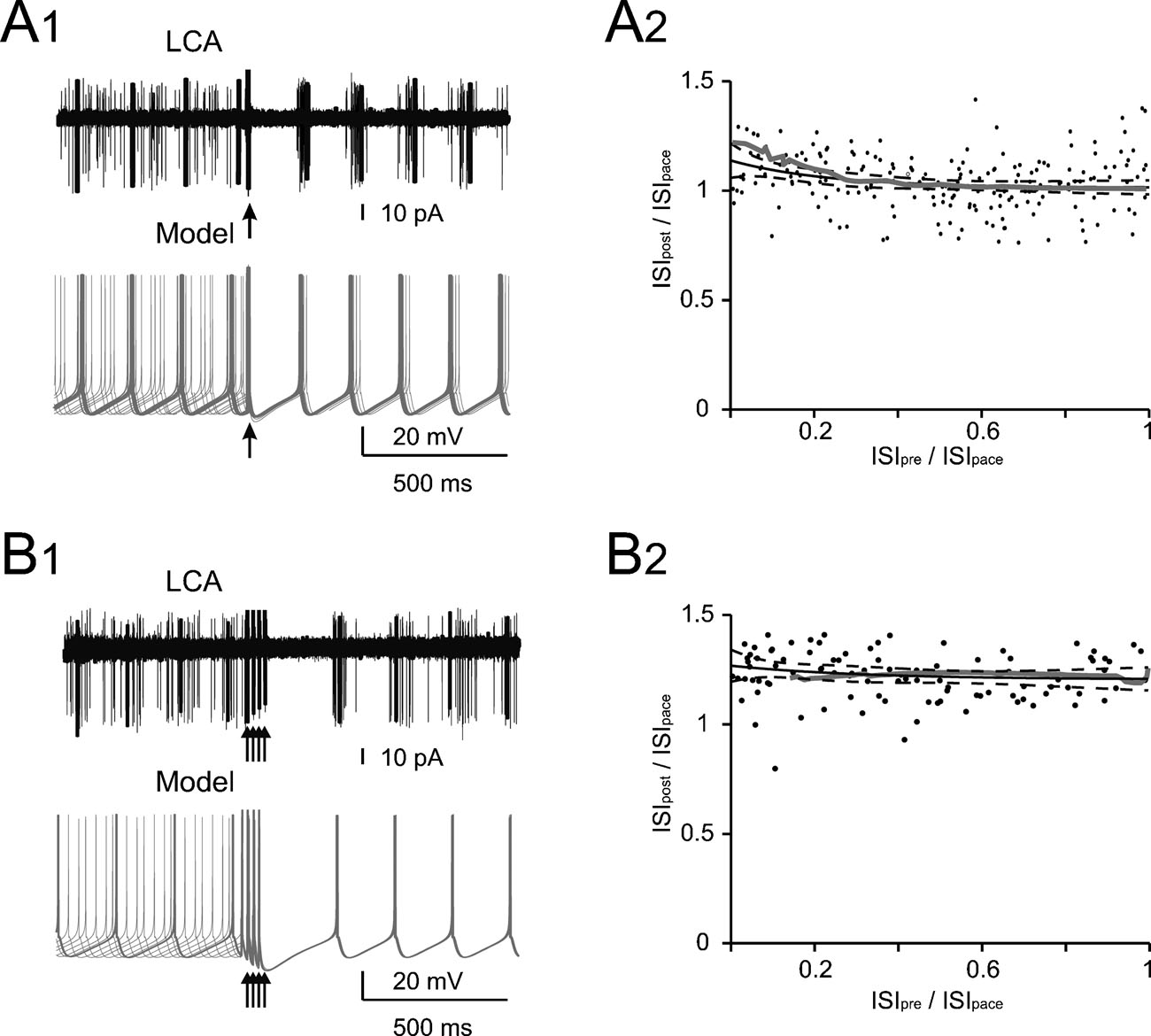
Figure 1. Phase reset of pacemaking. (A1 and B1) A Golgi cell recorded in LCA (black trace) shows autorhythmic firing when a single (A1) or four antidromic spikes at 50 Hz (B1) are elicited by axonal electrical stimulation (arrows). In different sweeps the stimulus was delivered at different phases of the pacemaker cycle. Nonetheless, following stimulation the Golgi cell is phase reset, i.e., restarts firing almost without memory of the preceding phase. The same behavior is observed in the model (gray traces) stimulated with 0.5 ms-long current pulses delivered at varying times during the ISI (the stimulus size is tuned as to inject the minimal charge required to elicit an AP according to the plot in Figure 2 B). (A2 and B2) The plots show summary data from 13 and 6 Golgi cells, respectively, to which antidromic stimulation was applied. The time interval between the resetting stimuli and the subsequent spike (ISIpost ) is compared to the time interval preceding the stimulus (ISIpre). Both ISIpre and ISIpost were normalized by the average ISI of pacemaking (ISIpace). ISIpost /ISIpace was independent from ISIpre . With 1 stimulus (B1) the correlation coefficient was −0.11 (not significantly different from 0, p>0.18, t-test; average ISIpost/ISIpace = 1.05). With four stimuli (B2) the correlation coefficient was 0.08 (not significantly different from 0, p > 0.7, t-test; average ISIpost /ISIpace = 1.15). In either case, the model (gray traces) predicted the experimental results (p > 0.1, t-test). The experimental data were fitted using a single exponential function (solid black trace, dashed black traces show the 95% confidence limits).
As explained in detail in the next section, equivalent experimental protocols were also applied to the model. The experimental data were corrected for a liquid junction potential of 10 mV (Forti et al., 2006 ).
Golgi cell and synaptic noise modeling
The Golgi cell model developed in the companion paper (Solinas et al., 2007, available at senselab.med.yale.edu∕modeldb∕) was adopted without modification to predict the mechanisms underlying the cell behaviors reported in the present in vitro experiments. Moreover, in order to reproduce the ISI irregularity observed during Golgi cell recordings in vivo (mean nCVISI = 0.43–0.45, depending on anesthesia; Vos et al., 1999a , see nCVISI definition therein), balanced synaptic noise was added to the model (Jaeger et al., 1997 ). The synapses were represented by a C0 gating scheme (τbinding = 0.4 ms, τunbinding = 3 ms; Koch and Segev, 1998 , see also Jacobson et al., 2005 ) activated by 0.3-ms 1-mM transmitter pulses. The reversal potential was 0 mV for excitatory and −60 mV for inhibitory synapses. Based on theoretical considerations, the model was endowed with a small number of strong synapses, which markedly raise the irregularity in the firing pattern (Maex and De Schutter, 1998 ; Maex et al., 2000 ). The maximum conductance of excitatory and inhibitory synapses was 4 and 8 nS, respectively (corresponding to peak conductance of 1.5 and 3 nS, respectively). The unitary excitatory and inhibitory post-synaptic current were 90 and 180 pA while holding the model at −60 and 0 mV in voltage clamp configuration, respectively. There were 26 excitatory and 13 inhibitory synapses on the terminal compartments of each one of the three dendrites. Each excitatory and inhibitory synapse was activated with random spike trains generated by a Poisson process having average rate of 0.53 and 8 Hz, respectively. This procedure effectively imitated the in vivo CVISI (nCVISI = 0.45 ± 0.05 in 2-second traces).
Data analysis
General analysis procedures are reported in Solinas et al., (2007). The charge injected into the model by action potentials was calculated as the time integral of the total current during their rising phase (i.e., from threshold to peak). The charge injected by EPSPs was calculated as the time integral between their onset and the minimum reached before the membrane potential increase toward the next spike (this limitation was due to the periodic reactivation of spikes during pacemaking).
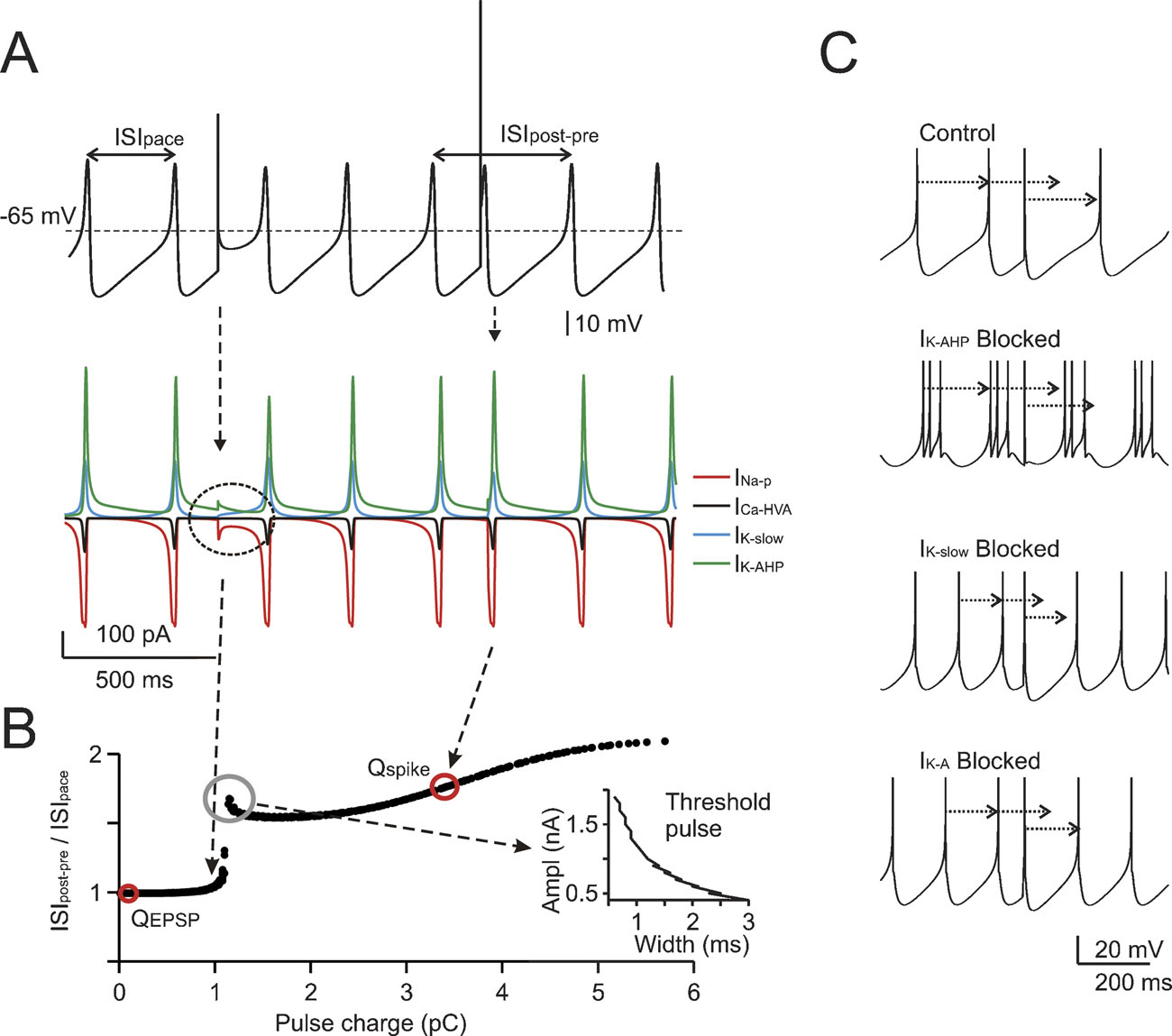
Figure 2. The mechanisms of phase-reset. (A) Phase-reset simulations were performed on subthreshold oscillations after blocking all voltage-dependent currents except for INa-p, ICaHVA, IK-AHP, and IK-slow . The simulations show that small current pulses (2 nA for 0.5 ms) do not alter the cycle, while larger perturbations (6.8 nA for 0.5 ms) reset the cycle of the subthreshold oscillation. The currents involved are shown at the bottom, revealing that currents comparable to those observed during spikes are generated only with the larger pulse. (B) The same protocol used in A was repetitively applied to the model by varying pulse width (Δt = 0.1-3 ms) and amplitude (ΔI = 0.1-2 nA). The plot shows ISIpost-pre /ISIpace (cf. Figure 1 ) as a function of charge Q = Δ I.Δt. A sudden step in the plot indicates a sharp phase reset threshold. The EPSC and spike charges are also reported. The inset shows that one point in the plot corresponds to a hyperbolic trajectory in a stimulus strength-duration graph. (C) The phase-reset mechanism was explored by simulating block of specific ionic currents (control is with all ionic currents active, spikes are truncated for clarity). While in control simulations (upper trace) a spike-like perturbation resets the pacemaker phase, this does not occur after IK-AHP blockage (note that in this condition the model fires short spike bursts). However, blocking IK-slow or IK-A (lower traces) does not alter the phase reset. It should be noted that the absence of noise in these simulations prevented the ISI irregularity that would have been introduced by IK-AHP blockage in real cells (see Forti et al., 2006 ; Solinas et al., 2007).
The match of model to experimental data was evaluated by testing the null hypothesis that their difference was a random sample from a normal distribution (Lilliefors test) with mean equal to 0 and unknown variance (Student's t-test). All data are reported as mean ± SD.
Results
The experimental analysis of Golgi cell pacemaking and electroresponsiveness demonstrated the coexistence of multiple ionic mechanisms operating of different time scales (Forti et al., 2006 ). Here, we investigate the implications of these properties in specific functional conditions relevant for Golgi cell activity in vivo. In order to bridge the gap between in vitro and in vivo cell behaviors we used the computational model developed previously (Solinas et al., 2007).
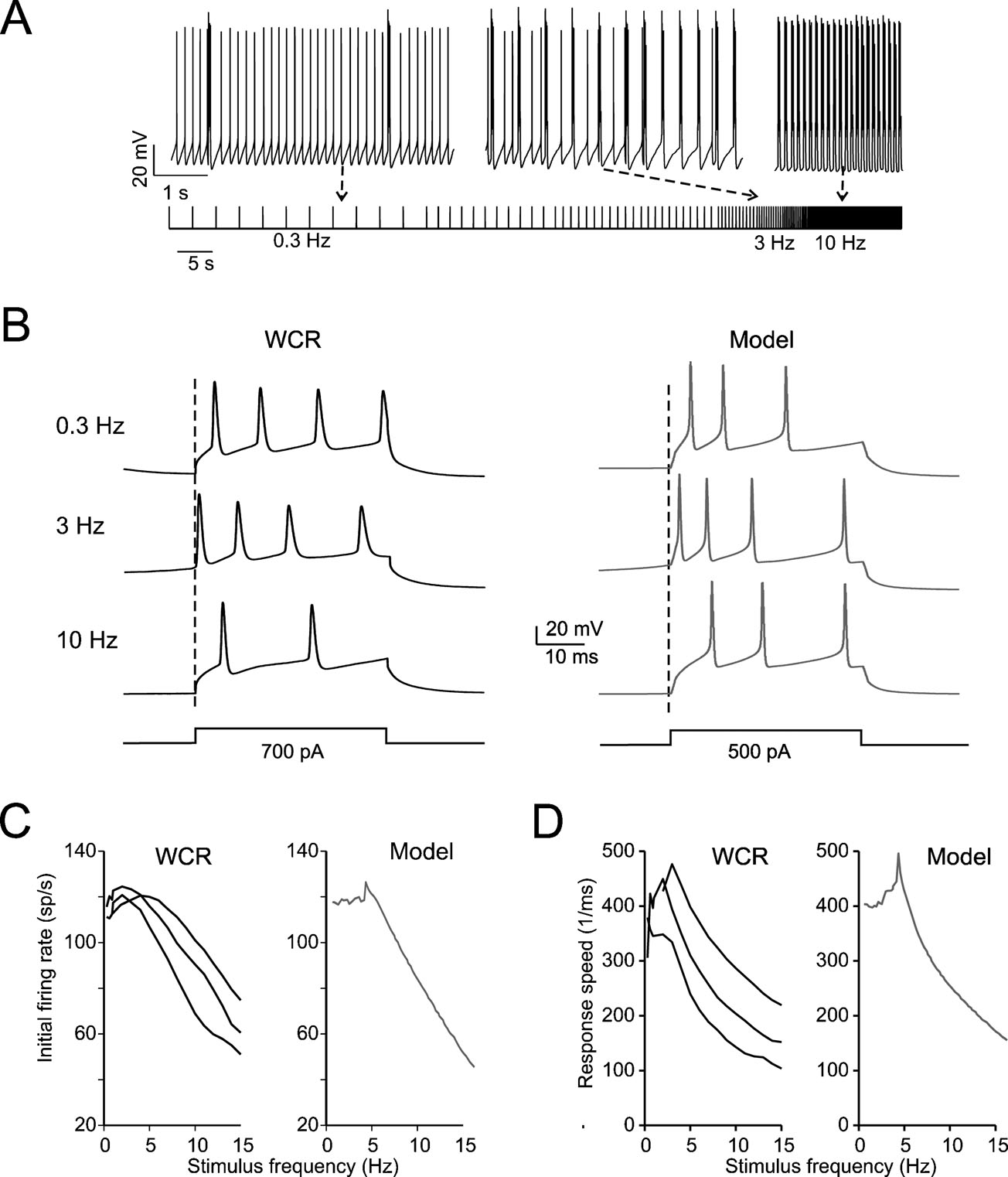
Figure 3. Intrinsic theta-frequency resonance. Intrinsic resonance was investigated by injecting short (40 ms) current steps at frequencies between 0.3 and 15 Hz. (A) A Golgi cell (WCR) in the pacemaking regime is repetitively driven to fire bursts of action potentials by injecting sequences of short (40 ms) current pulses. The pulses are repeated 10 times at each frequency (from 0.3 to 15 Hz). (B) Responses are intensified and show a shorter latency around 3 Hz. This experimental observation as also the resonance effects shown in panels C and D are reproduced by the model. (C) The initial firing rate (the inverse of the first ISI) is shown for three Golgi cell WCRs. The curves show resonance at 2.6 Hz. (D) The response speed (the inverse of first spike latency) is shown for the same three Golgi cells reported in C. The curves show resonance at around 3 Hz.
Pacemaking is phase-reset by spikes
To explore the interaction of spikes with low-frequency pacemaking, action potentials were elicited with retrograde stimulation while recording the Golgi cell in LCA. When a single perturbing action potential was evoked, the auto-rhythmic cycle was restarted after a delay precisely corresponding to the ISI (Figure 1 A1), a property called phase-reset. When a short burst of perturbing action potentials (four spikes at 50 Hz) was evoked to imitate in vivo Golgi cell responses to punctuate facial stimulation (Vos et al., 1999a ), the auto-rhythmic cycle was restarted after a delay slightly longer to the ISI (115%; Figure 1 B1). Interestingly, the phase reset was constant and independent of the phase of the preceding spike, so that the pause following the perturbation was almost constant. This also held true when the pause was normalized for the ISI in different Golgi cells (n = 13 for single pulses and n = 6 for quadruple pulses; Figures 1 A2 and 1 B2). The model faithfully reproduced phase-reset in response to single and multiple pulses (Figures 1 A1 and 1 B1) and its prediction was statistically indistinguishable from the experimental ISI distributions (Figures 1 A2 and 1 B2; p > 0.18 and p > 0.7, respectively, t-test).
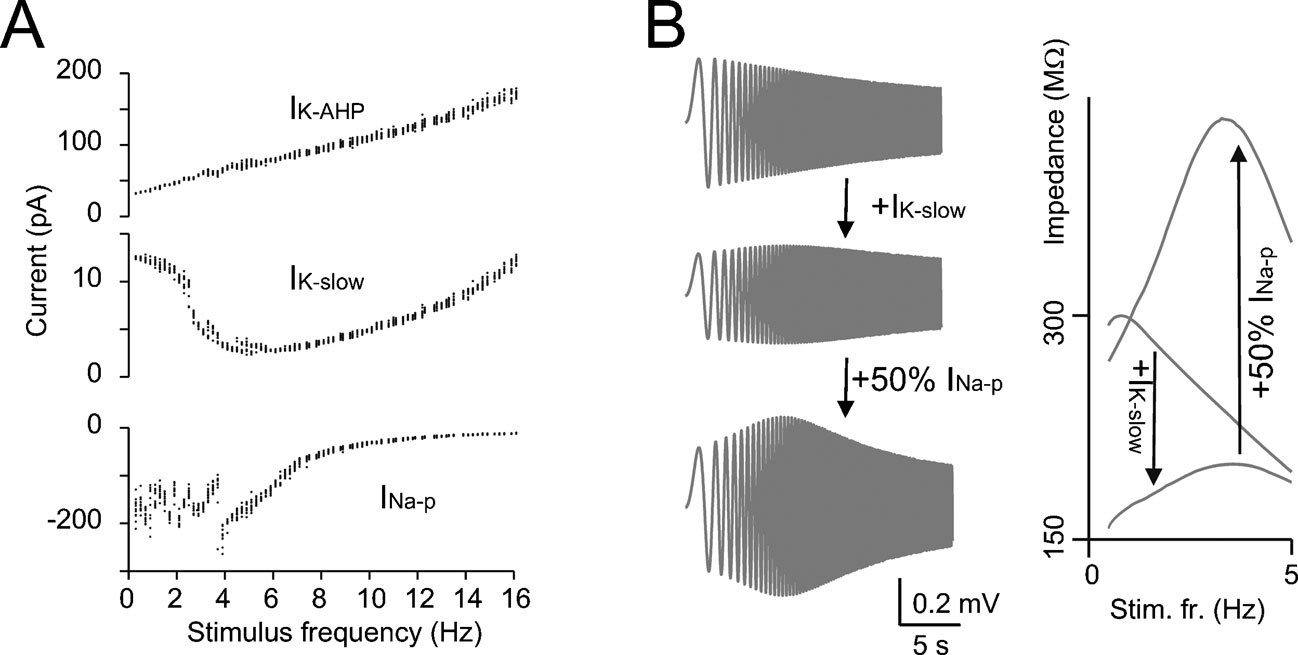
Figure 4. The mechanisms of resonance. (A) IK-AHP, IK-slow, and INa-p were measured in the model during the resonance protocol shown in Figure 3 (the mean values of IK-AHP and IK-slow were measured over the inter-pulse interval, the mean value of INa-p was measured over the first 5 ms of each depolarizing pulse). Note that IK-slow decreases while INa-p increases in the resonance region (since INa-p has fast activation dynamics, its measure is disturbed by spikes) while IK-AHP increases linearly with frequency. (B) In model simulations, resonance could be explored in the immediate subthreshold range (−65 mV) after blocking spike mechanisms (INa-t, IK-V, and IK-C ). The simulations show the ZAP response with all ionic current except for IK-slow and INap and after reintroducing IK-slow and INa-p (50% for graphical reasons) in sequence. The corresponding impedance profiles are shown at the right. The simulations show that IK-slow generates and INa-p amplifies resonance in the theta-frequency range.
The mechanisms of phase-reset were investigated in the model by blocking the spike and evaluating the effect of brief (0.5 ms) pulses of variable size on the phase of subthreshold oscillations (Figure 2 A). The subthreshold oscillation was phase-reset only when the perturbing pulse generated a depolarization comparable to that caused by a spike. An extended analysis of the stimuli capable of generating phase-reset is shown in Figure 2 B where phase-reset is plotted as a function of pulse charge. The analysis, which was performed for the specific phase of pulses shown in A, made use of different combinations of amplitude and duration (from 0.5 to 3 ms), so that one point in the plot corresponds to a hyperbolic trajectory in a stimulus strength-duration graph (see inset to Figure 2 B). Phase-reset could be obtained for charges greater than ∼1 pC, the trace break point. In the model, the influx of charge during the rising phase of spikes (3.4 pC) fell to the right of the break-point, while the charge equivalent to EPSPs (0.11 pC) fell to the left (see Materials and Methods). This analysis indicates that spikes (but not EPSPs) would phase reset the pacemaker.
The coupling of spikes to the slow AHP was largely determined by IK-AHP, which briskly activated after a full-blown spike and lasted until about half of the ISI (see Solinas et al., 2007). The specific involvement of IK-AHP in phase resetting was demonstrated by simulating the selective blockage of repolarizing ionic currents. Only blocking IK-AHP, but not IK-slow or IK-A, prevented phase-reset (Figure 2 C).
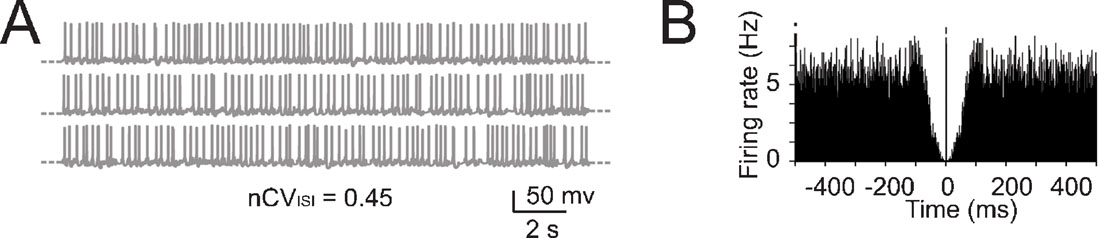
Figure 5. The effect of noise on pacemaking. (A) Pacemaking in the model was perturbed by injecting random balanced synaptic currents causing a marked ISI irregularity. (B) The autocorrelogram of a 60-second long simulation shows that the random synaptic input cancels the regularity of the pacemaker cycle.
Resonance with theta-frequency stimulus patterns
The expression of slow repolarizing currents suggests that Golgi cells could respond preferentially, i.e., be resonant, to stimuli delivered at low frequency (Buzsaki, 2006 ; Hutcheon and Yarom, 2000 ). Resonance in Golgi cells was investigated in vitro by applying sequences of 40-ms current steps, that elicited spike bursts composed of 2–3 spikes. This type of stimulus imitates the response to repetitive punctuate stimulation in vivo (Vos et al., 1999b ). The steps were repeated 10 times at a given frequency before moving to a different one, ranging from 0.3 to 15 Hz either in ascending or descending order (Figure 3 A; see Materials and Methods for details). The results were analyzed in terms of initial firing rate and first-spike latency and showed resonance peaking at 2.6 ± 1.1 Hz for the initial firing rate and at 3.0 ± 0.5 Hz for the inverse of the first-spike latency (Figures 3 B–3 D). The model, stimulated with the same step protocols, faithfully predicted the experimental results (Figures 3 B–3 D), matching the resonant frequencies (2.9 Hz for the initial firing rate and for the inverse of first spike latency).
The resonance mechanism was investigated using the model. IK-slow (measured along the inter-pulse interval) showed a minimum close to the peak of the resonance curve (Figure 4 A). Conversely, INa-p (measured during the depolarizing pulses) showed maximal activation around the peak of the resonance curve. IK-AHP showed only a monotonic increase with frequency. This suggests that IK-slow and INa-p played a critical role in determining resonance. The mechanism of resonance was further investigated in the model by blocking spikes and applying the ZAP protocol (Figure 4 B, see Materials and Methods and Buzsaki, 2006 ; D'Angelo et al., 2001 ; Hutcheon and Yarom, 2000 ) just below the membrane potential region generating subthreshold oscillations (Solinas et al., 2007). Experimental application of ZAP proved impractical in Golgi cells due to spike contamination (data not shown). At −65 mV, the resonance frequency was 3.2 Hz (Figure 4 B) close to the value measured in the firing regime. Subthreshold resonance reflected activation of IK-slow and was remarkably amplified by INa-p, as clearly observed in the corresponding impedance plots (Figure 4 B). Other currents, including IK-AHP, accentuated low-pass filtering but were not needed to determine the resonance peak. These results suggest that resonance originated in the subthreshold region from IK-slow activation at low frequency and was amplified by INa-p.
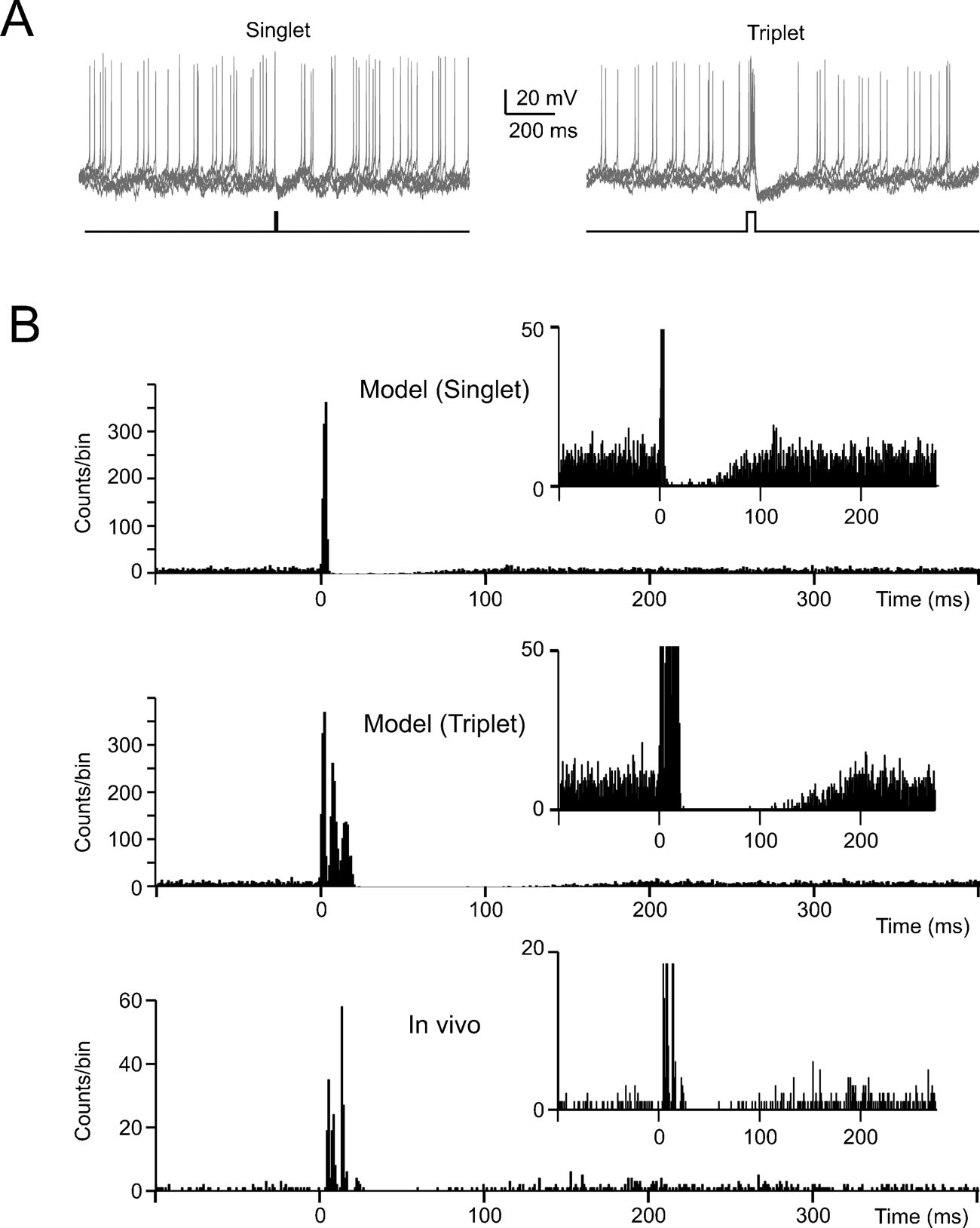
Figure 6. The effect of noise on phase-reset. (A) The model perturbed with balanced synaptic noise was stimulated by either 5-ms long or 30-ms long current pulses of 800 pA (lower traces show the stimulation protocols) to elicit a singlet or a triplet of spikes, respectively. Visual inspection shows an evident silent pause with the triplet but not with the singlet. (B) The PSTH for singlet shows a brief pause partly populated by spikes. The PSTH for triplets shows a pause roughly corresponding to the average pacemaker cycle free from any spikes. The insets show that the silent pause is short and unreliable with a singlet but not with a triplet. The bottom panel shows data recorded in vivo following vibrissal stimulation in the anaesthetized rat, which cause a brief spike sequence followed by a silent pause. Note the remarkable similarity between in vivo recordings and the model (triplet).
Pacemaking, phase reset and resonance with balanced synaptic noise
An important question is how the fundamental properties of Golgi cells are affected by synaptic noise generated by cerebellar network activity. Golgi cells are reported to fire spontaneously in vivo as in vitro, but beating in the anesthetized rat in vivo is more irregular than in vitro (with nCVISI rising to 0.43–0.45; Vos et al., 1999a , but see Edgley and Lidierth, 1987 ; Miles et al., 1980 ) and also slightly faster (Vos et al., 1999a , cf. Forti et al., 2006 ). We simulated the irregularity of spikes ISI by adding random balanced excitatory and inhibitory synaptic activity to the Golgi cell model (Figure 5 A; see Materials and Methods and Maex and De Schutter, 1998 ; Maex et al., 2000 ) until attaining nCVISI = 0.45. With this noise, the regular beating of the Golgi cell was no longer discernible in simulated traces and autocorrelograms (Figures 5 A–5 B).
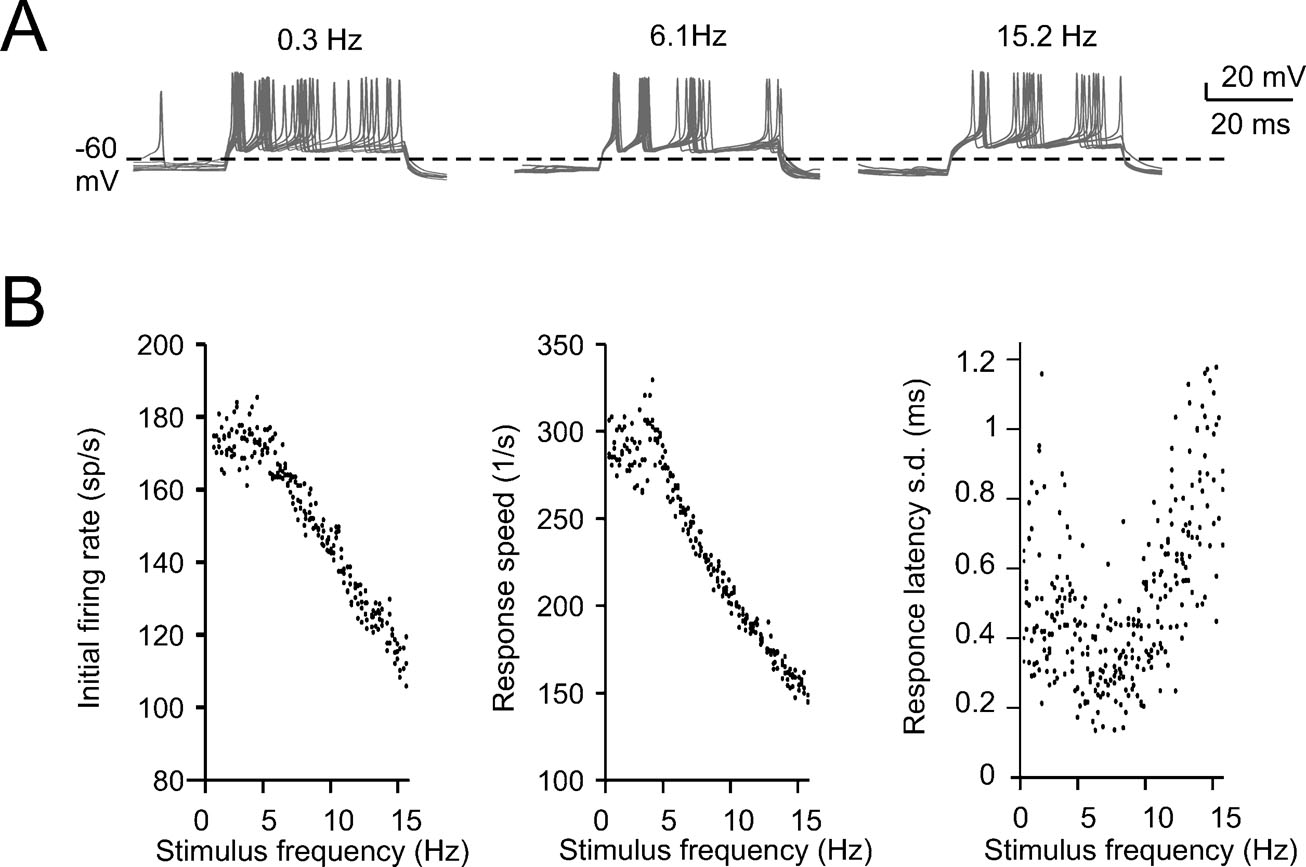
Figure 7. The effect of noise on resonance. (A) The resonance protocol reported in Figure 3 was also applied to the model perturbed with synaptic noise. The traces show the response to 800 pA current pulses taken from a sequence in which stimuli are delivered at increasing frequency. The traces at 6.2 Hz show greater precision of spike timing. (B) The plots show data from four simulations with different random seeds (there are four black circles for each tested stimulation frequency). The initial firing rate and the first spike delay do no longer show a clear resonance. However, the standard deviation of the first spike delay is clearly resonant with a peak at stimulation frequencies around 6 Hz.
In the presence of balanced synaptic noise, phase reset was induced with depolarizing pulses and peri-stimulus time histograms (PSTH) were constructed by repeating simulations with different random seeds. When the depolarizing pulses generated a single spike, phase-reset was not robust (Figure 6 A) as firing could restart just after the stimulus and the silent pause was not evident in the PSTH (Figure 6 B). However, phase reset became robust when the depolarizing pulses generated a spike triplet (Figure 6 B). In this case, the PSTH (Figure 6 B) became similar to those recorded in vivo following punctuate sensory stimulation (Vos et al., 1999a ; Volny-Luraghi et al., 2002 ) with a silent pause that had a duration similar to the average ISI (about 100 ms, see Figure 5 B). It should also be noted that the three spikes occurred at times and with precision similar to those recorded in vivo (interspike distances of 5–10 ms and time dispersion in the millisecond range, see inset). Slight differences, like the presence of rebound excitation or prolongation of the silent pause beyond the average ISI which are sometimes observed in vivo (Tahon et al., 2005 ), could be due to network effects (see Discussion).
Similar to the non-noisy case, periodic stimulation patterns in the presence of noise were able to unmask frequency-dependent properties of the Golgi cell model (Figure 7 A). Inspection of traces showed that the precision of spike timing in bursting responses was increased at intermediate frequencies, most evidently for the initial doublet. Indeed (Figure 7 B), while resonance of first-spike delay and initial firing frequency was partly corrupted by noise, the time-precision of the first spike was markedly enhanced around 6 Hz (SD of first spike latency at 0.3, 6.1, and 15.2 Hz was 0.788, 0.309, and 1.178 ms, respectively; and SD of second spike latency was 1.176, 0.513, and 2.78 ms, respectively). Thus a clear resonance of spike-timing precision was present at a frequency around 6 Hz. Clearly, when the inter-stimulus interval approaches the mean ISI of pacemaking and the duration of the silent pause, the probability of disturbances from incidental spikes is minimal.
In conclusion, these results predict that, in the presence of balanced synaptic noise, the fundamental properties of the Golgi cell revealed in vitro transform into an intrinsic irregular activity that can be phase-reset by short spike bursts. Within the bursts, the time-precision of the initial spike doublet is markedly improved when stimulation is repeated at theta-frequency. The implications of this finding for cerebellar network function are discussed.
Discussion
In this paper, we demonstrate that the theta-frequency pacemaking of cerebellar Golgi cells observed in vitro (Forti et al., 2006 ) can be phase-reset by stimuli evoking spikes and that resonance of output spike patterns is induced by input stimuli occurring at the pacemaker oscillation frequency. The functional implications of these response patterns were investigated using computational modeling based on a mechanistic reconstruction of the underlying ionic processes (Solinas et al., 2007). In the presence of balanced synaptic noise, assumed to mimic in vivo cerebellar network activity (De Schutter and Bower, 1994 ; Jaeger and Bower, 1999 ; Jaeger et al., 1997 ), the model spiked irregularly, resembling the non-periodic state observed in the cerebellum of anesthetized (Holtzman et al., 2006a ; Holtzman et al., 2006b ; Vos et al., 1999a ; Vos et al., 1999b ) and freely behaving rats (D. Cohen, personal communication). The irregular occurrence of spikes could be interrupted by strong stimuli that generate a short burst of activity followed by a silent pause with a duration roughly equivalent to the pacemaker cycle. Moreover, theta-frequency inputs proved optimal for fast, intense and precise discharges in the bursts. Thus the model predicts that the same elementary membrane properties generating regular pacemaking in vitro support quite different responses in vivo, allowing Golgi cells to exert an effective time-dependent control over the afferent patterns conveyed by mossy fiber activity.
Phase-reset in the model required IK-AHP, which has the property of coupling Ca2+ through HVA channels to spikes (Stocker, 2004 ), thereby counteracting the effect of noise and regularizing the pacemaker cycle. A similar action of SK channels on noise was observed also in various pacemaker neurons (review in Stocker, 2004 ; Walter et al., 2006 ). In simulations in the noisy regime, phase-reset emerged as a silent pause in response to short spike bursts. Since the bursts imitate the response to facial punctuate stimulation (e.g., Vos et al., 1999a , see below), this mechanism could be involved in the physiological processing of sensory signals (Tahon et al., 2005 ).
Resonance in the model required IK-slow activation at low frequencies and was strongly amplified by INa-p, resembling the mechanism previously reported in pyramidal cortical cells (Gutfreund et al., 1995 ) and cerebellar granule cells (D'Angelo et al., 2001 ). Interestingly, resonance regulated spike timing and frequency in bursting responses to repetitive stimuli and, in the noisy regime, markedly improved time-precision of the initial spike doublet. We therefore predict that repetitive activation of the Golgi cells at theta-frequency in vivo will produce more temporally precise discharge than activation at other frequencies.
The relevance of the intrinsic excitable properties of Golgi cells in the context of in vivo cerebellar physiology needs to be considered in relation to their responses to native mossy fiber inputs (Chadderton et al., 2004 ; Kase et al., 1980 ). It is somewhat surprising that the simple simulations reported in Figures 5 –7 are so successful at reproducing the Golgi cell response to brief tactile stimuli in vivo (Vos et al., 1999a ; Volny-Luraghi et al., 2002 ). For example, the timing of Golgi cell spikes in vivo is assumed to be related to differential delays in the afferent fibers (trigeminal and cortico-pontine mossy fibers: Vos et al., 2000 , see also Morissette and Bower, 1996 , as well as parallel fibers: Volny-Luraghi et al., 2002 ; Vos et al., 2000 ), but in our model intrinsic mechanisms tune the response toward the appropriate spike burst. Intrinsic mechanisms also provide the substrate of the silent pause in the model, but the response lacks the subsequent rebound in activity observed in vivo (Tahon et al., 2005 ; Vos et al., 1999a ), suggesting that the silent pause is enhanced by Golgi cell inhibition by molecular layer interneurons (Dumoulin et al., 2001 ; Palay and Chan-Palay, 1974 ). This inhibition may also explain the long-lasting depressions of firing evoked by strong electrical stimuli (Holtzman et al., 2006b ). Equally interesting is the finding that Golgi cell response to repetitive stimulation is anticipated, intensified and made more precise at theta frequency. Golgi cell theta-frequency oscillation and resonance, together with theta-frequency resonance in granule cells (D'Angelo et al., 2001 ) may intensify and improve time precision to theta-frequency cortical inputs during certain sensory-motor behaviors, like active whisking (for review see Kleinfeld et al., 2006 ). Resonance, in turn, could promote the coherent oscillation of granular layer neurons observed in awake rats and monkeys (Hartmann and Bower, 1998 ; Pellerin and Lamarre, 1997 ).
In conclusion, the present paper suggests that Golgi cell excitable properties revealed in vitro contribute to cerebellar processing in vivo, introducing time- and state-dependent components in cerebellar computations (cf. De Schutter and Bjaalie, 2001 ; Vos et al., 2000 for introductory concepts). Most strikingly, both phase-reset and resonance control Golgi cell spike timing and therefore the temporal precision of inhibition delivered to granule cells. Depending on input patterns (either solitary or repeated bursts proved particularly effective), the beginning and end of an inhibitory cycle are set with millisecond precision. This, together with rebound activation through molecular layer interneurons, could be particularly important to entrain the cerebellar network into oscillatory states exploiting time-windowing mechanisms in reverberating loops (Kistler and DeZeeuw, 2003 ). During a given time-window, granule cell inhibition wanes, so that consecutive stimuli would recover their effectiveness generating specific output patterns depending on the temporal relationships between mossy fiber and Golgi cell discharge (e.g., see Medina and Mauk, 2000 ). The precise relationship between excitation and inhibition may also have an impact on the induction of long-term plasticity at the mossy fiber–granule cell synapse (Mapelli and D'Angelo, 2007 ), suggesting the existence of spike-timing-dependent plasticity (STDP) in the cerebellar glomerulus. A secondary effect of Golgi cell spiking, for which precise timing becomes irrelevant, is to contribute to tonic inhibition. This is due to GABA accumulation in the cerebellar glomerulus and exerts a steady control on granule cell excitation (De Schutter, 2002 ; Rossi et al., 2003 ). It seems therefore that the random basal discharge of Golgi cells generated by noisy synaptic bombardment contributes to keep the granular layer under tonic inhibitory control, while patterned stimuli (like bursts repeated in specific sequences) would enhance communication within precise time-windows. The spatio-temporal coherence of signal processing could be extended by Golgi cell synchronization along the parallel fiber axis (Maex and De Schutter, 1998 ; Vos et al., 1999b ) and made cross-modal through the wide afferent parallel fiber input (Vos et al.,1999a ; Vos et al.,2000 ). Untangling the complex interactions between intrinsic cell electroresponsiveness and network activity will require further experimental testing in vitro and in vivo combined with the development of large-scale network simulations.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgements
This work was supported by grants from CEREBELLUM (QLG3-CT-2001-02256) and SENSOPAC (FP6-IST028056) of the European Commission, CNISM and Fondazione CARIPLO of Italy, and UA and FWO of Belgium, and OIST of Japan. L.F. was the percipient of an INGENIO fellowship from the European Social Fund, Ministero del Lavoro e della Previdenza Sociale and Regione Lombardia of Italy.
References
Chadderton, P., Margrie, T. W., Häusser, M. (2004). Integration of quanta in cerebellar granule cells during sensory processing. Nature 428, 856–860.
D'Angelo, E., Nieus, T., Maffei, A., Armano, S., Rossi, P., Taglietti, V., Fontana, A., and Naldi, G. (2001). Theta-frequency bursting and resonance in cerebellar granule cells: experimental evidence and modeling of a slow K+-dependent mechanism. J. Neurosci. 21, 759–770.
De Schutter, E. (2002). Cerebellar cortex: computation by extrasynaptic inhibition. Curr. Biol. 12, R363–R365.
De Schutter, E., and Bjaalie, J. G. (2001). Coding in the granular layer of the cerebellum. Prog. Brain Res. 130, 279–296.
De Schutter, E., and Bower, J. M. (1994). An active membrane model of the cerebellar Purkinje cell: II. Simulation of synaptic responses. J. Neurophysiol. 71, 401–419.
Dieudonné, S. (1998). Submillisecond kinetics and low efficacy of parallel fibre-Golgi cell synaptic currents in the rat cerebellum. J. Physiol. 510, 845–866.
Dumoulin, A., Triller, A., Dieudonné, S. (2001). IPSC kinetics at identified GABAergic and mixed GABAergic and glycinergic synapses onto cerebellar Golgi cells. J. Neurosci. 21, 6045–6057.
Eccles, J. C., Ito, M., Szentágothai, J. (1967). The Cerebellum as a neuronal machine (Berlin, Springer).
Edgley, S. A., and Lidierth, M. (1987). The discharges of cerebellar Golgi cells during locomotion in the cat. J. Physiol. 392, 315–332.
Forti, L., Cesana, E., Mapelli, J., D'Angelo, E. (2006). Ionic mechanisms of autorhythmic firing in rat cerebellar Golgi cells. J. Physiol. 574, 711–729.
Golgi, C. (1883). Sulla fina anatomia degli organi centrali del sistema nervoso IV. Sulla fina anatomia delle circonvoluzioni cerebellari. Riv. Sper. Freniatr. Med. Leg. Alien. Ment. 9, 1–17.
Gutfreund, Y., Yarom, Y., and Segev, I. (1995). Subthreshold oscillations and resonant frequency in guinea-pig cortical neurons: physiology and modelling. J. Physiol. 483, 621–640.
Hartmann, M. J., and Bower, J. M. (1998). Oscillatory activity in the cerebellar hemispheres of unrestrained rats. J. Neurophysiol. 80, 1598–1604.
Hartmann, M. J., and Bower, J. M. (2001). Tactile responses in the granule cell layer of cerebellar folium crus IIa of freely behaving rats. J. Neurosci. 21, 3549–3563.
Holtzman, T., Mostofi, A., Phuah, C. L., and Edgley, S. A. (2006a). Cerebellar Golgi cells in the rat receive multimodal convergent peripheral inputs via the lateral funiculus of the spinal cord. J. Physiol. 577, 69–80.
Holtzman, T., Rajapaksa, T., Mostofi, A., and Edgley, S. A. (2006b). Different responses of rat cerebellar Purkinje cells and Golgi cells evoked by widespread convergent sensory inputs. J. Physiol. 574, 491–507.
Hutcheon, B., and Yarom, Y. (2000). Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci. 23, 216–222.
Jacobson, G. A., Diba, K., Yaron-Jakoubovitch, A., Oz, Y., Koch, C., Segev, I., and Yarom, Y. (2005). Subthreshold voltage noise of rat neocortical pyramidal neurones. J. Physiol. 564, 145–160.
Jaeger, D., and Bower, J. M. (1999). Synaptic control of spiking in cerebellar Purkinje cells: dynamic current clamp based on model conductances. J. Neurosci. 19, 6090–6101.
Jaeger, D., De Schutter, E., and Bower, J. M. (1997). The role of synaptic and voltage-gated currents in the control of Purkinje cell spiking: a modeling study. J. Neurosci. 17, 91–106.
Kase, M., Miller, D. C., and Noda, H. (1980). Discharges of Purkinje cells and mossy fibres in the cerebellar vermis of the monkey during saccadic eye movements and fixation. J. Physiol. 300, 539–555.
Kistler, W. M., and De Zeeuw, C. (2003). Time windows and reverberating loops: a reverse engineering approach to cerebellar function. The Cerebellum 2, 44–54.
Kleinfeld, D., Ahissar, E., and Diamond, M. E. (2006). Active sensation: insights from the rodent vibrissa sensorimotor system. Curr. Opin. Neurobiol. 16, 435–444.
Koch, C., and Segev, I. (1998). Methods in neuronal modeling from ions to networks (Cambridge, MA, USA, MIT Press).
Llinás, R. R. (1988). The intrinsic electrophysiological properties of mammalian neurons: insights into central nervous system function. Science 242, 1654–1664.
Maex, R., and De Schutter, E. (1998). Synchronization of Golgi and granule cell firing in a detailed network model of the cerebellar granule cell layer. J. Neurophysiol. 80, 2521–2537.
Maex, R., and De Schutter, E. (2005). Oscillations in the cerebellar cortex: a prediction of their frequency bands. Prog. Brain Res. 148, 181–188.
Maex, R., Vos, B. P., and De Schutter, E. (2000). Weak common parallel fibre synapses explain the loose synchrony observed between rat cerebellar Golgi cells. J. Physiol. 523, 175–192.
Mapelli, J., D'Angelo, E. (2007). The spatial organization of long-term synaptic plasticity at the input stage of cerebellum. J. Neurosci. 27, 1285–1296.
Medina, J. F., and Mauk, M. D. (2000). Computer simulation of cerebellar information processing. Nat. Neurosci. 3, 1205–1211.
Miles, F. A., Fuller, J. H., Braitman, D. J., and Dow, B. M. (1980). Long-term adaptive changes in primate vestibuloocular reflex. III. Electrophysiological observations in flocculus of normal monkeys. J. Neurophysiol. 43, 1437–1476.
Morissette, J., and Bower, J. M. (1996). Contribution of somatosensory cortex to responses in the rat cerebellar granule cell layer following peripheral tactile stimulation. Exp. Brain Res. 109, 240–250.
Pellerin, J. P., and Lamarre, Y. (1997). Local field potential oscillations in primate cerebellar cortex during voluntary movement. J. Neurophysiol. 78, 3502–3507.
Puil, E., Gimbarzevsky, B., and Miura, R. M. (1986). Quantification of membrane properties of trigeminal root ganglion neurons in guinea pigs. J. Neurophysiol. 55, 995–1016.
Rossi, D. J., Hamann, M., and Attwell, D. (2003). Multiple modes of GABAergic inhibition of rat cerebellar granule cells. J. Physiol. 548, 97–110.
Solinas, S., Forti, L., Cesana, E., Mapelli, J., De Schutter, E., D'Angelo, E. (2008). Computational reconstruction of pacemaking and intrinsic electroresponsiveness in cerebellar Golgi cells. Front. Neurosci., 2: 2.
Stocker, M. (2004). Ca2+-activated K+ channels: molecular determinants and function of the SK family. Nat. Rev. Neurosci. 5, 758–770.
Tahon, K., Volny-Luraghi, A., and De Schutter, E. (2005). Temporal characteristics of tactile stimuli influence the responce profile of cerebellar Golgi cells. Neurosci. Lett. 390, 156–161.
Volny-Luraghi, A., Maex, R., Vos, B. P., and De Schutter, E. (2002). Peripheral stimuli excite coronal beams of Golgi cells in rat cerebellar cortex. Neuroscience 113, 363–373.
Vos, B. P., Volny-Luraghi, A., and De Schutter, E. (1999a). Cerebellar Golgi cells in the rat: receptive fields and timing of responses to facial stimulation. Eur. J. Neurosci. 11, 2621–2634.
Vos, B. P., Maex, R., Volny-Luraghi, A., and De Schutter, E. (1999b). Parallel fibers synchronize spontaneous activity in cerebellar Golgi cells. J. Neurosci. 19, RC6.
Vos, B. P., Volny-Luraghi, A., Maex, R., and De Schutter, E. (2000). Precise spike timing of tactile-evoked cerebellar Golgi cell responses: a reflection of combined mossy fiber and parallel fiber activation? Prog. Brain Res. 124, 95–106.
Keywords: golgi cell, resonance, phase-reset, cerebellum, granular layer, modeling
Citation: Sergio Solinas, Lia Forti, Elisabetta Cesana, Jonathan Mapelli, Erik De Schutter,and Egidio D'Angelo (2007). Fast-reset of pacemaking and theta-frequency resonance patterns in cerebellar Golgi cells: Simulations of their impact in vivo. Front. Cell. Neurosci. 1:4. doi: 10.3389/neuro.03/004.2007
Received: 26 November 2007;
Paper pending published: 1 December 2007;
Accepted: 7 December 2007;
Published online: 30 December 2007
Edited by:
Alexander Borst, Max-Planck-Institute of Neurobiology, GermanyReviewed by:
Hermann Cuntz, University College London, UKYosef Yarom, Hebrew University, Israel
Copyright: © 2007 Solinas, Forti, Cesana, Mapelli, De Schutter and D'Angelo. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Egidio D'Angelo, Department of Cellular and Molecular Physiological and Pharmacological Sciences, University of Pavia and CNISM, Via Forlanini 6, I-27100 Pavia, Italy. e-mail:ZGFuZ2Vsb0B1bmlwdi5pdA==





