1
Department of Neuroscience, Erasmus Medical Center, Rotterdam, The Netherlands
2
Department of Biomedical Engineering, Ben Gurion University of the Negev, Be’er Sheva, Israel
The compensatory eye movement (CEM) system maintains a stable retinal image, integrating information from different sensory modalities to compensate for head movements. Inspired by recent models of the physiology of limb movements, we suggest that CEM can be modeled as a control system with three essential building blocks: a forward model that predicts the effects of motor commands; a state estimator that integrates sensory feedback into this prediction; and, a feedback controller that translates a state estimate into motor commands. We propose a specific mapping of nuclei within the CEM system onto these control functions. Specifically, we suggest that the Flocculus is responsible for generating the forward model prediction and that the Vestibular Nuclei integrate sensory feedback to generate an estimate of current state. Finally, the brainstem motor nuclei – in the case of horizontal compensation this means the Abducens Nucleus and the Nucleus Prepositus Hypoglossi – implement a feedback controller, translating state into motor commands. While these efforts to understand the physiological control system as a feedback control system are in their infancy, there is the intriguing possibility that CEM and targeted voluntary movements use the same cerebellar circuitry in fundamentally different ways.
Compensatory eye movements (CEM) is a general term for a number of different reflexes that keep an image fixed on the retina during movements of the body and the head (e.g. Delgado-Garcia, 2000
). As such, these eye movements have a specific and well-defined goal: to prevent movement of the visual image on the retina, often called retinal slip, during fixation. The circuitry of the CEM system (Figure 1
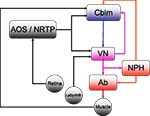
) is different from the circuitry for other eye movements such as saccades, although all the eye movement systems converge in the oculomotor nuclei of the brainstem (Buttner-Ennever and Buttner, 1992
). For horizontal eye movements these are the abducens nucleus (Ab) and the nucleus prepositus hypoglossi (NPH). All CEM-related input to these brainstem structures comes from the Vestibular Nuclei (VN).
Figure 1. The horizontal compensatory eye movement (CEM) system. Generally, this is described as two separate reflexes. The optokinetic reflex (OKR) uses visual input from the retina to stabilize the eye while the vestibulo-ocular reflex (OKR) responds to vestibular information from the labyrinth. This figure emphasizes the distinction between sensory feedback (black) and motor signals (red).Blue and purple represent central stages of processing, and are added for comparison with other figures. Cblm: cerebellar cortex; AOS/NRTP: accessory optic system and nucleus reticularis tegmentum pontis; VN: vestibular nucleus; NPH: neuclus prepositus hypoglossi; OMN/AB: oculomotor nucleus and abducens.
The optokinetic reflex (OKR) is a closed loop system that directly responds to retinal slip, generating eye movements with the direction and magnitude of measured retinal slip. Afferents from the retina project directly to the Accessory Optic System (AOS). The AOS, in turn projects to the VN and the cerebellum, through the Nucleus Reticularis Tegmenti Pontis (NRTP; Gerrits et al., 1984
; Langer et al., 1985
; Glickstein et al., 1994
). The OKR has a response delay of about 80 ms (e.g Winkelman and Frens, 2006
), mostly because of the inherent delay involved in visual processing (Graf et al., 1988
). In keeping with this, the OKR is only responsive to low velocity stimuli.
For compensation of higher velocity stimuli, the CEM system depends on the vestibulo-ocular reflex (VOR) which uses vestibular input to estimate head movement and generate oppositely directed eye movements. Vestibular afferents from the labyrinth project directly to the VN. The two systems are complementary: the VOR compensates for higher frequencies while the OKR compensates for the lower velocities (Collewijn, 1989
).
Both the VOR and OKR are adaptive, meaning that the mapping of stimulus to appropriate eye response can be tuned to match changing response properties of the eye and its supporting tissues (usually collectively called the “plant”) or changes in the sensitivity of the sensory organs (Blazquez et al., 2004
; Boyden et al., 2004
; Andreescu et al., 2005
; Gittis and du Lac, 2006
). Changes in either plant response properties, sensory sensitivity, or environmental changes in the relationship of vision and vestibular input to movement will change the appropriate mapping from stimulus to response and thus the system must change the mapping so that retinal slip continues to be appropriately compensated. There is ample evidence that the flocculus, a small section of the cerebellar cortex is critical in this plasticity (e.g. Lisberger et al., 1984
). The Purkinje cells (P-cells) of the flocculus project only to the VN. There are sites of plasticity both at the level of the parallel fibre synapses to these P-cells, as well as at the P-cell/VN synapses (Raymond et al., 1996
; Boyden et al., 2004
). In addition, the cerebellum has an important role in ongoing performance beyond its role in plasticity: the performance of the OKR decreases dramatically after floccular lesions (Takemori and Cohen, 1974
; Zee et al., 1981
), while the VOR is less affected (Waespe et al., 1983
; Van Neerven et al., 1989
).
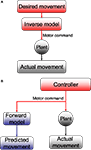
There has been a long history of using models based on the principles of control theory to describe the control of eye movements generally and CEM in particular. Starting with the seminal work of David Robinson (for review Robinson, 1981
), this tradition has generally posited a neural implementation of an inverse model that maps stimuli to command signals (Skavenski and Robinson, 1973
). An inverse model, literally speaking, is a control process that inverts the plant; that is, the plant converts control signals into motion, so an inverse model converts desired motion into the appropriate control signals (Jordan and Rumelhart, 1992
; Figure 2
A).
Figure 2. (A) Inverse and (B) forward models. The plant takes motor commands and produces movement. The inverse model inverts this process, producing the motor commands that are appropriate for a given movement. A forward model mimics this process, estimating the movement that will be produced by the plant.
The cerebellar floculus is thought by many to implement a form of inverse model (Kawato and Gomi, 1992
, and see also Lisberger, 2009
, for review of these ideas in relation to the smooth pursuit system). While this idea has many adherents, there are also alternative proposals. Perhaps most famously, Llinás (1988)
proposed that the cerebellum is involved in adjusting movement timing to facilitate coordination, rather than in generating compensatory movement commands. Similar ideas have been put forward recently. Specifically, Jacobson et al. (2008)
argued that synchrony and oscillatory activity in the inferior olive are compatible with a cerebellar timing mechanism driven by olivary harmonics. D’Angelo and De Zeeuw (2009)
in contrast, focus on the temporal dynamics of the cerebellar granular layer. A somewhat more eclectic model that also focuses on timing is Braitenberg’s model of the cerebellum as a system for generating sequences of movement in precise time relationship (Braitenberg et al., 1997
). While each of these models can legitimately claim to explain important data, there is no doubt that the inverse model understanding of the cerebellum in CEM is the most widely accepted. We will not consider the other models in developing our own ideas below. The controversy about timing models and adaptation models of the cerebellum has been going on for a long time (Miles and Lisberger, 1981
; Ivry and Keele, 1989
; Simpson et al., 1996
). There are those who believe the two different approaches are mutually compatible (Mauk et al., 2000
). It is not our intention, in any case, to take on this issue.
The inverse model framework can be contrasted with a forward model (Wolpert and Miall, 1996
; Todorov and Jordan, 2002
; See Figure 2
B) which simulates the activity of the plant: it converts the current state and the control signals into a prediction of what the plant will actually do. The bottom line is: inverse models output motor commands and forward models output estimates of state.
The focus on a neural inverse model of the oculomotor plant reflected a perspective that the central problem in oculomotor control is producing the appropriate motor commands once the goal is given. Researchers in other motor systems – notably arm movements – followed in the footsteps of the pioneering work in oculomotor research and focused on the inverse model problem and the question of how appropriate motor commands are generated, given a particular desired movement. This approach was reinforced by the explanatory power of hypothesized desired trajectories (Flash and Hogan, 1985
; Uno et al., 1989
), and the apparent tendency of subjects to correct movements (Shadmehr and Mussa-Ivaldi, 1994
; Donchin et al., 2003
).
However, the possibility that a forward model also plays a role has been hypothesized for a long time (e.g. Wolpert and Miall, 1996
; Kawato, 1999
). One recent radical proposal has been that the system does not work with either a “desired trajectory” or an inverse model (Todorov, 2004
). Under this approach, the problem of predicting the results of motor commands is no less central than the problem of generating those motor commands in the first place. The reason such state prediction is so important is because it allows stable feedback control. Feedback control is the use of the measured or predicted state of the system to generate ongoing motor commands. This form of control can be simpler and more flexible than open-loop control. However, control becomes unstable when it depends on delayed or noisy feedback. Since sensory systems are both slow and noisy, this is inevitably a problem in physiological motor control. A forward model can be faster and less noisy than the full sensory loop. However, predictions of the state must be combined with actual sensory feedback in order for the control loop to remain robust in the face of unpredicted perturbations.
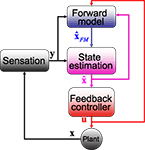
Thus, the framework (which we will call the state-predicting feedback control, SPFC, framework) is built out of three essential building blocks (Figure 3
; Todorov, 2004
; Shadmehr and Krakauer, 2008
). The forward model takes the current estimate of state and the motor commands and produces an initial prediction. The state estimator combines this prediction with actual sensory feedback to produce a better estimate of the current state. The feedback controller uses the current estimate of state in order to decide what motor commands to generate. It either replaces or incorporates the inverse model on which the tradition of Robinson had focused. We propose that this framework is an appropriate description of CEM control and that it can be mapped onto CEM physiology in a manner that is consistent with experimental evidence.
Figure 3. The SPFC framework proposes that a feedback controller is optimized to produce motor commands that achieve task goals. In order to do this effectively, it uses an estimate of the current situation that is derived from a combination of feedback from the sensory system and forward model estimation that depends on efferent copy.
How could such a computational scheme be implemented in the known anatomy and physiology of CEM? The boxology of Figure 3
doesn’t necessarily reflect separate neural stages or nuclei. Nevertheless, Shadmehr and Krakauer (2008)
have recently proposed that neural structures involved in the control of arm movements can, in fact, be mapped onto the control structure described by these boxes. They suggest that motor cortex, in combination with the basal ganglia, implements a feedback controller implementing a control policy that maximizes successful performance. They support this using data from patients with Parkinson’s disease (Mazzoni et al., 2007
), and hemiparesis (Raghavan et al., 2006
). State estimation is hypothesized to occur in parietal cortex based on findings in patients with parietal lesions (Wolpert et al., 1998
). Finally, on the basis of the cerebellar role in in-flight adjustment of saccades (Quaia et al., 2000
) and anticipatory postural adjustments (Nowak et al., 2007
), they claim the forward model is implemented in the cerebellum.
Since the CEM system is located in brain stem nuclei and the cerebellum, and neither motor cortex nor parietal cortex is instrumental, our effort to ascribe computational functions to physiological correlates in the CEM will necessarily produce different results. We will argue that, for CEM, the most suitable mapping would be that the oculomotor nuclei and integrators (Robinson’s “inverse plant”) combine to form a feedback controller. The cerebellar cortex (and not the whole cerebellum) generates a forward model, and the VN combine forward model output with current inputs to produce the state estimate.
The feedback controller maps current estimate of state onto the appropriate motor command. In the language of control system experts, this could be approximated as a transformation

where un is a vector of length ku describing the motor commands at the nth time step. In our case, this would be the command driving the ocular musculature; each element of un represents the activation directed at a single muscle. 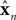 is a vector of length kx describing our current estimate of state; the elements of
is a vector of length kx describing our current estimate of state; the elements of 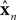 reflect variables like estimated eye position, eye velocity, and possibly include estimated head position and velocity and even desired eye position and velocity. Of course, both the state and the motor vectors could, in reality, be even more complicated. Ln is a function which maps each state onto the appropriate motor command. This mapping need not be linear or fixed in time. The point is that the feedback controller implements a function, L, that translates its input, an estimated state vector,
reflect variables like estimated eye position, eye velocity, and possibly include estimated head position and velocity and even desired eye position and velocity. Of course, both the state and the motor vectors could, in reality, be even more complicated. Ln is a function which maps each state onto the appropriate motor command. This mapping need not be linear or fixed in time. The point is that the feedback controller implements a function, L, that translates its input, an estimated state vector, 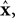 into its output, the motor command vector, u.
into its output, the motor command vector, u.
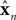 is a vector of length kx describing our current estimate of state; the elements of
is a vector of length kx describing our current estimate of state; the elements of 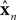 reflect variables like estimated eye position, eye velocity, and possibly include estimated head position and velocity and even desired eye position and velocity. Of course, both the state and the motor vectors could, in reality, be even more complicated. Ln is a function which maps each state onto the appropriate motor command. This mapping need not be linear or fixed in time. The point is that the feedback controller implements a function, L, that translates its input, an estimated state vector,
reflect variables like estimated eye position, eye velocity, and possibly include estimated head position and velocity and even desired eye position and velocity. Of course, both the state and the motor vectors could, in reality, be even more complicated. Ln is a function which maps each state onto the appropriate motor command. This mapping need not be linear or fixed in time. The point is that the feedback controller implements a function, L, that translates its input, an estimated state vector, 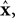 into its output, the motor command vector, u.
into its output, the motor command vector, u.By definition, the output of a controller is motor command so whatever produces the motor commands must necessarily be implementing a controller. In our case, motor command is the activity that drives the muscles, and the motoneurons of the Abducens Nucleus are the output of the feedback controller, at least for horizontal motion. A subtler question regards whether any other related nuclei are also included.
In CEM, the controller must know the desired fixation point and it must receive an estimate of the current eye position. It calculates the vectorial difference between these two and generates motoneuron activity which will move the eye in the direction indicated by this vector. The brainstem circuit that traditionally constitutes the inverse plant meets these requirements (Buttner-Ennever and Buttner, 1992
; Glasauer, 2007
), even though there is debate on how the computation in the plant is achieved (see below). The issue of its input, a state estimate, will be discussed below.
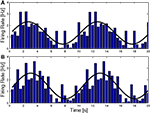
The traditional view is that a displacement or velocity input is directly fed to the abducens output neurons that project to the eye muscles. In order to overcome the low-pass filter properties of the plant, an integrated version of this input is linearly added to the direct projection. The so-called oculomotor integrators are responsible for this indirect pathway (e.g. McFarland and Fuchs, 1992
; Moschovakis, 1997
). Recent work on the NPH, the putative horizontal integrator, undermines this view since neurons in the NPH are found to encode the whole motor command, u, rather than only the integrated part (Green et al., 2007
; Ghasia et al., 2008
), as shown in Figure 4
. This makes the distinction between the NPH and the abducens unclear. One possibility, suggested by Green et al. is that NPH output serves feedback purposes. Indeed, on the basis of the finding that NPH feedback encodes “motor commands,” Green et al. propose that the feedback is updating a cerebellar forward model (see Figure 3
).
Figure 4. NPH neurons (dashed, orange) behave like the motor command, represented by the solid, red curve. The black lines show the activity of a hypothetical neuron that would encode eye position, with a constant gain and phase. NPH and Ab activity were taken from (Green et al., 2007
).
In both the Ab and the NPH, the CEM circuit is shared with the other eye movement systems (i.e. saccades and smooth pursuit). This fits the role of feedback controller, since the efference copy needed by the forward model should contain all oculomotor output in order to produce an optimal estimate of state (see below).
The Forward model updates our previous estimate of state. That is, we can use a forward model to generate an estimate about current state from our earlier estimate and our knowledge of system dynamics. We assume, for the purpose of simplicity, that the actual dynamics of the system can be described as linearly combining previous state and motor command:

x is the actual state, whose estimate is discussed above (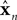 ). Both x and
). Both x and 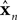 have the same size, but the latter is the brain’s estimate and the former is the actual quantity. A is a kx × kx matrix, B is a kx × kumatrix, and «n is a noise term. Under this assumption, the forward model estimate would be generated from the previous estimate using a similar equation
have the same size, but the latter is the brain’s estimate and the former is the actual quantity. A is a kx × kx matrix, B is a kx × kumatrix, and «n is a noise term. Under this assumption, the forward model estimate would be generated from the previous estimate using a similar equation
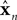 ). Both x and
). Both x and 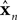 have the same size, but the latter is the brain’s estimate and the former is the actual quantity. A is a kx × kx matrix, B is a kx × kumatrix, and «n is a noise term. Under this assumption, the forward model estimate would be generated from the previous estimate using a similar equation
have the same size, but the latter is the brain’s estimate and the former is the actual quantity. A is a kx × kx matrix, B is a kx × kumatrix, and «n is a noise term. Under this assumption, the forward model estimate would be generated from the previous estimate using a similar equation
where 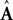 and
and 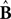 represent the forward model’s estimates of system dynamics. Notice that in this formulation, which is commonly used, the estimate of state used to calculate the forward model is not the same as the estimate produced by the forward model in the previous step. That is, we have
represent the forward model’s estimates of system dynamics. Notice that in this formulation, which is commonly used, the estimate of state used to calculate the forward model is not the same as the estimate produced by the forward model in the previous step. That is, we have 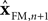 on the left side of the equation but
on the left side of the equation but 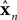 on the right hand side. What we mean by this is that we may improve the estimate generated by the forward model (for instance, by incorporating information from sensory inputs) before we use it in the forward model’s next step. This idea is demonstrated graphically in Figure 3
.
on the right hand side. What we mean by this is that we may improve the estimate generated by the forward model (for instance, by incorporating information from sensory inputs) before we use it in the forward model’s next step. This idea is demonstrated graphically in Figure 3
.
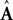 and
and 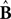 represent the forward model’s estimates of system dynamics. Notice that in this formulation, which is commonly used, the estimate of state used to calculate the forward model is not the same as the estimate produced by the forward model in the previous step. That is, we have
represent the forward model’s estimates of system dynamics. Notice that in this formulation, which is commonly used, the estimate of state used to calculate the forward model is not the same as the estimate produced by the forward model in the previous step. That is, we have 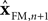 on the left side of the equation but
on the left side of the equation but 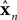 on the right hand side. What we mean by this is that we may improve the estimate generated by the forward model (for instance, by incorporating information from sensory inputs) before we use it in the forward model’s next step. This idea is demonstrated graphically in Figure 3
.
on the right hand side. What we mean by this is that we may improve the estimate generated by the forward model (for instance, by incorporating information from sensory inputs) before we use it in the forward model’s next step. This idea is demonstrated graphically in Figure 3
.One point requires clarification. The figure shows sensory input (black line) reaching the cerebellum in addition to the current estimates of state (purple) and efferent copy (red). This is drawn to reflect the realities described in Figure 1
, which shows that sensory input does reach the cerebellar cortex. This includes retinal input from AOS (which is routed through the inferior olive and climbing fibers) and NRTP (which comes through mossy fibers). It also includes proprioceptive information. Part of the visual input, especially the part arriving through AOS, may play a role in adaptation processes discussed below. On the other hand, sensory input that has a direct effect on cerebellar activity is not entirely consistent with Eq. 3. It may nevertheless be consistent with the cerebellum producing a predictive estimate of state based on all the available information.
We assume that the forward model has no knowledge of the random fluctuations in the state represented by the noise term. However, we expect the forward model to be plastic. That is, if the state prediction of the forward model is consistently wrong the model should change. The cerebellar cortex appears to have all of these characteristics.
It has been amply demonstrated that the cerebellum receives efference copy from many motor systems. Specifically, the cortical area responsible for CEM, the flocculus, receives direct projections from the NPH (Sato et al., 1983
; Langer et al., 1985
; McCrea and Baker, 1985
). Furthermore, it receives a strong input from the VN (Sato et al., 1983
; Langer et al., 1985
; Gerrits et al., 1989
; Barmack et al., 1993
), and we will argue later that this is the most likely candidate for a state estimator.
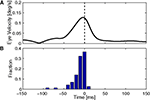
The key issue in claiming that cerebellar cortex produces a forward model is to show that the output uses efference copy to generate an estimate of state. This, we believe, is demonstrated by one important finding. Figure 5
shows that spike triggered averaging (STA) of the eye velocity reveals that the neural activity does not predict or follow the movement with a large latency. Rather, the correlation peaks at a latency close to zero, or even slightly negative (Winkelman and Frens, 2007
). Because the activity does not precede the eye movement, it cannot be causing it. Thus, floccular output is not part of the controller signal. Similarly, because it does not follow the eye movement, it cannot reflect purely sensory information. The flocculus thus processes efferent copy to produce an output that represents the current state faithfully, which is exactly what one expects from the forward model.
Figure 5. Timing of cerebellar activity. (A) Shows a simple spike triggered average of eye velocity in response to white noise optokinetic stimulation. The white noise stimulus was provided by a panaromic projector system and consisted of a hexagonal matrix of green patches that were rotated coherently around the animal according to a three dimensional gaussian white noise process filtered through a 20-Hz low-pass filter. Note that the curve of this neuron peaks slightly before 0 ms, i.e. the P-cell is active slightly after the actual movement. (B) Summarizes the timing of the peak in 71 Purkinje cells, showing activity that more or less coincides with the movement (Winkelman and Frens, 2007
).
Ultimately, state estimation requires combining two sources of information about the current state. The first source of information is the forward model, and the second source is sensory input. In our case, the latter includes vestibular, visual and possibly also proprioceptive inputs.
We can formalize the relationship between state and sensory input using the equation

yn is a vector of length ky whose components reflect all the different inputs from the head and eye. ηn is a noise term reflecting the fact that the activity in our sensory system is not a faithful representation of the state. The function H is meant to characterize the process of sensation.
In engineering applications, these two sources of information about state – the forward model and sensation or observation – are often combined using a Kalman filter

The Kalman filter uses the forward model’s estimate of the next state, 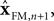 as a basis for the combined estimate. The forward model estimate is modified by the “sensory prediction error,”
as a basis for the combined estimate. The forward model estimate is modified by the “sensory prediction error,” 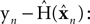 the difference between the actual observation, yn, and the observation expected from our current estimate of state,
the difference between the actual observation, yn, and the observation expected from our current estimate of state, 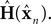 The matrix Kn, of size kx × ky, is called the Kalman gain and it quantifies both the way different sensors are relevant to different aspects of state and the relative reliability of sensation and forward model estimation.
The matrix Kn, of size kx × ky, is called the Kalman gain and it quantifies both the way different sensors are relevant to different aspects of state and the relative reliability of sensation and forward model estimation.
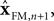 as a basis for the combined estimate. The forward model estimate is modified by the “sensory prediction error,”
as a basis for the combined estimate. The forward model estimate is modified by the “sensory prediction error,” 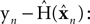 the difference between the actual observation, yn, and the observation expected from our current estimate of state,
the difference between the actual observation, yn, and the observation expected from our current estimate of state, 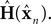 The matrix Kn, of size kx × ky, is called the Kalman gain and it quantifies both the way different sensors are relevant to different aspects of state and the relative reliability of sensation and forward model estimation.
The matrix Kn, of size kx × ky, is called the Kalman gain and it quantifies both the way different sensors are relevant to different aspects of state and the relative reliability of sensation and forward model estimation.In Box 1
, we also explain how sensory delays lead to alternative formulations for state estimation. Whatever the details of the calculation by which state is estimated, a number of essential points can be made regarding its physiological and behavioral correlates. First, sensory estimation is a combination of internal predictions and currently available sensory information. Second, the way those two sources of information are combined should reflect their reliability: if sensory input is noisy, then the system should rely more on the forward model and vice versa. Third, the input/output relations of the system give us insight into the specific calculation being performed.
Box 1
. The Kalman filter and sensory delays
The Kalman filter model is popular in engineering applications in part because it is possible, in certain circumstances, to calculate the optimal value for the Kalman gain, Kn, and, for this value, the estimate produced is as close as possible to the true value of the state. Indeed, properly speaking, Eq. 5 describes a Kalman filter only when the function H(x) is linear and the value of the gain is set to the Kalman gain. However, in the field of motor control the term is often used more loosely.
The Kalman filter updates the estimate of state produced by the forward model, 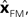 using the discrepancy between our prediction of sensory feedback,
using the discrepancy between our prediction of sensory feedback, 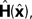 and the actual sensory feedback, y. This discrepancy is often called the sensory prediction error. One concern in using the Kalman filter as a model of the activity of the VN is that there is no evidence that VN actually calculates anything like the sensory prediction error.
In Eq. 5, two different estimates of state are used,
and the actual sensory feedback, y. This discrepancy is often called the sensory prediction error. One concern in using the Kalman filter as a model of the activity of the VN is that there is no evidence that VN actually calculates anything like the sensory prediction error.
In Eq. 5, two different estimates of state are used, 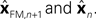 A true Kalman filter, uses only one of these estimates,
A true Kalman filter, uses only one of these estimates, 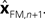 That is:
That is:
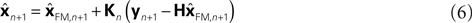 This is because the true Kalman filter doesn’t include sensory delay. In that case, the Kalman filter can be rewritten as a weighted average:
This is because the true Kalman filter doesn’t include sensory delay. In that case, the Kalman filter can be rewritten as a weighted average:
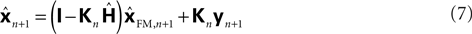 with I signifying the identity matrix. This version of the equation calculates a weighted average of prediction (
with I signifying the identity matrix. This version of the equation calculates a weighted average of prediction (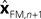 ) and sensation (yn+1) and does not calculate a sensory prediction error (
) and sensation (yn+1) and does not calculate a sensory prediction error (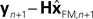 ). This means that a network that calculates a state estimate based on optimal mixing for forward model prediction and noisy sensory data does not need to calculate a sensory prediction error. While this may not make any difference computationally, it does make a difference in terms of our physiological predictions. Eqs 6 and 7 imply a different sort of synaptic connectivity.
It is interesting to consider solutions to the delay problem. If feedback is delayed by d time steps, then
). This means that a network that calculates a state estimate based on optimal mixing for forward model prediction and noisy sensory data does not need to calculate a sensory prediction error. While this may not make any difference computationally, it does make a difference in terms of our physiological predictions. Eqs 6 and 7 imply a different sort of synaptic connectivity.
It is interesting to consider solutions to the delay problem. If feedback is delayed by d time steps, then 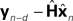 would compare predictions about the current state with sensory information from a while ago (we assume for this discussion that sensation H is linear). One class of solutions which includes the Smith predictor (Wolpert and Miall, 1996
) is to compare the delayed sensation, yn−d, to a delayed state estimate. In the brain, we do not have delay registers, but we can estimate the past state from the current one, or, for that matter from the output of the forward model,
would compare predictions about the current state with sensory information from a while ago (we assume for this discussion that sensation H is linear). One class of solutions which includes the Smith predictor (Wolpert and Miall, 1996
) is to compare the delayed sensation, yn−d, to a delayed state estimate. In the brain, we do not have delay registers, but we can estimate the past state from the current one, or, for that matter from the output of the forward model, 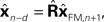 where
where 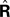 performs backwards linear estimation of the state such as estimating previous position from current position and velocity. Since d is substantial (around 100 ms), the estimating backward using the current output of the state estimate,
performs backwards linear estimation of the state such as estimating previous position from current position and velocity. Since d is substantial (around 100 ms), the estimating backward using the current output of the state estimate, 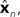 is relatively similar to using the current output of the forward model,
is relatively similar to using the current output of the forward model, 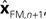 since both are relatively similar compared to
since both are relatively similar compared to 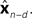 This leads us to a modified Kalman filter
This leads us to a modified Kalman filter
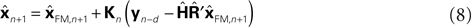 that can also be written as a weighted average
that can also be written as a weighted average
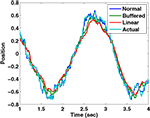
 We have simulated this process using a Kalman filter tracking a particle driven by a sinusoidal force with a frequency of 2 Hz, using a time step of 10 ms. The “normal” filter receives the noisy sensory data with 0 delay; the “buffered” filter receives the sensory data with a 100 ms delay, but keeps track of the last 10 estimates of state and updates them as the delayed sensory information arrives; the “linear estimator” follows Eq. 8. It is clear from Figure B1
that the linear estimator performs nearly as well as the buffered version in this case. The sum squared error of the buffered Kalman filter is 12 times greater than a filter without delay while that of the linear estimation filter is 15 times greater. This shows that a reasonable state estimator can be developed that is based primarily on weighted averages of the forward prediction and sensation, even in cases of significant delay. We suggest that the vestibular nucleus has the characteristics necessary for generating such an estimate.
We have simulated this process using a Kalman filter tracking a particle driven by a sinusoidal force with a frequency of 2 Hz, using a time step of 10 ms. The “normal” filter receives the noisy sensory data with 0 delay; the “buffered” filter receives the sensory data with a 100 ms delay, but keeps track of the last 10 estimates of state and updates them as the delayed sensory information arrives; the “linear estimator” follows Eq. 8. It is clear from Figure B1
that the linear estimator performs nearly as well as the buffered version in this case. The sum squared error of the buffered Kalman filter is 12 times greater than a filter without delay while that of the linear estimation filter is 15 times greater. This shows that a reasonable state estimator can be developed that is based primarily on weighted averages of the forward prediction and sensation, even in cases of significant delay. We suggest that the vestibular nucleus has the characteristics necessary for generating such an estimate.
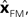 using the discrepancy between our prediction of sensory feedback,
using the discrepancy between our prediction of sensory feedback, 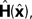 and the actual sensory feedback, y. This discrepancy is often called the sensory prediction error. One concern in using the Kalman filter as a model of the activity of the VN is that there is no evidence that VN actually calculates anything like the sensory prediction error.
In Eq. 5, two different estimates of state are used,
and the actual sensory feedback, y. This discrepancy is often called the sensory prediction error. One concern in using the Kalman filter as a model of the activity of the VN is that there is no evidence that VN actually calculates anything like the sensory prediction error.
In Eq. 5, two different estimates of state are used, 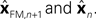 A true Kalman filter, uses only one of these estimates,
A true Kalman filter, uses only one of these estimates, 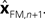 That is:
That is:
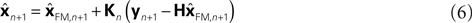 This is because the true Kalman filter doesn’t include sensory delay. In that case, the Kalman filter can be rewritten as a weighted average:
This is because the true Kalman filter doesn’t include sensory delay. In that case, the Kalman filter can be rewritten as a weighted average:
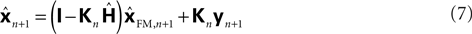 with I signifying the identity matrix. This version of the equation calculates a weighted average of prediction (
with I signifying the identity matrix. This version of the equation calculates a weighted average of prediction (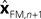 ) and sensation (yn+1) and does not calculate a sensory prediction error (
) and sensation (yn+1) and does not calculate a sensory prediction error (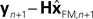 ). This means that a network that calculates a state estimate based on optimal mixing for forward model prediction and noisy sensory data does not need to calculate a sensory prediction error. While this may not make any difference computationally, it does make a difference in terms of our physiological predictions. Eqs 6 and 7 imply a different sort of synaptic connectivity.
It is interesting to consider solutions to the delay problem. If feedback is delayed by d time steps, then
). This means that a network that calculates a state estimate based on optimal mixing for forward model prediction and noisy sensory data does not need to calculate a sensory prediction error. While this may not make any difference computationally, it does make a difference in terms of our physiological predictions. Eqs 6 and 7 imply a different sort of synaptic connectivity.
It is interesting to consider solutions to the delay problem. If feedback is delayed by d time steps, then 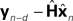 would compare predictions about the current state with sensory information from a while ago (we assume for this discussion that sensation H is linear). One class of solutions which includes the Smith predictor (Wolpert and Miall, 1996
) is to compare the delayed sensation, yn−d, to a delayed state estimate. In the brain, we do not have delay registers, but we can estimate the past state from the current one, or, for that matter from the output of the forward model,
would compare predictions about the current state with sensory information from a while ago (we assume for this discussion that sensation H is linear). One class of solutions which includes the Smith predictor (Wolpert and Miall, 1996
) is to compare the delayed sensation, yn−d, to a delayed state estimate. In the brain, we do not have delay registers, but we can estimate the past state from the current one, or, for that matter from the output of the forward model, 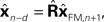 where
where 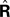 performs backwards linear estimation of the state such as estimating previous position from current position and velocity. Since d is substantial (around 100 ms), the estimating backward using the current output of the state estimate,
performs backwards linear estimation of the state such as estimating previous position from current position and velocity. Since d is substantial (around 100 ms), the estimating backward using the current output of the state estimate, 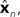 is relatively similar to using the current output of the forward model,
is relatively similar to using the current output of the forward model, 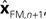 since both are relatively similar compared to
since both are relatively similar compared to 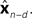 This leads us to a modified Kalman filter
This leads us to a modified Kalman filter
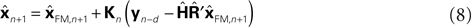 that can also be written as a weighted average
that can also be written as a weighted average
 We have simulated this process using a Kalman filter tracking a particle driven by a sinusoidal force with a frequency of 2 Hz, using a time step of 10 ms. The “normal” filter receives the noisy sensory data with 0 delay; the “buffered” filter receives the sensory data with a 100 ms delay, but keeps track of the last 10 estimates of state and updates them as the delayed sensory information arrives; the “linear estimator” follows Eq. 8. It is clear from Figure B1
that the linear estimator performs nearly as well as the buffered version in this case. The sum squared error of the buffered Kalman filter is 12 times greater than a filter without delay while that of the linear estimation filter is 15 times greater. This shows that a reasonable state estimator can be developed that is based primarily on weighted averages of the forward prediction and sensation, even in cases of significant delay. We suggest that the vestibular nucleus has the characteristics necessary for generating such an estimate.
We have simulated this process using a Kalman filter tracking a particle driven by a sinusoidal force with a frequency of 2 Hz, using a time step of 10 ms. The “normal” filter receives the noisy sensory data with 0 delay; the “buffered” filter receives the sensory data with a 100 ms delay, but keeps track of the last 10 estimates of state and updates them as the delayed sensory information arrives; the “linear estimator” follows Eq. 8. It is clear from Figure B1
that the linear estimator performs nearly as well as the buffered version in this case. The sum squared error of the buffered Kalman filter is 12 times greater than a filter without delay while that of the linear estimation filter is 15 times greater. This shows that a reasonable state estimator can be developed that is based primarily on weighted averages of the forward prediction and sensation, even in cases of significant delay. We suggest that the vestibular nucleus has the characteristics necessary for generating such an estimate.Estimated position and actual position as tracked by three different Kalman filters..
The state estimator receives input from the sensory organs and the forward model. Its output should be a state estimate that reflects more recent sensory input than the forward model.
If we accept that the flocculus generates a forward model, then the input requirements are met by the VN. All floccular output is directed to the VN, and sensory information about the head and eye converges here. As a matter of fact, the VN are quite inappropriately named. Vestibular information is just one of their many inputs.
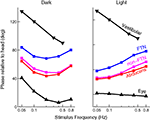
One key study that has looked into the exact properties of the output of the VN is Stahl and Simpson (1995)
. The neurons of the VN can be divided into two groups. They first receive input from the flocculus (FTNs) while the rest, 80% of the neurons in the VN, do not (non-FTNs). The two groups of neurons have distinctly different behaviors, as seen in Figure 6
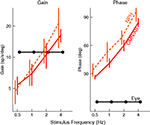
. The firing of the non-FTNs predicts (with almost zero lead) the firing of the neurons in the Abducens Nucleus. This, in combination with the fact that all non-FTNs project to the Abducens Nucleus, suggests that the non-FTNs might be a good candidate for the estimate of state that actually drives the feedback controller. The relationship of the FTNs to sensory (vestibular) input, motor output (Abducens Nucleus) and actual eye movement is more complex. First, the FTNs lead the non-FTNs, suggesting that they are the first step in a two step computation, or perhaps an earlier step in a complex computation. Roughly 60% do not project to the midbrain Stahl and Simpson (1995)
. Second, the relationship of FTN activity to actual eye movement is better in the dark than in the light, consistent with the idea that FTN activity reflects the predictions of a forward model which has a greater influence on the controller when sensory input is compromised. This suggestion is reinforced by the fact that the difference between light and dark nearly disappears when target velocity and acceleration are increased (the target oscillates at a higher frequency) because in these situations, the vestibular input is much more reliable than visual input, and so the importance of the forward model would not be different in the light and the dark.
Figure 6. Timing of activity of FTNs in the VN, compared to non-FTNs, Abducens nucleus, vestibular efferents, and the actual eye movement. All phases are given with respect to a vestibular stimulus that was either given in the dark (left panel), or in the light (right panel). Data from Stahl and Simpson (1995
).
Finally, the notion that these neurons carry the full 3D properties of the eye movement, while the actual motor command itself does not, suggests that the VN carries an estimate of state rather than a motor command (Ghasia et al., 2008
). This picture can be further complicated by a consideration of coordinate systems. Roy and Cullen (2004)
show that activity of vestibular neurons – that normally reflects gaze shifts – is suppressed during gaze shifts involving active head movements. This is consistent with the idea that the vestibular nucleus activity reflects the activity of a forward model incorporating efferent copy of commands to the neck muscles. It also has important repercussions for the coordinate system of representation. Cancellation of vestibular nucleus activity during active head movements suggests that vestibular nucleus activity reflects the position of the eyes in the head rather than the position of eyes in extrinsic space.
Only one more point needs to be made on the theoretical level. This concerns the issue of adaptation. In many control systems, the plant, the environment and the sensory system are not really fixed in time. For instance, in the case of eye movements, the physiological fluctuations in muscle strength change the effects of motor commands and putting on glasses (which change visual magnification and have different characteristics in different parts of visual space) or contact lenses (which change the weight of the eye) can change the way movements of the eye affect visual input. In such situations, the controller must adapt to changes in the plant. Generally, this may require adaptation of all three major components of the system. It is possible that the different forms of adaptation happen simultaneously: the forward model changes in response to sensory prediction error; the sensory prediction optimally re-weights sensation and prediction; the feedback controller adjusts the motor commands associated with the current state. Adaptation in nervous circuitry is generally supported by neural plasticity. Thus, we must be clear, when we discuss physiological correlates, to specify where we think plasticity may be taking place, and which neurons carry the signals that drive the plasticity and in what coordinates these signals are represented.
The mechanisms of plasticity of the cerebellar cortex have been well studied. The most widespread hypothesis is that climbing fibre (CF) projections (that produce Purkinje cell complex spikes) encode errors that modify the PF-PC synapses through LTD (Ito, 1986
, 2006
; Simpson et al., 1996
). There is evidence for other forms of plasticity as well (Hansel et al., 2001
; Coesmans et al., 2004
). Nonetheless, many researchers accept the role of the CF as a teacher signal.
If we accept that CF activity carries some form of error signal that drives plasticity, we must face the question of what sort of error it really carries. Until recently, CF projection to the flocculus was thought to contain retinal slip signals. This would be appropriate if the flocculus was calculating an inverse model. On the other hand, such a signal is not optimal for modifying a forward model (FM). Adaptation in a forward model should reduce discrepancies between the estimated and the actual state; it should adapt in response to an error that reflects such discrepancies. Consequently the CF should report unexpected retinal slip rather than any retinal slip (See Figure 7
for an example). Such signals have been found in the flocculus (Frens et al., 2001
; Winkelman and Frens, 2006
), as well as in the visual pathways projecting to the Inferior Olive (Ilg and Hoffmann, 1991
, 1996
).
Figure 7. Complex spike (CS) Modulation as a result of sinusoidal optokinetic stimulation. In (A) the stimulus was an oscillating pattern. In (B) the same pattern moved transparently over a static background. The behavior of the animal varied with the relative luminances of the moving and the static pattern. The frequency of the fi tted sine wave equals the frequency of the stimulus (0.1 Hz). Note that the modulation in (A) and (B) is virtually identical, as are the CEM made by the animal (gain 0.60 and 0.58, respectively). Consequently the predicted slip (caused by the eye movement over the static pattern) is not reflected in the CS (Frens et al., 2001
).
Plasticity in the VN (Pugh and Raman, 2006
, 2009
), guided by the cerebellar projection may be the mechanism underlying the weighting required for the optimal state estimation proposed in Box 1
. In a recent paper, Beraneck et al. (2008)
showed that early recovery of the VOR from labyrinthectomy is cerebellar independent while later recovery is cerebellar dependent. Of course, this argues strongly for non-cerebellar mechanisms of plasticity in the CEM system. Additionally, it allows our model to make a prediction. Beraneck et al. suggest that the early, non-cerebellar recovery reflects plasticity in the vestibular nucleus. Our model suggests that this may result from a reweighting of the different inputs to the state estimator. Indeed, our model makes a strong prediction: the early stage of recovery from VOR will not depend on calculations related to the forward model while the later stage will have such a dependence.
We were not able to find any studies of addressing the possibility of plasticity in the Ab or NPH. However, gaze stability is affected by VOR adaptation, and one reasonable explanation for this would be adaptation of the gain of the oculomotor integrator (Tiliket et al., 1994
).
We propose that CEM are generated by a SPFC framework where specific functional roles can be ascribed to specific nuclei in the CEM circuitry. The strength of the SPFC framework has been demonstrated by many groups (Wolpert and Miall, 1996
; Todorov and Jordan, 2002
; Shadmehr and Krakauer, 2008
). Recently, it has also been applied to describe eye movements (Glasauer, 2007
; Ghasia et al., 2008
). Because the physiology and anatomy underlying CEM is relatively well known, we are able to describe this mapping in more detail and with more precision than was possible in a similar attempt to describe the control of reaching movements (Shadmehr and Krakauer, 2008
). The timing and nature of the signals that can be recorded in the flocculus, the VN, and the brainstem structures support our hypothesis. Also, plasticity in the flocculus and in the VN and the purported olivary error signals can be understood in terms of this framework.
Our model can be contrasted with the classical approach, where the output of the cerebellum is an inverse model (Kawato and Gomi, 1992
). The difference in the role played in the cerebellar output is, perhaps, the most salient difference between the two approaches, but there are other differences as well. For instance, the classical approach does not explain the separate function of the three different areas – flocculus, vestibular nucleus, and brainstem motor nuclei – that generate a cascading series of motor commands. In contrast, the SPFC framework ascribes clear and distinct functions to each of these areas.
However, making an experimental distinction between the output of a forward model and the output of an inverse model can be quite difficult. Work by Kawato’s group has shown that position, velocity and acceleration regress onto firing rate with a combined r2 of above 0.7 (Shidara et al., 1993
). This has been widely regarded as evidence that the cerebellum implements an inverse model. However, in follow up work, the Kawato group disavows this idea and claims that the floccular output cannot represent the main part of the motor command to the eyes (Gomi et al., 1998
). Perhaps the two most convincing arguments in this respect come from our group and that of Dora Angelaki, as described above. Both of these lines of reasoning argue in favor of the forward model interpretation.
Our model enjoys a family resemblance with previously presented schemes, notably the Shadmehr and Krakauer (2008)
model of reaching movement control and the Green et al. (2007)
model for CEM. However, there are also key differences between our model and the others. Perhaps the most notable difference between our model and the Green et al. model is their suggestion that the vestibular nucleus implements an inverse model. One key issue in this regard is whether the output of the vestibular nucleus describes the upcoming motor command or the current estimate of state. Because CEM do not obey Listing’s law, the use of the representation of violation of Listing’s law (as was used to great effect in Ghasia et al., 2008
) to separate motor commands from state estimates cannot be used in this system. Nevertheless, (1) Ghasia et al. (2008)
do suggest that many neurons in the vestibular nucleus represent state, and (2) if the vestibular nucleus is implementing an inverse model and the flocculus is implementing a forward model, it is unclear where state and prediction should be combined.
Our model is also different from the one used by Shadmehr and Krakauer to describe reaching movements (Shadmehr and Krakauer, 2008
). Shadmehr and Krakauer suggest that the output of the deep cerebellar nuclei (DCN) reflects the output of a forward model ( ). This is necessary in their scheme because they propose, based on evidence from errors in reaching movements, that the parietal cortex calculates an estimate of state, and thus they propose that the forward model output from the cerebellum should drive this estimate of state. One might say that the DCN is considered the output of the forward model because it more directly projects to the cortex, although the role of the ventrolateral thalamus – which relays the DCN projection to cortex – is not considered in their framework. In our system, the VN seem to be located appropriately to combine forward model prediction based on efferent feedback with delayed sensory information. The VN are analogues of the DCN. Thus, in our system, it is not the cerebellum but specifically the cerebellar cortex which generates a forward model prediction. This difference between our hypothesis and that of Shadmehr and Krakauer might arise for a number of reasons as both models are speculative. Shadmehr and Krakauer did not consider the cerebellar cortex and DCN separately or ascribe any role at all to the thalamus relay station. Our model is more comprehensive, primarily because we are considering a simpler system. However, it is possible that the computation carried out by the cerebellum in the two systems is different and both models are correct.
). This is necessary in their scheme because they propose, based on evidence from errors in reaching movements, that the parietal cortex calculates an estimate of state, and thus they propose that the forward model output from the cerebellum should drive this estimate of state. One might say that the DCN is considered the output of the forward model because it more directly projects to the cortex, although the role of the ventrolateral thalamus – which relays the DCN projection to cortex – is not considered in their framework. In our system, the VN seem to be located appropriately to combine forward model prediction based on efferent feedback with delayed sensory information. The VN are analogues of the DCN. Thus, in our system, it is not the cerebellum but specifically the cerebellar cortex which generates a forward model prediction. This difference between our hypothesis and that of Shadmehr and Krakauer might arise for a number of reasons as both models are speculative. Shadmehr and Krakauer did not consider the cerebellar cortex and DCN separately or ascribe any role at all to the thalamus relay station. Our model is more comprehensive, primarily because we are considering a simpler system. However, it is possible that the computation carried out by the cerebellum in the two systems is different and both models are correct.
 ). This is necessary in their scheme because they propose, based on evidence from errors in reaching movements, that the parietal cortex calculates an estimate of state, and thus they propose that the forward model output from the cerebellum should drive this estimate of state. One might say that the DCN is considered the output of the forward model because it more directly projects to the cortex, although the role of the ventrolateral thalamus – which relays the DCN projection to cortex – is not considered in their framework. In our system, the VN seem to be located appropriately to combine forward model prediction based on efferent feedback with delayed sensory information. The VN are analogues of the DCN. Thus, in our system, it is not the cerebellum but specifically the cerebellar cortex which generates a forward model prediction. This difference between our hypothesis and that of Shadmehr and Krakauer might arise for a number of reasons as both models are speculative. Shadmehr and Krakauer did not consider the cerebellar cortex and DCN separately or ascribe any role at all to the thalamus relay station. Our model is more comprehensive, primarily because we are considering a simpler system. However, it is possible that the computation carried out by the cerebellum in the two systems is different and both models are correct.
). This is necessary in their scheme because they propose, based on evidence from errors in reaching movements, that the parietal cortex calculates an estimate of state, and thus they propose that the forward model output from the cerebellum should drive this estimate of state. One might say that the DCN is considered the output of the forward model because it more directly projects to the cortex, although the role of the ventrolateral thalamus – which relays the DCN projection to cortex – is not considered in their framework. In our system, the VN seem to be located appropriately to combine forward model prediction based on efferent feedback with delayed sensory information. The VN are analogues of the DCN. Thus, in our system, it is not the cerebellum but specifically the cerebellar cortex which generates a forward model prediction. This difference between our hypothesis and that of Shadmehr and Krakauer might arise for a number of reasons as both models are speculative. Shadmehr and Krakauer did not consider the cerebellar cortex and DCN separately or ascribe any role at all to the thalamus relay station. Our model is more comprehensive, primarily because we are considering a simpler system. However, it is possible that the computation carried out by the cerebellum in the two systems is different and both models are correct.One important aspect of the Shadmehr and Krakauer analysis of the reaching movement system has to do with the role they ascribe to the basal ganglia in determining the mapping of estimated state to motor command. Their framework explicitly uses the language of optimal feedback control, popularized in our field by Todorov (2004)
. In optimal feedback control, the controller produces a command which will lead to the best possible combination of task success and energy conservation. In different tasks or with different weight attached to energy conservation, the controller will map states onto motor commands differently. In the scheme put forward by Shadmehr and Krakauer, the role of the basal ganglia is to work with the motor cortex to learn to produce such optimal motor commands. There is no equivalent of the basal ganglia in the CEM system, and it is quite possible that the CEM does not implement an optimal controller: the CEM system is a reflex system and the cost function may be very consistent relative to the costs associated with reaching movements in different tasks.
Another way in which our model differs from previous theories is that we explicitly reject the widespread hypothesis that state estimation is computed using a Kalman filter (see Box 1
). Rather, it seems that the VN calculation of current state reflects a process with two or more stages, where floccular target neurons perform a first stage of estimation and are then integrated into the broader calculation. The use of a forward model is useful when sensory signals are either noisy or have a large delay. The latter is specifically the case for the retinal slip signals that drive the visual component of CEM (the OKR), which have a delay of 80 ms, whereas the vestibular afferents have a delay of only a few ms. This may explain why lesions of the flocculus primarily affect the OKR, and only influence the plasticity of the VOR, but not its performance (Waespe et al., 1983
; Van Neerven et al., 1989
).
Although the CEM circuit is well studied, there are still many holes in our knowledge. For instance, the projections of the VN are only beginning to be understood. It is known that different VN neurons project to the brain stem and to the flocculus. Perhaps the VN calculates two different state estimates or perhaps its projection forward to the brain stem motor nuclei includes partial calculation of the motor command. Resolving this issue will need to wait until more data is available.
Also the finding that there are neurons at two levels of signal processing that strongly resemble the firing of the Abducens (the non-FTNs in the VN, Stahl and Simpson, 1995
, and the cells in the NPH Green et al., 2007
) requires further experimentation, for instance during eye movements that are mechanically perturbed.
Plasticity in the Abducens Nucleus or NPH is a key prediction of this model. An SPFC framework cannot successfully adapt to changes in the plant unless the feedback controller can adapt. Since recent findings have obscured the functional difference between Abducens Nucleus and NPH (Green et al., 2007
; Ghasia et al., 2008
), one tempting hypothesis is that NPH serves as the adaptive component of the feedback controller. However, this is only speculation until some data on plasticity in the two nuclei becomes available.
Similarly, the difference between foveate and afoveate species should be addressed. Foveate species have smooth pursuit, which they can use to voluntarily reduce retinal slip. In the afoveate rabbit, for instance, in an experimental paradigm, where the visual environment rotates along with a vestibular stimulus, the VN modulate only at high frequencies, along with the actual eye movement (Stahl and Simpson, 1995
). In the (foveate) primate, this correlation is less robust (Miles, 1974
; Waespe and Henn, 1978
), since the smooth pursuit system can modify the eye movements. Thus, the VN appear to represent an estimate of the eye state faithfully in the rabbit (because CEM are the only eye movements present), but this relation is harder to study in primates, since CEM and SP are harder to distinguish.
In sum, we believe that the SPFC model for the CEM accounts for the available data on the anatomy and physiology of the brain areas involved. It solves important conundrums, especially the timing of the activity of P-cells involved in CEM. While the model remains speculative, it seems to us to be the most reasonable basis for continued exploration of the neural mechanisms involved in stabilizing the eye during fixation.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Part of this work was funded by the Israeli Science Foundation, grant number 624/06 (Opher Donchin), and the NWO-VIDI program (Maarten A Frens).