1
Adaptive and Regenerative Software Systems, Department of Computer Science and Electrical Engineering, Rostock, Germany
2
Laboratory of Cognitive Neuroscience, Brain Mind Institute, Swiss Federal Institute of Technology, Lausanne, Switzerland
3
Department of Neurology, University Hospital, Geneva, Switzerland
Neurological evidence suggests that disturbed vestibular processing may play a key role in triggering out-of-body experiences (OBEs). Little is known about the brain mechanisms during such pathological conditions, despite recent experimental evidence that the scientific study of such experiences may facilitate the development of neurobiological models of a crucial aspect of self-consciousness: embodied self-location. Here we apply Bayesian modeling to vestibular processing and show that OBEs and the reported illusory changes of self-location and translation can be explained as the result of a mislead Bayesian inference, in the sense that ambiguous bottom-up signals from the vestibular otholiths in the supine body position are integrated with a top-down prior for the upright body position, which we measure during natural head movements. Our findings have relevance for self-location and translation under normal conditions and suggest novel ways to induce and study experimentally both aspects of bodily self-consciousness in healthy subjects.
Out-of-body experiences (OBEs) are illusions, where people experience themselves as being located outside their physical body (disembodied self-location) and often report sensations of flying and to see the world from an elevated perspective. Investigating such neurological conditions is a promising approach to study the neuronal basis of the bodily self and might facilitate the development of neurobiological models of bodily self-consciousness (Ehrsson, 2007
; Lenggenhager et al., 2007
; Metzinger, 2008
; Vogeley and Fink, 2003
; Vogeley et al., 2004
). This has been demonstrated in recent experiments where key aspects of the bodily self (self-location and self-identification) have been manipulated experimentally (Ehrsson, 2007
; Lenggenhager et al., 2007
; Mizumoto and Ishikawa, 2005
), but further conceptual advances depend on explicitly modeling aspects of the bodily self.
For almost every sensory system, the bottom-up signals from the sensory periphery are ambiguous and need to be disambiguated based on previous experience (see Poggio et al., 1985
for a prominent example in vision). Such a disambiguation could be done in computationally different ways. For example, it could be computed close to the sensory periphery, where previous experience may have shaped neuronal circuits such that the interpretation of the ambiguous sensory signals is always biased towards the same most plausible interpretation. Other disambiguations have to be flexible if they depend on the particular context via, for example, signals from other modalities or the recent history of sensory stimulation. Top-down signals, which could change more rapidly than less adaptive processes closer to the sensory periphery, are a possible mechanism for the latter kind of computation.
The signals from the otholithic vestibular system are inherently ambiguous, because the otholiths cannot distinguish between gravity and acceleration. Since subjects are usually moving in their environment, the brain has to continuously disambiguate these signals. The way the brain performs this computation is currently not completely known. In order to estimate self-motion, however, the brain probably integrates vestibular bottom-up and top-down signals derived from, for example, other gravitoreceptors in the body, from the visual system (MacNeilage et al., 2007
), and at a subcortical level probably also from the semicircular canals (Angelaki et al., 2001
). The Bayesian approach is a natural framework to model this integration and has become a widely accepted analogy to information processing in the brain (Friston, 2005
; Knill and Richards, 1996
; Pouget et al., 2003
; Rao and Ballard, 1999
) as it is supported by experimental (Ernst and Banks, 2002
; Körding and Wolpert, 2004
; MacNeilage et al., 2007
; van Beers et al., 1996
) and theoretical studies relating it to neuronal activations (Denève et al., 2007
; Huys et al., 2007
; Ma et al., 2006
; Rao, 2004
; Sahani and Dayan, 2003
).
Here we apply the Bayesian approach to model the brain’s processing of vestibular signals (see also Laurens and Droulez, 2007
) as such processing has been proposed to encode not just location and movements of one’s body, but also aspects of the self such as self-location and the first-person perspective. Neurological evidence showed that the occurrence of OBEs in neurological patients is associated with disturbed otholithic processing (Blanke and Mohr, 2005
). The experienced spatial location of the self (self-location) is a key aspect of (self) consciousness (Blanke et al., 2004
), and it likely depends on self-motion signals like the vestibular signals via, for example, path integration mechanisms (McNaughton et al., 2006
). Recent behavioural and neuroimaging research has utilized the illusory characteristics of disembodied self-location during OBE to design experiments for the study of embodied self-location under normal conditions (Arzy et al., 2006
; Blanke et al., 2005
; Ehrsson, 2007
; Lenggenhager et al., 2007
). Using virtual reality, these studies showed that self-location can be manipulated systematically by multisensory mismatch of bodily information (Ehrsson, 2007
; Lenggenhager et al., 2007
) and that self-location depends on temporoparietal activity (Arzy et al., 2006
) compatible with neurological data (Blanke et al., 2004
; De Ridder et al., 2007
; Devinsky et al., 1989
; Maillard et al., 2004
). Here, we propose that OBEs and associated illusory changes in self-location can be explained as the result of a mislead Bayesian inference, in the sense that the ambiguous bottom-up signals from the vestibular otholiths in the supine body position are integrated with a top-down prior for the upright body position, which is not appropriate for the current (supine) body position.
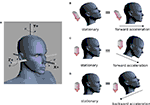
We then show that the variances of the top-down priors for the head acceleration and pitch rotation are crucially affecting an inferred illusory self-translation, which here we identify with pathological self-location. We measure these variances via analyzing natural head movements and find that illusory self-translations are predicted especially for subjects engaged in rapid sport-like activities, but less so for slowly walking or stationary subjects. Collectively, our results suggest a solid interpretation for pathological self-location and other vestibular illusions during OBEs. These findings also have relevance for embodied self-location under normal conditions and suggest novel ways to induce and study experimentally this crucial aspect of bodily self-consciousness in healthy subjects.
In order to obtain quantitative estimates of the top-down prior information for the upright position, we instructed nine subjects (seven male, age 29 ± 4) to perform three kinds of natural movements for a duration of 4–5 min each. In the standing condition, the subjects were standing and moved only their head and partly the upper torso in order to inspect all locations surrounding them. In the waiting condition, subjects walked continuously around the capture area (3 m × 3 m) as if they were waiting and looking for someone on a plaza. In the action condition, subjects were instructed to move as if they were playing tennis, such that they serve, play with the forehand and backhand, make fast movements to the net, etc.
Subjects were wearing a headband, on which we mounted n = 4 infrared markers. Each condition started with a period of 5 s, during which the subjects were standing and looking straight ahead. The time-averaged three-dimensional coordinates of the markers recorded during this period were then used as the base pose xi, i = 1,…, n. The base pose was translated such that 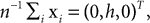 where we set h = 15 cm for all subjects. In other words, the base pose was shifted to the origin in the horizontal plane and 15 cm along the vertical axis. This way, rotations and translations of the base pose are relative to the approximate center of the head. We also used larger and smaller values of h, but the measured statistics did not depend strongly on these choices of h. As a recording device we used a ReActor 2 motion capture system (Ascension Technology) operating at a sampling rate of 30 Hz.
where we set h = 15 cm for all subjects. In other words, the base pose was shifted to the origin in the horizontal plane and 15 cm along the vertical axis. This way, rotations and translations of the base pose are relative to the approximate center of the head. We also used larger and smaller values of h, but the measured statistics did not depend strongly on these choices of h. As a recording device we used a ReActor 2 motion capture system (Ascension Technology) operating at a sampling rate of 30 Hz.
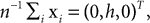 where we set h = 15 cm for all subjects. In other words, the base pose was shifted to the origin in the horizontal plane and 15 cm along the vertical axis. This way, rotations and translations of the base pose are relative to the approximate center of the head. We also used larger and smaller values of h, but the measured statistics did not depend strongly on these choices of h. As a recording device we used a ReActor 2 motion capture system (Ascension Technology) operating at a sampling rate of 30 Hz.
where we set h = 15 cm for all subjects. In other words, the base pose was shifted to the origin in the horizontal plane and 15 cm along the vertical axis. This way, rotations and translations of the base pose are relative to the approximate center of the head. We also used larger and smaller values of h, but the measured statistics did not depend strongly on these choices of h. As a recording device we used a ReActor 2 motion capture system (Ascension Technology) operating at a sampling rate of 30 Hz.Using this system, we measured for each time the translation and rotation of the recorded marker position relative to the base pose. While a few commercial products are available for this computations, we decided to implement our own postprocessing, since the implementation details are often only poorly documented. Details of our prostprocessing, which intentionally does not apply any temporal smoothing, are documented in the Supplementary Material.
The Otholiths as Gravitoinertial Sensors
We model the afferent signals as if coming from a single device sensing the gravitoinertial acceleration f = g −a , where g = (0,−9.81 m/s2,0)T is the gravitational vector and a is the acceleration of the head, i.e. −a is the inertial acceleration. Each of the vectors f, g and a are given in world-coordinates. In order to obtain the gravitoinertial acceleration x sensed by the otholiths, f needs to be transformed into the coordinate system of the head, which we assume to be a rotated version of the world-coordinate system. This transformation depends on the orientation of the head, which we always describe in terms of yaw, pitch and roll angles (see Materials and Methods for details). Let the rotation of the head be given by a pure rotation matrix R, such that R−1 = RT. Then, with
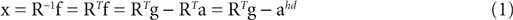
one obtains the sensed gravitoinertial acceleration x in head-coordinates. With ahd = RTa we refer to the acceleration of the head in head-centered coordinates. The conventions for the coordinate system and rotation angles are shown in Figure 1
A.
Figure 1. Conventions and illustration of otholith ambiguities. (A) We use a right-handed coordinate system with the y-axis pointing up. The yaw, pitch and roll angles are denoted by −π ≤ θ ≤ π,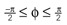 and
and 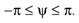 We follow the Fick-gimbal convention, where we first carry out the yaw rotation, then the pitch rotation in the rotated coordinate system, and finally the roll rotation in the coordinate system already rotated by yaw and pitch. The head is shown with θ = 0, φ = 0 and ψ = 0. Positive pitch corresponds to an upward tilt. (B–D) Illustration of three otholith ambiguities. In a stationary backward tilt, (B), the bending of the hair cells is the same as in an upright position with forward acceleration as it is the case for a stationary backward tilt and a forward acceleration in an upright position, (C), and for the stationary upright position and a forward acceleration with a forward tilt, (D) (see text for further detail).
We follow the Fick-gimbal convention, where we first carry out the yaw rotation, then the pitch rotation in the rotated coordinate system, and finally the roll rotation in the coordinate system already rotated by yaw and pitch. The head is shown with θ = 0, φ = 0 and ψ = 0. Positive pitch corresponds to an upward tilt. (B–D) Illustration of three otholith ambiguities. In a stationary backward tilt, (B), the bending of the hair cells is the same as in an upright position with forward acceleration as it is the case for a stationary backward tilt and a forward acceleration in an upright position, (C), and for the stationary upright position and a forward acceleration with a forward tilt, (D) (see text for further detail).
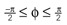 and
and 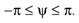 We follow the Fick-gimbal convention, where we first carry out the yaw rotation, then the pitch rotation in the rotated coordinate system, and finally the roll rotation in the coordinate system already rotated by yaw and pitch. The head is shown with θ = 0, φ = 0 and ψ = 0. Positive pitch corresponds to an upward tilt. (B–D) Illustration of three otholith ambiguities. In a stationary backward tilt, (B), the bending of the hair cells is the same as in an upright position with forward acceleration as it is the case for a stationary backward tilt and a forward acceleration in an upright position, (C), and for the stationary upright position and a forward acceleration with a forward tilt, (D) (see text for further detail).
We follow the Fick-gimbal convention, where we first carry out the yaw rotation, then the pitch rotation in the rotated coordinate system, and finally the roll rotation in the coordinate system already rotated by yaw and pitch. The head is shown with θ = 0, φ = 0 and ψ = 0. Positive pitch corresponds to an upward tilt. (B–D) Illustration of three otholith ambiguities. In a stationary backward tilt, (B), the bending of the hair cells is the same as in an upright position with forward acceleration as it is the case for a stationary backward tilt and a forward acceleration in an upright position, (C), and for the stationary upright position and a forward acceleration with a forward tilt, (D) (see text for further detail).The same sensed gravitoinertial acceleration could be produced by a multitude of head rotations and accelerations. Figures 1
B–D illustrate such ambiguities. For example, based only on the otholith signals the brain cannot distinguish between a stationary backward tilt and an upright body position with a forward acceleration (Figure 1
B). This ambiguity plays a key role in our explanation of illusory self-motion as reported in OBEs. If subjects are in a supine body position, but they internally assume to be upright, then the brain’s “explanation” for the sensory-bottom up signals consistent with the upright body position is a forward acceleration. Figures 1
C,D illustrate two other ambiguities for the stationary upright body position.
The Effect of a Non-Appropriate Upright Prior – Model
We consider the acceleration of the head, ahd, in the head-centered coordinate system and the rotation of the head, R, relative to gravity as the two relevant so-called hidden variables, which the brain may use to account for the sensed gravitoinertial acceleration. Given a particular sensed gravitoinertial acceleration x, the posterior for the two hidden variables is obtained by Bayes’ rule as
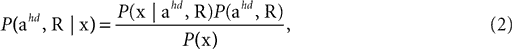
where
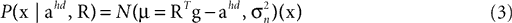
is the likelihood, which describes the way the two hidden variables give rise to a sensed gravitoinertial acceleration x. In other words, it is a forward model of the sensory signals, where we assume that these signals are perturbed by additive Gaussian noise. Here, N(μ, σ2)(x) denotes a Gaussian probability density with mean μ and covariance matrix σ2I evaluated at x. P(ahd, R) is the top-down prior assumed before any sensory signals are observed, and P(x) is the overall probability of x. When comparing different possible explanations of a particular value of x (in terms of values for ahd and R), P(x) becomes a constant factor not affecting such a comparison.
We now consider the case, where ahd and x are vectors in the xy-plane (see Figure 1
A), and the rotation matrix implementing only pitch rotations. We first set 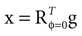 to the stimulation corresponding to a stationary upright position. In this case, the otholith signals do not distinguish between the correct stationary upright position and other alternatives (Figures 1
C,D).
to the stimulation corresponding to a stationary upright position. In this case, the otholith signals do not distinguish between the correct stationary upright position and other alternatives (Figures 1
C,D).
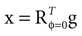 to the stimulation corresponding to a stationary upright position. In this case, the otholith signals do not distinguish between the correct stationary upright position and other alternatives (Figures 1
C,D).
to the stimulation corresponding to a stationary upright position. In this case, the otholith signals do not distinguish between the correct stationary upright position and other alternatives (Figures 1
C,D).For such a sensory stimulus, the likelihood for the accelerations in the x- and y-direction in head-centered coordinates are shown in the first two panels of Figure 2
A. In the first panel, the likelihood is plotted for no acceleration in the y-direction. The combination of the true values with no pitch, φ = 0, and no acceleration,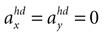 , has the highest likelihood. However, high values are also assigned to combinations with φ < 0 and
, has the highest likelihood. However, high values are also assigned to combinations with φ < 0 and 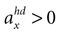 (forward tilt and forward acceleration) and φ > 0 and
(forward tilt and forward acceleration) and φ > 0 and 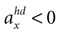 (backward tilt and backward acceleration). The second panel shows the likelihood with
(backward tilt and backward acceleration). The second panel shows the likelihood with 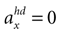 and varying acceleration in the y-direction. Again, high values are assigned to the true parameter combination with φ = 0 and
and varying acceleration in the y-direction. Again, high values are assigned to the true parameter combination with φ = 0 and 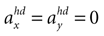 . However, an upside-down rotation of the head, φ = ±π, with an acceleration of
. However, an upside-down rotation of the head, φ = ±π, with an acceleration of 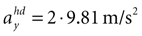 is also consistent with the stationary upright position and no forward acceleration.
is also consistent with the stationary upright position and no forward acceleration.
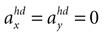 , has the highest likelihood. However, high values are also assigned to combinations with φ < 0 and
, has the highest likelihood. However, high values are also assigned to combinations with φ < 0 and 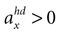 (forward tilt and forward acceleration) and φ > 0 and
(forward tilt and forward acceleration) and φ > 0 and 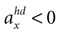 (backward tilt and backward acceleration). The second panel shows the likelihood with
(backward tilt and backward acceleration). The second panel shows the likelihood with 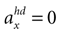 and varying acceleration in the y-direction. Again, high values are assigned to the true parameter combination with φ = 0 and
and varying acceleration in the y-direction. Again, high values are assigned to the true parameter combination with φ = 0 and 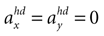 . However, an upside-down rotation of the head, φ = ±π, with an acceleration of
. However, an upside-down rotation of the head, φ = ±π, with an acceleration of 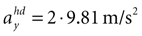 is also consistent with the stationary upright position and no forward acceleration.
is also consistent with the stationary upright position and no forward acceleration.Figure 2. The effect of an upright prior. (A) The first two panels show the likelihoods for the pitch angle φ and the accelerations in the x- and y-directions in head-centered coordinates for a sensory stimulus x corresponding to the upright position. The third panel shows the prior for these accelerations and the pitch angle. The last three panels show the posteriors with different variables being integrated over. (B) Panel order is the same as in (A), but for a sensory stimulus x corresponding to the supine position with 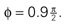 All priors are Gaussians with zero mean and σx = σy = 1 and σφ = 0.1. For the sensory noise we set σn = 1.
All priors are Gaussians with zero mean and σx = σy = 1 and σφ = 0.1. For the sensory noise we set σn = 1.
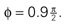 All priors are Gaussians with zero mean and σx = σy = 1 and σφ = 0.1. For the sensory noise we set σn = 1.
All priors are Gaussians with zero mean and σx = σy = 1 and σφ = 0.1. For the sensory noise we set σn = 1.The last three panels in Figure 2
A show the posterior for the two hidden variables, where we have integrated over 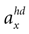 ,
,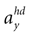 and φ, respectively. In other words, the last three panels are different views of the information one obtains about the state of the head in terms of the pitch φ and acceleration ahd, if the sensory data x is combined with the top-down prior. Here, the posterior assigns a high value to the true parameter combination. This is the expected result, because we set the sensory data x to a value corresponding to a stationary upright position, and the top-down prior implemented the assumption of a stationary upright position. In this scenario, there is no conflict between the sensory data and the top-down prior.
and φ, respectively. In other words, the last three panels are different views of the information one obtains about the state of the head in terms of the pitch φ and acceleration ahd, if the sensory data x is combined with the top-down prior. Here, the posterior assigns a high value to the true parameter combination. This is the expected result, because we set the sensory data x to a value corresponding to a stationary upright position, and the top-down prior implemented the assumption of a stationary upright position. In this scenario, there is no conflict between the sensory data and the top-down prior.
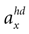 ,
,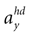 and φ, respectively. In other words, the last three panels are different views of the information one obtains about the state of the head in terms of the pitch φ and acceleration ahd, if the sensory data x is combined with the top-down prior. Here, the posterior assigns a high value to the true parameter combination. This is the expected result, because we set the sensory data x to a value corresponding to a stationary upright position, and the top-down prior implemented the assumption of a stationary upright position. In this scenario, there is no conflict between the sensory data and the top-down prior.
and φ, respectively. In other words, the last three panels are different views of the information one obtains about the state of the head in terms of the pitch φ and acceleration ahd, if the sensory data x is combined with the top-down prior. Here, the posterior assigns a high value to the true parameter combination. This is the expected result, because we set the sensory data x to a value corresponding to a stationary upright position, and the top-down prior implemented the assumption of a stationary upright position. In this scenario, there is no conflict between the sensory data and the top-down prior.Let us now consider the case of a sensory stimulation corresponding to a supine position, where we set 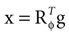 with
with 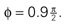 Figure 2
B shows the likelihoods, priors and posteriors. Again, the highest values for the likelihoods (first two panels in Figure 2
B) are for the parameter combination we actually used to compute the sensory stimulation x. However, due to the otholith ambiguity, other parameter combinations are also consistent with this sensory stimulation. With no acceleration in the y-direction, the face-down position with a forward acceleration of
Figure 2
B shows the likelihoods, priors and posteriors. Again, the highest values for the likelihoods (first two panels in Figure 2
B) are for the parameter combination we actually used to compute the sensory stimulation x. However, due to the otholith ambiguity, other parameter combinations are also consistent with this sensory stimulation. With no acceleration in the y-direction, the face-down position with a forward acceleration of 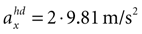 is consistent with the stationary supine position (first panel in Figure 2
B). For no acceleration in the x-direction, positions with an even further tilt backwards and positive accelerations
is consistent with the stationary supine position (first panel in Figure 2
B). For no acceleration in the x-direction, positions with an even further tilt backwards and positive accelerations 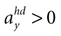 as well as less tilt backwards and negative accelerations
as well as less tilt backwards and negative accelerations 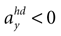 are also consistent with the stationary supine position (second panel in Figure 2
B). Now, however, there is a conflict between this bottom-up sensory information and the top-down prior, which we assume to implement the assumption of an upright position. How do they interact according to Bayesian inference and what are the predicted perceptual consequences in the sense of the posteriors?
are also consistent with the stationary supine position (second panel in Figure 2
B). Now, however, there is a conflict between this bottom-up sensory information and the top-down prior, which we assume to implement the assumption of an upright position. How do they interact according to Bayesian inference and what are the predicted perceptual consequences in the sense of the posteriors?
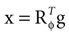 with
with 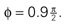 Figure 2
B shows the likelihoods, priors and posteriors. Again, the highest values for the likelihoods (first two panels in Figure 2
B) are for the parameter combination we actually used to compute the sensory stimulation x. However, due to the otholith ambiguity, other parameter combinations are also consistent with this sensory stimulation. With no acceleration in the y-direction, the face-down position with a forward acceleration of
Figure 2
B shows the likelihoods, priors and posteriors. Again, the highest values for the likelihoods (first two panels in Figure 2
B) are for the parameter combination we actually used to compute the sensory stimulation x. However, due to the otholith ambiguity, other parameter combinations are also consistent with this sensory stimulation. With no acceleration in the y-direction, the face-down position with a forward acceleration of 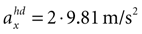 is consistent with the stationary supine position (first panel in Figure 2
B). For no acceleration in the x-direction, positions with an even further tilt backwards and positive accelerations
is consistent with the stationary supine position (first panel in Figure 2
B). For no acceleration in the x-direction, positions with an even further tilt backwards and positive accelerations 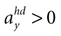 as well as less tilt backwards and negative accelerations
as well as less tilt backwards and negative accelerations 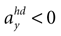 are also consistent with the stationary supine position (second panel in Figure 2
B). Now, however, there is a conflict between this bottom-up sensory information and the top-down prior, which we assume to implement the assumption of an upright position. How do they interact according to Bayesian inference and what are the predicted perceptual consequences in the sense of the posteriors?
are also consistent with the stationary supine position (second panel in Figure 2
B). Now, however, there is a conflict between this bottom-up sensory information and the top-down prior, which we assume to implement the assumption of an upright position. How do they interact according to Bayesian inference and what are the predicted perceptual consequences in the sense of the posteriors?The last three panels in Figure 2
B show the obtained posteriors. Two features are worth noting. First, the pitch rotations with the highest posterior probabilities are closer to the value φ = 0 for the upright position. Second, non-vanishing accelerations in the x- and y-directions are predicted. In other words, combining the ambiguous otholith signals in a supine position with a prior for the upright position leads to an inferred state of the head with a forward and downward acceleration in head-coordinates and less tilt backward than the supine position.
In our model, this prediction is a direct consequence of the multiplication of two Gaussians. Let 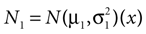 and N2=
and N2=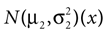 be two Gaussians for some random variable x with diagonal covariance matrices
be two Gaussians for some random variable x with diagonal covariance matrices 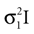 and
and 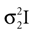 . Then, their product is given as
. Then, their product is given as
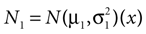 and N2=
and N2=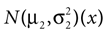 be two Gaussians for some random variable x with diagonal covariance matrices
be two Gaussians for some random variable x with diagonal covariance matrices 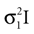 and
and 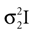 . Then, their product is given as
. Then, their product is given as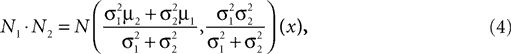
which is also a Gaussian, but with the new mean computed as the weighted sum of the means of the individual Gaussians. In particular, the variance 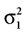 of the first Gaussian, normalized by
of the first Gaussian, normalized by 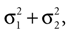 becomes the weight for the mean μ2 of the second Gaussian and vice versa. This basic relation is the key property of Bayesian models of multisensory integration (Alais and Burr, 2004
; Battaglia et al., 2003
; Ernst and Banks, 2002
). In such models, Eq. 4 describes the posterior (assuming a non-informative prior) over a state variable x of interest (like the location of a target), and N1 and N2 describe how x is inferred via the individual modalities (like vision and audition). Equation 4 shows how the reliability of the individual modalities, as quantified by their variances, affects the mean of the posterior distribution. If one modality becomes less reliable (the variance increases), then the mean of the posterior is shifted towards the mean predicted by the other modality. The same relation, however, also dictates how a Gaussian likelihood is combined with a Gaussian prior within a single modality, which is the case we are considering.
becomes the weight for the mean μ2 of the second Gaussian and vice versa. This basic relation is the key property of Bayesian models of multisensory integration (Alais and Burr, 2004
; Battaglia et al., 2003
; Ernst and Banks, 2002
). In such models, Eq. 4 describes the posterior (assuming a non-informative prior) over a state variable x of interest (like the location of a target), and N1 and N2 describe how x is inferred via the individual modalities (like vision and audition). Equation 4 shows how the reliability of the individual modalities, as quantified by their variances, affects the mean of the posterior distribution. If one modality becomes less reliable (the variance increases), then the mean of the posterior is shifted towards the mean predicted by the other modality. The same relation, however, also dictates how a Gaussian likelihood is combined with a Gaussian prior within a single modality, which is the case we are considering.
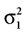 of the first Gaussian, normalized by
of the first Gaussian, normalized by 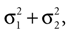 becomes the weight for the mean μ2 of the second Gaussian and vice versa. This basic relation is the key property of Bayesian models of multisensory integration (Alais and Burr, 2004
; Battaglia et al., 2003
; Ernst and Banks, 2002
). In such models, Eq. 4 describes the posterior (assuming a non-informative prior) over a state variable x of interest (like the location of a target), and N1 and N2 describe how x is inferred via the individual modalities (like vision and audition). Equation 4 shows how the reliability of the individual modalities, as quantified by their variances, affects the mean of the posterior distribution. If one modality becomes less reliable (the variance increases), then the mean of the posterior is shifted towards the mean predicted by the other modality. The same relation, however, also dictates how a Gaussian likelihood is combined with a Gaussian prior within a single modality, which is the case we are considering.
becomes the weight for the mean μ2 of the second Gaussian and vice versa. This basic relation is the key property of Bayesian models of multisensory integration (Alais and Burr, 2004
; Battaglia et al., 2003
; Ernst and Banks, 2002
). In such models, Eq. 4 describes the posterior (assuming a non-informative prior) over a state variable x of interest (like the location of a target), and N1 and N2 describe how x is inferred via the individual modalities (like vision and audition). Equation 4 shows how the reliability of the individual modalities, as quantified by their variances, affects the mean of the posterior distribution. If one modality becomes less reliable (the variance increases), then the mean of the posterior is shifted towards the mean predicted by the other modality. The same relation, however, also dictates how a Gaussian likelihood is combined with a Gaussian prior within a single modality, which is the case we are considering.For the sake of illustration, let us consider the Bayesian inference of only the head acceleration ahd with the true pitch φ* used to compute a sensory stimulation 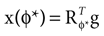 and the internally assumed pitch φ as parameters, and let us assume that the mean of the acceleration prior is zero, μacc = 0. Then, the posterior for the head acceleration ahd is given as
and the internally assumed pitch φ as parameters, and let us assume that the mean of the acceleration prior is zero, μacc = 0. Then, the posterior for the head acceleration ahd is given as
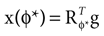 and the internally assumed pitch φ as parameters, and let us assume that the mean of the acceleration prior is zero, μacc = 0. Then, the posterior for the head acceleration ahd is given as
and the internally assumed pitch φ as parameters, and let us assume that the mean of the acceleration prior is zero, μacc = 0. Then, the posterior for the head acceleration ahd is given as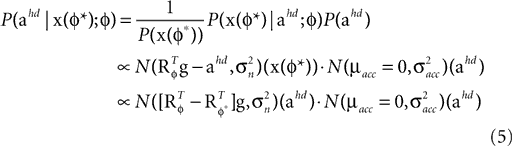
If φ* = φ, the mean of the head acceleration posterior is zero, independent of the values of 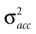 and
and 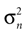 . In other words, if the internally assumed pitch φ and the true pitch φ* coincide,
. In other words, if the internally assumed pitch φ and the true pitch φ* coincide, 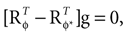 then the inferred head acceleration in terms of the mean of the posterior is zero (Figure 2
A). If φ ≠ φ*, however, then the mean of the posterior is a weighted sum (see Eq. 4) of μacc = 0 and
then the inferred head acceleration in terms of the mean of the posterior is zero (Figure 2
A). If φ ≠ φ*, however, then the mean of the posterior is a weighted sum (see Eq. 4) of μacc = 0 and 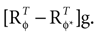 Here, large values of
Here, large values of 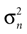 bias the solution of the otholithic ambiguity towards the zero head acceleration with μacc = 0. Conversely, large values of
bias the solution of the otholithic ambiguity towards the zero head acceleration with μacc = 0. Conversely, large values of 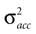 bias the solution of this ambiguity towards the non-zero head acceleration
bias the solution of this ambiguity towards the non-zero head acceleration 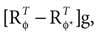 which can account for the mismatch between the internally assumed and the true pitch.
which can account for the mismatch between the internally assumed and the true pitch.
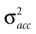 and
and 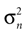 . In other words, if the internally assumed pitch φ and the true pitch φ* coincide,
. In other words, if the internally assumed pitch φ and the true pitch φ* coincide, 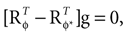 then the inferred head acceleration in terms of the mean of the posterior is zero (Figure 2
A). If φ ≠ φ*, however, then the mean of the posterior is a weighted sum (see Eq. 4) of μacc = 0 and
then the inferred head acceleration in terms of the mean of the posterior is zero (Figure 2
A). If φ ≠ φ*, however, then the mean of the posterior is a weighted sum (see Eq. 4) of μacc = 0 and 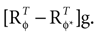 Here, large values of
Here, large values of 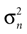 bias the solution of the otholithic ambiguity towards the zero head acceleration with μacc = 0. Conversely, large values of
bias the solution of the otholithic ambiguity towards the zero head acceleration with μacc = 0. Conversely, large values of 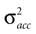 bias the solution of this ambiguity towards the non-zero head acceleration
bias the solution of this ambiguity towards the non-zero head acceleration 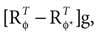 which can account for the mismatch between the internally assumed and the true pitch.
which can account for the mismatch between the internally assumed and the true pitch.This non-zero “compensatory acceleration” is shown in Figure 3
A in the xy-plane for the supine body position (the true pitch φ*), but different internally assumed pitch rotations. If φ* = φ (“face up” in Figure 3
A), then no compensatory acceleration is needed to account for the sensory signals, but if the internally assumed pitch is the upright position (“upright” in Figure 3
A), the brain has to assume a non-zero acceleration in order to account for the bottom-up signals in the supine body position. The absolute value of this compensatory acceleration is shown in Figure 3
B for different internally assumed pitch rotations.
Figure 3. Compensatory acceleration to account for the mismatch between the supine and upright position. (A) Compensatory acceleration in the xy-plane to account for the sensory signals in a stationary supine position in terms of accelerations in the upright position. (B) Magnitude of the compensatory acceleration as a function of the internally assumed pitch rotation. If the actual supine position, 90°, and the internally assumed position coincide, no compensatory acceleration is necessary. (C) Dependence of the compensatory acceleration on the variance of the acceleration and pitch priors.
In order to compute the full Bayesian acceleration posteriors (last panels in Figures 2
A,B) with the internally assumed pitch φ being also a random variable, one evaluates
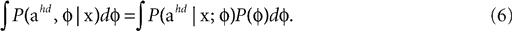
Now both the acceleration and the pitch are the hidden state variables of interest, which we assumed to be independent, i.e. P(ahd, φ) = P(ahd)P(φ). Interestingly, we find that the variance σpitch of the pitch prior P(φ) affects the strength of the inferred illusory self-translation, because the absolute value of the compensatory self-translation (Figure 3
B) depends in a non-linear way on the internally assumed pitch. In other words, P(φ) averages over a non-linear function (the compensatory acceleration for a given sensory stimulation x), and the range over which this averaging is performed affects its result. Figure 3
C shows that for large σpitch the absolute value of the illusory self-translation becomes smaller, because at the internally assumed upright position, φ = 0, the absolute value of the compensatory acceleration decays more rapidly towards the supine position than it increases towards further tilts forward. Figure 3
C also shows that for larger σacc, or conversely for smaller σn, the inferred illusory self-translation increases.
The Effect of a Non-Appropriate Upright Prior – Predictions
In the last section we have demonstrated, using a toy model of otholithic processing, that an otherwise optimal processing strategy can lead to illusory perceptions, when the internally assumed upright body position differs from the actual body position. In particular, if the actual body position is supine, but the internally assumed position is upright, then the brain may explain this discrepancy in terms of an illusory self-translation, which we predict to be forward and downward in head-centered coordinates. Moreover, we have derived two additional testable dependencies of the magnitude of the illusion. We predict that the illusion is stronger, if the subjects are more uncertain about their acceleration (larger values of σacc, Figure 3
C), and that the uncertainty regarding the pitch of the head should be minimized (small values of σpitch, Figure 3
C) for stronger illusions. While testing these predictions is a methodological challenge (see Discussion), a valuable first step is a characterization of the range these two values take in everyday life. We did this by measuring the head movements of subjects using a motion capture system.
The Effect of the Measured Upright Priors
We assume that the brain may have inferred the priors based on stimuli it is exposed to during everyday life. These priors certainly change on different time-scales and depend on the actual context. To the best of our knowledge, however, no statistics of natural head movements are reported in the literature. In order to obtain a first approximation to these statistics, we measured the head movements of subjects in the three different conditions standing, waiting and action (see Materials and Methods). The results are shown in Figures 4
A–D as histograms and Gaussian fits to the histograms. While the measured σpitch is similar for the waiting and action conditions, it is larger for the standing condition (Figure 4
A), where standing subjects moved their head in order to inspect their surrounding. The measured σacc is largest for the action, smaller for the waiting and even smaller for the standing condition (Figures 4
B–D). Hence, given the dependence of the illusory self-translation on σpitch and σacc, it will be largest for the action condition. Figures 4
E–G show that this is indeed the case. Interestingly, Figures 4
E–G show that in the waiting condition almost no illusory self-motion is predicted whereas in the action condition the larger values of σacc lead to a notable self-translation of approx. 1/2 g in magnitude. This dependence of the magnitude of the illusory self-translation in the supine position on the variance of the acceleration prior may also underlie the everyday experience of some vestibular aftereffects like, for example, illusory self-motion when lying in bed after a day in the theme park or after a day of skiing.
Figure 4. Estimated probabilities from the recorded head movements and the resulting posteriors. (A) Histogram for the pitch rotations in the casual condition as calculated with a parametrization of the fitted rotation matrices according to a Fick-gimbal convention and Gaussian fits obtained by minimizing the Kullback–Leibler divergence KL(p||q) between the Gaussian fits p and the histograms q (see Supplementary Material for the values). (B–D) Histograms and fits for the measured accelerations in head-coordinates. (E–G) Resulting acceleration posteriors for the standing, (E), waiting, (F), and action, (G), condition.
The main result of this paper is the interpretation of the vestibular component of OBEs as a mislead Bayesian inference and that this accounts for disembodied and elevated self-location. We have shown that a mismatch between the actual body position and an internally assumed upright body position can lead to illusory self-translations due to the otholithic ambiguity. While this ambiguity has been the subject of previous studies (see Angelaki et al., 2001
for a review), we have shown that illusory self-motions are also crucially affected by the variances of the accelerations and pitch priors. Since most previous studies have not considered these variances as candidates for the independent variable in experimental designs, our model makes strong testable predictions for future behavioral experiments with healthy subjects. Moreover, we have measured the top-down priors by analyzing natural head movements and determined the approximate values of these variances. Together with our model this data suggests that subjects who use a top-down acceleration prior corresponding to, for example, rapid sport-like movements may experience illusory self-translation in a supine body position.
Based on neurological observations, it has been proposed that the vestibular component of OBEs may both induce and allow distinguishing OBEs from related bodily illusions. OBEs have been induced by electrical stimulation of vestibular cortex (Blanke et al., 2002
; Penfield et al., 1955
) and share many similarities with bodily illusions of healthy subjects in microgravity conditions such as orbital and parabolic flights (Kornilova, 1997
; Lackner, 1992
). Hence, in terms of aspects relevant to the study of the bodily self, the present study suggests that using a top-down prior reflecting an upright body position in order to disambiguate otholith signals in a supine body position may account for the following key elements of an OBE. Disembodied self-location would be due to illusory self-translation affecting self-location by means of, for example, path integration mechanisms (McNaughton et al., 2006
), while the actual body position is static. Elevation of self-location would be due to the illusory upright body position while the actual body is in a supine position. However, it could also be a consequence of the illusory self-translation in the forward direction. The vestibular sensations of floating and flying would be a direct consequence of the predicted illusory self-translation.
We argue that the concept of combining empirically measured statistics of vestibular (and other sensory) signals with computational modeling is an important step towards the systematic and detailed description of how the brain computes a phenomenon like self-location by the integration of basic bodily sensory signals.
Signals from the Semicircular Canals and Other Modalities
An apparently strong limitation of our model is its focus on only the otholithic signals. We do not model the information from the semicircular canals, which signal angular acceleration and help to disambiguate the otholithic signals (Angelaki et al., 2001
). However, we are considering a scenario with a mismatch between the actual static supine position and an internally assumed upright position. The inferred orientation as described by the Bayesian posterior is almost upright as well. Hence, the semicircular canals are neither actually contributing sensory signals, nor would there be any further discrepancy between the inferred (almost) upright position and the upright position imposed by the prior in terms of canal signals. However, a more complete model would certainly have to account for the signals form the semicircular canals and how they interact with the otholithic signals. Moreover, an apparently arbitrary choice we made is setting the noise for the otholithic signals to 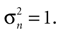 This sensory noise can be measured experimentally, but estimates for the detection threshold of movement onset vary widely depending on the method of measurement (Korhuber, 1974
). If our explanation of the vestibular component in OBEs is correct, we have to assume low sensory noise. Hence, we selected a value for the sensory noise, which corresponds to the upper end of measured range of detection threshold and is a conservative estimate.
This sensory noise can be measured experimentally, but estimates for the detection threshold of movement onset vary widely depending on the method of measurement (Korhuber, 1974
). If our explanation of the vestibular component in OBEs is correct, we have to assume low sensory noise. Hence, we selected a value for the sensory noise, which corresponds to the upper end of measured range of detection threshold and is a conservative estimate.
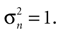 This sensory noise can be measured experimentally, but estimates for the detection threshold of movement onset vary widely depending on the method of measurement (Korhuber, 1974
). If our explanation of the vestibular component in OBEs is correct, we have to assume low sensory noise. Hence, we selected a value for the sensory noise, which corresponds to the upper end of measured range of detection threshold and is a conservative estimate.
This sensory noise can be measured experimentally, but estimates for the detection threshold of movement onset vary widely depending on the method of measurement (Korhuber, 1974
). If our explanation of the vestibular component in OBEs is correct, we have to assume low sensory noise. Hence, we selected a value for the sensory noise, which corresponds to the upper end of measured range of detection threshold and is a conservative estimate.In normal life, however, being in a supine position and imagining oneself standing does not induce OBE-like experiences. This is certainly due to the fact that the top-down priors used to disambiguate the otholithic signals (beside their subcortical interactions with the canal signals) change on many different time-scales and depend on the context. For example, visual signals (like optic flow) and proprioceptive signals (like neck muscle activity to sustain the head against gravity) are certainly used by the brain in order to infer self-location and self-translation. Moreover, when healthy subjects are lying awake in a supine position, they usually know that they are lying, which affects their interpretation of the sensory signals. Hence, our assumption of an upright prior in a supine position is a simplification, which may only be appropriate when signals from other modalities are attenuated. We hypothesize that this is the case in some neurological conditions leading to OBEs, but it may also be the case in dreams or transitions from wakefulness to sleep. In other words, in OBEs the actual processing of sensory and top-down information would still be intact (or even optimal in the Bayesian sense), but “wrong” inputs to an otherwise optimal processing could lead to illusions such as OBEs as suggested by the induction of OBE-like experiences via multisensory stimulation (Ehrsson, 2007
; Lenggenhager et al., 2007
). It is a methodological challenge to render other modalities non-informative when experimentally testing our model with healthy subjects.
The Analogy of Bayesian Inference
Bayesian inference is a mathematical theory rooted in logic and statistics (Cox, 1961
; Jaynes, 2003
), which deserves justification when used to model brain functions (Knill and Richards, 1996
). We selected it, because the Bayesian approach formalizes a task the brain has to solve during processing of sensory information and it provides a solution to it. The task is to infer the state of the body (or other objects in the world) based on ambiguous and noisy sensory signals in terms of values of hidden variables like the orientation of the head relative to gravity, which cannot be measured directly. Bayesian inference is the solution to this task, because within such a setting, where information can have different degrees of certainty, it can be derived as the optimal way of combining prior information with new (sensory) information (Cox, 1961
). Behavioral experiments have shown that in some sensory (Ernst and Banks, 2002
; MacNeilage et al., 2007
) and sensory-motor (Körding and Wolpert, 2004
; van Beers et al., 1999
) tasks the human performance is well described by the Bayesian posterior. In order to link this approach to OBEs we assumed that the posterior distributions are a proper description of subjects’ experiences. Sharing this assumption, a recent Bayesian model of vestibular processing (Laurens and Droulez, 2007
) explains a set of other vestibular illusions.
Linking our approach to brain activations is also possible, but at this point it is hindered for two reasons. First, although neuronal implementations of Bayesian computations have been suggested (Denève et al., 2007
; Huys et al., 2007
; Ma et al., 2006
; Rao, 2004
; Sahani and Dayan, 2003
), the mere similarity of the performance or perception of subjects to Bayesian inference does not imply that the brain indeed performs computations analogous to Bayesian inference. Second, the vestibular system is a distributed processing network (Guldin and Grüsser, 1998
) whose functions and patterns of activation have not been described in as much detail as those of other sensory systems (Berthoz, 1996
; Brandt and Dieterich, 1999
). This would complicate the interpretation of neuroimaging results using Bayesian modeling. The Bayesian approach, however, leads to clearly testable predictions for behavioral experiments. For example, illusory translations should occur if the top-down prior is manipulated such that it reflects an upright position (i.e. by manipulating visual inputs) and while subjects are in a supine body position, but such experiments may turn out to be challenging methodologically (see above).
Previous Work on OBEs and Self-Location
Strictly speaking, our model may be described only as a model of a vestibular illusion. But as its predictions are consistent with reported vestibular sensations during OBEs we expect merit for studying the bodily self under normal conditions. Possible conceptual advances could derive from our explicit postulate of identifying the Bayesian posterior with the experience of the subject as compared to a description of subjects’ behavioral performance. Consequently, here we suggest that the bodily self is a statistical model of body-related multisensory signals with the vestibular modality playing a key role, because it delivers information about the whole body in space. Does this perspective help to interpret previous empirical findings regarding the computational role of particular brain regions? Direct evidence for the causal implication of temporal-parietal cortex in OBEs came from the induction of OBEs by electrical stimulation of this area (Blanke et al., 2002
; De Ridder et al., 2007
; Penfield et al., 1955
) as well as brain damage to this area (Blanke et al., 2004
). These neurologically induced OBEs were characterized by disembodied and elevated self-location and first-person perspective as well as vestibular sensations. It is also activated when employing mental imagery using self-location (Arzy et al., 2006
; Blanke et al., 2005
) and mental perspective taking (Vogeley et al., 2004
). Hence, this brain region could be part of a (statistical) model of the bodily self. In other words, it may serve as an area representing aspects of the bodily self like self-location and self-translation relative to gravity, and its involvement in visuo-spatial perspective taking could reflect its role as the source for imagined self-motion signals.
Recently, it has been shown that self-location can be manipulated experimentally in healthy subjects by creating conflicts between multisensory bodily signals using virtual reality (Ehrsson, 2007
; Lenggenhager et al., 2007
). Extending a similar paradigm about the perception and integration of multisensory arm signals, the so-called “rubber hand illusion” (Botvinick and Cohen, 1998
; Tsakiris and Haggard, 2005
), to the entire body, changes in self-location and self-identification could be induced. In Lenggenhager et al. (2007)
subjects saw their own body (virtual body) in 3D through a head-mounted display (HMD) as if standing 2 m in front of them. They saw their virtual body being stroked synchronously or asynchronously with respect to a felt stroking on their back. This stimulation led to visual capture and systematic errors in self-location as the subjects localized themselves as drifted towards the virtual body in the synchronous condition but not in the asynchronous condition. Although, none of the subjects reported disembodied self-location (as in OBEs), these data suggest that participants localized their bodily self outside their corporeal borders. This was corroborated by participants’ heightened self-identification with the virtual body and self-attribution of the visual stimuli applied to the “skin” of the virtual body. These behavioural data as well as the present data suggest that self-location can be manipulated relatively easily using conflicting sensory stimulation. Hence, online processing of body-related multisensory information in the brain is more like ongoing puzzle solving of which the normally experienced embodied self-location is just a fragile and only temporarily stable solution, which is a setting that is naturally suited for the Bayesian approach to sensory information processing. However, in order to model the experimentally identified aspects of self-location one has to refer to particular coordinate systems. In our model, we assumed an body-centered coordinate system and identified the illusory self-motion with altered self-location. More precisely, we suggest that the illusory body-centered self-motion signals are used in predictive models (Kilner et al., 2007
; Rao and Ballard, 1999
; Wolpert et al., 1995
) for body- and world-related sensory signals. Since the physical body is not actually moving, this leads to prediction errors in other modalities, and those may correspond to other aspects of multisensory OBEs. By explaining disembodied self-location as illusory self-translation while the actual body position is static and elevated self-location during OBEs due to the illusory upright body position while the actual body is in a supine position our results suggest a solid interpretation for pathological self-location during OBEs. These findings are likely to have relevance for the continuously calculated embodied self-location and suggest novel ways to induce and study experimentally this crucial aspect of bodily self-consciousness under normal conditions.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supported by the Fondation de Famille Sandoz and DFG (803371). The authors like to thank Henning Sprekeler for carefully reading the manuscript and helpful comments.
Pose Determination
We have computed the statistics of the natural head movements in terms of motion parameters that the brain may use in order to estimate the orientation and movement of the body in space. In particular, we were interested in the statistics of the accelerations in head-centered coordinates, ahd, and the angles characterizing the rotation matrix R. However, these motion parameters could not be measured directly, but had to be estimated based on the three dimensional Cartesian coordinates of the markers we attached to the head of our subjects. In order to estimate the translation and rotation of the head relative to the base pose, we solved the so-called pose determination problem by means of a least-squares estimate: Given a base pose xi, i = 1,…,n, and another set of points yi, i = 1,…,n, for the locations of the n markers at some other time during the movement, we seek a rotation matrix R and a translation vector r such that
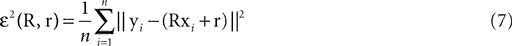

is a unique solution to Eq. 7, with 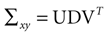 being a singular value decomposition of the covariance matrix
being a singular value decomposition of the covariance matrix
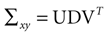 being a singular value decomposition of the covariance matrix
being a singular value decomposition of the covariance matrix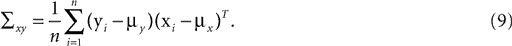
The diagonal matrix S in Eq. 8 is defined as
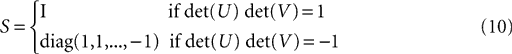
for rank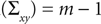 and
and
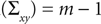 and
and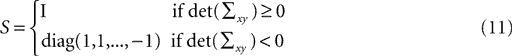
for rank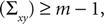 where m = 3 is the number of dimensions of the points xi and yi. In this way, we obtained for each time t during the movement a rotation matrix Rt and a translation rt by transforming the base pose to the measured coordinates of the markers at time t.
where m = 3 is the number of dimensions of the points xi and yi. In this way, we obtained for each time t during the movement a rotation matrix Rt and a translation rt by transforming the base pose to the measured coordinates of the markers at time t.
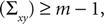 where m = 3 is the number of dimensions of the points xi and yi. In this way, we obtained for each time t during the movement a rotation matrix Rt and a translation rt by transforming the base pose to the measured coordinates of the markers at time t.
where m = 3 is the number of dimensions of the points xi and yi. In this way, we obtained for each time t during the movement a rotation matrix Rt and a translation rt by transforming the base pose to the measured coordinates of the markers at time t.Head Acceleration and Orientation
Given a sequence of rotation matrices Rt and translation vectors rt, we computed (1) the accelerations of the head in head-centered coordinates, ahd, and (2) the orientation of the head in terms of yaw, pitch, and roll angles. The accelerations are obtained by first computing the accelerations in world-coordinates based on the translation vectors rt. Then, these accelerations were transformed into the head-centered coordinate system.
The head orientations were characterized using yaw, pitch and roll rotations as follows: We denote the angles for the yaw, pitch and roll rotations as θ, φ and ψ, respectively. The corresponding rotation matrices for these individual rotations are given as
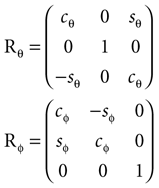
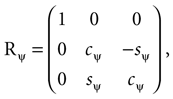
where we used shorthand notations cθ for cos (θ), sθ for sin (θ), etc. A rotation matrix R = (RθRφ)Rψ given as
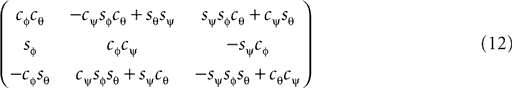
corresponds to a sequence of rotations, where we first carry out the yaw rotation in world coordinates, then the pitch rotation in the rotated coordinate system, and finally the roll rotation in the coordinate system already rotated by yaw and pitch rotations.
Now, for each rotation matrix R estimated using the least-squares estimate, we computed the values of θ, φ, and ψ. For |1 − R21| < 0.001 they are given as θ = arctan2(R13, R33),  and ψ = 0. For |−1 − R21| < 0.001 the values are θ = arctan2(R13, R33), and ψ = 0. Otherwise, they are given by
and ψ = 0. For |−1 − R21| < 0.001 the values are θ = arctan2(R13, R33), and ψ = 0. Otherwise, they are given by
 and ψ = 0. For |−1 − R21| < 0.001 the values are θ = arctan2(R13, R33), and ψ = 0. Otherwise, they are given by
and ψ = 0. For |−1 − R21| < 0.001 the values are θ = arctan2(R13, R33), and ψ = 0. Otherwise, they are given by
Here, arctan2 (y, x) is the four-quadrant inverse tangents. The case distinction was introduced in order to account for the singularities at the north and south pole. In other words, head orientations with a pitch of 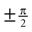 are described as only yaw and pitch, but no roll rotations.
are described as only yaw and pitch, but no roll rotations.
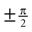 are described as only yaw and pitch, but no roll rotations.
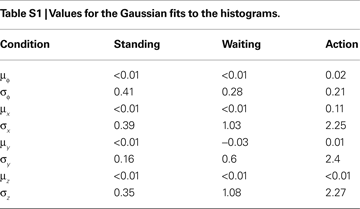
are described as only yaw and pitch, but no roll rotations.Gaussian Fits to the Histograms
As we were mainly interested in the variances of the priors, we subtracted the mean for the pitch angles and accelerations for each subjects before combining the histograms. Given histograms computed over all subjects, we derived Gaussian fits to these histograms by minimizing the Kullback–Leibler divergence (Cover and Thomas, 2006
) between the Gaussians fits and the histograms. The results of these fits are given in Table S1
.



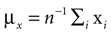 and
and 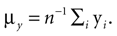 It has been shown (
It has been shown (