- Gatsby Computational Neuroscience Unit, UCL, UK
Humans can be instructed verbally to perform computationally complex cognitive tasks; their performance then improves relatively slowly over the course of practice. Many skills underlie these abilities; in this paper, we focus on the particular question of a uniform architecture for the instantiation of habitual performance and the storage, recall, and execution of simple rules. Our account builds on models of gated working memory, and involves a bilinear architecture for representing conditional input-output maps and for matching rules to the state of the input and working memory. We demonstrate the performance of our model on two paradigmatic tasks used to investigate prefrontal and basal ganglia function.
Introduction
There is much recent interest in understanding and modeling how subjects perform a range of tasks that pose graded computational challenges with respect to conditional input-output mappings (Badre et al., 2005 ; Badre and D'Esposito, 2007 ; Boettiger and D'Esposito, 2005 ; Fusi et al., 2007 ; Koechlin et al., 2003 ; Koechlin and Summerfield, 2007 ), working memory (Frank et al., 2001 ; O'Reilly and Frank, 2006 ), and even simple branching subroutines (Braver and Bongiolatti, 2002 ; Koechlin et al., 1999 ). One obvious fact about these experiments is the huge advantage that linguistically capable humans have over other animals (and most models), in that the former can be effectively “programmed” with just a few words to perform complex tasks; whereas animals require much longer periods of training, and even architectural (O'Reilly and Frank, 2006 ) and∕or training-based (Krueger and Dayan, 2007 ) hints. To use terminology borrowed from conditioning (Daw et al., 2005 ; Dickinson, 1985 ), the extensive training may be building a habit, or a collection thereof; by comparison, humans can presumably use rules more akin to a forward-model of the task (e.g., Bunge, 2004 ), and act according to a mixture of the output of this forward-model system and a more slowly trained, automatized, habitual control system (e.g., Anderson, 1982 ; Daw et al., 2005 ; Dickinson, 1985 ; Logan, 1988 ; Sloman, 1996 ).
The power of language as an input medium is obviously not to be denied. However, the question for this paper is what substrates for control might mediate the instant programmability which is conferred by language. That is, could there be a uniform architecture for control which can instantiate habits, but also provides an implementational substrate for simple rules? This question raises a host of issues to do with the initial creation of rules (Duncan, personal communication), which is analogous to compilation, and also the storage, recall, and matching of rules to the current state. The state is a combination of the internal representation of immediate sensory input and the contents of working memory. These are obviously very broad questions; we will seek only partial answers, and also in a relatively abstract treatment of the problem. In particular, we do not solve the compilation problem, but rather assume that a decomposition of a task into a set of rules can be provided.
We build a uniform architecture, and show how it can embody both habits and rules. Our model of habits was inspired by Frank et al. (2001) , O'Reilly and Frank (2006) , Rigotti and Fusi (2006) , and Rigotti et al. (2007) , using a bilinear architecture to instantiate an input-output mapping. Here, the input is the state mentioned above, which consists of the current sensory observations together with the contents of activity-based working memory, which, for our present purposes, stores information about past sensory observations. The output includes actions with external consequences, such as pressing a left or right lever, and ones with internal consequences, such as reading or gating (Frank et al., 2001 ) the current sensory observation into working memory, or indeed clearing some element of working memory. The bilinearity has a similar purpose to the hidden units used by Rigotti and Fusi (2006) and Rigotti et al. (2007) , allowing tasks with complex input-output contingencies to be executed.
Instead of specifying a task as a single, complex, input-output mapping, a set of rules allows it to be decomposed into a set of simple input-output mappings. Duncan (personal communication) cited the example of a board game; there is typically a moderate number of rules, each of which only applies in a restricted circumstance, and specifies a simple contingency. Using rules therefore requires a number of steps to be followed.
Our rules have two parts—one specifying the conditions under which they apply; the second indicating the contingency they seek to impose. These rules are stored in an episodic-like memory, and are retrieved via associative recall, based on similarity of their matching conditions with the full contents of the current state. However, the determinants of associative episodic recall are expected to be laxer than those precise conditions specified in the rules themselves, in particular not specifying aspects of the state that should not be present or be true. Therefore, there is an additional process of rule matching, which involves assessing whether the state is indeed appropriate for a rule to be activated. This can also be performed in a multilinear manner (i.e., in the form of another internally directed output), consistent with the uniformity of the architecture as a whole. If the rule matches in detail, then the contingency it demands is imposed as another, simple, input-output mapping, of exactly the same form as a habit, and learned in the same manner.
Using two paradigmatic examples from the literature, we show that bilinear habits can be acquired, along with the interactions necessary to implement individual rules.
This paper draws on three main traditions. The first is the extensive line of work into the psychological and neural substrates of complex tasks that are putatively dependent on extensive regions of prefrontal cortex (Badre and D'Esposito, 2007 ; Brass and von Cramon, 2002 , 2004 ; Bunge, 2004 ; Christoff and Gabrieli, 2000 ; Cohen et al., 1996 ; Cooper and Shallice, 2006 ; D'Esposito et al., 2000 ; Frank et al., 2001 ; Fuster, 1997 ; Koechlin and Jubault, 2006 ; Miller and Cohen, 2001 ; Rougier et al., 2005 ; Sakai and Passingham, 2003 ; Williams and Goldman-Rakic, 1995 ; Wood and Grafman, 2003 ). We model two cases—first, one of the conditional input-output tasks that Koechlin et al. (2003) and Koechlin and Summerfield (2007) used to investigate an apparent hierarchy of control structures in extensive regions of lateral prefrontal cortex; and second, the conditional one-back 12AX task invented by Frank et al. (2001) to elucidate the interaction between prefrontal cortex and the basal ganglia in an-homuncular control and working memory. Although I am not aware of any published psychological or functional neuro-imaging test of the 12AX task, it is a variant of the N-back working memory task (Braver et al., 2001 ; Cohen et al., 1997 ; Gevins and Cutillo, 1993 ; Rowe et al., 2000 ), which, along with other areas, is known to involve various prefrontal regions (see Owen et al., 2005 ). We chose these particular tasks since they present a range of computational challenges, and because they can both be captured using the same abstractions of sensory input and working memory.
The second tradition is the modeling work associated with such control problems. We borrow insights from two approaches: the pre-frontal, basal ganglia, working memory (PBWM) model that Frank et al. (2001) , Hazy et al. (2006 , 2007 ), and O'Reilly and Frank (2006) used to solve their illustrative 12AX task, and the working memory and control models of Fusi, Wang, and their colleagues (Fusi et al., 2007 ; Rigotti and Fusi, 2006 ; Rigotti et al., 2007 ; Wang, 2002 ). The analysis that led to PBWM started from the important difference between weight-based and activity-based storage, with the latter being analogous to working memory. Building on the ideas of Hochreiter and Schmidhuber (1997) , PBWM suggests that key to the use of working memory is the non-linear operation of gating (Braver and Cohen, 2000 ; Cohen et al., 1996 ; Frank et al., 2001 ); namely that cortico-striato-thalamo-cortical loops (Alexander and Crutcher, 1990 ) would allow cortical (and sub-cortical) control over whether information is stored in, or retrieved from, working memory cortical micro-circuits in prefrontal cortex (Durstewitz and Seamans, 2002 ; Miller and Cohen, 2001 ; Williams and Goldman-Rakic, 1995 ). This control mechanism permits the solution of sophisticated conditional input-output tasks, and also provides an account of the step-by-step, sequential performance required in many tasks involving extended working memory. Frank et al. (2001) originally set weights effectively by hand (a tactic we also borrow) to show that their overall model could support the computations required for the 12AX task; they later considered how such weights could emerge through on-line learning (Hazy et al., 2006 , 2007 ; O'Reilly and Frank, 2006 ; O'Reilly et al., 2007 ).
The other approach to working memory and control is less architecturally comprehensive than PBWM, but includes a more detailed view of working memory itself (Wang, 2002 ). It has also led to a more complete model (Fusi et al., 2007 ) of a particular, influential conditional visuo-motor task that has been administered to monkeys (Pasupathy and Miller, 2005 ). As mentioned above, both these modeling approaches have concentrated on habitual control; by contrast, we are mainly interested in the link between habitual and rule-based notions. However, our habitual architecture does owe a particular debt to Rigotti and Fusi (2006) and Rigotti et al. (2007) , who observed that the conditionality of conditional input-output tasks typically results in problems that are not linearly separable (like the famous XOR or negative patterning problem), and so demand something equivalent to hidden units. Multilinearity is one of the simplest examples of such a mechanism.
The elemental operations associated with multilinearity have been considered before. In particular, PBWM's central operation is gating, as applied to the control of the flow of information into specific and changeable parts of working memory. Given simple binary representations of inputs and working memory, gating is a primitive multiplicative operation. Here, we consider more general multilinear models, which were observed by Koenderink and Van Doorn (1997) to be the normatively correct abstraction for a wealth of psychophysical computations, further developed by Tenenbaum and Freeman (2000) as a powerful statistical modeling technique for a variety of self-supervised learning questions, and used by Dayan (2006) to capture the way the focus of attention operates in exploring the hierarchical analysis and synthesis of internal representations of visual objects.
The multiplicative operations inherent in multilinearity are also closely related to those used in multidimensional basis functions suggested by Poggio (1990) and Pouget (1997) , and also the shifter circuits of Olshausen et al. (1993) . Dayan's (2006) model was also inspired by work in the early days of connectionism (see Hinton, 1991 ) which considered issues in neural representation of, and computation with, structured information, including versions of habit- and rule-based processing (Hinton, 1990 ). However, we are not claiming that there is an obvious neural implementation of bilinearity or multilinearity, let alone of the way that rules are supposed to work by determining particular interactions. We suggest that the worth in our model is as a stepping-stone toward more realistic, though inevitably more complex, treatments.
In the next section, we describe the two tasks on which we focus, together with the constraints on the model they impose. We then describe the model in detail, together with the way we determined the existence of appropriate weights. Following that, we show that the model can indeed solve the tasks, using either rule-based or habitual mechanisms.Finally, we discuss the implications of the work, together with pressing future directions.
The Tasks
We consider two tasks, one, which we will call CIOM, used by Koechlin et al. (2003) , which emphasizes complex conditional input-output maps; and the other, the so-called 12AX task, from Frank et al. (2001) , which stresses the sequential interaction between the contents of working memory and direct stimulus input. We describe the tasks, and also possible rules underlying their satisfactory execution.
One reason for selecting these particular tasks is that, although they probe rather different parts of the space of cognitive problemse, they can be described in rather similar ways, involving similar classes of input and at least some aspects of working memory, and, most particularly, conditional input-output maps that potentially combine the entire contents of working memory with that of the current input to determine what action is required.
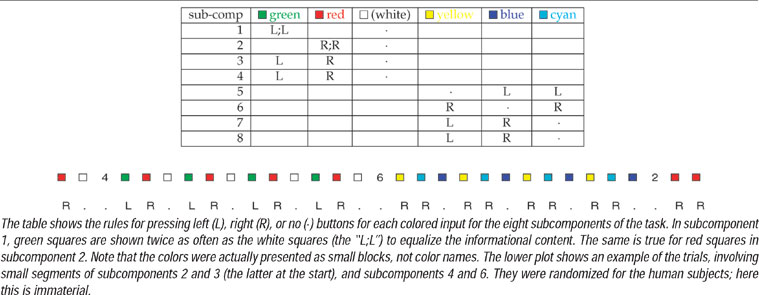
More particularly, both tasks can be seen as involving two different sorts or types of input stimuli. One of these indicates which of a number (eight for CIOM; two for 12AX) of task subcomponents is active for a block. This information needs to be read into and stored by working memory for the duration of the block. Stimuli of the other type (here represented as colors) indicate on an input-by-input basis what action is required of the subjects. The 12AX task demands that some of these stimuli are also read into working memory; the CIOM task does not. We will assume a working memory with separate parts (“stripes,” Frank et al., 2001 ; Lund et al., 1993 ; Pucak et al., 1996 ) for taskWM subcomponents and colorWM (using a sans-serif font and the subscript to indicate that these refer to working memory).
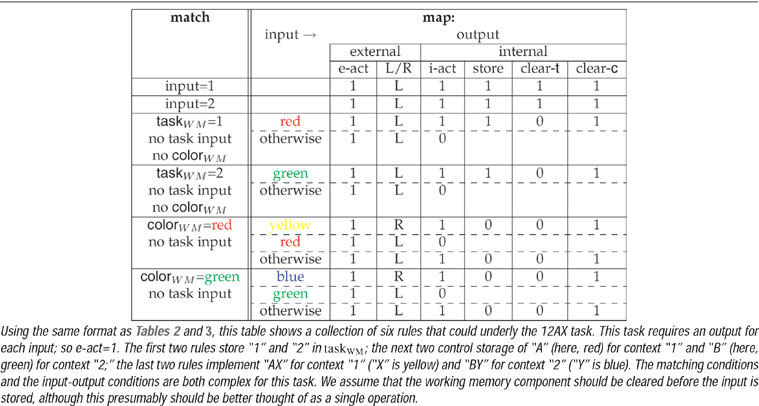
Actions can be externally directed (such as pushing a particular button) or internally directed (manipulating working memory). We will consider both classes as proceeding in two stages—first a choice of whether to execute any such action, and then a choice of which. This implies that there are six binary actions, two external (one we call e-act, which determines whether or not to act externally; and L∕R, which determines which button to push), and four internal (i-act, whether or not to act internally; store, which reads the current sensory input into working memory; and clear-t and clear-c, which clear the taskWM and colorWM components of working memory, respectively. We discuss the rationale for i-act and e-act in more detail below.
CIOM
Koechlin et al. (2003) sought to elucidate the contributions of different lateral prefrontal areas in control by designing a task with factorial demands associated with stimuli and responses. Their task involved 16 different subcomponents; we consider just the eight shown in Table 1 . Subjects would first see an identifier associated with whichever of the subcomponents was about to start; and would then see a number of colored squares (12 per subcomponent block) according to which they would have to press a left or a right button (L or R), or do nothing. The critical factors in the design are that:
- green, red, and white colors are always associated with a single action (left, right, or nothing, respectively), whereas yellow, blue, and cyan are associated with all three actions (with one being twice as frequent as the others);
- in tasks 1,2; 5,6, subjects need only prepare one possible active response (either a left or a right button press); in tasks 3,4; 7,8, they have to prepare both.
Koechlin et al. (2003) showed that subjects' reaction times (following learning of the task) implied a rough partial order of difficulty:
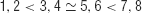
suggesting that both factors influence performance in a measured manner. They analyzed fMRI BOLD data using the factors to generate informative contrasts. We discuss the imaging findings in Section Discussion.
CIOM's rules are conceptually straightforward. The main requirement is to remember which of the eight possible subcomponents is active. This can be done by reading the identifier for the subcomponent into working memory when it occurs (clearing out the old identifier from the previous subcomponent if necessary) and storing it for the block. Conditioned on these contents of working memory, the remaining rules can all be specified as separate, albeit, potentially complex input-output mappings that can be represented in the form shown in Table 2 . This rule matches the task component of working memory (the “taskWM = 1”), provided that there is a color input, and instantiates a conditional map from this immediate input (i.e., the color) to the six binary outputs.
It will be important for the later discussion to note that there are different possible collections of rules that can implement the same task, but that place different demands on (the closely related operations of) matching and mapping. An example of two alternative rules is shown in Table 3 . These put all the onus on matching, whence the action map is formally trivial. Despite the functional equivalence of the different sets of rules, the demands on rule memory are, of course, different. In general, the different sets are different possible outcomes of the process of compilation—there is no single correct answer.
Note further that the second of Koechlin et al.'s (2003) factors implies an extra simplification in the rules. For tasks 1,2; 5,6, there is only one possible action for a whole subcomponent, and therefore no need to choose which externally directed action to do, because there is no competition. This is formally a Go∕NoGo task, whose striatal instantiation via direct and indirect, D1 and D2 circuits (e.g., Frank et al., 2004 ) may be rather different from the other cases, in which there is competition between different external actions. For Go∕NoGo, we assume that the decision can be based solely on the e-act action.
12AX
The 12AX task is a conditional version of the one-back task. In its original form, subjects see a sequence consisting of the numbers “1” and “2,” and the letters “A,” “B,” “C,” “X,” “Y,” and “Z.” Their task is to press one button (say L) for every input except that the “X” of “AX” in the case that the most recent number had been a “1,” and the “Y” of “BY” if the most recent number had been a “2” require R to be pressed. The “1” can be followed by a varying number of “AXs,” embedded in essentially random other letters before the “2” is shown. 1
We put this into the same framework as the CIOM task by treating the “1” and “2” as specifying different task subcomponents, and then substituting the six possible colors for the six possible letters. However, the sequential structure of the task means that the rules governing its evolution are now much more complicated. Again, there are various possibilities for rule sets. One example is given in Table 4 , this time involving two unconditional rules for storing the task subcomponents, and four input-conditional rules. Note that both external and internal actions are required for every single input for this task, unlike CIOM. The extra matching conditions associated with the lower four rules are to ensure that no more than one rule matches at a time. In general, precedence relations among rules may be necessary.
The Model
Figure 1 shows the basic architecture of the model. It comprises two main parts which are separately discussed below:
- A bilinear mapping from the state, defined by the contents of working memory and the input, to the six externally and internally directed actions that are described above, and shown in the rule tables.
- The rule recall and matching mechanisms. These are responsible for recalling rules from an episodic store based on associative similarity with the current state of working memory and stimulus input, and then for the bilinear process of matching to ensure that the precise conditions of the rule are met. A rule that matches is taken as determining an alternative bilinear input-output map that controls internally and externally directed responding.
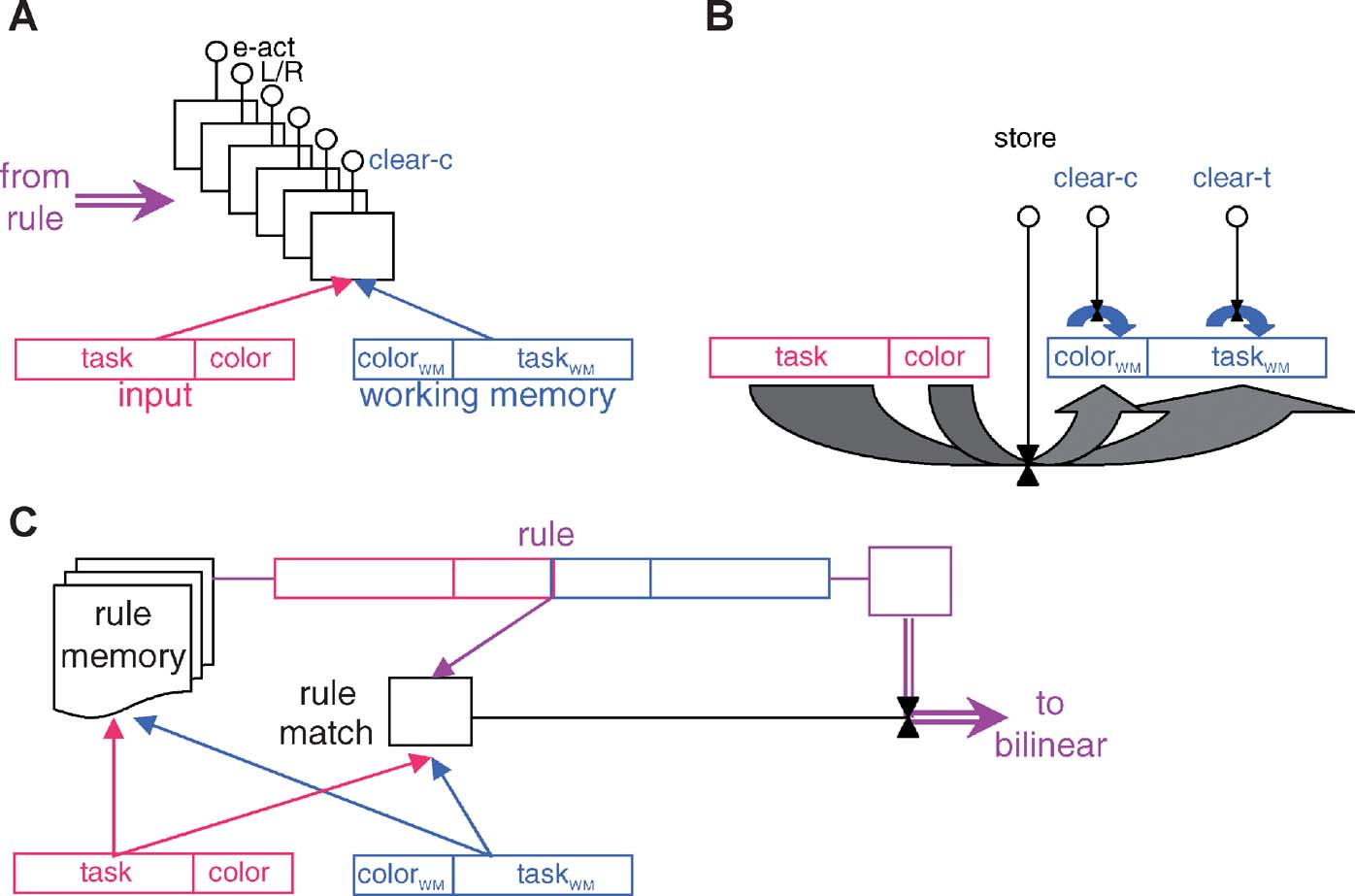
Figure 1. The model. To avoid overwhelming complexity, the three panels show three separate facets of the model. Complete details are provided in the Appendix. (A) The bilinear structure controlling ultimate execution. Input and working memory units are divided into separate components (stripes, Frank et al., 2001 ) for task and color inputs; the bilinear form has six binary output units. The arrow from the left allows the rule to instantiate a bilinear form. (B) Read into and clearing the working memory is under control of the three internally directed actions. (C) The rule memory, recall, and matching process showing the associative and exact matching processes, and the means for implementing the rule as the bilinear form in (A).
More complete details of the architecture and various training regimes are given in the Appendix.
As stressed above, it is obvious that these suggestions are much further removed from the neural substrate than those of the “parent” models of Frank et al. (2001) , Fusi et al. (2007) , and O'Reilly and Frank (2006) . The key notion that there are alternative bilinear mappings that can be imposed through the operation of a rule (or, if no rule is retrieved or matched, then by default as a habit) is particularly troubling in this respect. However, as also implied in the work of Dayan (2006) and Tenenbaum and Freeman (2000) , we suggest that this abstraction is useful, since it allows us to focus on the relationship between rules and habits, and, in the longer run, to consider the status of rules with respect to the overall statistical space of bilinear mappings.
Our notion of gated working memory is borrowed directly from PBWM, with the operations:
Store the current input into working memory. Both tasks require this; for the 12AX task in particular, the nature of the input determines which of the two components of working memory should be used.
Clear working memory. For the 12AX task, the option of clearing one of the two components without the other is required.
Frank et al. (2001) suggested the involvement of basal ganglia structures via their loops with cortex in implementing such gating operations. As also for them, we employ a localist (i.e., 1 of n) coding for both classes of input (task and color). This is largely for convenience; sparse distributed codes would also work.
The bilinear mapping
This network involves a standard bilinear mapping with binary output units. More formally, given (binary) input vector x, which includes the contents of working memory and the stimulus input, the output oc of unit c is determined stochastically according to:
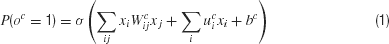
where σ(ζ) = 1∕(1 + exp, (−ζ)) is the conventional logistic sigmoid function. Here, the term involving Wc implements the bilinearity. There is one set of parameters Ωc = {Wc, uc, bc} for each of the output units oc. Note that the architectures of Rigotti and Fusi (2006) and Rigotti et al. (2007) use a different route to generate hidden units with related capacities.
Rather like Frank et al. (2001) themselves, we start by considering whether there is any settings of the whole collection of parameters Ω ={Ωc} that instantiates the required computational structure (we actually use a non-biological learning procedure to find such weights). 2 We do this by specifying a supervised training regime that could come, for instance, if observations of both internally and externally directed actions determined through the operation of the rules was available to the habit learner. In both cases, during training, information about errors in the externally directed actions would be available for each input. Thus, the key requirement is for the internally directed actions (such as preserving in working memory the identity of the current task subcomponent) to be made evident. This also arranges for a form of teaching-forcing (Williams and Zipser, 1989 ) to be effective, with the contents of working memory being determined correctly even when the habitual bilinear mapping is far from being accurate.
We used a gradient-based maximum likelihood method for determining appropriate weights. Outputs without supervision information (such as the non-existent choice between L and R button presses in tasks 1 and 2 of CIOM), do not generate errors and were not considered to be part of the training set. For CIOM, we generated a training set that completely describes all the contingencies. This is not so straightforward for the 12AX task because of the stochasticity associated with the switching between the subcomponents and the colored stimulus inputs themselves. Therefore, we generated a moderate-sized training set (with 384 elements in the sequence) exactly according to the stochastic rules for the task, and trained with that. As will be seen later, this was ample to ensure good quality generalization when we tested on novel input sequences.
The main formal difference between the training and testing regimes for the habits is associated with teacher forcing. During testing, outputs arising stochastically through the operation of the bilinear map are themselves used to determine the state of the working memory. For CIOM, this is very straightforward, because the task makes only such simple demands on working memory. The 12AX task has more complex temporal dependencies, and so this is more challenging.
Rule memory and matching
The rule memory is assumed to be a form of auto-associative storage and recall device. Rules share many computational commonalities with episodic memories, in that there is a large number of closely related patterns that need to be stored in such a way that they are very distinct, and then recalled based on similarity. Of course, other features associated with episodic memory, such as the notion of mental time travel (Tulving, 2002 ), and the explicit storage of substantial context surrounding a memory, are of less importance for rules. We adopt a similar abstraction to that employed by Kali and Dayan (2004) in their work on the relationship between a putatively hippocampal episodic memory and a cortical self-supervised, representational learner which acted as a form of statistical semantic memory.
Recall of potential rules is similar to recall of episodes. This is based on the associative match between the (matching portions of) items in the episodic memory for rules and aspects of the current state, which here includes both the working memory and the stimulus input. The expectation would be that only one, or at most a few, rules would arise as possible associative matches. However, episodic memories and rules differ in terms of the way that they should generalize. Rules should apply only in very particular circumstances that depend on precise matching between their preconditions and particular aspects of the current state. By contrast, episodic recall is less exclusive—a whole range of episodic memories may bear a relevant relationship to any particular state. In particular, rules can have exclusion conditions, that is, requirements that the input state not have a property. These are hard to enforce during associative recall, though easy during bilinear matching.
Therefore, we allow directly for the possibility that a number of rules is retrieved from memory, but allow their preconditions to be precisely tested to determine the existence of an exact match. At present, we only consider rule sets such that a single rule will actually match at any stage in the task; we consider more general possibilities in the discussion. In particular, there are three underlying possibilities for rule matching with respect to the current input state x. We will therefore describe rule r as ar with 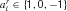 . A detailed match could require that xi = 1 (we use
. A detailed match could require that xi = 1 (we use 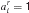 ), could require that xi = 0 (
), could require that xi = 0 (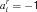 ) or not care (
) or not care (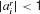 ). It turns out that this can be suitably computed by the bilinear threshold function:
). It turns out that this can be suitably computed by the bilinear threshold function:
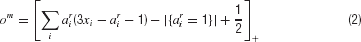
where the threshold can also be seen as the limit of a very steep logistic sigmoid function, and where the term |{ai = 1}| counts the number of required exact matches.
We model associative recall as eliminating all the exclusion conditions, and then using a form of k-winner takes all (similar to that adopted, for instance, by O'Reilly and Munakata, 2000 ). That is, we treat it as calculating
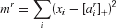
for each rule r, and reporting all those rules that have mr less than or equal to the 1st, 2nd, 3rd … kth, etc smallest, where k is a parameter. In this simple case, we set k = 1, although note that more than one rule can be retrieved if many are equidistant from the current state of input and working memory. Note that the competition embodied in this k-winner takes all rule can also be implemented using multilinearity (Fusi, personal communication).
Once a rule has been recalled and deemed an appropriate match, its associated conditional input-output map needs to be instantiated. In the current, highly simplified, version of the model, we accomplish this by learning an appropriate set of bilinear weights for each rule, and imposing those weights directly. As we will see, the input-output map associated with any particular rule is substantially simpler than (and often a subcomponent of) that associated with the task as a whole. We generate appropriate weights for each rule using the same training procedure as for habits, but based on training sets that are much simpler and smaller, since each rule only has a very limited domain.
We discuss the representational relationship between rules and habits later. Just as in standard accounts of proceduralization (e.g., Anderson, 1982 ), automatization (Logan, 1988 ), or habitization (Daw et al., 2005 ), we would expect the inferential relationship to be that rules would dominate in the early part of behavior, with habits dominating later. However, in the current version of the model, we do not maintain or propagate the uncertainty about the habits that is suggested by Daw et al. (2005) as underlying the switch in control from one system to the other, and therefore just show the separate rule-based and habit-based solutions to the two tasks.
Results
CIOM
As we have indicated, the CIOM task places strong emphasis on the nature of the conditional input-output maps, for the externally directed output, and rather less on the use of working memory. We may therefore expect that the rules and the habitual bilinear forms associated with the internally directed actions to be rather simple—the only requirement on working memory is to store (and preserve) the task identifier.
Habitual learning. Figure 2 shows the course of gradient descent learning (starting from zero weights and using a training set derived from the operation of the rules) for the habitual solution to the task. The output of the habitual model for any input is a probability of doing an action. However, the obvious experimental measure of performance is the reaction time; as reported, for instance, by Koechlin et al. (2003) . We therefore translate between the two for an action under the assumption that the psychologically and neurally popular drift diffusion decision-making model (Smith and Ratcliff, 2004 ) controls the decision, with the magnitude of the drift being determined by the input to the sigmoid for that action. For a simple drift-diffusion model (DDM), the RT and the probability of correct termination are two sides of the same coin. We stress that these RTs should not be thought of as much more than a way of illustrating the course of learning; not only do subjects' actual RTs have substantial non-decision-making components, but also they will likely reflect the operation of both rule-based and habitual control systems to a degree that will change over time (in favor of the latter). We do not attempt to model the reaction times for the rule-based solution, since the dynamics of associative rule retrieval and implementation are not so well explored.
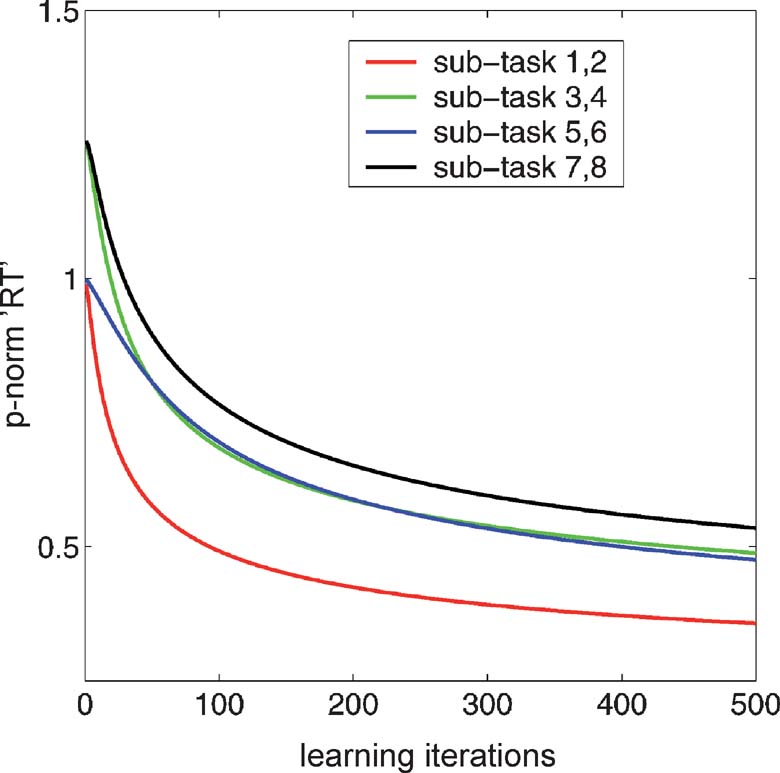
Figure 2. Nominal reaction times for the CIOM task. The curves show p-norm reaction times for the eight different subcomponents of the CIOM task as a function of learning iterations using simple gradient descent. The RTs associated with each individual binary output are derived from the underlying drift diffusion model; and, for the tasks involving an active L∕R choice, are combined using the 3norm. If the bilinear weights are allowed to get arbitrarily large, then the probabilities of each output unit tend toward 0 and 1, and the decision-making RT tends toward 0.
The four learning curves in Figure 2 show the DDM of the reaction times for the four different types of sub-task in the overall problem. For the sub-tasks with only one possible active button press (1,2; 5,6, in red and blue, respectively), the DDM controls the decision e-act about whether or not to perform an externally directed action. For these subcomponents, the decision to act is really a Go∕NoGo task.
For the sub-tasks with a choice between left and right button presses (3,4; 7,8, in green and black, respectively), the RTs reflect two decisions, one to act at all (e-act); and one declaring which action (L∕R). That is, with two different active outputs, the task is no longer merely Go∕NoGo, and so involves more complex, and (judging from Koechlin et al., 2003 ) more time-consuming competition. The RTs associated with the two decisions could be combined in various ways, from a sum to a max (or even as a first-past-the-post rule for the two diffusion processes), depending on the exact nature of the underlying decision-making structure. As a simple compromise, Figure 2 shows the p-norm of the two RTs (where p = 3). The graph shows well the large initial cost of this (black and green curves start substantially above the red and blue curves), although they all decrease appropriately. For this particular p-norm, the costs in terms of RT associated with the two separate factors that Koechlin et al. (2003) identified rapidly become almost equal. That is, the cost of having multiple choices active in a single sub-task (the green curve, for tasks 3,4) is roughly the same as having multiple possible choices across sub-tasks for a stimulus input (the blue curve). This is actually quite consistent with the true reaction times observed by Koechlin et al. (2003) . However, this identity is not strongly robust to the way that the two RTs are combined for the case of tasks 3,4. Nevertheless, the cost of the complexity of the rules in the task is clear in comparing the ease of learning for tasks 1,2 with that for tasks 5,6.
Figure 3 shows the bilinear weights that underlie the performance after all the learning trials in Figure 2 . The format of this plot is described in the Figure caption. As expected from the nature of the task, most of the complexity is shown in those weights for the externally directed output units (top row of Figure 3 ) that are associated with the stimulus input (second half of x). The only internally directed action is to store (and not forget) the identifier. The negative weights along the diagonal associated with the taskWM working memory for the i-act units arise because of the demands of not forgetting the identifier (this is particularly clear by comparison with the weights associated with the store output unit). An artefact of the training set is i.e., assumed that the working memory units had been zeroed between sub-tasks, and so these weights did not influence or affect the task of learning to execute i-act. In fact, these weights are adequate even if a taskWM working memory had still been present; however, this points out a key comparison between rules and habits to do with the former's ready invariance to irrelevant aspects of the (sub-)task.
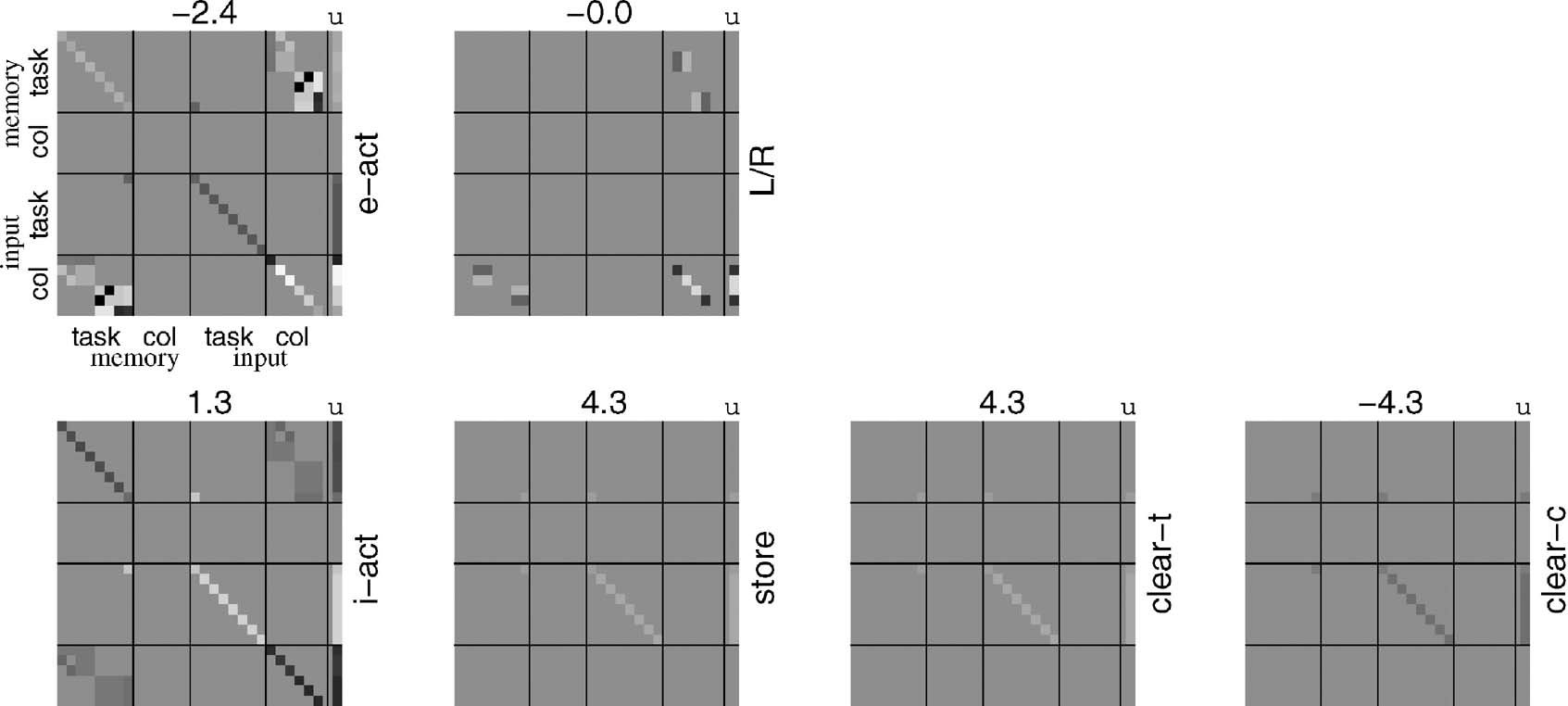
Figure 3. Habit-based weights for CIOM. Each block shows the weights associated with one of the output units; the main matrix shows W, with the state units xi ordered as shown; the last column shows u and the bias b for the unit is given as a number on top. The upper row of blocks is for the two externally directed actions (labels on the right); the lower row is for the four internally directed actions. The range of the gray-scale is determined by the biases ([-4,3,4.3]). Note that W is symmetrical; we show the full matrix for convenience.
Rules. As noted, this task can be solved with two classes of rules: one to store the identifiers, and eight to execute the subcomponents. Under our simple model, the most convenient way to store the identifiers is to have eight separate rules, each of which matches its associated identifier in the input, and then has a trivial input-output mapping which is to execute i-act, clear-t, and store. Matching is straightforward using Equation (2).
The execution of the subcomponents is more interesting. As described in the previous section, one way of doing it is to have matching conditions that depend on two factors: the contents of taskWM working memory being appropriate, and the input itself not being a new task identifier. Then the rules define conditional input-output mappings appropriate to each task subcomponent. Figure 4 shows the e-act and L∕R bilinear forms for four representative subcomponents. By comparison with the form in Figure 3 , they are very simple, since they only concern one part of the more complex overall map, and, indeed, are partly subsets of the dependencies in the full rule. Their forms are readily interpretable given the structure of the sub-tasks presented in Section The Tasks.
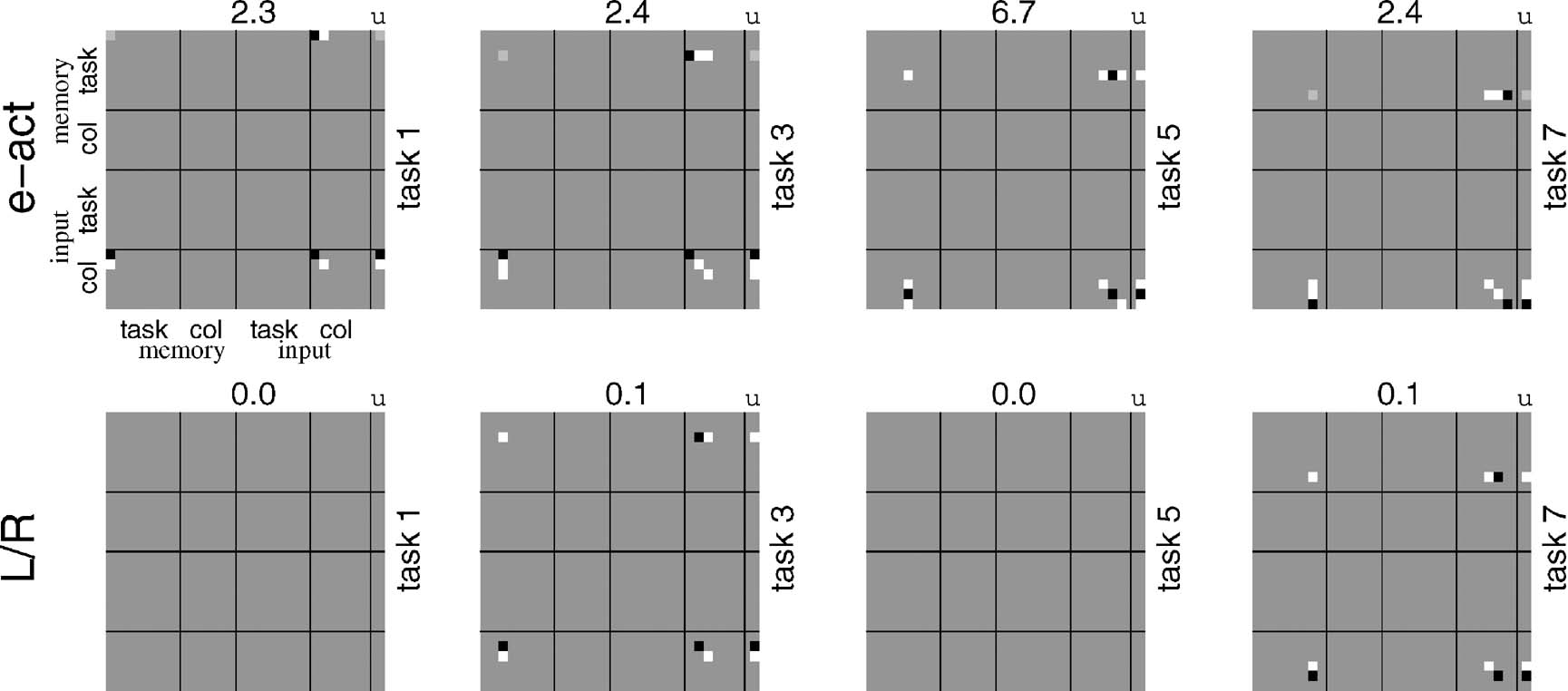
Figure 4. Rules for CIOM. These plots use the same form as in Figure 3 to show the rules for the two key output units, e-act and L∕R. The rules are simple in form, since they only concern individual rules, and also do not need to handle the additional matching conditions.
Figure 5 illustrates the operation of the rules. The top panel shows the inputs and the outputs produced by the model (all of which are correct). The middle panel indicates the number of the rule that matched. Numbers 1–8 are associated with their eponymous subcomponent; numbers 9–16 are the rules that are responsible for storing the task identifiers (1–8, respectively) when they arise. The bottom panel shows how many rules were extracted by the associative memory. During each subcomponent block, only the rule associated with that block is extracted from the rule memory. However, when the identifiers appear (at sequence points 14, 27, and 40 in the figure), the rule associated with switching the task subcomponent is extracted as well. This is because the extra condition that stops the first rule from matching in detail is that there should be no task input; and, as a negative condition, has no effect over associative recall.
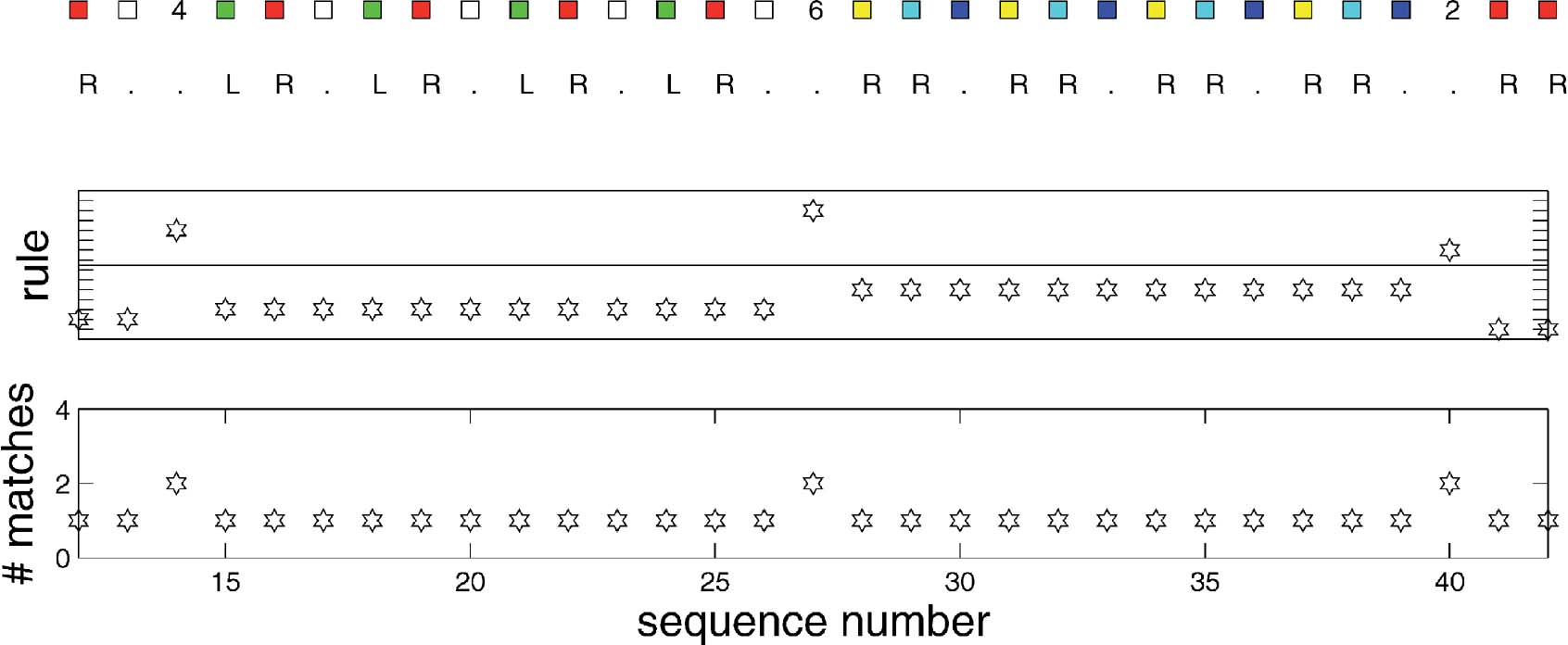
Figure 5. Rule execution for the conditioned input-output task. From the top, these plots show the inputs and output; the identify of the rule that matches, and the number of rules that were associatively extracted. Details in the text.
12AX task
The 12AX task imposes a much heavier burden on the intricacies of working memory than the CIOM task, and therefore we expect that the internally directed actions will exhibit a richer structure.
Habitual learning. Figure 6 shows the course of gradient descent learning for this task. As mentioned, for the 12AX task, it is not so straightforward to specify a complete training set, and so, instead, learning proceeded on the basis of a single, random, input sequence of 384 elements (in this case involving 27 subcomponents, and 57 “AX” or “BY” sub-sequences). The Figure shows the result of testing the bilinear model on fresh, random sequences, of length 200 (each point is the average over 10 different such sequences; the errorbars show the standard deviations), showing the accumulated errors based on stochastic draws from the probabilities associated with each output unit. This includes, for instance, the possibility of inappropriately failing to store the “1” or the “2,” and thereby omitting all the sub-sequences within the sequence. The network evidently learns to perform well.
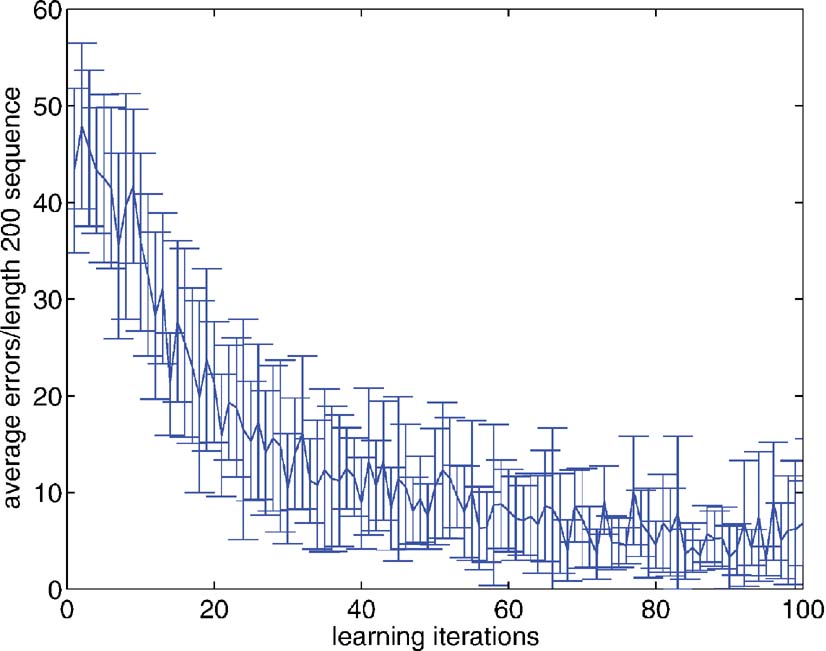
Figure 6. Errors over learning on the 12AX task. The graph shows the average number of errors committed by the network on untrained, random, sequences of length 200. The network was run stochastically, with the probability of executing the action associated with an output unit being determined by its probability.
Figure 7 shows weights suitable for executing the 12AX task, using the same format as in Figure 3 . As expected, the contingencies associated with acting on working memory are now more sophisticated than those associated with those acting externally. Note that only the first two subcomponents of the task input and working memory are involved, and so parts of the matrices are null. Further, an externally directed action is required on every trial, so e-act is driven mostly by its positive bias b.
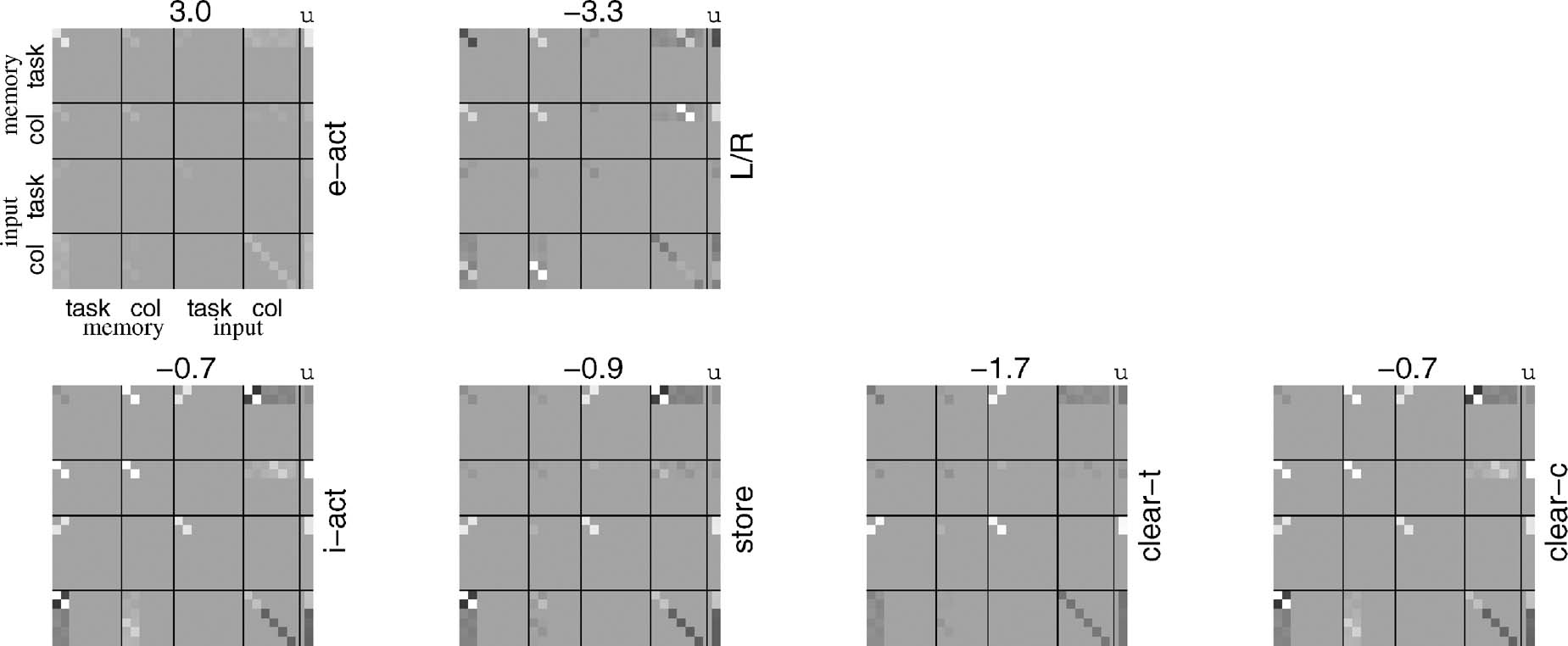
Figure 7. Habit-based bilinear weights for the 12AX task. Weights are shown in the same format as in Figure 3 . Again, the bias terms define the maximum and minimum values across the plots.
Rules. For the particular collection of rules shown in the previous Section, matching plays a greater part than do the conditional input-output maps themselves. For instance, Figure 8 shows an example of the bilinear form associated with the rule indicating what to do at the point “*” in a sequence such as “1 … A*.” The conditional map is simple—if an “X” is shown then press the right button, otherwise press the left button; but in either case, clear color component of working memory unless “A” is shown again. The process of matching deals with all the dependence on working memory; leaving a rule that only depends on the input color. The two conditional aspects of the rule are themselves evident in the L∕R and clear-c blocks in the figure.
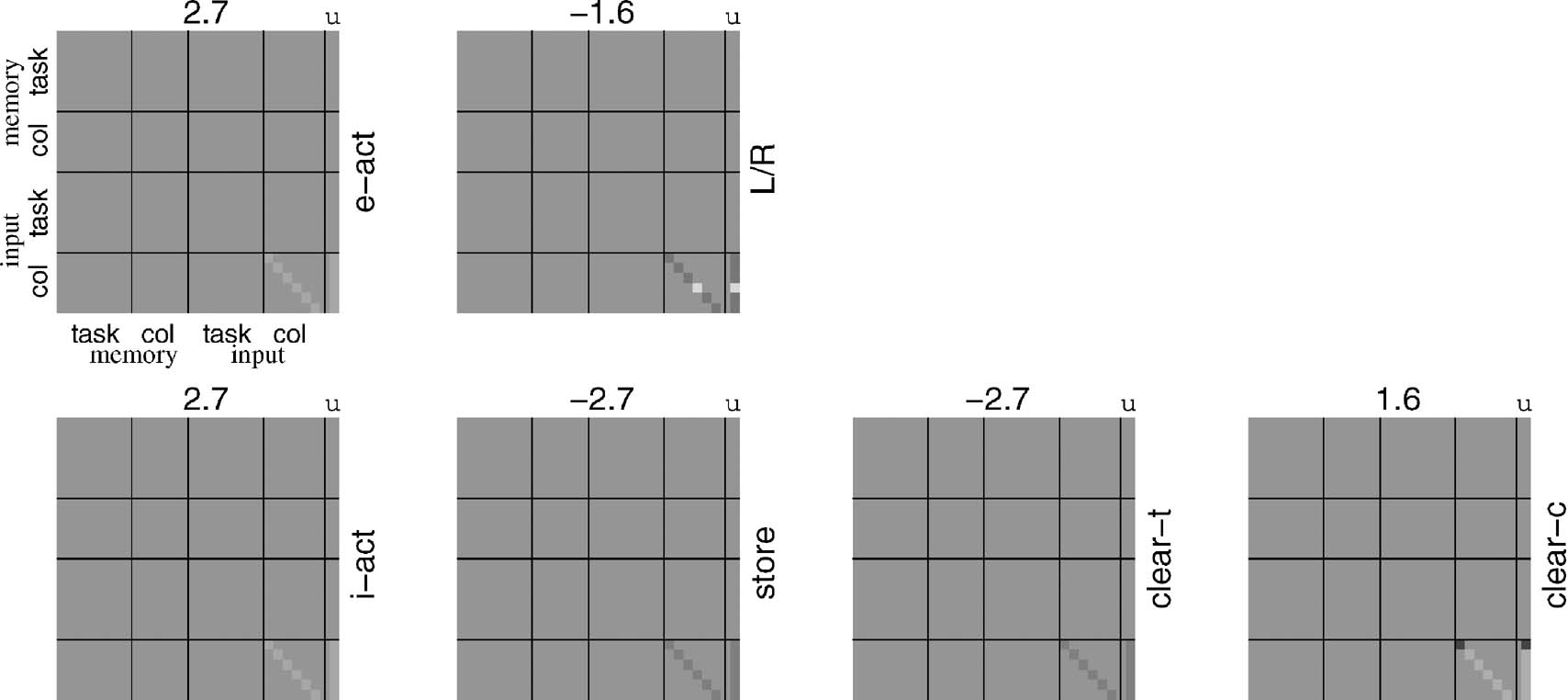
Figure 8. Bilinear form for the fifth rule for the 12AX task. This rule implements the simple input-output map that recognizes the “X” of “AX” in the appropriate subcomponent.
Figure 9 shows the execution of rules, using the same format as in Figure 5 . The much more complicated structure of rule execution is evident; however, it is seething under the bland surface of the near constant output “L.” Again, just a moderate number of rules is recalled from the associative rule memory at any point in the sequence; and, by design of the rules, only a single one matches.
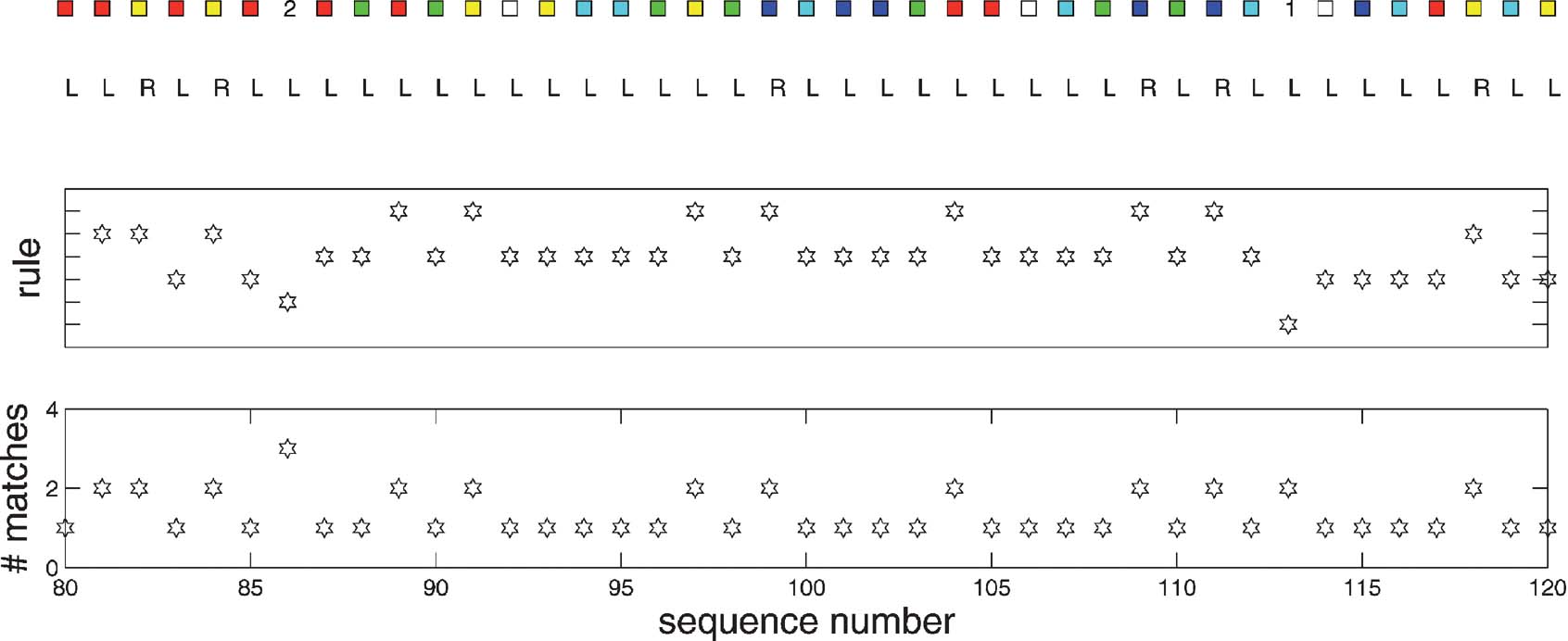
Figure 9. Rule execution for a snapshot of the 12AX task. The figure follows the same format as Figure 5 , showing, from top to bottom, a part of the sequence of inputs and outputs, the identity of the rule that matches, and the number of rules that were recalled from the associative store.
Discussion
Summary and lacunæ
Even though learned habits can allow us to negotiate even the most computationally complex of environments, we have a striking ability for flexible and near instantaneous (re-)programming. Here, we characterized this latter ability in terms of rules, and showed that it is possible to place habitual and rule-based control on a common functional footing with respect to execution. Our architecture has two closely related parts; one that implements conditional input-output mappings; the other that mediates the storage and recall of rules from an associative store, together with precise matching of the conditions of the rules to the state of the working memory and stimulus input. Both the conditional input-output mapping and the rule matching involved bilinear computations (followed by binary decisions), as a straightforward generalization away from a single, feedforward, layer of processing. We showed how habits and rules could solve two paradigmatic cognitive tasks that probe complex conditional input-output mappings and working memory, and contrasted properties of the solutions.
As already mentioned, the most significant lacuna in this work is the actual implementation of the bilinear mapping and matching processes. This part of the model was partly based on some general computational notions taken from work on multiplicatively gated working memory (Frank et al., 2001 ; Hazy et al., 2006 , 2007 ; O'Reilly and Frank, 2006 ) that has taken great pains with systems physiological verisimilitude; further, models such as basis function networks Olshausen et al. (1993) , Poggio (1990) , and Pouget (1997) shifter circuits embody nearly equivalent computations. The work of Rigotti and Fusi (2006) and Rigotti et al. (2007) shows another systematic approach to generating the required complexity of interactions. Of course, precise bilinearity is unlikely to be an algorithmically accurate description of underlying processes. Thus, one pressing direction for future work is to understand how it may be implemented, working on the basis of the conditional computations in models such as PBWM or those of Rigotti and Fusi (2006) and Rigotti et al. (2007) , but in the context of a much richer architecture of prefrontal connectivity and processing, as elucidated, for instance by Brass and von Cramon (2002 , 2004 ) and Bunge (2004) . A related lacuna is associated with learning; we mainly concentrated here on the existence of solutions, understanding how they can be credibly acquired is also critical.
Further, we made the tacit assumption that the execution of a rule ultimately depends on the same underlying bilinear architecture as the execution of a habit. Although as we discuss below, this is attractive from the statistical perspective of the relationship between rules and habits, it does pose a challenging issue about how habitual synaptic efficacies can be acquired in a structure whilst a different conditional input-output mapping is being instantiated.
Relationship to previous work
Close cousins of our work are the PBWM architecture and those of Rigotti and Fusi (2006) and Rigotti et al. (2007) , from which the habitual part of our model borrowed extensively. In particular, we purloined the nature and control of working memory from PBWM, that is, that input information separated into different types (task identifiers and colors) can be separately stored, that a major computational role is played by gating the storage of information into or out of activity-based, persistent working memory, and indeed that the control of external actions (such as pressing a response button) is of a piece with the control of internal actions (such as storing an input into working memory). PBWM implements gating in a rather particular manner, using striato-thalamo-cortical feedback in a stripe; we have considered a more abstract scheme, with multilinear interactions, which can implement more general input-output mappings. In this respect, our work is closer to that of Rigotti and Fusi (2006) and Rigotti et al. (2007) , who consider input-output rules of the form that we have studied, and investigate the importance of hidden units in solving complex cognitive tasks.
The most salient difference from these notions involves the rules themselves. In execution, each individual rule just specifies a rather simple input-output mapping; the problems arise in compiling the instructions provided for a task into a complete collection of rules; storing the rules in an associative memory; retrieving them based on similarity to the current state; testing their detailed match; and then executing them. Only the execution is as for a single input-output mapping in PBWM; the remaining tasks are different. We provided algorithmic solutions to all the problems apart from compilation, and have argued that they require not much more of the substrate than is typically assumed in other domains.
Koechlin et al. (2003) and Koechlin and Summerfield (2007) used their CIOM task to elucidate the localization of different aspects of control. They suggest that the various orthogonal factors underlying their task design were each separately represented in different areas in dorsolateral prefrontal cortex, creating an overall hierarchy. Hierarchical models of various sorts have long been of enduring interest—for instance, Badre and D'Esposito (2007) suggested a related representational hierarchy on the basis of an experiment that parametrically manipulated information about response, cues, and context. Since it is not based on these hierarchies, it is incomplete (although we do comment below about the hierarchical statistical decomposition of the bilinear forms). However, our model, like others, does pose a question about habitization in these tasks. There is no reason to think that even such a complex task would not, in the end, become habitized, like many others. It is not quite clear the point in the process at which the experimental data were collected, and thus how the conclusions about localization would change over the course of acquisition and expression. Any such changes might break the compelling link between the abstract, informational demands of the task, and the particular hierarchical realization across prefrontal cortex. Clearly, there remains an enduring requirement for working memory in the task; however, many structures, even outside prefrontal cortex (see, e.g., Major and Tank, 2004 ), exhibit persistent activity, the putative substrate of working memory (e.g., Fuster, 1997 ; Goldman-Rakic, 1995 ), and so the necessity for the persistent involvement of high level prefrontal structures is not clear.
We have concentrated on the links to suggestions about prefrontal cortical function and the relationship between habits and rules, but there are some relevant suggestions about implementing forms of (human) rule processing Anderson (1976) , Johnson-Laird (1983) , Newell and Simon (1972) , and Sacerdoti (1977) in neural-, or at least connectionist-like systems (see Hinton, 1991 ). For instance, Touretzky and Hinton (1988) suggested a model called Distributed Connectionist Production System (DCPS). DCPS involves a working memory consisting of a (possibly large) number of active “triples” over (abstract) entities (to be thought of as logical statements such as “ABC”) together with a number of rules that execute if they match the current set of triples, with the effect of adding new triples, or taking away some old ones. Both triples and rules are implemented using random distributed (binary) representations, and rule matching, which could also perform a primitive form of unification, involves an operation similar to that in our associative memory, namely settling in a Hopfield network (Hopfield, 1982 ) or Boltzmann machine (Hinton and Sejnowski, 1986 ), but in the context of a specific architectural design. DCPS is a very different solution to ours, designed more as a connectionist model of a general-purpose production system than as a model for cognitive computations. However, its use of distributed representations rather than localist ones as employed by us (following Frank et al., 2001 ) is important, as is the operation, though not the instantiation, of unification.
Shastri and Ajjanagadde (1993) suggested another interesting connectionist-inspired model of chains of first-order logical reasoning. This model employs a form of temporal encoding, using something akin to phases within an underlying, synchronous, oscillation to indicate the role that a literal plays (so, for instance, it encodes “John gives a book to Mary” by having units representing “John” and “giver” firing at one phase; “Mary” and “recipient” at another phase; and “Book” and “given-object” firing at a third phase). Rules are instantiated via explicit, phase-sensitive connections. Thus, unlike DCPS and our model, adding an extra rule involves quite some manipulation to the structure of the network, rather than just the contents of a rule memory; it also places heavy demands on temporally exact wiring and processing. However, the model does have substantial attractive logical prowess, performing variable unification and binding.
Extensions
Our model can be extended in various ways. First, part of the complexity of the rule sets was predicated on a requirement that only one rule should ultimately match at any point in a trial sequence. It would be more natural to specify a number of rules that all match, but to allow some to be more important than others. This would also allow a default rule, specifying the input-output mapping if nothing else matched at all. This could readily be achieved via the associative matching process, if the order in which it suggests possible rules is influenced by this hierarchy; implementing this may be less straightforward.
A second extension would be to uncertainty. A key facet of Daw et al.'s (2005)
discussion of goal-directed and habitual actions in conditioning experiments is that the decision between these two structures should depend on their relative uncertainties. As in standard normative treatments of Bayesian cue integration (Clark and Yuille, 1990
), the more certain a source of information, the greater the weight it should have in determining choice. In this paper, we did not model the uncertainties, and so did not capture the transfer of behavioral control through habitization. Certainty in the rule set could come along with imperfect knowledge about the rules and be captured using 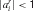 for matches and non-matches. Uncertainty in the habits could be learned though monitoring errors. However, as discussed by Daw et al. (2005)
, this would be much more difficult in the case of full sequential decision-making problems such as that posed by the 12AX task. We would definitely expect habitual performance ultimately to dominate, given the computational challenges and expense involved in the use of rules.
for matches and non-matches. Uncertainty in the habits could be learned though monitoring errors. However, as discussed by Daw et al. (2005)
, this would be much more difficult in the case of full sequential decision-making problems such as that posed by the 12AX task. We would definitely expect habitual performance ultimately to dominate, given the computational challenges and expense involved in the use of rules.
A third issue is a subtle constraint on the matching process itself. The two tasks we modeled can be solved in such a way that the matches are always prespecified (for instance, for the CIOM, matching the task stimulus input to a particular number). However, in more general cases it is desirable to make the matching conditions be variable—for instance, to require that the contents of the taskWM working memory match the task input, whatever it happens to be. For instance, at least given appropriate training, chimpanzees can learn an abstract delayed response task in which their responses at the time of a test stimulus array should depend on whether or not the two objects presented at the sample time were identical (Thompson et al., 1997 ). Computing such a match is a straightforward bilinear computation; specifying what should match with what could be more involved. There are potentially also even more complex aspects to matching, such as the variable specification that happens as part of the unification matching operation in prolog and that the systems of Shastri and Ajjanagadde (1993) and Touretzky and Hinton (1988) can instantiate. It is not clear how essential a component this would be for the range of cognitive tasks that have so far been used.
Fourth is the relationship between representational learning and both rules and habits. A conventional view of representational learning is that it proceeds in a self-supervised manner, providing representations that make task learning simpler (Hinton and Ghahramani, 1997 ). For instance, in CIOM, if the representation of the input stimulus was augmented with a bit indicating whether or not it was a subcomponent identifier, then the eight rules used to indicate the need to store these identifiers could be collapsed to a single rule. The associated habit form would also become substantially simpler. In this case, representational learning would be creating what Hinton (1981) called a microfeature—a semantically relevant component of the representation of a stimulus. In our simple case, this microfeature could, for instance, be learned from functional similarity between these stimuli; self-supervised learning can make representationally explicit, general facets of the statistics of the inputs.
A fifth extension would be to the more general use of episodic memory. At present, rules are assumed to be stored in a form of long-term memory, or at least to persist across the duration of each task as a whole. However, the observation that humans can execute rules with branching subroutines suggests that it is also interesting to consider whether information about the current state of working memory and rule execution could be stored in a shorter term episodic store at the initiation of a branch, and then recalled at the end. One prevalent (though not uncontested Burgess et al., 2007 ) idea is that fronto-polar cortex has a particular role to play in branching (e.g., Braver and Bongiolatti, 2002 ; Koechlin et al., 1999 ), and also in the links with episodic memory (reviewed in Christoff and Gabrieli, 2000 ); which may be a relevant confluence. Once coupled with this capacity, it would become particularly pressing to understand the formal computational capacity of the model, along with what would be necessary to make it more computationally universal.
Rules and habit statistics
The most essential structural extension to the present work has to do with more fundamental questions about the relationship between rules and habits. One attractive direction is to consider the structure of the overall statistical space of habits, and then to consider how rules fit into this structure. This approach has been considered in the domain of motor control (e.g., Sanger, 1995 ; Todorov, 2004 ), and has obvious application to cognitive control too.
We referred above to work on representational learning as potentially providing a source of semantically relevant microfeatures that would aid both rules and habits (Hinton and Ghahramani, 1997 ). The idea underlying this is that the sensory inputs occupy a low dimensional structure in the extremely high dimensional space of all inputs, and that learning identifies a new, typically non-linear, coordinate system that characterizes this structure. For instance, one popular such characterization is in terms of the independent components of the overall space (Bell and Sejnowski, 1995 ). The microfeatural representation of an input is then the location in this new coordinate system of an input; it will be useful if each coordinate captures something fundamental about the inputs as a whole. In one class of models, top-down connections in cortex instantiate a generative or synthetic model, indicating where a location in the new coordinate system maps to in input space; bottom-up connections an analytical or recognition model (Dayan et al., 1995 ; Hinton and Zemel, 1994 ; Hinton et al., 1995 ; Mumford, 1994 ; Neisser, 1967 ; Rao and Ballard, 1999 ), which implements the possibly complex map from a new input into its underlying coordinates.
In our case, self-supervised learning would determine a coordinate system appropriate to the statistical space of habits (i.e., the bilinear forms associated with them). Then the rules that we can be represented would be simply specified in terms of this coordinate system, with the top-down, generative, model provides the mechanism for instantiating a rule. This is exactly the scheme that Kali and Dayan (2004) employed in allowing the contents of medial temporal episodic memory to recreate a whole pattern in input posterior cortical units.
It is as (habitual) behavioral capacities grow that this statistical space, and therefore the space of rules, gets richer and more complex. In our case, the recognition process of determining the coordinates underlying a particular habit is not so critical. More important is the compilation process, taking a typically verbal description of a problem and turning it into the underlying rules and matching conditions, analogous to, just for instance, the way that Johnson-Laird et al. (1992) and Johnson-Laird (1983) consider parsing verbal descriptions and generating their preferred psychological construct (mental models). In studying complex tasks with very many rules, Duncan (personal communication) has pointed out that subjects may frequently not perform this compilation step adequately thoroughly, and thereby miss out important contingencies in the task. Indeed once the mechanisms for rule implementation are determined, it is compilation, and the rules and habits that underlie compilation, that will be the remaining homuncular mystery.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that should be construed as a potential conflict of interest.
Acknowledgements
I am very grateful to Kai Krueger for extensive discussions and comments on an earlier draft, to Stefano Fusi for a most thought-provoking exchange and helpful suggestions on the manuscript, to David Badre and Mark D'Esposito for sharing data prior to publication, and to Paul Burgess, Tim Shallice and Wako Yoshida and two reviewers for their constructive observations and comments. Funding was from the Gatsby Charitable Foundation.
Appendix
In this appendix we provide details of the model and the training regimes.
The network has 14 input units, one each for 8 possible task subcomponent identifiers (this is for the CIOM task; only 2 are used for 12AX) and the 6 input colors. These employ localist coding. There are also 14 working memory units. Output unit oc is defined by a collection of weights (28 × 28 for the bilinear form Wc; 28 for the linear term uc and 1 for the bias bc). In this case, this representation is redundant, since only the symmetric part of Wc affects the task; and, for binary inputs, 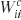 plays the same role as
plays the same role as 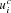 . However, we used the more general form for completeness, and it does not prevent the gradient descent learning rule from working.
. However, we used the more general form for completeness, and it does not prevent the gradient descent learning rule from working.
Learning of the weights for habits is supervised, as if successful execution of the rules of the task provided a correct assignment of all the output units o for each input in the sequence. As mentioned in the text, this includes the effect of teacher forcing, in the sense that the contents of working memory will always be set to be correct throughout learning, even at a point at which the habitual outputs are not yet appropriate.
For the CIOM, a complete training set can be specified, with one input-output case for storing the identifiers for each of the subcomponents; and then three input-output cases for each of the color-output mappings in each subcomponent (including the repeats for the subcomponents with only two possible inputs). The complete training set for CIOM is therefore 32 cases with 28 inputs defining the state (including the input and the working memory) and 6 outputs. Outputs that are immaterial (the blank entries in Table 2 ) do not generate errors and therefore do not influence the course of learning.
Learning used the conjugate gradient, line-search-based minimize routine kindly provided by Carl Rasmussen (http://www.kyb.tuebingen.mpg.de/bs/people/carl/code/minimize/ ). For Figure 2 for the CIOM task, nominal reaction times were calculated assuming a drift-diffusion decision-making process for which the probability pc = P(oc) for action c is turned into a reaction time rtc according to
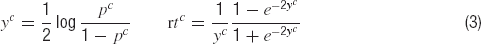
as if the drift rate of a DDM with unit noise is set to ensure the appropriate probability pc and the reaction time calculated. When habitual performance is tested, teacher forcing is not active, so store and clear-t (and, were it to have been used, clear-c) are under the direct control of the habitual output.
For the 12AX task, the sequential structure and randomness makes it hard to generate a compact, comprehensive training set. Instead, a pseudo-random sample of 384 input patterns was used, with a probability of switching between “1” and “2” sub-tasks of 1∕20 per pattern, and a probability of inserting a “AX” or a “BY” in each sub-task of 1∕5. Unlike some variants of the task, all the other letters were chosen at random, equiprobably. The rest of the training proceeded as for the CIOM task. When being tested, a new pseudo-random sequence of inputs, based on a new seed, was generated.
Each rule is implemented by a bilinear map that is just like the bilinear map of one of the habits that was just presented. However, the input-output mapping for each rule is substantially simpler than for the whole habit, since it only needs to represent a highly restricted set of cases (as apparent in Tables 2 and 4 ). These input-output mappings are taught to the network in the same manner as above, but using training sets that are restricted precisely to the domain of each rule. Thus, for instance, for the CIOM task, each rule for a subcomponent only involves three cases, one for each colored square that might be presented (including repeats for some subcomponents). Likewise, for the 12AX task, it is not necessary to generate random sequences of input patterns, since the sequential structure of the task arises from the matching and execution of the rules rather than the rules themselves. For example, each of the lower four rules in Table 4 only involves six training cases, one for each color.
Footnotes
- ^ There are obviously many possible variants of the task with different statistics for the different sub-parts. Although this is critical for some aspects of learning (Krueger and Dayan, 2007 ), it is not central for our present concerns.
- ^ Hazy et al. (2006 , 2007 ), O'Reilly and Frank (2006) , and O'Reilly et al. (2007) went on to show that the weights required for their model could be acquired through a modified form of reinforcement learning.
References
Alexander, G. E., and Crutcher, M. D. (1990). Functional architecture of basal ganglia circuits: neural substrates of parallel processing. Trends Neurosci. 13(7), 266–271.
Badre, D., D'Esposito, M. (2007). FMRI evidence for a hierarchical organization of the prefrontal cortex. J. Cogn. Neurosci. doi: 10.1162/jcon.2007.91201 .
Badre, D., Poldrack, R. A., Pare-Blagoev, E., Juliana amd Insler, R. Z., and Wagner, A. D. (2005). Dissociable controlled retrieval and generalized selection mechanisms in ventrolateral prefrontal cortex. Neuron 47(6), 907–918.
Bell, A. J., and Sejnowski, T. J. (1995). An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 7(6), 1129–1159.
Boettiger, C., D'Esposito, M. (2005). Frontal networks for learning and executing arbitrary stimulus-response associations. J. Neurosci. 25(10), 2723–2732.
Brass, M., and von Cramon, D. (2002). The role of the frontal cortex in task preparation. Cereb. Cortex 12(9), 908–914.
Brass, M., and von Cramon, D. (2004). Decomposing components of task preparation with functional magnetic resonance imaging. J. Cogn. Neurosci. 16(4), 609–620.
Braver, T., and Bongiolatti, S. (2002). The role of frontopolar cortex in subgoal processing during working memory. Neuroimage 15(3), 523–536.
Braver, T. S., Barch, D. M., Kelly, W. M., Buckner, R. L., Cohen, N. J., Mienzin, F., Snyder, A. Z., Ollinger, J. M., Akbudak, E., Conturo, T. E., and Petersen, S. E. (2001). Direct comparison of prefrontal cortex regions engaged in working and long-term memory tasks. NeuroImage 14, 48–59.
Braver, T. S., and Cohen, J. D. (2000). On the control of control: the role of dopamine in regulating prefrontal function and working memory. In Control of Cognitive Processes: Attention And Performance XVIII (Cambridge, MA, MIT Press), pp. 713–737.
Bunge, S. A. (2004). How we use rules to select actions: a review of evidence from cognitive neuroscience. Cogn. Affect. Behav. Neurosci. 4(4), 564–579.
Burgess, P. W., Simons, J. S., Dumontheil, I., and Gilbert, S. J. (2007). The gateway hypothesis of rostral prefrontal cortex (area 10) function. Trends Cogn. Sci. 11(7), 290–298.
Christoff, K., and Gabrieli, J. D. E. (2000). The frontopolar cortex and human cognition: evidence for a rostrocaudal hierarchical organization within the human prefrontal cortex. Psychobiology 28(2), 168–186.
Clark, J. J., and Yuille, A. L. (1990). Data fusion for sensory information processing systems. (Norwell, MA, Kulwer).
Cohen, J. D., Braver, T. S., O'Reilly, R. C. (1996). A computational approach to prefrontal cortex, cognitive control and schizophrenia: recent developments and current challenges. Philos. Trans. R. Soc. Lond. 351, 1515–1527.
Cohen, J. D., Perlstein, W. M., Braver, T. S., Nystrom, L. E., Noll, D. C., Jonides, J., and Smith, E. E. (1997). Temporal dynamics of brain activation during a working memory task. Nature 386(6625), 604–608.
Cooper, R., and Shallice, T. (2006). Hierarchical schemas and goals in the control of sequential behavior. Psychol. Rev. 113, 887–916.
Daw, N. D., Niv, Y., and Dayan, P. (2005). Uncertanty-based competition between prefrontal and dorsolateral striatal system for behavioral control. Nature Neurosci. 8(12), 1704–1711.
Dayan, P., Hinton, G. E., Neal, R. M., and Zemel, R. S. (1995). The Helmholtz machine. Neural Comput. 7, 889–904.
D'Esposito, M., Postle, B., and Rypma, B. (2000). Prefrontal cortical contributions to working memory: evidence from event-related fMRI studies. Exp. Brain Res. 133(1), 3–11.
Dickinson, A. (1985). Actions and habits: the development of behavioural autonomy. Philos. Trans. R. Soc. Lond. B Biol. Sci. 308(1135), 67–78.
Durstewitz, D., and Seamans, J. K. (2002). The computational role of dopamine D1 receptors in working memory. Neural Netw. 15(4–6), 561–572.
Frank, M. J., Loughry, B., O'Reilly, R. C. (2001). Interactions between frontal cortex and basal ganglia in working memory: a computational model. Cogn. Affect. Behav. Neurosci. 1(2), 137–160.
Frank, M. J., Seeberger, L. C., O'Reilly, R. C. (2004). By carrot or by stick: cognitive reinforcement learning in parkinsonism. Science 306(5703), 1940–1943.
Fusi, S., Assad, W. F., Miller, E. K., and Wang, X. J. (2007). A neural circuit model of flexible sensorimotor mapping: learning and forgetting on multiple timescales. Neuron 54(2), 319–333.
Fuster, J. M. (1997). The prefrontal cortex: anatomy, physiology, and neuropsychology of the frontal lobe, 3rd edn (New York, NY, Raven Press).
Gevins, A. S., and Cutillo, B. C. (1993). Neuroelectric evidence for distributed processing in human working memory. Electroencephalogr. Clin. Neurophysiol 87, 128–143.
Hazy, T. E., Frank, M. J., O'Reilly, R. C. (2006). Banishing the homunculus: making working memory work. Neuroscience 139(1), 105–118.
Hazy, T. E., Frank, M. J., O'Reilly, R. C. (2007). Toward an executive without a homunculus: computational models of the prefrontal cortex∕basal ganglia system. Philos. Trans. R. Soc. B 362(1485), 1601–1613.
Hinton, G. E. (1981). Implementing semantic networks in parallel hardware. In Parallel Models of Associative Memory, G. E. Hinton, and J. A. Anderson, eds. (Hillsdale, NJ, Lawrence Erlbaum), pp. 161–188.
Hinton, G. E. (1990). Mapping part-whole hierarchies into connectionist networks. Artif. Intell. 46(1–2), 47–75.
Hinton, G. E., Dayan, P., Frey, B. J., and Neal, R. M. (1995). The wake-sleep algorithm for unsupervised neural networks. Science 268(5214), 1158–1161.
Hinton, G. E., and Ghahramani, Z. (1997). Generative models for discovering sparse distributed representations. Philos. Trans. R. Soc. B 352(1358), 1177–1190.
Hinton, G. E., and Sejnowski, T. J. (1986). Learning and relearning in Boltzmann machines. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations, D. E. Rumelhart, and J. L. McClelland, eds. (Cambridge, MA, MIT Press), pp. 282–317.
Hinton, G. E., and Zemel, R. S. (1994). Autoencoders, minimum description length, and Helmholtz free energy. Adv. Neural Inf. Process. Syst. 6, 3–10.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Nat. Acad. Sci. 79(8), 2554–2558.
Johnson-Laird, P. N., Byrne, R. M. J., and Schaeken, W. (1992). Propositional reasoning by model. Psychol. Rev. 99(3), 418–439.
Kali, S., and Dayan, P. (2004). Off-line replay maintains declarative memories in a model of hippocampal-neocortical interactions. Nature Neurosci. 7(3), 286–294.
Koechlin, E., Basso, G., Pietrini, P., Panzer, S., and Grafman, J. (1999). The role of the anterior prefrontal cortex in human cognition. Nature 399(6732), 148–151.
Koechlin, E., and Jubault, T. (2006). Broca's area and the hierarchical organization of human behavior. Neuron 50(6), 963–974.
Koechlin, E., Ody, C., and Kouneiher, F. (2003). The architecture of cognitive control in the human prefrontal cortex. Science 302(5648), 1181–1185.
Koechlin, E., and Summerfield, C. (2007). An information theoretical approach to prefrontal executive function. Trends Cogn. Sci. 11(6), 229–235.
Koenderink, J. J., and Van Doorn, A. J. (1997). The generic bilinear calibration-estimation problem. Int. J. Comput. Vis. 23(3), 217–234.
Krueger, K. A., and Dayan, P. (2007). Flexible shaping: how learning in small steps helps. In COSYNE 2007.
Lund, J. S., Yoshioka, T., and Levitt, J. B. (1993). Comparison of intrinsic connectivity in different areas of macaque monkey cerebral cortex. Cereb. Cortex 3(2), 148–62.
Major, G., and Tank, D. (2004). Persistent neural activity: prevalence and mechanisms. Curr. Opin. Neurobiol. 14(6), 675–684.
Miller, E. K., and Cohen, J. D. (2001). An integrative theory of prefrontal cortex function. Ann. Rev. Neurosci. 24, 167–202.
Mumford, D. (1994). Neuronal architectures for pattern-theoretic problems. In Large-Scale Neuronal Theories of the Brain, C. Koch, and J. Davis, eds. (Cambridge, MA, MIT Press), pp. 125–152.
Olshausen, B. A., Anderson, C. H., and Van Essen, D. C. (1993). A neurobiological model of visual attention and invariant pattern recognition based on dynamic routing of information. J. Neurosci. 13(11), 4700–4719.
O'Reilly, R. C., and Frank, M. J. (2006). Making working memory work: a computational model of learning in the prefrontal cortex and basal ganglia. Neural Comput. 18(2), 283–328.
O'Reilly, R. C., Frank, M. J., Hazy, T. E., and Watz, B. (2007). PVLV: the primary value and learned value Pavlovian learning algorithm. Behav. Neurosci. 121(1), 31–49.
O'Reilly, R. C., and Munakata, Y. (2000). Computational explorations in cognitive neuroscience: understanding the mind by simulating the brain (MA, USA, MIT Press Cambridge).
Owen, A. M., McMillan, K. M., Laird, A. R., and Bullmore, E. (2005). N-back working memory paradigm: a meta-analysis of normative functional neuroimaging studies. Hum. Brain. Mapp. 25(1), 46–59.
Pasupathy, A., and Miller, E. K. (2005). Different time courses of learning-related activity in the prefrontal cortex and striatum. Nature, 433: 873–876.
Poggio, T. (1990). A theory of how the brain might work. Cold Spring Harb. Symp. Quant. Biol. 55, 899–910.
Pouget, A. (1997). Spatial transformations in the parietal cortex using basis functions. J. Cogn. Neurosci. 9(2), 222–237.
Pucak, M. L., Levitt, J. B., Lund, J. S., and Lewis, D. A. (1996). Patterns of intrinsic and associational circuitry in monkey prefrontal cortex. J. Comp. Neurol. 376(4), 614–630.
Rao, R. P. N., and Ballard, D. H. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nature Neurosci. 2(1), 79–87.
Rigotti, M., Ben Dayan Rubin, D., Wang, X.- J., and Fusi, S. (2007). The importance of neural diversity in complex cognitive tasks. In Society for Neuroscience Annual Meeting (Washington, DC, Society for Neuroscience).
Rigotti, M., and Fusi, S. (2006). Modeling event drives transitions between attractors of the neural dynamics. In Society for Neuroscience Annual Meeting, pp. 569.14∕LL5.Q4
Rougier, N. P., Noelle, N. P., Braver, T. S., Cohen, J. D., O'Reilly, R. C. (2005). Prefrontal cortex and flexible cognitive control: rules without symbols. Proc. Nat. Acad. Sci. 102(20). 7339–7343.
Rowe, J. B., Toni, I., Josephs, O., Frackowiak, R. S. J., and Passingham, R. E. (2000). The prefrontal cortex: response selection or maintenance within working memory? Science 288(5471), 1656.
Sakai, K., and Passingham, R. (2003). Prefrontal interactions reflect future task operations. Nature Neurosci. 6(1), 75–81.
Shastri, L., and Ajjanagadde, V. (1993). From simple associations to systematic reasoning: a connectionist representation of rules, variables, and dynamic bindings using temporal synchrony. Behav. Brain Sci. 16(3), 417–494.
Smith, P. L., and Ratcliff, R. (2004). Psychology and neurobiology of simple decisions. Trends Neurosci. 27(3), 161–168.
Tenenbaum, J. B., and Freeman, W. T. (2000). Separating style and content with bilinear models. Neural Comput. 12(6), 1247–1283.
Thompson, R., Oden, D., and Boysen, S. (1997). Language-naive chimpanzees (Pan troglodytes) judge relations between relations in a conceptual matching-to-sample task. J. Exp. Psychol. Anim. Behav. Process. 23(1), 31–43.
Touretzky, D., and Hinton, G. (1988). A distributed connectionist production system. Cognitive Sci. 12(3), 423–466.
Wang, X. J. (2002). Probabilistic decision making by slow reverberation in cortical circuits. Neuron 36(5), 955–968.
Williams, G. V., Goldman-Rakic, P. S. (1995). Modulation of memory fields by dopamine D1 receptors in prefrontal cortex. Nature 376, 572–575.
Williams, R. J., and Zipser, D. (1989). Experimental analysis of the real-time recurrent learning algorithm. Connect. Sci. 1(1), 87–111.
Keywords: habits, rules, bilinearity, working memory, prefrontal cortex, basal ganglia
Citation: Peter Dayan (2007). Bilinearity, rules, and prefrontal cortex. Front. Comput. Neurosci. 1:1. doi: 10.3389/neuro.10/001.2007
Received: 9 August 2007;
Paper pending published: 27 August 2007;
Accepted: 12 October 2007;
Published online: 2 November 2007.
Edited by:
Misha Tsodyks, Weizmann Institute of Science, Rehovot, IsraelReviewed by:
Stefano Fusi, Center for Theoretical Neuroscience, Columbia University, USA; Institute of Neuroinformatics, ETH Uni Zurich, Switzerland.Florentin Woergoetter, University of Goettingen, Goettingen, Germany
Copyright: © 2007 Dayan. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Peter Dayan, Gatsby Computational Neuroscience Unit, UCL, London, UK. e-mail:ZGF5YW5AZ2F0c2J5LnVjbC5hYy51aw==