Department of Physiology, University of Bern, Switzerland
The unsupervised categorization of sensory stimuli is typically attributed to feedforward processing in a hierarchy of cortical areas. This purely sensory-driven view of cortical processing, however, ignores any internal modulation, e.g., by top-down attentional signals or neuromodulator release. To isolate the role of internal signaling on category formation, we consider an unbroken continuum of stimuli without intrinsic category boundaries. We show that a competitive network, shaped by recurrent inhibition and endowed with Hebbian and homeostatic synaptic plasticity, can enforce stimulus categorization. The degree of competition is internally controlled by the neuronal gain and the strength of inhibition. Strong competition leads to the formation of many attracting network states, each being evoked by a distinct subset of stimuli and representing a category. Weak competition allows more neurons to be co-active, resulting in fewer but larger categories. We conclude that the granularity of cortical category formation, i.e., the number and size of emerging categories, is not simply determined by the richness of the stimulus environment, but rather by some global internal signal modulating the network dynamics. The model also explains the salient non-additivity of visual object representation observed in the monkey inferotemporal (IT) cortex. Furthermore, it offers an explanation of a previously observed, demand-dependent modulation of IT activity on a stimulus categorization task and of categorization-related cognitive deficits in schizophrenic patients.
Natural stimuli such as shapes, colors, tones, or flavors vary along a continuum. Humans are nevertheless able to classify objects according to these smoothly varying features into distinct categories via unsupervised stimulus exposure, without being taught what the categories should comprise. Furthermore, whether we can consistently classify the spectrum between red and green into different hues, for instance, depends on the level of attention and the desired classification granularity. Monkeys performing such a color categorization task in fact show different visual responses in the inferotemporal (IT) cortex to the same hue depending on how fine the required categorization is (Koida and Komatsu, 2007
). How, in general, can discrete categories form out of continuously changing features even if the statistics of stimulus appearance may not define clear category boundaries a priori? And how does the brain internally tune the granularity of categories that emerge from mere exposure to similar continua of stimuli?
Existing neural network models of stimulus classification do not adequately answer these questions. In particular, they do not explain the mechanisms via which the categories can be dynamically modulated by internal signals. Classical categorization networks, such as those used in vector quantization (see Hertz et al., 1991
for a review), assume a discrete number of pre-existing output units, each of which is intended to label a stimulus category after learning. A fixed number of pre-defined classes is also assumed in models studying the classification of continuously morphed objects in a feedforward network (Freedman et al., 2003
) or of discrete objects in a network with top-down modulation (Ardid et al., 2007
; Deco and Rolls, 2005
; Szabo et al., 2006
). The formation of new categories has been modeled by means of adding further output units to the network (Carpenter, 1987a,b
), although it is not clear how the process of adding these units can be implemented in neuronal terms. Instead, new categories may naturally emerge in a recurrently connected network when the stimuli are drawn from a clustered distribution (Rosenthal et al., 2001
) or from a distribution with temporal correlations (Bartlett and Sejnowski, 1998
). Neither work, however, has addressed the internal modulation of the number of emerging categories. Similarly, the deformation of pre-existing attractor networks by morphed stimuli has recently been studied (Bernaccia and Amit, 2007
; Blumenfeld et al., 2006
), but the question of how the categorization granularity may depend on internal cortical states remains an open issue. The notion of categorization granularity is related to the sparseness of cortical activity (Abeles et al., 1990
; Fuster, 1990
; Rolls and Tovee, 1995
), which is known to increase the memory capacity (Treves and Rolls, 1991
; Tsodyks and Feigel’mann, 1988
). The latter theoretical works, however, assumed clamping of the neuronal activities to the inputs and did not address the dynamic self-organization of the attractors.
Many experimental findings reveal that the stimulus representation is significantly modulated by internal cortical states, e.g., those reflecting awareness (Rodman et al., 1991
), emotions (Godinho et al., 2006
), attention (Fontanini and Katz, 2006
; Reynolds and Chelazzi, 2004
), or the task to be performed (Boudreau et al., 2006
; Koida and Komatsu, 2007
; Rainer et al., 2004
). Here we consider such a task- or attention-induced top-down modulation of the neuronal gain (McAdams and Maunsell, 1999
; Reynolds and Chelazzi, 2004
) and of the inhibitory feedback within a biologically plausible recurrently connected network model of IT (Dong et al., 2004
; Hestrin and Galarreta, 2005
). We show how this top-down modulation of the neuronal properties affects the formation of cortical categories under exposure to equiprobable, continuously varying stimuli. The category formation is enabled by slow homeostatic (Turrigiano and Nelson, 2004
) and Hebbian (Brown and Chatterji, 1994
) synaptic plasticity that equalize the average neuronal activity and stabilize simultaneously active neuronal ensembles in the network. As a result, the cortical network is divided in a self-organized manner into a discrete set of distinct subnetworks forming stable stimulus categories.
Top-down input indirectly modulates global competition among neurons in the network: the stronger the top-down input—resulting in stronger global inhibition—the fewer neurons can be active at the same time, and the greater number of distinct subnetworks will emerge, each representing a different category. The number of categories can be naturally adjusted because the categorical representation is based on attractor formation. Instead of labeling input patterns by single output units, classification is achieved by a prototype representation consisting of an ensemble of many neurons. This ensemble can be divided up or combined with other ensembles depending on the strength of the global modulatory signal, leading to fine or coarse stimulus classification.
Our model also captures several characteristic nonlinearities of cortical object representation observed in the monkey IT cortex, a higher visual area believed to extract categorical object information (Kiani et al., 2007
) and displaying persistent activity (Miyashita, 1988
). This area appears to represent objects not by the sum of the cortical columns representing the individual parts, but rather by a combination of activating and inactivating these columns (Tsunoda et al., 2001
). Furthermore, partial blockade of inhibition nonlinearly alters the stimulus selectivity for an individual IT neuron (Wang et al., 2000
). We show that these phenomena are simple consequences of cortical category formation in a competitive recurrent network endowed with Hebbian and homeostatic plasticity.
Finally, based on our model, we make a non-trivial prediction: a top down-induced global gain increase in the IT should not lead to an increase in neuronal activity, but, on the contrary, to the narrowing of the IT activity to smaller cortical patches, and hence to a general decrease in the neuronal activity. Such an activity decrease is in fact observed in the monkey IT on a task demanding finer classification in a color categorization experiment (Koida and Komatsu, 2007
). In the model this shrinking of activity arises due to a top-down-induced increase in competition mediated by global inhibition, and the same mechanisms may also apply to the experiment. The fact that the categorization granularity can be modulated by a global, unspecific signal also makes our model attractive for studying cognitive deficits related to the pathological lumping or splitting of categories as observed in schizophrenic patients (Keri et al., 1999
).
The model IT consists of N recurrently connected excitatory neurons and Q inhibitory feedback neurons. Each excitatory IT neuron further receives feedforward input from M excitatory (V1) neurons which also project via inhibitory neuron to IT (see Figure 1
). The number of neurons was chosen to be N = 100 (except in Figure 8
where N = 400), Q = 4, and M = 25.
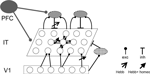
Figure 1. Model network. A two-dimensional sheet of neurons, e.g., representing the inferotemporal cortex (IT), receives bottom-up input from a lower visual area (for example, V1) as well as global top-down input, e.g., from prefrontal cortex (PFC), imposed by some global cortical state. V1 projects to IT through direct excitation (upwards arrows) and via global inhibition (checker oval). IT neurons are also recurrently connected via (semi-) global inhibitory neurons (shaded ovals). Top-down input uniformly increases the gain of the IT neurons and/or drives the recurrent inhibition. Synaptic weights marked with an arrow are subject to Hebbian plasticity. Synapses marked with a full arrow are additionally modulated by homeostatic plasticity which scales the connection strengths as a function of the average postsynaptic activity (Materials and Methods).
Dynamics of Excitatory IT Neurons
In view of the encoding in IT by mean firing rates (Aggelopoulos et al., 2005
), we describe the activity of our excitatory model IT neurons, yiE, by low-pass filtering the total excitatory and inhibitory synaptic currents, IiE and IiI. In addition to the noisy input patterns we also consider synaptic noise acting on the total synaptic currents (realized by the Gaussian variables ηi of mean 0 and standard deviation 0.1 per unit time, corresponding to 10% of the maximum activity level). The dynamics of the excitatory neurons are as follows:
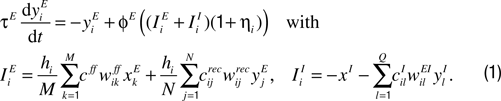
Here hi is a homeostatic factor which scales the excitatory synaptic inputs, xkE and xI represent the firing rates of the excitatory and inhibitory feedforward input neuron(s), and the ylI represent the firing rates of the recurrent inhibitory neurons. The w’s represent plastic synaptic efficacies between 0 and 1, and the c’s represent fixed connectivity parameters (see below). The neuronal time constant was set to τE = 20 ms. The connectivity parameters cff, cijrec and cilI specify the anatomical connections between the involved neurons. The feedforward connectivity is globally set to cff = 50 (for the recurrent connectivity see below).
The current-to-rate transfer function ΦE(I) was chosen to be the commonly used sigmoidal one:

with I0 = 0.5, and σ = 0.5, except for Figures 6 and 8
, where σ = 1. The maximum firing rate is set to fmax = 1 except for Figure 3
D where it was explicitly modulated. We assume that fmax (and thus of the gain of the input-output transfer function) can increase with the strength of the top-down input Itd, although we do not explicitly introduce this dependency into our model (but see Larkum et al., 2004
).
Dynamics of Feedforward Inhibition
In addition to direct feedforward excitation there is global feedforward inhibition of the IT neurons. This feedforward inhibition is mediated by a single model neuron representing a population of tightly connected inhibitory neurons (Hestrin and Galarreta, 2005
). It is linearly driven by the total stimulus activity,

with the time constant τI = 1 ms and connectivity parameter 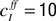 .
.
Dynamics of Feedback Inhibition
Competition among the IT neurons is enabled by inhibitory neurons which are driven by a large subset of excitatory IT neurons and feed back to them. The activity of these inhibitory feedback neurons is governed by
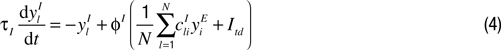
With a threshold-linear transfer function 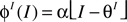 such that
such that 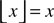 if x > 0 and
if x > 0 and 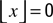 otherwise. The inhibitory transfer function ΦI is sketched in Figure 3
. The inhibitory threshold is set to θI = 4 in all simulations and α = 2, except for Figures 6 and 8
, where α = 1. The connectivity parameter cliI defines a rectangular projection field as explained below. The top-down input is set to Itd = 3 for Figures 4
, 6 and 8
. Otherwise, Itd is equal to 2.5 for Figure 2
C, 3.5 for Figure 2
D, and 3.75 for Figure 2
E and Figure 3
C. We further set Itd to 1.5 for Figure 2
F, and to 2 for Figures 3
B, 5
, and 9
. The top-down input Itd in the face categorization simulations (Figure 7
) was set from top to bottom by 3.5, 3 and 2.
otherwise. The inhibitory transfer function ΦI is sketched in Figure 3
. The inhibitory threshold is set to θI = 4 in all simulations and α = 2, except for Figures 6 and 8
, where α = 1. The connectivity parameter cliI defines a rectangular projection field as explained below. The top-down input is set to Itd = 3 for Figures 4
, 6 and 8
. Otherwise, Itd is equal to 2.5 for Figure 2
C, 3.5 for Figure 2
D, and 3.75 for Figure 2
E and Figure 3
C. We further set Itd to 1.5 for Figure 2
F, and to 2 for Figures 3
B, 5
, and 9
. The top-down input Itd in the face categorization simulations (Figure 7
) was set from top to bottom by 3.5, 3 and 2.
Hebbian Plasticity
All connection strengths to the excitatory neurons, 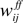 ,
, 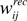 , and
, and 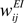 , are subject to Hebbian modifications. Hebbian long-term potentiation (LTP) is induced if the pre- and postsynaptic activity are both high, while long-term depression (LTD) is induced if the presynaptic activity is high, but the postsynaptic activity low. We also consider multiplicative synaptic bounds which restrict the weights to be within the interval [wmin, 1]. Formally, Hebbian plasticity takes the form
, are subject to Hebbian modifications. Hebbian long-term potentiation (LTP) is induced if the pre- and postsynaptic activity are both high, while long-term depression (LTD) is induced if the presynaptic activity is high, but the postsynaptic activity low. We also consider multiplicative synaptic bounds which restrict the weights to be within the interval [wmin, 1]. Formally, Hebbian plasticity takes the form
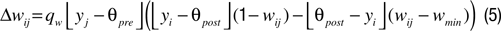
with modification thresholds θpre = 0.25 and θpost = 0.3, learning rate qw = 0.01, much slower that that of neuronal dynamics, and  defined as above. In all simulations we set wmin = 0.1, so that homeostatic plasticity could exercise its beneficial effects, while in Figures 4 and 5
we set wmin = 0.01 for wijrec. The synaptic weights were updated once per stimulus presentation based on the averaged activity (see below).
defined as above. In all simulations we set wmin = 0.1, so that homeostatic plasticity could exercise its beneficial effects, while in Figures 4 and 5
we set wmin = 0.01 for wijrec. The synaptic weights were updated once per stimulus presentation based on the averaged activity (see below).
Homeostatic Plasticity
Unlike Hebbian plasticity, homeostatic plasticity acts independently of presynaptic activity. It aims at maintaining the postsynaptic activity around a certain target value, here chosen to be the Hebbian modification threshold θpost given above. Including again multiplicative saturation the homeostatic variables change according to
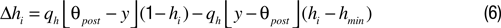
with minimal value hmin = 0.1 and a modification rate qh = 0.01 being the same as the rate for the Hebbian changes (cf. Discussion and Supplementary Material). Homeostatic updates are performed once per stimulus presentation together with the Hebbian updates.
Recurrent Excitatory Connectivity
To capture the 2-D structure we consider some mapping of the N excitatory neurons to the 2-D grid of size 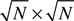 with integer-valued coordinates. Denoting the coordinates of neuron i by (ai, bi), the Euclidean distance between neuron i and j becomes
with integer-valued coordinates. Denoting the coordinates of neuron i by (ai, bi), the Euclidean distance between neuron i and j becomes 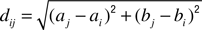 , and the connectivity parameter between these two neurons is set to cijrec = coexp(−dij|do), with do representing the connectivity decay length in terms of neurons. We set do = 7 and co = 415.8 for all figures, except Figure 8
A, where do = 0.7 and co = 2036.45 were used to prevent the lumping of IT activity into a single activity patch (we postulate a narrow type of excitation as compared to broad inhibition, as this was also assumed in other modeling studies, see, e.g., Miller, 1996
or Song and Abbott, 2000
). In Figure 8
the network was wired on a 2-D torus (so that the opposite edges became effectively adjacent) to minimize boundary effects. Note that with a mapping of 10 × 10 neurons onto an IT patch of 4 × 4 mm2 a decay length of 7 neurons maps to 2.8 mm, a number which is consistent with the axonal spread observed in IT (Tanigawa et al., 2005
).
, and the connectivity parameter between these two neurons is set to cijrec = coexp(−dij|do), with do representing the connectivity decay length in terms of neurons. We set do = 7 and co = 415.8 for all figures, except Figure 8
A, where do = 0.7 and co = 2036.45 were used to prevent the lumping of IT activity into a single activity patch (we postulate a narrow type of excitation as compared to broad inhibition, as this was also assumed in other modeling studies, see, e.g., Miller, 1996
or Song and Abbott, 2000
). In Figure 8
the network was wired on a 2-D torus (so that the opposite edges became effectively adjacent) to minimize boundary effects. Note that with a mapping of 10 × 10 neurons onto an IT patch of 4 × 4 mm2 a decay length of 7 neurons maps to 2.8 mm, a number which is consistent with the axonal spread observed in IT (Tanigawa et al., 2005
).
Recurrent Inhibitory Connectivity
Feedback inhibition is organized in Q = 4 semiglobal patches tiling the 2 D cortical sheet into 4 non-overlapping square-shaped subsheets indexed by l = 1,…,4. Each of these subsheets is associated with an inhibitory neuron forming uniform connections onto and from the excitatory neurons within the subsheet, but not to or from the others. The connectivity parameters for neuron i in subsheet l are set to be cilI = 20 and cliI = 10, and for a neuron j outside this subsheet cjlI = cljI = 0.
Stimuli
A stimulus was applied by clamping the activities xiE of the model V1 neurons to 0 or 1. In Figure 2
, the morphed stimuli were defined by sliding a bar of length 10 across the input array. Formally, for input pattern μ (μ = 1,…,10) the activity of the i’th neuron in the input array was set to xiE = xiE(μ) = 1 + ηi for μ ≤ i ≤ μ + 10 and otherwise 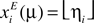 (with i = 1,…,M). Here, ηi is Gaussian random variable with mean 0 and standard deviation 0.05, yielding 5% of noise on the stimuli.
(with i = 1,…,M). Here, ηi is Gaussian random variable with mean 0 and standard deviation 0.05, yielding 5% of noise on the stimuli.
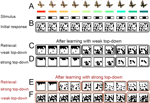
Figure 2. Emergence of distinct activity patterns in response to a continuum of stimuli is modulated by unspecific top-down input. (A) Strongly overlapping, continuously varying stimuli (bottom) with possible real-world counterparts (top, see also Koida and Komatsu, 2007
). (B) Before learning, all stimuli evoke the same random activity patterns in the IT model network (binarized activities, 400 ms after onset of stimulation with the pattern shown in the same column above; black is active, and white is silent). (C) After 2000 random presentations of the stimuli in the presence of weak top-down input, grouped network activity spontaneously appears forming 3 categories of contiguous stimuli (for convenience, solid lines are drawn around response patterns defining a distinct category). (D) The 3 cortical categories do not change immediately if the top-down input strength is increased, despite the increased competition which reduces the overall activity within each attractor. (E) If the top-down input is strong during learning, 5 instead of the 3 stable categories emerge. (F) These 5 categories can be merged again into 3 by reducing the top-down input without any need for re-learning.
To show that the model can also cope with input patterns of varying coding level we further chose a stimulus set with each pattern μ (μ = 1,…,P) being a subset of the next one as shown in Figure 3
A. Formally, we defined xiE = xiE(μ) = 1 + ηi for 1 ≤ i ≤ μ + 1 and 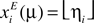 otherwise (with i = 1,…,M). This set consisted of P = 20 patterns and was applied from Figure 3
onwards. Noise was defined in the same way as for the first stimulus set.
otherwise (with i = 1,…,M). This set consisted of P = 20 patterns and was applied from Figure 3
onwards. Noise was defined in the same way as for the first stimulus set.
Learning Procedure
Prior to learning, all synaptic weights (wijff, wijrec and wijEI) were randomly and uniformly initialized in the interval [wmin, 1](with wmin = 0.1), except in Figure 4
where wijrec was initialized to [0.01, 0.25] and in Figure 5
where for convenience the initial values were set to a narrow interval for visualizing the synaptic dynamics. Similarly the homeostatic factors were randomly and uniformly initialized in [hmin, 1] (with hmin = 0.1). The neuronal activities at stimulus onset were initialized to 0, except in Figure 4
where prior to stimulus presentation the stimulus-free steady state activities evolved. A single stimulus presentation (‘trial’) lasted for at least 400 ms until steady-state activity was approached, at which stage the synaptic weights and homeostatic factors were updated based on the average activity across the last 100 ms.
All simulations were performed using the forward Euler method with a step size of dt = 0.2 ms.
The Model Network
We consider a recurrently connected network of excitatory neurons representing a two-dimensional cortical sheet and receiving synaptic input from a lower area (Figure 1
). Such a network could be realized in any cortical area where persistent activity is observed. To be specific, we think of the IT as a possible instantiation, with the input layer being some lower visual area, e.g., the primary visual cortex (V1).
There are two types of inhibition in the model, both are global and fast compared to the plasticity time scale (below). Feedforward inhibition is driven by the summed activity in the input layer and uniformly inhibits the excitatory neurons within the network. Because the strength of this inhibition scales with the total input activity, feedforward inhibition tends to keep the effective input (actual input together with feedforward inhibition) to the recurrent network constant. Recurrent inhibition, on the other hand, implements a negative feedback driven by the integrated activity of the excitatory neurons. This second type of inhibition introduces competition and leads to the suppression of weakly active neurons by the strongly active ones. The network can be further modulated for purposes of changing the categorization granularity. This is achieved by a modulation of global cortical states which, e.g., globally tunes the gain of the excitatory neurons or the excitability of the recurrent inhibition (see Materials and Methods). Here we assume that these changes are mediated by a top-down signal from the prefrontal cortex (PFC), but other modulatory signals are also conceivable.
We endowed the excitatory feedforward and recurrent synapses, as well as the inhibitory synapses mediating the recurrent inhibition, with slow, local Hebbian plasticity (Figure 1
). Hebbian plasticity increases the synaptic strength if both presynaptic and postsynaptic activities are high, and decreases it if the presynaptic activity is high, but the postsynaptic activity low. The excitatory feedforward and recurrent synaptic strengths onto each IT neuron are further scaled by a common homeostatic factor depending on the postsynaptic neuronal activity only, but not on that of any presynaptic neurons. Slow homeostatic plasticity decreases this synaptic factor whenever the postsynaptic activity is above some threshold, and strengthens it if the postsynaptic activity is subthreshold (Materials and Methods).
Formation of Cortical Categories
To test whether our recurrent network partitions a stimulus continuum into distinct categories, we randomly initialized all the synaptic strengths and repeatedly presented the stimuli in a random order (Figure 2
A, with morphed butterflies being a possible real-world analogue or color hues as used in Koida and Komatsu, 2007
). The IT model network is initially prone to converge to a unique attractor state, despite different stimuli being applied (Figure 2
B). After repeated stimulus presentations, however, distinct sets of contiguous input patterns are mapped to distinct sets of output neurons (cortical categories), with sharp transitions of the neural responses at the category boundaries (Figure 2
C).
This categorization emerges based on the fast recurrent dynamics and the slow joint effects of the homeostatic and Hebbian synaptic plasticity. Initially, there is only a single attractor. This attractor is formed by neurons each of which is predisposed to fire because initially it was randomly assigned a strong homeostatic factor, scaling all the excitatory inputs, and a weak recurrent inhibitory weight. These highly excitable neurons fire for all stimuli due to the strong recurrent connectivity and form the single attractor. The other neurons, initially less excitable, are suppressed by the recurrent inhibition driven by these highly excitable cells. During the ongoing presentation of stimuli the excitability of these neurons decreases due to the homeostatic plasticity, while the excitability of the non-activated neurons increases. Therefore, eventually every neuron in the network is enabled to be activated by some of the input patterns. Competition induced by the fast recurrent inhibition keeps the different response patterns apart as soon as they form, although the input patterns have strong overlaps. The ongoing slow Hebbian plasticity reinforces and stabilizes these response patterns and leads to the formation of distinct attractor subnetworks, each representing a separate category.
The number of emerging attractors depends on the strength of the competition during the learning process. A coarse-grained categorization with only a few attractors emerges if the competition is weak (Figure 2
C), and a fine-grained categorization if the competition is strong (Figure 2
E). Competition is strengthened by increasing the gain of the excitatory neurons or by increasing the excitability of the recurrent inhibitory feedback neurons. Both mechanisms are assumed to be induced by the top-down input. Increasing this modulatory input leads to an earlier recruitment of the recurrent inhibition by less active IT neurons and results in smaller attractor sizes. Since more of these smaller attractors are required to uniformly cover the whole network, more categories eventually emerge.
Once the categories have formed, one may ask whether the granularity of categorization can be dynamically changed by adjusting the top-down input, without further learning. It is in fact possible to ‘zoom out’ from a learned, fine-grained categorization, to a coarse-grained categorization by simply reducing the top-down input after learning (Figure 2
F). This dynamic top-down modulation of the categorization granularity may correspond to the demand-dependent IT activity observed in monkey experiments performing a fine or coarse-grained color categorization task (Koida and Komatsu, 2007
; see also Discussion). No dynamic increase in the number of categories is possible if the previous learning was only performed with weak top-down input. Increasing the strength of the top-down input during a subsequent recall then merely narrows each attractor, without refining the granularity of the categorization (Figure 2
D).
Estimating the Number of Emerging Categories
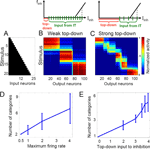
We next explored the impact of global network properties on tuning the granularity of categorization. In our model, we considered two ways in which the top-down input can affect the size and number of categories. First, a strong top-down input can depolarize the recurrent inhibitory neuron(s) to some subthreshold value, thus making them more responsive to the recurrent input (cf. the diagrams for weak and strong top-down input in Figure 3
, top). Alternatively, an additional gain increase in the excitatory IT neurons increases their impact on the recurrent inhibitory neurons so that the inhibition is activated by fewer presynaptic IT neurons. In either case, the same suppression level is therefore reached with a smaller number of active IT neurons (Figure 3
C) when the top-down input is stronger, resulting in a fine-grained categorization with more categories (each of which now contains fewer active cells). Thus, varying the maximum firing rate of the excitatory neurons (which also changes their gain) or the top-down drive to the recurrent inhibition independently results in modulating the size and number of emerging categories (Figures 3
D,E, respectively). In contrast to Figure 2
, we chose stimuli with varying mean activity level to show that the size of the emerging attractors does not depend on the activity level of the input. Note that each higher-numbered stimulus completely contains all the previous ones, yielding maximal overlap for stimuli with different mean activity.
We can also understand this modulation more quantitatively. Homeostatic plasticity forces the average activation of each neuron to be approximately the same across time and hence across stimuli (columns with fixed neuron in Figures 3
B,C). Moreover, due to the feedforward and feedback inhibition, the total number of active IT neurons, Nact, is approximately the same across stimuli (rows with fixed stimulus in Figures 3
B,C) given a certain top down input strength. The total postsynaptic current to an inhibitory feedback neuron, Iinh, is therefore approximately constant for different stimuli and takes the form Iinh = Itd + Nact · w · fmax, where Itd is the top-down input to recurrent inhibition, and Nact · w · fmax is the recurrent input generated by the active IT neurons which fire with saturation frequency fmax (model neurons tend to saturate due to strong recurrent connections) and project with synaptic weight w (fixed in all simulations) to the inhibitory neuron (cf. the diagrams in Figure 3
). The overall activity of the network is regulated by the strength of the feedback inhibition Iinh which itself remains approximately constant, independently of the top-down input. To understand why Iinh is constant, we consider the network in a stable equilibrium state, having learned in the presence of a certain value of Itd. As this equilibrium represents an isolated stable state of the recurrent dynamics, it is associated with a distinct value of the total drive Iinh to the global inhibition. If we now continuously change Itd, at least in a restricted range, this equilibrium drive Iinh must remain the same. Then, the change in Itd must be compensated by the corresponding change in the number of active neurons Nact, e.g., Nact must decrease if Itd increases.
To estimate the number of emerging categories we assume that the different attractor states approximately tile the whole IT network into distinct subnetworks. The total number of IT neurons, N, is therefore the sum of the neurons within these distinct subnetworks, N = C · Nact, where C is the number of subnetworks, and hence the number of categories. Solving the last two equations for the number of categories yields C = N · w · fmax /(Iinh − Itd). This confirms that the number of categories emerging from unsupervised learning is proportional to the top-down modulated maximum firing rate fmax of the excitatory IT neurons (cf. Figure 3
D). Similarly, more categories form by increasing the gain of the neuronal transfer function, being equivalent to increasing the connection strength w. The above formula also explains why the number of categories is a nonlinearly increasing function of the top-down input Itd to the inhibitory neurons (cf. Figure 3
E).
Figure 3. Top-down input can modulate the granularity of categorization via excitatory gain modulation or competitive inhibition. (A) Morphed input patterns with strong overlap and smoothly increasing activation level. (B) 3 stable categories develop after exposure to the stimuli (unsupervised learning during 2000 presentations). The initial connectivity was random. The excitatory neurons of the 2-D IT network are aligned along the X axis, sorted such that neurons activated by the same stimulus appear consecutively. Each row represents normalized IT response to the corresponding stimulus averaged across 300–400 ms after stimulus onset (at the end of learning) and each column, the individual neuronal responses to all stimuli. (C) Increasing the top-down input leads to the formation of 6 stable categories with partial overlaps. Diagrams above show the total postsynaptic current Iinh driving the inhibitory neuron at rate finh (dashed vertical line) for the cases of weak (left) and strong (right) top-down modulation. This current is composed of the top-down input (red bar) and the output of the active presynaptic IT neurons (green segments, stretched in the case of high gain). With strong top-down input, fewer IT neurons need to be active to produce the same inhibition. (D,E) Number of categories formed as a function of the maximum firing rate of the excitatory IT neurons and the top-down input to the inhibitory neurons, respectively.
Emergence of Persistent Activity
As we have demonstrated in the previous sections, the individual categories are represented by emergent distinct IT subnetworks. These subnetworks shrink when the categorization is fine-grained, and enlarge when it is coarse-grained. Each individual subnetwork represents an attractor that is activated by the multiple stimuli. Only due to the attractor property will different stimuli within the same category eventually activate the same network state.
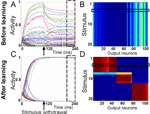
An interesting further possibility which we explored was whether the attractor states would remain stable not only in the presence of the stimuli, but after stimulus withdrawal as well. This would allow for an efficient memorization of the stimuli (represented by their category) by the same attractor states which also served for the categorization in the first place. We have found that such double functionality of the attractor states does in fact develop in our model network (Figure 4
).
Figure 4. Following learning, stimulus-selective network activity persists after stimulus withdrawal. (A) Prior to learning, the responses of the IT model neurons to a stimulus presentation decay when the stimulus is withdrawn 100 ms after stimulus onset. (B) Activity of the IT neurons after stimulus withdrawal, averaged across the time window highlighted with the dashed box in panel A. The horizontal box indicates the stimulus for which the neuronal responses are shown in panel A. (C) After learning, the activity of a stimulus-selective set of neurons stays high even when the stimulus has been withdrawn. (D) Post-stimulus activity as shown in panel B, but after 2000 pattern presentations. Categories have formed that are represented by stable attractor subnetworks. Thus, the input pattern has been memorized in the form of its category and is no longer required to maintain the same response of the network.
Throughout the learning process we assume that the presentation of a new stimulus resets the network activity to some low initial state. Prior to learning, neuronal activities that accumulated during an early part of the trial (single stimulus presentation) decay to some arbitrary, but stable activity levels after stimulus withdrawal (Figure 4
A). These activity states are the same for all input patterns and no stimulus selectivity develops (Figure 4
B). After learning, all the neurons are clearly separated into two groups, with stable high and low activities after stimulus removal, respectively (Figure 4
C). Note that in the first 30 ms after stimulus presentation the activity of IT neurons increases due to feedforward activation, while the recurrent excitatory connectivity and recurrent inhibition are responsible for the subsequent separation into the high and low activity states. The delay with which neuronal activities bifurcate into the high and low states depends on the ratio between excitatory and inhibitory connection strengths. The binary neuronal activities form an attractor state which is the same for a subset of stimuli (Figure 4
D). In the current example three stable attractor states, which classify the 20 input patterns into three categories, emerge.
Synaptic Dynamics Underlying Category Formation
The self-organized category formation in our network model stems from a dynamic interplay between homeostatic and Hebbian synaptic plasticity on the slow time scale. In this section, we consider individual synaptic time courses of all synapses in the network to uncover the role of each of the mechanisms underlying category formation. Synaptic efficacies are updated after each stimulus presentation based on the averaged activity at the end of the stimulus presentation (Materials and Methods). The homeostatic process first compensates for unequally distributed activities across neurons and transiently moves the synaptic dynamics to an unstable equilibrium point (Figure 5
A). The system then hovers near this point with little homeostatic change; Hebbian plasticity begins to dominate and eventually pushes the recurrent connections to either the upper or lower limit (Figure 5
B) while the overall activities of the neurons remain unchanged (as revealed by the homeostatic factor). The emerged discrete attractor structure remains stable during the ongoing presentation of the morphed stimuli: a tenfold extension of the learning phase to 50000 trials does not result in any significant changes (Figures 5
A–D). Such a long-run stability in response to morphed stimuli is not necessarily guaranteed in other attractor networks which do not involve stabilization mechanisms such as recurrent inhibition and homeostatic plasticity (cf. Blumenfeld et al., 2006
).
Figure 5. Evolution of synaptic variables during the course of unsupervised learning explains category formation. (A) Homeostatic factors hi modulate all excitatory input to the corresponding neurons and transiently correct for the initial random imbalance in the postsynaptic firing rates before settling to a new stable state. (B) After homeostatic plasticity has approximately equalized the activities of all neurons over time, Hebbian plasticity spontaneously separates recurrent synaptic weights 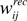 into high and low activity states, reinforcing some and weakening other connections. (C) Hebbian plasticity in recurrent inhibitory weights
into high and low activity states, reinforcing some and weakening other connections. (C) Hebbian plasticity in recurrent inhibitory weights 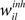 is functionally equivalent to the homeostatic process. (D) Hebbian plasticity in feedforwardsynaptic weights
is functionally equivalent to the homeostatic process. (D) Hebbian plasticity in feedforwardsynaptic weights 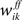 supports the formation of cortical categories, but due to the strongly overlapping stimuli the separation is incomplete. Each trial consists of a 400 ms presentation of a randomly chosen stimulus (shown in Figure 3
A). For better visualization the synaptic dynamics is only turned on after the first 50 trials.
supports the formation of cortical categories, but due to the strongly overlapping stimuli the separation is incomplete. Each trial consists of a 400 ms presentation of a randomly chosen stimulus (shown in Figure 3
A). For better visualization the synaptic dynamics is only turned on after the first 50 trials.
Different ways of implementing the slow synaptic processes could be considered in order to obtain category formation. Hebbian plasticity at the recurrent inhibitory synapses, for instance, has a somewhat similar effect of balancing the neuronal activity as that of the homeostatic plasticity at excitatory synapses, and in fact, the two processes have a similar learning time course (Figures 5
A,C). This arises because the presynaptic variable for Hebbian plasticity in the synapses projecting from the global inhibitory neurons is approximately constant across time. Hebbian plasticity at those synapses is therefore effectively determined by the postsynaptic activity, much like homeostatic plasticity. However, the homeostatic process acts multiplicatively on the excitatory inputs and therefore can reduce or enhance the overall drive to bring it to some relevant operating regime. In contrast, inhibitory Hebbian plasticity may fail to do so because it can only counteract the excitatory drive, without being able to strengthen it if it is subthreshold. Therefore, we find that a homeostatic process provides much more flexibility and robustnees and is necessary for distinct stable attractors to emerge. We have chosen to include the Hebbian plasticity at inhibitory synapses since it further enlarges the dynamic range of category formation, but we emphasize that it is not necessary and, if taken alone, such Hebbian plasticity, unlike homeostatic one, would not be an adequate mechanism of category formation. For reliable category formation, the homeostatic plasticity should operate on the same time scale as the Hebbian plasticity (see Discussion and Supplementary Material). Finally, Hebbian plasticity is also necessary in the feedforward and recurrent synaptic connections (to provoke symmetry breaking in the synaptic weights, Figure 5
B,D) although no clear separation in the feedforward synaptic strengths arises due to strong overlaps (Figure 5
D).
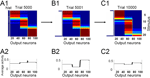
Categorization in a Dynamically Changing Environment
Given the stability of the categories considered above, one may ask whether and how new categories could evolve starting from a well formed cortical category structure. We address this question by changing the statistics of stimulus presentation after the stimuli have been categorized. If we begin as above with uniform input statistics, categories of the same size emerge after learning (Figure 6
A1), and the average activity of each output neuron across time (approximately reflecting its activation probability) is equalized (Figure 6
A2). When some of the stimuli are presented more often than others, the activation probability of the neurons across the network becomes transiently distorted (Figure 6
B2). However, after another learning epoch, the activation probabilities are again balanced at the same level due to the homeostatic plasticity (Figure 6
C2). Consequently, the number of stimuli comprising a category is adjusted to reflect the relative frequency of those stimuli. In particular, stimuli presented most frequently form the most selective category containing fewest stimuli (Figure 6
C1, rightmost category), and the stimuli presented least often form the least selective category (Figure 6
C1, middle category). The selectivity of the corresponding attractors self-organizes within the network such that each attractor, and therefore each neuron, shows the same average activation across time.
Figure 6. Cortical categories faithfully track changing probabilities of stimulus occurrence. (A1) The same steady-state responses of 100 model IT neurons for all input patterns (same inputs as in Figure 3
A) after 5000 pattern presentations, as in Figure 3
A. The uniform stimulus statistics (see histogram ‘hist’ along the stimulus axis) produce equal-sized cortical categories. (A2) The activation probabilities of the individual IT neurons are approximately equal due to homeostatic synaptic plasticity. (B1) Changing the stimulus statistics from trial 5001 on, with stimuli 1 and 20 presented 20% and 40% of the time, respectively (histogram in panel B1), does not perturb the categorical representations immediately as they result from slow Hebbian and homeostatic plasticity. (B2) However, the average activity of the IT neurons across time/patterns is transiently perturbed on a short time scale. (C1) After another epoch of 5000 stimulus presentations IT neurons responding to rare patterns extend their effective ‘tuning curves’ to adjacent patterns (middle category), while neurons responding to most frequent patterns become more selective (rightmost category). (C2) This reorganization of the cortical mapping equalizes the activation probabilities of the IT neurons (due to the homeostatic plasticity) in the changed environment to the same level as those prior to the change in the statistics.
Hierarchical Categorization of Clustered Input
So far we have considered the categorization of morphed stimuli with uniform or non-uniform temporal presentation frequencies. To test the behavior of our model for feature clustered stimuli, we also used the representation of human faces in V4 to mimic the natural input to IT. The V4 activity was generated by means of the nonnegative matrix factorization algorithm (Lee and Seung, 1999
) that encodes visual features similar to those observed in primate V4 (Desimone and Schein, 1987
; Kobatake and Tanaka, 1994
) (for further details see Supplementary Material). The set of 12 stimuli (corresponding to V1 activation) consisted of 1 female and 2 male faces, each twice with a serious and twice with a cheerful facial expression (Figure 7
).
Figure 7. By varying the top-down input strength to the model IT network, categories at different abstraction levels can be extracted. Images of human faces were converted into modeled V4 activity by nonnegative matrix factorization (Lee and Seung, 1999
). When this activity was presented as input to the IT network in the presence of a strong top-down input, 6 categories formed, separating different kinds of facial expressions of each individual. With an intermediate top-down input, each individual (but not the facial expressions) was represented by a single activity pattern in IT, leading to 3 categories. When the top-down input was weak, the two males were assigned to one of the two categories, and the female to the other. Images are from the CBCL (http://cbcl.mit.edu/software-datasets/FaceData2.html) database and the software generating the V4 activity was kindly provided by Sebastian Seung.
The V4 activity generated by these faces was repeatedly fed into our IT network while applying the top-down input of a specific strength (see Materials and Methods). For each top-down strength, the synaptic weights were randomly initialized and 2000 uniformly chosen samples of the 12 images were presented. After this unsupervised learning epoch the network was able to categorize the images at different abstraction levels depending on the strength of the top-down input during learning (Figure 7
). When the learning was performed with a strong top-down input, 6 categories emerged, each comprising a specific facial expression of the three subjects. At a medium top-down input strength, 3 categories emerged, each encompassing one subject, but not distinguishing among the facial expressions. When the top-down input strength was lowered even further, only 2 categories emerged, separating the genders only. The categories at the different abstraction levels could also be retrieved by dynamically changing the top-down input strength, provided it was sufficiently strong during the learning process.
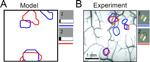
Non-Additive Feature Mapping
Global competition that can be modulated by top-down input is a key feature of our model. If competition is also essential in shaping activity in the monkey IT that we attempt to model, individual features should compete for representational space. The result would be object representation that is non-additive with respect to the individual features, i.e., the response to two features present at the same time would not be the same as the sum of the individual responses to each of the features. This is in fact observed both in experiments (Figure 8
B) by Tsunoda et al. (2001) and in our model (Figure 8
A). While this might be a general feature of nonlinear systems as such, more is true of both the experiment and the model: additional activity at the stimulus level does not necessarily result in adding more activity to the IT, but can in fact suppress previously active neurons (Figure 8
A). In contrast to the additive feature mapping as in the primary visual cortex, the mapping in IT consists of activating or inactivating cortical columns coding for individual features in the stimulus. The model suggests that the non-additive (and often subtractive) combination of individual features is in fact a salient property of category formation.
Figure 8. The response to a stimulus is not the sum of responses to its parts. (A) Contours of activity patches in the two-dimensional IT network (of 20 × 20 neurons) in response to two stimuli (shown on the right in panel A), with the first being a subset of the second. Contours are defined by a 70% activity level compared to saturation. Note that some groups of IT neurons that are activated by the narrow stimulus 1 (blue) are not activated by the wide stimulus 2 (red). This non additivity emerges from the competitive character of category formation and manifests itself in experiments. (B) Activity contours in the monkey IT in response to two visual stimuli shown on the right (adapted from Tsunoda et al., 2001
).
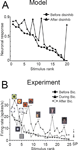
Non-Monotonic Stimulus Preferences
The non-additivity at the network level is related to nonlinearities at the neuronal level. To describe these neuronal nonlinearities we consider the “tuning curve” of a single model IT neuron while modulating inhibition. After the categories have formed, we choose an IT neuron with broad selectivity and plot its steady-state response to all stimuli, in descending order (Figure 9
A; for tuning curves of the other neurons see Figure 13
in Supplementary Material). Broad input selectivity arises in the presence of weak top-down input when attractors are wide. The stimuli are the same as in Figure 3
A. Next, we locally reduce the recurrent inhibitory synaptic strengths onto the chosen neuron and its four nearest neighbors by a factor of 0.5. This local disinhibition induces a reorganization of the neuronal response, resulting in a strong response increase for a few distinct input patterns independently of their ranking under control conditions.
Figure 9. Our model reproduces the non-monotonic modulation of neuronal stimulus preference via local disinhibition. (A) Response of a single model neuron with broad selectivity to the entire stimulus set, sorted in the descending magnitude-of-response order (filled circles). When inhibition is locally reduced, the responses increase non monotonically as a function of the stimulus rank (triangles). (B) In the monkey experiment, a similar non-monotonic distortion of the stimulus selectivity in IT neurons is observed when partially blocking inhibition via local injection of bicuculline (adapted from Wang et al., 2000
).
The same phenomenon is observed in the monkey experiment (Wang et al., 2000). When GABAergic transmission in the anterior part of IT was blocked, the stimulus selectivity of a nearby neuron varied non-monotonically (Figure 9
B). Taken as an isolated feature of the experiment these nonlinearities may look rather enigmatic. However, in the model they appear as a natural consequence of competitive self-organization in a recurrent network.
In the same way as a local decrease of inhibition changes the selectivity of a neuron, the stimulus selectivity may also be reshuffled when inhibition is globally decreased (as done in Figure 2
F). We therefore predict that global top-down signals nonlinearly modulate the stimulus selectivity of neurons in the monkey IT similarly to what is observed for the local GABA receptor blockade.
We investigated unsupervised category formation in a cortical network and its modulation by non-local intrinsic signals. The interplay between slow Hebbian and homeostatic plasticity in the presence of fast inhibition in a recurrent network leads to the formation of distinct subnetworks representing cortical categories of continuously varying stimuli. Depending on the strength of competition endowed by a global gain increase or a global drive of inhibition, more or fewer categories emerge (Figure 3
). The emerging categories reflect the stimulus occurrence statistics: rarely presented stimuli comprise broad categories, while frequent stimuli are mapped to narrow categories represented by highly selective neurons (Figure 6
). This enhanced neuronal selectivity to frequently presented stimuli can be viewed as an idealization of that observed in the monkey IT during extended discrimination training with some visual stimuli (Baker et al., 2002
). The categorical representation developing in our model network also reproduces the non-additivity of object representation in the IT (Figure 8 and Tsunoda et al., 2001
): a stimulus consisting of several features does not necessarily produce the sum of responses to the individual features, but may rather trigger a complete redistribution of cortical activity. This non-additivity is a hallmark of extracting categorical information instead of aggregating the individual features defining a specific object as in V1. In fact, object representation in the IT is claimed to be categorical (Kiani et al., 2007
). Similarly, local blockade of inhibition can lead to a complete reordering of a neuron’s stimulus selectivity (Figure 9
).
Attractor States Allow for Tuning Category Granularity
The representation of a category by an ensemble of neurons forming an attractor state (Amit et al., 1997
; Roudi and Latham, 2007
) relieves the need of explicitly adding or deleting output neurons (Carpenter, 1987a,b
) in order to change the number of categories. Instead, an attractor subnetwork can be divided up or combined with another attractor subnetwork depending on the strength of competition mediated by global inhibition. This global competition may depend on some internal cortical state (Fontanini and Katz, 2006
; Rodman et al., 1991
) and can be tuned, for instance, by a top-down signal changing the neuronal gain (Larkum et al., 2004
; McAdams and Maunsell, 1999
; Reynolds and Chelazzi, 2004
) or the balance of excitation and inhibition (Dong et al., 2004
; Hestrin and Galarreta, 2005
). Such an internal signal may allow for extracting categorical information on different abstraction levels. Weakening the top-down input could instantaneously convert a fine-grained categorization into a coarse-grained categorization through the merging of the attractors. In contrast to this merging process, splitting into finer categories requires that the fine-grained attractor configuration have already been formed during the course of prior learning. Learning in the presence of strong competition is therefore advantageous as it leads to a category hierarchy with deeply tunable abstraction levels. Although learning in the presence of weak competition stores fewer categories and does not allow for the same fine gradation of abstraction levels, it may instead leave some storage capacity of the network for the memorization of other stimuli in another context.
Synergies Between Homeostatic and Hebbian Plasticity
In our model, the formation of attractors that optimally exploit the storage capacity of the network relies on Hebbian and homeostatic processes to stabilize and equalize the network activity. The specific form of these processes is not crucial. Homeostatic plasticity, for instance, can either multiplicatively modulate the excitatory synaptic connections, or it can additively change the excitability of the model neurons, or it can even be replaced by Hebbian plasticity at inhibitory synapses driven by the total network activity. Different forms of homeostatic plasticity in fact seem to be present in cortical networks (Maffei et al., 2004
; Turrigiano and Nelson, 2004
). A necessary property revealed by our model, however, is that the time scales of Hebbian and homeostatic plasticity should not differ by more than an order of magnitude (see Supplementary Material). If homeostatic plasticity is much slower, category formation does not occur and all stimuli produce the same initial response pattern. At least during the critical period of symmetry breaking (early category formation), some form of fast homeostatic plasticity must be present which acts on a time scale of minutes, comparable to that for the induction of Hebbian changes (Sjöström et al., 2001
). Recent evidence reveals such a fast synaptic homeostasis at the Drosophila neuromuscular junction (Frank et al., 2006
), though it remains to be shown at cortical synapses. Alternatively, the internal calcium concentration may regulate the homeostatic time constant of synaptic plasticity such that it approaches the time constant of Hebbian plasticity during the critical period but is much slower at other times (Bienenstock et al., 1982
; Yeung et al., 2004
).
Monkey Categorization Experiments: A Prediction
Our model provides a possible explanation for the cortical data from monkeys performing a color categorization task with weak and strong demands (Koida and Komatsu, 2007
). If in these experiments a green color stimulus, for instance (say the second to last hue in Figure 2
A), has to be classified by a corresponding eye movement as being greenish or reddish, the IT responses to this stimulus are of similar strength as no task would be required (Koida and Komatsu, 2007
). If the task difficulty is increased by requiring a distinction between light and dark green, however, some of the previously active IT neurons are fully suppressed (Koida and Komatsu, 2007
). In our model, the same suppression of neuronal activity can be seen if an originally weak top-down input—mimicking a weak task demand—is replaced by a strong top-down input, allowing for a finer-grained stimulus representation and leading to the inactivation of the previously active neurons (see Figures 2
F,E, respectively).
The demand-dependent modulation of IT activity in the color classification task (Koida and Komatsu, 2007
) is in contrast to the demand-independent IT activity observed in classifying morphed images of animal-like objects (Suzuki et al., 2006
). One difference in the design of experiments is the order of stimulus presentation. Learning an easy and difficult discrimination tasks precedes the simple grouping task in Suzuki et al. (2006)
, as opposed to the alternation of the two demands during learning in the color classification experiment (Koida and Komatsu, 2007
). The preceding task of pure object discrimination in Suzuki et al. (2006)
can be performed using the same fine-grained representation in IT for both task demands, and instead employing a strategy based on a downstream readout network. When the switch to the simple grouping task (which may putatively relate to a coarse-grained stimulus representation) has been made, in the beginning such an untrained representation would lack the stability of the attractor states. To avoid mistakes, the monkey may adhere to the previously stabilized fine-grained stimulus representation, adapting only the downstream readout network. According to this interpretation, the IT responses under both the difficult and simple grouping tasks in Suzuki et al. (2006)
would be recorded in the presence of a strong top-down input to the IT. Our model therefore predicts that the same stimulus, presented without any task and thus without top-down input, will activate more IT neurons (cf. Figures 2
F,E). Such an activity increase in the IT has been in fact observed when switching from a difficult color categorization task to a pure fixation task (Koida and Komatsu, 2007
). In addition, demand-dependent IT activity is predicted for the object categorization experiment if the difficult and simple grouping tasks are learned simultaneously.
Models of Cortical Stimulus Representation and Categorization
Our network architecture shares many elements with other models studying cortical object representation. The idea that inhibition shapes the cortical representation has appeared in the context of self-organized feature mapping (Kohonen, 1982
), binocular rivalry (Bienenstock et al., 1982
) and cortical column formation (Miller, 1994
; Song and Abbott, 2001
). Top-down modulation of cortical stimulus representation has been modeled in the context of visual attention (Ardid et al., 2007
; Deco and Rolls, 2005
; Friston and Büchel, 2000
; Lee et al., 1999
), perception (Mechelli et al., 2004
; Szabo et al., 2006
), or perceptual learning (Schäfer et al., 2007
) (see Friston and Price, 2001
for a review). The formation of Hebbian ensembles in response to continuously varying stimuli has been recently attracting much interest (Bartlett and Sejnowski, 1998
; Bernaccia and Amit, 2007
; Blumenfeld et al., 2006
; Rosenthal et al., 2001
), but the internal modulation of the number and size of the emerging ensembles has not been addressed. Our model combines the self-organized feature mapping with unsupervised attractor formation by introducing and exploring the idea of modulating the granularity of categorization by global cortical states. In the special case in which the top-down signal tunes the model network so that two populations emerge, we obtain a decision-making network consisting of two recurrently connected populations that compete via global inhibition (Wang, 2002
). Models of categorical learning have also been studied in cognitive neuroscience with hierarchical layers extracting category information on different abstraction levels (Keri, 2003
; O’Reilly et al., 2002
).
Cognitive Deficits in Schizophrenia
Many mental disorders are believed to originate from an imbalance of neurotransmitter systems such as dopamine, serotonin, or noradrenalin (see, e.g., Sarter et al., 2007
). In vitro studies, in addition, show that these modulatory neurotransmitters affect the gain of cortical pyramidal neurons (Zhang and Arsenault, 2005
). It is therefore a distinct possibility that cognitive deficits observed in mental disorders are related to similar pathological modifications of neuronal properties (see also Loh et al., 2007
). Among the cognitive impairments in schizophrenia are in fact difficulties in categorizing graded stimuli (Keri et al., 1999
). Some of the most typical symptoms consist of formal thought disorders such as ‘incoherence’ or ‘loose associations’ which can be understood as the result of too fine or too coarse categorization, respectively. In the context of our model, such inappropriate category granularity can be explained by disrupted competition, caused, for instance, by a pathological dopamine-dependent gain modulation (Thurley et al., 2008
). Impaired dopamine regulation is in fact believed to underly many symptoms of schizophrenia (Guillin et al., 2007
). Our model explains how any alteration of neuronal properties that changes the approximate balance of excitation and inhibition can pathologically boost or prevent the formation of categories.
Homeostatic and Hebbian Time Constants must be Similar
We have investigated the range of Hebbian and homeostatic time constants where category formation was possible. We have found that homeostatic plasticity could not be slower than Hebbian plasticity by more than a factor of 10 for category formation to occur.
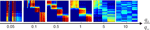
Each panel in Figure 10
shows the activities of the IT neurons for all the different patterns (see Figure 3
of the main text for further details). Category formation is possible if the ratio of the homeostatic and Hebbian rates, qh/qw, is in the range of 0.1–5. When homeostatic plasticity is too slow (qh<< qw, leftmost panel), some neurons never become activated and symmetry breaking in the neuronal responses does not occur. When homeostatic plasticity is too fast (qh >> qw, rightmost panel), on the other hand, Hebbian plasticity cannot partition different response patterns into distinct attractors and the activity becomes uniformly distributed for each moment in time.
Figure 10. Category formation is only possible if homeostatic plasticity operates on a time scale comparable to that of Hebbian plasticity. Here, we have fixed the learning rate of Hebbian plasticity to qw = 0.01 and modified qh, so that the ratio qh/qw varied from 0.05 to 10. The six panels show the activity of the IT neurons in response to the 20 input patterns in the same format as in Figure 3
of the main text. If the homeostatic scaling of the synaptic weights is 20 times slower than Hebbian plasticity (leftmost panel), several neurons remain silent, while some others are activated by all stimuli. Category formation occurs when the homeostatic process is from 10 times slower to 5 times faster than the Hebbian process. No distinct categories emerge if the homeostatic factor adapts 10 times faster than the Hebbian weights (rightmost panel). Other parameters are the same as the ones for Figure 3
B of the main text (see Materials and Methods).
Nature may employ different options to take into account the need for similar homeostatic and Hebbian time constants. In our simulations, homeostatic and Hebbian time constants are independent of the activation history of the neuron. In reality, both could be modulated, for instance, by some internal calcium concentration. This modulation may bring the time constants closer together during the critical period of symmetry breaking (see, e.g., Yeung et al., 2004
). Alternatively, homeostatic plasticity may be compensated by Hebbian plasticity at inhibitory synapses, which also leads to the normalization of the postsynaptic activity. Yet another option is that there is an additional fast homeostatic plasticity operating in the range of minutes, as is found in experimental preparations (Frank et al., 2006
).
Construction of the V4 Activity
In order to study how well our model would perform with more realistic, feature-clustered inputs, we used a model by Lee and Seung (1999)
to encode a natural image by its parts. This process is conceptually similar to the extraction of visual features in V4 (Desimone and Schein, 1987
; Kobatake and Tanaka, 1994
) and since V4 provides direct input to IT, V4 like activity represents an appropriate test for our model. Lee and Seung (1999)
employed a method called nonnegative matrix factorization (NMF) to obtain an encoding matrix H from a natural image W (Figure 11
A). We assume that this H could represent the activation of V4, whereas the original W would determine the selectivity of each V4 neuron. For each H, ten elements with the maximum activity were selected and set to 1 whereas the rest were set to 0. This binarized H served as the input to our model IT. In a biological context, the binarization could be performed by a multiple winner-take-all network.
Figure 11. Generation of V4 activity via nonnegative matrix factorization (NMF) of facial images. (A) Matrix W of a natural image and the encoding matrix H of the image. Taken from Lee and Seung (1999)
. (B) The input to the model IT network was obtained from the H matrix (representing a high-resolution activity of V4) by extracting the positions of ten largest elements. The input to the model IT at these positions was set to 1 and at the other positions to 0.
Blocking Inhibition Rearranges Neuronal Selectivity
Figure 8
A of the main text shows the modulation of the neuronal selectivity when recurrent inhibition is locally blocked. To find out how typical a non-monotonic reorganization of the neuronal selectivity is, we present the response curves for all the 10 × 10 model IT neurons (Figure 12
). To mimic the surface application of bicuculine, a GABAA antagonist (Wang et al., 2000
), we locally reduced the synaptic strength of the recurrent inhibitory synapses which are supposed to mediate inhibition within the superficial layers (Hestrin and Galarreta, 2005
). The local reduction of inhibition within a narrow region within the neuronal grid (marked with ovals in Figure 12
) was applied after learning. Each panel in Figure 12
shows the response curves of the corresponding IT neuron before and after the simulated bicuculine application. As revealed by this figure, a non-monotonic reordering of the neuronal selectivity as presented in Figure 8
A of the main text is a quite typical phenomenon.
Figure 12. Neuronal selectivity changes induced by reduced inhibition. In each panel, the X-axis shows the individually stimuli, and the Y-axis, the normalized neuronal responses before (blue) and after (red) the simulated bicuculine application. In the area indicated by the two ovals recurrent inhibition was reduced by 50%. This rearranged the selectivity of many neurons in a non-monotonic way. The neuron indicated by the black rectangle is shown as an example in Figure 8
A of the main text. For parameter values, see Materials and Methods in the main text.
Figure 13. Complete set of network responses corresponding to Figure 7
A of the main text. (A) Network responses of the 2-dimensional model IT network (20 × 20 neurons) to all 20 stimuli (ordered from left to right starting with the first row). The stimuli used were the same as in Figure 3
A in the main text. (B) Active spots were defined in the same way as for the experimental data (adapted from Tsunoda et al., 2001
), but points with activity level corresponding to 70% of the peak activity were connected. For Figure 7
A in the main text, responses to stimulus 4 and 6 were selected
.
Emergence of Activity Patches
In the experiment by Tsunoda et al. (2001)
, active spots were outlined by connecting pixels with one half the peak absorption value. In the model IT consisting of 20 × 20 neurons 20 continuously varying stimuli were presented to the network for learning and retrieval purposes. For parameter values see Materials and Methods in the main text.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We would like to acknowledge Stefano Fusi for his continuing support, especially in the initial phase of the work, for many inspiring discussions, and for critical comments on the manuscript. We also acknowledge Robert Urbanczik, Orna Rosenthal, Hans Peter Clamann, and Jürg Streit for helpful comments and critical reviewing of the manuscript, and we thank Sebastian Seung for providing the software for the nonnegative matrix factorization. We thank Takayuki Sato and Manabu Tanifuji for providing the data for Figure 8
B and also for the discussions. WS thanks Werner Strik and Thomas König for interesting discussions on schizophrenia and for sharing ideas on modulating the categorization granularity. The research was supported by the Swiss National Science Foundation (grant 3152A0-105966 for WS).