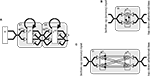1
Division of Engineering, King’s College London, London, UK
2
Centre for Brain and Cognitive Development, Birkbeck, University of London, London, UK
A simple variation of the standard biased competition model is shown, via some trivial mathematical manipulations, to be identical to predictive coding. Specifically, it is shown that a particular implementation of the biased competition model, in which nodes compete via inhibition that targets the inputs to a cortical region, is mathematically equivalent to the linear predictive coding model. This observation demonstrates that these two important and influential rival theories of cortical function are minor variations on the same underlying mathematical model.
Predictive coding (Jehee et al., 2006
; Rao and Ballard, 1999
) and biased competition (Desimone and Duncan, 1995
; Reynolds et al., 1999
) are two highly influential theories of cortical visual information processing. Both theories propose that perception involves the interaction between top-down expectation and sensory-driven analysis. However, predictive coding hypothesizes that cortical feedback connections act to suppress information predicted by higher-level cortical regions, so that only the residual error between the top-down prediction and the bottom-up input is propagated from one cortical region to the next along a processing pathway. In contrast, biased competition proposes that cortical feedback acts to enhance stimulus-driven neural activity that is consistent with top-down predictions in order to affect competition occurring between neural representations in each cortical area. These two theories are therefore presumed to be incompatible and to make a number of rival predictions. However, in this article it is demonstrated that predictive coding is mathematically equivalent to a particular form of biased competition model in which the nodes compete via negative feedback (Harpur and Prager, 1994
, 1996
; Spratling and Johnson, 2004
). This equivalence between the two models diffuses most of the distinctions that are assumed to exist. The only enduring difference concerns how the same underlying mathematical model is implemented in cortical hardware. In this respect, the neural architecture derived from the biased competition model seems most consistent with cortical physiology.
Biased Competition
The biased competition model (Desimone and Duncan, 1995
; Reynolds et al., 1999
) proposes that visual stimuli compete to be represented by cortical activity. Competition may occur at each stage along a cortical visual information processing pathway. The outcome of this competition is influenced not only by bottom-up, sensory-driven, activity but also by top-down, attention-dependent, biases. These top-down influences increase the amplitude and duration of the neural activity generated in response to an attended stimulus and thus affects the ongoing competition between cells (Luck et al., 1997
; Reynolds et al., 1999
).
Attention operates via cortical feedback pathways (Desimone and Duncan, 1995
; Mehta et al., 2000
; Treue, 2001
). These feedback connections convey a range of top-down and contextual information from different cortical areas. Hence top-down information, originating from a wide range of different sources, can potentially modulate neural activity and bias competition; resulting in effects similar to those observed during attentional tasks also being observed in non-attentional tasks (Galuske et al., 2002
; Hupé et al., 1998
; Lamme et al., 1998
; Lee et al., 1998
; Zipser et al., 1996
). The biased competition model can thus be extended to account for other contextual influences on perceptual processing (Bayerl and Neumann, 2004
; Roelfsema, 2006
; Spratling and Johnson, 2004
; Vecera, 2000
; Watling et al., 2007
), with the same mechanism of feedback modulation, which influences competition, proposed to account for contextual and top-down effects in general and not just attentional biases.
A simple neural network implementation of the biased competition model is shown in Figure 1
A. The diagram shows a two stage hierarchy, in which two neural populations represent neighboring cortical regions along an information processing pathway. The two populations are reciprocally connected by excitatory feedforward and feedback connections, and neurons within each population compete via lateral inhibitory connections. The lower region receives input from a more peripheral cortical or thalamic region, while the higher region sends feedforward connections to, and receives feedback connections from, subsequent stages in the cortical hierarchy. In a more complete model, each region might send feedforward connections to a number of higher-level regions and receive feedback from each of these regions. Furthermore, nodes in each higher level would receive convergent input from a population of nodes with spatially diverse receptive fields in the preceding level so that receptive field sizes increase from one stage of the hierarchy to the next.
Figure 1. (A) A common implementation of the biased competition model. Rectangles represent populations of neurons, open arrows signify excitatory connections, filled arrows indicate inhibitory connections, and large shaded boxes, with rounded corners, indicate different cortical areas or processing stages. Within each processing stage nodes compete to be active in response to the current pattern of feedforward activity received from the sensory input or previous processing stage. The outcome of this competition can be influenced by feedback activation received from subsequent processing stages and/or attentional signals. Two possible mechanisms of competition within a processing stage are illustrated in (B) and (C). (B) Lateral inhibition suppressing node outputs. Direct inhibitory connections are shown between two nodes within a neural population, however, functionally equivalent behavior results from inhibition that is pooled via inhibitory interneurons, or from a non-neurally implemented selection mechanism that chooses the most active node(s). (C) Lateral inhibition suppressing node inputs. The bottom-up input to a processing stage is routed via an additional population of nodes. These nodes provide a mechanism through which the output nodes can compete, via feedback inhibition, for the right to respond to inputs. Each inhibitory weight from a node in population y to a node in population e has the same strength as the reciprocal excitatory weight between the same nodes in populations e and y. In both (B) and (C) nodes are shown as circles, thin arrows show connections between individual nodes, while thick arrows illustrate multiple connections between populations of nodes.
In most neural implementations of the biased competition model, nodes within each processing stage compete by inhibiting the output activity generated by neighboring nodes (e.g., Bayerl and Neumann, 2007
; Corchs and Deco, 2002
; Deco and Rolls, 2005
; Deco et al., 2002
; Hahnloser et al., 2002
; Hamker, 2004, 2005
; Phaf et al., 1990
; Usher and Niebur, 1996
). This form of competition (see Figure 1
B) is common to a large number of neural network algorithms (see Spratling and Johnson, 2002
, for references). An alternative mechanism of competition is a form of lateral inhibition in which nodes suppress the inputs (rather than the outputs) of other nodes (Harpur and Prager, 1994
, 1996
; Spratling, 1999
; Spratling and Johnson, 2002
). In such a model (see Figure 1
C), activation is fed-back from a population of output nodes to subtractively inhibit the inputs to those nodes. For example, in Harpur’s “negative feedback network” (Harpur and Prager, 1994
, 1996
) the neural activity is determined using the following equations:
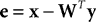
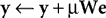
where y = [y1,…, yn]T is a vector of output activations, x = [x1,…, xm]T is a vector of input activations, e is a vector containing the inhibited values of the inputs, and W = [w1,…, wn]T is an n by m matrix of synaptic weight values, each row of which contains the weights received by a single node. Note that there is no restriction on the signs of either e or y and hence neurons in both populations can generate positive and negative responses. For each new input pattern, the output activations (y) are initialized to zero, and then the above equations are iterated (while x is held constant) to find the steady-state values for y and e. The parameter μ is a scale factor controlling the rate at which the output activations change during this iteration process. Although each output node inhibits its own inputs, this iterative process enables certain nodes to generate strong steady-state responses, while other nodes have their activations suppressed. In the steady-state, the output responses accurately reconstruct the inputs (i.e.,WTy = x), and hence e = 0 and the output responses stop changing. Prior to the steady-state, the elements of e are not all zero, and this causes the values of y to be adjusted up or down which will subsequently move the values of e closer to zero. A similar mechanism of inhibition, in which nodes suppress the inputs to neighboring nodes, has been used to successfully implement a biased competition model (Spratling and Johnson, 2004
). However in this previous model, the inhibition was proposed to take place within the dendrites of the output neurons rather than within a separate, error-detecting, neural population.
In order to employ negative feedback as the mechanism of competition in an implementation of the biased competition model, it is necessary to modify the equation for y above so that node activations in one cortical area are influenced by activity fed-back from higher areas. The simplest mechanism, which is used in many previous models of biased competition (e.g., Corchs and Deco, 2002
; Deco and Rolls, 2005
; Deco et al., 2002
; Hahnloser et al., 2002
; Phaf et al., 1990
; Usher and Niebur, 1996
), is to have the top-down bias add to the node activations. Hence, for an implementation of the biased competition model using negative feedback as the mechanism of competition, the network activity would be determined by the following equations applied to each stage of the hierarchy:

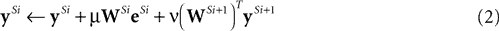
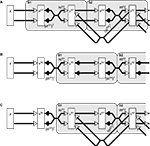
where superscripts of the form Si indicate processing stage i of the hierarchical neural network, yS0 = x, and ν is a constant scale factor controlling the strength of the top-down influence. The corresponding neural network architecture is illustrated in Figure 2
A.
Figure 2. Neural network architectures which each implement the same mathematical model but which vary in the neural mechanisms used. (A) The biased competition model implemented using negative feedback as the mechanism for intra-cortical competition. (B) A simplified diagram of the predictive coding model as implemented by Rao and Ballard (1999)
. (C) The reformulated predictive coding model [this architecture is identical to (A) except that the proposed mapping onto cortical areas – illustrated by the large shaded boxes with rounded corners – is shifted]. Note that although model (B) seems to differ from both (A) and (C) in not having excitatory feedback from one y population to the preceding y population, an identical effect is brought about by the negative weights from the e population to the preceding y population. This allows negative e values to have an excitatory effect on the y node activations. The symbols used are the same as in Figure 1
A, additionally crossed connections signify a many-to-many connectivity pattern between nodes in two populations, and parallel connections indicate a one-to-one mapping between the nodes in two populations.
In order to learn the matrix of synaptic weight values (W), Harpur and Prager (1996)
proposed the following learning rule:

This learning rule is essentially a Hebbian rule driven by the activity of the output nodes and the error-detecting nodes.
Predictive Coding
Rather than passively responding to the output activity generated by preceding stages of cortical processing, the predictive coding model hypothesizes that higher levels of cortex actively predict the input they expect to receive (Jehee et al., 2006
; Rao and Ballard, 1999
). Hence, it is proposed that cortical feedback connections convey predictions (outputted by a population of prediction nodes) while cortical feedforward connections convey residual errors between these top-down predictions and the bottom-up input (outputted by a population of error-detecting neurons).
Rao and Ballard (1999)
implemented this idea using a model in which the responses (y) of the prediction nodes (at a particular stage of the hierarchy, i.e., Si) were calculated using the following equation:
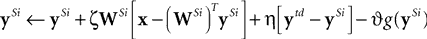
where 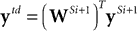 is the top-down prediction from the next highest stage,
is the top-down prediction from the next highest stage, 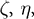 and
and 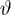 are constant scale factors, and g is a function of y that influences the sparsity of the output response (different functions were used in the different simulations reported by Rao and Ballard, 1999
). The above equation has been derived using Euler’s method to convert the differential equation actually proposed by Rao and Ballard (1999)
into a discrete time form suitable for numerical simulation and for comparison with the difference equation Harpur and Prager (1994
, 1996
) used to define their model. The dynamics of the original differential equation can be approximated to different degrees of precision by scaling parameters
are constant scale factors, and g is a function of y that influences the sparsity of the output response (different functions were used in the different simulations reported by Rao and Ballard, 1999
). The above equation has been derived using Euler’s method to convert the differential equation actually proposed by Rao and Ballard (1999)
into a discrete time form suitable for numerical simulation and for comparison with the difference equation Harpur and Prager (1994
, 1996
) used to define their model. The dynamics of the original differential equation can be approximated to different degrees of precision by scaling parameters 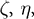 and
and 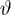 to effectively modify the time step used.
to effectively modify the time step used.
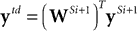 is the top-down prediction from the next highest stage,
is the top-down prediction from the next highest stage, 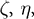 and
and 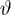 are constant scale factors, and g is a function of y that influences the sparsity of the output response (different functions were used in the different simulations reported by Rao and Ballard, 1999
). The above equation has been derived using Euler’s method to convert the differential equation actually proposed by Rao and Ballard (1999)
into a discrete time form suitable for numerical simulation and for comparison with the difference equation Harpur and Prager (1994
, 1996
) used to define their model. The dynamics of the original differential equation can be approximated to different degrees of precision by scaling parameters
are constant scale factors, and g is a function of y that influences the sparsity of the output response (different functions were used in the different simulations reported by Rao and Ballard, 1999
). The above equation has been derived using Euler’s method to convert the differential equation actually proposed by Rao and Ballard (1999)
into a discrete time form suitable for numerical simulation and for comparison with the difference equation Harpur and Prager (1994
, 1996
) used to define their model. The dynamics of the original differential equation can be approximated to different degrees of precision by scaling parameters 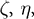 and
and 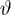 to effectively modify the time step used.
to effectively modify the time step used.Rao and Ballard (1999)
employed both a linear and a nonlinear version of the predictive coding model. In the linear model, 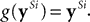 . Only this linear version of predictive coding will be considered further in this article. Hence, replacing g(ySi) with ySi, and substituting for ytd, the above equation can be re-written as:
. Only this linear version of predictive coding will be considered further in this article. Hence, replacing g(ySi) with ySi, and substituting for ytd, the above equation can be re-written as:
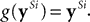 . Only this linear version of predictive coding will be considered further in this article. Hence, replacing g(ySi) with ySi, and substituting for ytd, the above equation can be re-written as:
. Only this linear version of predictive coding will be considered further in this article. Hence, replacing g(ySi) with ySi, and substituting for ytd, the above equation can be re-written as: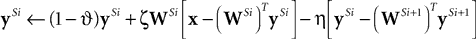
If we define:
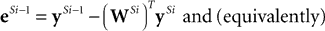

and set ySi−1 = x when i = 1, then the responses of the prediction nodes are given by:
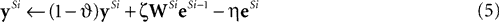
As with Harpur’s negative feedback algorithm, the values of y and e need to be iteratively updated (while the input, x, is held constant) in order to find the steady-state values for the node activations. Also, in common with Harpur’s algorithm, the activations of nodes in both the e and y populations can take both positive and negative values.
An illustration of a hierarchical neural network implementation of Eqs 4 and 5 is shown in Figure 2
B. As in the previous figures, only a simple hierarchy is shown for clarity, but a practical model would include a convergence of connections from nodes with smaller non-overlapping receptive fields in lower levels in order to provide nodes in higher levels with larger receptive fields. The neural implementation of the predictive coding model employed by Rao and Ballard (1999)
was more complicated than that shown in Figure 2
B. In their implementation each processing stage contained four separate populations of neurons. However, the network shown in Figure 2
B is equivalent to their model and retains its essential features such as feedforward excitation and feedback inhibition between the y and e populations within each processing stage and excitatory feedforward connections, and inhibitory feedback connections, between different processing stages. This network is also very similar to the architecture proposed by Friston (2005)
. Note that the error-detecting units can convey negative (as well as positive) values in order to enable feedback from prediction nodes at one stage to enhance (via negative feedback weights) the responses of prediction nodes at the preceding stage of the hierarchy.
We can reformulate the linear predictive coding model by substituting the definition of eSi from Eq. 4 into the third term on the right-hand-side of Eq. 5 to yield the following description:

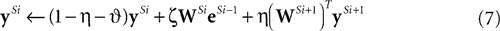
with an appropriate choice of parameters (i.e., 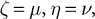 and
and 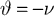 ) the reformulated linear predictive coding model (Eqs 6 and 7) can be seen to be mathematically identical to the biased competition model implemented using negative feedback as the mechanism of competition (Eqs 1 and 2). The only difference is the assignment of neural populations to processing stages (denoted by the superscripts). It should be noted that the different populations of error-detecting nodes can be re-labeled, by adding 1 to the processing stage each e population is assigned to, without having any effect on functionality.
) the reformulated linear predictive coding model (Eqs 6 and 7) can be seen to be mathematically identical to the biased competition model implemented using negative feedback as the mechanism of competition (Eqs 1 and 2). The only difference is the assignment of neural populations to processing stages (denoted by the superscripts). It should be noted that the different populations of error-detecting nodes can be re-labeled, by adding 1 to the processing stage each e population is assigned to, without having any effect on functionality.
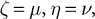 and
and 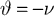 ) the reformulated linear predictive coding model (Eqs 6 and 7) can be seen to be mathematically identical to the biased competition model implemented using negative feedback as the mechanism of competition (Eqs 1 and 2). The only difference is the assignment of neural populations to processing stages (denoted by the superscripts). It should be noted that the different populations of error-detecting nodes can be re-labeled, by adding 1 to the processing stage each e population is assigned to, without having any effect on functionality.
) the reformulated linear predictive coding model (Eqs 6 and 7) can be seen to be mathematically identical to the biased competition model implemented using negative feedback as the mechanism of competition (Eqs 1 and 2). The only difference is the assignment of neural populations to processing stages (denoted by the superscripts). It should be noted that the different populations of error-detecting nodes can be re-labeled, by adding 1 to the processing stage each e population is assigned to, without having any effect on functionality.A neural network implementing Eqs 6 and 7 is shown in Figure 2
C. This has an identical architecture to the biased competition model depicted in Figure 2
A except that the grouping of neural populations into cortical regions (illustrated in the figure by the large shaded boxes with rounded corners) is shifted to the right.
The learning rule proposed by Rao and Ballard (1999)
was:
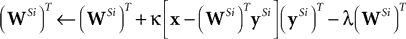
Substituting Eq. 6 for the term in square brackets, and taking the transpose of each side, gives:
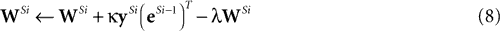
with the appropriate choice of parameter values (i.e., 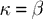 and
and 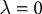 ), this rule is identical to that used by Harpur and Prager (1996)
(see Eq. 3). While it is clear that there is a strong similarity between the learning rules proposed for the predictive coding model and for the biased competition model implemented as a hierarchy of negative feedback networks, exact equivalence between these rules is only obtained when one parameter in the predictive coding model takes a fixed value (i.e., for a special case of predictive coding). In contrast, the equations for updating the node activations are equivalent for any parameter values as long as corresponding parameter values in the two sets of equations are equated (as described earlier in this section). The following discussion only assumes equivalence between the equations for calculating node activations.
), this rule is identical to that used by Harpur and Prager (1996)
(see Eq. 3). While it is clear that there is a strong similarity between the learning rules proposed for the predictive coding model and for the biased competition model implemented as a hierarchy of negative feedback networks, exact equivalence between these rules is only obtained when one parameter in the predictive coding model takes a fixed value (i.e., for a special case of predictive coding). In contrast, the equations for updating the node activations are equivalent for any parameter values as long as corresponding parameter values in the two sets of equations are equated (as described earlier in this section). The following discussion only assumes equivalence between the equations for calculating node activations.
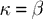 and
and 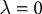 ), this rule is identical to that used by Harpur and Prager (1996)
(see Eq. 3). While it is clear that there is a strong similarity between the learning rules proposed for the predictive coding model and for the biased competition model implemented as a hierarchy of negative feedback networks, exact equivalence between these rules is only obtained when one parameter in the predictive coding model takes a fixed value (i.e., for a special case of predictive coding). In contrast, the equations for updating the node activations are equivalent for any parameter values as long as corresponding parameter values in the two sets of equations are equated (as described earlier in this section). The following discussion only assumes equivalence between the equations for calculating node activations.
), this rule is identical to that used by Harpur and Prager (1996)
(see Eq. 3). While it is clear that there is a strong similarity between the learning rules proposed for the predictive coding model and for the biased competition model implemented as a hierarchy of negative feedback networks, exact equivalence between these rules is only obtained when one parameter in the predictive coding model takes a fixed value (i.e., for a special case of predictive coding). In contrast, the equations for updating the node activations are equivalent for any parameter values as long as corresponding parameter values in the two sets of equations are equated (as described earlier in this section). The following discussion only assumes equivalence between the equations for calculating node activations.The preceding analysis has demonstrated that the linear predictive coding model and a particular implementation of biased competition are functionally equivalent. In other words, they are different implementations of the same mathematical model. Three different implementations of this mathematical model have been derived (Eqs 1 and 2, Eqs 4 and 5, and Eqs 6 and 7) which differ in the neural architectures they propose for their implementation. These three architectures are shown in Figures 2
A–C and will be referred to as the biased competition network, the predictive coding network, and the reformulated predictive coding network respectively. The underlying mathematical model will be referred to as the linear predictive coding/biased competition (linear PC/BC) model.
Demonstrating that a particular implementation of predictive coding (the linear model proposed by Rao and Ballard, 1999
) is mathematically identical to a particular implementation of biased competition (using the method of competition proposed by Harpur and Prager, 1994
, 1996
) highlights the similarity between predictive coding and biased competition in general, and enables analogies to be drawn between these two theories. However, it should be noted that other implementations of these two theories (or even two implementations of one of these theories) will differ mathematically, and are thus also likely to differ in the detailed behavior they produce. The degree of correspondence between other implementations would need to be investigated empirically through simulation.
Implementational Similarities
Since each network implements the same mathematical model it is not surprising that they all share many features in common. Specifically, all three of the possible neural implementations propose alternate populations of error-detecting and prediction/representation nodes. Within this hierarchy all the networks employ one-to-one excitatory connections between one population of y units and the subsequent population of e units. Furthermore, the proposed connectivity between one population of prediction nodes and the previous population of error-detecting nodes is identical: all the networks use feedforward excitation and feedback inhibition with reciprocal strengths between populations of y and e units. In the biased competition network, this subtractive feedback is viewed as a method for providing competition between the nodes generating the y values. Whereas in the predictive coding network, this inhibitory feedback is viewed as a method for prediction-error correction. However, the proposed mechanisms are mathematically equivalent so the only difference is one of interpretation. This correspondence between lateral inhibition and predictive coding has been noted previously (Koch and Poggio, 1999
; Lee, 2003
).
Implementational Differences
The three different implementations of the linear PC/BC model differ only in terms of the neural architecture that is required to implement them (as illustrated in Figures 2
A–C). These networks thus make different predictions about how the same underlying mathematical model could be implemented in cortical circuitry. This in turn has implications for the biological plausibility of each possible implementation.
The biased competition network and the reformulated predictive coding network differ from the predictive coding network in terms of the mechanism used to enable the activity in one population of y units to enhance the activity of nodes in the preceding population of y units. In the biased competition network, and the reformulated predictive coding network, strong activation of a particular prediction node at one stage in the hierarchy (e.g., 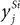 ) will cause excitatory feedback that directly enhances the responses of those nodes in the lower-level population
) will cause excitatory feedback that directly enhances the responses of those nodes in the lower-level population 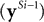 which, in turn, send feedforward excitation (via the eSi neurons) to that prediction node (
which, in turn, send feedforward excitation (via the eSi neurons) to that prediction node (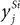 ). In the predictive coding network, the same effect is brought about indirectly through inhibitory feedback projections: high activity in node
). In the predictive coding network, the same effect is brought about indirectly through inhibitory feedback projections: high activity in node 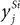 results in strong negative feedback to all the error-detecting nodes in the preceding level from which node
results in strong negative feedback to all the error-detecting nodes in the preceding level from which node 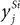 receives excitation. This results in negative activity values for a subset of error-detecting nodes, and hence, via the negative feedback connections to the preceding prediction nodes, will excite all the
receives excitation. This results in negative activity values for a subset of error-detecting nodes, and hence, via the negative feedback connections to the preceding prediction nodes, will excite all the 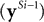 nodes which indirectly excite node
nodes which indirectly excite node 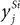 . Hence, the biased competition network, and the reformulated predictive coding network, propose direct excitatory feedback from one population of prediction nodes to the preceding one. In contrast, the predictive coding network generates a mathematically identical result via a two stage inhibitory feedback pathway (via the e neurons) from the y population in one stage to that in the preceding stage.
. Hence, the biased competition network, and the reformulated predictive coding network, propose direct excitatory feedback from one population of prediction nodes to the preceding one. In contrast, the predictive coding network generates a mathematically identical result via a two stage inhibitory feedback pathway (via the e neurons) from the y population in one stage to that in the preceding stage.
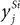 ) will cause excitatory feedback that directly enhances the responses of those nodes in the lower-level population
) will cause excitatory feedback that directly enhances the responses of those nodes in the lower-level population 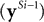 which, in turn, send feedforward excitation (via the eSi neurons) to that prediction node (
which, in turn, send feedforward excitation (via the eSi neurons) to that prediction node (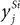 ). In the predictive coding network, the same effect is brought about indirectly through inhibitory feedback projections: high activity in node
). In the predictive coding network, the same effect is brought about indirectly through inhibitory feedback projections: high activity in node 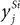 results in strong negative feedback to all the error-detecting nodes in the preceding level from which node
results in strong negative feedback to all the error-detecting nodes in the preceding level from which node 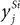 receives excitation. This results in negative activity values for a subset of error-detecting nodes, and hence, via the negative feedback connections to the preceding prediction nodes, will excite all the
receives excitation. This results in negative activity values for a subset of error-detecting nodes, and hence, via the negative feedback connections to the preceding prediction nodes, will excite all the 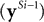 nodes which indirectly excite node
nodes which indirectly excite node 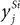 . Hence, the biased competition network, and the reformulated predictive coding network, propose direct excitatory feedback from one population of prediction nodes to the preceding one. In contrast, the predictive coding network generates a mathematically identical result via a two stage inhibitory feedback pathway (via the e neurons) from the y population in one stage to that in the preceding stage.
. Hence, the biased competition network, and the reformulated predictive coding network, propose direct excitatory feedback from one population of prediction nodes to the preceding one. In contrast, the predictive coding network generates a mathematically identical result via a two stage inhibitory feedback pathway (via the e neurons) from the y population in one stage to that in the preceding stage.The predictive coding network and the reformulated predictive coding network differ from the biased competition network in terms of how they group the error-detecting and prediction node populations into processing stages. In the biased competition network each processing stage consist of an e population followed by a y population (as shown in Figure 2
A). In contrast, in the predictive coding network each processing stage consists of a y population followed by a e population (as shown in Figure 2
B). The reformulated predictive coding network (Figure 2
C) proposes the same grouping of neural populations into processing stages as the predictive coding network from which it was derived (the manipulation carried out to derive Eq. 7 from Eq. 5 has the effect of replacing the two-stage negative feedback pathway described in the preceding paragraph with direct excitatory feedback from one population of prediction nodes to the preceding one, but has no effect on the assignment of neural populations to processing stages).
In Eqs 1–8 superscripts of the form Si have been used to denote the processing stage to which each neural population belongs. Hence, in the biased competition network the y values in stage Si are driven by the e values calculated in stage Si, whereas for the predictive coding network and reformulated predictive coding network the y values in stage Si are driven by the e values calculated in the preceding processing stage. The use of the superscripts to denote processing stages rather than the position of a population in the hierarchy irrespective of the proposed grouping, leads to the difference in the superscripts values of the e populations in the equations describing the reformulated predictive coding network (Eqs 6 and 7) compared to the equations describing the biased competition network (Eqs 1 and 2).
In previous work on the predictive coding network, processing stages have been equated with cortical regions (Friston, 2005
; Rao and Ballard, 1999
). Under such a literal interpretation, each of the three networks make distinct predictions about the cortical circuitry that would be required to implement the same mathematical model in neural hardware. In terms of the plausibility of each implementation, one notable way in which these predictions differ is in terms of the required functional role of cortical feedback connections. The biased competition network requires feedback from one cortical area to the preceding area to be excitatory. In contrast, the predictive coding network requires cortical feedback to be inhibitory. The reformulated predictive coding network requires both inhibitory feedback (targeting the e units), and excitatory feedback (targeting the y units). Cortical feedback connections are the axon projections of pyramidal cells and are therefore exclusively excitatory. The targets for these connections are also predominately pyramidal cells (Budd, 1998
; Johnson and Burkhalter, 1996
). It is possible that these top-down signals are “inverted” by the action inhibitory interneurons within the cortical area receiving the feedback. This could either occur via the small proportion of direct inhibitory contacts made by the feedback connections themselves, or via the pyramidal cells targeted by the feedback subsequently activating inhibitory interneurons (e.g., as proposed by Schwabe et al., 2006
to model surround suppression). However, the post-synaptic potentials generated by the activation of feedback connections are predominantly excitatory (Johnson and Burkhalter, 1997
; Shao and Burkhalter, 1996
). Hence, cortical feedback causes strong excitation and only weak inhibition, and this is incompatible with both the predictive coding network and reformulated predictive coding network. Hence, in this regard, the biased competition network appears to suggest the most biologically plausible neural architecture.
Based on the anatomy of cortical feedforward and feedback connections (Barbas and Rempel-Clower, 1997
; Barone et al., 2000
; Felleman and Van Essen, 1991
; Johnson and Burkhalter, 1997
) it is possible to propose a mapping of the biased competition network onto the cortical circuitry. Cortical feedforward connections originate from pyramidal cells in layers II and III and feedback connections terminate outside layer IV. This suggests that the prediction/representation units map to pyramidal cells in the superficial layers of cortex. Similarly, since cortical feedforward connections predominantly target the spiny-stellate cells in layer IV, it is possible to equate the error-detecting population of nodes with this cortical layer. However, it is also possible that the error-detection is performed in the dendrites of the supra-granular pyramidal cells (Spratling and Johnson, 2002
) rather than in a separate neural population.
Reconciling Predictions
The previous section has discussed differences between implementations of the linear PC/BC model at the hardware or implementation level of analysis. However, at the algorithmic level all the implementations are identical (they all implement the same mathematical model) and hence the behavior of these networks and the predictions they make about cortical function are the same. It should be emphasized that no new model has been proposed in this article: the model described is mathematically the same as the linear model proposed by Rao and Ballard (1999) and hence makes all the same predictions as that model. What this article does contribute is a new perspective on that existing algorithm which shows how biased competition and predictive coding theories can be unified.
From the perspective of predictive coding, reconciliation involves rearranging the equations describing the linear predictive coding model and changing the way in which the neural populations are grouped into processing stages. It is then possible to derive a mathematically equivalent implementation that can be interpreted as a form of biased competition model. By doing so, predictive coding can be seen to inherit the predictions made by biased competition and to benefit from a more intuitively appealing and biologically plausible interpretation.
Correspondingly, from the perspective of biased competition, reconciliation involves modifying a standard implementation of the biased competition model to use the method of competition proposed by Harpur and Prager (1994
, 1996
). This yields a form of biased competition that is mathematically equivalent to the original linear predictive coding model proposed by Rao and Ballard (1999)
. Hence, this particular implementation of biased competition inherits all the predictions of the linear predictive coding model and benefits from the information-theoretic elegance of the predictive coding theory.
The suggestion that predictive coding and biased competition actually make the same predictions may be controversial given the widespread belief that they are distinct, rival, theories. However, all three neural implementations of the linear PC/BC model propose that there is a population of error-detecting nodes and a population of representational nodes in each cortical region, and each network predicts that top-down knowledge can make the responses of the representational population more selective and also reduce the response of the error-detecting population by subtracting the top-down prediction from them. The linear PC/BC model thus predicts that when top-down knowledge accurately predicts the bottom-up inputs to a processing stage a sub-population of cells (the error-detecting neurons) in that cortical region will show suppression, while another sub-population (a specific subset of prediction neurons) will show an enhancement of response. The enhanced response of the subset of prediction nodes which encode information consistent with the top-down prediction is compatible with single-cell electrophysiological data showing enhanced neural activity resulting from attentional and contextual influences (Galuske et al., 2002
; Hupé et al., 1998
; Lamme et al., 1998
; Lee et al., 1998
; Luck et al., 1997
; McAdams and Maunsell, 2000
; Reynolds et al., 1999
; Zipser et al., 1996
).
Similarly, the model’s behavior is consistent with fMRI data showing a reduction in response of primary visual areas (correlated with an increase in response of higher-level areas) when visual information is coherent rather than incoherent (Harrison et al., 2007
; Murray et al., 2002
). The model proposes that neurons with larger receptive fields in higher cortical regions would be sensitive to coherent information and be able to feedback accurate predictions to cells with smaller receptive fields in the more peripheral region. This, in turn, would reduce the response of the error-detecting nodes in the lower-level area (Harrison et al., 2007
; Murray et al., 2002
; Olshausen, 2003
). It would also lead to a refinement in the representation formed by the prediction nodes in the lower-region due to excitatory feedback enhancing those few responses consistent with the top-down percept and suppressing, through competition, inconsistent representations (Kersten et al., 2004
; Murray et al., 2004
; Olshausen and Field, 2005
).
Previously, the predictive coding model has been criticized for being inconsistent with single-cell electrophysiology experiments showing top-down enhancement to neural responses (Hamker, 2006
; Koch and Poggio, 1999
). This is a mis-interpretation of the model, that may have resulted from the strong emphasis the predictive coding hypothesis places on the importance of the error-detecting nodes, and the corresponding under-emphasis on the role of the prediction nodes in maintaining an active representation of the stimulus. It may also result from the top-down excitation received by the prediction nodes in the original implementation of predictive coding being “disguised” as inhibition through the use of a two stage inhibitory feedback pathway. From the current analysis it is clear that predictive coding is consistent with cortical physiology and would predict that attention causes enhanced activity of neural responses consistent with the attended location or feature and that, furthermore, this enhanced activity will act to influence the outcome of the competition occurring between the prediction nodes within a cortical region.
Previously, the predictive coding model has been considered to be compatible with the fMRI data showing suppression of responses in early visual processing stages due to the mechanism of error-detection node suppression (Harrison et al., 2007
; Murray et al., 2002
; Olshausen, 2003
). The current analysis makes it clear that predictive coding is also compatible with suppression of the fMRI signal due to refinement of the representation formed in the prediction nodes (as previously noted by Friston, 2005
). Similarly, the biased competition model has previously been considered to be compatible with the fMRI data due to the mechanism of response refinement (Kersten et al., 2004
; Murray et al., 2004
; Olshausen and Field, 2005
). However, biased competition (when implemented using negative feedback as the mechanism of competition between the prediction nodes) is also compatible with an explanation in terms of a reduction in prediction error.
At first sight the biased competition and predictive coding theories seem to be diametrically opposed: one requires cortical feedback to be excitatory while the other proposes that feedback is suppressive. The predictive coding and biased competition models have therefore been considered as distinct theories of cortical function. However, a simple variation on the conventional neural network implementation of the biased competition model has been shown to be identical to the linear predictive coding model. Hence, a particular implementation of the biased competition model, in which nodes compete via inhibition that targets the inputs to a cortical region, is mathematically equivalent to linear predictive coding. These previously distinct, rival, theories of cortical function can thus be united.
The unified PC/BC model proposes that each cortical region along an information processing pathway represents hypotheses. These hypotheses might be either endogenously generated through expectation, priming, attention, etc., or exogenously generated through larger scale, contextual, information being integrated across the larger receptive fields of higher-level neurons. These hypotheses are continuously feeding-back to more peripheral cortical regions to bias the ongoing processing occurring in those areas. This will result in nodes representing information consistent with the higher-level hypotheses receiving top-down excitation. Such top-down bias may influence the outcome of competition occurring between nodes in the lower region so that the neural representations at each stage of the hierarchy reflect the integration of both bottom-up analyses and top-down hypotheses. When the top-down hypothesis is accurate, this will lead to a reduction in the error between the representation formed and the bottom-up input received. Hence, bottom-up information is combined with top-down priors in order to compute the most likely interpretation of ambiguous sensory data.
The need for top-down, contextual, biases for the processing of ambiguous visual information does not exclude the possibility that unambiguous data can be analyzed rapidly via the first feedforward wave of activity (Roelfsema, 2006
). It is also possible that, as has been observed psychophysically (Hochstein and Ahissar, 2002
; Oliva and Torralba, 2006
; VanRullen and Thorpe, 2001
), a neural representation encoding the gist of a scene, or a previously learned object category, might be sufficiently strongly activated via feedforward connections to allow it to be distinguished at short latencies. At longer latencies the model would predict that the initial representation becomes more refined through the influence of lateral and feedback connections, and that these effects would become apparent in the later, sustained, responses of neurons, as is observed in cortex (Hegdé and Van Essen, 2006
; Hochstein and Ahissar, 2002
; Hupé et al., 1998
; Lamme et al., 1998
; Lee et al., 1998
; Roelfsema, 2006
; Zipser et al., 1996
).
The PC/BC model described here is purely linear. A more powerful model might include nonlinearities and Rao and Ballard (1999)
proposes a nonlinear version of their implementation. Two other possible forms of nonlinearity could be introduced into the effects of higher-level predictions on lower-level predictions (i.e., the inter-regional feedback in the biased competition network) and into the effects of predictions on error-detecting nodes (i.e., the effects of competition in the biased competition network). For the former, top-down feedback might be allowed to multiplicatively modulate the bottom-up driven activation of lower-level nodes (Spratling and Johnson, 2004
). Such gain modulation is observed in cortex and there are plausible physiological mechanisms for its implementation (Friston, 2005
; Larkum et al., 2004
). The other possibility might be to employ a mechanism of competition in which nodes divisively modulate their inputs. This is the method used in the non-negative matrix factorization algorithm (Lee and Seung, 1999
) and has been shown to generate more accurate parsings of images into their elementary components than the subtractive feedback mechanism used in the current model (Spratling et al., sub
). An additional advantage of this mechanism is that it avoids the need for the error-detecting nodes to encode negative activity values, and hence overcomes a biological implausibility in the current model. Another direction for future development is the learning mechanism. The current learning rules proposed by both Rao and Ballard (1999) and Harpur and Prager (1996)
attempt to adjust synaptic weights in order to minimize the error between the input stimulus and the predicted input. Hence, in common with many other algorithms (e.g., Friston, 2005
; Lee and Seung, 1999
), both short-term responses and long-term weight changes are driven by the objective of error reduction. However, this form of error-driven learning fails to form meaningful representations of overlapping image components in the face of occlusion (Spratling et al., sub
) and, hence, fails to accurately encode the causal structure of the visual environment.
The author declares that the research was conducted in the absence of any commercial or financial relationships that should be construed as a potential conflict of interest.
Thanks to Raul Kompass and Walter Senn for stimulating discussions on this topic, and for insightful comments on a draft of this article. This work was funded by EPSRC Research Grants GR/S81339/01 and EP/D062225/1.