Network Biology Research Laboratories, Technion – Israel Institute of Technology, Haifa, Israel
In this perspective we provide an example for the limits of reverse engineering in neuroscience. We demonstrate that application of reverse engineering to the study of the design principle of a functional neuro-system with a known mechanism, may result in a perfectly valid but wrong induction of the system’s design principle. If in the very simple setup we bring here (static environment, primitive task and practically unlimited access to every piece of relevant information), it is difficult to induce a design principle, what are our chances of exposing biological design principles when more realistic conditions are examined? Implications to the way we do Biology are discussed.
Reverse engineering is a concept in software and hardware industry, denoting the process of detailed examination of a functional system, in the face of limited a-priori knowledge of its design principles. While in the above sense we (biologists) all do reverse engineering, there are aspects that significantly complicate matters in that context: Unlike reverse engineering of man-made apparatuses, in biological reverse engineering there is no prior knowledge of the relevant level of organization. Furthermore, biological systems are characterized by deep degeneracy; functional objects may be mapped to many different processes within a given level of organization as well as at many different levels.
Perhaps the most vivid example of reverse engineering in biology is that of neuroscience, the Holy Grail of which is to map the path from stimuli to action through the brain. In neuroscience, the above mentioned complications translate to difficulties in pointing at a relevant level of organization: To some of us it is the single neuron, single synapse or even a single membrane protein; to others it is large populations of neurons or global concentrations of chemicals. Furthermore, it has been repeatedly demonstrated that behavior (the function to be explained in the neurosciences) may be mapped to many different brain processes within and between many different levels of organization. These complications render the inherent difficulty of reverse engineering – that is, the undeterminability of inductive reasoning – a strong constraint on the entire endeavor of neuroscience; a constraint that we all, too often, tend to ignore.
Inductive reasoning has traditionally been defined as the process of inferring a general law from the observations of particular instances. David Hume was probably the first modern thinker to raise doubts about induction as a process of gaining knowledge about nature; his main argument revolved around the idea that any inductive process must make certain assumptions (e.g. uniformity) in order to apply. As he pointed out, these very assumptions cannot be justified on any “rational” grounds. These difficulties led Popper to suggest the principle of falsification as a guideline to the construction of scientific theories. In this sense, a scientist constructs a theory which must be falsifiable by some specific experiment. According to this idea, theories are never proved, but can be refuted by subjecting them to appropriate experimental conditions. These ideas have been cast in modern form within the mathematical theory of learning, which provides, under well defined settings, necessary and sufficient conditions for the success of the inductive process. A clear result of this theory is that based on any finite set of observations, it is impossible to generalize since many possible hypotheses may explain the data equally well. More interestingly, it can be shown that generalization may be impossible even after observing an infinite number of instances (Vapnik, 1998
). The point is that even if we know in advance that the instances were generated according to some rule within a class of possible rules, there may be no way for a learner to infer the rule, if the class of possible rules is too large. The main approach taken within Physics in order to improve the prospects of constructing a good theory is to use some form of Occam’s razor principle, suggesting that among several theories consistent with a set of observations, the “simplest” one should be selected. However, there is, unfortunately, no unequivocal notion of simplicity to be guided by. More fundamentally, the justification of this principle is itself subject to the same criticism raised by Hume. Finally, when it comes to biology, there seems to be no a-priori argument which suggests why “simple” solutions should be better.
In this commentary we provide an example for the limits of reverse engineering in neuroscience. We demonstrate that application of reverse engineering to the study of representation in a functional neuro-system with known design principles, may result in a perfectly valid but wrong induction of the system’s design principle. Of course, the commentary is not aimed at re-discovering the limits of inductive reasoning; rather, it offers an exercise in modesty. Probably some neuroscientists feel that they do not need such exercises; this commentary is intended for the rest of us.
We use a biological toy model, a realized Braitenberg Vehicle II (Braitenberg, 1984
). This is a continuously moving Lego robot that is equipped with two ultrasonic eyes that transmit their input to a large scale network of real, cultured biological cortical neurons (for review see Marom and Shahaf, 2002
). The task of the agent (the Lego apparatus together with the biological network) is to avoid running into obstacles in a static environment. Based on the electrical responses of neurons to the input from the ultrasonic eyes, a decision is taken (by a well-defined algorithm) as to which direction should the agent be driven (see caption of Figure 1
). This algorithm considers only the delay from stimulus time to first spike that is emitted by broadly-tuned neurons (i.e. neurons that responded to input from the right as well as the left ultrasonic eyes). The responding neurons are ranked based on the time to first spike, and the resulting rank order represents the input source. The algorithm, which is based on a reported analysis of response dynamics (for detailed explanation see Shahaf et al., 2008
), performs flawlessly in spatial input classification tasks. This is demonstrated in a movie file (Supportive Information Video S1 in Shahaf et al., 2008
) that shows the behaviour of the agent over 1500 s; Figure 1
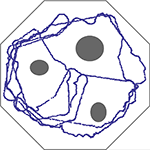
depicts the trajectory of the system over that period of time. The agent performs perfectly in the sense that it succeeds in its avoidance task. Importantly, no learning is involved; the representations of stimuli from the ultrasonic eyes are fixed by the rank-order.
Figure 1. Trajectory of the agent’s path, over 1500 s, in an obstacle avoidance task. Obstacles and walls are depicted in gray. Inputs from the two ultrasonic eyes of a Lego Mindstorms vehicle are sampled at 0.2 Hz and translated into stimulation of a large random network of cortical neurons at two different sites. The side corresponding to the nearest visual object (relative to the vehicle’s longitudinal axis) is classified using an Edit-distance metric based on the recruitment order of 8 neurons, similar to procedures shown in Figure 6 of Shahaf et al. (2008)
. Based on the classified activity, a command is sent to the appropriate motor attached to one of the wheels. See Video S1 in Shahaf et al. (2008)
for technical details.
To prove our point about the precariousness of reverse engineering in biology, let us test the validity of an interpretation that is “orthogonal” to the actual design principle (algorithm) of the above toy. The actual design principle of representation, as explained above, relies on the rank order of first spikes in a subset of identified broadly-tuned neurons. Now, suppose that a neurophysiologist wishes to test an hypothesis, according to which representation of the visual field is embedded in a population response rate. This idea of population rate differs from the actual design principle in several key aspects: Neuronal identities are ignored and temporal relations between spikes are ignored; only the temporal profile of total spike counts throughout the network, following input, is considered. Note that thus defined, there is practically no relation between this population-based representation scheme and the original (rank-order) scheme that drives the agent
1
. Figure 2
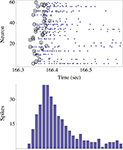
shows the process of data reduction.
There are several ways to test an hypothesis about the validity of a given representation scheme in neurophysiology. One very efficient and bias-free way is to use state-of-the-art non-linear classifiers. Indeed, our dedicated neurophysiologist uses the non-linear version of Support Vector Machine approach (Vapnik, 1998
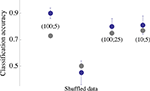
): Data is transformed to a space where linear classification is performed. To avoid over-fitting, only a fraction of the data is used for the construction of the classifier, and the efficacy of categorization by population response rate is evaluated by testing the classifier on the complementary (unseen) set of the data. The blue point of Figure 3
, denoted (100;5), shows the efficacy of categorization using vectors of population spike rate constructed over a 100 ms time window at 5 ms bin size; categorization is very good (accuracy 0.9), for all practical purposes. In other words, population response rate provides an accurate input categorization. So, concludes the neurophysiologist, population response rate is (or, “may be,” as a less cavalier physiologists would say) the scheme of representation, the “neural code.” But it is wrong; we know it is wrong because we have designed the machine otherwise. Of course, one might say that the neurophysiologist is too hasty in jumping to conclusions; but honestly, how many of us (physiologists) try to find an alternative design principle to one at hand that is 80–90% accurate in predicting the results? Moreover, if in the very simple neural setup examined here (static environment, primitive task and practically unlimited access to every piece of relevant information), it is difficult to induce a design principle, what are our chances of exposing biological design principles when more realistic conditions are examined?
Figure 2. The upper panel shows the spikes (blue dots) emitted by ∼60 neurons in response to one stimulus to the network. The stimulus was triggered by the right eye of the agent. Note that in this case there were no spontaneous spikes in the network immediately preceding the stimulus, although this need not be generally true. Black circles depict the first spikes (of each neuron) following the stimulus. The actual design principle is based on the rank-order of these first spikes, resulting in a unique “time-less” neuronal recruitment order; the recruitment order in the top panel example is 24, 17, 26, 25, 48, 1, 13,…. The bottom panel shows the population count histogram (“network spike”).
Figure 3. Accuracy of input classification (i. e. classification of the eye that triggered the network stimulation). A classifier (Gaussian kernel) was constructed using network spike profiles of the kind shown in the bottom panel of Figure 2
. Each blue point is the average classification accuracy obtained by 30 independent executions of the classification procedure (80% training set); error bars depict standard deviation. Parameters of the network spike histograms are depicted inside the plot: (x; y) is a network spike histogram computed over x ms, starting 10 ms following the stimulus, using y ms bin size. Analyses of (100;25) and (10;5) are shown, indicating that the result obtained by analyzing (100;5) is by and large valid under more restricted conditions. Gray points depict the classification of same data set using Euclidean distance based cluster analysis. All computations were carried out within Mathematica (Wolfram Research) environment.
An experienced biologists will immediately respond to the above heretical thought, coming up with two arguments: (i) “Your claim is based on a single, unique and quite esoteric setup;” and, (ii) “furthermore, do you have an alternative? Otherwise,” will say the experienced biologist “your claims are destructive!”
Well, to the first argument we answer that our example is strong enough to refute (at least) the naive reductionistic version of reverse engineering in biology, which is predominated by indeterminacy of data to theory. Under these circumstances, a more liberal approach that allows for coexistence of different models seems appropriate (e.g. Johnson and Omland, 2004
). Of course, in other domains of knowledge (e.g. machine learning and statistical inference) this approach is well-established.
To the second argument we say: it is not in our (scientists) mandate to find reasons to do wrong things when the right things to do are unclear. Reverse engineering is a pragmatical process; if it succeeds in extracting a predictor that works, irrespective of its relation to the actual design principle, the process is considered succesful. However, the business of Biology as a basic science is to uncover the actual design principles; this is where the naive version of reverse engineering fails.
But there might be an even stronger lesson here: maybe the degeneracy that is inherent to biological systems should not be considered as an obstacle to our capacity to decipher unique machineries. Rather, deep degeneracy at all levels is an integral part of biology, where machineries are developed through evolution to cope with a multiplicity of functions, and are therefore not necessarily optimized to the problem that we choose to reverse engineer. Viewed in this way, our limitation in reverse engineering a biological system might reflect our misconception of what a design principle in biology is. There are good reasons to believe that this conclusion is generally applicable to reverse engineering in a wide range of biological systems.
One reviewer of this position paper (E. Ahissar) proposed that perhaps what we named “deep redundancy,” where different models predict the agent’s behavior to a good enough degree, should be thought of as reflecting something that is akin to relations between theories in (for instance) physics; some are more universal compared to others (e.g. Einstein’s vs. Newtons). Therefore, an experiment can be designed such that the less universal theory is ruled out. Clearly, in the example we provided here, where we know that there is a single design principle, such an approach might reveal that principle, even if it “beats” other candidate principles only marginally. Note, however, that one of our key messages is that in the possible absence of such principles, pushing the experiment to various limits may not necessarily lead to the selection of one universal (“true”) model; in other words, different models may “win” in different extreme experimental conditions. Of course, we do not intend to claim that there are no laws underlying the dynamics of the system, laws that may (and indeed should) be discovered; rather, we raise the possibility that there are no design principles in a sense similar to the absence of design principles in evolution. In that respect our criticism is not merely on methodology, but on belief systems.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This study was partially supported by grants from the Israel Science Foundation (to SM, RM and EB) and the Etai Sharon Rambam Atidim Program for Excellence in Research (to DE).
- ^ In what sense we think of population rate code and rank order code as being “orthogonal” to each other? We start by realizing that the raw data that comes out of the recording system includes an ordered list of pairs of numbers: {id, t}, where id is the label of the neuron and t is the time at which that neuron evoked a spike. Note that there is no a-priori requirement on entailment between id and t. Thus, for instance, independent Poisson processes may generate such a list of pairs of numbers. The rank order code is constructed from the first term in each pair, the id. The population response rate code is constructed using only the second number of each pair, the time t. They are “uninformative” about each other; in that sense they are completely orthogonal. Having said that, complete orthogonality is not the main issue, nor a requirement for the argument presented in this paper.