Center for Memory and Brain, Boston University, Boston, MA, USA
Behavioral tasks are often used to study the different memory systems present in humans and animals. Such tasks are usually designed to isolate and measure some aspect of a single memory system. However, it is not necessarily clear that any given task actually does isolate a system or that the strategy used by a subject in the experiment is the one desired by the experimenter. We have previously shown that when tasks are written mathematically as a form of partially observable Markov decision processes, the structure of the tasks provide information regarding the possible utility of certain memory systems. These previous analyses dealt with the disambiguation problem: given a specific ambiguous observation of the environment, is there information provided by a given memory strategy that can disambiguate that observation to allow a correct decision? Here we extend this approach to cases where multiple memory systems can be strategically combined in different ways. Specifically, we analyze the disambiguation arising from three ways by which episodic-like memory retrieval might be cued (by another episodic-like memory, by a semantic association, or by working memory for some earlier observation). We also consider the disambiguation arising from holding earlier working memories, episodic-like memories or semantic associations in working memory. From these analyses we can begin to develop a quantitative hierarchy among memory systems in which stimulus-response memories and semantic associations provide no disambiguation while the episodic memory system provides the most flexible disambiguation, with working memory at an intermediate level.
Behavioral tasks are often used to experimentally study the different memory systems present in humans and animals (Eichenbaum and Cohen, 2001
) and are specifically designed to examine only a subset of the distinct memory systems that are hypothesized to exist in the brain (Schacter and Tulving, 1994
; Squire, 2004
; Squire and Zola-Morgan, 1991
). However, with this approach it is not necessarily clear that the subject is actually using the memory strategy that the experimenter desires. The theoretical study of memory systems is often carried out through simulations of different physiological systems at varying levels of detail to demonstrate that a model can show appropriate neural activity for the memory system in question (e.g., Deco and Rolls, 2005
; Fransén et al., 2002
) or that these types of neural activity can guide behavior in an agent performing appropriate tasks (Dayan, 2007
; Frank et al., 2001
; Hasselmo and Eichenbaum, 2005
; Moustafa and Maida, 2007
; O’Reilly and Frank, 2006
; Phillips and Noelle, 2005
; Zilli and Hasselmo, 2008a
).
An alternative theoretical approach (Marr, 1982
) would be to begin with both abstract characterizations of memory mechanisms and mathematical descriptions of tasks and determine if a particular memory mechanism is of use in solving a particular task. This type of implementation-agnostic approach allows general exploration of the ways that memory mechanisms may interact with each other and how they depend on the structure of tasks in ways that may not be clear from simulations of particular instantiations of the mechanism. Here we extend an earlier theoretical analysis of this type (Zilli and Hasselmo, 2008b
) to explore such interactions between memory mechanisms. An example of the utility of this approach is that it can inform theoretical models by identifying memory system interactions that are redundant or not useful, thus simplifying architectures without losing functionality or capability.
In particular, we consider interactions between the memory mechanisms for episodic memory and working memory described in Zilli and Hasselmo (2008a)
as well as a new, semantic-like memory mechanism. However, here we heed the advice of Baddeley (1986)
on the value of distinguishing between “a theoretically neutral description of a type of task and… the name of a theoretically controversial system that is assumed to be partially responsible for that task” by referring not to those memory system names but rather to mechanisms that may underlie them. Thus claims made about the mechanisms we focus on apply only to the memory systems inasmuch as these mechanisms actually are involved in the memory systems.
Episodic memory in humans is often characterized as the capability for mental time travel (Tulving, 1972
, 2002
; but see, e.g., Schwartz et al., 2005
for operational definitions used in animal studies). That is, it is the capability to mentally re-experience past events in their original spatial and temporal context, as opposed to the memory for specific facts, which lack a first person or experiential quality. To motivate our formal version of episodic memory, consider that mental time travel requires the selection of a “destination” and, intuitively, the destination would be identified in terms of the content of the episodic memory to be retrieved (we retrieve a memory at location X or regarding object or event X). We suggest that one cannot, however, retrieve memories that occurred at a specified time (unless awareness of the time was part of the episode) or occurring at a specific interval in the past (at least not without additional cognitive effort to reason out what the content of the memory should be for a particular interval). This property is called content-addressability. Thus we assume that the retrieval of an episodic memory always begins with some specified cue which is part of the memory to be retrieved. We assume that the memory retrieved is always the most recent occurrence of the cue for three reasons. First, intuitively, it seems as though the retrieved memory for a cue is always the most recent such memory (where multiple cues may be combined to identify the earlier episodes, e.g., the cue movie-theater should retrieve a memory no older than the combined cues movie-theater and blind-date). Second, this allows for the simplest analysis (although the analyses below could be adjusted for other possibilities, such as decreasing probabilities of retrieving each earlier instance of the cue). Third, previous simulations using this assumption have proven sufficient for modeling behavioral tasks (Hasselmo and Eichenbaum, 2005
; Zilli and Hasselmo, 2008a
). Episodic memory is also said to represent events in their original temporal context, so our formal model allows the agent to retrieve sequences of events one “frame” at a time. Although humans can retrieve sequences in either forward or reverse order, evidence suggests the two may be the result of distinct processes (Drosopoulos et al., 2007
; Li and Lewandowsky, 1995
) and we focus here on the forward direction of retrieval (although the analyses can be modified to allow for bi-directional retrieval). Retrieval may thus be advanced one frame at a time, and we assume that as each new frame is retrieved, the previous frames immediately pass out of awareness (unless specifically held in working memory, see below). We call any mechanism that has both of these properties a content-addressable, sequential retrieval memory (CASRM). A variety of such mechanisms have been used previously both in neural network modeling (Hasselmo, 2007
; Hasselmo and Eichenbaum, 2005
) and in reinforcement learning (RL) simulations (Zilli and Hasselmo, 2008a
), and in earlier analysis (Zilli and Hasselmo, 2008b
).
Working memory is the name for the mechanism that allows subjects to maintain task-relevant information in memory (Miyake and Shah, 1999
). In this case, we focus on gated, active maintenance memory (GAMM) of information about prior observations (Frank et al., 2001
; O’Reilly and Frank, 2006
), consistent with use of the term in models and experimental data focused on persistent spiking activity during the delay period of a behavioral task (Fransén et al., 2002
; Fuster, 1995
; Lisman et al., 1998
; Miller et al., 1996
; Zipser et al., 1993
). However, we do not specifically focus on the separate modality-specific components of working memory defined by Baddeley and Hitch (1974)
or working memory systems that hold multiple observations (Cowan, 2001
; Jensen and Lisman, 2005
; Miller, 1956
), though such components can easily be considered in this system by including multiple GAMMs. A practical limitation to the use of GAMMs is that they are not expected to be able to maintain information indefinitely for at least two reasons. First, an agent will generally have a limited number of GAMMs which eventually will have to be reused. Second, simulations usually use an action selection mechanism like ε-greedy or softmax (Sutton and Barto, 1998
) which occasionally selects random actions, thus unpredictably overwriting a GAMM’s contents.
Finally, we consider semantic-like associations (Eichenbaum and Cohen, 2001
; Tulving, 1972
, 1985
) in a very general sense as the ability for the agent to retrieve categories, relations, internal models, observations, etc. associated with some given observation through some unspecified process. This is analyzed as a set of static associations from observations to partially observable Markov decision processes (POMDPs), which we call a static association mechanism (SAM). Although POMDPs are generally used to represent task environments, they actually provide a powerful formalism for representing semantic information. If the states of a POMDP correspond to spatial locations and the actions to spatial movements, the POMDP can represent spatial knowledge. If the states correspond to views of an object and the actions to rotations of that object, the POMDP can represent knowledge of object shape and structure. POMDPs can also represent more abstract knowledge: if the states are countries or cities, the action “Capital” might lead from a country state to its capital city state. A static association memory is thus a collection of an arbitrary number of such POMDPs representing a static body of knowledge.
The analyses in Zilli and Hasselmo (2008b
) addressed the disambiguation problem (essentially the problem of choosing how to act given an observation that may correspond to multiple distinct underlying states) by considering each of these systems in isolation. We now consider disambiguation produced by different combinations of pairs of these memory systems. We ask how well the memory systems work together (i.e., when combined, how do the capabilities of an agent with the memory systems change?). Specifically, we identify which subset of states the agent can be in, given particular contents of the agent’s memory systems. The present analyses can answer questions such as: What information is provided by cuing CASRM using a static associate of some present observation? What information is provided by holding in GAMM some observation from a previously retrieved CASRM? These types of questions are important, because it may be that interactions among a small number of simple memory mechanisms can support a variety of complex strategies, allowing the decomposition of any particular strategy of interest into the mechanisms that support it.
We show there is a hierarchy of the three memory systems considered in terms of their flexibility in disambiguating observations in concert with other systems. This flexibility is defined in terms of the increased information provided by combinations of memory systems over using each of them on their own. The provided information, which we call disambiguation, relates the agent’s observation of the environment to the true states the environment can be in. Increased information or disambiguation means that there is a smaller set of possible hidden environmental states. Static associations of other memories are shown to never provide additional disambiguation, whereas CASRMs cued by memories from any of the systems can provide disambiguation beyond that provided by CASRMs cued by the current environment observation alone. GAMMs are shown to be slightly less flexible than CASRMs in the ways they can be usefully combined with other memory systems.
We first briefly review the Markov decision process framework and give our formal definitions of three memory systems to demonstrate how they function in this framework. Next we consider the utility of the CASRM system when its cue is provided by each of the three memory systems in turn. Then we examine the disambiguation provided when the contents of different memory systems are maintained in a GAMM. We conclude by summarizing the results and briefly considering their value.
By its nature, the analysis of interacting memory systems requires formal definitions of the analyzed memory mechanisms and of the ways they can be used. We express the models in the terms of RL theory (Sutton and Barto, 1998
). In this framework there is an agent which exchanges information with an environment. The agent selects actions that are sent to the environment, which changes its state in response to the action and sends the agent an observation reflecting its new state. The agent’s goal is to learn a policy (a function that produces an action, possibly probabilistically, given an observation) that maximizes the expected temporally discounted reward the agent will receive over time. Popular algorithms for learning such a policy are temporal difference methods (Sutton and Barto, 1998
) such as actor-critic learning or Q-learning (Watkins and Dayan, 1992
). Under reasonable assumptions, these algorithms provably converge to an optimal policy (Dayan, 1992
; Tsitsiklis, 1994
; Watkins and Dayan, 1992
). Though the environment can be any sort of system that receives actions and produces observations, one of the assumptions for the convergence proofs is that the environment has the Markov property, so environments are often represented as Markov decision processes (MDPs).
An MDP is a tuple 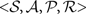 of, respectively, a set of states, a set of actions, a set of probabilities
of, respectively, a set of states, a set of actions, a set of probabilities 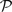 (s, a, s′) giving the probability of transitioning to state s′ after taking action a in state s, and a real-valued reward function defined on the state transitions.
(s, a, s′) giving the probability of transitioning to state s′ after taking action a in state s, and a real-valued reward function defined on the state transitions.
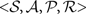 of, respectively, a set of states, a set of actions, a set of probabilities
of, respectively, a set of states, a set of actions, a set of probabilities 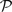 (s, a, s′) giving the probability of transitioning to state s′ after taking action a in state s, and a real-valued reward function defined on the state transitions.
(s, a, s′) giving the probability of transitioning to state s′ after taking action a in state s, and a real-valued reward function defined on the state transitions.In an MDP the complete state of the environment is always available to an agent. For animals, only a subset of the true state of the environment is usually available to the senses and even this information can be noisy. For this reason, environments can instead be represented as POMDPs (Kaelbling et al., 1998
; Monahan, 1982
). In this formalism, states and observations are separate sets (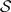 and
and 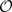 ), and each observation has a certain probability of appearing when the environment is in each state [taking action a from state s results in o observed in state s′ with probability
), and each observation has a certain probability of appearing when the environment is in each state [taking action a from state s results in o observed in state s′ with probability 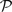 (s, a, s′, o)]. It is convenient to consider a map A from a hidden state s to the set of observations corresponding to that state A(s). The present work actually uses a simplification of POMDPs that we call aliased Markov decision processes (AMDPs). In an AMDP each state corresponds to only a single observation, | A(s) | = 1 for all s, although multiple states may correspond to the same observation. In this way, the probability of an observation is either 1.0 or 0.0, greatly simplifying the analyses.
(s, a, s′, o)]. It is convenient to consider a map A from a hidden state s to the set of observations corresponding to that state A(s). The present work actually uses a simplification of POMDPs that we call aliased Markov decision processes (AMDPs). In an AMDP each state corresponds to only a single observation, | A(s) | = 1 for all s, although multiple states may correspond to the same observation. In this way, the probability of an observation is either 1.0 or 0.0, greatly simplifying the analyses.
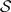 and
and 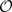 ), and each observation has a certain probability of appearing when the environment is in each state [taking action a from state s results in o observed in state s′ with probability
), and each observation has a certain probability of appearing when the environment is in each state [taking action a from state s results in o observed in state s′ with probability 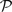 (s, a, s′, o)]. It is convenient to consider a map A from a hidden state s to the set of observations corresponding to that state A(s). The present work actually uses a simplification of POMDPs that we call aliased Markov decision processes (AMDPs). In an AMDP each state corresponds to only a single observation, | A(s) | = 1 for all s, although multiple states may correspond to the same observation. In this way, the probability of an observation is either 1.0 or 0.0, greatly simplifying the analyses.
(s, a, s′, o)]. It is convenient to consider a map A from a hidden state s to the set of observations corresponding to that state A(s). The present work actually uses a simplification of POMDPs that we call aliased Markov decision processes (AMDPs). In an AMDP each state corresponds to only a single observation, | A(s) | = 1 for all s, although multiple states may correspond to the same observation. In this way, the probability of an observation is either 1.0 or 0.0, greatly simplifying the analyses.In this more realistic formalism, convergence to an optimal policy is no longer guaranteed. It is possible to find an optimal policy on what is called the belief space of a POMDP by updating an estimate of the probability that the agent is in each state, but this is only useful to an agent that knows the complete details of the POMDP it is interacting with (Kaelbling et al., 1998
). Here we explore a different approach in which the contents of memory mechanisms can provide surrogate information which identifies the agent’s current state. This works without the agent needing to know information about the underlying states and transitions and immediate rewards (i.e., it is model free, although this information is needed in the following analyses to show why the approach works).
Memory Systems
The common way of including biologically inspired memory mechanisms into the RL framework (Dayan, 2007
; Moustafa and Maida, 2007
; O’Reilly and Frank, 2006
; Zilli and Hasselmo, 2008a
) is to treat each memory mechanism as a part of the environment in the sense that the agent interacts with the memory system through actions and the contents of memory are provided to the agent as part of the observation from the overall environment. Moustafa and Maida (2007)
called this the uniform selection hypothesis: putting cognitive and motor actions on equal footing for the purpose of action selection (based on an earlier idea from Frank et al., 2001 and Prescott et al., 2003
).
For action selection, the contents of each memory system must be combined with sensory observations to create a single state from which the agent’s policy can select an action. We call this combined information a policy-state. The number of possible policy-states grows combinatorically with the number of memory systems (or other environments included), causing increasingly slow learning rates as the number of systems increase (the curse of dimensionality). This suggests a general advantage for architectures with fewer memory mechanisms that can be flexibly combined to perform more complex functions.
The essence of the approach analyzed here is that if a policy-state is only attainable when the agent is in a particular hidden state, then the agent can act as though it knows its true sensory state and select an action appropriately. We call this disambiguation. The smaller the set of hidden states from which a given policy-state is reachable, the better the resulting disambiguation. The following analyses can determine these sets of hidden states corresponding to a particular policy-state and AMDP. This is done by first finding the policy-states that are reachable from a given sensory state and then identifying the corresponding hidden states.
When an agent has multiple memory systems, there are two general ways that the information from each may be combined. The simplest case is when each memory system acts in parallel, in which case each provides independent disambiguation. If one memory system indicates the agent is in one hidden state from a set S1 and another independently indicates the agent is in one hidden state from a set S2, then the agent must be in a state in the intersection of S1 and S2. The second possibility is when one memory system uses information from another, so the constraints are no longer independent, but rather one depends on the other. Most of the present analyses are of this condition: showing how the dependency is taken into account in the calculation of the set of possible hidden states.
We consider the following types of memory mechanisms: GAMM, CASRM, and static associations from observation to POMDPs (stimulus–stimulus memory, in a sense). Each is characterized by the actions it responds to and the observation it produces as a function of the agent’s history and actions taken. These mechanisms are treated as independent modules which can in theory be arranged in a variety of ways. Any particular arrangement of zero or more copies of zero or more modules we term an architecture.
That the present analysis is focused on these three memory mechanisms is not meant to suggest that these are the only three needed to solve all tasks. A number of other mechanisms might be included to more closely match the capabilities of animals. Some of these are mentioned in the Section “Discussion.”
Gated Active Maintenance
A gated active maintenance memory (GAMM) mechanism provides a single memory action to the agent which, when used, changes the state of the mechanism to a representation of the current observation of a target environment and maintains this representation over time until the action is taken again (when its contents are overwritten). The observation information it contributes to the policy-state is the currently maintained representation as well as the amount of time that representation has been held in memory. If the GAMM action was last taken at time t − i when the agent saw some observation ot−i, then the GAMM’s current observation is the pair (ot−i, i). Although simulations using this type of system in the past (Dayan, 2007
; Frank et al., 2001
; Moustafa and Maida, 2007
; O’Reilly and Frank, 2006
; Phillips and Noelle, 2005
; Zilli and Hasselmo, 2008a
) have not included age information and were nonetheless successful, an earlier analysis (Zilli and Hasselmo, 2008b
) suggests this age information can be very useful. GAMM is the only memory mechanism whose state is not cleared when the agent takes a motor action. That is, GAMMs provide the only means of keeping memory information directly accessible over time in the architectures described here. Including an action to clear the GAMM does not affect the results.
An architecture of memory mechanisms along with a specified sensory AMDP implicitly create a policy-state space. That is, the two together define the set of possible policy-states that an agent might experience and also identify which policy-states can lead to which others.
For example, an architecture containing only a GAMM that targets the sensory observation has a policy-state that can be written as the triple: (sensory observation, GAMM observation, age of item in GAMM) or, as above, (ot, ot−i, i). The policy-state (o, p, i) is only reachable at a state observed as o if observation p can actually occur i steps before o in the sensory AMDP. If one wanted to actually determine whether (o, p, i) is a valid policy-state, one could examine each sensory state that can be observed as o, find all states i steps before those and see whether any of those states can be observed as p.
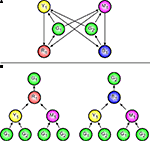
It can be convenient to abbreviate “all states i steps before states that can be observed as o” and similar statements. To do so, we introduce a function that looks a specified number of steps backward from a specified observation or state. We write bO(o, i) to mean the set of observations that can be found i steps before any state observed as o (see Appendix A). To refer to the set of states instead of the set of observations, we use a subscript S instead of O: bS(o, i). For instance, in Figure 1
A, bS(yellow, 1) = {G1, G2} and bO(green, 2) = {yellow, magenta}. Using this, we can say that (o, p, i) is valid if observation p is in the set bO(o, i).
Figure 1. Content-addressable, sequential retrieval memory (CASRM). (A) Example aliased Markov decision process (AMDP). States are circles identified by a letter and number and the corresponding observation by the color of the circle (which corresponds to the state’s letter). (B) Unwinding the AMDP for each of the two green observations G1 and G2. CASRM retrieval cued by green at a green observation (top of the “trees”) will begin at one of the green observation at the bottom of the tree and proceed upward as the memory is advanced. Regardless of the bottom state retrieval began at, the observation at the third level uniquely identifies the agent’s current state at the top of the tree.
If (o, p, i) turns out to be a valid policy-state, then an agent might actually experience it while performing a task. It could be that there are many states in the AMDP that are observed as o, but perhaps only one such state, s, is actually preceded i steps earlier by a state observed as p. For instance, consider idling at a street intersection where a left turn leads to home and a right turn to a pizzeria. The intersection is an observation corresponding to many hidden states: some states where going home is the optimal action, some where getting pizza is the optimal action, and perhaps others. Suppose the policy-state is actually: (intersection, text message “pick up pizza,” 30 s ago). A policy-state can correspond to a single state, so the policy-state becomes a useful proxy for learning values and selecting actions appropriate to the true, hidden state. In this example, the policy-state indicates that the agent is in a state where turning right is the optimal action. But this is not always the case: it could be that a state observed as p is always found i steps before a state observed as o, so the policy-state (o, p, i) would provide no extra information about the agent’s true state.
Content-Addressable, Sequential Retrieval
CASRM is a mechanism that allows the controlled retrieval of a sequence of observations starting from a point in time identified by a provided retrieval cue. The mechanism has one or more target environments whose observations it records. CASRM provides two actions to the agent. The first action cues retrieval by finding the most recent point in the past that the retrieval cue was present. The second action advances retrieval by one step, setting the observation of the CASRM to be the next observation in the sequence currently being retrieved.
Figure 1
demonstrates the CASRM system. Figure 1
A is a simple AMDP containing one ambiguous observation green, corresponding to two states: G1 and G2. In Figure 1
B the AMDP has been “unwound” separately for each of the two green states. For each state, a tree is made with that state as the root. Then the states just before the root state are added, then the states just before those are added, and so forth. A branch of the tree ends at a leaf when a state is reached with the same observation as the root. These leaf states are the states at which retrieval may begin when retrieval is cued from the root observation. Advancing retrieval corresponds to moving upward in the tree. The particular starting state of retrieval depends on the path the agent most recently followed. The utility of CASRM arises because sometimes an observation will only occur on a particular level for a subset of trees. In Figure 1
B, red only occurs in the third position when the agent is at G1, whereas yellow can occur in the second position for either state.
Formally, let ot be the observation of the target environment at time t, and let c = ot−x be a retrieval cue observation, which most recently occurred at time t − x (x > 0). A CASRM has an internal variable y indicating whether it is currently retrieving and, if so, what the time corresponding to the currently retrieved observation is (let y = −1 mean not retrieving). The effect of the cue retrieval action with cue c is to set y ← t − x and the CASRM’s observation becomes (oy, 0), where oy is the observation that occurred at time y. The effect of the advance retrieval action is to set y ← y + 1 and the CASRM’s observation becomes (oy, y − (t − x)). If advancing retrieval would set y > t, the action fails. The y − (t − x) element is a difference between times y and (t − x), reflecting the number of steps memory has been advanced, much as a GAMM’s observation indicates the age of the memory. And like the age of an item in GAMM, an earlier analysis suggests it may be useful, though simulations of this system (Zilli and Hasselmo, 2008a
) and of a simpler version of this system (Hasselmo and Eichenbaum, 2005
) have been successful without it. To see why it is useful, consider the agent at state X having just experienced either the sequence X-Y-X or X-Z-Y-X. If the agent cues CASRM with X, it can retrieve Y by advancing retrieval either one step or two step, and knowing the number of steps advanced allows it to disambiguate the two cases. When the agent takes a motor action, the state of CASRM is cleared (y ← −1).
An architecture containing only a CASRM that targets the sensory observation has a policy-state that can be written as the triple: (sensory observation, CASRM observation, number of steps retrieval has been advanced) or, as above, (ot, ot−x+j, j). It is straightforward to determine whether a particular policy-state is ever reachable in a given AMDP. Policy-state (o, q, j) is only reachable if observation q is reachable j steps after observation o. Again, this can be determined by examining whether any state observable as q can occur j steps after a state observable as o. For instance, in Figure 1
, (green, red, 2) is a valid policy-state because a red state is found two steps after a green state. Where above we defined a backward function bO, here we can use a forward function: we write fO(o, j) to represent the set of observations found j steps forward from any state observed as o (see Appendix A). So (o, q, j) is a valid policy-state if observation q is in fO(o, j).
Given such a valid policy-state, from which hidden sensory states is that policy-state reachable? Taking policy-state (o, q, j), in terms of trees like those shown in Figure 1
B, this asks for the states at the top of the trees in which q is found as the jth observation. Given a set of these trees, it is easy to determine the states (o, q, j) is reachable from. There are alternatives, however. Let q1, q2,… be states observed as q. Suppose only q1 and q2 are found j steps after an o observation. Also suppose, for instance, that q1 is in the trees for states o1, o3, o5,… and q2 is in the trees for states o2, o4, o6,…. Then if we formed a tree going forward from q1 and stopping the branches when hitting states observed as o, the leaves on this one tree would be o1, o3, o5,… (and similarly for q2). We will call the set of states in this tree the o-delimited, reachable states from q1 and write this as rS(q1, o) (see Appendix A). Or combining the trees for q1 and q2, we write rS(q, o). Now policy-state (o, q, j) is reachable from some state oi if oi is in rS(q, o) (where it will be a leaf on one of the trees with a q state as its root).
That is: can the agent retrieve q after j steps of retrieval while at state oi (i.e., is policy-state (o, q, j) reachable from oi)? It can if (1) at least one q state can occur j steps after at least one o state [i.e., (o, q, j) is a valid policy-state], and (2) oi is in the forward tree that stops at o states of one such q state [so oi is in rS(q, o)].
Static Associations
A SAM is modeled as a set of internal POMDPs that do not change on a behavioral time scale. Each observation o is associated with a POMDP P. Because POMDPs need not have connected state-space graphs, an observation can actually be associated with multiple POMDPs that are just treated as one large POMDP with specified probabilities for starting in each state in each sub-POMDP. The structures of the POMDPs are assumed to be learned over time in an unspecified manner, but do not change during performance of a task (they might change on a very slow timescale or change may require an off-task consolidation period, e.g., Squire and Alvarez, 1995
). A SAM has a target environment, and it has one cue action in addition to the actions of the POMDPs. When the cue action is taken, the state of the POMDP corresponding to the target environment’s observation is selected probabilistically per that POMDP’s starting state probabilities. The actions of the POMDP may then be taken and the state of the POMDP changes accordingly. A SAM also keeps track of the number of POMDP actions k that have been taken since the cue action was last taken. The observation from a SAM is (om, k) where om is the current observation of the POMDP. The state of SAM and k are cleared when the agent takes a motor action.
An architecture containing only a SAM has a policy-state we write as (ot, om, k). This policy-state is reachable only if observation om in ot’s SAM-associated POMDP is reachable in exactly k steps from one of the starting states in that POMDP.
In contrast to GAMMs or CASRMs, for SAM a policy-state reachable from one hidden sensory state is reachable from all hidden sensory states with the same observation, because the behavior of the SAM system does not depend on the agent’s history. Thus the use of SAM never provides more information regarding the agents hidden sensory state than does the sensory observation itself.
Interactions
Zilli and Hasselmo (2008b)
described an analysis of GAMM and CASRM (under the names working memory and episodic memory), giving, for example, the probability that the agent is in some hidden state s given that i steps ago it observed observation p and arranged these in a matrix with the past observations as rows and the hidden states as the columns. Of particular interest are those memory observations for which the corresponding policy-state is reachable only from a single hidden state, in which case the memory mechanisms allow the hidden state to be identified.
The rest of this manuscript extends this analysis to consider ways in which pairs of these mechanisms can interact. The general form of the analysis remains the same: an architecture (how many mechanisms are used and what their targets are) and the corresponding form of the policy-states (which information from the mechanisms is used in decision making) are determined. For a given sensory AMDP observation of interest (e.g., a choice point in a task), we first identify policy-states reachable from that observation, then relate the reachable policy-states to the possible hidden sensory states that may correspond to the observation of interest.
To formalize the interaction between mechanisms, we examine the policy-state of the architecture in response to a fixed sequence of memory actions and arbitrary motor actions that end in a state with a particular observation. For instance, we might consider the sequence “hold sensory observation in GAMM, take two motor actions, cue CASRM with observation in GAMM” which ends with the agent observing o and ask which policy-state might the agent be in and which hidden sensory states can policy-states correspond to. The analysis of GAMM in Zilli and Hasselmo (2008b)
would correspond to action sequences of the form “GAMM action, n motor actions.” The analysis of CASRM in Zilli and Hasselmo (2008b)
would correspond to action sequences “CASRM cue action, j CASRM advance retrieval actions.”
We have now introduced the formal memory systems and the basic concepts needed to consider interactions between these systems. Just as before, we are interested in the set of hidden states corresponding to a specified policy-state. More than that, we are interested in comparing the set of hidden states resulting from two memory systems interacting to the set of hidden states from one system on its own. This shows how the capabilities of an agent changes when memory systems can interact.
In the content-addressable, sequential retrieval system as previously described and analyzed (Zilli and Hasselmo, 2008a
,b
), only the agent’s current observation was usable as a retrieval cue. Everyday experience, however, suggests that the retrieval cues used for our episodic memories are not restricted to currently observed sensory cues: we can use internally evoked cues, such as static associates of observed stimuli (Polyn et al., 2005
) or we can use other, more complex cognitive processes to interact with episodic memory (Cabeza, 2008
; Ciaramelli et al., 2008
). This motivates the consideration of other ways in which the CASRM cue may come about.
Adapting the analysis to consider arbitrary retrieval cues is straightforward. Retrieval cued by the current observation o begins at the previous occurrence of an o in the agent’s history and identifies whether subsequent observations disambiguate which o state is currently occupied. If retrieval were cued by some general observation o′, retrieval could proceed no farther than the subsequent o′. Here there may be multiple occurrences of o within any path from one o′ to another. The fact that the states to be disambiguated are no longer the end states on the path is the cause of the largest modification needed. Previously, in Zilli and Hasselmo (2008b)
, occupancy of only the end states was of interest, but the present analysis of arbitrary cues focuses on occupancy of all states on the paths leading up to the end states (the o′-delimited reachable states).
Earlier we suggested the form of the policy-states for a CASRM-only architecture was (sensory observation, CASRM observation, number of steps retrieval has been advanced), but really this is the case only when the retrieval cue can only be the current sensory observation. When more than one retrieval cue can be used (e.g., if observations from other memory systems can be used as cues), then the cue can be included in the policy-state, giving the form (sensory observation, CASRM cue, CASRM observation, number of steps retrieval has been advanced).
This section considers three ways in which the retrieval cue for CASRM might come about. These correspond to the following types of action sequences: (1) Cuing retrieval with an observation from SAM: “k SAM actions, CASRM cue with SAM observation, j CASRM advance retrieval actions,” (2) Cuing retrieval with an observation from GAMM: “GAMM action, n motor actions, CASRM cue with GAMM observation, j CASRM advance retrieval actions,” and (3) Cuing retrieval with an observation retrieved with CASRM: “CASRM cue with sensory observation, i CASRM advance retrieval actions, CASRM cue with CASRM observation, j CASRM advance retrieval actions.”
In each of these action sequences, there is more than one possible cue observation that can arise from the memory systems used (e.g., more than one possible observation held in GAMM from n steps earlier, in the second sequence). For each cue, there is a separate set of policy-states, so each cue can be considered independent of the others. So, for each possible cue, the analysis is applied: the reachable policy-states are found, then their correspondence to hidden sensory states is found.
This can be informally summarized as follows. If observation o′ is used as a CASRM retrieval cue and retrieval is advanced j steps, which results in retrieved memory of observation q [one of possibly many memories that might be retrieved, specifically one from the set fO(o′, j)], then a particular policy-state including q and j results. The hidden state corresponding to the retrieved memory is one of the set of states that are observed as q and occur j steps after a state observed as o′ [the subset of fS(o′, j) which can be observed as q]. Finally, the set of o′-delimited, reachable states from the states found j steps after o′ that are observable as q is the set of states from which the policy-state containing q is reachable using cue o′. The analyses only differ in that each has a different set of possible cues o′, but this difference is important in practice.
If the retrieval cue itself were not included in the policy-state, an additional step would be needed. In this step, the sets of states from which a policy-state with a given retrieved observation q is reachable would be combined (unioned) over each possible cue value.
Allowing arbitrary observations to be used as cues does allow the agent to make one type of systematic error: the use of over-specific cues. For example, if an agent is attempting to recall what it had for breakfast this morning, consider the cue “morning” versus the cue “Thursday morning.” While the former may generally be successful, the latter will only work when today is actually Thursday. Roughly, an appropriate retrieval cue in this formalism should be an observation that occurs with the same frequency as the desired memory and which occurs just before or at the same time as the desired memory (because we only consider forward retrieval).
Though we do not specifically focus on CASRMs with limited capacities (i.e., a system where only the n most recent observations are retrievable), it is easy to see how a limited capacity can be accounted for. If the agent’s current sensory observation is o and observation o′ is used as a retrieval cue, but o′ most recently occurred far enough in the past that it is no longer retrievable, the agent’s policy-state may be written (o, o′, –, 0) (where the hyphen indicates no observation retrieved). This policy-state is reachable from a state s that can be observed as o only if the sensory AMDP allows a sequence of n observations ending with s in which o′ never occurs. Thus a failure to retrieve a memory given a cue is informative in that it indicates the cue observation has not been observed in a long time (the past n steps).
SAM cue for CASRM Retrieval
The policy-state for an agent with both SAM and CASRM combines the forms given earlier into (ot, ot−x+j, j, om, k) and the SAM observation om (which must be reachable in k steps from ot using SAM) used as a CASRM cue means ot−x = om for some lowest integer x for which this holds for the given om (assuming om has been observed in the past, otherwise retrieval fails). Holding ot, j, om, and k constant, we consider the possible values of ot−x+j. The hidden states corresponding to ot−x+j are fS(om, j). A particular retrieved memory o (and the policy-state containing it) corresponds to the subset S of the set of states fS(om, j) that can be observed as o. The hidden sensory states from which the policy-state (ot, o, j, om, k) is reachable are those in the set rS(S, om) that can be observed as or. Each of these policy-states would correspond to one row of a disambiguation matrix in the approach of Zilli and Hasselmo (2008b)
.
Because CASRM can only retrieve a memory given a cue, its potential use is limited by the cues presently available to the agent. Static associations can provide a larger pool of observations, allowing access to memories that would otherwise be unavailable in a particular situation.
As an example of a situation where this strategy can be useful, consider a Where Did I Park? task. In this task, the agent must recall in which parking lot its car is parked (it is assumed that recalling the lot is sufficient to find the car). On each trial the agent experiences three task-relevant states (and a number of irrelevant states). The agent begins in the car observation (parking its car) then is randomly presented with one of multiple parking lot observations, and then passes through perhaps many irrelevant observations (work, errands, etc.). Finally, it is presented with the test observation where it must recall where it parked. From this test observation (which corresponds to one of multiple hidden states: one for each parking lot), there is a “go to parking lot A” action, a “go to parking lot B” action, etc. The agent is rewarded for selecting the action corresponding to the lot where it parked its car (e.g., in the test observation corresponding to having parked in parking lot A, the parking lot A action is rewarded). The agent may then go on to experience a number of other task-irrelevant observations (car, driving to a warehouse, fight club, etc.) before eventually beginning the next trial.
While observing test, CASRM can only retrieve a memory beginning at the most recent past observation of test which does not easily provide the desired information regarding the car’s location. If the car observation has been learned as a static associate of the test observation, then car can be used as a CASRM retrieval cue when the agent is observing test. The particular parking lot observed on a particular trial occurs one step after the car observation, so after j = 1 retrieval step the agent will retrieve an observation of a parking lot. That is, fO(car, 1) is the set of the possible parking lots in the task (specifically, the set of observations that can follow a car observation). Suppose there are two such observations: Itchy lot and Scratchy lot and that the respective test states are testIL and testSL. rS(Itchy lot, test), the set of test-delimited, reachable-from-Itchy lot states, includes the Itchy lot state, the testIL state, and any states in between, but not the testSL state [and vice versa for rS(Scratchy lot, test)]. Thus the parking lot retrieved corresponds to the agent’s hidden sensory state. This result shows that using SAM to provide a retrieval cue for CASRM can be a successful strategy for efficiently solving the Where Did I Park? task. This success is true by virtue of the definition of the task. If the task were changed so that the agent’s car could randomly move to a different parking lot without the agent observing it, then both testIL and testSL would be in both sets rS(Itchy lot, test) and rS(Scratchy lot, test) and the retrieved memory would not be informative.
GAMM cue for CASRM Retrieval
The policy-state for an agent with both GAMM and CASRM combines the forms given earlier into (ot, ot−x+j, j, ot−i, i) and if the GAMM observation ot−i were being used as a CASRM cue, we would have x ≤ i. That is, the retrieved memory can begin no earlier than the time at which the cue was gated into GAMM. The analysis proceeds exactly as above, except that the set of possible cues is restricted to bO(ot, i) (the possible values of ot−o). Using a cue from GAMM drastically restricts the range of memories that can be retrieved, because CASRM retrieves the most recent sequence beginning with the cue, which will have appeared in the recent history of the agent for it to be maintained in GAMM.
A task where this strategy can be useful is immediate serial recall task (Baddeley, 1986
), in which a subject is presented with a sequential list of items and then immediately asked to recall them in order. Clearly maintaining the first item of the list in GAMM during the list presentation provides a cue for CASRM to retrieve the list directly. Of course, other strategies such as maintaining the whole list in GAMM would also be successful in this task. The primary advantage of using CASRM to retrieve the list is the greater capacity of CASRM. An agent will have a limited number of GAMMs and so must decide which information to store at the time it is presented, whereas CASRM allows a list to be retrieved repeatedly to find the relevant information at a particular time.
CASRM cue for CASRM Retrieval
The policy-state for an agent with a CASRM is of the form given earlier: (ot, ot−x, ot−x+j, j). If the cue ot−x is itself an observation retrieved in CASRM, then it must be j′ steps after some earlier cue ot−y, so ot−x = ot−y+j′. In the simplest case, the initial cue is ot so the possible subsequent cues are fO(ot, j′). In the same way that using SAM to provide a CASRM retrieval cue expands the set of possible cues, using a retrieved observation from CASRM itself can also provide a greater range of retrieval cues. And as in the case of a cue from GAMM, this subsequent cue ot−x can occur no earlier in time than the retrieved observation ot−y+j′ which became the new cue, which is to say x ≤ y + j′. If the cue observation was the most recent appearance of that observation, x = y + j′, then there is no effect and retrieval can proceed as usual. Essentially, using a retrieved observation as a cue allows retrieval to “skip ahead,” as the following example demonstrates.
Consider this strategy in the Where Did I Park? task. If the agent were to cue CASRM retrieval with the test observation, the retrieved memory would begin at the most recent test observation, which would be followed by the car observation, the driving home observation, and so forth through the whole night, eventually retrieving the most recent car observation and subsequently the desired parking lot observation. Notice that car, which is a useful cue in this situation, occurs after a single step of advancing retrieval. By then cuing CASRM retrieval with car, retrieval jumps ahead to the most recent car observation, after which one more step of advancing retrieval will retrieve the desired parking lot observation. This shows that using CASRM to provide a cue for CASRM is another successful strategy for solving the Where Did I Park? task.
Summary
In all of these cases of varying the retrieval cue for CASRM, there has been the potential for disambiguation beyond that provided by using only the current observation as a retrieval cue. So, although the restriction on the CASRM to only use presently available cues may seem overly limited, in reality other mechanisms available to an agent can make up for the limitation.
Having now examined the effect on CASRM of using cues from different memory systems, we next proceed to examining the maintenance of observations from different memory systems in a GAMM.
This section considers three ways in which an observation to be maintained in GAMM might come about. These correspond to the following types of action sequences: (1) Maintaining an observation from GAMM: “GAMM action, i′ motor actions, GAMM action, i motor actions,” (2) Maintaining an observation from SAM: “k SAM actions, GAMM action, i motor actions,” and (3) Maintaining an observation retrieved with CASRM: “CASRM cue with sensory observation, j CASRM advance retrieval actions, GAMM action, i motor actions.”
For simplicity it is assumed (unless otherwise specified) that a GAMM has a single target so that, if the GAMM contains o from i steps ago, it is clear which system originally contained o.
Consider the case of maintaining in GAMM an observation retrieved with CASRM. Intuitively the idea of this memory strategy is that, since CASRM can disambiguate a set of states, holding the retrieved observation in GAMM should let the agent carry that disambiguation information forward in time. For instance, suppose that through CASRM the agent knows it was at state sa and not state sb i steps ago (but sa and sb are observed as identical). Also suppose that sa leads to sy and sb to sz, both after i steps (and sy sz are observed as identical). Then, combined, the agent can behave as if it knows it is currently at sy and not sz.
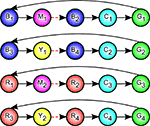
For a more concrete example, consider the following interpretation of the AMDP in Figure 2
in terms of packaging. An agent is presented with a closed box that is colored blue or red. It opens the box and places inside it a white ball drawn from either a magenta or a yellow drawer. Possibly much later in time (indicated by the red arrows), the box is closed and wrapped in cyan paper. A green light indicates that the packaging is completed and that the agent should press one of four buttons, depending on the color of the drawer and box. At this point in time, the current sensory input does not inform as to the color of the drawer or box. The observation from two steps in the past identifies the box color, partially disambiguating the green, and so is useful to maintain in GAMM. The observation of the drawer color, however, is potentially too old to have been maintained in GAMM. Nevertheless, CASRM at the recent observation of the box color can retrieve the memory of the color of the drawer. In fact, holding both the cue (box color) and the retrieved observation (drawer color) in GAMM can disambiguate the green states. For example, if one step of CASRM retrieval cued by blue retrieves magenta, the agent must be at B2 and, through GAMM, can carry that information forward to know it is at G1. Note that, properly, all the green states in Figure 2
should be connected to all of the left-most states to represent a case where the box color and drawer color are selected randomly. However, the analyses below only examines states during a single “trial” so these connections have no effect on the particular calculations carried out here.
Figure 2. Task used as an example of the use of holding earlier disambiguation (such as from content-addressable, sequential retrieval memory, CASRM) in gated, active maintenance memory. A behavioral interpretation as an agent wrapping packages is given in the text. The name of the each state is given as a letter and number within each colored circle and the color of the circle identifies the corresponding observation (with letters corresponding to colors as in B for blue or M for magenta). The red dashed arrows indicate places where additional states may be interposed without qualitatively affecting the results when CASRM is used (as long as no red or blue states are placed there).
The essence of these analyses is the same regardless of the original source of the observation in GAMM. When the observation was first placed in GAMM, the agent was at a particular policy-state which was reachable from a subset of hidden states in the AMDP. The agent then took i motor actions and arrives at a new policy-state. It is this policy-state and the hidden states from which it is reachable that are of interest.
Architectures with Two GAMMs
First, consider an architecture with a single GAMM. The set X of all states from which policy-state (o, p, i + i′) is reachable is a subset of the set of states that can be observed as o. Now consider an architecture with a second GAMM that can maintain the contents of both the sensory observation and the first GAMM. This agent could start at policy-state (o′, p, i′,…) (where the ellipses indicate irrelevant information), use its second GAMM action to move to policy-state (o′, p, i′, (o′, p, i′), 0), then take i motor actions and end up at (o, p, i + i′, (o′, p, i′), i). This policy-state is possibly more informative than the first because the set Y of states from which this policy-state is reachable is a subset of the set X (see Appendix B, Theorem B1). (Recall that since the agent’s policy is a function of its policy-state, a smaller set of hidden sensory states from which a policy-state is reachable results in less uncertainty about its state and a policy that may better reflect the true dynamics of the sensory AMDP).
But why is this the case? Since this architecture combined the observations of two mechanisms into the target for a single GAMM, it is worth considering which of the two (sensory observation or GAMM contents) are responsible for the increase in information.
If the second GAMM maintained only the sensory information, then the agent would end up in policy-state (o, p, i + i′, o′, i) [instead of (o, p, i + i′) if the agent had a single GAMM]. By the same logic as the case above, the policy-state with two GAMMs is potentially more informative than that with a single GAMM (see Appendix B, Theorem B2).
If the second GAMM maintained only the first GAMM’s information, the agent could start at policy-state (o′, p, i′,…), use its second GAMM action to move to policy-state (o′, p, i′, (p, i′), 0), then take i motor actions and end up at (o, p, i + i′, (p, i′), i). In this case where one GAMM maintains the contents of another, the architecture with one GAMM [ending at policy-state (o, p, i + i′)] is equally informative as that with two GAMMs [ending at policy-state (o, p, i + i′, (p, i′), i)]. From any state s from which (o, p, i + i′) is reachable, (o, p, i + i′, (p, i′), i) is also reachable, because the content of the second GAMM is redundant.
The primary purpose of these three cases is to show that the case of one GAMM maintaining the information from another GAMM is not useful, but that using two GAMMs to maintain information from two different times is useful.
GAMM for SAM
The form of the argument for the case where one GAMM maintains the content of a second also shows that using GAMM to maintain a static associate of an observation is at best equally informative (and at worst, less informative) than using a GAMM to maintain the original observation (at least for the specific characterization of informative used here, which relates policy-states to hidden sensory states). To show this, consider an agent with only a GAMM at policy-state (o, p, i) [where p is some observation in bO(o, i)] and let X be the set of hidden states from which this policy-state is reachable. Similarly, for an agent with a GAMM and an SAM at policy-state (o, m, i,…) [where m is some observation reachable through k SAM actions from some p in bO(o, i)], let Y be the set of hidden states from which this is reachable. The only relevant difference here is that p is the actual sensory observation from i steps in the past while m is a static associate of the actual sensory observation from i steps in the past. Here X ⊆ Y, which is to say that maintaining a static associate has possibly decreased the amount of information available (see Appendix B, Theorem B3).
Consider as an example a delayed matching task where a white oval sample stimulus is displayed and followed, a short time later, by another white oval (which, in a matching task, the agent should respond to). If the agent maintains in GAMM the white oval itself, it will be able to respond correctly. If the agent, on the other hand, maintained some other observation that is associated with a white oval, e.g., an egg or Kevin Bacon (who is associated with many observations, Fass et al., 1996
), then the agent has less information about the sample stimulus and may not be able to respond correctly.
GAMM for CASRM
We consider two cases of using GAMM to maintain the contents of CASRM, differing only in whether or not GAMM maintains only the retrieved observation and number of steps retrieval is advanced or if it also maintains the retrieval cue.
First, we will compare an architecture with a single GAMM to one with a GAMM that can maintain the retrieved CASRM observation and number of steps retrieval has been advanced. In the former case, the agent’s policy-state can be written as (o, p, i). For the latter case, the agent’s policy-state may be of the form (o, p, i, q, j). In this case suppose the agent is initially at policy-state (o,…, q, j), having advanced its CASRM retrieval j steps to retrieve q. Now if the agent uses its GAMM action to maintain q and j, it will be at policy-state (o, (q, j), 0, q, j), and i motor actions will take it to (o, q, j), i, −, −1) (where the hyphen and negative one are used to indicate that CASRM is not currently retrieving any memory). Comparison of the two architectures shows that their policy-states are independently informative, which is to say that the set of hidden states reachable from (o, p, i) is neither necessarily a superset nor a subset of the set of hidden states reachable from (o, (q, j), i, −, −1). Thus neither is strictly more informative than the other (see Appendix B, Theorem B4).
This is not the case, however, if GAMM includes the retrieval cue in addition to the retrieved observation and number of steps retrieval is advanced. This is apparent from the form of the policy-state that results. Taking actions exactly as above will result in the agent being at policy-state (o, (p, q, j), i, −, −1) versus (o, q, i), where the information of the latter is clearly contained within the former. In this case GAMM of CASRM is more informative than GAMM alone (see Appendix B, Theorem B5).
An example of the use of this strategy was given in the packaging example in the beginning of this section and in Figure 2
.
Summary
In contrast to the results from the previous section which discussed means by which CASRM retrieval cues could come about, there are cases where GAMM alone is equally informative as a more complicated architecture. These cases include GAMM maintaining the contents of another GAMM or a SAM (see middle row in Table 1
). On the other hand, using a GAMM to maintain the contents of CASRM can be more informative than using GAMM alone.
This concludes the analyses of interactions of the three memory systems considered here. We close with discussion on the results and our approach.
We have extended earlier analyses from Zilli and Hasselmo (2008b)
which dealt with separate memory systems by now analyzing a variety of combinations of memory systems. We first considered alternative cues for CASRM. This allows for the analysis of CASRM in a much larger range of tasks by loosening a major restriction of the earlier analysis.
We next considered the case of GAMM for memory observations that were produced at an earlier point in time. We showed that GAMM for another GAMM’s observation or static associations linked to some observation provides no improvement in information regarding the agent’s hidden sensory state over GAMM for the original observation. For GAMMs this occurs because the information is redundant and for static associations this arises because static associations themselves provide no additional information. On the other hand, GAMM for CASRM can provide increased information (particularly when both the retrieval cue and the retrieved memory are held in GAMM). These results are summarized in Table 1
.
These results provide insight both into the way that memory systems can be used in solving tasks and into the way the structure of tasks relate to the way particular memory systems work. By understanding the memory systems themselves and interactions between them in quantitative terms, we can hope to develop understanding of memory on a deeper level than that provided by, for instance, hierarchies of memory systems defined in often informal terms (Eichenbaum and Cohen, 2001
; Schacter and Tulving, 1994
; Squire, 2004
; Squire and Zola-Morgan, 1991
).
Additionally, the results inform as to useful memory architectures, which is information useful for both theoretical models and understanding the memory systems in animals. Increasing the complexity of a memory architecture in theoretical work will slow learning by virtue of the greater number of actions and expanded state space, so identifying redundant systems or interactions may help guide the design of models. Similarly, natural selection will likely have favored simple systems with the most flexible behavior, so a normative understanding of interactions between memory systems can aid in the understanding of memory mechanisms in animals.
Already this work can tentatively identify relationships between the considered mechanisms. Our analysis takes as a baseline level of disambiguation that provided only by an observation. Learning and behaving in an AMDP describing a task can be described in the RL framework in which action selection depends only on the current observation, and hence stimulus-response associations forms the base of any disambiguation hierarchy we might describe. We have seen that static associations provide no additional disambiguation of any states on their own, and so this system would be on the same level as stimulus-response associations. GAMM appears to provide the next level of disambiguation, as on its own it can reduce uncertainty about observations (by restricting the possible hidden states the agent may be at by virtue of the agent’s recent history) and has further use when used to hold previously retrieved CASRM observations. Finally, CASRM is the most powerful, providing the potential for additional disambiguation of observations using any of the memory systems here analyzed as a retrieval cue.
The present work has certainly not considered every possible mechanism involved in animal behavior. Other reasonable mechanisms that could be considered in the future include mechanisms for context, detecting identity-independent matching, dynamic associations, selective attention, familiarity or recognition, spatial memory, temporally extended motor patterns, etc. The analysis of these mechanisms and their potential use in behavioral simulations are a promising direction for future research.
We have provided a framework for analyzing the use and utility of biologically inspired memory mechanisms. These methods allow formal arguments about the capabilities and limitations of the mechanisms and may be useful both in understanding the brains and behavior of animals as well as in designing artificial systems with desired learning and memory abilities.
Appendix A
Here we provide quantitative definitions for the functions fS, bS, and rS in terms of POMDPs.
Recall that a POMDP is formally a tuple 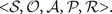 . The functions f, b, and r depend only on the way the states are connected and the observations that can correspond to those states. Thus it is convenient to extract from the tuple a simpler representation of the information needed.
. The functions f, b, and r depend only on the way the states are connected and the observations that can correspond to those states. Thus it is convenient to extract from the tuple a simpler representation of the information needed.
 . The functions f, b, and r depend only on the way the states are connected and the observations that can correspond to those states. Thus it is convenient to extract from the tuple a simpler representation of the information needed.
. The functions f, b, and r depend only on the way the states are connected and the observations that can correspond to those states. Thus it is convenient to extract from the tuple a simpler representation of the information needed.First, we find the matrix N of the connectivity of the state space. N is an |  |-by-|
|-by-|  | square matrix (one row and column for each state). Ni,j, the entry at row i and column j in N, is 1 if, for any action a and observation o in
| square matrix (one row and column for each state). Ni,j, the entry at row i and column j in N, is 1 if, for any action a and observation o in 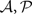 (si, a, sj, o) is nonzero; otherwise Ni,j = 0. Thus N is the adjacency matrix of the state space. Notice that the state space graph is directed, so the adjacency matrix is not necessarily symmetric.
(si, a, sj, o) is nonzero; otherwise Ni,j = 0. Thus N is the adjacency matrix of the state space. Notice that the state space graph is directed, so the adjacency matrix is not necessarily symmetric.
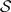 |-by-|
|-by-| 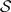 | square matrix (one row and column for each state). Ni,j, the entry at row i and column j in N, is 1 if, for any action a and observation o in
| square matrix (one row and column for each state). Ni,j, the entry at row i and column j in N, is 1 if, for any action a and observation o in 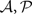 (si, a, sj, o) is nonzero; otherwise Ni,j = 0. Thus N is the adjacency matrix of the state space. Notice that the state space graph is directed, so the adjacency matrix is not necessarily symmetric.
(si, a, sj, o) is nonzero; otherwise Ni,j = 0. Thus N is the adjacency matrix of the state space. Notice that the state space graph is directed, so the adjacency matrix is not necessarily symmetric.The other piece of information needed is the set of observations that correspond to each state. We write this as a map 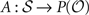 where P(
where P(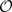 ) is the set of all subsets of
) is the set of all subsets of 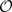 . For each state s in
. For each state s in 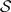 , A(s) is defined as the set
, A(s) is defined as the set 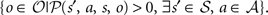 . To slightly abuse notation, we can define the inverse of this function as
. To slightly abuse notation, we can define the inverse of this function as 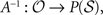 taking an observation and producing the set of states that can be observed as that observation.
taking an observation and producing the set of states that can be observed as that observation.
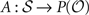 where P(
where P(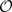 ) is the set of all subsets of
) is the set of all subsets of 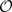 . For each state s in
. For each state s in 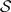 , A(s) is defined as the set
, A(s) is defined as the set 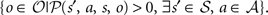 . To slightly abuse notation, we can define the inverse of this function as
. To slightly abuse notation, we can define the inverse of this function as 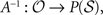 taking an observation and producing the set of states that can be observed as that observation.
taking an observation and producing the set of states that can be observed as that observation.The function fS(sa, i) gives the set of states found i steps forward from state sa. (Technically, the POMDP itself should also be a parameter to the function, but it is left implicit in this discussion for conciseness). These states are given by the nonzero entries in row a of the matrix Ni. Similarly, if X is a set of states which correspond to rows a, b, …in N, then fS(X, i) would be the set of states reachable in exactly i steps from any state in X. These would correspond to the states with nonzero entries in any of rows a, b, …in Ni. By analogy we can “overload” this function so that the first parameter is an observation instead of a state: fS(o, i), which is simply shorthand for fS(A−1(o), i). And with these we can define analogous functions to find observations i steps forward from a state or observation: fO(s, i) = A(fS(s, i)) and fO(o, i) = A(fS(o, i)).
The function bS(sa, i) gives the set of states found i steps backward from state sa. This is calculated as fS(sa, i) except the transpose of N is used: (NT)i. Analogous functions to the f functions can also be defined: bS(o, i) = A(bS(A−1(o), i)), bO(s, i) = A(bS(s, i)), and bO(o, i) = A(bS(o, i)).
Finally, we used a function rS(X, o) giving the o-delimited, reachable states from states in the set X, which corresponds to a forward tree expanding out of each state in X and stopping each branch when a state observed as o is reached. This entails finding, for each state in X, each state entered when walking along every possible path out of x and stopping only when a state that can be observed as o is reached. This set of reachable states can be found using a three step process. First, the connectivity matrix N can be adjusted so that the agent cannot exit states that can be observed as o. That is, we create a new matrix Nabs(o) in which rows corresponding to states A−1(o) are made absorbing (to borrow a term from Markov chain theory). If row r is made absorbing, all entries in the row are set to 0, except column r which is set equal to 1. If every row were made absorbing, the result would be the identity matrix.
In this way, row r of 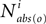 will always have only a single nonzero entry in column r, which means that the only state ever reachable from that state is the state itself. Some other row r′ not made absorbing will contain states reachable in i steps will also be affected if a state made absorbing is reachable from r′ in i or fewer steps. Thus this effectively provides the o-delimited aspect for a particular number of steps. To find all of the o-delimited, reachable states, we might sum
will always have only a single nonzero entry in column r, which means that the only state ever reachable from that state is the state itself. Some other row r′ not made absorbing will contain states reachable in i steps will also be affected if a state made absorbing is reachable from r′ in i or fewer steps. Thus this effectively provides the o-delimited aspect for a particular number of steps. To find all of the o-delimited, reachable states, we might sum 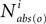 for all values of
for all values of 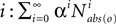 (where 0 < α < 1 prevents entries from going to infinity). But this does not match the definition of o-delimited, reachable states, because that definition applied the o-delimit only after the first step (in this definition, starting at a row corresponding to a state observed as o would stay in that state forever).
(where 0 < α < 1 prevents entries from going to infinity). But this does not match the definition of o-delimited, reachable states, because that definition applied the o-delimit only after the first step (in this definition, starting at a row corresponding to a state observed as o would stay in that state forever).
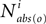 will always have only a single nonzero entry in column r, which means that the only state ever reachable from that state is the state itself. Some other row r′ not made absorbing will contain states reachable in i steps will also be affected if a state made absorbing is reachable from r′ in i or fewer steps. Thus this effectively provides the o-delimited aspect for a particular number of steps. To find all of the o-delimited, reachable states, we might sum
will always have only a single nonzero entry in column r, which means that the only state ever reachable from that state is the state itself. Some other row r′ not made absorbing will contain states reachable in i steps will also be affected if a state made absorbing is reachable from r′ in i or fewer steps. Thus this effectively provides the o-delimited aspect for a particular number of steps. To find all of the o-delimited, reachable states, we might sum 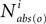 for all values of
for all values of 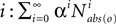 (where 0 < α < 1 prevents entries from going to infinity). But this does not match the definition of o-delimited, reachable states, because that definition applied the o-delimit only after the first step (in this definition, starting at a row corresponding to a state observed as o would stay in that state forever).
(where 0 < α < 1 prevents entries from going to infinity). But this does not match the definition of o-delimited, reachable states, because that definition applied the o-delimit only after the first step (in this definition, starting at a row corresponding to a state observed as o would stay in that state forever).This is avoided by simply left-multiplying this sum by the non-absorbing N, which essentially takes one step in the graph before considering the absorbing aspect. This, however, introduces yet another problem, because a state should be o-delimited, reachable from itself, but N may not allow a state to be reachable from itself. This is solved by adding the identity matrix I to the product.
In sum this gives the matrix 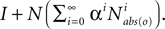 Row r in this matrix gives the o-delimited, reachable states from row r. To find the reachable states from a set of states a, b,…, rows corresponding to a, b,…can be added. The nonzero entries in the resulting vector correspond exactly (by construction) to the o-delimited, reachable states from X.
Row r in this matrix gives the o-delimited, reachable states from row r. To find the reachable states from a set of states a, b,…, rows corresponding to a, b,…can be added. The nonzero entries in the resulting vector correspond exactly (by construction) to the o-delimited, reachable states from X.
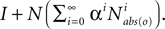 Row r in this matrix gives the o-delimited, reachable states from row r. To find the reachable states from a set of states a, b,…, rows corresponding to a, b,…can be added. The nonzero entries in the resulting vector correspond exactly (by construction) to the o-delimited, reachable states from X.
Row r in this matrix gives the o-delimited, reachable states from row r. To find the reachable states from a set of states a, b,…, rows corresponding to a, b,…can be added. The nonzero entries in the resulting vector correspond exactly (by construction) to the o-delimited, reachable states from X.Appendix B
The following theorems concern comparisons between pairs of architectures and focus on the relationship between the set of states from which a equivalent policy-states in the two architectures are reachable. When the set of states arising from one architecture are fully contained within the set of states from another, we say the architecture with the smaller set of states is more informative, because there is less uncertainty as to the actual state. However, it is important to keep in mind that this does not directly mean that the more informative architecture is always better. There can be situations where a particular memory strategy’s information actually increases the mean absolute deviation between the expected reward from the environment and the agent’s own expectation of that reward.
Consider four indistinguishable states from which an animal can perform a lever press. Let the lever press produce a reward of 0.5 in two of those states, 0 in one of those states, and 2 in one of those states. Suppose the agent is known to be in one of three states: one where a reward of 0.5 will result or one of the two states where a reward of 0 or 1 will result. If the agent knows it is in one of those three states, the expected reward will be 0.833 and the mean absolute deviation will be 0.778 (the expectation of the absolute value of the difference between the expected reward and the actual rewards). If the agent does not know it is in one of those three states, its expected reward will be 0.75, but the mean absolute deviation will be 0.75. Thus it has less information and has a lower expected reward, but its expected reward is closer to the reward it is actually expected to receive from those three states (and so its action value will be closer on average to the optimal action values).
Theorem B1. An architecture  with two GAMMs in which one GAMM targets the sensory input and the other targets both the sensory input and the contents of the first GAMM has more informative policy-states than an architecture
with two GAMMs in which one GAMM targets the sensory input and the other targets both the sensory input and the contents of the first GAMM has more informative policy-states than an architecture  with only a GAMM that targets the sensory input. Specifically, for architecture
with only a GAMM that targets the sensory input. Specifically, for architecture  let X be the set of states from which policy-state (o, p, i + i) is reachable and for architecture
let X be the set of states from which policy-state (o, p, i + i) is reachable and for architecture  let Y be the set of states from which policy-state (o, p, i + i′, (o′, p, i′), i) is reachable. Then Y ⊆ X.
let Y be the set of states from which policy-state (o, p, i + i′, (o′, p, i′), i) is reachable. Then Y ⊆ X.
 with two GAMMs in which one GAMM targets the sensory input and the other targets both the sensory input and the contents of the first GAMM has more informative policy-states than an architecture
with two GAMMs in which one GAMM targets the sensory input and the other targets both the sensory input and the contents of the first GAMM has more informative policy-states than an architecture  with only a GAMM that targets the sensory input. Specifically, for architecture
with only a GAMM that targets the sensory input. Specifically, for architecture  let X be the set of states from which policy-state (o, p, i + i) is reachable and for architecture
let X be the set of states from which policy-state (o, p, i + i) is reachable and for architecture  let Y be the set of states from which policy-state (o, p, i + i′, (o′, p, i′), i) is reachable. Then Y ⊆ X.
let Y be the set of states from which policy-state (o, p, i + i′, (o′, p, i′), i) is reachable. Then Y ⊆ X.Proof. x ∈ X means A(x) = o and p ∈ bO(x, i + i′). y ∈ Y means A(y) = o (y can be observed as o) and p ∈ bO(y, i + i′) [(o′, p, i′) is a valid policy-state] and for some z in A−1(o′), z is in bS(y, i) [y is reachable from a state from which (o′, p, i′) is reachable]. All y must be in X but there may be some x where no such z is in bS(x, i), so Y ⊆ X.
Theorem B2. An architecture  with two GAMMs in which both GAMMs target the sensory input has more informative policy-states than an architecture
with two GAMMs in which both GAMMs target the sensory input has more informative policy-states than an architecture  with only a GAMM that targets the sensory input. Specifically, for architecture
with only a GAMM that targets the sensory input. Specifically, for architecture  let X be the set of states from which policy-state (o, p, i + i) is reachable and for architecture
let X be the set of states from which policy-state (o, p, i + i) is reachable and for architecture  let Y be the set of states from which policy-state (o, p, i + i′, o′, i) is reachable. Then Y ⊆ X.
let Y be the set of states from which policy-state (o, p, i + i′, o′, i) is reachable. Then Y ⊆ X.
 with two GAMMs in which both GAMMs target the sensory input has more informative policy-states than an architecture
with two GAMMs in which both GAMMs target the sensory input has more informative policy-states than an architecture  with only a GAMM that targets the sensory input. Specifically, for architecture
with only a GAMM that targets the sensory input. Specifically, for architecture  let X be the set of states from which policy-state (o, p, i + i) is reachable and for architecture
let X be the set of states from which policy-state (o, p, i + i) is reachable and for architecture  let Y be the set of states from which policy-state (o, p, i + i′, o′, i) is reachable. Then Y ⊆ X.
let Y be the set of states from which policy-state (o, p, i + i′, o′, i) is reachable. Then Y ⊆ X.Proof. Let X be the set of states from which (o, p, i + i′) is reachable and Y the set of states from which (o, p, i + i′, o′, i) is reachable. x ∈ X means A(x) = o and p ∈ bO(x, i + i′). y ∈ Y means A(y) = o, p ∈ bO(y, i + i′) and o′ ∈ bO(y, i), and for some z in A−1(o′), z is in bS(y, i) [y is reachable from a state from which (o′, p, i′) is reachable]. All y must be in X, but there may be some x where no such z is in bS(x, i), so Y ⊆ X.
Theorem B3. An architecture  with a GAMM and a SAM in which GAMMs target the SAM and the SAM targets the sensory observation has equally or less informative policy-states than an architecture
with a GAMM and a SAM in which GAMMs target the SAM and the SAM targets the sensory observation has equally or less informative policy-states than an architecture  with only a GAMM that targets the sensory input. Specifically, for architecture
with only a GAMM that targets the sensory input. Specifically, for architecture  let X be the set of states from which policy-state (o, p, i) is reachable and for architecture
let X be the set of states from which policy-state (o, p, i) is reachable and for architecture  let Y be the set of states from which policy-state (o, m, i,…) is reachable. Then X ⊆ Y.
let Y be the set of states from which policy-state (o, m, i,…) is reachable. Then X ⊆ Y.
 with a GAMM and a SAM in which GAMMs target the SAM and the SAM targets the sensory observation has equally or less informative policy-states than an architecture
with a GAMM and a SAM in which GAMMs target the SAM and the SAM targets the sensory observation has equally or less informative policy-states than an architecture  with only a GAMM that targets the sensory input. Specifically, for architecture
with only a GAMM that targets the sensory input. Specifically, for architecture  let X be the set of states from which policy-state (o, p, i) is reachable and for architecture
let X be the set of states from which policy-state (o, p, i) is reachable and for architecture  let Y be the set of states from which policy-state (o, m, i,…) is reachable. Then X ⊆ Y.
let Y be the set of states from which policy-state (o, m, i,…) is reachable. Then X ⊆ Y.Proof. Let X be the set of states from which (o, p, i) is reachable and Y the set of states from which (o, m, i,…) is reachable. Because an observation may be considered a zero-step static associate of itself, all x from X must also be in Y. However, consider some state s where A(s) = o but p is not in bO(s, i). If there is some static associate m of some other p′ ≠ p in bO(s, i) then s is in Y but not X. Thus X ⊆ Y.
Theorem B4. An architecture  with a GAMM and a CASRM in which the GAMM targets the CASRM (maintaining only the retrieved observation and number of steps retrieval is advanced) and the CASRM targets the sensory observation has differently informative policy-states than an architecture
with a GAMM and a CASRM in which the GAMM targets the CASRM (maintaining only the retrieved observation and number of steps retrieval is advanced) and the CASRM targets the sensory observation has differently informative policy-states than an architecture  with only a GAMM that targets the sensory input. Specifically, for architecture
with only a GAMM that targets the sensory input. Specifically, for architecture  let X be the set of states from which policy-state (o, p, i) is reachable and for architecture
let X be the set of states from which policy-state (o, p, i) is reachable and for architecture  let Y be the set of states from which policy-state (o, (q, j), i, −, −1) is reachable. Then it is not necessarily true that either X ⊆ Y or Y ⊆ X.
let Y be the set of states from which policy-state (o, (q, j), i, −, −1) is reachable. Then it is not necessarily true that either X ⊆ Y or Y ⊆ X.
 with a GAMM and a CASRM in which the GAMM targets the CASRM (maintaining only the retrieved observation and number of steps retrieval is advanced) and the CASRM targets the sensory observation has differently informative policy-states than an architecture
with a GAMM and a CASRM in which the GAMM targets the CASRM (maintaining only the retrieved observation and number of steps retrieval is advanced) and the CASRM targets the sensory observation has differently informative policy-states than an architecture  with only a GAMM that targets the sensory input. Specifically, for architecture
with only a GAMM that targets the sensory input. Specifically, for architecture  let X be the set of states from which policy-state (o, p, i) is reachable and for architecture
let X be the set of states from which policy-state (o, p, i) is reachable and for architecture  let Y be the set of states from which policy-state (o, (q, j), i, −, −1) is reachable. Then it is not necessarily true that either X ⊆ Y or Y ⊆ X.
let Y be the set of states from which policy-state (o, (q, j), i, −, −1) is reachable. Then it is not necessarily true that either X ⊆ Y or Y ⊆ X.Proof. Let X be the set of states from which (o, p, i) is reachable and Y the set of states from which (o, (q, j), i,…) is reachable, where (q, j) is CASRM information. X is the set of states s where A(s) = o and p is in bO(s, i). Y is the set of states s where A(s) = o and there is some state s′ where A(s′) = q, s′ is in fS(o, j), and s is in rS(s′, o). We show that there may be some x not in Y and some y not in X. To see this, notice that both X and Y are subsets of A−1(o), but otherwise have independent constraints on membership. For instance, y does not constrain the set bO(y, i), so it may not contain p and y may not be in X. Similarly, x is not constrained by definition to be in Y. (The packaging example in the main text, Figure 2
, is also an demonstration of the claim).
Theorem B5. An architecture  with a GAMM and a CASRM in which GAMMs target the CASRM and the CASRM targets the sensory observation has more informative policy-states than an architecture
with a GAMM and a CASRM in which GAMMs target the CASRM and the CASRM targets the sensory observation has more informative policy-states than an architecture  with only a GAMM that targets the sensory input. Specifically, for architecture
with only a GAMM that targets the sensory input. Specifically, for architecture  let X be the set of states from which policy-state (o, p, i) is reachable and for architecture
let X be the set of states from which policy-state (o, p, i) is reachable and for architecture  let Y be the set of states from which policy-state (o, (p, q, j), i, −, −1) is reachable. Then Y ⊆ X.
let Y be the set of states from which policy-state (o, (p, q, j), i, −, −1) is reachable. Then Y ⊆ X.
 with a GAMM and a CASRM in which GAMMs target the CASRM and the CASRM targets the sensory observation has more informative policy-states than an architecture
with a GAMM and a CASRM in which GAMMs target the CASRM and the CASRM targets the sensory observation has more informative policy-states than an architecture  with only a GAMM that targets the sensory input. Specifically, for architecture
with only a GAMM that targets the sensory input. Specifically, for architecture  let X be the set of states from which policy-state (o, p, i) is reachable and for architecture
let X be the set of states from which policy-state (o, p, i) is reachable and for architecture  let Y be the set of states from which policy-state (o, (p, q, j), i, −, −1) is reachable. Then Y ⊆ X.
let Y be the set of states from which policy-state (o, (p, q, j), i, −, −1) is reachable. Then Y ⊆ X.Proof. Let X be the set of states from which (o, p, i) is reachable and Y the set of states from which (o, (p, q, j), i,…) is reachable, where (p, q, j) is CASRM information (p the cue and q the retrieved observation). X is the set of states s where A(s) = o and p is in bO(s, i). Y is the set of states s where A(s) = o, p is in bO(s, i) and there is some state s′ where A(s′) = q, s′ is in fS(o, j), and s is in rS(s′, o). We show that Y ⊆ X, i.e., there may be some x not in Y. To see this, notice simply that Y is defined as X with additional constraints on its membership and so all y are in X but not necessarily is a given x in Y.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was supported by Silvio O. Conte Center Grant NIMH MH71702, NIMH MH60013, NSF SLC SBE 0354378, and NIDA DA16454 (part of the CRCNS program). We also thank the three reviewers whose comments and suggestions greatly improved the clarity of the presentation of this material.