- 1New Frontiers of Sound Science and Technology Center, The University of Arizona, Tucson, AZ, United States
- 2Department of Mathematics, The University of Arizona, Tucson, AZ, United States
- 3Department of Materials Science and Engineering, The University of Arizona, Tucson, AZ, United States
The dynamical equations of motion for a discrete, one-dimensional harmonic chain with side restoring forces are analogous to the relativistic Klein–Gordon equation. Dirac factorization of the discrete Klein–Gordon equation introduces two equations with time reversal (T) and parity (P) symmetry-breaking conditions. The Dirac-factored equations enable the exploration of the properties of the solutions of the dynamic equations under PT symmetry-breaking conditions. The spinor solutions of the Dirac factored equations describe two types of acoustic waves: one with a conventional topology (Berry phase equal to 0) and the other with a non-conventional topology (Berry phase of π). In the latter case, the acoustic wave is isomorphic to the quantum spin of an electron, also known as an “acoustic pseudospin,” which requires a closed path, corresponding to two Brillouin zones (BZs), to restore the original spinor. We also investigate the topology of evanescent waves supported by the Dirac-factored equations. The interface between topologically conventional and non-conventional chains exhibits topological surface states. The Dirac-factored equations of motion of the one-dimensional harmonic chain with side springs can serve as a model for the investigation of the properties of acoustic topological insulators.
1 Introduction
A topological insulator cannot be adiabatically transformed into an ordinary insulator without passing through an intermediate conducting state (Qi and Zhang, 2011). While the bulk system is insulating, the surface can support conduction that is topologically protected, meaning that the surface states are insensitive to local perturbations (Hasan and Kane, 2010). Topological insulators can exhibit quantum mechanical properties such as the quantum spin Hall (QSH) effect (Qi and Zhang, 2010) and the anomalous quantum Hall (QH) effect, which occurs in the absence of an external magnetic field due to the breaking of time-reversal symmetry (Chang et al., 2023). Acoustic analogs of the QSH effect have been implemented (a) by tuning an accidental double Dirac cone in graphene-like lattices (He et al., 2016; Mei et al., 2016) and (b) via a BZ folding mechanism (Zhang et al., 2017; Yves et al., 2017; Xia et al., 2017; Deng et al., 2017). QH-related effects have been realized in acoustics by arranging circulating flows into periodic settings to form an acoustic lattice that breaks time reversal symmetry (Yang et al., 2015; Ni et al., 2015; Khanikaev et al., 2015).
Phononic structures can support elastic waves with non-conventional topology by breaking symmetry (Xue et al., 2022). Dirac factorization of the wave equation reveals potential topological properties that may result from symmetry breaking (which might be brought about by structural or external perturbations). For instance, the equations of motion of two coupled one-dimensional harmonic systems (Deymier and Runge, 2016) can be factored in the long wavelength limit as a product of two Dirac-like equations, each of which breaks parity symmetry and time reversal symmetry. Propagative wave solutions to each Dirac equation can satisfy two possible dispersion relations, giving rise to symmetric and anti-symmetric eigenmodes. The former exhibit the conventional character of Boson-like phonons, while the latter exhibit Fermion-like behavior of phonons (Deymier et al., 2015; Deymier et al., 2014). The topological properties of evanescent waves in product parity-time symmetry have also been investigated near exceptional points (Chen et al., 2024).
The wave equation for a two-dimensional plate coupled to a rigid substrate can also be subject to Dirac factorization (Deymier and Runge, 2022). These factors are analogous to the long-wavelength limit of the Qi, Wu, and Zhang (QWZ) model of the anomalous quantum Hall effect (Qi et al., 2006). The Dirac factorization reveals waves with spin-like degrees of freedom that have a gapped band structure, which is similar to the spin Hall effect. Kane and Lubensky (2014) demonstrate a method inspired by the Dirac factorization of the Klein–Gordon equation to establish a connection between topological mechanical modes and the topological band theory in electronic systems. This leads to the prediction of new topological bulk mechanical phases with distinct boundary modes. Topological phonons can also be classified using local symmetries (Süsstrunk and Huber, 2016) by adapting the classification of non-interacting electron systems to mechanical systems.
Here, we study solutions of the Dirac factorizations of the discrete one-dimensional harmonic chain with side restoring forces and investigate the appearance of edge modes at the interface of conventional and non-conventional topologies. In Section 2, we introduce the Dirac factorization of the discrete Klein–Gordon equation, and in Section 3, we find the dispersion relation and amplitude vectors corresponding to propagative wave solutions of the Dirac equations. Section 4 addresses evanescent wave solutions and their dispersion relation. In Sections 5 and 6, we compute the respective Berry phases of the amplitude vectors of the propagative and evanescent waves. Section 7 addresses the existence of edge modes at the interface between two topologically different semi-infinite media that obey the acoustic Dirac equation. Finally, in Section 8, we summarize and draw conclusions.
2 Model system and equation of motion for the discrete harmonic chain
We consider the model of the one-dimensional harmonic chain illustrated in Figure 1. We assume that the chain lies along the
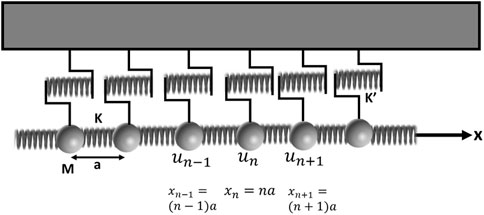
Figure 1. Schematic illustration of the one-dimensional harmonic chain attached elastically to a rigid substrate (top gray box). The side springs restore longitudinal motion.
We denote the displacement of the
Taking
The quantity
—where
Now, let us provide a physical interpretation of amplitude vectors with two components. We note that if
In order to achieve a factorization of the discrete Klein–Gordon equation as a product of Dirac-like equations, we will interpret the operator
Let
It can be verified that this product is the same as
—where
Now the solution to Equation 4
The tensor products of the matrices appearing in the above equation are as follows:
Taking
—where
3 Eigenvectors and dispersion relation
3.1 Dispersion relation
We will now find propagative solutions to the Dirac equations in Equation 5. Let us consider an ansatz taking the form of a plane wave with a
We have the matrices
In matrix form, Equation 7 becomes
The determinant of this 4 × 4 matrix is
and there exist non-zero solutions to Equation 8 if the determinant is zero. Equation 9 gives us
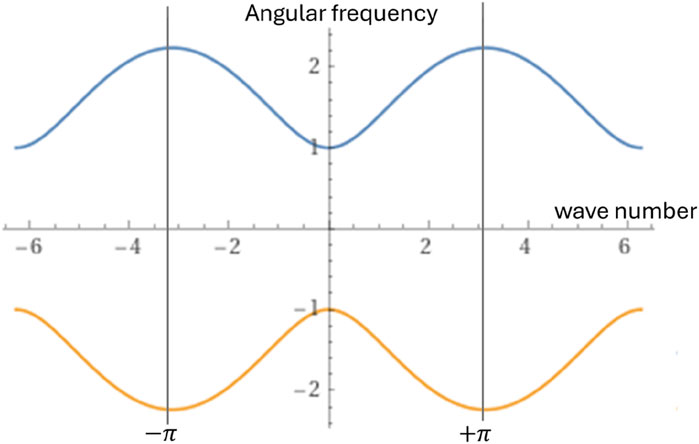
Equation 10 gives us the dispersion relations
The dispersion relation is illustrated in Figure 2.
3.2 Eigenvectors
We now solve Equation 8 for the components of the amplitude vector
To find solutions to the system of equations given by Equations 12 a–d, we hypothesize that
Recognizing that
4 Evanescent waves
In order to find non-propagative solutions of the Dirac equations (Equation 5), we consider the ansatz
We follow the procedure used in Section 3 to find the dispersion relation for waves of the form given by Equation 15:
When
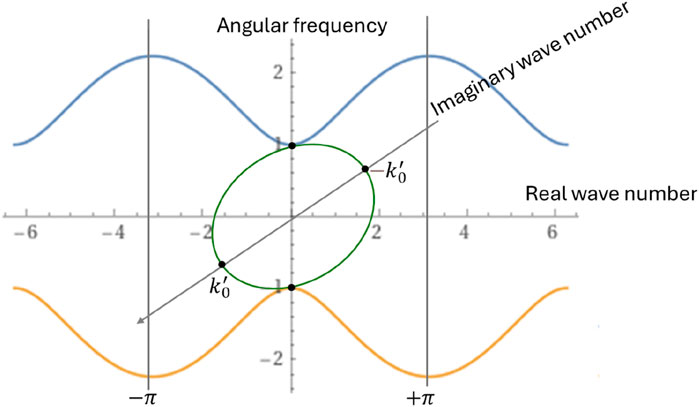
Figure 3. Schematic illustration of the discrete system dispersion relation for propagative waves (blue and yellow lines):
The normalized amplitude eigenvector is of the form
—where
5 Berry phase for propagative waves
5.1 Continuous contribution to the Berry phase
The contribution of the continuous part of the function,
Note that
5.2 Contribution of discontinuities in the eigenvectors to the Berry connection
The eigenvector given by Equation 14 contains components in the form of square roots—
The square root of a complex number is given by the formula
Here,
The phase of
If
If
Considering the component
In the case of
Their inner product gives
The Berry phase is a topological invariant of the system. Dirac-factored equations
6 Berry phase for evanescent waves
We now compute the Berry connection of the unit amplitude vector
We first compute the Berry connection along the top and the bottom halves of the loop, when
Case 1.
In this case, the unit amplitude vector is
We note that
Therefore, the Berry connection when
Case 2.
In this case, the unit amplitude vector is
Case 3. The Berry connection near the points where the loop intersects the
We wish to determine whether near
As
Similarly, when
Therefore, along the closed loop over the evanescent mode, the Berry phase amounts to
7 Interface modes
We now consider a system composed of two semi-infinite chains described by the acoustic Dirac equation, but differing only in the value of the parameter
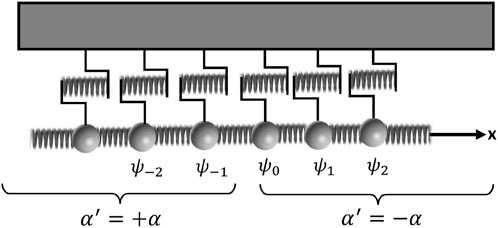
Figure 4. Schematic illustration of an interface between two topologically different semi-infinite media obeying the acoustic Dirac equation. The medium with
At the interface, the Dirac equations are
The Equations 19 a,b can be expanded as
We now seek solutions to these equations that take the form of evanescent waves decaying on both sides of the interface. These are solutions of the form
Equations 21 a,b give are solutions to the bulk acoustic Dirac equation of infinite chains, each with its respective values of
The existence of solutions in the forms given by Equations 22a,bwhich satisfy Equations 20a,b implies the existence of interface modes between the two chains with different topologies.
Inserting Equations 22a,b,b into Equations 20a,b,b gives us a system of eight linear equations in the eight unknowns
Equation 23 has solutions if the
Note that this determinant is independent of k’. To illustrate, let us set
The
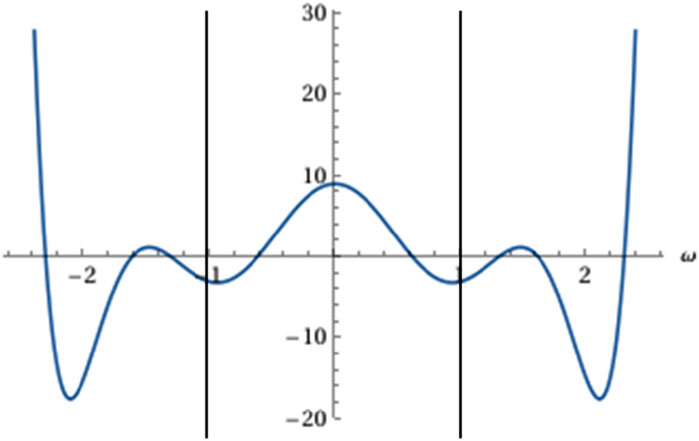
Figure 5. Plot of
8 Conclusion
We have here demonstrated that the Dirac factorization of the equations of motion of a mass and spring model exposes the potential for topological insulator behavior in acoustic systems. In particular, for a 1-d harmonic mass and spring chain attached elastically to a rigid substrate, the equations of motion give rise to a discrete version of the Klein–Gordon equation that can be factorized into Dirac equations with broken time-reversal and parity symmetry. Propagative and evanescent wave solutions of the Dirac factored equations were obtained. For propagative modes, the Berry phase for the Dirac equation with the + sign was found to be zero (conventional topology), and that with the – sign was found to be
Dirac factorization of classical wave equations exposes the possibility of topological insulators arising from broken symmetries. It reveals the possibilities offered by symmetry breaking in terms of the direction of wave propagation. However, additional physical conditions or mechanisms are needed to break T- or P-symmetry and realize one-way propagating waves in physical systems.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
AB: Writing – original draft, Writing – review and editing. KR: Writing – original draft, Writing – review and editing. PD: Writing – original draft, Writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Science and Technology Center New Frontiers of Sound (NewFoS) through NSF cooperative agreement # 2242925.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Berry, M. V. (1984). Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A39245–57. doi:10.1098/rspa.1984.0023
Calderin, L., Hasan, M. A., Jenkins, N. G., Lata, T., Lucas, P., Runge, K., et al. (2019). Experimental demonstration of coherent superpositions in an ultrasonic pseudospin. Sci. Rep. 9, 14156. doi:10.1038/s41598-019-50366-y
Chang, C.-Z., Liu, C.-X., and MacDonald, A. H. (2023). Colloquium: Quantum anomalous hall effect. Rev. Mod. Phys. 95 (1), 011002. doi:10.1103/RevModPhys.95.011002
Chen, Z., He, H., Li, H., Li, M., Kou, J., Lu, Y., et al. (2024). Observation of parity-time symmetry for evanescent waves. Commun. Phys. 7, 339. doi:10.1038/s42005-024-01816-1
Deng, Y., Ge, H., Tian, Y., Lu, M., and Jing, Y. (2017). Observation of zone folding induced acoustic topological insulators and the role of spin-mixing defects. Phys. Rev. B 96, 184305. doi:10.1103/PhysRevB.96.184305
Deymier, P., and Runge, K. (2016). One-dimensional mass-spring chains supporting elastic waves with non-conventional topology. Crystals 6 (4), 44. doi:10.3390/cryst6040044
Deymier, P. A., and Runge, K. (2022). Revealing topological attributes of stiff plates by dirac factorization of their 2D elastic wave equation. Appl. Phys. Lett. 120 (8), 081701. doi:10.1063/5.0086559
Deymier, P. A., Runge, K., Swinteck, N., and Muralidharan, K. (2014). Rotational modes in a phononic crystal with fermion-like behavior. J. Appl. Phys. 115, 163510. doi:10.1063/1.4872142
Deymier, P. A., Runge, K., Swinteck, N., and Muralidharan, K. (2015). Torsional topology and fermion-like behavior of elastic waves in phononic structures. Comptes Rendus Mécanique 343, 700–711. doi:10.1016/j.crme.2015.07.003
Hasan, M. Z., and Kane, C. L. (2010). Colloquium: topological insulators. Rev. Mod. Phys. 82 (4), 3045–3067. doi:10.1103/RevModPhys.82.3045
He, C., Ni, X., Ge, H., Sun, X.-C., Chen, Y.-B., Lu, M.-H., et al. (2016). Acoustic topological insulator and robust one-way sound transport. Nat. Phys. 12, 1124–1129. doi:10.1038/nphys3867
Kane, C. L., and Lubensky, T. C. (2014). Topological boundary modes in isostatic lattices. Nat. Phys. 10, 39–45. doi:10.1038/nphys2835
Khanikaev, A. B., Fleury, R., Mousavi, S. H., and Alù, A. (2015). Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat. Commun. 6, 8260. doi:10.1038/ncomms9260
Mei, J., Chen, Z., and Wu, Y. (2016). Pseudo-time-reversal symmetry and topological edge states in two-dimensional acoustic crystals. Sci. Rep. 6, 32752. doi:10.1038/srep32752
Ni, X., He, C., Sun, X.-C., Liu, X.-p., Lu, M.-H., Feng, L., et al. (2015). Topologically protected one-way edge mode in networks of acoustic resonators with circulating air flow. New J. Phys. 17, 053016. doi:10.1088/1367-2630/17/5/053016
Qi, X.-L., and Zhang, S.-C. (2010). The quantum spin hall effect and topological insulators. Phys. Today 63 (1), 33–38. doi:10.1063/1.3293411
Qi, X.-L., and Zhang, S.-C. (2011). Topological insulators and superconductors. Rev. Mod. Phys. 83 (4), 1057–1110. doi:10.1103/RevModPhys.83.1057
Qi, X.-L., Wu, Y.-S., and Zhang, S.-C. (2006). Topological quantization of the spin hall effect in two-dimensional paramagnetic semiconductors. Phys. Rev. B 74, 085308. doi:10.1103/PhysRevB.74.085308
Süsstrunk, R., and Huber, S. D. (2016). Classification of topological phonons in linear mechanical metamaterials. Proc. Natl. Acad. Sci. U.S.A. 113 (33), E4767–E4775. doi:10.1073/pnas.1605462113
Xia, B.-Z., Liu, T.-T., Huang, G.-L., Dai, H.-Q., Jiao, J.-R., Zang, X.-G., et al. (2017). Topological phononic insulator with robust pseudospin-dependent transport. Phys. Rev. B 96, 094106. doi:10.1103/PhysRevB.96.094106
Xue, H., Yang, Y., and Zhang, B. (2022). Topological acoustics. Nat. Rev. Mater 7, 974–990. doi:10.1038/s41578-022-00465-6
Yang, Z., Gao, F., Shi, X., Lin, X., Gao, Z., Chong, Y., et al. (2015). Topological acoustics. Phys. Rev. Lett. 114, 114301. doi:10.1103/PhysRevLett.114.114301
Yves, S., Fleury, R., Lemoult, F., Fink, M., and Lerosey, G. (2017). Topological acoustic polaritons: robust sound manipulation at the subwavelength scale. New J. Phys. 19, 075003. doi:10.1088/1367-2630/aa66f8
Keywords: topological insulator, Berry phase, Dirac equation, Klein-Gordon equation, interface mode
Citation: Basu A, Runge K and Deymier PA (2025) The acoustic Dirac equation as a model of topological insulators. Front. Acoust. 3:1615210. doi: 10.3389/facou.2025.1615210
Received: 20 April 2025; Accepted: 29 August 2025;
Published: 29 September 2025.
Edited by:
Michael J. Leamy, Georgia Institute of Technology, United StatesReviewed by:
Stefano Laureti, University of Calabria, ItalyZhang, Qicheng, Westlake University, China
Copyright © 2025 Basu, Runge and Deymier. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Abhirup Basu, YWJoaXJ1cC5iYXN1NTZAZ21haWwuY29t
 Abhirup Basu
Abhirup Basu Keith Runge
Keith Runge Pierre A. Deymier1,3
Pierre A. Deymier1,3