Efficient high-resolution microscopic ghost imaging via sequenced speckle illumination and deep learning from a single noisy image

This study presents a novel approach for achieving high-quality and large-scale microscopic ghost imaging by integrating deep learning-based denoising with computational ghost imaging techniques. By utilizing sequenced random speckle patterns of optimized sizes, we reconstructed large noisy images with fewer patterns while successfully resolving fine details as small as 2.2 μm on a USAF resolution target. To enhance image quality, we incorporated the Deep Neural Network-based Noise2Void (N2V) model, which effectively denoises ghost images without requiring a reference image or a large dataset. By applying the N2V model to a single noisy ghost image, we achieved significant noise reduction, leading to high-resolution and high-quality reconstructions with low computational resources. This method resulted in an average Structural Similarity Index (SSIM) improvement of over 324% and a resolution enhancement exceeding 33% across various target images. The proposed approach proves highly effective in enhancing the clarity and structural integrity of even very low-quality ghost images, paving the way for more efficient and practical implementations of ghost imaging in microscopic applications.

1 Introduction

Microscopy has transformed scientific research by enabling visualization of micro- and nanoscale structures, which is essential for biological studies and disease research. However, traditional optical microscopy is fundamentally limited by the Abbe diffraction limit, restricting achievable resolution (Abbe, 1873). While reducing the illumination wavelength and increasing the numerical aperture can improve resolution, imaging biological samples at the nanoscale requires XUV wavelengths (10–100 nm), which can damage samples and suffer from high absorption losses and limited optical components.

To overcome these challenges, ghost imaging (GI) has emerged as a promising technique. GI reconstructs images using correlated measurements from spatially separated detectors, making it attractive for lensless imaging and applications requiring low radiation doses. Originally developed with quantum entangled photons (Pittman et al., 1995), GI has since been demonstrated with classical light sources, broadening its applicability (Abouraddy et al., 2001; Bennink et al., 2002).

Advancements in computational techniques and single-pixel detectors have further enhanced GI. Computational ghost imaging (CGI) uses compressed sensing (CS) and reconstruction algorithms to recover images from fewer measurements (Shapiro, 2008; Katz et al., 2009), enabling lensless imaging in environments where traditional optics are impractical, such as with XUV sources. Despite using only, a single-pixel detector, CGI has enabled rapid computational imaging (Welsh et al., 2013). Simplified holography processes have also expanded the potential for 3D imaging and microscopy (Clemente et al., 2013).

Recent progress has extended GI into the x-ray and XUV regimes, including demonstrations with conventional x-ray sources (Yu et al., 2016; Pelliccia et al., 2016; Zhang A-X. et al., 2018), XUV free-electron lasers (Kim et al., 2020), and x-ray phase-contrast GI (Olbinado et al., 2021). Our recent work has enabled microscopic ghost imaging with a tabletop XUV source (Oh et al., 2025), and other studies have shown high-resolution GI of microscopic objects (Sun et al., 2019; Vinu et al., 2020; Dou et al., 2020). Techniques such as imaging at megahertz switching rates with cyclic Hadamard masks (Hahamovich et al., 2021) and novel phase microscopy approaches have significantly improved imaging speed and reduced system complexity (Zhao et al., 2023).

Nevertheless, many CGI methods rely on traditional pattern-based approaches, such as Hadamard and Fourier transforms, which require a large number of illumination patterns to achieve high resolution. For example, capturing Extended Graphics Array (XGA) resolution images (1,024 × 768 pixels) requires over 1.5 million patterns with the differential Hadamard method and over 3 million with the 4-step Fourier method (Duarte et al., 2008; Zhang et al., 2017; Gibson et al., 2020), resulting in long acquisition times and heavy computational loads. In contrast, our previous work with sequenced speckle illumination demonstrated that GI reconstruction is possible with significantly fewer patterns (Oh et al., 2023). In this study, we adopted sequenced speckle as the illumination strategy for our experiments to validate its effectiveness within the proposed framework.

Despite recent advances in deep learning for ghost imaging, existing approaches have notable limitations. Traditional deep learning methods typically require extensive training datasets, including paired low-resolution and reference images, which are often difficult to obtain in practical microscopic settings (Lyu et al., 2017; Wang et al., 2019; Hu et al., 2020). More recent methods, such as ghost imaging with deep neural network constraints (Wang et al., 2022), employ untrained networks and compressed sensing to reconstruct images directly from measurement data. However, these approaches still face significant challenges: they cannot fully exploit the spatial information inherent in speckle patterns, and they demand large volumes of measurement data and considerable computational resources. These limitations hinder the practical application of high-resolution, high-quality ghost imaging, especially when rapid or resource-efficient imaging is required.

To address these limitations, we introduce a denoising algorithm based on Noise2Void (N2V) (Krull et al., 2019), a deep learning method that requires only a single noisy image for training, eliminating the need for reference images. By combining ghost images obtained from random speckle patterns with the N2V model, we achieve high-quality, high-resolution images with fewer patterns and minimal computational resources. The N2V framework is built on the U-Net architecture (Ronneberger et al., 2015; Wu et al., 2024; Komatsu and Gonsalves, 2020; Jia et al., 2021), which is well-suited for image restoration and denoising, especially with limited training data.

We evaluated the quality of denoised images using Rayleigh, Abbe, and Sparrow criteria, and investigated how speckle pattern size affects microscopic ghost image quality. Our results reveal a clear relationship between speckle size and image resolution, demonstrating the effectiveness of our approach for efficient, high-quality microscopic ghost imaging.

2 Experimental setup and measurement principle

2.1 Experimental setup

Figure 1 illustrates the experimental setup. The experiments were conducted using a DMD-based CGI setup—specifically the Vialux^TM DLP V-Module V4100 board—which is capable of projecting sequenced speckle patterns at a rate of 50 frames per second. To enhance the randomness and diversity of the illumination, we employed sequenced speckle patterns with varying sizes. The DMD features a 0.7-inch diagonal array comprising 1,024 × 768 micromirrors, each with a pitch of 13.6 μm. A beam expander was used to illuminate the entire area of the DMD. The reflected light was directed through a positive lens (focal length = 125 mm) and then focused onto the object via an objective lens. For magnification, we used ZEISS A-Plan objectives with ×40 magnification (NA = 0.65, focal length = 4.1 mm, infinity-corrected). According to the Rayleigh criterion, the spatial resolution of the objective is $0.61\mathrm{\lambda }/NA$, which yields approximately 0.6 µm for a 632.8 nm He–Ne laser wavelength. The light transmitted through the object was collected by a focusing lens and measured by a bucket detector (Thorlabs, PDA36A-EC), which recorded the total transmitted intensity.

Figure 1

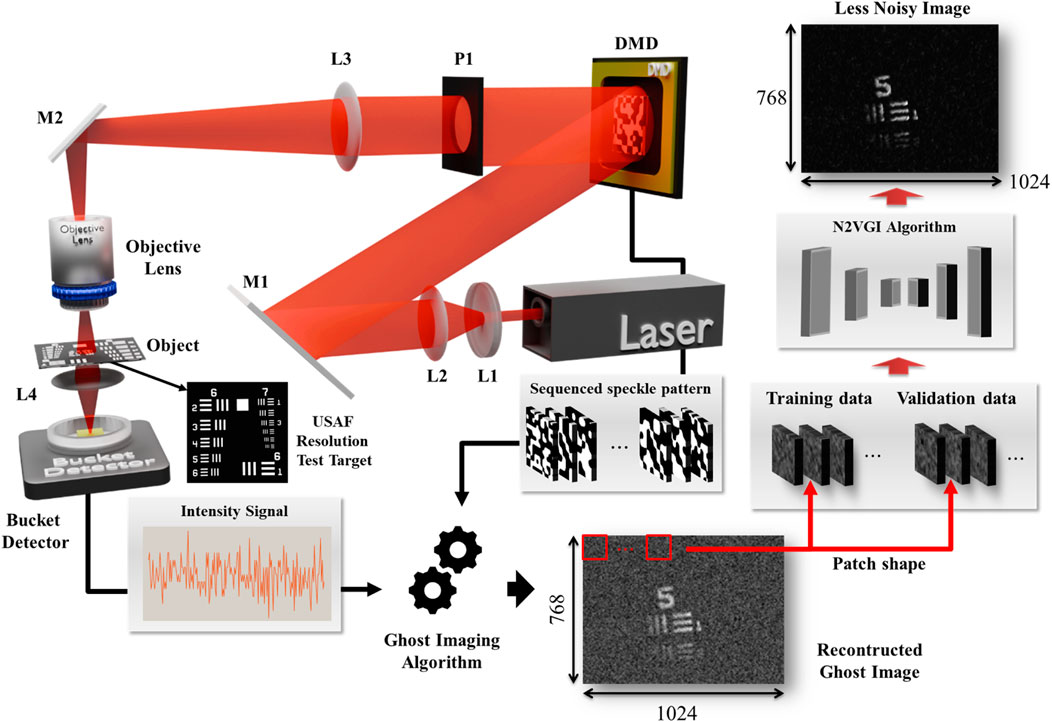
Figure 1. Experimental setup for computational microscopic ghost imaging enhanced with a neural network. A collimated beam from a He-Ne laser (λ = 632.8 nm) is shaped by lenses L1 and L2 before being directed towards a Digital Micromirror Device (DMD). The DMD, controlled by a computer, generates a sequence of speckle patterns. These patterns are focused by lens L3 (f = 125 mm) onto an objective lens (f = 4.1 mm, NA: 0.65), which illuminates the USAF-1951 resolution target. Light transmitted through the target is collected by a bucket detector, producing an intensity signal. This signal, along with the corresponding DMD patterns, is fed into a ghost imaging algorithm, specifically a Noise2Void Ghost Imaging (N2VGI) network. The N2VGI network is trained using a single reconstructed ghost image to reconstruct a less noisy ghost image of the target. The dimensions of the reconstructed image are 768 × 1,024 pixels. Mirrors M1 and M2 are used to direct the beam within the setup. P1: pinhole, L4: lens.

During the experimental procedure, sequential patterns were displayed on the DMD. The reconstructed ghost image was obtained by correlating the intensity signals detected by the bucket detector with the random speckle patterns displayed on the DMD. To validate the feasibility and performance of the CMGI technique, a USAF 1951 resolution target was used, featuring the smallest line width of 2.2 μm.

2.2 Principle of measurement

We utilize a DMD to generate pre-designed speckle patterns of specific sizes, which are then projected onto the target as speckle patterns denoted by In(x, y). It is important to note that the bucket detector records the total intensity, Sn, of the light transmitted by the object. The object image, G (x, y), can be reconstructed by calculating the second-order correlation function (Abouraddy et al., 2001; Oh et al., 2023) between the intensity distribution, In, illuminated onto the target, and the total intensity, Sn, recorded by the bucket detector, as shown in Equation 1. Here, N represents the total number of patterns used in each experiment.

$G\left(x,y\right)=\frac{1}{N}{\displaystyle \sum _{n=1}^N}\left(I_n\left(x,y\right)-〈I〉\right)S_n\left(x,y\right)(1)$

2.3 Noise2Void Ghost Imaging (N2VGI) algorithm

In this study, we propose a Noise2Void-based Ghost Imaging (N2VGI) framework to denoise reconstructed ghost images using a self-supervised U-Net architecture. Although U-Net was originally developed for biomedical image segmentation (Ronneberger et al., 2015), its encoder–decoder design with skip connections is highly effective in preserving spatial information. In ghost imaging, the reconstruction can reflect the illumination pattern; since we employ sequenced speckle illumination, the resulting images contain locally uncorrelated speckle noise—the kind of random variation that N2V can learn to remove.

While more advanced architectures such as U-Net++, ResUNet, Attention U-Net, Pix2Pix, MSGU-Net, and GA-UNet (Zhou et al., 2018; Zhang Z. et al., 2018; Oktay et al., 2018; Isola et al., 2017; Cheng et al., 2024; Kaur et al., 2021) have demonstrated superior performance in supervised or data-rich environments, they generally rely on clean ground truth data, complex training pipelines, and greater computational resources-requirements incompatible with our self-supervised setting, which operates on single noisy ghost images without access to clean references. In contrast, U-Net serves as the fundamental baseline architecture for image denoising and restoration tasks. Its simple yet powerful encoder–decoder structure with skip connections has been widely validated across diverse applications, making it the standard reference point for both performance and efficiency. U-Net is computationally efficient, converges quickly, and performs reliably even in unsupervised or self-supervised noise modeling with limited data (Wu et al., 2024; Komatsu and Gonsalves, 2020). Therefore, U-Net was selected as the most practical and effective choice, providing an optimal balance between simplicity, computational cost, and robust denoising performance under our experimental constraints.

The U-Net architecture used in our model is configured with a kernel size of 3, a network depth of 3, and an initial filter size of 32. This configuration facilitates multi-scale feature extraction, allowing the network to effectively learn complex noise distributions and improve image fidelity. The training dataset comprises non-overlapping patches of size 24 × 24 pixels, extracted from the input images. To evaluate generalization and mitigate overfitting, 1,000 patches are reserved for training, and the remainder are used for validation.

During training, batch normalization is applied to stabilize convergence. The loss function is defined as mean squared error (MSE), aiming to minimize reconstruction errors. The N2V manipulator is implemented using a median-based masking strategy, which replaces selected pixels with the median of their local neighborhood to prevent identity learning. The model is trained for 25 epochs with a batch size of 16. For noise estimation, 50% of the pixels in each patch are randomly selected, with a neighborhood radius of five pixels used to define local context during training.

Once the model is trained, as detailed in Table 1, it is integrated into an iterative reconstruction process to refine ghost images. Given a noisy ghost image G, the N2V model generates an estimated clean image L by identifying and suppressing noise. The residual noise component F is then computed F = G–L and further refined through a proximal operator, which applies soft-thresholding to enforce sparsity and enhance noise separation (Parikh and Boyd, 2014).

Table 1

Table 1. N2VGI Algorithm: Applying the Noise2Void (N2V) model to enhance reconstructed ghost images, leveraging a U-Net architecture to capture and reduce noise. The stopping criterion is defined by the epsilon (ε) threshold set at 0.5.

To improve robustness, the refined noise estimate is iteratively averaged with previous estimates, yielding an updated noise estimate R. The final reconstructed ghost image is obtained by subtracting the refined noise estimate from the original input. We empirically evaluated convergence thresholds in the range ε = 0.3–0.6 and found that ε = 0.5 offered the best balance between denoising quality and original feature preservation. Consequently, the iterative process continues until the convergence parameter—defined as the ratio of the noise-suppressed image norm to the original image norm—falls below ε = 0.5 or the maximum iteration limit is reached.

This approach effectively enhances ghost image reconstruction by leveraging deep-learning-based self-supervised denoising while preserving fine structural details. The integration of N2V with iterative refinement provides a robust noise suppression mechanism, improving the quality and reliability of reconstructed images in quantum and computational ghost imaging applications. Figure 2 shows the workflow of the N2VGI algorithm.

Figure 2

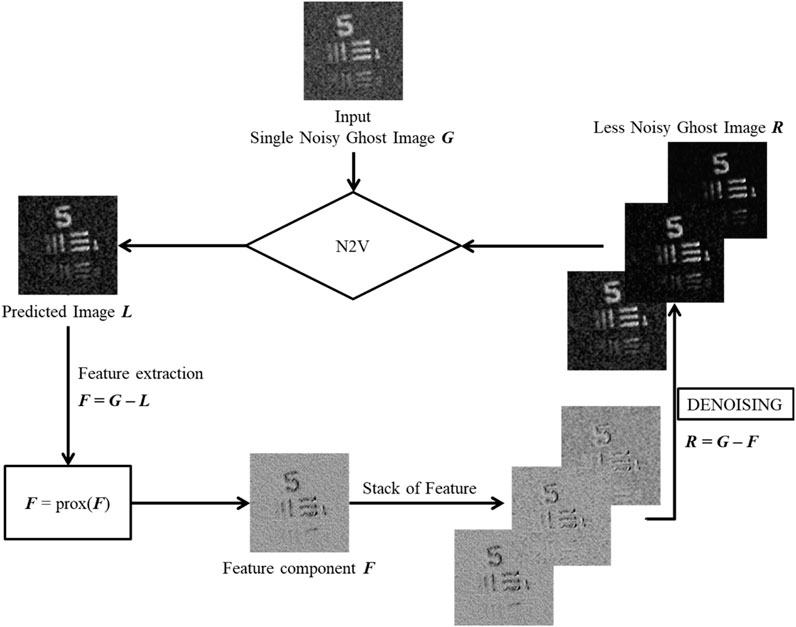
Figure 2. Denoising workflow of the N2VGI algorithm. The process begins with a single noisy ghost image G. The Noise2Void (N2V) model generates a predicted image L, which serves as an estimate of the clean image. The noise component F is extracted by computing the difference between the input image and the predicted image. This noise estimate is then refined using a proximal operator to suppress residual artifacts while preserving structural details. The refined noise estimate is iteratively subtracted from the input image, producing an updated ghost image R with progressively reduced noise. The iterative process continues until the convergence condition p < ϵ is satisfied or the maximum iteration limit is reached, ensuring an optimal balance between noise suppression and image fidelity.

2.4 Speckle size measurement and image quality evaluation criteria

To measure the speckle size, we employ a fast cross-correlation algorithm. This algorithm calculates the cross-correlation between consecutive input fields and then fits a Gaussian function to the cross-correlation result. The width and height parameters obtained from the Gaussian fitting provide information about the speckle size. The average speckle size within the input field is estimated based on the pitch size (13.6 μm) of the DMD used in the experiment. Using this methodology, we generated a total of 20 random patterns with varying speckle sizes ranging from 30 to 275 μm.

For a quantitative assessment of reconstructed image quality, the Structural Similarity Index (SSIM) is employed as a metric to evaluate the similarity between the reconstructed image and the reference image while considering luminance, contrast, and structural information. The SSIM is calculated using the following formula (Wang et al., 2004), as shown in Equation 2.

$SSIM\left(x,y\right)=\frac{\left(2{\mu }_x{\mu }_y+C_1\right)\left(2{\sigma }_{xy}+C_2\right)}{\left({\mu }_x^2+{\mu }_y^2+C_1\right)\left({\sigma }_x^2+{\sigma }_y^2+C_2\right)}(2)$

Here, ${\mu }_x$ and ${\mu }_y$ represent the mean intensity values of images x and y, respectively, while ${\sigma }_x^2$ and ${\sigma }_y^2$ denote their variances. The term ${\sigma }_{xy}$ represents the covariance between the two images. The constants $C_1$ and $C_2$ are small values included to prevent instability when the denominators are close to zero. By evaluating the SSIM, the quality of the reconstructed images can be effectively compared and assessed based on their structural similarity to the reference image, offering a perceptually relevant measure of image fidelity.

Figure 3 presents the resolution measurement of a ghost image. To evaluate the resolution of the ghost image in relation to changes in speckle size, we used the USAF resolution target as the object and measured the resolution based on the spatial resolution of the line pairs. The resolution value R is calculated using the following equation (Oh et al., 2023), as shown in Equation 3.

$R=\frac{2\left(p_2-p_1\right)}{W_2+W_1}(3)$

where $p_1$ and $p_2$ are the positions of the two peaks, and $W_1$ and $W_2$ are their respective widths. As shown in Figure 3, we outlined three lines and obtained an object profile through Gaussian fitting of these lines. To quantitatively evaluate the resolution value, we compare our approach R to the following criteria:

• Rayleigh Criterion: Applies when the central maximum of one Airy disk coincides with the first minimum of another. This corresponds to an R value of 0.5.

• Abbe Criterion: Determined by the full width at half maximum (FWHM) of the two overlapping Airy disks. This corresponds to an R value of 0.41.

• Sparrow Criterion: Observed when the overlapping Airy disks exhibit no discernible difference in their superimposed intensities across the entire resolution distance. This corresponds to an R value of 0.38.

Figure 3

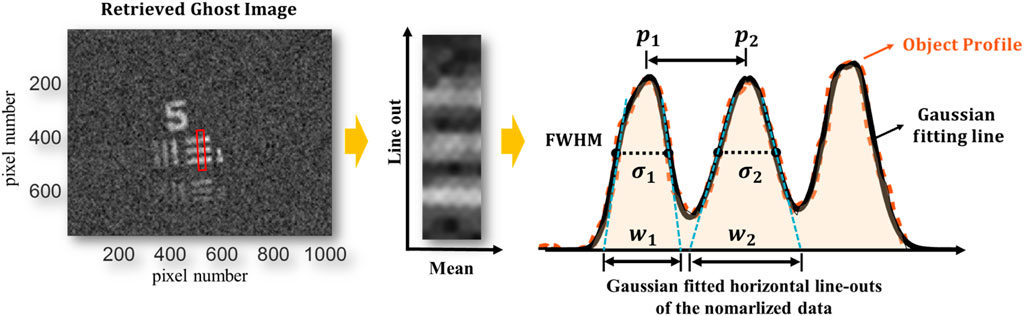
Figure 3. Resolution Measurement. Gaussian fitting is performed on line-outs of the noisy image to determine the resolution of two peaks. The separation between the peaks ($p_2-p_1$) and their widths ($W_1$ and $W_2$) are used to compute the resolution. To find the width at each peak in the normalized dataset, draw a straight line at the point that sets the Full Width at Half Maximum (FWHM) as the standard, and determine the width through the two points where the straight line intersects the baseline.

The R value serves as a measure of resolution for the reconstructed images. Specifically, a resolution value exceeding R > 0.5 indicates that the image surpasses conventional criteria (Advanced Microscopy, 2025). By comparing the R values, we can effectively assess the quality and resolution of the ghost images obtained through our method.

3 Experimental results

3.1 Microscopic ghost imaging

Figure 4 depicts the reconstructed microscopic ghost images for various object targets, with line widths ranging from 15.6 µm to 2.2 µm. These images were captured using a ×40 objective lens, resulting in a magnification range from 21.6 to 83.2. All images demonstrate sufficient spatial resolution, with the three lines clearly discernible to the naked eye.

Figure 4

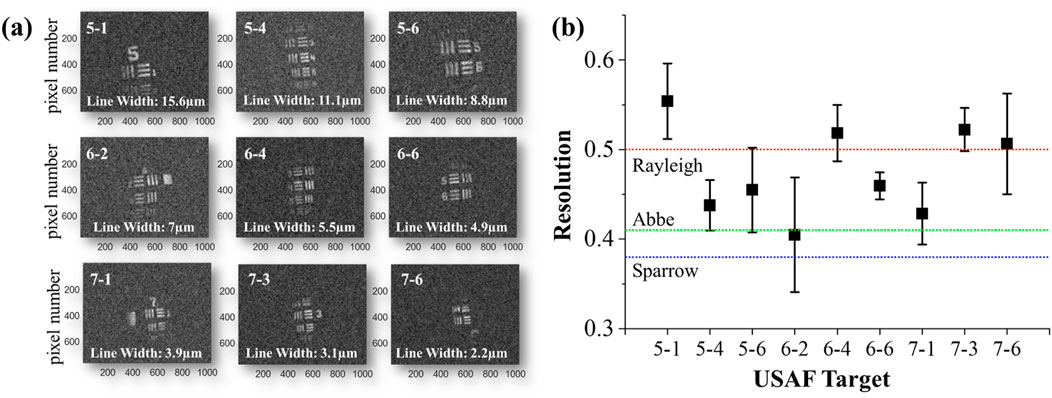
Figure 4. Microscopic Ghost Imaging. (a) Reconstructed ghost images obtained using random speckle patterns with 10,000 iterations for various resolution targets with line widths ranging from 15.6 μm to 2.2 μm. Even the target with the smallest line width (2.2 μm) was well reconstructed. (b) presents the R value for the USAF target alongside image quality criteria. The R value serves as a measure of resolution, with higher values indicating better resolution.

In Figure 4b, we present the quantitative resolution R values obtained by averaging 10 line-out sections per image. Images 5–1, 6–4, 7-3, and 7-6 all exhibit R values above the Rayleigh limit of 0.5, and, apart from case 6–2, every image exceeds the Abbe limit of 0.41. Case 6–2 corresponds to a 7 µm line width and the lowest effective magnification (∼21.6×), which decreases the sampling interval in the line-out analysis and leads to an underestimated R value. In contrast, all other cases benefited from higher effective magnifications, yielding R values that surpass conventional resolution criteria.

3.2 Exploring the influence of speckle size on microscopic ghost imaging

To further explore these effects, experiments were conducted by projecting random speckle patterns of known sizes onto resolution targets. Figure 5 shows this experimental result.

Figure 5

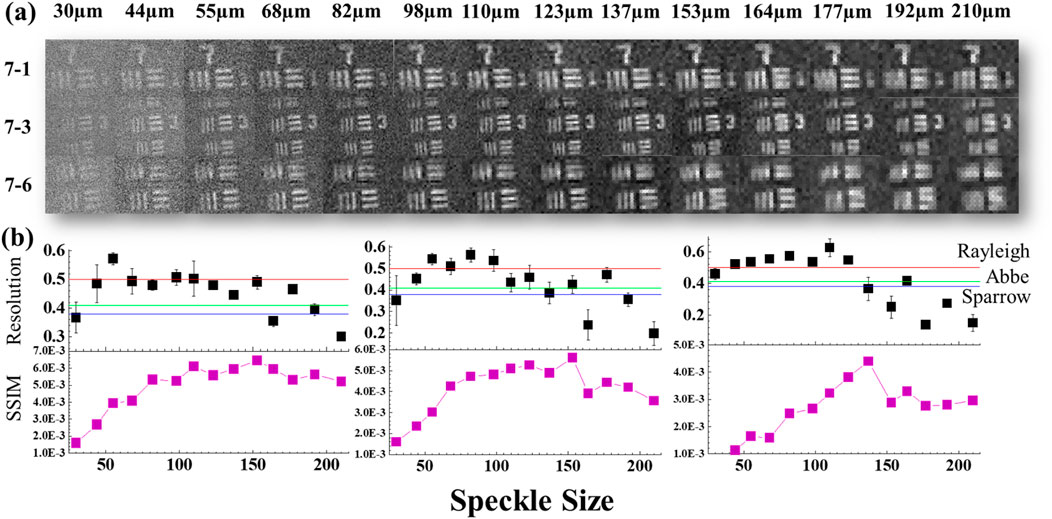
Figure 5. Impact of Speckle Size on Reconstructed Ghost Image. (a) illustrates the reconstructed images obtained using varying speckle sizes for resolution targets 7–1, 7-3, and 7–6. The impact of speckle size on the quality and resolution of the reconstructed ghost image is evaluated. (b) demonstrates the relationship between speckle size and two key metrics: The Resolution (R) and the Structural Similarity Index (SSIM). As speckle size increases, the R value exhibits a decreasing trend, indicating reduced resolution, while the SSIM value initially increases but plateaus beyond a specific threshold.

The upper section of Figure 5 illustrates the reconstructed ghost images for speckle sizes from 30 µm to 210 μm, demonstrating that larger speckles improve contrast but reduce sharpness. The lower section presents SSIM and R value curves, showing that increased speckle size enhances SSIM while diminishing R value. This trade-off arises because larger speckles reinforce low-frequency information—boosting overall image fidelity—whereas smaller speckles preserve high-frequency details essential for fine resolution. To balance these effects, an appropriate speckle size should be chosen to match the object’s spatial scale: use smaller speckles when maximum resolution is required and larger speckles when image contrast is paramount. Furthermore, following our earlier work on mixed-scale speckle illumination (Oh et al., 2023), a multiscale approach—projecting speckles of varying sizes sequentially or in combination—can simultaneously capture both high- and low-frequency content, thereby maximizing resolution and SSIM in a single dataset.

3.3 Enhancing GI quality through N2VGI algorithm optimization

We utilized the N2V model to enhance the image quality of GI by optimizing the experimental setup and speckle size in the initial reconstructed GI. In all reconstructed GI cases, we conducted 10,000 iterations. The number of patterns used is 10,000 for the random speckle pattern, which is only 0.6% of the patterns used in the differential Hadamard method and only 0.3% of the patterns used in the 4-step Fourier method. All reconstructed ghost images have a dimensional size of XGA, same to DMD (1,024 × 768). Initially, we divided the training and validation datasets with a single noisy image based on patch parameters. The patch size, determined by the average noise size of the reconstructed ghost image and the image’s dimensions, played a crucial role in determining the most optimal modelling parameters. Through iterative experiments, we developed an effective denoising N2V model. Subsequently, employing the N2VGI algorithm outlined in Table 1, we conducted iterative refinement until achieving the desired level of denoising. Figure 6 illustrates the impact of our N2V algorithm on individual images, with all images demonstrating a substantial reduction in noise, confirming the efficacy of our approach.

Figure 6

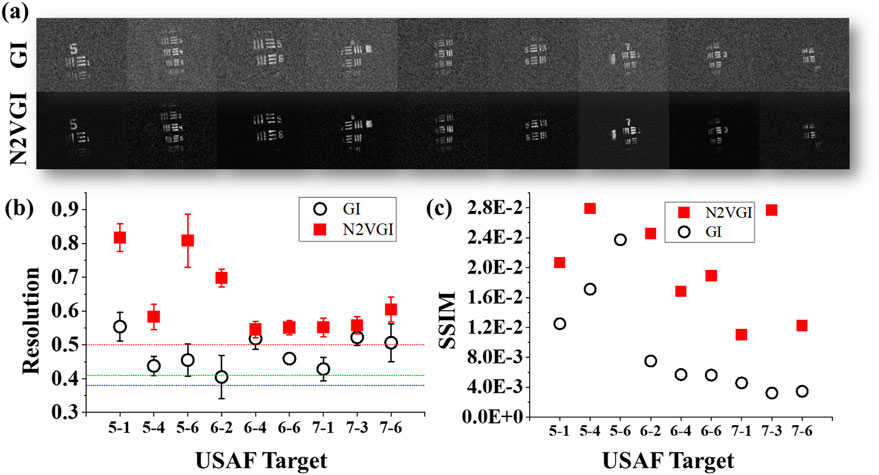
Figure 6. Denoising Noisy Ghost Images with the N2VGI Model. (a) compares the reconstructed image with the denoised image using the N2VGI model. The application of the N2VGI algorithm consistently enhances image quality in all cases. (b) The R value, a measure of resolution, is compared between GI and N2VGI. After applying the N2VGI algorithm, all images surpassed the resolution threshold defined by the Rayleigh standard. On average, the R value in all images subjected to the N2VGI algorithm was approximately 33% higher than the average R value in the initial GI. For image 5-6, the R value increased by approximately 78% compared to its previous value. (c) Similarly, the Structural Similarity Index (SSIM) value improved for all images after applying the N2VGI algorithm. The SSIM value, which quantifies structural fidelity relative to the ground truth, showed significant improvement, demonstrating the effectiveness of the N2VGI approach in preserving fine image details while suppressing noise.

In Figure 4, only four images surpassed the resolution threshold of 0.5, defined by the Rayleigh standard. However, after applying the N2VGI algorithm, all images exceeded the Rayleigh criteria. On average, the R value in all images subjected to the N2VGI algorithm was approximately 33% higher than the average R value in the initial GI. For image 5-6, the R value increased by approximately 78% compared to its previous value. When considering SSIM, the application of the N2VGI algorithm resulted in an increase in SSIM values for all images, with the average SSIM value across all targets increasing by 324% in N2VGI compared to GI. For image 7-3, the SSIM increased by approximately 854% compared to the original image.

Additionally, we conducted an experiment on GI reconstructed with 2000 iterations to validate the algorithm’s applicability to cases with extremely low image quality. Figure 7 presents the GI obtained with a low number of iterations and the results when the N2VGI algorithm is applied to the images.

Figure 7

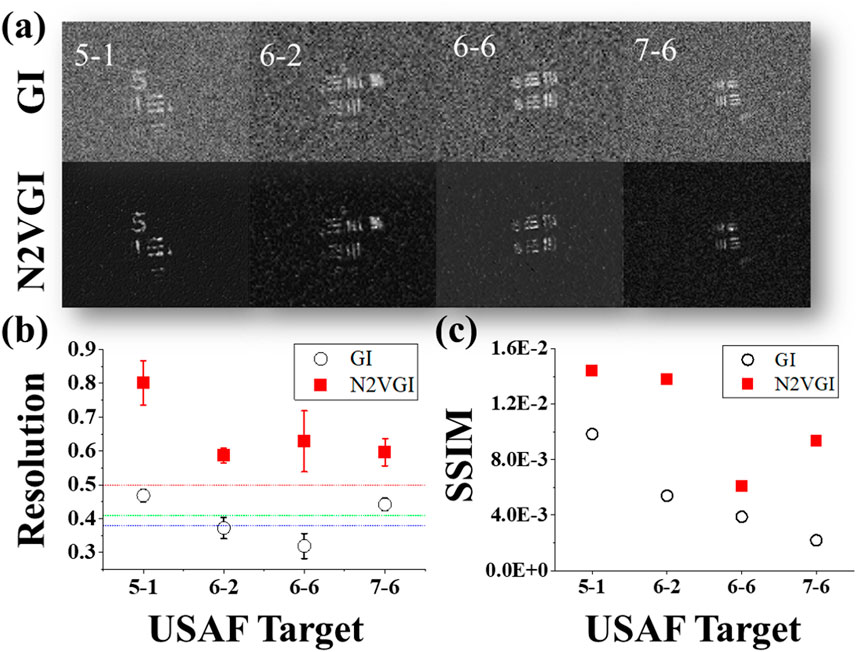
Figure 7. Denoising Noisy Ghost Images with the N2VGI Model for Low-Iteration GI. (a) This panel compares the reconstructed image with fewer iterations (2000) versus the denoised image from the N2VGI model. The application of the N2VGI algorithm consistently enhances image quality in all cases. (b) The R value comparison shows an increase in the denoised images by approximately 63% compared to GI. (c) Similarly, the overall SSIM value was increased in compared to the original images. While the image improved notably in noisy regions after applying the algorithm, some information was lost in the denoised image due to the limitations of the original image.

Figure 7 displays a low-iteration GI alongside an image enhanced with the N2VGI algorithm. The average R value of denoised images increased by approximately 63% compared to GI. In terms of SSIM, the average value increased by approximately 247% compared to the original images. While the algorithm notably improved the image in noisy regions, it is evident that some information was lost in the denoised image due to the limitations of the original data. Nonetheless, the N2VGI model demonstrates its effectiveness in enhancing even very low-quality GI images.

4 Conclusion

In conclusion, we demonstrated microscopic ghost imaging by optimizing both lens position and speckle size, achieving a smallest resolvable line width of 2.2 µm—well beyond conventional Rayleigh criteria. Our investigation revealed that as speckle size increases, resolution decreases while SSIM improves for certain target widths, with an optimal speckle scale maximizing both metrics. By combining speckle-based CGI with our self-supervised Noise2Void (N2VGI) U-Net algorithm, we successfully denoised images reconstructed from as few as 2,000–10,000 speckle patterns (under 1% of the patterns required by differential Hadamard or 4-step Fourier methods), without any reference images or large training sets. Despite this drastic reduction, N2VGI consistently delivered high-quality XGA-resolution (1,024 × 768) reconstructions using less computational resources. Because N2VGI relies on single-image training, there is a risk of overfitting to speckle-specific noise, which may degrade performance under low-contrast or highly correlated noise conditions. Future work will address these limitations by incorporating regularization techniques, multi-image strategies, and broader dataset validation to further improve robustness and extend applicability to light-sensitive biological imaging.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SO: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review and editing. TT: Data curation, Formal Analysis, Investigation, Software, Writing – review and editing. ZS: Conceptualization, Data curation, Formal Analysis, Investigation, Writing – review and editing. CS: Conceptualization, Formal Analysis, Funding acquisition, Methodology, Project administration, Supervision, Writing – original draft, Writing – review and editing, Validation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC 2051 (Project-ID 390713860), “Balance of the Microverse”; The Free State of Thuringia within the project “Quantum Hub Thüringen” (Funding ID 2021 FGI 0044); DAAD (Deutscher Akademischer Austauschdienst) German Academic Exchange Service, Funding programme/-ID: (57552340) Research Grants—Doctoral Programmes in Germany, 2021/22.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. For Proofreading.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbe, E. (1873). Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung. Arch. F. mikrosk Anat. 9, 413–468. doi:10.1007/bf02956173

CrossRef Full Text | Google Scholar

Abouraddy, A. F., Saleh, B. E. A., Sergienko, A. V., and Teich, M. C. (2001). Role of entanglement in two-photon imaging. Phys. Rev. Lett. 87, 123602. doi:10.1103/physrevlett.87.123602

PubMed Abstract | CrossRef Full Text | Google Scholar

Advanced Microscopy (2025). Super-resolution tutorial - education - advanced microscopy. Available online at: https://advanced-microscopy.utah.edu/education/super-res/ (Accessed 2025 May 5).

Google Scholar

Bennink, R. S., Bentley, S. J., and Boyd, R. W. (2002). “Two-Photon” coincidence imaging with a classical source. Phys. Rev. Lett. 89, 113601. doi:10.1103/physrevlett.89.113601

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, H., Zhang, Y., Xu, H., Li, D., Zhong, Z., Zhao, Y., et al. (2024). MSGU-Net: a lightweight multi-scale ghost U-Net for image segmentation. Front. Neurorobot 18, 1480055. doi:10.3389/fnbot.2024.1480055

PubMed Abstract | CrossRef Full Text | Google Scholar

Clemente, P., Durán, V., Tajahuerce, E., Andrés, P., Climent, V., and Lancis, J. (2013). Compressive holography with a single-pixel detector. Opt. Lett. 38, 2524. doi:10.1364/ol.38.002524

PubMed Abstract | CrossRef Full Text | Google Scholar

Dou, L.-Y., Cao, D.-Z., Gao, L., and Song, X.-B. (2020). Dark-field ghost imaging. Opt. Express 28, 37167. doi:10.1364/oe.408888

PubMed Abstract | CrossRef Full Text | Google Scholar

Duarte, M. F., Davenport, M. A., Takhar, D., Laska, J. N., Sun, T., Kelly, K. F., et al. (2008). Single-pixel imaging via compressive sampling. IEEE signal Process. Mag. 25, 83–91. doi:10.1109/msp.2007.914730

CrossRef Full Text | Google Scholar

Gibson, G. M., Johnson, S. D., and Padgett, M. J. (2020). Single-pixel imaging 12 years on: a review. Opt. Express 28, 28190. doi:10.1364/oe.403195

PubMed Abstract | CrossRef Full Text | Google Scholar

Hahamovich, E., Monin, S., Hazan, Y., and Rosenthal, A. (2021). Single pixel imaging at megahertz switching rates via cyclic Hadamard masks. Nat. Commun. 12, 4516. doi:10.1038/s41467-021-24850-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, H.-K., Sun, S., Jiang, L., Lin, H. Z., Lin, H.-Z., Lin, H.-Z., et al. (2020). Denoising ghost imaging under a small sampling rate via deep learning for tracking and imaging moving objects. Opt. Express 28, 37284–37293. doi:10.1364/oe.412597

PubMed Abstract | CrossRef Full Text | Google Scholar

Isola, P., Zhu, J.-Y., Zhou, T., and Efros, A. A. (2017). Image-to-image translation with conditional adversarial networks, 1125–1134.

Google Scholar

Jia, F., Wong, W. H., and Zeng, T. (2021). DDUNet: dense dense U-net with applications in image denoising, 354–364.

Google Scholar

Katz, O., Bromberg, Y., and Silberberg, Y. (2009). Compressive ghost imaging. Appl. Phys. Lett. 95, 131110. doi:10.1063/1.3238296

CrossRef Full Text | Google Scholar

Kaur, A., Kaur, L., and Singh, A. (2021). GA-UNet: UNet-based framework for segmentation of 2D and 3D medical images applicable on heterogeneous datasets. Neural Comput. and Applic 33, 14991–15025. doi:10.1007/s00521-021-06134-z

CrossRef Full Text | Google Scholar

Kim, Y. Y., Gelisio, L., Mercurio, G., Dziarzhytski, S., Beye, M., Bocklage, L., et al. (2020). Ghost imaging at an XUV free-electron laser. Phys. Rev. A 101, 013820. doi:10.1103/physreva.101.013820

CrossRef Full Text | Google Scholar

Komatsu, R., and Gonsalves, T. (2020). Comparing U-net based models for denoising color images. AI 1, 465–486. doi:10.3390/ai1040029

CrossRef Full Text | Google Scholar

Krull, A., Buchholz, T.-O., and Jug, F. (2019). Noise2Void - learning denoising from single noisy images. 2019 IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), 2124, 2132. doi:10.1109/cvpr.2019.00223

CrossRef Full Text | Google Scholar

Lyu, M., Wang, W., Wang, H., Wang, H., Li, G., Chen, N., et al. (2017). Deep-learning-based ghost imaging. Sci. Rep. 7, 17865. doi:10.1038/s41598-017-18171-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Oh, S., Mallick, M., Siefke, T., and Spielmann, C. (2025). Microscopic ghost imaging with a tabletop XUV source. doi:10.48550/arXiv.2505.13075

CrossRef Full Text | Google Scholar

Oh, S., Sun, Z., Tian, T., and Spielmann, C. (2023). Improvements of computational ghost imaging by using sequenced speckle. Appl. Sci. 13, 6954. doi:10.3390/app13126954

CrossRef Full Text | Google Scholar

Oktay, O., Schlemper, J., Folgoc, L. L., Lee, M., Heinrich, M., Misawa, K., et al. (2018). Attention U-net: learning where to look for the pancreas. doi:10.48550/arXiv.1804.03999

CrossRef Full Text | Google Scholar

Olbinado, M. P., Paganin, D. M., Cheng, Y., and Rack, A. (2021). X-ray phase-contrast ghost imaging using a single-pixel camera. Optica 8, 1538. doi:10.1364/optica.437481

CrossRef Full Text | Google Scholar

Parikh, N., and Boyd, S. (2014). Proximal algorithms. Found. trends® Optim. 1, 127–239. doi:10.1561/2400000003

CrossRef Full Text | Google Scholar

Pelliccia, D., Rack, A., Scheel, M., Cantelli, V., and Paganin, D. M. (2016). Experimental X-ray ghost imaging. Phys. Rev. Lett. 117, 113902. doi:10.1103/physrevlett.117.113902

PubMed Abstract | CrossRef Full Text | Google Scholar

Pittman, T. B., Shih, Y. H., Strekalov, D. V., and Sergienko, A. V. (1995). Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 52, R3429–R3432. doi:10.1103/physreva.52.r3429

PubMed Abstract | CrossRef Full Text | Google Scholar

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net: convolutional networks for biomedical image segmentation. Lect. Notes Comput. Sci., 234–241. doi:10.1007/978-3-319-24574-4_28

CrossRef Full Text | Google Scholar

Shapiro, J. H. (2008). Computational ghost imaging. Phys. Rev. A 78, 061802. doi:10.1103/physreva.78.061802

CrossRef Full Text | Google Scholar

Sun, Z., Tuitje, F., and Spielmann, C. (2019). Toward high contrast and high-resolution microscopic ghost imaging. Opt. Express 27, 33652. doi:10.1364/oe.27.033652

PubMed Abstract | CrossRef Full Text | Google Scholar

Vinu, R. V., Chen, Z., Singh, R. K., and Pu, J. (2020). Ghost diffraction holographic microscopy. Optica 7, 1697. doi:10.1364/optica.409886

CrossRef Full Text | Google Scholar

Wang, F., Wang, C., Chen, M., Gong, W., Zhang, Y., Han, S., et al. (2022). Far-field super-resolution ghost imaging with a deep neural network constraint. Light Sci. Appl. 11, 1. doi:10.1038/s41377-021-00680-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, F., Wang, H., Wang, H., Li, G., and Situ, G. (2019). Learning from simulation: an end-to-end deep-learning approach for computational ghost imaging. Opt. Express 27, 25560. doi:10.1364/oe.27.025560

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P. (2004). Image quality assessment: from error visibility to structural similarity. IEEE Trans. image Process. 13, 600–612. doi:10.1109/tip.2003.819861

PubMed Abstract | CrossRef Full Text | Google Scholar

Welsh, S. S., Edgar, M. P., Bowman, R., Jonathan, P., Sun, B., and Padgett, M. J. (2013). Fast full-color computational imaging with single-pixel detectors. Opt. Express 21, 23068. doi:10.1364/oe.21.023068

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Z., Li, J., Xu, C., Huang, D., and Hoi, S. C. H. (2024). RUN: rethinking the UNet architecture for efficient image restoration. IEEE Trans. Multimedia 26, 10381–10394. doi:10.1109/tmm.2024.3407656

CrossRef Full Text | Google Scholar

Yu, H., Lu, R., Han, S., Xie, H., Du, G., Xiao, T., et al. (2016). Fourier-transform ghost imaging with hard X rays. Phys. Rev. Lett. 117, 113901. doi:10.1103/physrevlett.117.113901

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, A.-X., He, Y.-H., Wu, L.-A., Chen, L.-M., and Wang, B.-B. (2018a). Tabletop x-ray ghost imaging with ultra-low radiation. Optica 5, 374. doi:10.1364/optica.5.000374

CrossRef Full Text | Google Scholar

Zhang, Z., Liu, Q., and Wang, Y. (2018b). Road extraction by deep residual U-net. IEEE Geoscience Remote Sens. Lett. 15, 749–753. doi:10.1109/lgrs.2018.2802944

CrossRef Full Text | Google Scholar

Zhang, Z., Wang, X., Zheng, G., and Zhong, J. (2017). Hadamard single-pixel imaging versus Fourier single-pixel imaging. Opt. Express 25, 19619. doi:10.1364/oe.25.019619

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y.-N., Hou, H.-Y., Han, J.-C., Gao, S., Cui, S.-W., Cao, D.-Z., et al. (2023). Single-pixel phase microscopy without 4 f system. Opt. Lasers Eng. 163, 107474. doi:10.1016/j.optlaseng.2023.107474

CrossRef Full Text | Google Scholar

Zhou, Z., Rahman Siddiquee, M. M., Tajbakhsh, N., and Liang, J. (2018). “UNet++: a nested U-net architecture for medical image segmentation,” in Deep learning in medical image analysis and multimodal learning for clinical decision support Editors D. Stoyanov, Z. Taylor, G. Carneiro, T. Syeda-Mahmood, A. Martel, and L. Maier-Hein (Cham: Springer International Publishing), 3–11.

CrossRef Full Text | Google Scholar