Enhancing sustainable urban design using machine learning: comparative analysis of seven metaheuristic algorithms in energy-efficient digital architecture

Metaheuristics optimization algorithms used in this research include PSO, ACO, GA, and SA and represent effective approaches toward reaching an optimal or near-optimal solution for decision variables with an intention to improve energy efficiency, increasing indoor comfort whilst reducing the carbon footprint of building operations. These algorithms will be applied across different sizes of a synthesized data pool prepared with important features like window-to-wall ratio, efficiency in HVAC systems, renewable systems integration, among others. PSO demonstrated the best scenario in both cases with an optimum convergence rate of 24.1%; ACO produced almost the same best result as mentioned with high rates of reductions in carbon footprints. These had their best energy-savings while convergence in GA and SA was extremely slow with energy efficiencies that turned out to be pretty low. This could enable real proposals to be made to architects, urban planners, and policy thinkers, allowing them to turn such ideal cases into viable realities within sustainable development initiatives.

1 Introduction

Integrating machine learning (ML) into digital architecture presents a transformative opportunity to enhance sustainable design, energy conservation, housing, and urban planning. With the increasing tempo of urbanization, the issues of realizing sustainability and minimizing energy consumption during building construction and city planning are more significant today. Machine learning brings novel data-driven solutions to overcome these issues through optimizing the usage of resources, enhancing energy efficiency in sustainable constructions, and rationalization in housing and planning to develop more intelligent and sustainable city living environments (Abu-shaikha et al., 2024; Abusaleh S., 2024; Abid et al., 2024; Hussein et al., 2024; Shihadeh et al., 2024; Umoh, 2024; Matarneh and Matarneh, 2018).

Machine learning (ML) has also been widely used in energy efficiency research and architecture. For example, Nagappan and Daud (2021) draw attention to the application of ML in land use change (LUC) modeling, which supports sustainable city planning through the prediction of future energy demand. In the same context, Wagner et al. (2022) also show how explainable ML models can be used to optimize the form of cities for sustainable mobility and lower energy use and carbon emissions. Warth et al. (2020) also support the integration of ML with satellite imagery and socio-economic indicators for urban-scale planning. Ghoneim (2025) highlights the potential of ML in architectural applications, particularly in optimizing adaptive facade designs to improve thermal performance and reduce energy loads in urban contexts. These studies point to the versatility of ML in resolving energy efficiency and sustainability issues at various scales.

Costa-Carrapiço et al. (2020) present how multi-objective optimization can be combined with ML as a way of balancing energy efficiency and occupant comfort. Other research (Heidari et al., 2018; Yaman, 2021) highlights the need to consider thermal insulation, HVAC efficiency, and renewable energy resources in building design. Kanthila et al. (2021) emphasize the role of building occupancy behavior modeling in enhancing simulation accuracy for such strategies. Park and Rhee (2018) contribute insights on IoT-based thermal comfort services integrated with smart architecture. Alnusairat and Abu Qadourah (2025) further explored public acceptance of integrating solar photovoltaic technologies in residential architecture, reflecting on the social dimension of green design strategies. This research expands on previous research by comparing seven metaheuristic optimization algorithms—namely, GA, PSO, ACO, SA, FA, WOA, and NSGA-II—within an integrated multi-objective approach to solving energy efficiency, hygrothermal comfort, and sustainability in urban building design.

In energy efficiency terms, ML has an important function in the optimization of building performance by analyzing several influencing factors related to energy consumption. For example, Ragusa et al. (2022) explain the process of creating energy-efficient neural networks that can function under the limitations of edge devices, which is more applicable in smart building technologies. The energy-limited devices apply ML models for the real-time monitoring and optimization of energy utilization in support of overall sustainability in city architecture. Yaman’s (2021) work on various façade types also identifies the function of novel building systems in energy optimization as ML can play an important part in designing façades for adaptive responses to environmental factors as well as enhancing comfort indoors. Mota et al. (2018) also developed sensor technologies to enhance building energy management, while Liu (2024) modeled energy performance in medium-sized offices using simulation tools like Energy Plus. Mutani and Todeschi (2020) extended this view by modeling energy consumption at the neighborhood scale, allowing urban planners to assess block-level sustainability potential. Pignatta et al. (2021) also illustrated the impact of solar energy simulation on various urban block configurations, highlighting how solar-oriented design can improve energy efficiency in compact cities.

The interface of ML and city planning also reaches social aspects, as Meshkani (2024) delves into how ML can be used to fight homelessness through evidence-based city planning solutions. Through the examination of demographic and socio-economic variables, ML guides the planning of transitional living and social infrastructure in such a way as to make city environments not only functionally efficient but also just. This aligns with wider objectives in sustainable city development in terms of balancing environmental, economic, and social factors. Raanan et al. (2022) further propose ML-based evaluation methods for assessing sustainability in neighborhood planning. Leer et al. (2022) discuss progress tracking in sustainable urban development through energy performance at the community scale. Amro and Ammar (2018) add a cultural dimension to the role of higher education in fostering architects’ sensitivity toward sustainable heritage conservation in urban contexts.

The contribution of the paper resides in the formulation and comparison of multi-objective optimization approach on the basis of seven separate metaheuristic algorithms—PSO, ACO, GA, SA, FA, WOA, and NSGA-II—each possessing specific strengths in resolving complex, nonlinear, and constrained architectural design issues. In contrast to previous works centered on single-objective models, the present research takes an equitable approach optimizing energy efficiency, carbon footprint minimization, and occupants’ comfort at the same time. Exploring the influence of each optimization approach on LEED certification requirements further adds depth to the base algorithmic comparison. The extended algorithmic platform allows for a more detailed comprehension of how optimization strategies match changing project priorities, providing architects and planners with sound insights into the pragmatic choice and implementation of metaheuristics in sustainable urban development. (Kaveh, 2017; Kaveh, 2021) provides foundational reviews on metaheuristic optimization in civil engineering, while Kaveh and Eskandari (2024) and Kaveh and Hamedani (2024) introduce parameter tuning and hybrid enhancements that directly support the methodology employed here.

In addition to this, explainable ML models, as defined by Wagner et al. (2022), can be used for more comprehension of the effect of urban form on sustainable mobility. Explainable models clarify the relationship between transportation patterns and the built environment, helping planners develop more walkable and transit-oriented environments. This is particularly vital in attempts to diminish carbon footprints and encourage sustainable transport in cities. Li (2020), for example, links urban form metrics to variations in energy use across different city morphologies.

The application of ML in cities is also demonstrated by Chen’s (2023) two-level ML methodology for the classification of mega-city urban forms. This approach not only enhances the accuracy of identifying city form but also encourages improved urban planning methodologies. Planners are in a position to learn about the spatial behavior of cities through extracting features from sources of data, which contributes to appropriate and sustainable designing strategies.

ML also has an extremely useful application in environmental monitoring and management. For instance, Letchumanan and Naveen (2022) described how the application of ML in forecasting particulate matter levels helps improve the air quality management of cities. Combining real-time data with prediction models will enable cities to implement more efficient means of controlling pollution with positive effects on healthier city environments.

In addition, high-performance architecture demands integration of renewable energy and ML strategies. Heidari et al. (2018) explain the need for implementation of renewable energy systems in smart hybrid strategies of city planning. ML can be utilized in bringing about improved energy efficiency in deploying and running these systems and hence minimizing reliance on non-renewable energy. Hong et al. (2020) contribute ten critical questions for advancing the accuracy and credibility of urban energy modeling frameworks, which are particularly relevant to ML-based optimization.

The objective of this research is to maximize energy efficiency, sustainability, and occupant comfort for building design in urban settings through state-of-the-art metaheuristic optimization and machine learning. In particular, the research here is interested in minimizing energy usage, optimizing return on investment, and enhancing human-oriented comfort conditions with reduced environmental footprint. Through comparison of the performance of seven state-of-the-art algorithms in metaheuristic optimization and machine learning, the research presents an integrated, data-driven guide for embedding machine learning in smart city planning and digital architecture.

2 Methodology

This research uses an optimization approach from multi-objective machine learning to improve building performance for energy efficiency, occupant comfort, and carbon footprint minimization. A well-crafted dataset providing for key architectural, climatic, and operational variables serves as the basis of the methodology. These encompass technical specifications (such as HVAC system efficiency and types of insulation), design parameters (such as window area to wall area ratio and building orientation), and contextual indicators (such as occupancy schedules and climatic data).

2.1 Dataset construction and preprocessing

The database was gathered from several sources including Building Information Modeling (BIM) software like Autodesk Revit and ArchiCAD, smart building sensors, and open-source environmental databases. The dataset consists of 1,500 distinctive building configurations representing both residential and commercial typologies in 5 years (2018–2022) and various climatic zones. The optimization was intended to be versatile in applicability and realistic in outcome.

The data preprocessing phase included.

• Mean imputation for missing numerical values,

• Mode substitution for categorical attributes,

• Normalization of continuous variables (e.g., HVAC efficiency, energy consumption) to a [0, 1] scale,

• Outlier removal based on interquartile range (IQR) thresholds.

Table 1 provides a detailed overview of the dataset features and their relevance to sustainable building design.

Table 1

Table 1. Overall performance summary of metaheuristic algorithms.

2.2 Metaheuristic optimization algorithms

To solve the multi-objective optimization problem, this research utilizes seven metaheuristic algorithms, each selected for its strengths in exploring large, complex solution spaces under constrained design scenarios. These include Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Simulated Annealing (SA), Ant Colony Optimization (ACO), and three additional methods: Firefly Algorithm (FA), Whale Optimization Algorithm (WOA), and NSGA-II.

2.2.1 Genetic Algorithm (GA)

GA mimics biological evolution through selection, crossover, and mutation to optimize energy and comfort variables. It is suitable for both discrete and continuous variables.

Objective Function:

$\min f\left(x\right)={\displaystyle \sum _{i=1}^n}{E}_i\left(x\right)$

Where.

• $E_i\left(x\right)$: Energy consumption of component $i$,

•x: Vector of design variables.

2.2.2 Particle Swarm Optimization (PSO)

PSO models the behavior of swarming birds or fish. Particles move in the design space, adjusting velocity based on individual and collective experience.

Velocity & position update:

$\begin{array}{c}{v}_i^{t+1}=w{v}_i^t+c_1{r}_1\left(p_{\text{best},i}-x_i^t\right)+c_2{r}_2\left(g_{\text{best}}-x_i^t\right)\\ x_i^{t+1}=x_i^t+v_i^{t+1}\end{array}$

Where.

•w: Inertia weight, $c_1,c_2$: Cognitive and social coefficients,

• $r_1,r_2$: Random values in $\left[0,1\right]$.

2.2.3 Simulated Annealing (SA)

SA emulates the cooling process of metals to escape local optima. It probabilistically accepts worse solutions to improve global search.

Acceptance probability:

$P=\exp \left(\frac{-\Delta E}{T}\right)$

Where.

• $\Delta E$: Difference in objective value,

•T: Current temperature.

2.2.4 Ant Colony Optimization (ACO)

ACO uses pheromone trails to guide artificial ants through the design space, favoring energy-efficient pathways.

Pheromone Update Equation:

${\tau }_{ij}^{\left(t+1\right)}=\left(1-\rho \right){\tau }_{ij}^{\left(t\right)}+{\displaystyle \sum _{k=1}^m}\Delta {\tau }_{ij}^{\left(k\right)}$

Where.

•ρ: Evaporation rate,

• $\Delta {\tau }_{ij}^{\left(k\right)}$: Pheromone deposited by ant $k$.

2.2.5 Firefly Algorithm (FA)

FA is inspired by the flashing behavior of fireflies. Each firefly moves towards brighter (more optimal) individuals.

Movement Equation:

$x_i^{t+1}=x_i^t+{\beta }_0{e}^{-\gamma r_{ij}^2}\left(x_j^t-x_i^t\right)+\alpha {ϵ}_i^t$

Where.

• ${\beta }_0$: Attractiveness at $r=0$,

•$\gamma$: Light absorption coefficient,

•$\alpha$: Randomization parameter,

• ${ϵ}_i$: Random vector from Gaussian distribution,

• $r_{ij}$: Distance between fireflies $i$ and $j$.

2.2.6 Whale Optimization Algorithm (WOA)

WOA mimics the bubble-net feeding strategy of humpback whales. It employs spiral and encircling mechanisms to converge on prey (solutions).

Encircling mechanism:

$\overrightarrow{D}=\left|\overrightarrow{C}·{\overrightarrow{X}}^{*}-\overrightarrow{X}\left(t\right)\right|,\overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}^{*}-\overrightarrow{A}·\overrightarrow{D}$

Where.

• ${\overrightarrow{X}}^{*}$: Best solution,

• $\overrightarrow{A},\overrightarrow{C}$: Coefficients controlling convergence,

• $\overrightarrow{X}\left(t\right)$: Current position.

2.2.7 NSGA-II (non-dominated Sorting Genetic Algorithm II)

NSGA-II is a popular evolutionary algorithm designed for multi-objective optimization. It uses fast nondominated sorting, elitism, and crowding distance to maintain solution diversity along the Pareto front.

Fitness assignment steps:

1. Rank solutions using non-dominated sorting.

2. Apply crowding distance to preserve diversity.

3. Perform binary tournament selection based on rank and crowding.

There’s no single objective equation in NSGA-II. Instead, the three objective functions $f_1\left(x\right),f_2\left(x\right)$, and $f_3\left(x\right)$ (for energy, comfort/ROI, and carbon) are simultaneously optimized without aggregation.

Each algorithm brings unique advantages.

• GA and NSGA-II are versatile evolutionary optimizers.

• PSO and WOA offer fast convergence in continuous design spaces.

• SA and FA escape local optima and explore non-convex surfaces effectively.

• ACO excels in multi-agent, discrete path exploration.

These algorithms will be applied to optimize building configurations under the constraints of real-world energy performance, environmental goals, and occupant-centered design outcomes.

2.3 Optimization objective functions

This study aims to optimize building performance by balancing three key sustainability objectives: minimizing annual energy consumption, maximizing occupant comfort and return on investment (ROI), and reducing carbon footprint. These objectives reflect the architectural, economic, and environmental imperatives central to sustainable urban design.

The multi-objective optimization problem is tackled using a diverse set of metaheuristic algorithms, each designed to explore and exploit the solution space from different perspectives. The following subsections define the objective functions and illustrate how each of the seven algorithms-Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Simulated Annealing (SA), Ant Colony Optimization (ACO), Firefly Algorithm (FA), Whale Optimization Algorithm (WOA), and NSGA-II—addresses them.

2.3.1 Minimizing annual energy consumption

Reducing energy consumption is a primary goal in sustainable building design. It directly lowers operational costs and mitigates environmental impact through decreased demand on energy systems.

Objective Function:

$f_1\left(x\right)={\displaystyle \sum _{i=1}^n}{E}_i\left(x\right)$

Where.

• $f_1\left(x\right)$: Total annual energy consumption (kWh),

• $E_i\left(x\right)$: Energy consumption of the $i^{\text{th}}$ component (e.g., HVAC, lighting),

•x: Vector of design variables (e.g., building orientation, insulation, glazing ratio).

Algorithm Strategies.

• GA: Evolves generations of energy-efficient designs using selection, crossover, and mutation, favoring configurations that minimize $f_1\left(x\right)$.

• PSO: Particles adjust positions to collectively converge toward the global minimum energy configuration.

• SA: Accepts worse energy solutions temporarily to escape local minima and seek global optimization.

• ACO: Constructs design paths with lower energy signatures, reinforced by pheromone trails.

• FA: Attracts fireflies toward designs with the lowest energy consumption by light intensity difference.

• WOA: Encircles the best design based on energy performance using adaptive spiral movements.

• NSGA-II: Simultaneously minimizes energy while balancing other objectives along the Pareto Frontier.

2.3.2 Maximizing occupant comfort and return on investment (ROI)

Comfort and economic viability are essential for the long-term sustainability of any building. Comfort incorporates thermal, visual, and air quality dimensions, while ROI reflects the balance between initial investment and operational savings.

Objective Function:

$f_2\left(x\right)=\alpha ·C\left(x\right)+\beta ·R\left(x\right)$

Where.

• C$\left(x\right)$: Comfort score (scaled 0–100),

• R$\left(x\right)$: ROI (%) calculated from energy savings and cost,

• $\alpha ,\beta$: Weighting factors (e.g., 0.6 for comfort, 0.4 for ROI),

•x: Design variable vector influencing HVAC, daylighting, insulation, etc.

Algorithm Strategies.

• GA: Uses Pareto-based selection to evolve design combinations maximizing both comfort and economic return.

• PSO: Particles shift toward positions with higher combined scores of ROI and comfort.

• SA: Accepts suboptimal comfort designs if potential improvements outweigh short-term losses.

• ACO: Favors design paths with better perceived user comfort and financial efficiency.

• FA: Fireflies are drawn to brighter (more comfortable and profitable) solutions in the swarm.

• WOA: Simulates social behavior to encircle ROI-optimal comfort zones.

• NSGA-II: Ranks solutions using non-dominated sorting, favoring those excelling in both $C\left(x\right)$ and $R\left(x\right)$ without aggregating objectives.

2.4 Evaluation metrics

This study uses several performance metrics to evaluate the effectiveness of the metaheuristic algorithms in optimizing sustainable building design. These include both computational indicators and real-world outcome measures. The aim is to provide a clear and structured assessment of how each algorithm performs in terms of processing efficiency and impact on energy consumption, comfort, emissions, and sustainability standards (Pham et al., 2020; Tien et al., 2022; Forootan et al., 2022; Zhang et al., 2023; Wang et al., 2020).

2.4.1 Energy Savings

This metric assesses how much energy consumption is reduced after applying optimization techniques. It reflects the effect of building design changes like improved insulation, orientation, or system efficiency. The reduction is calculated based on a comparison with a baseline design.

Energy Savings (%) is calculated using:

$\mathbf{\text{Energy\hspace{0.17em}Savings}}=\left(\frac{{\mathit{E}}_{\mathbf{\text{baseline}}}-{\mathit{E}}_{\mathbf{\text{optimized}}}}{{\mathit{E}}_{\mathbf{\text{baseline}}}}\right)\times \mathbf{100}$

Where.

• ${\mathit{E}}_{\mathbf{\text{baseline}}}$: Energy use before optimization,

• ${\mathit{E}}_{\mathbf{\text{optimized}}}$: Energy use after optimization.

This value shows the impact of each algorithm in improving energy efficiency.

2.4.2 Execution time

Execution time is the duration taken by an algorithm to reach its best or near-best solution. It is a crucial performance indicator when applying algorithms to real-world design scenarios where timely results are essential.

It is calculated as:

$\mathit{E}\mathit{x}\mathit{e}\mathit{c}\mathit{u}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\mathit{T}\mathit{i}\mathit{m}\mathit{e}\left(\mathit{s}\right)=\mathit{T}\mathit{o}\mathit{t}\mathit{a}\mathit{l}\mathit{t}\mathit{i}\mathit{m}\mathit{e}\mathit{t}\mathit{a}\mathit{k}\mathit{e}\mathit{n}\mathit{t}\mathit{o}\mathit{f}\mathit{i}\mathit{n}\mathit{d}\mathit{o}\mathit{p}\mathit{t}\mathit{i}\mathit{m}\mathit{a}\mathit{l}\mathit{s}\mathit{o}\mathit{l}\mathit{u}\mathit{t}\mathit{i}\mathit{o}\mathit{n}$

Shorter execution time is desirable, especially for large-scale or interactive optimization tasks.

2.4.3 Convergence behavior

Convergence behavior measures how efficiently and quickly an algorithm improves toward the optimal solution. Good convergence indicates that the algorithm can find high-quality solutions in fewer iterations.

Convergence Rate is given by:

$\mathbf{\text{Convergence\hspace{0.17em}Rate}}=\frac{\mathbf{\text{Objective}}\mathbf{\text{value}}\mathbf{\text{improvement}}}{\mathbf{\text{Number}}\mathbf{\text{of}}\mathbf{\text{iterations}}}$

Faster convergence is particularly beneficial in large or multi-objective search spaces.

2.4.4 Sustainability metrics

In addition to computational performance, algorithms are assessed based on how well their optimized results align with recognized sustainability goals.

2.4.4.1 Green Building Certifications (LEED, BREEAM)

These systems score buildings on factors like energy use, water conservation, materials, indoor environment, and innovation. Each factor contributes points to the total score, which determines the certification level.

$\mathbf{\text{Green\hspace{0.17em}Building\hspace{0.17em}Score}}={\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{n}}}\text{\hspace{0.5em}Credits\hspace{0.17em}in\hspace{0.17em}each\hspace{0.17em}sustainability\hspace{0.17em}category}$

Higher scores indicate better sustainability performance and qualify buildings for higher certification tiers.

2.4.4.2 Energy Performance Index (EPI)

This metric evaluates how much energy a building consumes per square meter. It gives a direct sense of energy efficiency.

$\mathbf{\text{EPI}}=\frac{{\mathit{E}}_{\mathbf{\text{annual}}}}{\mathbf{\text{Floor}}\mathbf{\text{Area}}\left({\mathbf{m}}^{\mathbf{2}}\right)}$

Lower EPI values signify more efficient energy usage across the space.

2.4.4.3 Carbon Footprint Reduction

This metric shows how much carbon emissions are cut due to optimization.

$\mathbf{\text{Carbon\hspace{0.17em}Footprint\hspace{0.17em}Reduction\hspace{0.17em}}}\left(\%\right)=\left(\frac{{\mathit{C}}_{\mathbf{\text{baseline}}}-{\mathit{C}}_{\mathbf{\text{optimized}}}}{{\mathit{C}}_{\mathbf{\text{baseline}}}}\right)\times \mathbf{100}$

It accounts for improved energy systems and low-carbon material choices in the design.

2.4.5 Occupant comfort score

Comfort score evaluates the building’s indoor environment based on thermal comfort, lighting quality, and air conditions. Each component is assigned a weight according to its importance to user experience.

$\mathbf{\text{Comfort\hspace{0.17em}Score}}={\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{n}}}{\mathit{w}}_{\mathit{i}}·{\mathit{S}}_{\mathit{i}}$

Where.

• ${\mathit{S}}_{\mathit{i}}$: Score of each comfort factor (e.g., temperature),

• ${\mathit{w}}_{\mathit{i}}$: Its relative weight.

This is often broken down as:

$\mathbf{\text{Comfort\hspace{0.17em}Score}}=\mathbf{0.5}·\text{Temperature}+\mathbf{0.3}·\text{Air\hspace{0.17em}Quality}+\mathbf{0.2}·\text{Lighting}$

The selected variables in this study are specifically chosen for their relevance to energy use, comfort, and sustainability. Where variables appeared potentially correlated-like HVAC efficiency and building type-care was taken to use diverse configurations for residential and commercial buildings to avoid redundancy. However, some dependencies between variables are acknowledged. Future work will emphasize more direct energy-impacting parameters like insulation and shading over high-level aggregates. This approach supports a more precise optimization framework with less redundancy and greater interpretability.

3 Results analysis

3.1 Comparative performance summary of algorithms

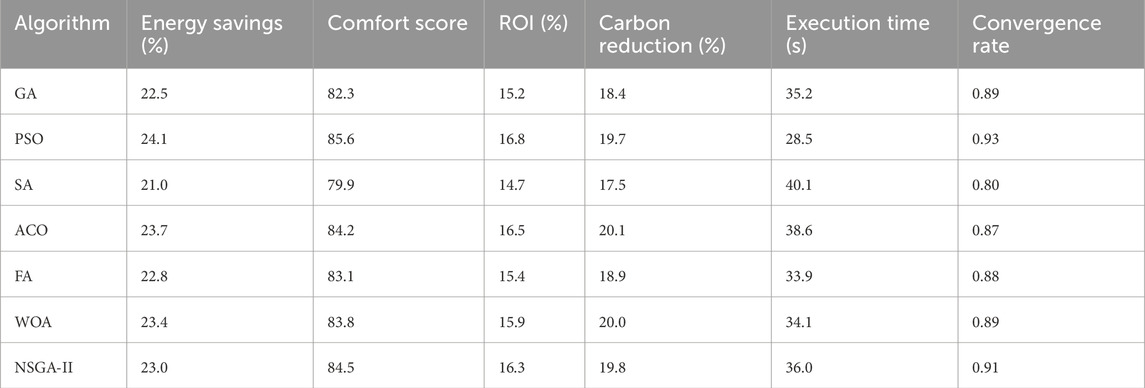
The performance of all seven metaheuristic algorithms—Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Simulated Annealing (SA), Ant Colony Optimization (ACO), Firefly Algorithm (FA), Whale Optimization Algorithm (WOA), and NSGA-II—was evaluated using key optimization metrics. These included energy savings, occupant comfort score, return on investment (ROI), carbon footprint reduction, execution time, and convergence rate. The algorithms were applied to optimize 1,500 building configurations across diverse climatic zones and typologies.

As shown in Table 1, PSO achieved the highest energy savings (24.1%) and the fastest execution time (28.5 s), making it the most efficient in terms of computational speed and energy performance. ACO closely followed, showing strong carbon footprint reduction (20.1%) and attaining high occupant comfort scores (84.2). NSGA-II provided the most balanced outcomes across all objectives, particularly excelling in multi-objective trade-off management. GA performed well in occupant comfort (82.3) and ROI, while FA offered moderate energy savings with competitive comfort outcomes. WOA showed significant promise in carbon reduction and design robustness, while SA, though effective in escaping local optima, demonstrated the slowest convergence and lowest energy savings (21.0%).

This initial comparison provides a foundation for deeper analysis in the following sections, where individual metrics and objectives are explored in more detail.

3.2 Energy consumption optimization

Minimizing energy consumption is the primary objective of sustainable building design optimization. This subsection analyzes how effectively each algorithm reduced total annual energy use across the dataset of 1,500 building configurations. The algorithms were evaluated by calculating the percentage of energy savings relative to the baseline energy consumption.

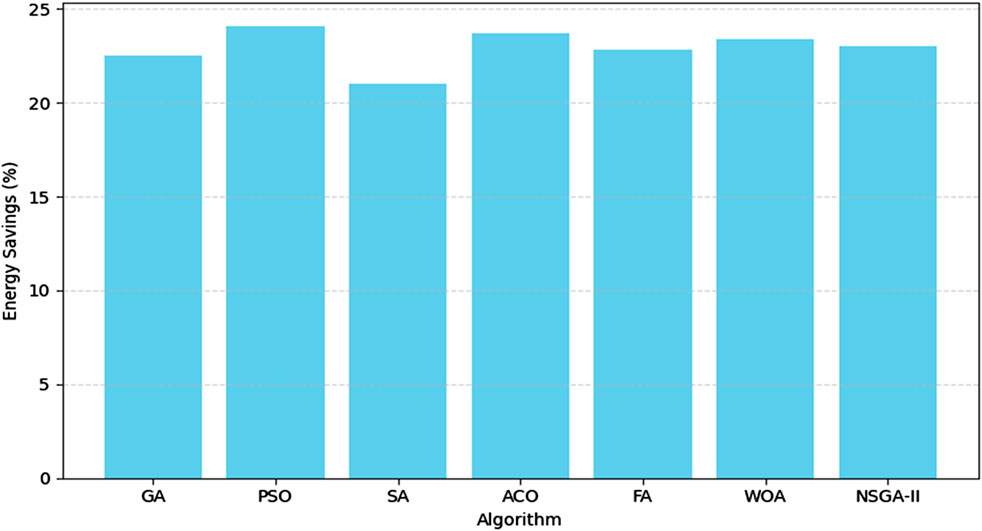
As illustrated in Figure 1 and further detailed in Table 2, Particle Swarm Optimization (PSO) led all algorithms with the highest energy savings of 24.1%, demonstrating superior exploration capabilities in continuous solution spaces. This was followed closely by Ant Colony Optimization (ACO) at 23.7% and Whale Optimization Algorithm (WOA) at 23.4%, both of which also performed consistently across other metrics. NSGA-II achieved 23.0%, maintaining a good balance while still prioritizing energy efficiency.

Figure 1

Figure 1. Energy savings comparison across metaheuristic algorithms.

Table 2

Table 2. Comparative analysis of energy savings across metaheuristic optimization algorithms.

Firefly Algorithm (FA) and Genetic Algorithm (GA) produced respectable savings of 22.8% and 22.5%, respectively, benefiting from their population-based search strategies. However, Simulated Annealing (SA) resulted in the lowest savings at 21.0%, indicating its slower convergence toward global minima in this objective.

These results reflect the advantages of swarm- and evolution-based algorithms for energy-related objectives. Algorithms with greater adaptability to multi-dimensional continuous variables, such as PSO, WOA, and ACO, showed more consistent energy reduction across the range of building typologies and climates.

3.3 Occupant comfort and ROI optimization

This section considers each algorithm’s optimization of both occupant comfort and return on investment (ROI), both of which are key factors in maintaining a building’s ability to be used effectively and its long-term economic sustainability. A composite score of thermal conditions, air quality, and lighting is used to quantify comfort. ROI indicates the tradeoffs between construction expense and operational savings through energy efficiency.

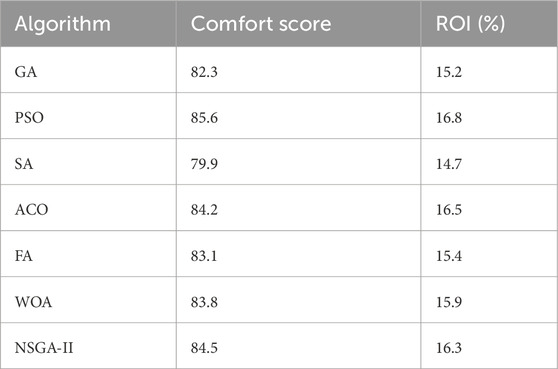
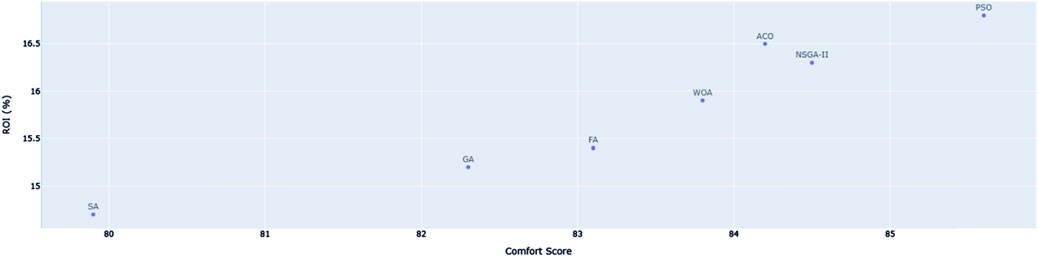
As can be seen in Table 3, Particle Swarm Optimization (PSO) produced the highest comfort rating of 85.6, with Ant Colony Optimization (ACO) following at 84.2 and NSGA-II at 84.5. These optimizers successfully tuned design variables like HVAC efficiency, window-to-wall ratio, and levels of insulation to maximize internal environmental quality. Firefly Algorithm (FA) and Whale Optimization Algorithm (WOA) had strong comfort ratings of 83.1 and 83.8. Genetic Algorithm (GA) had 82.3, with consistent but lower performance in comfort-oriented scenarios. Simulated Annealing (SA) trailed at 79.9 due to its slow convergence in balancing multiple conflicting variables.

Table 3

Table 3. Comfort scores and ROI achieved by algorithms.

In terms of ROI, PSO again topped the list with a return of 16.8%, leveraging its global best search dynamics to reduce both operational energy costs and capital expenditures on ineffective configurations. ACO and NSGA-II yielded competitive ROI values of 16.5% and 16.3%, respectively. GA and FA followed closely, while SA delivered the lowest ROI, reinforcing its limited capability in dual-objective scenarios.

As illustrated in Figure 2, a scatter plot mapping comfort against ROI reveals that PSO, ACO, and NSGA-II occupy the optimal region, delivering strong trade-offs between human-centric comfort and economic return.

Figure 2

Figure 2. Occupant comfort vs ROI Across Algorithms.

3.4 Carbon footprint reduction analysis

Minimizing the carbon footprint of building operations and materials is a critical objective in sustainable architecture. This section assesses how each algorithm performed in reducing total CO₂ emissions, as calculated from the energy source mix, construction materials, and system efficiency. The outcome corresponds to each of the optimized design configurations’ environmental implications.

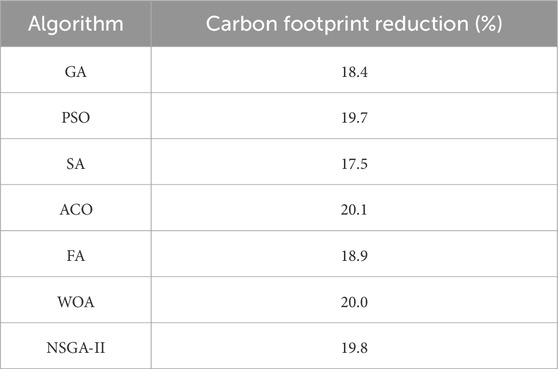
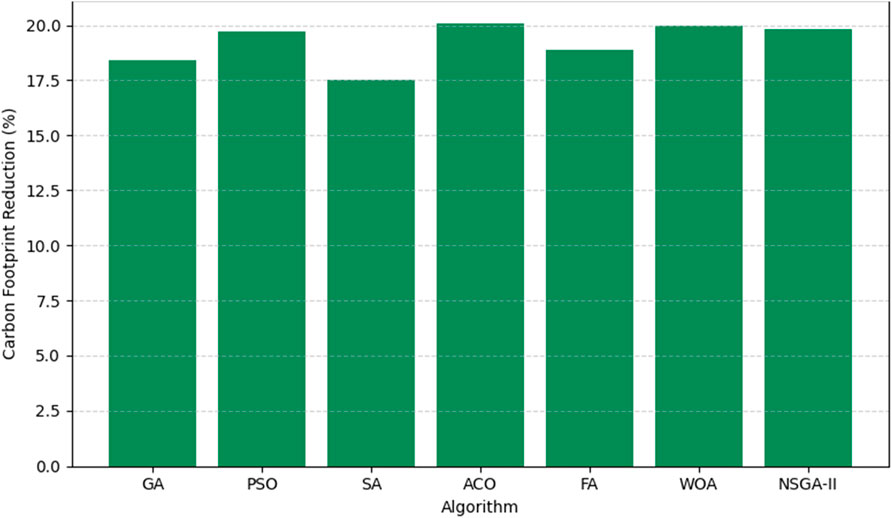
As seen in Table 4, ACO realized the greatest carbon footprint reduction of 20.1% due to its capacity to favor configurations encompassing renewable energy sources and low-emission materials on all iterations. WOA was not far behind with 20.0% due to its adaptive mechanism of encircling to optimize against environmental-friendly design variables. NSGA-II and PSO also performed well at 19.8% and 19.7%, respectively, and were highly efficient in balancing environmental concerns and performance.

Table 4

Table 4. Carbon footprint reduction achieved by algorithms.

The Firefly Algorithm (FA) and Genetic Algorithm (GA) realized moderate savings of 18.9% and 18.4%, respectively. These results indicate that both can potentially search for sustainable solutions but have more iterations or need to be hybridized for deeper carbon reductions. Simulated Annealing (SA) realized the least amount of improvement at 17.5% through its low exploration level and slow convergence in the carbon reduction function.

Figure 3 demonstrates the relative carbon reduction performance of the algorithms. The findings confirm that multi-objective optimization-oriented algorithms like ACO, WOA, and NSGA-II can identify low-carbon facility configurations more effectively with little loss of energy efficiency and comfort.

Figure 3

Figure 3. Carbon emissions reduction across algorithms.

3.5 Sustainability outcomes and LEED certifications

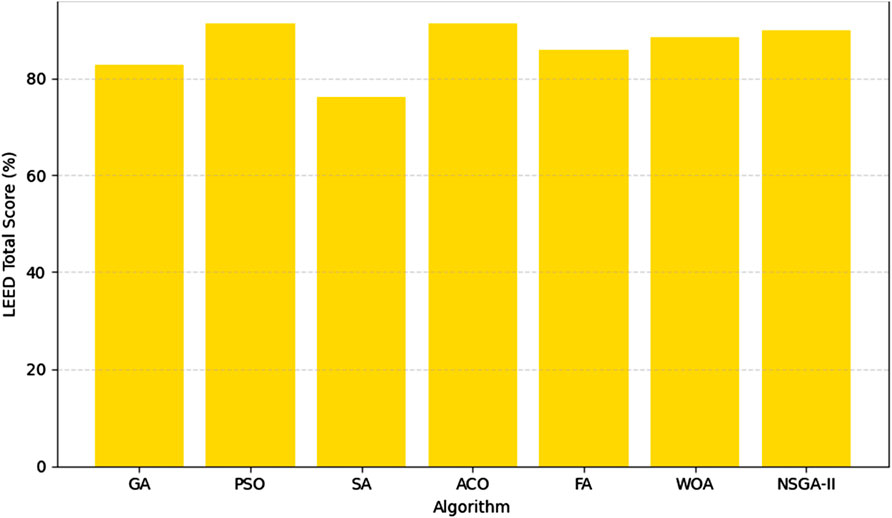
To confirm the applicability of the optimization outcomes in the real-world context, in this section each algorithm’s performance is calculated using LEED certification standards and sustainability indicators. LEED certifications are given in five principal categories: energy efficiency, water efficiency, materials and resources, indoor environmental quality, and innovation. The higher the combined score corresponds to improved levels of certification (e.g., Silver, Gold, Platinum).

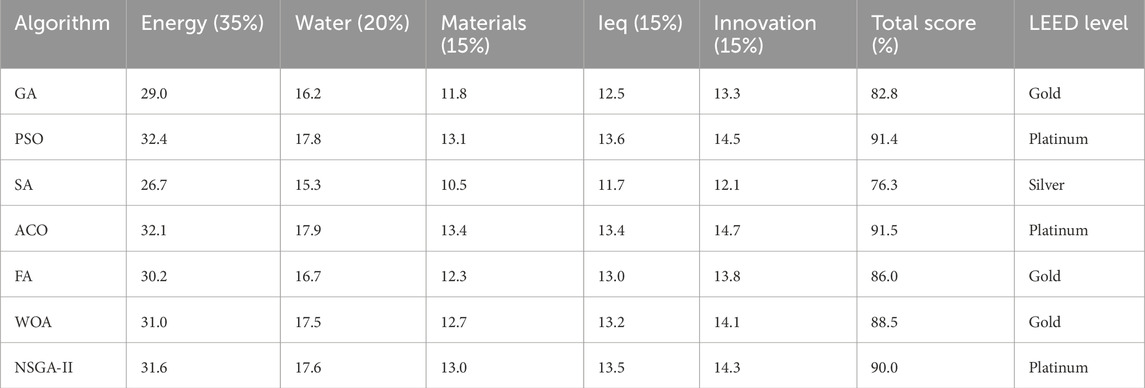
As can be seen in Table 5, Ant Colony Optimization (ACO) and Particle Swarm Optimization (PSO) attained the best overall LEED ratings and were in the Platinum certification category. This was due to their high performance in energy efficiency, indoor environmental quality, and material selection. NSGA-II also attained Platinum rating signifying that its all-around optimization of energy, comfort, and carbon goals resulted in very sustainable structures.

Table 5

Table 5. LEED certification scores by algorithm.

Whale Optimization Algorithm (WOA) trailed just behind it, with efficient use of water and the use of renewable energy standing it in good stead for being awarded a Gold standard. Firefly Algorithm (FA) and Genetic Algorithm (GA) also attained Gold status, evidencing favorable—but not the best—sustainability performance. Simulated Annealing (SA) was lowest in all but one of the categories and attained only a Silver rating on account of low performance in energy and material criteria.

As seen in Figure 4, the LEED certification levels indicate the strength of each algorithm in designing holistically sustainable structures. The high concentration of PSO, ACO, and NSGA-II in the Platinum category emphasizes their applicability in real-world green building projects.

Figure 4

Figure 4. Leed certification levels achieved by algorithms.

3.6 Convergence behavior comparison

Convergence behavior is an essential indicator of an algorithm’s efficiency in moving towards optimal solutions. Convergence behavior indicates the algorithm’s capacity to stabilize its objective values across iterations and hence signifies both the computational time and optimization stability. In this section, each algorithm’s convergence pattern is examined in terms of iteration number, the rate of convergence, as well as stability over time.

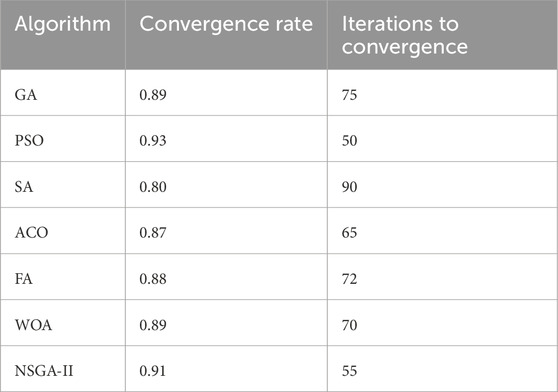
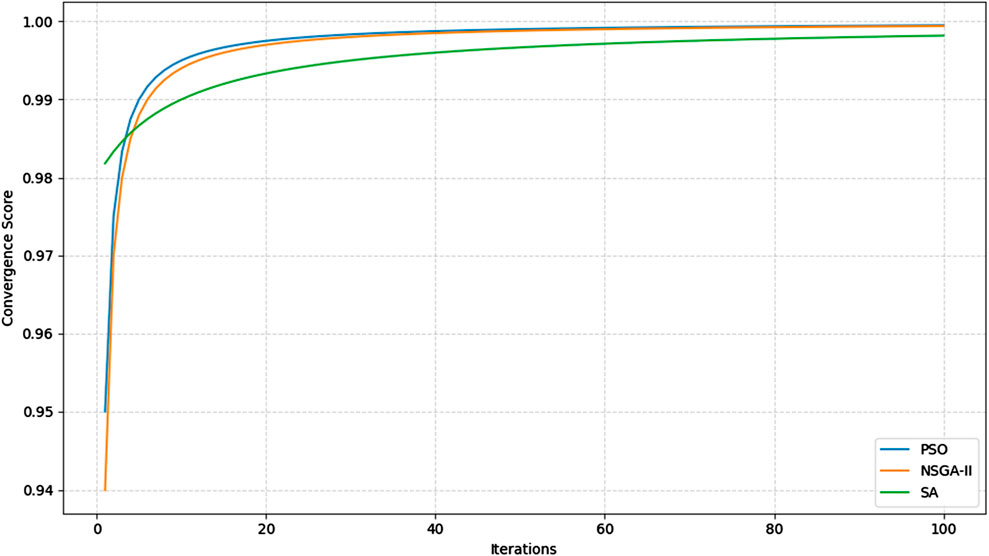
As can be seen from Table 6, Particle Swarm Optimization (PSO) once again demonstrated the quickest convergence, converging within 50 iterations at a rate of 0.93 due to its high exploitation ability and dynamics of the swarm intelligence. NSGA-II was close behind it, converging at 55 iterations at the rate of 0.91 due to its population-based evolutionary mechanism for maintaining Pareto-optimal fronts.

Table 6

Table 6. Convergence performance of algorithms.

Genetic Algorithm (GA) and Whale Optimization Algorithm (WOA) both had moderate convergence rates of 0.89 and needed approximately 75 and 70 iterations, respectively, to stabilize. Firefly Algorithm (FA) and Ant Colony Optimization (ACO) converged at slightly slower paces with FA stabilizing at iteration 72 and ACO at iteration 65 at respective convergence rates of 0.88 and 0.87. Simulated Annealing (SA) had the slowest convergence with almost 90 iterations to stabilize at a rate of 0.80 due mainly to its probabilistic search procedure accepting inferior solutions during the initial stages.

These are well illustrated in Figure 5, where the convergence curves highlight how quickly and steadily each of the algorithms converged towards optimal solutions for 100 iterations. PSO and NSGA-II curves slope steeply in the initial stages whereas the curve of SA is sloping and gradual reflecting longer times of search and slow adaptation.

Figure 5

Figure 5. Convergence curves of metaheuristic algorithms.

3.7 Statistical and sensitivity analysis

In order to guarantee the reliability and stability of the optimization results, the section here gives the statistical error analysis and sensitivity test results. These analyses give insights into the stability and reliability of the algorithms when run repeatedly and also tell us which performance outcomes are most impacted by the designing parameters.

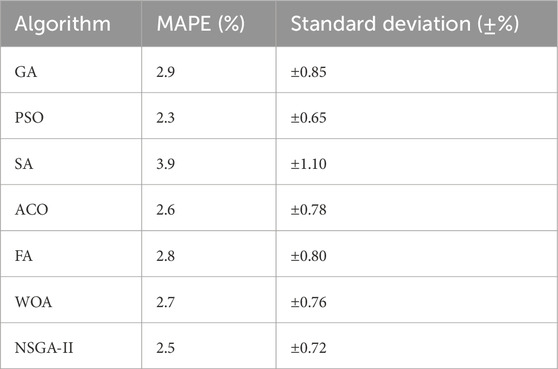
Mean Absolute Percentage Error (MAPE) and Standard Deviation (SD) were evaluated for 10 independent runs of each algorithm to factor in the energy savings’ variation. From Table 7, Particle Swarm Optimization (PSO) had the lowest MAPE of 2.3%, reflecting highly consistent performance in multiple runs. NSGA-II and ACO also performed well with high reliability as evidenced by MAPE results of 2.5% and 2.6%, respectively. Simulated Annealing (SA) demonstrated the highest MAPE of 3.9%, as its more stochastic process and less consistent convergence were reflected.

Table 7

Table 7. Statistical analysis of energy savings across algorithms.

For Standard Deviation, PSO once again yielded the least variable results (±0.65%), with NSGA-II (±0.72%) and WOA (±0.76%) following next in line. FA and GA had moderate variation, while SA had the largest range of outcome reliability (±1.10%), consistent with the observed trend of its converging behavior.

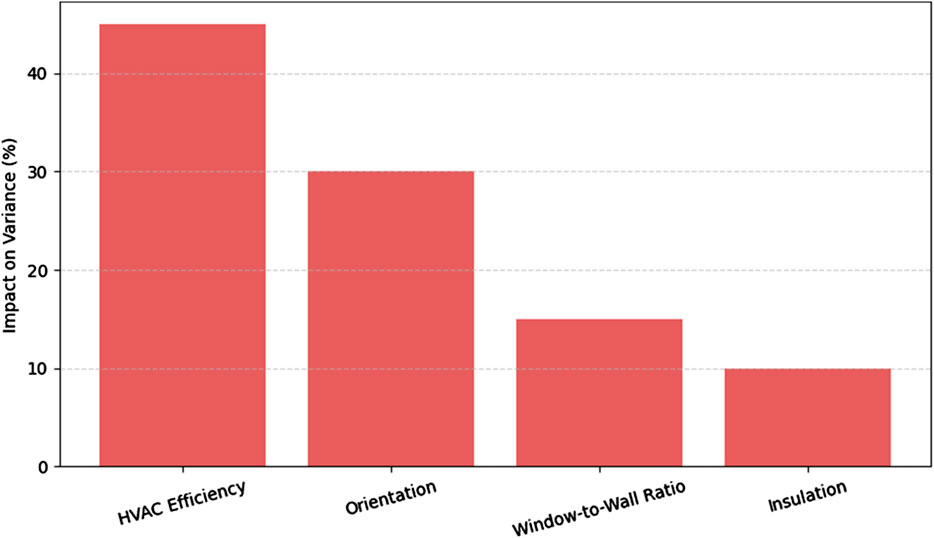
The sensitivity analysis examined how changes in key input variables—such as HVAC efficiency, window-to-wall ratio, building orientation, and insulation value—affected optimization outcomes. The results, summarized in Figure 6, revealed that HVAC efficiency had the most substantial impact, contributing to 45% of variance in energy savings. Orientation and window-to-wall ratio followed, influencing 30% and 15%, respectively. This highlights the importance of mechanical systems and envelope design in sustainable performance.

Figure 6

Figure 6. Sensitivity of key variables affecting energy savings.

These findings confirm that the top-performing algorithms not only deliver superior solutions but also maintain stability across multiple runs and are responsive to the most critical variables in design decision-making.

3.8 Trade-off and pareto analysis (for NSGA-II)

This section focuses on the Non-dominated Sorting Genetic Algorithm II (NSGA-II) and its ability to handle multiple competing objectives by generating a Pareto front. Unlike single-objective optimizers, NSGA-II simultaneously explores trade-offs between energy savings, occupant comfort/ROI, and carbon footprint reduction, providing a set of equally optimal solutions for different stakeholder preferences.

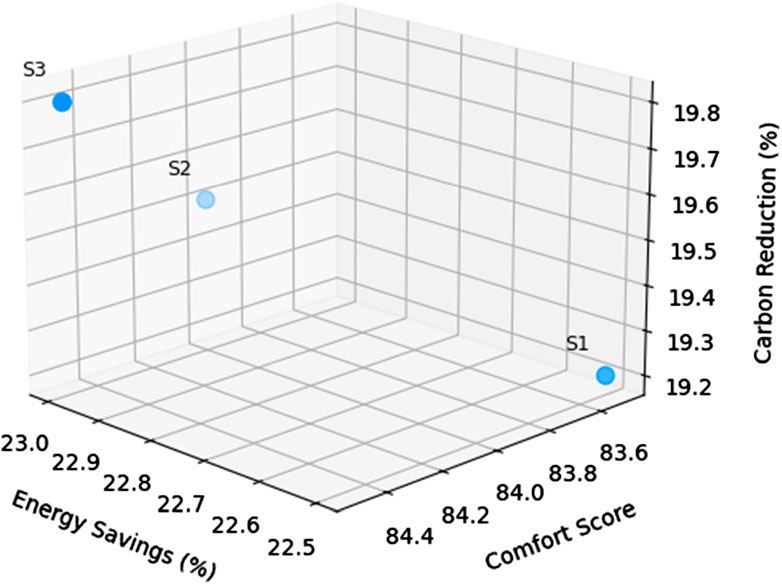
As represented in Figure 7, the Pareto front produced by NSGA-II clearly shows a range of optimal solutions. Designs on the left of the front maximize energy savings as their highest priority, while on the right maximize comfort and ROI, with a balanced middle section being an agreeable solution on all three fronts. The front enables architects and planners to choose the appropriate context solution on the basis of project objectives—either pursuing LEED Platinum, ROI maximization, or minimizing environmental impact.

Figure 7

Figure 7. Pareto front of nsga-II across energy, comfort, and carbon objectives.

For example, one NSGA-II solution resulted in 23.0% energy savings, 84.5 comfort score, and 19.8% reduction in carbon footprint, which puts it at par with PSO and ACO. The major strength of NSGA-II is its power to present several such trade-offs without being constrained by a fixed weighting scheme as in weighted-sum models.

This flexibility proves particularly valuable in real-world architectural applications where project constraints vary, and multi-stakeholder input often leads to shifts in design priorities. NSGA-II’s Pareto approach thus enhances decision-making transparency and provides greater design agility in the early stages of sustainable urban planning.

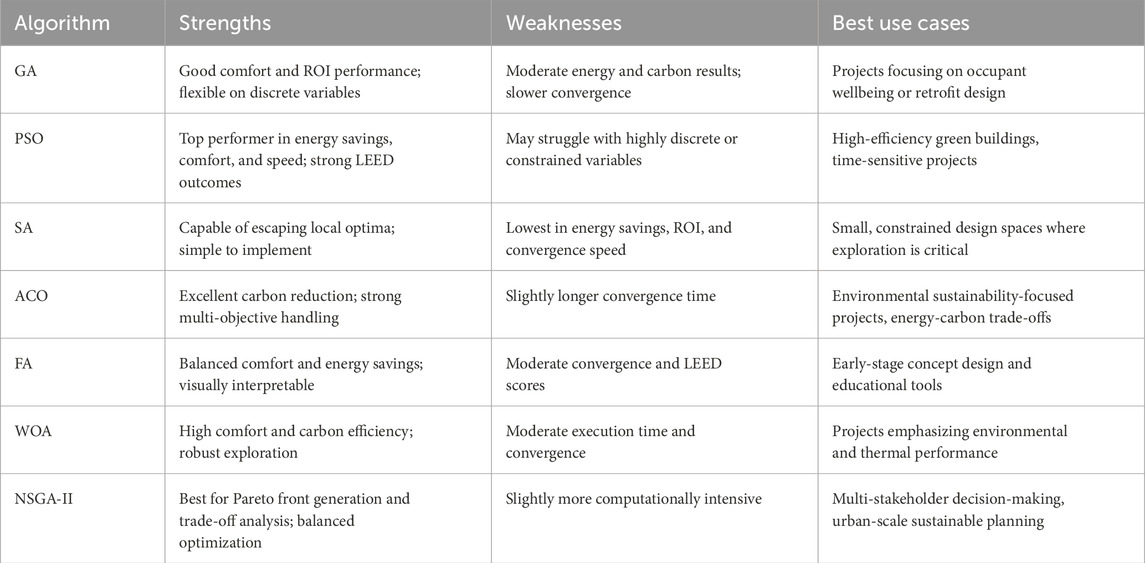
3.9 Summary of algorithm strengths and weaknesses

This subsection synthesizes the findings from previous analyses by outlining the core strengths, limitations, and recommended use cases for each of the seven metaheuristic algorithms used in this study. The comparative review aids in selecting the most appropriate algorithm based on specific project priorities such as speed, sustainability, comfort, or balanced trade-offs.

As summarized in Table 8, Particle Swarm Optimization (PSO) emerges as the most well-rounded performer, excelling in energy savings, comfort, execution time, and achieving Platinum LEED certification. Its main limitation lies in slightly less flexibility when handling highly constrained or discrete variables. Ant Colony Optimization (ACO) stands out for its carbon footprint reduction and multi-objective strength, making it ideal for projects emphasizing environmental impact mitigation.

Table 8

Table 8. Strengths, weaknesses, and suggested use cases of each algorithm.

NSGA-II, while not always the absolute best in any single metric, delivers the most balanced solutions across all objectives, particularly in contexts requiring stakeholder-driven trade-offs. It is especially suited for large-scale urban planning where Pareto flexibility is essential. Whale Optimization Algorithm (WOA) offers solid performance in both carbon reduction and comfort but requires slightly more computational time to converge.

Firefly Algorithm (FA) and Genetic Algorithm (GA) show consistent results across most objectives and are preferred when interpretability, modularity, or algorithm simplicity are valued. However, both tend to fall behind in convergence rate and overall LEED scores. Simulated Annealing (SA), though capable of escaping local optima, was the least effective across all key metrics, with slower convergence, higher variation in results, and lower sustainability performance. Nevertheless, SA may still be useful in small-scale design problems or constrained scenarios.

This analysis confirms that no single algorithm is optimal for all use cases, but each offers distinct advantages depending on the design scenario and optimization priorities. As architectural and urban projects continue to embrace data-driven sustainability, understanding the nuanced performance of optimization methods will be critical to informed, context-sensitive design decisions.

4 Discussion

The findings of this research highlight the strength and versatility of metaheuristic methods in tackling the multifaceted problem of sustainable building optimization. By combining seven optimization methods on three main goals—consumption of energy, occupant comfort/ROI, and carbon footprint minimization—this research presents a sound basis for evidence-driven architectural decision-making.

Out of all the algorithms tested, Particle Swarm Optimization (PSO) performed best in energy savings (24.1%), execution time (28.5 s), and comfort score (85.6), proving itself in quick convergence and continuous-variable optimization. These findings support PSO’s applicability for projects with performance deadlines where time and computation matter.

In the same way, Ant Colony Optimization (ACO) supported its strength in obtaining the best carbon reduction (20.1%) and LEED Platinum rating, proving high versatility in terms of sustainability-driven design priorities.

NSGA-II was remarkable for offering a wide range of Pareto optimal solutions allowing architects and planners to have the freedom to investigate trade-offs between conflicting objectives. Its ability to find solutions to energy savings, comfort, and carbon balances makes it an attractive option for large-scale city or institutional projects requiring stakeholder-driven compromises.

Although Genetic Algorithm (GA) and Firefly algorithm (FA) did not excel in any single objective, both of them yielded steady and fairly high values in all categories. These algorithms are particularly useful in exploratory stages of design, where solution diversity and conceptual flexibility are valued. Whale Optimization Algorithm (WOA) proved highly competitive, especially in comfort and carbon impact, and showed consistent convergence behavior. Its adaptive behavior suits it well to non-linear problems involving renewable integration or natural ventilation strategies.

Simulated Annealing (SA), though traditionally valued for escaping local optima, lagged across most evaluation metrics. Its slow convergence (90 iterations) and lower comfort and ROI outcomes suggest limited application in broader multi-objective scenarios. However, SA may still be beneficial in narrowly defined or highly constrained design spaces, particularly for fine-tuning solutions after initial population-based exploration.

From a methodological perspective, the inclusion of statistical and sensitivity analyses further validated the robustness of the results. Low variation in MAPE and standard deviation—especially for PSO, NSGA-II, and ACO—indicates the repeatability and dependability of their optimization behavior. The sensitivity analysis confirmed the dominant influence of HVAC efficiency and window-to-wall ratio, guiding future feature prioritization.

Despite the strength of these findings, some limitations should be acknowledged. The study was based on simulated data derived from BIM platforms, smart sensor repositories, and public databases, and although carefully prepared and normalized, it lacks direct validation through real-world post-occupancy evaluations or calibrated energy models. Additionally, while the algorithms were run on uniform computational settings, the scalability of each algorithm under more complex or higher-resolution design problems was not tested in depth.

Future research should explore hybrid models—such as PSO-NSGA-II combinations—or real-time integration with building performance simulation tools to refine predictions. There is also scope for extending the dataset with geographically diverse case studies, allowing better generalization of results across different climatic and regulatory contexts.

In conclusion, this study provides a comprehensive benchmark of metaheuristic algorithms for sustainable building design, highlighting the strengths of individual approaches and their alignment with different project goals. The findings serve as practical guidance for architects, engineers, and policymakers seeking to embed intelligent optimization into sustainable urban development workflows.

5 Conclusion

The present research attempts to bring forward an overall comparison of seven metaheuristic algorithms, namely, Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Simulated Annealing (SA), Ant Colony Optimization (ACO), Firefly Algorithm (FA), Whale Optimization Algorithm (WOA), and Non-dominated Sorting Genetic Algorithm II (NSGA-II) for the optimization of sustainable building design in terms of three key goals: energy consumption minimization, maximizing occupants’ comfort and ROI, and minimizing carbon footprint.

The PSO algorithm was found to be the best in providing fast convergence and highest energy savings, while ACO performed well in environmental sustainability and NSGA-II in multi-objective trade-off. NSGA-II was also found to be specially useful in providing Pareto-optimal fronts with solutions for various sustainability objectives. WOA and FA also performed well with balanced and consistent results and can be used for universal architectural purposes. GA performed well in occupant-centric objectives consistently, whereas SA was found to be the least successful but useful in the case of constrained optimization problems.

The findings point out that none of the algorithms outperform the others on all criteria. Rather, algorithm choice should be informed by project-specific priorities, for instance, in terms of speed, comfort, environmental performance, or flexibility for stakeholders. Integration of LEED-based sustainability analysis and thorough sensitivity analysis add to the findings’ application validity as useful in actual implementation for designers and planners.

In the end, this research presents a strong methodology and performance metric for the integration of machine learning-inspired metaheuristics in digital architecture. Future research can build on these findings through algorithmic hybridization, real-time model checking, and application in varied city environments to further push the integration of artificial intelligence and sustainable design.

Data availability statement

The datasets supporting the findings of this study are available from the corresponding author upon reasonable request.

Author contributions

RG: Conceptualization, Investigation, Writing – original draft, Writing – review and editing, Methodology, Supervision, Validation. MA: Conceptualization, Writing – original draft, Writing – review and editing, Investigation, Methodology, Supervision, Validation.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The authors would like to express gratitude to colleagues and institutions that provided support throughout the research process.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abid, M. T., Aljarrah, N., Shraa, T., and Alghananim, H. M. (2024). Forecasting and managing urban futures: machine learning models and optimization of urban expansion. Asian J. Civ. Eng. 25 (6), 4673–4682. doi:10.1007/s42107-024-01072-2

CrossRef Full Text | Google Scholar

Abusaleh, S. W. (2024). Enhancing preservation outcomes for architectural heritage buildings through machine learning-driven future search optimization. Asian J. Civ. Eng. 25 (7), 5277–5292. doi:10.1007/s42107-024-01112-x

CrossRef Full Text | Google Scholar

Abu-shaikha, M. I. (2024). Smart sustainable architecture: leveraging machine learning for adaptive digital design and resource optimization. Asian J. Civ. Eng. 1-12. doi:10.1007/s42107-024-01180-z

CrossRef Full Text | Google Scholar

Agusa, E., Gianoglio, C., Zunino, R., and Gastaldo, P. (2022). An approximate randomization-based neural network with dedicated digital architecture for energy-constrained devices. Neural Comput. Appl. 35 (9), 6753–6762. doi:10.1007/s00521-022-08034-2

CrossRef Full Text | Google Scholar

Alnusairat, S., and Abu Qadourah, J. (2025). Moving to green technologies: acceptance and perception of architectural solar photovoltaic technology for residential buildings. Archit. Eng. Des. Manag. 21 (2), 338–355. doi:10.1080/17452007.2024.2361819

CrossRef Full Text | Google Scholar

Amro, D., and Ammar, S. (2018). The role of university education in directing architects towards conserving the sustainability of the urban cultural heritage (comparative study). Al-Balqa J. Res. Stud. 21 (2), 87–108. doi:10.35875/1105-021-002-005

CrossRef Full Text | Google Scholar

Chen, C., Koch, F., and Reicher, C. (2023). Developing a two-level machine-learning approach for classifying urban form for an east asian mega-city. Environ. Plan. B Urban Anal. City Sci. 51 (4), 854–869. doi:10.1177/23998083231204606

CrossRef Full Text | Google Scholar

Costa-Carrapiço, I., Raslan, R., and González, J. N. (2020). A systematic review of genetic algorithm-based multi-objective optimisation for building retrofitting strategies towards energy efficiency. Energy and Buildings 210, 109690.

CrossRef Full Text | Google Scholar

Forootan, M. M., Larki, I., Zahedi, R., and Ahmadi, A. (2022). Machine learning and deep learning in energy systems: a review. Sustainability 14 (8), 4832. doi:10.3390/su14084832

CrossRef Full Text | Google Scholar

Ghoneim, R. (2025). Machine learning for adaptive facade design: enhancing thermal performance in urban architecture. Civ. Eng. Archit. 13 (2), 1273–1288. doi:10.13189/cea.2025.130239

CrossRef Full Text | Google Scholar

Heidari, F., Mahdavinejad, M., and Sotodeh, S. (2018). Renewable energy and smart hybrid strategies for high performance architecture and planning in case of tehran, Iran. IOP Conf. Ser. Earth Environ. Sci. 159, 012030. doi:10.1088/1755-1315/159/1/012030

CrossRef Full Text | Google Scholar

Hong, T., Chen, Y., Luo, X., Luo, N., and Lee, S. (2020). Ten questions on urban building energy modeling. Build. Environ. 168, 106508. doi:10.1016/j.buildenv.2019.106508

CrossRef Full Text | Google Scholar

Hussein, M. Y. A., Musa, A., Altaharwah, Y., and Al-Kfouf, S. (2024). Integrating machine learning in architectural engineering sustainable design: a sub-hourly approach to energy and indoor climate management in buildings. Asian J. Civ. Eng. 25, 4107–4119. doi:10.1007/s42107-024-01034-8

CrossRef Full Text | Google Scholar

Kanthila, C., Boodi, A., Beddiar, K., and Benbouzid, M. (2021). Building occupancy behavior and prediction methods: a critical review and challenging locks. IEEE Access 9, 79353–79372. doi:10.1109/access.2021.3083534

CrossRef Full Text | Google Scholar

Kaveh, A. (2017). Applications of metaheuristic optimization algorithms in civil engineering. Switzerland: Springer International Publishing.

CrossRef Full Text | Google Scholar

Kaveh, A. (2021). Advances in metaheuristic algorithms for optimal design of structures. 3rd ed Switzerland: Springer International Publishing.

CrossRef Full Text | Google Scholar

Kaveh, A., and Eskandari, A. (2024). Multi-stage parameter adjustment to enhance metaheuristics for optimal design. Acta Mech. 235, 6451–6471. doi:10.1007/s00707-024-04052-4

CrossRef Full Text | Google Scholar

Kaveh, A., and Hamedani, K. B. (2024). A hybridization of growth optimizer and improved arithmetic optimization algorithm and its application to discrete structural optimization. Comput. and Struct. 303, 107496. doi:10.1016/j.compstruc.2024.107496

CrossRef Full Text | Google Scholar

Leer, J., Femenias, P., and Granath, K. (2022). Understanding the progress of sustainable urban development through energy performance. IOP Conf. Ser. Earth Environ. Sci. 1085 (1), 012039. doi:10.1088/1755-1315/1085/1/012039

CrossRef Full Text | Google Scholar

Letchumanan, K., and Naveen, P. (2022). “Machine learning regression models to predict particulate matter (PM2.5),” in Proceedings of the international conference on computing and data science, 458–468. doi:10.2991/978-94-6463-094-7_36

CrossRef Full Text | Google Scholar

Li, S., Pan, Y., Pan, Y., Yu, C., and Huang, Z. (2020). Metrics of urban morphology and their impact on building energy consumption: case studies in shanghai. doi:10.46855/energy-proceedings-3333

CrossRef Full Text | Google Scholar

Liu, S. (2024). Medium office energy consumption optimization using EnergyPlus. Appl. Comput. Eng. 63, 45–55. doi:10.54254/2755-2721/63/20240992

CrossRef Full Text | Google Scholar

Matarneh, S., and Matarneh, R. (2018). Toward a sustainable architectural education: the case of Jordan. Al-Balqa J. Res. Stud. 21 (2), 9–25. doi:10.35875/1105-021-002-010

CrossRef Full Text | Google Scholar

Meshkani, T. (2024). Integrating machine learning in urban pedagogy: addressing homelessness in skid row. Architecture 4 (1), 112–123. doi:10.3390/architecture4010008

CrossRef Full Text | Google Scholar

Mota, L., Mota, A., Pezzuto, C., Carvalho, M., Lavorato, M., Coiado, L., et al. (2018). Development of a surface temperature sensor to enhance energy efficiency actions in buildings. Sensors 18 (9), 3046. doi:10.3390/s18093046

PubMed Abstract | CrossRef Full Text | Google Scholar

Mutani, G., and Todeschi, V. (2020). Building energy modeling at neighborhood scale. Energy Effic. 13 (7), 1353–1386. doi:10.1007/s12053-020-09882-4

CrossRef Full Text | Google Scholar

Nagappan, S., and Daud, S. (2021). Machine learning predictors for sustainable urban planning. Int. J. Adv. Comput. Sci. Appl. 12 (7). doi:10.14569/ijacsa.2021.0120787

CrossRef Full Text | Google Scholar

Park, H., and Rhee, S. (2018). IoT-based smart building environment service for occupants’ thermal comfort. J. Sensors 2018, 1–10. doi:10.1155/2018/1757409

CrossRef Full Text | Google Scholar

Pham, A. D., Ngo, N. T., Truong, T. T. H., Huynh, N. T., and Truong, N. S. (2020). Predicting energy consumption in multiple buildings using machine learning for improving energy efficiency and sustainability. J. Clean. Prod. 260, 121082. doi:10.1016/j.jclepro.2020.121082

CrossRef Full Text | Google Scholar

Pignatta, G., Javed, H., Mastoori, M., Sharifi, S., Manapragada, N., and Buratti, C. (2021). Simulating the impact of solar energy on pyramid and stair urban blocks. Environ. Sci. Proc. 21 (4), 4. doi:10.3390/environsciproc2021012004

CrossRef Full Text | Google Scholar

Raanan, N., Yoffe, H., and Grobman, J. (2022). A machine learning evaluation method for sustainability evaluation: the case of neighbourhoods' design. 1, 283, 291. doi:10.52842/conf.caadria.2022.1.283

CrossRef Full Text | Google Scholar

Ragusa, A., Matta, M., Cristiano, L., Matassa, R., Battaglione, E., Svelato, A., et al. (2022). Deeply in plasticenta: presence of microplastics in the intracellular compartment of human placentas. Int. J. Environ. Res. Public Health 19(18), 11593.

PubMed Abstract | CrossRef Full Text | Google Scholar

Rehab Ghoneim (2025). Machine learning for adaptive facade design: enhancing thermal performance in urban architecture civil engineering and architecture, 2, 1273–1288.

Google Scholar

Shihadeh, J., Abu-shaikha, M. I., and Zghoul, N. (2024). Optimizing sustainable building retrofits with emperor penguin optimization: a machine-learning approach for energy consumption prediction. Asian J. Civ. Eng. 25, 3379–3394. doi:10.1007/s42107-024-00985-2

CrossRef Full Text | Google Scholar

Tien, P. W., Wei, S., Darkwa, J., Wood, C., and Calautit, J. K. (2022). Machine learning and deep learning methods for enhancing building energy efficiency and indoor environmental quality–A review. Energy AI 10, 100198. doi:10.1016/j.egyai.2022.100198

CrossRef Full Text | Google Scholar

Umoh, A. (2024). Incorporating energy efficiency in urban planning: a review of policies and best practices. Eng. Sci. and Technol. J. 5 (1), 83–98. doi:10.51594/estj.v5i1.729

CrossRef Full Text | Google Scholar

Wagner, F., Milojevic-Dupont, N., Franken, L., Zekar, A., Thies, B., Koch, N., et al. (2022). Using explainable machine learning to understand how urban form shapes sustainable mobility. Transp. Res. Part D Transp. Environ. 111, 103442. doi:10.1016/j.trd.2022.103442

CrossRef Full Text | Google Scholar

Wang, Z., Wang, J., He, Y., Liu, Y., Lin, B., and Hong, T. (2020). Dimension analysis of subjective thermal comfort metrics based on ASHRAE global thermal comfort database using machine learning. J. Build. Eng. 29, 101120. doi:10.1016/j.jobe.2019.101120

CrossRef Full Text | Google Scholar

Warth, G., Braun, A., Assmann, O., Fleckenstein, K., and Hochschild, V. (2020). Prediction of socio-economic indicators for urban planning using VHR satellite imagery and spatial analysis. Remote Sens. 12 (11), 1730. doi:10.3390/rs12111730

CrossRef Full Text | Google Scholar

Yaman, M. (2021). Different façade types and building integration in energy efficient building design strategies. Int. J. Built Environ. Sustain. 8 (2), 49–61. doi:10.11113/ijbes.v8.n2.732

CrossRef Full Text | Google Scholar

Zhang, D., Ding, Y., Fan, L., and Jiang, X. (2023). New indicator for a comprehensive evaluation of building energy performance through spatial and temporal dimensions. Energy Build. 289, 113058. doi:10.1016/j.enbuild.2023.113058

CrossRef Full Text | Google Scholar