A comparative study between LSSVM, LSTM, and ANN in predicting the unconfined compressive strength of virgin fine-grained soil

The present investigation introduces a robust soft computing model by comparing twelve least square support vector machine (LSSVM), six long short-term memory (LSTM), and thirty-six artificial neural network (ANN) models to predict the unconfined compressive strength (UCS) of fine-grained soil. For that purpose, a database of fine content, dry unit weight, porosity, void ratio, degree of saturation, and specific gravity results of 85 soil specimens has been compiled from the literature. 75 and 10 soil specimens were trained and tested for each model. Six training databases have been prepared to analyze the effect of quality and quantity of training database by selecting 50%, 60%, 70%, 80%, 90%, and 100% of 75 soil specimens. The performance comparison demonstrated that the LSTM model (MD 113) requires fewer training datasets (50% of 75) than the LSSVM (MD 102 and MD 108) and ANN (MD 120, MD 127, MD 136, MD139, MD 148, and MD 150) models. Also, it was observed that the nonlinear LSSVM model (MD 108) is unaffected by multicollinearity in training datasets and predicted UCS better than the linear LSSVM model (MD 102). Furthermore, the Levenberg-Marquardt neural network model (MD 120) has outperformed the other ANN models with the root mean square error (RMSE) of 5.1214 N/cm², the mean absolute error (MAE) of 4.1379 N/cm², and correlation (R) of 0.9836. The overall performance comparison revealed that the LSTM model is more potent than the LSSVM and ANN models. The LSTM model predicted the UCS of fine-grained soil with the RMSE of 4.7539 N/cm², the MAE of 4.2461 N/cm², and R of 0.9880. Conversely, cosine amplitude sensitivity analysis demonstrated that the fine content and dry unit weight influence the prediction of virgin UCS of fine-grained soils.

1 Introduction

Unconfined compressive strength is the strength parameter of cohesive soils and is essential for any civil engineering project. The unconfined compressive strength of undisturbed, compacted, or remoulded soils is determined as per BIS (1991) and Standard (2017). The unconfined compressive strength test determines cohesion ($C^{\prime }$) and the internal friction angle of cohesive soils. In the UCS test, the soil sample is subjected to major principal stress $\left({\sigma }_1\right)$ and minor principal stress $\left({\sigma }_3=0\right)$, where the internal friction angle is ϕ = 0 (Gunaydin et al., 2010). Therefore, the Mohr circle reveals the undrained shear Equation 1 strength $s_u$.

${\mathit{s}}_{\mathit{u}}=\mathit{c}=\frac{{\mathit{q}}_{\mathit{u}}}{\mathbf{2}}(1)$

The experimental procedure for determining UCS of fine-grained soil is lengthy because it requires the optimum moisture content obtained from the standard or modified proctor test. A proctor test requires five to six attempts to reveal the soil’s OMC and MDD. Therefore, several researchers have developed different methods and methodologies to predict the unconfined compressive strength of the soil. Several researchers have established relationships between soil properties (index and compaction) and UCS of stabilized soil (Zumrawi and Mohammed, 2016; Khalid et al., 2015; Arumugam et al., 2013; Chan et al., 2012; Al-Kahdaar and Al-Ameri, 2010; Masada, 2009; Edil et al., 2009; Obasi and Anyaegbunam, 2005; Yılmaz, 2000). The nonlinear analysis demonstrates a better relationship between index properties and UCS of soil than the linear analysis. The physical properties and normalized shear strength can predict the unconfined compressive strength (Senoon and Hussein, 2019). In addition, Arumugam et al. (2013) have also mapped the relationship between the liquidity index and UCS and observed that the UCS decreases with the liquidity index. Most of the published research works are concerned with the application of artificial intelligence to predict the UCS of stabilized soil using geopolymer, cement, fly ash, kiln dust, reinforcing material, waste types, and micron fines (Tabarsa et al., 2021; Yildirim et al., 2021; Ngo et al., 2021; Salahudeen et al., 2020; Priyadarshee et al., 2020; Saputra and Putra, 2020; Bazazorde, 2018; Ghorbani and Hasanzadehshooiili, 2018; Javdanian and Lee, 2019; Sharma and Singh, 2018; Mahamaya et al., 2015; Mozumder and Laskar, 2015; Udo et al., 2014; Motamedi et al., 2015; Arumugam et al., 2013; Kalkan et al., 2009). On the other hand, the authors have compared the performance of artificial neural networks with different AI approaches and found that the prediction of geotechnical properties is very encouraging and acceptable using ANN. Gunaydin et al. (2010) have also applied ANN and regression approaches to predict UCS of soil using soil properties such as water content, natural unit weight, dry unit weight, void ratio, porosity, saturated unit weight, saturated degree, specific gravity, and permeability. The authors have derived a regression Equation 2, which predicted the UCS of soil with a COD of 0.88.

$\begin{array}{ll}\hfill \mathit{U}\mathit{C}\mathit{S}\left(\mathit{k}\mathit{P}\mathit{a}\right)& =-\mathbf{7287634}*\mathit{K}+\mathbf{12291.38}*\mathit{S}\mathit{G}-\mathbf{39.20}*\mathit{P}\hfill \\ \hfill & +\mathbf{172.28}*\mathit{S}\mathit{U}\mathit{W}-\mathbf{31130.39}\hfill \end{array}(2)$

In addition, the authors have mapped a coefficient of determination (0.71-0.92) between the different percentages of clay content and water content. Gunaydin et al. (2010) have reported that the ANN predicts UCS better than the regression model. On the other hand, numerous researchers have predicted the UCS of soil using field test parameters. The dynamic cone penetration index strongly correlates with unconfined compressive strength (Dirriba, 2017; Oljira et al., 2021). Adroja et al. (2017) have also confirmed that the DCPI, LL, PI, and OMC influence the UCS of soil. Saputra and Putra (2020) have mapped a strong correlation (>0.9) between index properties and UCS of Laterite soil. A brief description of the published models is given in Table 1.

Table 1

Table 1. Description of published models in the literature study.

The literature presented that the researchers mapped the relationship between the UCS and different soil properties/DCPI. Conversely, the applied artificial neural networks, gene expression programming, fuzzy, gradient boosting, support vector machine, and regression analysis approaches employed and predicted the UCS of stabilized soil. Still, least square support vector machine (LSSVM), long short-term memory (LSTM), and artificial neural network (ANN) approaches have not been utilized to predict the UCS of virgin fine-grained soil. Researchers have also been observed using compaction, consistency, CBR, and admixture content (RHA, C, PA, LC, etc.) to predict the UCS of virgin/stabilized fine-grained soils. Still, the FC, DUW, P, VR, DS, and SG parameters have not been selected to predict the UCS of virgin fine-grained soil. The soft computing approaches are black-box and data-driven models, affected by the quality and quantity of the database. Still, the impact of the quality and quantity of training databases has not been analyzed on the performance and overfitting of soft computing models. Based on the literature study, the following novelty statements have been drawn for the present research:

• This investigation analyzes the prediction capabilities of LSSVM (linear and polynomial kernel-based), LSTM, and ANN (configured by six backpropagation algorithms) models in predicting the UCS of fine-grained soil.

• This research demonstrates the impact of the quality and quantity of training databases on the performance and overfitting of the LSVVM, LSTM, and ANN models in estimating UCS of fine-grained soil.

• This work compares 54 soft computing models to introduce a robust soft computing model to predict the UCS of fine-grained soil to help geotechnical engineers and designers predict the UCS of fine-grained soil.

2 Research methodology

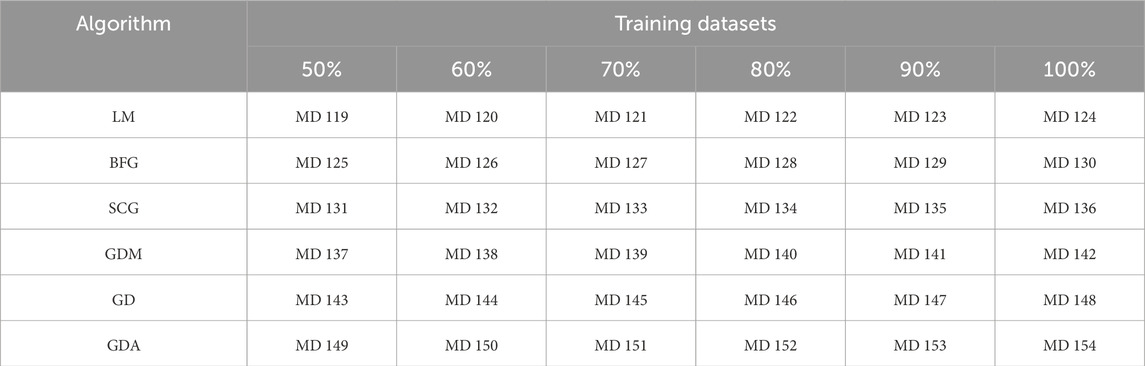
The present investigation introduces a robust soft computing model to predict the unconfined compressive strength of fine-grained soil. For that purpose, a database of fine-grained soil has been compiled from the literature. The database consists of fine content (FC in %), dry unit weight (DUW in g/cm³), porosity (P in %), void ratio (VR), degree of saturation (DS in %), specific gravity (SG), and unconfined compressive strength of (UCS in N/cm²) results of 85 soil specimens. The complete database has been preprocessed to remove the outliers and missing data points. Finally, the database has been normalized by the min-max function. The LSSVM, LSTM-RNN, and ANN models have been developed, trained, tested, and analyzed to introduce the robust soft computing model. Still, the effect of quality and quantity of training database on performance and overfitting of LSSVM, LSTM, and ANN models have not been analyzed and determined in predicting the UCS of fine-grained soil. Therefore, 75 and 10 soil specimens have been selected to create training and testing databases. To assess the effect of quality and quantity of training databases on the performance and overfitting of LSSVM, LSTM, and ANN models, the data proportionality method has created six training databases, selecting 50%, 60%, 70%, 80%, 90%, and 100% of 75 soil specimens. Thus, 54 models (6 linear LSSVM +6 polynomial LSSVM, 6 LSTM, and 36 ANN) have been developed, analyzed, and compared to determine the robust soft computing model to predict the UCS of fine-grained soil. The root mean square error (RMSE), mean absolute error (MAE), and performance (R) metrics have measured the training and testing performances of each model. Based on the performance comparison of 6 linear LSSVM, 6 polynomial LSSVM, 6 LSTM, 6 Levenberg-Marquardt-based neural network (LMNN), 6 Broyden-Fletcher-Goldfarb-Shanno-based neural network (BFGsNN), 6 Scaled Conjugate Gradient-based neural network (SCGNN), 6 Gradient Descent with Momentum-based neural network (GDMNN), 6 Gradient Descent-based neural network (GDNN), and 6 Gradient Descent with Adaptive Learning Rate-based neural network (GDANN), nine better performing models have been identified. These nine models have been analyzed by performing reliability and generalizability analyses. Finally, laboratory-tested soil specimens have validated a robust soft computing model.

3 Data compilation and analysis

The present research has been carried out by collecting the unconfined compressive strength datasets of fine-grained soil collected from the published articles of Gunaydin et al. (2010) to train and test the AI models. The soil specimens were collected from Mersin (İçel), Turkey. The investigators found that the soil specimens are a mixture of clay and silt particles, i.e., bentonite and quartz. Gunaydin et al. (2010) determined the liquid limit, plastic limit, shrinkage limit, plasticity index, specific gravity, permeability, silt content, and clay content of soil specimens as 65.63%, 25.27%, 17.33%, 40.36%, 2.76, 2.45 × 10⁻⁸, 55%, and 45%, respectively. The soil was classified as high plasticity clayey silt (CH) based on the consistency parameters. The database consists of fine content (FC in %), dry unit weight (DUW in g/cm³), porosity (P in %), void ratio (VR), degree of saturation (DS in %), specific gravity (SG), and unconfined compressive strength of (UCS in N/cm²) of 85 fine-grained soil specimens. The complete database has been preprocessed by removing outliers and missing values. The z-score method has been utilized to remove the outliers. In addition, the min-max function has normalized the complete database. Figure 1 illustrates the frequency distribution of geotechnical parameters of 85 fine-grained soil specimens.

Figure 1

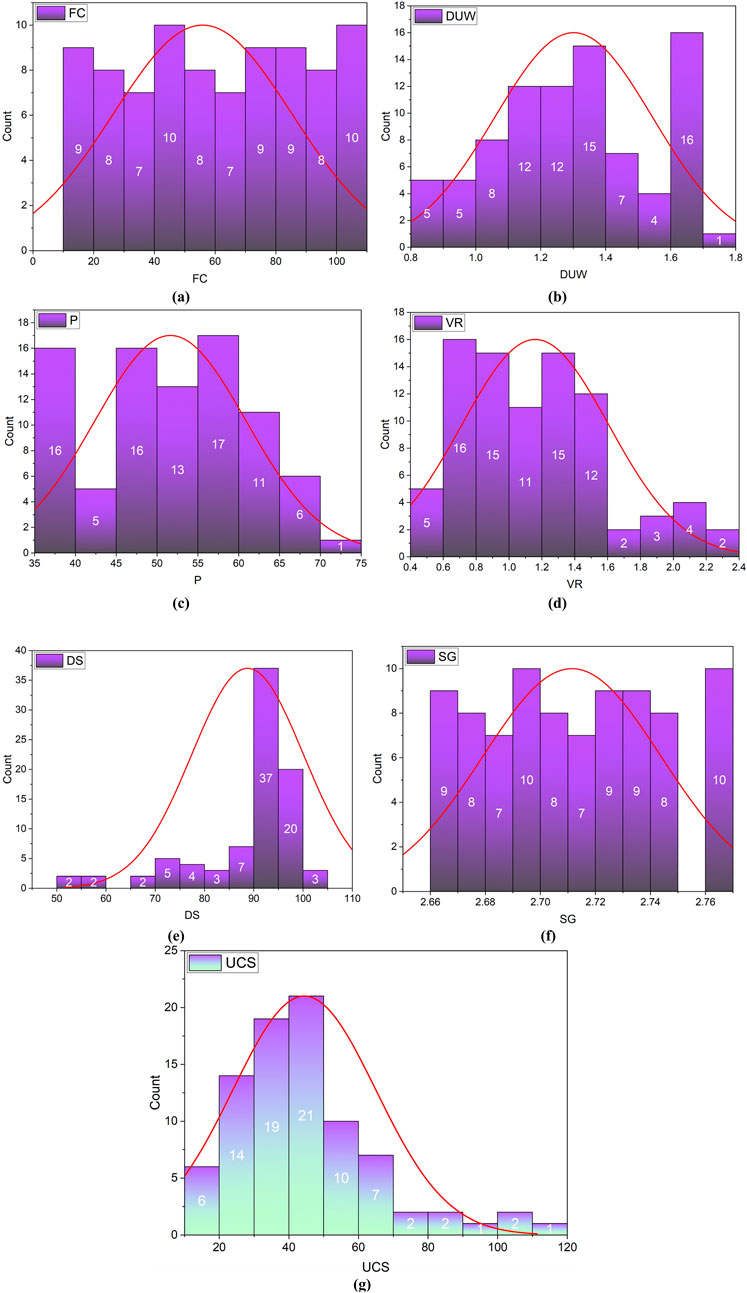
Figure 1. Illustration of the frequency distribution of (a) fine content, (b) dry unit weight, (c) porosity, (d) void ratio, (e) degree of saturation, (f) specific gravity, and (g) unconfined compressive strength.

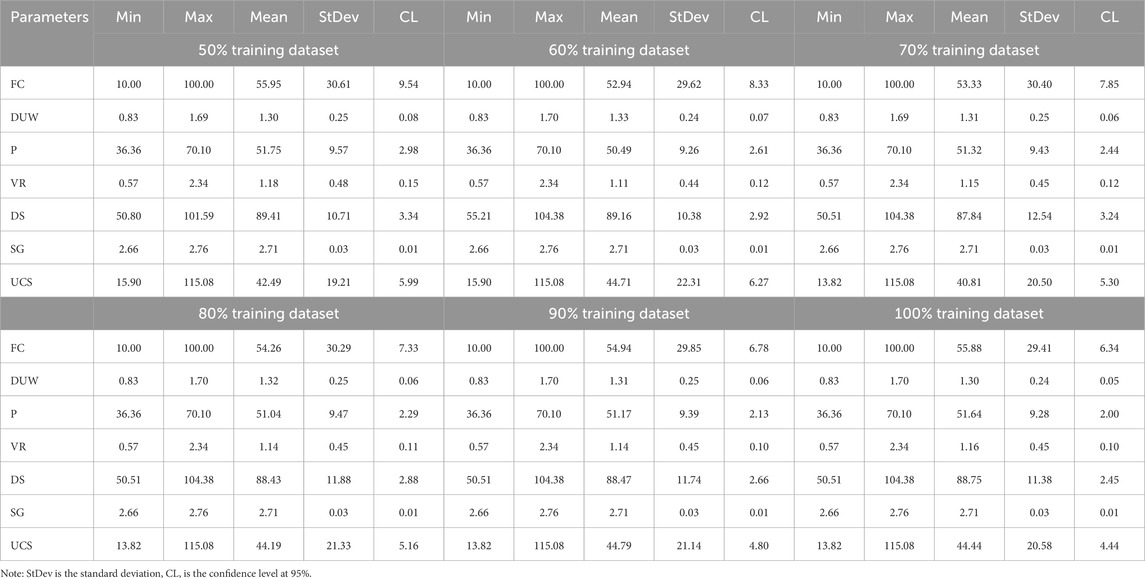
To develop, employ, and analyze the soft computing models, 75 and 10 data points have been randomly selected from 85 data points to create the training and testing datasets. Furthermore, to analyze the effect of quality and quantity of training database on the performance, accuracy, and overfitting of the soft computing model, the 50%, 60%, 70%, 80%, 90%, and 100% data points have been selected from 75 data points. Thus, six training databases have been created and statistically analyzed, as shown in Table 2.

Table 2

Table 2. Descriptive statistics of training UCS datasets.

Furthermore, the relationship between UCS and input parameters (FC, DUW, P, VR, DS, SG) was determined using Pearson’s product-moment correlation coefficient method. The range of correlation coefficients ±0.81 to ±1.00, ±0.61 to ±0.80, ±0.41 to ±0.60, ±0.21 to ±0.40, and ±0.00 to ±0.20 show a very strong, strong, moderate, weak and no relationship between pair of datasets, respectively (Hair et al., 2010). The relationship between parameters given in UCS datasets has been drawn, as shown in Figures 2a–f for each different percentage of training datasets.

Figure 2

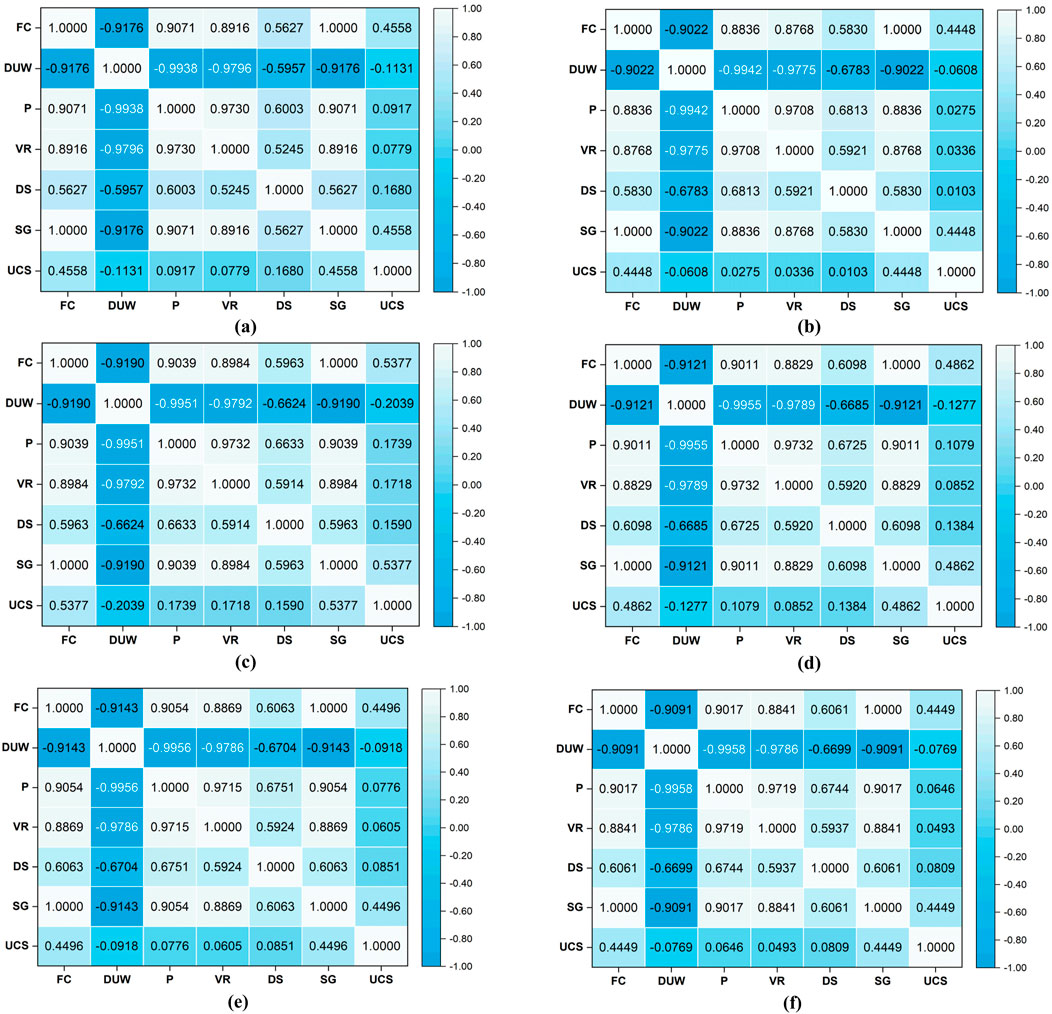
Figure 2. Illustration of the relationship between variables for (a) 50%, (b) 60%, (c) 70%, (d) 80%, (e) 90%, and (f) 100% training databases.

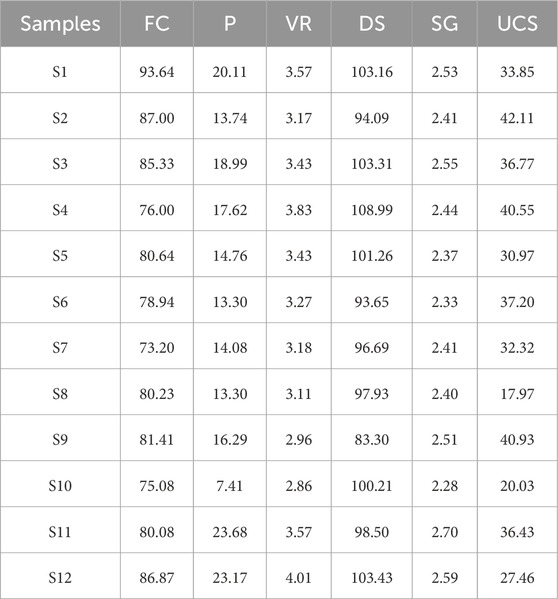
Figures 2a–f illustrates that the fine content has a very strong relationship with porosity, void ratio, and the specific gravity of fine-grained soils. Also, the porosity and void ratio have a very strong relationship with the specific gravity of soil. Figure 2 also depicts that dry unit weight strongly correlates with void ratio and specific gravity in every training dataset. In addition, the porosity and dry unit weight strongly relate to the degree of saturation. Furthermore, the fine content has a moderate relationship with the degree of saturation and UCS of fine-grained soil. Figure 2 shows that the dry unit weight, porosity, and void ratio have no relationship with the UCS of fine-grained soil. Multicollinearity was also determined for the UCS training dataset. The UCS training datasets contain the multicollinearity between specific gravity and porosity and void ratio. Also, the UCS has multicollinearity with porosity and void ratio in 70%, 80%, and 90% of 75 training datasets. The relationship between UCS and fine content and specific gravity shows moderate multicollinearity. On the other hand, the porosity and the void ratio have weak multicollinearity with the UCS of fine-grained soil. In addition, twelve fine-grained soil samples have been collected from and around Kota, Rajasthan, to validate the best architectural model of the unconfined compressive strength of the soil. The laboratory results of twelve fine-grained soil specimens are given in Table 3. The results of twelve soil specimens have been utilized to validate the prediction capabilities and accuracy of the robust soft computing model.

Table 3

Table 3. Laboratory test results of twelve fine-grained soil.

4 Applied soft computing approaches

The present research has adopted the least-square support vector machine, long short-term memory-recurrent neural network, and artificial neural network AI approaches to predict the strength parameters of fine-grained soil. The least-square support vector machine is a hybrid learning approach and the rest of the deep learning approaches.

4.1 Least-square support vector machine

The support vector machine is a supervised machine learning model associated with learning algorithms that analyze data for regression analysis and classification (Vapnik, 1999). LSSVM is a standard regression approach of the least-squares support vector machine. Several authors have used LSSVM to solve the complex problems of geotechnical engineering. Cai et al. (2021) have successfully applied the LSSVM approach optimized by GWO, DE, and GA optimization techniques to predict the liquefaction potential. Also, Hoang and Bui (2018) have predicted the earthquake-induced liquefaction potential of soil using the LSSVM approach optimized by KFDA. On the other hand, Tien Bui et al. (2019) have also predicted shear strength parameters for road construction using the LSSVM (optimized by CSO) approach. Alkroosh et al. (2015) have reported in the published research that the LSSVM approach predicts the bearing capacity of bored piles using pile geometry and cone penetration test results. Therefore, the LSSVM approach has been applied to predict the UCS of fine-grained soil in the present study. The LSSVM approach/code has been adopted by Wolter (2016). Furthermore, the linear and polynomial kernels have developed the LSSVM models in MATLAB R2020a. The published research by Khatti and Grover (2024), Khatti and Grover (2023) demonstrated that the LSSVM model achieved a performance of over 0.95 in predicting the compaction parameters and California bearing ratio of fine-grained soil. Therefore, the LSSVM models have been configured with gamma and sigma of 3 and 10, respectively, in this investigation. The hyperparameters mentioned in Table 4 have developed six LSSVM models for each linear and polynomial LSSVM approach. The model designation of the linear and polynomial LSSVM approach is mentioned in Table 4.

Table 4

Table 4. Model designation of LSSVM Models.

4.2 Long short-term memory neural network

The long-short-term memory recurrent neural network is a supervised learning approach. The LSTM solves the vanishing gradient problems, consisting of cells, elements, and label gates (Hochreiter and Schmidhuber, 1996; 1997). Based on the advantage of LSTM, many researchers have used the LSTM approach to predict the geotechnical parameters of soil. Filipović et al. (2022) have applied the LSTM approach to predict the moisture content of regional soil. In addition, Wang et al. (2021) have successfully employed the LSTM approach in predicting slurry pressure. Tang et al. (2021) have introduced the application of LSTM to predict slope displacement. Also, Jain (2020) has employed LSTM to predict the flow problems in unsaturated soil. Moreover, Yang et al. (2019) have developed LSTM models to predict landslide displacement using rainfall, reservoir level, and displacement datasets. The published work demonstrates the capabilities of the LSTM approach in solving geotechnical problems. Therefore, it has been decided to adopt the LSTM approach/code from Toan (2018) and develop models to predict the unconfined compressive strength of fine-grained soil. The LSTM models optimized by the Adam optimizer have been constructed in MATLAB R2020a in the present study. The mathematical formulation Equation 3 of the Adam optimizer is –

${\mathit{m}}_{\mathit{t}}={\mathit{\beta }}_{\mathbf{1}}{\mathit{m}}_{\mathit{t}-\mathbf{1}}+\left(\mathbf{1}-{\mathit{\beta }}_{\mathbf{1}}\right)\left[\frac{\mathit{\delta }\mathit{L}}{\mathit{\delta }{\mathit{w}}_{\mathit{t}}}\right]{\mathit{v}}_{\mathit{t}}={\mathit{\beta }}_{\mathbf{2}}{\mathit{v}}_{\mathit{t}-\mathbf{1}}+\left(\mathbf{1}-{\mathit{\beta }}_{\mathbf{2}}\right){\left[\frac{\mathit{\delta }\mathit{L}}{{\mathit{\delta }\mathit{w}}_{\mathit{t}}}\right]}^{\mathbf{2}}(3)$

where

$v_t={\beta v}_{t-1}+\left(1-\beta \right)*{\left[\frac{\delta L}{{\delta w}_t}\right]}^2$

$m_t$ the aggregate of the gradient at time t (initial equal to 0),

$m_{t-1}$ the aggregate of the gradient at time t-1 (previous),

$\beta$ moving average parameter,

$\delta w_t$ derivative of weights at time t,

$\delta L$ derivative of the loss function

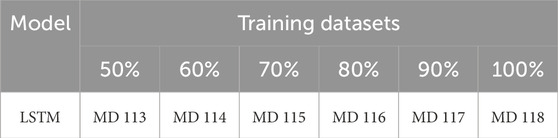
Each LSTM model has been configured with the sequenceinputlayer, lstmlayer, Adam optimizer, 500 epochs, 64 min batch size, 0.01 gradient threshold, 0.0001 initial learning rate, piecewise learning rate schedule, 125 learning rate drop period, 0.2 learning rate drop factor, and zero verbose. Table 5 presents the designation of LSTM models employed using 50%, 60%, 70%, 80%, 90%, and 100% of 75 training datasets.

Table 5

Table 5. Model designation of LSTM Models.

4.3 Artificial neural networks

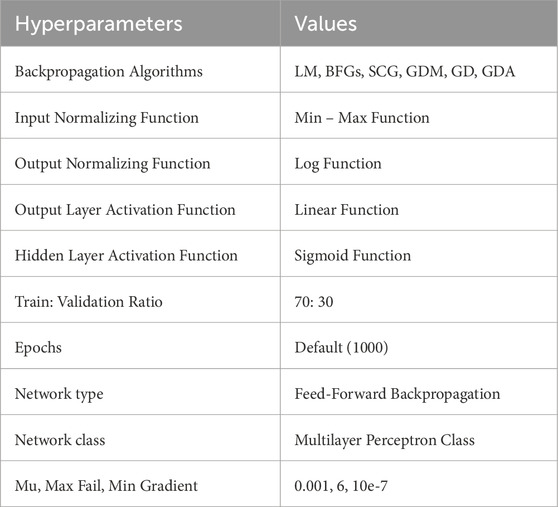
The artificial neural network is the most popular approach among geotechnical researchers. The artificial neural network is the machine learning approach based on supervised, unsupervised, and reinforced learning. The artificial neural network is a network of input, hidden, and output layers interconnected by neurons. Many researchers have applied the ANN to predict soil’s physical and mechanical properties (Taffese and Abegaz, 2021; Puri et al., 2018; Taleb Bahmed et al., 2019; Ranasinghe et al., 2017). The present research uses multilayer perceptron artificial neural networks to predict the UCS of fine-grained soil. The hyperparameters of the developed artificial neural network models are given in Table 6.

Table 6

Table 6. Hyperparameters of ANN models.

Each backpropagation algorithm, Levenberg-Marquardt (LM), Broyden-Fletcher-Goldfarb-Shanno (BFGs), Scaled Conjugate Gradient (SCG), Gradient Descent with Momentum (GDM), Gradient Descent (GD), and Gradient Descent with Adaptive Learning Rate (GDA), has developed six ANN models using 50%, 605, 70%, 80%, 90%, and 100% of 75 training datasets. The designation of the developed artificial neural network models is mentioned in Table 7.

Table 7

Table 7. Model designation of LSTM Models.

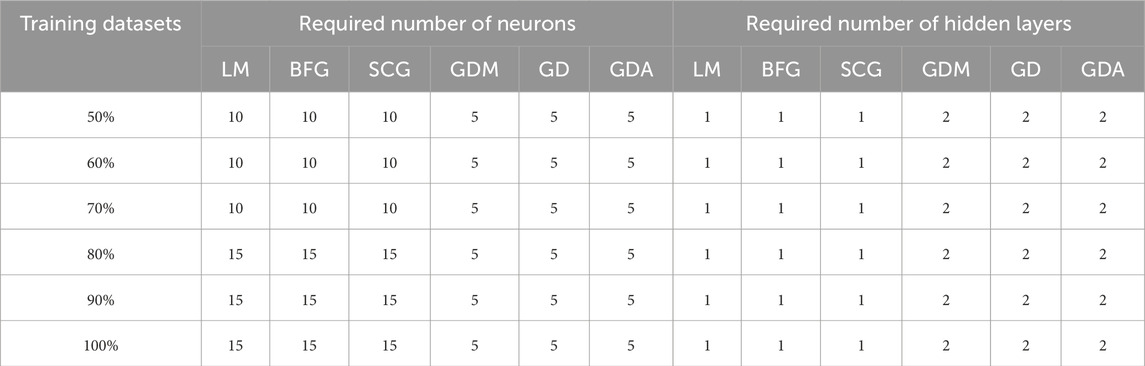
Albaradeyia et al. (2011), Erzin et al. (2010), Chen et al. (2009), Chang (2007), and Binaghi et al. (2004) derived the different formulas to determine the number of hidden layers using the number of databases. Khatti and Grover (2022) derived the formulas for determining the hidden layers and neurons for LM, BFG, SCG, GDA, GD, and GDM-configured ANN models for the first time. However, the present investigation demonstrates the effect of the quality and quantity of training databases on the performance of soft computing models. Therefore, the formulas derived by Khatti and Grover (2022) have determined the number of hidden layers and neurons for each ANN model. The formulas for calculating the number of neurons and hidden layers are as follows:

For LM, BFG, and SCG algorithms

${\mathit{N}}^{\prime }=\mathbf{5}+\sqrt{\mathit{I}+\mathit{O}}(4)$

$\mathit{H}\mathit{L}=\frac{{}^{\mathbf{3}}\sqrt{{\mathit{I}-\mathit{N}}^{\prime }+\mathbf{1}}}{\mathbf{4}}(5)$

For GDM, GD, and GDA algorithms

${\mathit{N}}^{\prime }=\sqrt{\mathit{I}+\mathit{O}}-\mathbf{5}(6)$

$\mathit{H}\mathit{L}=\frac{{}^{\mathbf{3}}\sqrt{{\mathit{I}-\mathit{N}}^{\prime }+\mathbf{1}}}{\mathbf{2}}(7)$

where N′ is the number of neurons; HL is hidden layers; I is the number of input dataset(s); O is the output(s). The present research has divided 75 training datasets into 50%, 60%, 70%, 80%, 90%, and 100%. Thus, the number of input datasets (I) is 38, 45, 53, 60, 68, and 75, and the output is O = 1 (UCS) for Equations 4–7. The required number of neurons and hidden layer is given in Table 8.

Table 8

Table 8. Required number of neurons and hidden layers.

Table 8 illustrates that the ANN model developed with the LM backpropagation algorithm requires one hidden layer interconnected with 15 neurons for 50% of 75 training datasets. Similarly, the GDA-NN model requires two hidden layers interconnected with five neurons to predict the UCS of fine-grained soil with better performance.

5 Results and discussion

In this investigation, the statistical quality parameters such as Root mean square error (RMSE), mean absolute error (MAE), and correlation coefficient (R) have computed the performance of developed fifty-four AI models in predicting UCS of fine-grained soils. The mathematical expression Equations 8–10 of RMSE, MAE, and R is –

$\mathit{R}\mathit{M}\mathit{S}\mathit{E}=\sqrt{\frac{\mathbf{1}}{\mathit{N}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}{\left({\mathit{T}}_{\mathit{i}}-{\mathit{P}}_{\mathit{i}}\right)}^{\mathbf{2}}}(8)$

$\mathit{M}\mathit{A}\mathit{E}=\frac{\mathbf{1}}{\mathit{N}}\left({\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}\mathit{a}\mathit{b}\mathit{s}\left({\mathit{T}}_{\mathit{i}}-{\mathit{P}}_{\mathit{i}}\right)\right)(9)$

$\mathit{R}=\frac{{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{N}}}\left({\mathit{T}}_{\mathit{i}}-\overline{\mathit{T}}\right)\left({\mathit{P}}_{\mathit{i}}-\overline{\mathit{P}}\right)}{\sqrt{{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{N}}}{\left({\mathit{T}}_{\mathit{i}}-\overline{\mathit{T}}\right)}^{\mathbf{2}}{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{N}}}{\left({\mathit{P}}_{\mathit{i}}-\overline{\mathit{P}}\right)}^{\mathbf{2}}}}(10)$

where N is the number of data points, T is the actual UCS, P is the predicted UCS, $\overline{T}$ is the mean of actual UCS, and $\overline{P}$ is the mean of predicted UCS. A soft computing model is the best architectural model if the RMSE = 0, MAE = 0, and R = 1.

5.1 LSSVM models

Figure 3 demonstrates the training (mentioned by TR) and testing (mentioned by T) performance comparison of LSSVM models. Figures 3a,b illustrate that model MD 102 (Linear LSSVM) has predicted UCS with the RMSE of 7.4724 N/cm², MAE of 6.4261 N/cm², and R of 0.9584. Thus, Figures 3c,d demonstrate that model MD 108 (Polynomial LSSVM) has predicted UCS with the RMSE of 5.5464 N/cm², MAE of 5.0261 N/cm², and R of 0.9766. The performance comparison of models MD 102 and MD 108 shows that the nonlinear LSSVM model (MD 108) predicts UCS of fine-grained soil with better performance (Senoon and Hussein, 2019; Arumugam et al. (2013). The polynomial LSSVM model outperformed the linear LSSVM model in this work because it has the capability to capture complex, nonlinear relationships between input variables and the target output. While the linear LSSVM is limited to fitting straight-line relationships, the polynomial LSSVM uses a kernel function to project the data into a higher-dimensional feature space, enabling it to model curved patterns and interactions among variables (Suykens and Vandewalle, 1999). This flexibility allows the polynomial model to fit better data where the underlying structure is not strictly linear, improving predictive accuracy (Schölkopf and Smola, 2002). As a result, it has been observed that the polynomial LSSVM typically yielded lower error and better generalization compared to its linear counterpart.

Figure 3

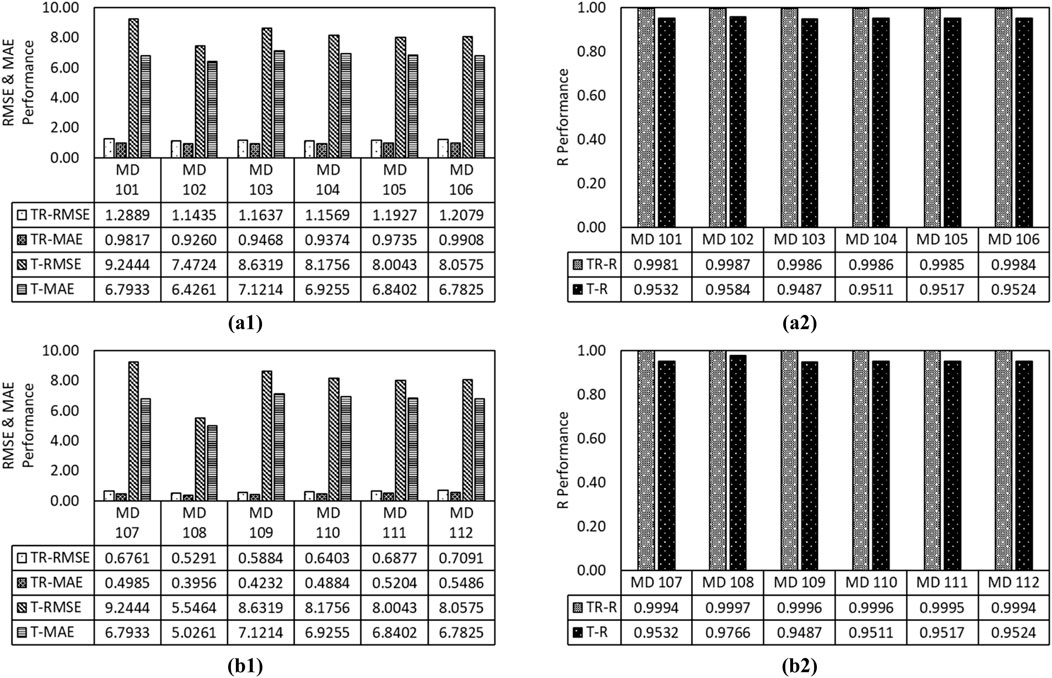
Figure 3. Illustration of performance comparison of (a) linear and (b) polynomial kernel-based LSSVM model in terms of (1) RMSE and MAE and (2) R.

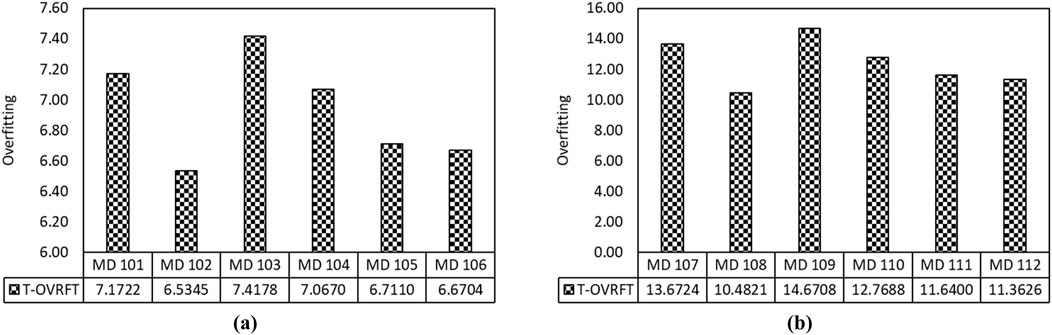
In addition, the overfitting of linear and polynomial LSSVM models has been calculated, as shown in Figure 4. Figures 4a,b show that models MD 102 and 108 have predicted UCS with overfitting of 6.5345 and 10.4821, respectively. However, models MD 102 and MD 108 are trained by 60% of 75 training datasets. The correlation coefficient study of 60% of 75 training datasets indicates that FC, DUW, P, and VR very strongly correlate with each other and specific gravity. On the other hand, DUW, P, and VR have no relationship with the unconfined compressive strength of fine-grained soils. Still, fine content has a moderate correlation with the UCS of fine-grained soil. Also, 60% of the 75-training dataset shows multicollinearity between specific gravity and porosity and void ratio.

Figure 4

Figure 4. Illustration of overfitting of (a) linear and (b) polynomial-based LSSVM models.

5.2 LSTM-RNN models

The LSTM-RNN models have predicted UCS of fine-grained soil, and Figures 5a,b show the performance comparison of LSTM-RNN models. Figures 5a,b demonstrate the performance comparison of LSTM-RNN models in predicting UCS of fine-grained soil. Figures 5a,b show that model MD 113 has predicted UCS with the RMSE of 4.7539 N/cm², MAE of 4.2461 N/cm², and R of 0.9880. Model MD 113 has been trained by 50% of 75 data points. The correlation between features and labels demonstrated that the features have a relationship from weak to moderate levels with the label. Still, the LSTM-RNN model achieved higher performance because it captures and learns temporal dependencies and hidden patterns in the data. Unlike linear models that rely heavily on strong direct correlations between input features and target outputs, LSTM-RNNs leverage their memory cells and gating mechanisms to retain and process information over time, enabling them to model nonlinear and sequential relationships effectively (Al-Selwi et al., 2024; Safonova et al., 2023). This capability is particularly beneficial when the feature-target correlation is less strong, as the model can still uncover indirect or lagged associations. Also, because LSTMs are good at handling noise and can learn complex patterns in data, they often perform well even with small datasets and features that are not strongly correlated with the target. This makes them a strong choice for regression problems where the relationships in the data are not immediately obvious or straightforward.

Figure 5

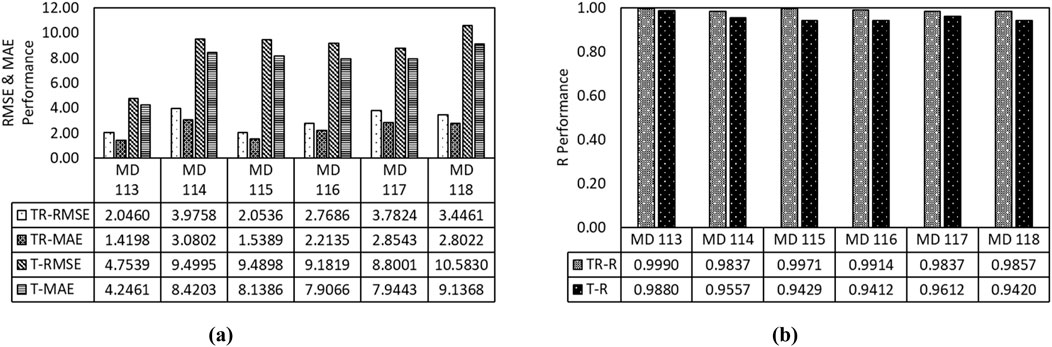
Figure 5. Illustration of performance comparison of LSTM-RNN models in terms of (a) RMSE and MAE and (b) R.

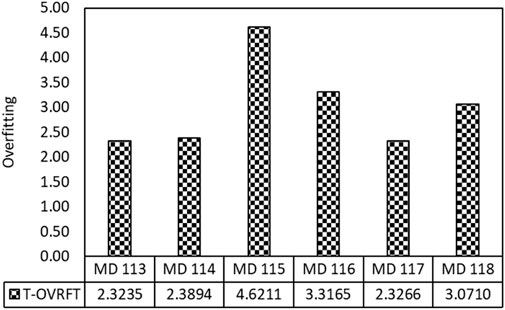
Furthermore, the overfitting of LSTM-RNN models in predicting the UCS of soil has been calculated, as shown in Figure 6. It depicts the comparison of overfitting of LSTM-RNN models in predicting UCS of fine-grained soil. Figure 6 illustrates that model MD 113 has predicted UCS with an overfitting of 2.3235, which is comparatively less than other LSTM-RNN models. However, model MD 113 has achieved a performance of 0.9880 after training by 50% of 75 training datasets. Model MD 113 has achieved high performance because the training dataset has a very strong relationship between input parameters. The fine content moderately correlates with the UCS of fine-grained soil. The input parameters FC, DUW, P, VR, DS, and SG have significantly less multicollinearity. Therefore, model MD 113 has outperformed other LSTM models with a performance (R) of 0.9880.

Figure 6

Figure 6. Illustration of overfitting of LSTM-RNN models.

5.3 ANN models

Thirty-six artificial neural network models have also been developed using different backpropagation algorithms, i.e., LM, BFG, SCG, GDM, GD, and GDA, to predict the UCS of fine-grained soil. Figures 7a to (1) shows the performance comparison of artificial neural networks in predicting UCS of soil. Figures 7a–f depicts that models MD 120 (LM_NN), MD 127 (BFG_NN), MD 136 (SCG_NN), MD 139 (GDM_NN), MD 148 (GD_NN), and MD 150 (GDA_NN) have predicted UCS of fine-grained soil with a correlation coefficient of 0.9836, 0.9321, 0.9684, 0.9746, 0.9722, and 0.9665, respectively. Models MD 120, MD 127, MD 136, MD 139, MD 148, and MD 150 have been trained by 60%, 70%, 100%, 70%, 100%, and 60% of 75 training datasets, respectively. The performance results of the artificial neural network show that the SCG and GD neural network models require a large training dataset (100% of 75) to predict UCS with a performance of more than 0.96. Still, the GDA_NN and LM_NN model predict UCS of fine-grained soil with a performance of more than 0.96 if the 60% training dataset has trained the GDA and LM neural network. On the other hand, BFG and GDM neural network models predict UCS with a performance of more than 0.93 if 70% of training datasets have trained BFG and GDM neural networks. The study demonstrates that the BFG_NN model (MD 127) has achieved the least testing performance, i.e., 0.9321, in predicting the UCS of soil. The present research demonstrates that the LM neural network model is better for predicting the UCS of fine-grained soil.

Figure 7

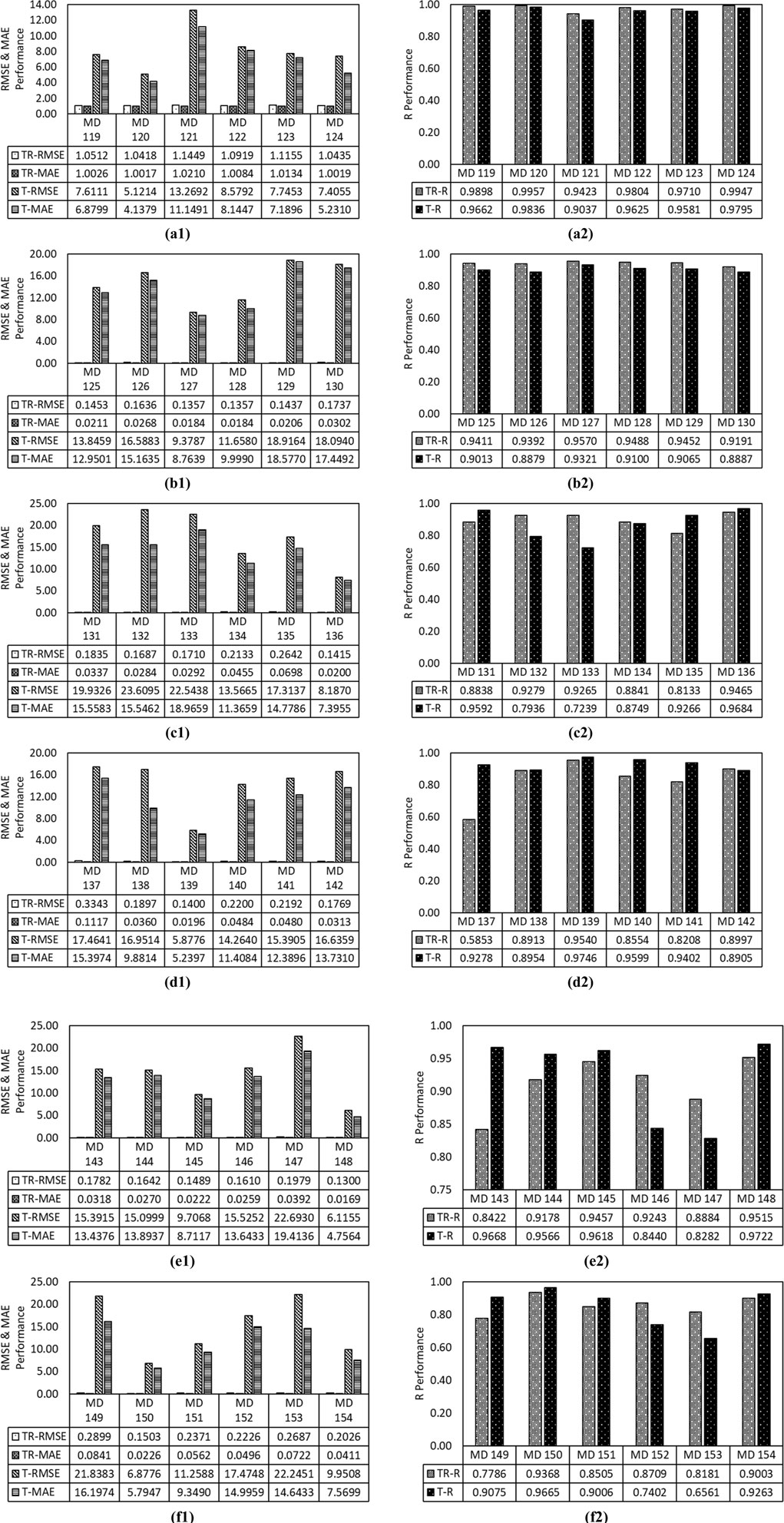
Figure 7. Illustration of performance comparison of (a) LM, (b) BFGs, (c) SCG, (d) GDM, (e) GD, and (f) GDA backpropagation-based ANN models in terms of (1) RMSE and MAE and (2) R.

The differences in performance among the neural network models mainly come down to the optimization algorithms they use during training. The Levenberg–Marquardt (LM) model (MD 120) achieved the best results (R = 0.9836) even though it was trained with just 60% of the data. This shows how effective LM is at quickly finding accurate solutions, thanks to its combination of Gauss-Newton and gradient descent methods (Ceryan et al., 2013). In contrast, the BFGS-based model (MD 127) had the lowest performance (R = 0.9321) despite having more training data (70%), likely because it's more sensitive to local minima and does not generalize as well with complex data like soil properties. The other models, like SCG_NN and GD_NN, needed all the training data (100%) to perform above R = 0.96, indicating that they rely heavily on larger datasets to learn effectively. However, models using adaptive methods, e.g., GDA_NN and GDM_NN, still performed well with 60%–70% of the data. Their strength lies in features like adaptive learning rates (GDA) and momentum (GDM), which help them learn faster and more efficiently (Tabarsa et al., 2021; Chopra et al., 2015). Overall, the LM algorithm is the most reliable and data-efficient choice for predicting fine-grained soils’ unconfined compressive strength (UCS). Therefore, the overfitting of neural network models has been calculated, as shown in Figure 8.

Figure 8

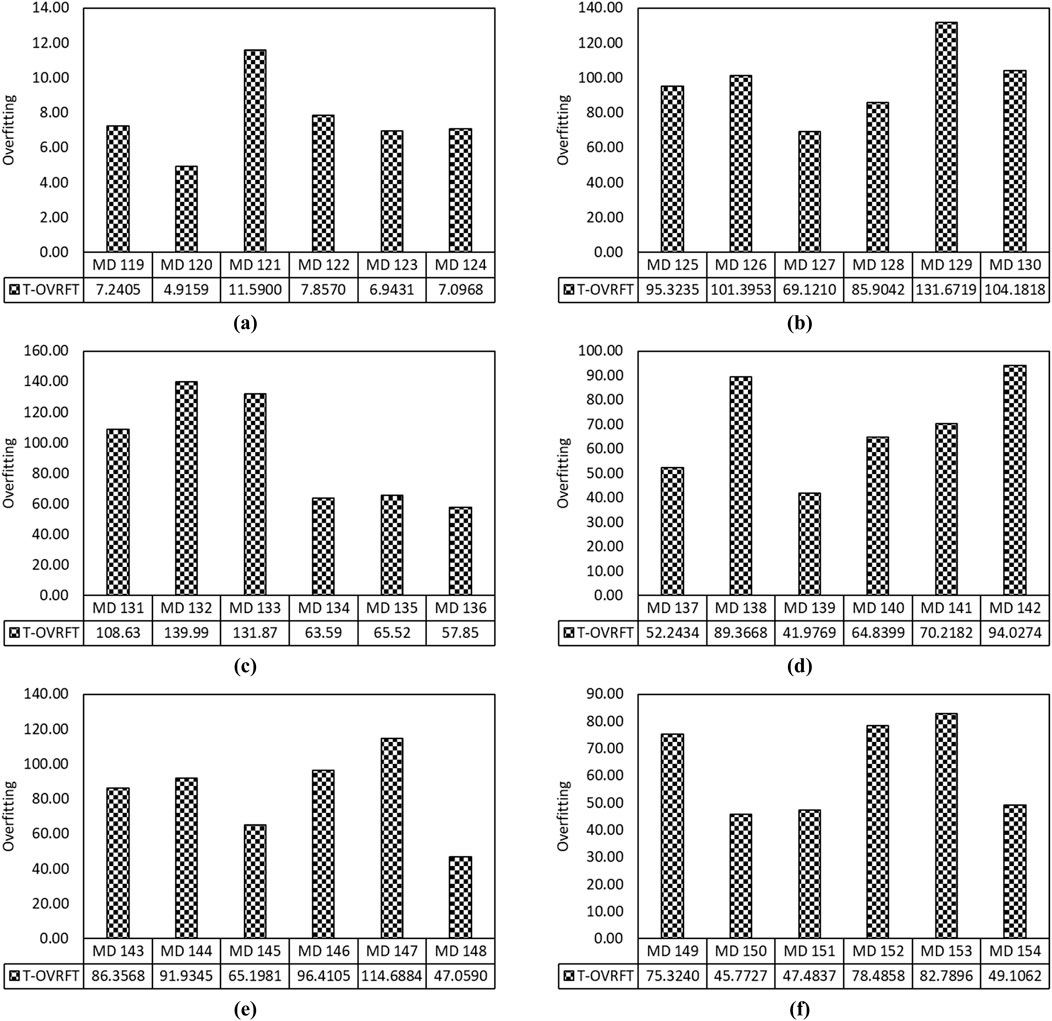
Figure 8. Illustration of overfitting comparison of (a) LM, (b) BFGs, (c) SCG, (d) GDM, (e) GD, and (f) GDA backpropagation-based ANN models.

Figure 8 shows an overfitting comparison of ANN models in predicting UCS of fine-grained soil. Models MD 120, MD 127, MD 136, MD 139, MD 148, and MD 150 have predicted UCS with overfitting of 4.9159, 69.121, 57.853, 41.977, 47.059, and 45.773, respectively. The performance comparison of ANN models has shown that the model MD 120 has predicted UCS with the R of 0.9836, which is comparatively better than other ANN models. However, model MD 120 has achieved maximum performance with an overfitting of 4.9159. The correlation coefficient study of the 60% training dataset shows specific gravity has multicollinearity with P and VR. In addition, the specific gravity has multicollinearity with fine content. Instead of multicollinearity, the LM_NN model has predicted UCS of fine-grained soil with R of 0.9836, RMSE of 5.1214 N/cm², and MAE of 4.1379 N/cm². Thus, the nine artificial intelligence best performance models, MD 102, MD 108, MD 113, MD 120, MD 127, MD 136, MD 139, MD 148, and MD 150, have been identified by comparing the RMSE, MAE, and R of AI models in predicting UCS of fine-grained soil. These nine of the best-performance AI models have been compared, as shown in Figure 9, in predicting UCS.

Figure 9

Figure 9. Performance comparison of the best performance AI models in predicting UCS.

Figure 9 illustrates that models MD 102, MD 108, MD 113, MD 120, MD 127, MD 136, MD 139, MD 148, and MD 150 have achieved a testing performance (R) of 0.9584, 0.9766, 0.9880, 0.9836, 0.9321, 0.9684, 0.9746, 0.9722, and 0.9665, respectively. The comparative study shows that model MD 113 has been identified as the robust soft computing model in predicting UCS of fine-grained soil.

5.4 Cross validation by computational cost

This investigation employs 54 soft computing models to determine the robust soft computing model to predict the UCS of fine-grained soil. The performance comparison demonstrated that the MD 113 model has been recognized as a robust soft computing model. Still, cross-validation of the prediction capabilities of these nine models is required before mentioning the MD 113 model as a robust soft computing model. However, all these models have been prepared with a k-fold value of 5. These nine models were re-configured for cross-validation with a 10k fold value, and the computational cost was measured and analyzed. These models have been developed using an HP pavilion G6 machine, configured with Intel Core i3-2350M (second gen), 2.3Ghz processor, 4GB RAM, 240SSD, Intel HD 3000GPU, AMD Radeon 7450M, and Windows 10 64bit. Figure 10 compares the computational cost of 5k and 10k fold configured nine models. Figure 10a presents that the MD 113 model has predicted UCS of fine-grained soil with the computational costs of 166.619s (configured with 5k-fold) and 214.404s (configured with 10k-fold), followed by the MD120 (137.814s for 5k, 198.120s for 10k), MD108 (123.094s for 5k, 179.192s for 10k), MD139 (100.649s for 5k, 138.277s for 10k), MD148 (73.533s for 5k, 120.291s for 10k), MD136 (59.151s for 5k, 106.588s for 10k), MD150 (46.493s for 5k, 99.767s for 10k), MD102 (39.217s for 5k, 93.091s for 10k), and MD127 models, in training phase. Conversely, Figure 10b demonstrates that the MD113 model has achieved the highest computational cost, i.e., 0.895 for 5k and 1.305 for 10k, in the testing phase. Model MD127 has predicted the UCS of fine-grained soil with the least computational cost, i.e., 0.180 for 5k and 0.205 for 10k and higher residuals. Hence, the MD113 model has been recognized as a robust soft computing model in predicting fine-grained soil.

Figure 10

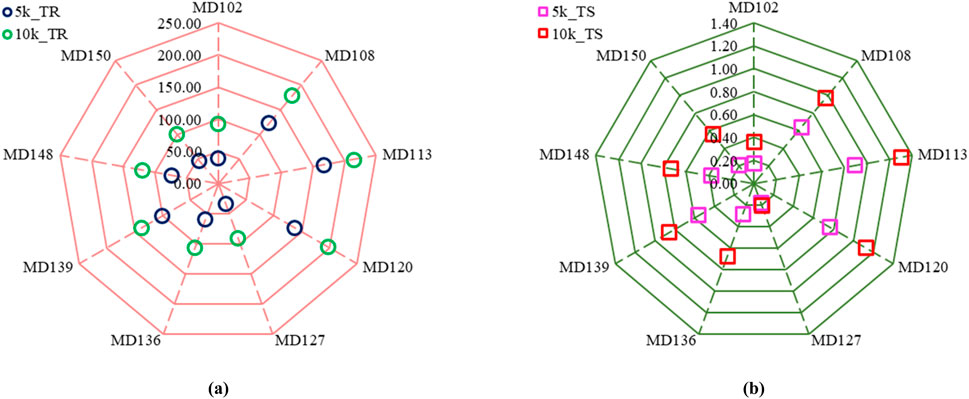
Figure 10. Illustration of comparison of the computational cost of nine models in (a) training and (b) testing phase.

5.5 Reliability analysis

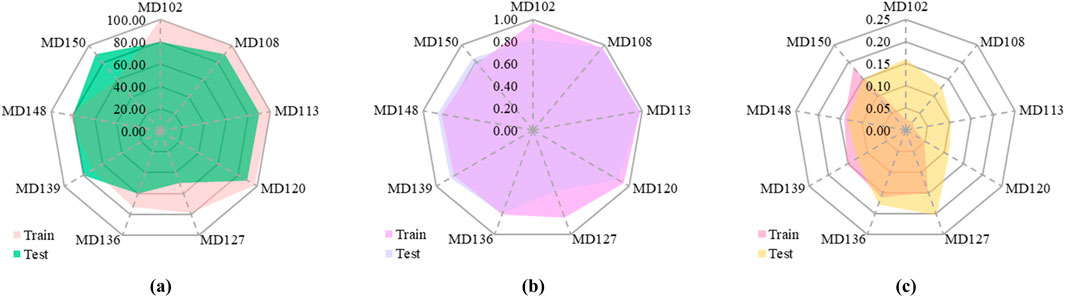
This study identifies the MD 102, MD 108, MD 113, MD 120, MD 127, MD 136, MD 139, MD 148, and MD 150 models as better-performing models to introduce a robust soft computing model to predict the UCS of fine-grained soil. The performance metrices have demonstrated that the MD113 has been recognized as a robust soft computing model. Still, it is required to determine and analyze the reliability of these models by implementing Equations 11–13 the index metrics, i.e., a20, scatter (IOS), and agreement (IOA), as mentioned below:

$\mathit{a}\mathbf{20}\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{x}=\frac{\mathit{m}\mathbf{20}}{\mathit{H}}(11)$

$\mathit{I}\mathit{O}\mathit{A}=\mathbf{1}-\frac{{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}\left({\mathit{P}}_{\mathit{i}}-{\mathit{T}}_{\mathit{i}}\right)}{\mathbf{2}{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}\left({\mathit{T}}_{\mathit{i}}-\overline{T}\right)}(12)$

$\mathit{I}\mathit{O}\mathit{S}=\frac{\mathit{R}\mathit{M}\mathit{S}\mathit{E}}{\mathit{A}\mathit{v}\mathit{g}.\mathit{o}\mathit{f}\mathit{A}\mathit{c}\mathit{t}\mathit{u}\mathit{a}\mathit{l}\mathit{V}\mathit{a}\mathit{l}\mathit{u}\mathit{e}\mathit{s}}(13)$

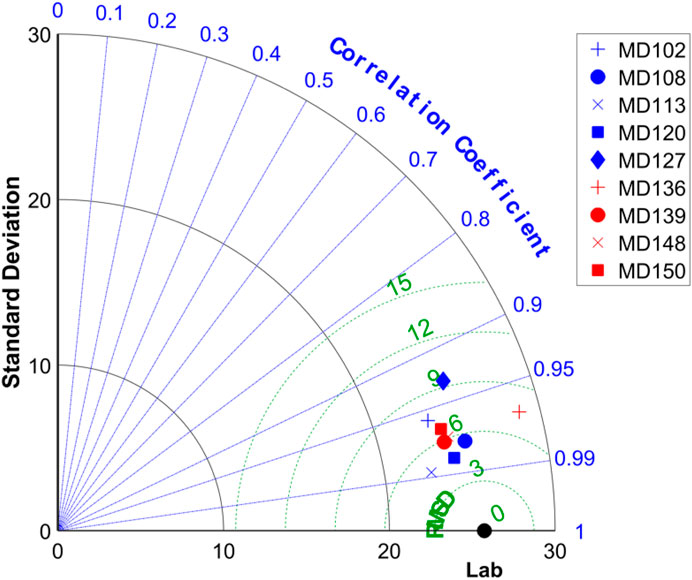
where m20 us the ratio of actual and predicted values varies between 0.8 and 1.2, and H is the total number of data samples. Figure 11 compares the a20 (Fig. a), IOA (Fig. b), and IOS (Fig. c) results and presents the robustness of each model. Figure 11a demonstrates that the MD113 model has predicted the UCS of fine-grained soil with the a20 index of 100 and 90 in the training and testing phase, respectively. Still, it is observed that the MD108 model also obtained an a20 index of 100 and 90 in the training and testing phases. Therefore, it is required to compare the IOA and IOS to achieve a robust soft computing model. Figure 11b illustrated that the MD113 model grained the IOA of 0.9738 and 0.9844 in the training and testing phase, respectively, comparatively higher than the MD108 model (0.9678 and 0.9747 in training and testing, respectively). Also, it can be observed that the MD113 model has predicted UCS of fine-grained soil with the IOS of 0.0204 and 0.1031 in the training and testing phase, respectively, as presented in Figure 11c. Thus, the MD113 model has been recognized as a robust soft computing model to predict the UCS of fine-grained soil.

Figure 11

Figure 11. Illustration of comparison of reliability indices (a) a20, (b) IOA, and (c) IOS.

5.6 Generalizability analysis

A generalizability analysis is performed to validate the robust soft computing model externally. The generalizability test confirms the overfitting of the model in the training phase and makes it reliable. Golbraikh and Tropsha (2002) proposed the theory with mathematical expression to investigate the accurate model, as given in Table 9.

Table 9

Table 9. Mathematical expression and condition of validation factors.

Where $d_i$ denotes the experimental UCS and $y_i$ denotes the predicted UCS, $k,$ and $k^{\prime }$ represent the slopes of the predicted versus actual UCS and actual versus predicted UCS concerning the origin. $R_o^2$ and ${R^{\prime }}_o^2$ denotes the coefficients of determination of the predicted versus actual UCS and actual versus predicted UCS. $m$ and $n$ represent the factors for estimating the predictive power of the proposed models. Table 10 consists of a generalizability test and reveals that the MD113 model presents superiority over the MD 102, MD 108, MD 120, MD 127, MD 136, MD 139, MD 148, and MD 150 models in predicting UCS of fine-grained soil.

Table 10

Table 10. Results of the generalizability test in the prediction of UCS.

5.7 Laboratory validation

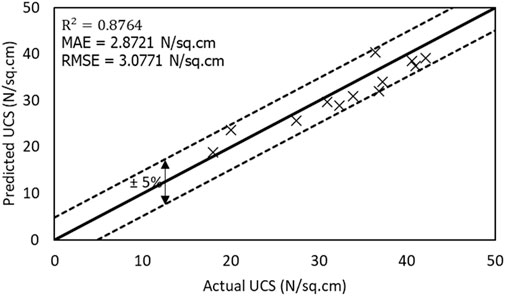
For the validation of the MD113 model, the UCS of twelve soil specimens has been predicted, as shown in Figure 12. Figure 12 illustrates that the no predicted UCS using MD 113 falls outside the ±5% confidence interval. In addition, model MD 113 has predicted UCS of twelve fine-grained soils with a COD of 0.8764 (R = 0.9362), RMSE of 3.0771 N/cm², and MAE of 2.8721 N/cm². Finally, model MD 113 has been recognized as the best architecture model for predicting the unconfined compressive strength of virgin fine-grained soil.

Figure 12

Figure 12. Actual vs. predicted UCS plot by MD 113 using laboratory data.

6 Model implication

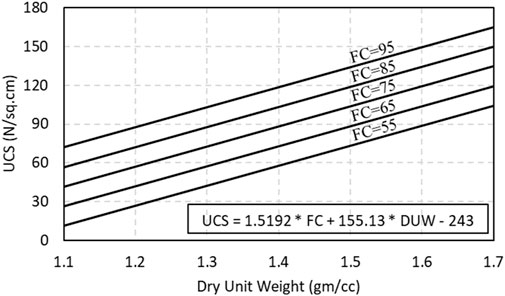
Cohesive soils’ fine content and dry unit weight influence the unconfined compressive strength. However, model MD 113 has been trained by 50% of 75 training datasets and identified as the best architecture model. Therefore, a multiple regression equation, Equation 14, has been derived using 50% of 75 training datasets.

$\mathit{U}\mathit{C}\mathit{S}\left(\mathit{N}/{\mathit{c}\mathit{m}}^{\mathbf{2}}\right)=\mathbf{1.5192}*\mathit{F}\mathit{C}+\mathbf{155.13}\mathit{D}\mathit{U}\mathit{W}-\mathbf{243}(14)$

Utilizing Equation 14, a nomogram has been drawn for fine content of 55%, 65%, 75%, 85%, and 95% to estimate the UCS of fine-grained soil. A nomograph, or nomogram, is a visual tool that helps to quickly assess the UCS to an equation by showing the relationship between three or more variables. It does not require a large computational process. It is just a straight edge to line up the values, as shown in Figure 13. Finally, the unconfined compressive strength of fine-grained soil can be estimated using these predicting curves shown in Figure 13.

Figure 13

Figure 13. Illustration of nomograph for estimating UCS of fine-grained soil.

7 Sensitivity analysis

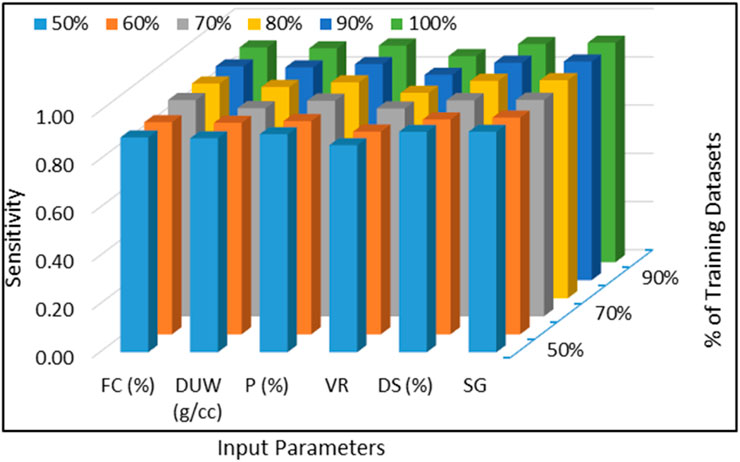
In the present study, the nonlinear AI models have performed better than linear AI models in predicting UCS of virgin fine-grained soil. Therefore, nonlinear sensitivity analysis has been performed using the cosine amplitude method. The sensitivity analysis is performed by Equation 15 (Ardakani and Kordnaeij, 2019)

$\mathit{S}\mathit{S}=\frac{{\sum }_{\mathit{c}=\mathbf{1}}^{\mathit{n}}\left({\mathit{X}}_{\mathit{i}\mathit{c}}*{\mathit{X}}_{\mathit{j}\mathit{k}}\right)}{\sqrt{{\sum }_{\mathit{c}=\mathbf{1}}^{\mathit{n}}{\mathit{X}}_{\mathit{i}\mathit{c}}^{\mathbf{2}}}{\sum }_{\mathit{c}=\mathbf{1}}^{\mathit{n}}{\mathit{X}}_{\mathit{j}\mathit{k}}^{\mathbf{2}}}(15)$

where $X_{ic}$ is input parameters FC, DUW, P, VR, DS and SG, and $X_{jk}$ is UCS of fine-grained soil. The input parameter highly influences the output parameter if the SS value is one or closer to 1. The present study used 50%, 60%, 70%, 80%, 90%, and 100% of 75 training datasets to train the AI models. Therefore, the sensitivity analysis was performed for 50%-100% of UCS training datasets, as shown in Figure 14.

Figure 14

Figure 14. Illustration of sensitivity of features in predicting UCS.

The present study, model MD 113, was identified as the best-performing AI architecture for predicting fine-grained soil’s unconfined compressive strength (UCS), trained with only 50% of the dataset. The sensitivity analysis results, as shown in Figure 12, reveal that the most influential input parameters on UCS prediction are fine content (FC), dry unit weight (DUW), plasticity (P), void ratio (VR), degree of saturation (DS), and specific gravity (SG), with sensitivity values of 0.8797, 0.8773, 0.8843, 0.8409, 0.8912, and 0.8989, respectively. These parameters are statistically significant and hold strong physical relevance in geotechnical engineering. For instance, FC and P directly influence the soil’s consistency and shear strength. At the same time, DUW, DS, and VR are key indicators of compaction and pore structure, which are directly linked to strength characteristics. SG reflects the mineralogical composition of the soil, further contributing to strength variation. Importantly, all these parameters are commonly measured or estimated in standard soil testing procedures in geotechnical practice. Therefore, their use in the proposed model enhances its feasibility and scalability for practical engineering applications, ensuring the model can be reliably implemented in real-world scenarios without needing advanced or inaccessible testing methods.

8 Summary and conclusion

Determining the unconfined compressive strength of soil is essential for any Civil Engineering Project. The laboratory procedures for determining the UCS of fine-grained soil are lengthy and costly in mega projects. Therefore, the present investigation employs LSSVM, LSTM, and ANN models to predict the UCS of fine-grained soil. The effect of the quality and quantity of the training database has been determined and analyzed to help geotechnical engineers and designers select the suitable database. Based on the overall analysis, the following conclusions are mapped.

• Prediction Capabilities–The performance comparison demonstrates that the linear LSSVM (MD 102), polynomial LSSVM (MD 108), LSTM-ANN (MD 113), LMNN (MD 120), BFGNN (MD 127), SCGNN (MD 136), GDANN (MD 139), GDNN (MD 148), and GDMNN (MD 150) models have gained the testing performance of 0.9584, 0.9766, 0.9880, 0.9836, 0.9321, 0.9684, 0.9746, 0.9722, and 0.9665, respectively.

• Effect of Quality and Quantity of Training Database–models MD 102, MD 108, MD 113, MD 120, MD 127, MD 136, MD 139, MD 148, and MD 150 models have been trained by 60%, 60%, 50%, 60%, 70%, 100%, 70%, 100% and 60% of 75 training datasets, respectively. The comparison of training datasets demonstrates that LSTM-RNN (MD 113) performs better using small (50% of 75) training datasets. The correlation coefficient for 50% of 75 training datasets shows that fine content and dry unit weight strongly correlate with void ratio and specific gravity (0.81 > R < 1.0). Also, fine content and dry unit weight moderately correlate with UCS. On the other hand, the degree of saturation is multicollinear, with porosity (0.9071) and void ratio (0.8916). The multicollinearity affects the performance and prediction of regression AI models. Instead of multicollinearity in training datasets, the model MD 113 has performed better than other adopted AI models with 50% of 75 training datasets.

• Robust Soft Computing Model–Based on the performance metrics, computational cost, reliability index, and generalizability analysis, the MD113 (LSTM) model has outperformed the LSSVM and ANN models in predicting the UCS of fine-grained soil in the present research. In the validation phase, the MD113 model predicted the UCS of twelve fine-grained soil specimens with an RMSE of 3.0771 N/cm², MAE of 2.8721 N/cm², and R of 0.9361. In addition, the performance comparison of Gunaydin O. et al. (2010) model and model MD 113 demonstrates that model MD 113 gives a slightly better testing performance (R = 0.9880) than the model (R = 0.9849) developed by Gunaydin O. et al. (2010).

To sum up, the present study introduces the long short-term memory (LSTM) model as a robust soft computing model, which predicts the UCS of fine-grained soil with ±5% confidence intervals. This investigation uses only the UCS results of 85 soil specimens, which is a limitation. This research may be extended by including more databases to determine the impact of large databases on the performance and overfitting of the soft computing model. This investigation may also be extended by optimizing the LSTM model to determine the impact of the optimization algorithm in predicting the UCS of fine-grained soil.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JK: Methodology, Writing – original draft, Software, Funding acquisition, Formal Analysis, Visualization, Supervision, Investigation, Resources, Validation, Conceptualization, Project administration, Data curation, Writing – review and editing. KG: Conceptualization, Investigation, Writing – review and editing, Methodology, Validation, Formal Analysis. PS: Software, Writing – review and editing, Investigation, Formal Analysis.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adroja, P. B., Solanki, R. V., and Shah, Y. U. (2017). Development of correlation between different engineering properties of subgrade soil. J. Emerg. Technol. Innovative Res. 4 (5), 177–180.

Google Scholar

Albaradeyia, I., Hani, A., and Shahrour, I. (2011). WEPP and ANN models for simulating soil loss and runoff in a semi-arid Mediterranean region. Environ. Monit. Assess. 180, 537–556. doi:10.1007/s10661-010-1804-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Al-Kahdaar, R. M., and Al-Ameri, A. F. I. (2010). Correlations between physical and mechanical properties of Al-Ammarah soil in Messan Governorate. J. Eng. 16 (4), 5946–5957. doi:10.31026/j.eng.2010.04.18

CrossRef Full Text | Google Scholar

Alkroosh, I. S., Bahadori, M., Nikraz, H., and Bahadori, A. (2015). Regressive approach for predicting bearing capacity of bored piles from cone penetration test data. J. Rock Mech. Geotechnical Eng. 7 (5), 584–592. doi:10.1016/j.jrmge.2015.06.011

CrossRef Full Text | Google Scholar

Al-Selwi, S. M., Hassan, M. F., Abdulkadir, S. J., Muneer, A., Sumiea, E. H., Alqushaibi, A., et al. (2024). RNN-LSTM: from applications to modeling techniques and beyond—systematic review. J. King Saud University-Computer Inf. Sci. 36, 102068. doi:10.1016/j.jksuci.2024.102068

CrossRef Full Text | Google Scholar

Ardakani, A., and Kordnaeij, A. (2019). Soil compaction parameters prediction using GMDH-type neural network and genetic algorithm. Eur. J. Environ. Civ. Eng. 23 (4), 449–462. doi:10.1080/19648189.2017.1304269

CrossRef Full Text | Google Scholar

Arumugam, R., Rashid, A., Yaacob, H., and Noor, N. (2013). Correlation between liquidity index (LI) and unconfined compressive strength of stabilized silty clay as subgrade. Aust. J. Basic Appl. Sci. 7 (10), 450–454.

Google Scholar

Bazazorde, S. (2018). UCS and CBR behaviour of Perth sandy soil reinforced with waste tyre fibres and cement.

Google Scholar

Binaghi, E., Boschetti, M., Brivio, P. A., Gallo, I., Pergalani, F., and Rampini, A. (2004). Prediction of displacements in unstable areas using a neural model. Nat. hazards 32, 135–154. doi:10.1023/B:NHAZ.0000026796.59079.1a

CrossRef Full Text | Google Scholar

BIS (1991). 2720 methods of test for soils: Part 10-determination of unconfined compressive strength. New Delhi, India: Bureau of Indian Standards, 1–4.

Google Scholar

Cai, M., Hocine, O., Mohammed, A. S., Chen, X., Amar, M. N., and Hasanipanah, M. (2021). Integrating the LSSVM and RBFNN models with three optimization algorithms to predict the soil liquefaction potential. Eng. Comput. 38, 3611–3623. doi:10.1007/s00366-021-01392-w

CrossRef Full Text | Google Scholar

Ceryan, N., Okkan, U., and Kesimal, A. (2013). Prediction of unconfined compressive strength of carbonate rocks using artificial neural networks. Environ. earth Sci. 68, 807–819. doi:10.1007/s12665-012-1783-z

CrossRef Full Text | Google Scholar

Chan, C. M., Kikuchi, Y., and Mizutani, T. A. (2012). Correlation between unconfined compressive strength and mixing quality of solidified clay. Int. J. Civ. Struct. Eng. 3 (2), 408.

Google Scholar

Chang, T. C. (2007). Risk degree of debris flow applying neural networks. Nat. hazards 42 (1), 209–224. doi:10.1007/s11069-006-9069-y

CrossRef Full Text | Google Scholar

Chen, C. H., Ke, C. C., and Wang, C. L. (2009). A back-propagation network for the assessment of susceptibility to rock slope failure in the eastern portion of the Southern Cross-Island Highway in Taiwan. Environ. Geol. 57, 723–733. doi:10.1007/s00254-008-1350-9

CrossRef Full Text | Google Scholar

Chopra, P., Sharma, R. K., and Kumar, M. (2015). Artificial neural networks for the prediction of compressive strength of concrete. Int. J. Appl. Sci. Eng. 13 (3), 187–204.

Google Scholar

Dirriba, A. (2017). Developing correlation between dynamic cone penetration index (DCPI) and unconfined compression strength (UCS) of the soils in alem gena town. Civ. Eng. Geotech. Eng.

Google Scholar

Edil, T. B., Benson, C. H., Li, L., Mickelson, D., and Camargo, F. F. (2009). Comparison of basic laboratory test results with more sophisticated laboratory and in-situ tests methods on soils in southeastern Wisconsin: final report.

Google Scholar

Erzin, Y., Rao, B. H., Patel, A., Gumaste, S. D., and Singh, D. N. (2010). Artificial neural network models for predicting electrical resistivity of soils from their thermal resistivity. Int. J. Therm. Sci. 49 (1), 118–130. doi:10.1016/j.ijthermalsci.2009.06.008

CrossRef Full Text | Google Scholar

Filipović, N., Brdar, S., Mimić, G., Marko, O., and Crnojević, V. (2022). Regional soil moisture prediction system based on Long Short-Term Memory network. Biosyst. Eng. 213, 30–38. doi:10.1016/j.biosystemseng.2021.11.019

CrossRef Full Text | Google Scholar

Ghorbani, A., and Hasanzadehshooiili, H. (2018). Prediction of UCS and CBR of microsilica-lime stabilized sulfate silty sand using ANN and EPR models; application to the deep soil mixing. Soils Found. 58 (1), 34–49. doi:10.1016/j.sandf.2017.11.002

CrossRef Full Text | Google Scholar

Golbraikh, A., and Tropsha, A. (2002). Beware of q2. J. Mol. Graph. Model. 20 (4), 269–276. doi:10.1016/S1093-3263(01)00123-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Gunaydin, O., Gokoglu, A., and Fener, M. (2010). Prediction of artificial soil's unconfined compression strength test using statistical analyses and artificial neural networks. Adv. Eng. Softw. 41 (9), 1115–1123. doi:10.1016/j.advengsoft.2010.06.008

CrossRef Full Text | Google Scholar

Hair, J. F., Ortinau, D. J., and Harrison, D. E. (2010). Essentials of marketing research, 2. New York, NY: McGraw-Hill/Irwin.

Google Scholar

Hoang, N. D., and Bui, D. T. (2018). Predicting earthquake-induced soil liquefaction based on a hybridization of kernel Fisher discriminant analysis and a least squares support vector machine: a multi-dataset study. Bull. Eng. Geol. Environ. 77 (1), 191–204. doi:10.1007/s10064-016-0924-0

CrossRef Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1996). LSTM can solve hard long time lag problems. Adv. neural Inf. Process. Syst. 9.

Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9 (8), 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Jain, S. (2020). Application of Machine Learning methods to flow problems in unsaturated soil Master's thesis. Trondheim, Norway: NTNU.

Google Scholar

Javdanian, H., and Lee, S. (2019). Evaluating unconfined compressive strength of cohesive soils stabilized with geopolymer: a computational intelligence approach. Eng. Comput. 35 (1), 191–199. doi:10.1007/s00366-018-0592-8

CrossRef Full Text | Google Scholar

Kalkan, E., Akbulut, S., Tortum, A., and Celik, S. (2009). Prediction of the unconfined compressive strength of compacted granular soils by using inference systems. Environ. Geol. 58 (7), 1429–1440. doi:10.1007/s00254-008-1645-x

CrossRef Full Text | Google Scholar

Khalid, U., Rehman, Z., Farooq, K., and Mujtaba, H. (2015). Prediction of unconfined compressive strength from index properties of soils. Sci. Int. (Lahore) 27 (5), 4071–4075.

Google Scholar

Khatti, J., and Grover, K. S. (2022). Determination of suitable hyperparameters of artificial neural network for the best prediction of geotechnical properties of soil. Int. J. Res. Appl. Sci. Eng. Technol. 10 (5), 4931–4961. doi:10.22214/ijraset.2022.43662

CrossRef Full Text | Google Scholar

Khatti, J., and Grover, K. S. (2023). Prediction of compaction parameters of compacted soil using LSSVM, LSTM, LSBoostRF, and ANN. Innov. Infrastruct. Solutions 8 (2), 76. doi:10.1007/s41062-023-01048-2

CrossRef Full Text | Google Scholar

Khatti, J., and Grover, K. S. (2024). CBR prediction of pavement materials in unsoaked condition using LSSVM, LSTM-RNN, and ANN approaches. Int. J. Pavement Res. Technol. 17 (3), 750–786. doi:10.1007/s42947-022-00268-6

CrossRef Full Text | Google Scholar

Mahamaya, M., Suman, S., Anand, A., and Das, S. K. (2015). Prediction of UCS and CBR values of cement stabilised mine overburden and fly ash mixture. Procedia Earth Planet. Sci. 11, 294–302. doi:10.1016/j.proeps.2015.06.064

CrossRef Full Text | Google Scholar

Masada, T. (2009). Shear strength of clay and silt embankments (No. FHWA/OH-2009/7). Ohio Res. Inst. Transp. Environ.

Google Scholar

Motamedi, S., Song, K. I., and Hashim, R. (2015). Prediction of unconfined compressive strength of pulverized fuel ash–cement–sand mixture. Mater. Struct. 48 (4), 1061–1073. doi:10.1617/s11527-013-0215-1

CrossRef Full Text | Google Scholar

Mozumder, R. A., and Laskar, A. I. (2015). Prediction of unconfined compressive strength of geopolymer stabilized clayey soil using artificial neural network. Comput. Geotechnics 69, 291–300. doi:10.1016/j.compgeo.2015.05.021

CrossRef Full Text | Google Scholar

Ngo, H. T. T., Pham, T. A., Vu, H. L. T., and Giap, L. V. (2021). Application of artificial intelligence to determined unconfined compressive strength of cement-stabilized soil in vietnam. Appl. Sci. 11 (4), 1949. doi:10.3390/app11041949

CrossRef Full Text | Google Scholar

Obasi, N. L., and Anyaegbunam, A. J. (2005). Correlation of the undrained shear strength. Niger. J. Technol. 24 (2), 1–11.

Google Scholar

Oljira, S. A., Tsige, D., and Quezon, E. T. (2021). Modeling unconfined compressive strength of fine grained soils: application of dynamic cone penetration to predict foundation soil strength. Appl. J. Environ. Eng. Sci. 7 (4), 7–4. doi:10.48422/IMIST.PRSM/ajees-v7i4.28114

CrossRef Full Text | Google Scholar

Priyadarshee, A., Chandra, S., Gupta, D., and Kumar, V. (2020). Neural Models for Unconfined Compressive Strength of Kaolin clay mixed with pond ash, rice husk ash and cement. J. Soft Comput. Civ. Eng. 4 (2), 85–102. doi:10.22115/SCCE.2020.223774.1189

CrossRef Full Text | Google Scholar

Puri, N., Prasad, H. D., and Jain, A. (2018). Prediction of geotechnical parameters using machine learning techniques. Procedia Comput. Sci. 125, 509–517. doi:10.1016/j.procs.2017.12.066

CrossRef Full Text | Google Scholar

Ranasinghe, R. A. T. M., Jaksa, M. B., Kuo, Y. L., and Nejad, F. P. (2017). Application of artificial neural networks for predicting the impact of rolling dynamic compaction using dynamic cone penetrometer test results. J. Rock Mech. Geotechnical Eng. 9 (2), 340–349. doi:10.1016/j.jrmge.2016.11.011

CrossRef Full Text | Google Scholar

Safonova, A., Ghazaryan, G., Stiller, S., Main-Knorn, M., Nendel, C., and Ryo, M. (2023). Ten deep learning techniques to address small data problems with remote sensing. Int. J. Appl. Earth Observation Geoinformation 125, 103569. doi:10.1016/j.jag.2023.103569

CrossRef Full Text | Google Scholar

Salahudeen, A. B., Sadeeq, J. A., Badamasi, A., and Onyelowe, K. C. (2020). Prediction of unconfined compressive strength of treated expansive clay using backpropagation artificial neural networks. Niger. J. Eng. 27 (1).

Google Scholar

Saputra, N. A., and Putra, R. (2020). The correlation between CBR (California Bearing Ratio) and UCS (Unconfined Compression Strength) laterite soils in palangka raya as heap material. IOP Conf. Ser. Earth Environ. Sci. 469 (1), 012093. doi:10.1088/1755-1315/469/1/012093

CrossRef Full Text | Google Scholar

Schölkopf, B., and Smola, A. J. (2002). Learning with kernels: support vector machines, regularization, optimization, and beyond. MIT press.

Google Scholar

Senoon, A. A. A., and Hussein, M. M. (2019). “Correlation between unconfined compression strength (UCS) and index properties of soil in assiut governorate, Egypt,” in Fifteenth international conference on structural and geotechnical engineering, faculty of engineering. Cairo, Egypt: Ain Shams University.

Google Scholar

Sharma, L. K., and Singh, T. N. (2018). Regression-based models for the prediction of unconfined compressive strength of artificially structured soil. Eng. Comput. 34 (1), 175–186. doi:10.1007/s00366-017-0528-8

CrossRef Full Text | Google Scholar

Standard, A. S. T. M. D. (2017). Standard test methods for compressive strength of molded soil-cement cylinders. West Conshohocken, PA: ASTM International.

Google Scholar

Suykens, J. A., and Vandewalle, J. (1999). Least squares support vector machine classifiers. Neural Process. Lett. 9, 293–300. doi:10.1023/A:1018628609742

CrossRef Full Text | Google Scholar

Tabarsa, A., Latifi, N., Osouli, A., and Bagheri, Y. (2021). Unconfined compressive strength prediction of soils stabilized using artificial neural networks and support vector machines. Front. Struct. Civ. Eng. 15 (2), 520–536. doi:10.1007/s11709-021-0689-9

CrossRef Full Text | Google Scholar

Taffese, W. Z., and Abegaz, K. A. (2021). Artificial intelligence for prediction of physical and mechanical properties of stabilized soil for affordable housing. Appl. Sci. 11 (16), 7503. doi:10.3390/app11167503

CrossRef Full Text | Google Scholar

Taleb Bahmed, I., Harichane, K., Ghrici, M., Boukhatem, B., Rebouh, R., and Gadouri, H. (2019). Prediction of geotechnical properties of clayey soils stabilised with lime using artificial neural networks (ANNs). Int. J. Geotechnical Eng. 13 (2), 191–203. doi:10.1080/19386362.2017.1329966

CrossRef Full Text | Google Scholar

Tang, L., Ma, Y., Wang, L., Zhang, W., Zheng, L., and Wen, H. (2021). Application of long short-term memory neural network and prophet algorithm in slope displacement prediction. ISSMGE Int. J. Geoengin. Case Hist. 6 (4), 48–66. doi:10.4417/IJGCH-06-04-04

CrossRef Full Text | Google Scholar

Tien Bui, D., Hoang, N. D., and Nhu, V. H. (2019). A swarm intelligence-based machine learning approach for predicting soil shear strength for road construction: a case study at Trung Luong National Expressway Project (Vietnam). Eng. Comput. 35 (3), 955–965. doi:10.1007/s00366-018-0643-1

CrossRef Full Text | Google Scholar

Toan (2018). Recurrent neural network. Available online at: https://github.com/toanhvu/matlab-rnn.217–257. doi:10.1007/978-1-4842-3564-5_10

CrossRef Full Text | Google Scholar

Udo, E., Udoh, N., and Kennedy, C. (2014). Composite stabilization and model prediction of CBR and UCS parameters of unyeghe residual soils, AkwaIbom state, Nigeria. Int. J. Eng. Innovation and Res. 3 (6), 854–862.

Google Scholar

Vapnik, V. (1999). The nature of statistical learning theory. Springer science and business media.

Google Scholar

Wang, Q., Xie, X., Yu, H., and Mooney, M. A. (2021). Predicting slurry pressure balance with a long short-term memory recurrent neural network in difficult ground condition. Comput. Intell. Neurosci. 2021, 6678355. doi:10.1155/2021/6678355

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolter, M. (2016). Least-square support vector machine. Bonn: HPCA Lab, Bonn University. Available online at: https://github.com/v0lta/svm/tree/master/LSSVMlabv1_8_R2009b_R2011a.

Google Scholar

Yang, B., Liu, Z., Lacasse, S., and Nadim, F. (2019). “Landslide displacement prediction based on wavelet transform and long short-term memory neural network,” in Proceedings of the XVII ECSMGE 2019: geotechnical engineering foundation of the future: European conference on soil mechanics and geotechnical engineering.

Google Scholar

Yildirim, E., Avci, E., and Tanbay, N. A. (2021). Prediction of unconfined compressive strength of microfine cement injected sands using fuzzy logic method. doi:10.21203/rs.3.rs-232296/v1

CrossRef Full Text | Google Scholar

Yılmaz, I. (2000). Evaluation of shear strength of clayey soils by using their liquidity index. Bull. Eng. Geol. Environ. 59 (3), 227–229. doi:10.1007/s100640000056

CrossRef Full Text | Google Scholar

Zumrawi, M. M., and Mohammed, L. A. (2016). “Correlation of placement conditions and soil intrinsic properties with shear strength of cohesive soils,” in 7th annual conference for postgraduate studies and scientific research-basic sciences and engineering studies. Khartoum, Sudan: Friendship Hall.

Google Scholar

Nomenclature

${\mathit{C}}^{\prime }$ Cohesion (N/mm²)

${\mathit{C}\mathit{B}\mathit{R}}_{\mathbf{10}}$ CBR of Soil Compacted with 10 Blows (%)

${\mathit{C}\mathit{B}\mathit{R}}_{\mathbf{30}}$ CBR of Soil Compacted with 30 Blows (%)

${\mathit{C}\mathit{B}\mathit{R}}_{\mathbf{65}}$ CBR of Soil Compacted with 65 Blows (%)

${\mathit{C}}^{\mathit{C}}$ Cement Condition

${\mathit{C}}_{\mathit{C}}$ Coefficient of Curvature

${\mathit{C}}^{\mathit{T}}$ Curing Period (days)

${\mathit{C}}_{\mathit{U}}$ Coefficient of Uniformity

${\mathit{C}}^{\mathit{c}\mathit{c}}$ Curing Condition

${\mathit{L}}^{\mathit{C}}$ Lime Content (%)

${\mathit{L}}_{\mathit{S}}$ Linear Shrinkage (%)

${\mathit{M}}^{\mathit{O}}$ Molar Concentration of Alkali Solution

${\mathit{M}}^{\mathit{S}}$ Micro Silica (%)

$\overline{\mathit{P}}$ Mean of the Values of the Y-Variable

${\mathit{P}}_{\mathit{i}}$ Estimated Values

$\overline{\mathit{T}}$ Mean of the Values of the X-Variable

${\mathit{T}}_{\mathit{i}}$ Actual Observations

${\mathit{V}}_{\mathit{p}}$ Primary Ultrasonic Wave Velocity (m/s)

${\mathit{s}}_{\mathit{u}}$ Undrained Shear Strength (N/mm²)

${\mathit{\gamma }}_{\mathit{w}}$ Wet Density (gm/cc)

${\mathit{\sigma }}_{\mathbf{1}}$ Major Principal Stress (N/mm²)

${\mathit{\sigma }}_{\mathbf{3}}$ Minor Principal Stress (N/mm²)

A/B Amount of Alkali to Binder

abs Absolute Function

AI Artificial Intelligence

ANN Artificial Neural Networks

ASTM American Standard for Testing and Materials

BFS Blast Furnace Slag (%)

C Clay Content (%)

CBR California Bearing Ratio (%)

COD Coefficient of Determination

CSO Cuckoo Search Optimization

D Sampling Depth

DCPI Dynamic Cone Penetration Index

DE Differential Equation

DS Degree of Saturation (%)

DUW Dry Unit Weight (gm/cc)

EPR Evolutionary Polynomial Regression

FA Fly Ash (%)

FC Fine Content (%)

GA Genetic Algorithm

GB Gradient Boosting

GGBS Ground Granulated Blast-furnace Slag

GMDH Group Method of Data Handling

GWO Grey Wolves Optimization

IS Indian Standards

K Permeability (m/s)

KFDA Kernel Fisher Discriminant Analysis

LL Liquid Limit (%)

MC Moisture Content (%)

MDD Maximum Dry Density (gm/cc)

MRA Multiple Regression Analysis

MVR Multi Variable Regression

N Total Number of Datasets

Na/Al Atomic Proportion of Na to Al

NF Neuro Fuzzy

NMC Natural Moisture Content (%)

OMC Optimum Moisture Content (%)

ɸ Diameter (m)

P Porosity (%)

PA Pond Ash (%)

PL Plastic Limit (%)

PSO Particle Swarm Optimization

RA Regression Analysis

RBF Radial Bias Function

RHA Rice Husk Ask (%)

SG Specific Gravity

Si/Al Atomic Proportion of Si to Al

SLR Simple Linear Regression

SUW Saturated Unit Weight (gm/cc)

SVM Support Vector Machine

UCS Unconfined Compressive Strength (N/cm²)

VR Void Ratio

W/c ratio Water/cement ratio

γ Density (gm/cc)

ϕ Internal Friction Angle (degree)