Effects of active vibration control of simply supported plates on sound radiation

This paper deals with the effects of different active vibration control strategies applied to a vibrating structure on its sound radiation, taking into account the effect of the position of the excitation force. This is done by means of numerical analyses of a simply supported plate, where both the sound pressure field and the radiated sound power are computed for both uncontrolled and controlled systems. Reflections of the sound waves from walls placed around the vibrating plate are considered using the image source method. Although the vibration mitigation of the plate is achieved by active control measures, it does not imply a reduction of the sound propagation. This means that if the vibration of the plate is attenuated, the sound radiated by the plate can be amplified, an effect that is usually undesirable in practice. By simulating different strategies of active control, the study shows that, among the analyzed approaches, direct velocity feedback control provides the best overall reduction in terms of structural vibration and acoustic radiation.

1 Introduction

Vibration control is a wide field of study that aims to modify the dynamic response of a system as desired Preumont (2018), Meirovitch (1990), Ogata (2010). This can be achieved by passive approaches, active approaches or a combination of both Pérez-Aracil et al. (2021), Zenz et al. (2013). Passive control can be accomplished by adding a mechanical element to the target structure and is a common topic in structural control Masnata and Pirrotta (2024), Schoeftner and Krommer (2012). However, its efficiency highly depends on the proper tuning of the passive devices (such as frequency and damping for tuned mass dampers Baader and Fontana (2017); Preumont (2018)). In addition, these devices can be quite large and heavy, which may not be feasible in practical implementations. In these cases, the adoption of active control strategies provides an alternative.

Unlike passive control, active approaches require an external power supply and consist of a set of actuators and sensors. An actuator interferes with the structure to be controlled and its input signal is generated based on measurement data from a sensor attached to the structure. Various approaches have been proposed for active vibration control (AVC), such as optimal control approaches Preumont (2018), acceleration feedback Díaz and Reynolds (2010), proportional-integral-derivative controllers Genari et al. (2017), Guo et al. (2022), Gattringer et al. (2003) and direct velocity feedback Hanagan and Murray (1997), Shahabpoor et al. (2011). Due to their simplicity in terms of hardware implementation, direct velocity feedback Alujević et al. (2019) and compensated velocity feedback Hirschfeldt et al. (2024) are widely discussed approaches in AVC.

The vibrating structure induces the propagation of waves in the medium in which the system is immersed, such as air or liquids Fahy and Gardonio (2007). In air, a common case for real-world scenarios, this variation of pressure is perceived as sound. Therefore, this structural sound source can result in large noise, which is mostly undesirable in everyday applications, making the study of acoustic control of great interest. Comparisons of different AVC approaches, such as direct velocity feedback, direct acceleration feedback, and compensated acceleration feedback in the literature Shin et al. (2013) usually focus only on the control effect on the structure, while the concomitant effect on the sound propagation is not considered. It should be emphasized that the reduction of structural vibrations by active measures does not imply a reduction of the sound radiated by the vibrating structure. That is, it is possible that active structural vibration control may amplify the radiated sound even though the vibration is attenuated. However, this has not yet been sufficiently investigated and therefore detailed studies are needed to assess the concomitant effect of AVC on sound propagation.

Active structural acoustic control (ASAC) deals with active control of the acoustic response of structures and is an active field of research. For example, Fuller (1991) shows by experimental comparisons that for noise radiated by vibrating structures, control through the vibrating structure reduces more efficiently the sound than control by acoustic sources. Meirovitch and Thangjitham (1990) apply active measures to control the structural modes that govern the sound propagation of a simply supported rectangular elastic plate. From their study, they conclude that as the number of actuators increases, the influence of actuator position on sound control performance becomes less important. However, only the suppression of farfield pressure radiation is examined, and the effects of the active sound pressure control on the response of the vibrating plate are not addressed. In Baumann et al. (1992) a farfield approach is proposed to estimate the sound power radiated by a vibrating system by measurements of the structural response. Using a vibrating clamped-clamped beam as an example, this study shows that an optimal control approach to minimize the radiated sound power can, in some cases, increase structural vibrations. On the other hand, Johnson and Elliott (1995) exploits volume velocity cancellation to perform acoustic control through a piezoelectric control actuator. In some cases, an increase in structural vibrations due to acoustic control was observed. However, it was shown that in a farfield approach this increase in structural vibration can be avoided by using a uniform force actuator with a volume velocity sensor.

In many studies of ASAC, only the farfield is considered to simplify the analysis. For instance, in Fuller (1990), point control forces applied directly to a circular plate and optimized control gains reduce the sound radiation globally, but limited to the farfield. Focusing on farfield effects allows for simplifications in sound propagation calculations and provides a suitable approach for several real-world applications. However, the present study also takes into account room acoustics by considering the vibrating plate as being in a closed room Kuttruff (2009), Savioja and Svensson (2015), where nearfield conditions must be accounted for Williams (1999). The influences of the different AVC approaches are therefore also relevant for these cases where sound wave reflections have to be taken into account.

The aim of this paper is to examine and compare the effects of different AVC approaches on the sound radiated by a vibrating structure through numerical analyses. In particular, a simply supported rectangular force excited plate equipped with a controller tuned to ensure vibration reduction and stability of the control system is considered. It is examined which of the selected control approaches provides the best effect in terms of both vibration and sound reduction. Room acoustics are also discussed, where wave reflections must be considered and a nearfield rather than a farfield approach is adopted.

In addition, the application point of the excitation force on the vibrating structure has a significant influence on structural vibration and sound propagation. Wrona et al. (2020) provides a passive optimization process for shaping the acoustic radiation of vibrating plates that can be combined with optimization of actuator and sensor positions for a passive-active control approach. In the present paper, the position of the force excitation on the plate is varied instead of the control point. The effects on the plate behavior and sound propagation can then be compared for uncontrolled and controlled systems.

The paper is organized as follows. Section 2 presents the vibroacoustic model considered in the study. Specifically, this is a simply supported plate immersed in air, where reflections of the sound waves from walls around the vibrating plate are also discussed, thus taking into account the impact of room acoustics. The same section also introduces the AVC approaches of interest, in particular proportional-integral-derivative controllers and direct velocity feedback control. Section 3 discusses the effects of these different AVC approaches on acoustic radiation, where they are also compared for cases with and without reflections. Finally, Section 4 provides the conclusions of this comparative study.

2 Methods

2.1 Modeling of the vibroacoustic system

This section presents the vibroacoustic model of a system consisting of a simply supported plate with surrounding air. While real structural elements such as floors and slabs typically have more complex boundary constraints (such as clamping or partial clamping), the simply supported plate model provides a good approximation in many cases. It is capable of accurately describing the dynamic behavior while still allowing for analytical comparisons with classical plate theory. This approach is therefore of interest for room acoustic applications, one of the objectives of this study. Acoustic radiation from the vibrating plate is discussed using the Rayleigh integral to obtain the propagating sound pressure and sound power. Reflections from walls around the vibrating plate are also introduced by the image source method.

2.1.1 Simply supported plate model

Kirchhoff’s theory of thin plates is used to derive the forced vibration of an undamped, isotropic, rectangular plate, which is governed by the differential equation Williams (1999).

$\rho h\frac{{\partial }^{2}w}{\partial t^2}+B\left(\frac{{\partial }^{4}w}{\partial x^4}+2\frac{{\partial }^{4}w}{\partial x^2\partial y^2}+\frac{{\partial }^{4}w}{\partial y^4}\right)=u(1)$

In this equation, $w(x,y,t)$ is the displacement of the plate from the reference state in the $z$-direction and $u(x,y,t)$ is the lateral load. The variable $B=E{h}^3/(12(1-{\nu }^2))$ denotes the bending stiffness of the plate, where $E$ is the Young’s modulus of the plate, $h$ is its thickness, and $\nu$ is Poisson’s ratio. Figure 1 shows the plate with length $l_x$, width $l_y$ and the origin of the coordinate system in the lower left corner of the plate. An arbitrary time-varying single force $f(t)$ applied at coordinates $(x_1,y_1)$ excites the plate to vibrations, i.e., $u(x,y,t)=\delta (x-x_1)\delta (y-y_1)f(t)$ with $\delta$ as the Dirac delta function.

Figure 1

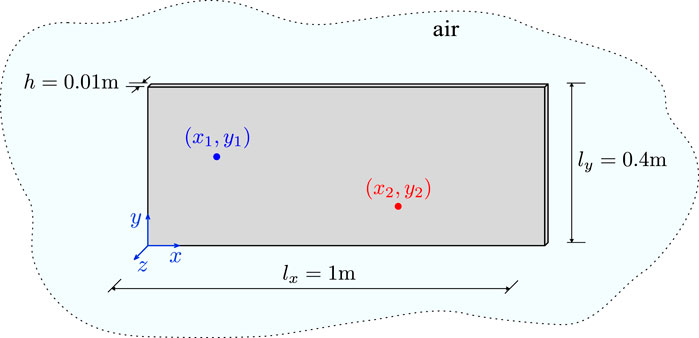
Figure 1. Simply supported rectangular plate immersed in air with the input force at point $(x_1,y_1)$ and the control force at point $(x_2,y_2)$.

The equation of motion Equation 1 is solved by modal analysis, which is based on the modal expansion of the deflection $w$,

$w\left(x,y,t\right)={\displaystyle \sum _{n,m=1}^{\infty }}{\varphi }_{nm}\left(x,y\right)q_{nm}\left(t\right)(2)$

Here, ${\varphi }_{nm}(x,y)$ denotes the $nm$-th mode shape satisfying the simply supported boundary conditions Leissat (1973),

${\varphi }_{nm}\left(x,y\right)=\sqrt{\frac{4}{l_x{l}_y}}\sin \left(n\frac{\pi x}{l_x}\right)\sin \left(m\frac{\pi y}{l_y}\right),n=\mathrm{1,2,3}\dots ,m=\mathrm{1,2,3}\dots (3)$

This procedure yields the modal oscillator equations in terms of the modal coordinates $q_{nm}(t)$ Wrona et al. (2020),

${\ddot{q}}_{nm}+2{\xi }_{nm}{\omega }_{nm}{\dot{q}}_{nm}+{\omega }_{nm}^2{q}_{nm}=\frac{1}{{\rho }_{p}h}{\varphi }_{nm}\left(x_1,y_1\right)f\left(t\right),n,m=\mathrm{1,2,3}\dots (4)$

where damping has been added in the form of modal damping with modal damping ratio ${\xi }_{nm}$ to account for independent energy dissipation of each mode (a reasonable approximation for lightly damped systems). For each mode $(n,m)$ the corresponding natural circular frequency is ${\omega }_{nm}=\sqrt{B/\rho h}\left[{\left(n\pi /l_x\right)}^2+{\left(m\pi /l_y\right)}^2\right]$. The modal oscillator equations Equation 4 are solved by standard procedures of structural dynamics. Inserting the resulting modal coordinates into Equation 2 and deriving the deflection with respect to the time $t$ yields the surface velocity distribution $v$ of the plate, which governs the emitted sound radiation.

In particular, an aluminum plate with the properties given in Table 1 is considered in this study. For this plate, Figure 2 shows the first six mode shapes according to Equation 3 up to a frequency of 750 Hz. The corresponding natural frequencies $f_{nm}={\omega }_{nm}/(2\pi )$ are 176.1 Hz, 248.9 Hz, 370.3 Hz, 540.3 Hz, 631.4 Hz, and 704.2 Hz.

Table 1

Table 1. Vibroacoustic system parameters.

Figure 2

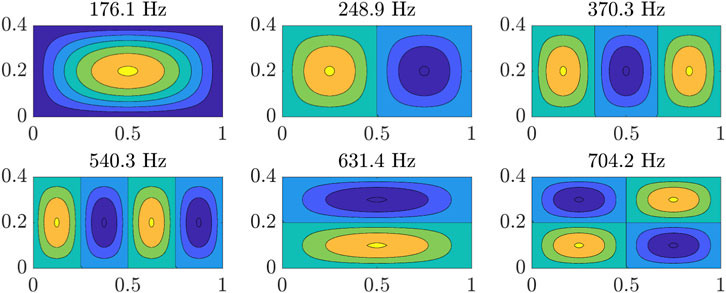
Figure 2. Mode shapes of the simply supported plate and corresponding natural frequencies in the frequency range of interest.

2.1.2 Acoustic radiation analysis using a nearfield approach

It is assumed that the vibrating plate is the only sound source and that the sound waves propagate in the positive direction of the $z$-axis (see Figure 1). Furthermore, the viscous interaction between the vibrating structure and the surrounding air is neglected. Since the viscous boundary layer is thin compared to the acoustic wavelength at common acoustic frequencies, the viscous shear stresses and energy dissipation are negligible when compared to the forces due to pressure and inertia. The air medium is therefore treated as an inviscid fluid.

Once the surface vibration velocity distribution of the plate has been computed according to Section 2.1.1, the sound pressure $p$ at a given point in space $\mathbf{r}=(x,y,z)$ in the frequency domain ($\omega$ in rad/s) can be determined by the Rayleigh integral Williams (1999), Fahy and Gardonio (2007).

$p\left(x,y,z,\omega \right)=\frac{i\omega {\rho }_a}{2\pi }{\int }_{S}v\left(x^{\prime },y^{\prime },0,\omega \right)g\left(R,\omega \right)dS(5)$

with

$g\left(R,\omega \right)=\frac{e^{-ikR}}{R}(6)$

Here, ${\mathbf{r}}_S=(x^{\prime },y^{\prime },0)$ is the position vector of the elemental surface $dS$, $v(x^{\prime },y^{\prime },0,\omega )$ is the normal velocity at this element, and $R=|\mathbf{r}-{\mathbf{r}}_s|$. Moreover, ${\rho }_a$ is the density of air, $k=\omega /c$ is the wave number (where $c$ is the speed of sound), and $i$ is the imaginary unit. The parameters used for the analysis of the acoustic radiation are given in Table 1.

For the computation of the sound pressure field, the vibrating structure is discretized into elemental vibration sources Fahy (1989), Elliott and Johnson (1993). Here, elemental radiators based on a linearly spaced grid with an area $A_e=0.02\times 0.02$ m are chosen, which yields reliable results for frequencies up to 1 kHz. Let $N$ be the number of elemental radiators and $\mathbf{v}={[v_1{v}_2\dots v_N]}^T$ a column vector of complex amplitudes of the velocities at the surface of the vibrating plate. Then, the column vector of the sound pressure $\mathbf{p}={[p_1{p}_2\dots p_N]}^T$ at a plane parallel to the plate is composed by elements of the form

$p_q\left(x_q,y_q,z_q,\omega \right)=\frac{i\omega {\rho }_a{A}_e{e}^{-ik{R}_{qj}}}{2\pi R_{qj}}{v}_j\left(x^{\prime },y^{\prime },0,\omega \right)(7)$

where $R_{qj}$ is the distance between the centers of the $q$th and $j$th elements. Since each elemental source contributes to the sound pressure at a single point in space, this procedure can be computationally expensive. The literature typically considers farfield conditions Baumann et al. (1992), where this equation is valid and can be further simplified. Since this study is aimed at room acoustics where typical nearfield conditions prevail Williams (1999), no simplification of Equation 5 can be used.

Since sound pressure is a field that varies with the observed point in space, it is common in acoustic studies to make use of the radiated sound power Fahy and Gardonio (2007) as position independent quantity. The time-averaged sound power $W$ is obtained by integrating the product of the surface velocity $v(x^{\prime },y^{\prime },0,\omega )$ and the surface sound pressure $p(x,y,0,\omega )$ over the panel, providing an approximation for the computation of sound power in nearfield conditions. This is given by

$W\left(\omega \right)=\frac{1}{2}{\int }_S\text{Re}\left\{v{\left(x^{\prime },y^{\prime },0,\omega \right)}^{*}p\left(x,y,0,\omega \right)\right\}dS(8)$

where the superscript ^* stands for the complex conjugate.

For the elemental radiators, $W$ in Equation 8 is taken to be the sum of the radiated sound power of each element such that

$W\left(\omega \right)=\frac{l_x{l}_y}{2N}\text{Re}\left\{{\mathbf{v}}^H\mathbf{p}\right\}(9)$

for a grid with element dimensions smaller than both the structural and acoustic wavelength, where $H$ indicates the Hermitian transpose (transpose and conjugate).

The radiated sound power can alternatively be computed by a set of radiation modes, a concept that is widely used in ASAC approaches Johnson and Elliott (1995), Elliott and Johnson (1993). These radiation modes are frequency-dependent, but independent from each other. Through them, radiation efficiencies can be computed, measures of how well the vibrating system produces sound for each of these modes. This approach is not followed here and is left for future studies.

2.1.3 Effects of reflections

To account for the effects of reflections from walls around the plate, the image source method is used Nagy et al. (2006). For each elemental radiator, the reflection is taken as an image source, where its distance is taken by mirroring this vibrating element with respect to the reflecting wall. Here, first order image sources are taken into account. Equation 6 must therefore be modified according to

$g\left(R_0,R,\omega \right)=\frac{e^{-ik{R}_0}}{R_0}+{\gamma }_1\left(\omega \right)\frac{e^{-ik{R}_1}}{R_1}+\cdots +{\gamma }_j\left(\omega \right)\frac{e^{-ik{R}_j}}{R_j}(10)$

where $R_j=|\mathbf{r}-{\mathbf{r}}_j|$ (${\mathbf{r}}_j$ denotes the position of the $j$th image source) and ${\gamma }_j(\omega )$ represents absorption effects. Figure 3 shows an example of this method for the present system, where reflections in a room are taken into account. A generic point “$\times$” is marked on the surface of the plate to illustrate this method.

Figure 3

Figure 3. Image source method representation for a vibrating simply supported plate in a room.

2.2 Active control approaches

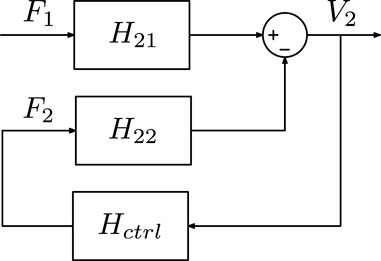
This section compares the effects resulting from AVC of the system shown in Figure 1. Different cases of proportional-integral-derivative (PID) controllers are implemented and their influence on the radiated sound pressure and sound power is discussed for a frequency range from 90 Hz to 750 Hz. Referring to Figure 1, at point $(x_1,y_1)$ the external force is applied. Meanwhile, point $(x_2,y_2)$ refers to the measurement point that provides the signal fed back to the controller as well as where the actuator force is applied.

Proportional-integral-derivative controller is a feedback control-loop technique composed of three contributions Ogata (2010), Srivastava and Pandit (2016). The control effect of the proportional (P) element is directly proportional to the instantaneous error of the control system, allowing for immediate response correction. In this control setup, the control force generated by this element is proportional to the surface velocity. Meanwhile, the integral (I) element accumulates error over time, providing long-term stability by correcting even small persistent errors. It generates a restoring effect, which in this control system means the return of the structure to the target average position. The derivative (D) element reacts to the rate of change, which here corresponds to the rate of change of the velocity error, i.e., the acceleration. This is a predictive component that can prevent overshoot and improve the stability of the control system. A PID controller thus has the form

$H_{\mathit{ctrl}}\left(s\right)=\left(g_P+\frac{g_I}{s}+g_{D}s\right)(11)$

where $g_P,g_I,g_D$ are real values of gain that can be tuned to the target system such that the balance of each one of these elements generates a desired behavior. PID controllers are advantageous due to their flexible tuning. Nevertheless, choosing a satisfying set of parameters for Equation 11 can be challenging for complex systems Wang (2012), Srivastava and Pandit (2016).

With $H_{ij}$ denoting the mobility transfer function with respect to the velocity at the $i$th degree of freedom (DoF) due to force at the $j$th DoF and the numbering mentioned above, the closed-loop transfer function is given by

$H_{21}^{cl}\left(s\right)=\frac{H_{21}\left(s\right)}{1+H_{\mathit{ctrl}}\left(s\right)H_{22}\left(s\right)}(12)$

The block diagram of the control system described by Equation 12 is given in Figure 4, where $V_2(s),F_1(s),F_2(s)$ are the Laplace transforms of the velocity at point $(x_2,y_2)$, the disturbance force, and control force, respectively.

Figure 4

Figure 4. Block diagram of the closed loop control system.

The proportional element in Equation 11, i.e., $H_{\mathit{ctrl}}=g_P$, is of particular interest because it corresponds to direct velocity feedback (DVF) in the present control setup. It introduces active damping effects into the control system. Because of its extensive use in real-world problems, DVF is used as the nomenclature to emphasize its relevance. DVF guarantees stability of the control system for a collocated configuration where the target point of vibration mitigation is located at the same position as the actuator applying control Preumont (2018). This is the case of the present control system. DVF is a popular approach because of its clear physical meaning and ease of tuning, but it usually needs to be combined with other control elements for complete system control.

3 Results

In this section, different cases of PID and DVF control are considered. The aim is to evaluate which type of AVC provides better performance in terms of sound propagation (here meaning sound reduction or at least lower levels of amplification) when structural vibration reduction is guaranteed.

3.1 Active vibration control of a simply supported plate

As shown in Figure 1, three scenarios are simulated with respect to the application point of the dynamic excitation: $(x_1,y_1)=(x_2,y_2)=(0.59,0.11)$, i.e., the application point of the excitation force and the control point on the plate are the same; $(x_1,y_1)=(0.63,0.15)$ and $(x_2,y_2)=(0.59,0.11)$, i.e., the application point of the excitation force is slightly away from the control point; $(x_1,y_1)=(0.3,0.24)$ and $(x_2,y_2)=(0.59,0.11)$, to account for application point of excitation force and control point far away from each other. The influence of the position of the excitation force can thus be discussed in terms of structural vibration control and sound propagation.

The gains for each control case were chosen to result in a smaller magnitude of vibration amplitude throughout the frequency range of interest in all cases analyzed. They also were chosen to provide stable responses for the control system and the same order of magnitude for the forces required to apply control. Figures 5–7 show the Bode plots of the mobility frequency response functions for the uncontrolled and controlled systems for different combinations of the PID controller and DVF control.

Figure 5

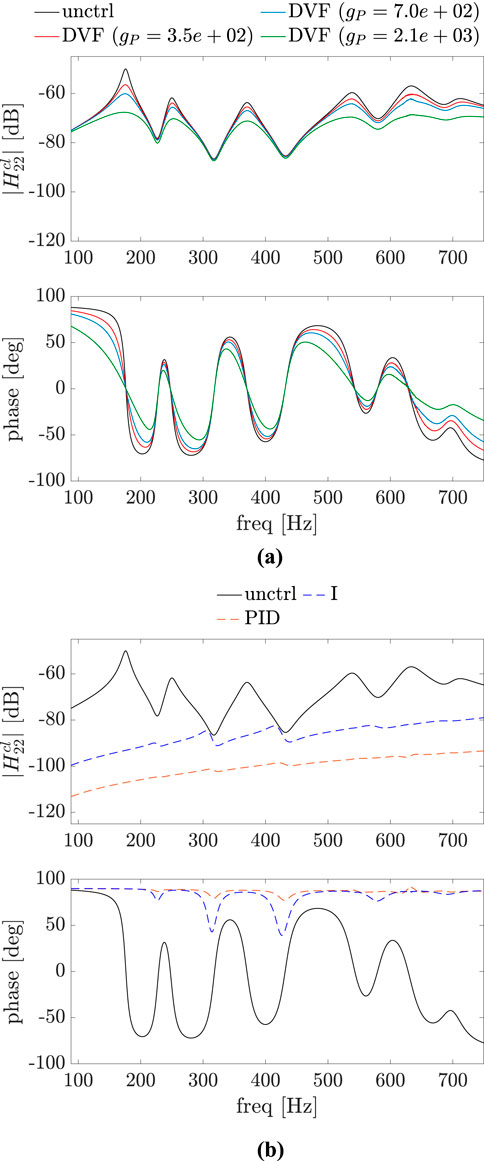
Figure 5. Bode plot of the uncontrolled (unctrl) and controlled systems, where the control point and the point of application of the force excitation are the same: $(x_1,y_1)=(x_2,y_2)=(0.59,0.11)$, see Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I control.

Figure 6

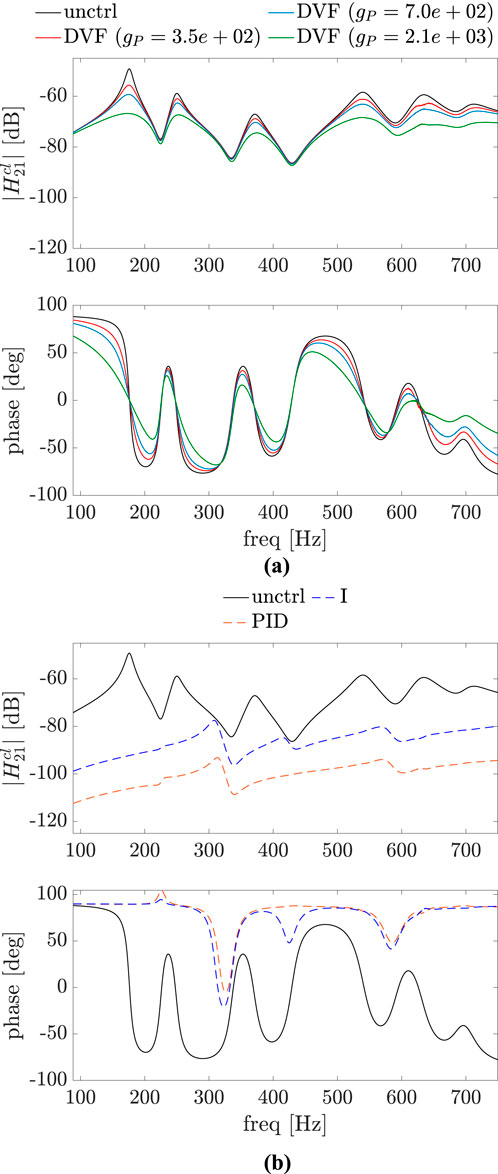
Figure 6. Bode plot of the uncontrolled (unctrl) and controlled systems, where the control point and the point of application of the force excitation are slightly different: $(x_1,y_1)=(0.63,0.15)$ and $(x_2,y_2)=(0.59,0.11)$, see Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I control.

Figure 7

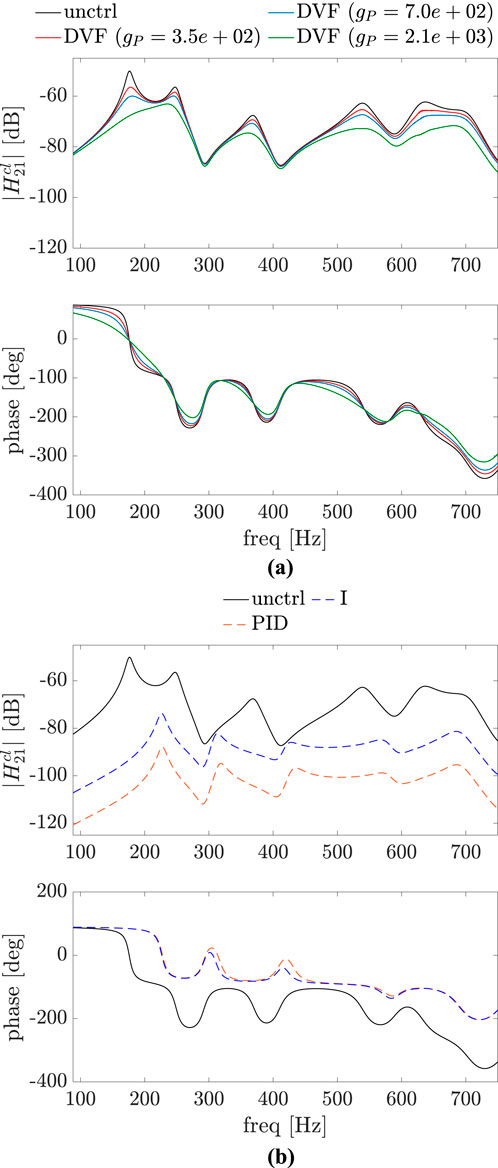
Figure 7. Bode plot of the uncontrolled (unctrl) and controlled systems, where the control point and the point of application of the force excitation are different: $(x_1,y_1)=(0.3,0.24)$ and $(x_2,y_2)=(0.59,0.11)$, see Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I control.

For DVF, three different gains are considered: $g_P=3.5e+02$, $g_P=7.0e+02$ and $g_P=2.1e+03$. As expected, Figures 5A, 6A are very similar since they involve frequency response functions from very close points on the plate. As the gain increases, a significant reduction in vibration amplitude is achieved by DVF. For example, for $g_P=7.0e+02$ in Figure 7A (for application point of excitation force and control point far away from each other) the damping ratios of the closed-loop system modes are 9.6$\%$, 4.6$\%$, 4.3$\%$, 5$\%$, 5.7$\%$ and 3.7$\%$ (compared to 3$\%$ damping in the uncontrolled system, see Table 1).

For the complete PID case, the gains used are $g_P=2.1e+03,g_I=2.5e+08,g_D=1$ and for the integral (I) case the gain is taken as $g_I=5.0e+07$. Both approaches provide a large reduction in magnitude and stable responses. However, the chosen gains are high enough to drastically change the damped natural frequencies and mode shapes of the system, as for the DVF controllers with $g_P=2.1e+03$.

3.2 Effects of active vibration control in acoustic radiation

In the following, the effects of these control approaches on acoustic radiation are examined. As mentioned previously, to compute the sound pressure by Equation 7, the influence of the velocities at all elemental sources must be taken into account. By doing this for both uncontrolled and controlled systems, it is possible to compare the influence of each AVC approach of Section 3.1 on the acoustic propagation. Furthermore, the sound power as given in Equation 9 is also computed and the reflections as described in Section 2.1.3 are discussed for uncontrolled system and different controlled approaches. Here, the mobility frequency response functions $H_{ij}(\omega )$ at the $i$th DoF due to force at the $j$th DoF are used to compute both sound pressure and sound power.

3.2.1 System without reflections

Figures 8–10 show the Bode plots of the frequency response function $P_i/F_j$ with respect to the target point of control and the disturbance for uncontrolled and controlled systems at a perpendicular distance $z=0.5$ m from the plate. They illustrate the three excitation force location scenarios described above.

Figure 8

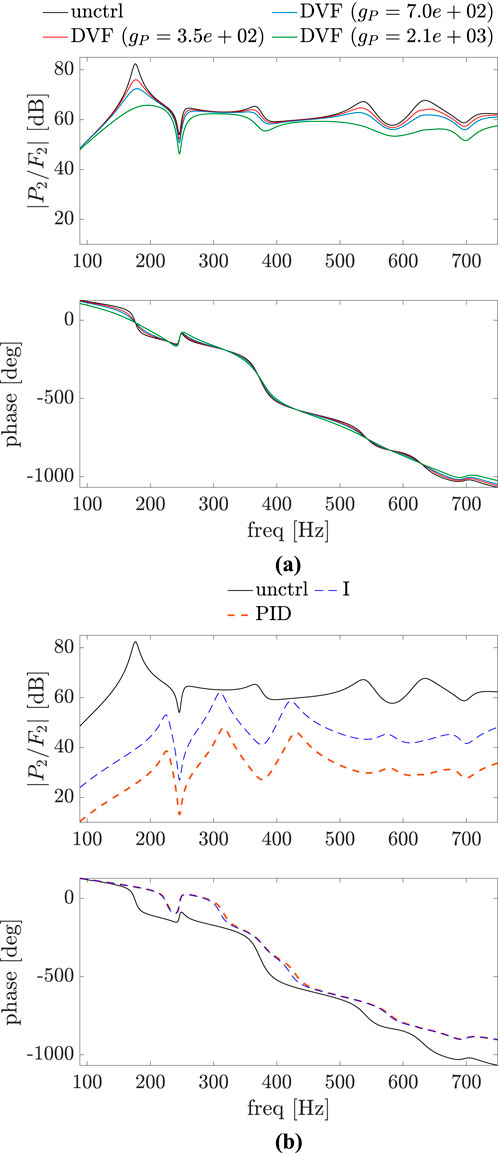
Figure 8. Bode plot of $P_2/F_2$ for uncontrolled (unctrl) and controlled systems for a perpendicular distance of $z=0.5$ m from the plate for $(x_1,y_1)=(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I control.

Figure 9

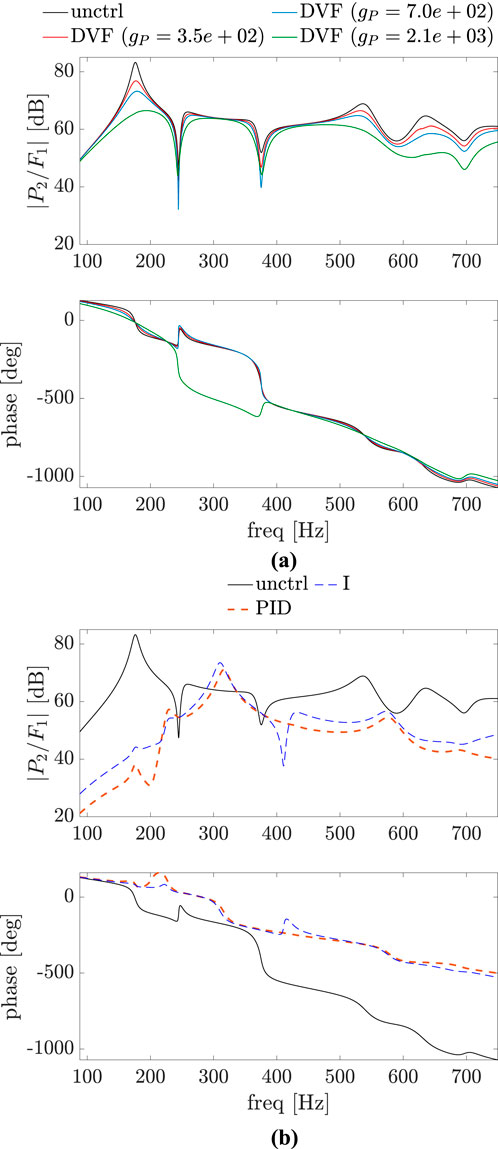
Figure 9. Bode plot of $P_2/F_1$ for uncontrolled (unctrl) and controlled systems for a perpendicular distance of $z=0.5$ m from the plate for $(x_1,y_1)=(0.63,0.15)$ and $(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I control.

Figure 10

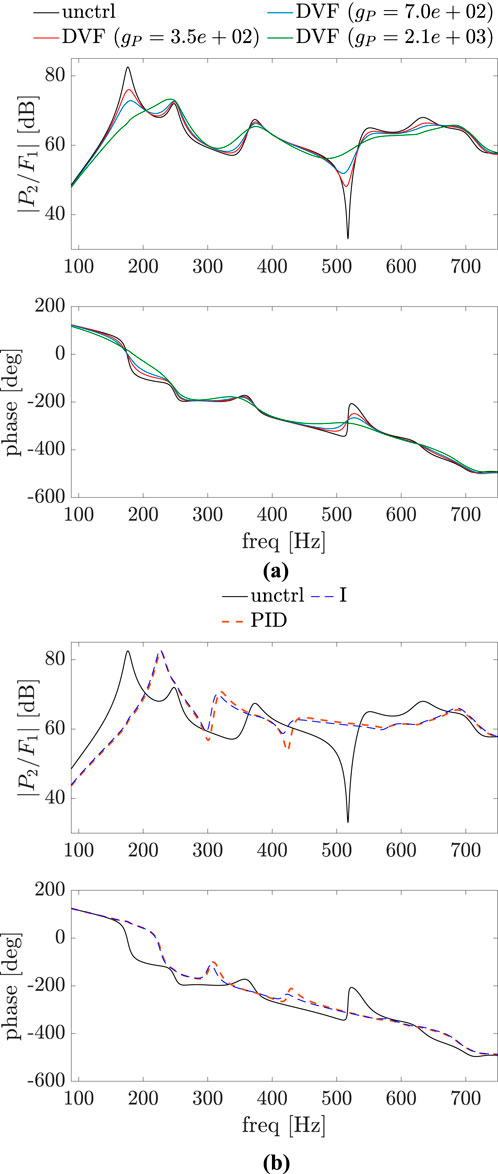
Figure 10. Bode plot of $P_2/F_1$ for uncontrolled (unctrl) and controlled systems for a perpendicular distance of $z=0.5$ m from the plate for $(x_1,y_1)=(0.3,0.24)$ and $(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I control.

A comparison of Figure 5 with Figure 8 shows that for all the control approaches there is a significant reduction in the magnitude of the sound pressure in the considered frequency range for this case of disturbance and control point at the same position on the plate. However, for a small deviation between these two points (Figures 6, 9) it is already noticeable that vibration reduction does not necessarily imply in sound pressure reduction for all the control approaches, as seen in Figure 9B in the frequency range between 240 Hz and 380 Hz. As the distance between the excitation force and control point increases, this is also true for DVF, as demonstrated in Figure 10. Also, the PID and I control approaches, which have a better performance in terms of structural vibration mitigation (see Figure 7), have a worse performance in terms of sound pressure propagation for frequencies between the natural frequencies of the uncontrolled plate.

To evaluate if this reduction/amplification of the sound pressure occurs for the whole $x-y$ plane at $z=0.5$ m and not only for a specific point Figure 11 shows the magnitude $|P_i/F_1|$ (for each $i$th element) in this plane for two frequencies. Only the uncontrolled, PID and DVF $(g_P=7.0e+02)$ cases are shown for the case of $(x_1,y_1)=(0.3,0.24)$ and $(x_2,y_2)=(0.59,0.11)$ (remote excitation force and control point, respectively). On the left column, the first natural frequency of the plate is considered, where a reduction in magnitude with respect to the uncontrolled system can be seen for all points in the two control approaches. Meanwhile, the right column refers to the frequency at which the PID results in the first peak in Figure 10B (226.5 Hz). For the DVF control, there is a decrease in magnitude for almost all points, while for the PID case, there is an increase in magnitude for all points in the plane.

Figure 11

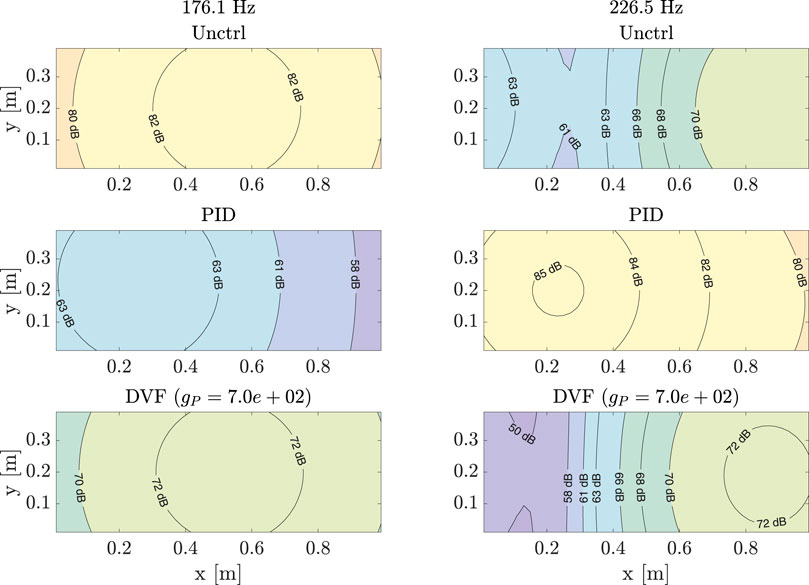
Figure 11. Magnitude $|P_i/F_1|$ (for each $i$th element) in the $x$-$y$ plane at a perpendicular distance from the plate of $z=0.5$ m for $(x_1,y_1)=(0.3,0.24)$ and $(x_2,y_2)=(0.59,0.11)$ as in Figure 1.

Using sound pressure directly as a measurement quantity in a feedback control setup is challenging due to its position dependency and the inherent time delay of the vibroacoustic system. The phase plots in Figures 8–10 show this delay due to the propagation of the sound wave in air. Compensation of time delay systems is an ongoing field of study and more details can be found in Wang (2012), Srivastava and Pandit (2016). In the current study, (direct) acoustic control is not considered.

Figures 12–14 show the magnitude $|W/F_j^2|$ of the radiated sound power for the uncontrolled system and the considered controlled systems for the three positions of excitation force. The change of the damped natural frequency peaks in Figures 8–10 is not only related to the sound pressure but also to the sound power. Similar to Figures 9, 10, although there is a reduction in magnitude around the peaks of the uncontrolled system, this is not necessarily true for all frequencies. This effect is clearly seen in the cases where the structural mode shapes of the controlled system differ too much from the uncontrolled one.

Figure 12

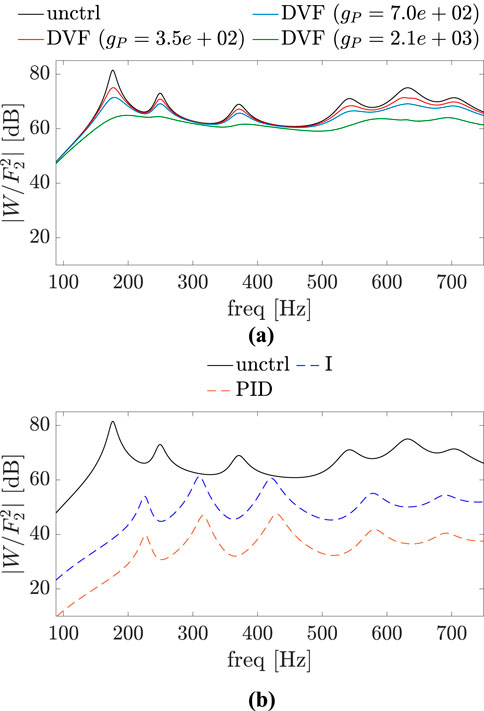
Figure 12. Magnitude plots of $W/F_2^2$ for uncontrolled (unctrl) and controlled systems for $(x_1,y_1)=(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I control.

Figure 13

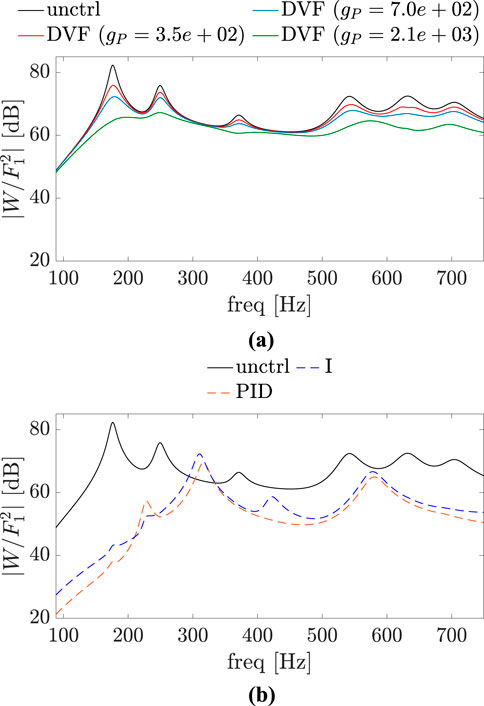
Figure 13. Magnitude plots of $W/F_1^2$ for uncontrolled (unctrl) and controlled systems for $(x_1,y_1)=(0.63,0.15)$ and $(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I controls.

Figure 14

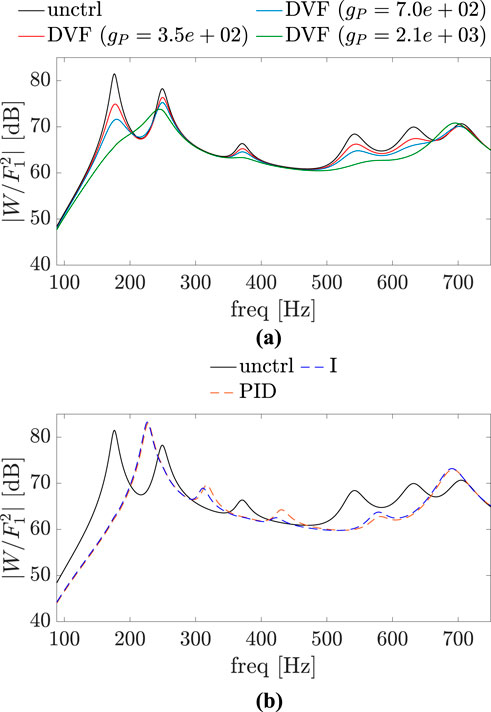
Figure 14. Magnitude plots of $W/F_1^2$ for uncontrolled (unctrl) and controlled systems for $(x_1,y_1)=(0.3,0.24)$ and $(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I controls.

The overall sound pressure level (SPL) at the observation point and the overall sound power level (SWL) for uncontrolled and controlled systems without considering reflections are also of interest. For the cases where excitation point and the control point are the same or very close, it can be seen in Figures 8, 9, 12, 13 that these overall levels decrease for all control approaches. However, this is not clear at first glance when these two points are far apart. SPL and SWL for this scenario are given in Table 2, where it is evident that the PID and I controllers result in a slight increase in both levels.

Table 2

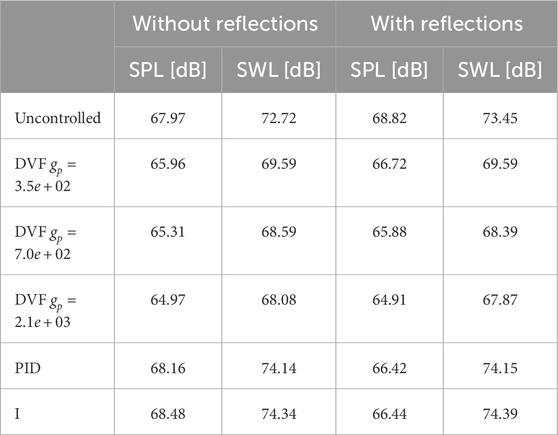
Table 2. Overall sound pressure level (SPL) at the observed point and overall sound power level (SWL) for uncontrolled and controlled systems.

3.2.2 System with reflections

To account for reflections, a constant ${\gamma }_j(\omega )=1$ in Equation 10 is used for all walls in Figure 3, i.e. complete reflections are assumed for all excitation frequencies. The considered walls are at a distance of 1 m from the plate. Figures 15–17 show the Bode plots of $P_2/F_j$ for reflections in a closed room. Compared to Figures 8–10, there is a change in phase. The peak sound pressure at the second resonance frequency of the plate would be reduced by the reflections in the uncontrolled system. Here, DVF control results in an increase in sound pressure in the controlled systems in Figure 17 (remote excitation and control points).

Figure 15

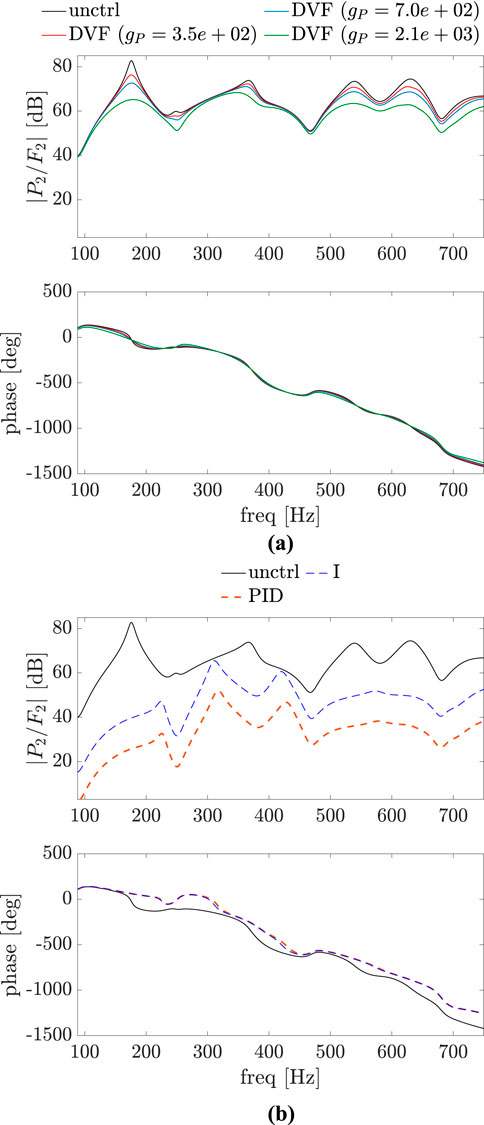
Figure 15. Bode plot of $P_2/F_2$ for the uncontrolled (unctrl) and controlled systems with reflections as in Figure 3 for a perpendicular distance of $z=0.5$ m for $(x_1,y_1)=(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I controls.

Figure 16

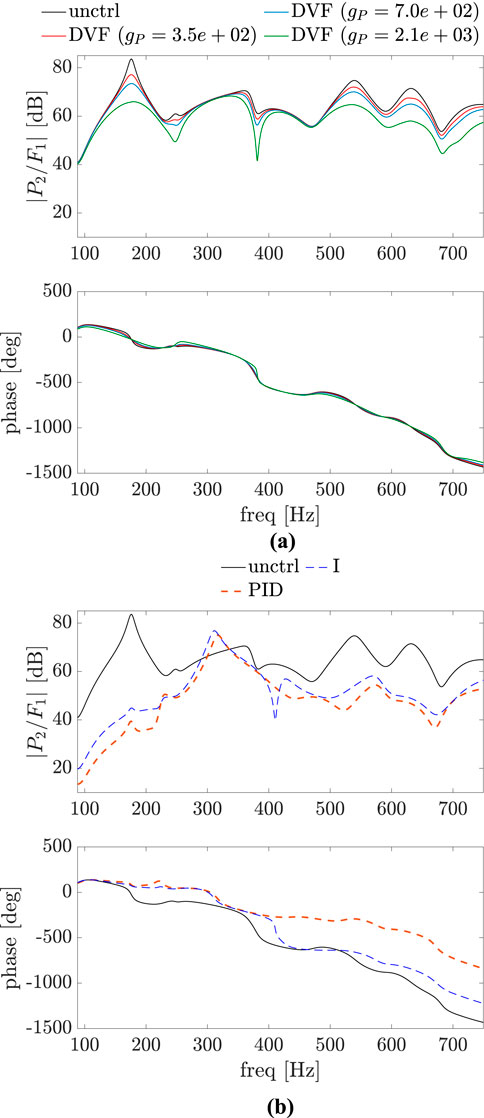
Figure 16. Bode plot of $P_2/F_1$ for the uncontrolled (unctrl) and controlled systems with reflections as in Figure 3 for a perpendicular distance of $z=0.5$ m for $(x_1,y_1)=(0.63,0.15)$ and $(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I controls.

Figure 17

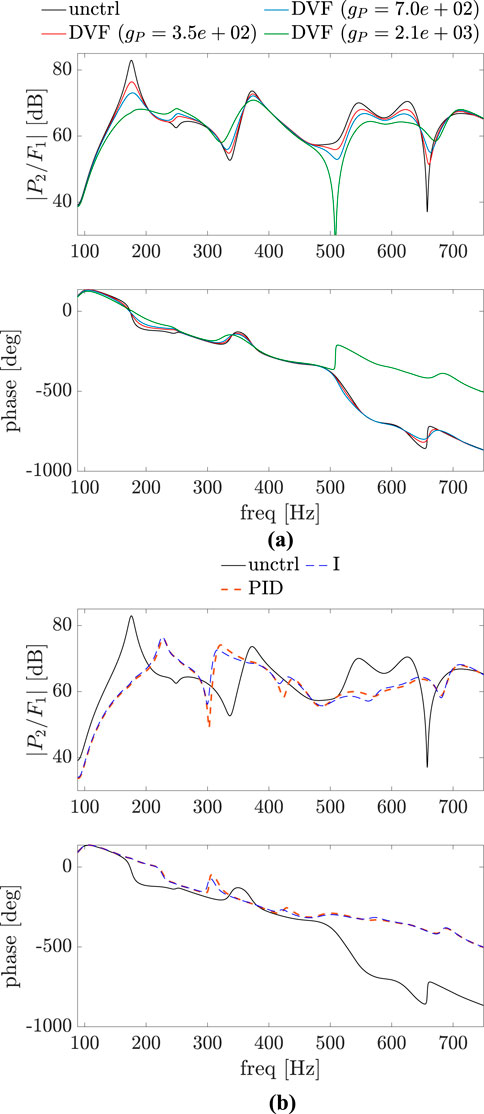
Figure 17. Bode plot of $P_2/F_1$ for the uncontrolled (unctrl) and controlled systems with reflections as in Figure 3 for a perpendicular distance of $z=0.5$ m for $(x_1,y_1)=(0.3,0.24)$ and $(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I controls.

Figure 18 shows the same configurations as in Figure 11, now with reflections considered. The magnitudes for all points in the plane for a vibrating frequency as the first damped natural frequency of the uncontrolled plate are reduced for both controlled approaches. However, for a frequency of 226.5 Hz this is not true for all points in the plane for the DVF approach, although the magnitude increases at the observed point.

Figure 18

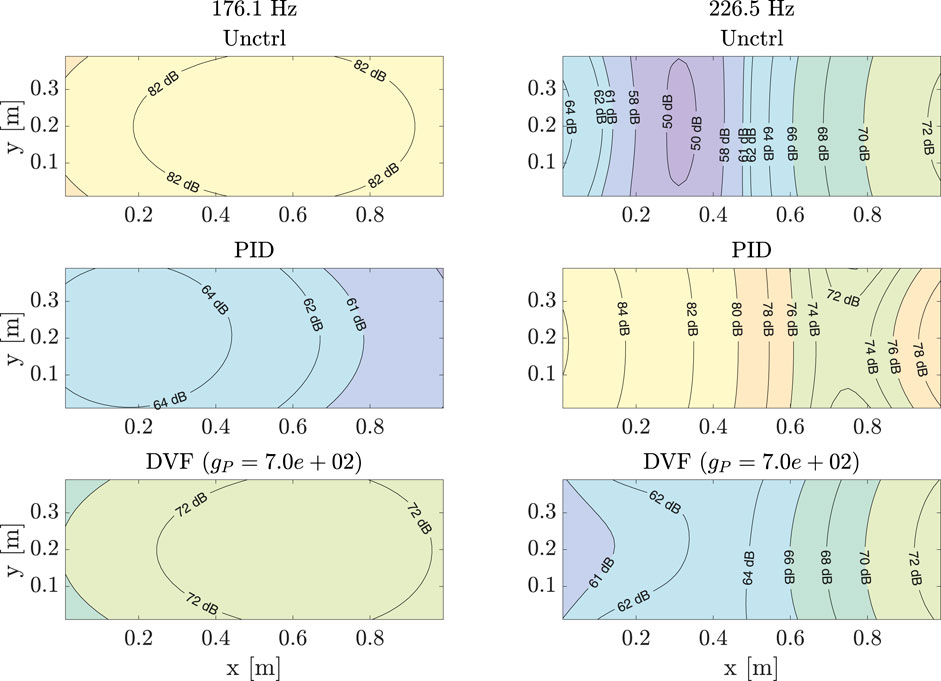
Figure 18. Magnitude $|P_i/F_1|$ (for each $i$th element) in the $x$-$y$ plane at a perpendicular distance from the plate of $z=0.5$ m with reflections as in Figure 3 for $(x_1,y_1)=(0.3,0.24)$ and $(x_2,y_2)=(0.59,0.11)$ as in Figure 1.

Figures 19–21 show magnitude plots of $W/F_j^2$ for the uncontrolled system and controlled systems with the different control approaches. Compared to the case without reflections, there is a slight decrease in magnitude at the second peak and a slight increase at the third and fourth peaks for the uncontrolled plate. At lower frequencies, a difference of about 7 dB can be observed between the uncontrolled structure with and without reflections.

Figure 19

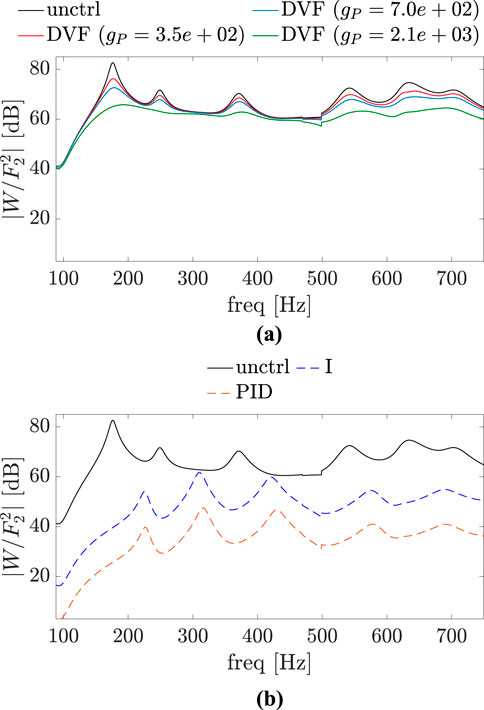
Figure 19. Magnitude plots of $W/F_2^2$ for uncontrolled (unctrl) and controlled systems with reflections as in Figure 3 for $(x_1,y_1)=(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I controls.

Figure 20

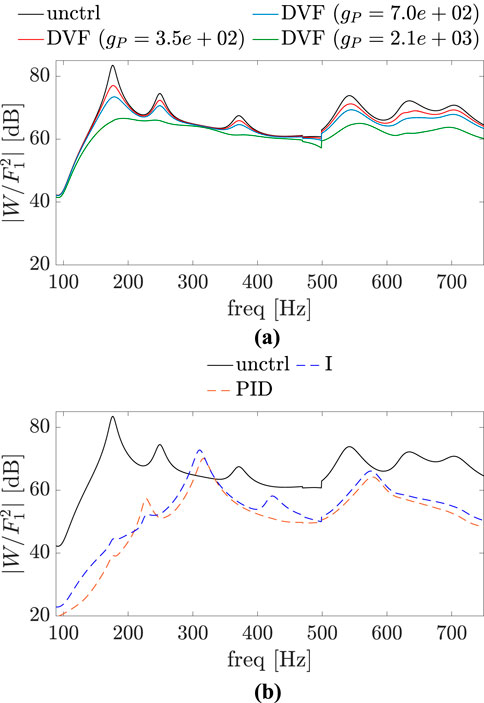
Figure 20. Magnitude plots of $W/F_1^2$ for uncontrolled (unctrl) and controlled systems with reflections as in Figure 3 for $(x_1,y_1)=(0.63,0.15)$ and $(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I controls.

Figure 21

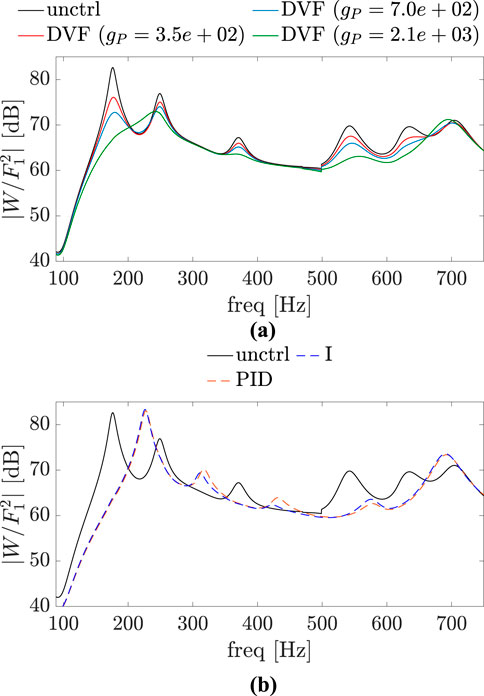
Figure 21. Magnitude plots of $W/F_1^2$ for uncontrolled (unctrl) and controlled systems with reflections as in Figure 3 for $(x_1,y_1)=(0.3,0.24)$ and $(x_2,y_2)=(0.59,0.11)$ as in Figure 1. (a) Control systems with DVF control. (b) Control systems with PID and I controls.

The SPL at the observed point and the SWL for the system with reflections are also given in Table 2 for $(x_1,y_1)=(0.3,0.24)$ and $(x_2,y_2)=(0.59,0.11)$ in Figure 1. Unlike the system without reflections, the SPLs for PID and I controllers at this specific point are now lower than the uncontrolled system. However, the SWLs are still slightly higher.

4 Conclusion

The present paper deals with the acoustic radiation of a simply supported vibrating plate, where the aim was to compare different AVC strategies in order to reduce the resultant sound field in nearfield conditions. By analyzing these effects not only on the sound pressure but also on the sound power, it can be concluded that if the goal is to reduce the sound propagation at a specific excitation frequency such as one of the natural frequencies of the plate, all control options provide a good performance. On the other hand, if the objective is to achieve an overall reduction in the frequency range of interest, the DVF control approach can provide better results for structural and sound reduction as a set. For gain values where the shape of the magnitude plots remain close to the uncontrolled cases, the responses of the control system are predictable and provide reliable means to achieve sound reduction with and without reflections.

The contributions of this study can be summarized as follows:

$•$ A nearfield approach to sound propagation was used to show that DVF control can provide better performance for structural and sound reduction as a set. A greater overall reduction in sound power in the frequency range of interest is achieved when compared to PID controllers, even though they provide better performance in terms of vibration mitigation;

$•$ Since the location of the external excitation is relevant to the sound propagation, the effects of its location on the sound pressure and sound power were also studied. It was shown that significant amplification of the sound propagation can occur for the excitation force far away from the control point. When the application point of the force excitation and the control point are at the same position on the plate, all control approaches for vibration and sound control are feasible and provide significant reductions for both. However, the performance of DVF for structural and sound reduction is superior as a set when these points are not the same;

$•$ The effects of reflections were also considered. Reflections in a room changed the sound pressure at certain points to a large extent, but the sound power remained similar in all cases. The same conclusions can be drawn as for the cases without reflections.

The effects of different dimensions of the plate would also be of interest. With larger width and/or length, the natural frequencies of the system shift to lower values, while with larger thickness there is a shift to higher frequencies. The process of applying AVC does not change. Therefore, the effects of structural control should be similar, but now different gain values must be used for both PID and DVF control to achieve vibration mitigation. These new gain values must to be chosen in the same way to ensure stability of the control system, reduction of vibration, and the same order of magnitude of the forces required to apply control. In terms of sound propagation, the biggest difference is in the cases with reflections for the same room described in the paper, now with a larger plate. Pressure and power levels will increase with increasing width/length due to interference from reflected sound waves. However, the same conclusion should hold: if the shape of the magnitude plots remains close to the uncontrolled system, DVF provides predictable responses that can result in sound reduction. Furthermore, the analysis of other types of boundary conditions is suggested for future work to consider more realistic setups than the simply supported plate.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

NH: Software, Formal Analysis, Writing – original draft, Visualization, Investigation, Data curation. TF: Writing – review and editing, Methodology, Supervision, Conceptualization, Investigation. CA: Writing – review and editing, Supervision, Conceptualization, Resources.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Open Access Funding provided by Universität Innsbruck.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alujević, N., Senjanović, I., Ćatipović, I., and Vladimir, N. (2019). The absence of reciprocity in active structures using direct velocity feedback. J. Sound Vib. 438, 251–256. doi:10.1016/j.jsv.2018.09.035

CrossRef Full Text | Google Scholar

Baader, J., and Fontana, M. (2017). Active vibration control of lightweight floor systems. Procedia Eng. 199, 2772–2777. doi:10.1016/j.proeng.2017.09.529

CrossRef Full Text | Google Scholar

Baumann, W. T., Ho, F.-S., and Robertshaw, H. H. (1992). Active structural acoustic control of broadband disturbances. J. Acoust. Soc. Am. 92, 1998–2005. doi:10.1121/1.405250

CrossRef Full Text | Google Scholar

Díaz, I. M., and Reynolds, P. (2010). Acceleration feedback control of human-induced floor vibrations. Eng. Struct. 32, 163–173. doi:10.1016/j.engstruct.2009.09.003

CrossRef Full Text | Google Scholar

Elliott, S. J., and Johnson, M. E. (1993). Radiation modes and the active control of sound power. J. Acoust. Soc. Am. 94, 2194–2204. doi:10.1121/1.407490

CrossRef Full Text | Google Scholar

Fahy, F. (1989). Sound intensity. England: Elsevier.

Google Scholar

Fahy, F., and Gardonio, P. (2007). Sound and structural vibration: radiation, transmission and response. 2 edn. London: Elsevier.

Google Scholar

Fuller, C. R. (1990). Active control of sound transmission/radiation from elastic plates by vibration inputs: I. Analysis. J. Sound Vibrafion 136, 1–15. doi:10.1016/0022-460X(90)90933-Q

CrossRef Full Text | Google Scholar

Fuller, C. R., Hansen, C., and Snyder, S. (1991). Active control of sound radiation from a vibrating rectangular panel by sound sources and vibration inputs: an experimental comparison. J. Sound Vibrafion 145, 195–215. doi:10.1016/0022-460X(91)90587-A

CrossRef Full Text | Google Scholar

Gattringer, H., Nader, M., Krommer, M., and Irschik, H. (2003). Collocative PD control of circular plates with shaped piezoelectric actuators sensors. J. Vib. Control 9, 965–982. doi:10.1177/10775463030098004

CrossRef Full Text | Google Scholar

Genari, H. F., Mechbal, N., Coffignal, G., and Nóbrega, E. G. (2017). A reconfigurable damage-tolerant controller based on a modal double-loop framework. Mech. Syst. Signal Process. 88, 334–353. doi:10.1016/j.ymssp.2016.11.015

CrossRef Full Text | Google Scholar

Guo, X., Volery, M., and Lissek, H. (2022). Pid-like active impedance control for electroacoustic resonators to design tunable single-degree-of-freedom sound absorbers. J. Sound Vib. 525, 116784. doi:10.1016/j.jsv.2022.116784

CrossRef Full Text | Google Scholar

Hanagan, L., and Murray, T. (1997). Active control approach for reducing floor vibrations. J. Struct. Eng. 123, 1497–1505. doi:10.1061/(ASCE)0733-9445(1997)123:11(1497)

CrossRef Full Text | Google Scholar

Hirschfeldt, N., Furtmüller, T., Adam, C., and Maderebner, R. (2024). Compensated velocity feedback for non-collocated active vibration control. Meccanica. doi:10.1007/s11012-024-01913-z

CrossRef Full Text | Google Scholar

Johnson, M. E., and Elliott, S. J. (1995). Active control of sound radiation using volume velocity cancellation. J. Acoust. Soc. Am. 98, 2174–2186. doi:10.1121/1.413332

CrossRef Full Text | Google Scholar

Kuttruff, H. (2009). Room acoustics. 5th edn. Boca Raton, FL: CRC Press.

Google Scholar

Leissat, A. W. (1973). The free vibration of rectangular plates. J. Sound Vib. 31, 257–293. doi:10.1016/S0022-460X(73)80371-2

CrossRef Full Text | Google Scholar

Masnata, C., and Pirrotta, A. (2024). Optimal design of inerter-based absorbers with amplified inertance: from the improved tuned liquid column damper inerter (ITLCDI) to the improved tuned mass damper inerter (ITMDI) and improved tuned inerter damper (ITID). Meccanica. doi:10.1007/s11012-024-01834-x

CrossRef Full Text | Google Scholar

Meirovitch, L. (1990). Dynamics and control of structures. (United States of America: John Wiley and Sons, Inc.).

Google Scholar

Meirovitch, L., and Thangjitham, S. (1990). Active control of sound radiation pressure. J. Vib. Acoust. 112, 237–244. doi:10.1115/1.2930118

CrossRef Full Text | Google Scholar

Nagy, A. B., Fiala, P., Márki, F., Augusztinovicz, F., Degrande, G., Jacobs, S., et al. (2006). Prediction of interior noise in buildings generated by underground rail traffic. J. Sound Vib. 293, 680–690. doi:10.1016/j.jsv.2005.12.011

CrossRef Full Text | Google Scholar

Ogata, K. (2010). Modern control engineering. 5 edn. New Jersey: Prentice Hall.

Google Scholar

Pérez-Aracil, J., Pereira, E., Díaz, I. M., and Reynolds, P. (2021). Passive and active vibration isolation under isolator-structure interaction: application to vertical excitations. Meccanica 56, 1921–1935. doi:10.1007/s11012-021-01342-2

CrossRef Full Text | Google Scholar

Preumont, A. (2018). Vibration control of active structures: an introduction. 4 edn, 246. Cham, Switzerland: Springer.

Google Scholar

Savioja, L., and Svensson, U. P. (2015). Overview of geometrical room acoustic modeling techniques. J. Acoust. Soc. Am. 138, 708–730. doi:10.1121/1.4926438

PubMed Abstract | CrossRef Full Text | Google Scholar

Schoeftner, J., and Krommer, M. (2012). Single point vibration control for a passive piezoelectric Bernoulli-Euler beam subjected to spatially varying harmonic loads. Acta Mech. 223, 1983–1998. doi:10.1007/s00707-012-0686-0

CrossRef Full Text | Google Scholar

Shahabpoor, E., Reynolds, P., and Nyawako, D. (2011). “A comparison of direct velocity, direct, and compensated acceleration feedback control systems in mitigation of low-frequency floor vibrations,” in Dynamics of civil structures (Jacksonville, Florida, USA: Springer New York), 4, 177–187. doi:10.1007/978-1-4419-9831-6_19

CrossRef Full Text | Google Scholar

Shin, C., Hong, C., and Jeong, W. B. (2013). Active vibration control of beams using filtered-velocity feedback controllers with moment pair actuators. J. Sound Vib. 332, 2910–2922. doi:10.1016/j.jsv.2012.12.037

CrossRef Full Text | Google Scholar

Srivastava, S., and Pandit, V. S. (2016). A PI/PID controller for time delay systems with desired closed loop time response and guaranteed gain and phase margins. J. Process Control 37, 70–77. doi:10.1016/j.jprocont.2015.11.001

CrossRef Full Text | Google Scholar

Wang, D. J. (2012). A PID controller set of guaranteeing stability and gain and phase margins for time-delay systems. J. Process Control 22, 1298–1306. doi:10.1016/j.jprocont.2012.05.019

CrossRef Full Text | Google Scholar

Williams, E. G. (1999). Fourier acoustics: sound radiation and nearfield acoustical holography. Cambridge: Academic Press.

Google Scholar

Wrona, S., Pawelczyk, M., and Qiu, X. (2020). Shaping the acoustic radiation of a vibrating plate. J. Sound Vib. 476, 115285. doi:10.1016/j.jsv.2020.115285

CrossRef Full Text | Google Scholar

Zenz, G., Berger, W., Gerstmayr, J., Nader, M., and Krommer, M. (2013). Design of piezoelectric transducer arrays for passive and active modal control of thin plates. Smart Struct. Syst. 12, 547–577. doi:10.12989/sss.2013.12.5.547

CrossRef Full Text | Google Scholar