Ca2+ waves in astrocytes: computational modeling and experimental data

This paper examines different computational models for Calcium wave propagation in astrocytes. Through a comparative analysis of models by Goldbeter, De Young-Keizer, Atri, Li-Rinzel, and De Pittà and of experimental data, the study highlights the model contributions for the understanding of Calcium dynamics. Tracing the evolution from simple to complex models, this work emphasizes the importance of integrating experimental data in order to further refine these models. The results allow to improve our understanding of the physiological functions of astrocytes, suggesting the importance of more accurate astrocyte models.

Introduction

The field of neuroscience, and more specifically computational neuroscience, has in recent decades focused almost exclusively on the study and modeling of neuronal components and dynamics at both the cellular and network levels, almost completely neglecting the role of astrocytes except for their metabolic and homeostatic activity. Recent studies have shown that astrocyte Ca²⁺ variation is associated with the modulation of neuronal signaling through the uptake and release of neurotransmitters (Haydon and Carmignoto, 2006; Volterra and Meldolesi, 2005; Khakh and Mccarthy, 2015; Pasti et al., 1997; Fiacco and Mccarthy, 2006; Kofuji and Araque, 2021; Semyanov et al., 2020; Verkhratsky and Nedergaard, 2018; Khakh and Sofroniew, 2015). A growing body of research demonstrates that astrocytes are more than merely passive read-out units (Temburni and Jacob, 2001); rather, they play a significant role in controlling the activity of neuronal synapses (Fellin et al., 2006; Perea et al., 2009; Clarke and Barres, 2013). Astrocytes have a sort of chemical excitability based on variations in intracellular Calcium concentration, despite not being electrically excitable cells that is, they cannot produce action potentials. Astrocytes control the number of neurotransmitters in the synaptic cleft by regulating intracellular and intercellular Calcium dynamics; thereby controlling the synaptic signal current between two neurons. It is now known that astrocyte Ca²⁺ signaling is essential for proper functioning of neuronal activity and dysfunction of astrocyte dynamics is implicated in the onset of neurodegeneration (Kang et al., 2005; Nadkarni and Jung, 2003; Tian et al., 2005; Verkhratsky et al., 2010; Eddleston and Mucke, 1993; Rappold and Tieu, 2010; Eid et al., 2008; Madinier et al., 2013; Mitroshina et al., 2022; Jiang et al., 2024).

The discovery that astrocytes are responsible for neuronal activity has led to the creation of various mathematical and computational models for simulating astrocyte dynamics. Of these, those relating to the modulation of intracellular Ca²⁺ waves occupy particular importance due to their importance in cell communication. Research on glia entered a new era with the fundamental discovery in the 1980s that astrocytes express a wide range of receptors for neurotransmitters. Subsequent research has shown that the release of neurotransmitters during synaptic activity can activate these receptors and cause an increase in Ca²⁺ in astrocytes. In turn, this mechanism can cause the release of gliotransmitters such as glutamate, ATP and D-serine, which are capable of activating neuronal receptors, thus modifying the electrical excitability of neurons and synaptic transmission, triggering intercellular communication between astrocytes and neurons (Araque et al., 1999; Fellin et al., 2004; Schipke and Kettenmann, 2004; Jourdain et al., 2007). Thanks to these findings, the theory of “tripartite synapses” was developed, which considers astrocytes as the third component of the signal integration unit (Volterra et al., 2002). Recently, much research has been conducted on the mechanism of chemical transmitter release from astrocytes. Of all the gliotransmitters, glutamate has undoubtedly attracted the most attention due to the fundamental discovery by Anne Cornell-Bell and colleagues that glutamate evokes increased Calcium concentrations in astrocytes (Cornell-Bell et al., 1990).

Various studies have been done to confirm that astrocytes possess specific receptors for glutamate on the outer surface of the plasma membrane (mGluRs) (Anderson and Swanson, 2000; Backus et al., 1989; Condorelli et al., 1997). The function of glial mGluRs is still almost unknown, on the contrary, there is much evidence on the role of ionotropic glutamate receptors in glial cells (Dantoni et al., 2008; Verkhratsky and Steinhäuser, 2000; Kondoh et al., 2001; Seifert and Steinhäuser, 2001). Astrocytes release glutamate, which diffuses into the extra synaptic space and binds to metabotropic glutamate receptors (mGluRs) or NMDA receptors (NMDARs) of neighboring presynaptic terminals in turn, they may respond to the glutamate released at the synaptic level with an increase in intracellular Ca²⁺ that may trigger the release of further glutamate by astrocytes (Malarkey and Parpura, 2008; Skowrońska et al., 2019; Santello and Volterra, 2009; Montana et al., 2006).

Modeling and theoretical study of Ca²⁺ dynamics involving the IP₃ receptor channel are the main topics of the review. It also provides a synopsis of the experimental results.

The models presented in this review are united by the fact that the dynamics of IP3 and the compartmental changes of Ca²⁺ are integrated in a set of ordinary differential equations. System parameters have a sensitive effect on the propagation of released Ca²⁺. Therefore, instead of reviewing the results of each study, we will present the ideas and techniques employed.

Section of models

The Goldbeter model

Pioneering models for intracellular Ca²⁺ signaling include the Goldbeter et al. model (Santello and Volterra, 2009), which predicts the occurrence of periodic spikes of the ion in the absence of IP₃ oscillations, indicating that repetitive Ca²⁺ spikes do not necessarily require a concomitant periodic change in IP₃ and can be induced by external stimulation. The model assumes the existence of two distinct internal stores, one sensitive to IP₃ and the other sensitive to Ca²⁺. The IP₃ produced by agonist stimulation leads to a release of Ca²⁺ from the IP₃-sensitive store via the IP₃Rs. The released Ca²⁺ will stimulate a further release from the Ca²⁺ sensitive store (see Figure 1), which self-amplifies above a threshold value for cytosolic Ca²⁺ concentration (C), representing a model for Induced Calcium Release (CIRC). Depletion of the Ca²⁺-sensitive pool (C_ER) limits the release. This model makes the critical assumption that the Ca²⁺ in the IP₃-sensitive store remains constant as the extracellular medium rapidly replenishes it. The model lacks a mechanism for IP₃-dependent Ca²⁺ inhibition. The two variables in the model are the concentration of free Ca²⁺ in the cytosol and in the IP3-insensitive repository (e.g., the endoplasmic reticulum or sarcoplasmic reticulum); these variables are denoted Z and Y, respectively. Assuming that buffering is linear with respect to Ca²⁺ concentration, the time evolution of the systems is governed by the two kinetic equations:

$\begin{array}{ll}\frac{dC}{dt}={\nu }_0+{\nu }_1\beta -{\nu }_2+{\nu }_3+k_{f}Y-k_Z& (1)\end{array}$

$\begin{array}{ll}\frac{d{C}_{ER}}{dt}={\nu }_2-{\nu }_3-k_{f}Y& (2)\end{array}$

Figure 1

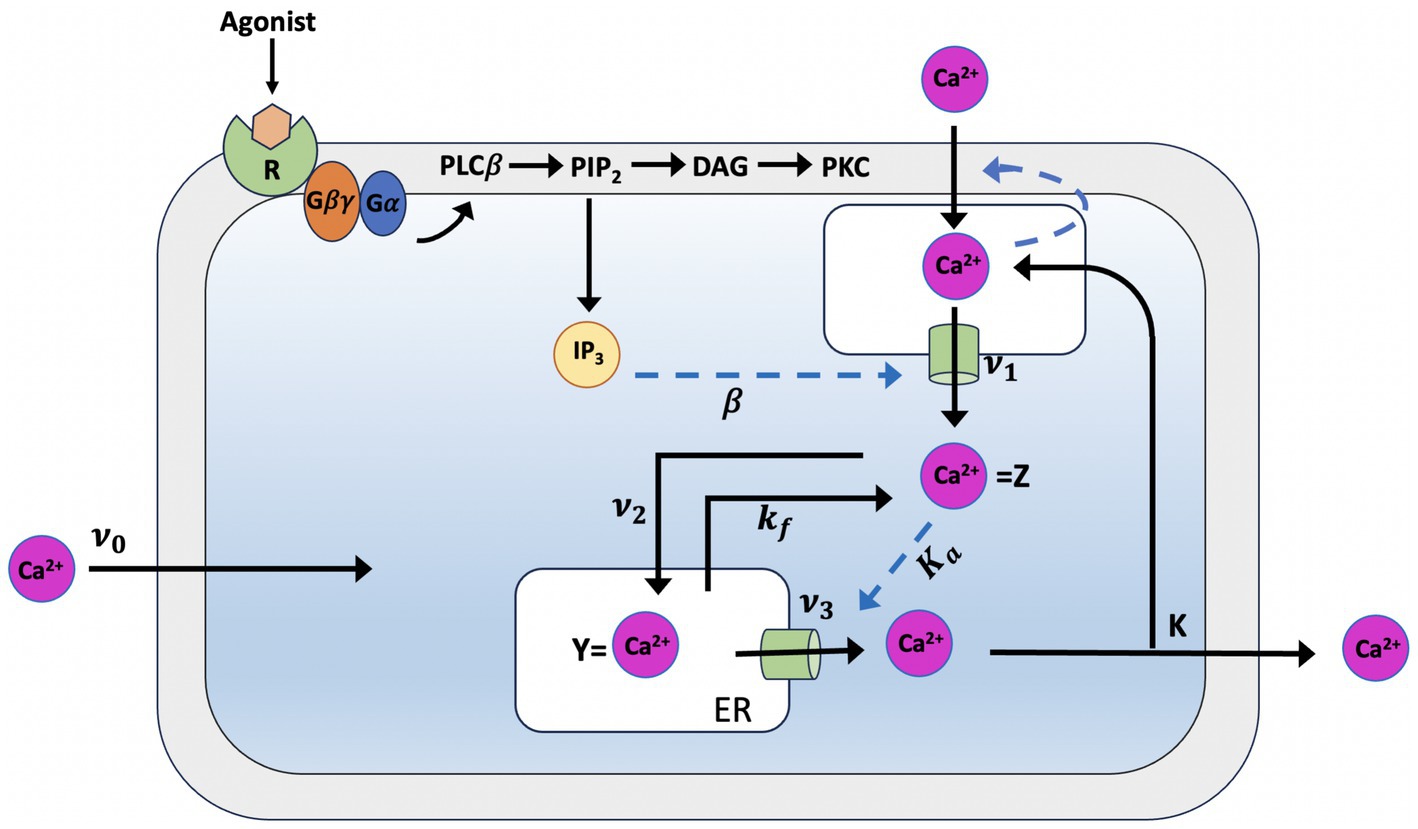
Figure 1. Illustration of the production mechanism of Ca²⁺ oscillations according to Goldbeter model, which is based on Ca²⁺ release induced by intracellular stores. Ca²⁺ release is modulated by IP₃ from an IP₃-sensitive store located in the cytosol $\left({\nu }_1\right)\text{,}$which also indirectly controls the influx of external Ca²⁺ into this store. In the model, ${\nu }_1$ determines the constant Ca²⁺ flux in the cytosol, which is controlled by each level of InsP3. Z, the cytosolic Ca²⁺ concentration, passes from a phase of low concentration, during which priming Ca²⁺ is transferred $\left({\nu }_2\right)$into the InsP3-insensitive pool, to a phase in which the Ca2+ stored in that pool (Y) is released into the cytosol $\left({\nu }_3\right)\text{;}$this phase is characterized by short peaks of Ca²⁺. The parameter ${\nu }_0$ refers to the influx of extracellular Ca²⁺ into the cytosol, $k$ to the influx of cytosolic Ca²⁺ from the cell to the extracellular space and $k_f$ to the passive loss of Y in Z (see text for details).

In Equation 1, the ν₀ parameter, which is assumed take constant, relates to the Ca²⁺ input from the extracellular medium into the cell; k_Z, which is assumed to be linear, pertains the outflow of Ca²⁺ into outflow from the cell, which occurs even in the absence of external stimulation. ν₁β denotes the InsPs-modulated release of Ca²⁺; ν₂ indicates the rate of ATP-driven pumping of Ca²⁺ from the cytosol into the InsP₃-insensitive store, while ν₃ represents the rate of transport from this pool into the cytosol; finally, the term k_fY refers to a nonactivated transport of C into C_ER.

When the cell receives an external signal, this triggers an increase in InsP₃, which leads to a rise in the saturation function β and, subsequently, to an increase in cytosolic Ca²⁺.

$\begin{array}{ll}{\nu }_2=V_{M2}\frac{Z^n}{K_2^n+Z^n}\mathrm{}{\nu }_3=V_{M3}\frac{Y^m}{K_R^m+Y^m}\cdot \frac{Z^P}{K_A^P+Z^P}& (3)\end{array}$

Were V_M2 and V_M3 denote, respectively, the maximum rates of Ca²⁺ pumping into and release from the intracellular store; these processes are described by Hill functions whose cooperativity coefficients are taken as n and m; p denotes the degree of cooperativity of the activation process; K₂, K_R, and K_A are threshold constants for pumping, release, and activation.

The Goldbeter model assumes that two different types of pools are required for Ca²⁺ oscillations, some of which are sensitive to InsP₃ and others with RyR and thus sensitive to Ca²⁺. Due to the InsP₃R’s inherent sensitivity to both Ca²⁺ and InsP₃, this proved unneeded. Subsequently, Dupont and Goldbeter formulated a version of the model that assumes the existence of a single pool in which Ca²⁺ and IP₃ are co-agonists for the induction of Ca²⁺ release (Dupont and Goldbeter, 1993; Table 1).

Table 1

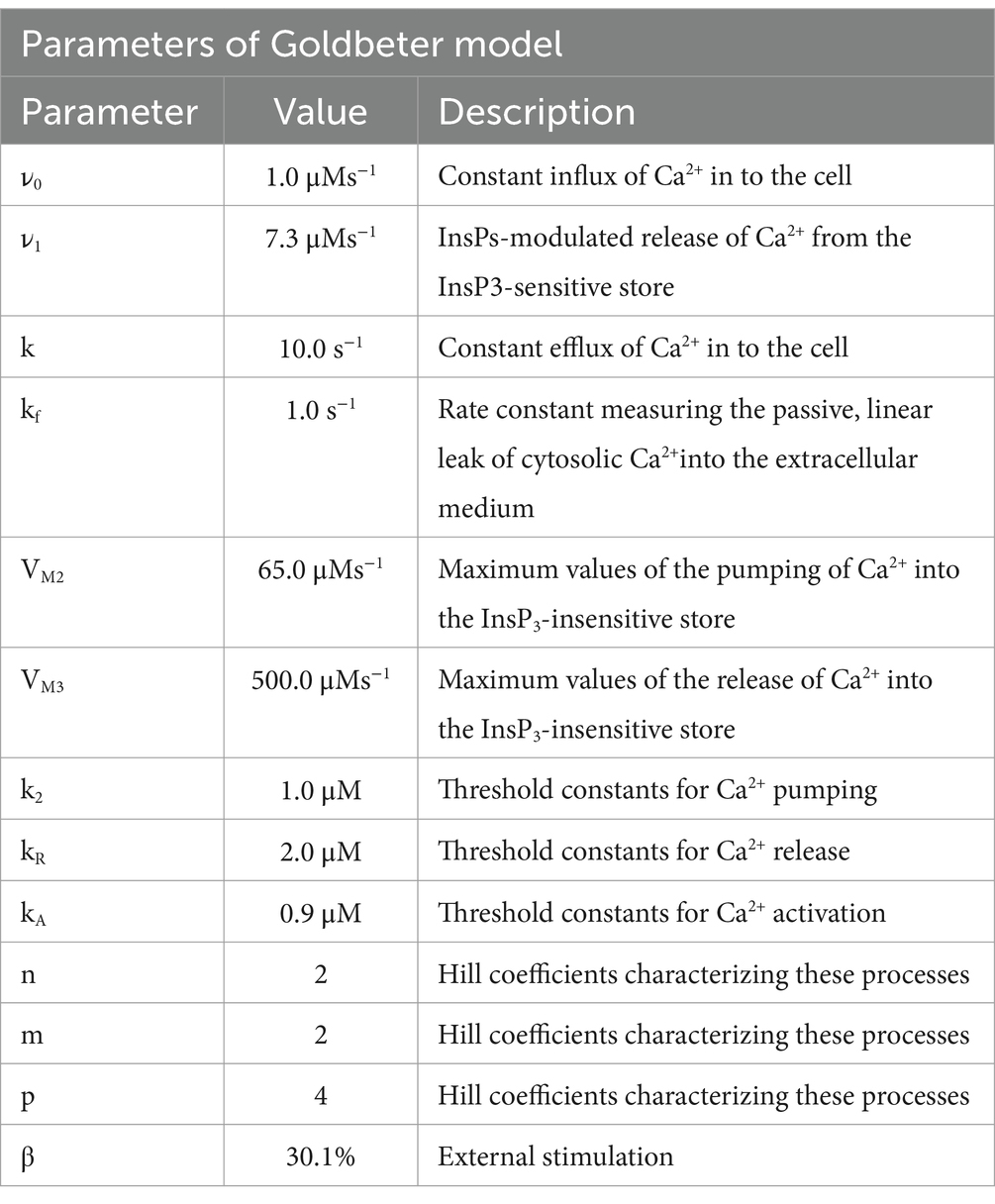
Table 1. Parameters of the Goldbeter model (Goldbeter et al., 1990).

The De Young-Keizer model

In 1992, the De Young-Keizer model (Young et al., 1992) studied the properties of the IP₃ receptor/ Ca²⁺ channel; in particular, it examined the biphasic response of the IP₃ receptor/channel to cytosolic Ca²⁺ and how this could be sufficient to induce Ca²⁺ oscillations. The rate constants in the equations were fitted to the kinetic and equilibrium data and the model successfully reproduced a series of in vivo and in vitro experiments (Berridge and Irvine, 1989; Mouillac et al., 1990; Smrcka et al., 1991; Taylor and Exton, 1987). The model incorporates a positive Ca²⁺ feedback mechanism on IP₃ production by phospholipase-C (PLC). It was noted that this enriches the properties of oscillations and leads to Ca²⁺ oscillations accompanied by IP₃ oscillations (see Figure 2). They created a simplified model of the IP₃ receptor/channel by assuming that Ca²⁺ conduction is mediated by three equivalent, independent subunits, all of which must be in a conducting state before the receptor allows Ca²⁺ to flow. There are three binding sites on each subunit, one for IP₃, one for Ca²⁺ activation and one for Ca²⁺ inactivation. Consequently, each subunit can exist in eight states, with transitions controlled by first and second order rate constants for association and dissociation, respectively. Each state is labeled with S_ijk the first index refers to the IP₃ binding site, the second to the Ca²⁺ activation site and the third to the Ca²⁺ inactivation site; i,j,k take the value 0 or 1 depending on whether the binding site is unoccupied or occluded (see Figures 3, 4).

Figure 2

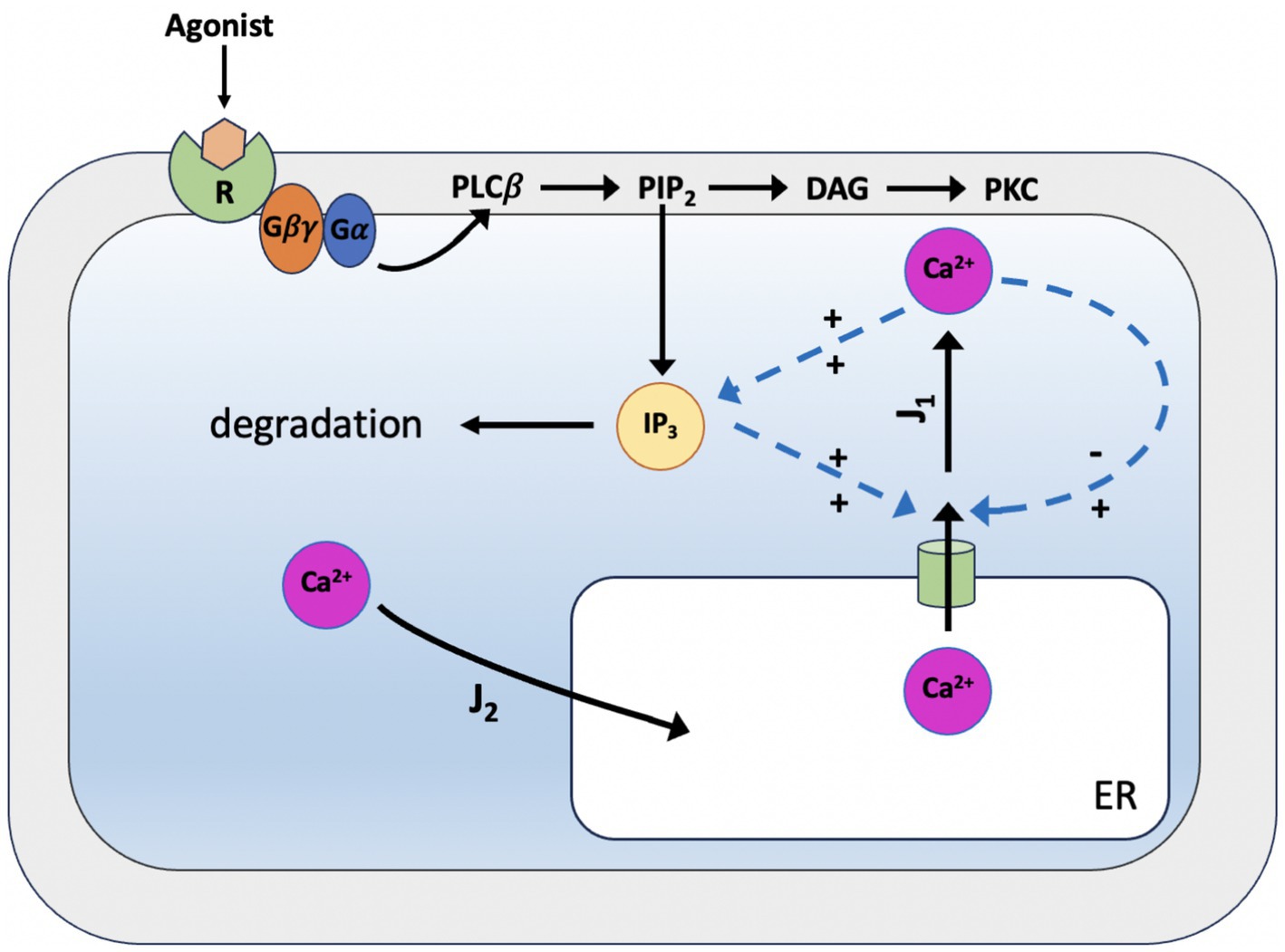
Figure 2. Scheme of the simplified De Young-Keizer kinetic model describing the properties of Ca²⁺ activation and inhibition by the inositol 1,4,5-trisphosphate (IP₃) receptor in the endoplasmic reticulum. J₁ is the outward flux of Ca²⁺, and J₂ is the inward flux. J₁ has two components, the Ca²⁺ flux through the IP₃ receptor/channel and a constant leak flux. J₂ represents the flux facilitated by the ATP-dependent Ca²⁺ pumps which actively transport Ca²⁺ from the cytosol back into the endoplasmic reticulum. The model incorporates the activity of Ca²⁺-ATPase, which is responsible for pumping Ca²⁺ back into the endoplasmic reticulum, and results in oscillations of cytoplasmic Ca²⁺ concentrations when the IP₃ concentration is held constant. This occurs with only a single pool of Ca²⁺ available for release from the endoplasmic reticulum.

Figure 3

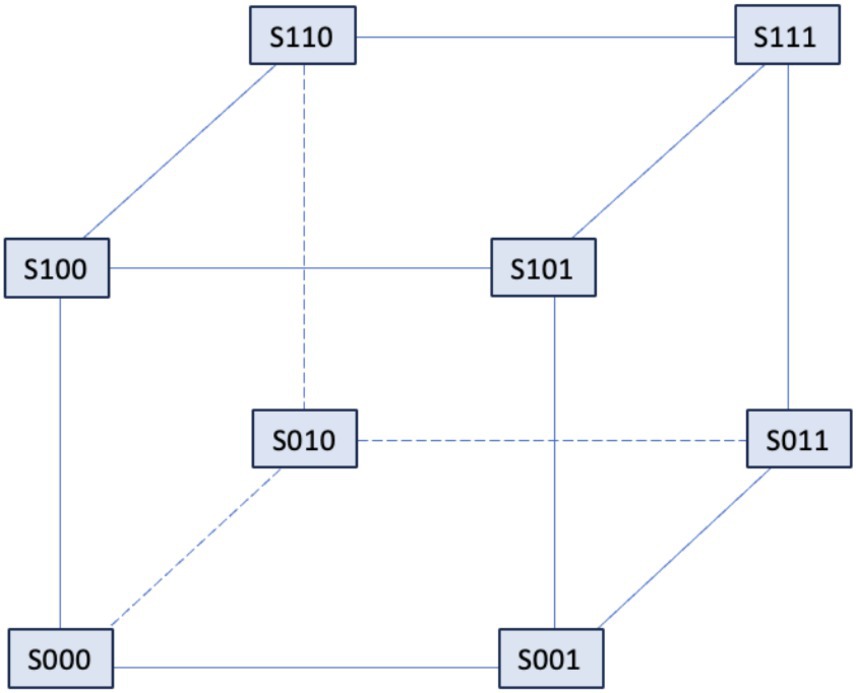
Figure 3. The IP3 receptor’s single unit’s binding mechanism. The probability that the component will be in one of the states [i,j,k], where i, j, and k can take the values 0 and 1, is shown by S_ijk. The IP₃ binding site’s condition is indicated by the first index, the activating Ca²⁺ binding site by the second, and the inhibitory Ca²⁺ binding site by the third. The corresponding binding site is unbound if an index is zero, and bound if an index is one.

Figure 4

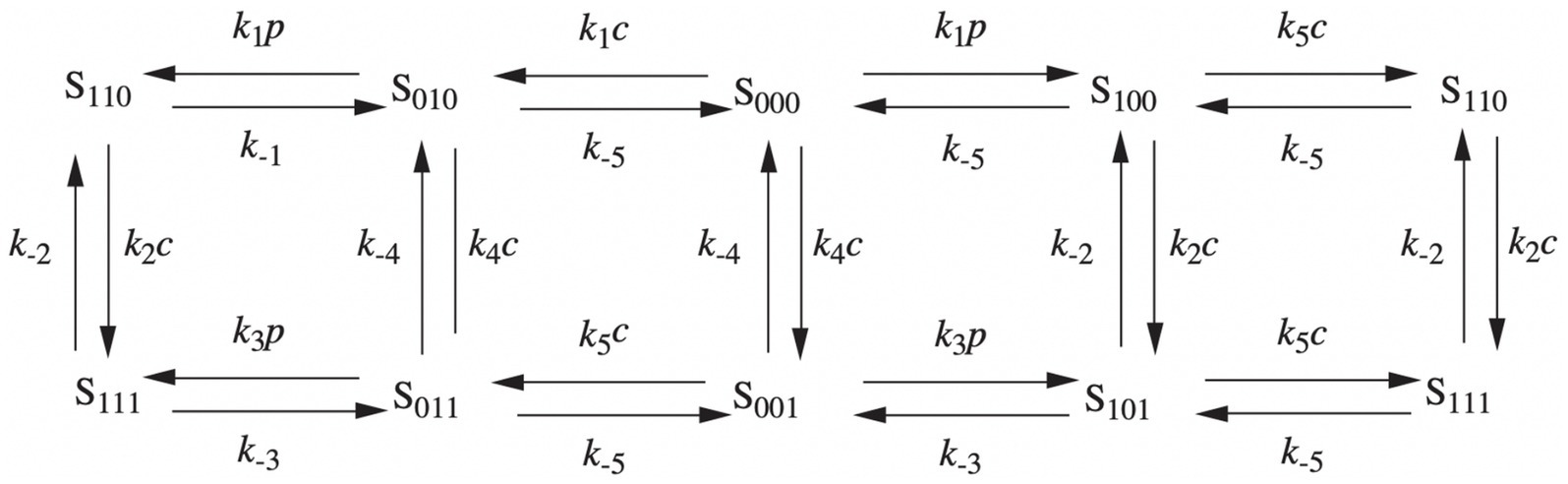
Figure 4. Binding diagram of De Young-Keizer IP₃ pattern in two dimensions. c stands for Ca²⁺ and p for IP₃.

The 24 not-all-independent speed constants of the model were reduced to 10 constants, $k_{\pm }1,\dots ,k_{\pm }5$ by introducing the following two assumptions:

i. the rate constants are independent of whether or not Ca²⁺ is bound to the activation site

ii. Ca²⁺ activation kinetics do not depend on IP₃ or Ca²⁺ inactivation.

Since experimental data indicate that the receptor subunits act cooperatively, for the channel to be open and in conduction, all three subunits must be in the S₁₁₀ state (one bound to IP₃ and one to activating Ca²⁺). The gives rise to seven differential equations for the receptor states. Although there are eight states, only seven are independent. As far as mass-action kinetics are concerned, the Ordinary Differential Equations (ODEs) for the receptor states have the present form:

$\begin{array}{l}\frac{d{x}_{000}}{dt}=\left(k_{-1}{x}_{100}-k_{1}p{x}_{000}\right)+\left(k_{-4}{x}_{001}-k_{4}c{x}_{000}\right)+\\ \mathrm{}\left(k_{-5}{x}_{010}-k_{5}c{x}_{000}\right)\end{array}\text{ (4)}$

where p denotes [IP₃] and c denotes [Ca²⁺].

The DeYoung and Keizer model consists of seven ODEs for receptor states with the following Equations 5–7 that describing the [Ca²⁺] handling of the IP₃-sensitive Ca²⁺ pool and the IP₃ production:

$\begin{array}{ll}\frac{\mathit{dc}}{dt}=J_1-J_2& (5)\end{array}$

where c is the cytosolic free Ca²⁺ concentration, J₁ is the outward flux of Ca²⁺ and J₂ is the inward flux (see Figure 2).

$\begin{array}{ll}{J}_1=c_1{\nu }_1{x}_{110}^3\left(c_{ER}-c\right)+c_1{\nu }_2\left(c_{ER}-c\right)& (6)\end{array}$

$\begin{array}{ll}{J}_2=\frac{{\nu }_3{c}^2}{c^2+k_3^2}& (7)\end{array}$

J₁ has two components, the Ca²⁺ flux through the IP₃ receptor/channel and a constant leak flux. c₁ is the ratio between the volume of the ER and the volume of the cytosol. c_ER and c are the Ca²⁺ in the ER and cytosolic Calcium, respectively; $\nu$ ₁ is the max Ca²⁺ channel flux, $\nu$ ₂ is the Ca²⁺ leak flux constant; $\nu$ ₃ is the Max Ca²⁺ uptake and K₃ is the Activation constant for ATP-Ca²⁺ pump (Table 2).

Table 2

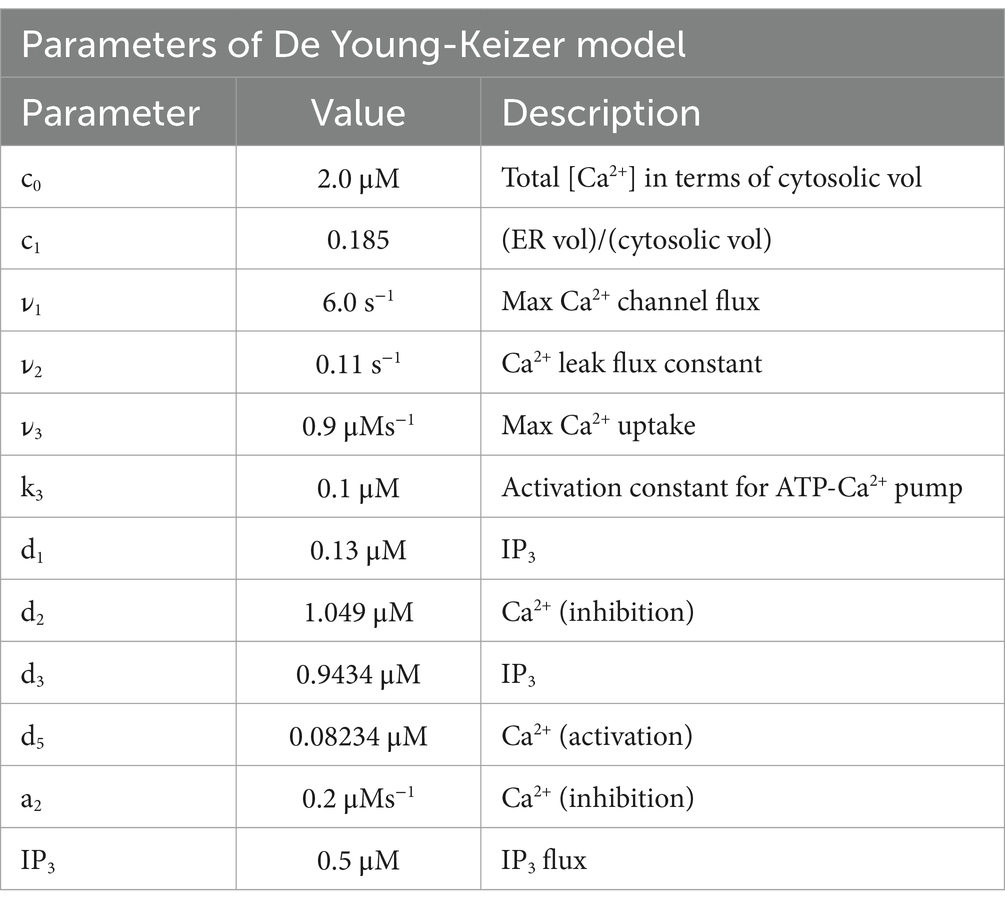
Table 2. Parameters of the De Young-Keizer model (Young et al., 1992).

The Atri model

In 1993, Atri et al. constructed a minimalist model for Ca²⁺ wave oscillations (Smrcka et al., 1991). The model, which served as the basis for a number of other models, proved simple enough to allow an understanding of the oscillatory phenomena underlying the spatio-temporal properties of Ca²⁺. A single intracellular Ca²⁺ pool that releases Ca²⁺ through the IP₃R is included in the model. It is believed that Ca²⁺ modulates the IP₃R in a biphasic manner, with intermediate Ca²⁺ acting to increase Ca²⁺ release while low and high Ca²⁺ act to block it (see Figure 5). The model takes its cue from Finch et al. (1991), and distinguishes between the time scales of channel activation and inactivation, where inactivation proceeds at a slower rate than activation. This temporal separation is critical for the spatial propagation of the Ca²⁺ signal, as inactivation must occur more gradually than activation to ensure the effective transmission of waves.

Figure 5

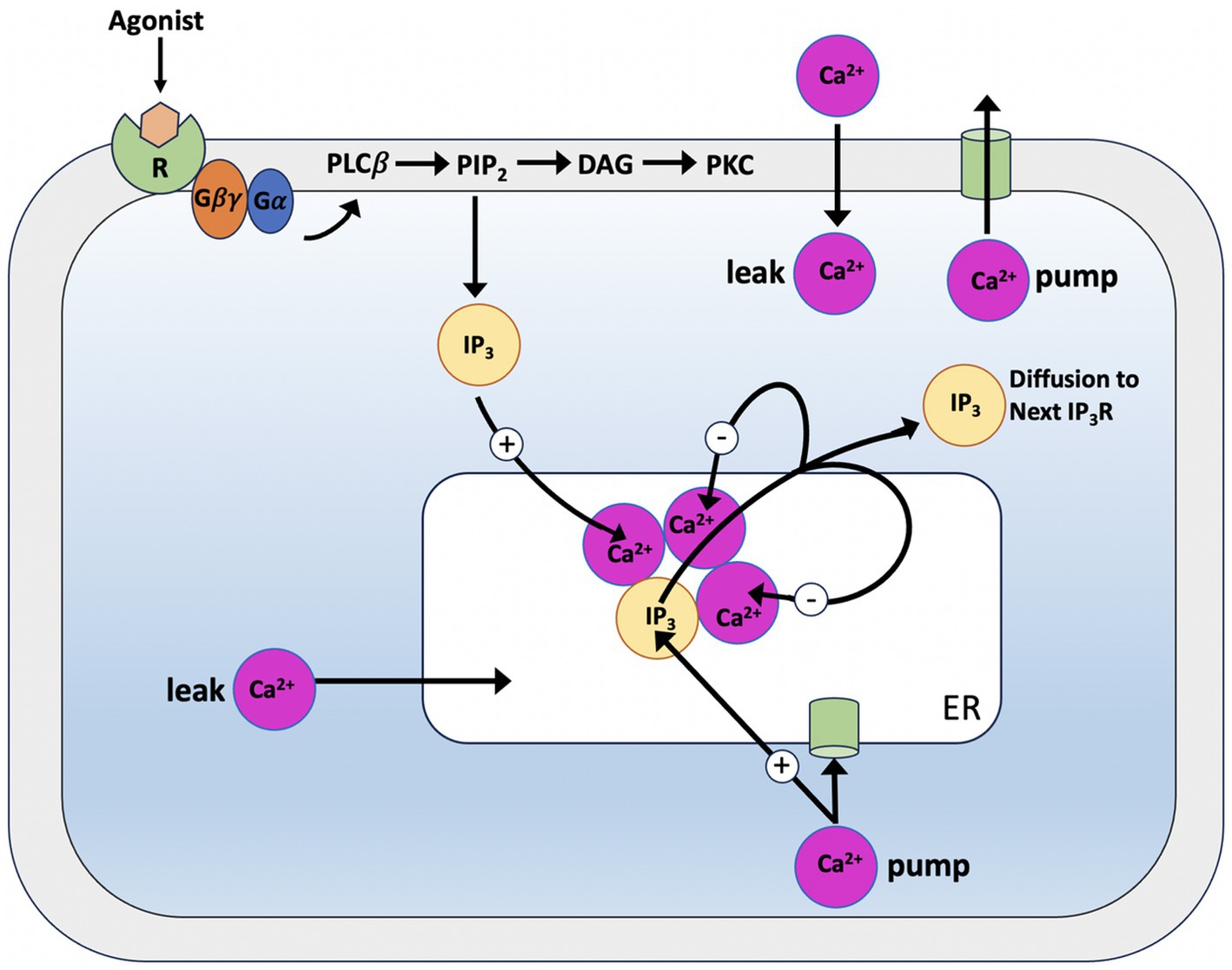
Figure 5. Schematic illustration of the Atri model. When IP₃ reaches the binding sites of the IP₃ receptor (IP₃R), it allows Calcium to leave the endoplasmic reticulum by opening a Calcium-permeable channel. After leaving the channel, Calcium diffuses to the next storage site, inactivating the channel (−) and increasing (+) the sensitivity of the IP₃R to IP₃. Ca²⁺ pumps are used to return Calcium to the storage site.

The model equation is:

$\begin{array}{ll}\frac{\mathit{dc}}{dt}=J_1+J_2-J_3& (8)\end{array}$

According to Atri et al., there are three binding domains on the IP₃ receptor, the first of which binds IP₃ and the other two bind Ca²⁺; when IP₃ is linked to domain 1 Ca²⁺ is attached to domain 2, but Ca²⁺ is not bound to domain 3, the receptor merely passes the Ca²⁺ current. Consequently, Ca²⁺ binds to domain 2 of the receptor to activate it and to domain 3 to deactivate it. Based on functionality, each binding domain consists of a certain number of binding sites. Assuming domain independence, the steady-state Ca²⁺ flux through the IP₃ receptor, J₁, is given by:

$\begin{array}{ll}{J}_1=k_f{p}_1{p}_2{p}_3& (9)\end{array}$

Where in Equation 9 $p_1$ is the probability that IP₃ is bound to domain 1, $p_2$ is the probability that Ca²⁺ is bound to domain 2 and 1; $p_3$ is the probability that Ca²⁺ is bound to domain 3; $k_f$ is a constant and represents the maximum total Ca²⁺ influx through the IP₃ receptors.

Thus, if we let c denote [Ca²⁺] can P denote [IP₃] then the following Equations 9–19 result:

$\begin{array}{ll}{p}_1={\mu }_0+\frac{{\mu }_{1}P}{k_{\mu }+P}& (10)\end{array}$

$\begin{array}{ll}{p}_2=b+\frac{V_{1}c}{k_1+c}& (11)\end{array}$

$\begin{array}{ll}{p}_3=1-\frac{c^2}{K_2^2+c^2}& (12)\end{array}$

Note that the expression of $p_3$ assumes that Ca²⁺ binds to the inactivating domain in a cooperative manner and while $p_1$ and $p_2$ are instantaneous functions of [Ca²⁺] and [IP₃], $p_3$ acts on a slower time scale, therefore:

$\begin{array}{ll}{J}_1=k_f{p}_1{p}_{2}n& (13)\end{array}$

The dimensionless variable $n$ represents the proportion of IP₃ that have not been closed by Ca²⁺ and it is described by:

$\begin{array}{ll}\frac{dn}{dt}=\frac{n_{\infty }\left(c\right)-n}{{\tau }_n}& (14)\end{array}$

$\begin{array}{ll}{n}_{\infty }c=1-\frac{c^2}{k_2^2+c^2}& (15)\end{array}$

$n_{\infty }\left(c\right)$is the steady-state value of $n$ as a function of the intracellular Calcium concentration c,

${\tau }_n$ is the time constant for the dynamics of $n$ (Table 3).

$\begin{array}{ll}{J}_1=k_{\mathit{flux}}\mu \left(\left[I{P}_3\right]\right)n\left(b+\frac{V_{1}c}{k_1+c}\right)& (16)\end{array}$

$\begin{array}{ll}{J}_2=\beta & (17)\end{array}$

$\begin{array}{ll}{J}_3=\frac{\gamma c}{k_{\gamma }+c}& (18)\end{array}$

$\begin{array}{ll}\mu \left(\left[I{P}_3\right]\right)={\mu }_0+\frac{{\mu }_1\left[I{P}_3\right]}{k_{\mu }+\left[I{P}_3\right]}& (19)\end{array}$

Table 3

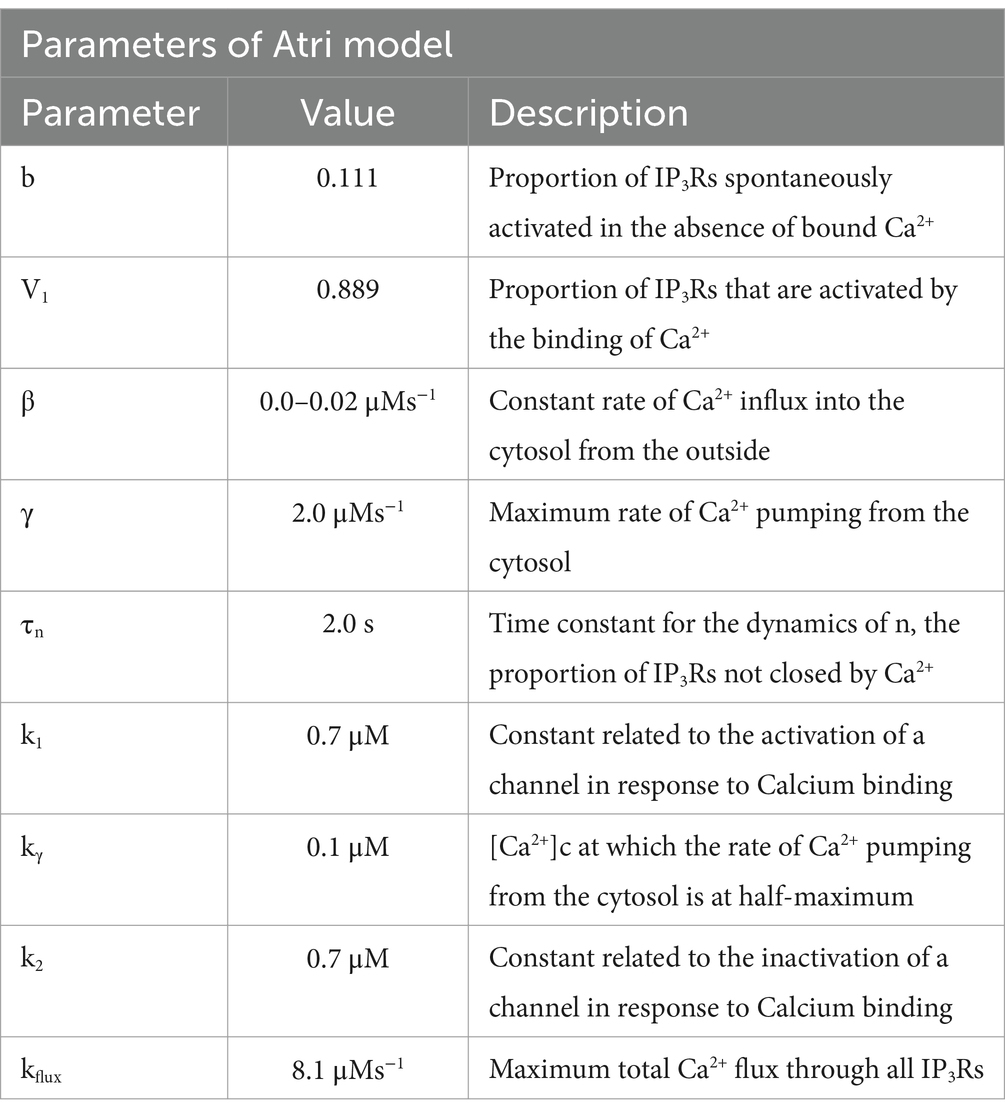
Table 3. Parameters of the Atri model (Atri et al., 1993).

The Li and Rinzel model

In 1994, Yue-Xian Li and John Rinzel deduced a model that reduces the De Young-Keizer model to a two-variable system to describe Calcium dynamics. This was mainly done by identifying the binding rates involving IP₃ and activating Ca²⁺ molecules as faster rates than the binding rate of deactivating Ca^2+. This made it possible to essentially split the model into two halves, with and without deactivating Ca²⁺ binding. The two dynamic variables of the LR model are the concentration of free cytosolic Ca²⁺ (C) and the fraction of open subunits of the inositol triphosphate receptor (h) (see Figure 6; Li and Rinzel, 1994); this result was obtained by using the method of multiple scales to solve the equations of the De Young-Keizer model on a succession of faster time scales to reduce it to a 2D system:

$\begin{array}{ll}\frac{\mathit{dc}}{dt}=J_1+J_2-J_3& (20)\end{array}$

Figure 6

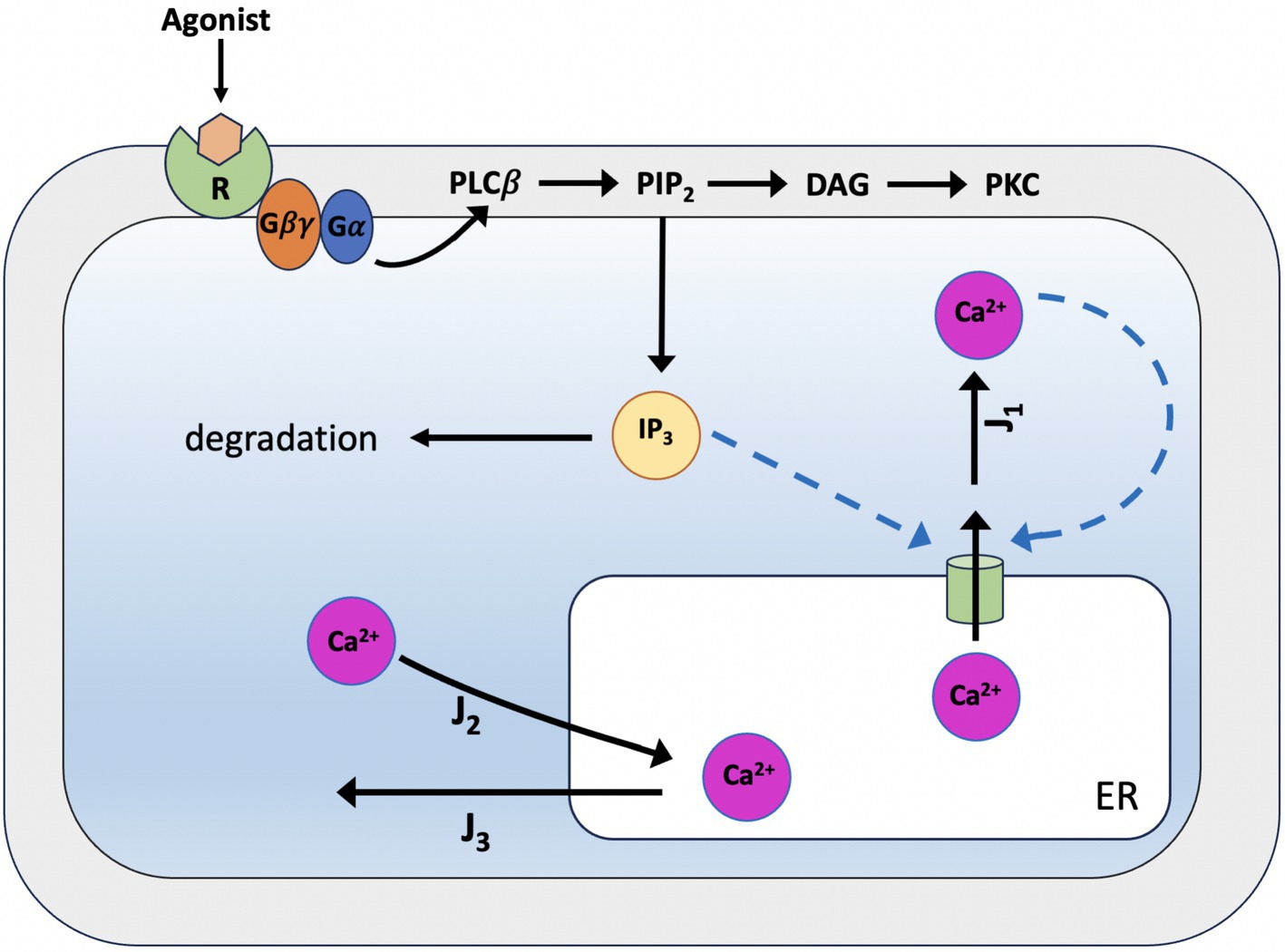
Figure 6. Schematic representation of Calcium dynamics according to the Li-Rinzel model. The model focuses on an individual cell situated within an extracellular environment devoid of Ca²⁺, thus negating the influx and efflux of Ca²⁺ through the cell membrane. Consequently, the intracellular Ca²⁺ dynamics are prompted by IP₃, which is initially required to open the IP₃ receptors on the ER membrane and prime the channels for Calcium-mediated feedback activation in the cytoplasm. Subsequently, the Calcium dynamics are governed by the interplay between Calcium-induced Calcium release (CICR), a non-linear amplification process regulated by the Calcium-dependent opening of channels to the ER’s Calcium stores, and the activity of the active SERCA pumps, which facilitate a reverse flow. Basal Ca²⁺ levels, on the other hand, are determined by the balance between a nonspecific passive loss of Ca²⁺ from the ER stores into the cytoplasm and the active uptake by SERCA pumps.

and

$\begin{array}{ll}\frac{dh}{dt}=\frac{h_{\infty }-h}{{\tau }_h}& (21)\end{array}$

with J1, J2, and J3 given by the equations:

$\begin{array}{ll}{J}_1=c_1{\nu }_1{m}_{\infty }^3{h}^3\left(c_{ER}-c\right)& (22)\end{array}$

$\begin{array}{ll}{J}_2=c_1{\nu }_2\left(c_{ER}-c\right)& (23)\end{array}$

$\begin{array}{ll}{J}_3=\frac{{\nu }_3{c}^2}{c^2+k_3^2}& (24)\end{array}$

Were J₁ is a release of Ca²⁺, mutually controlled by Ca²⁺ and by IP₃ concentration; J₂ is a passive loss of Ca²⁺ from the endoplasmic reticulum (ER) to the cytosol; and J₃ an active absorption of Ca²⁺ in ER due to the action of the pumps. Again, in Equation 22, $h=x_{000}+x_{100}+x_{010}+x_{110}$ is the fraction of channel not yet inactivated by Ca²⁺.

Along with the gating variables:

$\begin{array}{ll}{m}_{\infty }=\frac{I}{I+d_1}\frac{C}{C+d_5}& (25)\end{array}$

$\begin{array}{ll}{h}_{\infty }=\frac{Q_2}{Q_2+C}& (26)\end{array}$

$\begin{array}{ll}{T}_h=\frac{1}{a_2\left(Q_2+C\right)}& (27)\end{array}$

$\begin{array}{ll}{Q}_2=\frac{I+d_1}{I+d_3}{d}_2& (28)\end{array}$

Therefore, the level of IP₃ is directly controlled by the signals affecting the cell from its external environment. In turn, the level of IP₃ determines the dynamic behavior of the LR model. The Calcium signal can therefore be considered as coded information relating to the level of IP₃ (Table 4).

Table 4

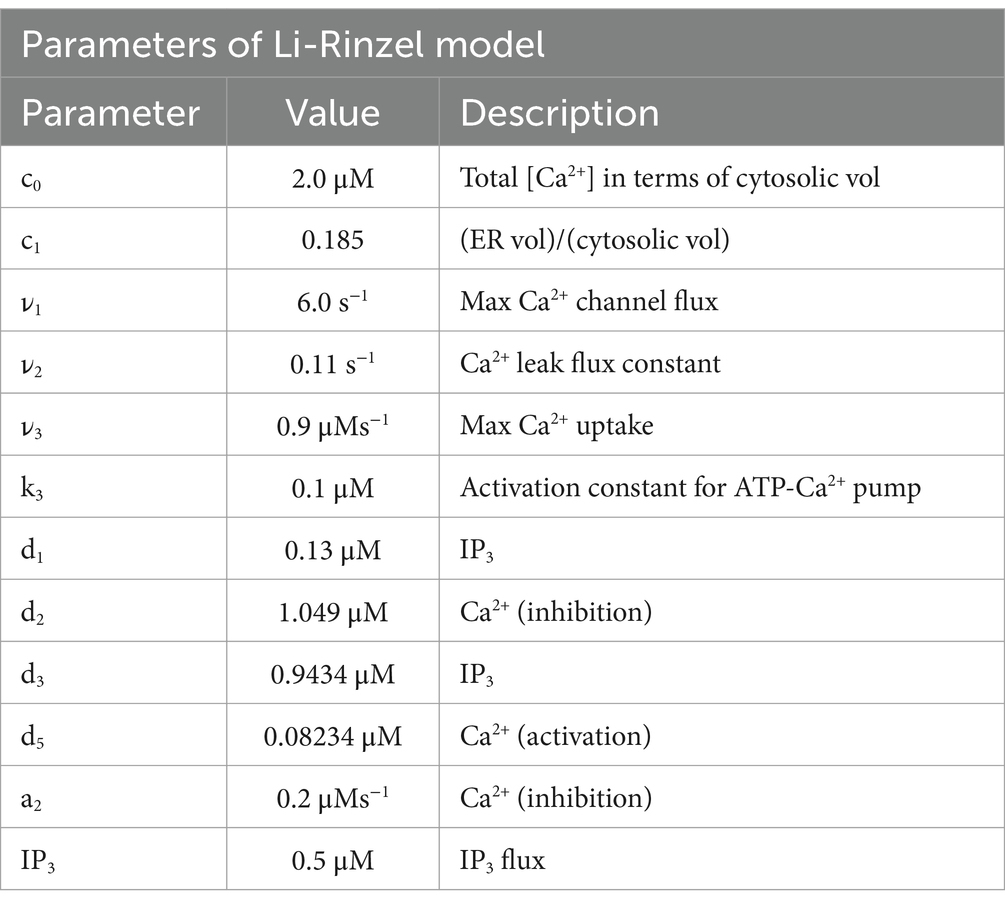
Table 4. Parameters of the Li-Rinzel model (Li and Rinzel, 1994).

Most models for Ca²⁺ dynamics are derived from the two-variable models mentioned so far. Since the realization of the pioneering models mentioned above, the intracellular dynamics of Ca²⁺ and IP₃ have been characterized much more comprehensively, and above all, specific and more sophisticated models for intracellular and extracellular Ca²⁺ dynamics in astrocytes have been realized. When astrocytes respond to stimulation, they register a variety of spatiotemporal dynamics of Ca²⁺ elevation, each of which may have its own coding. Understanding the biophysical mechanisms underlying the rich Ca²⁺ dynamics in astrocytes is important because distinct coding patterns may correspond to different downstream signaling, including gliotransmission and consequently control of synaptic function.

More recently, models have also been created for subcellular Ca²⁺ increases linked to metabotropic glutamate receptors (mluRs). Here, the models offer the possibility of establishing a link between the properties of mGluRs and their implication in intracellular Ca²⁺ dynamics.

Glutamate is the most abundant excitatory neurotransmitter in the brain and plays a crucial role in various physiological processes, including learning, memory, and synaptic plasticity.

As demonstrated by electron microscopy the outer surface of the plasma membrane of astrocytes has specific receptors for glutamate. Smith et al. (2014) showed that cultured astrocytes responded to extracellular glutamate with rapid and oscillatory elevations of intracellular free Ca²⁺ concentration (Innocenti et al., 2000; Dani et al., 1992; Charles et al., 1991). In 1994, Mennerick and Zorumski experimentally demonstrated that astrocytes are able to uptake and transport 90% of glutamate from the extracellular space (Mennerick and Zorumski, 1994); Parpura and Haydon subsequently demonstrated that astrocytes modulate neuronal excitability through the release of glutamate linked to physiologically relevant increases in Ca²⁺ (Shao and Mccarthy, 1994; Parpura and Haydon, 2000).

Metabotropic glutamate receptors (mGluRs) are membrane proteins capable of responding to glutamate, the central nervous system’s main excitatory neurotransmitter as a result, they are crucial in the transmission of signals between cells in the nervous system. Research employing in situ hybridization and immunocytochemistry reveals that mGluR3 is the most often expressed mGluR subtype in glia (Smith, 1992; Petralia et al., 1996; Wroblewska et al., 1998). Astrocytes express Group I mGluR subtypes, which includes mGluR1 and 5, reviews can be found in Barres, 1991 (Barres, 1991; Steinhäuser and Gallo, 1996; Parpura et al., 1994; Testa et al., 1995; Miller et al., 1995; Winder and Conn, 1996; Hermans and Challiss, 2001; Verkhratsky et al., 1998; Biber et al., 1999; Cai et al., 2000; Aronica et al., 2003; Perea and Araque, 2007; Araque and Navarrete, 2010; Sun et al., 2013).

It is interesting to note that cell lines that express the mGluR5 receptor are the primary source of concurrent InsP3 and Ca²⁺ oscillations. These glutamate-induced Ca²⁺ oscillations have unusual characteristics, so it is plausible that different oscillatory mechanisms prevail depending on the receptor type (Kummer et al., 2000; Lemon et al., 2003; De Pittà et al., 2009).

When glutamate binds to its membrane receptor, a sequence of events is set off: the ethorotrimeric G-protein, which is named for its three distinct polypeptide subunits, α, β, and γ, interacts with the receptor to create a receptor-G-protein complex on the inner membrane surface. When the α subunit interacts with the receptor, it undergoes a conformational shift that releases the GDP attached to it and replaces it with GTP. This, in turn, activates the phospholipase C-β (PI-PLCβ) that is specific to phosphatidyl-inositol. PI-PLCβ is located on the inner surface of the membrane, linked to the interaction between its PH domain and a PIP₂ molecule immersed in the bilayer. The PI-PLCβ enzyme catalyzes a reaction that cleaves PIP₂ into two molecules, inositol 1,4,5-triphosphate (IP₃) and diglycerol (DAG). The resultant IP₃ molecules diffuse into the cytoplasm and attach to a particular IP₃ receptor found on the smooth endoplasmic reticulum surface (Rosa et al., 2022). DAG stimulates PKC activity, which in turn phosphorylates the mGlu5 receptor at Ser-839. This phosphorylation leads to the uncoupling of the receptor from the G protein signaling cascade.

Modeling studies have not always been conducted in tandem with experimental research on mGlur receptor-mediated Ca²⁺ signaling; although mGlur receptors are highly expressed in the central nervous system (CNS) and have been linked to several pathophysiological processes as well as neuro-psychiatric disorders (Nicoletti et al., 2011; Spooren et al., 2001).

The De Pittà model

Young et al. (1992), Li and Rinzel (1994), and Höfer et al. (2002) models as a starting point, in De Pittà et al. (2009) constructed a generic model for glutamate-induced Ca²⁺ (Glu) dynamics in astrocytes, including additional biochemical processes relevant for a more realistic description of astrocyte activity. Such extensions include the production and degradation of IP₃ within the astrocyte cell, mediated by two membrane-associated enzymes, PLCβ and PLCδ (see Figure 7). Later, De Pittà and Berry (2019) further refined their model by focusing on the rate of IP₃ production following activation of glutamate receptors mGluRs, building a new model. The De Pittà model for IP₃/Ca²⁺ signaling is constituted by three ODES, respectively, for intracellular Ca²⁺ (C), the IP₃R gating (h), and the mass balance equation for intracellular IP₃ lumping terms. Regarding the differential equations for the variables C and h above, the De Pittà model considers the original Li-Rinzel model formulation described for the CICR and provides a more detailed description of IP₃ production and degradation, proposing a three-variable model for glutamate-induced intracellular Calcium dynamics caused by synaptic activity in astrocytes.

$\begin{array}{ll}\frac{\mathit{dc}}{dt}=J_1+J_2-J_3& (20)\end{array}$

$\begin{array}{ll}\frac{dh}{dt}=\frac{h_{\infty }-h}{{\tau }_h}& (21)\end{array}$

Figure 7

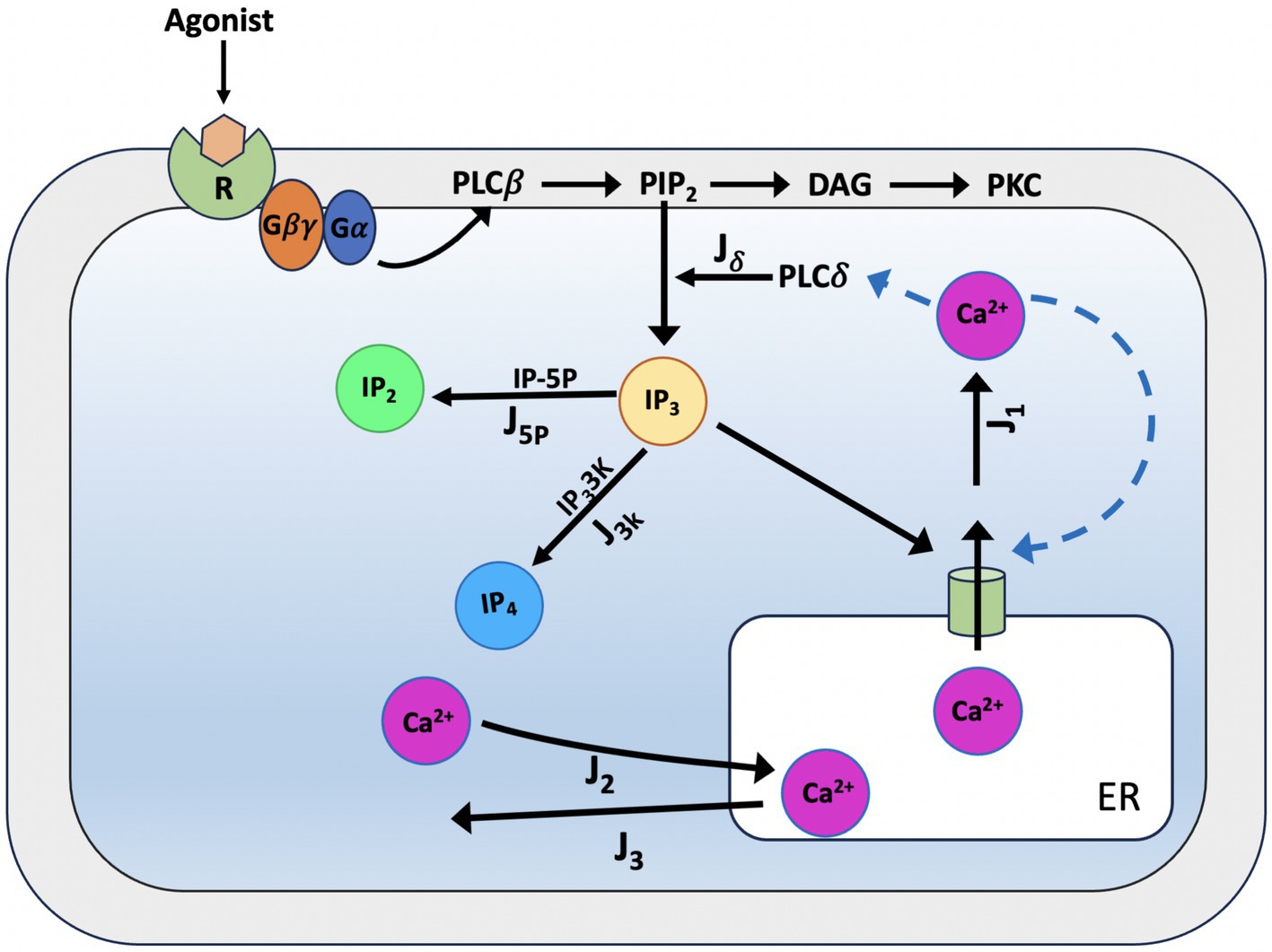
Figure 7. Schematic representation of Ca²⁺ dynamics and IP₃ production according to the De Pittà model. When glutamate binds to metabotropic glutamate receptors (mGluR1/5), the receptor activates a G_q protein, which subsequently stimulates phospholipase C-beta (PLC-β). PLC-β hydrolyses phosphatidylinositol 4,5-bisphosphate (PIP₂) into two second messengers: inositol 1,4,5-trisphosphate (IP₃) and diacylglycerol (DAG). IP₃ diffuses into the cytoplasm and binds to endoplasmic reticulum (ER) receptors (J_δ), triggering the release of Calcium ions (Ca²⁺) and initiating downstream cellular responses. IP₃ can then be degraded by IP₃-3-kinase (IP₃-3 K) (J_3K) to inositol 1,3,4,5-tetrakisphosphate (IP₄) or by inositol polyphosphate 5-phosphatase (IP-5P) (J_5p) to inositol 1,4-bisphosphate (IP₂), modulating the signaling cascade. For the CICR, the model considers the original formulation of the Li-Rinzel model (Li and Rinzel, 1994).

In astrocytes, IP₃ together with diacylglycerol (DAG) is produced by hydrolysis of phosphatidylinositol 4,5-bisphosphate (PIP₂) by two phosphoinositide-specific phospholipase C (PLC) isoenzymes, PLCβ and PLCδ (Rebecchi and Pentyala, 2000). PLCβ is primarily controlled by cell surface receptors; hence, its activity is linked to the level of external stimulation (i.e., the extracellular glutamate) and as such, it pertains to the glutamate-dependent IP₃ metabolism. PLCδ is the enzyme responsible of endogenous IP₃ production in astrocytes, it is essentially activated by increased intracellular Ca²⁺ levels (Rhee and Bae, 1997). The model proposed for PLCδ -mediated IP₃ production (J_δ) (Equation 29) derived from structural and mutational studies (Höfer et al., 2002; Pawelczyk and Matecki, 1998).

$\begin{array}{ll}{J}_{\delta }=O_{\delta }\left(1-\frac{I}{I+K_{\delta }}\right)\left(\frac{c^2}{c^2+K_{\delta }}\right)& (29)\end{array}$

where O_δ is the maximal rate of IP₃ production by PLCδ and K_δ is the inhibition constant of PLCδ activity. According to experiments, PLCδ activity is inhibited by high IP₃ concentrations (> 1 μM) because they compete with PIP₂ for the enzyme’s binding (Allen and Barres, 2009).

In astrocytes there are two several pathways for IP₃ degradation: the dephosphorylation of IP₃ by inositol polyphosphate 5-phosphatase (IP-5P), and the phosphorylation of phosphorylation of IP₃ by the IP₃3-kinase (IP₃-3 K). For the description of the two IP₃ degradation dynamics we use the relations given by Equations 30, 31:

$\begin{array}{ll}{J}_{5p}=O_{5p}\left(\frac{I}{I+K_{5p}}\right)& (30)\end{array}$

where O_5p is the maximal rate of IP-5P mediated IP₃ degradation in the linear approximation.

For IP₃-3 K degradation we can write:

$\begin{array}{ll}{J}_{3K}=O_{3K}\left(\frac{c_4}{c_4+K_{3K}^4}\right)\left(\frac{I}{I+K_{3K}}\right)& (31)\end{array}$

where O_3k is the maximal rate of IP₃ degradation by IP₃-3 K.

In summary, the De Pittà model of Ca²⁺ dynamics with endogenous IP₃ metabolism (Equation 32) is based on the two LR equations but the IP₃ concentration (I) is now provided by a third coupled differential Equations 20a, 20, 21, 21b, 33.

$\begin{array}{ll}\frac{dI}{dt}=J_{\delta }-J_{5p}-J_{3K}& (32)\end{array}$

$\begin{array}{l}\frac{dI}{dt}=O_{\delta }\left(1-\frac{I}{I+K_{\delta }}\right)\left(\frac{c^2}{c^2+K_{\delta }}\right)-O_{5p}\left(\frac{I}{I+K_{5p}}\right)-\\ \mathrm{}{O}_{3K}\left(\frac{c_4}{c_4+K_{3K}^4}\right)\left(\frac{I}{I+K_{3K}}\right)\end{array}\text{ (33)}$

The model highlights the complex biochemical reactions coupled with Ca²⁺ dynamics via the different second messengers (Table 5).

Table 5

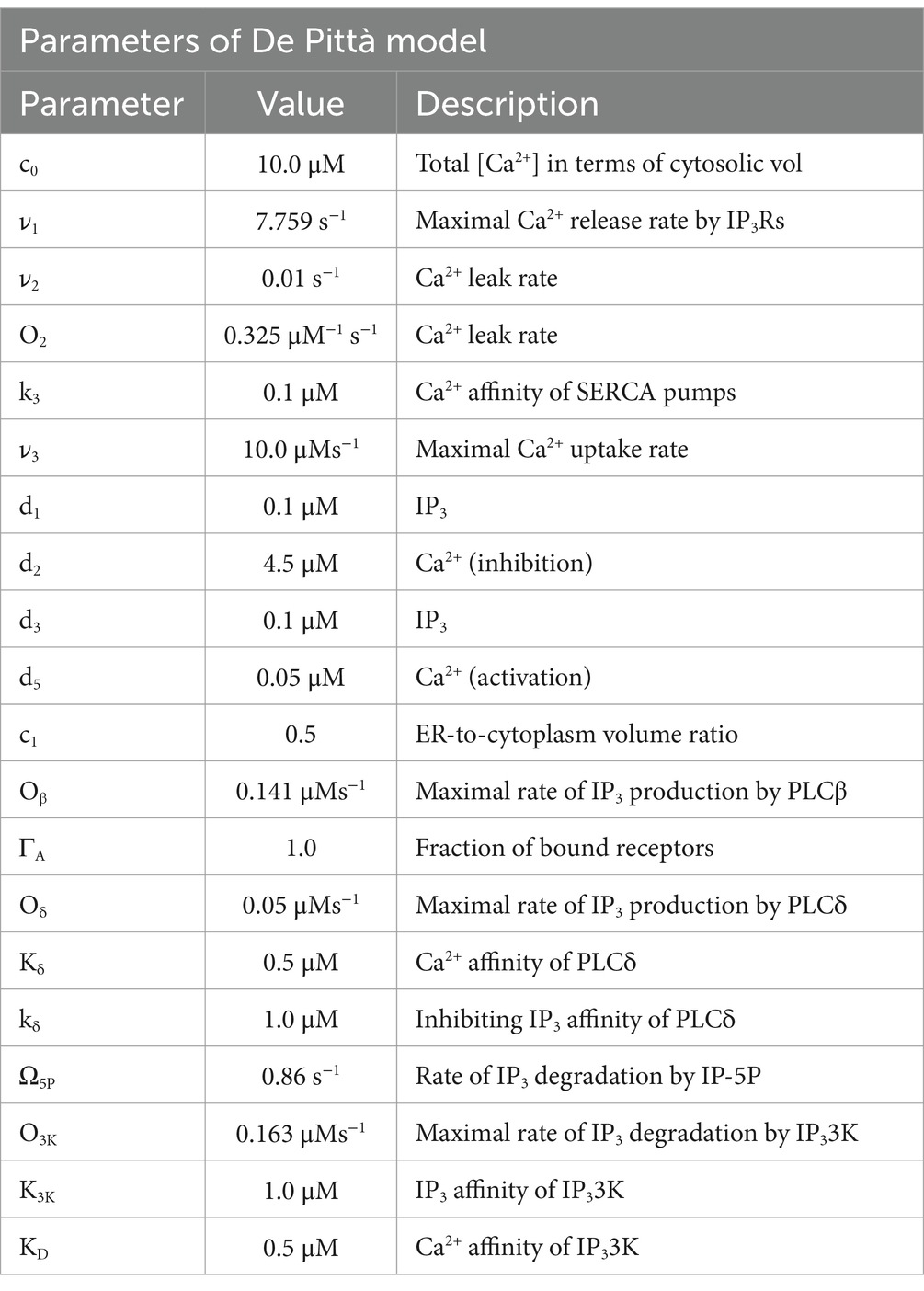
Table 5. Parameters of the De Pittà model (De Pittà and Berry, 2019).

Data sources

For the acquisition of experimental data, the methodology described in the article “Dynamics of Astrocytes Ca²⁺ Signaling: A Low-Cost Fluorescence Customized System for 2D Cultures” was adopted (Musotto et al., 2024), this study provides temporal and spatial data of Calcium signaling in astrocytes using an innovative and inexpensive fluorescence imaging system designed for two-dimensional (2D) cell cultures. The analysis was performed on immortalized human astrocytes, the raw data for all cells in the well analyzed are shown in Figure 8.

Figure 8

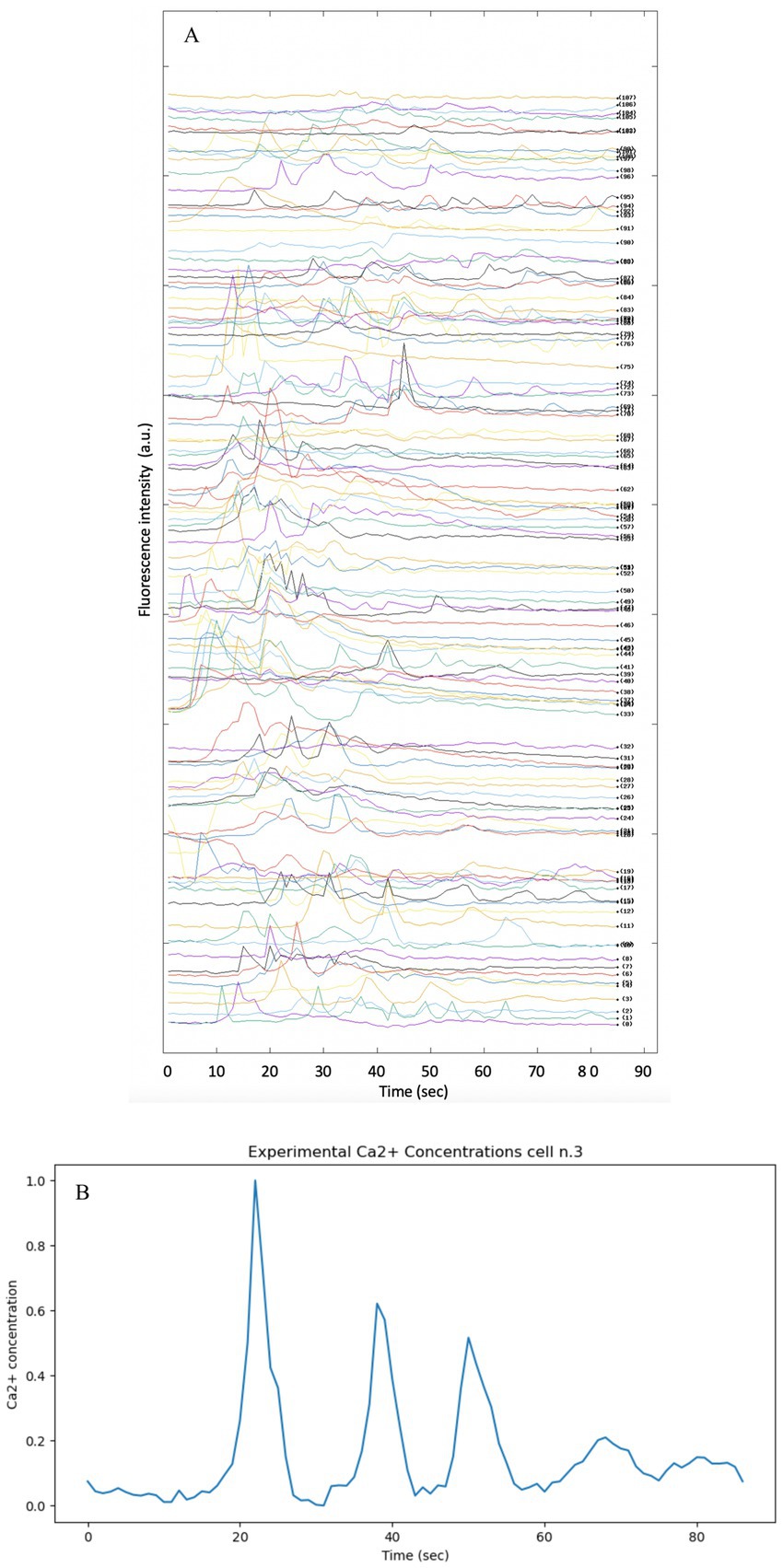
Figure 8. Fluorescence intensity profiles showing the spontaneous activity of intracellular Ca²⁺ in immortalized human astrocytes. The methodology and instrument described in Musotto et al. (2024) was used to produce the experimental data. (A) Split image of each Ca²⁺ cell present in the well under analysis. The Ca²⁺ signal of each cell present in the well was split in order to provide all data simultaneously. (B) Intensity vs. time profile of Ca²⁺ fluorescence intensity in cell n.3.

The background was subtracted from the raw data and normalized by calculating the change in fluorescence (ΔF) from baseline fluorescence (F₀) (Wamhoff et al., 2002). This normalization process is essential to ensure that the data reflect true physiological changes rather than artifacts introduced by variable dye loading.

In order to visualize the variables on different scales and to facilitate comparison between theoretical and experimental data, all data were scaled by the min-max normalization method in the range [0,1]. In order to compare the theoretical Ca²⁺ signal obtained from the models reported in the article, cell no. Three was chosen arbitrarily (see Figure 8B)

Comparing model predictions with experimental data makes it possible to assess the accuracy and reliability of models, identify discrepancies and refine models accordingly.

Results

The Goldbeter model

The Goldbeter model is known to describe intracellular Calcium oscillations, which in many biological situations exhibit regular and periodic behavior, but is highly sensitive to the parameters that govern it; in this form, it appears to be insufficient to explain the experimental data on Ca²⁺ dynamics in astrocytes. The theoretical model, as reported in the original article, describes the Calcium dynamics over a shorter time interval (10 s), while the experimental data cover a longer period (87 s). By extending the integration time of the model to 87 s, so as to be comparable with the experimental time, it can be observed that the Z oscillations persist throughout the interval with a fairly stable amplitude and frequency. The oscillations do not disappear and the system does not converge to a static equilibrium, but seems to maintain a repetitive oscillation pattern. The pattern is set to produce sustained oscillations that continue for longer times. The parameters of the pattern determine how fast Calcium enters, is released and is removed from the various compartments of the cell. To adapt the model to the much slower experimental Ca²⁺ dynamics, the model parameters must be modified. The experimental data provided show less regular behavior and more unpredictable amplitude variations. The large differences observed suggest that the actual biological system is more complex and requires optimization of model parameters or more refined modeling (Figure 9).

Figure 9

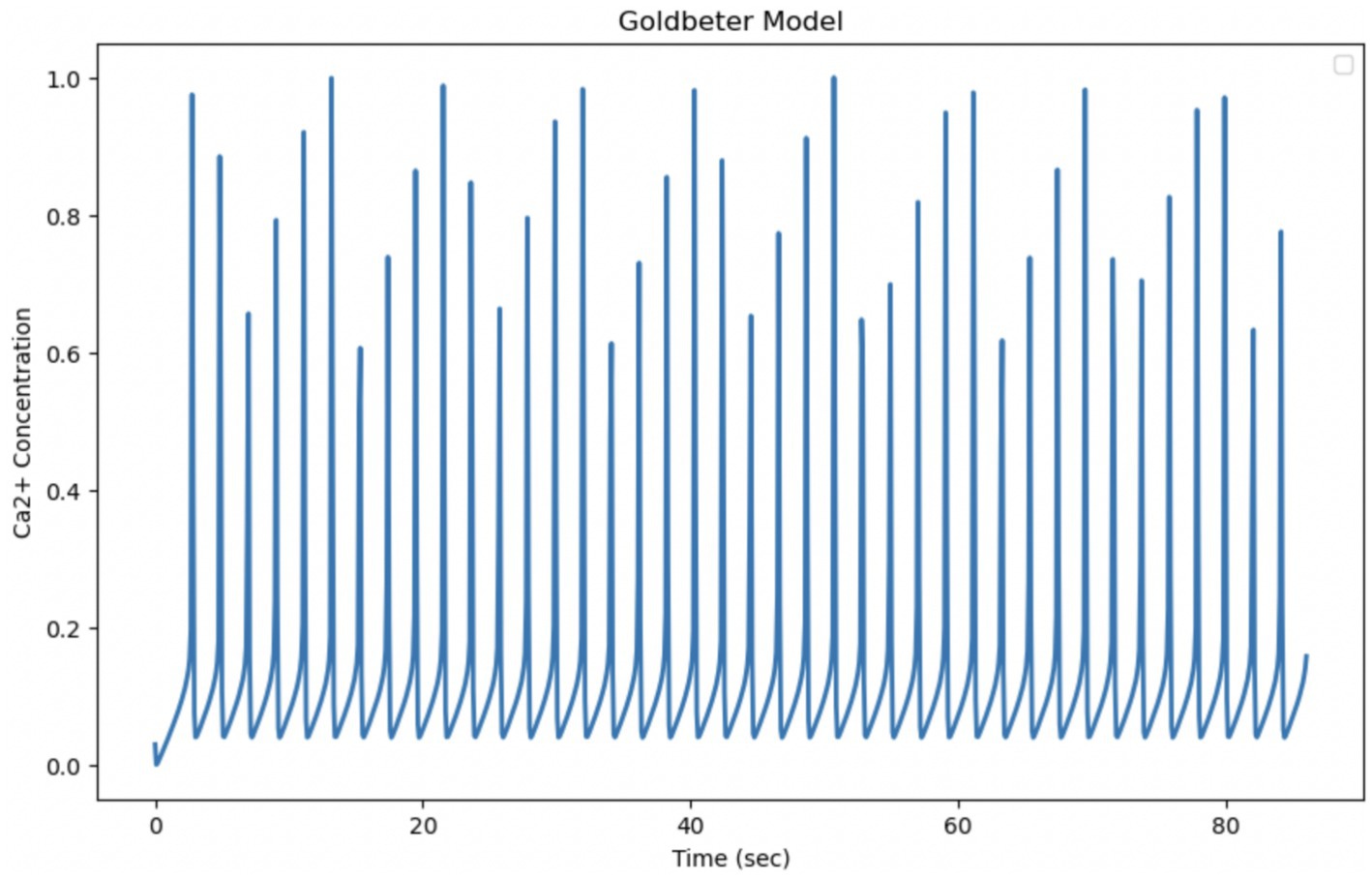
Figure 9. Simulation of the Golbeter model (Goldbeter et al., 1990). Curves obtained by integrating Equations 1 and 2 with the parameters shown in Table 1. Fluctuations of cytosolic Ca²⁺ concentration in 87 s, a time comparable to the experimental observation time. Goldbeter et al. obtained the reported fluctuations with an external stimulation β of 30.1%.

The Atri model

The Atri model is based on a simplified system of differential equations that mainly considers the release and pumping of intracellular Calcium. By extending the simulation of the model to make it temporally comparable with experimental data, whose observation time is equal to 87 s, it can be seen that the oscillations are regular, with stable amplitude and average frequency. The experimental data, on the other hand, show changes in the behavior of Calcium over a period of 87 s, with an initial activation phase, a maximum peak, and a subsequent decline. This indicates that the biological system may have richer temporal dynamics that the model cannot fully reproduce. These discrepancies suggest that the model, in its current form, fails to fully capture the complexity of the experimental behavior of intracellular Calcium in astrocytes. A key factor in the Atri model is the gating variable n, which regulates the opening of Calcium release channels. This variable introduces a feedback mechanism that can influence the frequency of oscillations, making the model more flexible with respect to the timing of oscillation (Figure 10).

Figure 10

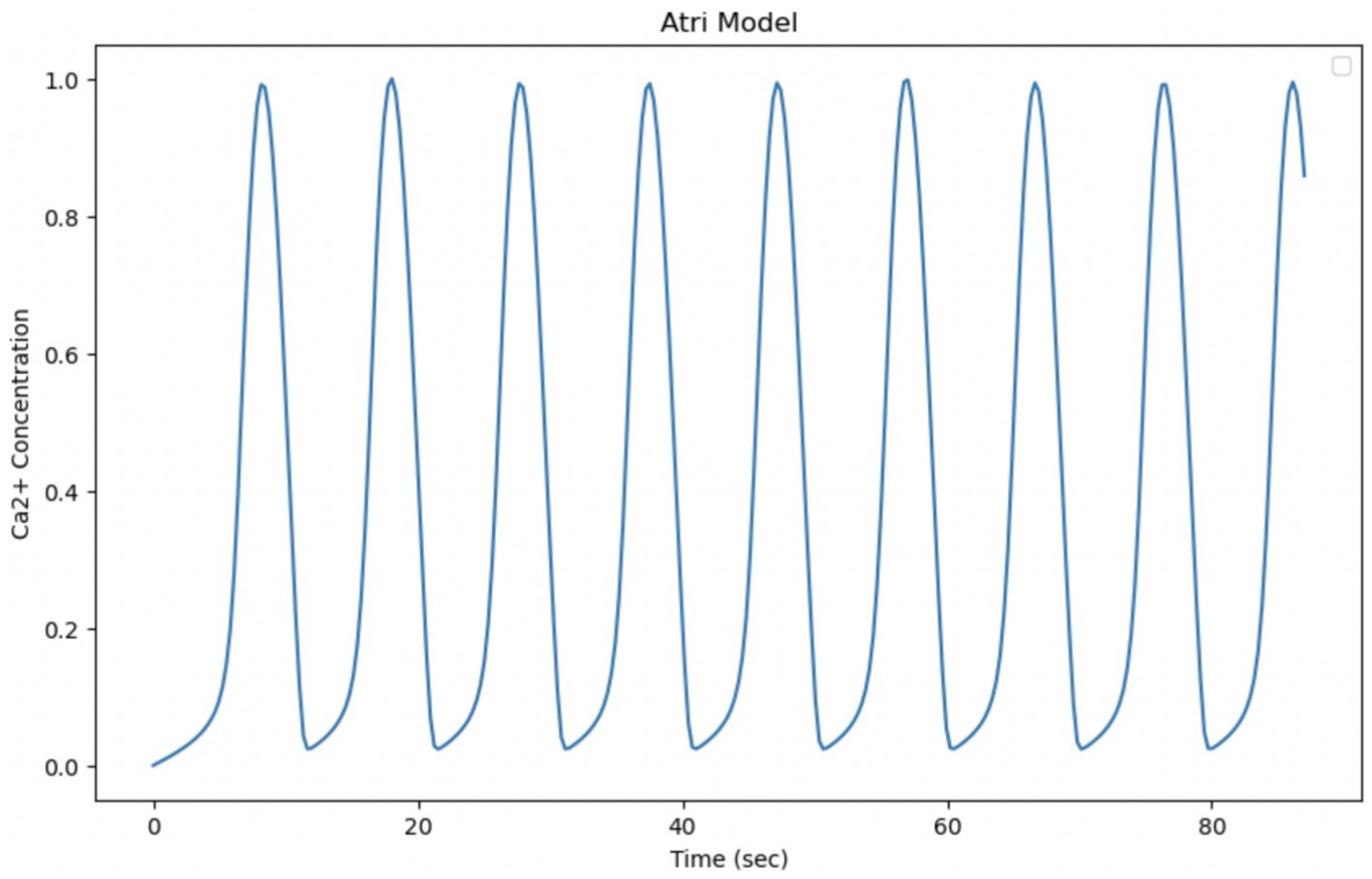
Figure 10. Simulation of the Atri model. Curves obtained by integrating Equations 8, 19 with the parameters shown in Table 3. Oscillation of cytosolic Ca²⁺ concentration in 87 s, time comparable with experimental observation time.

The Li-Rinzel model

The Li-Rinzel model originates from a reduction of the more complex model of De Young and Keizer, with the aim of simplifying the description of intracellular Calcium oscillations while maintaining the ability to reproduce experimentally observed phenomena. The model is particularly useful for describing the regulation of Calcium release via IP₃ receptors in the endoplasmic reticulum. It explicitly introduces the Calcium concentration in the endoplasmic reticulum as a dynamic variable, which makes it more detailed in its description of the Calcium release and reabsorption cycle and capable of reproducing more regular and structured oscillations than simpler models. The ability of the model to generate slow Ca²⁺ input-dependent oscillations, as in Figure 5 of the article “Equations for InsP, Receptor-mediated [Ca²⁺], Oscillations Derived from a Detailed Kinetic Model: A Hodgkin-Huxley Like Formalism,” makes it more suitable for comparison with our experimental data on Ca²⁺ signaling in astrocytes. However, the regularity of oscillations predicted by the model may be less realistic than experimentally observed oscillations, which tend to be more irregular and less predictable (Figure 11).

Figure 11

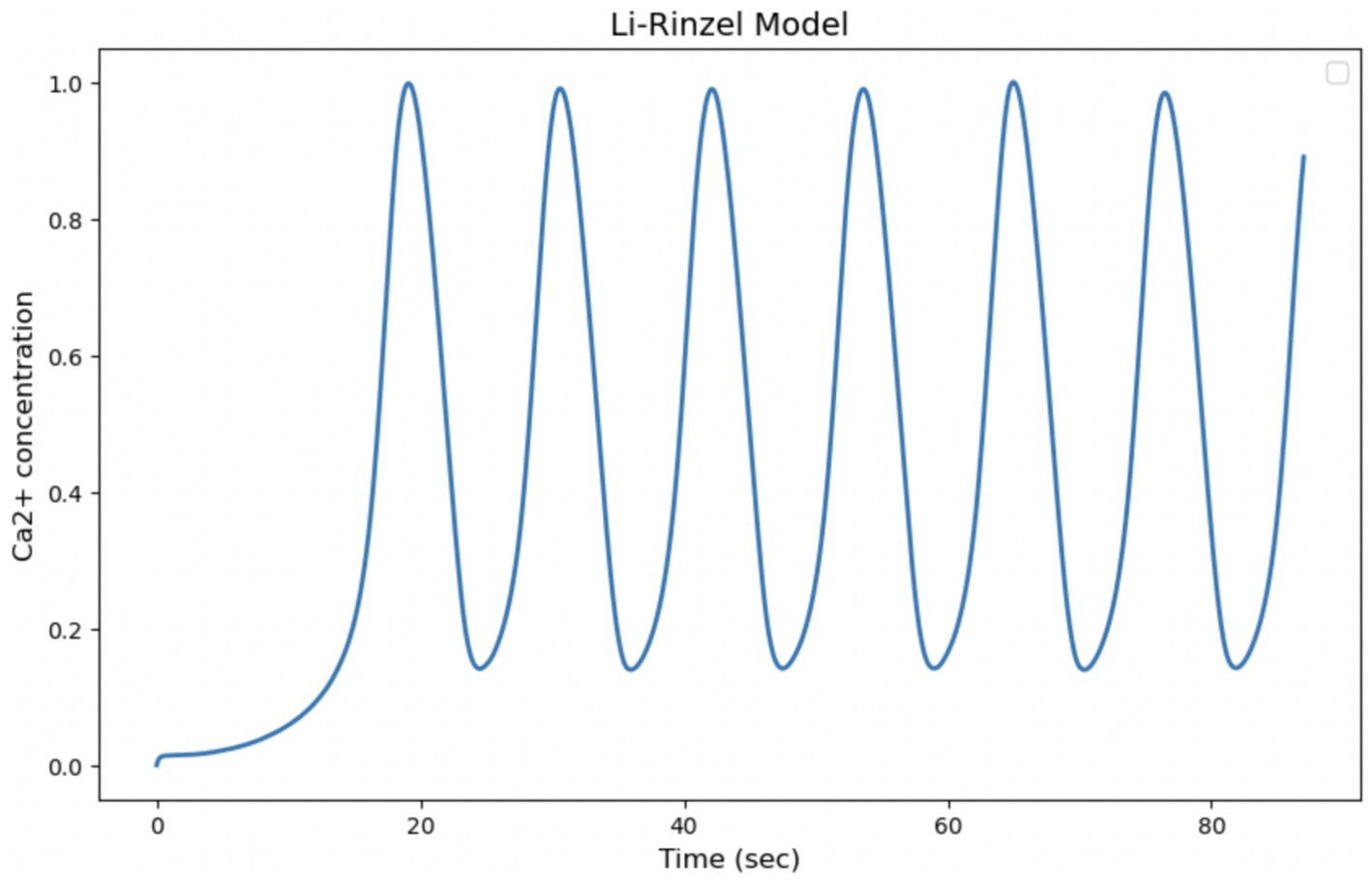
Figure 11. Simulation of the Li-Rinzel model. Curves obtained by integrating Equations 20, 21 with the parameters shown in Table 4. Oscillation of cytosolic Ca²⁺ concentration in 87 s, time comparable with experimental observation time.

The De Pittà model

The De Pittà model is a powerful tool to describe intracellular Calcium oscillations regulated by G-protein-coupled receptors. In the model, G-protein-coupled receptors, when activated, induce the release of IP₃, which in turn stimulates the release of Calcium from the endoplasmic reticulum. The released Calcium can further activate Calcium release channels through the process of induced Calcium release (CICR), creating positive feedback. Like many other Calcium oscillation models, De Pittà includes positive feedback (via CICR) and negative feedback (via Calcium reabsorption in the endoplasmic reticulum or degradation of the IP₃ signal). These mechanisms are crucial for the generation of regular oscillations. Although it provides a realistic description of IP₃ and CICR mediated Calcium release, it has some limitations compared to experimental data, particularly with regard to its ability to capture the irregularity and variability of Calcium oscillations. The experimental data show much more dynamic and complex behavior, with significant variations in amplitude and frequency that the model does not fully reproduce in its current form. In order to have a better fit to the experimental data, the parameters could be calibrated. Optimization of Calcium release and absorption rates, as well as IP₃ dynamics, could improve the fit of the model (Figure 12; Table 6).

Figure 12

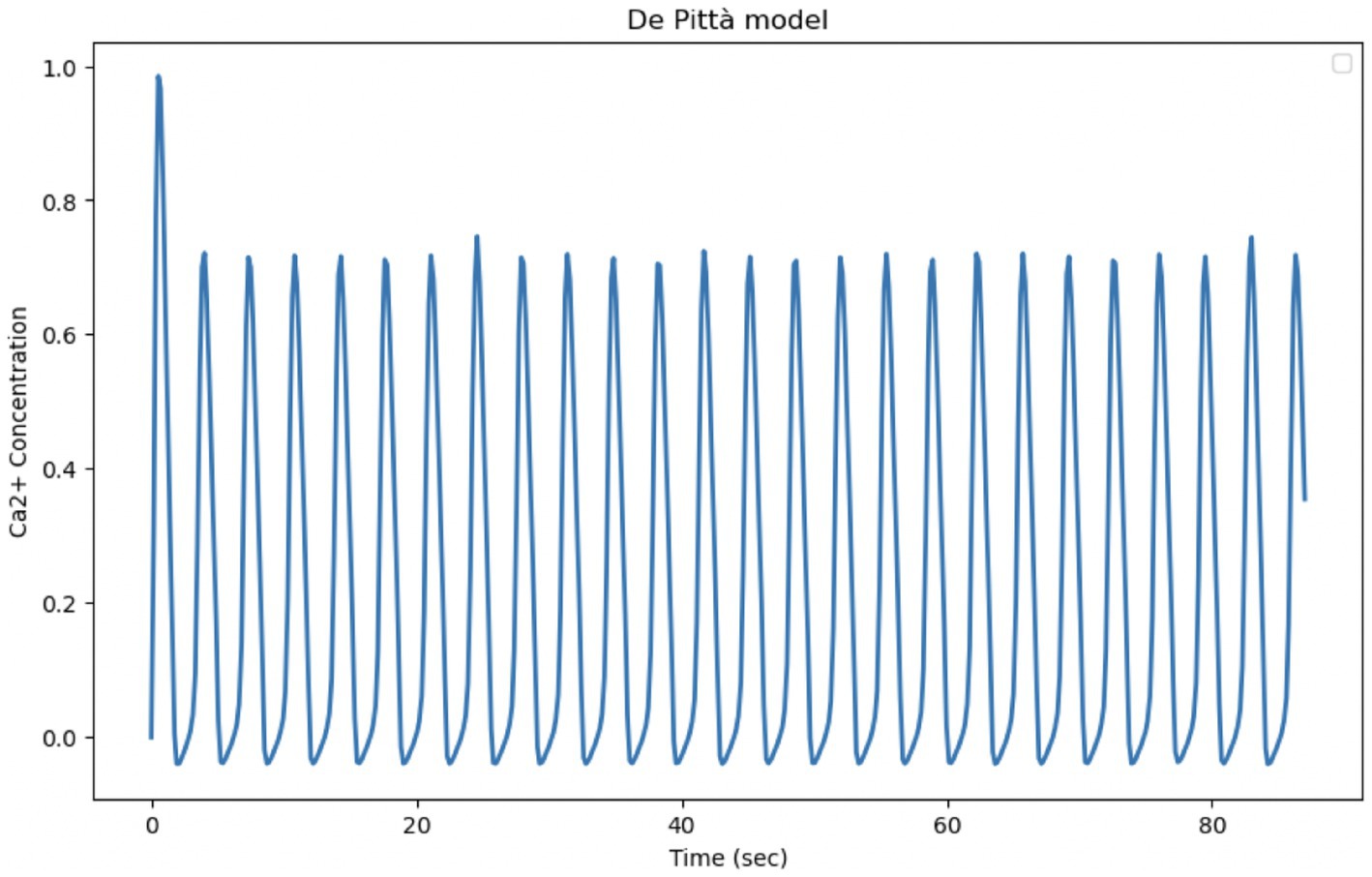
Figure 12. Reproduction of the De Pittà model. Curves obtained by integrating Equations 20, 21 of the Li-Rinzel model relating to Calcium-induced Calcium dynamics (CIRC) with Equation 31 relating to IP3 production and degradation. The model parameters are shown in Table 4. Oscillation of cytosolic Ca²⁺ concentration of the model in 87 s, time comparable with experimental observation time.

Table 6

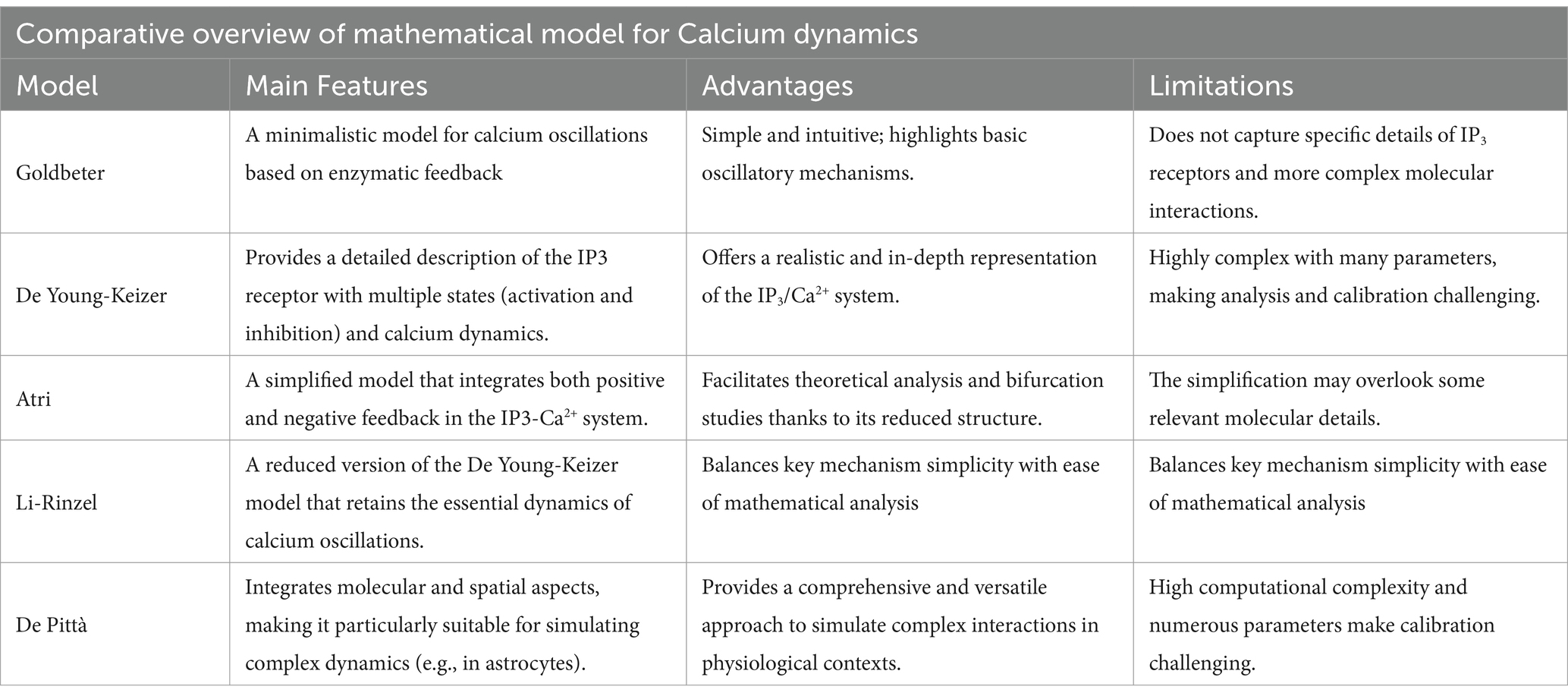
Table 6. This table summarizes the main features, advantages, and limitations of the Goldbeter, De Young-Keizer, Atri, Li-Rinzel, and De Pittà models, providing with a quick reference to understand the merits and constraints of each modeling approach.

Discussion

Over the past 20 years, many computational models for intracellular Ca²⁺ dynamics have been developed. They differ according to the level of description, from the microscopic level, for which stochastic models must be used, to the macroscopic level, which requires deterministic models. In this review, five models of intracellular Ca²⁺ dynamics were evaluated (Goldbeter et al., 1990; Young et al., 1992; Atri et al., 1993; Li and Rinzel, 1994; De Pittà and Berry, 2019), implementing the equations based on what was presented in the original publications. Our aim was to reproduce the simulation results of the original articles and compare them with the experimental data in our possession (Musotto et al., 2024) in order to determine which model was most suitable.

The aim of the mathematical models analyzed in this contribution is to interpret the emergence of complex intracellular Calcium dynamics as the result of interdependent Ca²⁺ fluxes between the cytosol and intracellular stores, driven by the interaction with IP₃. The models are described by systems of non-linear ordinary differential equations (ODEs), which are capable of supporting self-sustained Calcium oscillations. These phenomenological models have been developed to reproduce Calcium flow behavior comparable with available experimental data and have played a crucial role in the advancement of neuroscience, serving as a bridge between experimental observations and the development of more in-depth theories. All models discussed here are described by deterministic equations, meaning that the effects of stochastic fluctuations due to microscopic inhomogeneities and noise due to spatial localization or random fluctuations are neglected. Indeed, one of the limitations of deterministic models is that they produce oscillations that are too regular compared to those observed experimentally. The addition of stochastic components could improve the models’ ability to fit the experimental data. It has been shown that IP₃ channels are distributed in clusters on the ER membrane, generating Ca²⁺ signals on multiple scales, ranging from local puffs to global intra- and extracellular waves. It should be pointed out that our observation of intracellular Ca²⁺ dynamics in astrocytes is given by whole-cell oscillations. These signals are believed to include release from the multiple compartmentalized processes within the cell (Bindocci et al., 2017; Smith and Parker, 2009) that give rise to the observed global Ca²⁺ oscillations.

From the study of the models reported in this paper, a common problem emerges: the period of intracellular Ca²⁺ fluctuations are faster than that observed experimentally. The period of Calcium fluctuations in astrocytes is generally slower, often occurring within seconds or minutes. Research indicates that Calcium signals in astrocytes can be attributed to delayed release from internal stores, leading to slower kinetics than in neuron (Ma et al., 2021). Furthermore, astrocyte Calcium transients can be influenced by various signaling pathways, including those mediated by inositol trisphosphate (IP₃) and ryanodine receptors, which contribute to the complexity and variability of astrocyte Calcium dynamics (Stobart et al., 2018; Corkrum et al., 2019). The frequency and duration of these Calcium events can vary significantly depending on the physiological state of the astrocytes and the surrounding neuronal activity (Schnell et al., 2011; Mcdougal et al., 2013). In summary, while Calcium fluctuations in some cells and neurons are rapid and occur on the millisecond scale, astrocyte Calcium signaling operates on a slower time scale, typically between seconds and minutes, with the possibility of intercellular propagation of Calcium waves. Of the five models studied, only four were implemented, as the Li-Rinzel model is a simplification of the De Young-Keizer model and it was decided not to simulate the latter because it was too computationally expensive. The models analyzed in this review were simulated using the parameters reported in the original studies. Each model has unique mechanisms and parameters that influence the dynamics of Ca²⁺ signaling. A general comparison of the four implemented models shows that they have different abilities to modulate Ca²⁺ frequencies, varying in complexity and adaptability. Goldbeater model generates constant frequencies that depend on the parameters of Ca²⁺ release and accumulation without direct influence from IP₃. This model is suitable for constant and rhythmic cellular responses. In Atri model, the frequency of oscillations varies depending on the levels of IP₃ and the rate of binding of IP₃ to its receptors. The oscillations are influenced by spatial diffusion, which allows variable frequencies and the formation of Ca²⁺ waves ideal for complex communications between different cellular regions. In Li and Rinzel model, the frequency of Ca²⁺ oscillations are dependent on the concentration of IP₃. As IP₃ increases, the frequency of Ca²⁺ oscillations also increase. This model is used to analyze cellular responses that must vary gradually with external stimuli. The most complex of the models analyzed, the G-ChI model, describes the Ca²⁺ frequency as a result of the dynamic interaction between Ca²⁺, IP₃, and GPCR receptors. Oscillations in this model respond to different synaptic stimuli, with frequencies modulated by enzymes such as PLC and PKC. It therefore allows a highly adjustable frequency, ideal for neurobiological functions in astrocytes.

In the present contribution, a comparison of five models representing different modeling approaches, with the aim of identifying which of these bests fit our experimental data. The selected model will be used as a basis for developing a model with a structure derived from the application of physical principles as in Gawthrop and Crampin (2017). Considering the heterogeneity of astrocytes reported in the literature (Khakh and Sofroniew, 2015), future extensions of the model should include parameters representing the phenotypic and functional variability of the cells to obtain simulations that better reflect the complexity of astrocytic responses observed experimentally. Moreover, since Ca²⁺ puffs (irregular) and oscillations (much more regular) can be observed in the same cell for different stimulus levels, the study of Ca²⁺ dynamics offers the fascinating possibility of studying the transition from a stochastic to a deterministic regime.

It should also be pointed out that although in vitro models allow us to gain insight into the cellular mechanisms underlying Ca2+ regulation, they tend to simplify the cellular environment by isolating astrocytes from other cell types and their natural interactions. Indeed, as pointed out by Stogsdill et al. (2023), astrocytes are an integral part of complex neural networks, and their Ca²⁺ activity is influenced by signals from neurons and other glial cells. The use of computational models built by integrating both in vitro and in vivo experimental data allow a better understanding of Ca²⁺ signaling and its role in neuronal functions (Manninen et al., 2018).

Conclusion

The article reports the findings of a comparative study of some of the most significant models for Calcium dynamics in astrocytes. The evolution from minimal models to more complex models, that consider additional biochemical processes for a more realistic description of astrocyte activity, is discussed. We compared mathematical models and experimental data of Ca²⁺ in astrocytes. The experimental data reveal complex oscillatory dynamics with different frequencies and amplitudes, reflecting the intricate regulatory mechanisms of Ca²⁺ signaling in astrocytes. Our analysis shows that the Goldbeter model, although effective in generating stable oscillations, does not allow to capture the variability in measured frequency and amplitude. The Atri model introduces a spatial wave dynamic, which could mimic some variations in the dynamics of experimental oscillations, but fails to reproduce the full range of dynamic behavior. The Li-Rinzel model, through IP₃-dependent modulation, provides a closer approximation of the experimental data, allowing for frequency adjustments; however, it remains limited in capturing amplitude variability. The De Pittà model, on the other hand, aligns more closely with experimental observations, as it incorporates detailed GPCR and enzymatic feedback mechanisms that allow for both frequency and amplitude modulation. This latter model successfully replicates the observed changes in Ca²⁺ dynamics, making it suitable for studying the role of astrocytes in neural signaling and synaptic regulation.

It is important to note that astrocytes exhibit remarkable heterogeneity in their morphology, molecular expression, and functional responses, which varies across different brain regions and microcircuits (Khakh and Sofroniew, 2015). Incorporating this cellular diversity into computational models could enhance their ability to accurately reflect the range of astrocytic calcium dynamics observed experimentally.

Mathematical modeling of Ca²⁺ signaling in astrocytes has emerged as a critical tool for understanding the complex dynamics of the glial cells in the central nervous system. These models help elucidate the mechanisms by which astrocytes respond to neuronal activity and maintain homeostasis through Calcium signaling.

In summary, mathematical models of Ca²⁺ signaling in astrocytes are essential for deciphering the complex interactions between astrocytes and neurons. These models not only improve our understanding of normal physiological processes, but also provide a framework for studying the altered Calcium dynamics associated with various neurological disorders. Future research using these models will likely continue to reveal the intricate role of astrocytes in brain function and their potential as therapeutic targets in neurodegenerative diseases.

Author contributions

RM: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. UW: Data curation, Supervision, Writing – review & editing. GP: Resources, Supervision, Validation, Visualization, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the project “NeuroSuite: Un nuovo sistema intelligente e predittivo per il supporto alla decisione clinica nelle neuro-fragilità” (Cod. F/350230/01-05/X60), supported by the Italian Ministry of Enterprises and Made in Italy (Ministero delle Imprese e del Made in Italy).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allen, N. J., and Barres, B. A. (2009). Glia more than just brain glue. Nature 457, 675–677. doi: 10.1038/457675a

PubMed Abstract | Crossref Full Text | Google Scholar

Anderson, C. M., and Swanson, R. A. (2000). Astrocyte glutamate transport: review of properties, regulation, and physiological functions. Glia 32, 1–14. doi: 10.1002/1098-1136(200010)32:1<1::AID-GLIA10>3.0.CO;2-W

PubMed Abstract | Crossref Full Text | Google Scholar

Araque, A., and Navarrete, M. (2010). Glial cells in neuronal network function. Philos. Trans. R. Soc. B Biol. Sci. 365, 2375–2381. doi: 10.1098/rstb.2009.0313

PubMed Abstract | Crossref Full Text | Google Scholar

Araque, A., Sanzgiri, R. P., Parpura, V., and Haydon, P. G. (1999). Astrocyte-induced modulation of synaptic transmission. Can. J. Physiol. Pharmacol. 77, 699–706. doi: 10.1139/y99-076

Crossref Full Text | Google Scholar

Aronica, E., Gorter, J. A., Ijlst-Keizers, H., Rozemuller, A. J., Yankaya, B., Leenstra, S., et al. (2003). Expression and functional role of mGluR3 and mGluR5 in human astrocytes and glioma cells: opposite regulation of glutamate transporter proteins. Eur. J. Neurosci. 17, 2106–2118. doi: 10.1046/j.1460-9568.2003.02657.x

PubMed Abstract | Crossref Full Text | Google Scholar

Atri, A., Amundson, J., Clapham, D., and Sneyd, J. (1993). A single-pool model for intracellular calcium oscillations and waves in the Xenopus laevis oocyte. Biophys. J. 65, 1727–1739. doi: 10.1016/S0006-3495(93)81191-3

PubMed Abstract | Crossref Full Text | Google Scholar

Backus, K. H., Kettenmann, H., and Schachner, M. (1989). Pharmacological characterization of the glutamate receptor in cultured astrocytes. J. Neurosci. Res. 22, 274–282. doi: 10.1002/jnr.490220307

PubMed Abstract | Crossref Full Text | Google Scholar

Barres, B. A. (1991). Glial ion channels. Curr. Opin. Neurobiol. 1, 354–359. doi: 10.1016/0959-4388(91)90052-9

PubMed Abstract | Crossref Full Text | Google Scholar

Berridge, M. J., and Irvine, R. F. (1989). Inositol phosphates and cell signalling. Nature 341, 197–205. doi: 10.1038/341197a0

PubMed Abstract | Crossref Full Text | Google Scholar

Biber, K., Laurie, D. J., Berthele, A., Sommer, B., Tölle, T. R., Gebicke-Härter, P. J., et al. (1999). Expression and signaling of group I metabotropic glutamate receptors in astrocytes and microglia. J. Neurochem. 72, 1671–1680. doi: 10.1046/j.1471-4159.1999.721671.x

PubMed Abstract | Crossref Full Text | Google Scholar

Bindocci, E., Savtchouk, I., Liaudet, N., Becker, D., Carriero, G., and Volterr, A. (2017). Three-dimensional Ca²⁺ imaging advances understanding of astrocyte biology. Science 356:eaai8185. doi: 10.1126/science.aai8185

Crossref Full Text | Google Scholar

Cai, Z., Schools, G. P., and Kimelberg, H. K. (2000). Metabotropic glutamate receptors in acutely isolated hippocampal astrocytes: developmental changes of mGluR5 mRNA and functional expression. Glia 29, 70–80. doi: 10.1002/(SICI)1098-1136(20000101)29:1<70::AID-GLIA7>3.0.CO;2-V

PubMed Abstract | Crossref Full Text | Google Scholar

Charles, A. C., Merrill, J. E., Dirksen, E. R., and Sanderson, M. J. (1991). Intercellular signaling in glial cells: calcium waves and oscillations in response to mechanical stimulation and glutamate. Neuron 6, 983–992. doi: 10.1016/0896-6273(91)90238-U

PubMed Abstract | Crossref Full Text | Google Scholar

Clarke, L. E., and Barres, B. A. (2013). Emerging roles of astrocytes in neural circuit development. Nat. Rev. Neurosci. 14, 311–321. doi: 10.1038/nrn3484

PubMed Abstract | Crossref Full Text | Google Scholar

Condorelli, D. F., Dell'Albani, P., Corsaro, M., Giuffrida, R., Caruso, A., Salinaro, A. T., et al. (1997). Metabotropic glutamate receptor expression in cultured rat astrocytes and human gliomas. Neurochem. Res. 22, 1127–1133. doi: 10.1023/A:1027317319166

PubMed Abstract | Crossref Full Text | Google Scholar

Corkrum, M., Rothwell, P. E., Thomas, M. J., Kofuji, P., and Araque, A. (2019). Opioid-mediated astrocyte neuron signaling in the nucleus accumbens. Cells 8:586. doi: 10.3390/cells8060586

PubMed Abstract | Crossref Full Text | Google Scholar

Cornell-Bell, A. H., Finkbeiner, S. M., Cooper, M. S., and Smith, S. J. (1990). Glutamate induces calcium waves in cultured astrocytes: long-range glial signaling. Science 247, 470–473. doi: 10.1126/science.1967852

PubMed Abstract | Crossref Full Text | Google Scholar

Dani, J. W., Chernjavsky, A., and Smith, S. J. (1992). Neuronal activity triggers calcium waves in hippocampal astrocyte networks. Neuron 8, 429–440. doi: 10.1016/0896-6273(92)90271-E

PubMed Abstract | Crossref Full Text | Google Scholar

Dantoni, S., Berretta, A., Bonaccorso, C. M., Bruno, V., Aronica, E., Nicoletti, F., et al. (2008). Metabotropic glutamate receptors in glial cells. Neurochem. Res. 33, 2436–2443. doi: 10.1007/s11064-008-9694-9

PubMed Abstract | Crossref Full Text | Google Scholar

De Pittà, M., and Berry, H. (2019). A neuron–glial perspective for computational neuroscience. Comput. Gliosci., 3–35. doi: 10.1007/978-3-030-00817-8

Crossref Full Text | Google Scholar

De Pittà, M., Goldberg, M., Volman, V., Berry, H., and Ben-Jacob, E. (2009). Glutamate regulation of calcium and IP₃ oscillating and pulsating dynamics in astrocytes. J. Biol. Phys. 35, 383–411. doi: 10.1007/s10867-009-9155-y

PubMed Abstract | Crossref Full Text | Google Scholar

Dupont, G., and Goldbeter, A. (1993). One-pool model for Ca²⁺ oscillations involving Ca²⁺ and inositol 1, 4, 5-trisphosphate as co-agonists for Ca²⁺ release. Cell Calcium 14, 311–322. doi: 10.1016/0143-4160(93)90052-8

PubMed Abstract | Crossref Full Text | Google Scholar

Eddleston, M., and Mucke, L. (1993). Molecular profile of reactive astrocytes implications for their role in neurologic disease. Neuroscience 54, 15–36. doi: 10.1016/0306-4522(93)90380-X

PubMed Abstract | Crossref Full Text | Google Scholar

Eid, T., Williamson, A., Lee, T.-S. W., Petroff, O. A., and de Lanerolle, N. C. (2008). Glutamate and astrocytes key players in human mesial temporal lobe epilepsy? Epilepsia 49, 42–52. doi: 10.1111/j.1528-1167.2008.01492.x

PubMed Abstract | Crossref Full Text | Google Scholar

Fellin, T., Pascual, O., Gobbo, S., Pozzan, T., Haydon, P. G., and Carmignoto, G. (2004). Neuronal synchrony mediated by astrocytic glutamate through activation of extra synaptic NMDA receptors. Neuron 43, 729–743. doi: 10.1016/j.neuron.2004.08.011

PubMed Abstract | Crossref Full Text | Google Scholar

Fellin, T., Pascual, O., and Haydon, P. G. (2006). Astrocytes coordinate synaptic networks: balanced excitation and inhibition. Physiology 21, 208–215. doi: 10.1152/physiol.00161.2005

PubMed Abstract | Crossref Full Text | Google Scholar

Fiacco, T. A., and Mccarthy, K. D. (2006). Astrocyte calcium elevations: properties, propagation, and effects on brain signaling. Glia 54, 676–690. doi: 10.1002/glia.20396

PubMed Abstract | Crossref Full Text | Google Scholar

Finch, E. A., Turner, T. J., and Goldin, S. M. (1991). Calcium as a coagonist of inositol 1, 4, 5-trisphosphate-induced calcium release. Science 252, 443–446. doi: 10.1126/science.2017683

PubMed Abstract | Crossref Full Text | Google Scholar

Gawthrop, P. J., and Crampin, E. J. (2017). Bond graph modelling of chemoelectrical energy transduction. IET Syst. Biol. 11, 127–138. doi: 10.1049/iet-syb.2017.0006

Crossref Full Text | Google Scholar

Goldbeter, A., Dupont, G., and Berridge, M. J. (1990). Minimal model for signal-induced Ca²⁺ oscillations and for their frequency encoding through protein phosphorylation. Proc. Natl. Acad. Sci. 87, 1461–1465. doi: 10.1073/pnas.87.4.1461

PubMed Abstract | Crossref Full Text | Google Scholar

Haydon, P. G., and Carmignoto, G. (2006). Astrocyte control of synaptic transmission and neurovascular coupling. Physiol. Rev. 86, 1009–1031. doi: 10.1152/physrev.00049.2005

PubMed Abstract | Crossref Full Text | Google Scholar

Hermans, E., and Challiss, R. A. J. (2001). Structural, signalling and regulatory properties of the group I metabotropic glutamate receptors: prototypic family C G-protein-coupled receptors. Biochem. J. 359, 465–484. doi: 10.1042/bj3590465

Crossref Full Text | Google Scholar

Höfer, T., Venance, L., and Giaume, C. (2002). Control and plasticity of intercellular calcium waves in astrocytes: a modeling approach. J. Neurosci. 22, 4850–4859. doi: 10.1523/JNEUROSCI.22-12-04850.2002

PubMed Abstract | Crossref Full Text | Google Scholar

Innocenti, B., Parpura, V., and Haydon, P. G. (2000). Imaging extracellular waves of glutamate during calcium signaling in cultured astrocytes. J. Neurosci. 20, 1800–1808. doi: 10.1523/JNEUROSCI.20-05-01800.2000

PubMed Abstract | Crossref Full Text | Google Scholar

Jiang, H., Aćimović, J., Manninen, T., Ahokainen, I., Stapmanns, J., Lehtimäki, M., et al. (2024). Modeling neuron-astrocyte interactions in neural networks using distributed simulation.

Google Scholar

Jourdain, P., Bergersen, L. H., Bhaukaurally, K., Bezzi, P., Santello, M., Domercq, M., et al. (2007). Glutamate exocytosis from astrocytes controls synaptic strength. Nat. Neurosci. 10, 331–339. doi: 10.1038/nn1849

PubMed Abstract | Crossref Full Text | Google Scholar

Kang, N., Xu, J., Xu, Q., Nedergaard, M., and Kang, J. (2005). Astrocytic glutamate release-induced transient depolarization and epileptiform discharges in hippocampal CA1 pyramidal neurons. J. Neurophysiol. 94, 4121–4130. doi: 10.1152/jn.00448.2005

PubMed Abstract | Crossref Full Text | Google Scholar

Khakh, B. S., and Mccarthy, K. D. (2015). Astrocyte calcium signaling: from observations to functions and the challenges therein. Cold Spring Harb. Perspect. Biol. 7:a020404. doi: 10.11017/cshperspect.a020404

Crossref Full Text | Google Scholar

Khakh, B. S., and Sofroniew, M. V. (2015). Diversity of astrocyte functions and phenotypes in neural circuits. Nat. Neurosci. 18, 942–952. doi: 10.1038/nn.4043

PubMed Abstract | Crossref Full Text | Google Scholar

Kofuji, P., and Araque, A. (2021). G-protein-coupled receptors in astrocyte–neuron communication. Neuroscience 456, 71–84. doi: 10.1016/j.neuroscience.2020.03.025

PubMed Abstract | Crossref Full Text | Google Scholar

Kondoh, T., Nishizaki, T., Aihara, H., and Tamaki, N. (2001). NMDA-responsible, APV-insensitive receptor in cultured human astrocytes. Life Sci. 68, 1761–1767. doi: 10.1016/S0024-3205(01)00971-7

PubMed Abstract | Crossref Full Text | Google Scholar

Kummer, U., Olsen, L. F., Dixon, C. J., Green, A. K., Bornberg-Bauer, E., and Baier, G. (2000). Switching from simple to complex oscillations in calcium signaling. Biophys. J. 79, 1188–1195. doi: 10.1016/S0006-3495(00)76373-9

PubMed Abstract | Crossref Full Text | Google Scholar

Lemon, G., Gibson, W. G., and Bennett, M. R. (2003). Metabotropic receptor activation, desensitization and sequestration I: modelling calcium and inositol 1, 4, 5-trisphosphate dynamics following receptor activation. J. Theor. Biol. 223, 93–111. doi: 10.1016/S0022-5193(03)00079-1

PubMed Abstract | Crossref Full Text | Google Scholar

Li, Y.-X., and Rinzel, J. (1994). Equations for InsP3 receptor-mediated [Ca²⁺] oscillations derived from a detailed kinetic model: a Hodgkin-Huxley like formalism. J. Theor. Biol. 166, 461–473. doi: 10.1006/jtbi.1994.1041

PubMed Abstract | Crossref Full Text | Google Scholar

Ma, Z., Wei, L., Du, X., Hou, S., Chen, F., Jiao, Q., et al. (2021). Two-photon calcium imaging of neuronal and astrocytic responses: the influence of electrical stimulus parameters and calcium signaling mechanisms. J. Neural Eng. 18:046096. doi: 10.1088/1741-2552/ac1f2b

PubMed Abstract | Crossref Full Text | Google Scholar

Madinier, A., Bertrand, N., Rodier, M., Quirié, A., Mossiat, C., Prigent-Tessier, A., et al. (2013). Ipsilateral versus contralateral spontaneous post-stroke neuroplastic changes: involvement of BDNF? Neuroscience 231, 169–181. doi: 10.1016/j.neuroscience.2012.11.054

PubMed Abstract | Crossref Full Text | Google Scholar

Malarkey, E. B., and Parpura, V. (2008). Mechanisms of glutamate release from astrocytes. Neurochem. Int. 52, 142–154. doi: 10.1016/j.neuint.2007.06.005

PubMed Abstract | Crossref Full Text | Google Scholar

Manninen, T., Havela, R., and Linne, M. (2018). Computational models for calcium-mediated astrocyte functions. Front. Comput. Neurosci. 12:14. doi: 10.3389/fncom.2018.00014

PubMed Abstract | Crossref Full Text | Google Scholar

Mcdougal, D. H., Hermann, G. E., and Rogers, R. C. (2013). Astrocytes in the nucleus of the solitary tract are activated by low glucose or glucoprivation: evidence for glial involvement in glucose homeostasis. Front. Neurosci. 7:249. doi: 10.3389/fnins.2013.00249

PubMed Abstract | Crossref Full Text | Google Scholar

Mennerick, S., and Zorumski, C. F. (1994). Glial contributions to excitatory neurotransmission in cultured hippocampal cells. Nature 368, 59–62. doi: 10.1038/368059a0

PubMed Abstract | Crossref Full Text | Google Scholar

Miller, L. D., Petrozzino, J. J., and Connor, J. A. (1995). G protein-coupled receptors mediate a fast excitatory postsynaptic current in CA3 pyramidal neurons in hippocampal slices. J. Neurosci. 15, 8320–8330. doi: 10.1523/JNEUROSCI.15-12-08320.1995

PubMed Abstract | Crossref Full Text | Google Scholar

Mitroshina, Е. V., Pakhomov, A. M., Krivonosov, M., Yarkov, R. S., Gavrish, M. S., Shkirin, A. V., et al. (2022). Novel algorithm of network calcium dynamics analysis for studying the role of astrocytes in neuronal activity in Alzheimer’s disease models. Int. J. Mol. Sci. 23:15928. doi: 10.3390/ijms232415928

PubMed Abstract | Crossref Full Text | Google Scholar

Montana, V., Malarkey, E. B., Verderio, C., Matteoli, M., and Parpura, V. (2006). Vesicular transmitter release from astrocytes. Glia 54, 700–715. doi: 10.1002/glia.20367

PubMed Abstract | Crossref Full Text | Google Scholar

Mouillac, B., Balestre, M.-N., and Guillon, G. (1990). Positive feedback regulation of phospholiphase C by vasopressin-induced calcium mobilization in WRK1 cells. Cell Signal 2, 497–507.

Google Scholar

Musotto, R., Wanderlingh, U., D'Ascola, A., Spatuzza, M., Catania, M. V., De Pittà, M., et al. (2024). Dynamics of astrocytes Ca²⁺ signaling: a low-cost fluorescence customized system for 2D cultures. Front. Cell Dev. Biol. 12:1320672. doi: 10.3389/fcell.2024.1320672

Crossref Full Text | Google Scholar

Nadkarni, S., and Jung, P. (2003). Spontaneous oscillations of dressed neurons: a new mechanism for epilepsy? Phys. Rev. Lett. 91:268101. doi: 10.1103/PhysRevLett.91.268101

PubMed Abstract | Crossref Full Text | Google Scholar

Nicoletti, F., Bockaert, J., Collingridge, G. L., Conn, P. J., Ferraguti, F., Schoepp, D. D., et al. (2011). Metabotropic glutamate receptors: from the workbench to the bedside. Neuropharmacology 60, 1017–1041. doi: 10.1016/j.neurophar.2010.10.022

Crossref Full Text | Google Scholar

Parpura, V., Basarsky, T. A., Liu, F., Jeftinija, K., Jeftinija, S., and Haydon, P. G. (1994). Glutamate-mediated astrocyte-neuron signalling. Nature 369, 744–747. doi: 10.1038/369744a0

PubMed Abstract | Crossref Full Text | Google Scholar

Parpura, V., and Haydon, P. G. (2000). Physiological astrocytic calcium levels stimulate glutamate release to modulate adjacent neurons. Proc. Natl. Acad. Sci. 97, 8629–8634. doi: 10.1073/pnas.97.15.8629

PubMed Abstract | Crossref Full Text | Google Scholar

Pasti, L., Volterra, A., Pozzan, T., and Carmignoto, G. (1997). Intracellular calcium oscillations in astrocytes: a highly plastic, bidirectional form of communication between neurons and astrocytes in situ. J. Neurosci. 17, 7817–7830. doi: 10.1523/JNEUROSCI.17-20-07817.1997

PubMed Abstract | Crossref Full Text | Google Scholar

Pawelczyk, T., and Matecki, A. (1998). Localization of phospholipase C δ3 in the cell and regulation of its activity by phospholipids and calcium. Eur. J. Biochem. 257, 169–177. doi: 10.1046/j.1432-1327.1998.2570169.x

PubMed Abstract | Crossref Full Text | Google Scholar

Perea, G., and Araque, A. (2007). Astrocytes potentiate transmitter release at single hippocampal synapses. Science 317, 1083–1086. doi: 10.1126/science.1144640

PubMed Abstract | Crossref Full Text | Google Scholar

Perea, G., Navarrete, M., and Araque, A. (2009). Tripartite synapses: astrocytes process and control synaptic information. Trends Neurosci. 32, 421–431. doi: 10.1016/j.tins.2009.05.001

PubMed Abstract | Crossref Full Text | Google Scholar

Petralia, R. S., Wang, Y. X., Zhao, H. M., and Wenthold, R. J. (1996). Ionotropic and metabotropic glutamate receptors show unique postsynaptic, presynaptic, and glial localizations in the dorsal cochlear nucleus. J. Comp. Neurol. 372, 356–383. doi: 10.1002/(SICI)1096-9861(19960826)372:3<356::AID-CNE3>3.0.CO;2-1

PubMed Abstract | Crossref Full Text | Google Scholar

Rappold, P. M., and Tieu, K. (2010). Astrocytes and therapeutics for Parkinson's disease. Neurotherapeutics 7, 413–423. doi: 10.1016/j.nurt.2010.07.001

PubMed Abstract | Crossref Full Text | Google Scholar

Rebecchi, M. J., and Pentyala, S. N. (2000). Structure, function, and control of phosphoinositide-specific phospholipase C. Physiol. Rev. 80, 1291–1335. doi: 10.1152/physrev.2000.80.4.1291

PubMed Abstract | Crossref Full Text | Google Scholar

Rhee, S. G., and Bae, Y. S. (1997). Regulation of phosphoinositide-specific phospholipase C isozymes. J. Biol. Chem. 272, 15045–15048. doi: 10.1074/jbc.272.24.15045

PubMed Abstract | Crossref Full Text | Google Scholar

Rosa, M., Giovanni, P., and Ulderico, W. (2022). Neuron and astrocyte computational models for describing the brain complexity. Atti della Accademia Peloritana dei Pericolanti-Classe di Scienze Fisiche, Matematiche e Naturali. 100.2:1. doi: 10.1478/AAPP.1002LC1

Crossref Full Text | Google Scholar

Santello, M., and Volterra, A. (2009). Synaptic modulation by astrocytes via Ca²⁺-dependent glutamate release. Neuroscience 158, 253–259. doi: 10.1016/j.neuroscience.2008.03.039

PubMed Abstract | Crossref Full Text | Google Scholar

Schipke, C. G., and Kettenmann, H. (2004). Astrocyte responses to neuronal activity. Glia 47, 226–232. doi: 10.1002/glia.20029

PubMed Abstract | Crossref Full Text | Google Scholar

Schnell, C., Fresemann, J., and Hülsmann, S. (2011). Determinants of functional coupling between astrocytes and respiratory neurons in the pre-Bötzinger complex. PLoS One 6:e26309. doi: 10.1371/journal.pone.0026309

PubMed Abstract | Crossref Full Text | Google Scholar

Seifert, G., and Steinhäuser, C. (2001). Ionotropic glutamate receptors in astrocytes. Prog. Brain Res. 132, 287–299. doi: 10.1016/S0079-6123(01)32083-6

Crossref Full Text | Google Scholar

Semyanov, A., Henneberger, C., and Agarwal, A. (2020). Making sense of astrocytic calcium signals from acquisition to interpretation. Nat. Rev. Neurosci. 21, 551–564. doi: 10.1038/s41583-020-0361-8

PubMed Abstract | Crossref Full Text | Google Scholar

Shao, Y., and Mccarthy, K. D. (1994). Plasticity of astrocytes. Glia 11, 147–155. doi: 10.1002/glia.440110209

PubMed Abstract | Crossref Full Text | Google Scholar

Skowrońska, K., Obara-Michlewska, M., Zielińska, M., and Albrecht, J. (2019). NMDA receptors in astrocytes: in search for roles in neurotransmission and astrocytic homeostasis. Int. J. Mol. Sci. 20:309. doi: 10.3390/ijms20020309

PubMed Abstract | Crossref Full Text | Google Scholar

Smith, S. J. (1992). Do astrocytes process neural information? Prog. Brain Res. 94, 119–136.

Google Scholar

Smith, K. L., John, C. S., Elizabeth, S. I, Ongür, D., Cohen, B. M., Barry, S. M., et al. (2014). Exploring the role of central astrocytic glutamate uptake in ethanol reward in mice. Alcohol. Clin. Exp. Res. 38, 1307–1314. doi: 10.1111/acer.12361

PubMed Abstract | Crossref Full Text | Google Scholar

Smith, I. F., and Parker, I. (2009). Imaging the quantal substructure of single IP₃R channel activity during Ca²⁺ puffs in intact mammalian cells. Proc. Natl. Acad. Sci. 106, 6404–6409. doi: 10.1073/pnas.0810799106

PubMed Abstract | Crossref Full Text | Google Scholar

Smrcka, A. V., Hepler, J. R., Brown, K. O., and Sternweis, P. C. (1991). Regulation of polyphosphoinositide-specific phospholipase C activity by purified Gq. Science 251, 804–807. doi: 10.1126/science.1846707

PubMed Abstract | Crossref Full Text | Google Scholar

Spooren, W. P., Gasparini, F., Salt, T. E., and Kuhn, R. (2001). Novel allosteric antagonists shed light on mglu5 receptors and CNS disorders. Trends Pharmacol. Sci. 22, 331–337. doi: 10.1016/S0165-6147(00)01694-1

Crossref Full Text | Google Scholar

Steinhäuser, C., and Gallo, V. (1996). News on glutamate receptors in glial cells. Trends Neurosci. 19, 339–345. doi: 10.1016/0166-2236(96)10043-6

PubMed Abstract | Crossref Full Text | Google Scholar

Stobart, J. L., Ferrari, K. D., Barrett, M. J. P., Glück, C., Stobart, M. J., Zuend, M., et al. (2018). Cortical circuit activity evokes rapid astrocyte calcium signals on a similar timescale to neurons. Neuron 98, 726–735.e4. doi: 10.1016/j.neuron.2018.03.050

PubMed Abstract | Crossref Full Text | Google Scholar

Stogsdill, J. A., Harwell, C. C., and Goldman, S. A. (2023). Astrocytes as master modulators of neural networks: synaptic functions and disease-associated dysfunction of astrocytes. Ann. N. Y. Acad. Sci. 1525, 41–60. doi: 10.1111/nyas.15004

PubMed Abstract | Crossref Full Text | Google Scholar

Sun, W., McConnell, E., Pare, J.-F., Xu, Q., Chen, M., Peng, W., et al. (2013). Glutamate-dependent neuroglial calcium signaling differs between young and adult brain. Science 339, 197–200. doi: 10.1126/science.1226740

Crossref Full Text | Google Scholar

Taylor, S. J., and Exton, J. H. (1987). Guanine-nucleotide and hormone regulation of polyphosphoinositide phospholipase C activity of rat liver plasma membranes. Bivalent-cation and phospholipid requirements. Biochem. J. 248, 791–799. doi: 10.1042/bj2480791

PubMed Abstract | Crossref Full Text | Google Scholar

Temburni, M. K., and Jacob, M. H. (2001). New functions for glia in the brain. Proc. Natl. Acad. Sci. 98, 3631–3632. doi: 10.1073/pnas.081073198

PubMed Abstract | Crossref Full Text | Google Scholar

Testa, C. M., Standaert, D. G., Landwehrmeyer, G. B., Penney, J. B. Jr., and Young, A. B. (1995). Differential expression of mGluR5 metabotropic glutamate receptor mRNA by rat striatal neurons. J. Comp. Neurol. 354, 241–252. doi: 10.1002/cne.903540207

PubMed Abstract | Crossref Full Text | Google Scholar

Tian, G.-F., Azmi, H., Takano, T., Xu, Q., Peng, W., Lin, J., et al. (2005). An astrocytic basis of epilepsy. Nat. Med. 11, 973–981. doi: 10.1038/nm1277

PubMed Abstract | Crossref Full Text | Google Scholar

Verkhratsky, A., and Nedergaard, M. (2018). Physiology of astroglia. Physiol. Rev. 98, 239–389. doi: 10.1152/physrev.00042.2016

PubMed Abstract | Crossref Full Text | Google Scholar

Verkhratsky, A., Olabarria, M., Noristani, H. N., Yeh, C. Y., and Rodriguez, J. J. (2010). Astrocytes in Alzheimer's disease. Neurotherapeutics 7, 399–412. doi: 10.1016/j.nurt.2010.05.017

PubMed Abstract | Crossref Full Text | Google Scholar

Verkhratsky, A., Orkand, R. K., and Kettenmann, H. (1998). Glial calcium: homeostasis and signaling function. Physiol. Rev. 78, 99–141. doi: 10.1152/physrev.1998.78.1.99

PubMed Abstract | Crossref Full Text | Google Scholar

Verkhratsky, A., and Steinhäuser, C. (2000). Ion channels in glial cells. Brain Res. Rev. 32, 380–412. doi: 10.1016/S0165-0173(99)00093-4

PubMed Abstract | Crossref Full Text | Google Scholar

Volterra, A., Magistretti, P. J., and Haydon, P. G. (2002). The tripartite synapse: glia in synaptic transmission : Oxford University Press.

Google Scholar

Volterra, A., and Meldolesi, J. (2005). Astrocytes, from brain glue to communication elements: the revolution continues. Nat. Rev. Neurosci. 6, 626–640. doi: 10.1038/nrn1722

PubMed Abstract | Crossref Full Text | Google Scholar

Wamhoff, B. R., Dixon, J. L., and Sturek, M. (2002). Atorvastatin treatment prevents alterations in coronary smooth muscle nuclear Ca²⁺ signaling in diabetic dyslipidemia. J. Vasc. Res. 39, 208–220. doi: 10.1159/000063686

PubMed Abstract | Crossref Full Text | Google Scholar

Winder, D. G., and Conn, P. J. (1996). Roles of metabotropic glutamate receptors in glial function and glial-neuronal communication. J. Neurosci. Res. 46, 131–137. doi: 10.1002/(SICI)1097-4547(19961015)46:2<131::AID-JNR1>3.0.CO;2-I

PubMed Abstract | Crossref Full Text | Google Scholar

Wroblewska, B., Santi, M. R., and Neale, J. H. (1998). N-acetylaspartylglutamate activates cyclic AMP-coupled metabotropic glutamate receptors in cerebellar astrocytes. Glia 24, 172–179. doi: 10.1002/(SICI)1098-1136(199810)24:2<172::AID-GLIA2>3.0.CO;2-6

PubMed Abstract | Crossref Full Text | Google Scholar

Young, D., Gary, W., and Keizer, J. (1992). A single-pool inositol 1, 4, 5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca²⁺ concentration. Proc. Natl. Acad. Sci. 89, 9895–9899. doi: 10.1073/pnas.89.20.9895

PubMed Abstract | Crossref Full Text | Google Scholar