Effect of quenched disorder on the absorbing transition in contact processes on a comb lattice

Power-law behavior frequently emerges in physical, biological, and social systems, particularly near continuous phase transitions characterized by diverging correlation lengths and universal scaling. The contact process is a prototypical model for studying absorbing-state phase transitions, typically belonging to the directed percolation (DP) universality class in its clean form. In this study, we investigate how quenched disorder influences the absorbing-state transition of the contact process on a one-dimensional comb lattice, a minimal geometry that incorporates structural inhomogeneity while remaining analytically and computationally tractable. In our model, activity spreads over a fraction of the branches q and is blocked in the rest. Without disorder, the system belongs to the directed percolation (DP) universality class. Introducing quenched disorder leads to significant changes in the critical dynamics. For q≤0.15, the system develops a Griffiths phase characterized by algebraic decay away from the critical point and logarithmic scaling at criticality, indicating a transition to the activated scaling universality class. In contrast, for q>0.15, the contact process on the comb lattice shows power-law decay of the order parameter only at the critical point, demonstrating a clean transition with standard critical dynamics and no extended Griffiths region. The results show that quenched disorder induces non-universal slow dynamics for small q, while larger values of q suppress the disorder-driven effects, restoring standard DP-like criticality. This transition underscores the role of lattice geometry and disorder strength in shaping nonequilibrium phase transitions.

1 Introduction

The continuous phase transitions from a fluctuating phase to an absorbing state in nonequilibrium systems have garnered significant attention over the years. Once the system reaches the absorbing state, it cannot escape it. These transitions are classified into various universality classes, with the directed percolation (DP) universality class being the most prominent (Henkel, 2008). The ubiquity of the DP behavior was independently conjectured by Grassberger (1981) and Janssen (1981), where any system with a single absorbing state, a single-order parameter, short-range interaction in time and space, no translational invariance, and an absence of multicritical points invariably falls into the DP universality class. The order parameter follows conventional power-law scaling behavior only at the critical point. Below this, the order parameter decays exponentially to the absorbing state. Above the critical point, the order parameter attains a steady, non-zero value. The characteristic critical exponents of the one-dimentional DP universality class are $\beta =0.276$, ${\nu }_{\perp }=1.09$, and ${\nu }_{\Vert }=1.73$. These exponents are universal features that remain invariant under the microscopic details of the model. The DP class exhibits remarkable robustness even when several underlying assumptions are relaxed (Bhoyar et al., 2022).

However, the experimental realization of the DP universality class is limited, requiring an extreme fine-tuning of parameters. In real systems, inhomogeneity and intrinsic defects can significantly influence critical behavior, often causing the system to deviate from DP universality. According to Harris criterion, the quenched disorder is a relevant perturbation if the spatial correlation length exponent satisfies the relation ${\nu }_{\perp }<\frac{2}{d}$ for the pure (disorder-free) system (Harris, 1974). This inequality holds for DP in all dimensions $d<4$; therefore, quenched disorder is relevant and may alter the critical scaling.

Vojta (2006) provided a comprehensive review, including nonequilibrium systems, and provided a theoretical foundation and understanding of the change of universality class in disordered systems, leading to the Griffiths phase. The concept of the Griffiths phase was first introduced by R. B. Griffiths in 1969 within the framework of equilibrium statistical mechanics (Griffiths, 1969). In the context of nonequilibrium systems undergoing absorbing state transitions, such as the contact process, the Griffiths phase originates as an effect of the presence of rare regions. These locally ordered regions can persist near the critical point, even when the overall system remains disordered. Thus, activity may prevail in the rare region, although the system is globally in the absorbing phase. This leads to a power-law decay in a range of parameters in the absorbing phase. This power-law exponent can be complex. Griffiths phase with a generic complex critical exponent was reported in our earlier work (Bhoyar and Gade, 2020; 2021). Logarithmic periodic oscillations are observed over and above the usual power laws obtained over a parametric range. We refer to this parameter range as the complex Griffiths phase.

Here, we study the dynamic behavior of the contact process on a comb lattice with topological disorder. The contact process is a basic stochastic model in the DP class, which is widely used to describe the spread of activity such as epidemics, forest fires, and opinions (Pastor-Satorras and Vespignani, 2001; Henkel, 2008; Ódor, 2000). A one-dimentional comb can be thought of as an infinite backbone chain with finite side branches attached at each site. Extending this idea, a two-dimentional comb is built by attaching a chain at every point along the backbone. In our case, since the side branches have finite lengths, the system effectively behaves like a one-dimentional structure.

The comb lattice is an anisotropic geometry that is often used to model branched or polymer-like systems. It has been applied to problems such as anomalous transport (Méndez et al., 2015), drug diffusion in biological tissues (Marsh et al., 2008), and materials with dendritic or branched structures (Frauenrath, 2005). Its geometry leads to subdiffusive motion along the backbone as particles are temporarily trapped in the branches. Bénichou et al. (2015) showed that a tracer particle in such a lattice exhibits subdiffusion along the backbone, with normal diffusion restored at longer times. In Shang’s studies of the hierarchical lattice, the different sites are connected, with a probability dependent on the distance between the sites. In one study, it decays as a power law with distance. In another, the connections are also dependent on the weights assigned to each vertex. The exact thresholds for critical percolation are obtained in both cases. We do not consider distance-dependent connections or connections dependent on weights assigned to each vertex. Instead, we consider a nearest-neighbor connection on the comb lattice. We study the contact process, which is a time-dependent nonequilibrium phenomenon rather than simple geometric percolation.

Geometry-induced slow dynamics and anisotropic spreading are closely linked to changes in scaling behavior seen in many systems. Moreover, introducing quenched disorder in the form of random but fixed variations in branch length or spacing can model structural heterogeneities found in real materials. Examples include irregular dendritic structures in biology, uneven branching in porous rocks, and imperfections in microfluidic devices. Studying quenched disorder helps us understand how structural variability affects transport, diffusion, and search processes in such systems. The inhomogeneity and anisotropic connectivity of the comb lattice introduce naturally slow dynamics, which are further enhanced when quenched topological disorder is introduced. In our model, the activity is allowed in only a fraction of the branches $q$, while the rest are blocked. We find that the dynamic behavior of the model strongly depends on $q$. The structure of this study is as follows: Section 2 describes the system and simulation details, Section 3 presents the results for different disorder strengths, and Section 4 summarizes the conclusions.

2 Model and simulation

We investigate the critical behavior of the contact process on a one-dimentional comb lattice, a comb structure composed of a backbone of length L and teeth (or branches) of finite length K. We consider the cellular automaton model of the contact process proposed by Domany and Kinzel (1984). The state of each site at time t is represented by $v_{i,k}(t)\in$ {0,1}, where $v=0$ is an inactive, healthy, or dry site, and $v=1$ is an active, infected, or wet site.

The update rules are symmetric: a site can be activated if either of its neighboring sites is active. To explore the effect of quenched disorder, we introduce topological defects into the lattice by randomly allowing activity in the $q$ fraction of the teeth and blocking activity in the ($1-q$) fraction of the teeth.

We initialize the system with a random configuration, where half the lattice sites are set as active by using a pseudo-random number generator. Figure 1 illustrates the comb lattice. The horizontal axis $i=\mathrm{1,2,3}\dots L$ represents the backbone, and the vertical axis $j=\mathrm{1,2,3}\dots K$ represents the teeth or branches. Red dot denotes active sites, and purple dots denote inactive sites. The black cross denotes the blocked branch (quenched disorder). A backbone site is activated with probability $p$ if at least one of its neighbors is active (either to its immediate left or right on the backbone or on the first site of the associated branch, provided that activity is allowed in that branch). A site within a branch where activity is permitted updates its state with probability $p$ if either of its adjacent vertical neighbors is active. The conditional probabilities of sites on the backbone and teeth $P_B$ and $P_T$, respectively, are defined below.

Figure 1

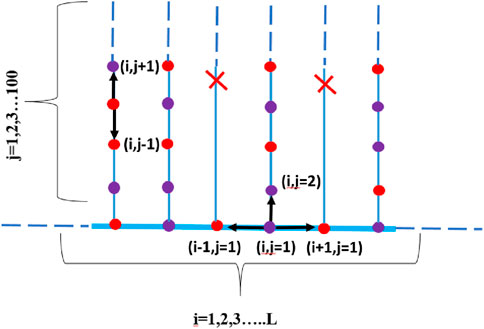
Figure 1. One-dimensional comb lattice of length L with a finite branch length K. The active and inactive sites are represented by red and purple dots, respectively, while the arrows indicate possible interaction pathways. The branch marked with a red cross corresponds to an inactive branch, illustrating quenched disorder.

$P_B(x_{i,1}(t+1)|x_{i-\mathrm{1,1}}(t)+x_{i+\mathrm{1,1}}(t)+x_{i,2}(t))$

and

$P_T(x_{i,j}(t+1)|x_{i,j+1}(t)+x_{i,j-1}(t))$

It should be noted that $P_B(1|0)=P_B(0|1)=P_B(1|1)=p$, and $P_T(1|0)=P_T(0|1)=P_T(1|1)=p$ and $p\ne 0$. Of course, for disordered case, if a branch is blocked, all sites on that branch remain uninfected forever. The boundary conditions are periodic: if $i<1$ then $i=L$; if $i>L$ then $i=1$; if $j>K$ then $j=1$; if $j-1=0$, then $j=K$. Sites belonging to different branches cannot directly influence each other’s state, only neighboring sites within the same branch or on the backbone can interact.

All simulations are carried out on a comb lattice having a backbone length of $L=50000$ and a branch length of $K=100$ over a long period of $t=10^6$. The average is computed over at least 500 independent disorder configurations and initial conditions. The order parameter is the fraction of active sites at time t, given by $\rho (t)=\frac{1}{N}{\sum }_{i=1}^L{\sum }_{j=1}^K{x}_{i,j}(t)$, where $N=L\times K$. We present a detailed analysis of how the system’s dynamics evolve for different values of $q$, revealing various critical regimes and universality classes.

3 Results and discussion

3.1 q = 0 and q = 1

Let us first consider the two simple cases that are expected to belong to the DP universality class:

Case (i) $q=0$.

Here, all the branches are blocked. Activity is confined only to the backbone. As a result, the comb lattice is a one-dimentional lattice of length L with symmetric nearest-neighbor connections. The system undergoes a continuous phase transition from the fluctuating phase to the absorbing phase at the critical activation probability $p_c=0.7055$. At the critical point, the order parameter exhibits power law decay $\rho (t)\sim t^{-\delta }$, where the decay exponent $\delta$ = 0.153. For $p<p_c$, the system relaxes to the absorbing phase, $\rho (t)\to 0$, and for $p>p_c$, a finite steady-state density $\rho (\infty )$ is observed (Figure 2a).

Figure 2

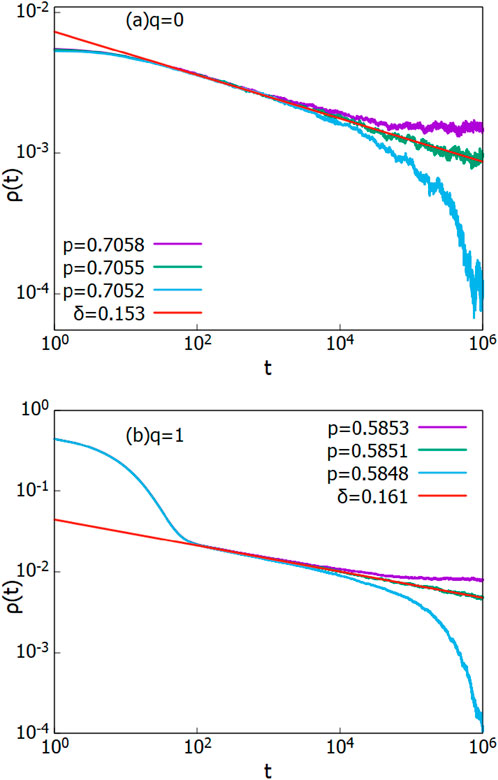
Figure 2. Time evolution of the order parameter $\rho (t)$ for activation probabilities $p>p_c$, $p=p_c$, and $p<p_c$ (top to bottom) on a log–log scale. (a) For $q=0$ (one-dimensional chain), the system undergoes power-law decay $\rho (t)\sim t^{-\delta }$ at $p_c$ = 0.7055 with $\delta =0.153\pm 0.000084$. (b) For $q=1$, the system undergoes power-law decay at $p_c$ = 0.5851 with $\delta =0.161\pm 0.000029$. In both cases, the dynamics are consistent with the directed percolation (DP) universality class. In both cases, the system sustains a finite steady-state density for $p>p_c$, indicating an active phase. Similarly, for $p<p_c$, the density decays rapidly to zero, corresponding to the absorbing phase.

Case (ii) $q=1$.

In this case, none of the branches are blocked. The comb lattice resembles a rectangular lattice of finite width. Each branch site is connected to one neighboring site above and below, while each site on the backbone has symmetric connections to its lateral neighbors and a connection to a branch site above. The system undergoes a continuous phase transition at the critical point $p_c=0.5851$. At criticality, the order parameter decays as $\rho (t)\sim t^{-\delta }$, with $\delta$ = 0.161 (Figure 2b). For $p<p_c$, $\rho (t)\to 0$, and for $p>p_c$, the system reaches a steady state, $\rho (\infty )>0$. In both cases, the value of the decay exponent $\delta$ is consistent with the known value of one-dimentional DP. Thus, the system belongs to the DP universality class in both cases.

3.2 $q=0.75,0.5,0.25$

In this section, we examine cases in which activity is allowed in at least 25$\%$ of the branches. For all $q\ge 0.25$, the system undergoes a clean continuous phase transition from the fluctuating phase to the absorbing phase. Figure 3 shows the time evolution of the order parameter $\rho (t)$ for several values of activation probabilities $p>p_c$, $p_c$, and $p<p_c$ for $q=0.75,0.5,0.25$. As $q$ increases, the critical point $p_c$ decreases. This reflects enhanced connectivity due to more active branches. We observe a clean critical transition to the absorbing phase in each of these cases. The decay exponent $\delta$ varies slightly; however, its value remains close to the one-dimentional DP value ($\delta$ = 0.158). Specifically:

Figure 3

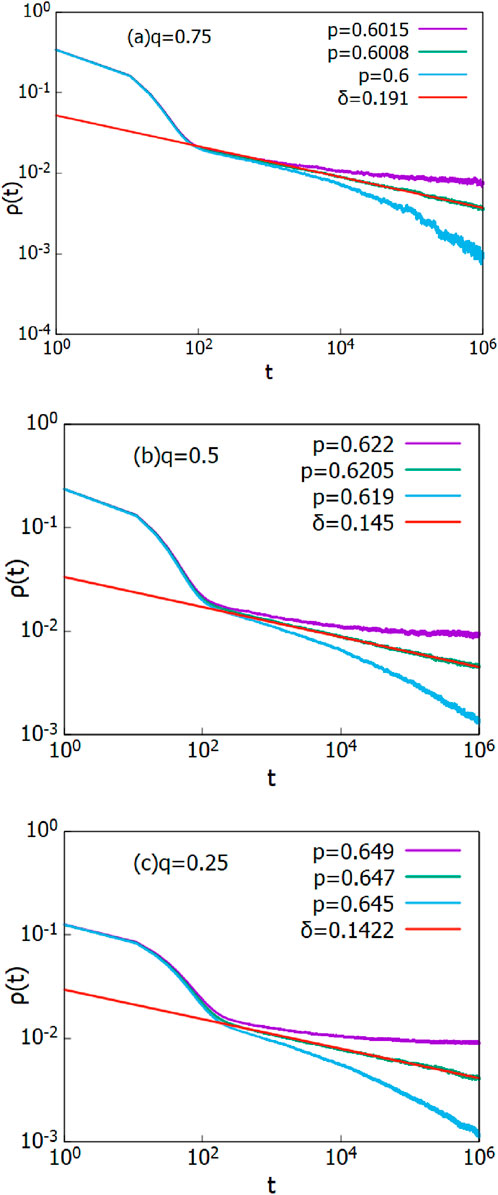
Figure 3. Evolution of the order parameter $\rho (t)$ with time on the log–log scale for activation probabilities $p>p_c$, $p_c$ and $p<p_c$ (top to bottom). A power-law decay $\rho (t)\sim t^{-\delta }$ is observed at $p=p_c$. (a) For $q=0.75$, $p_c=0.6008$ and $\delta =0.191\pm 0.000038$. (b) For $q=0.5$, $p_c=0.6205$ and $\delta =0.145\pm 0.000035$. (c) For $q=0.25$, $p_c=0.647$ and $\delta =0.142\pm 0.000044$. As $q$ decreases, the critical activation probability increases, reflecting reduced connectivity in the system.

for $q=0.75$, $p_c=0.6008$ and $\delta =0.191$.

for $q=0.5$, $p_c=0.6205$ and $\delta =0.145$.

for $q=0.25$, $p_c=0.647$ and $\delta =0.142$.

We explore the case $q=0.25$ and calculate the critical exponents $\beta$, ${\nu }_{\Vert }$, and $z$. To determine $\beta$, we analyze the steady-state density $\rho (\infty )$ for several values of $p>p_c$. In Figure 4a, the steady-state value $\rho (\infty )$ is plotted against $|p-p_c|$. The obtained value of $\beta =0.457\pm 0.0119$. This value is significantly higher than the one-dimentional DP value and slightly lower than the two-dimentional DP value ($\beta =0.583$). The errors have been calculated using the Gnuplot fitting function. This uses the nonlinear least-squares method, specifically the Marquardt–Levenberg algorithm, to adjust the parameters in a user-defined function so that it best fits the given data points. Off-critical scaling yields the value of the temporal correlation length exponent ${\nu }_{\Vert }$. We plot $\rho (t){\mathrm{\Delta }}^{-\delta {\nu }_{\Vert }}$ versus $t{\mathrm{\Delta }}^{{\nu }_{\Vert }}$ on log–log scale for several values of $p>p_c$ and $p<p_c$. Here $\mathrm{\Delta }=|p-p_c|$. The best collapse is obtained for ${\nu }_{\Vert }$ = 0.5 and $\delta =0.1422$ (see Figure 4b). However, the hyperscaling relation $\beta \ne \delta {\nu }_{\Vert }$ is not satisfied, suggesting that simple scaling relations may break down in this hybrid geometry.

Figure 4

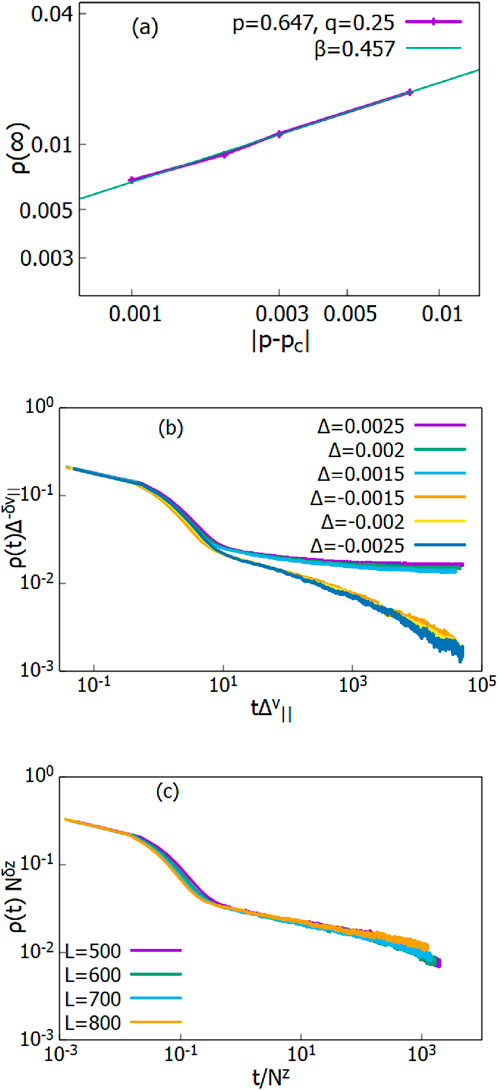
Figure 4. (a) Plot of steady-state density $\rho (\infty )$ vs. $|p-p_c|$ on log–log scale. The obtained value of $\beta =0.457\pm 0.0119$. (b) Off-critical scaling analysis is shown by plotting $t{\mathrm{\Delta }}^{{\nu }_{\Vert }}$ vs. $\rho (t){\mathrm{\Delta }}^{-\delta {\nu }_{\Vert }}$. The best collapse is obtained with ${\nu }_{\Vert }$ = 0.5 and $\delta$ = 0.1422. (c) Finite-size scaling plot $t/N^z$ vs. $\rho (t)N^{\delta z}$ is shown for different sizes $N=L\times K$. Here, L = 500, 600, 700, 800, and K = 100. The optimal collapse is obtained for $z=1$.

To extract the dynamic exponent z, we perform finite-size scaling. We plot $t/N^z$ versus $\rho (t)N^{\delta z}$ on a log–log scale. Here, $N=L\ast K$. We plot several lattice sizes L = 500,600,700,800 (Figure 4c). Here, $K=100$. The best collapse is achieved for $z=1$, which indicates an almost linear spread of defects.

The steady-state density $\rho (\infty )$ is a global time-averaged measure. It indicates that the long-term exploration of both the backbone and side branches results in quasi-2D behavior. The temporal correlation length exponent ${\nu }_{\Vert }$ is small and indicates strong correlations. The quenched disorder and the anisotropic geometry of the comb lead to retention of memory in the backbone. The value of $z={\nu }_{\Vert }/{\nu }_{\perp }=1$ implies that ${\nu }_{\perp }$ is also small and that there are strong correlations over time. This occurs because the particles are trapped in the teeth. At the same time, trapped particles in the teeth produce a decay exponent close to the one-dimentional value. Overall, the rich critical behavior emerges from the interplay between the backbone’s limited connectivity and the increasing influence of side branches.

3.3 q = 0.15

In this section, we present the results for $q=0.15$, which exhibits dynamic behavior that diverges from the DP universality class. At this value of $q$, activity is allowed in 15% of the branches, while the remaining 85% are blocked. A substantial obstruction of this kind may lead to the formation of isolated regions in the lattice. These regions may trap active sites and persist for a long time, even if the bulk is in the absorbing phase. We find that the order parameter $\rho (t)$ undergoes power-law decay $\rho (t)\sim t^{-\delta }$ over a range of activation probability values $p$ rather than exclusively at a single critical point. This extended power-law decay over a range of parameter values is known as the “Griffiths phase”. Figure 5a shows the temporal decay of $\rho (t)$ on a log–log scale for various values of $p$ in the range 0.658–0.662. The decay exponent $\delta$ varies continuously with $p$. The decay is logarithmic at the critical point $p_c$ = 0.662.

Figure 5

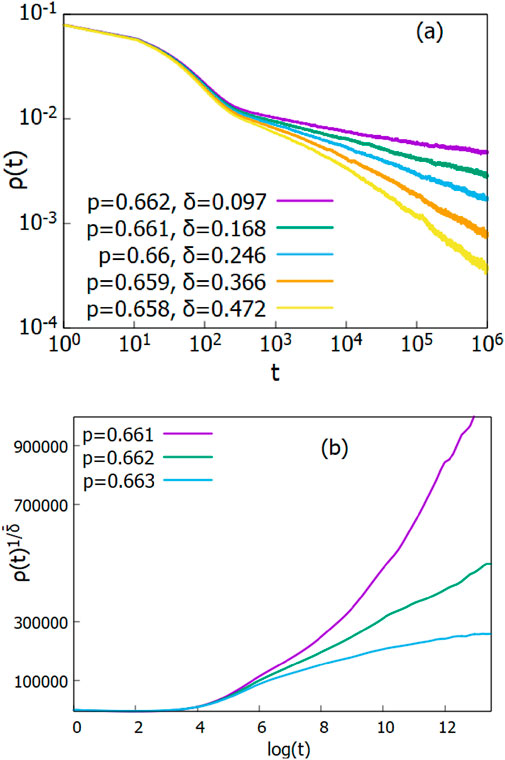
Figure 5. (a) Evolution of the order parameter $\rho (t)$ with time on a log–log scale at various activation probabilities $p$ in the range 0.662–0.658 (from top to bottom). The order parameter undergoes power-law decay, $\rho (t)\sim t^{-\delta }$ for all $p$ in this range. The decay is logarithmic at the critical point $p_c=0.662$. (b) Plot of $\rho {(t)}^{-\bar{\delta }}$ vs. $\log (t)$ for $p<p_c$, $p_c$ and $p>p_c$ (top to bottom). We observe linear behavior only at the critical point with $\bar{\delta }$ = 0.381.

In such a scenario, the transition to the absorbing phase is expected to fall within the activated scaling universality class. This class describes a distinct type of critical behavior that emerges in nonequilibrium systems subjected to strong disorder. Unlike conventional scaling, which features power-law relationships between time and spatial scales, activated scaling is governed by logarithmic scaling laws. It is characterized by the following three scaling relations:

$\rho {(t)}^{1/\bar{\delta }}\sim \log (t)$, $P_s{(t)}^{1/\bar{\delta }}\sim \log (t)$, and $N{(t)}^{1/\theta }\sim \log (t)$

where $\rho (t)$ denotes the order parameter, $P_s(t)$ is the survival probability, and $N(t)$ is the average number of active particles in the cluster originating from a single active seed. The survival probability $P_s(t)$ is defined as the fraction of the cluster that survives until time t. The values of the critical exponents of the activated scaling class are $\bar{\delta }$ = 0.381 and $\theta$ = 1.236 (Hooyberghs et al., 2003). $\rho (t)$ is measured on the full lattice starting with a random initial configuration. The other two quantities, $P_s(t)$ and $N(t)$, are obtained by initiating dynamics with a single active site placed at the center of the backbone.

We present the analysis of the activated scaling behavior for $q=0.15$. We plot $\rho {(t)}^{1/\bar{\delta }}$ as a function of $\log (t)$ (Figure 5b). Linear behavior is observed only at the critical point for $\bar{\delta }$ = 0.381. Figure 6a shows the plot of $P_s{(t)}^{1/\bar{\delta }}$ as a function of $\log (t)$ for the comb lattice initialized with a single active seed at the center of the backbone. Again, we obtain linear behavior only at the critical point for $\bar{\delta }$ = 0.381. Figure 6b shows the plot of $N{(t)}^{1/\theta }$ as a function of $\log (t)$ for several values of the activation probabilities $p<p_c$, $p=p_c$, and $p>p_c$. Linear behavior appears exclusively at the critical point $p_c=0.662$, for $\theta$ = 1.236. The obtained values of $\bar{\delta }$ = 0.381 and $\theta$ = 1.236 are in excellent agreement with those of the activated scaling class. These results indicate that for $q=0.15$, there exists a range of the activation probability $p$ that separates the active and absorbing phases, within which the system exhibits a generic power-law decay, which is characteristic of the Griffiths phase. The topology of the comb lattice plays a crucial role in this behavior. Due to the blocking of the majority of the branches, the lattice fragments into spatially rare regions. These isolated clusters can trap activity and persist for exponentially long times, even when the bulk of the system is in the absorbing phase. The natural formation of these rare regions along the “teeth” of the comb leads to inherently slow relaxation dynamics, reinforcing the classification of the transition within the activated scaling framework.

Figure 6

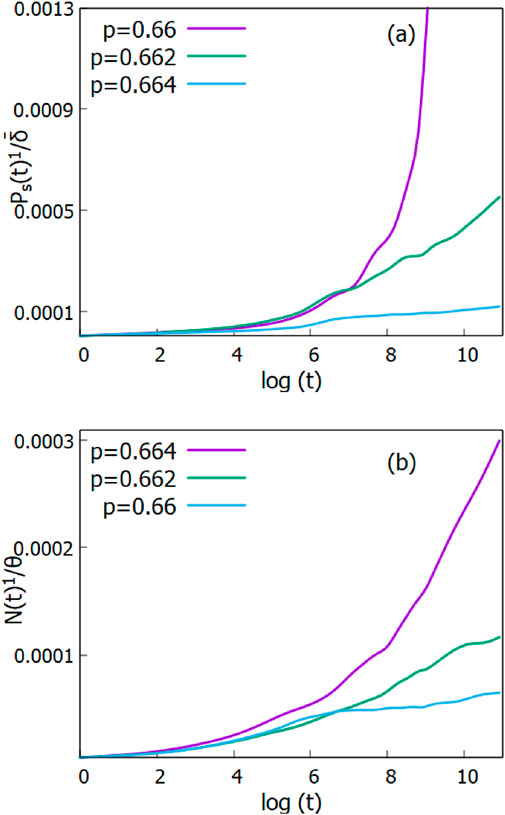
Figure 6. (a) Plot of $P_s{(t)}^{1/\bar{\delta }}$ vs. $\log (t)$ for $p<p_c$, $p_c$ and $p>p_c$ (top to bottom). Linear behavior is obtained only at the critical point with $\bar{\delta }$ = 0.381. (b) Plot of $N{(t)}^{1/\theta }$ vs. $\log (t)$ for $p>p_c$, $p_c$ and $p<p_c$ (top to bottom). Linear behavior is obtained only at the critical point with $\theta$ = 1.236. These values are consistent with those of the activated scaling class.

4 Conclusion

Power-law behavior is ubiquitous in space and time. However, the presence of quenched disorder can significantly alter this behavior. Quenched disorder is inherent in any real system; therefore, understanding how it influences the dynamic behavior of a system has attracted much attention in statistical physics. In particular, quenched disorder can induce a change in the universality class. In this article, we studied the Domany–Kinzel model of the contact process on a one-dimensional comb lattice with topological disorder. Comb lattices are naturally inhomogeneous structures with anisotropic geometry that slow down dynamic processes. By introducing disorder in the form of missing branches, we increase structural complexity and explore the combined effects of geometry and quenched disorder on system behavior. We varied the fraction of missing branches $q$ and observed distinct dynamical regimes. The cases $q=0$ and $q=1$ are simple. As expected, they showed a continuous phase transition from the fluctuating to the absorbing phase within the DP universality class. For $q\ge 0.25$, the order parameter $\rho (t)$, the fraction of active sites at time t, underwent a continuous phase transition only at the critical point $p_c$. Interestingly, the exponent $\delta$ was found to be close to the one-directional DP value, but the exponents $\beta$, ${\nu }_{\Vert }$, and $z$ changed. This indicates that the disorder in the structure is a meaningful perturbation and that the steady-state properties do not depend solely on the backbone at this value of $q$.

As blocking was further increased, a clear departure from the DP universality class was observed for $q=0.15$. We obtained the Griffiths phase, which is characterized by power-law decay with continuously changing exponents over a range of $p$ values. At the critical point, the order parameter decayed logarithmically in time. The critical exponents obtained were $\bar{\delta }=0.381$ and $\theta$ = 1.236, which are consistent with the activated scaling class. The blockade in a large number of branches led to the effective fragmentation of the lattice, which eventually led to the rare region effect. Rare regions are locally favorable clusters that remain active longer than the bulk. The collective behavior of rare regions led to ultra-slow dynamics in the Griffiths regime. Our results demonstrate that the interplay between limited connectivity along the backbone and the increasing influence of the side branches with increasing $q$ leads to this rich critical behavior.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors on resonable request.

Author contributions

PB: Writing – original draft, Formal Analysis, Resources, Project administration, Writing – review and editing, Data curation, Investigation, Methodology, Validation, Funding acquisition. PG: Conceptualization, Validation, Supervision, Methodology, Resources, Writing – review and editing, Project administration, Visualization, Formal Analysis, Writing – original draft.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. PDB acknowledges Rashtrasant Tukadoji Maharaj Nagpur University for providing financial assistance (RTMNU/RDC/2024/242).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bénichou, O., Illien, P., Oshanin, G., Sarracino, A., and Voituriez, R. (2015). Diffusion and subdiffusion of interacting particles on comblike structures. Phys. Rev. Lett. 115, 220601. doi:10.1103/physrevlett.115.220601

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhoyar, P. D., and Gade, P. M. (2020). Dynamic phase transition in the contact process with spatial disorder: griffiths phase and complex persistence exponents. Phys. Rev. E 101, 022128. doi:10.1103/physreve.101.022128

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhoyar, P. D., and Gade, P. M. (2021). Emergence of logarithmic-periodic oscillations in contact process with topological disorder. Phys. Rev. E 103, 022115. doi:10.1103/physreve.103.022115

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhoyar, P. D., Warambhe, M. C., Belkhude, S., and Gade, P. M. (2022). Robustness of directed percolation under relaxation of prerequisites: role of quenched disorder and memory. Eur. Phys. J. B 95, 64. doi:10.1140/epjb/s10051-022-00326-9

CrossRef Full Text | Google Scholar

Domany, E., and Kinzel, W. (1984). Equivalence of cellular automata to ising models and directed percolation. Phys. Rev. Lett. 53, 311–314. doi:10.1103/physrevlett.53.311

CrossRef Full Text | Google Scholar

Frauenrath, H. (2005). Dendronized Polymers—Building a new bridge from molecules to nanoscopic objects. Prog. Polym. Sci. 30, 325–384. doi:10.1016/j.progpolymsci.2005.01.011

CrossRef Full Text | Google Scholar

Grassberger, P. (1981). “On phase transitions in schlögl’s second model,” in Nonlinear phenomena in chemical dynamics: proceedings of an international conference, bordeaux, France, September 7–11, 1981 (Springer), 262.

Google Scholar

Griffiths, R. B. (1969). Nonanalytic behavior above the critical point in a random ising ferromagnet. Phys. Rev. Lett. 23, 17–19. doi:10.1103/physrevlett.23.17

CrossRef Full Text | Google Scholar

Harris, A. B. (1974). Effect of random defects on the critical behaviour of ising models. J. Phys. C Solid State Phys. 7, 1671–1692. doi:10.1088/0022-3719/7/9/009

CrossRef Full Text | Google Scholar

Henkel, M. (2008). Non-equilibrium phase transitions. Springer.

Google Scholar

Hooyberghs, J., Iglói, F., and Vanderzande, C. (2003). Strong disorder fixed point in absorbing-state phase transitions. Phys. Rev. Lett. 90, 100601. doi:10.1103/physrevlett.90.100601

PubMed Abstract | CrossRef Full Text | Google Scholar

Janssen, H.-K. (1981). On the nonequilibrium phase transition in reaction-diffusion systems with an absorbing stationary state. Z. für Phys. B Condens. Matter 42, 151–154. doi:10.1007/bf01319549

CrossRef Full Text | Google Scholar

Marsh, R., Riauka, T., and McQuarrie, S. (2008). A review of basic principles of fractals and their application to pharmacokinetics. Q. J. Nucl. Med. Mol. Imaging 52, 278–288. Available online at: https://pubmed.ncbi.nlm.nih.gov/18551095/

PubMed Abstract | Google Scholar

Méndez, V., Iomin, A., Campos, D., and Horsthemke, W. (2015). Mesoscopic description of random walks on combs. Phys. Rev. E 92, 062112. doi:10.1103/physreve.92.062112

PubMed Abstract | CrossRef Full Text | Google Scholar

Ódor, G. (2000). Critical behavior of the one-dimensional pair contact process with diffusion. Phys. Rev. E 62, R3027. doi:10.1103/PhysRevE.62.R3027

PubMed Abstract | CrossRef Full Text | Google Scholar

Pastor-Satorras, R., and Vespignani, A. (2001). Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203. doi:10.1103/physrevlett.86.3200

PubMed Abstract | CrossRef Full Text | Google Scholar

Vojta, T. (2006). Rare region effects at classical, quantum and nonequilibrium phase transitions. J. Phys. A Math. General 39, R143–R205. doi:10.1088/0305-4470/39/22/r01

CrossRef Full Text | Google Scholar