- 1 Institute of Psychology, University of Münster, Münster, Germany
- 2 Department of Computer Science, Chemnitz University of Technology, Chemnitz, Germany
Visual working memory (WM) tasks involve a network of cortical areas such as inferotemporal, medial temporal and prefrontal cortices. We suggest here to investigate the role of the basal ganglia (BG) in the learning of delayed rewarded tasks through the selective gating of thalamocortical loops. We designed a computational model of the visual loop linking the perirhinal cortex, the BG and the thalamus, biased by sustained representations in prefrontal cortex. This model learns concurrently different delayed rewarded tasks that require to maintain a visual cue and to associate it to itself or to another visual object to obtain reward. The retrieval of visual information is achieved through thalamic stimulation of the perirhinal cortex. The input structure of the BG, the striatum, learns to represent visual information based on its association to reward, while the output structure, the substantia nigra pars reticulata, learns to link striatal representations to the disinhibition of the correct thalamocortical loop. In parallel, a dopaminergic cell learns to associate striatal representations to reward and modulates learning of connections within the BG. The model provides testable predictions about the behavior of several areas during such tasks, while providing a new functional organization of learning within the BG, putting emphasis on the learning of the striatonigral connections as well as the lateral connections within the substantia nigra pars reticulata. It suggests that the learning of visual WM tasks is achieved rapidly in the BG and used as a teacher for feedback connections from prefrontal cortex to posterior cortices.
Introduction
During object-based visual search, target templates stored in visual working memory (WM) can bias attentional processing in visual areas to favorize the relevant objects (Desimone and Duncan, 1995 ; Woodman et al., 2007 ). Visual WM can be investigated through a number of different tasks in rats, primates or humans, among which change detection, recall procedures, delayed matching-to-sample (DMS), delayed nonmatching-to-sample (DNMS) or delayed pair-association (DPA) tasks are frequently used. These experiments have allowed to shed light on the psychophysical mechanisms involved in visual WM (Luck and Vogel, 1997 ) as well as to delineate the neural substrates subserving these functions (Ranganath, 2006 ). Visual WM has several computational aspects: encoding of the relevant items (potentially in an abstract manner), maintenance of the items through time in face of distractors, retrieval of the sensory content of the item, abstraction of the underlying rule. It faces both a structural credit assignment problem (which item to store and retrieve) and a temporal assignment problem (how to link encoding in WM with the delayed delivery of reward).
Specific attention has been directed towards the prefrontal cortex which is well-known to be involved in WM maintenance and manipulation in various modalities (Fuster and Alexander, 1971 ; Funahashi et al., 1989 ). Prefrontal lesions do not totally eliminate visual WM but impairs the ability to maintain it during long delays or in front of distractors (Petrides, 2000 ; D’Esposito et al., 2006 ). Neurons in PFC exhibit robust object-specific sustained activities during the delay periods of visual WM tasks like DMS or DNMS (Miller et al., 1996 ). However the informational content of WM-related activities in PFC is still unclear (Romanski, 2007 ). Inferotemporal (IT) neurons have been shown to encode object-specific information (Nakamura et al., 1994 ) as they are located at the end of the ventral visual pathway (Ungerleider and Mishkin, 1982 ). They have been shown to be critical for visual WM (Fuster et al., 1981 ; Petrides, 2000 ) and also exhibit sustained activation during the delay period, even if their responses can be attenuated or cancelled by intervening distractors (Miller et al., 1993 ), what can be partly explained by feedback cortico-cortical connections originating from PFC (Fuster et al., 1985 ; Webster et al., 1994 ).
The medial temporal lobe (MTL, composed of perirhinal, PRh; entorhinal, ERh and parahippocampal, PH cortices) also plays an important also not essential role in visual WM. Compared to IT, a greater proportion of neurons in PRh and ERh exhibit sustained activation during the delay period (Nakamura and Kubota, 1995 ) and are robust to distractors (Suzuki et al., 1997 ). They are especially crucial when visual objects are novel and complex (Ranganath and D’Esposito, 2005 ). Particularly, PRh cells are more strongly involved in visual recognition when it requires visual WM processes (Lehky and Tanaka, 2007 ). They are reciprocally connected with IT neurons and can provide them with information about novelty or category membership since they can rapidly encode relationship between visual features (Murray and Bussey, 1999 ; Rolls, 2000 ), as well as the association of objects to reward (Mogami and Tanaka, 2006 ). Ranganath (2006) provided a complete account of the functional relationship between IT, PFC and MTL in visual WM. He considers that the visual aspects of the remembered object are maintained in the ventral pathway at various levels of complexity (low-level features in V1 or V4, object-related representations in IT) through sustained activation of cells. Top-down activation of these neurons by MTL would provide them with information about novelty and help to reconstruct a coherent mental image of the objects composing the visual scene, thanks to the link between MTL and hippocampus. Top-down activation by PFC helps the ventral stream to maintain representations in face of distraction and also allows stimulus–stimulus associations (like in the delayed pair-association task) in IT (Gutnikov et al., 1997 ).
A structure that is absent in this scheme but that is nevertheless very important in visual WM is the basal ganglia (BG), a set of nuclei in the basal forebrain. Human patients with BG disorders (such as Parkinson’s disease) show strong deficits in delayed response tasks (Partiot et al., 1996 ). Several experiments have recorded visual WM-related activities in various structures composing the BG, especially the striatum (STR) (Hikosaka et al., 1989 ; Mushiake and Strick, 1995 ; Lewis et al., 2004 ; Chang et al., 2007 ). Almost all cortical areas send projections to the input nuclei of BG (STR and the subthalamic nucleus, STN), while the output nuclei of BG (the internal segment of globus pallidus, GPi and the substantia nigra pars reticulata, SNr) tonically inhibit various thalamic nuclei, allowing selective modulation of corticothalamic loops (Parent and Hazrati, 1995 ). The BG are organized through a series of closed loops, which receive inputs from segregated cortical regions and project back to them quite independently (see Haber, 2003 for a review). The number and functional domain of these loops is still an open issue (Alexander et al., 1986 ; Lawrence et al., 1998 ; Nambu et al., 2002 ), but two of them are of particular relevance for our model. The executive loop involves the dorsolateral part of PFC (dlPFC), the head of the caudate nucleus (CN, a region of the dorsal striatum), GPi-SNr and the mediodorsal nuclei of thalamus (MD). The structures involved in this loop have all been shown to be involved in WM processes in various modalities and provide a basis for the maintenance and manipulation of items in cognitive tasks (see Frank et al., 2001 , for a review about the functional requirements of WM). The visual loop involves the IT and extrastriate occipital cortices, the body and tail of the CN, SNr and the ventral–anterior nucleus of the thalamus (VA) (Middleton and Strick, 1996 ; Seger, 2008 ). This loop is particularly involved in visual categorization and visual discrimination, but also sends output to premotor areas to link category learning with appropriate behavior. In addition to IT neurons, the body of the CN is involved in visual WM tasks, what suggests a role of the entire visual loop in visual WM (Levy et al., 1997 ).
What remains unknown is how these two loops can interact together in order to subserve visual WM functions in the context of efficient behavior. Previous models have particularly addressed the updating of WM content as part of the executive BG loop (e.g. Brown et al., 1999 or O’Reilly and Frank, 2006 ). We here focus on how such memory content can be used to bias the visual loop allowing for a goal-directed memory recall in the context of rewarded tasks such as DMS, DNMS or DPA. Among the different mechanisms by which two BG loops can interact, we focus on the overlapping projection fields of cortical areas: a cortical area sends principally projections to a limited region of the striatum, but its axons send collaterals along the surface of the striatum. In particular, the body of the caudate, which is part of the visual loop and principally innervated by IT projection neurons, also receives connections from the dorsolateral prefrontal cortex (Selemon and Goldman-Rakic, 1985 ). This model is thus composed of the visual loop linking PRh with BG and the thalamus, while the executive loop is reduced to sustained activation in dlPFC which projects on the region of the striatum belonging to the visual loop. The model is alternatively presented with specific combinations of visual cues and tasks symbols that allow the system to perform actions leading to the delivery of reward (as proposed by Gisiger and Kerszberg, 2006 ). Our emphasis is on the reward-modulated self-organization of connectivity between distributed populations. The model provides hypotheses about how sustained representations in dlPFC can bias learning in the visual loop so that object-related activities in the ventral visual pathway can be retrieved through thalamic stimulation in the context of a particular cognitive task to provide anticipatory top-down signals for the visual system, as observed physiologically (Naya et al., 2003 ; Takeda et al., 2005 ). In particular, self-organization in the model relies on the competitive selection of relevant cortical representations in the output structures of the BG.
Materials and Methods
Architecture of the Model
Each structure used in this model is composed of a set of dynamical neurons, whose membrane potential is governed by a time-dependent differential equation and transformed into a mean firing rate through a non-linear transfer function. These neurons therefore exchange a real instantaneous value instead of spikes, as it saves considerably computational costs and allows to use efficient learning rules that are not yet available for spiking neurons. Although we do not capture some biophysical details, this paradigm is sufficiently complex to show the emergence of dynamic behaviors through the interaction of distributed computational units (Rougier, 2009 ). The differential equation that rules the evolution of the activity of each neuron is discretized according to the Euler method with a time-step of 1 ms and is evaluated asynchronously to allow stochastic interactions between functional units (Rougier and Vitay, 2006 ).
Biological details gave us some insights on the choice of certain parameters, such as the time constants for the different neurons, as we know for example that striatal cells are faster than cortical cells (Plenz and Aertsen, 1996 ). Other parameters have been set to bring the model into a functionally meaningful range. Control simulations showed that minor variations on their values do not change qualitatively the results presented here.
The architecture of the model is depicted in Figure 1 A. Visual inputs are temporally represented in the perirhinal cortex (PRh), each cell firing for a particular visual object. These perirhinal representations project to the prefrontal cortex (dlPFC) where they are actively maintained for the duration of the task. These sustained activations in dlPFC are artificially controlled by a set of gating signals, leaving unaddressed the temporal credit assignment problem. PRh and dlPFC both project extensively to the CN, which learns to represent them in an efficient manner according to the task requirements. Depending on reward delivery in the time course of learning, each active striatal cell learns to integrate perirhinal and prefrontal information in a competitive manner due to inhibitory lateral connections. This mechanism leads to the formation through learning of clusters of striatal cells that represent particular combinations of cortical information depending on their association to reward. These CN cells send inhibitory projections to the SNr, whose cells are tonically active and learn to become selective for specific striatal patterns. This learning between CN and SNr is also dependent on reward delivery. Learning of the lateral connections between SNr cells additionally allows to limit the number of simultaneously inhibited SNr cells. These cells in SNr tonically inhibit thalamic cells (VA) which have reciprocal connections with PRh. The connections from SNr to VA and between VA and PRh are not learned but focused (one-to-one connection pattern), meaning that the inhibition of one SNr cell leads to the thalamic stimulation of a unique cell in PRh. A dopaminergic cell (SNc) receives information about the delivered reward (R) and learns to associate it with striatal activities. Its signal modulates learning at the connections between cortical areas (PRh and dlPFC) and CN, between CN and SNr, as well as within SNr. We now present in detail each structure and the differential equations followed by their neurons.
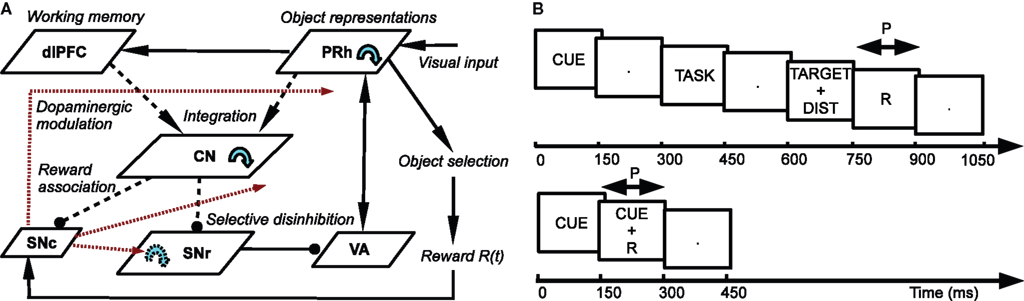
Figure 1. (A) Architecture of the model. Pointed arrows denote excitatory connections and rounded arrows denote inhibitory ones. Dashed arrows denote plastic connections. Blue circular arrows within an area represent lateral connections between the cells of this area. Red arrows represent dopaminergic modulation of learning. (B) Time course of the visual inputs presented to the network. Top: rewarded trials like DMS, DNMS or DPA. Bottom: delay conditioning.
Perirhinal cortex
The input of our model is a high-level visual area with mnemonic functions which is able to bias processing in the ventral visual stream. In general, the area TE of the IT cortex is a potential candidate, but we particularly focused on PRh, as it has been shown to be preferentially involved in recognition tasks that require visual WM (Lehky and Tanaka, 2007 ). We previously designed a detailed computational model of PRh that is able to learn object-related representations in clusters of cells based on partial information (Vitay and Hamker, 2008 ). These clusters linked through lateral connections are able to exhibit sustained activation when the dopamine (DA) level in the network is within an optimal range. The visual information that they contain can also be easily retrieved through a partial stimulation coming from the thalamus. We hypothesize that this memory retrieval through thalamic stimulation under an accurate level of DA can be a basis for the guidance of visual search.
Here, we reduced the size of PRh to eight cells, each of them representing a particular object that is presented to the network (see “Experiments” for the description of these objects). In our previous model, PRh contained hundreds of cells and each object was represented by a cluster of different cells. Each cell i has a membrane potential mi(t) and an instantaneous firing rate 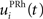 which are governed by the following equations:
which are governed by the following equations:
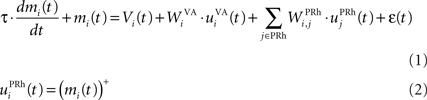
where τ = 20 ms is the time constant of the cell, Vi(t) its visual input (see Experiments) and 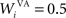 the weight of a connection coming from the corresponding thalamic cell whose firing rate is
the weight of a connection coming from the corresponding thalamic cell whose firing rate is 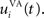 ε(t) is an additional noise whose value varies uniformly at each time-step between −0.3 and 0.3. The transfer function used for perirhinal cells is simply the positive part of the membrane potential ()+. Each perirhinal cell additionally receives inhibitory lateral connections from the seven neighboring perirhinal cells with a fixed weight of
ε(t) is an additional noise whose value varies uniformly at each time-step between −0.3 and 0.3. The transfer function used for perirhinal cells is simply the positive part of the membrane potential ()+. Each perirhinal cell additionally receives inhibitory lateral connections from the seven neighboring perirhinal cells with a fixed weight of 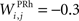 to induce competition between the perirhinal cells.
to induce competition between the perirhinal cells.
Dorsolateral prefrontal cortex
We do not model explicitly the executive loop and rather use a very simple WM representation in dlPFC, including mechanisms of updating and resetting. Future work will address these questions in the context of WM gating in the executive loop (Frank et al., 2001 ; Gruber et al., 2006 ). The dlPFC is here composed of eight cells which keep track of activity in PRh through temporal integration:
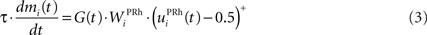
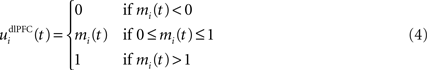
where τ = 10 ms is the time constant of the cell and G(t) a gating signal allowing the entry of an item in WM. Each dlPFC cell receives only one connection from a PRh cell with the weight . As soon as the activity of a PRh cell exceeds 0.5, it is integrated in the corresponding prefrontal cell, whose activity saturates to a maximum value of 1.0 thanks to the transfer function and stays at this value even if the perirhinal stimulation ends. The gating signal G(t) is manually set to a value of 1.0 when objects have to be maintained in WM and to a value of 0.0 otherwise. The activity of the prefrontal cells is manually reset to zero at the end of a trial.
Ventral–anterior thalamus
The portion of the ventral–anterior nucleus of the thalamus we consider here is represented by eight cells that are reciprocally connected with PRh. Its eight cells send and receive a connection with only one perirhinal cell, forming segregated thalamocortical loops. In a more biologically detailed model, we would have to take into account the difference in the number of cells between VA and PRh, as well the more diffuse pattern of connections from thalamus to cortex. However, this simplification is justified by our previous detailed model of PRh, where we have shown that a thalamic cell can activate a functional cluster of cells representing a single object (Vitay and Hamker, 2008 ). The membrane potential and firing rate of these thalamic cells are ruled by the following equations:
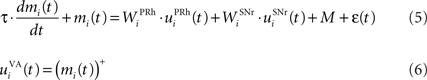
where τ = 15 ms and M = 0.8. In addition to the connection coming from one PRh cell with a weight of 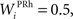 a thalamic cell also receives an inhibitory connection from one cell of SNr with a weight of
a thalamic cell also receives an inhibitory connection from one cell of SNr with a weight of 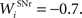
Caudate nucleus
The CN of the striatum learns to represent the cortical information in PRh and dlPFC in an efficient manner based on dopaminergic signaling of reward-related information in SNc. Although some evidences suggest that the DA level can even influence the firing rate of striatal cells (Nicola et al., 2000 ), we here exclusively focus on the effect of DA on the synaptic learning of corticostriatal connections (Di Filippo et al., 2009 ). The striatum is mostly composed of medium spiny neurons that integrate cortical information and directly inhibit several structures such as the substantia nigra or the globus pallidus. These cells have also lateral inhibitory connections, either directly or through fast-spiking interneurons (Tepper et al., 2008 ). Caudate nucleus contains here 64 cells ruled by the following equations:
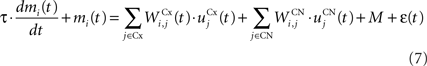

where τ = 10 ms and M = 0.3. Each striatal cell receives inhibitory lateral connections from the 63 other striatal cells with a weight 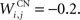 of The corticostriatal connections
of The corticostriatal connections 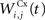 coming either from PRh or dlPFc are learned according to a homeostatic covariance learning rule:
coming either from PRh or dlPFc are learned according to a homeostatic covariance learning rule:
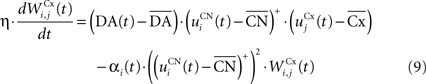
where η = 100 is the rate of learning, DA(t) represents the synaptic level of DA (considered equal to the activity of the SNc cell),  the baseline activity of the SNc cell,
the baseline activity of the SNc cell, 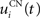 the firing rate of the striatal cell,
the firing rate of the striatal cell,  the mean firing rate of the CN cells,
the mean firing rate of the CN cells, 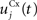 the firing rate of the cortical cell,
the firing rate of the cortical cell,  the mean firing rate of the considered cortical area and αi(t) a cell-dependent regularization factor. The weights are randomly initialized with a value between −0.1 and 0.1.
the mean firing rate of the considered cortical area and αi(t) a cell-dependent regularization factor. The weights are randomly initialized with a value between −0.1 and 0.1.
The first part of the right term of Eq. 9 is a classical Hebbian learning rule (correlation between the activities of the presynaptic and postsynaptic cells) modulated by the DA level. The positive function applied to the striatal activity ensures that only the cells which are significantly activated compared to the rest of the population will update their selectivity for cortical patterns. The exact influence of DA on corticostriatal learning is still a matter of debate and depends on the type of dopaminergic receptor (D1 or D2) involved, the state of the membrane potential of the striatal cell (“up” and “down” states) and on the cortical patterns (Calabresi et al., 2007 ). We do not model in detail these mechanisms and consider that a phasic burst of DA (transient activity of the SNc cell above its baseline) globally favorizes long-term potentiation (LTP) of corticostriatal synapses, while DA depletion (activity below baseline) globally induces long-term depression (LTD) of the same synapses (Reynolds and Wickens, 2000 ).
The second part of the right term of Eq. 9 performs a homeostatic regularization of the corticostriatal synapses. Its shape is similar to the classical Oja (1982) learning rule to avoid an infinite increase of the weight values, but the difference is that the regularization factor αi(t) is not fixed but varies with the activity of the cell (Vitay and Hamker, 2008 ). Homeostatic plasticity allows cells to adapt their learning behavior to ensure stability (Turrigiano and Nelson, 2004 ). In our case, we want to avoid that the striatal cells fire too much in order to save energy, by scaling down proportionally the weights of all the connections. αi(t) therefore becomes positive when the firing rate of the cell exceeds a defined threshold uMAX:
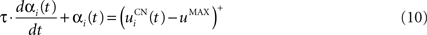
with τ = 20 ms and 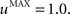 In addition to dynamically and locally normalizing the afferent connections to the cells, this homeostatic regularization term also allows to sharpen the selectivity of the cell. Homeostatic plasticity has been observed in the nucleus accumbens, a part of the striatum (Ishikawa et al., 2009
).
In addition to dynamically and locally normalizing the afferent connections to the cells, this homeostatic regularization term also allows to sharpen the selectivity of the cell. Homeostatic plasticity has been observed in the nucleus accumbens, a part of the striatum (Ishikawa et al., 2009
).
Substantia nigra pars compacta
The dopaminergic cells contained in SNc have the property to respond to the delivery of unexpected rewards by a phasic burst of activity above baseline (Mirenowicz and Schultz, 1994 ). However, in conditioning tasks, the amplitude of this response to primary rewards gradually decreases through learning and is transferred to the appearance of the conditioned stimulus (Pan et al., 2005 ). In addition, when reward is omitted, these dopaminergic cells show a phasic depletion of activity (below baseline) at the time reward was expected (Schultz et al., 1997 ). Several theories have tried to explain this behavior related to reward expectation, including an analogy with the error signal of the temporal difference (TD) algorithm of reinforcement learning (Suri and Schultz, 1999 ) or more biologically detailed models (Brown et al., 1999 ; O’Reilly et al., 2007 ). The TD analogy considers that DA phasic activation or depletion at the time of reward delivery or conditioned stimulus appearance are due to a unique mechanism. The more biologically detailed approaches contrarily highlight the role of afferent structures in the different components of this behavior: the phasic activation to primary rewards may be due to excitatory connections coming from the pedunculopontine tegmental nucleus, and its amplitude is gradually decreased by the learning of the reward expectation through inhibitory connections coming from the striatum. In these models, the DA phasic activation for the appearance of a conditioned stimuli is provoked by different mechanisms than for the delivery of primary rewards. The depletion in DA activity when reward is omitted is controlled by an external timing mechanism, presumably computed by an intracellular calcium-dependent mechanism in striatal cells (Brown et al., 1999 ) or by an external signal computed in the cerebellum (O’Reilly et al., 2007 ). We followed the assumptions of these models, but did not model explicitly this timing signal.
We used only one cell in SNc, which receives information about the received reward R(t) and learns to predict its association with striatal representations through learnable inhibitory connections. The activity of this cell is ruled by the following equations:
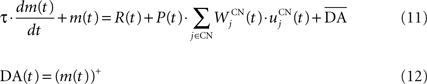
where τ = 10 ms, 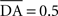 The reward R(t) (set to 0.5 when received, 0.0 otherwise) and the timing of its occurrence P(t) (set to 1.0 when expected, 0.0 otherwise) are external to the neuronal model. When reward is delivered, R(t) will drive the activity of the cell above its baseline but this effect will be reduced by the learning of the inhibitory connections between the striatum and SNc. When reward is expected but not delivered, the striatal inhibition will force the cell to exhibit an activity below baseline. The connections between CN and SNc are learned according to the following rule:
The reward R(t) (set to 0.5 when received, 0.0 otherwise) and the timing of its occurrence P(t) (set to 1.0 when expected, 0.0 otherwise) are external to the neuronal model. When reward is delivered, R(t) will drive the activity of the cell above its baseline but this effect will be reduced by the learning of the inhibitory connections between the striatum and SNc. When reward is expected but not delivered, the striatal inhibition will force the cell to exhibit an activity below baseline. The connections between CN and SNc are learned according to the following rule:
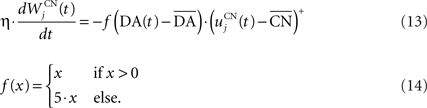
where η = 10000. The weights are initialized with a value of 0.0, so that striatal representations have initially no association to reward. When DA(t) is above baseline (reward has been delivered), the inhibitory connections are further decreased, which means that the striatal representation increases its associative value. When DA(t) is below baseline (reward has been omitted), the same striatal representation decreases its association to reward. This dopaminergic signal is used to modulate learning in CN and SNr.
Substantia nigra pars reticulata
The output nuclei of the BG (GPi and SNr) have the particularity to be tonically active (with an elevated firing rate of 25 Hz at rest and pause in firing when inhibited by striatal activity). They send inhibitory projections to ventral thalamic nuclei as well as various subcortical structures such as the superior colliculi. The SNr cells are selective for particular motor programs and can disinhibit various thalamocortical loops (Chevalier and Deniau, 1990 ). Their selectivity is principally due to the inhibitory connections originating from the striatum and GPe, but they also receive excitatory inputs from the STN. However, the SNr cells also tonically inhibit each other, with a particular connectivity pattern suggesting they may subserve an important functional role (Mailly et al., 2003 ). When a SNr cell is inhibited by striatal activation, it stops inhibiting the other SNr cells, who consequently increase their firing rate and inhibit more strongly their efferent thalamic cells. Inhibitory connections within SNr may therefore help focusing on the disinhibition of the desired thalamocortical loop by suppressing the competing other loops (Gulley et al., 2002 ). Instead of considering the inhibitory effect of high nigral activity, we modeled this competition between SNr cells by an excitatory effect of low nigral activity, what is functionally equivalent. The eight cells in SNr evolve according to the following equations:
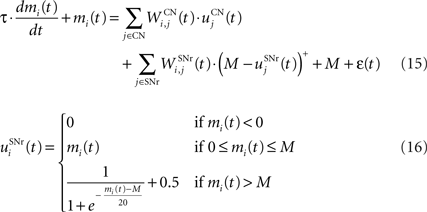
where τ = 10 ms, M = 1.0 and ε(t) is an additional noise randomly picked between −0.3 and 0.3. The excitatory connections from neighboring SNr cells are active when their corresponding activity is below baseline. The transfer function ensures that activities exceeding M saturate to a value of 1.5 with a sigmoidal shape. The inhibitory connections originating in CN are learned according to an equation similar to Eq. 9. Even if little is known about synaptic learning in SNr, the strong dopaminergic innervation of nigral cells (Ibañez-Sandoval et al., 2006 ) makes it reasonable to hypothesize that DA modulates the learning of striatonigral connections in a way similar to the corticostriatal ones.
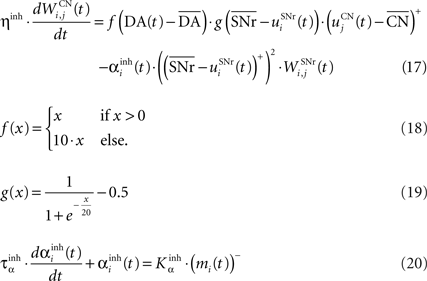
where ηinh = 500,  is the mean activity of all the cells in SNr,
is the mean activity of all the cells in SNr, 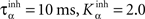 and ()− is the negative part of the membrane potential. The weights are randomly initialized between −0.15 and −0.05 and later restricted to negative values. Dopamine depletion (below baseline) has been given a greater influence in the learning rule through the f() function, because at the beginning of learning DA depletion has a much smaller amplitude than the DA bursts. Contrary to the classical Hebbian learning rule, the postsynaptic activity influences here the learning rule through a sigmoidal function g(), what makes it closer to the BCM learning rule (Bienenstock et al., 1982
). Similarly to BCM, there is a threshold (here the mean activity of the nuclei) on the postsynaptic activity that switches the learning rule from LTD to LTP. This learning rule is meant to increase the selectivity of each SNr cell regarding to its neighbors as well as the signal-to-noise ratio in the population. Another way for the nigral cells to increase their selectivity is competition through their lateral connections. There are two different learning rules used depending on whether the DA level is above or below baseline. When DA is above its baseline, the lateral connections are updated according to the following equation:
and ()− is the negative part of the membrane potential. The weights are randomly initialized between −0.15 and −0.05 and later restricted to negative values. Dopamine depletion (below baseline) has been given a greater influence in the learning rule through the f() function, because at the beginning of learning DA depletion has a much smaller amplitude than the DA bursts. Contrary to the classical Hebbian learning rule, the postsynaptic activity influences here the learning rule through a sigmoidal function g(), what makes it closer to the BCM learning rule (Bienenstock et al., 1982
). Similarly to BCM, there is a threshold (here the mean activity of the nuclei) on the postsynaptic activity that switches the learning rule from LTD to LTP. This learning rule is meant to increase the selectivity of each SNr cell regarding to its neighbors as well as the signal-to-noise ratio in the population. Another way for the nigral cells to increase their selectivity is competition through their lateral connections. There are two different learning rules used depending on whether the DA level is above or below baseline. When DA is above its baseline, the lateral connections are updated according to the following equation:
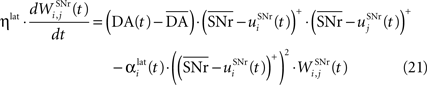
where ηlat = 500. The weights are initially set to 0.0. This rule is similar to a classical anti-Hebbian learning, as it favorites the competition between two cells when they frequently have simultaneously low firing rates. In the case of a DA depletion, an important feature of the model is that the symmetry of the lateral connections between two inhibited cells has to be broken. Dopamine depletion has then a punishing effect on the most inhibited cells, which will later receive much more excitation from previously moderately inhibited cells:
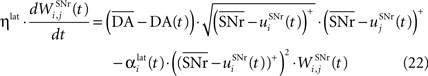
In both cases, two simultaneously inhibited cells will increase their reciprocal lateral connections. However, in the case of DA depletion, the square root function applied to the postsynaptic activity breaks the symmetry of the learning rule and the most inhibited cell will see its afferent lateral connections relatively more increased than the other cells. Thus, the inhibited cells which won the competition through lateral connections but provoked a DA depletion will be more likely to loose competition at the next trial. The effect of these asymmetric learning rules will be presented in Section “Effect of Late Competition in SNr”, where we will show that they are able to eliminate distractors. Both learning rules use the same equation for the updating of the regularization factor:
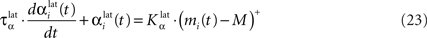
where 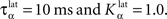
Experiments
In order to test the ability of our model to perform visual WM tasks, we focused on three classical experimental paradigms: the delayed matching-to-sample (DMS), the delayed nonmatching-to-sample (DNMS) and the delayed pair-association (DPA) tasks. These three tasks classically consist in presenting to the subject a visual object (called the cue), followed after a certain delay by an array of objects, including a target towards which a response should be made (either a saccade or a pointing movement or a button press). In DMS, the target is the same object as the cue; in DNMS, the target is the object that is different from the cue; in DPA, the target is an object artificially but constantly associated to the cue. These three tasks are known to involve differentially IT, MTL, PFC and BG (Sakai and Miyashita, 1991 ; Elliott and Dolan, 1999 ; Chang et al., 2002 ).
Similarly to the mixed-delayed response (MDR) task of Gisiger and Kerszberg (2006) , we want our model to acquire knowledge about contextual information, allowing it to learn concurrently these three tasks with the same cued visual objects. We therefore need to provide the network with a symbol specifying which task has to be performed. The meaning of this symbol is however initially not known by the model and must be acquired through the interaction within the tasks. The top part of Figure 1 B shows the time course of the visual inputs presented to the network during a trial. Each trial is decomposed into periods of 150 ms. During the first period, a cue is presented to the network, followed by a delay period without visual stimulation. A visual object representing which task to perform (DMS, DNMS or DPA) is then presented, followed by the same delay period. During this presentation phase, the signal G(t) in Eq. 3 is set to 1.0 to allow the sustained activation in dlPFC of these two objects.
In the choice period, two objects are simultaneously presented to the network: the target (whose identity is defined by the cue and the task symbol) and a distractor chosen randomly among the remaining cues. At the end of this period, the response of the network is considered to be performed, and reward is given accordingly through a probabilistic rule during the following reward period. For the entire duration of this reward period, the signal R(t) in Eq. 11 is set to 0.5 if reward is given and to 0.0 otherwise. P(t) is set to 1.0, denoting that reward is expected to occur. This reward period is followed by another delay period, the activities in dlPFC being manually reset to their baseline, allowing the network to go back to its resting state before performing a new trial.
In these experiments, we use four different cues (labeled A, B, C and D) and three task symbols (DMS, DNMS and DPA) that stimulate each a different cell in PRh. The corresponding cells will therefore be successively activated according to the time course of the trial described on the top part of Figure 1 B. In the Results section, we will only consider subsets of combinations of cues and tasks. For example, we define DMS-DNMS_AB as a combination of four different trials: A followed by DMS (A + DMS), A followed by DNMS (A + DNMS), B followed by DMS (B + DMS) and B followed by DNMS (B + DNMS). These four different trials are randomly interleaved during the learning period. In the DMS trials, the target of the task is the same as the cue, the distractor being chosen in the remaining possible cues. In the DNMS trials, the target is the object that is different from the cue. In the DPA task, the target is an object artificially associated to the cue. In DMS-DPA_AB, the target of the trial A + DPA is C and the one of B + DPA is D.
Each PRh cell is stimulated by its corresponding visual object by setting the signal Vi(t) in Eq. 1 to a value of 1.0 during the whole period. In the choice period, Vi(t) is limited to 0.5 for both cells (to mimic competition in the lower areas). To determine the response made by the system, we simply compare the activities of the two stimulated PRh cells at the end of the choice period. If the activity of the cell representing the target is greater than for the distractor, we hypothesize that this greater activation will feed back in the ventral stream and generate an attentional effect that will guide a saccade toward the corresponding object (Hamker, 2003 , 2005b ). We assume that this selection is noisy, what is modeled by introducing a probabilistic rule for the delivery of reward that depends on the difference of PRh activity for the two presented stimuli.
If we note utarget the activity of the PRh cell representing the target at the end of the choice period and udist the activity of the cell representing the distractor, the signal R(t) in Eq. 11 has the following probability to be delivered during the reward period:

This probability is of course limited to values between 0.0 and 1.0. When the activities of the two cells are equal, reward is delivered randomly, as we consider that a saccade has been performed randomly towards one of the two objects, as the feedback from PRh to the ventral pathway is not sufficiently distinct to favorite one of the two targets. When the activity of the target cell becomes relatively higher, the probability of executing the correct saccade and receiving reward is linearly increased. When reward is delivered, the signal R(t) has a value of 0.5 during the whole reward period, whereas it is set to 0.0 otherwise. We do not consider here the influence of rewards with different amplitudes.
In delay conditioning, reward is delivered randomly with a fixed probability during the presentation of a visual object (called X). The time course of this task is depicted on the bottom part of Figure 1 B. This task is described in Section “Reward-Related Clustering in CN” to study the effect of the probability of reward delivery on striatal representations and reward prediction in SNc.
In Section “Influence of the Number of Cells in SNr”, we will study the influence of the number of cells in SNr on the performance of the network. While this number is equal to 8 in the previous experiments, we vary it here from 6 to 16. When the number of cells in SNr exceeds 8, we simply added cells in SNr which receive striatal inhibition and compete with the others, but which do not inhibit any thalamic cell. When there is only 6 cells, we suppressed in SNr and VA the cells corresponding to the objects DPA and X, which are not used in this experiment.
Results
Concurrent Learning of the Different Tasks
Figure 2 A shows the learning behavior of the model when different combinations of tasks are presented. Each network was fed 1000 times with randomly alternated trials. The Y-axis represents the rank of the last trial during the learning sequence where the network produced a incorrect answer, which is a rather conservative measurement of behavior. After this last mistake, the performance of all networks are stable, even when more than 1000 trials are presented as further tests have shown. We represent here the performance of different combinations of tasks: DMS-DNMS_AB, DMS-DPA_AB, DMS-DNMS_ABC, DMS_ABCD, DNMS_ABCD and DPA_ABCD. For each combination of tasks, we used 50 different networks that were initialized randomly. One can notice that the different networks learn at very variable speeds, as shown by the standard deviation. For example, for the DMS-DNMS_AB task, some networks converged after 200 different trials whereas a few others needed 800 trials, what denotes the influence of initialization as well as the one of noise. The only significant difference between the combinations of tasks is that DMS-DNMS_AB is learned faster than DMS-DNMS_ABC, DMS_ABCD, DNMS_ABCD and DPA_ABCD (two-sample KS test, P < 0.05). However, this can be simply explained by the fact that DMS-DNMS_ABC uses six different trials instead of four for DMS-DNMS_AB (C + DMS and C + DNMS have to be learned at the same time), and that DMS_ABCD, DNMS_ABCD and DPA_ABCD use a bigger set of possible distractors during the choice period. In the current state of the model, more complex combinations of tasks (such as DMS-DNMS-DPA_ABCD) do not converge systematically in a reasonable amount of time, probably due to too strong constraints on the competition between the cells in SNr. We will investigate in Section “Effect of Late Competition in SNr” the influence of distractors on performance. The distributions of the numbers of trials needed to learn for each combination have no significant shape, though a Gaussian fit can not be rejected (χ2-test, 0.2 ≤ P ≤ 0.6).
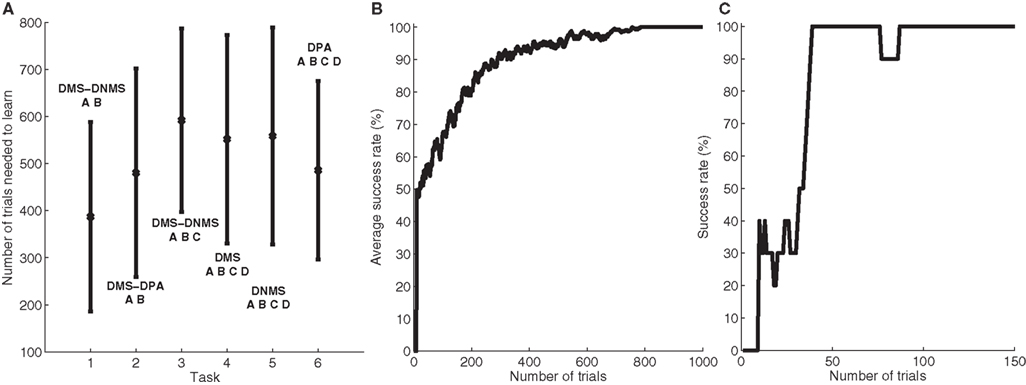
Figure 2. Different success rates. (A) Mean value and standard deviation of the last incorrect trial during learning of 50 randomly initialized networks for different combinations of cues and tasks: (1) DMS-DNMS_AB; (2) DMS-DPA_AB; (3) DMS-DNMS_ABC; (4) DMS_ABCD; (5) DNMS_ABCD; (6) DPA_ABCD. (B) Average success rate of 50 networks presented with DMS-DNMS_AB. (C) Success rate of a particular network which learned DMS-DNMS_AB, but computed only on the trials composed of A as a cue followed by DNMS as a task symbol.
Figure 2 B shows the average success rate of 50 networks presented with the DMS-DNMS_AB task. The success rate of a network is computed after each trial during learning as the percentage of rewarded trials for the last 10 trials: if the last 10 trials were rewarded, the success rate is 100%, if only one trial was not rewarded, the success rate is 90% and so on. All networks have reached the maximum success rate before the 800th trial, but some only need 200 trials. At the beginning of learning, the success rate is 50%, as the network does not really select a response and reward is given randomly according to the probabilistic rule of reward we use. This success rate quickly increases to a high value in around 300 trials, followed by a more flat phase where the competition in SNr temporarily deteriorates the performance of the networks.
This flattening of the average success rate can be explained by observing Figure 2 C. We represent the success rate of a particular network which learned DMS-DNMS_AB, but this success rate is plotted for analysis purpose only from trials composed of A as a cue followed by DNMS as a task symbol. We see that the network performs this task accurately after only 40 trials and stays at this maximum until it makes a mistake shortly before the 80th trial. We will later show that this temporary decrease in performance is mostly due to the late involvement of selection in SNr. To quantify this behavior, we examined the success rates of the 50 networks used in Figure 2 B and decomposed them regarding to the four types of trials involved in the learning phase (A followed by DMS and so on). We found that 32.5% of trial-specific networks showed this type of behavior, by reaching success in at least 10 successive trials before performing again a mistake. This criterion of 10 successive trials has been chosen sufficiently big to avoid pure chance in success (because of the probabilistic reward delivery rule) and sufficiently small to observe this decrease in performance. In average, these trial-specific networks reach stable success after only 14 trials and stay successful for 17 trials before performing a mistake. They then need on average 47 other trials before reaching definitely 100% success (last mistake after the 78th trial). In comparison, the other trial-specific networks (67.5%) perform their last mistake at the 64th trial on average, which is significantly shorter (χ2-test, P ≤ 0.05).
Temporal Evolution of the Activities After Learning
Once a network has successfully learned a particular combination of tasks, its neurons are able to retrieve the correct answer given the cue and the task symbol and obtain reward systematically. During learning, the selectivity of CN cells developed to represent the different combinations of cues and task symbols through clusters of cells (see Reward-Related Clustering in CN). SNr cells also became selective for some of these clusters and the learned competition between them ensured that only one SNr cell can be active at the same time in this context. After learning, when presented with a cue and a task symbol, the response of the network is already observable before the presentation of the choice array by the thalamic stimulation of the corresponding target. This anticipation of the correct response is typical of the BG mechanism of memory retrieval and is observed in all networks for all combinations of tasks. Two additional systematic observations are the sustained activation of the perirhinal cell representing the target after its disappearance and the tendency of the network to maintain the cue after its presentation through thalamic stimulation.
To better describe this common behavior, Figure 3 shows the temporal evolution of some cells of a particular network that successfully learned DMS-DNMS_AB. The learning phase consisted of 1000 randomly interleaved trials. The temporal evolution of the activity of the cells on Figure 3 was recorded during the course of a trial using A as a cue and DNMS as a task symbol. However, this pattern is qualitatively observed in every network that successfully learned the task and similar activation patterns occur for different tasks. The cells which are not shown on this figure do not exhibit significant activity after learning.
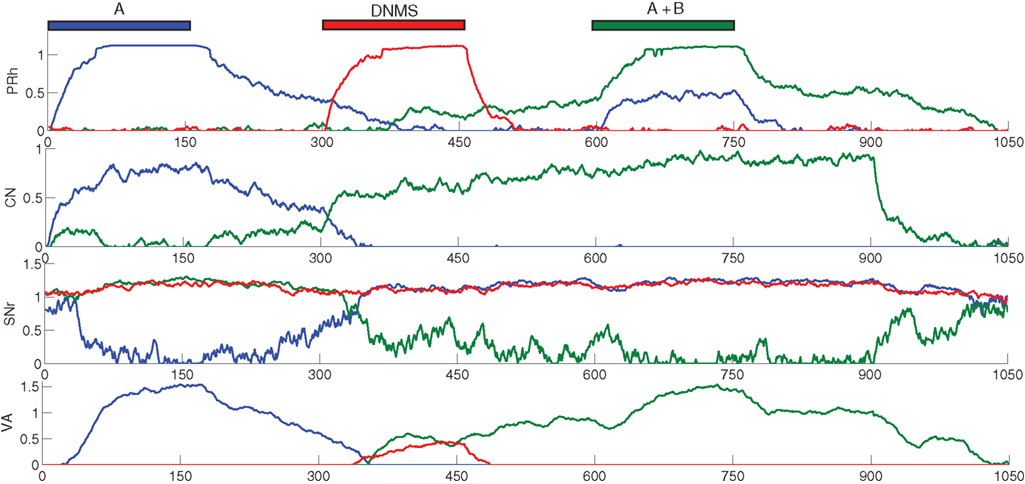
Figure 3. Temporal evolution of the activity of several cells in a network which successfully learned DMS-DNMS_AB. The activities are plotted with regard to time (in ms) during a trial consisting of A as a cue, DNMS as a task symbol and B as a target. The first row represents the activities of three cells in PRh which are respectively selective for A (blue line), DNMS (red line) and B (green line). The second row shows the activities of two cells in CN, one being selective for the pair A + DMS (blue line), the other for the pair A + DNMS (green line). The third row represents the activities of three cells in SNr which are respectively selective for A (blue line), DNMS (red line) and B (green line). The fourth row represents the activities of three cells in VA which are respectively selective for A (blue line), DNMS (red line) and B (green line).
When the object A is presented as a cue in PRh (and simultaneously enters the WM in dlPFC), it excites a cluster of cells in CN which, in this example, represents the couple A + DMS (blue line). This cluster inhibits the cell representing A in SNr which in turn stops inhibiting the corresponding cell in VA. The thalamocortical loop is then disinhibited and the two cells representing A in PRh and VA excite each other. After 150 ms, the stimulation corresponding to the cue ends and the activity of the cells representing A slowly decreases to their baseline. At 300 ms, the object specifying the task (DNMS) stimulates a cell in PRh and enters WM in dlPFC. This information biases processing in CN so that a new cluster representing A + DNMS gets activated (green line) and disinhibits through SNr the cell in VA representing the object B, which is the target of the task. At 600 ms, when both objects A (distractor) and B (target) stimulates PRh, the perirhinal cell A only receives visual information, while the cell B receives both visual and thalamic stimulation. Consequently, its activity is higher than the cell A and will be considered as guiding a saccade toward the object B. The cell representing DNMS in SNr never gets inhibited because it has never been the target of a task during learning. The corresponding thalamic cell only shows a small increase during the presentation of the object in PRh because of the corticothalamic connection. In the Discussion, we will come back on the fact that, in this particular example, the system has learned to select B instead of avoiding A as it should do in a DNMS task.
Three features are particularly interesting in this temporal evolution and have been observed for every network used in Section “Concurrent Learning of the Different Tasks”. The first one is that the perirhinal and thalamic cells corresponding to the object B are activated in advance to the presentation of the target and the distractor. The network developed a predictive code by learning the input, context and target association. For example, the behavior of the perirhinal cell correlates with the finding of pair-recall activities in IT and PRh during DPA tasks: some cells visually selective for the associated object have been shown to exhibit activation in advance to its presentation (Naya et al., 2003 ). Similarly, the behavior of the thalamic cell can be compared to the delay period activity of MD thalamic cells (part of the executive loop) during oculomotor WM tasks (Watanabe and Funahashi, 2004 ). The second interesting observation is the sustained activation of the perirhinal cell B after the disappearance of the target (between 750 and 900 ms on the figure) which is solely provoked by thalamic stimulation (as the WM in dlPFC still excites CN), whereas classical models of visual WM suggest that it is due a direct feedback from dlPFC (Ranganath, 2006 ).
The third interesting feature is the fact that the network, when only the cue was presented in PRh and dlPFC, already started to disinhibit the corresponding thalamic cell, somehow anticipating to perform the DMS task. We tested the 50 networks used in Section “Concurrent Learning of the Different Tasks” after learning the DMS-DNMS_AB task and presented them with either A or B for 200 ms. By subsequently recording the activity of the corresponding cells in SNr, we noticed that they all tended to perform DMS on the cue, i.e. disinhibiting the corresponding thalamic cell. This can be explained by the fact that the representation of the cue in PRh is also the correct answer to the task when DMS is required, and the projection from PRh to CN therefore favorites the selection of the striatal cluster representing A + DMS compared to A + DNMS. This can be interpreted such that the “normal” role of the visual loop is to maintain the visually presented objects, but that this behavior can be modified by additional prefrontal biasing (here the entry of DNMS into WM and its influence on striatal activation), as suggested by Miller and Cohen (2001) .
Effect of Late Competition in SNr
We focus now on what happens around the late incorrect trial in Figure 2 C to show that the first phase of learning corresponds to the selective learning of connections from cortex to CN and from CN to SNr, whereas the second one corresponds to the learning of lateral connections within SNr to decorrelate the activities in the structure. Figure 4 shows the evolution of some internal variables of SNr cells between the trials around the mistake produced at the trial number 77 of Figure 2 C. These trials are all composed of A as a cue, DNMS as a task symbol and therefore B as a target. Figure 4 A shows that the preceding and following trials were rewarded, but not the trial 77. Figure 4 B shows the activity of four SNr cells at the exact time when reward is delivered or expected to be delivered (750 ms after the beginning of the trial on Figure 3 ). These cells are selective respectively for A (blue line), B (green line), C (red line) and D (turquoise line). The four remaining cells in SNr are not plotted for the sake of readability, but they are not active anymore at this stage of learning. Figure 4 C represents the inhibition received by these cells at the same time, which means the weighted sum of inhibitory connections coming from CN. Figure 4 C represents the competition term received by these cells, which means the weighted sum of lateral connections in SNr (see Eq. 15).
Figure 4. Evolution of internal variables in SNr for trials surrounding the mistake performed by the network on Figure 2 C. (A) Reward received at each trial. (B) Activity of four SNr cells at the time reward is received or expected during the trial. These cells are selective respectively for A (blue line), B (green line), C (red line) and D (turquoise line). (C) Striatal inhibition received by these four cells. (D) Competition term received by the same four cells.
Through learning in the 76 first trials consisting in A followed by DNMS, the cells B and C became strongly inhibited during the choice period. In the rest of the article, we will call “active” a cell of SNr which is strongly inhibited and has an activity close to 0.0. Both cells receive a strong inhibition from the same CN cluster but they still do not compete enough with each other so that only one remains active. As B is a target, this provokes the disinhibition of the thalamocortical loop corresponding to B, so that the cell B in PRh is much more active than the cell A, leading to a correct response and subsequent reward. The cell C is not involved in this particular task, so it is just a distractor: its activation does not interfere with the current task. However, this cell may be useful in other tasks, but the strong striatal inhibition it receives will make it harder to recruit. At the trial 77, the cell C in SNr competes sufficiently with the cell B so that the activity of the cell B becomes close to its baseline (around 0.7 on Figure 4 B). The difference between the activities of cells A and B in PRh becomes small, leading to an omission of reward on Figure 4 A according to the probabilistic rule we used. This omission has two effects through the depletion of DA: first, it reduces the striatal inhibition received by the two active cells, as seen on Figure 4 C; second, it increases the competition between the two active cells, but in an asymmetrical manner (Figure 4 B). According to Eq. 22, the excitatory connection from the cell B to C will be much more increased than the one from the cell C to the cell B, as the cell C is much more inhibited than the cell B. Consequently, at trial 78, the cell C receives much more excitation from the cell B and its activity is pushed above baseline. The cell B is then strongly inhibited by the same cluster in CN and generates a correct rewarded response. In the following trials, the cell B will further increase its selectivity for this cluster, whereas the other cells in SNr (including the cell C) will totally lose theirs and can become selective for other clusters.
What happened around this trial shows the selection of a unique cell in SNr, even when the network already had a good performance. This selection relies on four different mechanisms. First, the network should have selected a number of cells in SNr which produce a correct answer. These cells include the target, but also distracting cells that are also selective for the same cluster in CN but which disinhibit irrelevant thalamocortical loops. Second, as the network produces correct answers, the cluster in CN becomes associated to a high reward-prediction value in SNc. The amplitude of phasic DA bursts is accordingly reduced. However, omission of reward will generate a greater depletion of the DA signal, compared to the beginning of learning when CN clusters had no association to reward and provoked no DA depletion. Third, omission of reward reduces the striatal inhibition received by active cells in SNr. However, if this was the only “punishing” mechanism, all the active cells will lose their selectivity. In this particular example, the cell B would gradually stop receiving inhibition from CN and all the preceding learning would be lost. Fourth, the learning of lateral connections in SNr is asymmetric with respect to DA firing: when a distractor progressively wins the competition until the response associated to the target is attenuated, this distractor becomes disadvantaged in the competition with the target. This is an indirect memory effect: as the cell corresponding to the target was previously activated and provoked reward delivery, the cease of its activation (provoking reward omission) is transmitted to the other cells in SNr through DA depletion, which “understand” that their activation is irrelevant and “get out” of the competition.
It is important to note that this competition between cells in SNr stays completely local to the cells: there is no winner-take-all algorithm or supervising mechanism deciding which cell should be punished. This competition emerges only through the interaction of the cells and the learning of their reciprocal connections. As stated in Section “Concurrent Learning of the Different Tasks”, a temporary decrease in performance occurs during learning in 32.5% of the networks we studied after they were able to obtain reward in at least 10 successive trials. This criterion was chosen as a compromise between being sufficiently high to avoid pure lucky success because of the probabilistic rule of reward delivery, and sufficiently low to catch all networks exhibiting a loss in performance due to lateral competition in SNr similar to the network presented in Figure 4 . In these networks, the target cell in SNr temporarily loses the competition before being reselected. However, contrary to this particular example, most of these networks perform more than one mistake after the initial one: they need 47 trials on average before reaching again stable success. Two behaviors are observed empirically: either the target directly wins the competition, the distractors fade and there is no degradation in performance, or another group of cells becomes instead active while still receiving reward because of the probabilistic rule of reward delivery, provoking a decrease in striatal inhibition of the target cell. This later case leads to a long period of instability for the network, where it has to find again that the target cell leads to systematic reward. These different types of learning behavior can explain the great variability in the number of trials needed to learn correctly all the tasks on Figure 2 A.
In order to better describe these two schemes of learning, we show on Figure 5 the magnitude of weight changes in CN and SNr during learning for two different networks. This magnitude is computed for each trial in the learning session by summing the absolute values of the discretized variations of weight values (|dWi,j(t)| in Eqs. 9, 17, 21 and 22) for all neurons in the considered area and for all computational time-steps in the entire trial (1050 in our design). These two networks have both learned the DMS-DNMS_AB task, but we represent here only the magnitude of weight changes occurring during A + DMS trials. The top row represents the magnitude of weight changes for striatal cells (Eq. 9), the middle row for the inhibitory connections from CN to SNr (Eq. 17) and the bottom one for lateral connections within SNr (both Eqs. 21 and 22). The absolute amplitude of these weight changes is meaningless, as it depends on the number of cells in each areas and the number of afferent connections. On Figure 5 A, the network shows an early learning phase in the first 30 trials where both striatal and pallidal cells show great variations in weight values, denoting that the network tries to find a correct answer to the task. After this first period, the connections from CN to SNr cease to fluctuate, while the connections from PRh and dlPFC to CN gradually stabilize (rather slowly, knowing that the computed magnitude also takes into account the regularization term in Eq. 9, as the striatal cells always tend to overshoot, and that this magnitude only decays with the association to reward). However, after the 50th trial, the lateral connections within SNr show another peak of variation. This corresponds to the simultaneous activation of two SNr cells, including the target. In this case, the correct target wins the competition and eliminates the distractor without provoking a mistake. The task has been correctly learned and the network slowly stabilizes its learning.
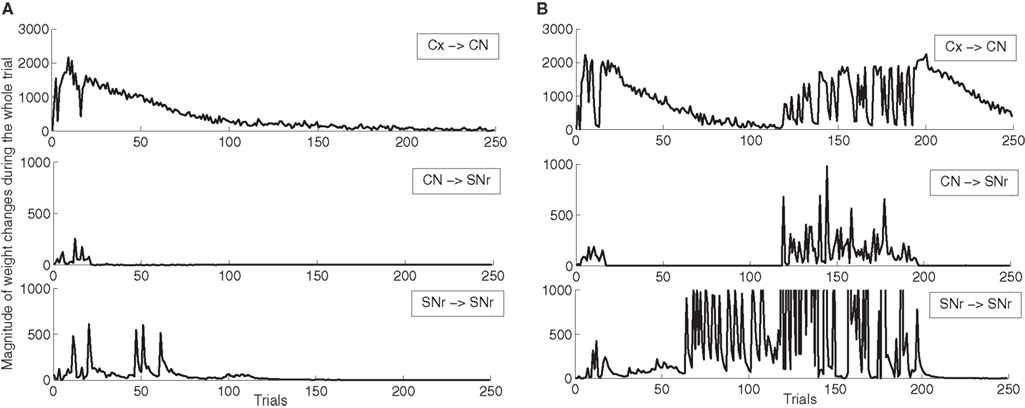
Figure 5. Magnitude of weight changes during learning of DMS-DNMS_AB for two different networks, plotted here only for A + DMS trials. The top line corresponds to global weight changes in CN (projections from PRH and dlPFC), the middle one to the connections from CN to SNr, the bottom one to lateral connections within SNr. (A) Network showing a late competition mechanism in SNr selecting directly the correct target without provoking a mistake. (B) Network showing a late competition mechanism in SNr that led to the performance of mistakes and to a long period of instability. The amplitude of lateral weight changes has been thresholded during this unstable phase (it reaches up to 5000) in order to allow a better comparison with the first network.
Oppositely, the network shown on Figure 5 B has the same early phase of learning, but the late increase in magnitude of lateral weight changes is much higher between the 70th and 120th trials. This increase is due to interference with lateral learning in another trial (here B + DMS), but provokes no mistake for the task. However, around the 120th trial, this increased competition between the target cell and a distractor leads the network to perform a mistake (as what happens in Figure 4 ), and the connections within the network vary for a certain number of trials before finding the correct solution and stabilizing. The instability in lateral weights induced by learning in another trial is due to the fact that, in the DMS + DNMS_AB combination of tasks, there are only two target cells for four different trials: they have to eliminate different distractors in each trial. The first scheme of learning is the most frequently observed (with often a longer duration), while the second one corresponds empirically to the 32.5% of networks found in Section “Concurrent Learning of the Different Tasks” (in some cases, there are no interactions between trials). We observed a third infrequent scheme of learning similar to the second one, but where only the connections from CN to SNr are modified in the second phase of learning, not the lateral ones. This can be explained by the fact that the target and the distractor have already learned to compete with each other during the learning of another trial.
Influence of the Number of Cells in SNr
As the number of possible distractors in SNr may influence the number of trials needed to learn the tasks, we investigated the influence of the number of cells in SNr (method described in Experiments). Figure 6 A shows the average number of trials needed to learn DMS-DNMS_AB by 50 randomly initialized networks. One can observe that the mean number of trials needed to learn increases monotonically with the number of cells in SNr, but in a quite flat manner: from 360 trials with 6 cells to 510 trials with 16 cells (regression analysis y = 15.16 × x + 271.9, with x the number of cells in SNr and y the time needed to learn, r2 = 0.25). This rather slow increase can be explained by the fact that the selection process in SNr through lateral connections do not concern cells two-by-two as shown on Figure 4 , but can eliminate several distractors at the same time. In addition, the variability of these numbers of trials is rather high, and some networks with 16 cells in SNr converge faster than some networks with only 6 cells depending on initialization and noise.
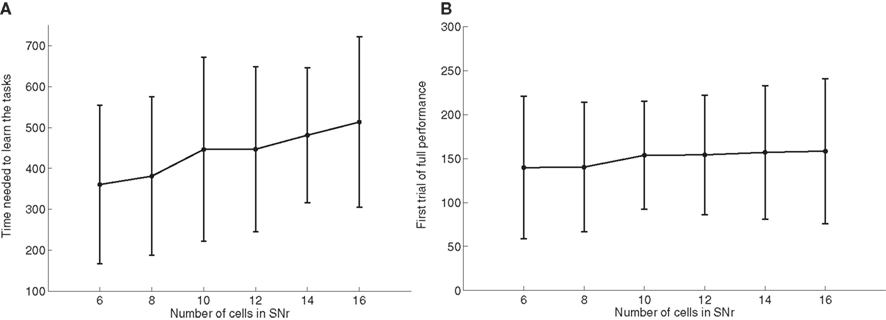
Figure 6. Influence of the number of cells in SNr. (A) Mean value and standard deviation of the last incorrect trial during learning of 50 randomly initialized networks learning DMS-DNMS_AB, depending on the number of cells in SNr. (B) Rank of the first trial during learning which got a success rate of 100% (computed on the 10 preceding trials), depending on the number of cells in SNr.
As a matter of comparison, Figure 6 B shows for the same networks the rank of the first trial in the learning sequence where the success rate was 100% (10 preceding trials were rewarded). One can observe that this first successful trial occurs on average at the same time in the learning sequence (around 150 trials), independently of the number of cells in SNr. We estimated the proportion of trial-specific networks that reached an early phase of success during at least 10 consecutive trials before performing a mistake again. This proportion stays rather constant with the number of cells in SNr, the minimum being 32.5% for 8 cells and the maximum 40% for 14 cells. Taken together, the result presented here confirm that there are globally two stages of learning regarding SNr: a first stage of parallel search independent of the number of cells in SNr, where the system selects through striatal inhibition an ensemble of cells in SNr able to obtain rewards (including the target and several distractors) and a second stage of partially sequential search that depends on the number of cells in SNr, where the system tries to eliminate the distractors through lateral competition, what needs more time when the number of possible distractors increases.
Reward-Related Clustering in CN
The CN cells learn to represent cortical information from PRh and PFC during the first stage of learning, together with the parallel selection in SNr. As the competition between CN cells is not very strong, a cluster of a few CN cells gradually become selective for a particular pattern of cortical activity which is rewarded. Each rewarded combination of cue and task symbols in the cortical areas gets represented by two to five cells in CN, whose identity may change through learning depending on reward delivery. Figure 7 shows the receptive fields (connection pattern with the cortical neurons) of several cells in CN after learning DMS-DNMS_AB. One can observe that some cells developed a very sharp selectivity to the cue and task symbols in dlPFC, as well as for the target in PRh. They have very strong positive connection weights to these cells, and relatively strong negative connection weights to the others. For example, the four cells on the top of the figure are selective for A and DNMS in dlPFC and B in PRh. After learning, this cluster will selectively inhibit the cell B in SNr and generate a correct response towards B.
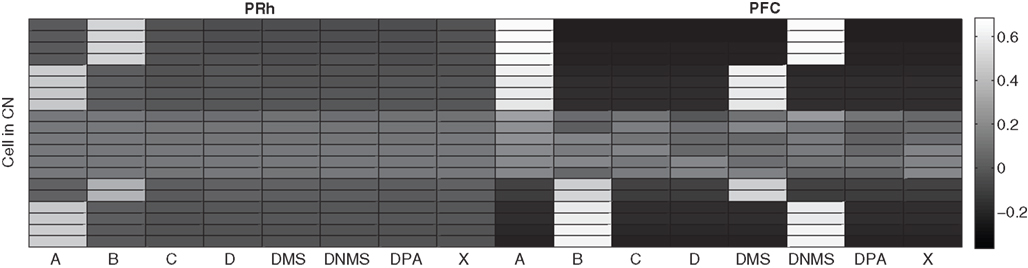
Figure 7. Receptive fields of some CN cells after learning DMS-DNMS_AB. The X-axis represent the cells in PRh and dlPFC and the Y-axis the different cells in CN. A white color represents a positive weight for the connection, grey represents a weight close to zero and black a negative weight.
According to these receptive fields, when a cue (e.g. A) is presented at the beginning of a trial, it will be represented in both PRh and dlPFC and therefore activate preferentially the cluster in CN selective for A + DMS. This explains the activation pattern of CN cells on Figure 3 : the presentation of the cue favorites the DMS-related clusters. However, when DNMS or DPA appear, they tend to inhibit these clusters so that the correct cluster can emerge from the competition. This tendency of the network to perform the DMS task even when the task is not known may have some advantages: a cue which is reliably associated to reward will see its representation in PRh enhanced through disinhibition of its thalamocortical loop, compared with visual objects which were never associated with rewards. This is coherent with the findings of Mogami and Tanaka (2006) who showed that the representation of visual objects in PRh is modulated by their association to reward.
At the end of the learning phase, the clusters in CN are fully associated with reward, which means that they totally cancel the phasic DA bursts and could generate a maximal depletion of DA if reward was omitted. The question that arises is whether all rewarded objects get represented equally in CN. In order to investigate this issue, we now use the trace conditioning that we presented in Section “Experiments”. This task consists in presenting to the network a visual object X which is randomly associated to reward with a fixed probability, whatever the response of the system. This trace conditioning task is randomly intermixed with the learning of DMS-DNMS_AB, for a total number of 1000 trials. Figure 8 A shows the sum of the activities of all CN cells at the time reward is given or expected, averaged over the last 50 conditioning trials of the learning sequence. Even with a low probability of reward like 0.1, the object X gets represented in CN by a sum of activity comprised between 3.0 and 5.0. This value must be compared to the sum of activities in CN when reward is never given (1.1) and which solely consists in weight initialization and noise. This sum of activities can represent a cluster of three to six cells depending on their activity.
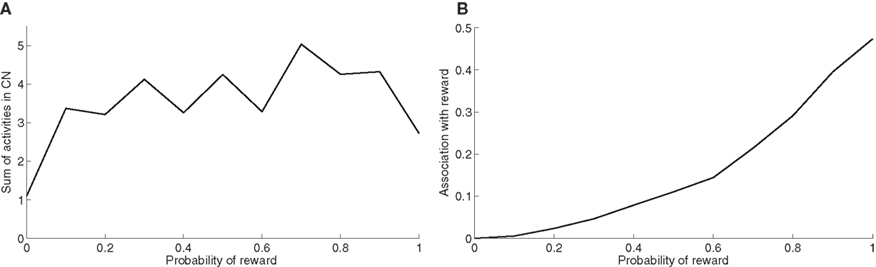
Figure 8. (A) Sum of activities in CN depending the probability of reward associated to the object X. (B) Association with reward of the cluster representing X in CN, depending on the probability of reward delivery.
Figure 8 B shows the association with reward associated of the object X at the time reward is given or expected, averaged over the last 50 conditioning trials of the learning sequence. This prediction of reward is computed as the absolute value of the weighted sum of connections from CN to SNc. Contrary to the striatal representations, this association to reward strongly depends on the probability of reward. It explains that even rarely rewarded objects can get represented in CN: the received reward generates a DA burst of activity that increases the corresponding corticostriatal connections, but it never becomes sufficiently associated to reward to generate a DA depletion that would decrease the same connections.
Discussion
We designed a computational model inspired by the functional anatomy of the visual loop connecting a high-level visual cortical area (PRh), some structures of BG (CN, SNc and SNr) and the corresponding thalamic nuclei (VA). The functioning of this closed loop is biased by the sustained activation of some prefrontal cells (dlPFC) which here artificially keep track of activity in PRh. This model is able to learn a mixture of visual WM tasks like DMS, DNMS and DPA in the context of reinforcement learning, where only a reward signal is delivered when the system answers correctly. This reward signal drives the activity of a dopaminergic cell which modulates Hebbian learning in the connections between the neurons of the model. With the combinations of tasks we tested, the network was able to learn perfectly the tasks after an average of 500 trials. Even if this number of trials may seem huge in comparison to experimental data on human adults, one has to consider that the system has absolutely no prior knowledge about the task: the symbols representing the tasks to perform within a trial are initially meaningless and the system only sees a couple of visual objects before being forced to make a choice in an array of objects.
Even if the architecture of the visual BG loop has been simplified compared to the known literature (only the direct pathway is implemented) and some known mechanisms have not been taken into account (like the modulation of the activity of striatal cells by DA firing), this model is able to exhibit some interesting emergent behaviors which can be considered as predictions. First, we have observed sustained activation of PRh cells which is only due to thalamic stimulation. As we hypothesized in (Vitay and Hamker, 2008 ), the observed sustained activation in PRh (and IT) may not only be the consequence of direct feedback from prefrontal areas to temporal areas, but may also pass through the thalamus via the BG in order to gain more control on the relevance of this behavior during the reinforced learning phase. After this learning phase, the fronto-temporal connections may replace the BG-thalamus system and directly provoke the sustained activation. Second, the tendency of the model after learning to start performing DMS right after the presentation of the cue (as the cue is represented both in PRh and dlPFC) enhances the perirhinal representation of items that are reliably associated to reward, what is in agreement with the findings of Mogami and Tanaka (2006) . It suggests that the default role of the visual loop of the BG is to favorite the representation of rewarded visual objects that are present in the visual scene, and that the role of the connections from dlPFC to the visual loop is to bias this behavior towards cognitively defined targets, as suggested by Miller and Cohen (2001) . Third, cells in PRh and VA corresponding to the target in the task are activated in advance of the presentation of the search array. Especially in DNMS and DPA where the target differs from the cue, this behavior reminds the pair-recall activities found in IT and PRh (Naya et al., 2003 ), as well as the presaccadic activities in the mediodorsal nucleus (MD) of the thalamus (Watanabe and Funahashi, 2004 ). We have not found similar results concerning the VA nucleus of the thalamus, but we predict that VA cells responsive for paired target of a DPA task will exhibit pair-recall activity.
There are three different stages of learning in the model. The first stage consists in the representation of cortical information by the striatal cells based on the delivered reward. This striatal representation combines the content of the WM (a representation of the cue and the task in dlPFC) with the perirhinal representation of the target through the activation of a cluster of cells. These clusters are composed of a limited number of cells due to competition among striatal cells. The second stage of learning consists in the selective inhibition of a group of SNr cells by these clusters of striatal cells. This selective inhibition is strongly modulated by reward delivery, so that the inhibited SNr cells are able to disinhibit the perirhinal representation of the target but not the distractor. This phase is performed in a parallel manner which does not depend on the number of cells in SNr. The third stage of learning is the enhanced competition between SNr cells to decorrelate their activities. This phase is sometimes characterized by a temporary degradation of the performance of the network until the target cell gets selected by the competitive mechanism, what makes this phase sequential with regard to the number of cells in SNr. This phase strongly relies on the learned reward-association value of striatal clusters in SNc, so that omission of reward can generate a depletion of DA. However, this distinction into three different stages is made a posteriori, as all cells learn all the time through the experiments without any change of parameters in the learning rules.
The role of the learned competition in SNr is to ensure that only the useful thalamocortical loop is disinhibited according to task requirements. Without this competition, several SNr cells would be inhibited by the same striatal cluster because the initialization of the connections between CN and SNr is randomly distributed. This could provoke parasitic disinhibition of thalamocortical loops, leading to involuntary movements or visual hallucinations. Without an additional self-organization of thalamocortical connections, the search for the target cell requires the progressive elimination of those distractors that strongly compete with the target, eventually leading to DA depletion to resolve the ambiguity. When different concurrently learned trials use the same targets, we even observed in Section “Effect of Late Competition in SNr” an interaction between them leading to a degradation of performance, what raises the issue of single-unit representations in SNr. For large real-world networks, one potential way to keep the sequential search in a reasonable bound would be to consider the topographical projections from cortex to striatum as well as from striatum to SNr. In our model, these projections are all-to-all and only become selective for particular patterns through learning. Zheng and Wilson (2002) showed that adjacent cells in striatum have very little common input, leading to a sparse representation of cortical information. Similarly, projections from striatum to GPi and SNr also have a sparse connectivity (Bar-Gad et al., 2003 ), although some GPi cells have been shown to receive input from functionally different striatal regions (Flaherty and Graybiel, 1994 ). Wickens and Oorschot (2000) observed that striatal cells are organized into small assemblies of neurons that have mutually inhibitory connections. The number of such compartments is remarkably similar to the number of GPi neurons, what could suggest a topographical pattern of convergence from cortex to SNr through striatum that could allow to limit this competition in SNr to limited sets of functionally related cells instead of the whole population. This would be in agreement with the found pattern of lateral connections between SNr cells belonging to the same or adjacent functional subdivision (Mailly et al., 2003 ).
To our knowledge, this model is the first to address the issue of learning at the level of SNr, either from striatum to SNr or within SNr. The late selection of the useful-only SNr cells may allow the prediction that the mean activity of the SNr population will be lower during learning than after, in the sense that more SNr cells will be inhibited in the first stages of learning than when the competition takes place. In addition, one may observe that the performance of the subject could temporarily be degraded after a certain number of successful trials, due to the late involvement of competition in SNr. This degradation of performance would be further enhanced when different tasks using the same targets are concurrently learned, as suggested the magnitude of weights changes observed in Section “Effect of Late Competition in SNr”. From a computational point of view, our model assigns a new functional role to SNr (and GPi) in the general framework of BG functioning and may guide to the development of a new class of BG models.
The model currently solves the DNMS task by learning to select the target, not by learning to avoid the cue. If a novel target were presented together with the cue after the learning phase, the system would not respond systematically towards it. In this respect, what is learned by the model when DNMS is required is more a version of DPA that associates cues together than truly DNMS. In order to learn DNMS, we would have to close the thalamocortical loop corresponding to the cue even more strongly than when SNr cells are at their baseline level. That could be achieved by exciting strongly the SNr cell corresponding to the cue, therefore inhibiting the neighboring cells in SNr which can then let other thalamocortical loops become active. The indirect pathway of BG is a possible candidate to truly learn DNMS: the additional inhibitory relay through GPe allows striatal activation to indirectly excite the output nuclei GPi/SNr (Albin et al., 1989 ; DeLong, 1990 ). This indirect pathway is also particularly involved in the processing of DA depletion, as the striatal cells participating in this pathway have mainly D2-type DA receptors and are globally inhibited by DA release. Dopamine depletion could then favorite this pathway and signal precisely to the output nuclei the omission of the expected reward. Incorporating this indirect pathway could allow us to truly learn DNMS and might also allow to simplify the learning rules in SNr which treat differentially over- and below-baseline DA activities. The balance between the direct and indirect pathway may signal more elegantly these two different situations, without modifying the principal results presented here.
On top of this possible influence of the indirect pathway on learning DNMS, Elliott and Dolan (1999) showed that DMS and DNMS involve differentially cortical or subcortical structures, the MD nuclei of the thalamus (part of the executive loop) being for example more implicated in DNMS than DMS. This raises the issue of the involvement of the executive loop in solving these rewarded visual WM tasks. In the current model, only the connections originating from dlPFC (which simply stores perirhinal information) bias representations in CN to perform the tasks. The purpose of this model is only to show that it is possible to retrieve object-related information in high-level visual areas like IT or PRh through behaviorally-relevant BG gating. The role of the executive loop in rewarded visual WM tasks is obviously much more complex than just maintaining perirhinal representations: gating the entry of items in WM (if a distractor is systematically presented during the task but has no behavioral relevance, it should not enter WM), manipulating them (abstracting sensory information and applying rules) and eventually actively suppressing items from WM (at the end of a trial or when a new item makes it obsolete). Gating and suppression of items are manually performed in our current dlPFC model but can be learned through the loop linking dlPFC with the corresponding BG structures modulated by DA firing (O’Reilly and Frank, 2006 ). Manipulating and abstracting representations is a harder issue that involves specifically the prefrontal cortex, but some computational models have already started to address this problem (Rougier et al., 2005 ). It would be also interesting not only to learn to represent specific combinations of cues and task symbols, but also to abstract the rule behind the task: if a new cue is presented, the system has to learn again this specific combination. This generalization to novel cues may be the role of the executive loop which may bias the visual loop in a more abstract manner than just storing cues and task symbols. This view is supported by the findings of Parker et al. (1997) which showed that MD (thalamic nuclei part of the executive loop) is crucial for learning DMS when the set of cues is big, but not when the set is small (what could be learned solely in the visual loop).
An extension of our model that would be able to fully learn the DMS, DNMS and DPA (with generalization to novel cues for all tasks and avoidance of the cue instead of selection of the target for DNMS) would therefore be composed of the visual and executive loops of the BG, both incorporating at least the indirect pathway. The role of the visual loop would be to retrieve the visual information associated to rewarded objects in the temporal lobe, acting by default on visually presented objects. The role of the executive loop would be to bias this processing, either by forbidding the visual loop to perform its automatic behavior (as in DNMS) or by guiding this behavior towards objects retrieved from memory (as in DPA). The executive loop would also be responsible for managing the task in time (gating and updating the entry of items into WM) in order to solve the temporal credit assignment problem, which is hard-coded in the current model. It would also manage the generalization of the learned task to bigger sets of cues and ultimately abstract the underlying rule. The interaction between the executive and visual loops will still rely on overlapping projection fields from PRh and dlPFC on the CN, but their synchronized learning will require to explore the spiraling pattern of connections between dopaminergic cells in SNc and the striatum discovered by Haber (2003) , suggesting a hierarchical organization of BG loops in guiding behavior. However, we expect the principal results of the current model to remain true in this extended version: the sustained activation of the target is only due to the classical disinhibition mechanism of the BG; the anticipatory activities in the thalamus are due to the maintenance of cues and task symbols in the executive loop; and the split of learning in two phases at the level of SNr should not affected by the incorporation of the indirect pathway, whose role would be rather a simplification of the treatment of DA depletion than a modification of the competition mechanism.
The way we modeled the dopaminergic firing in SNc is rather simple from a computational point of view. It receives information about the delivery of reward and learns to associate it with striatal representations. This reward association progressively cancels through learning the amplitude of the phasic DA bursts and provokes DA depletion at the time reward is expected (through an external timing signal) but not delivered. This behavior is consistent with the observations of Schultz et al. (1997) about DA firing at the time of reward in conditioning tasks. It does not reproduce the observed phasic burst that appears after learning at the presentation of the conditioned stimuli (or cue in our case). However, contrary to the classical approach comparing DA firing with the error signal of the TD algorithm (Suri and Schultz, 1999 ), we consider that this pattern of activation is computed by a separate mechanism, presumably by the selective entry in WM of the cue in the executive loop, as suggested by Brown et al. (1999) and O’Reilly and Frank (2006) . This entry of the cue in the executive loop will provide a timing signal which, combined with the reward association of the corresponding CN representation, is able to gradually provoke a DA phasic burst at the appearance of a cue which is reliably associated to reward. From a conceptual point of view, our current implementation of the DA firing considers that DA firing only enables the learning of the link between a context (here the content of WM), an action (the response made by the system) and the consequences of this action (here the delivery of reward), as suggested by Redgrave and Gurney (2006) .
The DA phasic burst generated by the executive loop could allow to signal the behavioral relevance of a stimulus instead of its association to reward. In the trace conditioning that we performed, even rarely rewarded stimuli get represented in CN, although they do not acquire a strong association to reward. By signaling that these stimuli may be rewarded but do not have a great importance for behavior, this cue-related DA firing may allow to reduce or even suppress their representation in CN so that the corresponding cells can focus on more important events. This DA-mediated behavioral relevance may act on the learning of corticostriatal connections (as we implemented it) or through the modulation of the membrane potential of striatal cells through the activation of D1 or D2 receptors (Calabresi et al., 2007 ). Linking striatal representations to behavioral relevance instead of just reward-association may allow a more efficient and selective encoding of external events that can occur in natural scenes.
A few computational models have addressed the issue of memory retrieval in the context of delayed visual WM tasks (Morita and Suemitsu, 2002 ; Mongillo et al., 2003 ; Gisiger and Kerszberg, 2006 ). These models are mainly attractor networks which focus on the interplay between IT and prefrontal cortices, but do not consider the influence of BG on learning through reinforcement. The model by Gisiger and Kerszberg (2006) learns concurrently DMS and DPA with a paradigm similar to the one we used. It is composed of three interconnected cortical structures performing respectively visual representation, WM and planning, and is able to reproduce electrophysiological data on IT and PFC functioning. However, it only learns to associate visual representations together, without learning to schedule the tasks. For example, the execution in time of DPA compared to DMS is controlled by manually computed gating signals, whereas, in our model, the only external gating signals concern the entry of visual representations into WM, independently of the particular task. Even if our model does not either solve the temporal credit assignment problem, we consider that the BG loops are an important site where the temporal execution of a task is learned, and that this functioning in time has important consequences on the content of cortical processing itself, such as anticipatory activities.
A comparison with other BG models is more difficult as we apply our model to a different paradigm. Some models deal with the influence of BG on reinforcement learning, particularly in classical or operant conditioning. The model of Suri and Schultz (1999) principally focuses on the computational aspects of DA firing which is considered similar to the error signal of the TD algorithm and which biases a direct mapping between stimuli and actions, within an actor-critic architecture. The model of Brown et al. (1999) is more biologically detailed and proposes a distinction between the different sources of information reaching SNc. The rest of the architecture of the BG is nonetheless kept simple and learning occurs only at the corticostriatal level. Other models focus more on the executive loop, especially with regard to WM gating and maintenance. Similarly to our approach, the model of O’Reilly and Frank (2006) uses the BG as a gating device for specific thalamocortical loops. It is successfully applied to complex WM tasks such as 1-2-AX, where it learns to generate a binary motor response depending on the content of WM. It is also applied to the store ignore recall (SIR) task, where it is presented with successions of visual objects, together with task symbols like “store” (where it should copy the object into WM) or ignore (where it should not copy). When the “recall” signal is presented alone, the system should respond towards the object that is currently stored in WM, whereas ordinarily it should just respond towards what is visually available. This task is similar to how we simulated DMS (PRh represents the visual input except when thalamic stimulation tells the opposite), but their model has the additional ability to ignore intervening distractors by selectively updating the content of WM depending on task requirements. The main differences with our model is that the output of their model is segregated from the input and that cues and task symbols have to be presented simultaneously. Adding an efficient executive loop to our model may allow us to better compare with this model. The model of Ashby et al. (2005) also focuses on WM maintenance (although in the spatial modality) through selective disinhibition of thalamocortical loops by the direct pathway only and considers elegantly the role of the feedback connections between PFC and posterior cortices. A very functionally different model was proposed by Gurney et al. (2001) , who place the STN at a very central place in the functioning of the BG. They claim that STN mediates the interplay between the selection pathway (similar to the direct pathway in other models) and the control pathway which biases processing in the selection pathway instead of acting in the opposite direction as suggested in the classical direct/indirect (or Go/NoGo) dichotomy. Although DA has there only a tonic effect, the concepts introduced in this model allow to reconsider the functional connectivity between BG structures.
Our proposed model is coherent with most cortical functional models of visual WM, such as Ranganath (2006) . It considers that relevant visual objects are actively maintained in dlPFC and fed back in high-level visual areas. These visual areas themselves modulate visual processing in the ventral pathway through feedback connections, in order to create object-based attention that helps selecting the correct target in space (Hamker, 2005a ). However, we propose that in the first phase of learning, BG learns to associate prefrontal representations with visual representations through reinforced trial-and-error learning in order to acquire the correct behavior. In parallel, but more slowly, the top-down connections from PFC to IT or PRh learns the same task in a supervised manner, BG acting as the teacher. After this second stage of learning, this prefrontal feedback on high-level visual areas can become the unique source of memory retrieval, as suggested by the results of Tomita et al. (1999) .
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work has been supported by the German Research Foundation (Deutsche Forschungsgemeinschaft) grant “A neurocomputational systems approach to modeling the cognitive guidance of attention and object/category recognition” (DFG HA2630/4-1) and by the EC Project FP7-ICT “Eyeshots: Heterogeneous 3-D Perception across Visual Fragments”.
References
Albin, R. L., Young, A. B., and Penney, J. B. (1989). The functional anatomy of basal ganglia disorders. Trends Neurosci. 12, 366–375.
Alexander, G. E., DeLong, M. R., and Strick, P. L. (1986). Parallel organization of functionally segregated circuits linking the basal ganglia and cortex. Annu. Rev. Neurosci. 9, 357–381.
Ashby, F. G., Ell, S. W., Valentin, V. V., and Casale, M. B. (2005). FROST: a distributed neurocomputational model of working memory maintenance. J. Cogn. Neurosci. 17, 1728–1743.
Bar-Gad, I., Morris, G., and Bergman, H. (2003). Information processing, dimensionality reduction and reinforcement learning in the basal ganglia. Prog. Neurobiol. 71, 439–473.
Bienenstock, E. L., Cooper, L. N., and Munroe, P. W. (1982). Theory of the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. J. Neurosci. 2, 32–48.
Brown, J., Bullock, D., and Grossberg, S. (1999). How the basal ganglia use parallel excitatory and inhibitory learning pathways to selectively respond to unexpected rewarding cues. J. Neurosci. 19, 10502–10511.
Calabresi, P., Picconi, B., Tozzi, A., and Filippo, M. D. (2007). Dopamine-mediated regulation of corticostriatal synaptic plasticity. Trends Neurosci. 30, 211–219.
Chang, C., Crottaz-Herbette, S., and Menon, V. (2007). Temporal dynamics of basal ganglia response and connectivity during verbal working memory. Neuroimage 34, 1253–1269.
Chang, J. Y., Chen, L., Luo, F., Shi, L. H., and Woodward, D. J. (2002). Neuronal responses in the frontal cortico-basal ganglia system during delayed matching-to-sample task: ensemble recording in freely moving rats. Exp. Brain Res. 142, 67–80.
Chevalier, G., and Deniau, J. M. (1990). Disinhibition as a basic process in the expression of striatal functions. Trends Neurosci. 13, 277–280.
D’Esposito, M., Cooney, J. W., Gazzaley, A., Gibbs, S. E. B., and Postle, B. R. (2006). Is the prefrontal cortex necessary for delay task performance? Evidence from lesion and FMRI data. J. Int. Neuropsychol. Soc. 12, 248–260.
DeLong, M. R. (1990). Primate models of movement disorders of basal ganglia origin. Trends Neurosci. 13, 281–285.
Desimone, R., and Duncan, J. (1995). Neural mechanisms of selective visual attention. Annu. Rev. Neurosci. 18, 193–222.
Di Filippo, M., Picconi, B., Tantucci, M., Ghiglieri, V., Bagetta, V., Sgobio, C., Tozzi, A., Parnetti, L., and Calabresi, P. (2009). Short-term and long-term plasticity at corticostriatal synapses: implications for learning and memory. Behav. Brain Res. 199, 108–118.
Elliott, R., and Dolan, R. J. (1999). Differential neural responses during performance of matching and nonmatching to sample tasks at two delay intervals. J. Neurosci. 19, 5066–5073.
Flaherty, A. W., and Graybiel, A. M. (1994). Input-output organization of the sensorimotor striatum in the squirrel monkey. J. Neurosci. 14, 599–610.
Frank, M. J., Loughry, B., and O’Reilly, R. C. (2001). Interactions between frontal cortex and basal ganglia in working memory: a computational model. Cogn. Affect. Behav. Neurosci. 1, 137–160.
Funahashi, S., Bruce, C. J., and Goldman-Rakic, P. S. (1989). Mnemonic coding of visual space in the monkey’s dorsolateral prefrontal cortex. J. Neurophysiol. 61, 331–349.
Fuster, J. M., and Alexander, G. E. (1971). Neuron activity related to short-term memory. Science 173, 652–654.
Fuster, J. M., Bauer, R. H., and Jervey, J. P. (1981). Effects of cooling inferotemporal cortex on performance of visual memory tasks. Exp. Neurol. 71, 398–409.
Fuster, J. M., Bauer, R. H., and Jervey, J. P. (1985). Functional interactions between inferotemporal and prefrontal cortex in a cognitive task. Brain Res. 330, 299–307.
Gisiger, T., and Kerszberg, M. (2006). A model for integrating elementary neural functions into delayed-response behavior. PLoS Comput. Biol. 2, e25. doi: 10.1371/journal.pcbi.0020025.
Gruber, A. J., Dayan, P., Gutkin, B. S., and Solla, S. A. (2006). Dopamine modulation in the basal ganglia locks the gate to working memory. J. Comput. Neurosci. 20, 153–166.
Gulley, J. M., Kosobud, A. E. K., and Rebec, G. V. (2002). Behavior-related modulation of substantia nigra pars reticulata neurons in rats performing a conditioned reinforcement task. Neuroscience 111, 337–349.
Gurney, K., Prescott, T. J., and Redgrave, P. (2001). A computational model of action selection in the basal ganglia. I. A new functional anatomy. Biol. Cybern. 84, 401–410.
Gutnikov, S. A., Ma, Y. Y., and Gaffan, D. (1997). Temporo-frontal disconnection impairs visual-visual paired association learning but not configural learning in macaca monkeys. Eur. J. Neurosci. 9, 1524–1529.
Haber, S. N. (2003). The primate basal ganglia: parallel and integrative networks. J. Chem. Neuroanat. 26, 317–330.
Hamker, F. (2003). A dynamic model of how feature cues guide spatial attention. Vision Res. 44, 501–521.
Hamker, F. H. (2005a). The emergence of attention by population-based inference and its role in distributed processing and cognitive control of vision. J. Comput. Vis. Image Underst. 100, 64–106.
Hamker, F. H. (2005b). The reentry hypothesis: the putative interaction of the frontal eye field, ventrolateral prefrontal cortex, and areas V4, IT for attention and eye movement. Cereb. Cortex 15, 431–447.
Hikosaka, O., Sakamoto, M., and Usui, S. (1989). Functional properties of monkey caudate neurons. III. Activities related to expectation of target and reward. J. Neurophysiol. 61, 814–832.
Ibañez-Sandoval, O., Hernández, A., Florán, B., Galarraga, E., Tapia, D., Valdiosera, R., Erlij, D., Aceves, J., and Bargas, J. (2006). Control of the subthalamic innervation of substantia nigra pars reticulata by D1 and D2 dopamine receptors. J. Neurophysiol. 95, 1800–1811.
Ishikawa, M., Mu, P., Moyer, J. T., Wolf, J. A., Quock, R. M., Davies, N. M., Hu, X. T., Schlter, O. M., and Dong, Y. (2009). Homeostatic synapse-driven membrane plasticity in nucleus accumbens neurons. J. Neurosci. 29, 5820–5831.
Lawrence, A. D., Sahakian, B. J., and Robbins, T. W. (1998). Cognitive functions and corticostriatal circuits: insights from Huntington’s disease. Trends Cogn. Sci. (Regul. Ed.) 2, 379–388.
Lehky, S. R., and Tanaka, K. (2007). Enhancement of object representations in primate perirhinal cortex during a visual working-memory task. J. Neurophysiol. 97, 1298–1310.
Levy, R., Friedman, H. R., Davachi, L., and Goldman-Rakic, P. S. (1997). Differential activation of the caudate nucleus in primates performing spatial and nonspatial working memory tasks. J. Neurosci. 17, 3870–3882.
Lewis, S. J. G., Dove, A., Robbins, T. W., Barker, R. A., and Owen, A. M. (2004). Striatal contributions to working memory: a functional magnetic resonance imaging study in humans. Eur. J. Neurosci. 19, 755–760.
Luck, S. J., and Vogel, E. K. (1997). The capacity of visual working memory for features and conjunctions. Nature 390, 279–281.
Mailly, P., Charpier, S., Menetrey, A., and Deniau, J. M. (2003). Three-dimensional organization of the recurrent axon collateral network of the substantia nigra pars reticulata neurons in the rat. J. Neurosci. 23, 5247–5257.
Middleton, F. A., and Strick, P. L. (1996). The temporal lobe is a target of output from the basal ganglia. Proc. Natl. Acad. Sci. U.S.A. 93, 8683–8687.
Miller, E., and Cohen, J. (2001). An integrative theory of prefrontal cortex function. Annu. Rev. Neurosci. 24, 167–202.
Miller, E., Erickson, C., and Desimone, R. (1996). Neural mechanisms of visual working memory in prefrontal cortex of the macaque. J. Neurosci. 16, 5154–5167.
Miller, E. K., Gochin, P. M., and Gross, C. G. (1993). Suppression of visual responses of neurons in inferior temporal cortex of the awake macaque monkey by addition of a second stimulus. Brain Res. 616, 25–29.
Mirenowicz, J., and Schultz, W. (1994). Importance of unpredictability for reward responses in primate dopamine neurons. J. Neurophysiol. 72, 1024–1027.
Mogami, T., and Tanaka, K. (2006). Reward association affects neuronal responses to visual stimuli in macaque TE and perirhinal cortices. J. Neurosci. 26, 6761–6770.
Mongillo, G., Amit, D. J., and Brunel, N. (2003). Retrospective and prospective persistent activity induced by Hebbian learning in a recurrent cortical network. Eur. J. Neurosci. 18, 2011–2024.
Morita, M., and Suemitsu, A. (2002). Computational modeling of pair- association memory in inferior temporal cortex. Brain Res. Cogn. Brain Res. 13, 169–178.
Murray, E. A., and Bussey, T. J. (1999). Perceptual-mnemonic functions of the perirhinal cortex. Trends Cogn. Sci. (Regul. Ed.) 3, 142–151.
Mushiake, H., and Strick, P. L. (1995). Pallidal neuron activity during sequential arm movements. J. Neurophysiol. 74, 2754–2758.
Nakamura, K., and Kubota, K. (1995). Mnemonic firing of neurons in the monkey temporal pole during a visual recognition memory task. J. Neurophysiol. 74, 162–178.
Nakamura, K., Matsumoto, K., Mikami, A., and Kubota, K. (1994). Visual response properties of single neurons in the temporal pole of behaving monkeys. J. Neurophysiol. 71, 1206–1221.
Nambu, A., Kaneda, K., Tokuno, H., and Takada, M. (2002). Organization of corticostriatal motor inputs in monkey putamen. J. Neurophysiol. 88, 1830–1842.
Naya, Y., Yoshida, M., Takeda, M., Fujimichi, R., and Miyashita, Y. (2003). Delay-period activities in two subdivisions of monkey inferotemporal cortex during pair association memory task. Eur. J. Neurosci. 18, 2915–2918.
Nicola, S. M., Surmeier, J., and Malenka, R. C. (2000). Dopaminergic modulation of neuronal excitability in the striatum and nucleus accumbens. Annu. Rev. Neurosci. 23, 185–215.
O’Reilly, R. C., and Frank, M. J. (2006). Making working memory work: a computational model of learning in the prefrontal cortex and basal ganglia. Neural. Comput. 18, 283–328.
O’Reilly, R. C., Frank, M. J., Hazy, T. E., and Watz, B. (2007). PVLV: the primary value and learned value Pavlovian learning algorithm. Behav. Neurosci. 121, 31–49.
Oja, E. (1982). A simplified neuron model as a principal component analyze. J. Math. Biol. 15, 267–273.
Pan, W. X., Schmidt, R., Wickens, J. R., and Hyland, B. I. (2005). Dopamine cells respond to predicted events during classical conditioning: evidence for eligibility traces in the reward-learning network. J. Neurosci. 25, 6235–6242.
Parent, A., and Hazrati, L. N. (1995). Functional anatomy of the basal ganglia. I. The cortico-basal ganglia-thalamo-cortical loop. Brain Res. Brain Res. Rev. 20, 91–127.
Parker, A., Eacott, M. J., and Gaffan, D. (1997). The recognition memory deficit caused by mediodorsal thalamic lesion in non-human primates: a comparison with rhinal cortex lesion. Eur. J. Neurosci. 9, 2423–2431.
Partiot, A., Vrin, M., Pillon, B., Teixeira-Ferreira, C., Agid, Y., and Dubois, B. (1996). Delayed response tasks in basal ganglia lesions in man: further evidence for a striato-frontal cooperation in behavioural adaptation. Neuropsychologia 34, 709–721.
Petrides, M. (2000). Dissociable roles of mid-dorsolateral prefrontal and anterior inferotemporal cortex in visual working memory. J. Neurosci. 20, 7496–7503.
Plenz, D., and Aertsen, A. (1996). Neural dynamics in cortex-striatum co-cultures – i. anatomy and electrophysiology of neuronal cell types. Neuroscience 70, 861–891.
Ranganath, C. (2006). Working memory for visual objects: complementary roles of inferior temporal, medial temporal, and prefrontal cortex. Neuroscience 139, 277–289.
Ranganath, C., and D’Esposito, M. (2005). Directing the mind’s eye: prefrontal, inferior and medial temporal mechanisms for visual working memory. Curr. Opin. Neurobiol. 15, 175–182.
Redgrave, P., and Gurney, K. (2006). The short-latency dopamine signal: a role in discovering novel actions? Nat. Rev. Neurosci. 7, 967–975.
Reynolds, J. N., and Wickens, J. R. (2000). Substantia nigra dopamine regulates synaptic plasticity and membrane potential fluctuations in the rat neostriatum, in vivo. Neuroscience 99, 199–203.
Rolls, E. T. (2000). Hippocampo-cortical and cortico-cortical backprojections. Hippocampus 10, 380–388.
Romanski, L. M. (2007). Representation and integration of auditory and visual stimuli in the primate ventral lateral prefrontal cortex. Cereb. Cortex 17(Suppl. 1), i61–i69.
Rougier, N. P., Noelle, D. C., Braver, T. S., Cohen, J. D., and O’Reilly, R. C. (2005). Prefrontal cortex and flexible cognitive control: rules without symbols. Proc. Natl. Acad. Sci. U.S.A. 102, 7338–7343.
Rougier, N. P., and Vitay, J. (2006). Emergence of attention within a neural population. Neural Netw. 19, 573–581.
Sakai, K., and Miyashita, Y. (1991). Neural organization for the long-term memory of paired associates. Nature 354, 152–155.
Schultz, W., Dayan, P., and Montague, P. R. (1997). A neural substrate of prediction and reward. Science 275, 1593–1599.
Seger, C. A. (2008). How do the basal ganglia contribute to categorization? Their roles in generalization, response selection, and learning via feedback. Neurosci. Biobehav. Rev. 32, 265–278.
Selemon, L. D., and Goldman-Rakic, P. S. (1985). Longitudinal topography and interdigitation of corticostriatal projections in the rhesus monkey. J. Neurosci. 5, 776–794.
Suri, R. E., and Schultz, W. (1999). A neural network model with dopamine-like reinforcement signal that learns a spatial delayed response task. Neuroscience 91, 871–890.
Suzuki, W. A., Miller, E. K., and Desimone, R. (1997). Object and place memory in the macaque entorhinal cortex. J. Neurophysiol. 78, 1062–1081.
Takeda, M., Naya, Y., Fujimichi, R., Takeuchi, D., and Miyashita, Y. (2005). Active maintenance of associative mnemonic signal in monkey inferior temporal cortex. Neuron 48, 839–848.
Tepper, J. M., Wilson, C. J., and Kos, T. (2008). Feedforward and feedback inhibition in neostriatal GABAergic spiny neurons. Brain Res. Rev. 58, 272–281.
Tomita, H., Ohbayashi, M., Nakahara, K., Hasegawa, I., and Miyashita, Y. (1999). Top-down signal from prefrontal cortex in executive control of memory retrieval. Nature 401, 699–703.
Turrigiano, G. G., and Nelson, S. B. (2004). Homeostatic plasticity in the developing nervous system. Nat. Rev. Neurosci. 5, 97–107.
Ungerleider, L. G., and Mishkin, M. (1982). “Two cortical visual systems,” in Analysis of Visual Behavior, eds D. J. Ingle, M. A. Goodale, and R. J. W. Mansfield (Cambridge, MA: The MIT Press), 549–586.
Vitay, J., and Hamker, F. H. (2008). Sustained activities and retrieval in a computational model of the perirhinal cortex. J. Cogn. Neurosci. 20, 1993–2005.
Watanabe, Y., and Funahashi, S. (2004). Neuronal activity throughout the primate mediodorsal nucleus of the thalamus during oculomotor delayed-responses. I. Cue-, delay-, and response-period activity. J. Neurophysiol. 92, 1738–1755.
Webster, M. J., Bachevalier, J., and Ungerleider, L. G. (1994). Connections of inferior temporal areas TEO and TE with parietal and frontal cortex in macaque monkeys. Cereb. Cortex 4, 470–483.
Wickens, J., and Oorschot, D. (2000). “Neuronal dynamics and surround inhibition in the neostriatum: a possible connection,” in Brain Dynamics and the Striatal Complex, eds R. Miller and J. Wickens (Amsterdam, Netherlands: Harwood Academic Publishers), 141–150.
Woodman, G. F., Luck, S. J., and Schall, J. D. (2007). The role of working memory representations in the control of attention. Cereb. Cortex 17, 118–124.
Keywords: basal ganglia, perirhinal cortex, visual working memory, reinforcement learning, memory retrieval, delayed rewarded tasks, attention
Citation: Vitay J and Hamker FH (2010) A computational model of basal ganglia and its role in memory retrieval in rewarded visual memory tasks. Front. Comput. Neurosci. 4:13. doi: 10.3389/fncom.2010.00013
Received: 18 August 2009;
Paper pending published: 26 November 2009;
Accepted: 30 April 2010;
Published online: 28 May 2010
Edited by:
Peter Dayan, University College London, UKReviewed by:
Kai Krueger, University College London, UKJeremy Reynolds, University of Denver, USA
Copyright: © 2010 Vitay and Hamker. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Fred H. Hamker, Department of Computer Science, Chemnitz University of Technology, Straße der Nationen 62, D-09107 Chemnitz, Germany. e-mail:ZnJlZC5oYW1rZXJAaW5mb3JtYXRpay50dS1jaGVtbml0ei5kZQ==

