- 1State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang, China
- 2Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang, China
- 3University of Chinese Academy of Sciences, Beijing, China
- 4Beijing Key Laboratory of Applied Experimental Psychology, School of Psychology, Beijing Normal University, Beijing, China
- 5State Key Laboratory of Cognitive Neuroscience and Learning, Beijing Normal University, Beijing, China
- 6School of Systems Science, Beijing Normal University, Beijing, China
- 7Chinese Institute for Brain Research, Beijing, China
Brain activities often follow an exponential family of distributions. The exponential distribution is the maximum entropy distribution of continuous random variables in the presence of a mean. The memoryless and peakless properties of an exponential distribution impose difficulties for data analysis methods. To estimate the rate parameter of multivariate exponential distribution from a time series of sensory inputs (i.e., observations), we constructed a hierarchical Bayesian inference model based on a variant of general hierarchical Brownian filter (GHBF). To account for the complex interactions among multivariate exponential random variables, the model estimates the second-order interaction of the rate intensity parameter in logarithmic space. Using variational Bayesian scheme, a family of closed-form and analytical update equations are introduced. These update equations also constitute a complete predictive coding framework. The simulation study shows that our model has the ability to evaluate the time-varying rate parameters and the underlying correlation structure of volatile multivariate exponentially distributed signals. The proposed hierarchical Bayesian inference model is of practical utility in analyzing high-dimensional neural activities.
1 Introduction
Decoding of the states of neural systems is a critical task for many applications in neural engineering, ranging from cognitive assessment, brain–machine interface to deep brain stimulation (Haynes and Rees, 2006; Qi et al., 2019; Yousefi et al., 2019; Xu et al., 2021; Zhang et al., 2022; Pan et al., 2022; Li and Le, 2017). However, there are several critical challenges faced by mental state decoding methods. First, brain activities are highly non-stationary, often showing transient dynamics. Second, responses of different brain regions are correlated, due to the dense complex anatomical connectivity patterns. Third, imaging processes of brain activities imposed additional spatial temporal transformations on neural signals, calling for appropriate inference methods to uncover the underlying brain states. To tackle these difficulties, methods that are capable of tacking and inferring multi-dimensional dynamic brain signals are indispensable.
Brain activities are shown to follow particular types of distributions that are distinctive from Gaussian distributions (Roxin et al., 2011). Extracellular recordings of brain voltage signals of various brain regions from different animals could be described by an exponential family of distributions, with tails falling off according to exponential distributions (Swindale et al., 2021). The distributions of the electromyography and electroencephalography signals from human subjects are found to have fatter tails than that of a Gaussian distribution and are fitted well by a generalized extreme value distribution (Nazmi et al., 2015). The innate statistics of the measured neural activities lead the direct application of classic tracking and inference methods, such as Kalman filtering, to be suboptimal (Li et al., 2009; Malik et al., 2010). It is therefore a valuable research direction to develop inference methods that closely match the characteristics of brain activities.
Exponential distributions well describe empirical data in neuroscience. Neurons in many regions, such as middle temporal and medial superior temporal visual areas in monkeys, fire in a Poisson-like fashion, with exponential distributed interspike intervals (Maimon and Assad, 2009; Ouyang et al., 2023). The sleep episode durations of human and other mammals, such as cats and rats, follow exponential distributions (Lo et al., 2004). The locomotion activity of cells in vitro displays a universal exponential distribution (Czirók et al., 1998). In addition, exponential distribution provides a good description of waiting times in the physical world, including lifespans, counts within a finite time period and so on. Therefore, researchers employ exponential distribution as lifetime distribution model to describe the lifetimes of manufactured products (Davis, 1952; Epstein and Sobel, 1953; Varde, 1969) and the survival or remission times in chronic diseases (Shanker et al., 2015). In physics, an exponential distribution is the best model of the times between successive flaps of a flag for a variety of wind speeds (McCaslin and Broussard, 2007). In finance, accumulating evidences have suggested that financial data can be quantified by exponential distributions. A study of tax and census data shows an exponential distribution of individual income in the United States (Drăgulescu and Yakovenko, 2001). An exponential distribution also agrees well with income for families with two earners (Drăgulescu and Yakovenko, 2001).
In this article, we aim to develop an inference model particularly to deal with the problem of volatility and multi-dimensionality in data space. Importantly, we assume that the data follow a multivariate exponential distribution, capturing the fat tail characteristics of neural signals. The proposed model can be applied to state estimation tasks in psychophysics, brain activity analysis, as well as other non-linear time series modeling tasks.
In probability theory, exponential distribution is a maximum entropy distribution of a continuous random variable with a bounded mean (Jaynes, 1982; Conrad, 2004; Stein et al., 2015). The exponential distribution has several interesting and important properties (Johnson et al., 2002; Ibe, 2014; Marshall and Olkin, 1967b):
• An exponential distribution is governed by a rate parameter (interpreted as the inverse of average waiting time). The mean of an exponential random variable is equal to the standard deviation (std).
• Exponential distribution is peakless. The probability density function of an exponential distribution is monotonously decreasing. The expectation of an exponential random variable is not at the maximum point of its probability density function. This means that samples drawn from an exponential distribution contain high noise, resulting in a fat tail.
• An exponential random variable is memoryless, i.e.,
In a Poisson process, this memoryless property means that the probability of waiting time until the next event is not affected by start time (Kingman, 1992). All waiting times are independently identically distribution (iid).
Due to these characteristics, fitting models of multivariate exponential distribution is a difficult problem encountered in various disciplines. The Marshall–Olkin exponential distribution is introduced based on shock models and the constraint that residual life and age are independent (Marshall and Olkin, 1967a). An exponential distribution with exponential minimums provides a model to describe the reliability of a coherent system (Esary and Marshall, 1974). A bivariate generalized exponential distribution is also introduced to analyze lifetime data in two dimensions (Kundu and Gupta, 2009). However, these models are complex in form and are not robust for non-stationary data. More importantly, the interactions among the components of a multivariate exponential variable are not trivial to estimate. These classical studies took the assumption of static distributions, without considering the dynamic changes of the underlying distributions. Robust methods for the estimation of multivariate exponential distribution in volatile environments are still sparse.
“Observing the observer” is a meta Bayesian framework (Daunizeau et al., 2010b,a) and furnishes a unified programming and modeling framework that unites perception and action based on the variational free energy principle (Beal, 2003; Friston, 2010; Mathys et al., 2011; Friston et al., 2017). Perceptual and response models are two major parts of this framework. Inversion of the perceptual and response models can map from sensory inputs (i.e., observations) into response actions. Following this framework, the general hierarchical Brownian filter (GHBF) was proposed as a model for state estimate in dynamic multi-dimensional environments with Gaussian distribution assumption (Zhu et al., 2025). An important function of this model is to capture temporal dynamics of lower order interactions among sensory inputs (i.e., observations).
In this article, we extend the general hierarchical Brownian filter to non-Gaussian case and develop an inference model for volatile multivariate exponentially distributed signals. The inference model incorporates a hierarchical perceptual model and a response model into the “observing the observer” framework. The model receives a series of multidimensional sensory inputs or observations and is asked to infer rate parameter of a multivariate exponential distribution in a complex volatile environment. The perceptual model represents rate parameter and covariance of the logarithm of rate parameter. The response model is a stochastic mapping to reproduce a series of sensory inputs. Compared with previous hierarchical Bayesian methods (Beal, 2003; Friston, 2010; Mathys et al., 2011; Friston et al., 2017), the proposed model is able to deal with multidimensional signals and dynamically uncover the potential correlation structure in the data.
The contribution of this article is two-fold. First, we develop a hierarchical Bayesian model to estimate the parameters of multivariate exponential distributions which are subject to dynamic changes. Through variational Bayesian learning, the model infers the rate parameters and the pairwise correlations of multivariate exponentially distributed signals at the same time; therefore, it is able to robustly track the distribution dynamically. The proposed model is valuable for its potential applications in estimating neural and behavioral responses. Second, the efficiency and the robustness of the proposed inference model is tested in simulations with synthetic dynamic data. Compared with a simplified model of constant volatility parameters, the proposed model is better in explaining the data, demonstrating the importance role of higher order variables, such as correlations, in estimating the parameters of the signal.
The rest of this article is structured as follows. The mathematical notations used in this study is defined in Section 2. Section 3 introduces the hierarchical Bayesian perceptual model in multivariate exponential distribution environment. Section 4 derives a set of closed form update equations for perceptual inference. Simulations results are given in Section 6. Finally, the article is concluded after discussions.
2 Notations
Throughout this article, we use the following conventional mathematical notations:
• A bold capital letter is a matrix while a bold lowercase letter is a vector.
• A hollow capital letter denotes a set, which is also denoted by {}.
• A probability density function (PDF) is denoted by q(·) or p(·).
• A multivariate Gaussian PDF of x is denoted by with mean μ and variance Σ, while a multivariate Gaussian random vector is denoted by .
• An multivariate exponential PDF of x can be denoted by with a rate parameter r, while an multivariate exponential random vector is denoted by .
• A sequence of variables over time are denoted by “:,” for example,
• Eq(x)(v) means the expectation of v under the distribution q(x).
• The operator ⊙ is the Hadamard product, the operation diag(v) is to transform a vector v into a diagonal square matrix with the elements of v on the principal diagonal.
• The function vec(Mm×n) is the vectorization of a matrix M, a linear operation, to obtain a column vector of length m×n by concatenating the columns of the matrix M consecutively from column 1 to column n. The operator ⊗ is the Kronecker product.
• The function lvec(L) is to transform a lower triangular matrix L into a column vector lvec(L) obtained by stacking columns without zero elements in the upper triangle part of the matrix.
3 Hierarchical Bayesian perceptual model
3.1 Parameterization of multivariate exponential distribution
Given a random multivariate exponential variable x0 without cross dimension interactions among components, we can easily get the joint probability of all components by directly multiplying all marginal exponential distributions:
where is the i-th component (i.e., random exponential variable) of x0. The rate parameter is the expectation of the i-th random exponential variable . r0 is the expected rate vector of random vector x0. The integer d0 is the number of dimensions of the random vector x0. However, this independent model is incapable of capturing the pairwise probabilistic correlation among the components of x0. If we introduce non-independent exponential model with interactions among the components of x0, it will lead to high model complexity. Since the rate parameter r0 is of primary interest, we aim to learn the rate parameter by explicitly considering the pairwise interactions among the components of r0. To keep the positive constraint of the rate parameter, we convert the constrained learning problem into an unconstrained learning in logarithmic space. More specifically, the rate r0 is mapped from a point x1 in its log-space
where the notation exp(·) denotes the element-wise exponential function. The coefficient matrix W1 is a diagonal matrix with positive elements on the principal diagonal. This matrix represents the coupling strength between x0 and x1. The bias b1 is a shift parameter.
3.2 Perceiving tendency and volatility of the rate parameter
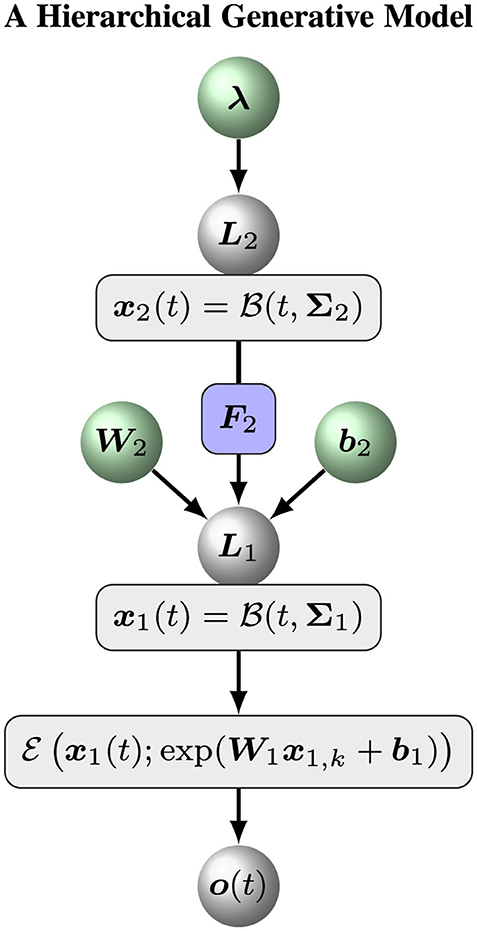
Volatile signals fluctuate over time, showing variations. The fluctuations of the signals are again subject to changes, and so forth. The nested nature of volatility is a hallmark of collective phenomena as observed in many complex systems like brain network, animal swarm and financial market. To quantitatively describe volatility and pairwise correlations of multi-dimensional signals, general hierarchical volatility model could be constructed based on nested Brownian motions (Zhu et al., 2025). The basic idea is that the variable of interest is represented by a Brownian motion, while the changes of the variable is predicted by higher order variables that are again subject to Brownian motions. Following this framework, we develop a hierarchical perceptual model to estimate the tendency and volatility of multivariate exponentially distributed signals (Figure 1). More specifically, the logarithms of rate parameters x1 of the underlying multivariate exponential distribution is modeled by a general Brownian motion with diffusion matrix
This Brownian motion captures the tendency of the learned parameter vector x1. The volatility (i.e., uncertainties and pairwise correlations) in x1 is given by , which is a symmetric positive definite matrix by definition. Considering the fact that the diffusion matrix Σ1 is a symmetric positive definite matrix, it could be uniquely represented by a lower triangular matrix according to Cholesky decomposition (Tanabe and Sagae, 1992; Jung and O'Leary, 2006):
To further evaluate the volatility Σ1 in x1, we assume that its decomposition L1 is modeled by a general Brownian motion in its parameterized space. To be exact, the elements of L1 is parametrized by a d2 = d1(d1+1)/2 dimensional vector y2, which results from concatenating the lower triangle elements of L1 in a column-wise fashion. The element in i-th row and j-th column of L1 is parameterized by
where sinh(·) denotes the hyperbolic sine function. Note that Equation 4 transforms L1 into logarithmic space, while conserving non-negativity for diagonal elements and allowing arbitrary values for off-diagonal elopements of L1.
The vector y2 represents the volatility of the signal in logarithmic space, therefore constitutes a parameterization of the volatility. y2 is given by the following mapping in the second level of the model:
where b2 and represent the trend and time-varying fluctuation in log-volatility of x1, respectively. The coefficient matrix W2 is a d2-by-d2 diagonal matrix representing the coupling strength from level two to level one. W2 can simply take the form of a diagonal matrix spanned from a column vector w2 with all positive elements
We can rewrite the coupling (Equations 4, 5) as
In the second level of the model, we further assume that x2 evolves as a general Brownian motion with diffusion matrix
The diffusion matrix Σ2 is chosen as a diagonal matrix for simplicity. Let be the unique Cholesky decomposition of Σ2. We simply assume that L2 is a constant diagonal matrix spanned by vector with all elements being positive.
Figure 1 shows an overview of the hierarchical perceptual model. With this model, a Bayesian agent receives a series of sensory inputs or observations o1:T. At time tk, the sensory input ok to the agent is determined by a delta distribution δ(·)
The initial priori states p(x1, 0, x2, 0) are Gaussian distributions as follows:
In summary, the hierarchical perceptual model constitutes a generative model for sensory observations o(t) based on hidden representations of the tendency (x1) and the volatility (x2) of the observations. . To simplify the notations, we introduced the notation X to denote the set of all hidden states, ℙ for the hyperparameters and the prior states of the model:
where μ1, 0, C1, 0, μ2, 0, andC2, 0 are the prior states of the model defined in Equation 8 and Supplementary material Section 2.
4 Perceptual inference approximated by variational approximation
The aforementioned hierarchical perceptual model is constructed based on general continuous Brownian motions. It remains to derive update rules to estimate the posterior distributions for the hidden representations x1 and x2. In order to derive a family of analytical and efficient update rules, we discretize continuous Brownian motions by applying the Eulerian method. The sampling interval (SI) ϵk = tk−tk−1 is defined by the time that elapses between the arrival of consecutive sensory inputs ok−1 and ok.
We use the variational Bayesian method (Beal, 2003; Friston, 2010; Daunizeau et al., 2010b; Mathys et al., 2011) to reach an approximation to the posterior distributions of x1(t) and x2(t) given the sensory input o(t) (i.e., observation). To this end, we maximize the negative free energy, which is the lower bound of log-model evidence, to yield variational approximation posterior (cf. Supplementary material Section 1):
where is a normalization constant. Vh(xh, k) is the variational energy given by
Here we introduced the notation X\h, k for excluding xh, k from the set Xk, Then under Brownian and Gaussian assumptions, the approximation variational posterior (Zhu et al., 2025) is
Under this approximation, the inference of the posterior distributions of xh is reduced to the estimation of the mean μh, k and the covariance matrix Ch, k, or equivalently the precision matrix . Following (Zhu et al., 2025), the update rules for the posterior distributions of x1 and x2 are derived.
At the bottom (zeroth) level of the hierarchical perceptual model, we can directly determine multivariate exponential distribution q(x0, k) with the expectation:
At the first level, following Equation 10, V1(x1) is calculated as
where 1 is a d0 dimensional column vector in which all elements are 1. Here we use the approximation
with computed from the second level
The variational energy V1(x1, k) is not a standard Gaussian quadratic form, so we have to employ a Gaussian quadratic form to approximate it (Zhu et al., 2025). To obtain this approximation form, we give the gradient and Hessian matrix of V1(x1, k) as follows:
and
Under the Gaussian quadratic form approximation, which is based on a single step Newton method (Zhu et al., 2025), the tendency of x0, k is captured by
where PE0, k is the prediction error:
is the prediction given by the mapping in Equation 2:
Unpacking prediction error PE0, k results in a meaningful formula,
The inverse of the predicted rate gives the expectation of sensory input, and the ratio measures the accuracy of the prediction. If the ratio is greater than 1 (i.e., the predicted expectation of sensory input is less than the actual sensory input), the prediction error is negative, and the agent should decrease . If the ratio is less than 1, the prediction error is positive, the agent should increase , so that the predicted expectation of sensory input could be decreased. Ideally, the ratio is equal to 1,and the prediction error vanishes, which means that the predicted expectation of the sensory input is equal to the actual sensory input.
In Equation 18, the prediction error is scaled and rotated by the covariance matrix C1, k of the approximate Gaussian distribution, which is converted from the precision matrix:
Here prediction precision is given by
Note that the off-diagonal elements of the inverse prediction precision matrix give the prediction correlations.
At the second level, the volatility, consisting of the uncertainties and pairwise correlations in natural parameters, is inferred by similar variational approximation method (Zhu et al., 2025). The mean is updated by
Here Δ1, k is given by
The constant matrix Id1 is a d1-by-d1 unit square matrix. PE1, k is the prediction error on the hidden state x1
is given by
where the constant vector e2(d2) is a -dimension column vector. The j-th component in is 1 if j = i or 0 if j≠i. The column vector is the i-th row in the coefficient matrix W2. is defined as
The precision matrix is updated by
where
The precision matrix of the prediction is given by
The notation Kmn denotes a mn-by-mn commutation matrix (Magnus and Neudecker, 1979).
5 Variational Bayesian learning
A model with a set of parameters ℙ receives and encodes sensory input o(t). We can arrange all elements of ℙ into a vector ξ. Here, we introduce the following mean field approximation to fit the parameters of the model with the sensory inputs o1:K
Then
We use the Lagrange multiplier method to work out the optimal variational posterior as follows:
Then we execute a Laplacian approximation to determine a Gaussian approximation of the variational posterior solution (Equation 33)
where is the logarithm of the predictive distribution and is given by
Finally, the maximum value of the negative free energy is given by
6 Simulation study
To verify the effectiveness of the proposed model, we conducted simulations on synthetic data to assess the model's ability to capture time-varying rate parameters of multivariate exponential distribution. The purpose of using simulation is to validate the model on precisely defined data, so that the results given by the model could be compared with ground truth.
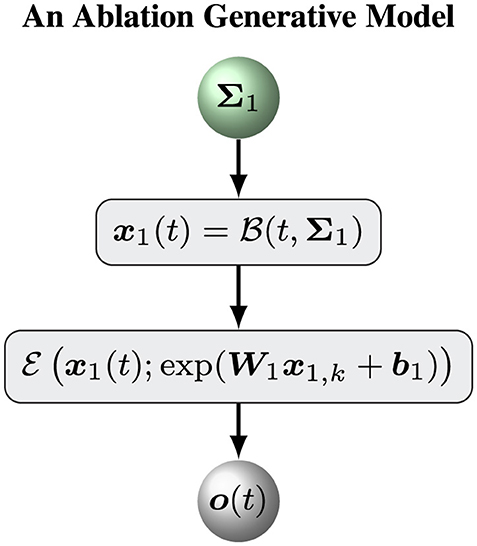
6.1 An ablation model
To assess the ability of our hierarchical Bayesian model , we define an ablation model as a baseline model to evaluate the role of the top (volatility) level of the hierarchical Bayesian model . Put simply, an ablation model is the simple version of the hierarchical Bayesian model with a constant volatility x2(t) = μ2. In this case, we can remove the variable x2, k and keep a constant likelihood matrix Σ1. The model can be defined by Equations 1–3. Figure 2 shows the overall framework of the ablation model .
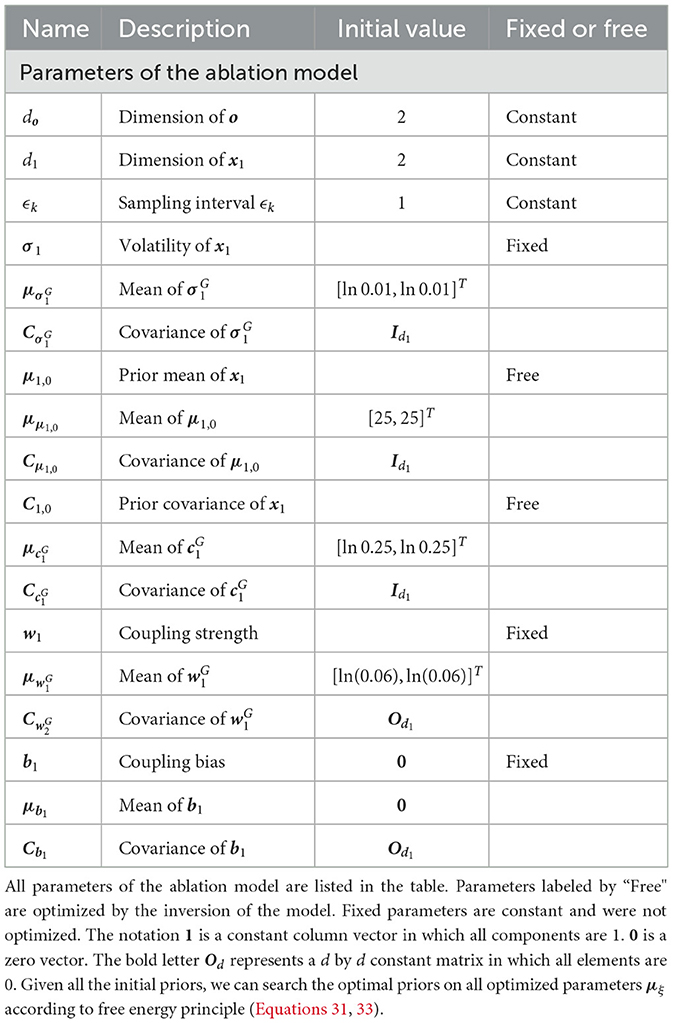
The update equations for the ablation model are similar to Equations 12, 18–22 with . Put simply, we assume that Σ1 is a diagonal matrix with positive diagonal elements. Therefore, Σ1 can be determined by a vector σ1 with positive elements. The prior distribution of Σ1 is defined by
where μlnσ1, Clnσ1 are the parameters of the prior distribution. Other parameters of this model are the same prior model with the above hierarchical Bayesian model (cf. Supplementary material Section 2).
6.2 Simulation setup
In detail, simulations were carried out in four steps as follows:
1. Generating synthetic sensory inputs. We randomly generated a sequence of bivariate exponential variable o1:K = o(t1), o(t2), o(t3), ⋯ , o(tK) (K = 400) (Figure 3):
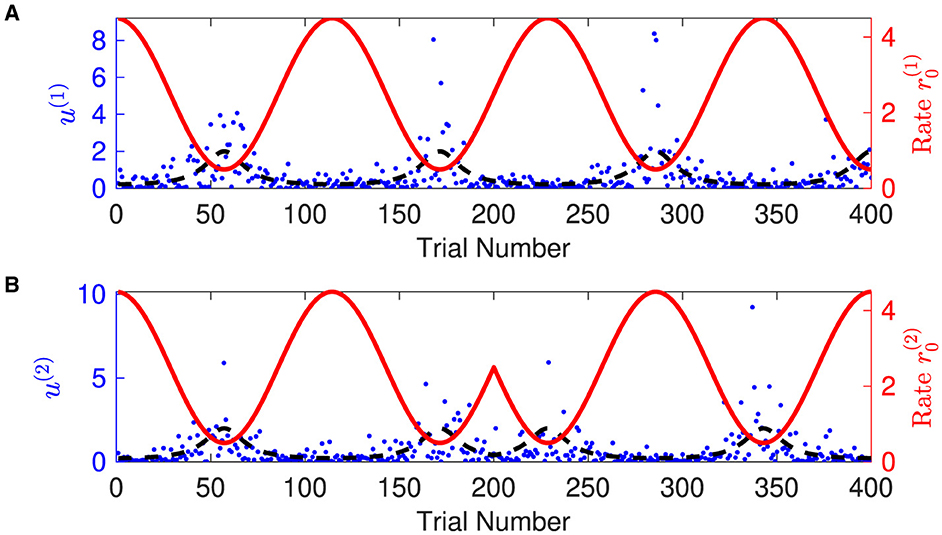
Figure 3. Time-varying rate parameter and sensory inputs of volatile multivariate exponentially distributed signals. Panels (A, B) represent two dimensions of input signal. In each panel, blue dots are the sensory inputs o(i) of the i-th dimension of the signal. Red lines represent the expected rate . The black dashed lines are the expectation of the sensory input o(i), i.e., the inverse of the expected rate . Note that the expected rate in the two dimensions fluctuates in time, synchronously before and anti-synchronously after trial 200.
where the time-varying rate vector r0(t) was governed by cosine waves and was defined by
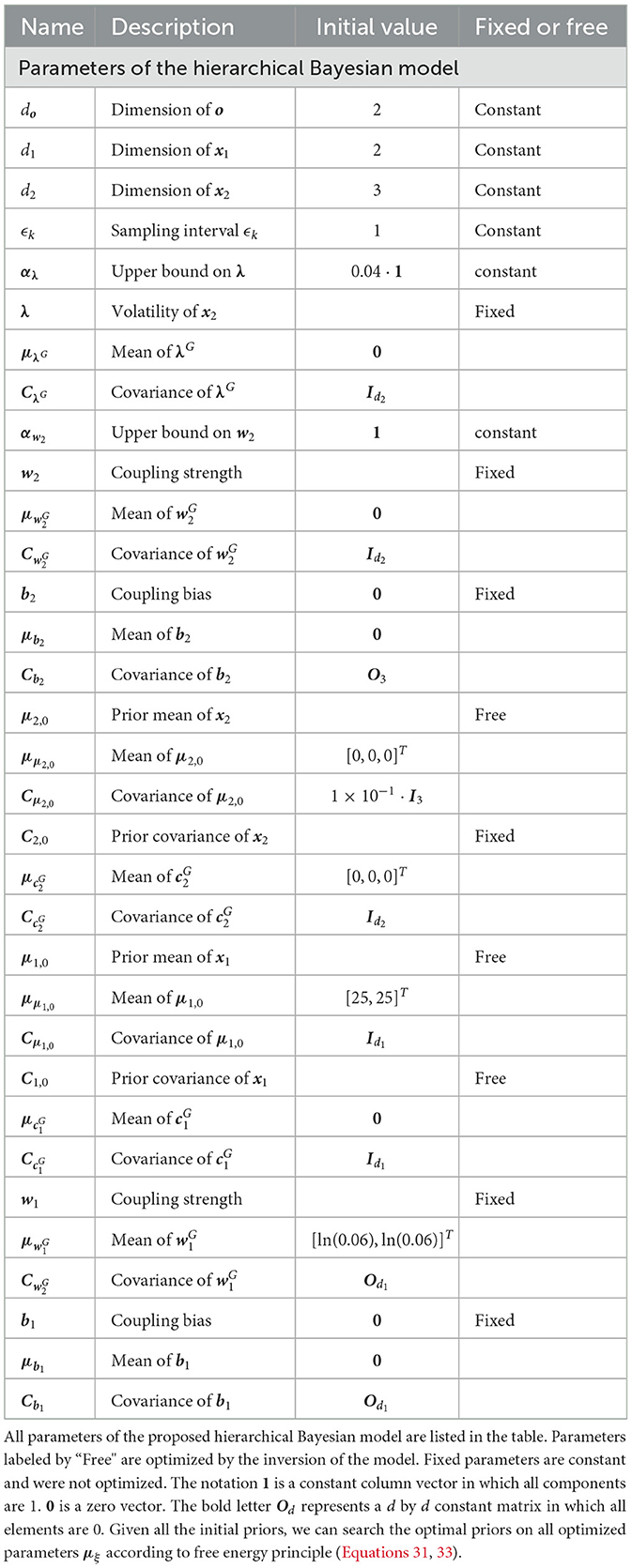
2. Initializing the sufficient statistics of all random parameters. We must choose particular initial sufficient statistics of a parameter vector ξ (Table 1 for the hierarchical Bayesian model and Table 2 for the ablation model) to make the models work well on a sequence of sensory inputs. Then we determined the prior distribution of ξ. All parameter configurations for the two models (Figures 1, 2) are shown in Tables 1, 2.
3. Maximizing negative free energy. We employed optimization methods to obtain the optimal sufficient statistics (μξ, Cξ) of the prior parameter ξ. The quasi-Newton Broyden-Fletcher-Goldfarb-Shanno method based on a line search framework (Nocedal and Wright, 2006) was adopted to maximize negative free energy (Equations 31, 33, 34) (Beal, 2003; Friston, 2010).
4. Generating the optimal trajectories of all states. We use the optimal prior parameters μξ to characterize a particular model (Figures 1, 2). The two models are compared on inference and decision-making tasks.
6.3 Perceiving volatile multivariate exponentially distributed signals
The proposed hierarchical Bayesian inference model endowed with the optimal parameter μξ constitutes a hierarchical Bayesian agent. We asked the hierarchical Bayesian agent to perceive volatile multivariate exponentially distributed signals as shown in Figure 3.
The dynamic tendency μ1(t) of the log-rate vector x1(t) is tracked online by the hierarchical Bayesian agent (Figure 4). μ1 follows the varying trend of the expected rate in logarithmic space. The uncertainty of μ1(t) is stable (light-red shaded area in Figure 4). The prediction error PE1 fluctuates around a baseline (blue line in Figure 4).
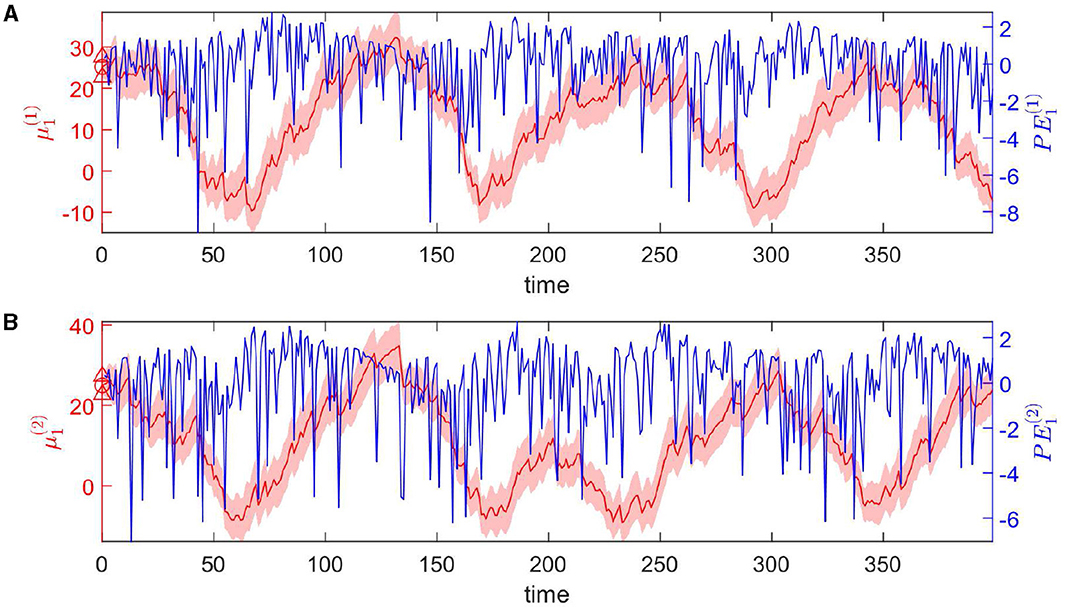
Figure 4. Temporal dynamics of the tendency μ1 of the log-rate vector x1(t) at the first level. Panels (A, B) represent two dimensions of the expectation μ1. In details, each panel shows one component of μ1 in red, and PE1 in blue. The light-red shaded area represents the uncertainty of each component (i.e., ). The red markers △, ° represent the priors on the standard deviation and the mean of each component respectively.
Overall, the agent perceives the expected rate vector well (Figure 5). For a majority of the trials, both of the belief expectations (solid lines in Figures 5A, C) fluctuates around the expected rate (dashed lines in Figures 5A, C). In the initial stage, the agent quickly adjusts itself to adapt to the input signal and tracks the expected states. Due to the stochasticity, the sample rate intensity in sensory inputs deviates from the expected rate intensity, leading to the estimated belief rate intensity to deviate from the expected rate intensity. From trial 120 to trial 165, the sample rate intensity in sensory inputs o(1) is larger than the expected rate intensity in Figure 3A. The agent's belief is higher than the expected rate (Figure 5A). From trial 116 to trial 158 (trial 296 to trial 308), the sample rate intensity in sensory inputs o(2) is greater than the expected rate intensity in Figure 3B, leading the agent to have higher belief of the rate intensity than the expected rate value.
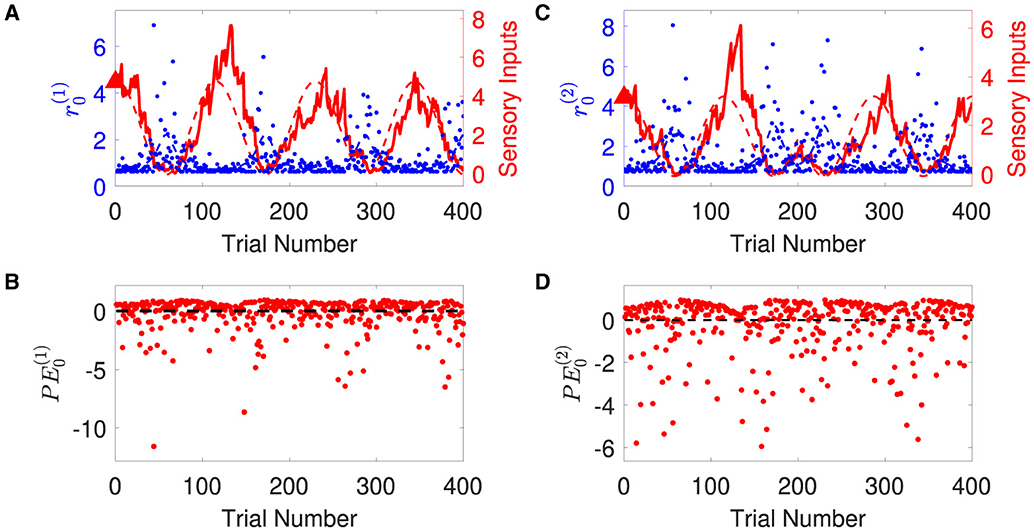
Figure 5. Temporal dynamics of the expectation of the logarithm of volatility μ2 in the state x1 at the second level. Panels (A–C) represent three dimensions of the expectation μ2. Each panel shows the evolution of one element of μ2 in red and the corresponding element of PE2 in blue. Light-red shaded area represents the uncertainty of each dimension (i.e., ). The red markers △, ° represent the priors of the standard deviation and mean of each dimension.
The expectations of log-volatilities in the logarithms of the rate vector ( and , i.e., internal representation of the expected states) has notable changes, stabilized for most of the time (Figure 6). From trial 1 to trial 200, changes in rate are consistent with changes in rate (Figure 3). In theory, they are positively correlated during this period. From trial 1 to trial 186, the prediction correlation continues to increase (Figure 7). From trial 187 to trial 200, asynchronous local fluctuations (or noise) lead to a decrease in prediction correlation . From trial 201 to trial 400, changes in rate are the opposite with the changes in rate (Figure 3). The two dimensions of the signal are negatively correlated during this period. As a result, the prediction correlation of the agent continues to decrease from trial 201 to trial 359. From trial 359 to trial 365, prediction errors are positive numbers, and drive prediction correlation to jump to a larger value (Figure 7). The hierarchical Bayesian agent therefore is able to uncover the correlation structures of the signal dynamically.
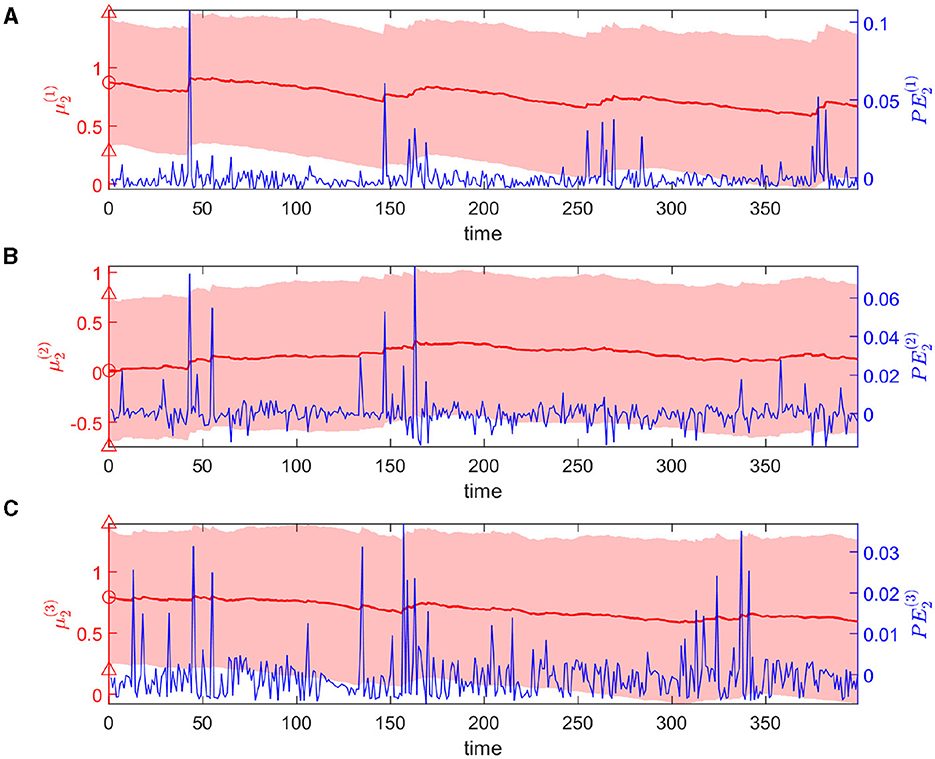
Figure 6. Temporal dynamics of the expectation of the logarithm of volatility μ2 in the state x1 at the second level. Each panel shows the evolution of one element of μ2 in red and the corresponding element of PE2 in blue. Light-red shaded area represents the uncertainty of each dimension (i.e., ). The red markers △, ° represent the priors of the standard deviation and mean of each dimension.
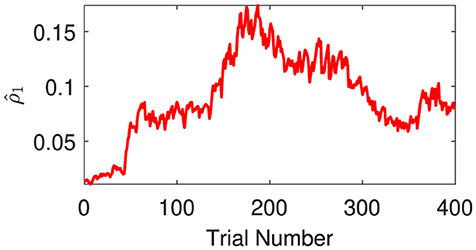
Figure 7. Prediction correlation is extracted from the inverse prediction precision generated by the second (log-volatility) level.
6.4 Bayesian model selection
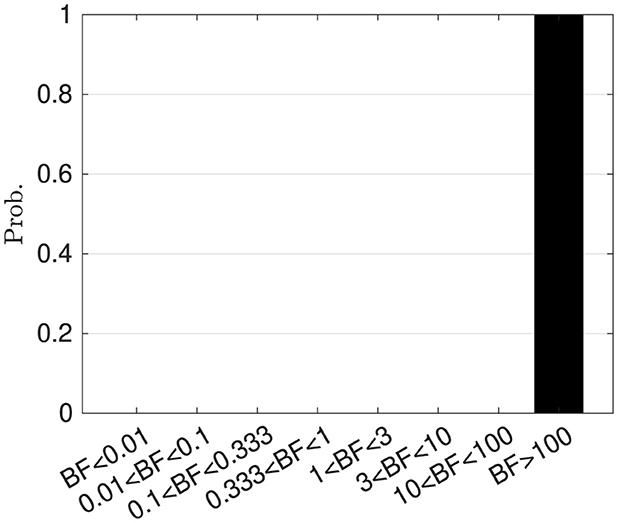
To compare the performance of the proposed hierarchical Bayesian model and the ablation model , we performed 100 independent simulations for each model using different seeds of random number generators. Based on these simulations, Bayesian factors were calculated. Figure 8 shows the histogram of the Bayesian factors . According to the criteria suggested by Harold Jeffreys (cf. Supplementary material Section 4), is better than .
7 Discussion
7.1 Contributions of this study
In this article, we developed a hierarchical Bayesian model to infer and track online the tendency and volatility in multivariate exponential signals. The bottom level of the hierarchical Bayesian model is to learn the expected rate parameter vector of the multivariate exponential signal. The logarithm of the rate parameter vector x1 is modeled to evolve as a general Brownian motion at the first level. Under the Brownian and Gaussian assumption on x1, the volatility in x1 can be computed by the Cholesky decomposition of the diffusion matrix of the Brownian motion x1. Therefore, we introduce a parameterization of the volatility in x1 in logarithmic space after the Cholesky decomposition of the diffusion matrix of x1. The volatility in x1 can be represented by x2, which again evolves as a Brownian motion. The low-order interactions among the components of the log-rate parameter vector and uncertainties are captured by x2 at the second level of the model.
The hierarchical Bayesian model assumes that the log-rate parameter vector x1(t) evolves as a general Brownian motion and can be updated by Equation 18, where prediction error PE0, k drives the agent to diminish the difference between the agent's belief and the sensory input. The coefficient matrix W1 plays the role of scaling factors to weight prediction error PE0, k. The covariance C1, k functions as complex adaptive learning rate in Equation 21.
In principle, the proposed model could be easily generalized to a Bayesian framework for decision making in high-dimensional volatile environments by defining appropriate form of response models (Berger, 2013; Mathys et al., 2014; Zhu et al., 2022). In this article, we define a simple random response model based on bivariate exponential distribution. For other problems of interest, it is sufficient to construct a compatible response model addressing the particular optimization criteria of the question.
7.2 Limitations and strengths
The peakless and memoryless properties of the exponential distribution bring difficulties for an online agent to predict, since historical sensory inputs can only provide weak evidence for a prediction. The proposed hierarchical Bayesian agent internally integrates historical sensory inputs and the current sensory input to infer the changes in the signal. The agent estimates the dynamic volatility in the sensory inputs and adjusts the learning rate based on the evidence of the volatility, so that the information from the signal is integrated into the internal states efficiently. The proposed hierarchical Bayesian agent is able to efficiently and accurately capture the characteristics of volatile multivariate exponentially distributed signals.
In the simulation, we observed that the proposed hierarchical Bayesian agent has good suppression effect on small volatility, but it is also swayed by the local variation of the rate intensity caused by the stochasticity of the signal. The prediction correlation is not only determined by changes in the trend of the sensory inputs but is also affected by volatility. Large local fluctuations can also cause jumps in prediction correlations. Asynchronous persistent small local fluctuations will also reduce the prediction correlation, while synchronous persistent small fluctuations will increase the prediction correlation.
In this study, we simply considered simulated data, which aims to capture dynamic and multidimensional aspects of nonstationary multivariate exponential signals and cannot cover other important features observed in real data set. The results obtained from simulations pave ways for further investigations of many estimation problems in neuroscience research. The possible applications of the method include firing rate estimation, functional brain connection estimation, etc.
8 Conclusions
We have introduced the mathematical basis of a hierarchical Bayesian model for inferring and tracking rate intensity parameter of multivariate exponential signals and illustrated its functionality. A family of interpretable closed form update rules were derived. In particular, we provided a full theoretical scenario that consists of inference in the perceptual model and learning optimal hyper-parameters by inversion of the hierarchical Bayesian model. The proposed theoretical framework was validated on synthetic data, and it turned out that the hierarchical Bayesian model worked well in tracking volatile multi-variate exponential signals. The preliminary study here points to the practical utility of our approach in analyzing high-dimensional neural activities, which often follow as distributions in exponential family.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
CZ: Conceptualization, Investigation, Software, Writing – original draft, Writing – review & editing, Methodology. KZ: Writing – original draft, Writing – review & editing. FT: Writing – original draft, Writing – review & editing. YT: Writing – original draft, Writing – review & editing. XL: Methodology, Writing – original draft, Writing – review & editing. BS: Conceptualization, Funding acquisition, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by STI2030-Major Projects 2022ZD0205005.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fncom.2025.1408836/full#supplementary-material
Abbreviations
GHBF, general hierarchical Brownian filter; STD, standard deviation; iid, independently identically distribution; SI, sampling interval; PDF, probability density function.
References
Beal, M. J. (2003). Variational Algorithms for Approximate Bayesian Inference [PhD thesis]. University College London (UCL), London.
Berger, J. O. (2013). Statistical Decision Theory and Bayesian Analysis. Cham: Springer Science & Business Media.
Conrad, K. (2004). Probability distributions and maximum entropy. Entropy 6:10. Available online at: https://kconrad.math.uconn.edu/blurbs/analysis/entropypost.pdf
Czirók, A., Schlett, K., Madarász, E., and Vicsek, T. (1998). Exponential distribution of locomotion activity in cell cultures. Phys. Rev. Lett. 81, 3038–3041. doi: 10.1103/PhysRevLett.81.3038
Daunizeau, J., Den Ouden, H. E., Pessiglione, M., Kiebel, S. J., Friston, K. J., and Stephan, K. E. (2010a). Observing the observer (II): deciding when to decide. PLoS ONE 5:e15555. doi: 10.1371/journal.pone.0015555
Daunizeau, J., den Ouden, H. E. M., Pessiglione, M., Kiebel, S. J., Stephan, K. E., and Friston, K. J. (2010b). Observing the observer (I): meta-Bayesian Models of learning and decision-making. PLoS ONE 5:e15554. doi: 10.1371/journal.pone.0015554
Davis, D. J. (1952). An analysis of some failure data. J. Am. Stat. Assoc. 47, 113–150. doi: 10.1080/01621459.1952.10501160
Drăgulescu, A., and Yakovenko, V. M. (2001). Evidence for the exponential distribution of income in the USA. Eur. Phys. J. B-Condens. Matter Complex Syst. 20, 585–589. doi: 10.1007/PL00011112
Epstein, B., and Sobel, M. (1953). Life testing. J. Am. Stat. Assoc. 48, 486–502. doi: 10.1080/01621459.1953.10483488
Esary, J. D., and Marshall, A. W. (1974). Multivariate distributions with exponential minimums. Ann. Stat. 2, 84–98. doi: 10.1214/aos/1176342615
Friston, K. (2010). The free-energy principle: a unified brain theory? Nat. Rev. Neurosci. 11, 127–138. doi: 10.1038/nrn2787
Friston, K., FitzGerald, T., Rigoli, F., Schwartenbeck, P., and Pezzulo, G. (2017). Active inference: a process theory. Neural Comput. 29, 1–49. doi: 10.1162/NECO_a_00912
Haynes, J.-D., and Rees, G. (2006). Decoding mental states from brain activity in humans. Nat. Rev. Neurosci. 7, 523–534. doi: 10.1038/nrn1931
Ibe, O. (2014). Fundamentals of Applied Probability and Random Processes. Cambridge, MA: Academic Press. doi: 10.1016/B978-0-12-800852-2.00012-2
Jaynes, E. T. (1982). On the rationale of maximum-entropy methods. Proc. IEEE 70, 939–952. doi: 10.1109/PROC.1982.12425
Johnson, R. A.Wichern, D. W., et al. (2002). Applied Multivariate Statistical Analysis. Upper Saddle River, NJ: Prentice Hall.
Jung, J. H., and O'Leary, D. P. (2006). Cholesky Decomposition and Linear Programming on a GPU. Scholarly Paper. College Park, MD: University of Maryland.
Kingman, J. F. C. (1992). Poisson Processes, Volume 3. Oxford: Clarendon Press. doi: 10.1093/oso/9780198536932.001.0001
Kundu, D., and Gupta, R. D. (2009). Bivariate generalized exponential distribution. J. Multivar. Anal. 100, 581–593. doi: 10.1016/j.jmva.2008.06.012
Li, S., and Le, W. (2017). Milestones of parkinson's disease research: 200 years of history and beyond. Neurosci. Bull. 33, 598–602. doi: 10.1007/s12264-017-0178-2
Li, Z., O'Doherty, J. E., Hanson, T. L., Lebedev, M. A., Henriquez, C. S., Nicolelis, M. A., et al. (2009). Unscented kalman filter for brain-machine interfaces. PLoS ONE 4:e6243. doi: 10.1371/journal.pone.0006243
Lo, C.-C., Chou, T., Penzel, T., Scammell, T. E., Strecker, R. E., Stanley, H. E., et al. (2004). Common scale-invariant patterns of sleep-wake transitions across mammalian species. Proc. Nat. Acad. Sci. 101, 17545–17548. doi: 10.1073/pnas.0408242101
Magnus, J. R., and Neudecker, H. (1979). The commutation matrix: some properties and applications. Ann. Stat. 7, 381–394. doi: 10.1214/aos/1176344621
Maimon, G., and Assad, J. A. (2009). Beyond poisson: Increased spike-time regularity across primate parietal cortex. Neuron 62, 426–440. doi: 10.1016/j.neuron.2009.03.021
Malik, W. Q., Truccolo, W., Brown, E. N., and Hochberg, L. R. (2010). Efficient decoding with steady-state kalman filter in neural interface systems. IEEE Trans. Neural Syst. Rehabil. Eng. 19, 25–34. doi: 10.1109/TNSRE.2010.2092443
Marshall, A. W., and Olkin, I. (1967a). A generalized bivariate exponential distribution. J. Appl. Probab. 4, 291–302. doi: 10.2307/3212024
Marshall, A. W., and Olkin, I. (1967b). A multivariate exponential distribution. J. Am. Stat. Assoc. 62, 30–44. doi: 10.1080/01621459.1967.10482885
Mathys, C. D., Daunizeau, J., Friston, K. J., and Stephan, K. E. (2011). A Bayesian foundation for individual learning under uncertainty. Front. Hum. Neurosci. 5:39. doi: 10.3389/fnhum.2011.00039
Mathys, C. D., Lomakina, E. I., Daunizeau, J., Iglesias, S., Brodersen, K. H., Friston, K. J., et al. (2014). Uncertainty in perception and the hierarchical Gaussian filter. Front. Hum. Neurosci. 8:825. doi: 10.3389/fnhum.2014.00825
McCaslin, J. O., and Broussard, P. R. (2007). Search for chaotic behavior in a flapping flag. arXiv. Available online at: https://arxiv.org/abs/0704.0484
Nazmi, N., Mazlan, S. A., Zamzuri, H., and Rahman, M. A. A. (2015). Fitting distribution for electromyography and electroencephalography signals based on goodness-of-fit tests. Procedia Comput. Sci. 76, 468–473. doi: 10.1016/j.procs.2015.12.317
Ouyang, G., Wang, S., Liu, M., Zhang, M., and Zhou, C. (2023). Multilevel and multifaceted brain response features in spiking, erp and erd: experimental observation and simultaneous generation in a neuronal network model with excitation-inhibition balance. Cogn. Neurodyn. 17, 1417–1431. doi: 10.1007/s11571-022-09889-w
Pan, H., Fu, Y., Zhang, Q., Zhang, J., and Qin, X. (2022). The decoder design and performance comparative analysis for closed-loop brain-machine interface system. Cogn. Neurodyn. 18, 147–164. doi: 10.1007/s11571-022-09919-7
Qi, Y., Liu, B., Wang, Y., and Pan, G. (2019). “Dynamic ensemble modeling approach to nonstationary neural decoding in brain-computer interfaces,” in Advances in Neural Information Processing Systems, Vol. 32, eds. H. Wallach, H. Larochelle, A. Beygelzimer, F. d' Alché-Buc, E. Fox, and R. Garnett (Curran Associates, Inc.). Available online at: https://proceedings.neurips.cc/paper_files/paper/2019/file/3f7bcd0b3ea822683bba8fc530f151bd-Paper.pdf
Roxin, A., Brunel, N., Hansel, D., Mongillo, G., and Vreeswijk, C. V. (2011). On the distribution of firing rates in networks of cortical neurons. J. Neurosci. 31, 16217–16226. doi: 10.1523/JNEUROSCI.1677-11.2011
Shanker, R., Hagos, F., and Sujatha, S. (2015). On modeling of lifetimes data using exponential and Lindley distributions. Biom. Biostat. Int. J. 2, 1–9. doi: 10.15406/bbij.2015.02.00042
Stein, R. R., Marks, D. S., and Sander, C. (2015). Inferring pairwise interactions from biological data using maximum-entropy probability models. PLoS Comput. Biol. 11:e1004182. doi: 10.1371/journal.pcbi.1004182
Swindale, N. V., Rowat, P., Krause, M., Spacek, M. A., and Mitelut, C. (2021). Voltage distributions in extracellular brain recordings. J. Neurophysiol. 125, 1408–1424. doi: 10.1152/jn.00633.2020
Tanabe, K., and Sagae, M. (1992). An exact cholesky decomposition and the generalized inverse of the variance-covariance matrix of the multinomial distribution, with applications. J. R. Stat. Soc. B (Methodological) 54, 211–219. doi: 10.1111/j.2517-6161.1992.tb01875.x
Varde, S. D. (1969). Life testing and reliability estimation for the two parameter exponential distribution. J. Am. Stat. Assoc. 64, 621–631. doi: 10.1080/01621459.1969.10501000
Xu, L., Xu, M., Jung, T.-P., and Ming, D. (2021). Review of brain encoding and decoding mechanisms for EEG-based brain-computer interface. Cogn. Neurodyn. 15, 569–584. doi: 10.1007/s11571-021-09676-z
Yousefi, A., Basu, I., Paulk, A. C., Peled, N., Eskandar, E. N., Dougherty, D. D., et al. (2019). Decoding hidden cognitive states from behavior and physiology using a Bayesian approach. Neural Comput. 31, 1751–1788. doi: 10.1162/neco_a_01196
Zhang, Y.-J., Yu, Z.-F., Liu, J. K., and Huang, T.-J. (2022). Neural decoding of visual information across different neural recording modalities and approaches. Mach. Intell. Res. 19, 350–365. doi: 10.1007/s11633-022-1335-2
Zhu, C., Zhou, K., Han, Z., Tang, Y., Tang, F., Si, B., et al. (2025). General Hierarchical Brownian Filter in Multi-dimensional Volatile Environments. submitted.
Keywords: online Bayesian learning, hierarchical filter, Brownian motion, exponential distribution, adaptive observation
Citation: Zhu C, Zhou K, Tang F, Tang Y, Li X and Si B (2025) A hierarchical Bayesian inference model for volatile multivariate exponentially distributed signals. Front. Comput. Neurosci. 19:1408836. doi: 10.3389/fncom.2025.1408836
Received: 23 April 2024; Accepted: 14 October 2025;
Published: 12 November 2025.
Edited by:
Kechen Zhang, Johns Hopkins University, United StatesReviewed by:
Guozhang Chen, Graz University of Technology, AustriaDodi Devianto, Andalas University, Indonesia
Copyright © 2025 Zhu, Zhou, Tang, Tang, Li and Si. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bailu Si, YmFpbHVzaUBibnUuZWR1LmNu
 Changbo Zhu
Changbo Zhu Ke Zhou
Ke Zhou Fengzhen Tang1,2,3
Fengzhen Tang1,2,3 Yandong Tang
Yandong Tang Bailu Si
Bailu Si