- 1School of Biological Sciences, Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
- 2Pasargad Institute for Advanced Innovative Solutions (PIAIS), Tehran, Iran
1 Introduction
Time delays in signal propagation represent a fundamental aspect of neuronal communication that profoundly influences information processing and learning (Gerstner et al., 1993, 1996, 1997). Synaptic delays, in particular, arise from the physical constraints of axonal conduction and dendritic integration. Dendritic and axonal delays within and between brain areas can vary significantly and are not necessarily identical. For instance, dendritic delays tend to be typically shorter than axonal delays, ranging from sub-millisecond to a few milliseconds (Agmon-Snir and Segev, 1993; Schierwagen and Claus, 2001). Axonal delays, on the other hand, can range from a few milliseconds in thalamo-cortical and cortico-tectal connections (Cleland et al., 1976; Swadlow and Weyand, 1987), to as much as tens of milliseconds in cortico-cortical connections (Swadlow, 1990; Stoelzel et al., 2017).
One key aspect of these delays pertains to the modulation of neuronal dynamics. Delays introduce temporal offsets in signal arrival, affecting synchronization and oscillation patterns within neuronal ensembles, as demonstrated in several influential theoretical and computational studies (Ernst et al., 1995; Crook et al., 1997; Ermentrout and Kopell, 1998; Yeung and Strogatz, 1999; Roxin et al., 2005; DHuys et al., 2008; Gilson et al., 2010; Popovych et al., 2011). In plastic networks, however, delays play a dual role: they modulate the temporal dynamics of neuronal activity while simultaneously shaping the adaptive processes underlying neuroplasticity (Gerstner et al., 1993; Debanne et al., 1998; Senn et al., 2002; Morrison et al., 2008; Madadi Asl et al., 2017, 2018b,c).
In oscillatory networks, short delays may decouple synchronous firing, promoting diverse activity states (Lubenov and Siapas, 2008; Kozloski and Cecchi, 2010; Knoblauch et al., 2012; Babadi and Abbott, 2013), whereas longer delays can enhance inter-regional synchronization, facilitating coherent information processing (Knoblauch and Sommer, 2003, 2004). In this way, dendritic and axonal delays may determine phase relationships between neurons. This temporal structuring is crucial for phenomena like gamma oscillations in cortical networks, where precise timing underlies sensory binding and attention mechanisms (Engel and Singer, 2001; Buzsáki and Wang, 2012; Madadi Asl and Valizadeh, 2025). By incorporating these delays, computational models can replicate a rich dynamical repertoire, such as multistable attractors where networks switch between qualitatively different dynamical states based on initial conditions (Kim et al., 1997; Ernst et al., 1998; Madadi Asl et al., 2018a). Such models underscore how delays act as a regulatory mechanism, enabling flexible network reconfiguration as well as transitions between different states (Khoshkhou and Montakhab, 2019; Madadi Asl and Ramezani Akbarabadi, 2023).
Traditional models sometimes simplify or neglect these delays to reduce computational complexity, but their presence is crucial for capturing realistic brain behaviors. For instance, in networks governed by spike-timing-dependent plasticity (STDP) (Gerstner et al., 1996; Markram et al., 1997b; Bi and Poo, 1998), where the synaptic weights are adjusted based on the precise timing of pre- and postsynaptic spikes, delays can alter the effective time lags between spike pairs. This ultimately leads to emergent connectivity patterns that differ markedly from delay-free scenarios (Lubenov and Siapas, 2008; Kozloski and Cecchi, 2010; Knoblauch et al., 2012; Babadi and Abbott, 2013; Madadi Asl et al., 2017), revealing how delay-induced temporal mismatches contribute to learning, memory, and adaptive responses.
More precisely, in STDP frameworks, the outcome of synaptic modification, i.e., long-term depression (LTD) or long-term potentiation (LTP), hinges on the relative spike timing of neuron pairs (Markram et al., 1997b; Bi and Poo, 1998). However, delays modify this timing at the synaptic site, potentially reversing or amplifying expected changes. Analytical studies of two reciprocally coupled neurons demonstrate that the combination of dendritic and axonal delays can shift spike ordering, leading to unconventional STDP outcomes like mutual potentiation or depression in loops (Senn et al., 2002; Morrison et al., 2008; Babadi and Abbott, 2013). This modulation is particularly evident in plastic networks subjected to pair-based STDP, where delays facilitate the preservation of strong bidirectional connections or loop elimination (Madadi Asl et al., 2017, 2018a). These effects scale up in larger recurrent networks, fostering motifs such as strong bidirectional loops when dendritic delays exceed axonal ones, or loosely connected structures in the reverse scenario (Madadi Asl et al., 2017, 2018a).
In this piece, I discuss a crucial aspect of modeling plastic networks, i.e., the differentiation between dendritic and axonal delays. These delays must be taken into account separately in computational models because they contribute uniquely to signal propagation and plasticity. In fact, their sum modulates neuronal dynamics as the total delay affecting signal transmission from the presynaptic neuron to the postsynaptic cell, while their difference determines the time lag perceived at the synapse, influencing the efficacy of synaptic modifications. Incorporating distinct dendritic and axonal delays into computational models significantly improves simulation methodologies. For instance, by accurately representing these delays, models can better replicate the temporal precision observed in biological neuronal networks, leading to more realistic simulations of learning and memory processes. This approach also enables computational studies to explore how disruptions in delay dynamics—such as those caused by neurological disorders—affect brain structure and function. For example, increased axonal delays in conditions like multiple sclerosis, due to demyelination, leads to a reduction of conduction velocity of signals along the axon (Waxman, 2006). This can disrupt reliable signal transmission, leading to impaired oscillatory responses (Lefebvre et al., 2025). Models that account for these delays can advance our understanding of brain function and refine tools for studying complex neuronal systems.
2 Incorporating delays into computational models
2.1 Delays change spike timings perceived at the synapse
As illustrated in Figure 1A, consider that the presynaptic neuron (1) is connected to the postsynaptic neuron (2), characterized by the coupling weight w21. If the presynaptic neuron fires at tpre = t1 and the postsynaptic neuron fires at tpost = t2, both the forward signal propagated along the presynaptic axon (denoted by the green arrow) and the backward signal backpropagated through the dendrite of the postsynaptic neuron (denoted by the red arrow) are essential for inducing synaptic modifications in the form of LTD or LTP (also see Figure 1B) (Sjöström and Häusser, 2006; Clopath and Gerstner, 2010; Froemke et al., 2010). However, when delays are taken into account, the spike times arriving at the synapse (Figures 1C1–C3, solid markers) may significantly differ from those initiated at the cell bodies (Figures 1C1–C3, dashed markers), depending on the trade-off between dendritic and axonal delays. Specifically, as shown in Figures 1C1–C3, when a presynaptic spike is generated at t1, it must first travel down the axon before reaching the synapse, thus arriving at , where τa is the axonal delay. By the same token, a postsynaptic spike generated at t2 must backpropagate through the dendrite before arriving at the synapse at , where τd is the dendritic delay. Consequently, this delay-induced time shift in spikes arrival may significantly affect the outcome of timing-dependent learning paradigms such as STDP (Gerstner et al., 1993; Senn et al., 2002; Morrison et al., 2008; Madadi Asl et al., 2017), as discussed below.
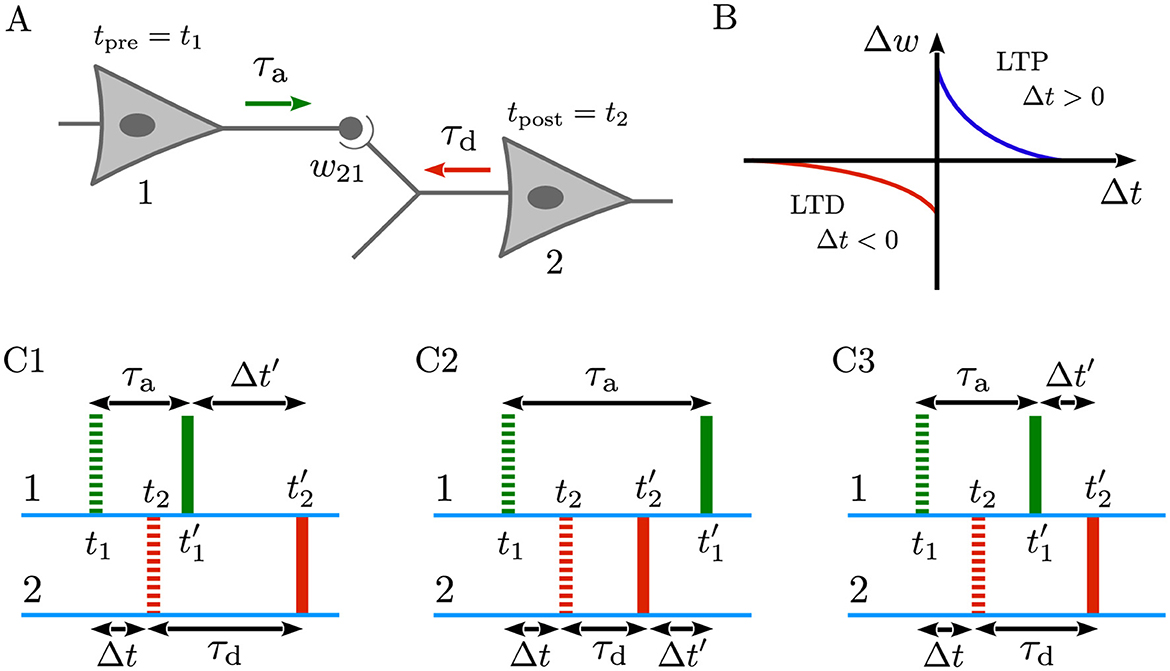
Figure 1. Dendritic and axonal delays change spike timings arriving at the synapse. (A) Representation of a neuron pair comprising a presynaptic neuron (1) connected to a postsynaptic neuron (2) with the coupling weight w21. The presynaptic neuron fires at tpre = t1, and the postsynaptic neuron fires at tpost = t2. These spike times arrive at the synapse at , after axonal delay (τa) in the forward direction (green arrow), and at , after dendritic delay (τd) in the backward direction (red arrow). (B) Schematics of a generic, temporally asymmetric STDP learning window where Δt = tpost−tpre = t2−t1 is the non-delayed time lag between the pre- and postsynaptic spike pairs, and Δw is the resultant synaptic change. According to Equation 1, pre-before-post spike pairing (Δt>0) induces LTP (Δw>0; blue), whereas post-before-pre pairing (Δt < 0) leads to LTD (Δw < 0; red). (C1–C3) Green and red dashed (solid) markers indicate the non-delayed, t1 and t2 (delayed, and ) forward spike time of the presynaptic neuron and the time of backpropagated potential of the postsynaptic neuron at the synaptic site, respectively. The spike times of the pre- and postsynaptic neurons are separated by a small, non-delayed time lag Δt such that pre-before-post ordering of spikes leads to the potentiation of synapse. Taking into account the effect of dendritic and axonal delays, the delayed time lag perceived at the synapse is Δt′ = Δt+ξ, where ξ = τd−τa. (C1) When τd>τa, the pre-before-post orderings of delayed and non-delayed spikes are identical and, therefore, the synapse is potentiated. (C2) When τd < τa, the backpropagated potential of the postsynaptic neuron (solid red) arrives sooner than the forward spike time of the presynaptic neuron (solid green) at the synapse. Thus, according to the STDP rule, the synapse undergoes depression. (C3) If τd = τa, the situation resembles the non-delayed scenario since ξ = 0, and Δt′ = Δt, and the synapse is potentiated due to the pre-before-post spike timing.
2.2 Delay-induced wiring patterns in plastic networks
In plastic networks, the synaptic weights (w) between neurons are continually modified based on neuronal activity. Consequently, in the presence of STDP, the synaptic weight between the pre- and postsynaptic neurons in Figure 1A is updated at each step of the simulation (w→w+Δw) according to the following temporally asymmetric learning window (Bi and Poo, 1998), as depicted in Figure 1B:
where Δw is the synaptic change, and Δt = tpost−tpre = t2−t1 represents the non-delayed time lag between the spikes of the presynaptic neuron (1) and the postsynaptic neuron (2). The parameters A+(A−) and τ+(τ−) denote the learning rate and the effective time window for synaptic potentiation (depression), respectively. The generic form of the STDP learning window is characterized by a greater potentiation amplitude (A+>A−) and longer depression time constant (τ+ < τ−) such that A+τ+<A−τ− (Bi and Poo, 1998). For biological reasons, synaptic weights in computer simulations are typically constrained within the range wmin<w<wmax by imposing soft or hard bound saturation constraints to ensure they remain within their allowed limits (Gerstner et al., 1996; Kempter et al., 1999; Song et al., 2000; Van Rossum et al., 2000; Rubin et al., 2001; Gütig et al., 2003). According to the STDP rule in Equation 1, when the presynaptic spikes precedes the postsynaptic spike the synapses is strengthened (Δt>0 → Δw>0; blue), whereas the synapse is weakened in the reverse scenario (Δt < 0 → Δw < 0; red) (Markram et al., 1997b). In the absence of delays, when the spike times of the pres- and postsynaptic neurons are separated by a small, non-delayed time lag (as shown by the dashed markers in Figures 1C1–C3), the pre-before-post ordering of spikes leads to the potentiation of synapse.
When dendritic and axonal delays come to play, the perceived time lag at the synapse (Δt′) is not typically the same as the non-delayed time lag (Δt). This difference can be formulated as follows:
where ξ = τd−τa, is the difference between dendritic and axonal delays (Madadi Asl et al., 2017), which alters the time lag used by the STDP rule, directly impacting synaptic weight evolution. Therefore, generally, Δt in Equation 1 can be replaced by Δt′. In the absence of delays, ξ = 0 and Δt is recovered. It is important to note that this differs from the sum of dendritic and axonal delays (τ = τd+τa), which indicates the total delay needed for signals to be transmitted from presynaptic neurons to postsynaptic cells. Theoretically, in the presence of delays three different scenarios can occur:
• τd>τa: As illustrated in Figure 1C1, the pre-before-post orderings of delayed and non-delayed spikes are identical and, therefore, the synapse is potentiated but with a different magnitude compared to the non-delayed case, since |Δt′|>|Δt|.
• τd < τa: In this case, the backpropagated potential of the postsynaptic neuron (Figure 1C2, solid red) arrives sooner than the spike time of the presynaptic neuron (Figure 1C2, solid green) at the synapse. This leads to the depression of the synapse based on the STDP rule in Equation 1.
• τd = τa: If dendritic and axonal delays are identical in a special case, as shown in Figure 1C3, the delayed and non-delayed time lags are also identical (Δt′ = Δt), and the synapse is potentiated due to the pre-before-post spike timing.
These arguments demonstrate that a synapse shared between two neurons (as in Figure 1A) can be strengthened or weakened, depending on the values of dendritic and axonal delays. Intriguingly, in situations where the two neurons are reciprocally connected to each other even more complex connectivity scenarios can occur, including the emergence of strong bidirectional loops (where both the outgoing and incoming synapses are potentiated), loosely connected structures (where both synapses are depressed), and unidirectional connections (where one synapses is potentiated and the other is depressed) (Madadi Asl et al., 2017). STDP is a local learning rule in which synaptic modifications depend solely on the joint pre- and postsynaptic activity of neurons (Gerstner et al., 1996; Markram et al., 1997b; Bi and Poo, 1998). However, these two-neuron connectivity patterns can build up and significantly influence the global dynamics of large networks of neurons, leading to the emergence of qualitatively different wiring patterns, as shown previousely (Izhikevich et al., 2004; Morrison et al., 2007; Gilson et al., 2009, 2010).
2.3 Delays shape the coevolution of neuronal and synaptic dynamics
In computational models of plastic neuronal networks, at least two sets of equations are present: one set describes neuronal dynamics, as in Equation 3a, such as the evolution of the membrane potential of a neuron (v) or, more generally, the phase dynamics of neuronal oscillators, while the other describes synaptic dynamics, as in Equation 3b, specifically the time evolution of synaptic weights (w). A crucial point is, then, the need to differentiate between dendritic and axonal delays, treating them as distinct components of synaptic delay rather than combining them into a single parameter. First, their sum represents the total delay (τ = τd+τa) required for signal transmission between neurons, which modifies neuronal dynamics in Equation 3a. Second, as argued above, their difference (ξ = τd−τa) represents the delayed spike times of neurons arriving at the synapse which modifies the synaptic dynamics in Equation 3a, determining the emergent connectivity patterns due to plasticity. This leads to the coevolution of the neuronal and synaptic dynamics (Aoki and Aoyagi, 2009; Madadi Asl et al., 2018c), which can be representatively shown as follows:
where I have deliberately omitted other functionals to emphasize the crucial role of dendritic and axonal delays. Given the initial conditions including the synaptic weights and delays, Equation 3a determines the time course of neuronal activity, as reflected in their spike trains. These spike times are then input into Equation 3b, which calculates the activity-dependent changes in the synaptic weights. These updated synaptic weights are subsequently fed back into Equation 3a to refine the activity dynamics, creating a continuous feedback loop simultaneously shaping neuronal and synaptic dynamics.
3 Discussion
A critical emphasis in modeling plastic networks is the necessity to discriminate between dendritic and axonal delays, incorporating them separately rather than as a lumped parameter. In this piece, I clarified the dual purpose of dendritic and axonal delays in computational modeling of neuroplasticity. The first facet of this dual role pertains to the modulation of neuronal dynamics. The sum of dendritic and axonal delays represents the total delay (denoted as τ = τd+τa) required for the transmission of signals from presynaptic neurons to the postsynaptic cells. This parameter modifies neuronal dynamics by introducing temporal offsets in the arrival of the synaptic currents. Transitioning to the synaptic domain, delays exert a profound influence on plasticity mechanisms, forming the second pillar of their dual role. By changing the spike timings arriving at the synapse, dendritic and axonal delays can shape different connectivity patterns in plastic networks. The difference between dendritic and axonal delays (denoted as ξ = τd−τa) plays a key role in this process. This dual functionality not only refines our simulations but also deepens insights into brain processes which crucially depend on temporal resolutions.
Beyond basic dynamics, the inclusion of discriminated delays enhances our understanding of brain function by bridging gaps between theoretical models and empirical observations. Failing to distinguish these can lead to inaccurate predictions; for instance, classic STDP models without delays might overlook the emergence of bidirectional motifs prevalent in cortical networks (Abbott and Nelson, 2000; Song and Abbott, 2001; Lubenov and Siapas, 2008; Kozloski and Cecchi, 2010; Knoblauch et al., 2012; Babadi and Abbott, 2013), leading to discrepancies with experimental data (Markram et al., 1997a; Song et al., 2005). By integrating delays, it is possible to uncover how temporal propagation shapes attractor landscapes - stable states that networks converge to - determining basins of attraction influenced by delay configurations (Ernst et al., 1995; Crook et al., 1997; Ermentrout and Kopell, 1998; Yeung and Strogatz, 1999; Roxin et al., 2005; DHuys et al., 2008). In computational setups, separate parameterization allows for exploring how imbalances, such as prolonged axonal delays in demyelinating diseases, affect plasticity, revealing vulnerabilities in network stability (Lefebvre et al., 2025).
On the methodological front, incorporating dendritic and axonal delays crucially improves simulation methodologies in computational neuroscience. Traditional approaches, often reliant on instantaneous transmission, yield oversimplified dynamics that diverge from biological realism. However, biologically plausible models can benefit from delay inclusion by generating emergent patterns like frustrated antiphase states or preserved recurrent loops (Esfahani et al., 2016; Madadi Asl et al., 2017). Moreover, parameterizing dendritic and axonal delays separately allows for sensitivity analyses, identifying critical thresholds where small changes in ξ precipitate qualitative shifts in network behavior, akin to delay-induced bifurcations in dynamical systems.
This insight extends to computational models with precise time delay representations, providing a framework for hypothesizing therapeutic interventions, such as targeted stimulation to restore optimal timing and shift network dynamics from diseased states to healthy attractors. These advancements are applicable, for instance, to theory-based brain stimulation paradigms where the time-delayed onset of stimuli enables stimulation of two or multiple neuronal ensembles, allowing for precise targeting of specific subsets of neurons with a time delay (Tass, 2003; Tass and Majtanik, 2006; Schmalz and Kumar, 2019; Madadi Asl et al., 2023). In fact, as shown computationally, adjusting stimulation timing to compensate for abnormal neuronal synchronization can desynchronize aberrant oscillations and rewire pathological connectivity patterns, for example, in Parkinson's disease models (Ebert et al., 2014; Manos et al., 2021; Asadi et al., 2024; Madadi Asl and Lea-Carnall, 2025), potentially integrating both short- and long-term synaptic plasticity dynamics during and after electrical stimulation (Madadi Asl and Lankarany, 2025).
Ultimately, multiple plasticity mechanisms at different levels may regulate neuronal and synaptic dynamics in the brain (Zenke et al., 2015). While STDP, a form of Hebbian learning that emphasizes the precise timing of neuronal spikes, is significant, it is crucial to consider other plasticity models influenced by temporal delays. For example, structural plasticity does not strictly conform to Hebbian or anti-Hebbian paradigms (Butz et al., 2009). However, certain forms of structural plasticity may be phenomenologically linked to Hebbian plasticity due to their activity dependence (Fauth and Tetzlaff, 2016). This relationship implies a close interplay between STDP and structural plasticity, where temporal delays in neuronal signaling can significantly influence these processes, potentially altering the timing and effectiveness of synaptic modifications. Delays might affect the synchronization of neuronal firing, thereby impacting the conditions under which structural plasticity is activated, as demonstrated by computational studies employing integrated models of structural plasticity and STDP (Deger et al., 2012, 2018). At another level, synaptic rewiring induced by STDP necessitates stabilization through compensatory mechanisms, such as activity-dependent homeostatic plasticity (Turrigiano and Nelson, 2004; Turrigiano, 2008, 2012). The dynamic adaptation of network activity patterns is closely linked to the STDP rule (Izhikevich and Desai, 2003), as homeostatic plasticity can modulate synaptic strengths in response to changes in overall neuronal activity. Importantly, temporal delays can crucially influence the effectiveness of homeostatic adjustments, as they may disrupt the timely feedback necessary for these mechanisms to respond appropriately, potentially leading to imbalances in synaptic strengths and affecting network stability. Furthermore, learning models such as reinforcement learning with modulated STDP (Florian, 2007; Farries and Fairhall, 2007), which focus on the role of reward signals in shaping behavior and synaptic strengths, operate under different principles and can be affected by delays in feedback. Additionally, rate-based learning models, which depend on the average firing rates of neurons rather than precise spike timing, may also exhibit sensitivity to temporal dynamics (Burkitt et al., 2004; Gilson et al., 2011). Exploring these diverse learning models in the context of delays could provide valuable insights into the broader mechanisms of synaptic plasticity and learning in neuronal networks, highlighting how different strategies adapt to the complexities of temporal interactions.
In conclusion, the dual role of delays in neuronal and synaptic dynamics underscores their critical position in computational models of neuroplasticity. By simultaneously modulating neuronal spike timings perceived at the synaptic site and the strength of synapses, dendritic and axonal delays orchestrate the brain's symphony of activity, while their discrimination ensures models reflect biological intricacies. This approach not only enriches our comprehension of brain function, but also propels simulation methodologies toward greater accuracy and applicability. Discriminating dendritic and axonal delays in computational models will unlock deeper insights into the neuronal code, paving the way for a more realistic and biologically plausible modeling of neuronal and synaptic dynamics.
Author contributions
MM: Visualization, Formal analysis, Writing – original draft, Investigation, Conceptualization, Writing – review & editing, Methodology.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbott, L. F., and Nelson, S. B. (2000). Synaptic plasticity: taming the beast. Nat. Neurosci. 3, 1178–1183. doi: 10.1038/81453
Agmon-Snir, H., and Segev, I. (1993). Signal delay and input synchronization in passive dendritic structures. J. Neurophysiol. 70, 2066–2085. doi: 10.1152/jn.1993.70.5.2066
Aoki, T., and Aoyagi, T. (2009). Co-evolution of phases and connection strengths in a network of phase oscillators. Phys. Rev. Lett. 102:034101. doi: 10.1103/PhysRevLett.102.034101
Asadi, A., Madadi Asl, M., Valizadeh, A., and Perc, M. (2024). Dynamics of parkinsonian oscillations mediated by transmission delays in a mean-field model of the basal ganglia. Front. Cell. Neurosci. 18:1344149. doi: 10.3389/fncel.2024.1344149
Babadi, B., and Abbott, L. F. (2013). Pairwise analysis can account for network structures arising from spike-timing dependent plasticity. PLoS Comput. Biol. 9:e1002906. doi: 10.1371/journal.pcbi.1002906
Bi, G. Q., and Poo, M. M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998
Burkitt, A. N., Meffin, H., and Grayden, D. B. (2004). Spike-timing-dependent plasticity: the relationship to rate-based learning for models with weight dynamics determined by a stable fixed point. Neural Computation 16, 885–940. doi: 10.1162/089976604773135041
Butz, M., Worgotter, F., and Van Ooyen, A. (2009). Activity-dependent structural plasticity. Brain Res. Rev. 60, 287–305. doi: 10.1016/j.brainresrev.2008.12.023
Buzsáki, G., and Wang, X.-J. (2012). Mechanisms of gamma oscillations. Annu. Rev. Neurosci. 35, 203–225. doi: 10.1146/annurev-neuro-062111-150444
Cleland, B., Levick, W., Morstyn, R., and Wagner, H. (1976). Lateral geniculate relay of slowly conducting retinal afferents to cat visual cortex. J. Physiol. 255, 299–320. doi: 10.1113/jphysiol.1976.sp011281
Clopath, C., and Gerstner, W. (2010). Voltage and spike timing interact in stdp-a unified model. Front. Synapt. Neurosci. 2:25. doi: 10.3389/fnsyn.2010.00025
Crook, S. M., Ermentrout, G. B., Vanier, M. C., and Bower, J. M. (1997). The role of axonal delay in the synchronization of networks of coupled cortical oscillators. J. Comput. Neurosci. 4, 161–172. doi: 10.1023/A:1008843412952
Debanne, D., Gähwiler, B. H., and Thompson, S. M. (1998). Long-term synaptic plasticity between pairs of individual ca3 pyramidal cells in rat hippocampal slice cultures. J. Physiol. 507(Pt 1):237. doi: 10.1111/j.1469-7793.1998.237bu.x
Deger, M., Helias, M., Rotter, S., and Diesmann, M. (2012). Spike-timing dependence of structural plasticity explains cooperative synapse formation in the neocortex. PLoS Comput. Biol. 8:e1002689. doi: 10.1371/journal.pcbi.1002689
Deger, M., Seeholzer, A., and Gerstner, W. (2018). Multicontact co-operativity in spike-timing-dependent structural plasticity stabilizes networks. Cereb. Cortex 28, 1396–1415. doi: 10.1093/cercor/bhx339
DHuys, O., Vicente, R., Erneux, T., Danckaert, J., and Fischer, I. (2008). Synchronization properties of network motifs: influence of coupling delay and symmetry. Chaos 18:2953582. doi: 10.1063/1.2953582
Ebert, M., Hauptmann, C., and Tass, P. A. (2014). Coordinated reset stimulation in a large-scale model of the stn-gpe circuit. Front. Comput. Neurosci. 8:154. doi: 10.3389/fncom.2014.00154
Engel, A. K., and Singer, W. (2001). Temporal binding and the neural correlates of sensory awareness. Trends Cogn. Sci. 5, 16–25. doi: 10.1016/S1364-6613(00)01568-0
Ermentrout, G. B., and Kopell, N. (1998). Fine structure of neural spiking and synchronization in the presence of conduction delays. Proc. Natl. Acad. Sci. 95, 1259–1264. doi: 10.1073/pnas.95.3.1259
Ernst, U., Pawelzik, K., and Geisel, T. (1995). Synchronization induced by temporal delays in pulse-coupled oscillators. Phys. Rev. Lett. 74:1570. doi: 10.1103/PhysRevLett.74.1570
Ernst, U., Pawelzik, K., and Geisel, T. (1998). Delay-induced multistable synchronization of biological oscillators. Phys. Rev. E 57:2150. doi: 10.1103/PhysRevE.57.2150
Esfahani, Z. G., Gollo, L. L., and Valizadeh, A. (2016). Stimulus-dependent synchronization in delayed-coupled neuronal networks. Sci. Rep. 6:23471. doi: 10.1038/srep23471
Farries, M. A., and Fairhall, A. L. (2007). Reinforcement learning with modulated spike timing-dependent synaptic plasticity. J. Neurophysiol. 98, 3648–3665. doi: 10.1152/jn.00364.2007
Fauth, M., and Tetzlaff, C. (2016). Opposing effects of neuronal activity on structural plasticity. Front. Neuroanat. 10:75. doi: 10.3389/fnana.2016.00075
Florian, R. V. (2007). Reinforcement learning through modulation of spike-timing-dependent synaptic plasticity. Neural Comput. 19, 1468–1502. doi: 10.1162/neco.2007.19.6.1468
Froemke, R. C., Letzkus, J. J., Kampa, B. M., Hang, G. B., and Stuart, G. J. (2010). Dendritic synapse location and neocortical spike-timing-dependent plasticity. Front. Synapt. Neurosci. 2:29. doi: 10.3389/fnsyn.2010.00029
Gerstner, W., Kempter, R., Van Hemmen, J. L., and Wagner, H. (1996). A neuronal learning rule for sub-millisecond temporal coding. Nature 383, 76–78. doi: 10.1038/383076a0
Gerstner, W., Kreiter, A. K., Markram, H., and Herz, A. V. (1997). Neural codes: firing rates and beyond. Proc. Natl. Acad. Sci. 94, 12740–12741. doi: 10.1073/pnas.94.24.12740
Gerstner, W., Ritz, R., and Van Hemmen, J. L. (1993). Why spikes? Hebbian learning and retrieval of time-resolved excitation patterns. Biol. Cybernet. 69, 503–515. doi: 10.1007/BF00199450
Gilson, M., Burkitt, A., and van Hemmen, J. L. (2010). Stdp in recurrent neuronal networks. Front. Comput. Neurosci. 4:23. doi: 10.3389/fncom.2010.00023
Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and Van Hemmen, J. L. (2009). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks iv: structuring synaptic pathways among recurrent connections. Biol. Cybernet. 101, 427–444. doi: 10.1007/s00422-009-0346-1
Gilson, M., Masquelier, T., and Hugues, E. (2011). Stdp allows fast rate-modulated coding with poisson-like spike trains. PLoS Comput. Biol. 7:e1002231. doi: 10.1371/journal.pcbi.1002231
Gütig, R., Aharonov, R., Rotter, S., and Sompolinsky, H. (2003). Learning input correlations through nonlinear temporally asymmetric hebbian plasticity. J. Neurosci. 23, 3697–3714. doi: 10.1523/JNEUROSCI.23-09-03697.2003
Izhikevich, E. M., and Desai, N. S. (2003). Relating stdp to bcm. Neural Comput. 15, 1511–1523. doi: 10.1162/089976603321891783
Izhikevich, E. M., Gally, J. A., and Edelman, G. M. (2004). Spike-timing dynamics of neuronal groups. Cereb. Cortex 14, 933–944. doi: 10.1093/cercor/bhh053
Kempter, R., Gerstner, W., and Van Hemmen, J. L. (1999). Hebbian learning and spiking neurons. Phys. Rev. E 59:4498. doi: 10.1103/PhysRevE.59.4498
Khoshkhou, M., and Montakhab, A. (2019). Spike-timing-dependent plasticity with axonal delay tunes networks of izhikevich neurons to the edge of synchronization transition with scale-free avalanches. Front. Syst. Neurosci. 13:73. doi: 10.3389/fnsys.2019.00073
Kim, S., Park, S. H., and Ryu, C. (1997). Multistability in coupled oscillator systems with time delay. Phys. Rev. Lett. 79:2911. doi: 10.1103/PhysRevLett.79.2911
Knoblauch, A., Hauser, F., Gewaltig, M.-O., Körner, E., and Palm, G. (2012). Does spike-timing-dependent synaptic plasticity couple or decouple neurons firing in synchrony? Front. Comput. Neurosci. 6:55. doi: 10.3389/fncom.2012.00055
Knoblauch, A., and Sommer, F. T. (2003). Synaptic plasticity, conduction delays, and inter-areal phase relations of spike activity in a model of reciprocally connected areas. Neurocomput. 52, 301–306. doi: 10.1016/S0925-2312(02)00792-0
Knoblauch, A., and Sommer, F. T. (2004). Spike-timing-dependent synaptic plasticity can form zero lag links for cortical oscillations. Neurocomputing 58, 185–190. doi: 10.1016/j.neucom.2004.01.041
Kozloski, J., and Cecchi, G. A. (2010). A theory of loop formation and elimination by spike timing-dependent plasticity. Front. Neural Circuits 4:727. doi: 10.3389/fncir.2010.00007
Lefebvre, J., Clappison, A., Longtin, A., and Hutt, A. (2025). Myelin-induced gain control in nonlinear neural networks. Commun. Phys. 8:145. doi: 10.1038/s42005-025-02055-8
Lubenov, E. V., and Siapas, A. G. (2008). Decoupling through synchrony in neuronal circuits with propagation delays. Neuron 58, 118–131. doi: 10.1016/j.neuron.2008.01.036
Madadi Asl, M., and Lankarany, M. (2025). A novel computational model for integrating dynamics of short- and long-term synaptic plasticity during and after electrical stimulation. Brain Stimul. 18:248. doi: 10.1016/j.brs.2024.12.105
Madadi Asl, M., and Lea-Carnall, C. A. (2025). Rhythmic modulation of subthalamo-pallidal interactions depends on synaptic rewiring through inhibitory plasticity. Phys. Rev. Res. 7:023128. doi: 10.1103/PhysRevResearch.7.023128
Madadi Asl, M., and Ramezani Akbarabadi, S. (2023). Delay-dependent transitions of phase synchronization and coupling symmetry between neurons shaped by spike-timing-dependent plasticity. Cogn. Neurodyn. 17, 523–536. doi: 10.1007/s11571-022-09850-x
Madadi Asl, M., and Valizadeh, A. (2025). Entrainment by transcranial alternating current stimulation: insights from models of cortical oscillations and dynamical systems theory. Phys. Life Rev. 53, 147–176. doi: 10.1016/j.plrev.2025.03.008
Madadi Asl, M., Valizadeh, A., and Tass, P. A. (2017). Dendritic and axonal propagation delays determine emergent structures of neuronal networks with plastic synapses. Sci. Rep. 7:39682. doi: 10.1038/srep39682
Madadi Asl, M., Valizadeh, A., and Tass, P. A. (2018a). Delay-induced multistability and loop formation in neuronal networks with spike-timing-dependent plasticity. Sci. Rep. 8:12068. doi: 10.1038/s41598-018-30565-9
Madadi Asl, M., Valizadeh, A., and Tass, P. A. (2018b). Dendritic and axonal propagation delays may shape neuronal networks with plastic synapses. Front. Physiol. 9:1849. doi: 10.3389/fphys.2018.01849
Madadi Asl, M., Valizadeh, A., and Tass, P. A. (2018c). Propagation delays determine neuronal activity and synaptic connectivity patterns emerging in plastic neuronal networks. Chaos 28:106308. doi: 10.1063/1.5037309
Madadi Asl, M., Valizadeh, A., and Tass, P. A. (2023). Decoupling of interacting neuronal populations by time-shifted stimulation through spike-timing-dependent plasticity. PLoS Comput. Biol. 19:e1010853. doi: 10.1371/journal.pcbi.1010853
Manos, T., Diaz-Pier, S., and Tass, P. A. (2021). Long-term desynchronization by coordinated reset stimulation in a neural network model with synaptic and structural plasticity. Front. Physiol. 12:716556. doi: 10.3389/fphys.2021.716556
Markram, H., Lübke, J., Frotscher, M., Roth, A., and Sakmann, B. (1997a). Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. J. Physiol. 500, 409–440. doi: 10.1113/jphysiol.1997.sp022031
Markram, H., Lübke, J., Frotscher, M., and Sakmann, B. (1997b). Regulation of synaptic efficacy by coincidence of postsynaptic aps and epsps. Science 275, 213–215. doi: 10.1126/science.275.5297.213
Morrison, A., Aertsen, A., and Diesmann, M. (2007). Spike-timing-dependent plasticity in balanced random networks. Neural Comput. 19, 1437–1467. doi: 10.1162/neco.2007.19.6.1437
Morrison, A., Diesmann, M., and Gerstner, W. (2008). Phenomenological models of synaptic plasticity based on spike timing. Biol. Cybernet. 98, 459–478. doi: 10.1007/s00422-008-0233-1
Popovych, O. V., Yanchuk, S., and Tass, P. A. (2011). Delay-and coupling-induced firing patterns in oscillatory neural loops. Phys. Rev. Lett. 107:228102. doi: 10.1103/PhysRevLett.107.228102
Roxin, A., Brunel, N., and Hansel, D. (2005). Role of delays in shaping spatiotemporal dynamics of neuronal activity in large networks. Phys. Rev. Lett. 94:238103. doi: 10.1103/PhysRevLett.94.238103
Rubin, J., Lee, D. D., and Sompolinsky, H. (2001). Equilibrium properties of temporally asymmetric hebbian plasticity. Phys. Rev. Lett. 86:364. doi: 10.1103/PhysRevLett.86.364
Schierwagen, A., and Claus, C. (2001). Dendritic morphology and signal delay in superior colliculus neurons. Neurocomputing 38, 343–350. doi: 10.1016/S0925-2312(01)00417-9
Schmalz, J., and Kumar, G. (2019). Controlling synchronization of spiking neuronal networks by harnessing synaptic plasticity. Front. Comput. Neurosci. 13:61. doi: 10.3389/fncom.2019.00061
Senn, W., Schneider, M., and Ruf, B. (2002). Activity-dependent development of axonal and dendritic delays, or, why synaptic transmission should be unreliable. Neural Comput. 14, 583–619. doi: 10.1162/089976602317250915
Sjöström, P. J., and Häusser, M. (2006). A cooperative switch determines the sign of synaptic plasticity in distal dendrites of neocortical pyramidal neurons. Neuron 51, 227–238. doi: 10.1016/j.neuron.2006.06.017
Song, S., and Abbott, L. F. (2001). Cortical development and remapping through spike timing-dependent plasticity. Neuron 32, 339–350. doi: 10.1016/S0896-6273(01)00451-2
Song, S., Miller, K. D., and Abbott, L. F. (2000). Competitive hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926. doi: 10.1038/78829
Song, S., Sjostrom, P. J., Reigl, M., Nelson, S., and Chklovskii, D. B. (2005). Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 3:e68. doi: 10.1371/journal.pbio.0030068
Stoelzel, C. R., Bereshpolova, Y., Alonso, J.-M., and Swadlow, H. A. (2017). Axonal conduction delays, brain state, and corticogeniculate communication. J. Neurosci. 37, 6342–6358. doi: 10.1523/JNEUROSCI.0444-17.2017
Swadlow, H. A. (1990). Efferent neurons and suspected interneurons in s-1 forelimb representation of the awake rabbit: receptive fields and axonal properties. J. Neurophysiol. 63, 1477–1498. doi: 10.1152/jn.1990.63.6.1477
Swadlow, H. A., and Weyand, T. G. (1987). Corticogeniculate neurons, corticotectal neurons, and suspected interneurons in visual cortex of awake rabbits: receptive-field properties, axonal properties, and effects of eeg arousal. J. Neurophysiol. 57, 977–1001. doi: 10.1152/jn.1987.57.4.977
Tass, P. A. (2003). A model of desynchronizing deep brain stimulation with a demand-controlled coordinated reset of neural subpopulations. Biol. Cybernet. 89, 81–88. doi: 10.1007/s00422-003-0425-7
Tass, P. A., and Majtanik, M. (2006). Long-term anti-kindling effects of desynchronizing brain stimulation: a theoretical study. Biol. Cybernet. 94, 58–66. doi: 10.1007/s00422-005-0028-6
Turrigiano, G. (2012). Homeostatic synaptic plasticity: local and global mechanisms for stabilizing neuronal function. Cold Spring Harbor Perspect. Biol. 4:a005736. doi: 10.1101/cshperspect.a005736
Turrigiano, G. G. (2008). The self-tuning neuron: synaptic scaling of excitatory synapses. Cell 135, 422–435. doi: 10.1016/j.cell.2008.10.008
Turrigiano, G. G., and Nelson, S. B. (2004). Homeostatic plasticity in the developing nervous system. Nat. Rev. Neurosci. 5, 97–107. doi: 10.1038/nrn1327
Van Rossum, M. C., Bi, G. Q., and Turrigiano, G. G. (2000). Stable hebbian learning from spike timing-dependent plasticity. J. Neurosci. 20, 8812–8821. doi: 10.1523/JNEUROSCI.20-23-08812.2000
Waxman, S. G. (2006). Axonal conduction and injury in multiple sclerosis: the role of sodium channels. Nat. Rev. Neurosci. 7, 932–941. doi: 10.1038/nrn2023
Yeung, M. S., and Strogatz, S. H. (1999). Time delay in the kuramoto model of coupled oscillators. Phys. Rev. Lett. 82:648. doi: 10.1103/PhysRevLett.82.648
Keywords: dendritic delay, axonal delay, neuronal dynamics, synaptic plasticity, computational modeling
Citation: Madadi Asl M (2025) Time delays in computational models of neuronal and synaptic dynamics. Front. Comput. Neurosci. 19:1700144. doi: 10.3389/fncom.2025.1700144
Received: 06 September 2025; Accepted: 27 October 2025;
Published: 10 November 2025.
Edited by:
Prosenjit Kundu, Dhirubhai Ambani Institute of Information and Communication Technology, IndiaReviewed by:
Sharon Crook, Arizona State University, United StatesCopyright © 2025 Madadi Asl. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mojtaba Madadi Asl, bS5tYWRhZGlAaXBtLmly
 Mojtaba Madadi Asl
Mojtaba Madadi Asl